Abstract
Per- and polyfluoroalkyl substances (PFAS) are receiving a great deal of attention from regulators, water utilities, and the general public. Anion-exchange resins have shown high capacities for removal of these substances from water, but there is currently a paucity of ion-exchange treatment models available to evaluate performance. In this work, important theoretical and practical considerations are discussed for modeling PFAS removal from drinking water using gel-type, strong-base anion-exchange resin in batch and column processes. Several important limitations found in the literature preclude movement toward model development, including the use of inappropriate isotherms, inappropriate kinetic assumptions, and experimental conditions that are not relevant to drinking water conditions. Theoretical considerations based on ion-exchange fundamentals are presented that will be of assistance to future researchers in developing models, designing batch and column experiments, and interpreting results of batch and column experiments.
Keywords: drinking water, ion exchange, modeling, PFAS
1 |. INTRODUCTION
Per- and polyfluoroalkyl substances (PFAS) in drinking water are an emerging issue due to recent regulations, toxicity guidelines, and public concern (Crone et al., 2019; Rahman et al., 2014). Although the number of chemicals that fall under the PFAS umbrella may include thousands of chemicals (USEPA, 2018), several PFAS of interest, including perfluorooctanesulfonic acid (PFOS) and perfluorooctanoic acid (PFOA), are perfluoroalkyl acids. These acids are ionized at pH levels relevant to drinking water and are therefore amenable to treatment in ion-exchange systems (Zhang et al., 2019). Some results show strong-base anion-exchange resins can effectively remove PFAS from source water (Carter & Farrell, 2010; Deng et al., 2010; Senevirathna et al., 2010; Zaggia et al., 2016), but much work remains to optimize ion exchange as a treatment process for PFAS in a given application.
Pilot-scale studies are a common technique for estimating efficacy of full-scale treatment systems for individual water sources (Liu et al., 2019; Woodard et al., 2017), but these are extremely costly and time consuming. Given the large and increasing number of potential PFAS of interest, it is not practical to run pilot-scale studies for each PFAS with every possible source water. Also, pilot scale studies are limited to the design of the study and the influent water and characteristics present during the study. As an alternative to pilot studies, carefully designed laboratory experiments can efficiently produce useful data and maximize use of available data. The design of such experiments is aided by fundamental understanding of the experimental systems, which is typically achieved with the help of theory, modeling, validation, and simulation in a recursive loop. Unfortunately, the usefulness of the current literature on drinking water treatment using sorption techniques, particularly ion exchange, is limited by several widespread errors and misunderstandings (Inglezakis et al., 2019; Tran et al., 2017). The most widespread and relevant of these errors involve the use of isotherms and kinetic models that are incorrect or uninformative for the experiments conducted. These conceptual errors often lead to omission of useful information from publications. For example, major inorganic anions in drinking water sources (e.g., chloride, sulfate, nitrate, and bicarbonate) are known to play an important role in the effectiveness of ion-exchange processes but are often omitted or ignored from experiments or analysis. These errors continue to occur despite the availability of general resources for mathematical modeling of ion exchange (Helfferich, 1995; SenGupta, 2017; Slater, 2013; Zagorodni, 2006).
To assist researchers in avoiding these pitfalls, this article provides an overview of the most important considerations for modeling PFAS removal from drinking water using strong-base anion-exchange resins. This article focuses on those aspects that are important to using single–use (i.e., non-regenerable) gel anion-exchange resins, as these are commonly being piloted in the United States for use in treatment of drinking water and remediation applications (Liu et al., 2019; Woodard et al., 2017). The following main points will be addressed: (1) fundamental theory of ion-exchange equilibria; (2) limitations and pitfalls affecting selection and application of ionexchange isotherms, including considerations for competition from divalent ions such as sulfate; (3) the importance of mass transfer mechanisms for the kinetics of batch and column experiments; and (4) important gaps in tools and knowledge that, if resolved, would improve the effectiveness of ion-exchange modeling.
2 |. ION-EXCHANGE EQUILIBRIA FUNDAMENTALS
2.1 |. Law of mass action and competitive Langmuir equation
To simulate ion exchange, including maximum contaminant uptake and competition effects between contaminants, it is important to understand the particulars of ion-exchange equilibria and how they might differ from other types of adsorption. For exchange of two ionic species, A and B, with charges ZA and ZB, equilibrium between the resin (denoted by overbar) and liquid phases can be described using Equation (1). Applying the law of mass action based on Equation (1) results in the thermodynamic equilibrium constant given by Equation (2).
| (1) |
| (2) |
In Equation (2), the curly braces indicate activities of the ionic species in the resin and liquid phases. Because of the difficulty of assessing the activities of ions in the resin phase and because liquid-phase ionic strengths are typically low in drinking water, Equation (3) is commonly used (Zagorodni, 2006).
| (3) |
In Equation (3), q is the concentration of ionic equivalents per volume of the resin phase (e.g., meq/L of swollen [hydrated] resin), and C is the concentration of ionic equivalents per volume of the liquid phase (e.g., meq/L of water). The apparent equilibrium constant (KB,A) is usually referred to as the “selectivity coefficient” (SenGupta, 2017). It is important to note that KB,A is dependent on ionic concentration so it is not the thermodynamic equilibrium constant Noncanceling activity effects cause KB,A not to be constant with respect to overall ionic concentration in the case of heterovalent exchange (i.e., exchange of ions having differing charges). Accordingly, experimentally determined values of KB,A for heterovalent ion exchange are valid only over a certain range of ionic compositions.
While KB,A does have the conceptual advantage of correspondence with the actual exchange reaction, it does not lend itself to intuitive prediction of selectivity series for ions of mixed valence. For that purpose, the chromatographic separation factor (αB,A, Equation 4) is typically used (SenGupta, 2017; Zagorodni, 2006).
| (4) |
When dealing with a system containing only monovalent ions, KB,A and αB,A are equivalent. Otherwise, their relationship depends on overall ionic concentration. For a monovalent reference ion (A) and a multivalent ion (B), KB,A can be written in terms of αB,A (Equation 5).
| (5) |
Equation (5) depends on the relative ionic composition as well as overall liquid-phase equivalent concentration. For a given total liquid-phase concentration, the heterovalent (i.e., divalent/monovalent) ion-exchange isotherm (Figure S1, solid line) can be approximated by a constant separation factor (Figure S1, dashed line). This causes some error when using an approximate separation factor to simulate processes that involve large portions of the ion-exchange isotherm. However, much more serious errors can result if the approximate separation factor is applied to situations with different total liquid-phase concentrations (Equation 7 and Figure S1, dotted line). The dependence of the heterovalent separation factor on overall total liquid-phase concentration can result in re-ordering of selectivity series and even change a favorable isotherm to an unfavorable one. Additional equations comparing divalent/monovalent and monovalent/monovalent exchange isotherms can be found in Derivation 1 in the Appendix S1.
In addition to the stoichiometric assumption of ion-exchange equilibrium, nonstoichiometric descriptions involving more detailed discretization of the resin phase have been developed and are arguably closer to physical reality (Horst et al., 1990; Okada, 1998; Ståhlberg, 1999). However, serious disagreements between these descriptions and approaches based on the law of mass action are rarely encountered. Due to their relative complexity, further discussion and analysis of these nonstoichiometric techniques is beyond the scope of this article.
By combining the expressions for total charge concentrations in the resin (qT, Equation 6) and liquid (CT, Equation 7) phases with the definition of equilibrium (Equations 3 and 4), expressions for the ion-exchange isotherms are obtained. For binary, monovalent ion exchange, the isotherm for species B can be expressed using Equation (8).
| (6) |
| (7) |
| (8) |
Because the total number of ionic equivalents in the liquid phase is unchanged during the ion-exchange process, Equation (8) can alternatively be written as Equation (9).
| (9) |
By recognizing that in ion exchange, as opposed to general adsorption (e.g., granular activated carbon), all adsorption sites are always occupied, Equations (8 and 9) can also be derived from a two-component, competitive Langmuir equation (Misak, 1993).
2.2 |. Limitations of single-component Langmuir and Freundlich isotherms
At a minimum, ion exchange is a competition for adsorption sites between two ions (i.e., the ion currently on the resin and the one trying to replace it). Therefore, using single-component isotherms to simulate ion exchange is inherently empirical (i.e., parameter estimates are limited to the conditions tested and not generalizable or comparable between studies). To date, batch isotherm experiments using anion exchange with PFAS (summarized in Table 1) have ignored this distinction and have used either single-component Langmuir or Freundlich isotherms in data analysis instead of competitive isotherms.
TABLE 1.
List of example publications reporting per- and polyfluoroalkyl substances batch isotherm experiments with anion exchange
| Isotherm used |
||||
|---|---|---|---|---|
| Study | PFAS investigated | Freundlich | Langmuir | None |
| Yu et al. (2009) | PFOA & PFOS | ✓ | ✓ | |
| Carter and Farrell (2010) | PFBS & PFOS | ✓ | ||
| Deng et al. (2010) | PFOS | ✓ | ✓ | |
| Senevirathna et al. (2010) | PFOS | ✓ | ||
| Chularueangaksorn et al. (2013) | PFOS | ✓ | ||
| Chularueangaksorn et al. (2014a) | PFOA | ✓ | ||
| Chularueangaksorn et al. (2014b) | PFBS & PFOS | ✓ | ||
| Yao et al. (2014) | PFOA & PFOS | ✓ | ||
| Conte et al. (2015) | PFBA, PFBS, PFOA, & PFOS | ✓ | ||
| Du et al. (2015) | PFCAsa & PFOS | ✓ | ||
| Wang et al. (2016) | PFOA & PFOS | ✓ | ✓ | |
| Zaggia et al. (2016) | PFBA, PFBS, PFOA, & PFOS | ✓ | ||
| Gao et al. (2017) | PFOS | ✓ | ✓ | |
| Kothawala et al. (2017) | 13 PFASb | ✓ | ||
| Schuricht et al. (2017) | PFOS | ✓ | ✓ | |
| Maimaiti et al. (2018) | PFBA, PFBS, PFHxA, PFHxS, PFOA, & PFOS | ✓ | ||
| Yang et al. (2018) | PFOA | ✓ | ||
| Dixit et al. (2019) | PFOA & PFOS | ✓ | ||
| Wang, Maimaiti, et al. (2019) | GenX & PFOA | ✓ | ✓ | |
| Wang, Mi, et al. (2019) | PFBA, PFBS, PFOA, PFOS, & GenX | ✓ | ||
| Dixit et al. (2020) | GenX, PFMOPrA, & PFMOBA | ✓ | ||
Abbreviations: FOSA, perfluorooctanesulfonamide; GenX, perfluoro-2-propoxypropanoic acid; PFBA, perfluorobutanoic acid; PFBS, perfluorobutanesulfonic acid; PFCAs, perfluorinated carboxylic acids; PFDA, perfluorodecanoic acid; PFDoDA, perfluorododecanoic acid; PFHpA, perfluoroheptanoic acid; PFHxA, perfluorohexanoic acid; PFHxS, perfluorohexanesulfonic acid; PFMOBA, perfluoro-4-methoxybutanoic acid; PFMOPrA, perfluoro-3-methoxypropanoic acid; PFNA, perfluorononanoic acid; PFOA, perfluorooctanoic acid; PFOS, perfluorooctanesulfonic acid; PFPeA, perfluoropentanoic acid; PFUnDA, perfluoroundecanoic acid
Washing wastewater dominated by PFHxA, PFHpA, & PFOA.
PFBA, PFPeA, PFHxA, PFHpA, PFOA, PFNA, PFDA, PFUnDA, PFDoDA, PFBS, PFHxS, PFOS, & FOSA.
Equation (10) is a single-component Langmuir isotherm, which does not reflect the stoichiometric nature of ion exchange.
| (10) |
In Equation (10), bL and QL are the Langmuir constants. The single-component Langmuir isotherm produces an ascending curve that plateaus at high liquid-phase concentration. This curve shape is similar enough to a binary (monovalent/monovalent and favorable) ion-exchange isotherm to provide a decent representation of experimental data under a narrow range of conditions. However, the estimated parameters from such a fit are often meaningless. Theoretically, QL is usually thought of as the maximum occupancy of adsorber, which might tempt one to equate qT and QL. However, inspection of Equations (8 and 10) reveals that this equality is not strictly true, only occurring when CB is large enough that the first term in the denominators of both Equations (8 and 10) can be neglected. Therefore, QL does not correspond to the concentration of sites in the resin, and thus the estimation of QL becomes purely empirical and dependent on the final concentration of the presaturant (ion A). Furthermore, the bL parameter does not correspond to a separation factor or ion-exchange equilibrium constant, and bL will also not be constant across changes in liquid-phase composition (Hekmatzadeh et al., 2012; Misak, 2000).
The commonly used Freundlich isotherm (Equation 11) is similarly unhelpful for describing ion-exchange equilibria beyond empirical results specific to the experiment conducted. In Equation (11), KF and n are the Freundlich constants.
| (11) |
This isotherm does not account for competition with species A nor does it assume a maximum number of sites in the resin phase. The values of the Freundlich constants are not expected to be constant with solution composition. Accordingly, the Freundlich isotherm cannot be relied upon to make predictions for ion-exchange behavior under different conditions.
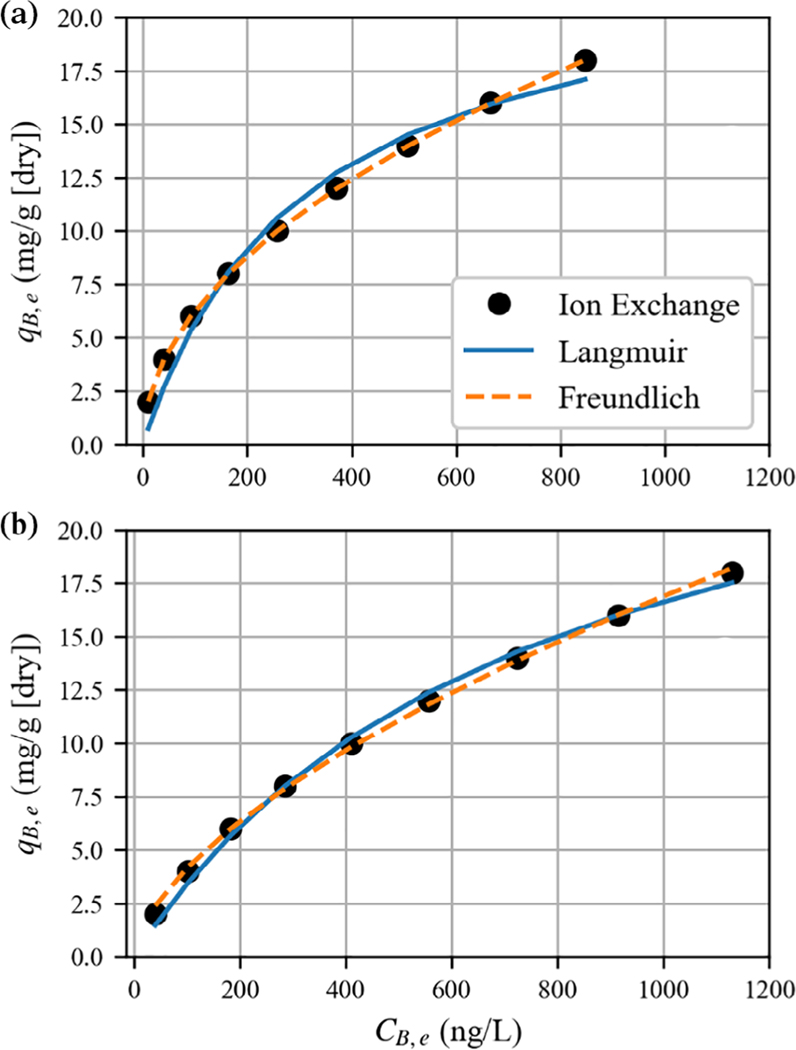
The above points can be illustrated by fitting Equations (10 and 11) to a hypothetical ion-exchange isotherm simulated for a monovalent chemical (B) exchanging for chloride (A) on an anion-exchange resin (Figure 1). For this example, the Freundlich isotherm provides an excellent representation of the simulated data while the single-component Langmuir is not as good but still serviceable. However, the estimated isotherm parameters are dependent on initial liquid-phase chloride concentration (Figure 1(a) vs. (b)). The example illustrates that while the fits using the single-component Langmuir or Freundlich isotherm may provide a reasonable representation of the experimental data, these fits provide little physical insight into the ion-exchange process.
FIGURE 1.
Nonlinear fits of single-component Langmuir and Freundlich isotherms to simulated binary ion-exchange isotherm data between a hypothetical monovalent ion (B) and chloride (A) for two different initial concentrations of chloride. The simulated conditions are as follows: qT = 1.3 eq/L of resin, αB,A = 100. The liquid volume was 1 L, and the resin-phase volume was 65 μl. The mass of a dry resin pellet per volume of a wet resin pellet was 0.65 g/ml, and the equivalent weight of ion B was 200 g/eq. Using this information, the units on q can be converted from eq/L of wet resin phase to units more commonly found in the literature, mass of B per gram of dry resin. Accordingly, in mass units, qT = 400 mg/g (dry). The initial concentration of ion B in solution ranged from 0.2 to 1.8 mg/L. The initial chloride concentrations in solution were (a) CA,0 = 0 and (b) CA,0 = 3 μeq/L. The best fit parameters were: (a) bL = 3.25 × 10−3 L/ng, QL = 23.3 mg/g; KF = 0.65 [(mg/g)/(ng/L)1/n], n = 2.03; (b) bL = 1.32 × 10−3 L/ng, QL = 29.3 mg/g; KF = 0.25 [(mg/g)/(ng/L)1/n], n = 1.64
2.3 |. Multispecies isotherms
So far, this discussion has been limited to isotherm expressions involving only two species at most. Drinking water contains multiple anion species (e.g., nitrate, sulfate, etc.) capable of competing with PFAS for ion-exchange sites. For monovalent exchange, the isotherm presented above (Equation 8) can be generalized to handle multiple species (Equation 12). The symbol αj,i is the separation factor between the jth and ith component in the mixture. Alternately, Equation (13) can be used if the liquid-phase concentrations are of interest. Note that the indexing order for separation factor is reversed from that of Equation (12) and that αi,jαj,i = 1.
| (12) |
| (13) |
It is not necessary to measure all possible separation factors in the mixture. It is only necessary to know the separation factors compared with a single reference ion (A) because of the relationship shown in Equation (14).
Equation (14) allows information obtained from binary isotherms to be used when multiple species are present.
| (14) |
Expressions for heterovalent ion exchange can become more complicated. These problems require finding solutions to systems of equations. Further discussion of solving such problems will be presented in later sections.
3 |. MODELING BATCH EXPERIMENTS
Batch adsorption experiments are commonly used to generate experimental data for use in estimating ionexchange isotherm parameters for use in designing ionexchange processes (SenGupta, 2017). Procedures for designing these experiments are available elsewhere (Tripp et al., 2003). One of the most important considerations when conducting a batch isotherm experiment is running the experiment long enough to reach conditions representative of equilibrium. If the experiment is stopped prematurely, erroneous values for the isotherm parameters will be determined. Therefore, it is important to understand the kinetics of the ion-exchange reaction to appropriately design isotherm experiments.
3.1 |. Batch kinetics
When discussing kinetics of adsorption processes, three potential rate-determining mechanisms are (1) external mass transfer, (2) internal mass transfer, and (3) chemical reaction. In ion exchange, the mass transfer steps are typically much slower than the actual ion exchange (i.e., chemical reaction) (Helfferich, 1995). Thus, the derivation here will focus on the two mass transfer mechanisms (steps 1 and 2).
There exists a considerable body of literature dedicated to determining which of the two mass transfer mechanisms dominates and then making appropriate model simplifications (Inglezakis et al., 2019). The relative contributions of film transfer and internal diffusion depend on factors such as resin affinity and the diffusion behavior in the bead interior. However, neither of these factors are well understood for PFAS, which are a diverse group of contaminants with varying chemical parameters and are present in drinking water under a varying range of conditions, background constituents, and concentrations. Thus, it cannot be taken as a given that a single mechanistic model would be appropriate for all PFAS and situations. Therefore, this section initially describes a general mixed mechanism model, which can be represented schematically (Figure 2). Then, the section discusses application of two simplified, single-mechanism models, and how they can assist the use of the more general model.
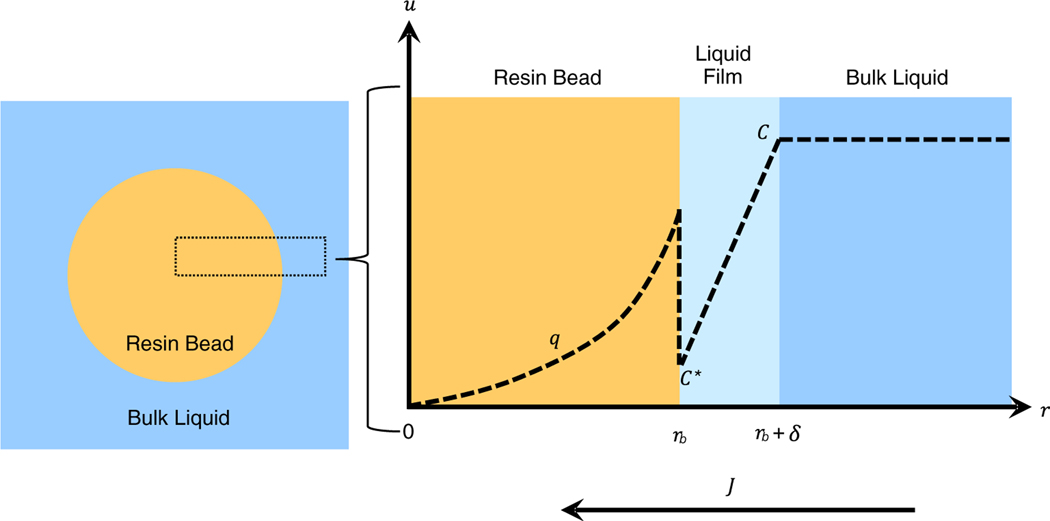
FIGURE 2.
Conceptual diagram of mass transfer model. r is the coordinate axis along the resin bead’s radius. rb is the bead radius, δ is the thickness of the liquid film layer, u is the concentration axis, C is the concentration in the bulk liquid, C* is the liquid concentration in equilibrium with the surface of the resin bead, q is the concentration in the resin bead, and J is the flux across the resin bead’s surface
For the general mixed mechanism model, the change in liquid-phase concentration in the batch reactor over time can be written (see Derivation 2 in the Appendix S1, Equation S2.4) in terms of the resin-phase concentration and the porosity within the batch reactor (ε) is Equation (15).
| (15) |
Equation (15) can also be recast in terms of the bead radius (rb) and the ionic flux (J) between the resin and the solution, using Appendix S1 (Equations S2.5 and S2.6) and resulting in Equation (16).
| (16) |
3.2 |. Expressions for flux (J)
One of the more rigorous models for concentration, and coupled ionic diffusion is the Nernst-Plank equation (Equation 17) where T is temperature, F is the Faraday constant, R is the ideal gas constant, Ψ is the electric potential, and Di, Ci, and Zi are the interdiffusion coefficient, charge of species i, respectively.
| (17) |
Using Equation (17) requires knowledge of the interdiffusion coefficients (Di) for all ionic species involved. Solving the fluxes in this equation is a complicated task (Franzreb et al., 1993) and potentially comes with a high computational cost (Bachet et al., 2014). Use of these equations may be necessary for high-accuracy predictions of breakthrough curves for major ions, especially when heterovalent ion exchange is involved. However, PFAS are almost always present as minority ions. Their low concentrations cause the electric field term in the above expression to become vanishingly small. Thus, the Nernst-Plank equations are not expected to provide more meaningfully accurate flux predictions over those provided by simpler Fickian approximations.
If a linear concentration profile is assumed (Sircar & Huftonin, 2000) and the diffusive layer surrounding the resin is thin enough that curvature can be neglected, the flux expression can be written as Equation (18) where C* is the liquid-phase concentration in equilibrium with the surface of the resin bead and kL is the liquid film mass transfer coefficient. Determination of C* involves some nuance and will be discussed in its own section.
| (18) |
We now focus on adding internal mass transfer resistance to the model. Diffusion in the interior of a spherical resin bead can be described using Fick’s second law (Equation 19) where Ds is the diffusion coefficient in the resin phase.
| (19) |
The boundary condition at the center of the sphere is given by Equation (20) and represents that there is no concentration gradient at the resin bead’s center.
| (20) |
This leaves only ∂q/∂t at the surface to solve. A boundary condition for the bead surface can be derived by assuming continuity between the flux due to liquid film transport and the flux from intraparticle diffusion (Equation 21a), resulting in the boundary condition (Bellot & Condoret, 1991) at the surface given by Equation (21b).
| (21a) |
| (21b) |
The exact mathematical expression for ∂q/∂t at the bead surface depends on the discretization scheme and method of solution for the differential equations, which will not be covered in detail here. The model described up to this point is essentially a heterogeneous surface diffusion model (HSDM) and is appropriate for application to gel-type resins. When describing transport in macroporous ion-exchange resins, however, it may be necessary to include considerations for diffusion within the macropores. A mathematical model for doing so has been described at length elsewhere (Hokanson et al., 1995) and will not be reproduced here.
3.3 |. Calculating C*
The liquid-phase equilibrium concentration at the bead’s surface of the ith component can be found using a slight modification of Equation (13), resulting in Equation (22).
| (22) |
As discussed previously, this expression is only strictly valid for monovalent ion exchange. Drinking water commonly contains divalent ions (e.g., sulfate). It is therefore important to properly handle heterovalent exchange. It is possible to solve for C* based on K. For strictly monovalent exchange, K can be directly substituted in for α. Otherwise, one must solve a system of equations. A procedure for this calculation has been described in detail elsewhere (Jia & Foutch, 2004). For convenience, example formulas for monovalent/divalent ion exchange with a monovalent reference ion are presented here.
If the apparent equilibrium constants (Ki,A) are defined relative to a monovalent reference ion (A), it is possible to write Equation (23).
| (23) |
Solving Equation (23) for liquid-phase concentration yields Equation (24).
| (24) |
For a mixture of N counterions, there will be N − 1 such equations. One more equation is required to solve for the interfacial liquid-phase concentrations. During ion exchange, the total charge in the solution is unchanged (Equation 7) and excluding the reference ion (A) from the charge summation yields Equation (25).
| (25) |
Substituting in the equilibrium expression (Equation 24) into Equation (25) yields Equation (26).
| (26) |
Solving Equation (26) for results in a quadratic expression (Equations 27a–d).
| (27a) |
| (27b) |
| (27c) |
| (27d) |
Provided that at least one of the divalent species has a nonzero resin phase concentration, Equations (27a–d) can be solved using the standard quadratic formula. Because all concentrations must be positive, this quadratic has only one physically relevant solution (Equation 28).
| (28) |
Once has been determined, it can then be substituted back into the N − 1 equilibrium expressions to find the interfacial liquid concentrations for the remaining counterions. Now that a method for determining ∂q/∂t has been completely defined, it is possible to integrate Equation (16) using standard numerical methods. Implementation of numerical models is reviewed in Bellot and Condoret (1991).
3.4 |. Batch kinetics: Limiting cases
Fitting the general kinetic model to data from batch kinetic experiments can be challenging and may be an ill-posed problem without some prior knowledge of the isotherm and kinetic parameters. While an independent estimate of the isotherm parameters may be acquired from batch isotherm experiments conducted until equilibrium is reached, estimation of the two kinetic parameters (kL and Ds) bears further discussion.
There are some limiting cases that are potentially instructive for conducting batch sorption experiments involving PFAS. These limiting cases fall into two broad categories based on whether liquid film diffusion (i.e., external mass transfer) or intraparticle diffusion (i.e., internal mass transfer) controls the mass transfer. When one of the mass transfer parameters dominates, simultaneous regression on both mass transfer parameters using the general model can lead to ill-determined parameter estimates. Therefore, it is helpful to identify and understand batch experiments that fall into these two limiting cases.
For a contaminant (B) present at trace concentrations ( and ) which would be applicable to drinking water conditions where PFAS are several orders of magnitude lower in concentration than inorganic anions, the ion-exchange isotherm is often nearly linear over the operating range of the batch experiment, and the rate-determining mechanism can be approximately determined using the Biot number (SenGupta, 2017) (Equation 29, Derivation 3 in the Appendix S1).
| (29) |
If , the kinetics are expected to be limited by intraparticle diffusion (Hand et al., 1984). If , the kinetics are expected to be limited by liquid film diffusion (Hand et al., 1984). For intermediate Biot numbers, mixed diffusion mechanisms are expected (i.e., HSDM). Inspection of Equation (29) suggests that Bi is inversely proportional to αB,A. Accordingly, a high αB,A pushes the system toward liquid film control.
An analytical solution for intraparticle diffusion-limited batch experiments involving linear isotherms has been provided by Crank (1975). If , the kinetics should be limited by intraparticle diffusion, and the HSDM and Crank result should agree (Figure S2).
In this solution, the fractional progress to equilibrium (U) is defined by Equation (30) and has the analytical solution given by Equations (31a–d). In Equations (31a–d), Vl is the liquid volume in the reactor, Vx is the volume of the resin phase, λB is the equilibrium distribution coefficient, and un are the nonzero roots of Equation (32).
| (30) |
| (31a) |
| (31b) |
| (31c) |
| (31d) |
| (32) |
Another analytical solution is given by Helfferich (1995) for film diffusion-limited batch kinetics, assuming a linear isotherm (Equations 33a, b). If , the kinetics should be limited by liquid film diffusion, and the HSDM and Helfferich solution should agree (Figure S2).
| (33a) |
| (33b) |
Provided the ion-exchange isotherm can be considered linear, an analytical solution (Equations 34a, b) also exists for the HSDM (LeVan et al., 2018). The pn in Equation (34a) are the positive roots of Equation (35).
| (34a) |
| (34b) |
| (35) |
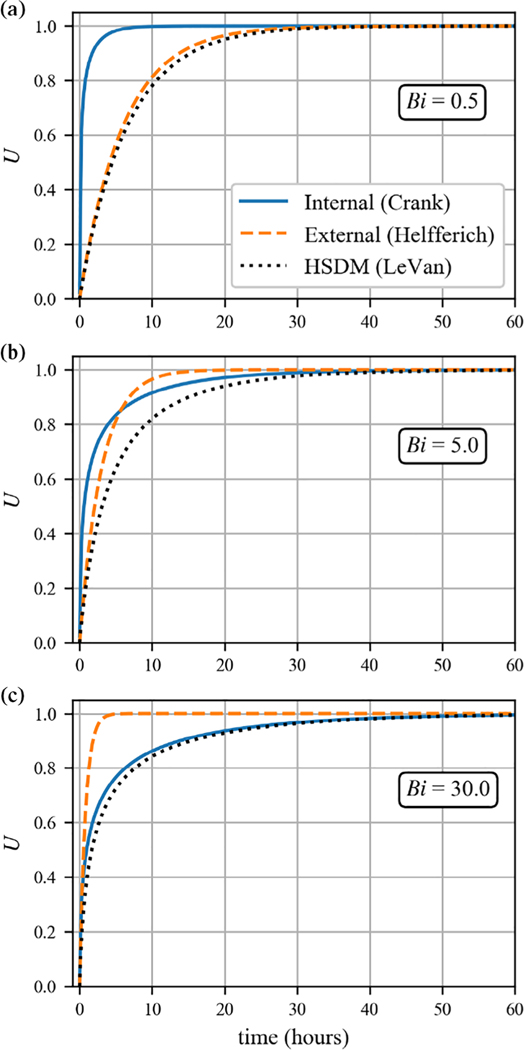
Comparisons of the Crank model, Helfferich model, and the analytical HSDM for several values of Bi are presented in Figure 3. The Helfferich model displays the characteristic slow initial rise and comparatively rapid final approach to equilibrium characteristic of film-limited diffusion. The Crank model displays the rapid initial rise and slow final approach to equilibrium characteristic of intraparticle diffusion. The slow approach to equilibrium can make it difficult to determine when a batch isotherm experiment has essentially reached equilibrium. Depending on the circumstances, this difficulty can lead to experimenters ending experiments prematurely and thus underestimating selectivity (Figure S3). Another important observation from Figure 3 is that the rate-limiting mechanism can change during the experiment. That is, some batch experiments can be initially dominated by film diffusion, yet still display a slow final approach to equilibrium. In these cases, predictions based on Crank’s and Helfferich’s analytical solutions will likely lead to poor and potentially misleading fits of experimental data, resulting in the need for the HSDM.
FIGURE 3.
Comparison of batch kinetic predictions for single mechanism models classified for opposite mass transfer resistance assumptions. The solid line represents the solution given by Crank, which assumes internal mass transfer is rate determining. The dashed line represents the solution given by Helfferich, which assumes external mass transfer is rate determining. The dotted line represents the solution given by the HSDM. The parameters used are as follows: rb = 3.5 × 10−2 cm, λB = 1.4 × 103, Vl/Vx = 1 × 104. For panel (a), Ds = 1.0 × 10−8cm2/s, kL = 2.0 × 10−3cm/s; panel (b), Ds = 2 × 10−9cm2/s, kL = 4.0 × 10−3cm/s; panel (c), Ds = 1.25 × 10−9cm2/s, kL = 1.5 × 10−2cm/s. These parameters were selected arbitrarily for illustration purposes
If the mechanistic character of the mass transfer in the batch experiment is not evident from the kinetic data, some insight into the controlling mechanism of a batch experiment may be obtained using interruption tests (Kressman & Kitchener, 1949; Kunin & Myers, 1947). In these experiments, the ion-exchange resins are removed from the solution before equilibrium is achieved. The resin beads are later reintroduced into the solution. If the uptake curve continues at the same rate as before the interruption, the dominating mechanism is likely film transfer. Discontinuities in the uptake rate suggest that intraparticle diffusion has at least some effect on the overall kinetics.
Analogous experiments can be performed in column studies by interrupting flow through the column (Brusseau et al., 1989).
4 |. COLUMN MODELS
Drinking water ion-exchange treatment occurs in continuous–flow columns (i.e., pressure vessels) rather than batch. Columns have the advantage of providing complete removal of contaminants of even moderate selectivity (provided the column is long enough to contain the mass transfer zone and therefore avoid incipient breakthrough). One of the most important questions to be answered regarding a column is how long the column can operate before the contaminant breaks through. Assuming a favorable exchange isotherm, the expected number of bed volumes until the concentration at the column outlet reaches 50% of the concentration in the feed solution for the ith species (Γi) is given by Equations (36a, b) (Zagorodni, 2006) where ε is the bed porosity and qi is the resin phase concentration for the ith species in equilibrium with the influent solution.
| (36a) |
| (36b) |
The estimate for run time to 50% breakthrough (tc) is then given in terms of column length (L) and superficial flow velocity (v) by Equation (37).
| (37) |
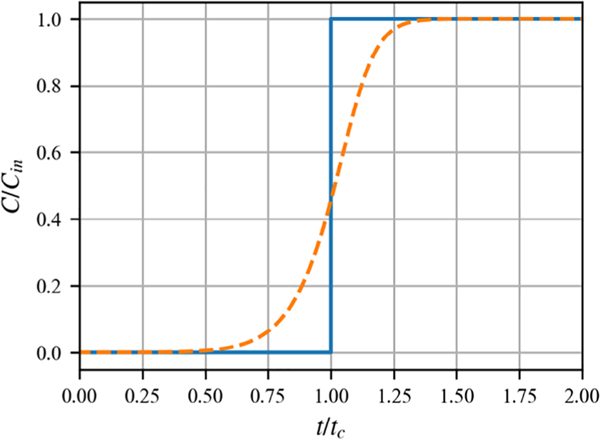
The quantity L/v is commonly referred to as the empty bed contact time. While this formula is of some use in experimental design, it is of little direct utility for drinking water operations because it does not take chromatographic effects (repartitioning as species move along the column) into account. Thus, it is not applicable to feed components that face meaningful competition with higher affinity species. Furthermore, this approximation does not provide any information about the temporal shape of the breakthrough curve. Depending on the efficiency of the column process, a breakthrough level of concern may occur well before 50% breakthrough (Figure 4). Predicting the profile of the breakthrough curve requires more sophisticated models.
FIGURE 4.
Conceptual diagram illustrating the difference between ideal (solid line) and dispersed (dashed line) breakthrough curves. C and Cin are the concentrations of the contaminant of interest in the effluent and influent, respectively, and t and tc and are the actual run time and run time to achieve 50% breakthrough, respectively
4.1 |. Column models that include mass transfer kinetics
The overall mass balance in an ion-exchange column can be described by adding flow advection and flow dispersion to the batch equation (Equation 38).
| (38) |
In Equation (38), z is the axial coordinate, ε is the resin bed porosity, and Dz is the axial dispersion coefficient. Axial dispersion is expected to be minor when vL/Dz > 40. For practical systems, this should be true when L > 40rb (Raghavan & Ruthven, 1983). Axial dispersion effects can also potentially arise in narrow columns. However, edge effects in the form of channeling along the column walls only start to become significant when the column radius is <30rb (Schwartz & Smith, 1953). Accordingly, the plug flow assumption should be valid for pilot- and full-scale systems. A detailed review of dispersion in packed beds can be found elsewhere (Delgado, 2006). Based on the arguments above, it is expected that dispersion of the breakthrough curve in water treatment systems is due primarily to nonequilibrium behavior rather than hydraulic dispersion. Therefore, it is possible to simplify Equation (38) by neglecting axial flow dispersion (setting ∂2C/∂z2 = 0). Making this simplification and solving Equation (38) for the time derivative of the liquid-phase concentration (∂C/∂t) yields Equation (39).
| (39) |
Equation (39) can be solved by providing influent concentrations at z = 0 and using expressions for the time derivative of the resin phase concentration (∂q/∂t) as described in the section on batch experiments.
4.2 |. Equilibrium models: Plates/tanks
In addition to mass transfer kinetic models, ion-exchange columns have also been described using models built from theory of chromatographic plates (Guter, 1984; Guter & Hardan, 1985) or stirred tanks in equilibrium (Hokanson, 2004). In these models, dispersion of the breakthrough curve is fit by increasing or decreasing the number of plates/tanks (Usher et al., 2008). For accurate prediction, these models require equilibrium between the bulk-liquid and the average resin-phase concentrations. However, due to the significant mass transfer resistances in typical applications, there is little reason to expect this assumption to hold for adsorption of PFAS from drinking water. If equilibrium is not achieved, these models will predict artificially sharp breakthrough curves (Özdural et al., 2004). This is problematic during the early part of the breakthrough curve, which is likely of primary concern for drinking water utilities who may target relatively low effluent PFAS concentrations.
5 |. PRACTICAL APPLICATION, LIMITATIONS, KNOWLEDGE GAPS, AND RESEARCH NEEDS
The above discussion of ion-exchange theory represents the known framework for modeling PFAS sorption consistent with the fundamentals of ion exchange. However, several outstanding issues challenge and limit the framework’s application to practical situations, particularly for water treatment studies for PFAS.
5.1 |. Obtaining necessary parameters to apply models
The governing equations described include parameters that are necessary to apply the equations in practice. Finding high-quality values for these parameters can represent a challenge to ready application of the models if a particular contaminant is not well-studied. Many PFAS fall into this category. PFAS/chloride (or other reference ion) separation factors and PFAS/resin mass transfer parameters, which are critical for predicting ion-exchange behavior, are extremely scarce in the literature.
There is currently no known method for estimating resin selectivity ab initio. Therefore, carefully designed isotherm experiments are needed to address data gaps in this area. Several methods for conducting these experiments are discussed in general ion-exchange textbooks (Helfferich, 1995; SenGupta, 2017).
Methods for determining the mass transfer parameters (kL and Ds) in fixed-bed processes have already been extensively reviewed (Liu & Weber Jr, 1981; Weber & Smith, 1987). These methods are typically discussed for general fixed-bed adsorption experiments and do not account for effects of ion composition on diffusion behavior. However, because interdiffusion in ion exchange is dominated by minority species (Helfferich, 1995), most of the general fixed-bed, mass-transport literature cited here should be relevant to experiments involving PFAS at trace concentration.
Under certain circumstances, it is possible to design bench column experiments to determine kL and Ds simultaneously (Weber Jr & Liu, 1980). It is also possible to arrive at useful estimates of kL using readily available empirical correlations (Cornel et al., 1986). These correlations typically estimate kL using the Sherwood number (Sh) and the ion’s diffusivity in water (DL), Equation (40).
| (40) |
The simplified Gnielinski correlation (Roberts et al., 1985), for example, estimates Sh using the Reynolds (Re) and Schmidt (Sc) numbers for the system (Equation 41).
| (41) |
The simplified Gnielinski correlation is valid for Re < 100 and 0.6 < Sc < 104. To the best of our knowledge, no such reliable correlations exist for predicting Ds in gel-type ion-exchange resins. However, Ds obtained from appropriately designed batch kinetic experiments should also apply to column experiments as Ds does not depend on column hydraulics. On the other hand, it is not possible to generalize kL from batch experiments to column experiments due to the differing hydraulic conditions.
Resin capacity (qT) is usually supplied by resin manufacturers. If not, it can be determined using standard methods (ASTM, 2017). Resin capacity will typically be reported as capacity of the packed bed, also known as filter capacity (qF), and qF is related to qT by ε (Equation 42).
| (42) |
Typical values for ε are generally in the range 0.35 to 0.40, depending on the sphericity and size distribution of the resin and packing method of the resin bed (Cornel et al., 1986; Helfferich, 1995).
5.2 |. Effects of natural organic matter
Some natural organic matter (NOM) molecules, such as humic and fulvic acids commonly found in drinking water sources, contain anionic groups at drinking water pHs and thus can compete for sites on ion-exchange resin (Bolto et al., 2004; Levchuk et al., 2018). These species can reduce the effectiveness of PFAS sorption by competing for sites on the ion-exchange resin (Gagliano et al., 2019). Competition due to NOM is difficult to model because important properties like molecular weight, valence, and selectivity of NOM are usually ill defined, and this challenge is accentuated by the extremely heterogeneous nature across the NOM spectrum. Additionally, NOM can reduce the effectiveness of ion-exchange resin through fouling. These molecules can adhere to the surface of strong-base anion-exchange resins and can effectively convert them into cation-exchange resins, resulting in degraded kinetics and loss of capacity (SenGupta, 2017). To the best of the authors’ knowledge, there is currently no widely accepted theoretical description of this performance degradation. Thus, quantitative prediction of ion-exchange performance using models described in this paper are most applicable to systems with low- NOM sources or featuring adequate pretreatment for NOM.
Given enough high-quality column data for waters containing well-characterized NOM, it is potentially possible to develop correlations, or hypothetical component approaches, to account for the impacts of NOM. A hypothetical component approach could be mechanistic but could suffer from necessary grouping assumptions. The correlation approach can account for unknown chemistries but would suffer due to lack of confidence that all mechanisms are adequately addressed in the training sets. Component and correlation approaches have been developed for activated carbon adsorption (Bhuvendralingam, 1992; Magnuson & Speth, 2005; Sontheimer et al., 1988) with some success. Although these specific models cannot be directly be applied to ion exchange, they could potentially be used as a starting point for developing analogous models.
5.3 |. Nonideal PFAS behavior
Some investigators have reported anomalous behavior (such as nonstoichiometric sorption or failure of qT to correspond to useable sorption capacity) for longer-chain PFAS (e.g., PFOS) during ion-exchange experiments (Du et al., 2014; Maimaiti et al., 2018; Zaggia et al., 2016). For instance, sorption of PFOS in excess of chloride release has been reported at high PFOS concentrations (Deng et al., 2010). This behavior is puzzling because, while hydrophobic sorption is expected for experiments involving nonfunctionalized resins or PFAS that are weak or nonelectrolytes, the Donnan potential generally prevents nonexchange sorption of ionized species onto strong-base anion-exchange resins (Harland, 1994; Helfferich, 1995). Thus, hydrophobic interactions with the resin backbone might be expected to affect the selectivity of strong-base resin for a given ion but would not normally be expected to result in altered sorption capacity. However, at high solution concentrations, it might be possible for PFAS to form aggregates on the resin surface. To explain the observed nonstoichiometric sorption of PFOS, some of authors have presented arguments involving hemi–micelle or micelle formation and critical micelle concentration of PFAS, which are related to PFAS chain length (Kunieda & Shinoda, 1976; López-Fontán et al., 2005; Shinoda et al., 1972). Intuition suggests that this hypothesis is more relevant to site remediation, which can involve comparatively high concentrations of PFAS, than it is for drinking water treatment. Indeed, recent reports of closely stoichiometric ion exchange of PFAS at lower concentrations support this intuition (Dixit et al., 2019, 2020). The micellization hypothesis, however, may impact ion-exchange studies, which can use (and historically have used) higher concentrations of such PFAS as a necessity of the study design—possibly resulting in unexpected deviations in PFAS selectivity or resin capacity.
Another theoretically possible source of nonideal behavior would be exclusion of PFAS from the gel interior—either by a coating of micelles, a coating of NOM, or by size exclusion due to a high degree of crosslinking in the gel (Harland, 1994). The latter of these mechanisms could be investigated by comparing isotherm results for varying bead sizes for gel-type resins or by attempting to fully convert a sample of resin to a PFAS form. In any case, the precise cause of the anomalous results and implications for modeling sorption of PFAS are currently areas of ongoing investigation.
5.4 |. Tools for implementation of ion exchange models
To the authors’ knowledge, very few computer tools are available to assist researchers in designing batch and column experiments for ion exchange. Currently available design tools mostly consist of proprietary software from sorbent vendors. Often, the use of these programs is limited to current customers. Furthermore, the underlying assumptions used by these programs are usually concealed as confidential business information. As such, these proprietary tools are of limited utility to the research community. Developing and sharing tools in an open–source manner would be a valuable resource for the drinking water research community. Furthermore, code to allow kinetic parameter estimation and simulation of batch and column experiments would be valuable for both experimental design and analysis.
5.5 |. Challenges in leveraging existing data
Because it is not currently possible to rigorously determine isotherm and mass transfer parameters ab initio, results of efforts to model PFAS sorption from drinking water using available literature can be reliant on the quality, quantity, and relevance of experimental results presented. Complicating the matter and as previously discussed, all PFAS isotherm studies (Table 1) conducted thus far have used single-parameter isotherm models that make determined parameters not generalizable, limiting their use as a basis to design experiments. Additionally, the concentrations of other anions present in solution often go unreported, making it difficult or impossible to determine ion-exchange parameters from the data presented. Consequently, there is a need for ion-exchange isotherm data and intraparticle diffusion coefficients under drinking water conditions for PFAS in commonly available ion-exchange resins. Specifically, isotherms conducted with equilibrium PFAS concentrations between 10 and 1,000 ng/L are of interest as those represent ranges seen in drinking water and current/proposed regulatory limits (Crone et al., 2019). There is also a subsequent need for pilot- or full-scale column data in laboratory and natural waters where the water characteristics are known. These data would allow for validation of the model (laboratory waters) and potential application of the model accounting for the influence of NOM and other relevant issues found in the field (natural waters).
6 |. SUMMARY
To quantitatively simulate breakthrough of PFAS on strong-base anion-exchange columns during drinking water treatment, it is desirable for predictive models to (1) use rigorous ion-exchange isotherms that are fundamentally based; (2) determine kinetics using mass transfer mechanisms; and (3) account for nonequilibrium conditions. Once equipped with appropriate isotherm and kinetic data, such model(s) should be able to produce reasonable simulations regarding PFAS breakthrough curves for pilot systems at any site, so long as the anion concentrations in the source water are known and the concentration of NOM is low. For waters where NOM has a significant influence, it is possible that additional correlations, or hypothetical components, could be added to the model to account for this influence, or at least improve uncertainty estimates for performance predictions.
However, the development and useful application of such a model is contingent on availability of theoretically useful isotherm and kinetic data. The current lack of such data in the literature is due in part from not considering basic ion-exchange theory during design and analysis of experiments. It is the sincere hope of the authors that this article will provide investigators with the tools needed to fill important gaps and improve the general understanding of the mechanisms governing removal of PFAS from drinking water.
Supplementary Material
ACKNOWLEDGMENT
The U.S. Environmental Protection Agency (EPA) through its Office of Research and Development funded the research described herein. It has been subjected to the Agency’s review and has been approved for publication. Note that approval does not signify that the contents necessarily reflect the views of the Agency. Any mention of trade names, products, or services does not imply an endorsement by the U.S. Government or EPA. The EPA does not endorse any commercial products, services, or enterprises.
Funding information
Office of Research and Development; U.S.
Environmental Protection Agency Associate Editor: Detlef R. U. Knappe
Footnotes
CONFLICT OF INTEREST
The authors have no conflict of interest to declare.
DATA AVAILABILITY STATEMENT
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
SUPPORTING INFORMATION
Additional supporting information may be found online in the Supporting Information section at the end of this article.
REFERENCES
- ASTM (2017). Standard test methods and practices for evaluating physical and chemical properties of particulate ion-exchange resins. In ASTM Standard D2187-17. ASTM International. [Google Scholar]
- Bachet M, Jauberty L, De Windt L, Tevissen E, De Dieuleveult C, & Schneider H. (2014). Comparison of mass transfer coefficient approach and Nernst–Planck formulation in the reactive transport modeling of Co, Ni, and Ag removal by mixed-bed ion-exchange resins. Industrial & Engineering Chemistry Research, 53(27), 11096–11106. 10.1021/ie5009663 [DOI] [Google Scholar]
- Bellot J, & Condoret J. (1991). Liquid chromatography modelling: A review. Process Biochemistry, 26(6), 363–376. 10.1016/0032-9592(91)85027-L [DOI] [Google Scholar]
- Bhuvendralingam S. (1992). A decision algorithm for optimizing granular activated carbon adsorption process design (PhD Dissertation). Michigan Technological University. [Google Scholar]
- Bolto B, Dixon D, & Eldridge R. (2004). Ion exchange for the removal of natural organic matter. Reactive and Functional Polymers, 60, 171–182. 10.1016/j.reactfunctpolym.2004.02.021 [DOI] [Google Scholar]
- Brusseau ML, Rao P, Jessup R, & Davidson J. (1989). Flow interruption: A method for investigating sorption nonequilibrium. Journal of Contaminant Hydrology, 4(3), 223–240. 10.1016/0169-7722(89)90010-7 [DOI] [Google Scholar]
- Carter KE, & Farrell J. (2010). Removal of perfluorooctane and perfluorobutane sulfonate from water via carbon adsorption and ion exchange. Separation Science and Technology, 45(6), 762–767. 10.1080/01496391003608421 [DOI] [Google Scholar]
- Chularueangaksorn P, Tanaka S, Fujii S, & Kunacheva C. (2013). Regeneration and reusability of anion exchange resin used in perfluorooctane sulfonate removal by batch experiments. Journal of Applied Polymer Science, 130(2), 884–890. 10.1002/app.39169 [DOI] [Google Scholar]
- Chularueangaksorn P, Tanaka S, Fujii S, & Kunacheva C. (2014a). Adsorption of perfluorooctanoic acid (PFOA) onto anion exchange resin, non-ion exchange resin, and granular-activated carbon by batch and column. Desalination and Water Treatment, 52(34–36), 6542–6548. 10.1080/19443994.2013.815589 [DOI] [Google Scholar]
- Chularueangaksorn P, Tanaka S, Fujii S, & Kunacheva C. (2014b). Batch and column adsorption of perfluorooctane sulfonate on anion exchange resins and granular activated carbon. Journal of Applied Polymer Science, 131(3), 1–7. 10.1002/app.39782 [DOI] [Google Scholar]
- Conte L, Falletti L, Zaggia A, & Milan M. (2015). Polyfluorinated organic micropollutants removal from water by ion exchange and adsorption. Chemical Engineering Transactions, 43, 2257–2262. 10.3303/CET1543377. [DOI] [Google Scholar]
- Cornel P, Sontheimer H, Summers RS, & Roberts PV (1986). Sorption of dissolved organics from aqueous solution by polystyrene resins—II. External and internal mass transfer. Chemical Engineering Science, 41(7), 1801–1810. 10.1016/0009-2509(86)87059-2 [DOI] [Google Scholar]
- Crank J. (1975). The mathematics of diffusion (2nd ed.). Clarendon Press. [Google Scholar]
- Crone BC, Speth TF, Wahman DG, Smith SJ, Abulikemu G, Kleiner EJ, & Pressman JG (2019). Occurrence of per-and polyfluoroalkyl substances (PFAS) in source water and their treatment in drinking water. Critical Reviews in Environmental Science and Technology, 49(24), 2359–2396. 10.1080/10643389.2019.1614848 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delgado J. (2006). A critical review of dispersion in packed beds. Heat and Mass Transfer, 42(4), 279–310. 10.1007/s00231-005-0019-0 [DOI] [Google Scholar]
- Deng S, Yu Q, Huang J, & Yu G. (2010). Removal of perfluorooctane sulfonate from wastewater by anion exchange resins: Effects of resin properties and solution chemistry. Water Research, 44(18), 5188–5195. 10.1016/j.watres.2010.06.038 [DOI] [PubMed] [Google Scholar]
- Dixit F, Barbeau B, Mostafavi SG, & Mohseni M. (2019). PFOA and PFOS removal by ion exchange for water reuse and drinking applications: Role of organic matter characteristics. Environmental Science: Water Research & Technology, 5(10), 1782–1795. 10.1039/C9EW00409B [DOI] [Google Scholar]
- Dixit F, Barbeau B, Mostafavi SG, & Mohseni M. (2020). Efficient removal of GenX (HFPO-DA) and other perfluorinated ether acids from drinking and recycled waters using anion exchange resins. Journal of Hazardous Materials, 384, 121261. 10.1016/j.jhazmat.2019.121261 [DOI] [PubMed] [Google Scholar]
- Du Z, Deng S, Bei Y, Huang Q, Wang B, Huang J, & Yu G. (2014). Adsorption behavior and mechanism of perfluorinated compounds on various adsorbents—A review. Journal of Hazardous Materials, 274, 443–454. 10.1016/j.jhazmat.2014.04.038 [DOI] [PubMed] [Google Scholar]
- Du ZW, Deng SB, Chen YG, Wang B, Huang J, Wang YJ, & Yu G. (2015). Removal of perfluorinated carboxylates from washing wastewater of perfluorooctanesulfonyl fluoride using activated carbons and resins. Journal of Hazardous Materials, 286, 136–143. 10.1016/j.jhazmat.2014.12.037 [DOI] [PubMed] [Google Scholar]
- Franzreb M, Höll WH, & Sontheimer H. (1993). Liquid-phase mass transfer in multi-component ion exchange I. Systems without chemical reactions in the film. Reactive Polymers, 21(1– 2), 117–133. 10.1016/0923-1137(93)90059-0 [DOI] [Google Scholar]
- Gagliano E, Sgroi M, Falciglia PP, Vagliasindi FG, & Roccaro P. (2019). Removal of poly-and perfluoroalkyl substances (PFAS) from water by adsorption: Role of PFAS chain length, effect of organic matter and challenges in adsorbent regeneration. Water Research, 115381, 1–31. 10.1016/j.watres.2019.115381 [DOI] [PubMed] [Google Scholar]
- Gao YX, Deng SB, Du ZW, Liu K, & Yu G. (2017). Adsorptive removal of emerging polyfluoroalky substances F-53B and PFOS by anion-exchange resin: A comparative study. Journal of Hazardous Materials, 323, 550–557. 10.1016/j.jhazmat.2016.04.069 [DOI] [PubMed] [Google Scholar]
- Guter G. (1984). Estimation of effects of resin and water composition on column performance in nitrate ion exchange. Paper presented at the Proceedings of 1984 AWWA Annual Conference, Dallas. [Google Scholar]
- Guter G, & Hardan D. (1985). Computer simulation of nitrate removal by ion exchange. Paper presented at the Proceedings of 1985 AWWA Annual Conference, Washington. [Google Scholar]
- Hand DW, Crittenden JC, & Thacker WE (1984). Simplified models for design of fixed-bed adsorption systems. Journal of Environmental Engineering, 110(2), 440–456. 10.1061/(ASCE)0733-9372(1984)110:2(440) [DOI] [Google Scholar]
- Harland CE (1994). Ion exchange: Theory and practice. Royal society of Chemistry. [Google Scholar]
- Hekmatzadeh A, Karimi-Jashani A, Talebbeydokhti N, & Kløve B. (2012). Modeling of nitrate removal for ion exchange resin in batch and fixed bed experiments. Desalination, 284, 22–31. 10.1016/j.desal.2011.08.033 [DOI] [Google Scholar]
- Helfferich FG (1995). Ion exchange. Courier Corporation. [Google Scholar]
- Hokanson DR (2004). Development of ion exchange models for water treatment and application to the International Space Station water processor. [Google Scholar]
- Hokanson DR, Clancey BL, Hand DW, Crittenden JC, Carter DL, & Garr JD (1995). Ion exchange model development for the International Space Station water processor (SAE Technical Paper 0148–7191). doi: 10.4271/951628 [DOI] [Google Scholar]
- Horst J, Höll WH, & Eberle SH (1990). Application of the surface complex formation model to exchange equilibria on ion exchange resins. Part I. Weak-acid resins. Reactive Polymers, 13 (3), 209–231. 10.1016/0923-1137(90)90092-I [DOI] [Google Scholar]
- Inglezakis V, Fyrillas M, & Park J. (2019). Variable diffusivity homogeneous surface diffusion model and analysis of merits and fallacies of simplified adsorption kinetics equations. Journal of Hazardous Materials, 367, 224–245. 10.1016/j.jhazmat.2018.12.023 [DOI] [PubMed] [Google Scholar]
- Jia Y, & Foutch GL (2004). True multi-component mixed-bed ion-exchange modeling. Reactive and Functional Polymers, 60, 121–135. 10.1016/j.reactfunctpolym.2004.02.017 [DOI] [Google Scholar]
- Kothawala DN, Köhler SJ, Östlund A, Wiberg K, & Ahrens L. (2017). Influence of dissolved organic matter concentration and composition on the removal efficiency of perfluoroalkyl substances (PFASs) during drinking water treatment. Water Research, 121((Supplement C)), 320–328. 10.1016/j.watres.2017.05.047 [DOI] [PubMed] [Google Scholar]
- Kressman T, & Kitchener J. (1949). Cation exchange with a synthetic phenolsulphonate resin. Part V. Kinetics. Discussions of the Faraday Society, 7, 90–104. 10.1039/DF9490700090 [DOI] [Google Scholar]
- Kunieda H, & Shinoda K. (1976). Krafft points, critical micelle concentrations, surface tension, and solubilizing power of aqueous solutions of fluorinated surfactants. The Journal of Physical Chemistry, 80(22), 2468–2470. 10.1021/j100563a007 [DOI] [Google Scholar]
- Kunin R, & Myers RJ (1947). Rates of anion exchange in ion-exchange resins. The Journal of Physical Chemistry, 51(5), 1111–1130. 10.1021/j150455a006 [DOI] [PubMed] [Google Scholar]
- LeVan MD, Carta G, Ritter JA, & Walton KS (2018). Adsorption and ion exchange. In Green DW & Southard MZ (Eds.), Perry’s chemical engineers’ handbook. McGraw-Hill. [Google Scholar]
- Levchuk I, Màrquez JJR, & Sillanpää M. (2018). Removal of natural organic matter (NOM) from water by ion exchange–a review. Chemosphere, 192, 90–104. 10.1016/j.chemosphere.2017.10.101 [DOI] [PubMed] [Google Scholar]
- Liu CJ, Werner D, & Bellona C. (2019). Removal of per-and polyfluoroalkyl substances (PFASs) from contaminated groundwater using granular activated carbon: A pilot-scale study with breakthrough modeling. Environmental Science: Water Research & Technology, 5(11), 1844–1853. 10.1039/C9EW00349E [DOI] [Google Scholar]
- Liu K-T, & Weber WJ Jr. (1981). Characterization of mass transfer parameters for adsorber modeling and design. Journal (Water Pollution Control Federation), 53(10), 1541–1550. [Google Scholar]
- López-Fontán JL, Sarmiento F, & Schulz PC (2005). The aggregation of sodium perfluorooctanoate in water. Colloid and Polymer Science, 283(8), 862–871. 10.1007/s00396-004-1228-7 [DOI] [Google Scholar]
- Magnuson ML, & Speth TF (2005). Quantitative structure− property relationships for enhancing predictions of synthetic organic chemical removal from drinking water by granular activated carbon. Environmental Science & Technology, 39(19), 7706–7711. 10.1021/es0508018 [DOI] [PubMed] [Google Scholar]
- Maimaiti A, Deng S, Meng P, Wang W, Wang B, Huang J, Wang Y, & Yu G. (2018). Competitive adsorption of perfluoroalkyl substances on anion exchange resins in simulated AFFF-impacted groundwater. Chemical Engineering Journal, 348, 494–502. 10.1016/j.cej.2018.05.006 [DOI] [Google Scholar]
- Misak NZ (1993). Langmuir isotherm and its application in ion-exchange reactions. Reactive Polymers, 21(1–2), 53–64. 10.1016/0923-1137(93)90054-J [DOI] [Google Scholar]
- Misak NZ (2000). Some aspects of the application of adsorption isotherms to ion exchange reactions. Reactive and Functional Polymers, 43(1–2), 153–164. 10.1016/S1381-5148(99)00046-2 [DOI] [Google Scholar]
- Okada T. (1998). Interpretation of ion-exchange chromatographic retention based on an electrical double-layer model. Analytical Chemistry, 70(9), 1692–1700. 10.1021/ac970655r [DOI] [PubMed] [Google Scholar]
- Özdural AR, Alkan A, & Kerkhof PJ (2004). Modeling chromatographic columns: Non-equilibrium packed-bed adsorption with non-linear adsorption isotherms. Journal of Chromatography A, 1041(1–2), 77–85. 10.1016/j.chroma.2004.05.009 [DOI] [PubMed] [Google Scholar]
- Raghavan N, & Ruthven D. (1983). Numerical simulation of a fixed-bed adsorption column by the method of orthogonal collocation. AICHE Journal, 29(6), 922–925. 10.1002/aic.690290608 [DOI] [Google Scholar]
- Rahman MF, Peldszus S, & Anderson WB (2014). Behaviour and fate of perfluoroalkyl and polyfluoroalkyl substances (PFASs) in drinking water treatment: A review. Water Research, 50, 318–340. 10.1016/j.watres.2013.10.045 [DOI] [PubMed] [Google Scholar]
- Roberts PV, Cornel P, & Summers RS (1985). External mass-transfer rate in fixed-bed adsorption. Journal of Environmental Engineering, 111(6), 891–905. 10.1061/(ASCE)0733-9372(1985)111:6(891) [DOI] [Google Scholar]
- Schuricht F, Borovinskaya ES, & Reschetilowski W. (2017). Removal of perfluorinated surfactants from wastewater by adsorption and ion exchange—influence of material properties, sorption mechanism and modeling. Journal of Environmental Sciences, 54, 160–170. 10.1016/j.jes.2016.06.011 [DOI] [PubMed] [Google Scholar]
- Schwartz CE, & Smith J. (1953). Flow distribution in packed beds. Industrial & Engineering Chemistry, 45(6), 1209–1218. 10.1021/ie50522a025 [DOI] [Google Scholar]
- Senevirathna STMLD, Tanaka S, Fujii S, Kunacheva C, Harada H, Shivakoti BR, & Okamoto R. (2010). A comparative study of adsorption of perfluorooctane sulfonate (PFOS) onto granular activated carbon, ion-exchange polymers and non-ion-exchange polymers. Chemosphere, 80(6), 647–651. 10.1016/j.chemosphere.2010.04.053 [DOI] [PubMed] [Google Scholar]
- SenGupta AK (2017). Ion exchange in environmental processes: Fundamentals, applications and sustainable technology. John Wiley & Sons. [Google Scholar]
- Shinoda K, Hato M, & Hayashi T. (1972). Physicochemical properties of aqueous solutions of fluorinated surfactants. The Journal of Physical Chemistry, 76(6), 909–914. 10.1021/j100650a021 [DOI] [Google Scholar]
- Sircar S, & Hufton J. (2000). Why does the linear driving force model for adsorption kinetics work? Adsorption, 6(2), 137–147. 10.1023/A:1008965317983 [DOI] [Google Scholar]
- Slater MJ (2013). Principles of ion-exchange technology. Butterworth-Heinemann. [Google Scholar]
- Sontheimer H, Crittenden JC, & Summers RS (1988). Activated carbon for water treatment. American Water Works Association. [Google Scholar]
- Ståhlberg J. (1999). Retention models for ions in chromatography. Journal of Chromatography A, 855(1), 3–55. 10.1016/S0021-9673(99)00176-4 [DOI] [PubMed] [Google Scholar]
- Tran HN, You S-J, Hosseini-Bandegharaei A, & Chao H-P (2017). Mistakes and inconsistencies regarding adsorption of contaminants from aqueous solutions: A critical review. Water Research, 120, 88–116. 10.1016/j.watres.2017.04.014 [DOI] [PubMed] [Google Scholar]
- Tripp A, Clifford D, Roberts D, Cang Y, Aldridge L, Gillogly T, & Boulos L. (2003). Treatment of perchlorate in groundwater by ion exchange technology. AWWA and AwwaRF. [Google Scholar]
- USEPA. (2018). Long-chain perfluoroalkyl carboxylate and perfluoroalkyl sulfonate chemical substances; significant new use rule. https://www.reginfo.gov/public/do/eAgendaViewRule?pubId=201810&RIN=2070-AJ99.
- Usher KM, Simmons CR, & Dorsey JG (2008). Modeling chromatographic dispersion: A comparison of popular equations. Journal of Chromatography A, 1200(2), 122–128. 10.1016/j.chroma.2008.05.073 [DOI] [PubMed] [Google Scholar]
- Wang BY, Lee LS, Wei CH, Fu HY, Zheng SR, Xu ZY, & Zhu DQ (2016). Covalent triazine-based framework: A promising adsorbent for removal of perfluoroalkyl acids from aqueous solution. Environmental Pollution, 216, 884–892. 10.1016/j.envpol.2016.06.062 [DOI] [PubMed] [Google Scholar]
- Wang W, Maimaiti A, Shi HL, Wu RR, Wang R, Li ZL, Qi D, Yu G, & Deng SB (2019). Adsorption behavior and mechanism of emerging perfluoro-2-propoxypropanoic acid (GenX) on activated carbons and resins. Chemical Engineering Journal, 364, 132–138. 10.1016/j.cej.2019.01.153 [DOI] [Google Scholar]
- Wang W, Mi X, Zhou ZM, Zhou SX, Li CL, Hu X, Qi D, & Deng SB (2019). Novel insights into the competitive adsorption behavior and mechanism of per- and polyfluoroalkyl substances on the anion-exchange resin. Journal of Colloid and Interface Science, 557, 655–663. 10.1016/j.jcis.2019.09.066 [DOI] [PubMed] [Google Scholar]
- Weber W Jr., & Liu K. (1980). Determination of mass transport parameters for fixed-bed adsorbers. Chemical Engineering Communications, 6(1–3), 49–60. 10.1080/00986448008912520 [DOI] [Google Scholar]
- Weber WJ, & Smith EH (1987). Simulation and design models for adsorption processes. Environmental Science & Technology, 21(11), 1040–1050. 10.1021/es00164a002 [DOI] [Google Scholar]
- Woodard S, Berry J, & Newman B. (2017). Ion exchange resin for PFAS removal and pilot test comparison to GAC. Remediation Journal, 27(3), 19–27. 10.1002/rem.21515 [DOI] [Google Scholar]
- Yang YQ, Ding Q, Yang MH, Wang Y, Liu N, & Zhang XD (2018). Magnetic ion exchange resin for effective removal of perfluorooctanoate from water: Study of a response surface methodology and adsorption performances. Environmental Science and Pollution Research, 25(29), 29267–29278. 10.1007/s11356-018-2797-1 [DOI] [PubMed] [Google Scholar]
- Yao Y, Volchek K, Brown CE, Robinson A, & Obal T. (2014). Comparative study on adsorption of perfluorooctane sulfonate (PFOS) and perfluorooctanoate (PFOA) by different adsorbents in water. Water Science and Technology, 70(12), 1983–1991. 10.2166/wst.2014.445 [DOI] [PubMed] [Google Scholar]
- Yu Q, Zhang R, Deng S, Huang J, & Yu G. (2009). Sorption of perfluorooctane sulfonate and perfluorooctanoate on activated carbons and resin: Kinetic and isotherm study. Water Research, 43(4), 1150–1158. 10.1016/j.watres.2008.12.001 [DOI] [PubMed] [Google Scholar]
- Zaggia A, Conte L, Falletti L, Fant M, & Chiorboli A. (2016). Use of strong anion exchange resins for the removal of perfluoroalkylated substances from contaminated drinking water in batch and continuous pilot plants. Water Research, 91, 137–146. 10.1016/j.watres.2015.12.039 [DOI] [PubMed] [Google Scholar]
- Zagorodni AA (2006). Ion exchange materials: Properties and applications. Elsevier. [Google Scholar]
- Zhang D, Zhang W, & Liang Y. (2019). Adsorption of perfluoroalkyl and polyfluoroalkyl substances (PFASs) from aqueous solution-a review. Science of the Total Environment, 694, 133606. 10.1016/j.scitotenv.2019.133606 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.