Non-monetary valuation using Multi-Criteria Decision Analysis: Using a strength-of-evidence approach to inform choices among alternatives

Abstract

This article demonstrates an approach to Multi-Criteria Decision Analysis that compares non-monetary ecosystem service (ES) outcomes for environmental decision making. ES outcomes are often inadequately defined and characterized by imprecision and uncertainty. Outranking methods enrich our understanding of the imperfect knowledge of ES outcomes by allowing decision makers to closely examine and apply preference measures to relationships among the outcomes. We explain the methodological assumptions related to the Preference Ranking Organization METHod for Enrichment Evaluation (PROMETHEE) method, and apply it to a wetland restoration planning study in Rhode Island, USA. In the study, we partnered with a watershed management organization to evaluate four wetland restoration alternatives for their abilities to supply five ES: flood water regulation, scenic landscapes, learning opportunities, recreation, and birds. Twenty-two benefit indicators were identified for the ES as well as one indicator for social equity and one indicator for reliability of ES provision. We developed preference functions to characterize the strength of evidence across estimated indicator values between pairs of alternatives. We ranked the alternatives based on these preferences and weights on ES relevant to different planning contexts. We discuss successes and challenges of implementing PROMETHEE, including feedback from our partners who utilized the methods.

1. Introduction

Interest in the non-monetary valuation of ecosystem services (ES) is growing, especially in the context of evaluating environmental management alternatives for decision-making purposes (Bagstad et al., 2013; Chan et al., 2012). A significant research challenge concerns how to effectively capture and evaluate the different ways people benefit from natural ecosystems using non-monetary or non-dollar estimates (Wainger and Mazzotta, 2011). An additional challenge is how to cope with uncertainty in non-monetary ES outcomes and measures (Hamel and Bryant, 2017).

There are many sources of uncertainty in modeling and measuring ES (e.g., measurement error, sampling error, systematic error, natural ecosystem variation, model assumptions, subjective judgments; Regan et al., 2002). While statistical or Bayesian techniques are typically applied to address these sources of uncertainty, uncertainty must also be acknowledged and addressed when choosing between alternative courses of action. In approaches to environmental decision making, it is customary to integrate multiple monetary and non-monetary metrics to assess tradeoffs in ES outcomes in terms of the potential costs or benefits gained or lost by choosing one management alternative over another (Nelson et al., 2009; for a recent review, see Grêt-Regamey et al., 2017). Evaluating tradeoffs can be easier if alternatives are compared using a common metric; however, this requires ES analysts to transform ES data into commensurable measures.

In this article, we examine approaches to making choices among management alternatives using Multi-Criteria Decision Analysis (MCDA). In the context of ES assessments, these approaches transform ES measures into a common metric and apply preference measures to ES, so that alternatives can be more effectively evaluated for decision-making purposes. Linear and non-linear value functions (e.g., multi-attribute value functions; Keeney and von Winterfeldt, 2007) and qualitative value functions (e.g., analytic hierarchy process; Saaty, 1990) are popular methods to develop common metrics that can be aggregated and easily compared, especially for ES assessments (Langemeyer et al., 2016). Value functions produce numerical representations of preference (i.e., scores) for each measured outcome. Additive value functions are commonly used to aggregate scores and rank alternatives, which tells us the “value” or “worth” of each alternative relative to others.

ES outcomes are, to a large extent, imperfectly known, meaning that they can be ambiguous, difficult to define, imprecise, and/or uncertain (Roy et al., 2014). MCDA approaches aim to cope with the imperfect nature of measures of ES outcomes in various ways. While a preferred approach may be to seek more complete information about the outcomes themselves, this may not be possible or feasible. Some approaches assign prediction probabilities to scores to reflect uncertainties that arise from measurements (e.g., decision trees with multi-attribute utility functions; Keeney and Raiffa, 1976; for a relevant application, see Maguire and Boiney, 1994). Other approaches account for imprecision by allowing for fuzziness in the way decision makers score outcomes (e.g., distance-based functions based on the concept of a best compromise for each outcome; Benayoun et al., 1970; Zeleny, 1973; for a relevant application, see Martin et al., 2016). These approaches fit within the family of additive aggregation functions, which are the most common methods for MCDA and especially useful when decision makers want a single cumulative score for each management alternative.

The usefulness of additive aggregation functions relies on the assumption that a single score adequately takes decision maker preferences over imperfectly-known ES into account (Roy, 1971). There are limitations to these types of approaches, especially when decision makers do not have strong preferences when comparing some or all of the ES outcomes.. Once the scores are aggregated, any inherent ambiguity, imprecision, or uncertainty in the outcomes has been masked, and the degree to which the magnitude of changes in outcomes across management alternatives influences their ranking may be masked as well (Roy, 1989). Additive aggregation functions treat a larger aggregated score as unambiguously better than a smaller aggregated score; yet, it may not make sense to say that one alternative is strictly better than another based on its overall score alone (Roy, 1990). For example, decision maker preferences may not be well-defined for choosing an alternative that saves 100 species over an alternative that saves 99 species. Although sensitivity analysis can address some of these challenges, results are sensitive to the choice of scoring and aggregation technique (Martin and Mazzotta, 2018), and it is not always clear whether decision makers are aware of the implications of the mathematical assumptions that underlie scoring and aggregation. In this paper, we present the use of outranking methods for MCDA as an alternative approach to addressing imperfect knowledge in ES outcomes when making choices among alternatives.

1.1. Outranking methods

The main objective of outranking methods for MCDA is to deconstruct the way decision makers make choices. In the context of ES assessments, this is achieved by assigning different types of preferences to relationships between ES outcomes. This makes the role of ambiguity, imprecision, and uncertainty in how ES are measured and used for decision making more transparent (Roy, 1989). With outranking methods, decision makers assign preference measures directly to comparisons across ES outcomes, based on explicit consideration of strength of evidence across those outcomes (Roy, 1991).

Using traditional additive aggregation, two types of preference relationships exist for making choices between two alternatives a,b (Table 1): strict preference (aPb) and indifference (aIb), which may refer to comparisons of numerically different and identical aggregated scores, respectively. Outranking methods were developed to allow for two additional preference relationships (Table 1; Roy and Vincke, 1987): fuzzy preference (a⧘P⧘b), meaning that it is difficult to say that one alternative is strictly preferred to another because the strength of evidence is incomplete (i.e., there are thresholds where decision makers vacillate between indifference and strict preference); and incomparability (aRb), meaning that some comparisons cannot be clearly distinguished because of insufficient strength of evidence. These latter two relationships allow decision makers to incorporate insufficient information, allowing for choices to be more nuanced in some cases of comparing ES outcomes.

Table 1.

Binary preference relationships between two alternatives a,b (adapted from Figueira et al., 2013).

Relationship	Notation	Description
Indifference	$aIb$	no difference in preference between alternatives a and b
Strict preference	$aPb$	alternative a is strictly preferred to b
Fuzzy preference	a⧘P⧘b	the degree to which alternative a is preferred to b is distinguished by some function reflecting ambiguity in preferences over uncertain outcomes
Incomparable	$aRb$	special situation in which a preference relationship cannot be determined without additional information

Outranking methods can provide more flexibility than scoring and aggregation, for instance, in situations where aggregated scores are too close to judge that one alternative is better than another, or where decision makers want to closely examine the actual differences in ES outcomes. Decision maker preferences for a large change in outcome (100 vs. 1 species saved) can be much stronger than for a small change (100 vs. 99 species saved). Accounting for such differences eliminates some of the undesirable effects of aggregation (Brans and Mareschal, 2005). Outranking methods force decision makers to focus their judgment on actual measurements and the degree of change, not scores, which can more fully inform choices among alternatives.

In the remainder of this article, we describe the basics of outranking methods, focusing on the PROMETHEE methods (Preference Ranking Organization METHod for Enrichment Evaluation; Brans et al., 1986). Applications of ES assessments using outranking methods are rare and require empirical testing (Langemeyer et al., 2016). We describe the PROMETHEE methods and their assumptions using a real-world ES assessment to plan for wetland restoration in Rhode Island, USA.

1.2. Study area

The Woonasquatucket River flows southeast through northern Rhode Island, into the city of Providence, the state’s capital (Fig. 1). The river is threatened by development pressures and water quality degradation. We partnered with the Woonasquatucket River Watershed Council (WRWC), a non-profit watershed organization whose mission is to support and promote sustainable development in the watershed. Among its many initiatives, the WRWC is seeking to research and plan for wetland restoration in the watershed. Following guidelines set forth in The American Heritage Rivers initiative, the WRWC is considering options to restore previously damaged or destroyed wetlands for their social benefits. Implementing restoration requires the WRWC to secure funding. Because they often have opportunities to write grant proposals to perform restoration, having a set of “shovel-ready” projects identified with potential ES benefits to provide justification is most useful for them. Therefore, our objective with the partnership was to develop research methods, including a rapid assessment approach (Mazzotta et al., 2016), estimate the social benefits of ecological restoration, and test how decision-focused methods are applied to aid the WRWC in ecological restoration planning (Martin et al., 2018).

Fig. 1.

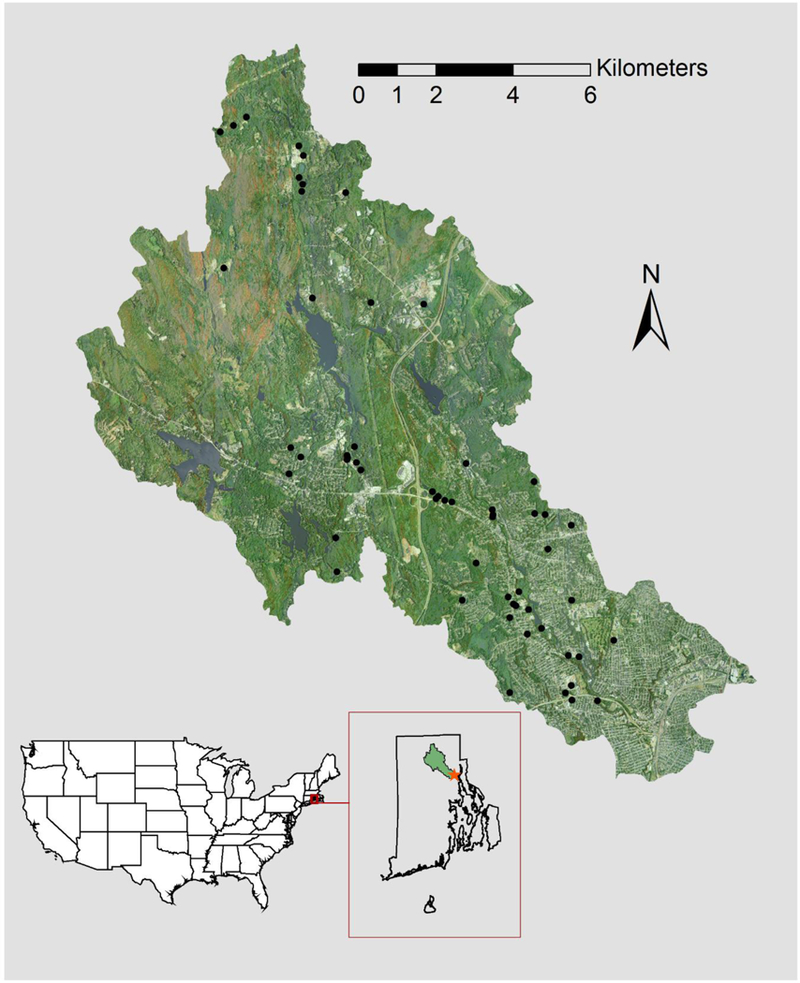
Map of Woonasquatucket River watershed, with 65 candidate restoration sites shown as black points. Reproduced with permission from Martin et al. (2018).

Many conversations within and outside the WRWC (Druschke and Hychka, 2015) were used to select five ES to analyze candidate wetland restoration sites (Fig. 1; Mazzotta et al., 2016): flood risk reduction (FR), scenic views (SV), environmental education (E), recreation (R), bird watching (BW). The ES are not comprehensive; they were identified based on availability of information and preferences of the WRWC and other restoration managers in Rhode Island. ES benefits and 22 associated benefit indicators were identified with conceptual modeling and measured using spatial analysis at the restoration sites (Table 2; Martin et al., 2018). Two additional benefit indicators were developed and measured using spatial analysis to reflect social equity – referring to whether socially vulnerability populations could have access to and benefit from ES – and reliability – referring to whether an ES will continue to be available at a site in the future (Table 2). Because this assessment was based on a rapid approach, there are various potential sources of inaccuracy in developing the performance measures and uncertainty in measuring the indicators (Mazzotta et al., 2016).

Table 2.

Benefit indicators and metrics for planning study.

Category	Benefit indicator	Description/Metric1	Preference direction	References
Flood risk reduction	FR1 beneficiaries	Number of addresses (homes and businesses) in the floodplain within 4km radius and downstream from site	Maximize	Bousquin et al. (2015)
	FR2 retention capacity	Size (hectares) of site	Maximize
	FR3 substitution	Number of dams/levees 4km radius and downstream from site	Minimize
	FR4 substitution	Percent area of wetlands within 4km radius of site	Minimize
Scenic views	SV1 beneficiaries	Number of addresses (homes and businesses) within 50m of site	Maximize	Mazzotta et al. (2016)
	SV2 beneficiaries	Number of addresses (homes and businesses) between 50–100m of site	Maximize
	SV3 access	Roads or trails within 100m of site	Yes
	SV4 complementarity	Number of natural land use types within 200m of site	Maximize
	SV5 substitution	Percent area of wetlands within 200m of site	Minimize
Education	E1 beneficiaries	Number of educational institutions within 402m radius of site	Maximize	Mazzotta et al. (2016)
	E2 substitution	Percent area of wetlands within 805m of site	Minimize
Recreation	R1 beneficiaries (walking)	Number of addresses (homes and businesses) within 536m of site	Maximize	Mazzotta et al. (2016)
	R2 beneficiaries (driving)	Number of addresses (homes and businesses) between 536–805m of site	Maximize
	R3 beneficiaries (driving)	Number of addresses (homes and businesses) between 805m-10km of site	Maximize
	R4 access	Bike trails within 536m of site	Yes
	R5 access	Bus stops within 536m of site	Yes
	R6 recreational quality	Size (hectares) of site and adjacent green space	Maximize
	R7 substitution	Percent area of green space within 1.1km but not adjacent to site	Minimize
	R8 substitution	Percent area of green space between 1.1–1.6km but not adjacent to site	Minimize
	R9 substitution	Percent area of green space between 1.6–19km but not adjacent to site	Minimize
Bird watching	BW1 beneficiaries	Number of addresses (homes and businesses) within 322m of site	Maximize	Mazzotta et al. (2016)
	BW2 access	Roads or trails within 322m of site	Yes
Social equity	S1 social vulnerability	Proximity-based percent of total area of social vulnerability to environmental hazards within 4km of site; based on demographics (e.g., race, class, wealth, age, ethnicity, employment) and other factors	Maximize2	NOAA3
Reliability	RE1 reliability	Assurance that a site will continue to provide benefits over time, in the face of development stressors. Measured in size of property within 152m of site designated with conservation, parks & open space, reserve, or water land use categories	Maximize	Mazzotta et al. (2016)

¹All metrics were converted from English units

²We used the “Medium” vulnerability percentages as non-monetary values. Higher values for this category are less able to recover from environmental hazards because they are areas identified as lower income and ethnically diverse. A higher percentage is preferable because the site provides access to people who are less able to access benefits otherwise.

³National Oceanic and Atmospheric Administration: https://coast.noaa.gov/dataregistry/search/collection/info/sovi

In previous work, we developed a tool to evaluate 65 candidate restoration sites using the compromise programming method for MCDA (Zeleny, 1973), which scored and aggregated the benefit indicator values for each site based on their geometric distance to a best compromise set of indicator values in multidimensional space (Martin et al., 2018). The tool was developed so that our partners could evaluate the sites under different planning scenarios. Each scenario incorporated different WRWC-defined importance weights for the indicators. The weights attributed to the ES were equally distributed among the indicators for each service. Numerous scenarios were evaluated in many informal meetings and based on specific preferences for getting restoration funded. This resulted in sorting and ranking the candidate sites. However, we and the WRWC noticed that four of the restoration sites were often the highest ranking sites in many different scenarios (Fig. 2; Martin et al., 2018). Likewise, when we applied equal weights to all indicators, we noticed that the aggregated indicator values of the four sites were close to uniform, which made it hard to discriminate which site was better than another.

Fig. 2.

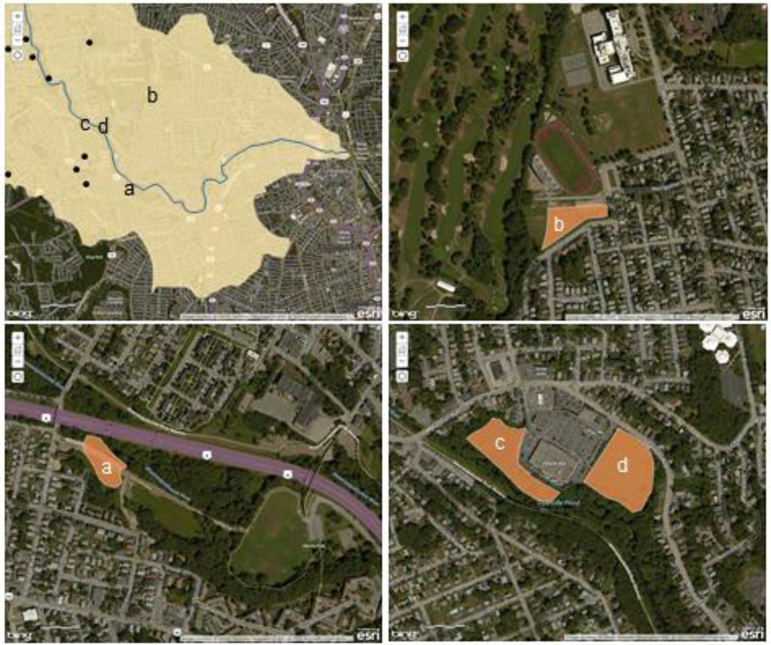
Four highest ranking candidate restoration alternatives based on previous work (reproduced with permission from Martin et al., 2018). In the upper left panel, locations are identified by letter, the Woonasquatucket River is identified by a blue line, and locations of other damaged and destroyed wetlands in the area are shown as black points. Polygons for each alternative are shown in the other panels. Alternative a is located on a former mill complex along the river and near an urban park and residential development, b is located near a tributary to the river and on a public school property and near a golf course and residential development, c and d are located along the river and adjacent to urban commercial and residential development.

Building on our previous work, we and the WRWC investigated the four candidate restoration sites to further distinguish their preferences between the sites. We tested the outranking approach to make this distinction transparent. The additional evaluation incorporated the PROMETHEE methodology and preference measures attributed to the differences in indicator values among the four sites, hereafter referred to as alternatives.

2. Methods

We used the following set of assumptions and notations for applying PROMETHEE in the study:

• We consider the problem to rank a finite set A of four alternatives $a,b,c,d\in A$, where each alternative is characterized by a finite set F of benefit indicators $j=1,\dots ,24$. Since set A is finite, we can organize the data into an evaluation table of indicator values $x_j\left(a,b,c,d\right)$, shown in Table 3.

• Outranking methods develop numerical representations of binary strength-of-evidence relationships between alternatives, for each indicator. To simplify our explanation of the methods, we use the notation $\left(a,b\right)$ to signify one alternative being compared to another in the set A. In practice, we performed pairwise comparisons between all alternatives $a,b,c,d\in A$.

• Most of the methods for MCDA assign numerical weights $w_j$ to each indicator. Weights generally reflect the relative importance of each indicator for decision making. Weights can be directly assigned by decision makers or other stakeholders based on their preferences for the indicators, or they may be constructed based on tradeoffs that stakeholders are willing to make among the indicators. The concept of weights and possible uncertainty associated with appropriately assigning weights will not be discussed in this article (see Choo et al., 1999; Belton and Stewart, 2002).

Table 3.

Non-monetary indicator values of restoration alternatives (a,b,c,d) and preference function relationships for planning study.

Benefit indicator	Min/Max (Yes/No)	a	b	c	d	Preference function type (Fig. 3)	Threshold q (Fig. 3)	Threshold p (Fig. 3)
FR1 beneficiaries (addresses)	Max	662	423	389	434	III	--	100
FR2 retention capacity (hectares)	Max	0.63	0.68	1.38	1.91	V	0.06	0.2
FR3 substitution (number of dams)	Min	3	0	3	3	I	--	--
FR4 substitution (percent)	Min	5.63	4.04	5.56	5.38	II	5	--
SV1 beneficiaries (addresses)	Max	1	15	18	14	II	2	--
SV2 beneficiaries (addresses)	Max	30	34	38	42	III	--	10
SV3 access (roads or trails)	Yes	Yes	Yes	Yes	Yes	I	--	--
SV4 complementarity (number of natural land use types)	Max	4	2	4	4	I	--	--
SV5 substitution (percent)	Min	5.94	0	2.71	4.03	II	5	--
E1 beneficiaries (number of institutions)	Max	0	2	1	1	I	--	--
E2 substitution (percent)	Min	2.57	0.25	3.55	2.63	II	5	--
R1 beneficiaries (addresses)	Max	1,006	1,025	1,014	852	II	100	--
R2 beneficiaries (addresses)	Max	1,336	1,203	828	933	II	100	--
R3 beneficiaries (addresses)	Max	139,151	143,780	135,326	137,402	III	--	5,000
R4 access (bike trails)	Yes	Yes	No	Yes	Yes	I	--	--
R5 access (bus stops)	Yes	Yes	Yes	Yes	Yes	I	--	--
R6 recreational quality (hectares)	Max	3.48	68.83	15.88	17.53	II	4.05	--
R7 substitution (percent)	Min	18.37	30.84	30.22	31.04	II	3	--
R8 substitution (percent)	Min	18.24	13.74	18.38	18.40	II	3	--
R9 substitution (percent)	Min	52.19	52.91	53.64	53.41	II	3	--
BW1 beneficiaries (addresses)	Max	418	402	470	398	III	--	100
BW2 access (roads or trails)	Yes	Yes	No	Yes	Yes	I	--	--
S1 index (percent)	Max	67.80	67.77	75.43	73.27	II	3	--
RE1 index (score)	Max	14.31	52.52	14.98	12.30	II	3	--

Note: indicator values are rounded to nearest hundredths; Yes/No values were transformed into 1/0 numbers for analytical comparison

2.1. PROMETHEE

The most common outranking methods for MCDA are ELimination and Choice Expressing the REality (ELECTRE; Figueira et al., 2013) and PROMETHEE. The PROMETHEE methods require decision makers to specify fewer parameters, and therefore include less trial and error than other common outranking methods (e.g., ELECTRE). For these reasons, we chose to implement PROMETHEE for the planning study. In this section, we cover basic principles of the first two PROMETHEE methods, PROMETHEE I and PROMETHEE II. These basic principles are used in the remaining PROMETHEE methods (III-VI), which are more specific to decision contexts (Brans and Mareschal, 2005). A spreadsheet with calculations for this study is available in the Supplementary material.

In PROMETHEE, a preference function $P_j\left(a,b\right)$ is selected for each indicator to represent intensity of preference. The preference function uses the decision maker’s evaluation of strength of evidence to assign a binary numerical (0–1) relationship to comparisons between pairs of alternatives $a,b,c,d\in A$ per indicator. This relationship is a function $f_j$ of the positive distance $d_j$ between two indicator values (Brans et al., 1986):

$$P_j\left(a,b\right)=f_j\left(d_j\right)\forall a,b,c,d\text{∈}A$$ (1)

$$d_j=\begin{array}{ll}\left|x_j\left(a\right)-x_j\left(b\right)\right|\hfill & if\hspace{0.17em}{x}_j\left(a\right)\hspace{0.17em}outperforms\hspace{0.17em}{x}_j\left(b\right)\hfill \\ 0\hfill & otherwise\hfill \end{array}$$ (2)

for all indicators $j=1,\dots ,24$; where $x_j$ is the indicator value for a given alternative in the set $jϵF$.

In this context, a preference function value of $P_j\left(a,b\right)=0$ indicates that alternative a is not preferred to alternative b for a specific indicator j. When this is true, it is also true that either $P_j\left(b,a\right)=0$ (b is not preferred to a) or $P_j\left(b,a\right)>0$ (b is preferred to a), for that indicator. A preference function value of $P_j\left(a,b\right)=1$ indicates strict preference of a over b, and $0<P_j\left(a,b\right)<1$ indicates fuzzy preference of a over b; these relationships imply that $P_j\left(b,a\right)=0$ (b is not preferred to a). In terms of fuzzy preference, preference function values closer to 0 indicate a weaker preference relationship between alternatives, whereas values closer to 1 indicate a stronger preference relationship.

Preference function relationships can take many forms (Fig. 3). Depending on decision maker preferences and strength of evidence between indicator values, preference functions require the specification of three threshold parameters: indifference parameter q, strict preference parameter p, and standard deviation parameter σ (Fig. 3).

Fig. 3.

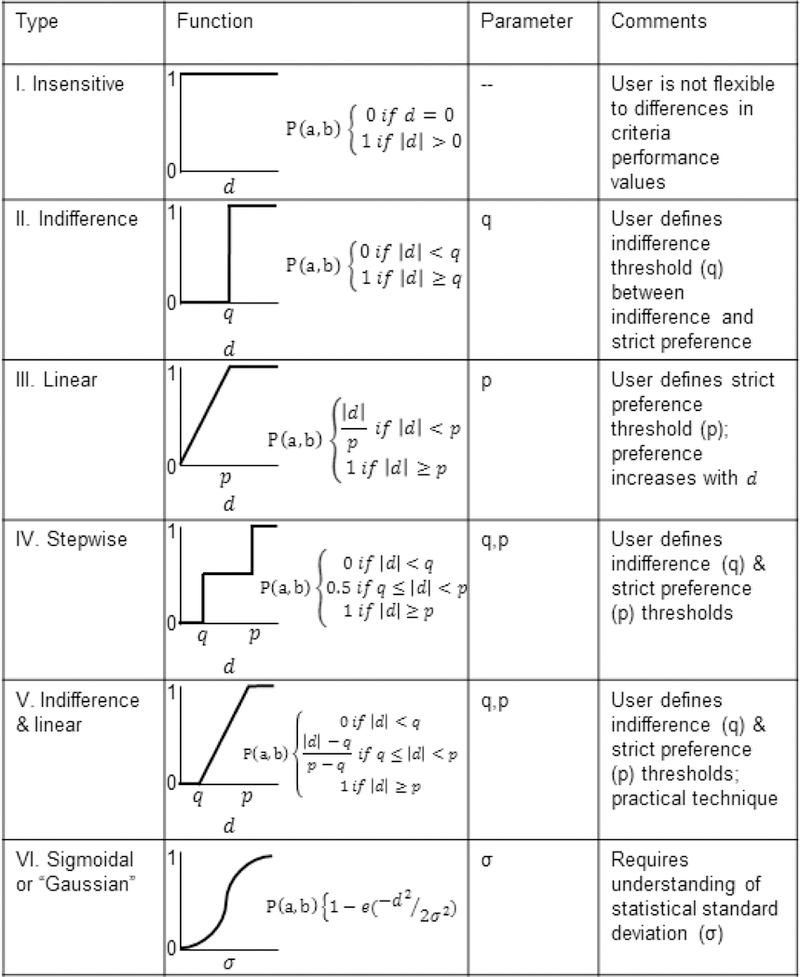
Preference functions in the PROMETHEE methodology that specify the degree of preference that one alternative a outranks another b for each indicator (adapted from Brans et al., 1986). The parameter d is defined by Eq. (2).

We aided the WRWC in identifying preference function relationships and threshold parameter values for each benefit indicator (Table 3, columns 7–9). To illustrate, we consider the first four benefit indicator values $x_j$ for flood risk reduction benefits (FR indicators; Table 3).

To express their preferences across the predicted outcomes, the WRWC chose to compare the beneficiaries indicator (FR1; number of addresses within 4km downstream radius; Table 2) using the linear (type III) preference function (Fig. 3) with strict threshold parameter p = 100 (Table 3). According to WRWC preferences, alternative a was undoubtedly the better alternative for this indicator; its value was $x_{FR1}\left(a\right)=662$, which exceeds the values for the other three alternatives by more than 100. The type III preference function allows for fuzzy preferences for differences that are less than 100; this allowed the WRWC to account for potential variability and imprecision in the indicator values between alternatives b, c, and d, with values $x_{FR1}\left(b\right)=423$, $x_{FR1}\left(c\right)=389$, and $x_{FR1}\left(d\right)=434$. Because the differences in these measures were close, and given that the exact consequence cannot be fully known, WRWC did not want the small differences to control how the alternatives were compared and, consequently, the results. By assigning this preference function, alternative d was weakly preferred, but not indifferent, to b, or $P_{FR1}\left(d,b\right)=\frac{\left|434-423\right|}{100}=0.11$; alternative d was moderately preferred over c, or $P_{FR1}\left(d,c\right)=\frac{\left|434-389\right|}{100}=0.45$; and alternative b was weakly preferred over c, or $P_{FR1}\left(b,c\right)=\frac{\left|423-389\right|}{100}=0.34$.

For the water retention capacity indicator (FR2; size of site; Table 3), two alternatives were close in indicator value: a = 0.63 hectares, and b = 0.68 hectares. Estimates for alternatives c (1.38 hectares) and d (1.91 hectares) were notably better than alternatives a and b. However, these measures are from spatial data using existing conditions, and it is unknown whether the size of alternatives will change after implementing restoration. Therefore, we assigned an indifference and linear (type V) preference function (Fig. 3) with indifference threshold parameter q = 0.06 and strict threshold parameter p = 0.2 (Table 3). This preference function resulted in an indifference preference relationship between alternatives a and b, or $P_{FR2}\left(a,b\right)=0$ and $P_{FR2}\left(b,a\right)=0$ and strict preference relationships between alternatives c and d and a and b, or $P_{FR2}\left(c,a\right)=1$, $P_{FR2}\left(d,a\right)=1$, $P_{FR2}\left(c,b\right)=1$, and $P_{FR2}\left(d,b\right)=1$.

For the first substitution indicator (FR3; number of dams in the floodplain and within 4km downstream; Table 2), alternatives a, c, and d had the same indicator values (3 dams), whereas there are no dams downstream from b (Table 3). Because fewer downstream dams theoretically indicates a higher value, alternative b is clearly better than the others. The WRWC chose not to consider more complete information about the dams downstream from each alternative and compared the alternatives for this indicator using the insensitive (type I) preference function (Fig. 3) with no specification of a threshold parameter (Table 3). This means that alternative b was strictly preferred to the other alternatives and the other alternatives were indifferent to each other.

For the second substitution indicator (FR4; percent area of wetlands within 200m; Table 2), the differences in indicator values for all alternatives were too close to judge that one alternative was better than another based on the potential imprecision and variability in these point estimates (Table 3): $x_{FR4}\left(a\right)=5.63$, $x_{FR4}\left(b\right)=4.04$, $x_{FR4}\left(c\right)=5.56$, and $x_{FR4}\left(d\right)=5.38$. Therefore, the WRWC chose to count those comparisons as equal by assigning an indifference (type II) preference function (Fig. 3) with indifference parameter q = 5 (Table 3).

In a similar manner to that described above, we worked with the WRWC to assign preference functions to all other indicators (Table 3). Although we could have performed a sensitivity analysis on the types of preference functions and threshold parameters (e.g., Martin et al., 2015), the WRWC were comfortable in defending these preferences in cases in which they had the opportunity to implement restoration. Therefore, they did not see the need for such a sensitivity analysis. We then computed the preference functions for every paired comparison of alternatives in the multidimensional dataset (Table 3). Using the PROMETHEE method, we computed a weighted global preference function $\pi \left(a,b\right)$ as a weighted sum of these calculations. This provides a measure of the strength of evidence that one alternative outranks another, over all indicators:

$$\pi \left(a,b\right)=\sum w_j{P}_j\left(a,b\right)$$ (3)

for all indicators $j=1,\dots ,24$, alternatives $a,b,c,d\in A$, where $\sum w_j=1$.

We arranged the weighted global preference function values for each pairwise comparison in a square table with rows and columns $A\times A$ (Table 4). The table depicts a set of numbers related to decision maker preferences, which are used to identify two different summations of strength of evidence that an alternative is preferred to others, referred to as outranking flow relationships. These are calculated for each alternative by summing each row and column. The positive outranking flow value ${\varphi }^{+}$ quantifies the extent to which a single alternative $a$ outranks all others $z$, whereas the negative outranking flow value ${\varphi }^{-}$ quantifies the extent to which a single alternative $a$ is outranked by all others $z$:

$${\varphi }^{+}\left(a\right)=\sum _{zϵA}\pi \left(a,z\right)$$ (4)

$${\varphi }^{-}\left(a\right)=\sum _{zϵA}\pi \left(z,a\right)$$ (5)

for all alternatives $a,b,c,d\in A$, where z refers to all other alternatives being compared to a single alternative. In our study context, ${\varphi }^{+}$ denotes the WRWC’s strength of preference for one alternative’s ability to maximize the performance of ES compared to all other alternatives. Likewise, ${\varphi }^{-}$ denotes the WRWC’s strength of preference for all other alternatives’ ability to maximize the performance of ES as compared to a single alternative. According to this logic, higher ${\varphi }^{+}$ values and lower ${\varphi }^{-}$ values represent better alternatives (Brans et al., 1986).

Table 4.

Square table showing global preference function calculations for the planning study using Eq. (3) and outranking flow values using Eq. (4,5,7) using equal weights.

	a	b	c	d	${\varphi }^{+}$	${\varphi }^{-}$	$\varphi$
a	0	0.19	0.08	0.10	0.38	1.05	−0.67
b	0.37	0	0.33	0.33	1.03	0.91	0.12
c	0.36	0.39	0	0.1	0.84	0.49	0.35
d	0.32	0.33	0.09	0	0.74	0.53	0.21

Note: numbers are rounded to hundredths

We performed variations of these calculations based on a series of informal meetings with the WRWC, where they selected different importance weights for each benefit indicator, using the same preference function relationships. In one meeting, we walked through the preference function types and assignments; in the next meeting we generated a prototype spreadsheet to illustrate the method; and in several subsequent meetings we walked through a more complete spreadsheet, directly applying weights to the indicators with sensitivity analysis according to several WRWC points of view, and discussed results. We and WRWC performed this informal case study to test how outranking methods might be used to evaluate ES tradeoffs that resulted from our previous work (Martin et al., 2018).

Weighting was based on specific planning contexts of interest to the WRWC, to identify alternatives that would be good choices for funding programs they are likely to encounter (e.g., funding to reduce risk of flooding of urban residents, to enhance recreational access, or to provide educational benefits). An initial scenario iteration used equal weights for each of the ES, social equity, and reliability indicators (Table 4) to illustrate obvious choices based on the preferences functions alone, referred to as within-indicator preferences. This scenario was contrasted with weighting scenarios that used a combination of importance weights across indicators to meet the needs of a planning context. We were directed by the WRWC to modify these weighting schemes in sub-iterations, to distinguish whether the results were sensitive to slight changes in indicator weights. A subset of results of the different weighting scenarios are discussed in Sections 3 and 4.

2.1.1. PROMETHEE I – partial ranking

PROMETHEE is based on three types of binary outranking relationships among the alternatives (Brans et al., 1986):

$$\begin{gathered} aPb\left(a outranks b\right)\begin{array}{c}if {\varphi }^{+}\left(a\right)>{\varphi }^{+}\left(b\right) and {\varphi }^{-}\left(a\right)<{\varphi }^{-}\left(b\right),\\ or {\varphi }^{+}\left(a\right)>{\varphi }^{+}\left(b\right) and {\varphi }^{-}\left(a\right)={\varphi }^{-}\left(b\right),\\ or {\varphi }^{+}\left(a\right)={\varphi }^{+}\left(b\right) and {\varphi }^{-}\left(a\right)<{\varphi }^{-}\left(b\right)\end{array} \\ aIb\left(a indifferent to b\right)if {\varphi }^{+}\left(a\right)={\varphi }^{+}\left(b\right) and {\varphi }^{-}\left(a\right)={\varphi }^{-}\left(b\right) \\ aRb\left(a and b incomparable\right)otherwise \end{gathered}$$ (6)

Several features of PROMETHEE I are noteworthy. The method does not guarantee a complete ranking relationship; some alternatives may remain incomparable. For this reason, we refer to results from PROMETHEE I as a partial ranking outcome. This point is critical because useful information about the alternatives could be obscured by combining metrics, as with PROMETHEE II (Section 2.1.2). Often a partial ranking outcome can be used to identify preferred alternatives without lumping information together for a complete ranking relationship (Brans et al., 1986).

In addition to this feature, the magnitudes of the outranking flow values do not influence the partial ranking outcome, which is a useful non-compensatory feature of the method. In an MCDA context, compensation refers to the extent to which undesirable indicator values are compensated by desirable values of other indicators (Bouyssou, 1986). Defining non-compensation, according to the axioms of Fishburn (1976), requires that the overall preference of an alternative a over b is not due to the magnitude of the differences between the within-indicator relationships of those alternatives; few methods for MCDA strictly conform to this conception (Bouyssou et al., 1997). That conception was revised to a simpler axiomatic foundation such that methods can maintain features on some continuum between possessing purely compensatory and purely non-compensatory features (Bouyssou et al., 1997). In Eq. (6), the global preference relationships of a over b are put into the same class of outranking relationship as global preference relationships of b over a; that is, the summed global preference relationships between all pairs of alternatives $a,b,c,d\in A$ are assigned one of three outcomes: aPb, aIb, aRb. This feature of PROMETHEE I, and most outranking methods in general, satisfies this non-compensatory property (Bouyssou et al., 1997).

2.1.2. PROMETHEE II – complete ranking

Decision makers may desire a complete ranking of the alternatives such that there are no instances of alternatives being incomparable. In these situations, PROMETHEE II establishes a net outranking flow $\varphi \left(a\right)$, which is the difference between positive and negative outranking flow values (Table 4):

$$\varphi \left(a\right)={\varphi }^{+}\left(a\right)-{\varphi }^{-}\left(a\right)$$ (7)

for all alternatives $a,b,c,d ϵ A$.

Two binary outranking relationships are possible using the net outranking flow values:

$$\begin{gathered} aPb if \varphi \left(a\right)>\varphi \left(b\right) \\ aIb if \varphi \left(a\right)=\varphi \left(b\right) \end{gathered}$$ (8)

We performed these calculations to yield a complete ranking outcome of the alternatives in order of maximizing $\varphi$.

Like standard aggregation techniques (e.g., value functions), PROMETHEE II provides a complete ranking of alternatives. However, the PROMETHEE methodology is based on comparing each alternative in turn to all others in the set, while standard aggregation techniques develop independent scores for each alternative and then rank them (Brans and Mareschal, 2005). We would expect rankings to differ based on these and other methodological assumptions (sensu Martin and Mazzotta, 2018). It is also important to note that combining the positive and negative outranking flow values into a single metric results in a loss of information on their individual values. Brans and Mareschal (2005) suggested considering results from both partial ranking (PROMETHEE I) and complete ranking (PROMETHEE II) so that any incomparability in partial ranking outcomes can be further clarified using complete ranking outcomes.

3. Results

A sub-set of results from the scenario analysis is given in Fig. 4. We were unable to distinguish between alternatives b and c with PROMETHEE I calculations using equal weights, although PROMETHEE II calculations with equal weights provided a complete ranking of all four alternatives (Fig. 4a). For all other calculations, a preferred alternative could be identified using both PROMETHEE I and PROMETHEE II.

Fig. 4.

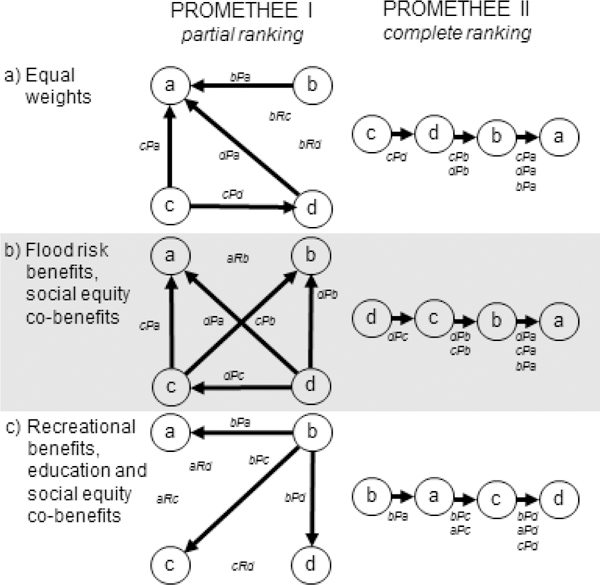
PROMETHEE results for candidate wetland restoration alternatives using different combinations of indicator weights. Arrow points from preferred alternative to non-preferred alternative, indicating a preference relationship (e.g.,$aPb$); no arrow indicates an incomparable relationship (e.g.,$aRb$). Panel a shows the iteration using equal weights as a baseline. Panel b shows an iteration where reducing flood risk and social equity were weighted, with greater weight assigned to flood risk benefit indicators than to the social equity benefit indicators. Panel c shows an iteration where recreation, education, and social equity were weighted, with greater weight assigned to recreation benefit indicators than to education and social equity benefit indicators. See the Supplementary material for indicator weights and calculations.

In each iteration of PROMETHEE I, there were incomparable alternatives (aRb), although many scenarios still allowed us to select a preferred alternative. Only strict preference relationships (aPb) were encountered using PROMETHEE II. When the WRWC chose a scenario that weighted flood risk and social equity, with more weight on flood risk as a benefit and less weight on social equity (all other indicators given zero weight), alternative d was clearly preferred for planning restoration, using both methods (Fig. 4b; Supplementary material). The results of this weighting scenario are likely to influence which sites the WRWC will choose to implement stormwater management projects in the future. Similarly, in a scenario focusing on recreation, education, and social equity, by putting more weight on recreation and less weight on education and social equity (all other indicators given zero weight), alternative b is clearly preferred for planning restoration (Fig. 4c). The results of this weighting scenario are likely to influence which alternatives the WRWC will use to support community projects near or in the city of Providence. Although alternatives b and d are preferred in two of the weighting scenarios, they are incomparable according to the partial ranking outcome using equal weights (Fig. 4a).

4. Discussion

We used the planning study with the WRWC to test the application of MCDA methods for ES assessment. Applying PROMETHEE facilitated the comparison of candidate wetland restoration alternatives and their benefit indicator values in a more detailed way than our previous use of additive aggregation techniques. The results were easier to explain to our partners than our previous work, which scored and aggregated the indicator values to a common scale (Martin et al., 2018). We determined that screening the 65 candidate sites using additive aggregation was useful to sort through a large number of alternatives and eliminate less valuable ones, but the WRWC acknowledged the benefit of comparing the actual indicator values using preference functions on a reduced number of sites (Table 3) to determine which comparisons were significant and which were not. It is important to note, however, that decision makers who use preference functions and assign discriminating types of thresholds will likely require decision aides, or experts who have built trust with decision makers and can work in close collaboration to inform them about ways to address the imperfect knowledge of ES outcomes, taking into account the way that the outcomes were developed and may perform after they have been implemented, for decision making purposes (Roy et al., 2014).

The results provided our partners with additional information they found helpful in evaluating the alternatives. For instance, we could suggest that, based on within-indicator preferences (using preference functions) and across-indicator preferences (using weights), the WRWC would not be taking a risk if they eliminated alternative a from further consideration because it is outranked by other alternatives in most scenario iterations (Fig. 4). Analytically, this alternative had very high negative outranking flow values ${\varphi }^{-}$ in most scenario iterations and negative net outranking flow values $\varphi$ in all scenario iterations (Table 4; Supplementary material), meaning that there is good strength of evidence that alternatives b, c, and d outrank a given the WRWC’s preferences on the indicator values. If the WRWC wanted to equally balance all ES indicators rather than placing more importance on specific ES (using equal weights), then they could be taking a risk if they eliminated alternative b because it is incomparable to c based on strength of evidence that alternative b outranks the other alternatives but also strength of evidence that alternative d is not outranked by the other alternatives, over all indicator values (Table 4). This result occurred in comparisons among many alternatives in other scenario iterations.

These examples point to a more intuitive assessment of choices among management alternatives using outranking methods. PROMETHEE allowed us to explicitly compare the indicator values as expressions of decision maker preferences, and the methods were beneficial to construct the WRWC’s point of view and create meaningful results, rather than using scoring and aggregation methods to discover results (Roy, 1990).

The partial ranking outcome using equal weights shows that alternatives c and b are incomparable; yet, the complete ranking outcome shows that those alternatives rank first and third, respectively (Fig. 4a). The differences in result between partial and complete ranking are due in part to the uncombined non-compensatory features of PROMETHEE I, which is related to how each method uses the same outranking flow calculations to evaluate the alternatives (Section 2.1.1). This is a general advantage of PROMETHEE I over some of the additive aggregation functions for MCDA (e.g., linear value functions), especially in situations where decision makers do not desire to offset poor ES outcomes by sufficiently large ES outcomes. The non-compensatory feature can be traced to decision maker preferences on actual ES outcomes, which makes PROMETHEE I a meaningful non-compensatory technique versus some non-linear additive aggregation functions that also have non-compensatory features (e.g., compromise programming; see Martin and Mazzotta, 2018). The choice of appropriate method will depend on decision makers, how comfortable they are with the methodological assumptions of each method, and how much effort they want to invest in incorporating within- and across-indicator preferences.

This evaluation appeared to be straightforward and understandable to our partners, with the exception of conveying the meaning of fuzzy preference function numbers of $0<P_j\left(a,b\right)<1$ for some of the indicator comparisons. We found that describing fuzzy preference functions was uncomplicated to the extent that they represented a preference of one alternative over another that is not “strict” or “indifferent,” but deciding what function to assign a “weak” or “strong” preference for a specific pairwise relationship was a challenge.

Although it makes sense to scale non-monetary values to comparable units (sensu additive aggregation techniques), establishing numerical representations of strength of evidence between alternatives requires additional effort and justification as to which comparisons should be assigned weakly preferable or strongly preferable numbers of $0<P_j\left(a,b\right)<1$. For these reasons, threshold parameters (p/q/σ; Fig. 3) are critical for analyzing and communicating the relationships between ES outcomes in a transparent way. We all agreed that incorporating some level of preference in the comparison of indicator values was needed, and WRWC decided that threshold parameters associated with a linear function (preference function types III and V; Fig. 3) was an appropriate assumption for the analysis. In some cases, however, it might be useful to conduct sensitivity analysis on the threshold parameters (e.g., Martin et al., 2015).

It is important to note that incorporating different ES weights into the method resulted in easily identifying preferred alternatives. In our experience, we find that using weights to emphasize the importance of particular ES can yield a similar ranking of alternatives, no matter which method for MCDA is used (additive aggregation or outranking methods) because weights tend to override the analytical features of the methods. Analysts may choose a method that could rank alternatives in the same way as other methods but without meaningful assumptions. In other words, the results may reflect across-indicator preferences but not within-indicator preferences, including the mathematical assumptions underlying the selected method, which have different implications for results (Martin and Mazzotta, 2018). We benefitted from maintaining trust and transparency with the WRWC, and our results were meaningful for their needs and in reflecting within- and across-indicator preferences.

7. Conclusions

Non-monetary valuation of ES is an emerging field. Incorporating non-monetary values into environmental decision making can allow for more comprehensive assessments, but addressing uncertainty in potential ES outcomes, among other sources of imperfect knowledge, is a challenge. Using outranking methods for MCDA that assign decision maker preferences to outcomes is a promising approach that contributes to addressing this challenge, alongside the more traditional statistical approaches to measurement and modeling uncertainty.

Outranking methods require analysts to aid decision makers in selecting parameters that determine the degree to which imperfect knowledge in outcome matters in choices among management alternatives. This allows for a more nuanced comparison of ES outcomes, where small changes can be parameterized to have less of an effect on results than more substantial changes. In this way, outranking methods can deal with imprecision and uncertainty in ES measures. They also allow for fuzzy preference orderings, incomparability between outcomes, and non-compensation between outcomes. While these features may make the decision process seemingly less straightforward, it provides a more realistic assessment and allows for better incorporation of decision makers’ knowledge and preferences for implementing environmental management.

Ecosystem service assessments such as the one described in this article may be contained within planning and decision-making frameworks (e.g., Gregory et al., 2012). The research and planning study described herein is part of such a process (Martin et al., 2018), which is of practical significance to environmental conservation and restoration worldwide (Schwartz et al., 2017). The outranking approach aims to dig deeper into what we are actually measuring and to allow decision makers to resolve a lack of information in a transparent and logical way. This can contribute to the growing body of work on evaluating ES using both monetary and non-monetary measures.