Personalized computational models of tissue-rearrangement in the scalp predict the mechanical stress signature of rotation flaps

Abstract

Objective:

To elucidate the mechanics of scalp rotation flaps through 3D imaging and computational modeling. Excessive tension near a wound or sutured region can delay wound healing or trigger complications. Measuring tension in the operating room is challenging, instead, non-invasive methods to improve surgical planning are needed.

Design:

Multi-view stereo (MVS) allows creation of 3D patient-specific geometries based on a set of photographs. The patient-specific 3D geometry is imported into a finite element (FE) platform to perform a virtual procedure. The simulation is compared with the clinical outcome. Additional simulations quantify the effect of individual flap parameters on the resulting tension distribution.

Participants:

Rotation flaps for reconstruction of scalp defects following melanoma resection in two cases are presented. Rotation flaps were designed without preoperative FE preparation.

Main Outcome Measure:

Tension distribution over the operated region.

Results:

The tension from FE shows peaks at the base and distal ends of the scalp rotation flap. The predicted geometry from the simulation aligns with postoperative photographs. Simulations exploring the flap design parameters show variation in the tension. Lower tensions were achieved when rotation was oriented with respect to skin tension lines (horizontal tissue fibers) and smaller rotation angles.

Conclusions:

Tension distribution following rotation of scalp flaps can be predicted through personalized FE simulations. Flaps can be designed to reduce tension using FE, which may greatly improve the reliability of scalp reconstruction in craniofacial surgery, critical in complex cases when scalp reconstruction is essential for coverage of hardware, implants, and/or bone graft.

Introduction

Over 34 million surgeries are performed in the US annually, each one requiring optimal wound healing (Aarabi et al., 2007; Sen et al., 2009). Tissue tension, also termed mechanical stress, is one of the factors contributing to wound complications costing more than four billion dollars annually (Wong, Levi, et al., 2012). Animal and in vitro studies have demonstrated that excessive mechanical stress leads to hypertrophic scarring, wound dehiscence, and tissue necrosis (Paterno et al., 2010; Wong, Longaker, et al., 2012). However, we are still unable to quantitatively predict skin stress and deformation during wound closure in routine clinical practice (Paul et al., 2016). Surgeons rely on tactile sensation and experience to estimate acceptable tension and soft tissue deformation at closure. Anticipating stress distribution of skin tissues based on preoperative information can thus help optimize individualized treatment plans. Planning in the head and neck region is challenging for large skin lesions because of the anatomical constraints, complex three-dimensional (3D) geometry, and unique surgical plan and skin mechanics for each patient. Hence, measuring stress distribution and the overall healing result is currently impossible in the head and neck. To bridge this gap, computational tools and simulation of virtual surgeries have been proposed as a powerful means to anticipate stress profiles over realistic skin geometries (Sifakis et al., 2009; Tepole, Gosain, et al., 2014).

Multiple aspects of craniofacial surgery also require understanding of soft tissue changes under uncertain conditions, such as complex craniofacial cases. A number of predictive methods using 3D imaging techniques have been described to estimate changes in soft tissue after craniofacial reconstruction (Abe et al., 2015; Lo et al., 2018), yet none of them calculate the soft tissue deformation under mechanical stress but rather approximate the shape of soft tissues with entirely geometric approaches.

We present two cases of skin cancer reconstruction on the scalp for which random pattern rotation flaps were used as advanced proof of concept to showcase our methodology for modeling soft tissue stresses. We chose to focus in small to moderate size scalp defects in order to identify fundamental principles that could subsequently be applied to reconstruction of more extensive scalp defects. For this study we restrict our attention to adjacent tissue transfer of random pattern flaps. Our methodology relies on obtaining 3D patient-specific geometries using multi-view stereo (MVS) (Hiep et al., 2009; Tepole et al., 2015), a flexible and powerful algorithm from computer vision that relies on feature matching across photographs taken from different angles. A commercial finite element (FE) analysis framework is used to perform the virtual procedure (Lee, Turin, et al., 2018). To investigate the effect of anisotropy, a fiber distribution field according to Cox’s lines is imposed (Cox, 1941). Relaxed skin tension lines (RSTL), the parameter with which clinicians are most familiar, are parallel to the underlying fiber orientation as delineated by Cox’s lines. We also investigate the flap design in idealized geometries in order to isolate the effect of individual flap parameters on the resulting stress distribution.

Materials and methods

Clinical cases of melanoma resection in the scalp

Two patients undergoing melanoma resection in the scalp volunteered to participate in this IRB-approved study. Patient 1 was a 73-year-old adult male, and patient 2 was a 62-year-old adult male. Both patients were scheduled for surgical removal of melanoma lesions in the scalp. On the day of surgery, photographs of the patient’s geometry were acquired preoperatively for 3D geometry reconstruction. A standard digital camera was used to collect approximately 30 photographs of the patients’ head and neck region from different angles, making sure that the patients remained static during photograph acquisition.

Intraoperatively, the melanoma lesions were excised together with surrounding tissue. In case 1, two regions were excised, one in the frontal scalp measuring approximately 4.8 cm in diameter, and a second region in the posterior scalp with a diameter of 2.5 cm. In case 2, a single lesion was excised, 3.6 cm in diameter, in the posterior scalp. Rotation flaps were performed in both scenarios to close the wounds.

In both cases the amount of skin removed prevented primarily closure of the wounds. In patient 1, the frontal defect was too large to attempt any tissue rearrangement strategy, and this wound was instead treated with a skin graft. The rotation flap in the posterior defect was closed without inducing unacceptably high tension for patient 1. In patient 2, the rotation flap was not fully sutured closed to prevent excessive tension in the skin.

Patient-specific computational models of tissue rearrangement

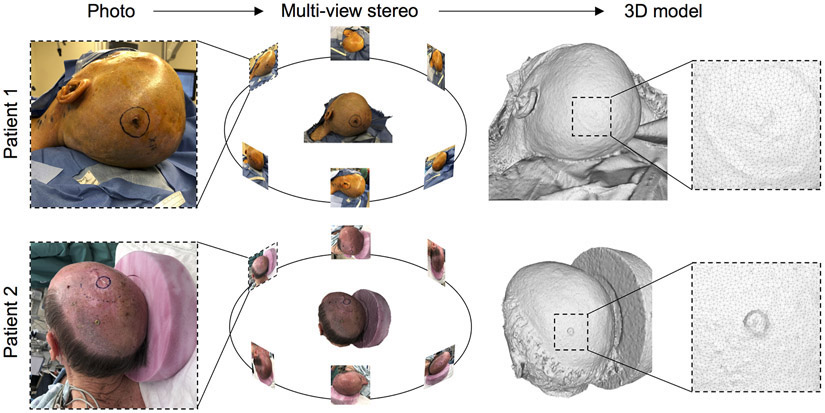
Preoperative photographs were processed with MVS to produce patient-specific geometries (Figure 1). MVS identifies common points in photographs taken from different angles and uses these correspondences to solve for the camera positions and orientations (Seitz et al., 2006). Then, an optimization routine expands the set of feature points to recreate a detailed 3D surface of the scene (Strecha et al., 2008).

Figure 1.

Preoperative, patient-specific 3D geometry reconstruction of two clinical cases of melanoma resection: 73-year-old adult male (patient 1) and 62-year-old adult male (patient 2) were photographed from different angles and MVS was used to extract the preoperative 3D scalp geometry.

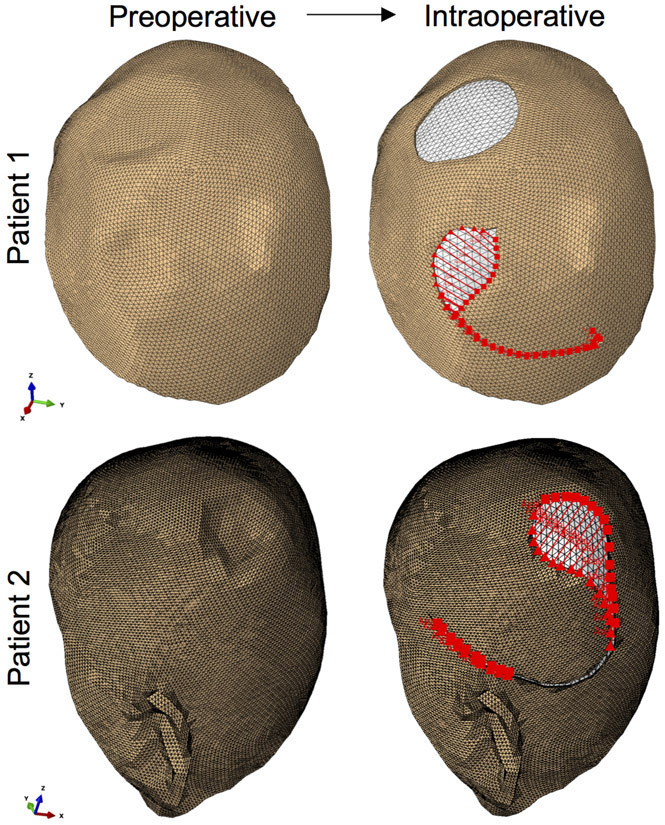
The preoperative models were used to perform virtual procedures according to the treatment plan of the patients (Figure 2). Namely, in patient 1, excision of the two lesions and the surrounding tissue was executed, and the incision pattern corresponding to a rotation flap for the posterior scalp defect was also created. For patient 2, a circular region in the posterior scalp was removed and a rotation flap designed.

Figure 2.

Preoperative patient-specific models were processed to virtually execute the treatment plan. Patient 1 underwent resection of two skin lesions, one posterior and one anterior, of 2.5 cm and 4.8 cm size respectively. A posterior 3.8 cm defect was removed in the scalp of patient 2. Sutures are imposed in a finite element framework to closely recreate the clinical setting.

Volume models were created from the surfaces by considering a thickness of 3 and 3.3 mm for patients 1 and 2 respectively. The final discretization of the model corresponding to patient 1 consisted of 35,466 tetrahedral elements and 12,278 nodes. The model for patient 2 was made of 75,282 elements and 25,394 nodes. In addition to modeling the skin, a skull geometry was generated to constraint the deformation and motion of the skin during the simulation. The 3D skull geometry was considered as a rigid body, i.e., no deformation of the bone was allowed.

Finite element analysis

Skin, like all soft connective tissues in the human body, shows nonlinear and anisotropic mechanical behavior dominated by the preferred orientation of collagen fibers in the dermis (Lanir and Fung, 1974; Tong and Fung, 1976; Jor et al., 2013). We incorporate this response into our model using the material model proposed by Gasser, Ogden and Holzapfel (GOH) (Holzapfel et al., 2000; Limbert, 2017). The FE simulations were run using the commercial software package Abaqus Standard (Dassault Systems, Waltham, MA).

Mechanical properties of skin change with age, gender, anatomical location, and even from one patient to another. Based on measurements of skin mechanics available in the literature, and considering the age and gender of both patients in this study, parameters for a 44 year old male from the literature were assigned (Ní Annaidh et al., 2012; Tonge, Atlan, et al., 2013; Tonge, Voo, et al., 2013). Unfortunately, the experimental datasets of skin mechanics in vivo are still limited and patient specific parameters were unavailable. Tissue anisotropy was also taken into consideration. Similarly to the choice of material properties, the fiber orientation, or RSTL, was assigned based on previous work which showed that Cox’s lines are a suitable indicator of anisotropy in the scalp (Cox, 1941).

The FE simulations solves the mechanical equilibrium problem corresponding to the manipulation of the tissue and closing of the defect. To closely match the clinical procedure, sutures are imposed by constraining the nodes on the opposite edges of the flap (red lines in Figure 2). During the virtual tissue rearrangement process, the skin is allowed to slide over the skull geometry assuming frictionless contact.

For validation of the FE model for the two cases shown here, we additionally replicated the measurements of scalp tension measured experimentally for simple advancement of scalp flaps under different undermining conditions (Raposio et al., 1998). Raposio et al. created Y-shaped incisions on the scalp of ten individuals. They then pulled on the scalp and measured the force needed to advance the edge of the flap a given distance. Thus, this dataset offers both deformation and force measurements of the scalp for a simple advancement scenario. We created a geometric model matching the experiment from Raposio et al. and used the material properties from our study. The simulations done without any calibration replicated the force measurements from Raposio et al., showing that the baseline material properties are representative of adult scalp tissue. Discrepancy of our simulation with respect to the data from Raposio et al. can be explained by patient variability. We calibrated the mechanical properties to match the experiments in order to show that, by tuning material parameters, the simulation can capture the force-deformation data very accurately (see Supplementary material). In the patient specific geometries shown here we did not have individual material properties. Therefore, showing that even without finely tuned parameters we can still capture the force-deformation response for advancement of the scalp as reported by Raposio et al., we are confident of the validity of the rotation flap results.

Rotation flap design optimization

In the two patient-specific scenarios, the design of the flap was based on the preoperative plan. However, one of the advantages of computer models is the ability to simulate alternative scenarios. We created a general simulation of a rotation flap with the parameters shown in Figure 3. We then investigated the sensitivity of the predicted tissue tension by varying the parameters of the flap design. We varied three parameters: the angle of rotation ϕ, the orientation of the flap with respect to the skin tension lines (RSTL) θ, and the normalized length of the back-cut c/r.

Figure 3.

General rotation flap design parameterized by three variables: rotation angle ϕ, orientation with respect to skin tension lines (RSTL) θ, and relative back-cut length c/r. The edge at the back-cut is referred to as proximal, while the edge that is rotated is referred to as distal.

Results

Patient specific models

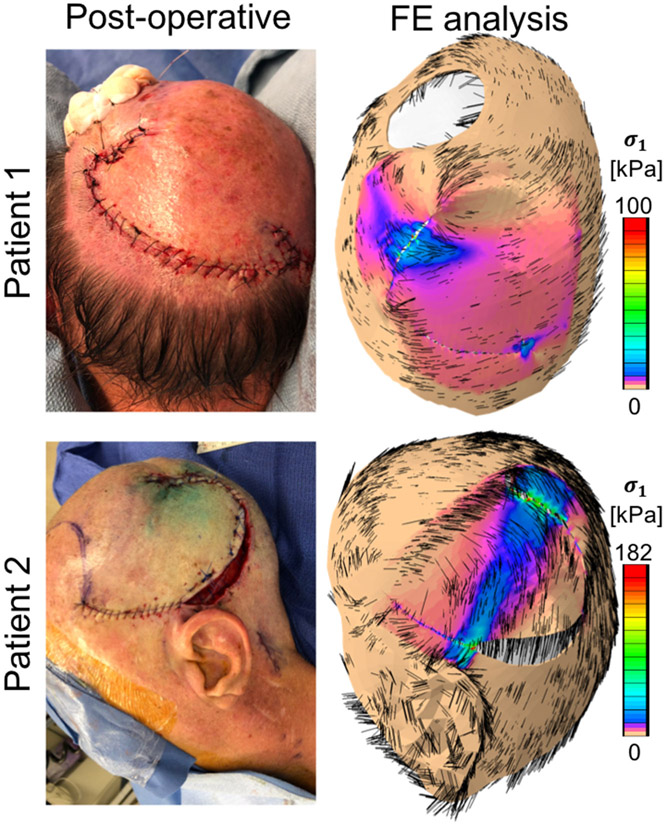
Figure 4 shows the comparison between the postoperative result obtained with the virtual model, and the real postoperative geometry. The contour plots on the FE model represent the mechanical stress distribution on the skin. In particular, here we show the maximum principal stress distribution, which is a metric of stress typically used in engineering design.

Figure 4.

Postoperative geometries for the two clinical cases presented in this study. The left column shows photographs taken immediately after the tissue rearrangement procedure. The results of the finite element (FE) simulation predict final geometries consistent with the real procedure as well as associated mechanical stress contours. For patient 1, a stress concentration occurs at the distal end, with maximum principal stress averaging 30 kPa. For patient 2, a band of high stress connects the proximal and distal regions.

The geometries predicted in Figure 4 align with the postoperative photographs. For patient 1, the stress profile is approximately 30 kPa near the distal end. Only a few points exceeded stress values of 100 kPa. There is also a small stress concentration at the base of the flap. The simulation for patient 2 shows higher stresses compared to patient 1. For patient 2, the distal end of the flap in patient 2 show stresses around 90 kPa, with a few points reaching 180 kPa. The reason for this difference can be attributed to the anatomical constraints present in the second case. The rotation flap for patient 2 was designed close to the left ear. As a consequence, skin was stretched more in order to close the flap of patient 2, inducing larger stress, and preventing closure along the entire flap contour, just as it occurred during the actual procedure. For comparison, previous work on a porcine model established that stresses of approximately 200 kPa led to hypertrophic scarring (Wong, Levi, et al., 2012). No similar data exists for human wounds.

Despite differences in defect size and patient geometry, the rotation flap in the patient geometries induced high stress at the distal end. In the second patient, this tension extended to the proximal end of the flap, forming a continuous band of high stress. In patient 1, on the other hand, while there was a stress concentration at the base of the flap, there was not a band of high tension across the entire flap.

General rotation flap model

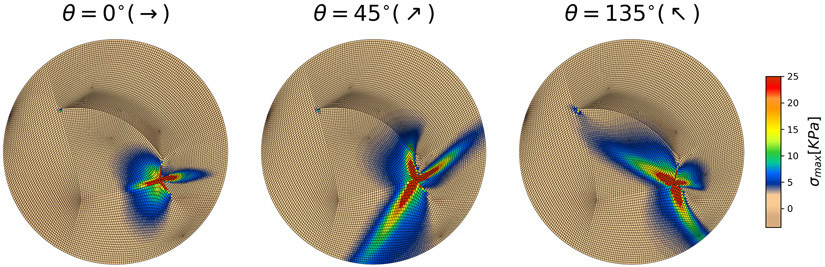
The general model depicted in Figure 3 is used to evaluate the influence of individual flap parameters on the mechanical stress distribution. For consistency, we refer to the edge adjacent to the backcut (c) as the proximal edge of the flap, and the edge towards the defect into which the flap is to be rotated (r) as the distal edge of the flap (see Figure 3). Simulations with variation of all parameters are shown as Supplementary material. Based on our simulations, we identified the orientation of the flap with respect to the skin tension lines to be the most important choice during flap design. Therefore, Figure 5 shows three simulations of the general rotation flap for three flap orientations θ = 0°, 45°, 135° with respect to the direction of skin tension lines (anisotropy). In all cases we see a stress concentration at the proximal edge of the flap, with a band of high stress aligned with the fiber orientation. These results suggest that, in an ideal setting, the rotation flap should not lead to high stress at the distal edge. Instead, higher stresses are expected at the proximal edge of the flap. However, if the skin tension lines extend across the flap, from the proximal edge to the distal edge, a band of high stress can connect the two ends. Comparison between the ideal flap design and the patient-specific simulations also underscores the importance of anatomical constraints in the patient cases. Based on the simulations shown in Figure 5 and the supplementary information Figures S3, S4, S5, orientation the flap such that the tension lines are horizontal with respect to the rotation, θ = 0°, and designing the flap with the smallest angle of rotation, ϕ = 30° in this case, leads to the smallest tension.

Figure 5.

General flap simulations show that flap orientation with respect to the relaxed skin tension lines (RSTL; anisotropy direction) is the most important parameter. Depending on flap orientation there is either no stress at the distal end, or, in the worst-case scenario, a stress band can extend from the proximal to the distal end.

Discussion

The objective of this study was to create patient-specific FE models to anticipate tension distributions resulting from tissue rearrangement surgeries. The present study evaluated two cases with small-to-moderate size scalp defects to showcase application of finite element analysis to scalp reconstruction. This allowed us to analyze quantitatively the effect of flap orientation with respect to relaxed skin tension lines on the resulting stress distribution. In the future we wish to extend these principles to applications of more extensive scalp defects for which conventional non-anatomic techniques (e.g., back cutting, galeal scoring, interpolated flap designs) would be needed alongside distant tissue recruitment. Our purpose in this study is not to obviate the more conventional techniques for scalp advancement, but rather to understand fundamental flap biomechanics and optimize flap design even in the more intuitive cases using FE simulations. This study shows that FE can be used to minimize tension in the simple design by adjusting flap orientation with respect to RSTL, possibly reducing the need for additional non-anatomic techniques, and offers a stepping-stone to subsequently extend these methods to more extensive scalp defects. The conventional techniques mentioned as well as those described in the present study apply to random pattern flaps, which are very well-tolerated in the scalp due to excellent perfusion. In contrast, the design of axial pattern flaps based on the inclusion of identified axial blood vessels rather than simply minimizing tension for adjacent tissue transfer is a future area of research. We realize that axial pattern or distant flap transfer for scalp reconstruction would follow the vascular pattern of the respective flaps. Consideration of features such as vascular pattern into the FE model is possible and we have started work in that direction (Sree et al., 2019).

The models of two skin cancer patients were created based on the preoperative geometry captured via MVS. This computer vision technology relies only on a set of photographs taken with any standard digital camera. In the cases presented here, a smartphone camera was used. We have previously shown that MVS reconstruction induces small errors, less than 10% (Tepole, Gart, et al., 2014), and with an average of 2% (Tepole et al., 2016). Therefore, MVS offers a flexible and easy-to-use methodology to create accurate preoperative models of reconstructive surgery (Lee, Turin, et al., 2018). Alternatives include 3D cameras, which are becoming common in clinical practice (Camison et al., 2018; Lee, Vaca, et al., 2018).

The simulation of the tissue rearrangement step requires the definition of the skin’s material behavior. The lack of patient-specific material properties is certainly one limitation of the present study. The parameters used here were based on reports of skin mechanical properties available in the literature (Ní Annaidh et al., 2012; Tonge, Atlan, et al., 2013; Tonge, Voo, et al., 2013). However, material parameters are expected to vary with age, gender, and anatomical location (Luebberding et al., 2014). Therefore, measuring individual properties is essential to create truly patient-specific models. Fortunately, new technologies are being developed, which enable noninvasive measurement of skin mechanics in vivo (Weickenmeier et al., 2015; Müller et al., 2018). Even in the absence of patient-specific material properties, the predicted geometry from our simulations matched qualitatively the postoperative photographs. We also validated our FE model against experimental measurements of tension needed to advance skin in the scalp with different undermining (Supplementary material Figure S1). Our simulations showed that, due to the anatomical constraints in the second scenario, higher stresses were expected for patient 2 compared to patient 1. In fact, the rotation flap for patient 2 could not be fully sutured due to concerns that the tension on the skin was too high. Furthermore, the values of stress we computed align with what has been reported for porcine models of excisional wounds closed under tension (Gurtner et al., 2011; Wong, Levi, et al., 2012).

The most interesting finding from this study is the critical effect of anisotropy and anatomical constraints in the resulting mechanical stress pattern. We created simulations of a general rotation flap design and varied three parameters. We found that, in the ideal case, the rotation flap should not lead to high stress at the distal edge when the angle of rotation is small and the flap is oriented such that skin tension lines are horizontal with respect to the direction of rotation. Conversely, we saw that if the skin tension lines are aligned obliquely, a band of high stress can extend over the flap, towards the distal edge, potentially leading to complications. The ideal rotation flap simulations showcase the use of FE to optimize flap designs, but, at the same time, comparison with patient-specific cases revealed the importance of individual anatomical constraints. This information is essential to optimize outcomes of flap design in areas where high tension is anticipated, which is often seen in scalp reconstruction. Although techniques such as galeal scoring and wide undermining can also decrease final tissue tension (see also validation simulations in the Supplementary material Figure S1), orientation of the flap relative to tissue tension lines is a key parameter which is often overlooked during flap design. On table expansion can be utilized to further stretch the flap, and this technique could be incorporated through preoperative FE analysis of flap design. Pre-planning flap orientation with the aid of FE analysis can optimize the final reconstruction and extend the outcomes of traditional means for relaxing tissues during flap transfer.

These two cases of reconstruction after cancer resection demonstrate the workflow in the simplest setting – i.e. one layer of skin (ignoring galea) over a non-deformable surface (the calvarium). By incorporating the multiple planes of the face and their respective tissue qualities, we hope to apply these concepts to modeling soft tissue stress as applied to all areas of head and neck reconstruction. Reliable scalp reconstruction is essential for coverage of hardware, implants, and/or bone graft in craniofacial surgery, and by facilitating preoperative planning for scalp advancement, significant complications could be avoided.

Conclusions

Mechanical stress profiles over patient-specific geometries can be achieved through personalized FE simulations. Furthermore, simulations of defects treated with rotation flaps show that smaller rotation angles and orienting the flap such that the skin tension lines are horizontal with respect to the flap leads to the lowest tension. Such applications of FE models could significantly improve outcomes of scalp reconstruction. Our analysis shows that flap orientation with respect to skin tension lines and anatomical constraints are crucial to minimize excessive tension.