Genetic architecture and adaptation of flowering time among environments

Summary

• The genetic basis of flowering time changes across environments, and pleiotropy may limit adaptive evolution of populations in response to local conditions. However, little is known about how genetic architecture changes among environments.

• We used genome-wide association studies (GWAS) in Boechera stricta (Graham) Al-Shehbaz, a relative of Arabidopsis, to examine flowering variation among environments and associations with climate conditions in home environments. Also, we used molecular population genetics to search for evidence of historical natural selection.

• GWAS found 47 significant quantitative trait loci (QTLs) that influence flowering time in one or more environments, control plastic changes in phenology between experiments, or show associations with climate in sites of origin. Genetic architecture of flowering varied substantially among environments. We found that some pairs of QTLs showed similar patterns of pleiotropy across environments. A large-effect QTL showed molecular signatures of adaptive evolution and is associated with climate in home environments. The derived allele at this locus causes later flowering and predominates in sites with greater water availability.

• This work shows that GWAS of climate associations and ecologically important traits across diverse environments can be combined with molecular signatures of natural selection to elucidate ecological genetics of adaptive evolution.

Plain Language Summary:

Plant traits change among environments, but the genetic basis of these changes are poorly understood. We identify genetic polymorphisms associated with flowering time and local climates, combining this with molecular evidence of adaptative evolution.

Introduction

Genetic architecture refers to the polymorphic genes that influence phenotypic variation, their frequencies, the magnitude of their allelic effects, and their pleiotropic impact on other traits and on trait expression in different environments (Barghi et al., 2020). While genetic control of most ecologically important traits is highly polygenic (Barghi et al., 2020), some large-effect polymorphisms may influence complex phenotypes, especially for traits closely connected to physiology or development (e.g., Kettunen et al., 2012; Prasad et al., 2012). Large-effect polymorphisms may have deleterious pleiotropic effects that limit their adaptive potential (Orr, 2005). Because environments are spatially and temporally heterogeneous, pleiotropic genetic architecture in different environments may constrain adaptive evolution, and alleles with fewer pleiotropic effects across environments may be favored (Orr, 2000; Hansen & Houle, 2008; Josephs, 2018).

Plasticity occurs when average trait expression of a genotype differs from one environment to another (Des Marais et al., 2013). Plasticity may evolve (Gomulkiewicz & Kirkpatrick, 1992; Gage et al., 2017), and it may be adaptive or non-adaptive (Ghalambor et al., 2015; Wagner & Mitchell-Olds, 2018; Kelly, 2019). To understand the role of plasticity in adaptive evolution, more information is needed on the genetic mechanisms that influence plastic expression of traits in lab and field (Des Marais et al., 2013; Sommer, 2020).

Genotype-environment associations occur when climate in the home location is correlated with plant traits expressed under common garden conditions. For example, environments with summer drought might be inhabited by genotypes that flower early, but accessions from habitats with abundant rainfall might delay flowering and accumulate more resources during the growing season. Such patterns suggest a history of adaptive evolution by natural selection (Mitchell-Olds & Schmitt, 2006). Studies of genotype-environment association can provide several insights. At the level of complex traits, we can infer heritabilities and genetic correlations, as well as genotype-by-environment interaction (GxE) among different environments (Falconer & Mackay, 1996). In addition, genome-wide association studies identify some of the loci contributing to trait variation within and among environments. In some natural plant populations QTLs may identify specific genes or candidate loci responsible for complex trait variation (Troth et al., 2018; Chhetri et al., 2019). GWAS across several environments can identify specific genes (or a handful of candidates) responsible for interactions between QTLs and environments.

Flowering time is a complex trait that is well-understood at the molecular level (Leal Valentim et al., 2015; Grimm et al., 2017; Sasaki et al., 2018; Zan & Carlborg, 2019), providing an experimentally tractable context for questions in evolutionary ecology. Age at reproduction often experiences natural selection in the wild (Brachi et al., 2010; Wadgymar et al., 2017; Troth et al., 2018), and flowering time shows plastic changes among environments (Weinig et al., 2002; Brachi et al., 2010; Anderson & Gezon, 2015; Cho et al., 2017; Guo et al., 2020; Yan et al., 2020). Local adaptation occurs when genotypes have higher fitness in their original environments and lower fitness elsewhere (Kawecki & Ebert, 2004). Flowering time can reflect local adaptation associated with elevation (Kooyers et al., 2015; Vidigal et al., 2016; Wadgymar et al., 2017), latitude (Ågren et al., 2017), and other environmental characteristics.

When plant populations are adapted to local environments, the causal polymorphisms may be associated with temperature, precipitation, or other aspects of climate. In some cases GWAS may identify associations between climate and responsible genes or single nucleotide polymorphisms (SNPs) (Romero Navarro et al., 2017; Vasseur et al., 2018; Ferrero-Serrano & Assmann, 2019). Here we use GWAS in Boechera stricta, a native, perennial relative of Arabidopsis thaliana, to ask three questions: (1) How does genetic architecture of flowering time vary among environments? (2) Are flowering QTLs associated with climate in their home environments? (3) Is there population genetic evidence of adaptive evolution at flowering time QTLs?

Materials and Methods

Study Species

Boechera stricta (Graham) Al-Shehbaz (Brassicaceae) is a close relative of Arabidopsis and Capsella (Huang et al., 2016), and is predominantly self-pollinating (F_IS = 0.9 and F_IT = 0.9) (Song et al., 2006). It is a short-lived perennial (Rushworth et al., 2011) native to relatively undisturbed sites in western North America (Anderson et al., 2010). B. stricta shows local adaptation to elevation gradients (Anderson et al., 2015) and historical climates (Anderson & Wadgymar, 2020). In the field, B. stricta displays substantial phenotypic plasticity in age at first flowering in response to temperature, elevation, snow pack, as well as the length of winter and the arrival time of spring (Anderson & Gezon, 2015; Wadgymar et al., 2018). Selection on flowering time may show tradeoffs between viability and fecundity selection (Wadgymar et al., 2017). In a reciprocal transplant between Colorado and Idaho, Anderson et al. (2010) found selection for earlier flowering, and alleles at the nFT (near-FT) QTL showed local adaptation, with higher rates of flowering in the home environments. Field experiments have documented GxE and plasticity in nature (Anderson & Gezon, 2015; Wagner & Mitchell-Olds, 2018).

In B. stricta, whole-genome resequencing data is available from 517 inbred genotypes (Wang et al., 2019a). Three genomic regions comprising about 10% of the genome show elevated polymorphism and enrichment for immune-related genes, indicating long-term balancing selection (Wang et al., 2019a). Here, these regions are excluded from population genetic analyses. B. stricta is subdivided into four genetically and geographically differentiated groups (COL, UTA, NOR, and WES), as well as some admixed (ADM) genotypes (Supporting Information Fig. S1). Here, “PopGroup” refers to these categorical genetic groups. Linkage disequilibrium (LD) in B. stricta COL and UTA groups decays within 50kb, but is more extensive in NOR and WES (Wang et al., 2019a). Due to its geographic distribution, Pleistocene history (Lee et al., 2017; Wang et al., 2019a), and perennial life cycle, we hypothesized that some polymorphic loci might be locally adapted to climate in their sites of origin. Therefore, we used GWAS to search for genetic association with climate metrics in home environments.

We performed 11 experiments to examine genetic variation for flowering time changes among environments in B. stricta (Tables 1 and 2). One experiment (B2) had short days and showed little flowering, so ten experiments are reported. These experiments were conducted in growth chambers (“Phytotron”) or glasshouse, with different container size, soil type, nutrient application, water availability, day length, temperature, length of cold vernalization period, and the number of cold vernalization periods (“winters”). Table 1 details these conditions.

Table 1:

Growth conditions for 10 flowering time experiments with the Boechera stricta GWAS population. Cold vernalization ("winter") was applied to all experiments before initiation of flowering. Experiments B1, B2, and B3 had a single flowering season, and their surviving plants had a second vernalization period, and a second flowering season (experiments B4, B5, and B6, respectively.)

Experiment	Num replicates	Weeks vern	Num winters	Location	Containers	Soil type	Fertilizer	Water avail	Day length	Temperature (day/night)
E1	10	8	1	GH	48-cell flats	MMF4*	normal	water daily	16h	21C
W1	5	6	1	GH	small cone-tainers	Fafard 4P	normal	water daily	16h	21C
W2	6	6	1	GH	96-cell flats	Fafard 4P	restricted	water daily	16h	21C
W3	5	6	1	GH	48-cell flats	Fritted clay	normal	2six day drt	16h	21C
W4	6	6	1	GH	48-cell flats	Fafard 4P	normal	2six day drt	16h	21C
B1	5	6	1	Phy	96-cell flats	MMF4	normal	water daily	16h	18C/14C
B2	5	6	1	Phy	96-cell flats	MMF4	normal	water daily	12h	18C/14C
B3	5	6	1	Phy	96-cell flats	MMF4	normal	water daily	16h	22C/18C
B4	5	6	2	GH	96-cell flats	MMF4	normal	water daily	16h	21C
B5	5	6	2	GH	96-cell flats	MMF4	normal	water daily	16h	21C
B6	5	6	2	GH	96-cell flats	MMF4	normal	water daily	16h	21C

^*Abbreviations: MMF4 = Metro-Mix 200 + Fafard 4P; vern = vernalization; Num winters = Number of winters; GH = Glasshouse; Phy = Phytotron; 2six day drt = Two six day drought cycles; Water avail = Water availability

Table 2:

Size of experiments, mean flowering age, and broad sense heritability in Boechera stricta. Means are reported +/− standard error.

Experiment	Number of genotypes flowered	Number of plants flowered	Mean flowering age	Heritability
E1	380	3,220	20.0 +/− 0.06	77.0%
W1	450	1,475	33.6 +/− 0.3	47.0%
W2	384	1,673	22.8 +/− 0.12	50.9%
W3	428	1,167	26.1 +/− 0.35	59.0%
W4	356	1,303	25.5 +/− 0.22	64.4%
B1	384	1,561	29.9 +/− 0.16	71.1%
B2	--	--	--	--
B3	390	1,536	31.8 +/− 0.22	64.9%
B4	430	2,117	21.5 +/− 0.09	59.3%
B5	432	2,208	19.5 +/− 0.08	59.3%
B6	424	1,982	22.0 +/− 0.08	59.9%

Experiment B2 had little flowering and was not analyzed.

Plant Cultivation

We used 488 sequenced B. stricta inbred line genotypes (Wang et al., 2019a) from across the western USA, grown in a range of glasshouse or growth chamber environments that alter factors known to influence plant growth and flowering (vernalization, number of growing seasons, soil type, planting density, container size, nutrients, water availability, day length, and temperature). We sought to produce a diverse range of environmental challenges, rather than to dissect the consequences of particular environmental contrasts, as we have done previously (Anderson et al., 2010; Lee et al., 2015). In total, these 10 experiments vary eight environmental factors with a total of 22 levels. The number of genotypes analyzed in each experiment varies slightly depending on seed availability. These experiments used either 5, 6, or 10 replicates per genotype (Table 1). Prior to experimentation, all genotypes were grown in the greenhouse for at least one generation to minimize maternal effects. Seeds were stratified in Petri dishes with damp filter paper, and then moved to a dark room at 4°C for 8 days, and finally placed in a growth chamber for 6 days (day length: 16h; night length: 8h; humidity: 70%; temperature: 30°C). Germinated seedlings were randomized into soil-filled containers (Table 1). Different experiments used flats 27.8 cm × 54.5 cm × 6.2 cm deep (Hummert International, Earth City, MO, USA) with either 48 or 96 cells, or else used cone-tainers from Stuewe and Sons, Tangent, OR, USA. Cone-tainers were 2.5 cm diameter × 16 cm deep in racks, with 1,076 plants per m². After watering, flats and racks were covered with clear plastic domes for 9 days to maintain humidity. Seedlings were watered and fertilized regularly until rosettes reached about 6 cm in diameter. Cold vernalization entailed 4°C, 40% relative humidity (RH), 12h day length for either 6 or 8 weeks.

We performed five experiments (E1, W1, W2, W3, W4) in the greenhouse at Duke University (day length: 16h; night length: 8h; temperature: 21°C). Three other experiments (B1, B2, B3) were grown in the phytotron (Table 1) with day length and temperatures as follows: 18h day length (B1: 18°C, B3: 14°C) and 6h night length (B1: 14°C, B3:18°C). After flowering ended, these three experiments were vernalized for a second “winter” for 6 weeks and labeled B4, B5 and B6, then moved to the greenhouse for a second flowering season (Table 1).

Soils used include Metro-Mix 200, Fafard 4P, fritted clay, with fertilization applied at 300 ppm of N (J. R. Peters, Inc., Allentown, PA, USA) once per week. Experiment W2 was subject to fertilizer limitation, growing without fertilization until nutrient deprivation appeared extreme. Experiments were either watered daily or subject to drought. Experiments W3 and W4 were subject to two sequential rounds of six days without water, separated by 1 day of watering to saturation. Experiment W3 was grown in fritted clay potting medium (Profile Porous Ceramic Greens Grade, Profile Products, Buffalo Grove, IL, USA), which releases water more evenly than potting soil. When powdery mildew occurred in the greenhouse bay, Biofungicide 3336F (Cleary Chemical Corp., Dayton, NJ, USA) was applied following manufacturer instructions. Age at first flowering was calculated as the number of days to flowering after removal from cold vernalization. First flowering was scored at least three times weekly, and more frequently during the peak stage of flowering.

Analysis of phenotypic data

We grew plants in randomized complete blocks designs, using log10 transformed age at first flowering (LogFlrAge) to improve normality. For experimental tractability, we used five sets in the largest experiment (E1), each planted on a different day, within a single week. Blocks were nested within sets. Analyses included random effects for genotype, block, and set (or rack). Analyses were performed in R version 3.6.2 (R_Core_Team, 2017) using restricted maximum-likelihood (REML) in lme4 and lmerTest (Kuznetsova et al., 2017). Differences between environments were modeled as fixed effects using type III sums of squares in lmerTest. Using function ranef in lmerTest, we estimated best linear unbiased predictors (BLUPs) to summarize age at first flower of each genotype. Broad sense heritability was estimated from the ratio of variance components due to genotype (accession) and total variation. This genetic component combines variation due to population groups and genotypes within groups. Using package GGally in R, genetic correlations were estimated as the cross-environment correlation between BLUPs, since there is no shared environmental covariance between experiments (Falconer & Mackay, 1996).

Genome-wide Association Studies

For GWAS analysis of 10 experiments we used EMMAX software (Kang et al., 2010). We used PLINK v1.90b3n 64-bit software (Purcell et al., 2007) to create the genotype file, and emmax-kin to estimate the SNP-based kinship matrix. We extracted genotypes of 488 individuals from Wang et al. (2019b), imputed and phased using Beagle v4.1 (Browning & Browning, 2013) with default settings. Results from EMMAX were summarized by Manhattan plots using CMplot (https://github.com/YinLiLin/CMplot) or custom scripts in R. We used 658,414 SNPs with minor allele frequency (MAF) > 0.05, and a conservative genome-wide Bonferroni threshold for statistical significance at −Log10(P) = 8.0. For significant flowering time QTLs in these environments, we computed a genotype matrix containing the most significant SNP for each flowering time QTL. In addition, we used the congeneric Boechera retrofracta genome (Kliver et al., 2018) to infer the ancestral allele at these SNPs. For GWAS of plasticity between environments we analyzed z_i = x_i - y_i , the difference between flowering time BLUPs of the i-th genotype in two environments. We examined six pairs of environments: E1W3 (with the largest sample size and the most divergent environment, respectively). Then, excluding the divergent W3 environment, we analyzed five additional environment pairs with the lowest correlations: B1W1, B1W2, B4W4, W1W2, and W2E1.

Using package raster (Fick & Hijmans, 2017) in R 3.6.2 we downloaded 19 abiotic variables for our genotype collection sites using 2.5 minutes of degree resolution (www.worldclim.org/data/bioclim.html). Based on the zero-centered, standardized correlation matrix, we used R to perform principal component analysis (PCA) on these climate variables to explore the association between abiotic environment and flowering time. Two separate principal component analyses are referred to as “flowering PCs” for principal components across the 10 flowering environments (Supporting Information Table S1), and “climate PCs” for principal components of 19 climate metrics (Supporting Information Table S2). Five climate PC scores were treated as traits of each genotype and analyzed in GWAS. To avoid models with many predictor variables, we used a sequential approach to reduce multicollinearity of gene-climate analyses (Rushworth et al., 2018), while simultaneously controlling for population structure. We analyzed BLUPs for log10 flowering age using the W1 experiment, which has data from the largest number of locations. First, we considered models with PopGroup, latitude, and elevation, and then with five climate PCs. Next, we excluded PC5 (weakly correlated with all climate metrics) and non-significant predictors. Finally, we predicted flowering time based on the leading Bioclim metrics that load on significant climate PCs (e.g., Yoder et al., 2014; Rushworth et al., 2018). Such analyses using many correlated predictor variables provide a first approximation to causal relationships, which must be verified by further research.

Genetic Architecture

EMMAX estimates the effect size of each QTL in each environment. We did not analyze effect sizes of qtl3.1, qtl3.2, and qtl4.1 since their MAF < 0.05 in some experiments. We report the magnitude of QTL effect sizes, making these experiments directly comparable. Also, we compared patterns of pleiotropy between QTLs by computing the cross-environment correlation of effect sizes for each pair of QTLs. This quantifies how a QTL with flowering effects in some environments may show patterns of pleiotropy similar to other QTLs. In addition, we asked whether results from these significant QTLs are representative for typical SNPs across the genome. We examined the top 100 SNPs that have largest effect sizes and data from at least six experiments. We computed pairwise correlations of effect sizes across environments for pairs of top SNPs, and compared the among-SNP correlations to the among-QTL correlations by randomization test. For a two-tailed P-value we compared the observed mean correlation among six QTLs (excluding qtl3.1, qtl3.2, and qtl4.1) to the distribution of correlations in 25,000 permuted samples of six SNPs.

Molecular Population Genetics:

We asked whether selection has influenced nucleotide variation near each QTL peak. Except for Extended Haplotype Homozygosity (EHH, Sabeti et al., 2002) and H12 (Garud et al., 2015), all selection analyses used un-imputed and un-phased data. For SNPs with MAF > 0.05 (Wang et al., 2019a) we quantified EHH that might surround a new, favored allele. By comparison to B. retrofracta we inferred the ancestral allele for seven QTL SNPs (qtl1.1, qtl2.1, qtl3.1, qtl3.2, qtl4.1, qtl6.2, and qtl7.2), and computed EHH using selscan v1.2.0a (Szpiech & Hernandez 2014) with default parameters. We also calculated linkage disequilibrium (LD) between each pair of SNPs in a 500 kb region centered on each QTL peak. Population genetic statistics were calculated within groups, or were not calculated if frequency of the minor or derived allele was low (MAF or DAF < 0.05; Supporting Information Table S3). LD, π, and H12 were calculated in COL for qtl1.1, qtl3.1, qtl3.2, qtl4.1, qtl6.1, qtl6.2 and qtl7.2, in WES for qtl7.1, and in COL and UTA for qtl2.1. EHH was calculated in the COL group for qtl1.1, qtl2.1, qtl3.1, qtl3.2, qtl4.1, qtl6.2, and qtl7.2), and in UTA for qtl2.1. The ancestral allele is unknown for qtl6.1 or qtl7.1, so EHH, Fst, and d_XY were not calculated.

We calculated π in 20 kb windows across the genome, estimating means and standard deviations of π for 200 kb regions centered on QTLs or genome-wide target SNPs (excluding balancing selection regions)(Wang et al., 2019a). In some windows π could not be calculated, so we use data from 4-10 windows for each 200kb QTL and target SNP region. H12 and H1/H2 were calculated for each SNP across the genome. Mean and standard deviation were estimated across all SNPs in QTL regions and intervals genome-wide. We calculated Fst and d_XY in 200kb windows centered on each target SNP. Genome-wide mean and standard deviation were computed based on 10,000 SNPs sampled genome-wide, each centered in a 200kb window.

For Fst and d_XY we compared divergence between haplotypes centered on the ancestral vs. derived peak SNP in a QTL region. These haplotypes may have diverged due to hitchhiking, and therefore may be more divergent than genomic regions surrounding neutral SNPs. We calculated Fst and d_XY between groups homozygous for the ancestral vs. derived allele when at least 10 homozygotes were available for each group. We calculated Fst and d_XY in COL for qtl1.1, qtl3.1, qtl3.2, qtl4.1, qtl6.2 and qtl7.2. We considered a ±100 kb window flanking the peak SNP, comparing Fst and d_XY for QTLs versus the distribution of ancestral-derived F_ST and d_XY values around 10,000 randomly chosen genome-wide SNPs matched for allele frequency (0.10 ≤ DAF ≤ 0.35). For each QTL we used one-tailed t-tests to ask whether Fst and d_XY for flowering QTL haplotypes showed higher ancestral-derived divergence than for 10,000 genome-wide SNP windows. For π, scaled π, H12, and H2/H1 we compared 100kb regions around the QTL peaks vs 10,000 genome-wide 100kb windows for these four statistics using the Wilcoxon test in R.

Data accessibility

We archived our data in Dryad Digital Repository (doi:10.5061/dryad.5tb2rbp3f).

Results

Quantitative genetics

Based on 18,242 flowering plants, we found high broad sense heritabilities (H²) of flowering time across experiments, as well as geographic variation in flowering phenology (Table 2, Fig. 1) and extensive GxE (e.g., Supporting Information Fig. S2). Flowering time showed positive genetic correlations among all environments (Supporting Information Fig. S3). Using a Bonferroni significance threshold, all pairwise correlations are individually significant (experiment-wide P < 0.0002). Even with substantial sample sizes (244 genotypes in common, each with ≥ 4 individuals), environments W2 and W3 showed the lowest correlation, r = 0.384. Finally, flowering of plants in their first versus second seasons (B1 and B3 versus B4 and B6, respectively) is similar to other pairwise correlations between experiments. The between-year genetic correlations r_{(B1, B4)} = 0.617 and r_{(B3, B6)} = 0.674 are near the overall mean of pairwise correlations (r = 0.604), and roughly midway within the total range (r = 0.384 - 0.819). Therefore, we treat these between-year pairs as statistically independent.

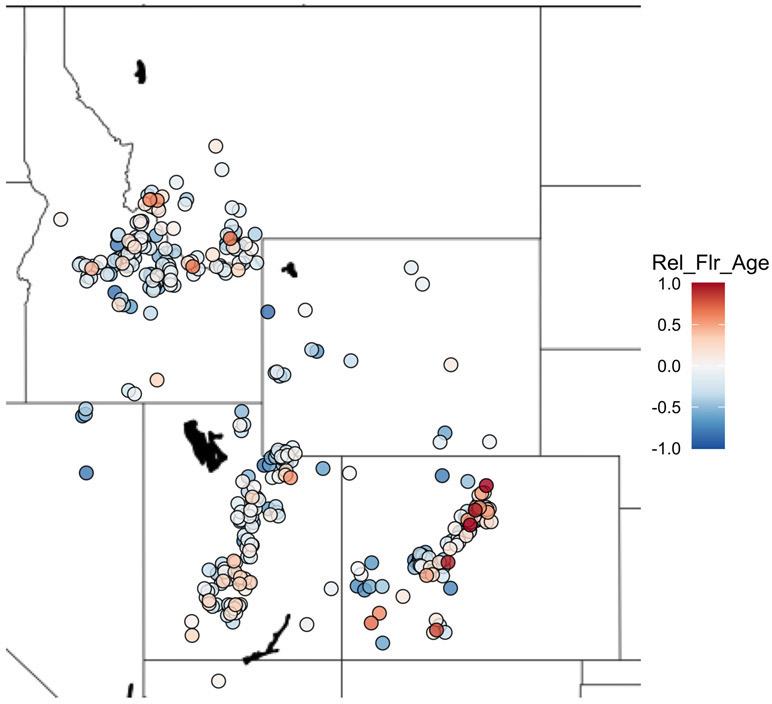
Fig. 1.

Flowering time for B. stricta genotypes in experiment W1. Geographic locations are shown with minor jitter to improve visibility. Relative flowering age is scaled from early (blue) to late (red). N = 401 genotypes. One early flowering mutant in Flowering Locus C (Lee et al., 2018) is not shown.

Flowering PC loadings are shown in Supporting Information Table S1. Five PCs summarize 88.7% of total variation. PC1 (67.2% of variance) is positively loaded on flowering time in all environments, PC2 (8.4% of variation) identifies a contrast between flowering times in W3 versus other environments, and PC3 (4.8% of variance) identifies a contrast between flowering times in W1 versus B1 and B4.

We used a biplot to summarize flowering time of principal components of individual genotypes among environments, as well as the environmental influences of each experiment on flowering time (Fig. 2). Flowering PC1 is highly correlated with effects of all environments except W3 (drought treatment in fritted clay), which has divergent effects on flowering time. Together, the PC1 and PC2 axes summarize 75.5% of genetic variance in flowering time.

Fig. 2.

BiPlot showing B. stricta flowering time across 10 environments. Principal components (PC1 and PC2) show genotype means in two orthogonal axes of greatest genetic variation in flowering time. Points indicate the average flowering phenotype of each accession in multivariate space. Arrows summarize the average flowering time in each environment. Arrows have been stretched 4X to improve visibility. Experiment W3 is labeled, and the remaining experiments are tightly clustered in the center right.

Genome-wide Association Studies

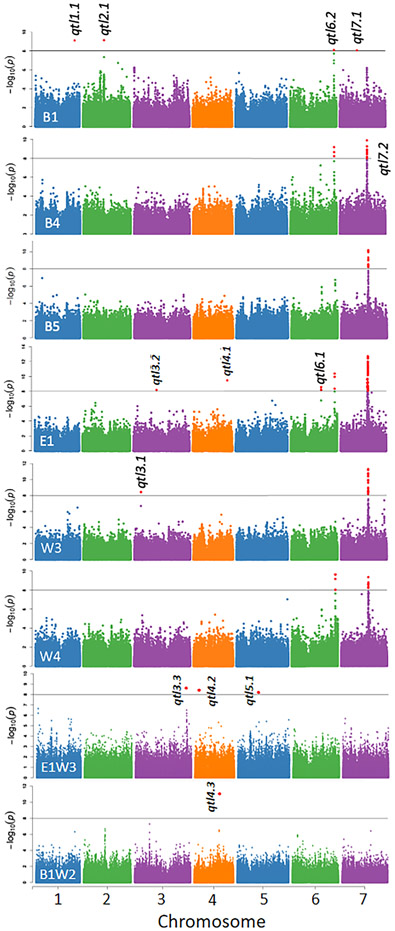
We found nine significant QTLs that influence flowering time (Fig. 3; Supporting Information Table S4) in at least one environment. Quantile plots were in accord with statistical expectation. Differences in flowering time between environments are controlled by four significant GxE QTLs that control plastic changes in flowering time between environment pairs E1W3 or B1W2 (Fig. 3). The remaining environments (B3, B6, W1, W2) and environment pairs (B4W4, B1W1, W2E1, W1W2) showed no significant peaks. Among 13 significant QTLs controlling flowering time or GxE between environments, eight QTL peaks (62%) are within 100 kb of known flowering time genes (Supporting Information Table S4) (Bouche et al., 2016). Most flowering QTLs showed narrow peaks of significant SNPs; only qtl7.2 showed a broad peak of significant SNPs that encompassed many annotated loci (Supporting Information Fig. S4).

Fig. 3.

Genome-Wide Association Study (GWAS) showing significant B. stricta Quantitative Trait Loci (QTLs) influencing flowering time across environments. Dots show significance level of each Single Nucleotide Polymorphism (SNP). Red dots exceed the Bonferroni significance threshold (horizontal line) at −log₁₀P = 8.0. Top six panels show significant flowering time QTLs. Panels are labeled by experiment (B1 to W4). Bottom two panels test for GxE, showing GWAS on the difference in flowering time between a pair of environments. These panels are labeled by the pair of environments compared (E1W3 and B1W2, respectively). GWAS analyses without significant QTLs are not shown.

Focusing on the genetically variable southern population groups (COL and UTA), we asked how much of the variation in flowering time is explained by significant QTLs. In our largest experiment (E1), 77% of flowering variation is under genetic control. Nine QTLs control 30% of total phenotypic variation, and 47% of trait variability reflects polygenic “background.”

Five significant flowering QTLs are close to candidate flowering genes (Supporting Information Table S4). qtl4.1: ATVOZ2 encodes a zinc finger transcription factor in Arabidopsis, regulating the transition between vegetative growth and flowering (Celesnik et al., 2013). TSF and JMJ14 are two separate flowering time genes very close to the most significant SNP for qtl7.2. Twin Sister of Flowering Locus T (TSF) is a paralog of FLOWERING LOCUS T (FT), which promotes the onset of flowering in Arabidopsis (Wickland & Hanzawa, 2015). Jumonji14 is a floral repressor (Lu et al., 2010) that also influences growth (Cattaneo et al., 2019). qtl6.2: candidate gene Terminal Flower 1 (TFL1) is a floral repressor interacting with FT to control meristem identity and flowering time (Hanzawa et al., 2005; Ahn et al., 2006; Wickland & Hanzawa, 2015) The remaining flowering time QTLs had no clear candidate genes.

Finally, although our sample size is close to other recent studies in ecological genetics (e.g., Exposito-Alonso et al., 2019), it is important to recognize stochastic variation among individual experiments, and reduced replication when we focus on the more polymorphic southern population groups. In order to infer general patterns regarding how genetic architecture changes across environments, larger experiments are needed.

Climatic influences on flowering time

Climate PC1 – PC5 explain 91.0% of climatic variation among the home environments of studied genotypes. Focusing on the loadings with largest absolute magnitudes for each axis, climate PC1 contrasts cool-wet vs. hot-dry locations. Climate PC2 is an indicator of continentality, loading on annual temperature range and winter temperature. Climate PC3 reflects high daily temperature fluctuations and low summer temperatures. Climate PC4 correlates with warmer summers and snowy winters, contrasting with cold winters and more summer rainfall. Finally, climate PC5 quantifies a complex mixture of climate metrics.

To examine correlations between flowering time of genotypes and climate in their home environments, we focused on LogFlrAge in Experiment W1, which has data from the largest number of locations. Flowering time in common garden is predicted by PopGroup, latitude and elevation at collection sites (all P < 0.004 by ANCOVA, Supporting Information Table S5a); earlier flowering genotypes come from more northerly and higher elevation sites. Among these climate PCs, PC2, PC4, and PC5 are significantly associated with flowering time (all P < 0.003 by ANCOVA, Supporting Information Table S5b). Finally, the leading climate metrics (Supporting Information Table S2) for PC2 and PC4 are significantly predicted by Bio7 (Temperature Annual Range, t = 8.18; df = 382; P = 0.0045) and Bio18 (Precipitation of Warmest Quarter, t = 19.06; df = 382; P = 1.60E-05); Bio6 (Min Temperature of Coldest Month) is marginally significant (t = 3.86; df = 382; P = 0.0502; Supporting Information Table S5c). Thus, in common garden, genotypes flower later from places with warmer winter temperatures, wider annual temperature range, and wetter summers.

We performed GWAS for climate PC1 – PC5 (Fig. 4). We found at least 34 significant QTL peaks, including 11 significant peaks associated with PC4 at the site of origin, and 21 significant peaks for PC2. Nineteen (56%) of these are within 100kb of known flowering genes (Supporting Information Table S6).

Fig. 4.

Genome-wide association with principal components (PC1-PC5) of abiotic climate (WorldClim data) at the sites of origin for each B. stricta accession. Dots show significance level of each Single Nucleotide Polymorphism (SNP). Red dots exceed the Bonferroni significance threshold (horizontal line) at −log₁₀P = 8.0. None of these climate Quantitative Trait Loci (QTLs) collocate with the nine flowering QTLs in Fig. 3.

Genetic variation for flowering time

We examined how nine flowering QTLs predict flowering time in environment E1 using ANOVA. Because WES and NOR populations showed little polymorphism at the SNPs underlying significant QTLs (Supporting Information Table S3), we used data from southern (COL and UTA) genotypes. Because B. stricta has low levels of heterozygosity (F_IS = 0.9 and F_IT = 0.9) (Schranz et al., 2005; Song et al., 2006), genotypes that are heterozygous for the minor allele (2.15% of total) were pooled with homozygotes for the minor allele. In experiment E1, heritability of flowering time was 77% (Table 2). Using PopGroup to control for population structure, these QTLs explain 39.5% of genetic variation for flowering time, and other polygenic variation accounts for 60.5% of genetic variance. The two largest QTLs (qtl6.2 and qtl7.2) explain 14.6% and 9.0% of genetic variation in flowering time, respectively. In this environment qtl6.2 has an effect size (between alternate homozygotes) of 1.29 phenotypic standard deviations and qtl7.2 has effect size of 1.43 standard deviations. Thus, both QTLs have large effects on flowering time, and their derived alleles delay flowering. Geographically, the derived alleles at these QTL SNPs are widely distributed in montane regions of Colorado and central Utah (Fig. 5; Supporting Information Fig. S5).

Fig. 5.

Geographic range of B. stricta qtl6.2 alleles. Shown are sites of origin for ancestral (red) and derived (blue) alleles. Genotypes from COL and UTA population groups are shown.

We tested whether these QTLs of large effect (qtl6.2 and qtl7.2) are associated with principal components of climate in home environments (Supporting Information Table S7). We found highly significant QTL-climate associations of both QTLs with climate PC4 (P < 0.004 by ANOVA) and a significant association for qtl7.2 with PC2 (F_1,222 = 4.09; P = 0.044). Climate PC4 shows highest loadings on Bio8 (mean temperature of wettest quarter) and Bio18 (precipitation of warmest quarter). For Bio8, we found no significant association with either QTL (t = 226; df = 222; P > 0.3). In contrast (Supporting Information Table S8), Bio18 showed highly significant association with qtl6.2. (t = 3.15, df = 222, P < 0.0018).

Genetic Architecture

We asked how genetic architecture of flowering time changes among environments, and thus whether genetic constraints may influence adaptive spatial and temporal responses. QTL effect sizes in 10 environments (Fig. 6) show substantial divergence among experiments. For example, qtl7.1 has large effects in environment B1, but has small effects of opposite sign in B3, B5 and W2. Furthermore, large-effect qtl6.2 and qtl7.2 show consistently positive effects, suggesting strong genetic constraints. In contrast, qtl7.1 has variable effects that are quite large in some environments.

Fig. 6.

Pleiotropic Quantitative Trait Locus (QTL) effect sizes across environments. Effect sizes of six B. stricta QTLs are shown in 10 different environments. The vertical axis shows log10 flowering time in days, multiplied by −10 for clarity. This axis ranges from −1 to +9 for each panel. QTLs are shown in the same order in each panel, from left to right: qtl1.1, qtl2.1, qtl6.1, qtl6.2, qtl7.1, qtl7.2. Three QTLs are not shown due to missing data: qtl3.1, qtl3.2, qtl4.1 (see the Materials and Methods section). Experiments are labeled as in Tables 1 and 2.

We asked whether some pairs of QTLs showed similar patterns of pleiotropy across environments (Fig. 7). Correlated cross-environment effects between pairs of QTLs ranged from near zero to strongly positive. Next, we compared cross-environment correlation of pleiotropic effects among QTL pairs versus similar pairings among the top 100 genome-wide SNPs. A permutation test shows that mean cross-environment correlation among QTL pairs (r_QTLs = 0.361) is significantly less than mean correlation among SNP pairs (r_SNPs = 0.715) (P = 0.0419). Therefore, the genes that underlie QTLs show less similar patterns of pleiotropy across environments than pairs of SNPs sampled genome-wide.

Fig. 7.

Correlation of pleiotropic Quantitative Trait Locus (QTL) effects in ten environments. Each panel shows the effect sizes (−10 x flowering age in log10 days) for a pair of B. stricta QTLs in 10 environments. (See Fig. 6 for single-environment portrayal.) Density plots (smoothed histograms) are shown on the diagonal. Upper triangular cells indicate the correlation coefficient for each pair of QTLs. Three QTLs are not shown due to missing data: qtl3.1, qtl3.2, qtl4.1 (see the Materials and Methods section).

Selection on QTLs

We tested for signatures of selection within genetic groups for each QTL with MAF > 0.05 (Supporting Information Table S9a). We used the EHH test for hard selective sweeps favoring new, derived QTL alleles within genetic groups. Overall, flanking regions around these SNPs showed little evidence for hard selective sweeps (Supporting Information Figure S6). Likewise, we found only modest LD flanking the QTL peaks (Supporting Information Figure S7), consistent with neutrality or selection on standing genetic variation. In addition, we compared nucleotide diversity π and scaled π in 200 kb regions centered on the QTL SNPs, versus genome-wide SNP regions (Wang et al., 2019a). Two QTL regions show significant changes in π or scaled π (qtl1.1 and qtl3.1; Supporting Information Table S9b). π in the qtl1.1 region is significant elevated, but this QTL occurs within a larger region of elevated polymorphism, so this is unlikely due to locus-specific selection.

We also checked for possible soft selective sweeps from standing genetic variation on QTL haplotypes (Supporting Information Table S9b). In COL, mean H2/H1 in QTL regions was 0.54 – 0.83 in qtl1.1, qtl2.1, qtl4.1, and qtl7.2 (P < 0.03), suggesting soft selective sweeps acting on multiple haplotypes, rather than hard selective sweeps favoring a single new mutation. Nevertheless, inferences regarding soft sweeps are sensitive to demographic models (Jensen, 2014), so results may be difficult to interpret.

Finally, to explore possible selection on six QTLs we contrasted levels of genetic variation between ancestral vs. derived QTL allele-groups for ±100 kb flanking haplotypes, and compared this to variation in regions flanking genome-wide SNPs (Supporting Information Table S9c). In the COL group, relative genetic differentiation (F_ST) was significantly higher between ancestral vs. derived haplotypes at qtl7.2 than for comparable haplotype comparisons genome-wide (P < 2.2E-16). At qtl1.1, absolute genetic differentiation, d_XY, is significantly higher between ancestral and derived haplotypes than for regions flanking genome-wide SNPs (P < 2.2E-16), consistent with historical balancing selection in the region (Wang et al., 2019a).

Discussion

Genetic control of flowering time

Across 10 diverse experiments we used 488 Boechera stricta genotypes and 18,242 plants to study how contrasting environments alter genetic architecture of flowering time. GWAS found 9 QTLs that influence flowering time in one or more environments (Fig. 3), four QTLs that control GxE between pairs of environments, and many QTLs that show associations with climate in sites of origin (Fig. 4).

We found extensive quantitative genetic and GxE variation for flowering time (Supporting Information Fig. S2). Among flowering QTLs, two loci have large effects on flowering time: qtl6.2 homozygotes differ by 1.29 phenotypic standard deviations, and qtl7.2 has effect size of 1.43 standard deviations. The derived alleles are widely distributed in Colorado and Utah (Fig. 5 and Supporting Information Fig. S5) across ~500 km. Because Boechera disperses most seeds less than one meter (Bloom et al., 2002), the derived, late flowering alleles probably originated tens or hundreds of thousands of years ago. The early- and late-flowering alleles of qtl6.2 show significant niche partitioning among habitats with drier versus wetter summers, respectively (Fig. 8; P = 0.0018, Supporting Information Table S8), suggesting local adaptation at this locus.

Fig. 8.

Climate association for B. stricta alleles at qtl6.2. Controlling for population structure, locations with more summer precipitation are associated with the derived allele at qtl6.2. (t = 3.15, df = 222; P = 0.0018; Supporting Information Table S8).

Some Arabidopsis GWAS find a simple quantitative genetic architecture with a few large-effect genes controlling most phenological variation (Tabas-Madrid et al., 2018), while other GWAS have found many flowering time QTLs with small to moderate effects (Brachi et al., 2010). Typically (Josephs et al., 2017), GWAS in outcrossing species find small-effect QTLs (e.g., Peiffer et al., 2014), while inbred species often find large-effect QTLs (e.g., Dixit et al., 2014), and large-effect mutations may be favored in specific environments (Taylor et al., 2019). B. stricta is largely inbreeding and we found two large-effect flowering QTLs across 10 environments.

Genotype-Environment Association

Genotype-environment associations, such as correlations between climate at sites-of-origin and trait values in common garden, suggest that genetic control of flowering time reflects adaptation to local climates (Mitchell-Olds & Schmitt, 2006). We found that later flowering genotypes are associated with home climates with warmer winter temperatures, wider annual temperature range, and wetter summers.

B. stricta genotypes from higher elevation and more northerly latitude flower earlier in common garden. In contrast, A. thaliana in Spain shows the opposite relationship between elevation and flowering time, with earlier flowering in low elevation genotypes (Montesinos-Navarro et al., 2011). This difference is probably explained by length of the growing season (Wadgymar et al., 2018): plants flower earlier where growing seasons are shorter, limited by temperature in high elevation B. stricta, or by water availability in low elevation A. thaliana in Spain (Bernier & Périlleux, 2005).

Recent GWAS analyses have found associations between climate and particular loci (Romero Navarro et al., 2017; Vasseur et al., 2018; Ferrero-Serrano & Assmann, 2019; Li et al., 2020). Here, we used GWAS to analyze genetic association between SNP variation and climate at sites of origin. GWAS for climate PC1 – PC5 found at least 34 significant QTL peaks (Fig. 5). A majority (56%) of these climate QTLs are close to known flowering genes (Supplementary Information Table S6), showing an important role for flowering pathways in adaptation to climate. Alternatively, focusing on large-effect flowering QTLs, both qtl6.2 and qtl7.2 are significantly associated with climate PC4 (P < 0.004, Supporting Information Table S7). Precipitation in the warmest quarter (Bio18) is correlated with PC4, and showed highly significant association with qtl6.2 (t = 3.15, P < 0.0018; Supporting Information Table S8). Furthermore, the derived allele at this SNP predominates in sites with higher summer precipitation (Fig. 8), and genotypes with the derived allele flower later, consistent with adaptation to greater water availability during the summer.

Genotype-by-Environment Interaction

Flowering genes that interact with environmental conditions have been studied widely (Des Marais et al., 2013; Zan & Carlborg, 2019; Guo et al., 2020), but less is known about plasticity genes that control changes between environments without causing trait variation within single environments. Our analysis of differences in flowering time between six environment pairs found four significant QTLs controlling flowering time changes between environments. None of these QTLs had significant effects on flowering time within a single environment. Three of these QTLs are close to known flowering gene candidates (Supporting Information Table S4) and in each case they function in regulation of flowering (Imaizumi et al., 2005; Goralogia et al., 2017; Romera-Branchat et al., 2020). This suggests that regulatory genes may play an important role in plasticity of complex traits.

Genetic Architecture

These analyses facilitate two questions about genetic architecture: (1) How does pleiotropic expression of a QTL change across environments? And (2) do different QTLs show similar cross-environment changes in effect sizes?

First, QTL effect sizes showed substantial divergence among 10 environments (Fig. 6). For example, QTLs may show large effects in one environment, but small effects of opposite sign in other environments. Furthermore, some large-effect QTLs have consistent effects across environments, while other QTLs have variable effects that are sometimes quite large. Overall, QTL effects are variable, or show conditional neutrality, but we find little sign of antagonistic pleiotropy. Perhaps evolutionary tradeoffs are more common among natural environments following generations of selection.

We also examined similarity of pleiotropic effects between QTLs across environments (Fig. 7). Correlated effects among pairs of QTLs ranged from near zero to strongly positive. Thus, some pairs of loci may drive cross-environment correlated responses to selection. Such shared pleiotropic effects might occur if a QTL in a key flowering network has large effects, and is correlated with other QTLs in the same network. Alternatively, similar patterns of pleiotropy among many SNPs might be caused by deleterious variants in diverse pathways, which could reduce growth and progress towards flowering, causing a common outcome of delayed flowering.

Selection and Adaptation

Based on geographical and ecological patterns, genotype-environment associations are compatible with local adaptation for some of these QTLs, favoring alternate alleles in different abiotic environments. For example, the derived allele at qtl6.2 has higher frequency in sites with greater summer precipitation, while the ancestral allele is most common in sites with drier summers (Fig. 8).

In addition, we found several lines of evidence supporting soft selective sweeps on standing variation (Stephan, 2019) rather than hard selective sweeps. First, moderate linkage disequilibrium flanking the QTL peaks (Supporting Information Fig. S7) and rapid decline of derived EHH haplotypes provide little evidence for hard selective sweeps (Supporting Information Figs. S7 and S8). Second, for qtl7.2 in the COL group, relative divergence (F_ST) between derived vs. ancestral haplotypes is 38% higher than for haplotypes genome-wide (P < 2.2E-16), but genetic diversity near qtl7.2 is comparable to genome-wide background, consistent with selection from standing variation (Barrett & Schluter, 2008). In COL group H2/H1 near qtl7.2 differs significantly from genome-wide patterns (P < 10E-11), suggesting a soft selective sweep near this complex trait locus.

Selection on standing variation for complex traits is well documented (e.g., McManus et al., 2017). It has been proposed that adaptation is faster from standing variation than from de novo mutation, because beneficial alleles are available at higher frequency immediately after the start of selection (Barrett & Schluter, 2008). This could be more significant for species like B. stricta with small effective population size, in which the waiting time for a new mutation (as a function of the mutation rate and N_e) is very long (McCandlish, 2018), so standing variation may be more important for rapid evolution.

These results are compatible with selection in heterogeneous montane habitats, since the ecological time-scale of changing allele frequency and local adaptation (Anderson & Gezon, 2015) may be faster than the evolutionary time scale of accumulating nucleotide polymorphism or recombination (Wang et al., 2019a). Other examples suggesting variable selection on flowering time in A. thaliana come from Spain (Exposito-Alonso et al., 2018), Sweden, and Italy (Ågren et al., 2017), as well as antagonistic pleiotropy and temporal heterogeneity of selection in Mimulus (Troth et al., 2018).

GWAS Population

Seeds from >400 sequenced accessions are available from the Arabidopsis Biological Resource Center, providing a public domain resource for GWAS in an ecological model system that is widely distributed in natural populations across western North America.

Supplementary Material

Supporting Information

Fig. S1 Geographic locations of five population groups.

Fig. S2 Norm of reaction for flowering time.

Fig. S3 Cross-environment correlations of flowering time.

Fig. S4 Statistical significance of SNPs near flowering time QTLs.

Fig. S5 Geographic range of qtl7.2 alleles.

Fig. S6 Extended Haplotype Homozygosity (EHH) for seven QTLs.

Fig. S7 LD: Linkage disequilibrium around QTL regions.

Table S1 Loadings of flowering principal components on flowering time BLUPs.

Table S2 Loadings of climate principal components at original genotype locations.

Table S3 Minor allele frequencies by population group for each QTL.

Table S4 QTLs for flowering and GxE.

Table S5 Analysis of climate data.

Table S6 Climate-associated QTLs that have candidate genes.

Table S7 Association between climate components and QTLs.

Table S8 Association of qtl6.2 and qtl7.2 with precipitation in warmest quarter (Bio18).

Table S9 Molecular population genetic analyses.