Hydrogen embrittlement in ferritic steels

Abstract

Hydrogen will be a crucial pillar in the clean-energy foundation, and therefore, the development of safe and cost-effective storage and transportation methods is essential to its success. One of the key challenges in the development of such storage and transportation methods is related to the interaction of hydrogen with structural materials. Despite extensive work, there are significant questions related to the hydrogen embrittlement of ferritic steels due to challenges associated with these steels, coupled with the difficulties with gauging the hydrogen content in all materials. Recent advancements in experimental tools and multi-scale modeling are starting to provide insight into the embrittlement process. This review focuses on a subset of the recent developments, with an emphasis on how new methods have improved our understanding of the structure–property–performance relationships of ferritic steels subjected to mechanical loading in a hydrogen environment. The structure of ferritic steels in the presence of hydrogen is described in terms of the sorption and dissociation processes, the diffusion through the lattice and grain boundaries, and the hydrogen–steel interactions. The properties of ferritic steels subjected to mechanical loading in hydrogen are also investigated; the effects of test conditions and hydrogen pressure on the tensile, fracture, and fatigue properties of base metal and welds are highlighted. The performance of steels in hydrogen is then explored via a comprehensive analysis of the various embrittlement mechanisms. Finally, recent insights from in situ and high-resolution experiments are presented and future studies are proposed to address challenges related to embrittlement in ferritic steels.

I. INTRODUCTION

A transformation of the energy market from coal, petroleum fuel, and natural gas to more environmentally-friendly primary energy sources and cleaner intermediates is taking place on the international stage. In feet, in a recent policy forum, the former President of the United States Barack Obama suggested that the trend toward a clean-energy economy and reduction of greenhouse gas emissions is imminent,¹ citing decoupled emissions and economic growth, private sector emission reductions, market forces in the power sector, and global momentum as the main economic drivers for the movement The technological grounds for the shift are just as profound, e.g., recent advances have pushed the power conversion efficiency of perovskite/silicon tandem solar cells to 28.0%² and the annual onshore capacity of wind farms to 500 GW.³ Together, these advances have driven increases in energy consumption and production from renewable energy sources; in 2018, the U.S. Energy Information Administration reported that renewable energy accounts for 11.4% of primary energy consumption and 12.3% of primary energy production, which represent up to 50% increases from a decade ago.⁴ Despite the progress, a critical challenge involved with these energy types is still the feet that the peaks and valleys in production differ from the peaks and valleys in demand. One answer to this issue involves the conversion of any excess energy to fuel, and more specifically, the electrolysis of water to hydrogen and oxygen.⁵ The hydrogen functions as an energy storage medium, storing energy until its conversion back to electricity through a fuel cell or engine, or combines with CO₂ to produce synthetic natural gas for power plants or transportation applications. Given its utility, it is likely that hydrogen will be a crucial pillar in the clean-energy foundation, and as such, the development of safe and cost-effective H₂ storage and transportation methods will be essential to its success.

One of the key challenges in the development of such storage and transportation methods is related to the interaction of H₂ with structural materials. Over a century ago, Johnson reported on remarkable changes in the physical properties of iron and steel after immersion in hydrochloric and sulfuric acids.⁶ The author reported significant decreases to both the fracture toughness and breaking strain, but also revealed that the effects were reversible (i.e., the material regained its original properties with a lapse of time). Furthermore, it was shown that the decrease in toughness was more severe in higher-strength materials. Two observations supported the idea that hydrogen was the cause of the changes in behavior: only acids that evolve H₂ invoked the changes and gas bubbles from the process burned with a distinctive H₂ flame. Since that time, it has been recognized that the phenomenon now known as “hydrogen embrittlement” is ubiquitous in metals, with only a few notable exceptions (e.g., Ag, Cu, and Au). Unfortunately, this means that most structural materials, of which ferritic steels are an important class, are susceptible to hydrogen embrittlement.

The extent of embrittlement is dependent on several factors related to the test conditions and the hydrogen–material interaction. Under the test conditions, the method and extent of H₂ charging has been shown to have an appreciable impact on the mechanical properties of steel. There are two means of charging materials with hydrogen: electrochemical charging, which involves simpler equipment to execute, and gas charging, which is more representative of in-service conditions, but which only a few laboratories in the world can perform. A concern remains that it is not simple to translate the environmental conditions represented by electrochemical charging to an equivalent gas charging pressure. The effect of hydrogen is also dependent on the test temperature and loading rate; in ferritic steels, embrittlement is most severe at temperatures between 200 and 300 K⁷ and strain rates below 10⁻³ to 10⁻⁵ s⁻¹.⁸ On the influence of hydrogen–material interaction, the structure of ferritic steels is important in determining its mechanical response to hydrogen. Unlike austenitic stainless steels or nickel-based alloys, ferrite is body-centered cubic (BCC) in structure. This lowers the solubility of hydrogen and increases its rate of diffusion through the material by several orders of magnitude.⁹ The low solubility translates to ferritic steels being more sensitive to small amounts of hydrogen in the environment and the high rate of hydrogen motion through the material means the behavior is more sensitive to the effects of microstructural features.⁹ Ferritic steels encompass a wide range of possible microstructures, marking a wide range of hydrogen susceptibilities.

Despite the many reports on the effects of the test conditions and the hydrogen–material interaction, there is still considerable debate on the mechanism responsible for the observed trends. In fact, several mechanisms have been suggested to explain hydrogen embrittlement,⁷ with no consensus in the literature as to which are dominant, or even which are dominant under the given conditions, apart from a couple of very specific cases. As a result, recent work has centered on new methods for high-throughput¹⁰ and in situ^11,12 mechanical testing in hydrogen gas, as well as high-resolution spectroscopy,¹³ microscopy^14,15, and tomography^16,17 of hydrogen–material behavior after testing in hydrogen. These advancements have not only provided insight into the mechanism, but have also enabled updates to the H₂ storage and transportation standards.^18,19

This review will focus on a subset of the recent developments, with an emphasis on how the new methods have improved our understanding of hydrogen embrittlement in ferritic steels. The review will be a material-focused paper, and thus mainly concerned with the structure–property–performance relationships of steels subjected to mechanical loading in a H₂ environment. Section II highlights the structure of hydrogen in steel; the behavior of hydrogen on and in a metal is described via sorption and dissociation, diffusion through the lattice and grain boundaries, and hydrogen–steel interactions. Section III examines the properties of steel subjected to mechanical loading in hydrogen, with an emphasis on tensile, fracture toughness, and fatigue properties and performance of welds. Section IV considers efforts to predict the performance of steel in hydrogen through a comprehensive understanding of the embrittlement mechanism. Section V highlights recent progress in expanding the understanding of hydrogen–material behavior via technological advances in experimentation and Sec. VI provides conclusions and suggestions for future work.

At this juncture, it is important to note that there are multiple degradation phenomena in metals that are caused by hydrogen. This includes hydrogen-induced cracking and blistering^20–22 where aggressive electrochemical charging conditions (often aided by H₂S) result in the precipitation of gaseous hydrogen in pressurized cracks in the metal; high temperature hydrogen attack,^23–25 where, at temperatures above 350 °C, hydrogen reacts with the carbides in carbon steel to form gaseous methane (CH₄), usually along grain boundaries, causing failure of these boundaries; stress corrosion cracking,^26–28 where sub-critical crack growth occurs in metals exposed to a corrosive environment, and these cracks are thought to be affected by hydrogen; and conventional hydrogen embrittlement, which is the focus of this review. The first three phenomena occur under different environmental conditions, including different hydrogen charging conditions, temperatures, and applied stress conditions. As such, they should be treated as separate phenomena, and will not be covered here. Instead, this review focuses on the fourth phenomenon in ferritic steels, which is defined here as the deleterious effects of hydrogen on the room temperature (200 to 300 K) mechanical properties, especially ductility.

II. HYDROGEN BEHAVIOR IN METALS

The susceptibility of ferritic steels to hydrogen depends on a host of factors, including the microstructure of the steel, the mechanism in which hydrogen is incorporated in the steel (i.e., electrochemical charging or gaseous charging), temperature, and kinetics of the deformation (e.g., strain rate or fatigue frequency). Ultimately, these factors control the true root parameters that govern hydrogen susceptibility, namely the concentration of hydrogen in steel and hydrogen kinetics.^29,30 The fact that these two factors, in particular, are the parameters which govern the hydrogen susceptibility is evidenced by the success of modeling of embrittlement utilizing as input parameters, the interaction of hydrogen with the steel surface, the kinetics of hydrogen entering the steel, and the transport kinetics within the steel framework (including in the crystal lattice, near dislocations, grain boundaries, and vacancies).^29,30 In this section, we review the experimental and computational studies of these parameters.

Although the exact physical mechanisms of hydrogen embrittlement in ferritic steel are not yet agreed upon by the community, the mechanism by which hydrogen enters the material is generally well-accepted.³¹ Diatomic hydrogen first adsorbs on the surface of the solid, then dissociates into atomic hydrogen at the surface and chemisorbs. The hydrogen then diffuses either through the metal lattice or through grain boundaries and accumulates near internal stress centers, such as dislocations or crack tips. At this stage, the behavior of hydrogen is less well understood, and its influences on the metal are still debated.

A. Adsorption of H on ferritic steel

In the initial stage, hydrogen from the gas phase adsorbs on the steel surface as a diatomic molecule. Under gas charging, the gas-phase to incorporated hydrogen reactions are

$${\text{H}}_2\left(g\right)\leftrightarrow {\text{H}}_2\left(\text{ads}.\right),$$ (1)

$${\text{H}}_2\left(\text{ads}.\right)\leftrightarrow \text{2H}\left(\text{chem}.\right).$$ (2)

The adsorption of H₂ on pure Fe at 77 K has been shown by Ransom and Ficalora to conform to a Langmuir isotherm for localized adsorption with a binding energy E_b = 60 kJ/mol and vibration frequency of ν = 24 GHz.³² In the Langmuir model, the surface coverage of adsorbed molecules, θ, is given by

$$\theta =\frac{P_{\mathrm{vapor}}\chi }{1+P_{\mathrm{vapor}}\chi },$$ (3)

where P_vapor is the gas pressure, χ is the Langmuir constant at a temperature T given by

$$\chi =\frac{e^{\frac{E_b}{k_{B}T}}}{\prod _{i=1}^3\sinh \left(\frac{h{\nu }_i}{k_{B}T}\right)}\sqrt{\frac{h^6}{{\left(8\pi M\right)}^3{\left(k_{B}T\right)}^5}},,$$ (4)

where E_b is the binding energy, ν_i is the vibrational frequency in the ith direction (with i = x, y, z), M is the reduced mass, h is the Planck constant, and k_B is the Boltzmann constant. At room temperature, hydrogen reaches near full surface coverage (1:1 H/Fe) at pressures above ≈0.05 MPa.

Ab initio calculations of hydrogen desorption temperatures and energies on the (100), (110), (111), and (211) surfaces³³ indicate an average hydrogen binding energy on Fe of 274.5 kJ/mol, with the largest binding energy (282.4 kJ/mol) on the (110) surface and the lowest binding energy (266.9 kJ/mol) on the (111) surface.

Under cathodic charging, in which the hydrogen exists within an aqueous solution as a cation, the reaction is

$${\text{H}}^{+}\left(\mathrm{aq}\right)+e^{-}\leftrightarrow \left(\frac{1}{2}\right){\text{H}}_2\left(g\right)\leftrightarrow \text{H}\left(\mathrm{chem}.\right).$$ (5)

Though the process in which H enters the steel is different between gas charging and cathodic charging, both types of charging can lead to similar effects in terms of hydrogen embrittlement in steels. Some efforts have been made to relate electrochemical charging conditions to an effective gas-charging pressure (or fugacity). Atrens et al. utilized thermal desorption spectroscopy (TDS) to measure the hydrogen concentration as a function of charging potential and as a function of gas pressure in a 980DP steel and a 3.5NiCrMoV steel. It was shown that the hydrogen concentration increases both with the negative charging potential as well as with hydrogen gas pressure.^34,35

B. Kinetics of adsorption and chemisorption

The sorption of H₂ is a two-step process in which molecular H₂ first adsorbs onto the surface and then dissociates to atomic H. The total chemisorption rate of H₂ onto thin iron films was measured through chemisorption-induced changes in the electrical resistivity described in Ref. 36 and modeled according to the coupled differential equations:

$$\frac{\text{d}{\Theta }^{*}}{\mathrm{dt}}=k_{\text{a}}p\left(1-{\Theta }^{*}\right)-k_{\text{d}}{\Theta }^{*}-\frac{1}{2}\frac{\text{d}\Theta }{\mathrm{dt}}$$ (6)

and

$$\frac{1}{2}\frac{\text{d}\Theta }{\mathrm{dt}}=k_1{\left(1-\Theta \right)}^2-k_2{\Theta }^2\left(1-{\Theta }^{*}\right),$$ (7)

where Θ* is the coverage (the number of adsorbed species per adsorption site) of molecular H₂, Θ is the coverage of chemisorbed H, k_ap is the rate of adsorption from the gas phase molecular H₂ to adsorbed H₂, k_d is the rate constant for desorption of H₂ to the gas phase, k₁ is the rate constant for dissociation of adsorbed H₂ to atomic H, and k₂ is the rate of recombination from atomic, chemisorbed H to molecular, physisorbed H₂. The quantity k_a is given by

$$k_a=\frac{\alpha }{\stackrel{\_}{n}\sqrt{2\pi M{k}_{B}T}},$$ (8)

where α is the “sticking probability” and $\stackrel{\_}{n}$ is the average number of sites per unit area. Figure 1(a) shows the adsorbed coverage as a function of time for Fe exposed to hydrogen gas at pressures 1.7 and 5.5 MPa. Fully adsorbed hydrogen coverage occurs in tens of nanoseconds. Figure 1(b) shows the chemisorbed coverage as a function of time, which from the coupled differential equations can be shown to be largely independent of pressure unless at very low gas pressures (< 1 Pa). Chemisorbed hydrogen requires tens of seconds to reach full coverage. Thus, chemisorption is the rate limiting step in determining the amount of hydrogen at the surface for incorporation in steel.

FIG. 1.

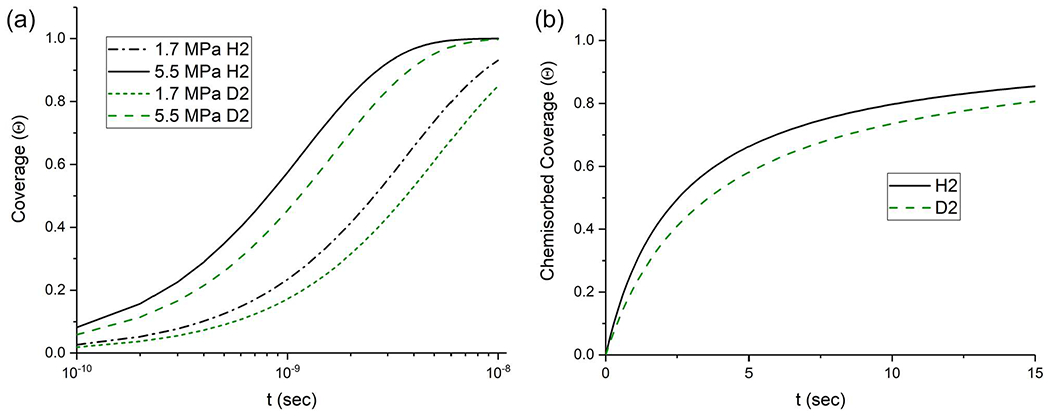
(a) Adsorbed coverage of H and D as a function of time for Fe exposed to hydrogen gas pressures of 1.7 and 5.5 MPa, respectively. It can be observed that fully adsorbed hydrogen coverage occurs in tens of nanoseconds. (b) Chemisorption of H from the adsorbed H₂ state, which occurs on the order of seconds. Note that for pressures above ≈1 Pa, the chemisorption rate is independent of pressure. The rate of adsorption is orders of magnitude faster than the rate of chemisorption, where full adsorption saturation of the surface occurs on the timescale of nanoseconds while dissociation of the adsorbed molecule occurs on the order of seconds. Reprinted from Connolly et al., Mater. Sci. Eng., A 753, 331 (2019).³⁷ Copyright 2019 Elsevier.

Figure 1 also shows the adsorption and chemisorption rates for the hydrogen isotope deuterium. Chemically identical to hydrogen, deuterium differs from hydrogen only in the inclusion of a neutron in the nucleus, which essentially doubles its mass. The increased mass suppresses the rate of diffusion, chemisorption, and adsorption. The differences between hydrogen and deuterium have been shown to have little effect on embritdement in tensile tests, but a drastic effect on fatigue properties depending on the gas pressure, where deuterium was shown not to increase the fatigue crack growth rate (FCGR) of an X70 steel at 1.7 MPa, but it did increase the fatigue crack growth rate at 5.5 MPa.³⁷

These calculations have been performed, assuming pure H₂ gas on a pristine Fe surface. Surface contaminates (e.g., oxides) affect both the adsorption and dissociation of hydrogen on steel.^38–40 In particular, ab initio calculations suggest oxygen is preferentially adsorbed onto Fe surfaces, preventing hydrogen adsorption and dissociation.⁴⁰ The prevention of hydrogen dissociation and subsequent diffusion into steel is likely the reason impurity levels of oxygen in the H₂ gas have been shown to decrease susceptibility to hydrogen embritdement and hydrogen affected-fatigue crack growth rate.^41,42 Calculations predict a similar effect on hydrogen dissociation kinetics by carbon monoxide,⁴² which has a similar hydrogen-susceptibility depressing effect. On the other hand, the calculations do not show a strong prevention of hydrogen dissociation due to CH₄ or CO₂, and incidentally, hydrogen susceptibility has been shown to not be largely influenced by CH₄ and CO₂ gases.⁴³ Thus, the kinetics of hydrogen adsorption, dissociation, and chemisorption seem to play a very large role in hydrogen embrittlement

C. Hydrogen diffusion in steel

Once the H₂ gas has adsorbed, dissociated, and chemisorbed on the steel surface, the monoatomic hydrogen begins to diffuse within the steel framework. In ferrite, hydrogen is small enough to occupy interstitial sites, especially tetrahedral sites. The diffusion is typically modeled by Fick’s law

$$J=-D\frac{d\left[H\right]}{dx},$$ (9)

where J is the flux, D is the hydrogen diffusivity, and [H] is the hydrogen concentration. Under stress-free conditions, the hydrogen concentration is given by Sievert’s Law^44,45

$${\left[H\right]}_0=\frac{\Phi }{D}{\left(P\right)}^{1/2},$$ (10)

where Φ is the hydrogen permeability and P is the hydrogen pressure of the surrounding gaseous environment. In the presence of a hydrostatic stress, the stress-assisted hydrogen concentration [H]_σ is given by

$${\left[H\right]}_{\sigma }={\left[H\right]}_0{e}^{{\sigma }_{h}V/RT}=\frac{\Phi }{D}{\left(P_H\right)}^{1/2}{e}^{{\sigma }_{h}V/RT},$$ (11)

where σ_h is the hydrostatic stress, R is the gas constant, and V = 2.0 × 10⁻⁶ m⁻³/mol is the partial molar volume of hydrogen in body-centered cubic (BCC) Fe.^46,47 At room temperature, Φ = 10¹³ atoms/m·s·MPa^½ for hydrogen gas. It has been shown that hydrogen trapping energy is sensitive to shear stress as well as hydrostatic stress.⁴⁸ Dislocations are areas with high shear stress, indicating that hydrogen accumulation occurs along the entire slip plane around a dislocation core.

However, as illustrated in Fig. 2, permeation tests of hydrogen in iron, unlike most other metals like nickel or vanadium, show a large range in the diffusion rate, especially at temperatures near room temperature.⁹ At the higher end, the trend appears to follow an Arrhenius relationship consistent with the higher temperature data, which also corresponds to ab initio calculations of hydrogen diffusion in BCC iron, suggesting a diffusible hydrogen rate on the order of 10⁻⁵ cm²/s at room temperature.^49–53 To explain the scatter of data at lower temperatures showing slower diffusion, the theory of hydrogen trap sites was developed.^54,55

FIG. 2.

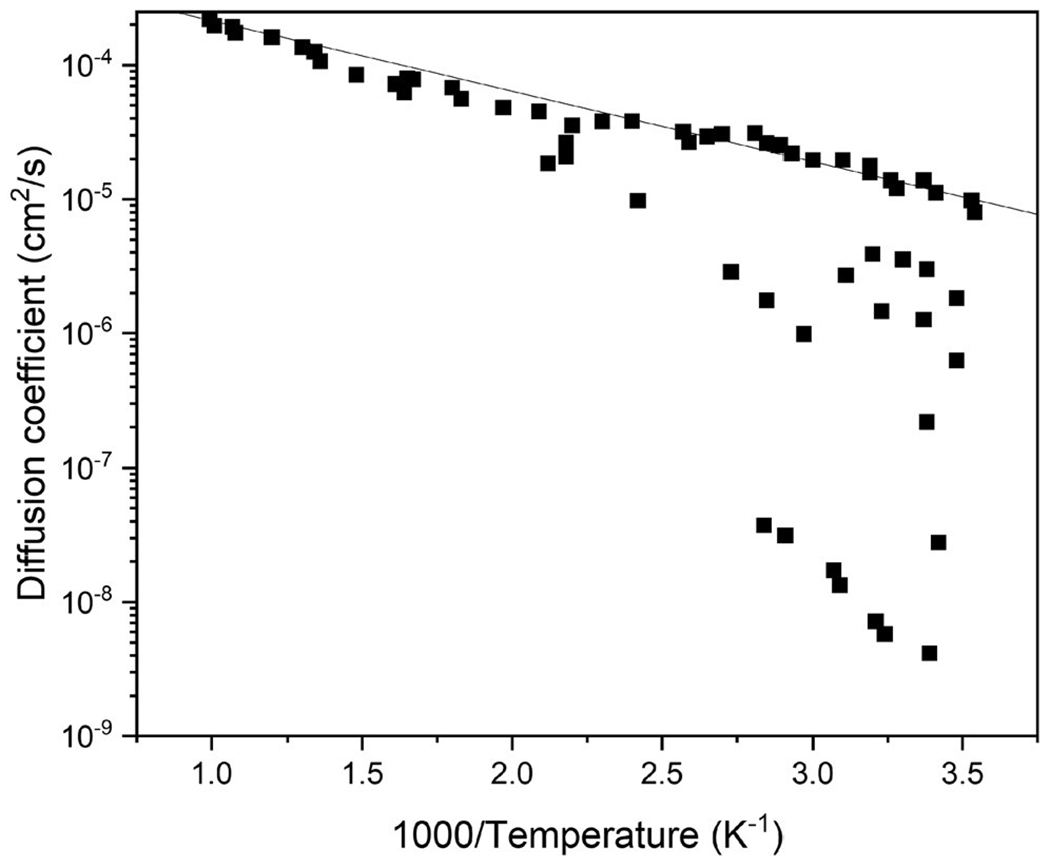
Literature data of hydrogen diffusivity in iron. It can be observed that permeation tests of hydrogen in iron, unlike most other metals (e.g., nickel and vanadium) show a large range in diffusion rates, especially close to room temperature. The straight line represents the ideal Arrhenius relationship fitted to the higher temperature data. The “noise” in the data falling below the line is due to microstructural trapping at lower temperature. Adapted from Volkl and Alefeld, in Diffusion in Solids: Recent Developments, edited by A. S. Nowick (Academic Press, New York, 1975), pp. 231–302.⁹ Copyright 1975 Academic Press.

Trap theory states that while hydrogen diffuses rapidly within the iron lattice even at room temperature, it amasses at microstructural defects such as voids, dislocations, grain boundaries, and precipitates^56,57 (Fig. 3), which act as traps. Depending on the characteristics of the defects and traps, the effect on the diffusing hydrogen can vary significantly. Some traps are attractive, subjecting the hydrogen to an attractive force that influences the diffusion; others are physical in nature, with no long-range forces such that the hydrogen randomly falls into the trap.⁵⁴ The other characteristic of traps is the “depth” or the binding energy of the trap. Irreversible traps have high trapping energies, and below a certain temperature, hydrogen cannot escape from the trap; reversible traps with low binding energies may retard the motion of the hydrogen for longer than an interstitial site, but the hydrogen will eventually continue moving through the metal.⁵⁵

FIG. 3.

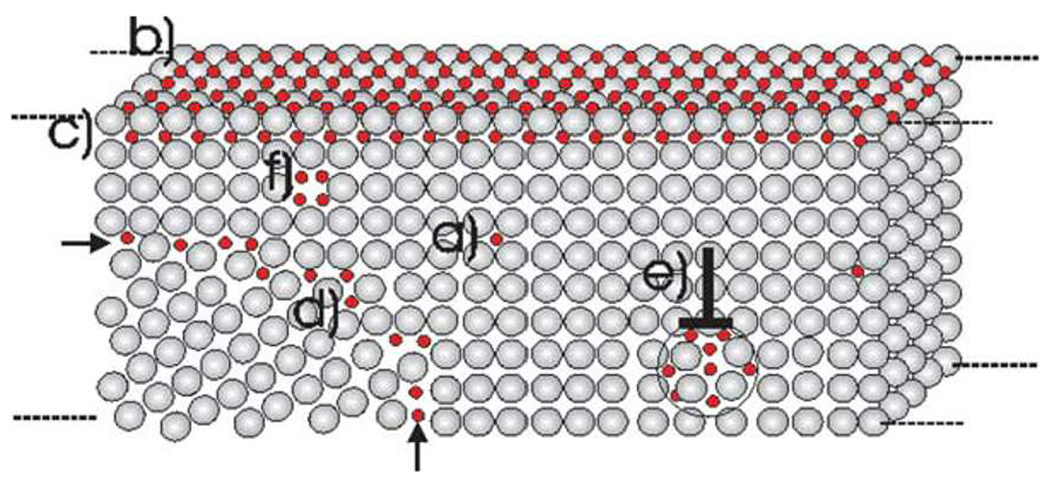
Trap theory states that hydrogen amasses at microstructural defects such as voids, dislocations, grain boundaries, and precipitates, which in turn act as traps. In this figure, we show a schematic demonstrating the hydrogen accumulation at different microstructural features, including (a) normal interstitial lattice sites, (b) surface sites, (c) subsurface sites, (d) grain boundaries, (e) dislocations, and (f) vacancies. It is observable that, depending on the characteristics of the defects and traps, the effect on the diffusing hydrogen can vary significantly. Some traps are attractive, subjecting the hydrogen to an attractive force that influences the diffusion; others are physical in nature, with no long-range forces such that the hydrogen randomly falls into the trap. Reprinted from Pundt and Kirchheim, Annu. Rev. Mater. Res. 36, 555 (2006).⁵⁸ Copyright 2006 Annual Reviews.

The trapping characteristics of grain boundaries seem to depend on the character of the boundary. Low-Σ (high symmetry) grain boundaries have interstitial sites which are energetically similar to the bulk interstitial sites, while high-Σ grain boundaries have higher binding energies.⁵⁹ There has also been a question as to whether grain boundaries can also act as fast diffusion pathways. Some experimental studies have shown enhanced diffusion along grain boundaries;^60,61 others have shown the opposite,⁶² while still others show a dependence on the boundary character.⁶³ While this question remains open, understanding the hydrogen behavior at grain boundaries is particularly important, as the accumulation of hydrogen can lead to a lower cohesive energy between grains. Dislocations are considered a mixed trap, with the strain field acting as an attractive trap, and the dislocation core acting as a physical trap.⁵⁴ As dislocations form networks, it has been proposed that they could act as short-circuit diffusion paths through the material.⁶⁴ But, perhaps more importantly to hydrogen distribution, dislocations are generally mobile under an applied stress. It has been proposed that moving dislocations can transport hydrogen.^55,65 Modeling suggests that this could result in significantly different hydrogen distributions than can be achieved by Fidrian diffusion alone.⁶⁶ Hydrogen is also strongly trapped by vacancies. The interaction of hydrogen with vacancies is circular and self-perpetuating—hydrogen acts to increase the likelihood of vacancy formation and stabilizes vacancy clusters, and vacancies act to trap hydrogen.^67,68

The role of trap sites on hydrogen embrittlement is still under debate.³⁰ On the one hand, trap sites cause a relatively high local concentration of hydrogen, and areas of high concentration are the suggested active sites of most proposed mechanisms of embrittlement.⁶⁹ Furthermore, weakly-trapped hydrogen can become released during service, and then diffuse to and accumulate at more susceptible locations. On the other hand, trap sites slow the overall diffusion of hydrogen, and irreversible traps can potentially keep it away from critical sensitive locations, which may decrease the degradation of the steel due to hydrogen.³⁰ The role of traps requires further investigation, as the H–Fe interactions that lead to low diffusion rates also lead to high local solubilities, indicating that a “Goldilocks” trapping energy that would lower hydrogen susceptibility may exist by providing a sufficiently slow diffusion combined with low hydrogen accumulation.

III. MECHANICAL PROPERTIES

For engineers designing parts in contact with hydrogen and scientists trying to understand the effects of hydrogen on materials, mechanical property data are of clear importance. Scientists and engineers study the relationships between mechanical properties, microstructures, and processing parameters. What is generically categorized as hydrogen embrittlement can apply not only to the reduction of area (RA) or lessening of elongation to failure, but also to any degradation of mechanical properties by hydrogen. However, the main mechanical properties used in design indude the reduction of area, elongation to failure, fatigue crack growth rate, fracture toughness, threshold for sustained load cracking, fatigue threshold, and stress-life. Yield strength and ultimate tensile strength (UTS) are also necessary properties for design, but it is unclear whether hydrogen, particularly in the gas phase, has a significant effect on these properties when considering smooth specimens of ferritic steels.

A. Tensile testing

There are a number of important variables associated with the determination of the effects of hydrogen on mechanical properties. These indude loading conditions, test temperature, and hydrogen environmental conditions. There is a wealth of mechanical property data in the literature from monotonic tensile testing.^52,70–78 This test provides yield strength, elastic modulus, ultimate tensile strength, and tensile ductility parameters such as elongation to failure and reduction of area, all of which are useful in design. As the strength of steel increases, hydrogen embrittlement, measured as the relative reduction of area of a smooth specimen in monotonic tensile testing, also increases, as shown in Fig. 4. Hydrogen has little effect on the strength of ferritic steels, particularly for structural steels such as pipeline steels.^70–75,77 However, the effect of hydrogen on strength may have a relationship with the microstructure. For instance, data from Hoffman and Rauls of tensile tests on 0.22% carbon steels at a 15.2 MPa hydrogen gas pressure⁷⁹ show results for the cold-drawn condition where there is a decrease in tensile strength, compared to that in air, as the hydrogen gas pressure increases, while results for a normalized steel of the same type showed no change in hydrogen compared to air. There is a pressure effect on tensile properties for ferritic steels, which can be seen for both smooth and notched specimens, where an increase is observed in the change in reduction of area as the hydrogen gas pressure increases, up to a plateau.^52,75,80

FIG. 4.

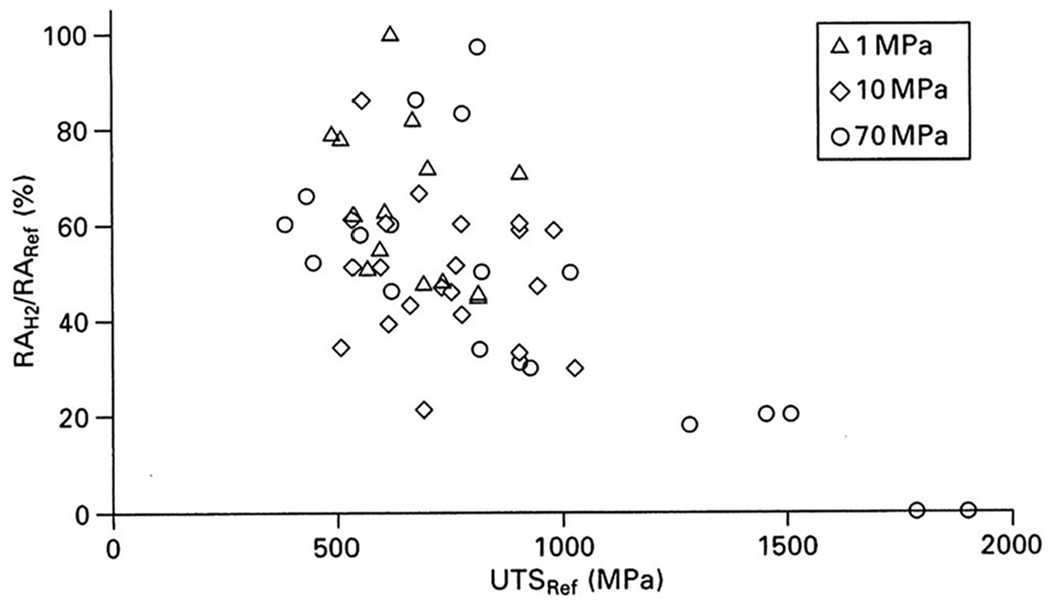
Depending on the strength of the steel, hydrogen embrittlement, measured as the relative reduction of area of a smooth specimen in monotonic tensile testing, also increases (shown herein). The figure emphasizes the relative reduction of area in hydrogen as a function of ultimate tensile strength of some ferritic steels. Reprinted from Gangloff and Somerday, Gaseous Hydrogen Embrittlement of Materials in Energy Technologies: The Problem, its Characterisation and Effects on Particular Alloy Classes (Woodhead Publishing, 2012).⁸ Copyright 2012 Woodhead Publishing.

Notched specimens show a significant reduction in both yield and tensile strength. Notched tensile testing is used to show the susceptibility to hydrogen embrittlement and how susceptibility changes as a function of mechanical stress concentration and local hydrogen concentration,^81–83 which are varied by changing the notch shape. In this case, the susceptibility to hydrogen is manifested by a reduction in notch strength, as shown in Fig. 5. However, notch strength is not a material property, and thus, notch testing has the most value in ranking the hydrogen susceptibility of materials or investigating effects such as stress or hydrogen concentrations.

FIG. 5.

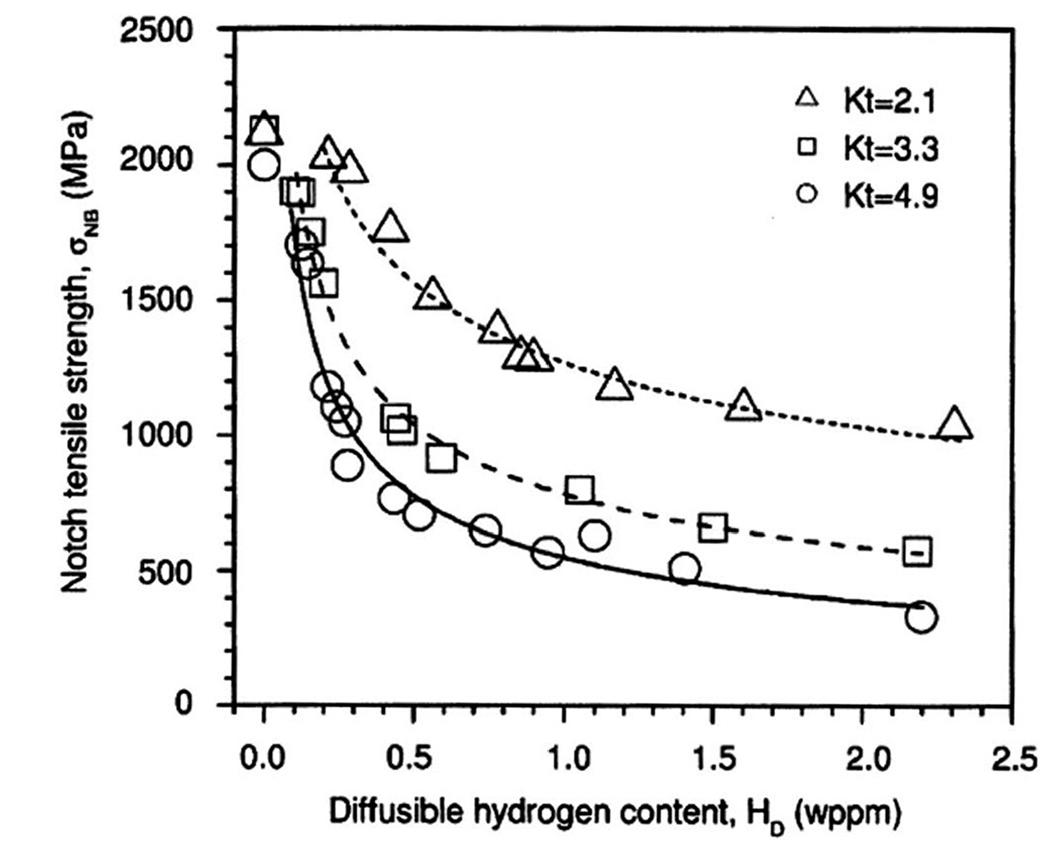
It has been observed that notched specimens show a significant reduction in both yield and tensile strength. Notched tensile testing is used to show susceptibility to hydrogen embrittlement and how susceptibility changes as a function of mechanical stress concentration and local hydrogen concentration,^81–83 which are varied by changing the notch shape. Here, the susceptibility to hydrogen is manifested by a reduction in notch strength. This figure shows a dependence of notch tensile strength on the diffusible hydrogen content for specimens with different stress concentration factors. Reprinted from Wang et al., Mater. Sci. Eng., A 398, 37 (2005).⁸¹ Copyright 2005 Elsevier.

Tensile tests also provide data on reduction of area and elongation to failure.^52,70–78 Hydrogen embrittlement is typically defined by the relative reduction of area of the cross section of a specimen that failed in a tensile test. Reduction of area itself is defined as the percentage of cross-sectional area of a fractured specimen at the point of fracture and consequently the smallest cross section after fracture, compared with the original cross-sectional area of the gauge section. The relative reduction of area is the ratio of the reduction of area in hydrogen to the reduction of area in air or inert gas.⁸ Reduction of area is not a material property and is not used in design. However, as with notch strength, reduction of area is commonly used to rank materials as to the degree of hydrogen embrittlement. Elongation to failure can also be used to rank the hydrogen embrittlement of materials. Elongation to failure is generally reported as a percentage and a gauge length because that percentage is dependent upon the gauge length with shorter gauge lengths, yielding larger percentages of elongation to failure. Some representative tensile data are given in Fig. 6 and Table I.⁸⁰ In Fig. 6, it can be seen that elongation to failure generally decreases as the hydrogen gas pressure increases, and that this effect seems to plateau. Also note that there is no change in yield strength as a function of pressure, and that changes in ultimate tensile strength do not show a definite correlation with pressure.

FIG. 6.

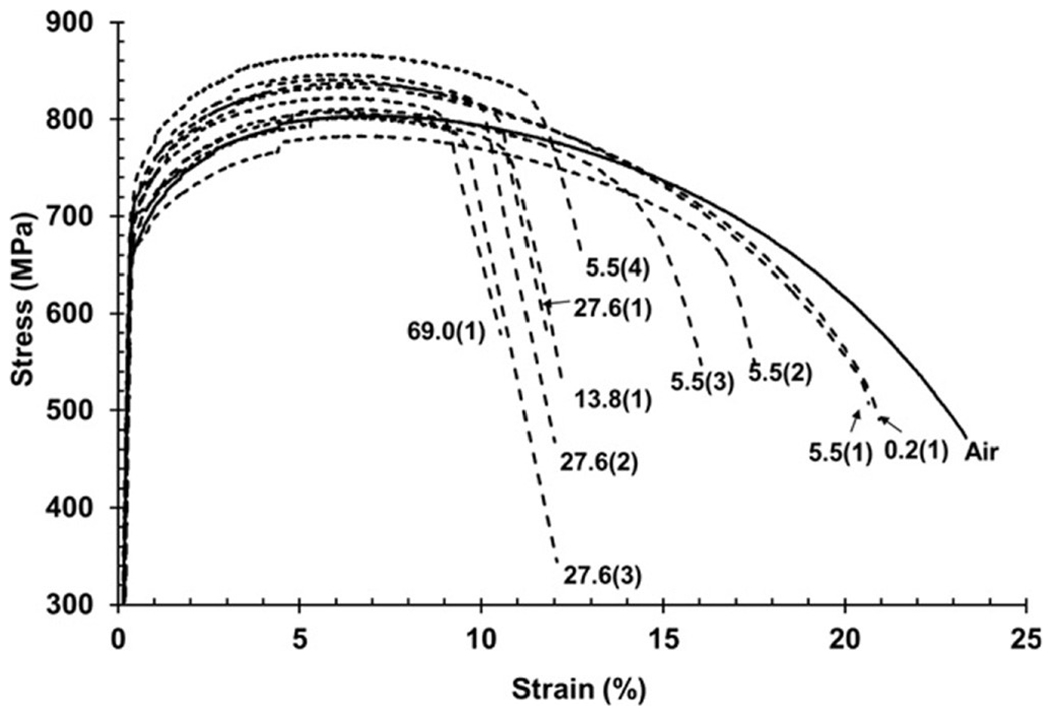
Tensile curves from longitudinal X100 steel specimens tested in hydrogen at different gas pressures and a strain rate of 7 × 10⁻³ s⁻¹. The hydrogen gas pressure in MPa is provided at the end of each tensile curve. Numbers in parentheses represent repeat specimens. This figure demonstrates that elongation to failure generally decreases as the hydrogen gas pressure increases, and that this effect seems to plateau. Moreover, there is no change in yield strength as a function of pressure, and that changes in ultimate tensile strength do not show a definite correlation with pressure. Reprinted from Nanninga et al., Corros. Sci. 59, 1 (2012).⁸⁰

TABLE I.

Tensile data from longitudinal X100 steel specimens at a strain rate of 7 × 10⁻³ s⁻¹, σ_{y 0.2%} = yield strength, UTS = ultimate tensile strength, E_f = elongation at failure, and RA = reduction of area (final area/original area). Reprinted from Nanninga et al., Corros. Sci. 59, 1 (2012).⁸⁰ Copyright 2012 Elsevier.

Gas	Pressure (MPa)	σy 0.2% (MPa)	UTS (MPa)	Ef (%)	RA (%)
Air	~0.08	665	792	21	75
Air	~0.08	674	804	23	78
Air	~0.08	698	810	22	75
Average		679	802	22	76
Standard deviation		17.1	9.2	1.0	1.9
H2	0.2	719	834	21	68
H2	5.5	747	867	11	24
H2	5.5	685	811	16	28
H2	5.5	670	783	18	39
Average		701	820	15	30
Standard deviation		40.8	42.8	3.2	7.8
H2	13.8	693	808	11	19
H2	27.6	704	803	9	28
H2	27.6	707	837	11	21
H2	27.6	731	846	12	20
Average		714	829	11	23
Standard deviation		14.8	22.7	1.3	4.2
H2	69.0	715	823	9	16

B. Fracture toughness

The threshold stress intensity factor K_TH is defined as the stress intensity below which crack propagation is unlikely in hydrogen. K_TH is measured either by what is commonly called a wedge-opening-load (WOL) test, where a specimen with a machined notch and fatigue precrack is loaded with a bolt to within a prescribed range of the fracture toughness (in air) of the material or with a rising load test. Therefore, loading is displacement-controlled for the WOL test.⁸⁴ Both tests provide conservative results for high strength steels with low fracture thresholds, but only the rising load test provides conservative results for a wide range of materials.⁸⁵ This parameter is used for the design of pressure vessels within a fracture-mechanics-based approach. For example, Article KD-10 in Sec. VIII, Division 3 of the ASME Boiler and Pressure Vessel code requires K_TH for the fracture-mechanics-based design of pressure vessels in hydrogen service.⁸⁶ For ferritic steels, K_TH generally decreases as the hydrogen gas pressure increases or alloy strength increases.^87,88 However, the correlation with the hydrogen gas pressure is more complicated.^75,89 It has been observed that for an X100 steel, a plateau is seen in the effect of hydrogen gas pressure on K_TH, whereas for a DOT 3T steel, only a small decrease in K_TH was observed as the hydrogen gas pressure increased,⁹⁰ although more data would be needed to rule out that the DOT 3T steel was not already in the plateau at a 40 MPa gas pressure. Additionally, it has been shown that K_TH is sensitive to the initial applied load on the specimen, and the sensitivity increases as the strength of the steel decreases.^90,91

The trends seen in fracture toughness testing in hydrogen generally follow the trends in the measurement of the threshold stress intensity factor.⁷⁵ While the most common property reported in the literature is K_IC, other properties are J_IC, crack growth resistance (J–R curves), or dJ/da.⁷⁸ The fracture toughness of steels in hydrogen gas is significantly reduced compared to that in air or inert environments. In general, the fracture toughness in air is at least twice as high as that in hydrogen gas at 5.5 MPa or higher.^92,93 A decrease in fracture toughness is seen in many cases as a function of increasing hydrogen gas pressure, but there is not a strong sensitivity to pressure.^78,92,94,95 Figure 7 shows the fracture toughness data over a modest range of gas pressure where the pressure effect is small. However, significant decreases in fracture toughness are seen for large increases in gas pressure, and a general trend is that reduced fracture toughness roughly follows the square root of pressure because of the fugacity–pressure relationship.^96,97

FIG. 7.

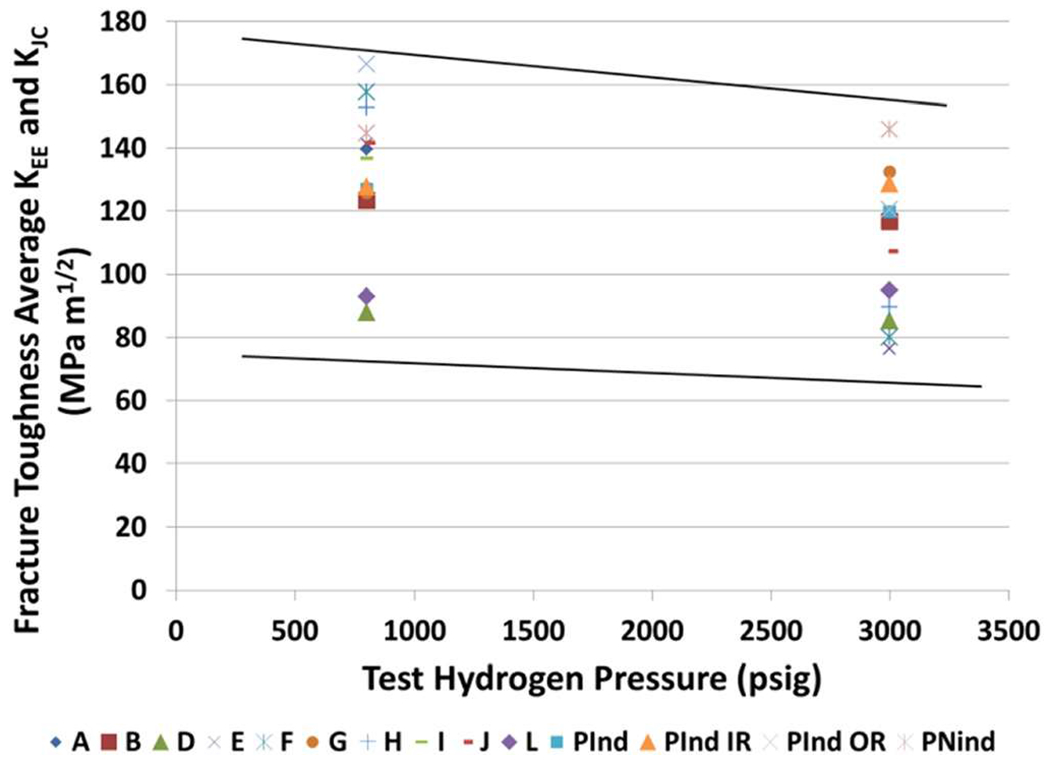
Fracture toughness of ferritic steels as a function of hydrogen gas pressure. (3000 psig = 21 MPa). As discussed above, the fracture toughness of steels in hydrogen gas is significantly reduced compared to that in air or inert environments. In air, fracture toughness is at least twice as high as that in hydrogen gas at 5.5 MPa or higher.^92,93 A decrease in fracture toughness is seen in many cases as a function of increasing hydrogen gas pressure, but there is no strong sensitivity to pressure.^78,92,94,95 Herein, we show fracture toughness data over a modest range of gas pressures where the pressure effect is small. However, significant decreases in fracture toughness are seen for large increases in gas pressure, and a general trend is that reduced fracture toughness roughly follows the square root of pressure because of the fugacity–pressure relationship. Reprinted from Stalheim et al., in Proceedings of the 9th International Pipeline Conference (American Society of Mechanical Engineers, 2012), p. 275.⁹² Copyright 2012 ASME.

Alvarez et al. studied the effect of displacement rate on fracture toughness of a C–Mn structural steel and a quench and tempered (ferrite–martensite) steel.⁹⁸ These steels were pre-charged with hydrogen gas at elevated temperature. For both steels, fracture toughness decreased as the displacement rate of the test decreased. The decrease was small for ferrite–pearlite steel, but large for ferrite–martensite steel. Similar results for displacement rate effects on quench and tempered steds have been observed.⁹⁹ In many cases, fracture toughness does not seem to correlate with yield strength.^92,94 While some studies show a correlation between increasing alloy strength and decreasing fracture toughness, the effect has only been seen in very high-strength alloys.⁹⁹

C. Fatigue

Fatigue crack growth rate (FCGR) testing provides information that can be used to calculate the remaining lifetime of a pipeline or pressure vessel, given an initial flaw size. Additionally, FCGR data are used in fracture-mechanics-based design. Both the ASME Boiler Pressure Vessel code Article KD-10 and the ASME B31.12 Hydrogen piping and pipelines code use FCGR data for design and compliance.^86,100 Three major variables for FCGR testing are stress intensity range ΔK, loading frequency, and gas pressure. Other variables, such as the load waveform, stress ratio, steel strength, and microstructure can also affect the FCGR.^101,102 Load waveform has a minor effect on hydrogen-assisted fatigue crack growth rate (HA-FCGR), where there is little to no effect at high values of stress intensity and more effect for slow-rising waveforms than fast-rising waveforms at low stress ratios.^101,103 Stress ratio, or load ratio, has little effect on the plateau region of the HA-FCGR.¹⁰⁴ However, an increase in stress ratio causes a lowering of the stress intensity required for the onset of crack acceleration (which is tied to the maximum stress intensity factor) and causes a lowering of the stress for the onset of stage III FCGR,¹⁰⁴ shown in Fig. 8. Steel strength is not generally considered to track with the HA-FCGR.^102,105,106 Slifka et al. measured the HA-FCGR of ferritic steels with yield strengths ranging from 325 to 800 MPa, at a hydrogen gas pressure of 5.5 MPa, a loading frequency of 1 Hz, and a stress ratio of 0.5 and found no correlation between the yield strength and HA-FCGR, as shown in Fig. 9.¹⁰⁶ The effect of microstructure on the HA-FCGR of ferritic steels seen in the literature is complex and may depend upon more dominant experimental factors such as ΔK, loading frequency, and gas pressure. Krishnamurthy et al. found little difference in the HA-FCGR when comparing microstructures including bainite, martensite, and dual-phase (ferrite–martensite) at similar strength levels.¹⁰⁷ Carroll and King found no correlation between the microstructure and HA-FCGR when tested in hydrogen gas near atmospheric pressure at a frequency of 0.1 Hz and a stress ratio of 0.5 for C–Mn pipeline steels with a range of strengths.¹⁰⁸ However, Cialone and Holbrook compared an X42 steel (ferrite–pearlite) with a fully-ferritic steel and a fully-pearlitic steel in 6.9 MPa hydrogen gas tested at a frequency of 1 Hz and a stress ratio of 0.1 and found significant differences in the HA-FCGR.^109,110 Additionally, Amaro et al. found that the percent polygonal ferrite in pipeline steels correlates with the HA-FCGR for tests in 5.5 MPa hydrogen gas at a frequency of 1 Hz and a stress ratio of 0.5, shown in Fig. 10.¹¹¹

FIG. 8.

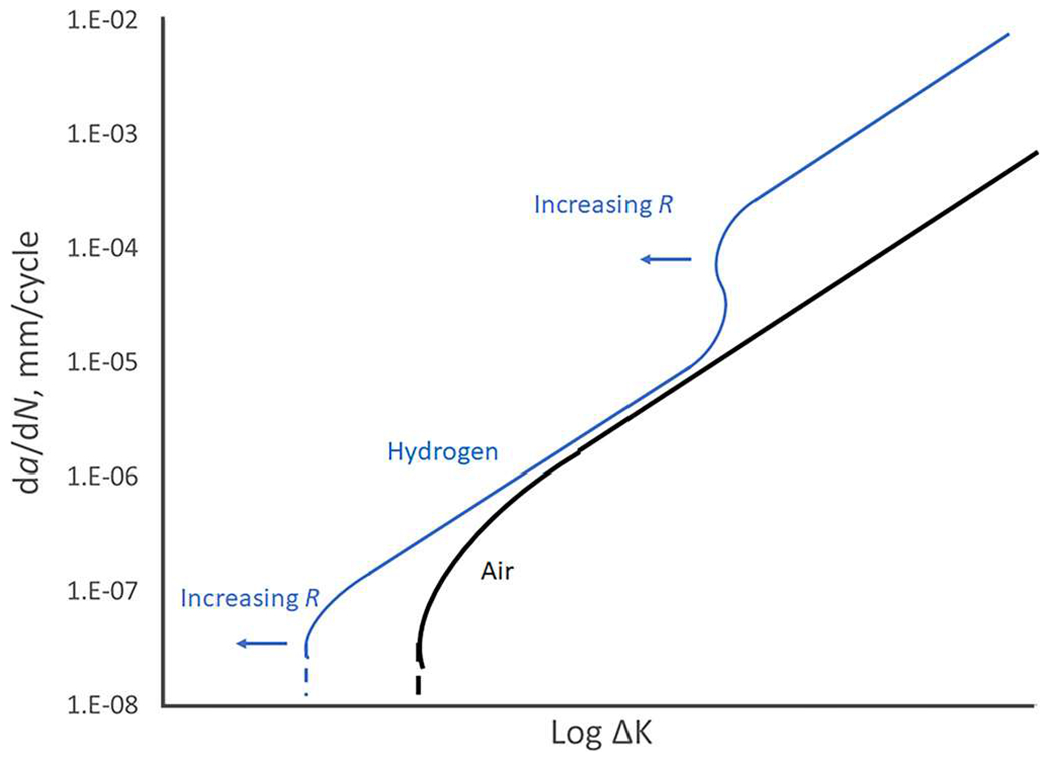
Diagram of the effect of stress ratio on the HA-FCGR. An increase in stress ratio causes a lowering of the stress intensity required for the onset of crack acceleration (which is tied to the maximum stress intensity factor) and causes a lowering of the stress for the onset of stage III FCGR.¹⁰⁴ Note that there is no effect of stress ratio on the FCGR in air or inert environments. Adapted from Suresh and Ritchie, Met. Sci. 16, 529 (1982).¹⁰⁴ Copyright 1982 Taylor and Francis.

FIG. 9.

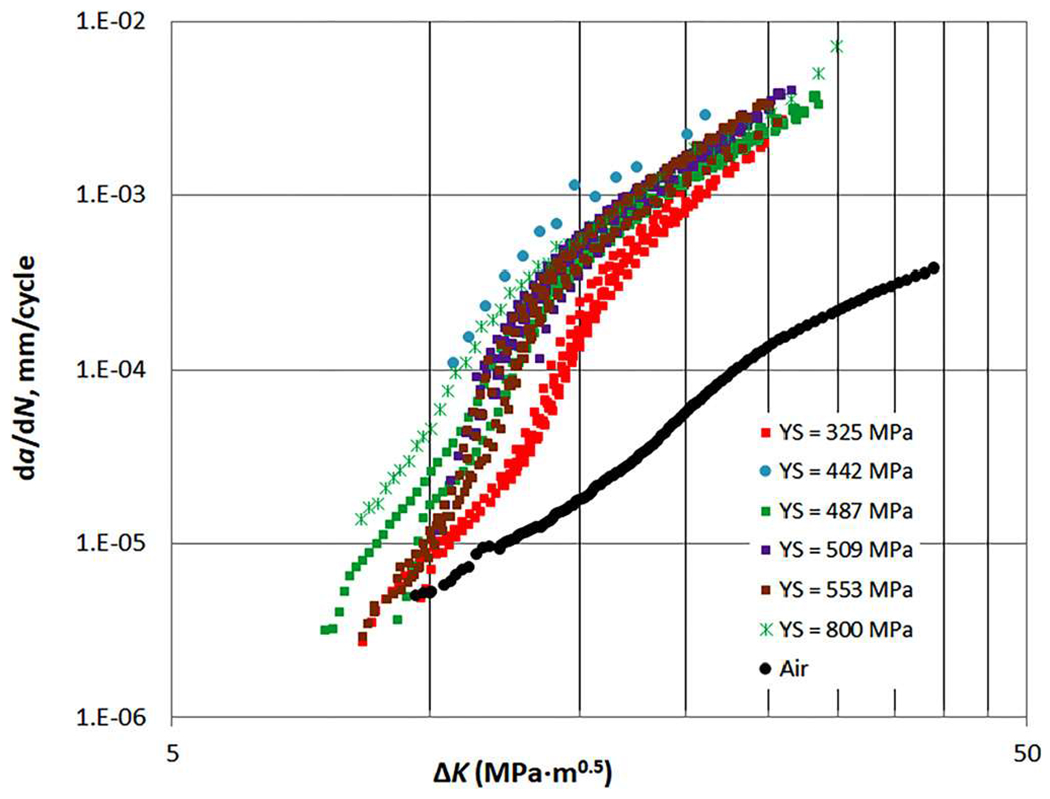
HA-FCGR at a hydrogen gas pressure of 5.5 MPa, loading frequency of 1 Hz, and stress ratio of 0.5 for pipeline steels with yield strengths ranging from 325 MPa to 800 MPa. As shown in Ref. 106, Slifka et al., measured the HA-FCGR of ferritic steels with yield strengths ranging from 325 to 800 MPa, at a hydrogen gas pressure of 5.5 MPa, loading frequency of 1 Hz, and a stress ratio of 0.5, and found no correlation between the yield strength and HA-FCGR. Reprinted from Slifka et al., J. Pressure Vessel Technol. 140, 011407 (2018).¹⁰⁶

FIG. 10.

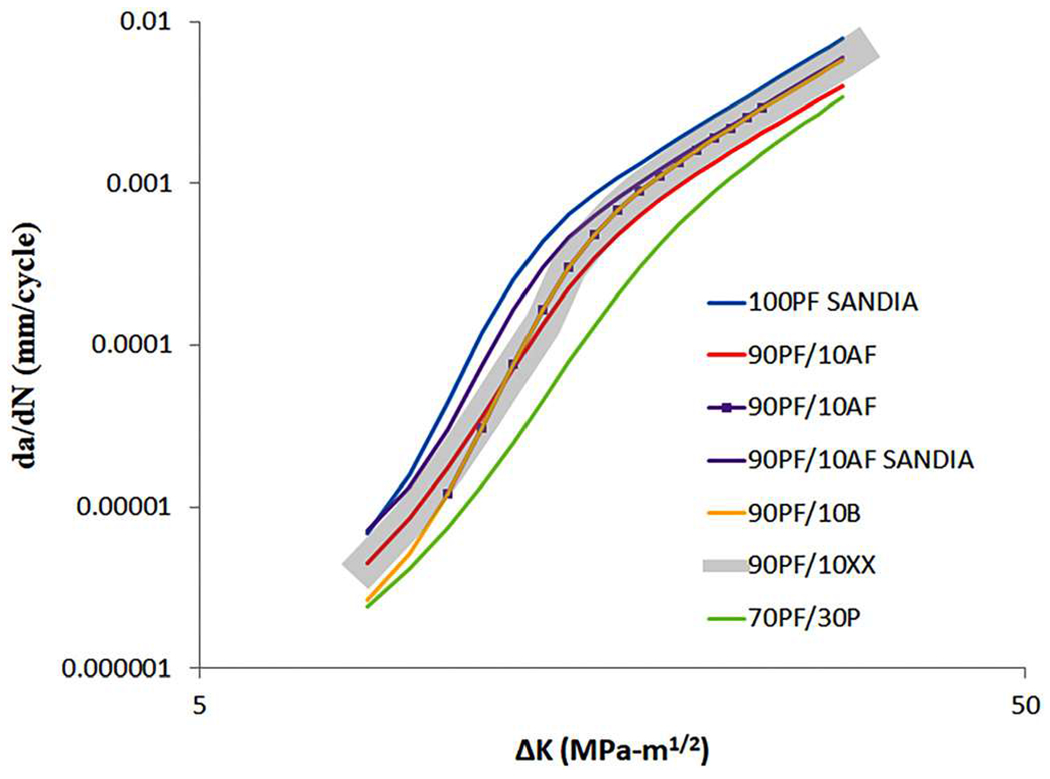
HA-FCG of pipeline steels with varying amounts of polygonal ferrite (PF) tested at a hydrogen gas pressure of 5.5 MPa, loading frequency of 1 Hz, and stress ratio of 0.5. AF = acicular ferrite, B = bainite, P = pearlite, and XX = all secondary potential constituents. It has been found that the percent polygonal ferrite in pipeline steels correlates well with the HA-FCGR for these tests. Reprinted from Amaro et al., J. Pressure Vessel Technol. 140, 021403 (2018).¹¹¹

In general, FCGRs increase in hydrogen environments (H₂ pressures of 1.7 MPa or more) by a factor of 10 or more over that in air or inert environments,^{70,75,78,95,102,104,112,113} as shown in Fig. 11. The effect of the gas pressure on the HA-FCGR observed in the literature varies. Plain carbon ferritic steels generally show an increase in FCGR as the hydrogen gas pressure increases.^74,114 On the other hand, San Marchi et al. concluded that there is little pressure dependence on the HA-FCGR for a range of ferritic steels.⁹⁶ Another study shows only modest increases in HA-FCGR with an increase in hydrogen gas pressure, but variation in sensitivity based on the microstructure.¹⁰⁶ At high ΔK (>30 MPa√m), measurements show ferritic steels converging to the same HA-FCGRs irrespective of the hydrogen gas pressure over a range from 6.9 to 103.4 MPa.⁷⁸ The loading frequency can have an effect on the HA-FCGR, but it is generally not a large effect. For ferritic steels, some steels show little or no effect, while some show a small effect which can be modeled with a power law factor.¹¹⁵ For quench and temper steels, Peral et al. found that some steels had little change with loading frequency, but some had significant increases in the HA-FCGR as frequency decreased.¹¹⁶ The decrease in some steels and not in others was correlated with the microstructure and diffusion through hydrogen traps.

FIG. 11.

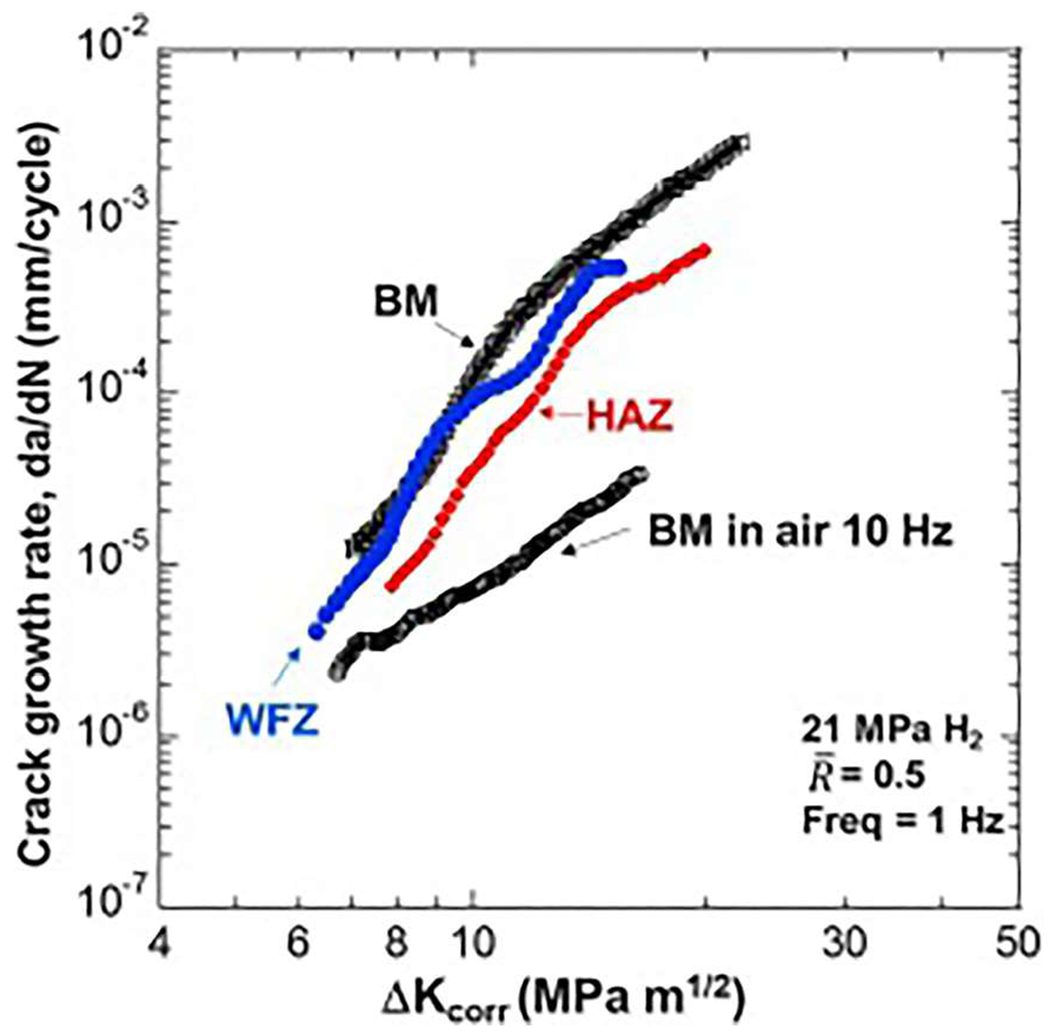
FCGR for a X100 pipeline steel, weld, and heat-affected zone, corrected for residual stress. In general, the FCGRs increase in hydrogen environments by a factor of 10 or more over that in air or other inert environments. Reprinted from Ronevich et al., Int. J. Fatigue 82, 497 (2016).¹¹⁷ Copyright 2016 Elsevier.

D. Performance of welds

For many ferritic steels, welds can he a particular consideration for effects of hydrogen due to inclusions and gradient microstructures.¹¹⁸ The combination of acute local heating, potentially uncontrolled cooling rates, and various diffusible impurity/dopant elements, such as carbon and sulfur, means that a wide variety of secondary phases and combinatory microstructures can occur due to the welding processes. These secondary phases and differing microstructures may be more susceptible to hydrogen embrittlement. The time period of the weldment can have a great influence over the qualities of the weld. For instance, older welds tend to have more inclusions than newer welds. Welding processes since the 1990s produce cleaner microstructures with finer grain sizes and more uniformity than older welds. However, all welds typically show higher aspect ratio ferrite grains and much more variation in grain size than base metals. Most welds consist of either Widmanstätten ferrite or acicular ferrite with Widmanstätten side plates with allotriomorphic ferrite (of varying width) on prior austenite grain boundaries.¹¹⁹ Welds may also contain pearlite, with older welds having more pearlite than newer welds. Friction stir welds are made from the base metal itself, so they tend to have finer grains than the base metal, but can contain more carbides.¹²⁰ Electrical resistance welds (ERWs) are virtually indistinguishable in many cases from the base metal, as long as the ERW process did not induce large voids.

In addition to the welds themselves, the surrounding metal undergoes heating and cooling due to the welding process. This can create an extensive heat-affected zone (HAZ) with gradient microstructures related to the amount of heating received and the local rate of cooling. HAZs on older steels range from martensite with varying morphologies and degrees of tempering near the fusion zone to various degrees of degeneration of pearlite as the HAZ gets closer to the base metal. Grain size can also vary widely in the HAZ with grains an order of magnitude larger than those in the base metal down to several times smaller than in the base metal, sometimes occurring along the gradient of the HAZ.¹¹⁹

Most mechanical tests in hydrogen on welds have been in the form of FCGR testing.¹²⁰ In most cases, welds did not perform much differently in hydrogen than the base metal, particularly for modern welds (from the 2000s to the present).^113,119 However, some effects of inclusions were seen, such as pinning of the crack reducing the FCGR, and particularly effects from residual stresses may be significant.^119,120 The welds of austenitic steels in hydrogen have been widely researched, but little has been measured for ferritic steels. Olden et al. found that the fracture toughnesses were similar for welds and base metal for an X70 steel pipe.¹²¹ HAZs for both X52 and X70 pipes were tested and modeled for fracture toughness, with the base metals being at least as susceptible to hydrogen as the heat-affected zones.¹²²

IV. FAILURE MECHANISMS

While the focus of this review is on ferritic steels, the exclusion of studies of all other material classes in any discussion of embrittlement mechanisms is impossible. Most researchers agree that, with a couple of exceptions, given the universality of hydrogen’s effect on structural materials, any hydrogen embrittlement mechanism must be equally universal. As such, several studies were done on model materials, such as nickel, with a brief follow-up study to show that the results were equally valid in BCC materials. Therefore, while this section focuses on ferritic steels, studies referring to results in other materials are also discussed in context. It should be noted that there are several extensive reviews focusing on the history and details of particular mechanisms; these are cited in the appropriate sections for readers desiring more depth.

A. Hydrogen enhanced decohesion

One of the oldest and longest-established contemporary mechanisms, the concept of decohesion, was first proposed by Troiano in 1960.¹²³ The basic premise is that dissolved hydrogen lowers the cohesive strength of metal bonds, enabling these bonds to rupture at lower applied stresses.¹²⁴ There are arguably two types of decohesion: lattice decohesion and boundary decohesion.

The decohesion of boundaries, whether grain boundaries or those around secondary phases, is one of the relatively undisputed mechanisms of hydrogen embrittlement, particularly in certain materials. Hydrogen has been clearly shown to be trapped at secondary phases, such as carbide precipitates in steels,^17,125,126 as well as at grain boundaries.^127,128 As hydrogen is trapped and accumulates in the boundaries of secondary phases or grain boundaries, it reduces the cohesive strength of the boundaries leading to failure.¹²⁹ In nickel, it has been observed that by simply allowing enough hydrogen to accumulate at the grain boundaries through aging, a high percentage of the fracture is intergranular.¹³⁰ In dissimilar metal welds, it was observed that “cleavage-like” failure through the “feature-less” zone of the weld [a free-centered cubic (FCC) metal that should not show cleavage failure] was actually due to the hydrogen-assisted boundary failure of crystallographically-aligned 100-nm needle-shaped carbide precipitates, causing the weld material to fail much like perforated paper.¹³¹ There are arguments over whether carbides, titanium, and/or vanadium rich, act as useful sinks that keep hydrogen away from critical areas, or whether they are critical fracture initiation sites. Martin et al.¹⁵ showed a case where carbides, though near the surface, clearly did not impact the fracture path.

However, intergranular failure is less common in ferritic steels than in face-centered cubic (FCC) austenitic alloys or nickel-based alloys.^129,132 It is observed under conditions of aggressive electrochemical charging¹³³ and under fatigue.^112,134 However, calculations of the reduction in boundary cohesive strength due to the presence of hydrogen show that the equivalent of a large hydrogen gas pressure is needed to produce a meaningful reduction in the cohesive energy of the boundary,¹³⁵ suggesting that other factors are necessary to produce intergranular failure.

Hydrogen-enhanced decohesion (HEDE) of the lattice is more strongly debated. There is no question that, in ferritic steels, the addition of sufficient hydrogen under the right loading conditions results in a transition from ductile failure (usually microvoid coalescence) to a brittle-appearing transgranular failure.^{14,15,136,137} Some authors^29,138 have described the effect of hydrogen as a ductile-to-brittle transition, similar to that which occurs around 100 to 120 K (−150 to −170 °C) in ferritic steels,¹³⁹ but dependent on hydrogen rather than temperature.

The HEDE model postulates that hydrogen reduces the cohesive strength of the lattice, such that bonds will rupture at lower applied stresses.¹²³ This reduction in cohesion is postulated to be directly correlated with the amount of local hydrogen; the greater the hydrogen concentration, the greater the reduction in cohesion, though the exact relationship between the degree of reduction of cohesion and hydrogen concentration is still not known.^140,141 As such, the critical point would be directly ahead of a crack tip, where the stresses are the greatest, leading to a higher hydrogen concentration.¹⁴² Higher stresses than expected by classical continuum mechanics are proposed by taking into account strain gradient plasticity.^143,144 Dislocation emission from the crack tip is proposed to shield the crack tip, moving the maximum stress further ahead of the crack tip where large triaxial stresses can cause very high concentrations of hydrogen even with low bulk concentrations.¹⁴⁵ Due to the very high proposed stresses (near theoretical stress of the material), it is proposed that the decohesion effect of the hydrogen (present in high concentrations) does not have to be very great to be effective.¹⁴⁵ Atomistic modeling suggests that a couple of mechanisms by which the presence of hydrogen encourages brittle fracture include the formation of a brittle “nanohydride” phase at the crack tip⁵³ or hydrogen suppression of dislocation emissions from the crack tip.²⁹

Because of the relative simplicity of the model and the brittleness of failure, it is claimed that the HEDE mechanism is the only mechanism that can predict the effect of hydrogen on cracking threshold and rates.¹⁴⁶ However, a truly predictive mechanistic understanding is missing from all proposed mechanisms. A part of the problem with creating a mechanistic model is that there are no measurements of the effect of hydrogen on cohesive strength; only first principles calculations exist, and these may be “insufficient to provide quantitative results for real materials.”¹⁴⁷

B. Hydrogen enhanced localized plasticity

The hydrogen enhanced localized plasticity (HELP) model was put forward by Birnbaum, Robertson, Sofronis, and co-workers in the 1980s and 1990s; see Refs. 148 and 149 for comprehensive reviews. Careful in situ transmission electron microscopy (TEM) experiments showed that the introduction of hydrogen gas to the vacuum of the TEM caused changes in the dislocation behavior in nearly every metal observed, including iron.¹⁵⁰ Multiple effects were observed, especially increased dislocation velocity, closer dislocation spacing,¹⁵¹ reduced cross-slip, and slight reduction in stacking fruit energy. The dislocation velocity was observed to increase with increasing H₂ pressure surrounding the sample.¹⁵⁰ Interestingly, reduced cross-slip was found to not be an effect of hydrogen on the stacking fault energy, as that was found to be too small to have a significant effect,¹⁵² suggesting another factor must be at play. Modeling work came up with the hydrogen shielding model, by which hydrogen forms an atmosphere around the dislocation (similar to a Cottrell atmosphere) and alters the elastic field of the dislocation such that it alters the interaction between the dislocation and other obstacles, such as grain boundaries, interstitial atoms, secondary phases, and other dislocations.¹⁵³ The hydrogen forming the atmosphere is thought to be strongly attracted to the core of an edge-type dislocation, which is both a physical and an attractive trap, and once around the core, it stabilizes the dislocation in this edge configuration. The stabilization of the edge component of dislocations would explain the reduction in cross-slip.

While there are mixed results for whether solid-solution hydrogen causes hardening or softening, a few studies show clear softening in high purity iron,¹⁵⁴ though the degree of softening was dependent on temperature. This is consistent with the idea that hydrogen-enhanced plasticity is related to hydrogen embrittlement, as both are constrained to a particular temperature and strain-rate range. This is proposed to be the same range at which the hydrogen atmosphere can both form and keep pace with dislocation movement, as opposed to being too diffuse or acting as a pinning agent. Work in nickel¹⁵⁵ even showed serrated flow under certain conditions due to hydrogen pinning of the dislocations. The idea of a particular range of temperature and strain rate is consistent with other interstitial solute work, such as the effect of carbon in iron, known to cause dislocation pinning, which showed softening in a particular temperature range.¹⁵⁶ Further support comes from stress relaxation tests, which show increased relaxation rates in the presence of hydrogen compared to in its absence in iron,¹⁵⁷ stainless steel,¹⁵⁸ and nickel.¹⁵⁹ Increased relaxation rates suggest increased dislocation mobility. In fact, in nickel, while there was an increase in stress relaxation in the presence of hydrogen, the introduction of carbon to the material showed a decrease in stress relaxation.

The one point that early studies were unable to address was how increased local plasticity can lead to globally brittle behavior. The original idea for hydrogen-enhanced plasticity was first proposed by Beachem in 1972¹⁶⁰ based on evidence of plasticity that he observed on hydrogen-assisted fracture surfaces. Beachem postulated that hydrogen locally assisted the deformation processes, leading to locally ductile failure with a macroscopically brittle appearance. Recent studies in the past decade have started to reveal how that could be possible. Recent work, summarized in Ref. 148, examined the microstructure direcdy underneath hydrogen-induced fracture features, which revealed evidence of highly-developed plasticity exceeding that expected based on the brittle nature of the fracture surface features. In the case of nickel intergranular failure, the intergranular facets had slip traces suggesting a planar slip, but underneath the fracture surface, a dense dislocation structure existed, suggesting that the material had undergone more strain than suggested by the mechanical response.¹⁶¹ This cell structure extended several mm away from the fracture surface, suggesting that this accelerated plasticity occurred throughout the strained material, not just immediately at the fracture surface.¹⁴⁹ Nearly identical results were found beneath intergranular features in iron,¹³³ and similar results were found underneath “brittle” transgranular fracture features in ferritic steel.^14,15

Therefore, how might differences in dislocation motion, such as increased mobility, increased packing, and decreased cross-slip, influence failure? To start with, it would be expected that a difference in the microstructural development with strain would occur. The simplest effect would be an increased dislocation density, as an increased velocity allows for increased multiplication from dislocation sources.¹⁶² But other effects are also possible, as closer spacing will change dislocation organization, such as cell walls, and reduced cross-slip will affect when transitions between different stages of deformation occur. Not only has an increase in dislocation density with increasing hydrogen concentration been observed,¹⁶³ and delays in transitions between different stages of deformation with hydrogen,^164,165 but differences in dislocation cell development, local crystal rotation, and grain rotation and grain shape development with strain have been observed with hydrogen.¹⁶⁶ Additionally, since the hydrogen atmospheres would be expected to move with the dislocations, this could lead to different distributions of hydrogen than would occur if only classical Fickian diffusion dominated. Some experiments on single crystals^167,168 have shown that accelerated diffusion could be associated with dislocation activity, though studies on polycrystalline materials were more ambiguous,^169,170 likely due to grain boundary and dislocation interactions. Modeling suggests that higher concentrations and larger distributions could occur if dislocation transport of hydrogen occurred.⁶⁶ By changing the microstructure of the material and distribution of the hydrogen, it is reasonable to expect that circumstances for accelerated failure could occur.

The exact mechanism by which hydrogen influences dislocation motion is still debated in the literature. There are arguments as to whether enough hydrogen forms around dislocations to have an influence on the motion,¹⁷¹ though a counter argument from modeling has suggested that hydrogen–hydrogen attractive interaction, suggested by thermodynamic considerations,¹⁷² could account for the needed concentration.¹⁷³ It is understandable that, without direct evidence of where hydrogen gathers around the dislocations, the exact mechanism by which hydrogen influences the dislocation activity will still be an active part of scientific debates. However, evidence clearly shows that dislocation motion is affected, and that microstructural evolution is affected. As cracks in engineering materials do not propagate through virgin, undeformed materials, this difference in the evolution in microstructure should be considered when describing the action of hydrogen on failure.

C. Hydrogen-enhanced strain-induced vacancies

The discovery of increased vacancy generation in the presence of hydrogen and the concept that these vacancies may be critical to the mechanism of embrittlement can be attributed primarily to the work of Nagumo and co-workers (See Ref. 174 for a comprehensive overview).

Due to their small size, vacancies are difficult to image or detect directly. Through careful TDS, Nagumo et al. noticed that plastic deformation in the presence of hydrogen resulted in a “superabundance” of vacancies compared with the equilibrium in iron.¹⁷⁵ This superabundance was a concentration of vacancies more than 15 orders of magnitude above the equilibrium concentration at room temperature. This high concentration of vacancies has been found by other researchers and in other materials.^176,177 First-principles calculations show that binding with hydrogen reduces the formation energy of vacancies,¹⁷⁸ which leads to higher concentrations. The trap sites detected by TDS were determined to be vacancies because the absorption capacity of the strained sample was reduced by annealing at low temperature, in other words, the traps were removed from the sample at lower temperatures than would remove microstructural defects such as dislocations. The use of low temperature TDS, which can provide better definition between lower temperature traps, produced data that suggest multiple lower energy traps, which were interpreted to be different sized dusters of these vacancy–hydrogen complexes.^174,179

Another method for detecting vacancies is positron annihilation spectroscopy. Inhomogeneities such as vacancies or microstructural defects such as dislocations and grain boundaries can trap positrons leading to higher numbers of positrons with higher mean lifetimes, and each defect traps differently. The analysis of mean positron lifetimes in a material can resolve the distribution of traps. Tensile straining of iron leads to an increased mean positron lifetime, and this lifetime is further enhanced by hydrogen-precharging prior to tensile straining.^179,180 It is proposed that hydrogen enhances the dislocation activity, which in turn increases the vacancies, which are formed as debris in the dislocations’ wakes. These vacandes are stabilized by the presence of hydrogen, and further collect into clusters.

The association of vacancies with embrittlement mechanisms is seen in combined tensile and heating experiments.¹⁷⁴ Iron or Incond 625, which is pre-strained in hydrogen to induce damage, shows loss in ductility when strained to failure. Some ductility is regained when aged to rdease hydrogen, as expected. However, full recovery occurred after aging at an elevated temperature, which was high enough to remove the hydrogen–vacancy complexes, but not high enough to influence dislocation structures. It is because of this evidence that Nagumo argues that it is the accumulation of vacandes, not the developed microstructure, which is critical to hydrogen embrittlement.

Failure has been proposed to be a finer scale version of ductile microvoid coalescence. Some groups have dubbed this phenomenon the nano-void coalescence (NVC) model,¹³⁶ illustrated in Fig. 12. Vacancy dusters coalesce into nano-voids, which, when large enough and closely spaced enough, coalesce similarly to microvoids in traditional macroscale ductile fracture. This is proposed to happen in areas of intense strain localization, such as slip bands.¹⁷⁴ An example of this failure is the “quasi-cleavage” failure of ferritic steel.¹³⁶ However, it is worth noting that this study is very similar to the material and conditions proposed by Martin et al.,¹⁵ who drew different conclusions as to the mechanism, and did not find evidence of nano-voids, even surrounding carbides near the fracture surface, which would be expected nucleation points.

FIG. 12.

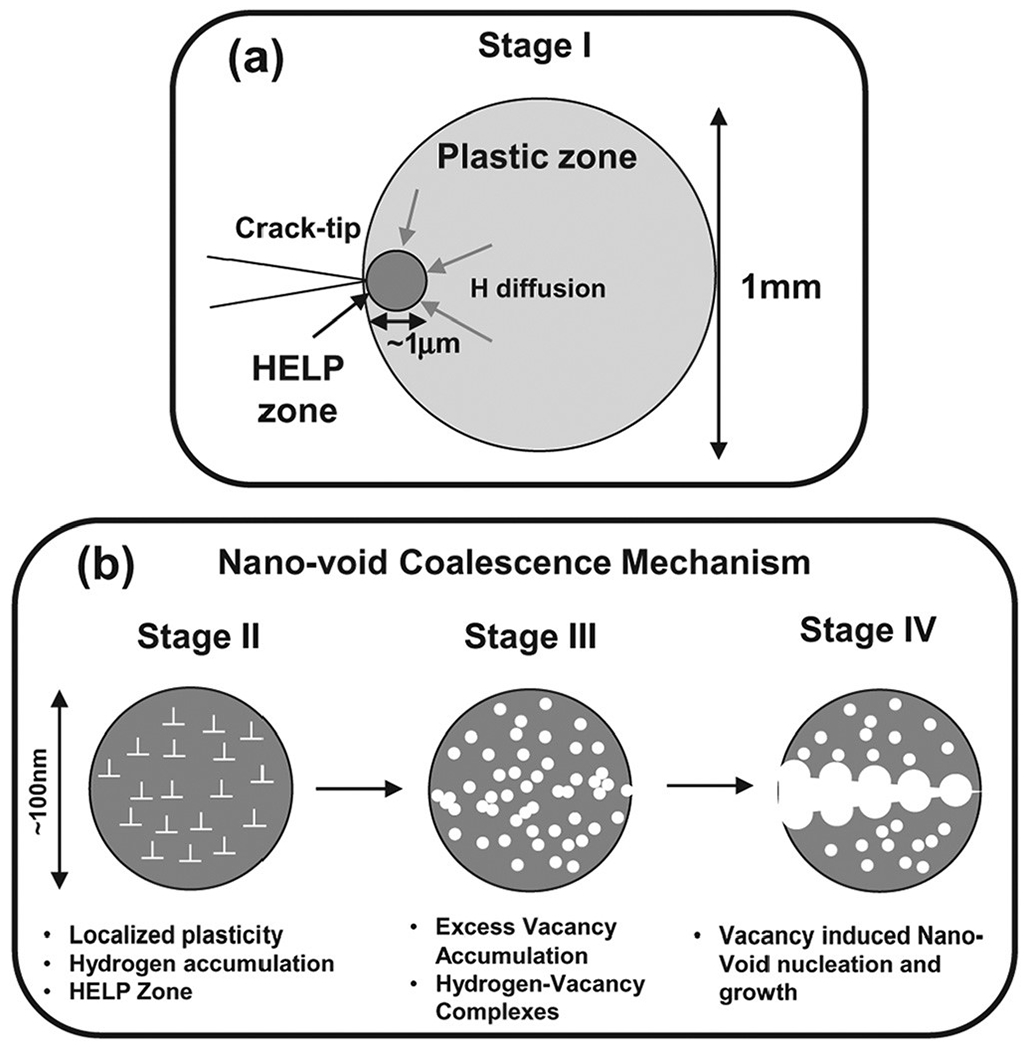
Schematic of a nano-void coalescence model. Vacancy clusters coalesce into nano-voids, which, when large enough, and closely spaced enough, coalesce similar to microvoids in traditional macroscale ductile fracture. This is proposed to happen in areas of intense strain localization, such as slip bands. In (a) a plastic zone, including the locally hydrogen-affected region, is shown forming ahead of the crack tip. (b) Plasticity leads to enhanced vacancy formation, and the vacancies coalesce to form voids, leading to bulk failure. Adapted from Neeraj et al., Acta Mater. 60, 5160 (2012).¹³⁶ Copyright 2012 Elsevier.

Though indirect, the evidence of large concentrations of vacancies after straining in hydrogen is overwhelming. Therefore, the connections between dislocations and vacancies cannot be ignored. Accelerated dislocation activity, as described above, leads to the accelerated formation of higher concentrations of vacancies.¹⁸¹ These vacandes in turn affect grain boundaries¹⁷⁶ and dislocations, promoting climb and jog formation as they annihilate in reactions with dislocations.¹⁸² This increased climb, which could allow bypassing of obstacles, and increased jog formation could contribute to the differences in microstructure development observed during deformation with hydrogen.

D. Hydrides/phase transformations

Hydride formation and cleavage is one of the few undisputed mechanisms, but only for hydride-forming materials, such as Group Vb metals (vanadium, niobium, and tantalum), titanium, zirconium, and their alloys.^183–187 The low hydrogen solubility of the materials leads to the precipitation of a brittle hydride phase, which can deave along crystallographic planes under stress.¹⁸³ Crack tip stresses may also induce hydride predpitation by creating a region of tensile stress into which the hydride expansion can be accommodated. Here, the morphology of the hydride can influence the crack direction.¹⁸⁸

Metal hydrides can form in other metallic systems, such as nickel, under conditions of high stress or high hydrogen fugacity, such as under aggressive charging conditions.^189,190 These hydrides are typically metastable. Based on atomistic simulations, some researchers⁵³ have suggested that nanohydrides can form ahead of crack tips. If this were the case, it would be expected that failures would conform to specific crystallographic planes. In the case of nickel, failures typically go from ductile to intergranular failure (with an increasing percentage of intergranular failure with increasingly aggressive environments),^130,191 with no “brittle transgranular” regime. In ferritic steels, recent work¹⁵ looking at “brittle” transgranular features has shown that they do not correspond to crystallographic planes and are not even planar. Also, in iron, hydrides have been observed under at least 3.5 GPa of hydrogen gas.¹⁹² While this was shown to be a brittle phase, the high pressures necessary for the formation of the hydride makes their presence likely not relevant to most hydrogen embrittlement conditions. Therefore, models that suggest crack-tip hydrides in iron or iron alloys are not suitable, as stresses, even ahead of crack tips, will not reach that level of stress, but will instead cause dislocation emission.

A second type of hydrogen-induced phase transformation is found in austenitic stainless steels, where hydrogen assists in the formation of martensitic phases.^193–195 The importance of this phase transformation to the hydrogen embrittlement is still under debate.^196,197 As ferrite is a more stable phase than austenite or martensite over the temperature range in which hydrogen embrittlement occurs, this mechanism is not available to ferritic steels.

E. Defactant concept

The “Defactant” concept, as developed by Kirchheim and co-workers,^198–200 is a thermodynamics framework that addresses solute–defect interactions, and can be specifically applied to hydrogen embrittlement. The concept is that hydrogen (or solutes more generally) acts on defects analogous to surfactants acting on surfaces (the term DEFect ACTing AgeNT is taken from the etymology of SURFace-ACTing AgeNT), reducing the formation energy of defects. The higher the chemical potential of hydrogen (related to concentration), the greater the effect. One way to interpret this is taking an alternative view of trapping theory;^54,55 instead of considering how the hydrogen solute atom reduces its energy by finding trapping (lower energy) sites, consider that the defect trap gains energy by trapping the hydrogen. One result would be that vacancies are stabilized²⁰¹ (supporting the results associated with the vacancy mechanism). Another effect would be an increase in dislocation motion, especially in BCC metals, by increasing double kink-formation due to a decrease in the line energy of dislocations¹⁹⁹ (supporting the results associated with the HELP mechanism). As such, various aspects of the mechanisms described above could be considered specific cases of the “Defactant” mechanism, with the chemical potential of hydrogen and the available defects determining the dominant effect. While, as currently formulated, this model cannot currently predict which condition will be dominant, this may be due to the fact that it currently lacks kinetic considerations.

F. Combinations of mechanisms

While there has always been a certain degree of agreement that different mechanisms could be operating under different conditions, and that understanding the regimes is critical to describing embrittlement, it is more recently that the idea of multiple mechanisms working together has been accepted.^202,203 One of the first studies to clearly delineate how different mechanisms could be cooperative was by Novak et al.²⁰⁴ In this work, the authors proposed a model whereby a dislocation pileup impinges on a grain boundary precipitate whose interface decoheres, leading to a crack.

In the case of intergranular failure, there is a difference in materials and conditions. Studies on nickel show that increasing the aging time of hydrogen in nickel increases the percentage of intergranular failure.¹³⁰ In other words, if there is sufficient hydrogen accumulated at the grain boundaries of nickel, the boundaries will fail brittlely with minimal strain. However, many other cases consider more dynamic conditions where the hydrogen does not have time to accumulate sufficiently, and yet intergranular failure still occurs. And in the case of iron, it can occur, but only under particular conditions. Atomistic modeling has calculated that hydrogen causes a reduction in the cohesive strength of grain boundaries dependent on the external H₂ gas pressure,¹³⁵ but, except for at very high pressures (significantly higher than 500 MPa), this reduction is insufficient to cause intergranular failure, suggesting other mechanisms are at play. Studies looking at the microstructure immediately underneath the intergranular fracture surface in iron,¹³³ as well as in nickel,¹⁶¹ found a highly developed dislocation structure indicative of strains significantly larger than expected, based on the strain at failure. Further studies showed that this dislocation structure exists more than three mm away from the fracture surface,¹⁴⁹ confirming that this is not a crack tip concentration effect. The HELP mechanism influenced the dislocation structure development leading to accelerated deformation. Dislocation–grain boundary interactions are very complicated,²⁰⁵ but can have the characteristic of multiple dislocations absorbed into a grain boundary prior to a single dislocation being ejected from the grain boundary. This would likely have two results: the first is distortion of the grain boundary due to the dislocation interactions, and the second would be deposition of hydrogen into the grain boundary, as more dislocations carrying hydrogen coming in than leaving the grain boundary would result in a net deposition of hydrogen. Both of these results would lead to lowering of the cohesive strength of the grain boundary.²⁰⁶ In this scenario, the reduction of the grain boundary cohesive strength is critical to intergranular failure but would not have occurred without the HELP-accelerated deformation. This was seen again in martensitic steels^207–209 where “quasi-cleavage” failures were found to actually be martensitic lath boundary failures, and the boundaries that failed were strongly disturbed by extensive dislocation activity in the form of shear bands, illustrated in Fig. 13.

FIG. 13.

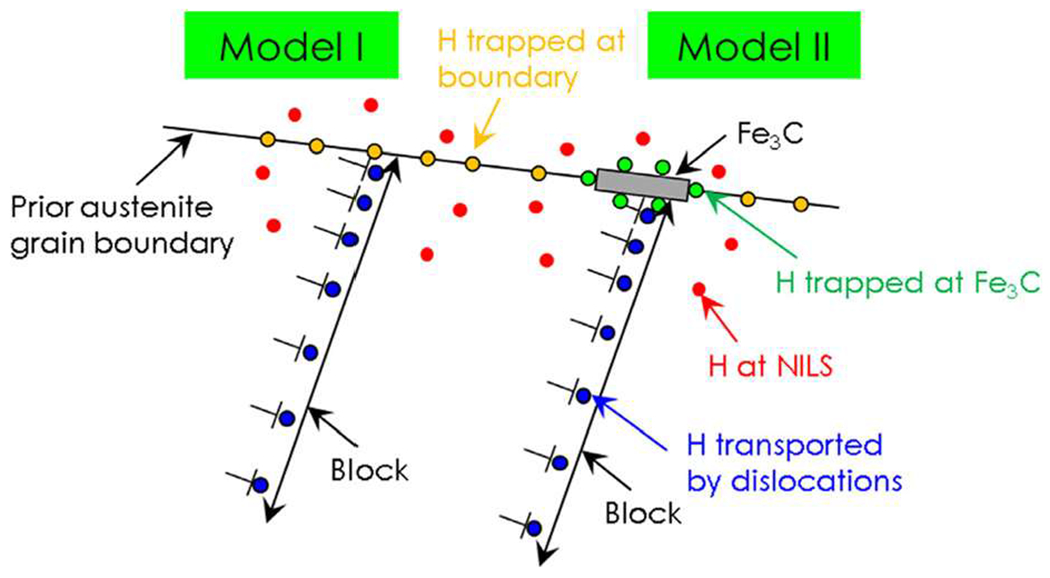
Schematic of HELP-assisted decohesion in martensitic steel. Hydrogen is transported to boundaries while the dislocations depositing the hydrogen also deform the boundaries. In martensitic steels, “quasi-cleavage” failures were found to actually be martensitic lath boundary failures, and the boundaries that failed were strongly disturbed by extensive dislocation activity in the form of shear bands. Adapted from Nagao et al., J. Mech. Phys. Solids 112, 403 (2018).²⁰⁹ Copyright 2018 Elsevier.

Other potential connections between different mechanisms could exist and are directions for further research.²⁰³

V. RECENT PROGRESS AND INSIGHT

The deleterious effects of hydrogen on the physical properties of iron and steel have now been realized for over a century;⁶ however, despite the extensive work over that time period, there are still significant questions related to the structure–property–performance relationships of steels subjected to hydrogen embrittlement. These questions have largely remained unanswered for ferritic steels due to specific challenges associated with these steels coupled with the global difficulties with gauging the hydrogen content in all materials. Perhaps the primary challenge, ferritic steels are known to have large diffusivities and small solubilities with respect to H₂, often leading to specimens that exhibit in-air properties shortly after (≈45 min) removal from an H₂ environment.²¹⁰ As such, recent effort has focused on specialized test chambers capable of in situ mechanical testing via neutron and x-ray measurements in gaseous hydrogen. There are several experimental difficulties with the direct observation of hydrogen in structural materials, both from limitations in spatial and temporal resolution²¹¹ and the abundance of “background” H₂ in high vacuum chambers.²¹² Thus, significant work has centered on high-resolution spectroscopy, microscopy, and atom probe tomography (APT) of ferritic steels after H₂ testing, with an emphasis on assessing the H₂ content, location, and binding states, and distinguishing environmentally-derived background H₂ from test-induced H₂. This section will highlight the recent progress and insight gained from both the in situ tests and high-resolution measurements. For information on other currently-used methods for hydrogen detection in steels (e.g., TDS, Ag reduction/decoration, hydrogen imprint technique, and neutron radiography), readers are directed to a recent review paper²¹¹ and a portion of the references therein.^213–216

A. In situ mechanical testing

Connolly et al.^11,12 designed, fabricated, and validated a gas-pressure chamber capable of in situ mechanical tests of steel specimens subjected to neutron scattering and x-ray diffraction measurements. In addition to the usual concerns of safety with a gas-pressure chamber, the walls of the chamber also needed to be adequately transparent to neutrons and x-rays. A monolithic 6061-T6 aluminum chamber with a 3.175 mm wall thickness met the necessary requirements. The authors used the chamber while conducting neutron-diffraction-based mapping of the strain field near fatigue crack tips in X70 steel C(T) samples in both hydrogen and air.¹¹ The resulting strain maps in hydrogen and air are shown in Fig. 14. The results suggest that the effect of hydrogen is to enhance crack-tip elastic strain for a given far-field load beyond that noted in air, which would be consistent with the HEDE theory that Fe–Fe interaction energy is decreased by hydrogen.

FIG. 14.

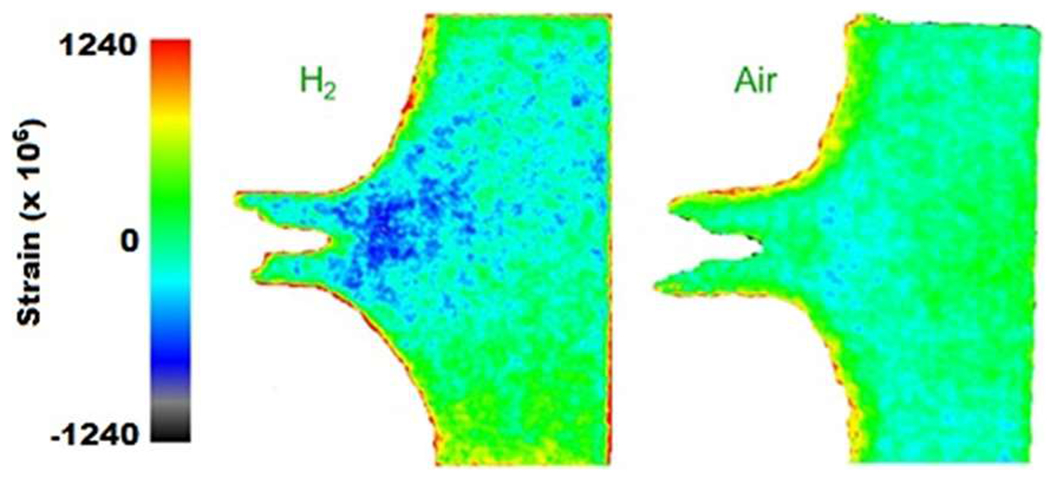
Strain mapping of an X70 steel C(T) sample under mechanical load in both hydrogen and air by neutron scattering. The results suggest that the effect of hydrogen is to enhance crack-tip strain for a given load beyond that noted in air. Adapted from Connolly et al., Rev. Sci. Instrum. 88, 063901 (2017).¹¹ Copyright 2017 AIP Publishing.

The chamber also allowed synchrotron x-ray diffraction measurements of the differences in the strain fields near the fatigue crack tip in AISI 4130 steel generated in air and in hydrogen.¹² In this study, the authors were able to determine the y-component and x-component strains, as well as the dislocation density, as a function of distance from the crack tip. There are significant differences in the air and hydrogen dislocation density profiles ahead of the crack tips, suggestive of the HELP mechanism. Together, the results from the neutron scattering and x-ray diffraction measurements allude to a combination of the HEDE and HELP mechanisms, with HEDE driven by an increase in hydrogen concentration through HELP.

While these and other studies²¹⁷ have shown the usefulness of x-ray and neutron diffraction, the diffracted beam is only one part of the scattered x-ray or neutron beam. While the diffracted beam, corresponding to zero energy transfer between the sample and the beam, provides information about the structure of a sample, scattering with non-zero energy transfer provides information about the dynamics. Quasi-elastic neutron scattering can provide hydrogen diffusion coefficients specific to particular components of a material’s microstructure, as shown for the case of dislocations.²¹⁸ Inelastic scattering (both x-ray and neutron) may provide insights into the effect of hydrogen on atomic bonding of the host metal; most of our current understanding of hydrogen’s effect on metal–metal bonds comes from first-principles modeling. Neutron imaging, which measures the attenuation of the transmitted neutron beam rather than the scattered beam, is particularly powerful in mapping hydrogen concentrations due to the strong interaction between neutrons and hydrogen.²¹⁹ The strength and usefulness of this field of study to understanding hydrogen embrittlement will likely depend on the continuing efforts and ingenuity of researchers in combining measurements (e.g., in situ mechanical testing with strain mapping).

B. High-resolution microscopy

The disparate scales involved in relating macroscale mechanical responses to nanoscale microstructural responses understandably result in difficulty in relating effects over the numerous length scales. An example of this disparity is the difficulty of relating enhanced dislocation motion of the HELP mechanism to brittle-appearing fracture surfaces and reduced mechanical ductility. Advances in microscopy technology and techniques have allowed correlation between length scales and different aspects of fracture in ways that were previously unfeasible. For instance, by looking at different length scales, Bertsch et al.¹⁶⁶ showed that the higher dislocation density in TEM measurements due to loading in hydrogen was arranged such that larger-scale scanning electron microscopy (SEM) measurements of grain orientation showed less reorientation in H₂ than in air. In other words, at a finer scale, the evidence was for increased plasticity, but manifested at the coarser scale in a way that would suggest less plasticity.

In particular, the combination of high-resolution techniques has led to insight into mechanisms of hydrogen-assisted fracture. Martin et al.^14,15 utilized high-resolution SEM, TEM, and atomic force microscopy (AFM) to examine the different morphologies on hydrogen-induced fracture surfaces for ferritic steels. These studies focused on quasi-cleavage features, a classical feature of hydrogen embrittlement in ferritic steels, but separated them into two morphologies: “quasi-cleavage,” which they defined as covered with river patterns, and “flat,” which were comparatively featureless. By using focused ion-beam (FIB) machining to extract samples directly from fracture surfaces, Martin et al. were able to correlate surface features with microstructural features immediately beneath the fracture surface. In the case of the “quasi-cleavage” features, the river patterns were found to be ridges whose faces were parallel with dislocation structures along slip planes. In the case of the “flat” features, the fracture surface did not follow any crystallographic planes, while beneath the surfaces was a high density of dislocations which extended several micrometers from the surface with no discernable gradient, as shown in Fig. 15. Neeraj et al.¹³⁶ conducted similar high-resolution SEM, TEM, and AFM on ferritic steel fracture surfaces, but suggested a different failure mechanism based on an interpretation of the fracture surface features and sub-surface microstructures. While reaching different conclusions on the principal mechanism of failure, both sets of studies revealed that this combination of techniques results in insight into the fracture features, and that the microstructure beneath hydrogen-assisted fracture surfaces is not indicative of purely brittle processes.

FIG. 15.

TEM images of the microstructure and dislocation density below the hydrogen-induced “flat” fracture surface in a ferritic steel. Selected areas on the left are magnified on the right. The images shown in the insets are taken at depths of (a) 250 nm and (b) 1500 nm from the fracture surface. In Refs. 14 and 15, the authors examined different morphologies on hydrogen-induced fracture surfaces in ferritic steels. These studies focused on quasi-cleavage features, a classical feature of hydrogen embrittlement in ferritic steels, but separated them into two morphologies: “quasi-cleavage” and “flat.” The authors were able to correlate surface features with microstructural features immediately beneath the fracture surface. In the case of “quasi-cleavage” features, the river patterns were found to be ridges whose faces were parallel with dislocation structures along slip planes. In the case of the “flat” features, the fracture surface did not follow any crystallographic planes, while beneath the surfaces was a high density of dislocations which extended several micrometers from the surface with no discemable gradient Reprinted from Martin et al., Acta Mater. 59, 3680 (2011).¹⁵ Copyright 2011 Elsevier.

As a further example of insight from this technique, Wang et al.¹³³ studied the embrittlement of commercial-grade pure iron under electrochemical charging to induce intergranular failure. The dislocation cell structure found underneath the fracture surface was indicative of more plasticity than expected for a brittle intergranular process at 5% strain-to-failure. Undoubtedly, a more advanced microstructure than is indicated by the fracture surface processes develops in the presence of hydrogen. This is supported by similar studies in other classes of materials such as nickel,¹⁶¹ martensitic steels,^207,208 and austenitic stainless steels.²²⁰ This suggests that conclusions about the developing microstructure under environment-enhanced fracture surfaces cannot be made by examination of the fracture surface features alone.²²¹

In addition to the fabrication of site-specific TEM foils, FIB machining can also he used to produce small-scale samples of various geometries for in situ studies. Nanopillar compression tests,²²² microcantilever fracture toughness tests,²²³ and even small-scale tensile tests²²⁴ can provide insight into behaviors of single crystals or model materials, and could be expanded to local behavior of engineering materials.

Other in situ microscopy tools have been developed to examine the permeation and release of hydrogen in ferritic steels with nanoscale lateral resolutions. For example, Senöz et al.²²⁵ highlighted the efficacy of scanning Kelvin probe force microscopy (SKPFM) as a highly sensitive tool for detecting hydrogen in metals. The method was based largely on the Devanathan–Stachurski permeation cell,^226,227 where the bottom side of a sample is potentiostatically or galvanostatically charged with hydrogen (entry side) and the top side of the sample is polarized anodically to oxidize the permeating hydrogen (exit side), and this exit side of the sample is scanned with an AFM tip to measure the surface work function. By looking at duplex (ferrite–austenite) steels, they observed potential changes that they could attribute to the different diffusion behaviors between the two phases.^206,228

Krieger et al.²²⁹ used SKPFM, TDS, and electron microscopy to identify and analyze hydrogen trapping sites in a ferritic steel subjected to annealing, cold rolling, and recrystallization. The three mechanical and thermal treatments enabled a systematic study of trapping at vacancies, dislocations, grain boundaries, and inclusions without changing the chemical composition of the material. Comparing the SKPFM results to those of a known technique allowed elucidation of the behavior of different traps with a finer degree. For instance, as desorption was only observed from some inclusions by SKPFM, shown in Fig. 16, and TDS results suggest trapping vacancies, it was argued that desorption was dominated by the hydrogen released from vacancies at the oxide–matrix interface, as opposed to trapping and desorption from the oxide inclusions.

FIG. 16.

Topography (top row) and SKPFM (bottom three rows) images of (a) annealed, (b) cold rolled, and (c) recrystallized ferritic steel as a function of time. The samples were charged electrochemically with hydrogen, covered with a palladium detection layer, and tested in a nitrogen environment. In Ref. 229, the authors used SKPFM, TDS, and electron microscopy to identify and analyze hydrogen trapping sites in a ferritic steel subjected to annealing, cold rolling, and recrystallization. Comparing the SKPFM results to those of a known technique allowed elucidation of the behavior of different traps with a finer degree. As desorption was only observed from some inclusions by SKPFM, and TDS results suggest trapping vacancies, it was argued that desorption was dominated by the hydrogen released from vacancies at the oxide–matrix interface, as opposed to trapping and desorption from the oxide inclusions. Reprinted from Krieger et al., Acta Mater. 144, 235 (2018).²²⁹ Copyright 2018 Elsevier.

The advances in microscopy techniques combined with the ingenuity of researchers to combine these techniques in novel ways has led to advances in understanding how hydrogen interacts with materials. While some of these results, it could be argued, merely confirm accepted theories, the fact that direct evidence for these theories can now be observed and measured is an important development.

C. High-resolution spectroscopy

While the previous microscopy studies are able to give some indirect information on the location of hydrogen, the exact location of hydrogen within a metal microstructure remains an elusive unknown. However, new techniques in two-dimensional mapping by secondary ion mass spectrometry (SIMS) show promise to be able to answer the question of where hydrogen lies in a material.

An early study by Takai et al.²³⁰ used secondary ion mass spectrometry (SIMS) to observe hydrogen and deuterium trapping sites in high-strength steel specimens. While there is some debate whether deuterium has the same effect on metals as hydrogen,^37,231 it is still invaluable as a tracer for hydrogen, given its similar chemical characteristics and limited presence in test chambers. The authors were able to measure hydrogen ion counts at non-metallic inclusions, grain boundaries, and segregation bands that were 11.0×, 7.8×, and 5.0× higher than in the adjacent matrix. Takai et al.²³² later used SIMS to visualize the distribution and desorption of hydrogen and deuterium in ferrite and pearlite. At room temperature, the resulting SIMS maps showed a smaller deuterium concentration in ferrite than in pearlite, which was ascribed to a smaller number of trapping sites. After heating and cooling, the SIMS maps revealed that deuterium desorbs from the ferrite at lower temperatures than from the pearlite and related that to the likely difference in trapping between the two microstructures. In both cases, the authors showed that SIMS was able to visualize the distribution and desorption of hydrogen and deuterium but was limited for ferritic steels due to large diffusivities in the material and small lateral resolutions for the method (2 μm). More recent work has focused on decreasing the diffusivity via cryogenic testing and increasing the lateral resolution through improvements in the SIMS technique.

On cryogenic testing, Nishimoto et al.²³³ used a cold trap and stage cooling system to study the hydrogen uptake in a ferritic steel via SIMS at 83 K. From the SIMS, it was shown that the hydrogen secondary ion intensity in hydrogen-charged specimens was ≈2× larger than in uncharged specimens. This quantitative assessment was only possible at cryogenic temperatures, as this decreased both the H₂ diffusivity and background and obviated the need for deuterium as a surrogate. In addition, the authors demonstrated that H₂ sensitivity can be further improved via changes to the sputtering rate. This provides yet another tool for improving the overall sensitivity of the method and, by association, the chances of success for measuring hydrogen in ferritic steels via SIMS.

On lateral resolution, Sobol et al.²³⁴ utilized time-of-flight SIMS (ToF-SIMS) to study deuterium-assisted cracking in a duplex stainless steel; ToF-SIMS data were combined with electron microscopy to impart insight into the distribution and desorption of deuterium as a function of microstructure at lateral resolutions of ≈100 nm. The ToF-SIMS data suggested that austenite grains exhibit higher deuterium secondary ion yields than ferrite grains, as expected based on the differences in diffusivity and solubility. These gradients likely resulted in the cracking and delamination shown in Fig. 17(a). Figure 17(b) shows a cross-sectional image for one such plate, where the cracking morphology of a delamination in a high deuterium concentration region can be observed.

FIG. 17.

(a) SEM topographic image and ToF-SIMS PC1 deuterium data for a duplex stainless steel. The arrow-head shaped plates reveal cracks and microtwins with significantly higher deuterium concentrations. (b) Secondary ion cross-sectional profile for one such plate; the primary and secondary cracks likely occurred from rapid diffusion through the ferrite and subsequent trapping at the ferrite–austenite interface. Adapted from Sobol et al., Mater. Sci. Eng., A 676, 271 (2016).²³⁴ Copyright 2016 Elsevier.

McMahon et al.¹³ used nanoscale SIMS (NanoSIMS) to investigate deuterium distributions in stainless steel after fatigue tests at an even finer lateral resolution. Although many of the findings may be specific to austenite, it is important to note that the ≈50 nm lateral resolution was sufficient to image areas near crack tips and inclusions, thereby providing the ability to draw conclusions as to the underlying mechanisms for hydrogen embrittlement. For example, the authors showed enhanced deuterium levels at crack tips with highly localized regions of dislocation tangles, which suggests that dislocation tangles are trap sites for deuterium. Similar results were detected near inclusions. A logical next step in the use of SIMS on ferritic steels is cryogenic NanoSIMS. This combination would decrease the deuterium diflfusivity and increase the lateral resolution over previous studies, which may provide an analogous mechanistic understanding for hydrogen embrittlement in this class of materials.

A limitation of SIMS, particularly with regard to ferritic steels, is that it derives only chemical information, not crystallographic or microstructural information. As shown in Fig. 17, other microscopy techniques such as imaging of etched steel surfaces, electron channeling contrast imaging to see grain structures and secondary phases, or even electron backscattered diffraction mapping²³⁵ can provide additional information to complement the chemical mapping of SIMS and provide a complete picture of hydrogen distribution in complicated steel microstructures.

D. High-resolution tomography

Researchers have recently been working to decrease the deuterium diffusivity and increase the lateral resolution in another method, namely atom probe tomography (APT). APT is a unique measurement tool, in that it combines a field ion microscope with a mass spectrometer to enable three-dimensional imaging and chemical composition measurements at the atomic scale, even for light elements like hydrogen.²³⁶ As with the SIMS measurements, deuterium is used as a surrogate for hydrogen in APT. Using this scheme, Gemma et al.¹⁶ took an important step toward the application of APT on ferritic steels via a study on the deuterium profile in Fe/V films. The authors found that the analysis temperature significantly affects the measured deuterium concentration profile, and as such, great care is required to minimize temperatures and transfer times during APT on deuterium-loaded samples, especially for materials like ferritic steels.

Takahashi et al.¹⁷ addressed the issue through the development of a deuterium charging cell and novel-charging scheme for APT measurements on a TiC precipitation-hardening ferritic steel. With the high resolution of APT, and the ability to maintain hydrogen/deuterium in the samples, they were able to observe that deuterium atoms were distributed along the broad surfaces of TiC platelets in charged samples, but only around precipitates larger than 3 nm. The authors leveraged this length-scale dependence to suggest two possibilities on the origin of trapping: carbon vacancies on the TiC surface or misfit dislocations at the TiC–matrix interface. Takahashi et al.¹²⁵ later used the method to study trapping in vanadium carbide (VC) precipitation ferritic steels. In the samples where the VC platelets were 10 to 20 nm in length, deuterium atoms were observed in the platelet and on its (001) broad interfaces. In samples where the VC platelets were smaller, they observed no correlation to the location of the deuterium atoms. The authors surmised that the trapping sites were misfit dislocation cores, based on previous evidence for misfit dislocations at a given platelet size.²³⁷ However, more recent work by the same group has reversed this hypothesis, in light of a more systematic study on the dependence of trapping behavior on precipitate size using TDS, high-resolution TEM, and APT.²³⁸ TEM provided evidence that misfit dislocations were not present on the broad interfeces between the VC platelets and ferrite matrix. APT data also provided direct evidence for a distinct change in the C/V stoichiometry, as shown in Fig. 18, suggestive of differences in the number of carbon vacancies. A hydrogen peak for deep trapping appeared in the TDS analysis, thus linking hydrogen trapping with carbon vacancies. The carbon vacancies likely exist near the precipitate surfaces, given the diffusion barriers for hydrogen into bulk sites.²³⁹

FIG. 18.

APT (a) elemental maps and (b) mass-to-charge spectrum of a deuterium-charged VC-precipitation ferrite steel aged for 8h. The deuterium atoms are distributed along the broad surface of the platelet. (c) The concentration profiles of carbon and vanadium. The C/V atomic ratio was about 0.74, which suggested a chemical composition of V₄C₃. Reprinted from Takahashi et al., Acta Mater. 153, 193 (2018).²³⁸ Copyright 2018 Elsevier.

More recently, Chen et al.²⁴⁰ used APT to investigate hydrogen-trapping sites in a ferritic steel with finely-dispersed carbide precipitates. From the APT data, the positions of the deuterium atoms showed a strong correlation to the proposed trapping sites for this material,¹²⁵ either in the precipitates or on its broad interfaces. To establish a more quantitative metric for the locations of the trapping sites, the authors exploited a statistical procedure for combining information from multiple precipitates into a single dataset. The resulting normalized data suggested that the deuterium was restricted to the interior of the carbide, in direct contrast to previous work on VC-precipitation steels,²³⁸ which suggested trapping at carbon vacancies near the precipitate surfaces. A similar debate has emerged from neutron scattering measurements, with some measurements suggesting trapping in the interior²⁴¹ and others pointing toward trapping at the surface.²⁴² Chen et al.²⁴³ potentially resolved the debate via APT measurements on a steel subjected to different heat treatments to induce ferritic and martensitic states. From the ferritic data, the authors surmised that the trapping location was largely dependent on the characteristics of the precipitates; larger, incoherent precipitates allow trapping at the surface, whereas smaller, coherent precipitates enable trapping in their interior. The results from the martensitic state provided evidence for trapping at dislocation cores and grain boundaries, as shown in Fig. 19. In all, APT shows great promise as a high-resolution tool to study hydrogen trapping at dislocations, grain boundaries, and precipitates in ferritic steels, given the recent advances in charging methods and cryogenic transfer.

FIG. 19.

APT analyses of deuterium-charged martensite steel. The first dataset [(a)–(d)] contains only dislocations, whereas the second dataset [(e)–(h)] contains both dislocations and grain boundaries. The dislocations and grain boundaries are highlighted by transparent blue and red isosurfaces, respectively. Reprinted from Chen et al., Science 367, 171 (2020).²⁴³ Copyright 2020 AAAS.

One disadvantage of APT is that, due to the limited detection rate of atoms, microstructural defects, such as grain boundaries and dislocations, cannot be detected. In some cases, as shown in Fig. 19, chemical segregation of secondary elements (carbon, in this case) can be used as a proxy for certain microstructural features. However, this technique would miss critical information about which features do not show segregation and what parameters dictate the degree of segregation. TEM now has a similar chemical spatial resolution to APT (for Z > 5, i.e., not hydrogen), and also allows imaging of defects by diffraction contrast.²⁴⁴ As APT samples are thin enough for TEM, the combination of TEM imaging with APT analysis²⁴⁵ could provide critical information in mapping chemical segregation at microstructural features.

VI. CONCLUSIONS AND OUTLOOK

In conclusion, hydrogen embrittlement is a complex phenomenon dependent on many different interactions between hydrogen and the host metal. This complexity requires multiple techniques to probe and deconvolute the various interactions and the result of those interactions. After many decades, the understanding of the community has developed significantly, but it is in the last decade in which impressive advances have been made, generally due to the development of new experimental capabilities. While many recent results come under the heading of confirming existing accepted theory, the direct evidence for theories such as hydrogen trapping mean that modeling of mechanisms can progress, confident in the established science behind them. As new experimental techniques are refined, it can be expected that the field will continue to develop at a remarkable pace. A notable theme that seems to run through recent developments has been that combining different techniques has been a powerful tool in expanding understanding.

There are still pieces missing that would help definitively answer what the working mechanisms are, and to what degree does each operate under given circumstances. Perhaps the biggest unanswered question is the location of hydrogen in the host metal. While decades of research have given us an idea of the trapping locations of hydrogen, understanding where the hydrogen goes under strain in a bulk material would be critical to answering the remaining questions on embrittlement mechanisms. Another missing piece is a measurement of the degree of the influence of hydrogen on bonding in metals. Without an actual measurement, most decohesion calculations are still hypotheses, and understanding the influence on bonding may answer questions about influences on dislocation motion. While newer techniques, such as APT, SIMS, and neutron diffraction, show promise for answering these questions, they remain unsolved due to complications of working with hydrogen. This is especially true in ferritic steels where the rapid diffusion rates mean that retaining sufficient hydrogen during measurements often requires special considerations, such as in situ charging. While simulations, both atomistic and molecular dynamics, may be useful to help confirm or deny certain aspects of hydrogen embrittlement mechanisms, care must be taken that models reflect the actual experimental conditions and real-world situations. Especially, since hydrogen embrittlement occurs in a specific temperature, strain-rate, and concentration range, this must be reflected in the models. As such, there remains work to be done to understand the mechanisms by which hydrogen influences the mechanical response of susceptible metals, and from that understanding, to be able to successfully design against failures by this phenomenon.

The ultimate goal for measurements of hydrogen interactions with steel, and in turn the elucidation of hydrogen embrittlement mechanisms and the conditions in which they are dominant, is to provide accurate lifetime predictions of existing steels for hydrogen service and to inform the development of novel materials for future use. To this end, the modeling of failure in steels for hydrogen service must evolve from a phenomenological-based approach, which often relies on time-consuming mechanical tests, to a physics-based approach. Recent advances have allowed for the incorporation of specific microstructures into, for example, finite element models. However, microstructure-specific physical properties including diffusion rates, solubilities, and concentrations are still needed as model inputs. Therefore, going forward, the most powerful measurements of these properties will have the ability to probe information specific to different surfaces, grains, grain boundaries, dislocations, and vacancies. Two routes to microstructure-specific information are through clever sample design or through techniques in which data can be deconvoluted to connect specific microstructure components to their associated signals.

Finally, mechanical properties are used both by industry for design and code compliance and by researchers trying to understand damage mechanisms and how to design new alloys with increased hydrogen resistance. Future measurement needs include test designs for a more accurate representation of in-service conditions, such as how single-edge notch tensile testing provides crack compliance closer to that of a pipeline than most other tests done with tensile loading. As mentioned earlier, measurements are needed to provide input data for physics-based models, such that these models can be used to predict new alloy designs. For fully-predictive models, measurements at multiple size scales, but especially at small and meso-scales, are needed to provide the material properties and behaviors of individual micro- and nano-constituents and boundaries.

Hopefully, as the need for hydrogen infrastructure increases in the next few decades, the field will develop to the point of being able to predict hydrogen-induced behavior, thus enabling intelligent material design and selection.