Doubly Stochastic Normalization of the Gaussian Kernel Is Robust to Heteroskedastic Noise

Abstract

A fundamental step in many data-analysis techniques is the construction of an affinity matrix describing similarities between data points. When the data points reside in Euclidean space, a widespread approach is to from an affinity matrix by the Gaussian kernel with pairwise distances, and to follow with a certain normalization (e.g. the row-stochastic normalization or its symmetric variant). We demonstrate that the doubly-stochastic normalization of the Gaussian kernel with zero main diagonal (i.e., no self loops) is robust to heteroskedastic noise. That is, the doubly-stochastic normalization is advantageous in that it automatically accounts for observations with different noise variances. Specifically, we prove that in a suitable high-dimensional setting where heteroskedastic noise does not concentrate too much in any particular direction in space, the resulting (doubly-stochastic) noisy affinity matrix converges to its clean counterpart with rate m^−1/2, where m is the ambient dimension. We demonstrate this result numerically, and show that in contrast, the popular row-stochastic and symmetric normalizations behave unfavorably under heteroskedastic noise. Furthermore, we provide examples of simulated and experimental single-cell RNA sequence data with intrinsic heteroskedasticity, where the advantage of the doubly-stochastic normalization for exploratory analysis is evident.

1. Introduction

1.1. Affinity matrix constructions

Given a dataset of points in Euclidean space, a useful approach for encoding the intrinsic geometry of the data is by a weighted graph, where the vertices represent data points, and the edge-weights describe similarities between them. Such a graph can be described by an affinity (or adjacency/similarity) matrix, namely a nonnegative matrix whose (i, j)’th entry holds the edge-weight between vertices i and j. To measure the similarity between pairs of data points, one can employ the Gaussian kernel with pairwise (Euclidean) distance. In particular, given data points ${\mathbf{x}}_1,\dots ,{\mathbf{x}}_n\in {\mathbb{R}}^m$, we consider the matrix $K\in {\mathbb{R}}^{n\times n}$ given by

$$K_{i,j}=\{\begin{array}{cc}\text{exp}(-\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2∕\epsilon ),\hfill & i\ne j,\hfill \\ 0,\hfill & i=j,\hfill \end{array}\phantom{\}}$$ (1)

for i, j = 1, … , n, where ε is the kernel width parameter. For many applications it is a common practice to normalize K, so to equip the resulting affinity matrix with a useful interpretation and favourable properties. Two such normalizations, which are closely related to each other, are the row-stochastic and the symmetric normalizations:

$$(\mathbf{Row}\text{-}\mathbf{stochastic}\mathbf{normalization})W^{(\mathrm{r})}\stackrel{\text{def}}{=}\text{diag}(\mathbf{r})K,r_i=\frac{1}{{\sum }_{j=1}^n{K}_{i,j}},$$ (2)

$$(\mathbf{Symmetric}\mathbf{normalization})W^{(s)}\stackrel{\text{def}}{=}\sqrt{\text{diag}(\mathbf{r})}K\sqrt{\text{diag}(\mathbf{r})},$$ (3)

where r = [r₁, … , r_n], and diag(r) is a diagonal matrix with r on its main diagonal.

Notably, the matrix W^(r) is row-stochastic, i.e., the sum of every row of W^(r) is 1, which allows for a useful interpretation of W^(r) as a transition-probability matrix (in the sense of a Markov chain). An important characteristic of the row-stochastic affinity matrix W^(r) is its relation to the heat kernel and the Laplace-Beltrami operator on a manifold [4, 12, 24, 46, 53]. Specifically, under the “manifold assumption” – where the points x₁, … , x_n are uniformly sampled from a smooth low-dimensional Riemannian manifold embedded in the Euclidean space – W^(r) approximates the heat kernel on the manifold, and the matrix L^(r) = I−W^(r) (known as the random-walk graph Laplacian) approximates the Laplace-Beltrami operator. This property of the row-stochastic normalization establishes the relation between W^(r) and the intrinsic local geometry of the data, thereby justifying the use of W^(r) as an affinity matrix.

The affinity matrix W^(s) (obtained by the symmetric normalization) is closely-related to W^(r), and in particular, since W^(s) = [diag(r)]^−1/2W^(r)[diag(r)]^1/2, W^(s) shares the spectrum of W^(r), and their eigenvectors are related through the vector r. Even though W^(s) is not a proper transition-probability matrix, it enjoys symmetry, which is advantageous in various applications.

We also mention that the row stochastic and symmetric normalizations can be used in conjunction with a kernel with variable width, i.e., when a different value of ε is taken for each row or column of K (see for instance [6] and references therein). We further discuss one such variant in the example in Section 3.2.

The matrices W^(r) and W^(s) (or equivalently, their corresponding graph Laplacians I − W^(r) and I − W^(s)) are used extensively in data processing and machine learning, notably in non-linear dimensionality reduction (or manifold learning) [4, 12, 38, 33], community detection and spectral-clustering [44, 39, 42, 55, 20, 43, 29], image denoising [9, 40, 37, 31, 47], and in signal processing and supervised-learning over graph domains [45, 13, 23, 15, 7].

1.2. The doubly-stochastic normalization

In this work, we focus on the doubly-stochastic normalization of K:

$$(\mathbf{Doubly}\text{-}\mathbf{stochastic}\mathbf{normalization})W^{(\mathrm{d})}\stackrel{\text{def}}{=}\text{diag}(\mathbf{d})K\text{diag}(\mathbf{d}),$$ (4)

where d = [d₁, … , d_n] > 0 is a vector chosen such that W^(d) is doubly-stochastic, i.e., such that the sum of every row and every column of W^(d) is 1. The problem of finding d such that W^(d) has prescribed row and column sums is known as a matrix scaling problem, and the entries of d are often referred to as scaling factors. Matrix scaling problems have a rich history, with a long list of applications and generalizations [2, 27]. Since the scaling factors are defined implicitly, their existence and uniqueness are not obvious, and depend on the zero-pattern of the matrix to be scaled. For the particular zero-pattern of K, existence and uniqueness are established by the following lemma.

Lemma 1 (Existence and uniqueness). Suppose that $A\in {\mathbb{R}}^{n\times n}$, n > 2, is symmetric with zero main diagonal and strictly positive off-diagonal entries. Then, there exist scaling factors d₁, … , d_n > 0 such that ${\sum }_{j=1}^n{d}_i{A}_{i,j}{d}_j=1$ for all i = 1, … , n, and moreover, $\{d_i{\}}_{i=1}^n$ are unique.

The proof can be found in Appendix A, and is based on the simple zero-pattern of A and on a lemma by Knight [30]. On the computational side, the scaling factors d can be obtained by the classical Sinkhorn-Knopp algorithm [48] (known also as the RAS algorithm), or by more recent techniques based on optimization (see [1] and references therein). We detail a lean variant of the Sinkhorn-Knopp algorithm adapted to symmetric matrices (see [30]) in Algorithm 1 below, and briefly discuss its convergence and computational complexity in Remark 1.

Algorithm 1 Sinkhorn-Knopp algorithm for symmetric matrices [30]

$$\begin{array}{cc}\hfill & \mathrm{Input}:\text{Symmetric nonnegative}n\times n\text{matrix}K,\text{tolerance}\delta >0.\hfill \\ \hfill & 1:\text{Initialize:}{d}_i^{(0)}=(\sum \begin{array}{c}n\hfill \\ j=1\hfill \end{array}{K}_{i,j}{)}^{-1},d_i^{(1)}=(\sum \begin{array}{c}n\hfill \\ j=1\hfill \end{array}{K}_{i,j}{d}_j^{(0)}{)}^{-1},d_i^{(2)}=(\sum \begin{array}{c}n\hfill \\ j=1\hfill \end{array}{K}_{i,j}{d}_j^{(1)}{)}^{-1},\tau =2.\hfill \\ \hfill & 2:{\text{While max}}_{1\le i\le n}\mid d_i^{(\tau -2)}∕d_i^{(\tau )}-1\mid >\delta ,\text{do:}\hfill \\ \hfill & •d_i^{(\tau +1)}=(\sum \begin{array}{c}n\hfill \\ j=1\hfill \end{array}{K}_{i,j}{d}_j^{(\tau )}{)}^{-1},\text{for}i=1,\dots ,n.\hfill \\ \hfill & •\text{Update}\tau \leftarrow \tau +1.\hfill \\ \hfill & 3:\text{Return}{d}_i=\sqrt{d_i^{(\tau )}{d}_i^{(\tau -1)}},\text{for}i=1,\dots ,n.\hfill \end{array}$$

By definition, W^(d) is a symmetric transition-probability matrix. Hence, it naturally combines the two favorable properties that W^(r) and W^(s) hold separately. It is worthwhile to point-out that W^(d) is in fact the closest symmetric and row-stochastic matrix to K in KL-divergence [8, 58], and interestingly, it can also be obtained by iteratively re-applying the symmetric normalization (3) indefinitely (see [57]). Another appealing interpretation of the doubly-stochastic normalization is through the lens of optimal transport with entropy regularization [14], summarized by the following proposition.

Proposition 2 (Optimal transport interpretation). W^(d) from (4) is the unique solution to

$$\begin{gathered} \underset{W\in {\mathbb{R}}_{+}^{n\times n}}{Minimize}\sum _{i,j=1}^n\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2{W}_{i,j}+\epsilon H(W), \\ Subjectto:W1=1,W^{T}1=1,W_{i,i}=0,i=1\dots ,n, \end{gathered}$$ (5)

where 1 is a column vector of n ones, and $H(W)={\sum }_{i,j=1}^n{W}_{i,j}\log W_{i,j}$ is the negative entropy.

The proof of Proposition 2 follows very closely with the proof of Lemma 2 in [14], with the additional use of Lemma 1 (to account for the constraint W_i,i = 0), and is omitted for the sake of brevity. In the optimal transport interpretation of the problem (5), each point x_i holds a unit mass that should be distributed between all the other points x_j ≠ x_i, while minimizing the transportation cost between the points (measured by the pair-wise distances ∥x_i − x_j∥²). The outcome of this process is constrained so that each point ends up holding a unit mass. In this context, the matrix W describes the distribution of the masses from all points to all other points, and is therefore required to be doubly-stochastic. The negative entropy regularization term εH(W) controls the “fairness” of the mass allocation, such that each mass is distributed more evenly between the points for large values of ε.

The optimization problem (5) can also be interpreted as an optimal graph construction. In this context, the term ${\sum }_{i,j=1}^n\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2{W}_{i,j}$ can be considered as accounting for the regularity of the data (as a multivariate signal) with respect to the weighted graph represented by W, while the negative entropy term εH(W) controls the approximate sparseness of W. Since the solution to (5) is a symmetric matrix, W^(d) can be thought of as describing the undirected weighted graph that optimizes the “smoothness” of the dataset, under the constraints of prescribed entropy (or approximate sparseness), no self-loops, and stochasticity (i.e., so that W^(d) is a transition-probability matrix).

In the context of manifold learning, the relation between the doubly-stochastic normalization and the heat kernel (or the Laplace-Beltrami operator) on a Riemannian manifold has been recently established in [36]. That is, under the manifold assumption (and under certain conditions) W^(d) is expected to approximate the heat kernel on the manifold, and therefore to encode the local geometry of the data much like W^(r). The doubly-stochastic normalization was also demonstrated to be useful for spectral clustering in [3], where it was shown to achieve the best clustering performance on several datasets. Last, we note that several other constructions of doubly-stochastic affinity matrices have appeared in the literature [56, 58], typically involving a notion of closeness to K other than KL-divergence (e.g. Frobenius norm).

Remark 1 (Computational complexity of Algorithm 1). It is evident that the computational complexity of each iteration in Algorithm 1 is dominated by the matrix-vector multiplication Kd^(τ), and is therefore $\mathcal{O}(n^2)$. As for the number of iterations required, in [30] it was shown that if the matrix to be scaled is fully indecomposable, then the scaling factors in the Sinkhorn-knopp algorithm admit a linear convergence whose rate is equal to the squared subdominant eigenvalue of the resulting doubly-stochastic matrix (see Theorem 4.4 in [30]). In the proof of Lemma 1 in Appendix A we show that K from (1) is indeed fully indecomposable, hence the number of iterations in Algorithm 1 is expected to be $\mathcal{O}(1∕\log (\mid {\lambda }_2\{W^{(d)}\}{\mid }^{-1}))$, where λ₂{W^(d)} is the subdominant eigenvalue of W^(d).

1.3. Robustness to noise

When considering real-world datasets, it is desirable to construct affinity matrices that are robust to noise. Specifically, suppose that we do not have access to the points x₁, … , x_n (which are non-random in our setting), but rather to their noisy observations ${\tilde{\mathbf{x}}}_1,\dots ,{\tilde{\mathbf{x}}}_n$, given by

$${\tilde{\mathbf{x}}}_i={\mathbf{x}}_i+{\eta }_i,$$ (6)

where ${\eta }_1,\dots ,{\eta }_n\in {\mathbb{R}}^m$ are pairwise independent noise vectors satisfying

$$\mathbb{E}[{\eta }_i]=0,\mathbb{E}[{\eta }_i{\eta }_i^T]={\Sigma }_i,$$ (7)

for all i = 1, … , n, where 0 is the zero column vector in ${\mathbb{R}}^m$, and Σ_i is the covariance matrix of η_i. We then define ${\tilde{W}}^{(r)}$, ${\tilde{W}}^{(s)}$, ${\tilde{W}}^{(d)}$, $\tilde{K}$, and {${\tilde{d}}_i$} analogously to W^(r), W^(s), W^(d), K , and {d_i}, respectively, when replacing {x_i} in (1) with {${\tilde{\mathbf{x}}}_i$}. For the noise model described above, we say that the noise is homoskedastic if Σ₁ = Σ₂ = … = Σ_n, and heteroskedastic otherwise.

The influence of homoskedastic noise on kernel matrices (such as K) was investigated in [16], and the results therein imply that ${\tilde{W}}^{(r)}$ and ${\tilde{W}}^{(s)}$ are robust to high-dimensional homoskedastic noise. Specifically, in the high-dimensional setting considered in [16], $\tilde{K}$ converges to a biased version K where all the off-diagonal entries of $\tilde{K}$ admit the same multiplicative bias. Such bias can therefore be corrected by applying either the row-stochastic or the symmetric normalizations (see [17]). However, this is not the case in the more general setting of heteroskedastic noise.

Heteroskedastic noise is a natural assumption for many real-world applications. For example, heteroskedastic noise arises in certain biological, photon-imaging, and Magnetic Resonance Imaging (MRI) applications [10, 41, 22, 19], where observations are modeled as samples from random variables whose variances depend on their means, such as in binomial, negative-binomial, multinomial, Poisson, or Rice distributions. In natural image processing, heteroskedastic noise occurs due to the spatial clipping of values in an image [18]. Additionally, heteroskedastic noise is encountered when the experimental setup varies during the data collection process, such as in spectrophotometry and atmospheric data acquisition [11, 49]. Generally, many modern datasets are inherently heteroskedastic as they are formed by aggregating observations collected at different times and from different sources. Last, we mention that heteroskedastic noise can be considered as a natural relaxation to the popular manifold assumption. In particular, heteroskedastic noise arises whenever data points are sampled from the high-dimensional surroundings of a low-dimensional manifold embedded in the ambient space, where the size of the sampling neighborhood (in the ambient space) around the manifold is determined locally by the manifold itself. See Figure 4 and the corresponding example in Section 3.1.2.

Figure 4:

Typical array of clean and noisy data points for n = 1000, m = 2, and additive noise sampled uniformly from a sphere whose radius depends on the angle of the corresponding clean point (on the unit circle) according to (18).

1.4. Contributions

Our main contribution is to establish the robustness of the doubly-stochastic normalization of the Gaussian kernel (with zero main diagonal) to high-dimensional heteroskedastic noise. In particular, we prove that in the high-dimensional setting where the number of points n is fixed, the dimension m is increasing, and the noise does not concentrate too much in specific direction in space, ${\tilde{W}}^{(d)}$ converges to W^(d) with rate m^−1/2. See Theorem 3 in Section 2. An intuitive justification of the robustness of the doubly-stochastic normalization to heteroskedastic noise, and also why zeroing-out the main diagonal of K is important, can be found in Section 2, equations (9)-(10). The proof of Theorem 3, see Appendix B, relies on a perturbation analysis of the doubly-stochastic normalization.

We demonstrate the robustness of ${\tilde{W}}^{(d)}$ to heteroskedastic noise in several examples (see Section 3). In Section 3.1.1 we corroborate Theorem 3 numerically, and exemplify that W^(r) and W^(s) suffer from inherent point-wise bias due to heteroskedastic noise (see Figures 1-3). In Section 3.1.2 we demonstrate the robustness of the leading eigenvectors of W^(d) to heteroskedastic noise whose characteristics depend locally on the manifold of the clean data (see Figures 4-6). In Section 3.2 we apply the doubly-stochastic normalization for both simulated and experimental single-cell RNA sequence data with inherent heteroskedasticity, showcasing its ability to accurately recover the underlying structure of the data despite the noise (see Figures 7,8,9,10).

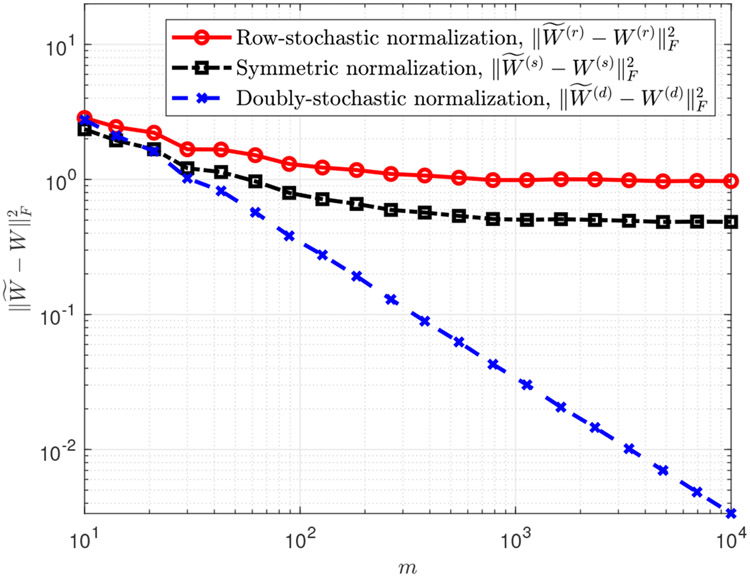
Figure 1:

Squared Frobenius loss (averaged over 10 trials) between clean and noisy affinity matrices from different normalizations, versus the dimension m. The dataset is the unit circle embedded in different dimensions (see (14), with n = 10³ and heteroskedastic noise simulated according to (15)-(17)

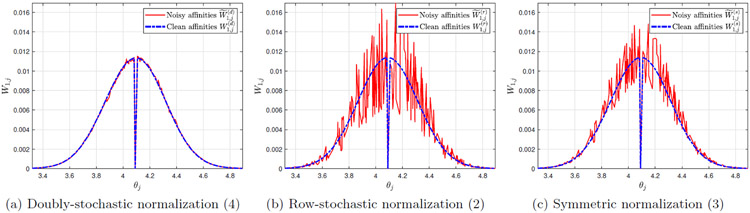
Figure 3:

First row of the clean and noisy affinity matrices obtained using different normalizations. The dataset is the unit circle (see (14), with n = 10³, m = 10⁴, and heteroskedastic noise simulated according to (15)-(17).

Figure 6:

Two-dimensional embedding using the second and third eigenvectors (corresponding to the second- and third-largest eigenvalues) of affinity matrices obtained from different normalizations. The dataset is the unit circle, with n = 10³, m = 500, and heteroskedastic noise generated according to (18).

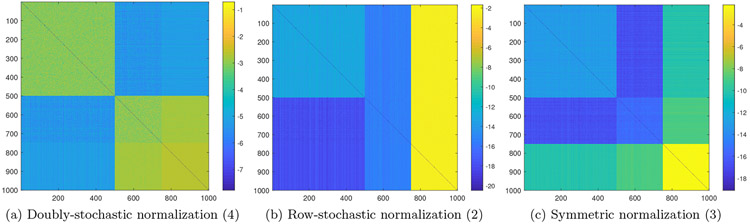
Figure 7:

Entries of the affinity matrices obtained from different normalizations in logarithmic scale (from left to right: ${\log }_{10}({\tilde{W}}^{(d)})$, ${\log }_{10}({\tilde{W}}^{(r)})$, ${\log }_{10}({\tilde{W}}^{(s)})$), for single-cell RNA sequence data simulated according to (19)-(21), with n = 1000, m = 4000.

Figure 8:

Two-dimensional visualization from t-SNE with different perplexity values (Figures 8a,8b,8c), and from t-SNE modified to use the doubly-stochastic affinity matrix ${\tilde{W}}^{(d)}$ (Figure 8d). The dataset is a simulated single-cell RNA sequence data (see (19)-(21) with n = 1000, m = 4000.

Figure 9:

Entries of the affinity matrices obtained from different normalizations in logarithmic scale (from left to right: ${\log }_{10}({\tilde{W}}^{(d)})$, ${\log }_{10}({\tilde{W}}^{(r)})$, ${\log }_{10}({\tilde{W}}^{(s)})$), computed from 1000 CD14 cells and 1000 CD34 cells from the purified PBMC dataset [61].

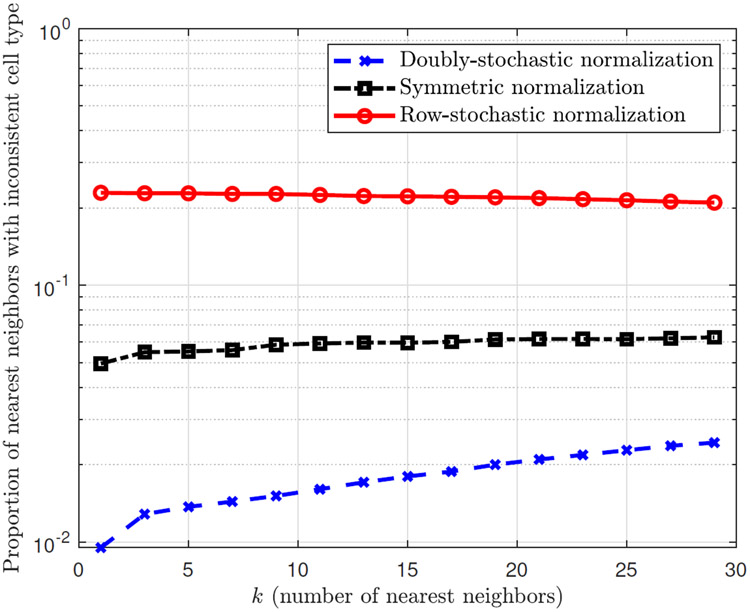
Figure 10:

Inconsistency between the type of a cell and the types of its nearest neighbours, according to each of the affinity matrices ${\tilde{W}}^{(d)}$, ${\tilde{W}}^{(r)}$, ${\tilde{W}}^{(s)}$, and using 1000 CD14 cells and 1000 CD34 cells from the purified PBMC dataset [61]. The x-axis is the number of nearest neighbors chosen for each cell (according to the largest entries in each row of a given affinity matrix), and the y-axis is the proportion of these nearest neighbors with a cell type that is different from the type of the reference cell (whose nearest neighbors are considered), averaged over all cells in the dataset and over 20 randomized trials (of sampling from the CD14 cells and the CD34 cells).

2. Main result

We now place ourselves in the high-dimensional setting where the dimension m is increasing while the number of points n and the kernel parameter ε are fixed. Formally, let ${\mathbf{x}}_i^{(m)}$, ${\tilde{\mathbf{x}}}_i^{(m)}$, ${\eta }_i^{(m)}$, ${\Sigma }_i^{(m)}$, K^(m), ${\tilde{K}}^{(m)}$, W^(d),(m), and ${\tilde{W}}^{(d),(m)}$ be the same as x_i, ${\tilde{\mathbf{x}}}_i$, η_i, Σ_i, K, $\tilde{K}$, W^(d), and ${\tilde{W}}^{(d)}$, respectively, and consider a sequence of each of the former quantities (with superscript (m)) in m = M, M + 1, … , ∞, where M is a positive integer. Our main result is as follows, where ${\mathcal{O}}_p$ stands for order in probability [35] (or stochastic boundedness).

Theorem 3 (Convergence of ${\tilde{W}}^{(d),(m)}$ to W^(d),(m)). Suppose that $\Vert {\mathbf{x}}_i^{(m)}\Vert \le 1$ and $\Vert {\Sigma }_i^{(m)}{\Vert }_2\le C_{\eta }{m}^{-1}$ for all i = 1, …, n and m ≥ M, where C_η is a universal constant (independent of m). Then,

$$\Vert {\tilde{W}}^{(d),(m)}-W^{(d),(m)}{\Vert }_F={\mathcal{O}}_p(m^{-1∕2}).$$ (8)

In other words, under the conditions in Theorem 3, it follows that for any probability p > 0 there exist a constant C′ and an integer M′ (both of which may depend on n, p, ε, and C_η) such that for all m ≥ M′ we have $\text{Pr}\{\Vert {\tilde{W}}^{(d),(m)}-W^{(d),(m)}{\Vert }_F>C^{\prime }{m}^{-1∕2}\}\le p$. The proof of Theorem 3 is detailed in Appendix B. For simplicity of the presentation, we omit the superscript (m) from all quantities in the rest of this section, as it should be clear that all quantities associated with Theorem 3 are sequences in the dimension m (where n and ε are fixed).

We now provide some remarks on the conditions in Theorem 3. Evidently, the constant 1 in the condition ∥x_i∥ ≤ 1 is arbitrary and can be replaced with any other constant (since ${\tilde{\mathbf{x}}}_i$ can always be normalized appropriately). Additionally, note that even though the quantities ∥Σ_i∥₂ are required to decrease with m, the expected noise magnitudes $\mathbb{E}\Vert {\eta }_i{\Vert }^2$ (which are equal to Tr{Σ_i}) can remain constant, and can possibly be large compared to the magnitudes of the clean data points ∥x_i∥². For example, if we have Σ_i = m⁻¹I_m for all i, where I_m is the m×m identity matrix, then it follows that $\mathbb{E}\Vert {\eta }_i{\Vert }^2=\text{Tr}\{{\Sigma }_i\}=1$, asserting that the magnitude of the noise is greater or equal to that of the clean data points (under the condition ∥x_i∥ ≤ 1). In this regime of non-vanishing high-dimensional noise, the condition ∥Σ_i∥2 ≤ C_ηm⁻¹ guarantees that the noise spreads-out in Euclidean space, and does not concentrate too much in any particular direction (observe that ∥Σ_i∥₂ is the largest singular value of Σ_i, and is therefore the variance of the noise in the direction where it is largest). Hence, the condition ∥Σ_i∥₂ ≤ C_ηm⁻¹ is primarily a convenience for considering noise that has bounded magnitude regardless of the ambient dimension (since $\mathbb{E}\Vert {\eta }_i{\Vert }_2^2\le C_{\eta }$), and whose variance in any particular direction is not too large. In many situations, the data can be normalized appropriately to satisfy this condition, see Remark 2 below and the discussion in Section 3.2.3. Clearly, the setup of Theorem 3 accommodates for heteroskedastic noise, and importantly, the ratios between the noise magnitudes $\mathbb{E}\Vert {\eta }_i{\Vert }^2$ for different data points can be arbitrary.

The main reason behind the robustness of the doubly-stochastic normalization to high-dimensional heteroskedastic noise, is that it is invariant to the type of bias introduced by heteroskedastic noise. Specifically, our analysis in the proof of Theorem 3 (see Appendix B) shows that for i ≠ j,

$$\Vert {\tilde{\mathbf{x}}}_i-{\tilde{\mathbf{x}}}_j{\Vert }^2\stackrel{p}{\to }\mathbb{E}\Vert {\tilde{\mathbf{x}}}_i-{\tilde{\mathbf{x}}}_j{\Vert }^2=\mathbb{E}\Vert {\eta }_i{\Vert }^2+\Vert x_i-x_j{\Vert }^2+\mathbb{E}\Vert {\eta }_j{\Vert }^2,$$ (9)

where $\stackrel{p}{\to }$ stands for convergence in probability, and correspondingly,

$${\tilde{K}}_{i,j}\stackrel{p}{\to }\text{exp}(-\mathbb{E}\Vert {\eta }_i{\Vert }^2∕\epsilon )\cdot K_{i,j}\cdot \text{exp}(-\mathbb{E}\Vert {\eta }_j{\Vert }^2∕\epsilon ),$$ (10)

for all i, j (since ${\tilde{K}}_{i,i}=K_{i,i}=0$). Crucially, $\tilde{K}$ in (10) is biased by symmetric diagonal scaling, which is precisely the type of bias corrected automatically by the doubly-stochastic normalization (4).

Equations (9) and (10) also highlight why zeroing-out the main diagonal of the Gaussian kernel (see Eq. (1) is important. Without it, the entries on the main diagonal of $\tilde{K}$ would be 1, while the off-diagonal entries of $\tilde{K}$ would be small due to the bias in the noisy pairwise distances (9). Thus, $\tilde{K}$ would be close to the identity matrix, which would render any normalization (row-stochastic, symmetric, or doubly-stochastic) ineffective.

Remark 2. Consider an alternative setting for high-dimensionality where the noise is only required to have bounded variance in each direction, i.e., ∥Σ_i∥₂ ≤ C_η for some universal constant C_η. This assumption holds, for instance, in the standard model where η_i has bounded variance in each coordinate and is uncorrelated between different coordinates. In addition, as the dimension m increases, suppose that the newly-added clean data coordinates are determined by a latent variable that is sampled from some underlying distribution. Specifically, suppose that each clean observation x_i is given by

$${\mathbf{x}}_i=[F_i(y_1),\dots ,F_i(y_m){]}^T,$$ (11)

where F_i is a bounded function, and y₁, … , y_m are i.i.d samples from some latent “coordinate” random variable Y (which can be multivariate or reside in a non-Euclidean space). In this case, one has

$$\Vert {\mathbf{x}}_i{\Vert }^2=\sum _{k=1}^m(F_i(y_k){)}^2=m\left({\mathbb{E}}_{y\sim Y}(F_i(y){)}^2+{\mathcal{O}}_p(m^{-1∕2})\right),$$ (12)

$$\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2=\sum _{k=1}^m(F_i(y_k)-F_j(y_k){)}^2=m\left({\mathbb{E}}_{y\sim Y}\mid F_i(y)-F_j(y){\mid }^2+{\mathcal{O}}_p(m^{-1∕2})\right),$$ (13)

which is due to Hoeffding’s inequality [25] (for sums of independent and bounded random variables). Evidently, a natural distance between x_i and x_j in this setting is ${\mathbb{E}}_{y\sim Y}\mid F_i(y)-F_j(y){\mid }^2$ as it does not depend on the ambient dimension m and allows for a constant kernel parameter ε to be used for all m. This suggests that the noisy observations ${\tilde{\mathbf{x}}}_i$ should be normalized by $\sqrt{m}$, which places us in the setting of Theorem 3 since $\Vert {\mathbf{x}}_i∕\sqrt{m}{\Vert }^2={\mathbb{E}}_{y\sim Y}(F_i(y){)}^2+{\mathcal{O}}_p(m^{-1∕2})={\mathcal{O}}_p(1)$, and ∥Σ_i/m∥₂ ≤ C_ηm⁻¹.

3. Examples

3.1. Example 1: The unit circle embedded in high-dimensional space

In our first example, we sampled n = 10³ points uniformly from the unit circle in ${\mathbb{R}}^2$, and embedded them in ${\mathbb{R}}^m$, for m ∈ [10, 10⁴], using randomly-generated orthogonal transformations. In more details, we first sampled angles θ₁, … , θ_n independently and uniformly from [0, 2π]. Then, for each embedding dimension m, we generated a random orthogonal matrix $R_m\in {\mathbb{R}}^{m\times 2}$ (i.e., such that $R_m^T{R}_m=I_m$), and computed the data points {x_i} as

$${\mathbf{x}}_i=R_m\cdot \left[\begin{array}{c}\hfill \cos ({\theta }_i)\hfill \\ \hfill \sin ({\theta }_i)\hfill \end{array}\right],i=1,\dots ,n.$$ (14)

Note that as a result, the magnitude of all points is constant, with ∥x_i∥ = 1 for all 1 ≤ i ≤ n and embedding dimension m.

3.1.1. Gaussian noise with arbitrary variances

We begin by demonstrating Theorem 3 numerically. Towards that end, we created the noise as follows. For every embedding dimension m, we set ${\Sigma }_i=\text{diag}([{\sigma }_{i,1}^2,\dots ,{\sigma }_{i,m}^2])$ (so that the noise is uncorrelated between coordinates), and generated the noise standard-deviations σ_i,j according to

$${\sigma }_{i,j}=\sqrt{\frac{{\alpha }_i{\beta }_j}{m}},$$ (15)

where $\{{\alpha }_i{\}}_{i=1}^n$, $\{{\beta }_j{\}}_{j=1}^m$ were sampled (independently) from the uniform distribution over [0.05, 0.5]. Therefore, the noise magnitudes $\mathbb{E}\Vert {\eta }_i{\Vert }^2$ satisfy

$$\frac{1}{400}\le \mathbb{E}\Vert {\eta }_i{\Vert }^2\le \frac{1}{4},$$ (16)

for all 1 ≤ i ≤ n, and can take any values in that range. Importantly, the noise magnitudes can vary substantially between data points, which is key in our setting. Then, {η_i[j]}_i,j were sampled (independently) according to

$${\eta }_i[j]\sim \mathcal{N}(0,{\sigma }_{i,j}^2),i=1,\dots ,n,j=1,\dots ,m,$$ (17)

where η_i[j] stands for the j’th entry of η_i. Once we generated the noisy data points ${\tilde{\mathbf{x}}}_1,\dots ,{\tilde{\mathbf{x}}}_n$ according to (6), we formed the clean and noisy kernel matrices K and $\tilde{K}$ with ε = 0.1, and computed W^(d), ${\tilde{W}}^{(d)}$ using Algorithm 1 with δ = 10^–12. Last, we also evaluated W^(r), W^(s) and ${\tilde{W}}^{(r)}$, ${\tilde{W}}^{(s)}$ using K and $\tilde{K}$, respectively, according to (2) and (3).

The behavior of the errors $\Vert {\tilde{W}}^{(d)}-W^{(d)}{\Vert }_F^2$, $\Vert {\tilde{W}}^{(r)}-W^{(r)}{\Vert }_F^2$, $\Vert {\tilde{W}}^{(s)}-W^{(s)}{\Vert }_F^2$ as a function of m can be seen in Figure 1. It is evident that for m > 100 the error for the doubly-stochastic normalization is substantially smaller than that for the row-stochastic normalization or for the symmetric normalization. Additionally, the error for the doubly-stochastic normalization decreases linearly in logarithmic scale, while the errors for the row-stochastic and the symmetric normalizations reach saturation and never fall below a certain value. In this experiment, the slope of $\log (\Vert {\tilde{W}}^{(d)}-W^{(d)}{\Vert }_F^2)$ versus log m (between m = 10² and m = 10⁴) was −0.9996, matching the slope suggested by the upper bound in Theorem 3 (which implies a slope of −1 for the squared Frobenius norm).

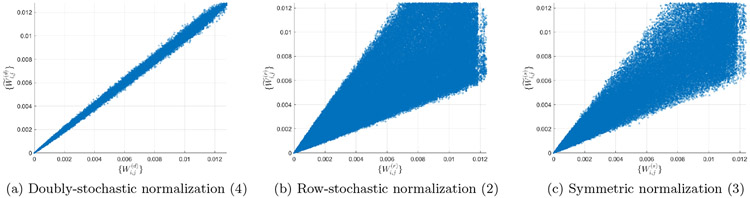
In Figure 2 we depict the noisy affinities ${\tilde{W}}_{i,j}^{(d)}$, ${\tilde{W}}_{i,j}^{(r)}$, ${\tilde{W}}_{i,j}^{(s)}$ versus their corresponding clean affinities $W_{i,j}^{(d)}$, $W_{i,j}^{(r)}$, $W_{i,j}^{(s)}$ for m = 10⁴. It can be observed that the noisy affinities from the doubly-stochastic normalization concentrate near their corresponding clean affinities, while the noisy affinities from the row-stochastic and symmetric normalizations deviate substantially from their clean counterparts, particularly for larger affinity values.

Figure 2:

Entries of the noisy affinity matrices (y-axis) versus the corresponding entries in the clean affinity matrices (x-axis), using different normalizations. The dataset is the unit circle (see (14), with n = 10³, m = 10⁴, and heteroskedastic noise simulated according to (15)-(17).

Last, in Figure 3 we visually demonstrate the first row of the clean and noisy affinity matrices W^(d), W^(r), W^(s) and ${\tilde{W}}^{(d)}$, ${\tilde{W}}^{(r)}$, ${\tilde{W}}^{(s)}$, using m = 10⁴. Note that we only display about a quarter of all the entries, since all the other entries are vanishingly small. It can be seen that the clean row-stochastic, clean symmetric, and clean doubly-stochastic affinities are all very similar, and resemble a Gaussian. This is explained by the fact that both W^(d) and W^(r) are expected to approximate the heat kernel on the unit circle (see [12, 36] and other related references given in the introduction), which is close to the Gaussian kernel with geodesic distance (for sufficiently small ε). Additionally, since the sampling density on the circle is uniform, diag(r) (from (2)) is close to a multiple of the identity, and hence W^(s) is expected to be close to W^(r) (recall that W^(s) = [diag(r)]^−1/2W^(r)[diag(r)]^1/2). Indeed, we found that $\Vert W^{(d)}-W^{(r)}{\Vert }_F^2\approx \Vert W^{(d)}-W^{(s)}{\Vert }_F^2\approx 0.01$.

Importantly, the doubly-stochastic normalization recovers the true affinities with high accuracy, with an almost perfect match between the corresponding clean and noisy affinities. On the other hand, there is an evident discrepancy between the corresponding clean and noisy affinities from the row-stochastic normalization and from the symmetric normalization.

3.1.2. Noise sampled uniformly from a ball with smoothly varying radius

Next, we proceed by demonstrating the robustness of the leading eigenvectors from the doubly-stochastic normalization under heteroskedastic noise, and in particular, in the presence of noise whose magnitude depends on the local geometry of the clean data. Specifically, we simulated heteroskedastic noise whose magnitude varies smoothly according to the angle θ_i of each point x_i on the circle (see (14), according to

$${\eta }_i\sim U({\mathcal{B}}_{\rho ({\theta }_i)}),\rho (\theta )=0.01+0.99\frac{1+\cos (2\theta )}{2},$$ (18)

where $U({\mathcal{B}}_r)$ stands for the uniform distribution over ${\mathcal{B}}_r$, which is a ball with radius r in ${\mathbb{R}}^m$ (centered at the origin). That is, every noisy observation ${\tilde{\mathbf{x}}}_i$ is sampled uniformly from a ball whose center is x_i and its radius is ρ(θ_i) from (18). Consequently, the maximal noise magnitude varies smoothly between 0.01 (for θ = π/2, 3π/2) and 1 (for θ = 0, π). A typical array of clean and noisy points arising from the noise model (18) for dimension m = 2 can be seen in Figure 4.

We generated the noisy data points ${\tilde{\mathbf{x}}}_1,\dots ,{\tilde{\mathbf{x}}}_n$ according to (6) for dimension m = 500, and formed the noisy kernel matrix $\tilde{K}$ with ε = 0.1. We next computed ${\tilde{W}}^{(d)}$ using Algorithm 1 with δ = 10⁻¹², and evaluated ${\tilde{W}}^{(r)}$, ${\tilde{W}}^{(s)}$ using $\tilde{K}$ according to (2) and (3).

Figure 5 displays the five leading (right) eigenvectors of W^(d), W^(r), W^(s), denoted by $\{{\psi }_k^{(d)}{\}}_{k=1}^5$, $\{{\psi }_k^{(r)}{\}}_{k=1}^5$, $\{{\psi }_k^{(s)}{\}}_{k=1}^5$, respectively, and the five leading (right) eigenvectors of ${\tilde{W}}^{(d)}$, ${\tilde{W}}^{(r)}$, ${\tilde{W}}^{(s)}$, denoted by $\{{\tilde{\psi }}_k^{(d)}{\}}_{k=1}^5$, $\{{\tilde{\psi }}_k^{(r)}{\}}_{k=1}^5$, $\{{\tilde{\psi }}_k^{(s)}{\}}_{k=1}^5$, respectively. It can be seen that the leading eigenvectors from the doubly-stochastic normalization are almost unaffected by the noise, and approximate sines and cosines, which are the eigenfunctions of the Laplace-Beltrami operator on the circle. As sines and cosines are advantageous for expanding periodic functions, it is natural to employ the eigenvectors of ${\tilde{W}}^{(d)}$ for the purposes of regression, interpolation, and classification over the dataset. It is important to mention that other useful bases and frames can potentially be constructed from ${\tilde{W}}^{(d)}$ (see [13, 23]). On the other hand, the eigenvectors obtained from ${\tilde{W}}^{(r)}$ and ${\tilde{W}}^{(s)}$ are strongly biased due to the heteroskedastic noise, and exhibit undesired effects such as discontinuities and localization. Specifically, as evident from Figure 5, the leading eigenvectors of ${\tilde{W}}^{(r)}$ are discontinuous at θ = 0 and θ = π, and the leading eigenvectors of ${\tilde{W}}^{(s)}$ are localized around θ = π/2 and θ = 3π/2 (i.e., their values are close to 0 around θ = 0 and θ = π). Clearly, this behaviour of the leading eigenvectors of ${\tilde{W}}^{(r)}$ and ${\tilde{W}}^{(s)}$ does not reflect the geometry of the clean data, but rather the characteristics of the noise (since the noise variance is smallest at θ = π/2, 3π/2 and largest at θ = 0, π).

Figure 5:

Eigenvectors corresponding to the five largest eigenvalues of the clean and noisy affinity matrices obtained from different normalizations. The top row corresponds to clean affinity matrices (from left to right: W^(d), W^(r), W^(s)) and the bottom row corresponds to noisy affinity matrices (from left to right: ${\tilde{W}}^{(d)}$, ${\tilde{W}}^{(r)}$, ${\tilde{W}}^{(s)}$). The dataset is the unit circle, with n = 10³, m = 500, and heteroskedastic noise generated according to (18).

In Figure 6 we illustrate the two-dimensional embedding of the noisy data points ${\tilde{\mathbf{x}}}_1,\dots ,{\tilde{\mathbf{x}}}_n$ using the second and third eigenvectors of ${\tilde{W}}^{(d)}$, ${\tilde{W}}^{(r)}$, and ${\tilde{W}}^{(s)}$ (corresponding to their second- and third-largest eigenvalues). That is, the x-axis and y-axis values for each embedding are given by the entries of ${\tilde{\psi }}_2^{(d)}$ and ${\tilde{\psi }}_3^{(d)}$ for the doubly-stochastic normalization, ${\tilde{\psi }}_2^{(r)}$ and ${\tilde{\psi }}_3^{(r)}$ for the row-stochastic normalization, and ${\tilde{\psi }}_2^{(s)}$ and ${\tilde{\psi }}_3^{(s)}$ for the symmetric normalization (see also [4, 12]). It is clear that the embedding due to the doubly-stochastic normalization reliably represents the intrinsic structure of the clean dataset – a unit circle with uniform density, whereas the embeddings due to the row-stochastic and the symmetric normalizations are incoherent with the geometry and density of the clean points.

3.2. Example 2: Single-cell RNA sequence data

Single-cell RNA sequencing (scRNA-seq) is a revolutionary technique for measuring target gene expressions of individual cells in large and heterogeneous samples [50, 34]. Due to the method’s high resolution (single-cell level) it allows for the discovery of rare cell populations, which is of paramount importance in immunology and developmental biology. A typical scRNA-seq dataset is an m × n nonnegative matrix corresponding to n cells and m genes, where its (i, j)’th entry is an integer called the read count, describing the expression level of i’th gene in the j’th cell. Importantly, the total number of read counts (or in short total reads) per cell (i.e., column sums) may vary substantially within a sample [28]. We next exemplify the advantage of using the doubly-stochastic normalization for exploratory analysis of scRNA-seq data.

3.2.1. Simulated data

We begin with a simple prototypical example where the gene expression levels of cells are measured in two different batches, such that the number of total reads (per cell) within each batch is constant, but is substantially different between the batches. Therefore, the noise variance (modeled by the variance of the multinomial distribution, to be described shortly) differs between the observations in the two batches, giving rise to heteroskedastic noise. Such a scenario can arise naturally in scRNA-seq, either from the intrinsic read count variability common to such datasets, or when two datasets from two independent experiments are merged for unified analysis.

We consider a simulated dataset which includes only two cell types, denoted by p₁, ${\mathbf{p}}_2\in {\mathbb{R}}_{+}^m$, with m = 4000 genes. The prototypes p₁ and p₂ were created by first sampling their entries uniformly (and independently) from [0, 1], and then normalizing them so that they sum to 1. That is,

$${\mathbf{p}}_1[j]=\frac{{\mathbf{z}}_1[j]}{{\sum }_{k=1}^m{\mathbf{z}}_1[k]},{\mathbf{p}}_2[j]=\frac{{\mathbf{z}}_2[j]}{{\sum }_{k=1}^m{\mathbf{z}}_2[k]},{\mathbf{z}}_1[j],{\mathbf{z}}_2[j]\sim U[0,1],j=1,\dots ,m.$$ (19)

Next, each noisy observation ${\tilde{\mathbf{x}}}_i$ was drawn from a multinomial distribution using either p₁ or p₂ as the probability vector, and normalized to sum to 1, as described next. First, we generated a batch containing 500 observations of p₁ and 250 observations of p₂, each with 1000 multinomial trials. Second, we added a batch containing 250 observations of p₂ only, each with 10⁴ multinomial trials. To summarize, the total number of observations is n = 1000, given explicitly by

$${\tilde{\mathbf{x}}}_i=\frac{{\widehat{\mathbf{x}}}_i}{{\sum }_{j=1}^m{\widehat{\mathbf{x}}}_i[j]},{\widehat{\mathbf{x}}}_i\sim \{\begin{array}{cc}\text{Multinomial}({10}^3,{\mathbf{p}}_1),\hfill & 1\le i\le 500,\hfill \\ \text{Multinomial}({10}^3,{\mathbf{p}}_2),\hfill & 501\le i\le 750,\hfill \\ \text{Multinomial}({10}^4,{\mathbf{p}}_2),\hfill & 751\le i\le 1000.\hfill \end{array}\phantom{\}}$$ (20)

Therefore, the dataset consists of 500 (normalized) multinomial observations of p₁, followed by 500 (normalized) multinomial observations of p₂. While all observations of p₁ are with 10³ multinomial trials, the observations of p₂ are split between 250 observations with 10³ multinomial trials, and 250 observations with 10⁴ multinomial trials. Evidently, we can write

$${\tilde{\mathbf{x}}}_i=\mathbb{E}[{\tilde{\mathbf{x}}}_i]+{\eta }_i={\mathbf{p}}_{{\ell }_i}+{\eta }_i,{\ell }_i=\{\begin{array}{cc}1,\hfill & 1\le i\le 500,\hfill \\ 2,\hfill & 501\le i\le 1000,\hfill \end{array}\phantom{\}}$$ (21)

where η_i is a zero-mean noise vector (arising from the multinomial sampling) satisfying that $\mathbb{E}\Vert {\eta }_i{\Vert }^2$ is significantly smaller (by a factor of 10 roughly) for 751 ≤ i ≤ 1000 compared to 1 ≤ i ≤ 750.

Using the noisy observations ${\tilde{\mathbf{x}}}_1,\dots ,{\tilde{\mathbf{x}}}_n$, we formed the noisy kernel matrix $\tilde{K}$ of (1) with ε = 2 · 10⁻⁵, computed the corresponding matrix ${\tilde{W}}^{(d)}$ using Algorithm 1 with δ = 10⁻¹², and evaluated the matrices ${\tilde{W}}^{(r)}$, ${\tilde{W}}^{(s)}$ according to (2) and (3). Our methodology for choosing ε was to take it to be the smallest possible such that Algorithm 1 converges within the desired tolerance (specifically, in this experiment we set a maximum of 10⁶ iterations for the algorithm). We note that if ε is too small, then $\tilde{K}$ becomes too sparse (approximately), and the doubly-stochastic normalization may become numerically ill-posed.

Figure 7 illustrates the values (in logarithmic scale) of the obtained affinity matrices ${\tilde{W}}^{(d)}$, ${\tilde{W}}^{(r)}$, ${\tilde{W}}^{(s)}$. It is evident that the affinity matrix from the doubly-stochastic normalization accurately describes the relationships between the data points. That is, ${\tilde{W}}^{(d)}$ indicates the similarities within the two groups of cell types (i.e., p₁ and p₂), but also the dissimilarities between them, regardless of batch association. On the other hand, the affinity matrices from the row-stochastic and the symmetric normalizations are not loyal to the grouping according to cell types, but rather to batch association. In particular, ${\tilde{W}}^{(r)}$ and ${\tilde{W}}^{(s)}$ highlight the observations from the second batch (observations 751–1000) as being most similar to all other observations. Clearly, the fundamental issue here is the heteroskedasticity of the noise, and specifically, the fact that the noise in the last 250 observations is considerably smaller than the noise in all the other observations.

One of the main goals of exploratory analysis of scRNA-seq data is to identify different cell types. Towards that end, non-linear dimensionality reduction techniques are often employed, among which t-distributed stochastic neighbor embedding (t-SNE) [33] is perhaps the most prominent [32, 51, 54, 21]. For its operation, t-SNE employs an affinity matrix which is a close variant of the row-stochastic normalization (2), where the kernel width parameter ε in (1) is allowed to vary between different rows of K, and the resulting row-stochastic matrix is symmetrized by averaging it with its transpose. The different kernel widths are determined by a parameter called the perplexity, which is related to the entropy of each row of the resulting affinity matrix.

Even though the affinity matrix employed by t-SNE is a modification of the standard row-stochastic normalization, and uses a different value of ε for each row, it is still expected to suffer from the inherent bias observed in Figure 9b. Specifically, note that the order of the entries in each row of ${\tilde{W}}^{(r)}$ (when sorted by their values) does not depend on ε, and only on the noisy pair-wise distances $\Vert {\tilde{\mathbf{x}}}_i-{\tilde{\mathbf{x}}}_j{\Vert }^2$, which are strongly biased by the magnitudes of the noise, as evident from Figure 9b.

In Figures 8a,8b,8c we demonstrate the two-dimensional visualization obtained from t-SNE for the dataset ${\tilde{\mathbf{x}}}_1,\dots ,{\tilde{\mathbf{x}}}_n$, using typical perplexity values of 10, 30, 100. We used MATLAB’s standard implementation of t-SNE, activating the option of forcing the algorithm to be exact (i.e., without approximating the affinity matrix). All other parameters of t-SNE were set to their default values suggested by the code (we also mention that the default suggested perplexity is 30).

In Figure 8d we display the two-dimensional visualization obtained from t-SNE when replacing its default affinity matrix construction with the doubly-stochastic matrix ${\tilde{W}}^{(d)}$ (obtained using ε = 2 · 10⁻⁵), while leaving all other aspects of t-SNE unchanged. Since the optimization procedure in t-SNE is affected by randomness, we ran the experiment several times to verify that the results we exhibit are consistent.

While there are only two types of cell in the data (p₁ and p₂), no clear evidence of this fact can be found in the visualizations by t-SNE (Figures 8a,8b,8c). Furthermore, the visualizations by t-SNE do not provide any noticeable separation between the cell types. On the other hand, the visualization obtained by modifying the t-SNE to employ the doubly-stochastic affinity matrix ${\tilde{W}}^{(d)}$ (Figure 8d) allows one to easily identify and distinguish between the two cell types.

3.2.2. Experimental data

In our second example for scRNA-seq, we use an experimental dataset of purified Peripheral Blood Mononuclear Cells (PBMC) [61], which includes 94654 cells and 32733 genes. This dataset is particularly advantageous for our purposes since each cell in the experiment was labeled according to a known cell type (with 10 different types in total). While this particular dataset does not include different experimental batches (as in the previous simulated example), there is nonetheless inherent variability in the read counts associated with different cell types. To demonstrate the advantage of the doubly-stochastic normalization over the row-stochastic or symmetric normalizations, we focus on the two cell types in the data that have the largest difference in their read counts (on average), which are the CD14 and CD34 cells. Specifically, the CD34 cells have roughly four times more read counts on average than the CD14 cells.

We randomly sampled n₁ = 10³ cells out of all CD14 cells, sampled n₂ = 10³ cells out of all CD34 cells, and concatenated their gene expressions (using all genes) into a matrix of size 32733 × (n₁ + n₂). We then normalized each column of this matrix to sum to 1 (which is a standard procedure used in scRNA-seq for normalizing the read count of each cell, see also Section 3.2.1), and denoted the resulting columns by ${\tilde{\mathbf{x}}}_1,\dots ,{\tilde{\mathbf{x}}}_{n_1+n_2}$. That is, ${\tilde{\mathbf{x}}}_1,\dots ,{\tilde{\mathbf{x}}}_{n_1}$ are the normalized gene expressions of the sampled CD14 cells, and ${\tilde{\mathbf{x}}}_{n_1+1},\dots ,{\tilde{\mathbf{x}}}_{n_1+n_2}$ are the normalized gene expressions of the sampled CD34 cells. We then formed the kernel matrix $\tilde{K}$ of (1) with ε = 5 · 10⁻⁴, computed the corresponding matrix ${\tilde{W}}^{(d)}$ using Algorithm 1 with δ = 10⁻¹², and evaluated the matrices ${\tilde{W}}^{(r)}$, ${\tilde{W}}^{(s)}$ according to (2) and (3). We mention that other values of ε produce similar results to what we report next.

Figure 9 illustrates the values (in logarithmic scale) of the obtained affinity matrices ${\tilde{W}}^{(d)}$, ${\tilde{W}}^{(r)}$, ${\tilde{W}}^{(s)}$. It is evident that the affinity matrices form the doubly-stochastic and the symmetric normalizations accurately reflect the structure of the data, as they assign large affinities between cells of the same type and small affinities between cells of different type. The row-stochastic normalization, on the other hand, assigns large affinities between CD14 cells and CD34 cells, which is clearly a bias from the fact that the CD34 cells are less noisy compared to the CD14 cells (due to the difference between their read counts).

Aside from the qualitative differences between the affinity matrices depicted in Figure 9, it is of interest to quantitatively assess their accuracy. Even though we do not have access to the corresponding clean affinity matrices W^(d), W^(r), W^(s), we can make use of the logical reasoning that the nearest neighbors of any given reference cell, defined as the cells with largest affinities to that reference cell, should belong to the same cell type as the reference cell. Following this logic, for each cell i we first found its k nearest neighbors, which are given by the k indices with largest entries in the i’th row of a given affinity matrix (${\tilde{W}}^{(d)}$, ${\tilde{W}}^{(r)}$, or ${\tilde{W}}^{(s)}$). Then, as a measure of error, for each cell i we found the proportion of its k nearest neighbors that do not share its cell type. We averaged this proportion for all cells i = 1, … , n₁ + n₂, and furthermore averaged these results over 20 randomized trials of sampling from the CD14 and CD34 cells.

Figure 10 depicts the resulting proportions of inconsistent cell types as a function of the number of nearest neighbors k for each of the affinity matrices ${\tilde{W}}^{(d)}$, ${\tilde{W}}^{(r)}$, and ${\tilde{W}}^{(s)}$. It is evident that according to our measure of cell type consistency, the affinity matrix from the doubly-stochastic normalization provides the lowest proportion of incorrectly determined near neighbors for all choices of k, establishing the advantage of the doubly-stochastic normalization. In particular, the proportion of the nearest neighbor (i.e., k = 1) with inconsistent cell type using the doubly-stochastic normalization is about 5 times less than that of the symmetric normalization, and about 20 times less than that of the row-stochastic normalization.

3.2.3. Validity of the asymptotic model for scRNA-seq

We conclude our scRNA-seq example with a brief discussion on the validity of Theorem 3 in an asymptotic setting of scRNA-seq, where the number of cells n and the kernel width ε are fixed, and the number of genes m is increasing. Suppose that the gene expression levels for each cell are sampled from a multinomial variable [52], where the number of multinational trials may differ between cells. That is, let ${\widehat{\mathbf{x}}}_i$ ~ Multinomial(r_i, p_i), where r_i is the read count for the i’th cell, p_i[j] is the underlying proportion for the expression level of the j’th gene in the i’th cell, and ${\sum }_{j=1}^m{\mathbf{p}}_i[j]$ for all i. When preprocessing scRNA-seq data, an important first step is to normalize the gene expression levels by the number of read counts. Hence, we define ${\tilde{\mathbf{x}}}_i={\widehat{\mathbf{x}}}_i∕r_i$, so that $\mathbb{E}[{\tilde{\mathbf{x}}}_i]={\mathbf{x}}_i={\mathbf{p}}_i$. In this case, the matrix ${\Sigma }_i=\mathbb{E}[{\eta }_i{\eta }_j^T]$ is equal to the covariance matrix of the multinomial ${\widehat{\mathbf{x}}}_i$ divided by $r_i^2$. Using Theorem 1 in [5] (which provides an inequality on the eigenvalues of the covariance of a multinomial),

$$\Vert {\Sigma }_i{\Vert }_2\le \underset{j=1,\dots ,m}{\max }{\mathbf{p}}_i[j]∕r_i\le 1∕r_i.$$ (22)

To consider an asymptotic setting, we think of an experimental setup where an increasing number of genes is sequenced. It is clear that in this experimental setup the number of read counts r_i for each cell needs to be controlled appropriately as a function of m. Since $\Vert {\mathbf{x}}_i{\Vert }_2^2={\sum }_{j=1}^m({\mathbf{p}}_i[j]{)}^2\le {\sum }_{j=1}^m{\mathbf{p}}_i[j]=1$, it is evident that the conditions in Theorem 3 hold if r_i = Ω(m), a condition which was recently identified as important for large-scale scRNA-seq experiments [60].

4. Summary and discussion

In this work, we investigated the robustness of the doubly-stochastic normalization to heteroskedastic noise, both from a theoretical perspective and from a numerical one. Our results imply that the doubly-stochastic normalization is advantageous over the popular row-stochastic and symmetric normalizations, particularly when the data at hand is high-dimensional and suffers from inherent heteroskedasticity. Moreover, our experiments suggest that incorporating the doubly-stochastic normalization into various data analysis, visualization, and processing techniques for real-world datasets can be worthwhile. The doubly-stochastic normalization is particularly appealing due to is simplicity, solid theoretical foundation, and resemblance to the row-stochastic/symmetric normalizations (which proved useful in countless applications).

The results reported in this work naturally give rise to several possible future research directions. On the theoretical side, it is of interest to characterize the convergence rate of ${\tilde{W}}^{(d)}$ to W^(d) also in terms of the number of points n and the covariance matrices {Σ_i} explicitly. As a particular simpler case, one may consider the high-dimensional setting where both n and m tend to infinity, while the quantity n/m is fixed (or tends to a fixed constant). On the practical side, it is of interest to investigate how to best incorporate the affinity matrix from the doubly-stochastic normalization into data analysis and visualization techniques. To that end, it is desirable to derive a method for picking the kernel parameter ε automatically, or in more generality, to determine how to make use of a variable kernel width (similarly to [59]) while retaining the robustness to heteroskedastic noise.

Appendix

Appendix A. Proof of Lemma 1

We first recall the definition of a fully indecomposable matrix [2]. A matrix B is called fully indecomposable if there are no permutation matrices P and Q such that

$$PBQ=\left[\begin{array}{cc}\hfill B_1\hfill & \hfill 0\hfill \\ \hfill B_2\hfill & \hfill B_3\hfill \end{array}\right],$$ (23)

with B₁ square. We now proceed to show that A from Lemma 1 is fully indecomposable. Since the only zeros in A are on its main diagonal, there is only one zero in every row and every column of A. Consequently, any permutation of the rows and columns of A would retain this property, namely have a single zero in every row and every column. Therefore, if n > 2, it is impossible to find P and Q such that (23) would hold for B = A, since there cannot be a block of zeros in PAQ whose number of rows or columns is greater than 1. Hence, A is fully indecomposable, and the existence and uniqueness of d = [d₁, … , d_n] > 0 follows from Lemma 4.1 in [30].

Appendix B. Proof of Theorem 3

Throughout this proof we omit the superscript (m) from the quantities ${\mathbf{x}}_i^{(m)}$, ${\tilde{\mathbf{x}}}_i^{(m)}$, ${\eta }_i^{(m)}$, ${\Sigma }_i^{(m)}$, K^(m), ${\tilde{K}}^{(m)}$, W^(d),(m), ${\tilde{W}}^{(d),(m)}$, and it should be noted that the resulting notation corresponds to sequences in the dimension m where n and ε are fixed.

Let us define

$$u_i=d_i\text{exp}(-\Vert {\mathbf{x}}_i{\Vert }^2∕\epsilon ),H_{i,j}=\{\begin{array}{cc}\text{exp}(2\langle {\mathbf{x}}_i,{\mathbf{x}}_j\rangle ∕\epsilon ),\hfill & i\ne j,\hfill \\ 0,\hfill & i=j,\hfill \end{array}\phantom{\}}$$ (24)

for i, j = 1, …, n. By the definition of W^(d) in (4), for i ≠ j we can write

$$W_{i,j}^{(d)}=d_i\text{exp}(-\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2∕\epsilon )d_j=d_i{e}^{-\Vert {\mathbf{x}}_i{\Vert }^2∕\epsilon }{e}^{2\langle {\mathbf{x}}_i,{\mathbf{x}}_j\rangle ∕\epsilon }{e}^{-\Vert {\mathbf{x}}_j{\Vert }^2∕\epsilon }{d}_j=u_i{H}_{i,j}{u}_j.$$ (25)

Analogously, we define ${\tilde{H}}_{i,j}$ and ${\tilde{u}}_i$ by replacing {x_i} and {d_i} in (24) with {${\tilde{\mathbf{x}}}_i$} and {${\tilde{d}}_i$}, respectively, and we have that ${\tilde{W}}_{i,j}={\tilde{u}}_i{\tilde{H}}_{i,j}{\tilde{u}}_j$.

Let ⨀ denote the Hadamard (element-wise) product, u = [u₁, … , u_n]^T, and $\tilde{\mathbf{u}}=[{\tilde{u}}_1,\dots ,{\tilde{u}}_n{]}^T$. We can write

$$\begin{gathered} \Vert {\tilde{W}}^{(d)}-W^{(d)}{\Vert }_F=\Vert \text{diag}(\tilde{\mathbf{u}})\tilde{H}\text{diag}(\tilde{\mathbf{u}})-\text{diag}(\mathbf{u})H\text{diag}(\mathbf{u}){\Vert }_F \\ =\Vert ({\mathbf{uu}}^T)\odot (\tilde{H}-H)+\tilde{H}\odot (\tilde{\mathbf{u}}{\tilde{\mathbf{u}}}^T-{\mathbf{uu}}^T){\Vert }_F \\ \le \underset{i,j}{\max }\{u_i{u}_j\}\cdot \Vert \tilde{H}-H{\Vert }_F+\underset{i,j}{\max }\{{\tilde{H}}_{i,j}\}\cdot \Vert \tilde{\mathbf{u}}{\tilde{\mathbf{u}}}^T-{\mathbf{uu}}^T{\Vert }_F. \end{gathered}$$ (26)

We begin by bounding the quantity $\Vert \tilde{H}-H{\Vert }_F$, which is the subject of the following Lemma.

Lemma 4. For all i ≠ j,

$$\mid {\tilde{H}}_{i,j}-H_{i,j}\mid ={\mathcal{O}}_p(m^{-1∕2}).$$ (27)

Proof. Let us write

$$\langle {\tilde{\mathbf{x}}}_i,{\tilde{\mathbf{x}}}_j\rangle =\langle {\mathbf{x}}_i,{\mathbf{x}}_j\rangle +\langle {\mathbf{x}}_i,{\eta }_j\rangle +\langle {\eta }_i,{\mathbf{x}}_j\rangle +\langle {\eta }_i,{\eta }_j\rangle .$$ (28)

According to (7) and the conditions in Theorem 3, for i ≠ j we have

$$\mathbb{E}\{\langle {\mathbf{x}}_i,{\eta }_j\rangle +\langle {\eta }_i,{\mathbf{x}}_j\rangle +\langle {\eta }_i,{\eta }_j\rangle \}=0,$$ (29)

$$\text{Var}\{\langle {\mathbf{x}}_i,{\eta }_j\rangle \}=\mathbb{E}[{\mathbf{x}}_i^T{\eta }_j{\eta }_j^T{\mathbf{x}}_i]={\mathbf{x}}_i^T{\Sigma }_j{\mathbf{x}}_i\le \Vert {\mathbf{x}}_i{\Vert }^2\Vert {\Sigma }_j{\Vert }_2\le C_{\eta }{m}^{-1},$$ (30)

$$\text{Var}\{\langle {\mathbf{x}}_j,{\eta }_i\rangle \}=\mathbb{E}[{\mathbf{x}}_j^T{\eta }_i{\eta }_i^T{\mathbf{x}}_j]={\mathbf{x}}_j^T{\Sigma }_i{\mathbf{x}}_j\le \Vert {\mathbf{x}}_j{\Vert }^2\Vert {\Sigma }_i{\Vert }_2\le C_{\eta }{m}^{-1},$$ (31)

$$\begin{gathered} \text{Var}\{\langle {\eta }_i,{\eta }_j\rangle \}=\mathbb{E}[{\eta }_i^T{\eta }_j{\eta }_j^T{\eta }_i]=\sum _{k=1}^m\sum _{\ell =1}^n\mathbb{E}[{\eta }_i[k]{\eta }_i[\ell ]]]\mathbb{E}[{\eta }_j[k]{\eta }_j[\ell ]] \\ =\text{Tr}\{{\Sigma }_i{\Sigma }_j\}\le m\Vert {\Sigma }_i{\Sigma }_j{\Vert }_2\le m\Vert {\Sigma }_i{\Vert }_2\Vert {\Sigma }_j{\Vert }_2\le C_{\eta }^2{m}^{-1}. \end{gathered}$$ (32)

Therefore,

$$\text{Var}\{\langle {\mathbf{x}}_i,{\eta }_j\rangle +\langle {\eta }_i,{\mathbf{x}}_j\rangle +\langle {\eta }_i,{\eta }_j\rangle \}\le \frac{6C_{\eta }+3C_{\eta }^2}{m},$$ (33)

where we used the inequality (a + b + c)² ≤ 3(a² + b² + c²). Consequently, Chebyshev’s inequality yields that for any p > 0

$$\text{Pr}\left\{\mid \langle {\mathbf{x}}_i,{\eta }_j\rangle +\langle {\eta }_i,{\mathbf{x}}_j\rangle +\langle {\eta }_i,{\eta }_j\rangle \mid >\sqrt{\frac{6C_{\eta }+3C_{\eta }^2}{m(1-p)}}\right\}\le p,$$ (34)

which implies

$$\mid \langle {\mathbf{x}}_i,{\eta }_j\rangle +\langle {\eta }_i,{\mathbf{x}}_j\rangle +\langle {\eta }_i,{\eta }_j\rangle \mid ={\mathcal{O}}_p\left(m^{-1∕2}\right).$$ (35)

Using the above for i ≠ j, a first-order Taylor expansion of exp(y) around y = 0 gives

$$\text{exp}\{2(\langle {\mathbf{x}}_i,{\eta }_j\rangle +\langle {\eta }_i,{\mathbf{x}}_j\rangle +\langle {\eta }_i,{\eta }_j\rangle )∕\epsilon \}=1+{\mathcal{O}}_p(m^{-1∕2}),$$ (36)

and by (28) we have

$${\tilde{H}}_{i,j}=e^{2\langle {\tilde{\mathbf{x}}}_i,{\tilde{\mathbf{x}}}_j\rangle ∕\epsilon }=e^{2\langle {\mathbf{x}}_i,{\mathbf{x}}_j\rangle ∕\epsilon }(1+{\mathcal{O}}_p(m^{-1∕2}))=H_{i,j}(1+{\mathcal{O}}_p(m^{-1∕2}))=H_{i,j}+{\mathcal{O}}_p(m^{-1∕2}),$$ (37)

where we used H_i,j = e^{⟨x_i,x_j⟩/ε} ≤ e^{∥x_i∥∥x_j∥/ε} ≤ e^1/ε in the last equality. □

Using Lemma 4 and applying the union bound on the off-diagonal entries of $\tilde{H}-H$, we obtain

$$\Vert \tilde{H}-H{\Vert }_F={\mathcal{O}}_p(m^{-1∕2}),$$ (38)

Continuing, we bound the quantities max_i,j{u_iu_j} and ${\max }_{i,j}\{{\tilde{H}}_{i,j}\}$ from (26). Towards that end, we have the following result.

Proposition 5. Under the conditions of Theorem 3, {H_i,j}_i≠j and $\{u_i{\}}_{i=1}^n$ are upper- and lower-bounded by positive constants independent of m.

Proof. Observe that for i ≠ j and for all m,

$$0<e^{-1∕\epsilon }\le H_{i,j}=e^{\langle {\mathbf{x}}_i,{\mathbf{x}}_j\rangle ∕\epsilon }\le e^{1∕\epsilon }.$$ (39)

Since the set of n × n matrices satisfying the above is compact, and using the fact that {u_i} > 0 can be uniquely determined by H (from Lemma 1 applied to H), there must exist constants c_u, C_u independent of m such that

$$0<c_u\le u_i\le C_u,$$ (40)

for all i and m. □

Consequently, Proposition 5 together with Lemma 4 guarantee that

$$\underset{i,j}{\max }\{u_i{u}_j\}={\mathcal{O}}_p(1),\underset{i,j}{\max }\{{\tilde{H}}_{i,j}\}=\underset{i,j}{\max }\{H_{i,j}\}+{\mathcal{O}}_p(m^{-1∕2})={\mathcal{O}}_p(1),$$ (41)

Next, we turn to bound the quantity $\Vert \tilde{\mathbf{u}}{\tilde{\mathbf{u}}}^T-{\mathbf{uu}}^T{\Vert }_F$ from (26). From Lemma 1 applied to H and $\tilde{H}$, it follows that u and $\tilde{\mathbf{u}}$ are unique. Additionally, by Lemma 4 it is clear that $\tilde{H}\stackrel{p}{\to }H$. Therefore, we also have that $\tilde{\mathbf{u}}\stackrel{p}{\to }\mathbf{u}$ (as otherwise we have a contradiction to the uniqueness of u and $\tilde{\mathbf{u}}$). Since ${\tilde{W}}^{(d)}$ is doubly-stochastic, we have

$$\sum _{j=1}^n{\tilde{W}}_{i,j}^{(d)}=\sum _{j=1}^n{\tilde{u}}_i{\tilde{H}}_{i,j}{\tilde{u}}_j=1.$$ (42)

Let us define the multivariate functions $\{f_i(A,\mathbf{v}){\}}_{i=1}^n$, where $A\in {\mathbb{R}}^{n\times n}$, $\mathbf{v}\in {\mathbb{R}}^n$, as

$$f_i(A,\mathbf{v})=\sum _{j=1}^m{v}_i{A}_{i,j}{v}_j.$$ (43)

To bound the error $\Vert \tilde{\mathbf{u}}-\mathbf{u}\Vert$, we expand f_i(A, v) around (H, u) using a first-order Taylor expansion. Towards that end, Proposition 5 can be used to verify that the second-order partial derivatives of f_i in the vicinity of (H, u) are bounded by constants independent of m. In particular,

$$\underset{(A,\mathbf{v})\in {\mathcal{B}}_1(H,\mathbf{u})}{\max }\mid \frac{{\partial }^2{f}_i}{\partial v_k\partial v_j}\mid ={\mathcal{O}}_p(1),\underset{(A,\mathbf{v})\in {\mathcal{B}}_1(H,\mathbf{u})}{\max }\mid \frac{{\partial }^2{f}_i}{\partial v_k{A}_{m,j}}\mid ={\mathcal{O}}_p(1),\frac{{\partial }^2{f}_i}{\partial A_{k,j}{A}_{m,\ell }}=0,$$ (44)

for all i, j, k, m, ℓ, where ${\mathcal{B}}_1(H,\mathbf{u})$ is a ball of radius 1 in Euclidean space around (H, u):

$${\mathcal{B}}_1(H,\mathbf{u})=\{(A,\mathbf{v}):\Vert A-H{\Vert }_F^2+\Vert \mathbf{v}-\mathbf{u}{\Vert }^2\le 1\}.$$ (45)

The choice of the radius of the ball ${\mathcal{B}}_1(H,\mathbf{u})$ is arbitrary, and is only required to guarantee that the point $(\tilde{H},\tilde{\mathbf{u}})$ is included in ${\mathcal{B}}_1(H,\mathbf{u})$ for sufficiently large m. Therefore, by (42) and (44), the first-order Taylor expansion of f_i(A, v) around (H, u) gives

$$\begin{gathered} {\phantom{\mid }1=f_i(\tilde{H},\tilde{\mathbf{u}})=f_i(H,\mathbf{u})+\sum _{j=1}^n\frac{\partial f_i}{\partial v_j}\mid }_{(H,\mathbf{u})}{\phantom{\mid }({\tilde{u}}_j-u_j)+\sum _{k,j=1}^n\frac{\partial f_i}{\partial A_{k,j}}\mid }_{(H,\mathbf{u})}({\tilde{H}}_{k,j}-H_{k,j}) \\ +{\mathcal{O}}_p(\Vert \tilde{\mathbf{u}}-\mathbf{u}{\Vert }^2)+{\mathcal{O}}_p(\Vert \tilde{H}-H{\Vert }_F^2). \end{gathered}$$ (46)

where

$${\phantom{\mid }\frac{\partial f_i}{\partial v_j}\mid }_{(H,\mathbf{u})}=\{\begin{array}{cc}\frac{1}{u_i},\hfill & j=i,\hfill \\ u_i{H}_{i,j},\hfill & j\ne i,\hfill \end{array}\phantom{\}}{\phantom{\mid }\frac{\partial f_i}{\partial A_{k,j}}\mid }_{(H,\mathbf{u})}=\{\begin{array}{cc}{u}_i{u}_j,\hfill & k=i,\hfill \\ 0,\hfill & k\ne i,\hfill \end{array}\phantom{\}}$$ (47)

and we used the fact that ${\sum }_{j=1}^n{u}_i{H}_{i,j}{u}_j=1(W^{(d)}$ is doubly-stochastic). Next, using that f_i(H, u) = 1, denoting ${\tilde{u}}_j-u_j≔e_j$, and multiplying both hand sides of (46) by u_i (u_i is bounded according to Proposition 5), we can write

$$e_i=-\sum _{j\ne i}^n{u}_i^2{H}_{i,j}{e}_j-\sum _{j=1}^n{u}_i^2{u}_j({\tilde{H}}_{i,j}-H_{i,j})+{\mathcal{O}}_p(\Vert \mathbf{e}{\Vert }^2)+{\mathcal{O}}_p(\Vert \tilde{H}-H{\Vert }_F^2),$$ (48)

where e = [e₁, … , e_n]^T. Consequently, since H_i,i = 0, writing (48) in matrix form gives

$$(I_n+[\text{diag}(\mathbf{u}){]}^{2}H)\mathbf{e}=-[\text{diag}(\mathbf{u}){]}^2(\tilde{H}-H)\mathbf{u}+{\mathcal{O}}_p(\Vert \mathbf{e}{\Vert }^2)+{\mathcal{O}}_p(\Vert \tilde{H}-H{\Vert }_F^2),$$ (49)

where I_n is the n × n identity matrix. In order to bound the vector e, we must be able to invert the matrix

$$G≔I_n+[\text{diag}(\mathbf{u}){]}^{2}H,$$ (50)

which is the subject of the following Lemma.

Lemma 6. Under the conditions of Theorem 3, the matrix G from (50) is invertible for all m, and ∥G⁻¹∥₂ ≤ C_G for some constant C_G independent of m.

Proof. Notice that G is similar to the matrix

$$[\text{diag}(\mathbf{u}){]}^{-1}G\text{diag}(\mathbf{u})=I_n+\text{diag}(\mathbf{u})H\text{diag}(\mathbf{u})=I_n+W^{(d)}.$$ (51)

Therefore, G is invertible if I_n + W^(d) is invertible. Since W^(d) is symmetric and doubly-stochastic, its largest eigenvalue is exactly 1, and λ_min{W^(d)} ≥ −1. Moreover, since W_i,j > 0 for all i ≠ j, we have that {(W^(d))²}_i,j > 0 for all i, j. Therefore, by Lemma 8.4.3 in [26] W^(d) has only one eigenvalue with maximal absolute-value (which is 1). Hence, λ_min{W^(d)} > −1, and we obtain that

$${\lambda }_{\text{min}}\{G\}={\lambda }_{\text{min}}\{I_n+W^{(d)}\}=1+{\lambda }_{\text{min}}\{W^{(d)}\}>0.$$ (52)

The fact that ∥G⁻¹∥₂ is bounded by some constant independent of m is established by Proposition 5 (since the set of all possible matrices G that satisfy (39) and (40) is compact). □

Using (49) together with Lemma 6 and Proposition 5, we have that

$$\begin{gathered} \Vert \mathbf{e}\Vert \le C_G\Vert [\text{diag}(\mathbf{u}){]}^2(\tilde{H}-H)\mathbf{u}\Vert +{\mathcal{O}}_p(\Vert \mathbf{e}{\Vert }^2)+{\mathcal{O}}_p(\Vert \tilde{H}-H{\Vert }_F^2) \\ \le C_G\Vert \text{diag}(\mathbf{u}){\Vert }_2^2\cdot \Vert \tilde{H}-H{\Vert }_2\cdot \Vert \mathbf{u}{\Vert }_2+{\mathcal{O}}_p(\Vert \mathbf{e}{\Vert }^2)+{\mathcal{O}}_p(\Vert \tilde{H}-H{\Vert }_F^2) \\ ={\mathcal{O}}_p(\Vert \tilde{H}-H{\Vert }_F)+{\mathcal{O}}_p(\Vert \mathbf{e}{\Vert }^2)+{\mathcal{O}}_p(\Vert \tilde{H}-H{\Vert }_F^2), \end{gathered}$$ (53)

where we used the inequality $\Vert \tilde{H}-H{\Vert }_2\le \Vert \tilde{H}-H{\Vert }_F$. From (38), (53), and the fact that $\tilde{H}\stackrel{p}{\to }H$, $\tilde{\mathbf{u}}\stackrel{p}{\to }\mathbf{u}$, it follows that

$$\Vert \mathbf{e}\Vert =\Vert \tilde{\mathbf{u}}-\mathbf{u}\Vert ={\mathcal{O}}_p(m^{-1∕2}).$$ (54)

Consequently,

$$\Vert \tilde{\mathbf{u}}{\tilde{\mathbf{u}}}^T-{\mathbf{uu}}^T{\Vert }_F=\Vert (\mathbf{u}+\mathbf{e})(\mathbf{u}+\mathbf{e}{)}^T-{\mathbf{uu}}^T{\Vert }_F=\Vert \mathbf{e}{\mathbf{u}}^T+\mathbf{u}{\mathbf{e}}^T+{\mathbf{ee}}^T{\Vert }_F\le 2\Vert \mathbf{u}\Vert \cdot \Vert \mathbf{e}\Vert +\Vert \mathbf{e}{\Vert }^2={\mathcal{O}}_p(m^{-1∕2}),$$ (55)

where we used Proposition 5 to bound ∥u∥. Overall, substituting (55), (38), and (41) into (26), we arrive at the required result

$$\Vert {\tilde{W}}^{(d)}-W^{(d)}{\Vert }_F={\mathcal{O}}_p(m^{-1∕2}).$$ (56)