Abstract
Biomolecular condensates appear throughout the cell serving a wide variety of functions. Many condensates appear to form by the assembly of multivalent molecules, which produce phase separated networks with liquid-like properties. These networks then recruit client molecules, with the total composition providing functionality. Here we use a model system of poly-SUMO and poly-SIM proteins to understand client-network interactions and find that the structure of the network plays a strong role in defining client recruitment, and thus functionality. The basic unit of assembly in this system is a zipper-like filament composed of alternating poly-SUMO and poly-SIM molecules. These filaments have defects of unsatisfied bonds that allow for both the formation of a 3D network and the recruitment of clients. The filamentous structure constrains the scaffold stoichiometries and the distribution of client recruitment sites that the network can accommodate. This results in a non-monotonic client binding response that can be tuned independently by the client valence and binding energy. These results show how the interactions within liquid states can be disordered yet still contain structural features that provide functionality to the condensate.
Graphical Abstract
Introduction
Many cellular structures have been shown to form by the spontaneous condensation of biomolecules into liquid-like states,1,2 often through liquid-liquid phase transitions. While these condensates may contain hundreds of different molecules, typically only a small number of molecules with high interaction valence and high connectivity to other molecules contribute strongly to phase separation.3–5 These are said to have “scaffold-like” properties depending on how strongly they promote phase separation. The remaining molecules, which exhibit “client-like” properties, are recruited through interactions with scaffolds.6,7 Together, the collection of molecules in a condensate determines its functionality.
Since the molecules driving phase separation are multivalent, polymer-like species, many treatments of condensate formation are based on polymer theories.8–11 In particular, scaffold condensation can be understood as the interaction between attractive “stickers” separated by inert “spacers”.11,12 These efforts explain universal features of condensates, such as how multivalency can amplify the effect of weak interactions to tune the phase coexistence line to lie within physiologically relevant regions of phase space (e.g. physiological concentrations).8 However, condensates have been shown to perform diverse functions, and the evolutionary pressure to optimize these specific functions implies that there will also be non-universal features.2,7,13–16 This begs the question of how the disordered network of interactions within a liquid structure can affect its properties.
The disorder in biomolecular condensates poses a challenge for structural biology to determine what features of the assembly are functionally relevant. In previous work, we showed that analytic theory can be used to deduce structural features in these systems.17 This approach is analogous to conventional methods like NMR and crystallography in that experimental constraints are used to refine a structural model. A major difference is that the model does not specify spatial coordinates, but instead, describes the network connectivity. This is encoded in a free energy model that uses system-specific order parameters to capture structural features as well as regions that remain disordered. Here we apply this approach to condensates formed by poly-SUMO and poly-SIM, a synthetic system composed of repeating units of either SUMO or its binding partner, SIM, that was developed to study the recruitment of client molecules.6 In both poly-SUMO and poly-SIM the modules are separated by a short, disordered linker of 12 amino acids. This system captures the features of the common sticker-and-spacer topology, and the 1:1 binding stoichiometry between SUMO and SIM modules eliminates the ambiguity in identifying the sticker moieties that complicates the study of natural systems. We find that SUMO/SIM condensates have a zipper-like microstructure that differs from the brush-like microstructure of SPOP/DAXX or the random network of FUS-like proteins.11,17 This microstructure dictates how client recruitment varies with changes in valence and affinity, and suggests that the composition, and thus function, of a condensate can be changed through modulation of its internal structure independent of its propensity to undergo phase separation. These results show how functionally relevant structures can be embedded within liquid-like disorder.
Based on these results, we propose a general model in which functional properties emerge from hierarchical assembly within a condensate. In this model, strong interactions drive the formation of molecular complexes with functional properties. These complexes then condense into a fluid state via weaker interactions. This combination of strong and weak interactions combines the best features of both interactions modes. Strong interactions provide the structural specificity needed for functional properties to emerge, while weaker interactions allow the formation of a high density state without the kinetic arrest that would accompany assembly driven strictly by strong interactions.
Results
Zipper-like filaments allow most modules to form bonds within a sparse network.
Our initial attempts to model SUMO/SIM condensates employed Flory-Huggins theory with three components representing SUMO, SIM, and solvent. Flory-Huggins is a lattice mean-field model representing a maximally disordered system. We refer to Flory-Huggins and similar theories for associative polymers11,12,18 as “random network” models, reflecting the fact that each binding site randomly searches the nearby volume for interaction partners, which results in uncorrelated binding. The Flory-Huggins lattice constant is determined by the dimensions of the macromolecular repeat units.19 In this case, estimates for the linker radius of gyration and module size yield repeat units on the order of 3 nm. We found that any realistic combination of interaction parameters, which account for excluded volume, binding energies, and spacer entropy, yields lattice occupancies of at least 70%, and usually much greater. With a 3 nm lattice constant, this corresponds to a droplet module concentration on the order of 50 mM, much greater than the observed concentration of ~ 2 mM.6 To account for the finite valence of the SUMO and SIM modules, we modified our model for SPOP/DAXX assemblies to account for decavalent scaffolds and, again, obtained results consistent with a dense phase module concentration near 50 mM. Electrostatic repulsion was considered as a swelling mechanism and rejected on the grounds that the repeat unit dimensions are greater than the ~ 1 nm Debye screening length, which eliminates long range interactions (short range effects are accounted for in the module binding affinity).
The experimentally measured module concentration implies that the volume per decavalent scaffold is (2 nM/10)−1 ≃ (20 nm)3. Since, this is larger than the random walk volume of a scaffold, this separation would allow only a small fraction of intermolecular bonds to be satisfied if the molecules are randomly oriented. For bond energies strong enough to drive phase separation, on the order of kBT, the penalty for this many unsatisfied bonds is prohibitive. Therefore, we were forced to reject the hypothesis of randomly oriented scaffolds.
The alternative to randomly oriented scaffolds is that SUMO/SIM networks satisfy most binding sites by aligning the scaffolds. Therefore, we developed a theory to describe aligned molecules. Fig. 1a,b shows a model where the molecules are aligned to form zipper-like structures. By comparing the predictions of this model to the experiments of6 we can learn the extent to which this “zipper model” describes SUMO/SIM condensates.
Figure 1: Poly-SUMO and poly-SIM assemble into zipper-like filaments.
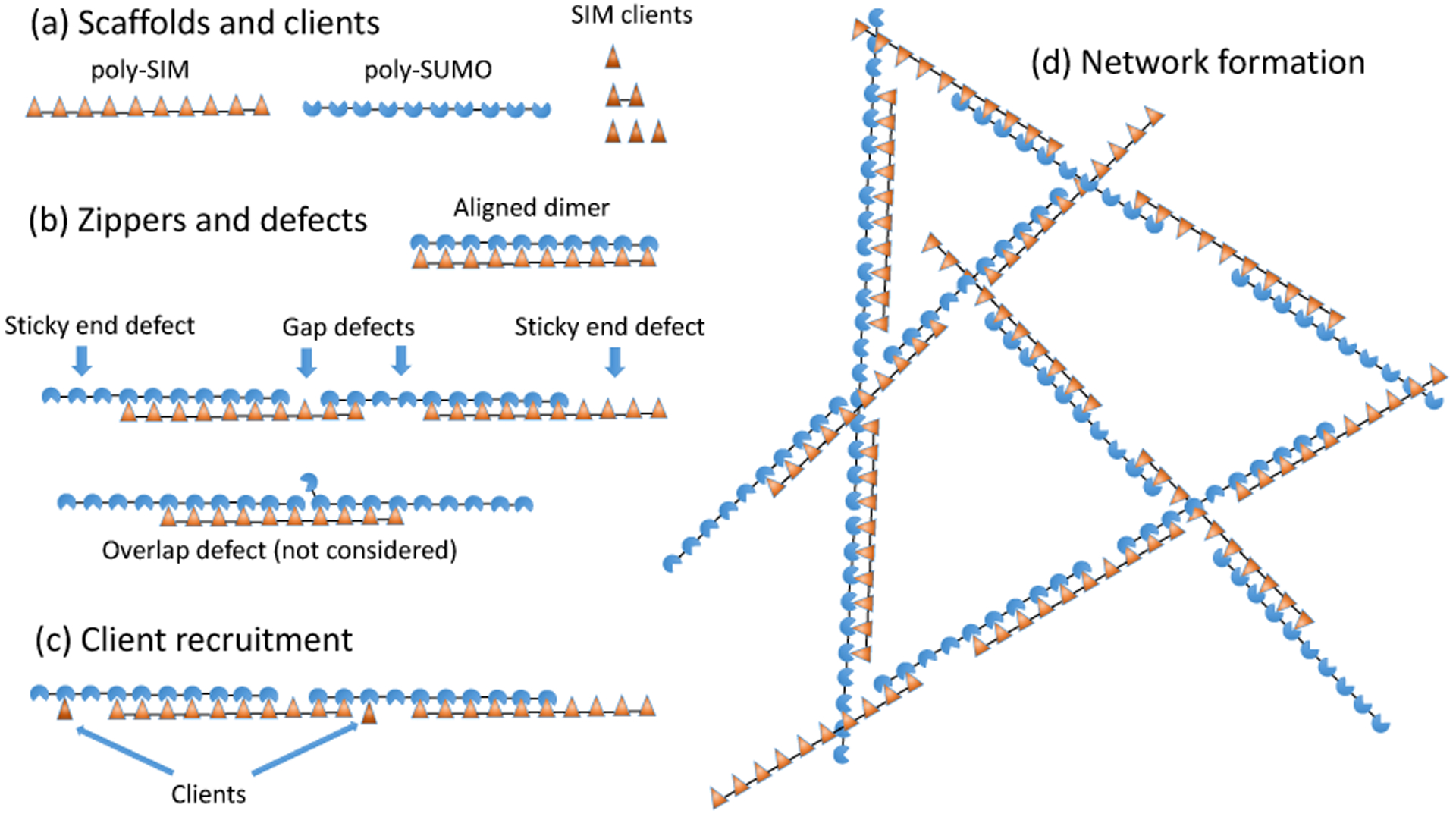
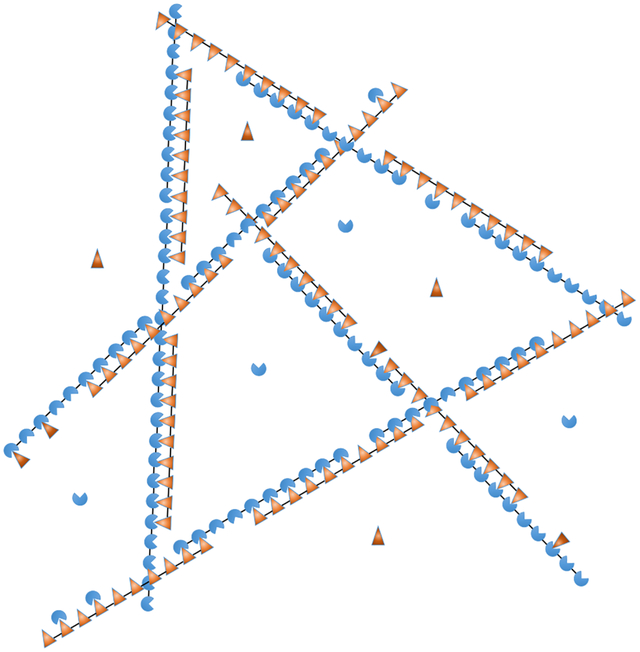
(a) SUMO/SIM droplets are composed of decavalent scaffolds and clients of valence 1, 2, and 3. (b) Intermolecular bonding is most efficient when the scaffolds align to form zipper-like structures. The zippers have bonding defects including sticky ends and gaps. Overlap defects are also possible but neglected in our calculation. (c) Zipper defects provide binding sites to recruit clients or (d) assemble the zippers into a 3D network. The short linker connecting modules favors consecutive bonds with the same molecule rather than the formation of a random network.
Thermal fluctuations require that SUMO/SIM zippers will have defects in the bonding structure that provide recruitment sites for clients as well as enable the 1D filaments to assemble into a 3D network (Fig. 1c,d). Therefore, the properties of the zippers determine the properties of the larger scale droplets. Notably, the defects will have a spacing on the order of the scaffold dimension, consistent with the (20 nm)−3 scaffold concentration. Fig. 1b shows two defects considered in this work, gaps and sticky ends, as well as an overlap defect that we neglect. Overlap defects incur a binding energy penalty identical to a gap, but are further suppressed by the steric clash between the two modules competing for the same binding partner. Therefore, we expect, and our results confirm, that sticky ends and gaps are the dominant defect in the zipper structure.
The filament partition function can be calculated with transfer matrices.
Due to the 1D nature of the zippers, their properties can be conveniently calculated using a transfer matrix formalism.20,21 To illustrate this approach, consider a tetravalent (v = 4) system (in subsequent calculations we use v = 10 to compare to the experiments of6) and define QN(j) as the partition function of a filament containing N molecules that terminates with a sticky end of j unpaired sites. Next, we construct a v − 1 dimensional vector, V(N), whose elements are the statistical weights QN(j) for sticky ends of each length, j. This vector obeys a recursion relation V(N + 1) = MiV(N), where the transfer matrix Mi generates the possible states upon addition of a molecule to the filament
| (1) |
where ϵ is the SUMO-SIM binding free energy (all energies are expressed in units of kBT) and zi is the fugacity of the added molecule. Matrix elements below the antidiagonal leave gap defects which can bind clients or form crosslinks with other filaments. This is accounted for by the gap partition function gi(m), where m is the size of the gap. Since we have two scaffold molecules, the grand partition function for a filament of N + 1 poly-SUMO and N + 1 poly-SIM molecules can be generated by alternately applying the matrices for the two species and applying vectors VL/R to collapse the matrix product into a scalar polynomial (see Appendix). This operation is given by QN+1 = VL(MUMI)NVR, where the U/I subscripts denote SUMO/SIM.
The most important parameter in Eq. 1 is the module binding affinity, which can be obtained from dilute solution measurements6 as follows. Consider the dimer association constant between scaffolds of valence v, , where c2v is the concentration of scaffold dimer. Here the reference concentration c0 gives the equilibrium constant appropriate units and enters the matrix formalism through the fugacity zi = ci/c0 (valid for dilute solution when the monomer free energy is set to zero). The dimerization free energy is given by the dimer partition function , where the terms represent the perfectly aligned state and successively larger mis-alignments. Plotting lnK2v vs. v (Fig. 2), we can extract ϵ = −2.23 kBT from the slope and c0 = 64 μM from the intercept. Note that accounts for both the binding affinity between modules, as well as the entropic cost of constraining the connecting spacers.
Figure 2: Model parameters are obtained from poly-SUMO/poly-SIM dimerization experiments.
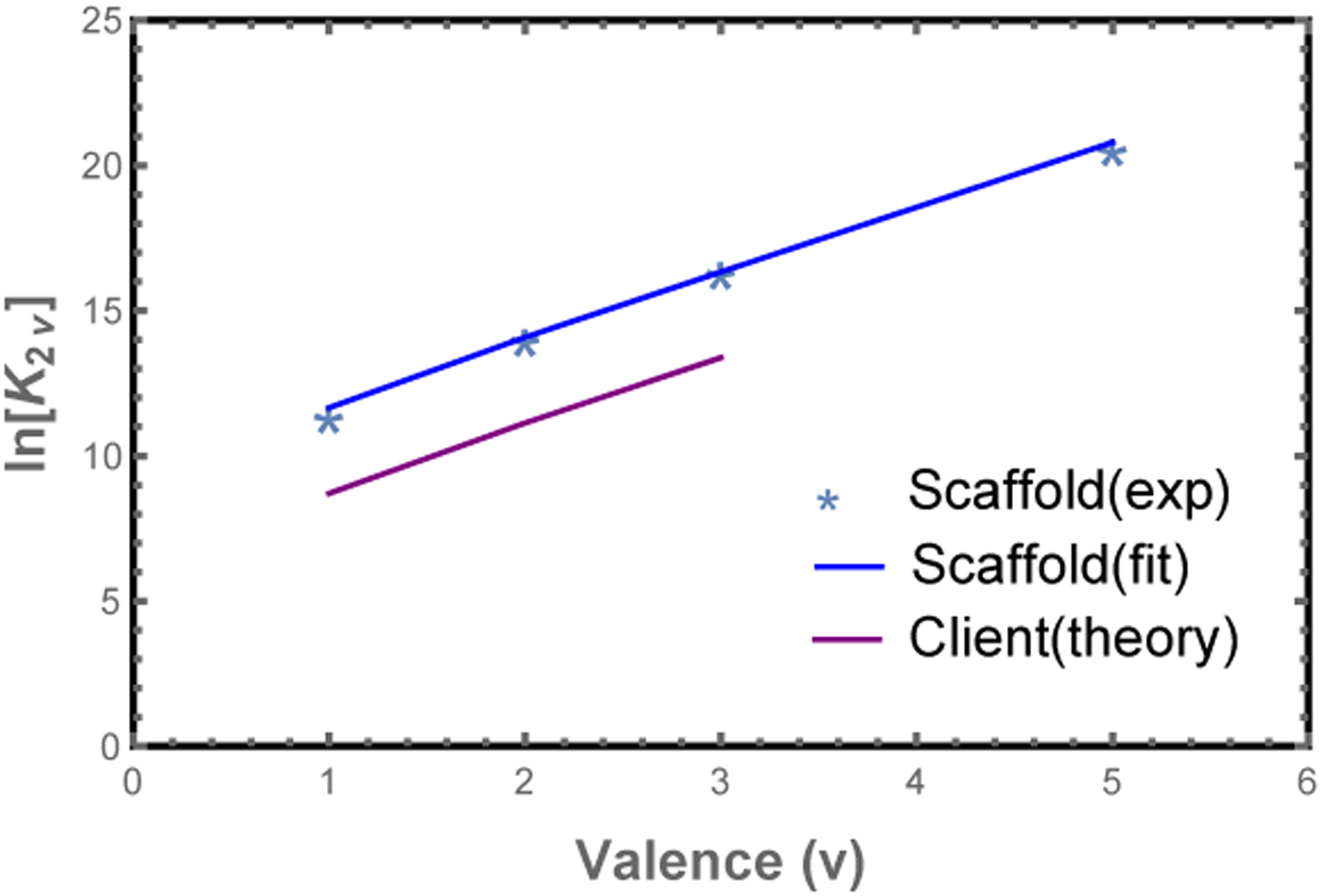
Plot of the dimer association constant, K2v,6 vs. the valence, v. The module binding free energy, ϵ, is obtained from the slope of lnK2v (blue line), while the intercept provides the reference concentration c0. Clients (mono-, bi-, or trivalent SIM) have a lower binding affinity than scaffolds in the droplet phase, which we attribute to steric interactions between the network and the fluorescent labels. We account for this with a free energy offset, fRFP, for clients in the dense phase (purple line).
To compute solution properties we construct the grand partition function
| (2) |
where the first two terms represent the monomers, the third term represents the perfectly aligned dimer, and the two sums represent filaments starting with SUMO and SIM respectively. The matrices Mi and end vectors V are given in the Methods section.
The condensed phase has structural features emerging on different length scales.
On length scales larger than the scaffold dimension the droplet resembles a random network of zippers (Fig. 1d). On this scale the only structural feature is the mesh size, which is determined by the crosslink density. Since the zipper motif fully satisfies the SUMO and SIM binding sites, the crosslinks can only form at defect sites. This limits the affinity of crosslink bonds, so the crosslinks are relatively weak and rapidly break and reform due to thermal fluctuations. This rapid reconfiguration is responsible for the liquid properties of the dense phase. In contrast, the cooperative binding within the zipper gives them a persistent structure that provides crucial functional characteristics. The zippers have considerable disorder, due to the many ways that the scaffolds can be aligned, but the essential structural features can be described by two quantities. The first is the defect density, which describes the capacity of the filaments to bind clients or crosslink into a 3D network. Using the substitution gi(m) = gm so that g is the statistical weight of an unbound module, the density of unpaired sites per scaffold molecule is given by . This gives ρg ≃ 0.6 unbound sites per decavalent scaffold at equimolar scaffold mixtures (Fig. 3a). Using this defect density, the zippers can be described in the sticker/spacer framework where the defects are stickers and the spacers are zippers with a length of 10/ρg ≃ 17 modules. The expected radius of gyration of these spacers is , which is consistent with, but somewhat smaller than, the 20 nm average molecular spacing. We attribute this discrepancy to the fact that not every defect will be involved in a crosslink and zippers will be less flexible than individual scaffolds due to the double linkage and increased charge density, so the spacer radius of gyration will be larger than our 12 nm estimate.
Figure 3: Filament length and defect density depend on stoichiometry.
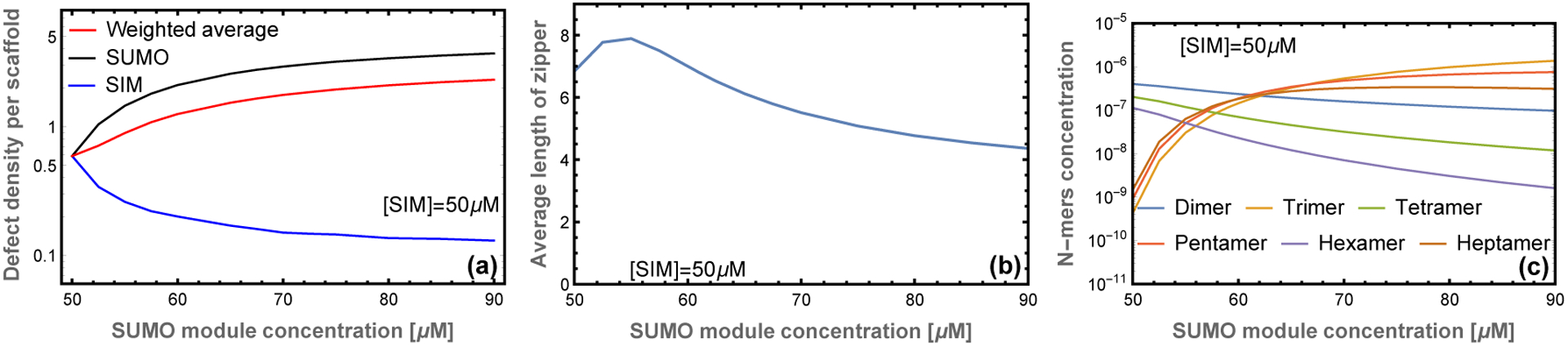
(a) At equal stoichiometry most scaffolds are fully bound resulting in few defects. As the stoichiometric imbalance increases, the number of unbound SUMO modules increases while the number of unbound SIM sites decreases. (b) The average length of filaments is a non-monotonic function of scaffold stoichiometry. A small excess of one scaffold leads to an increase in the filament length because unpaired scaffolds are available to stabilize sticky ends resulting from mis-aligned states. Larger stoichiometric mismatches result in a decline in filament length, which provides more sticky ends to bind the excess scaffold. (c) Filaments with equal number of SUMO and SIM scaffolds are favored at symmetric mixing, but unequal stoichiometries favor odd length filaments.
The second useful quantity to describe the zipper structure is the average number of scaffolds in a zipper. This is obtained from . The total assembly size Ntot = 〈NI +NU〉 is plotted in Fig. 3b. The most energetically favored state is the perfectly aligned dimer which allows all binding sites to be satisfied (Fig. 1b). This competes with the misaligned states, which have a higher entropy due to the many possible alignments. This is particularly true upon the formation of filaments with Ntot ≥ 3 because the unpaired sites can be distributed throughout the filament rather than localized at the ends. At sufficiently high concentration the entropic gain of misalignment can overcome the energetic cost of defects allowing the formation of large assemblies.
Asymmetric scaffold stoichiometries promote filaments over perfectly aligned dimers.
The combined behavior of the defect density and the filament length can be understood by looking at the populations of different filament lengths (Fig. 3c). At equal stoichiometries, the solution is dominated by perfectly aligned dimers resulting in a small average complex size. This is similar to the “magic number” effect seen in the simulations of EPYC1 and Rubisco in which phase separation is inhibited when the concentration and valence of scaffolds are matched.22,23 At unequal stoichiometries the energetic penalty for misalignments is reduced because excess scaffolds are available to bind one of the sticky ends, which facilitates the formation of longer complexes. As the stoichiometry mismatch increases, the system becomes dominated by odd-length complexes which are initially large before trimer (2:1 stoichiometry) states dominate at large stiochiometric mismatches. The decrease in filament size at large stoichiometric asymmetry can be understood as an abundance of filaments that have two sticky ends of the same type, which prevents them from joining into larger assemblies. The shortening of filaments causes an increase in sticky ends and, therefore, an increase in the concentration of defect sites (Fig. 3a). The defect density increases rapidly at first, then slows at SUMO module concentrations above 70 μM as the 2:1 trimer begins to dominate.
Asymmetry in scaffold stoichiometry can only be accommodated at the filament ends.
Our matrix formalism does not allow for direct calculation of the assembly of filaments into a 3D network within the droplet. However, we can compute the ratio of SUMO to SIM scaffold in the droplet by assuming that the monomer and perfectly aligned dimer remain in the bulk solution, , while all other complexes are in the droplet, . The calculated stoichiometry is compared to the experimentally measured droplet composition in Fig. 4a. The droplet SUMO/SIM ratio has downward curvature indicating that the droplet is unable to accommodate the stoichiometry mismatch of the bulk solution. This is a consequence of the filamentous structure because the interior of the filament is constrained to a 1:1 stoichiometry, so stoichiometric imbalance can only be accommodated at the filament ends. The filament calculation has somewhat more curvature than the experimental ratio (Fig. 4a, solid line) suggesting that the approximation of purely 1D assembly breaks down when the SUMO/SIM ratio is greater than ~ 1.4. The cause of the failure emerges upon comparing the monomer scaffold concentration (Fig. 4b) to the binding affinity of the modules, .6 This comparison reveals that when the SUMO concentration exceeds 80 μM the monomer concentration is sufficiently high that scaffold binding to gap defects cannot be neglected. A simple correction, allowing monovalent binding to the gap defects (see Appendix), resolves the discrepancy (Fig. 4a, dashed line). This calculation provides a valuable consistency check for our model. It shows that below 80:50 SUMO/SIM ratios the 1D zipper model provides an excellent representation of the droplet. However, above this ratio the 1D model will underestimate the SUMO scaffold content.
Figure 4: Model captures the droplet scaffold composition observed in experiment.
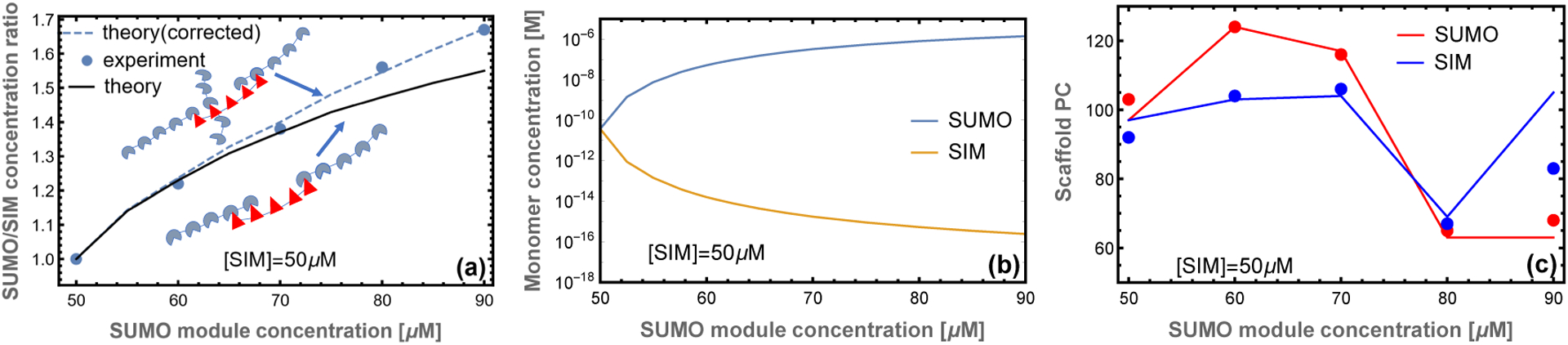
(a) The ratio of poly-SUMO to poly-SIM (NU/NI) calculated from our theory agrees well with the droplet stoichiometry in experiments.6 At high stoichiometric mismatches the approximation of purely 1D filaments breaks down because the concentration of free scaffolds is high enough to allow binding in the gaps. A correction accounting for monovalent scaffold-gap binding (inset cartoon) resolves the discrepancy with experiment (dotted line). (b) Excess SUMO scaffold accumulates in the dilute phase and depletes the concentration of monomeric SIM scaffolds. (c) Small stoichiometric mismatches promote increased scaffold accumulation in the droplet phase, but the trend reverses as the average filament size drops. The discrepancy at 90 μM can be explained by a breakdown of the 1D approximation as depicted in the cartoons of panel (a). In all panels lines indicate theory and circles denote the experiments of6
A related calculation is to compare the scaffold partition coefficient (PC), defined as the concentration in the dense phase to the concentration in the dilute phase. The fractional composition in each phase is Ni/(NU + NI), where i = U or I. In order to compare with experiments we weight this quantity by the experimentally determined total module concentration in each phase. Fig. 4c plots the quantities
| (3) |
Where and are the total module concentration in bulk and droplet phase respectively.6 The initial rise in the scaffold partitioning is due to the increase in filament lengths, but the trend reverses with the accumulation of smaller filaments at large stoichiometric asymmetry. The excellent agreement between theory and experiment without free parameters provides strong evidence supporting the zipper structural model. Notably, the partition coefficients in Fig. 4c underestimate SUMO recruitment at 90 μM, which is consistent with the breakdown of the 1D model observed in Fig. 4a,c.
Clients can bind to filament defects.
We next examined how the structural properties of scaffold assemblies in the droplet and bulk phases influence partitioning of mono-, di-, and trivalent SIM molecules employed as clients by Banani et al.6 In particular, we sought to understand the curious observation that high-valence clients show non-monotonic partitioning behavior as the SUMO/SIM scaffold ratio changes.6 To account for the recruitment of clients to the droplet we add client binding to the gap partition function. The form of the gap partition function depends on the valence and the concentration, ccl, of the clients as follows
| (4) |
| (5) |
| (6) |
In the case of monovalent clients, each gap site is independent, which gives a simple binomial with the two terms representing the empty and client-bound states. For multivalent clients we have the more involved process of counting the number of ways to add Nc clients to m sites and summing over the number of clients that will fit in a gap (see Appendix). While the binding energies in the above expression are same as those for the scaffolds due to the same underlying SUMO-SIM interaction, the binding affinity of clients is lower in the droplet than in the bulk.6 We attribute this to the entropy cost of confining the bulky RFP fluorescent tag within the droplet network. This steric penalty is included in our model with the factor fRFP. A least squares fit of the client partitioning yields fRFP = +3.15 kBT (Fig. 1b). fRFP is the only free parameter in our model.
Accounting for bound and unbound client in each phase, the client partition coefficient can be expressed as
| (7) |
where are the free client concentrations in the droplet and bulk, respectively, and and are the bound client concentration in the bulk and droplet phase, respectively. The average number of bound clients per scaffold is computed as . The bound client concentration is obtained by multiplying ρc times the experimentally determined scaffold concentration.6 Similarly, the bound client concentration in the dilute phase can be calculated from the total number of clients per scaffold in the dilute phase multiplied by the corresponding scaffold monomer concentration in the bulk phase.
Note that the concentrations cU, cI, and ccl appearing in the partition functions all represent the concentration of molecules that have not formed intermolecular bonds. These values must be determined by numerically solving the equations .for scaffolds and for the client. Here Ctot is the total (bound and unbound) concentration of the relevant molecule and ϕ is the volume fraction occupied by the droplet phase. The droplet volume fraction can be determined from the experimental values6 of the dilute and droplet protein concentrations using Ctot = ϕCdroplet+(1−ϕ)Cdilute.
The client partitioning provides further evidence for our structural model (Fig. 5). The 1D calculation captures the relative peak heights and locations, neither of which are sensitive to the free parameter. With the aid of the free parameter, the calculation quantitatively agrees with experiments for SUMO concentrations less than 80 μM. Above this concentration, the calculation systematically underestimates client recruitment, which again is consistent with increased SUMO scaffold content as the 1D approximation fails.
Figure 5: The scaffold composition that optimizes client recruitment depends on the client valence.
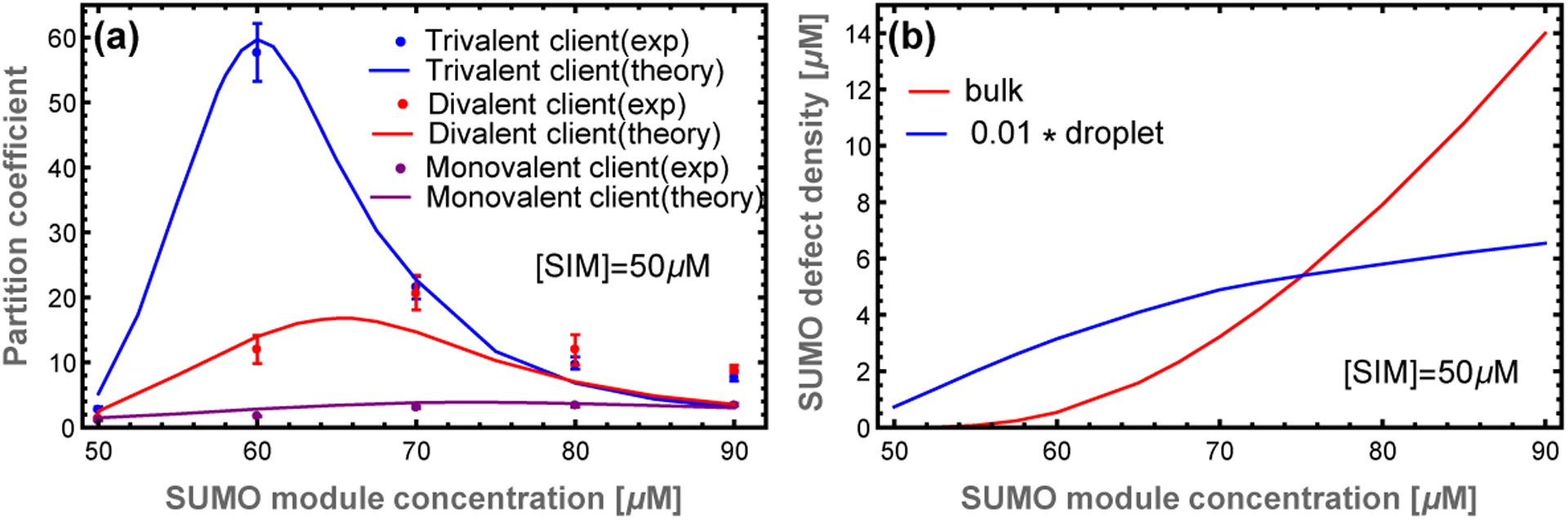
(a) The transfer matrix theory (lines) captures the shift in the experimental (dots) partition coefficient peak as the client valence increases. The high affinity of trivalent clients is more sensitive to both the appearance of defects in the droplet and the presence of free scaffold in the bulk. Experimental data from.6 (b) Concentration of unbound SUMO modules in the dense and dilute phases. Excess scaffolds, and associated defect sites, are initially bound in the droplet as shown by the blue curve (given by ρg times the droplet poly-SUMO concentration). However, above 70 μM additional poly-SUMO accumulates primarily in the bulk phase, which has a defect density of 10cU (red). The scaling factor applied to the droplet curve is approximately equal to the ~ 0.01 volume fraction of the droplets. Therefore, these curves approximately represent the number of defects sites in each phase.
Filament defects compete with soluble scaffold molecules for client binding.
The most striking feature of the PC is the non-monotonic dependence on the poly-SUMO concentration (Fig. 5a). This can now be understood as follows. Small excesses of poly-SUMO scaffold are readily incorporated in the droplet, which increases the PC by providing more sites for SIM clients to bind. However, as previously discussed, the 1D filaments are limited in their ability to accommodate unequal stoichiometry. As the filament ends become saturated with the abundant scaffold species, excess scaffold monomers are forced to accumulate in the dilute phase (Fig. 4b). At SUMO concentrations above 75 μM the number of unpaired SUMO modules in the dilute phase exceeds those in the dense phase (Fig. 5b). These free scaffolds compete for clients, which increases client concentration in the dilute phase and lowers the PC.
The client binding response is sensitive to the valence and binding affinity of the clients. Increasing the client valence increases the maximum value of the PC and shifts the peak toward equal scaffold stoichiometry. The increased affinity of clients through higher valence allows them to bind more readily to the sticky ends that appear with a small excess of complementary scaffold. However, the larger valence of these clients means that there is comparatively lower configuration entropy when binding to small defects. Therefore, when free scaffolds appear in the dilute phase, the favorable entropy provided by 10 consecutive binding sites overwhelms gap binding. Conversely, low valence clients have lower affinity, requiring a higher defect density for appreciable recruitment. But, they do not feel a confinement entropy in small defects, so they are sensitive only to the total number of available binding sites in the two phases (Fig. 5).
Network structure can provide binding specificity.
Not surprisingly, increasing the client’s specific affinity enhances client recruitment and increases the PC (Fig. 6a,b). Therefore, the zipper microstructure of the droplet provides independent mechanisms to tune the magnitude (via the affinity) and concentration (via the valence) of the maximial PC. These orthogonal methods of tuning client recruitment provide a mechanism by which the structure of the network influences the recruitment of clients, and thus function of the droplets. Fig. 6c shows PC curves for a monovalent and trivalent client where the binding affinities have been tuned to have similar peak recruitment. However, because the peaks in the PC curves occur at different scaffold stoichiometries, the network will predominantly recruit either one client or the other at different scaffold ratios. This means that, despite the liquid characteristics of the condensate, there is enough structure to specifically select between two closely related clients. This is because the zipper structure produces correlations in the location of available binding sites that biases the ensemble of binding states for multivalent clients. These structural correlations are not captured by random network models or the original mass action model of Banani et al.6
Figure 6: Increasing the client module binding affinity enhances client recruitment with minimal effect on the location of the peak.
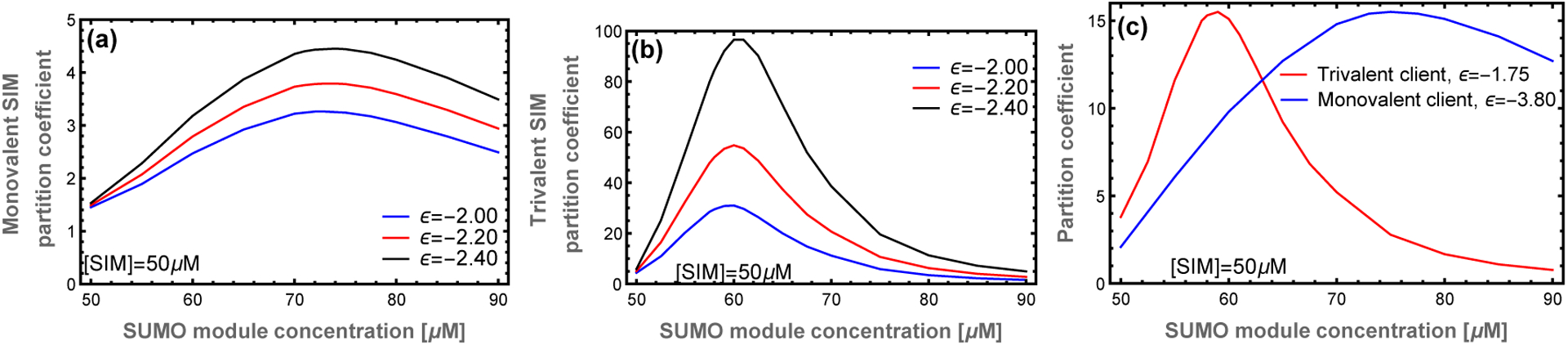
This provides separate mechanisms to tune the location and magnitude of client recruitment. (a) Monovalent SIM and (b) Trivalent SIM at different module binding affinities. The different effects of client valence and affinity on the PC curve allow the network to switch between the recruitment of different clients. (c) With tuned client affinities, it is possible for the network to selectively recruit either the monovalent or trivalent client in different regimes of parameter space.
Discussion
Interactions stabilizing liquid states impart functionally relevant condensate properties.
Comparing these results to the recently determined microstructure of SPOP/DAXX condensates,17 an interesting trend emerges. Both the SUMO/SIM and SPOP/DAXX systems can be described as sticker and spacer motifs,24,25 yet the underlying networks have very different connectivity (Fig. 7). Despite the superficial differences, both systems assemble in a hierarchical manner; strong interactions form molecular complexes and weaker interactions drive the condensation of the complexes. In the SPOP/DAXX system, strong SPOP-DAXX interactions result in the formation of brush-like assemblies that condense into a liquid phase via weaker DAXX-DAXX interactions. However, at higher SPOP-DAXX ratios, DAXX crosslinks SPOP into rigid bundles that associate into a gel state. These distinct states allow the scaffold stoichiometry to serve as a kinetic switch between fluid and arrested states.17 In contrast, in the poly-SUMO/poly-SIM system the same SUMO-SIM interactions drive the strong zipper formation and the weaker network crosslinks, with the presence or lack of cooperative binding providing the two different energy scales. Also, the filamentous structure, which is favored by a spacer that is much shorter than the mean intermolecular spacing, allows for a sensitive control over client recruitment. In both systems the assemblies are disordered at the length scales of both the strong and weak interactions. However, the hierarchy gives structure to the fluid in a way that provides functional properties.
Figure 7: The microscopic connectivity of biomolecule condensates imparts specific properties.
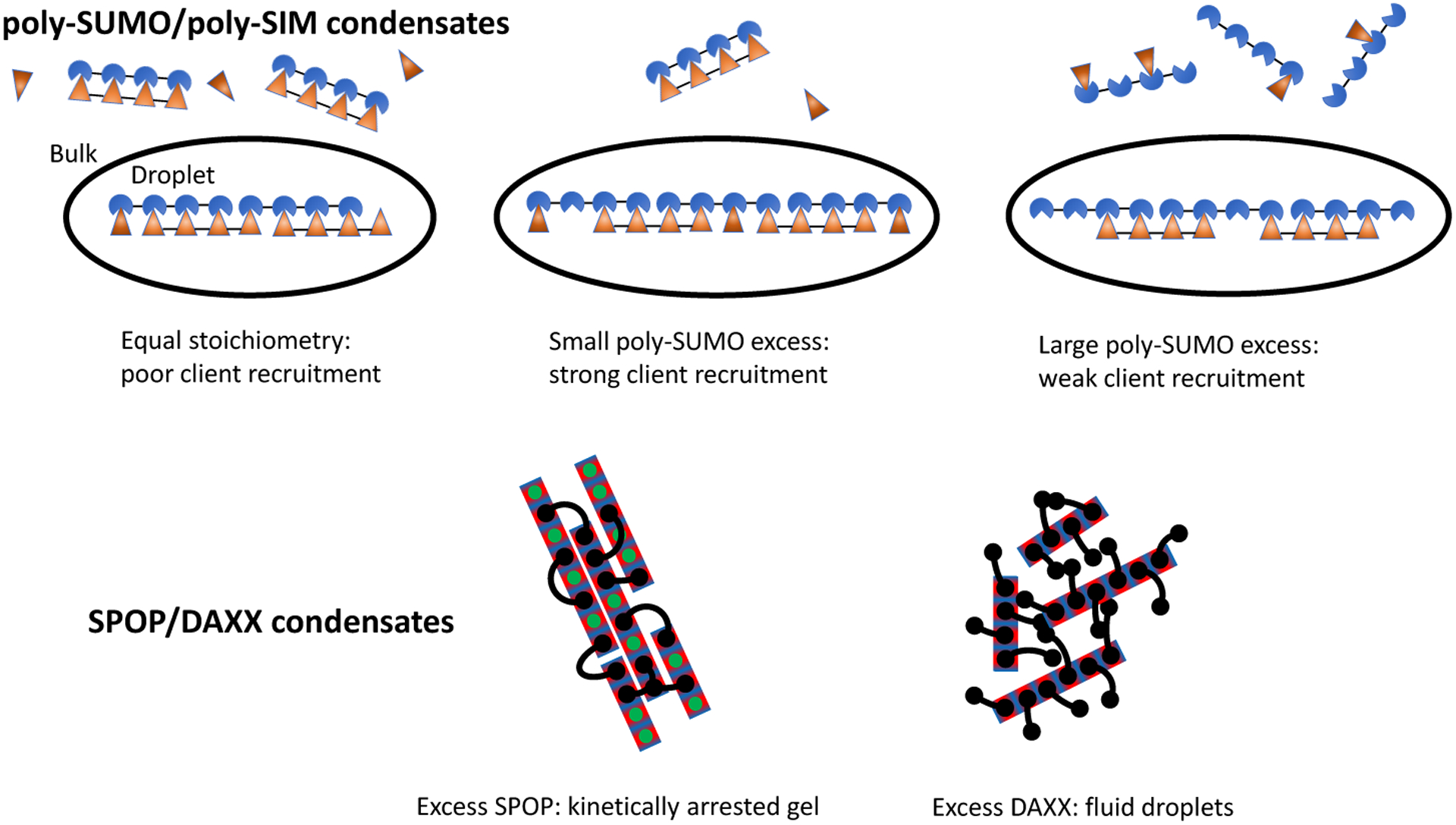
While both poly-SUMO/poly-SIM and SPOP/DAXX condensates form by the association of multivalent molecules, the assemblies have very different properties. Poly-SUMO/poly-SIM condensates are composed of linear filaments that provide a client binding response that is sensitive to the scaffold stoichiometry. SPOP/DAXX assemblies contain a “kinetic switch” that allows the system to convert between gel states with arrested dynamics and fluid droplets.17 Here the black lines represent bivalent DAXX molecules, while the rectangles represent polymerized SPOP rods. Adapted with permission from.17 Copyright 2020 by the American Chemical Society.
We conclude that even within a conserved sticker and spacer framework, differences in the scaffold valence, linker length, rigidity etc. can result in networks with widely different properties. It is inevitable that evolution will exploit these differences to optimize each condensate for its specific biological function. This inspires the question of how to identify functionally relevant structure within networks that are visually disordered. Here we have shown that theoretical modeling is a powerful tool for this task because parameters like Ntot and ρg emerge naturally to describe structural features in a way that connects to droplet function.
Acknowledgements:
This work was supported by NIH Grant R01GM107487 (to J.D.S), a postdoctoral fellowship from the Cancer Research Institute (to J.K.), a grant from the Welch Foundation (I-1544 to M.K.R.) and the Howard Hughes Medical Institute.
Appendix: detailed calculations
End Vectors and Transfer Matrices
Total grand partition function (Eq. 2) of the system is:
| (8) |
| (9) |
The two summation terms represent filaments starting with SUMO or SIM modules. In our formalism, filaments begin at the right end and grow right to left by application of the transfer matrices. The starting vectors VUR and VIR initiate the assembly with an imperfectly aligned dimer. These dimers have v −1 different states where v is the valence of the scaffolds. These states have free energy e−(v−n)ϵgi(n) where n = 1, 2, 3.…v − 1, and gi(n) is the gap partition function for the sticky end defect at right end of the filament. These alignment states comprise the elements of the right vectors
| (10) |
and
| (11) |
VUR and VIR are identical apart from the client species that can bind in the gap partition functions gU and gI, where the gap partition functions are labeled with subscripts that describe the client that they bind.
The transfer matrix Mi for deccavalent (v = 10) scaffolds is given by
Where zi is the fugacity of the attached molecule and gi(n) is the gap partition function for a gap of n unbound modules. Again, the matrices MU and MI are identical apart from the fugacity of the added molecule and the client species that binds in the gap. Since adding a SUMO molecule will leave a gap of unbound SIM modules, the gap partition function gU describes the binding of clients composed of SUMO modules.
Applying N transfer matrices to the right vector generates a vector V(N + 2) describing a filament containing N + 2 scaffold molecules. Each element of the vector is a polynomial giving the partition function of a filament terminating with a different length sticky end. The left vectors, ViL, serve three purposes. First, they collapse the filament vector into a scalar polynomial that gives the complete partition function of the filament. Secondly, the left vector provides the statistical weights for client binding at the left sticky end. These two functions can be served by a vector of the form
The third function of the left vector is that it must account for the fact that a filament can terminate with either species of scaffold. That means that the final left vectors are given by
| (12) |
| (13) |
Client binding entropy
The binding entropy of clients in a gap arises from the degeneracy of arranging the clients and unbound sites. We can treat the clients and vacancies as two particle types. When Nc clients of valence v bind to a gap of m sites, there are Nv = m − vNc unoccupied sites. So the total number of particles is Nt = Nc +Nv = m − (v − 1)Nc. The number of permutations is, therefore, the number of ways to select Nv particles from Nt positions. This degeneracy is gives the binomial coefficients appearing in Eqs. 5, 6.
Monomer Concentration vs total concentration
The quantities cU and cI appearing in our calculations represent the concentration of scaffold molecules that have not formed intermolecular bonds. In contrast, the more experimentally accessible quantity is the total scaffold concentration Ctot, which includes molecules that have formed assemblies. These quantities are related as follows
| (14) |
| (15) |
Fig 4b plots the free scaffold concentrations as a function of the total SUMO module concentration. There are several observations to make from this plot. First, when the scaffold concentrations are equal the monomer concentrations are very low, on the order of 10−10 M. This is much lower than the dilute phase concentration reported by.6 The discrepancy is due to the fact that most molecules in the dilute phase are in the perfectly aligned dimer state. This state satisfies all the available bonding sites, rendering the scaffolds inert to further assembly processes.
Second, when one scaffold is in excess, SUMO in this case, the monomer concentrations diverge widely (note the logarithmic vertical axis). This is because the low concentration scaffolds are mostly consumed in complexes with the higher concentration module. The depletion of low concentration modules results in an excess of high concentration modules that increases as the stoichiometry asymmetry increases.
Third, it is useful to compare the concentrations in Fig 4b to the 105 M−1 affinity for monovalent SUMO-SIM binding.6 At equal scaffold stoichiometry, the scaffold monomer concentrations are much too low for monovalent binding to occur. This justifies our approximation of strictly 1D filament formation because most of the gaps only have one or two unbound sites. However, when the SUMO module concentration reaches 90 μM (a 9:5 excess over SIM), the concentration of free SUMO module scaffolds is ≃ 14 μM. This is comparable to the ≃ 0.1 μM concentration of clients, so monovalent binding cannot be neglected.
Excess monomer scaffold binding at defect sites
When the scaffolds are present at unequal stoichiometries, the excess scaffold accumulates at concentrations where monovalent binding in the gaps becomes significant. At large asymmetry, the excess scaffold monomer concentration (≃ 1 μM) is about ten times greater than the total client concentration (≃ 0.1 μM) so that monomer scaffold binding is more favorable than client binding at defect sites. Therefore, we need to correct our 1D filament model to allow for perpendicular binding of scaffolds. As a first correction, we consider the “t” configuration illustrated in Fig. 8. This correction only allows for monovalent binding, which we expect to dominate given the small size of gaps in the filament.
Figure 8:

Excess monomer scaffold concentration binding at defect sites in crosslinked fashion.
The concentration of scaffolds that bind in the “t” configuration is calculated as
Where is the monovalent SUMO-SIM binding affinity.6 This affinity is multiplied by a factor of 10 to account for the degeneracy of binding of a decavalent scaffold to a single-site defect. cU is the scaffold monomer concentration (Figure 4b) and is the concentration of SIM defects in the network droplet. The latter quantity is calculated from the concentration of SIM scaffolds in the droplets, ,6 and the density of defect sites per SIM scaffold, which is calculated from , where we have used the substitution to define gU as the statistical weight of an unbound SIM module. Again, the subscript follows from our definition of gap partition functions based on the client that they bind. Note that this correction has not been applied to our PC calculations, which explains the systematic underestimate of the PC at high SUMO concentration.
References
- (1).Alberti S, “Phase separation in biology,” Current Biology, vol. 27, no. 20, pp. R1097–R1102, 2017. [DOI] [PubMed] [Google Scholar]
- (2).Brangwynne CP, Tompa P, and Pappu RV, “Polymer physics of intracellular phase transitions,” Nature Physics, vol. 11, pp. 899–904, 2015. [Google Scholar]
- (3).Yang P, Mathieu C, Kolaitis R-M, Zhang P, Messing J, Yurtsever U, Yang Z, Wu J, Li Y, Pan Q, and et al. , “G3bp1 is a tunable switch that triggers phase separation to assemble stress granules,” Cell, vol. 181, no. 2, pp. 325–345.e28, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Xing W, Muhlrad D, Parker R, and Rosen MK, “A quantitative inventory of yeast p body proteins reveals principles of compositional specificity,” bioRxiv, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Case LB, Ditlev JA, and Rosen MK, “Regulation of transmembrane signaling by phase separation,” Annual Review of Biophysics, vol. 48, no. 1, pp. 465–494, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Banani SF, Rice AM, Peeples WB, Lin Y, Jain S, Parker R, and Rosen MK, “Compositional control of phase-separated cellular bodies,” Cell, vol. 166, no. 3, pp. 651–663, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).George-Hyslop PS, Lin JQ, Miyashita A, Phillips EC, Qamar S, Randle SJ, and Wang G, “The physiological and pathological biophysics of phase separation and gelation of rna binding proteins in amyotrophic lateral sclerosis and fronto-temporal lobar degeneration,” Brain Research, vol. 1693, pp. 11–23, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Shin Y and Brangwynne CP, “Liquid phase condensation in cell physiology and disease,” Science, vol. 357, no. 6357, 2017. [DOI] [PubMed] [Google Scholar]
- (9).Lin Y-H, Song J, Forman-Kay JD, and Chan HS, “Random-phase-approximation theory for sequence-dependent, biologically functional liquid-liquid phase separation of intrinsically disordered proteins,” Journal of Molecular Liquids, vol. 228, pp. 176–193, 2017. [Google Scholar]
- (10).Harmon TS, Holehouse AS, Rosen MK, and Pappu RV, “Intrinsically disordered linkers determine the interplay between phase separation and gelation in multivalent proteins,” eLife, vol. 6, p. e30294, November 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Wang J, Choi J-M, Holehouse AS, Lee HO, Zhang X, Jahnel M, Maharana S, Lemaitre R, Pozniakovsky A, Drechsel D, and et al. , “A molecular grammar governing the driving forces for phase separation of prion-like rna binding proteins,” Cell, vol. 174, no. 3, pp. 688–699.e16, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Semenov AN and Rubinstein M, “Thermoreversible gelation in solutions of associative polymers.1.statistics,” Macromolecules, vol. 31, pp. 1373–1385, 1998. [Google Scholar]
- (13).Mao YS, Zhang B, and Spector DL, “Biogenesis and function of nuclear bodies,” Trends in Genetics, vol. 27, no. 8, pp. 295–306, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Boeynaems S, Alberti S, Fawzi NL, Mittag T, Polymenidou M, Rousseau F, Schymkowitz J, Shorter J, Wolozin B, Bosch LVD, and et al. , “Protein phase separation: A new phase in cell biology,” Trends in Cell Biology, vol. 28, no. 6, pp. 420–435, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Feric M, Vaidya N, Harmon TS, Mitrea DM, Zhu L, Richardson TM, Kriwacki RW, Pappu RV, and Brangwynne CP, “Coexisting liquid phases underlie nucleolar subcompartments,” Cell, vol. 165, no. 7, pp. 1686–1697, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Su X, Ditlev JA, Hui E, Xing W, Banjade S, Okrut J, King DS, Taunton J, Rosen MK, and Vale RD, “Phase separation of signaling molecules promotes t cell receptor signal transduction,” Science, vol. 352, no. 6285, pp. 595–599, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Schmit JD, Bouchard JJ, Martin EW, and Mittag T, “Protein network structure enables switching between liquid and gel states,” Journal of the American Chemical Society, vol. 142, no. 2, pp. 874–883, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Choi J-M, Holehouse AS, and Pappu RV, “Physical principles underlying the complex biology of intracellular phase transitions,” Annual Review of Biophysics, vol. 49, no. 1, pp. 107–133, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Dill KA and Bromberg S, Molecular driving forces : statistical thermodynamics in biology, chemistry, physics, and nanoscience. CRC Press, Taylor & Francis Group, 2011. [Google Scholar]
- (20).Zimm BH and Bragg JK, “Theory of the phase transition between helix and random coil in polypeptide chains,” The Journal of Chemical Physics, vol. 31, no. 2, pp. 526–535, 1959. [Google Scholar]
- (21).Pendry JB, “Transfer matrices and conductivity in two- and three-dimensional systems. i. formalism,” Journal of Physics: Condensed Matter, vol. 2, pp. 3273–3286, April 1990. [Google Scholar]
- (22).Rosenzweig ESF, Xu B, Cuellar LK, Martinez-Sanchez A, Schaffer M, Strauss M, Cartwright HN, Ronceray P, Plitzko JM, F¨rster F, and et al. , “The eukaryotic co2-concentrating organelle is liquid-like and exhibits dynamic reorganization,” Cell, vol. 171, no. 1, pp. 148–162.e19, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Xu B, He G, Weiner BG, Ronceray P, Meir Y, Jonikas MC, and Wingreen NS, “Rigidity enhances a magic-number effect in polymer phase separation,” Nat Commun, vol. 11, p. 1561, 2020 March 25 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Marzahn MR, Marada S, Lee J, Nourse A, Kenrick S, Zhao H, Ben-Nissan G, Kolaitis R, Peters JL, Pounds S, and et al. , “Higher-order oligomerization promotes localization of spop to liquid nuclear speckles,” The EMBO Journal, vol. 35, pp. 1254–1275, 6 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Bouchard JJ, Otero JH, Scott DC, Szulc E, Martin EW, Sabri N, Granata D, Marzahn MR, Lindorff-Larsen K, Salvatella X, and et al. , “Cancer mutations of the tumor suppressor spop disrupt the formation of active, phase-separated compartments,” Molecular Cell, vol. 72, no. 1, pp. 19–36.e8, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]


