The linearized disposition index augments understanding of treatment effects in diabetes

Abstract

The disposition index, calculated by multiplying measures of insulin secretion and insulin sensitivity, is widely applied as a sensitivity-adjusted measure of insulin secretion. We have recently shown that linearizing the underlying relationship uniquely permits identification of terms relating to maximal insulin secretion capacity and the secretion-coupling relationship, with both terms separately contributing to differences in the secretion-sensitivity relationship across gradations of glycemia. Here, we demonstrate the application of this linearized equation to the evaluation of treatment-induced changes in the insulin secretion-sensitivity relationship. We applied a combination of repeated-measures multivariate linear regression (evaluating treatment-induced changes in the joint relationship of insulin sensitivity and secretion) plus mixed-model repeated measures (evaluating treatment effects on maximal secretion capacity and on the secretion-sensitivity coupling slope) and compared against a usual application of the disposition index calculated from the same measurements. This novel approach allows a more informative description of treatment-induced changes compared with the usual disposition index, including isolating the source of change within the mutually adjusted relationship and identifying treatment-induced changes in the secretion-sensitivity coupling slope and in maximal insulin secretion. Application of this linearized approach provides an expanded understanding of treatment-induced changes in the insulin sensitivity-secretion relationship.

NEW & NOTEWORTHY The linearized insulin secretion-sensitivity relationship allows separate evaluation of the secretion-sensitivity slope and of maximal insulin secretion. Here, we demonstrate the application of this methodology to the evaluation of clinical trial data, showing that it provides an expanded understanding of treatment-induced changes compared with the disposition index.

BACKGROUND

The disposition index (DI) is widely used as an integrated measure of β-cell function (insulin response at a given insulin sensitivity) in studies of glucose metabolism. The underlying relationship embodied in the disposition index (DI) relates insulin secretion and insulin sensitivity via an inverse hyperbola. The DI term itself is a proportionality constant that is understood to represent a “set point” of β-cell function. The inverse relationship between secretion and sensitivity was long recognized but defined in the formalization of the disposition index concept by an exponent equal to −1, such that the relationship describes a “square” hyperbola (1–3). We and others have explored these relationships with data from clinical trials and cross-sectional studies (4–9). We have shown that applying a logarithmic transformation to the DI equation allows extraction and interpretation of the exponential term relating secretion and sensitivity, which is the secretion-sensitivity coupling slope (more fully explained later in the methods and in the appendix) (8). This approach also allows a more direct interpretation of the proportionality constant (analogous to the original DI term) as the y-axis intercept, representing a measure of maximal insulin secretion (i.e., a theoretical maximum at zero insulin sensitivity, here termed MaxSec). In short, these added variables improve the detail in understanding group differences in β-cell responses.

In cross-sectional analyses, we showed that the insulin secretion-sensitivity coupling slope is informatively different by physiological state, with stepwise reductions in secretion-sensitivity coupling slopes across groups of individuals with normal glucose tolerance, impaired glucose tolerance, and type 2 diabetes (8). These slope differences are distinct from concurrent differences in the y intercept terms (maximum secretion, MaxSec), which also vary importantly by glycemic status. This separation of the maximal secretion and insulin sensitivity-secretion coupling terms presents an advance in understanding between-group differences in metabolic physiology.

This methodology has not yet been applied to the evaluation of prospective changes in the insulin secretion-sensitivity relationship. As a means of demonstrating and evaluating this application of the linearized DI equation, here we apply this methodology to the evaluation of treatment responses in the Early Diabetes Intervention Program (EDIP), a previously published double-blinded, randomized, placebo-controlled trial of acarbose versus placebo in individuals with screen-detected diabetes mellitus (described in detail in Data Source below) (10–12). Using EDIP participant data, we applied this new methodology to evaluate prospective changes in insulin secretion, insulin sensitivity, and their secretion-sensitivity coupling relationship and compared this with treatment effects analyzed using the traditional DI approach. The EDIP data served primarily as a test bed for the new methodology, allowing us to evaluate differences in the outcomes with established and new methods.

METHODS

Data Source

We evaluated data from hyperglycemic clamp procedures and oral glucose tolerance testing performed in EDIP. EDIP participants were obese with elevated 2-h glucose levels following a standard 75-g oral glucose load [body mass index (BMI), 35.2 ± 7.1 kg/m²; 2-h glucose levels, 236.2 ± 31 mg/dL; fasting glucose levels, 121.4 ± 13/7 mg/dL; HbA1c levels, 6.34 ± 0.64%] (11). All participants received exercise and weight loss education, with diet reporting and weighing at study visits. Participants were randomized 1:1 to receive acarbose or matched placebo and followed for up to 5 years. In the first year of treatment, there was a divergence of weight and fasting glucose values, favoring the acarbose-treated group; nevertheless, at 5 years, there was no significant difference in the overall rate of progressive worsening of fasting glucose. Participants had annual 75-g oral glucose tolerance testing, and half of the cohort was randomly selected at baseline to also have hyperglycemic clamp procedures annually.

In EDIP, the largest on-treatment changes from baseline in weight and glucose were observed at year 1 following randomization (10–12), and we, therefore, elected to apply the new methodology to compare changes in the secretion-sensitivity relationships between baseline and year 1. We have previously published results evaluating the treatment effects on insulin sensitivity and insulin secretion using traditional analytic methodologies (10–12); in brief, early-phase insulin secretion measures were modestly, but not statistically, increased (with no treatment group differences) at 1 year after randomization when assessed either as the oral glucose tolerance testing (OGTT)-derived disposition index or the clamp-derived disposition index. In contrast, late-phase responses declined significantly when assessed at 1 year after randomization using total OGTT insulin secretion responses and were nonsignificantly reduced when assessed as second-phase glucose clamp responses (10). The late-phase secretion responses were inversely associated with concurrent change in insulin sensitivity, but the early-phase responses were independent of changes in insulin sensitivity (10). The original studies were performed following written signed informed consent, under the surveillance of the Indiana University and Washington University Institutional Review Boards.

Linearization of the DI Relationship

The methodology we have used applies a logarithmic transformation of the commonly used DI relationship. The common expression as DI = secretion × sensitivity is more explicitly expressed as y = k × x^α such that the y and x are secretion and sensitivity terms, respectively; the DI term is the k proportionality constant; and the exponent α is substituted for (−1) implicit in the inversion of the sensitivity term (see appendix) (8).

The logarithmic transformation of this generalized form of the equation is as follows:

$$\text{l}\mathbf{n}\hspace{0.17em}\left(y\right)=\text{l}\mathbf{n}\hspace{0.17em}\left(k\right)-\alpha *\ln \hspace{0.17em}\left(x\right)$$ (1)

In this linear equation, the slope relating the secretion (y) and sensitivity (x) terms (i.e., α) is the insulin secretion-sensitivity coupling slope. We have shown that this slope differs by the nature of the secretion and sensitivity terms being combined and by physiological features of the individuals contributing data and is not necessarily equal to −1 (8). Also, with this approach, the constant k is isolated from the secretion and exponential sensitivity terms, and by virtue of representing the y-axis intercept is interpretable as a measure of maximum insulin secretion. This y-axis intercept is related to but distinct from the DI term and is, therefore, given a separate name (MaxSec).

Analytic Methodology

In general, the analytic approach taken with concurrent measures of insulin secretion and sensitivity has been to evaluate the DI and the contributing secretion and sensitivity terms independently. Recently, a statistical methodology has been advanced that accounts for the two-dimensional dependency of secretion and sensitivity in evaluating change over time; specifically, a multivariate analysis (with secretion and sensitivity both entered as dependent variables) is applied to evaluate concurrent treatment-induced changes in both factors (13–15). This method allows appropriate simultaneous evaluation of the interrelated terms, specifically evaluating the mutually adjusted changes in both variables, as the approach to evaluating concurrent change in both components; where a joint change is observed, post hoc analyses can indicate whether one or both of the contributing terms is the source of change.

We have incorporated this analytic approach into the current analysis and also leveraged the advantages of the linearized DI equation to evaluate the full set of relevant physiological components, namely, the two-dimensional relationship between secretion and sensitivity; the secretion and sensitivity terms separately, where a change in the two-dimensional relationship is observed; the secretion-sensitivity coupling slope; and the intercept representing maximal insulin secretion. To allow comparison against traditional methodology, we have also evaluated the historical DI terms.

All testing was performed using repeated-measures methodologies to assess treatment effects. First, multivariate linear regression was applied to assess the two-dimensional relationship between sensitivity and secretion. This was done using repeated-measures ANOVA, specifying secretion and sensitivity terms as dependent variables, repeated over time, with treatment group and other variables entered as covariates. Hotelling’s T-squared test was used to determine whether there was significant within-subject change with treatment, and treatment-group interactions were evaluated to determine whether any significant change differed by treatment group (13–15). Post hoc univariate testing of these multivariate relationships allowed us to determine whether significant mutually adjusted changes occurred in the contributing secretion or sensitivity terms. Notably, the individual secretion and sensitivity terms were not evaluated in isolation, owing to their natural interdependence.

Second, the linear relationships between secretion and sensitivity terms were evaluated using a repeated-measures mixed-model approach to evaluate treatment effects on slopes and intercepts. Secretion was specified as the dependent variable, and sensitivity was specified as an independent variable, so that the slope term was directly tested as the sensitivity factor. The group effect in models including the sensitivity term provided the statistical test for the group-specific intercept, and each of these was evaluated for a time and/or treatment group interaction.

Third, treatment effects on the calculated disposition indices were also evaluated using repeated-measures mixed modeling, with the DI term as the dependent variable, testing a main effect of treatment and evaluating possible treatment-group differences using an interaction term.

For comparison against prior analyses performed using traditional methodologies, we repeated these analyses including relevant covariates in all three of these steps. For all testing, a nominal P value of <0.05 was considered statistically significant. No adjustments were made for multiple testing.

Insulin Secretion and Sensitivity Terms

This set of statistical tests was applied to four pairs of insulin secretion and sensitivity terms, derived from OGTT or hyperglycemic clamp testing. We evaluated early and late or total insulin secretion measures from each method together with sensitivity measures from the same method:

• OGTT early phase: combining the insulinogenic index [(insulin30 − insulin0)/(glucose30 − glucose0)] with inverse fasting insulin;

• OGTT total secretion: combining incremental insulin area under the curve (AUC; calculated using the trapezoidal rule) with inverse fasting insulin;

• clamp first phase: combining the first-phase response (average insulin concentrations from the first 10 min following the initiating glucose bolus) with clamp-derived sensitivity (M/I; steady-state glucose disposal rate divided by the achieved insulin concentrations); and

• clamp second phase: combining average insulin concentrations at steady state with M/I as earlier.

In each instance, the untransformed values were combined by multiplication into a traditional DI term. This term plus each component secretion and sensitivity term were log-transformed for inclusion in the evaluations described earlier, as previously described (8). Negative values can result from OGTT-derived secretion calculations, and logarithms are not evaluable for negative values. Also, values between 0 and 1 introduce nonlinearities in the logarithmic transformation. The original scale data were, therefore, linearly shifted according to (|min|+1) or multiplied by factors of 10 as needed to provide pretransformation data values greater than 1.

RESULTS

A summary of EDIP participant characteristics is presented in Table 1, which presents native scale (untransformed) data for the OGTT-derived and clamp-derived measures of insulin secretion and insulin sensitivity that were used in the current analyses. Evaluations of the treatment effects on insulin secretion and sensitivity in EDIP using traditional methodologies have been previously published (10).

Table 1.

Characteristics of the EDIP population at baseline and following 12 months’ randomized treatment

	Acarbose—Month 0	Acarbose—Month 12	Placebo—Month 0	Placebo—Month 12	P (Time)	P (Time × Group)
OGTT Data (n = 219)
Age, yr	53.7		53.7
White	84		84
Female	73		72
Male	36		38
Weight, kg	97.4	93.04	99.4	95.1	<0.001	0.094
BMI, kg/m2	35.1	33.6	35.3	33.7	<0.001	0.099
HbA1c, %	6.35	6.17	6.33	6.24	0.187	0.031
Fasting OGTT glucose, mg/dL	121.4	112.6	120.3	116.8	<0.001	0.035
2-h OGTT glucose, mg/dL	234.9	201.3	234.2	214.5	<0.001	0.086
Inverse fasting insulin, mL/μU	0.070	0.085	0.074	0.092	0.146	0.903
IGI, mU · mL−1 · mg−1 · dL	0.496	0.396	0.572	0.370	0.026	0.446
DI-IGI, mg−1 · dL	0.029	0.033	0.030	0.034	0.343	0.926
iAUCins/iAUCgluc, µU/mL/mg/dL	0.910	0.949	1.074	0.829	0.283	0.137
DI-iAUCins/iAUCgluc, mg−1 · dL	0.050	0.071	0.058	0.073	0.038	0.684
Clamp Data (n = 104)
Age, yr	51.2		56.0
White	38		42
Female	35		32
Male	17		20
Weight, kg	97.1	93.4	96.6	94.2	<0.001	0.306
BMI, kg/m2	35.5	34.2	34.1	33.3	<0.001	0.545
HbA1c, %	6.38	6.19	6.24	6.21	<0.001	0.607
Clamp M/I, mg · kg−1 · min−1 · μU−1 · mL	2.08	2.706	2.36	2.36	0.140	0.200
First phase, μU/mL	25.56	25.47	29.26	34.83	0.354	0.337
DI-first phase, mg−1 · kg · min	39.16	47.22	48.10	57.46	0.091	0.898
Second phase, μU/mL	61.72	58.56	80.49	64.35	0.135	0.313
DI-second phase, μU−1 · mL	94.64	102.25	100.49	105.66	0.113	0.759

P (Treatment) indicates a comparison of the repeated-measures effect of treatment overall. P (Treatment × Group) assesses whether this treatment effect differed by randomized treatment group. AUC, area under the curve for insulin; BMI, body mass index; DI, disposition index; EDIP, Early Diabetes Intervention Program; HbA1c, hemoglobin A1c; IGI, insulinogenic index; M/I, insulin sensitivity derived from clamp measures of glucose disposal rate (M) and insulin concentrations (I); OGTT, oral glucose tolerance testing. Statistically significant values are presented in bold for convenience.

OGTT-Derived Insulin Secretion-Sensitivity Pairs

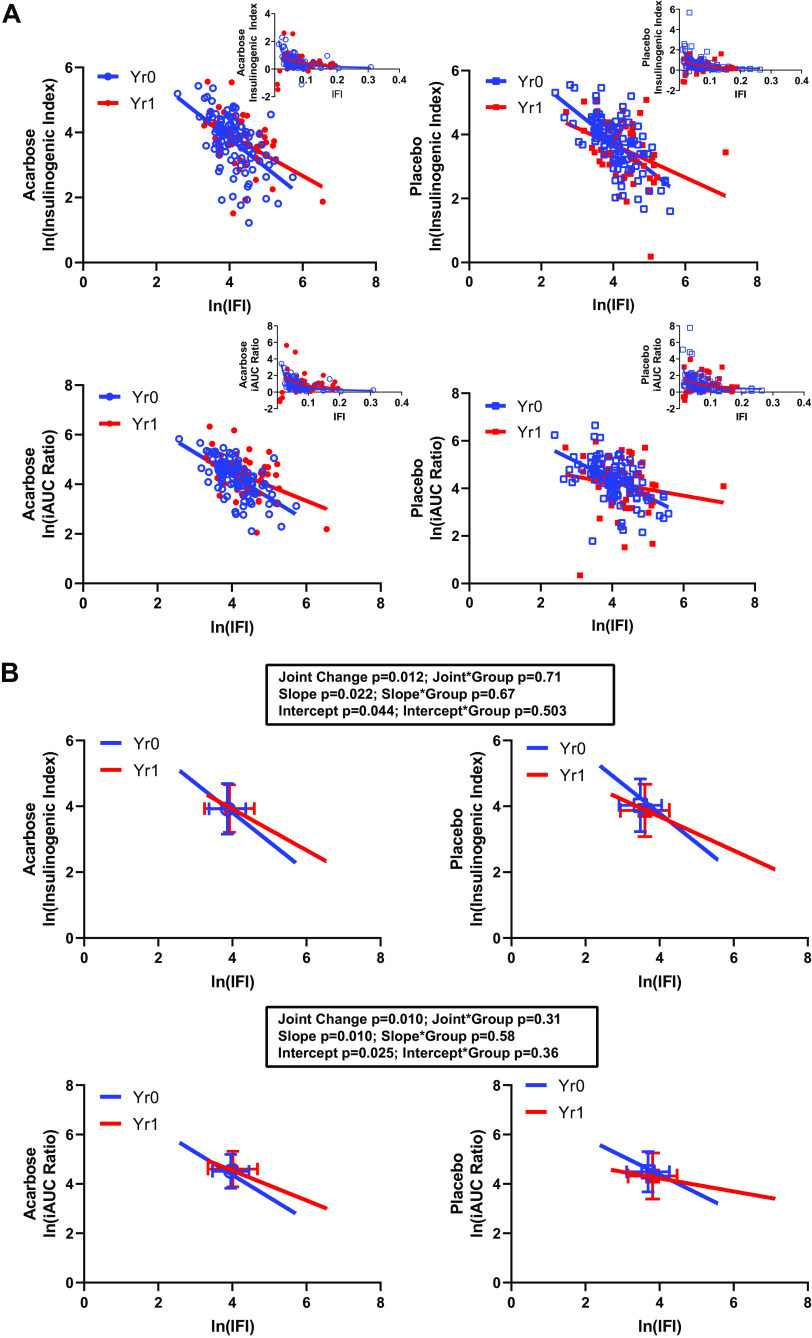
The relationships of secretion-sensitivity pairs derived from OGTT data are presented in Fig. 1, with the top panels providing data for the early-phase response (the insulinogenic index together with inverse fasting insulin, IGI-IFI), and the bottom panels presenting the integrated early- and late-phase responses (ratio of incremental AUCs for insulin and glucose with inverse fasting insulin, iAUC ratio-IFI). The mean treatment effects are represented by the colored squares in Fig. 1B, demonstrating a modest rightward shift in the two-dimensional relationship for early-phase relationships (top) and for integrated early- and late-phase relationships (bottom). Statistical testing of these changes is presented in Table 2 and summarized in the figure. The multivariate evaluation revealed significant changes in the joint secretion-sensitivity relationships (IGI-IFI P = 0.012; iAUC ratio-IFI P = 0.010), not different between treatment groups; this is reflected in the shifted location of the means of the data distributions (the square boxes in the figures). The changes in the early-phase (IGI-IFI) and integrated early- and late-phase (iAUC ratio-IFI) response relationships were driven by a change in insulin sensitivity but not secretion (Table 2). These joint and univariate effects were not different between groups.

Figure 1.

OGTT-derived insulin secretion–sensitivity relationships. A: presents the raw data for the linearized relationships, together with overlaid fitted lines. The inserts present the untransformed data and fitted lines. The underlying data were in units of mU · mL⁻¹ · mg⁻¹ · dL (IGI, insulinogenic index; top), iAUCins/iAUCgluc µU · mL⁻¹ · mg⁻¹ · dL (iAUC ratio; incremental area under the curve for insulin over incremental area under the curve for glucose; bottom), and mL · μU⁻¹ (IFI, inverse fasting insulin). Natural logarithmic transformations were applied as described in methods. Data for each treatment group are presented separately for clarity. B: presents the fitted lines for the linearized relationships, together with the summary results for each set of analyses. The box and whiskers represent the x–y means ± SD for each set of data points. Analyses are presented showing the effect of time on the secretion-sensitivity relationship (joint change), on the slope, and on the intercept of each underlying pair. The effect of treatment group is presented as an interaction term for each of these factors. OGTT = oral glucose tolerance testing.

Table 2.

Evaluating mutual changes in secretion and sensitivity

Multivariate Tests
Within-subjects effect	Measure	IGI with IFI	iAUC Ratio with IFI	Phase 1 with M/I	Phase 2 with M/I
Time	Joint secretion and sensitivity	0.012	0.010	0.009	0.038
Time × Group	Joint secretion and sensitivity	0.708	0.309	0.670	0.888
Post Hoc Univariate Tests
Source	Measure	IGI with IFI	iAUC with IFI	Phase 1 with M/I	Phase 2 with M/I
Time	Secretion	0.169	0.247	0.718	0.159
Sensitivity	0.003	0.004	0.034	0.024
Time × Group	Secretion	0.889	0.166	0.487	0.804
Sensitivity	0.408	0.518	0.973	0.985

Values in cells are P values. Evaluations were performed using log-transformed secretion and sensitivity terms as described in methods. Analyses used multivariate methodology to first compare the simultaneous changes in secretion and sensitivity (top) and post hoc univariate testing to isolate the source of significant change (bottom table). In each instance, a Time × Group interaction term was evaluated to determine whether observed effects differed by randomized treatment group. Values achieving statistical significance are presented in boldface. iAUC ratio, incremental area under the curve for insulin divided by incremental area under the curve for glucose; IGI, insulinogenic index; IFI, inverse fasting insulin; M/I, clamp steady-state glucose disposal rate divided by steady-state insulin concentrations. Statistically significant values are presented in bold for convenience.

Also evident in Fig. 1 is an apparent time-related change in the linear relationships between the OGTT-derived terms, with a reduction in slopes and intercepts. Results of linear mixed modeling of these relationships are presented in Table 3. For both pairs of secretion-sensitivity terms, there was a time effect on the intercept (P = 0.044 and P = 0.025 for IGI-IFI and iAUC ratio-IFI, respectively) and in slope (P = 0.022 and P = 0.010) without a significant effect of treatment group to modify these time-dependent changes.

Table 3.

Evaluating changes in secretion-sensitivity relationships using new and traditional methods

	Intercept		Slope		DI
	Time	Group * Time	Time	Group * Time	Time	Group * Time
IGI with IFI	0.044	0.503	0.022	0.674	0.259	0.227
iAUC ratio with IFI	0.025	0.357	0.010	0.581	0.158	0.159
Phase 1 with M/I	0.025	0.037	<0.001	0.047	<0.001	0.599
Phase 2 with M/I	0.169	0.095	0.432	0.086	0.003	0.982

Values in cells are P values. Evaluations were performed using log-transformed secretion and sensitivity terms and repeated-measures mixed modeling as described in methods. In each instance, a Group × Time interaction term was evaluated to determine whether observed effects differed by time and/or study treatment. Values achieving statistical significance are presented in boldface. DI, disposition index; iAUC ratio, incremental area under the curve for insulin divided by incremental area under the curve for glucose; IGI, insulinogenic index; IFI, inverse fasting insulin; M/I, clamp steady-state glucose disposal rate divided by steady-state insulin concentrations. Statistically significant values are presented in bold for convenience.

Table 3 also presents the results of statistical analyses using the traditional approach of calculating a DI term (by simple multiplication) from the contributing secretion-sensitivity pairs, log transforming those data to normalize the distribution, and then evaluating time and group effects using the same linear mixed modeling methodology. In contrast to the significant time effects seen on the slope and the intercept, there was no significant time effect on the DI terms or a treatment group interaction with the time effect.

Supplemental Tables S1 to S3 (see https://doi.org/10.5281/zenodo.3970751) present an evaluation of the concurrent effects of covariates (weight, fasting glucose, 2-h glucose, and triglyceride-to-HDL ratio) that have been previously shown to be relevant to the treatment effects on glycemia in this data set (12). Concordant with previous results, these analyses reveal significant and informative effects of these factors to modulate the joint relationships (Supplemental Table S1), the intercept and slope results with the regression analyses (Supplemental Table S2), and the DI analyses (Supplemental Table S3). This set of analyses highlights the opportunity to evaluate covariates together with primary evaluation of the relationship of insulin secretion and sensitivity using this methodology.

Clamp-Derived Insulin Secretion-Sensitivity Pairs

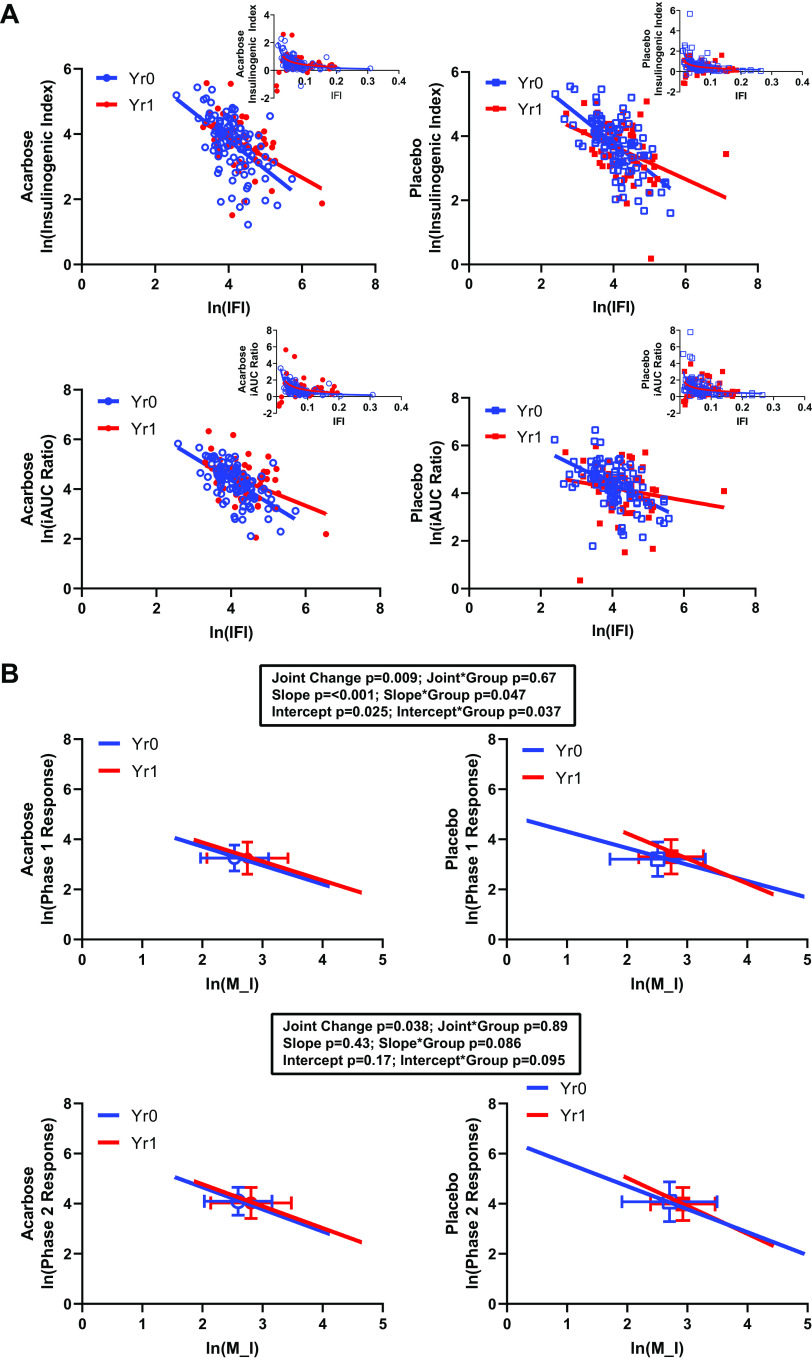
The secretion-sensitivity pairs derived from clamp data are presented in Fig. 2 (first phase-M/I, top; second phase-M/I, bottom). Similar to OGTT-derived measures, there was a rightward shift in the secretion-sensitivity relationships with time. Table 2 presents the multivariate evaluation of these joint relationships, revealing significant changes in both of these joint secretion-sensitivity relationships, indicating significant overall time effects for first- and second-phase insulin response (first phase-M/I P = 0.009; second phase-M/I P = 0.038; Table 2). In parallel with the results obtained using OGTT-derived measures, these effects were driven by changes in sensitivity but not secretion (Table 2). Also, in parallel with the results from the OGTT, there were no treatment group differences in these joint effects or in the individual secretion and sensitivity changes.

Figure 2.

Hyperglycemic clamp-derived insulin secretion-sensitivity relationships. A: presents the raw data for the linearized relationships, together with overlaid fitted lines. The inserts present the untransformed data and fitted lines. The underlying data were in units of μU · mL⁻¹ (phase 1 insulin response; top), μU · mL⁻¹ (phase 2 insulin response; bottom), and mg · kg⁻¹ · min⁻¹ · μU⁻¹ · mL (M/I, glucose disposal rate divided by the steady-state insulin concentration). Natural logarithmic transformations were applied as described in methods. Data for each treatment group are presented separately for clarity. B: presents the fitted lines for the linearized relationships, together with the summary results for each set of analyses. The box and whiskers represent the x–y means ± SD for each set of data points. Analyses are presented showing the effect of time on the secretion–sensitivity relationship (joint change), on the slope, and on the intercept of each underlying pair. The effect of treatment group is presented as an interaction term for each of these factors.

As shown in Fig. 2B, the slope and intercepts for the first phase-M/I relationship changed with time, significantly different between treatment groups and qualitatively different from what was seen in the OGTT analyses. Qualitatively similar effects that did not reach significance were seen with the second phase-M/I relationships (Fig. 2, Table 3). The DI derived from these terms showed effects of time for early and late secretion responses but did not reveal the treatment group interactions that were evident in the linearized regression approach (Table 3).

Covariate-adjusted analyses for these insulin secretion-sensitivity pairs are presented in Supplemental Tables S1 to S3. As with the OGTT-derived measures of β-cell function, the evaluated covariates demonstrated informative relationships with clamp-derived measures within the different components of the analyses performed here.

DISCUSSION

The inverse relationship between insulin secretion and sensitivity is hyperbolic or pseudohyperbolic in nature. Terms derived from this nonlinear relationship such as the DI and the power slope of the relationship are difficult to directly interpret in terms of the underlying physiology, particularly in the case of interventions that might change multiple components of these relationships including the power slope itself. We have developed a linearization of the DI equation that allows explicit interpretation of the intercept as a theoretical maximum secretion term MaxSec and that allows informative estimation of the secretion-sensitivity slope term (8). This approach allows visualization and interpretation of the relationship of insulin sensitivity and secretion as different slopes across varying degrees of glycemic control (8). Here, we demonstrate the application of this methodology to data from a previously published prospective treatment study in diabetes, as a test case for applying this methodology to compare treatment effects on secretion and sensitivity terms derived from OGTT and hyperglycemic clamp procedures. The new approach provides granularity in understanding the treatment responses and other changes over time not readily extracted from the traditional analysis of DI alone.

This methodology was successful in demonstrating treatment-related changes in the paired secretion-sensitivity relationship for early- and integrated early- and late-phase insulin secretion measures derived from OGTT and from first- and second-phase secretion from hyperglycemic clamp testing. Using statistically rigorous mutually adjusted analyses, we identified overall treatment-related changes attributed to changes in insulin sensitivity with treatment. In addition, the regression approach enabled separate evaluation of treatment effects on the intercepts (an index of maximal insulin secretion capacity) and on the secretion-sensitivity coupling slopes. Beyond the conceptual advantage of isolating these components of the secretion-sensitivity relationship compared with the traditional DI methodology, there appears to be a statistical advantage in that the DI alone does not uniformly reveal these effects of study treatment, randomized treatment group, or relevant covariates.

The extraction of the secretion-sensitivity slope applies established repeated-measures linear regression methodologies that are not suitable for use with nonlinearly related data. The main alternative analytic approach that has been proposed for evaluation of untransformed data is to apply nonlinear regression to extract the slope as a power term (4). Even if such nonlinear regression methodology were widely available, and suitable for application in repeated-measures designs, the problem remains of interpreting the power term thus derived. Also, in that analytic approach, the intercept component is not separately evaluable, relying instead on concurrent evaluation of a traditional DI term (discussed below).

The current analyses were enhanced by the application of statistical methods that better account for the interdependent nature of changes in insulin secretion and insulin sensitivity (13–15). This analytic method is not itself new but is not yet widely applied in the analysis of the measurement of β-cell function (i.e. concurrent analysis of insulin secretion and sensitivity). As with other parametric statistical tools, these methods are well suited to analysis of the linearized relationships presented here. The combination of statistical testing used here illustrates a pathway to a more rigorous and comprehensive evaluation of measures of β-cell function than has been previously applied.

The DI as traditionally calculated is a simple multiplication of insulin secretion and inverse sensitivity terms, with the power relationship embedded in the DI result (see appendix). In contrast, the logarithmic expression of the DI equation (Eq. 1) allows a separation of the intercept term from the slope of the relationship, thereby allowing statistical evaluation of both factors separately, and not assuming that the sensitivity exponent is (−1). One clear advantage of this approach is the simplified interpretation of the intercept term as an index of insulin secretion capacity (i.e., MaxSec); in contrast to the DI, the component of the relationship that depends on insulin sensitivity is separated into the slope term, which is separately evaluable. This is, therefore, conceptually simpler than the vague “sensitivity-adjusted secretion” interpretation that includes both of these, together with an exponential slope term, in the same DI value.

This approach expressly allows evaluation of treatment effects on the intercept and on the insulin secretion-sensitivity coupling slopes. In the current analyses, the hyperglycemic clamp data revealed modest differences in the effect of treatment group on the secretion-sensitivity slope relating first-phase insulin secretion to insulin sensitivity and no time- or group-related change in the slope relating second-phase insulin secretion to insulin sensitivity. In contrast, the OGTT data revealed significant reductions over time in the secretion-sensitivity coupling slopes for early and total insulin secretion measures, not different by treatment group. These differences in the apparent treatment effects between the clamp and OGTT approaches to measurement methods are unexpected, particularly in the contrasting directionality of change in the clamp data (improvement over time) versus the OGTT data (worsening over time). In EDIP, fewer participants underwent glucose clamp studies than OGTT studies, a design choice that was made owing to the known differences in precision of measurements between these methods. Applying OGTT analyses only to the subset of individuals that participated in clamp studies did not shift the pattern of response using OGTT-derived terms to mimic the clamp results (data not shown), excluding the possibility that this is a subgroup-specific difference in response. The greater variability of OGTT measurements (16) could contribute to this apparent difference between measurement methods, but in general, more statistical noise would be expected to mask rather than reveal a contrasting treatment effect. There are well-recognized biological differences between the nature of β-cell stimulation that arises from enterally delivered glucose versus intravenously delivered glucose (the incretin effect) (17), and it is possible that this approach to evaluation is revealing a previously unappreciated difference in the response to shifts in insulin sensitivity (or to weight loss in association with shifts in insulin sensitivity as previously described for this data set) (12). This could be compounded by the imperfect separation of first-phase secretion responses from the beginnings of the second-phase responses, with both contributing to the early secretion response assessed in the OGTT. Also, the extended exposure to hyperglycemia under glucose clamp conditions versus the dynamic and transient exposure under OGTT conditions could be influencing this observed difference. Further work evaluating changes in insulin secretion-sensitivity slopes, and differences in effects measured using enteral versus intravenous glucose delivery, will be needed to better understand these differences. The current results suggest that our new approach to analysis seems better suited to identifying and exploring these differences than the traditional approach using DI alone.

SUMMARY AND CONCLUSIONS

We have used data from a previously published pharmacologic intervention study to evaluate the utility of the linearized disposition index relationship in evaluating treatment effects, demonstrating the value of this approach to provide a more thorough evaluation of treatment-related changes in measures of β-cell response. The present results demonstrate that treatment-related changes in intercept and slope of the linearized relationship can be identified and contribute independent information to understanding physiological changes in response to study interventions. Therefore, this methodology brings added value to what has been traditionally obtained with evaluations of the disposition index alone.

GRANTS

T. S. Hannon, R. V. Considine, and K. J. Mather were supported by the Translation Core of the IU Diabetes Research Center Grant (2P30DK097512). C. Hanna was supported by an institutional training grant from the NIH (T35HL110854).

DISCLOSURES

At the time of publication, K. J. Mather was an employee of Eli Lilly and Company. The work presented was performed prior to this employment and was analyzed and produced independent of Eli Lilly and Company.

AUTHOR CONTRIBUTIONS

T.S.H., M.S.K., Y.P., and K.J.M. conceived and designed research; A.J.K., C.H., Y.P., and K.J.M. analyzed data; A.J.K., C.H., T.S.H., M.S.K., R.V.C., Y.P., and K.J.M. interpreted results of experiments; A.J.K., C.H., and K.J.M. prepared figures; A.J.K., T.S.H., Y.P., and K.J.M. drafted manuscript; A.J.K., C.H., T.S.H., M.S.K., R.V.C., Y.P., and K.J.M. edited and revised manuscript; A.J.K., C.H., T.S.H., M.S.K., R.V.C., Y.P., and K.J.M. approved final version of manuscript.

APPENDIX: DERIVATION OF THE LINEARIZED EQUATION

In general, insulin secretion and insulin sensitivity are inversely related

$$Secretion\alpha \frac{1}{Sensitivity}$$ (A1)

Including a proportionality constant and expressing the inversion as an exponent

$$Secretion=k•Sensitivit{y}^{-1}$$ (A2)

Generalizing this formula to allow exponents other than −1 [see reference (8)] provides

$$Secretion=k•Sensitivit{y}^{-\alpha }$$ (A3)

Rearranging to isolate the proportionality constant, we get

$$Secretion•Sensitivit{y}^{\alpha }=k$$ (A4)

The usual formulation of the disposition index is

$$DI=Secretion•Sensitivity$$ (A5)

Which is equivalent to Eq. A4, except that the exponent is not explicitly handled. Because of this, the DI incorporates both the proportionality constant and the exponent of the underlying relationship.

The DI is calculated for a single pair of secretion and sensitivity terms. For a collection of secretion-sensitivity data point pairs, the exponent will be expressed in the two-dimensional relationship and can be estimated using regression methodologies.

Taking the logarithm of Eq. A3 gives a traditional linear equation

$$\mathit{log}(\mathit{S}\mathit{e}\mathit{c}\mathit{r}\mathit{e}\mathit{t}\mathit{i}\mathit{o}\mathit{n})=\mathit{log}(k)-(\alpha )•\mathit{log}(\mathit{S}\mathit{e}\mathit{n}\mathit{s}\mathit{i}\mathit{t}\mathit{i}\mathit{v}\mathit{i}\mathit{t}\mathit{y})$$ (A6)

Thus, fitting a simple linear regression to log-transformed secretion and log-transformed sensitivity data pairs allows derivation of the secretion-sensitivity slope α, which can then be compared between groups and conditions. Further, this formulation isolates the y-axis intercept [log(k)], which reflects a theoretical maximum secretion (i.e., MaxSec), and can also be compared between groups and conditions.