Marginal Treatment Effects from a Propensity Score Perspective

Abstract

We offer a propensity score perspective to interpret and analyze the marginal treatment effect (MTE). Specifically, we redefine MTE as the expected treatment effect conditional on the propensity score and a latent variable representing unobserved resistance to treatment. As with the original MTE, the redefined MTE can be used as a building block for constructing standard causal estimands. The weights associated with the new MTE, however, are simpler, more intuitive, and easier to compute. Moreover, the redefined MTE immediately reveals treatment effect heterogeneity among individuals at the margin of treatment, enabling us to evaluate a wide range of policy effects.

1. Introduction

An essential feature common to all empirical social research is variability across units of analysis. Individuals differ not only in background characteristics, but also in how they respond to a particular treatment, intervention, or stimulation. Moreover, individuals may self-select into treatment on the basis of their anticipated treatment effects in a way that is not captured by observed covariates. This is likely when individuals (or their agents) possess more knowledge than the researcher about their gains (or losses) from treatment and act on it (Roy 1951; Bjorklund and Moffitt 1987; Heckman and Vytlacil 2007a). To study heterogeneous treatment effects in the presence of unobserved self-selection, Heckman and Vytlacil (1999, 2001a, 2005, 2007b) have developed a structural approach that builds on the marginal treatment effect (MTE). Under a latent index model of treatment assignment, the MTE is defined as the expected treatment effect given observed covariates and a latent variable representing unobserved, individual-specific resistance to treatment. A wide range of “causal parameters,” such as the average treatment effect (ATE) and the treatment effect of the treated (TT), can be expressed as weighted averages of MTE. Moreover, MTE can be used to evaluate average treatment effects for individuals at the margin of indifference to treatment, thus allowing the researcher to assess the efficacy of marginal policy changes (Carneiro, Heckman, and Vytlacil 2010, 2011).

In the MTE framework, the latent index model ensures that all unobserved determinants of treatment status be summarized by a single latent variable, and that the variation of treatment effect by this latent variable capture all of the unobserved treatment effect heterogeneity that may cause selection bias. Our basic intuition is that, under this model, treatment effect heterogeneity that is consequential for selection bias occurs only along two dimensions: (a) the observed probability of treatment (i.e., the propensity score), and (b) the latent variable for unobserved resistance to treatment. In other words, after unobserved selection is factored in through the latent variable, the propensity score is the only dimension along which treatment effect may be correlated with treatment status. Therefore, to identify population-level and subpopulation-level “causal effects” such as ATE and TT, it would be sufficient to model treatment effect as a bivariate function of the propensity score and the latent variable. In this paper, we show that such a bivariate function is not only analytically sufficient, but also crucial to the evaluation of policy effects.

Specifically, we redefine MTE as the expected treatment effect conditional on the propensity score (instead of the entire vector of observed covariates) and the latent variable representing unobserved resistance to treatment. This redefinition offers a novel perspective to interpret and analyze MTE that supplements the current approach. First, although projected onto a unidimensional summary of covariates, the redefined MTE is sufficient to capture all of the treatment effect heterogeneity that is consequential for selection bias. Thus, as with the original MTE, it can also be used as a building block for constructing standard causal parameters such as ATE and TT. The weights associated with the new MTE, however, are simpler, more intuitive, and easier to compute. Second, by discarding treatment effect variation that is orthogonal to the two-dimensional space spanned by the propensity score and the latent variable, the redefined MTE is a bivariate function, easier to visualize than the original MTE. Finally, the redefined MTE immediately reveals treatment effect heterogeneity among individuals who are at the margin of treatment. As a result, it can be used to evaluate a wide range of policy effects with little analytical twist, and to design policy interventions that optimize the marginal benefits of treatment. To facilitate practice, we also provide an R package, localIV, for estimating the redefined MTE as well as the original MTE via local instrumental variables (Zhou 2018).

For sure, this paper is not the first to characterize the selection problem using the propensity score. Since the seminal work of Rosenbaum and Rubin (1983), propensity-score-based methods, such as matching, weighting, and regression adjustment, have been a mainstay strategy for drawing causal inferences in the social sciences. In a series of papers, Heckman and his colleagues have established the key roles of the propensity score in a variety of econometric methods, including matching, control functions, instrumental variables, and the MTE approach (Heckman and Robb 1986; Heckman and Hotz 1989; Heckman and Navarro-Lozano 2004; Heckman 2010). In the MTE approach, for example, incremental changes in the propensity score serve as “local instrumental variables” that identify the MTE at various values of the unobserved resistance to treatment. Moreover, the weights with which MTE can be aggregated up to standard causal parameters depend solely on the conditional distribution of the propensity score given covariates. In this paper, we show that the propensity score offers not only a tool for identification, but also a perspective from which we can better summarize, interpret, and analyze treatment effect heterogeneity due to both observed and unobserved characteristics.

2. Marginal Treatment Effects: A Review

The MTE approach builds on the generalized Roy model for discrete choices (Roy 1951; Heckman and Vytlacil 2007a). Consider two potential outcomes, Y₁ and Y₀, a binary indicator D for treatment status, and a vector of pretreatment covariates X. Y₁ denotes the potential outcome if the individual were treated (D = 1) and Y₀ denotes the potential outcome if the individual were not treated (D = 0). We specify the outcome equations as

$$Y_0={\mu }_0(X)+ϵ$$ (1)

$$Y_1={\mu }_1(X)+ϵ+\eta$$ (2)

where ${\mu }_0(X)=\mathbb{E}\left[Y_0\mid X\right]$, ${\mu }_1(X)=\mathbb{E}\left[Y_1\mid X\right]$, the error term ϵ captures all unobserved factors that affect the baseline outcome (Y₀), and the error term η captures all unobserved factors that affect the treatment effect (Y₁ − Y₀). Treatment assignment is represented by a latent index model. Let I_D be a latent tendency for treatment, which depends on both observed (Z) and unobserved (V) factors:

$$I_D={\mu }_D(Z)-V$$ (3)

$$D=\mathbb{I}\left(I_D>0\right),$$ (4)

where μ_D(Z) is an unspecified function, V is a latent random variable representing unobserved, individual-specific resistance to treatment, assumed to be continuous with a strictly increasing distribution function. The Z vector includes all of the components of X, but it also includes instrumental variables (IV) that affect only the treatment status D. The key assumptions associated with equations (1–4) are

Assumption 1.

(ϵ, η, V) are statistically independent of Z given X (Independence).

Assumption 2.

μ_D(Z) is a nontrivial function of Z given X (Rank condition).

The latent index model characterized by equations (3) and (4), combined with assumptions 1 and 2, is equivalent to the Imbens-Angrist (1994) assumptions of independence and monotonicity for the interpretation of IV estimands as local average treatment effects (LATE) (Vytlacil 2002).

To define the MTE, it is best to rewrite the treatment assignment equations (3) and (4) as

$$\begin{array}{l}D=\mathbb{I}\left(F_{V\mid X}\left({\mu }_D(Z)\right)-F_{V\mid X}(V)>0\right)\\ =\mathbb{I}(P(Z)-U>0),\end{array}$$ (5)

where F_V|X(·) is the cumulative distribution function of V given X, and P(Z) = Pr(D = 1|Z) = F_V|X(μ_D(Z)) denotes the propensity score given Z. U = F_V|X(V) is the quantile of V given X, which by definition follows a standard uniform distribution. From equation (5) we can see that Z affects treatment status only through the propensity score P(Z). The MTE is defined as the expected treatment effect conditional on pretreatment covariates X = x and the normalized latent variable U = u:

$$\begin{gathered} \mathrm{MTE}(x,u)=\mathbb{E}\left[Y_1-Y_0\mid X=x,U=u\right] \\ =\mathbb{E}\left[{\mu }_1(X)-{\mu }_0(X)+\eta \mid X=x,U=u\right] \\ ={\mu }_1(x)-{\mu }_0(x)+\mathbb{E}[\eta \mid X=x,U=u]. \end{gathered}$$

Since U is the quantile of V, the variation of MTE(x, u) over values of u reflects how treatment effect varies with different quantiles of the unobserved resistance to treatment.

A wide range of causal parameters, such as ATE and TT, can be expressed as weighted averages of MTE(x, u). To obtain population-level causal effects, MTE(x, u) needs to be integrated twice, first over u given X = x and then over x. The weights for integrating over u are detailed in Heckman, Urzua, and Vytlacil (2006). It bears noting that the estimation of weights can be challenging in practice (except for the ATE case) as it involves estimating the conditional density of P(Z) given X and the latter is usually a high-dimensional vector.

Given assumptions 1 and 2, MTE(x, u) can be nonparametrically identified using the method of local instrumental variables (LIV).¹ Specifically, for any (x, u) within the support of the joint distribution of X and P(Z), MTE(x, u) can be identified as the partial derivative of $\mathbb{E}[Y\mid X=x,P\text{(}Z\text{)=}p\text{]}$ with respect to p:

$$\mathrm{MTE}(x,u)={\frac{\partial \mathbb{E}[Y\mid X=x,P(Z)=p]}{\partial p}|}_{p=u}.$$

In practice, however, it is difficult to condition on X nonparametrically, especially when X is high-dimensional. Therefore, in most empirical work using LIV, it is assumed that (X, Z) is jointly independent of (ϵ, η, V) (e.g., Carneiro and Lee 2009; Carneiro, Heckman, and Vytlacil 2011; Maestas, Mullen, and Strand 2013). Under this assumption, the MTE is additively separable in x and u:

$$\begin{array}{l}\mathrm{MTE}(x,u)={\mu }_1(x)-{\mu }_0(x)+\mathbb{E}[\eta \mid X=x,U=u]\\ ={\mu }_1(x)-{\mu }_0(x)+\mathbb{E}[\eta \mid U=u].\end{array}$$ (6)

The additive separability not only simplifies estimation, but also allows MTE(x, u) to be identified over supp(X)×supp(P(Z)) (instead of supp(X, P(Z))). The above equation also suggests a necessary and sufficient condition for the MTE to be additively separable:

Assumption 3.

$\mathbb{E}[\eta \mid X=x,U=u]$ does not depend on x (Additive separability).

This assumption is implied by (but does not imply) the full independence between (X, Z) and (ϵ, η, V) (see Brinch, Mogstad, and Wiswall 2017 for a similar discussion).

In most applied work, the conditional means of Y₀ and Y₁ given X are further specified as linear in parameters: ${\mu }_0(X)={\beta }_0^{T}X$ and ${\mu }_1(X)={\beta }_1^{T}X$. In this case, $\mathbb{E}[Y\mid X=x,P(Z)=p]$ can be written as

$$\mathbb{E}[Y\mid X=x,P(Z)=p]={\beta }_0^{T}x+{\left({\beta }_1-{\beta }_0\right)}^{T}xp+\underset{K(p)}{\underbrace{{\int }_0^p\mathbb{E}[\eta \mid U=u]du}},$$

where K(p) can be estimated either nonparametrically or with some functional form restrictions.² The MTE is then estimated as

$$\widehat{\mathrm{MTE}}(x,u)={\left({\widehat{\beta }}_1-{\widehat{\beta }}_0\right)}^{T}x+{\widehat{K}}^{\prime }(u),$$ (7)

where K′(u) is the derivative of K(p) evaluated at u. Heckman, Urzua, and Vytlacil (2006) provide a detailed discussion of different estimation methods.

3. A Redefinition of MTE

Under the generalized Roy model, a single latent variable U not only summarizes all unobserved determinants of treatment status but also captures all the treatment effect heterogeneity by unobserved characteristics that may cause selection bias. In fact, the latent index structure implies that all the treatment effect heterogeneity that is consequential for selection bias occurs only along two dimensions: (a) the propensity score P(Z), and (b) the latent variable U representing unobserved resistance to treatment. This is directly reflected in equation (5): a person is treated if and only if her propensity score exceeds her (realized) latent resistance u. Therefore, given both P(Z) and U, treatment status D is fixed (either 0 or 1) and thus independent of treatment effect:

$$Y_1-Y_0\text{⫫}D\mid P(Z),U.$$

Thus, to characterize selection bias, it is sufficient to model treatment effect as a bivariate function of the propensity score and the latent variable U. We redefine MTE as the expected treatment effect given P(Z) and U:

$$\widetilde{\mathrm{MTE}}(p,u)\triangleq \mathbb{E}\left[Y_1-Y_0\mid P(Z)=p,U=u\right].$$

Compared with the original MTE, $\widetilde{\mathrm{MTE}}(p,u)$ is a more parsimonious representation of all the treatment effect heterogeneity that is relevant for selection bias. Moreover, by discarding treatment effect variation that is orthogonal to the two-dimensional space spanned by P(Z) and U, $\widetilde{\mathrm{MTE}}(p,u)$ is a bivariate function, easier to visualize than MTE(x, u).

As with MTE(x, u), $\widetilde{\mathrm{MTE}}(p,u)$ can also be used as a building block for constructing standard causal parameters such as ATE and TT. However, compared with the weights on MTE(x, u), the weights on $\widetilde{\mathrm{MTE}}(p,u)$ are simpler, more intuitive, and easier to compute. The weights for ATE, TT, and TUT are shown in the first three rows of Table 1.³ To construct ATE(p), we simply integrate $\widetilde{\mathrm{MTE}}(p,u)$ against the marginal distribution of U — a standard uniform distribution. To construct TT(p), we integrate $\widetilde{\mathrm{MTE}}(p,u)$ against the truncated distribution of U given U < p. Similarly, to construct TUT(p), we integrate $\widetilde{\mathrm{MTE}}(p,u)$ against the truncated distribution of U given U ⩾ p. To obtain population-level ATE, TT, and TUT, we further integrate ATE(p), TT(p), and TUT(p) against appropriate marginal distributions of P(Z). For example, to construct TT, we integrate TT(p) against the marginal distribution of the propensity score among treated units.

Table 1:

Weights for Constructing ATE, TT, TUT, PRTE, and MPRTE from $\widetilde{\mathrm{MTE}}(p,u)$

Quantities of Interest	Weight
ATE(p)	hATE(p, u) = 1
TT(p)	$h_{\text{TT}}(p,u)=\frac{1(u<p)}{p}$
TUT(p)	$h_{\text{TUT}}(p,u)=\frac{1(u⩾p)}{1-p}$
PRTE(p, λ(p))	$h_{\text{PRTE}}(p,u)=\frac{1(p⩽u<p+\lambda (p))}{\lambda (p)}$
MPRTE(p)	hMPRTE(p, u) = δ(u − p)

Note: ATE=Average Treatment Effect; TT=Treatment Effect of the Treated; TUT=Treatment Effect of the Untreated; PRTE=Policy Relevant Treatment Effect; MPRTE=Marginal Policy Relevant Treatment Effect. δ(·) is the Dirac delta function.

4. Identification and Estimation of $\widetilde{\text{MTE}}(p,u)$

As with MTE(x, u), the regions over which $\widetilde{\mathrm{MTE}}(p,u)$ is identified depend on whether assumption 3 (additive separability) is invoked.⁴ Let us first look at the case without additive separability. From assumption 1, we know U ⫫ P(Z)|X. Since U follows a standard uniform distribution for each X = x, we also have U ⫫ X. By the rules of conditional independence, we have U ⫫ X|P(Z). Using this fact and the law of total expectation, we can write $\widetilde{\mathrm{MTE}}(p,u)$ as

$$\begin{gathered} \widetilde{\mathrm{MTE}}(p,u)={\mathbb{E}}_{X\mid P(Z)=p,U=u}\mathbb{E}\left[Y_1-Y_0\mid P(Z)=p,U=u,X\right] \\ ={\mathbb{E}}_{X\mid P(Z)=p}\mathbb{E}\left[{\mu }_1(X)-{\mu }_0(X)+\eta \mid P(Z)=p,U=u,X\right] \\ ={\mathbb{E}}_{X\mid P(Z)=p}\mathbb{E}\left[{\mu }_1(X)-{\mu }_0(X)+\eta \mid U=u,X\right](\text{because}(\eta ,U)⫫P(Z)\mid X) \\ ={\mathbb{E}}_{X\mid P(Z)=p}\mathrm{MTE}(X,u). \end{gathered}$$ (8)

Thus $\widetilde{\mathrm{MTE}}(p,u)$ is no more than the conditional expectation of MTE(X, u) given P(Z) = p. As discussed earlier, with assumptions 1 and 2, MTE(x, u) is identified over the support of the joint distribution of X and P(Z). Thus for a given u, MTE(x, u) is identified if and only if x ∈ supp(X|P(Z) = u). Yet, to evaluate $\widetilde{\mathrm{MTE}}(p,u)$ from equation (8), we need to know MTE(x, u) for all x ∈ supp(X|P(Z) = p). Therefore, for a given (p, u) pair, we can identify $\widetilde{\mathrm{MTE}}(p,u)$ if supp(X|P(Z) = p) ⊆ supp(X|P(Z) = u). For general p ≠ u, this condition can be quite restrictive. However, for the particular case in which p = u, this condition is trivially satisfied. Thus for any p ∈ supp(P(Z)), $\widetilde{\mathrm{MTE}}(p,u)$ can be identified as

$$\widetilde{\text{MTE}}(p,p)={\mathbb{E}}_{X\mid P(Z)=p}\frac{\partial \mathbb{E}[Y\mid X,P(Z)=p]}{\partial p},$$

which is a univariate function of p that reflects the effects of treatment among individuals who are at the margin of indifference to treatment. As we will see, it plays a prominent role in the evaluation of policy effects.

When assumption 3 is invoked (as in most empirical work with MTE), MTE(x, u) is identified for any (x, u) ∈ supp(X)×supp(P(Z)). That is, for each u ∈ supp(P(Z)), MTE(x, u) is identified over the marginal support of X. Thus for any (p, u) ∈ supp(P(Z)) × supp(P(Z)), we can identify $\widetilde{\mathrm{MTE}}(p,u)$ through equation (8). Since MTE(x, u) can now be partitioned into a function of x and a function of u, evaluation of equation (8) will be straightforward. For example, when μ₀(X) and μ₁(X) are specified as linear in parameters, MTE(x, u) can be estimated as equation (7). To obtain estimates of $\widetilde{\mathrm{MTE}}(p,u)$, we need only one more step: Fit a nonparametric curve of ${\left({\widehat{\beta }}_1-{\widehat{\beta }}_0\right)}^{T}x$ with respect to $\widehat{p}$ (e.g., using a local linear regression) and combine it with existing estimates of K′(u).

5. Policy Relevant Causal Effects

The redefined MTE can be used not only to recover standard causal parameters, but, in the context of program evaluation, also to draw implications for the ways in which the program should be revised in the future. To predict the impact of an expansion (or a contraction) in program participation, one needs to examine treatment effects for those individuals who would be affected by such an expansion (or contraction). To formalize this idea, Heckman and Vytlacil (2001b, 2005) define the Policy Relevant Treatment Effect (PRTE) as the mean effect of moving from a baseline policy to an alternative policy per net person shifted into treatment, that is,

$$\text{PRTE}\triangleq \frac{\mathbb{E}(Y\mid \text{Alternative}\text{Policy})-\mathbb{E}(Y\mid \text{Baseline}\text{Policy})}{\mathbb{E}(D\mid \text{Alternative}\text{Policy})-\mathbb{E}(D\mid \text{Baseline}\text{Policy})}\text{.}$$

They further show that under the generalized Roy model, the PRTE depends on a policy change only through its impacts on the distribution of the propensity score P(Z). Specifically, conditional on X = x, the PRTE can be written as a weighted average of MTE(x, u), where the weights depend only on the distribution of P(Z) before and after the policy change. Within this framework, Carneiro, Heckman, and Vytlacil (2010) further define the Marginal Policy Relevant Treatment Effect (MPRTE) as a directional limit of the PRTE as the alternative policy converges to the baseline policy. Denoting by F(·) the cumulative distribution function of P(Z), they consider a set of alternative policies indexed by a scalar α, $\left\{F_{\alpha }:\alpha \in ℝ\right\}$ such that F₀ corresponds to the baseline policy. The MPRTE is defined as

$$\text{MPRTE}=\underset{\alpha \to 0}{\lim }\text{PRTE}\left(F_{\alpha }\right).$$

We follow their approach to analyzing policy effects but without conditioning on X. While Carneiro, Heckman, and Vytlacil (2010) assume that the effects of all policy changes are through shifts in the conditional distribution of P(Z) given X, we focus on policy changes that shift the marginal distribution of P(Z) directly. In other words, we consider policy interventions that incorporate individual-level treatment effect heterogeneity by values of P(Z), whether their differences in P(Z) are determined by their baseline characteristics X or the instrumental variables Z\X. In a companion paper (Zhou and Xie 2018), we provide a more detailed comparison between these two approaches.

Specifically, let us consider a class of policy changes under which the ith individual’s propensity of treatment is boosted by λ(p_i) (in a way that does not change her treatment effect), where p_i denotes her propensity score P(z_i), and λ(·) is a positive, real-valued function such that p + λ(p) ≤ 1 for all p ∈ [0, 1). Thus the policy change nudges everyone in the same direction, and two persons with the same baseline probability of treatment share an inducement of the same size. For such a policy change, the PRTE given P(Z) = p < 1 and λ(p) becomes

$$\mathrm{PRTE}(p,\lambda (p))=\mathbb{E}\left[Y_1-Y_0\mid p(Z)=p,p⩽U<p+\lambda (p)\right].$$

As with standard causal parameters, PRTE(p, λ(p)) can be expressed as a weighted average of $\widetilde{\mathrm{MTE}}(p,u)$:

$$\mathrm{PRTE}(p,\lambda (p))=\frac{1}{\lambda (p)}{\int }_p^{p+\lambda (p)}\widetilde{\mathrm{MTE}}(p,u)du.$$

Here, the weight on u is constant (i.e., 1/λ(p)) within the interval of [p, p + λ(p)) and zero elsewhere.

To examine the effects of marginal policy changes, let us consider a sequence of policy changes indexed by a real-valued scalar α. Given P(Z) = p, we define the MPRTE as the limit of PRTE(p, αλ(p)) as α approaches zero:

$$\begin{gathered} \mathrm{MPRTE}(p)=\underset{\alpha \to 0}{\lim }\mathrm{PRTE}(p,\alpha \lambda (p)) \\ =\mathbb{E}\left(Y_1-Y_0\mid p(Z)=p,U=p\right) \\ =\widetilde{\mathrm{MTE}}(p,p). \end{gathered}$$

Hence, we have established a direct link between MPRTE(p) and $\widetilde{\mathrm{MTE}}(p,u)$: at each level of the propensity score, the MPRTE is simply the $\widetilde{\mathrm{MTE}}$ at the margin where u = p. As shown in the last row of table 1, MPRTE(p) can also be expressed as a weighted average of $\widetilde{\mathrm{MTE}}(p,u)$ using the Dirac delta function. This quantity, as noted in the previous section, can be nonparametrically identified even without the assumption of additive separability.

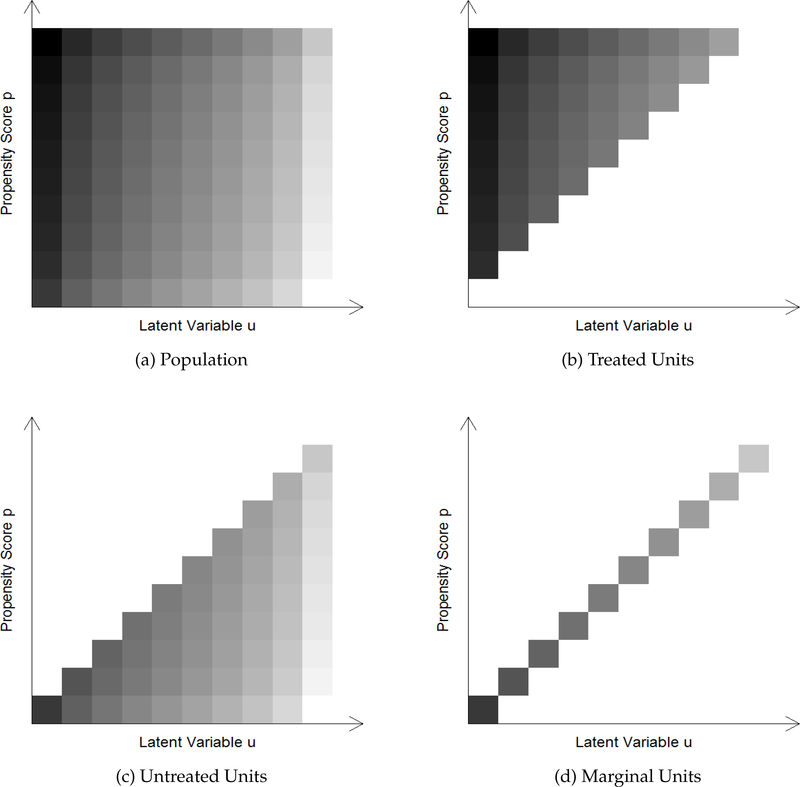
The relationships between ATE, TT, TUT, and MPRTE are illustrated graphically in Figure 1. Panel (a) shows a shaded grey plot of $\widetilde{\mathrm{MTE}}(p,u)$ for heterogeneous treatment effects in a hypothetical setup. In this plot, both the propensity score p and the latent resistance u (both ranging from 0 to 1) are divided into ten equally-spaced strata, yielding 100 grids, and a darker grid indicates a higher treatment effect. The advantage of such a shaded grey plot is that we can use subsets of the 100 grids to represent meaningful subpopulations. For example, we present the grids for treated units in panel (b), untreated units in panel (c), and marginal units in panel (d). Thus, evaluating ATE, TT, TUT, and MPRTE simply means taking weighted averages of $\widetilde{\mathrm{MTE}}(p,u)$ over the corresponding subsets of grids.

Figure 1:

Illustration of Treatment Effect Heterogeneity by Propensity Score P(Z) and Latent Variable U. A Darker Color Means a Higher Treatment Effect.

6. Treatment Effect Heterogeneity among Marginal Entrants

For policymakers, a key question of interest would be how MPRTE(p) varies with the propensity score p. To gain some intuition, let us consider the functional structure of MPRTE(p) under the assumption of additive separability. Substituting equation (6) into equation (8), we can see that MPRTE(p) consists of two components:

$$\mathrm{MPRTE}(p)=\text{E}\left[{\mu }_1(X)-{\mu }_0(X)\mid P(Z)=p\right]+\text{E}(\eta \mid U=p).$$

The first component reflects treatment effect heterogeneity by the propensity score, and the second component reflects treatment effect heterogeneity by the latent resistance U. Among marginal entrants, P(Z) is equal to U so that these two components fall on the same dimension.

To see how the two components combine to shape MPRTE(p), let us revisit the classic example on the economic returns to college. In the labor economics literature, a negative association has often been found between η and U, suggesting a pattern of “positive selection,” i.e., individuals who benefit more from college are more motivated than their peers to attend college (e.g., Willis and Rosen 1979; Blundell, Dearden, and Sianesi 2005; Moffitt 2008; Carneiro, Heckman, and Vytlacil 2011; Heckman, Humphries, and Veramendi 2016). In this case, the second component of equation (9) would be a decreasing function of p. On the other hand, the literature has not paid much attention to the first component, concerning whether individuals who by observed characteristics are more likely to attend college also benefit more from college. A number of observational studies have suggested that nontraditional students, such as racial and ethnic minorities or students from less-educated families, experience higher returns to college than traditional students, although interpretation of such findings remains controversial due to potential unobserved selection biases (e.g., Bowen and Bok 1998; Attewell and Lavin 2007; Maurin and McNally 2008; Brand and Xie 2010; Dale and Krueger 2011). However, if the downward slope in the second component were sufficiently strong, MPRTE(p) would also decline with p. In this case, we would, paradoxically, observe a pattern of “negative selection”: among students who are at the margin of attending college, those who by observed characteristics are less likely to attend college would actually benefit more from college.

To better understand the paradoxical implication of self-selection, let us revisit Figure 1. From panel (a), we can see that in the hypothetical data, treatment effect declines with u at each level of the propensity score, suggesting an unobserved self-selection. In other words, individuals may have self-selected into treatment on the basis of their anticipated gains. On the other hand, at each level of the latent variable u, treatment effect increases with the propensity score, indicating that individuals who by observed characteristics are more likely to be treated also benefit more from the treatment. This relationship, however, is reversed among the marginal entrants. As shown in panel (d), among the marginal entrants, those who appear less likely to be treated (bottom left grids) have higher treatment effects. This pattern of “negative selection” at the margin, interestingly, is exactly due to an unobserved “positive selection” into treatment.

7. Policy as a Weighting Problem

In section 5, we used λ(p) to denote the increment in treatment probability at each level of the propensity score p. Since MPRTE(p) is defined as the pointwise limit of PRTE(p, αλ(p)) as α approaches zero, the mathematical form of λ(p) does not affect MPRTE(p). However, in deriving the population-level (i.e., unconditional) MPRTE, we need to use λ(p) as the appropriate weight. To see this, let us consider the overall PRTE for a given α. Since given P(Z) = p, the size of inducement αλ(p) reflects the share of individuals that are induced into treatment (“compliers”), the overall PRTE is a weighted average of PRTE(p, αλ(p)) with weights αλ(p):

$${\mathrm{PRTE}}_{\alpha }=\frac{{\int }_0^1\alpha \lambda (p)\mathrm{PRTE}(p,\alpha \lambda (p))d{F}_P(p)}{{\int }_0^1\alpha \lambda (p)d{F}_P(p)}=\frac{{\int }_0^1\lambda (p)\mathrm{PRTE}(p,\alpha \lambda (p))d{F}_P(p)}{{\int }_0^1\lambda (p)d{F}_P(p)},$$

where F_P(·) denotes the marginal distribution function of the propensity score. We then define the population-level MPRTE as the limit of PRTE_α as α approaches zero. Under some regularity conditions,⁵ we can take the limit inside the integral:

$$\begin{gathered} \text{MPRTE}=\underset{\alpha \to 0}{\lim }{\text{PRTE}}_{\alpha } \\ =\frac{{\int }_0^1\lambda (p)\underset{\alpha \to 0}{\lim }\mathrm{PRTE}(p,\alpha \lambda (p))d{F}_P(p)}{{\int }_0^1\lambda (p)d{F}_P(p)} \\ =\frac{{\int }_0^1\lambda (p)\mathrm{MPRTE}(p)d{F}_P(p)}{{\int }_0^1\lambda (p)d{F}_P(p)}. \end{gathered}$$

Thus, given the estimates of MPRTE(p), a policymaker may apply the above formula to design an expression for λ(·) to boost the population-level MPRTE. For example, if it were found that the marginal return to college declines with the propensity score p, a college expansion targeted at students with lower values of p (say, a means-tested financial aid program) would be more effective overall than a uniform expansion of college attendance in the population (Zhou and Xie 2018).⁶

In practice, for a given policy λ(p), we can evaluate the above integral directly from sample data, using

$$\text{MPRTE}\approx \frac{{\sum }_i\mathrm{MPRTE}\left({\widehat{p}}_i\right)\lambda \left({\widehat{p}}_i\right)}{{\sum }_i\lambda \left({\widehat{p}}_i\right)},$$

where ${\widehat{p}}_i$ is the estimated propensity score for unit i in the sample. When the sample is not representative of the population by itself, sampling weights need to be incorporated in these summations.

8. Conclusion

Through a redefinition of MTE using the propensity score, we presented a new perspective to interpret and analyze heterogeneous treatment effects in the presence of unobserved selection. The redefined MTE treats observed and unobserved selection symmetrically, and parsimoniously summarizes all of the treatment effect heterogeneity that is relevant for selection bias. As with the original MTE, the redefined MTE can serve as a building block for evaluating aggregate causal effects. Yet the weights associated with the new MTE are simpler, more intuitive, and easier to compute. Finally, the new MTE immediately reveals treatment effect heterogeneity among individuals who are at the margin of treatment, thus enabling us to design more cost-effective policy interventions.