Abstract
An essential feature common to all empirical social research is variability across units of analysis. Individuals differ not only in background characteristics, but also in how they respond to a particular treatment, intervention, or stimulation. Moreover, individuals may self-select into treatment on the basis of their anticipated treatment effects. To study heterogeneous treatment effects in the presence of self-selection, Heckman and Vytlacil (1999, 2001a, 2005, 2007b) have developed a structural approach that builds on the marginal treatment effect (MTE). In this paper, we extend the MTE-based approach through a redefinition of MTE. Specifically, we redefine MTE as the expected treatment effect conditional on the propensity score (rather than all observed covariates) as well as a latent variable representing unobserved resistance to treatment. As with the original MTE, the new MTE can also be used as a building block for evaluating standard causal estimands. However, the weights associated with the new MTE are simpler, more intuitive, and easier to compute. Moreover, the new MTE is a bivariate function, and thus is easier to visualize than the original MTE. Finally, the redefined MTE immediately reveals treatment effect heterogeneity among individuals who are at the margin of treatment. As a result, it can be used to evaluate a wide range of policy changes with little analytical twist, and to design policy interventions that optimize the marginal benefits of treatment. We illustrate the proposed method by estimating heterogeneous economic returns to college with National Longitudinal Study of Youth 1979 (NLSY79) data.
1. Introduction
An essential feature common to all empirical social research is variability across units of analysis. Individuals differ not only in background characteristics, but also in how they respond to a particular treatment, intervention, or stimulation. In the language of causal inference, the second type of variability is called treatment effect heterogeneity. Due to the ubiquity of treatment effect heterogeneity, all statistical methods designed for drawing causal inferences can identify causal effects only at an aggregate level while overlooking within-group, individual-level heterogeneity (Holland 1986; Xie 2013). Moreover, when treatment effects vary systematically by treatment status, the average difference in outcome between the treated and untreated units is a biased estimate of the average treatment effect in the population (Winship and Morgan 1999).
Depending on data and assumptions about how individuals select into treatment, three major approaches have been proposed to studying heterogeneous treatment effects. First, we can simply include interaction terms between treatment status and a set of effect modifiers in a standard regression model. A drawback of this approach is that the results may be sensitive to the functional form specifying how treatment and covariates jointly influence the outcome of interest. Fortunately, recent developments in nonparametric modeling have allowed the idea to be implemented without strong functional form restrictions (e.g., Hill 2011). Second, recent sociological studies have focused on how treatment effect varies by the propensity score, i.e., the probability of treatment given a set of observed covariates (e.g., Brand and Xie 2010; Xie, Brand and Jann 2012). The methodological rationale for this approach is that under the assumption of ignorability, the interaction between treatment status and the propensity score captures all of the treatment effect heterogeneity that is consequential for selection bias (Rosenbaum and Rubin 1983). Treatment effect heterogeneity along the propensity score also has profound policy implications. For instance, if the benefits of a job training program are greater among individuals who are more likely to enroll in the program, expanding the size of the program may reduce its average effectiveness.
The above two approaches for studying heterogeneous treatment effects both rely on the assumption of ignorability, that is, after controlling for a set of observed confounders, treatment status is independent of potential outcomes. This assumption is strong, unverifiable, and unlikely to be true in most observational studies. Two types of unobserved selection may invalidate the ignorability assumption. On the one hand, if treatment status is correlated with some fixed unobserved characteristics such that treated units would have different outcomes from untreated units even without treatment, traditional regression and matching methods would lead to biased estimates of average causal effects. This bias is usually called pretreatment heterogeneity bias or Type I selection bias (Xie, Brand and Jann 2012). As Breen, Choi and Holm (2015) show, this type of selection could easily contaminate estimates of heterogeneous treatment effects by observed covariates or the propensity score. A variety of statistical and econometric methods, such as instrumental variables (IV), fixed effects models, and regression discontinuity (RD) designs, have been developed to address pretreatment heterogeneity bias.
The second type of unobserved selection arises when treatment status is correlated with treatment effect in a way that is not captured by observed covariates. This is likely when individuals (or their agents) possess more knowledge than the researcher about their individual-specific gains (or losses) from treatment and act on it (Roy 1951; Bjorklund and Moffitt 1987; Heckman and Vytlacil 2005). The bias associated with this type of selection has been termed treatment-effect heterogeneity bias or Type II selection bias (Xie, Brand and Jann 2012). For example, research considering heterogeneous returns to schooling has argued that college education is selective because it disproportionately attracts young persons who would gain more from attending college (e.g., Willis and Rosen 1979; Moffitt 2008; Carneiro, Heckman and Vytlacil 2011). Similar patterns of self-selection have been observed in a variety of contexts, such as migration (Borjas 1987), secondary schooling tracking (Gamoran and Mare 1989), career choice (Sakamoto and Chen 1991), and marriage dissolution (Smock, Manning and Gupta 1999).
The third approach, developed by Heckman and Vytlacil (1999, 2001a, 2005, 2007b), accommodates both types of unobserved selection through the use of a latent index model for treatment assignment. Under this model, all of the treatment effect heterogeneity relevant for selection bias is captured in the marginal treatment effect (MTE), a function defined as the conditional expectation of treatment effect given observed covariates and a latent variable representing unobserved, individual-specific resistance to treatment. This approach has been called the MTE-based approach (Zhou and Xie 2016). As Heckman, Urzua and Vytlacil (2006) show, a wide range of causal estimands, such as the average treatment effect (ATE) and the treatment effect of the treated (TT), can be expressed as weighted averages of MTE. Moreover, MTE can be used to evaluate average treatment effects among individuals at the margin of indifference to treatment, thus allowing the researcher to assess the efficacy of marginal policy changes (Carneiro, Heckman and Vytlacil 2010). For example, using data from the National Longitudinal Survey of Youth (NLSY) 1979, Carneiro, Heckman and Vytlacil (2011) found that if a policy change expanded each individual’s probability of attending college by the same proportion, the estimated return to one year of college education among marginal entrants to college would be only 1.5%, far lower than the estimated population average of 6.7%.
In the MTE framework, the latent index model ensures that all unobserved determinants of treatment status are summarized by a single latent variable, and that the variation of treatment effect by this latent variable captures all of the treatment effect heterogeneity that may cause selection bias. Our basic intuition is that, under this model, treatment effect heterogeneity that is consequential for selection bias occurs only along two dimensions: (a) the observed probability of treatment (i.e., the propensity score), and (b) the latent variable for unobserved resistance to treatment. In other words, after unobserved selection is factored in through the latent variable, the propensity score is the only dimension along which treatment effect may be correlated with treatment status. Therefore, to identify population-level and subpopulation-level causal effects such as ATE and TT, it would be sufficient to model treatment effect as a bivariate function of the propensity score and the latent variable. In this paper, we show that such a bivariate function is not only analytically sufficient, but also essential to the evaluation of policy effects.
Specifically, we redefine MTE as the expected treatment effect conditional on the propensity score (rather than the entire vector of observed covariates) and the latent variable representing unobserved resistance to treatment. This redefinition offers a novel perspective to interpret and analyze MTE that supplements the current approach. First, although projected onto a unidimensional summary of covariates, the redefined MTE is sufficient to capture all of the treatment effect heterogeneity that is consequential for selection bias. Thus, as with the original MTE, it can also be used as a building block for constructing standard causal estimands such as ATE and TT. The weights associated with the new MTE, however, are simpler, more intuitive, and easier to compute. Second, by discarding treatment effect variation that is orthogonal to the two-dimensional space spanned by the propensity score and the latent variable, the redefined MTE is a bivariate function, thus easier to visualize than the original MTE. Finally, and perhaps most importantly, the redefined MTE immediately reveals treatment effect heterogeneity among individuals who are at the margin of treatment. As a result, it can be used to evaluate a wide range of policy effects with little analytical twist, and to design policy interventions that optimize the marginal benefits of treatment. To facilitate practice, we also provide an R package, localIV, for estimating the redefined MTE as well as the original MTE via local instrumental variables (Zhou 2018), which is available from the Comprehensive R Archive Network (CRAN).
For sure, this paper is not the first to characterize the problem of selection bias using the propensity score. Since the seminal work of Rosenbaum and Rubin (1983), propensity-score-based methods, such as matching, weighting, and regression adjustment, have been a mainstay strategy for drawing causal inferences in the social sciences. In a series of papers, Heckman and his colleagues have also established the key roles of the propensity score in a variety of econometric methods, including control functions, instrumental variables, and the MTE approach (Heckman and Robb 1986; Heckman and Hotz 1989; Heckman and Navarro-Lozano 2004; Heckman 2010).1 In the MTE approach, for example, incremental changes in the propensity score serve as “local instrumental variables” that identify the MTE at various values of the unobserved resistance to treatment. Moreover, the weights with which MTE can be aggregated up to standard causal estimands depend solely on the conditional distribution of the propensity score given covariates. In this paper, we show that the propensity score offers not only a tool for identification, but also a perspective from which we can better summarize, interpret, and analyze treatment effect heterogeneity due to both observed and unobserved characteristics.
The rest of the paper is organized as follows. In section 2, we review the MTE-based approach for studying heterogeneous treatment effects. Specifically, we discuss the generalized Roy model for treatment selection, the definition and properties of MTE, and the estimation of MTE and related weights. In Section 3, we present our new approach that builds on the redefinition of MTE. The redefined MTE enables us to directly examine the variation of ATE, TT, and policy relevant causal effects across individuals with different values of the propensity score. In this framework, designing a policy intervention boils down to weighting individuals with different propensities of treatment. In Section 4, we illustrate our new approach by estimating heterogeneous economic returns to college with NLSY79 data. The final section concludes the paper.
2. The MTE-based Approach: A Review
2.1. The Generalized Roy Model
The MTE approach builds on the generalized Roy model for discrete choices (Roy 1951; Heckman and Vytlacil 2007a). Consider two potential outcomes, Y1 and Y0, a binary indicator D for treatment status, and a vector of pretreatment covariates X. Y1 denotes the potential outcome if the individual were treated (D = 1) and Y0 denotes the potential outcome if the individual were not treated (D = 0). We specify the outcome equations as
| (1) |
| (2) |
where , , the error term ϵ captures all unobserved factors that affect the baseline outcome (Y0), and the error term η captures all unobserved factors that affect the treatment effect (Y1 − Y0). In general, the error terms ϵ and η need not be statistically independent of X, although they have zero conditional means by construction. The observed outcome Y can be linked to the potential outcomes through the switching regression model (Quandt 1958, 1972):
| (3) |
Treatment assignment is represented by a latent index model. Let ID be a latent tendency for treatment, which depends on both observed (Z) and unobserved (V) factors:
| (4) |
| (5) |
where μD(Z) is an unspecified function, V is a latent random variable representing unobserved, individual-specific resistance to treatment, assumed to be continuous with a strictly increasing distribution function. The Z vector includes all of the components of X, but it also includes some instrumental variables (IV) that affect only the treatment status D. The key assumptions associated with equations (1–4) are
Assumption 1. (ϵ, η, V) are statistically independent of Z given X (Independence).
Assumption 2. μD(Z) is a nontrivial function of Z given X (Rank condition).
The latent index model characterized by equations (4) and (5), combined with assumptions 1 and 2, is equivalent to the Imbens-Angrist (1994) assumptions of independence and monotonicity for the interpretation of IV estimands as local average treatment effects (LATE) (Vytlacil 2002). Given assumptions 1 and 2, the latent resistance V is allowed to be correlated with ϵ and η in a general way. For example, research considering heterogeneous returns to schooling has argued that individuals may self-select into college on the basis of their anticipated gains. In this case, V will be negatively correlated with η, as individuals with higher values of η tend to have lower levels of unobserved resistance U.2
2.2. Marginal Treatment Effects
To define the MTE, it is best to rewrite the treatment assignment equations (4) and (5) as
| (6) |
where FV|X(·) is the cumulative distribution function of V given X, and P(Z) = Pr(D = 1|Z) = FV|X(Z) denotes the propensity score given Z. U = FV|X(V) is the quantile of V given X, which by definition follows a standard uniform distribution. From equation (6) we can see that Z affects treatment status only through the propensity score P(Z).3
The MTE is defined as the expected treatment effect conditional on pretreatment covariates X = x and the normalized latent variable U = u:
| (7) |
Since U is the quantile of V, the variation of MTE(x, u) over values of u reflects how treatment effect varies with different quantiles of the unobserved resistance to treatment. Alternatively, MTE(x, u) can be interpreted the average treatment effect among individuals who are indifferent between treatment or not with covariates X = x and the propensity score P(Z) = u.
A wide range of causal estimands, such as ATE and TT, can be expressed as weighted averages of MTE(x, u) (Heckman, Urzua and Vytlacil 2006). To obtain population-level causal effects, MTE(x, u) needs to be integrated twice, first over u given X = x and then over x. The weights for integrating over u are shown in Table 1. Note that these weights are conditional on X = x. To estimate overall ATE, TT, and TUT, we need to further integrate estimates of ATE(x), TT(x), and TUT(x) against appropriate marginal distributions of X.
Table 1:
Weights for Constructing ATE(x), TT(x), and TUT(x) from MTE(x, u)
| Quantities of Interest | Weight |
|---|---|
| ATE(x) | hATE(x, u) = 1 |
| TT(x) | |
| TUT(x) |
Note: ATE=Average Treatment Effect; TT=Treatment Effect of the Treated; TUT=Treatment Effect of the Untreated.
The estimation of MTE(x, u), however, is not straightforward since neither the counterfactual outcome nor the latent variable U is observed. Moreover, the estimation of weights can be practically challenging (except for the ATE case) as it involves estimating the conditional density of P(Z) given X and the latter is usually a high-dimensional vector. We turn to these estimation issues now.
2.3. Estimation of MTE and Weights in Practice
Given assumptions 1 and 2, MTE(x, u) can be nonparametrically identified using the method of local instrumental variables (LIV).4 To see how it works, let us first write out the expectation of the observed outcome Y given the covariates X = x and the propensity score P(Z) = p. According to equation (3), we have
| (8) |
Taking the partial derivative of equation (8) with respect to p, we have
Since is a function of observed (or estimable) quantities, the above equation means that MTE(x, u) is identified as long as u falls within supp(P(Z)|X), the conditional support of P(Z) given X = x. In other words, MTE(x, u) is nonparametrically identified over supp(X, P(Z)), the support of the joint distribution of X and P(Z).
In practice, however, it is difficult to condition on X nonparametrically, especially when X is high-dimensional. Therefore, in most empirical work using LIV, it is assumed that (X, Z) is jointly independent of (ϵ, η, V) (e.g., Carneiro and Lee 2009; Carneiro, Heckman and Vytlacil 2011; Maestas, Mullen and Strand 2013). Under this assumption, the MTE is additively separable in x and u:
| (9) |
The additive separability not only simplifies estimation, but also allows MTE(x, u) to be identified over supp(X)×supp(P(Z)) (instead of supp(X, P(Z))). The above equation also suggests a necessary and sufficient condition for the MTE to be additively separable:
Assumption 3. does not depend on x (Additive separability).
This assumption is implied by (but does not imply) the full independence between (X, Z) and (ϵ, η, V) (see Brinch, Mogstad and Wiswall 2017 for a similar discussion).
In most applied work, the conditional means of Y0 and Y1 given X are further specified as linear in parameters: and . Given the linear specification and assumptions 1–3, , can be written as
| (10) |
where K(p) is an unknown function that can be estimated either parametrically or nonparametrically.5
First, in the special case where the error terms (ϵ, η, V) are assumed to be jointly normal with zero means and an unknown covariance matrix S, the generalized Roy model characterized by equations (1), (2), (4), and (5) is fully parameterized, and the unknown parameters (β1, β0, γ, Σ) can be jointly estimated via maximum likelihood.6 This model specification has a long history in econometrics and is usually called the “normal switching regression model” (Heckman 1978; see Winship and Mare 1992 for a review). With the joint normality assumption, equation (9) reduces to
| (11) |
where σηV is the covariance between η and V, σV is the standard deviation of V, and Φ−1(·) denotes the inverse of the standard normal distribution function.7 By plugging in the maximum likelihood estimates (MLE) of (β1, β0, σηV, σV), we obtain an estimate of MTE(x, u) for any combination of x and u.
The joint normality of error terms is a strong and restrictive assumption. When errors are not normally distributed, imposition of normality may lead to substantial bias in estimates of the model parameters (Arabmazar and Schmidt 1982). To avoid this problem, Heckman, Urzua and Vytlacil (2006) proposed to fit equation (10) semiparametrically using a double residual procedure (Robinson 1988). In this case, the estimation of MTE(x, u) can be summarized in four steps:
Estimate the propensity scores using a standard logit/probit model, denote them as 8
Fit local linear regressions of Y, X, and on and extract their residuals eY, eX, and ;
Fit a simple linear regression of eY on eX and (with no intercepts) to estimate the parametric part of equation (10), i.e., (β0, β1 − β0), and store the remaining variation of Y as .
Fit a local quadratic regression (Fan and Gijbels 1996) of on to estimate K(p) and its derivative K′(p)
The MTE is then estimated as
| (12) |
With estimates of MTE(x, u), we still need appropriate weights to estimate aggregate causal effects such as ATE and TT. As shown in Table 1, most of the weights involve the conditional density of P(Z) given X. Since the latter is often a high-dimensional vector, direct estimation of these weights is practically challenging. In their empirical application, Carneiro, Heckman and Vytlacil (2011) conditioned on an index of X, , instead of X per se. In other words, they used as an approximation to f [P(Z)|X]. To estimate the former, we can first estimate the bivariate density using kernel methods, and then divide the estimated bivariate density by the marginal density . As we will see, these ad hoc methods for estimating weights are no longer needed with our new approach.
3. A Propensity Score Perspective
3.1. A Redefinition of MTE
Under the generalized Roy model, a single latent variable U not only summarizes all unobserved determinants of treatment status but also captures all of the treatment effect heterogeneity by unobserved characteristics that may cause selection bias. In fact, the latent index structure implies that all of the treatment effect heterogeneity that is consequential for selection bias exists only along two dimensions: (a) the propensity score P(Z), and (b) the latent variable U representing unobserved resistance to treatment. This is directly reflected in equation (6): a person is treated if and only if her propensity score exceeds her (realized) latent resistance u. Therefore, given both P(Z) and U, treatment status D is fixed (either 0 or 1) and thus independent of treatment effect:
This expression resembles the Rosenbaum-Rubin (1983) result on the sufficiency of the propensity score except that we now condition on U in addition to P(Z). Thus, to characterize selection bias, it would be sufficient to model treatment effect as a bivariate function of the propensity score (rather than the entire vector of covariates) and the latent variable U. We redefine MTE as the expected treatment effect given P(Z) and U:
| (13) |
Compared with the original MTE, has two immediate advantages. First, because it conditions on the propensity score P(Z) rather than the whole vector of X, it captures all of the treatment effect heterogeneity that is relevant for selection bias in a more parsimonious way. Second, by discarding treatment effect variation that is orthogonal to the two-dimensional space spanned by P(Z) and U, is a bivariate function, thus easier to visualize than MTE(x, u).
As with MTE(x, u), can also be used as a building block for constructing standard causal estimands such as ATE and TT. However, compared with the weights on MTE(x, u), the weights on are simpler, more intuitive, and easier to compute. The weights for ATE, TT, and TUT are shown in the first three rows of Table 2. To construct ATE(p), we simply integrate against the marginal distribution of U — a standard uniform distribution. To construct TT(p), we integrate against the truncated distribution of U given U < p. Similarly, to construct TUT(p), we integrate against the truncated distribution of U given U ⩾ p. To obtain population-level ATE, TT, and TUT, we further integrate ATE(p), TT(p), and TUT(p) against appropriate marginal distributions of P(Z). For example, to construct TT, we integrate TT(p) against the marginal distribution of the propensity score among treated units.
Table 2:
Weights for Constructing ATE, TT, TUT, PRTE, and MPRTE from
| Quantities of Interest | Weight |
|---|---|
| ATE(p) | hATE(p, u) = 1 |
| TT(p) | |
| TUT(p) | |
| PRTE(p, λ(p)) | |
| MPRTE(p) | hMPRTE(p, u) = δ(u − p) |
Note: ATE=Average Treatment Effect; TT=Treatment Effect of the Treated; TUT=Treatment Effect of the Untreated; PRTE=Policy Relevant Treatment Effect; MPRTE=Marginal Policy Relevant Treatment Effect. δ(·) is the Dirac delta function.
In practice, can be estimated as a “by-product” of MTE(x, u). Under assumptions 1–3,9 can be written as:
| (14) |
A proof of equation (14) is given in Appendix A. Comparing equation (14) with equation (9), we can see that the only difference between the original MTE and is that the first component of is now the conditional expectation of μ1(X) − μ0(X) given the propensity score rather than μ1(X) − μ0(X) per se. Therefore, to estimate , we need only one more step after implementing the procedures described in Section 2.3: Fit a nonparametric curve of with respect to (e.g., using a local linear regression), and combine it with existing estimates of K′(u).
3.2. Policy Relevant Causal Effects
The redefined MTE can be used not only to recover traditional causal estimands, but, in the context of program evaluation, also to draw implications for how the program should be revised in the future. To predict the impact of an expansion (or a contraction) in program participation, one needs to examine treatment effects for those individuals who would be affected by such an expansion (or contraction). To formalize this idea, Heckman and Vytlacil (2001b, 2005) define the Policy Relevant Treatment Effect (PRTE) as the mean effect of moving from a baseline policy to an alternative policy per net person shifted into treatment, that is,
They further show that under the generalized Roy model, the PRTE depends on a policy change only through its impacts on the distribution of the propensity score P(Z). Specifically, conditional on X = x, the PRTE can be written as a weighted average of MTE(x, u), where the weights depend only on the distribution of P(Z) before and after the policy change. Within this framework, Carneiro, Heckman and Vytlacil (2010) further define the Marginal Policy Relevant Treatment Effect (MPRTE) as a directional limit of the PRTE as the alternative policy converges to the baseline policy. Denoting by F(·) the cumulative distribution function of P(Z), they consider a set of alternative policies indexed by a scalar α, such that F0 corresponds to the baseline policy. The MPRTE is defined as
We follow their approach to analyzing policy effects but without conditioning on X. While Carneiro, Heckman and Vytlacil (2010) assume that the effects of all policy changes are through shifts in the conditional distribution of P(Z) given X, we focus on policy changes that shift the marginal distribution of P(Z) directly. In other words, we consider policy interventions that incorporate individual-level treatment effect heterogeneity by values of P(Z), whether their differences in P(Z) are determined by their baseline characteristics X or the instrumental variables Z\X. In Section 3.5, we compare these two approaches in more detail and discuss some major advantages of our new approach.
Specifically, let us consider a class of policy changes under which the ith individual’s propensity of treatment is boosted by λ(pi) (in a way that does not change her treatment effect), where pi denotes her propensity score P(zi), and λ(·) is a positive, real-valued function such that p + λ(p) ≤ 1 for all p ∈ [0, 1). Thus the policy change nudges everyone in the same direction, and two persons with the same baseline probability of treatment share an inducement of the same size. For such a policy change, the PRTE given P(Z) = p < 1 and λ(p) becomes
As with standard causal estimands, PRTE(p, λ(p)) can be expressed as a weighted average of :
Here, the weight on u is constant (i.e., 1/λ(p)) within the interval of [p, p + λ(p)) and zero else-where.
To examine the effects of marginal policy changes, let us consider a sequence of policy changes indexed by a real-valued scalar α. Given P(Z) = p, we define the MPRTE as the limit of PRTE(p, αλ(p)) as α approaches zero:
| (15) |
Hence, we have established a direct link between MPRTE(p) and : at each level of the propensity score, the MPRTE is simply the at the margin where u = p. As shown in the last row of Table 2, MPRTE(p) can also be expressed as a weighted average of using the Dirac delta function.
The relationships between ATE, TT, TUT, and MPRTE are illustrated in Figure 1. Panel (a) shows a shaded grey plot of for heterogeneous treatment effects in a hypothetical setup. In this plot, both the propensity score p and the latent resistance u (both ranging from 0 to 1) are divided into ten equally-spaced strata, yielding 100 grids, and a darker grid indicates a higher treatment effect. The advantage of such a shaded grey plot is that we can use subsets of the 100 grids to represent meaningful subpopulations. For example, we present the grids for treated units in panel (b), untreated units in panel (c), and marginal units in panel (d). Thus, evaluating ATE, TT, TUT, and MPRTE simply means taking weighted averages of over the corresponding subsets of grids.
Figure 1:
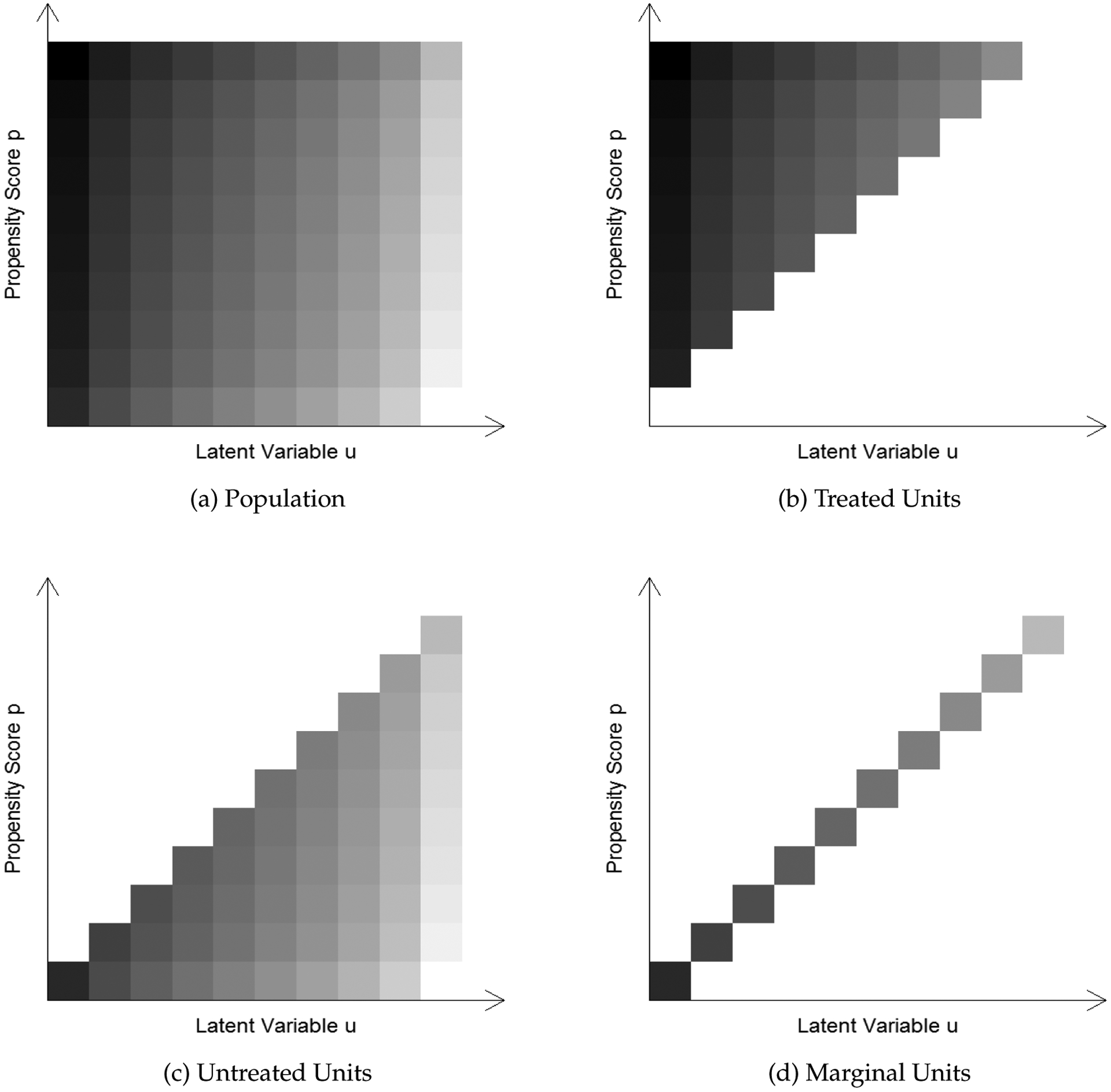
Demonstration of Treatment Effect Heterogeneity by Propensity Score P(Z) and latent variable U. A Darker Color Means a Higher Treatment Effect.
3.3. Treatment Effect Heterogeneity among Marginal Entrants
For policymakers, a key question of interest would be how MPRTE(p) varies with the propensity score p. From equations (14) and (15), we can see that MPRTE(p) consists of two components:
| (16) |
The first component reflects how treatment effect varies by the propensity score, and the second component reflects how treatment effect varies by the latent resistance U. Among marginal entrants, P(Z) is equal to U so that these two components fall on the same dimension.
To see how the two components combine to shape MPRTE(p), let us revisit the classic example on the economic returns to college. In the labor economics literature, a negative association has often been found between η and U, suggesting a pattern of “positive selection,” i.e., individuals who benefit more from college are more motivated than their peers to attend college in the first place (e.g., Willis and Rosen 1979; Blundell, Dearden and Sianesi 2005; Moffitt 2008; Carneiro, Heckman and Vytlacil 2011; Heckman, Humphries and Veramendi 2016). In this case, the second component of equation (16) would be a decreasing function of p. On the other hand, the literature has not paid much attention to the first component, concerning whether individuals who by observed characteristics are more likely to attend college also benefit more from college. A number of observational studies have suggested that nontraditional students, such as racial and ethnic minorities or students from less-educated families, experience higher returns to college than traditional students, although interpretation of such findings remains controversial due to potential unobserved selection biases (e.g., Bowen and Bok 1998; Attewell and Lavin 2007; Maurin and McNally 2008; Dale and Krueger 2011; see Hout 2012 for a review).10 However, if the downward slope in the second component were sufficiently strong, MPRTE(p) would also decline with p. In this case, we would, paradoxically, observe a pattern of “negative selection” (Brand and Xie 2010): among students who are at the margin of attending college, those who by observed characteristics are less likely to attend college would actually benefit more from college.
To better understand the paradoxical implication of self-selection, let us revisit Figure 1. From panel (a), we can see that in the hypothetical data, treatment effect declines with u at each level of the propensity score, suggesting an unobserved self-selection. In other words, individuals may have self-selected into treatment on the basis of their anticipated gains. On the other hand, at each level of the latent variable u, treatment effect increases with the propensity score, indicating that individuals who by observed characteristics are more likely to be treated also benefit more from the treatment. This relationship, however, is reversed among the marginal entrants. As shown in panel (d), among the marginal entrants, those who appear less likely to be treated (bottom left grids) have higher treatment effects. This pattern of “negative selection” at the margin, interestingly, is exactly due to an unobserved “positive selection” into treatment.
3.4. Policy as a Weighting Problem
In section 3.2, we used λ(p) to denote the increment in treatment probability at each level of the propensity score p. Since MPRTE(p) is defined as the pointwise limit of PRTE(p, αλ(p)) as α approaches zero, the mathematical form of λ(p) does not affect MPRTE(p). However, in deriving the population-level (i.e., unconditional) MPRTE, we need to use λ(p) as the appropriate weight, that is,
| (17) |
Here FP(·) is the marginal distribution function of the propensity score, and is a normalizing constant (see Appendix B for a derivation). Thus, given the estimates of MPRTE(p), a policymaker may use the above equation to design a formula for λ(·) to boost the population-level MPRTE. This is especially useful if MPRTE(p) varies systematically with the propensity score p. For example, if it were found that the marginal return to college declines with the propensity score p, a college expansion targeted at students with relatively low values of p (say, a means-tested financial aid program) would yield higher average marginal returns than a universal expansion of college enrollment regardless of student characteristics.11
In practice, for a given policy λ(p), we can evaluate the above integral directly from sample data, using
| (18) |
where is the estimated propensity score for unit i in the sample. When the sample is not representative of the population by itself, sampling weights need to be incorporated in these summations.
3.5. Comparison with Carneiro, Heckman and Vytlacil (2010)
In the above discussion, PRTE and MPRTE are defined for a class of policy changes in which the intensity of policy intervention depends on the individual’s propensity score P(Z). In other words, inducements are differentiated between individuals with different values of P(Z), whether their differences in P(Z) are determined by the baseline covariates X or the instrumental variables Z\X. This approach to defining MPRTE contrasts sharply with the approach taken by Carneiro, Heckman and Vytlacil (2010, 2011), who stipulate that all policy changes have to be “conditioned on X.” In their approach, inducements are allowed to vary across individuals with different values of Z\X but not across individuals with different values of X. For convenience, we call Carneiro, Heckman and Vytlacil’s approach the conditional approach and our approach the unconditional approach. Compared with the conditional approach, the unconditional approach to studying policy effects has several major advantages.
First, as noted above, preferential policies under the conditional approach only distinguish individuals with different instrumental variables (Z\X) but not individuals with different baseline characteristics (X). To see the limitation of such policies, let us revisit the college education example and consider a simplistic model where the only baseline covariate X is family income and the only instrumental variable Z\X is the presence of four-year colleges in the county of residence. In this case, an “affirmative” policy — a policy that favors students with lower values of P(Z) — would be a policy that induces students who happen to live in a county with no four-year colleges, regardless of family income. Given that P(Z) equals U at the margin, this policy benefits students with relatively low U’s at all levels of family income. To the extent that there is self-selection into college (i.e., Cor(η, U) < 0), this policy would yield a larger MPRTE than a neutral policy. However, if P(Z) was largely determined by family income rather than by the local presence of four-year colleges (a plausible scenario), the variation of P(Z) conditional on X would be very limited, and so would be the gain in MPRTE from a preferential policy. In contrast, the unconditional approach distinguishes individuals with different values of P(Z), most of which may be driven by X rather than Z\X. Since P(Z) equals U at the margin, this approach can effectively sort out marginal entrants with different levels of U. Therefore, preferential policies under the unconditional approach are more effective in exploiting unobserved heterogeneity in treatment effects.
Second, since treatment effect in general depends on the observed covariates X as well as the latent resistance U, an ideal policy intervention should exploit the variation of treatment effect along both dimensions. The conditional approach, however, differentiates only individuals with different U’s but not individuals with different observed characteristics (at least in practice). In contrast, by focusing on the propensity score P(Z), the unconditional approach accounts for treatment effect heterogeneity in both observed and unobserved dimensions. Because P(Z) equals U at the margin, the bivariate function degenerates into a univariate function of p among marginal entrants (see equation (16)). Thus, by weighting individuals with different values of P(Z), the unconditional approach captures the “collision” of observed heterogeneity and unobserved heterogeneity at the margin. To see why the latter is more effective, consider an extreme scenario where there is no unobserved sorting (i.e., E(η|U) is constant) but treatment effect varies considerably by X. In this case, the unconditional approach can partly exploit the variation of treatment effect by X (through the first component of equation (16)) whereas the conditional approach cannot (since it focuses exclusively on the second component of equation (16)).
Finally, the unconditional approach is computationally simpler. Since , no further step is needed to estimate MPRTE(p) once we have estimates of . The conditional approach, by contrast, needs to build MPRTE(x) on MTE(x, u) using policy-specific weights. As shown in Table 3, these policy-specific weights generally involve the conditional density of P(Z) given X. Because X is usually a high-dimensional vector, estimation of these weights is practically difficult and often tackled with ad hoc methods (see Section 2.3).
Table 3:
Weights for Constructing MPRTE(x) from MTE(x, uD)
| Parameters of Interest | Weight |
|---|---|
| MPRTE(x): P* = P + α | hMPRTE(x, u) = fP(Z)|X=x(u) |
| MPRTE(x): P* = (1 + α)P | |
4. Illustration with NLSY Data
To illustrate the new approach, we reanalyze the data from Carneiro, Heckman and Vytlacil’s (2011) study on economic returns to college education. In what follows, we first describe the data, then demonstrate treatment effect heterogeneity using the newly defined , and finally, evaluate the effects of different marginal policy changes.
4.1. Data Description
We reanalyze a sample of white males (N=1,747) who were 16–22 years old in 1979, drawn from the NLSY 1979. Treatment (D) is college attendance defined by having attained any post-secondary education by 1991. By this definition, the treated group consists of 865 individuals, and the comparison group consists of 882 individuals. The outcome Y is the natural logarithm of hourly wage in 1991.12 Following the original study, we include in pretreatment variables (in both X and Z) linear and quadratic terms of mother’s years of schooling, number of siblings, the Armed Forces Qualification Test (AFQT) score adjusted by years of schooling, permanent local log earnings at age 17 (county log earnings averaged between 1973 and 2000), permanent local unemployment rate at age 17 (state unemployment rate averaged between 1973 and 2000), as well as a dummy variable indicating urban residence at age 14 and cohort dummies. Also following Carneiro, Heckman and Vytlacil (2011), we use the following instrumental variables (Z\X): (a) the presence of a four-year college in the county of residence at age 14, (b) local wage in the county of residence at age 17, (c) local unemployment rate in the state of residence at age 17, and (d) average tuition in public four-year colleges in the county of residence at age 17, as well as their interactions with mother’s years of schooling, number of siblings, and the adjusted AFQT score. In addition, four variables are included in X but not in Z: years of experience in 1991, years of experience in 1991 squared, local log earnings in 1991, and local unemployment rate in 1991. More details about the data can be found in the online appendix of Carneiro, Heckman and Vytlacil (2011).
4.2. Heterogeneity in Treatment Effects
To estimate the bivariate function , we first need estimates of MTE(x, u). In Section 2, we discussed both a parametric method and a semiparametric method for estimating MTE(x, u). Here, we examine treatment effect heterogeneity with the semiparametric estimates of MTE(x, u) (equation (12)) and thus .13 Figure 2 presents our key results for the estimated with a shaded gray plot in which a darker grid indicates a higher treatment effect. The effect heterogeneity by the two dimensions — the propensity score and the latent resistance to treatment — exhibits a pattern that is easy to interpret but also surprising. On the one hand, we find that at each level of the propensity score, a higher level of the latent variable u is associated with a lower treatment effect, indicating the presence of self-selection based on idiosyncratic returns to college. This pattern of “sorting on gain” echoes the classic findings reported in Willis and Rosen (1979) and also Carneiro, Heckman and Vytlacil (2011). On the other hand, the color gradient along the propensity score suggests that given the latent resistance to attending college, students who by observed characteristics are more likely to go to college also tend to benefit more from attending college.
Figure 2:
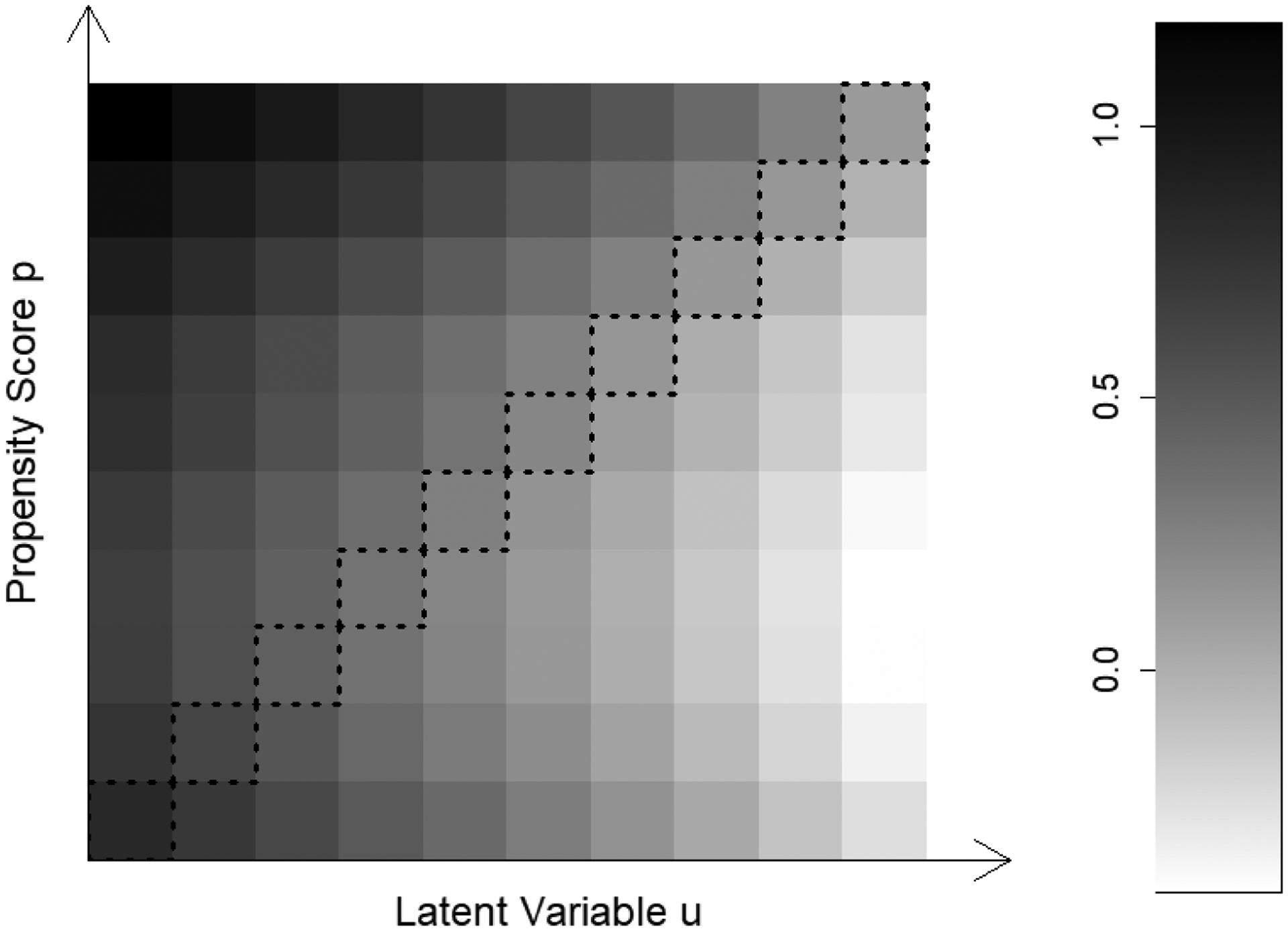
Treatment Effect Heterogeneity based on Semiparametric Estimates of .
If we read along the “diagonal” of Figure 2, however, we find that among students who are at the margin of indifference between attending college or not, those who appear less likely to attend college would benefit more from a college education, that is, MPRTE(p) declines with the propensity score p. Figure 3 shows smoothed estimates of MPRTE(p) as well as its two components (see equation (16)). We can see that the negative association between h and the latent resistance U more than offsets the positive association between (β1 − β0)TX and the propensity score P(Z), resulting in the downward slope of MPRTE(p). Echoing our discussion in Section 3.3, it is unobserved “sorting on gain” that leads to the negative association between the propensity score and returns to college among students at the margin.
Figure 3:
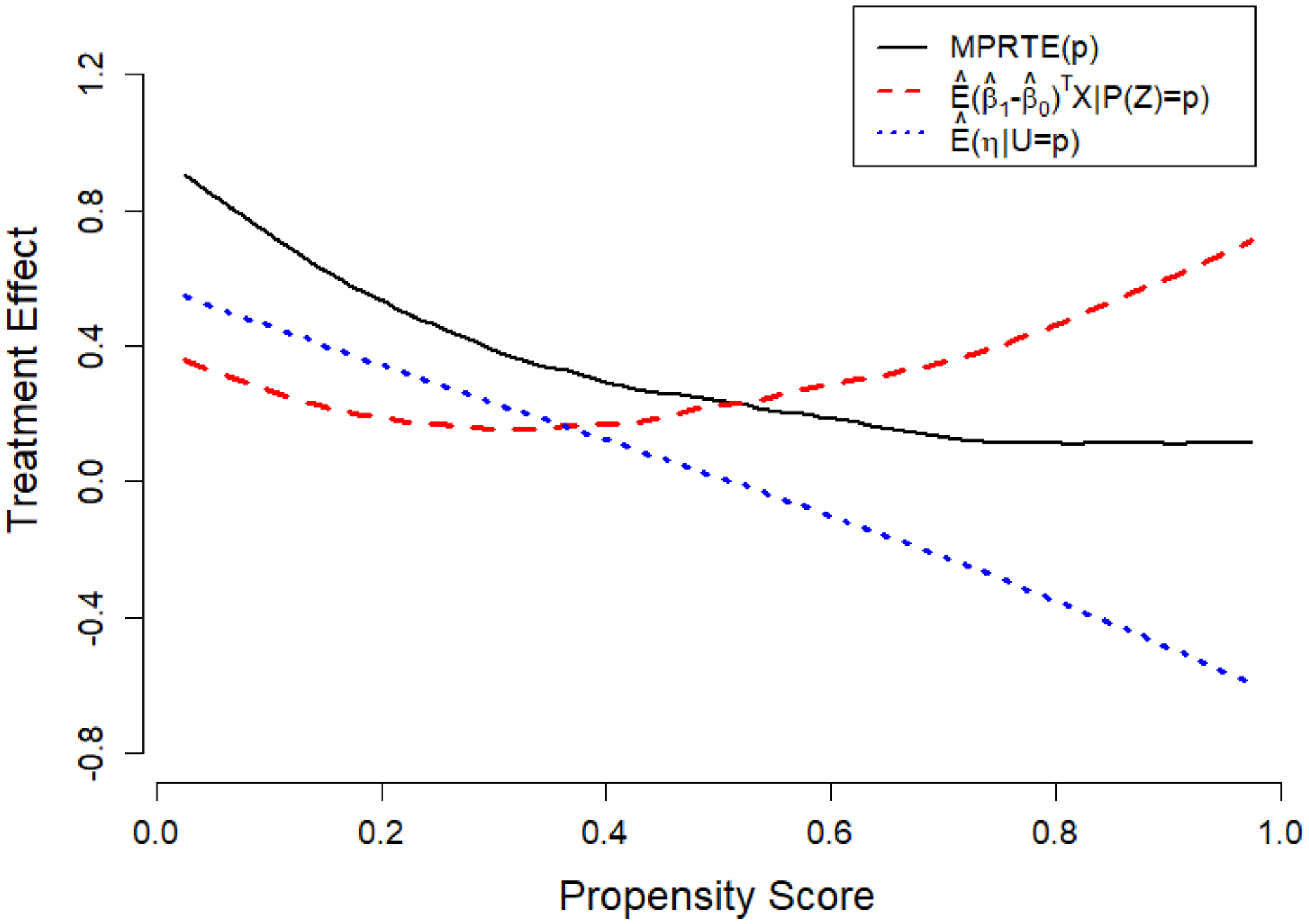
Decomposition of MPRTE(p) Based on Semiparametric Estimates of .
We use weights given in Table 2 to estimate ATE, TT, and TUT at each level of the propensity score. Figure 4 shows smoothed estimates of ATE(p), TT(p), TUT(p), as well as MPRTE(p). Several patterns are worth noting. First, there is a sharp contrast between ATE(p) and MPRTE(p): a higher propensity of attending college is associated with a higher return to college on average (solid line) but a lower return to college among marginal entrants (dotdash line). Second, TT(p) (dashed line) is always larger than TUT(p) (dotted line), suggesting that at each level of the propensity score, individuals are positively self-selected into college based on their idiosyncratic returns to college. Finally, TT(p) and TUT(p) converge to ATE(p) and MPRTE(p) at the extremes of the propensity score. When p approaches 0, TT(p) converges to MPRTE(p) and TUT(p) converges to ATE(p). At the other extreme, when p approaches 1, TT(p) converges to ATE(p) and TUT(p) converges to MPRTE(p). Looking back at figure 1, we can see that these relationships simply reflect compositional shifts in the treated and untreated groups as the propensity score changes from 0 to 1.
Figure 4:
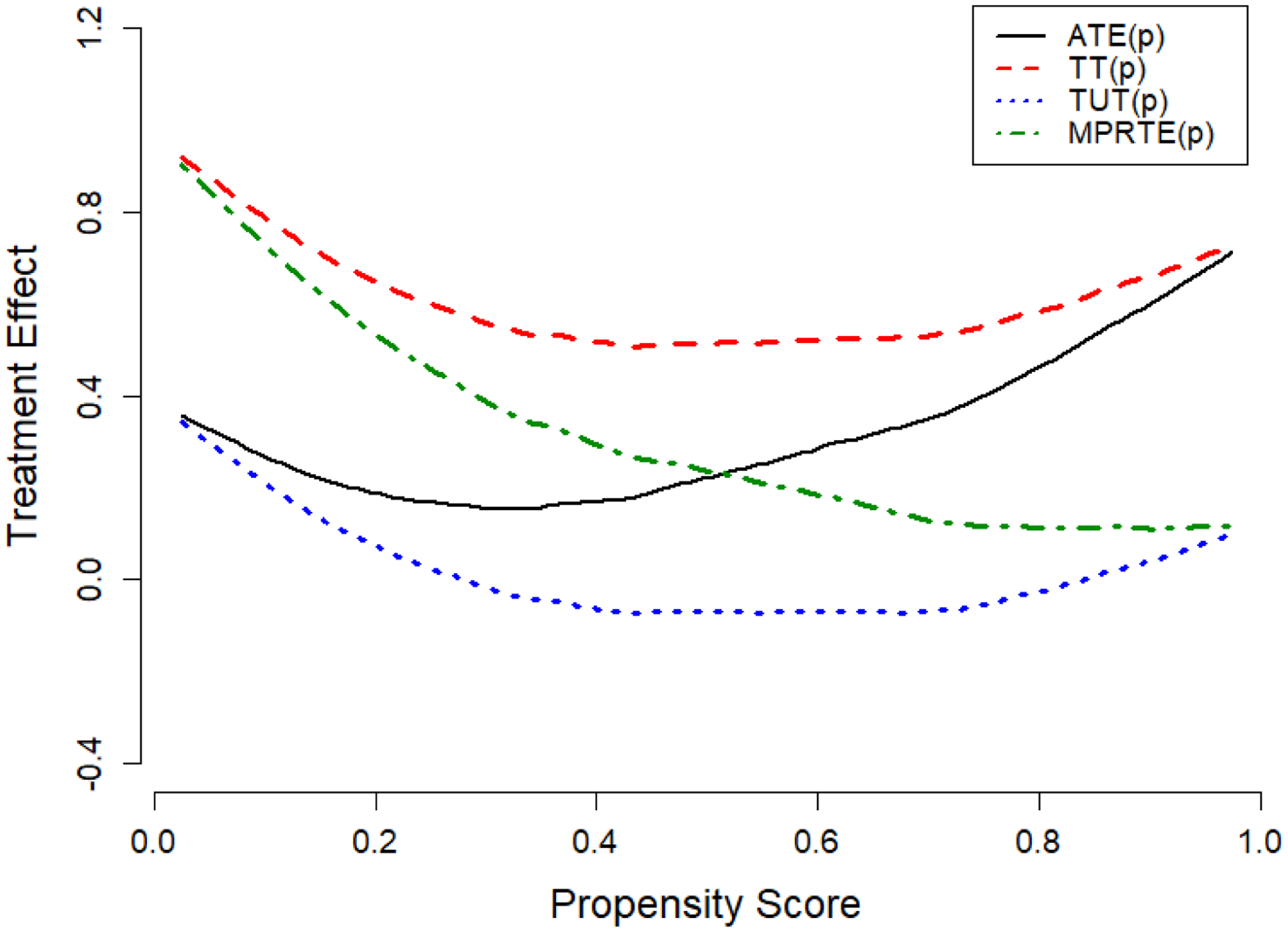
Heterogeneity in ATE, TT, TUT, and MPRTE(p) by Propensity Score based on Semiparametric Estimates of .
4.3. Evaluation of Policy Effects
Given the estimates of ATE(p), TT(p), TUT(p), we construct their population averages using appropriate weights across the propensity score. For example, to estimate TT, we simply integrate TT(p) against the marginal distribution of the propensity score among those who attended college. Moreover, the estimates of MPRTE(p) allow us to construct different versions of MPRTE, depending on how the policy change weights students with different propensities of attending college (see equation 18). Table 4 reports our estimates of ATE, TT, TUT, and MPRTE under different policy changes from both the parametric and the semiparametric estimates of MTE(x, u). To compare our new approach with Carneiro, Heckman and Vytlacil’s (2011) original approach, we show estimates built on as well as those built on MTE(x, u). Following Carneiro, Heckman and Vytlacil (2011), we annualize the returns to college by dividing all parameter estimates by four, which is the average difference in years of schooling between the treated and untreated groups.
Table 4:
Estimated Returns to One Year of College
| Parametric (Normal) | Semiparametric | |||
|---|---|---|---|---|
| Building Block | MTE(x, u) | MTE(x, u) | ||
| ATE | 0.066 (0.038) |
0.066 (0.038) | 0.082 (0.041) |
0.082 (0.041) |
| TT | 0.139 (0.035) |
0.142 (0.035) |
0.165 (0.048) |
0.167 (0.049) |
| TUT | −0.006 (0.067) |
−0.009 (0.067) |
0.000 (0.067) |
0.000 (0.061) |
| MPRTE | ||||
| λ(p) = α | 0.066 (0.038) |
0.065 (0.039) |
0.084 (0.041) |
0.083 (0.041) |
| λ(p) = αp | 0.061 (0.050) |
0.050 (0.048) |
||
| λ(p) = α(1 − p) | 0.068 (0.033) |
0.116 (0.042) |
||
| 0.080 (0.035) |
0.155 (0.055) |
|||
Note: ATE=Average Treatment Effect; TT=Treatment Effect of the Treated; TUT=Treatment Effect of the Untreated; MPRTE=Marginal Policy-Relevant Treatment Effect. Numbers in parentheses are bootstrapped standard errors (250 replications).
The first three rows of Table 4 indicate that TT>ATE>TUT≈0. That is, returns to college are higher among those who actually attended college than among those who attended only high school, for whom the average returns to college are virtually zero. We also find that using either the parametric or semiparametric estimates of MTE(x, u), our new approach and the original approach yield nearly identical point estimates and bootstrapped standard errors. The consistence between the two approaches affirms our argument that preserves all of the treatment effect heterogeneity that is consequential for selection bias. Although the redefined MTE seems to contain less information than the original MTE (as it projects (β1 − β0)TX onto the dimension of P(Z)), the discarded information does not contribute to the identification of average causal effects.
The last four rows of Table 4 present our estimates of MPRTE under four stylized policy changes: (1) λ(p) = α, (2) λ(p) = αp, (3) λ(p) = α(1 − p), and (4) . Put in words, the first policy change increases everyone’s probability of attending college by the same amount; the second policy change favors those students who appear more likely to go to college; the third policy change favors those students who appear less likely to go to college; and the last policy change targets only those students whose observed likelihood of attending college is less than 30%. For each of these policy changes, the MPRTE is defined as the limit of the corresponding PRTE as α goes to zero. The first policy change is also the first policy change considered by Carneiro, Heckman and Vytlacil (2011, p. 2760), i.e., Pα = P + α (see also the first row of Table 3). For this case, we estimated the MPRTE using both the original approach and our new approach. As expected, the two approaches yield the same results. However, the other three policy changes considered here cannot be readily accommodated within the original framework (see Section 3.5). Thus, we evaluate their effects using only our new approach, i.e., via equation (18).
We can see that although the estimates of TUT are close to zero, all four policy changes imply substantial marginal returns to college. For example, under the first policy change, the semiparametric estimate of MPRTE is 0.083, suggesting that one year of college would translate into an 8.3% increase in hourly wages among the marginal entrants. However, the exact magnitude of MPRTE depends heavily on the form of the policy change, especially under the semiparametric model. Whereas the marginal return to a year of college is about 5% if we expand everyone’s probability of attending college proportionally (policy change 2), it can be as high as 15.5% if we only increase enrollment among students whose observed likelihood of attending college is less than 30% (policy change 4). Figure 5 shows graphically how different policy changes produce different compositions of marginal college entrants. Since students who benefit the most from college are located at the low end of the propensity score, a college expansion targeted at those students will yield the highest marginal returns to college. Fortuitously, similar policy implications were reached by earlier research that did not account for the presence of unobserved selection (Brand and Xie 2010).
Figure 5:
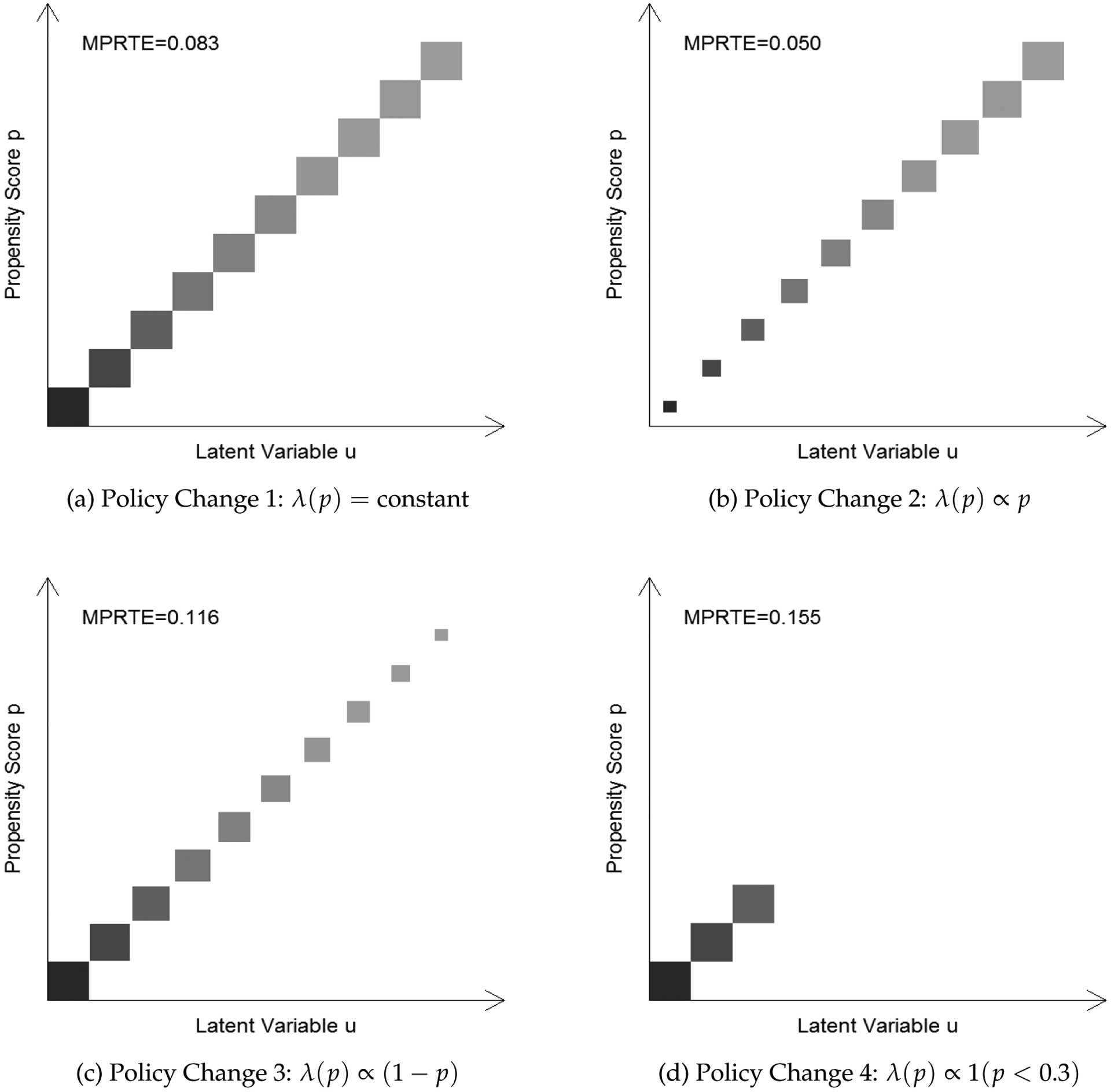
Semiparametric Estimates of MPRTE under Four Policy Changes.
5. Discussion and Conclusion
Due to the ubiquity of population heterogeneity in social phenomena, it is impossible to evaluate causal effects at the individual level. All efforts to draw causal inferences in social science must be at the group level. Yet with observational data, even group-level inference is plagued by two types of selection bias: individuals in the treated and comparison groups may differ systematically not only in their baseline outcomes but also in their treatment effects. Depending on whether unobserved selection is assumed away, traditional methods for causal inference from observational data can be divided into two classes, as shown in the first row of Table 5. The first class, including regression adjustment, matching, and inverse-probability-of-treatment weighting (Robins, Hernan and Brumback 2000), rest on the assumption of ignorability: after controlling for a set of observed covariates, treatment status is independent of both baseline outcomes and treatment effects. The second class of methods, including instrumental variables (IV), regression discontinuity (RD) designs (Thistlethwaite and Campbell 1960; Hahn, Todd and Van der Klaauw 2001), and fixed effects models, allow for unobserved selection into treatment but require exogenous variation in treatment status — either between or within units — to identify causal effects.
Table 5:
Methods for Identifying and Estimating Causal Effects from Observational Data
| Allowing for Unobserved Selection? | |||
|---|---|---|---|
| No* | Yes | ||
| Systematically Modeling Treatment Effect Heterogeneity? | No | regression adjustment, matching, IPW, etc. | IV, RD design, fixed effects models, etc. |
| Yes |
, |
MTE(x, u), |
|
Note: IV=Instrumental Variables, RD=Regression Discontinuity, IPW = Inverse Probability Weighting, MTE=Marginal Treatment Effect.
When there is unobserved selection by treatment effect but not by the baseline outcome, matching and weighting methods can still be used to consistently estimate TT (but not ATE).
While both classes of methods allow treatment effects to vary in the population, in common practices neither of them systematically models treatment effect heterogeneity.14 When treatment effects are heterogeneous, some of these methods estimate quantities that are not of primary interest to the researcher. For example, when treatment effect varies according to the level of a covariate, main-effects-only regression models cannot recover standard causal estimands such as ATE or TT, but instead estimate a conditional-variance-weighted causal effect that has little substantive meaning (Angrist and Pischke 2008; Elwert and Winship 2010). Moreover, it is widely known that when treatment effect is heterogeneous, IV and RD designs can only identify the average causal effect among individuals whose treatment status is influenced by the IV (Imbens and Angrist 1994), or, in the case of fuzzy RD designs, by whether the running variable surpasses the “cutoff point.” (Hahn, Todd and Van der Klaauw 2001). Similarly, fixed effects models can only identify the average causal effect among individuals who change their treatment status over the study period.
The second row of Table 5 summarizes the four approaches that can be used to systematically study treatment effect heterogeneity, especially treatment effect heterogeneity by pretreatment characteristics. The first approach, denoted as , includes the longstanding practice of adding interaction terms between treatment status and covariates in conventional regression models as well as recent proposals to fit nonparametric surfaces of potential outcomes and their difference (e.g. Hill 2011). The second approach, denoted as E(Y1 − Y0|P), models treatment effect as a univariate function of the propensity score (e.g., Xie, Brand and Jann 2012; Zhou and Xie 2016). Since the propensity score is the only dimension along which treatment effect may be correlated with treatment status, this approach not only provides a useful solution to data sparseness, but also facilitates projection of treatment effects beyond particular study settings (Stuart et al. 2011, Xie 2013). However, as noted earlier, these two approaches rely on the assumption of ignorability. When ignorability breaks down, interpretation of the observed heterogeneity in treatment effects becomes ambiguous (Breen, Choi and Holm 2015).
The latter two approaches, i.e., the MTE-based approach and our extension of it, accommodate unobserved selection through the use of a latent index model for treatment assignment. In this model, a scalar error term is used to capture all of the unobserved factors that may induce or impede treatment. As a result, treatment status is determined by the “competition” between the propensity score P(Z) and the latent variable U representing unobserved resistance to treatment. Therefore, the propensity score P(Z) and the latent variable U are the only two dimensions along which treatment status may be correlated with treatment effects. The MTE, as in the original formulation of Heckman and Vytlacil (1999, 2001a, 2005, 2007b), is asymmetrical with respect to these two dimensions, as it conditions on the entire vector of observed covariates X as well as the latent variable U. As a result of this asymmetry, the original MTE-based approach has a number of drawbacks, including (1) an exclusive attention (in practice) to unobserved heterogeneity in treatment effects, (2) difficulty of implementation due to unwieldy weight formulas, and (3) inflexibility in the modeling of policy effects (see Section 3.5).
To overcome these limitations, we presented an extension of the MTE framework through a redefinition of MTE. By conditioning on the propensity score P(Z) and the latent variable U, the redefined MTE not only treats observed and unobserved selection symmetrically, but more parsimoniously summarizes all of the treatment effect heterogeneity that is consequential for selection bias. As a bivariate function, it can be easily visualized. As with the original MTE, the redefined MTE can also be used as a building block with which for evaluating aggregate causal effects. Yet the weights associated with the new MTE are simpler, more intuitive, and easier to compute (compare Table 2 with Tables 1 and 3). Finally, the new MTE immediately reveals heterogeneous treatment effects among individuals who are at the margin of treatment, thus allowing us to design more cost-effective policy interventions.
For sure, our extension of the MTE approach is not a panacea. Like the original approach, it hinges on credible estimates of MTE(x, u) in the first place. Identification of MTE(x, u) requires at least a valid IV in the treatment assignment equation. Moreover, under either the parametric or the semiparametric model, the statistical efficiency of estimates of MTE(x, u) depends heavily on the strength of IVs (Zhou and Xie 2016). When the IVs are relatively weak in determining treatment status, MTE-based estimates of aggregate causal effects can be imprecise. Nonetheless, as long as valid instruments are present, more precise estimates can always be brought by a larger sample size.
Acknowledgments
Research reported in this publication was supported by the Eunice Kennedy Shriver National Institute of Child Health & Human Development of the National Institutes of Health under Grant Number R01-HD-074603-01. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The authors benefited from communications with Daniel Almirall, Matthew Blackwell, Jennie Brand, James Heckman, Jeffrey Smith, and Edward Vytlacil.
Appendix A: Identification of under Assumptions 1–3
From assumption 1, we know V ⫫ X. Since U and P(Z) are functions of V and Z respectively, U ⫫ P(Z)|X. Since U follows a standard uniform distribution for each X = x, we also have U ⫫ X. By the rules of conditional independence, we have U ⫫ X|P(Z). Using this fact and the law of total expectation, we can write as
| (19) |
Thus is simply the conditional expectation of MTE(X, u) given P(Z) = p. Given assumption 3, MTE(X, u) can be written as equation (14). Substituting it into (19) yields
Appendix B: Derivation of Equation (17)
To see why equation (17) holds, let us consider the overall PRTE for a given α. Since given P(Z) = p, the size of inducement αλ(p) reflects the share of individuals that are induced into treatment (“compliers”), the overall PRTE is a weighted average of PRTE(p, αλ(p)) with weights αλ(p):
where FP(·) denotes the marginal distribution function of the propensity score. We then define the population-level MPRTE as the limit of PRTEα as α approaches zero. Under some regularity conditions,15 we can take the limit inside the integral
Denoting , we obtain equation (17).
Footnotes
Heckman and Robb (1986) also framed propensity score matching as a special case of control function methods.
In the classic Roy model (Roy 1951), ID = Y1 − Y0. In that case, Z = X and V = −η.
The property that Z affects treatment status only through the propensity score in an additively separable latent index model is called index sufficiency (Heckman and Vytlacil 2005)
An alternative method to identify the MTE nonparametrically is based on separate estimation of and (see Heckman and Vytlacil 2007b; Brinch, Mogstad and Wiswall 2017).
In estimating K(p), we need to impose constraints on β0 and β1 such that K(0) = K(1) = 0. K(0) = 0 is from its definition. .
The maximum likelihood estimation can be easily implemented in R using the sampleSelection package. See Toomet and Henningsen (2008).
Since the treatment assignment model is now a probit model, σV is usually normalized to 1.
More flexible methods, such as generalized additive models and boosted regression trees, can also be used to estimate propensity scores (e.g., McCaffrey, Ridgeway and Morral 2004).
In a companion paper (self-identifying reference), we discuss the regions over which can be nonparametrically identified with and without the assumption of additive separability.
Studies that use compulsory schooling laws, differences in the accessibility of schools, or similar features as instrumental variables also find larger economic returns to college than do least squares estimates (Card 2001). However, this comparison does not reveal how returns to college vary by covariates or the propensity score.
Admittedly, the discussion here provides no more than a theoretical guide to practice. In the real world, designing specific policy instruments to produce a target form of λ(p) can be a challenging task.
Hourly wage in 1991 is defined as an average of deflated (to 1983 constant dollars) non-missing hourly wages reported between 1989 and 1993.
Results based on parametric estimates of MTE(x, u) (equation (11)) are substantively similar.
Although matching and weighting methods are well equipped to estimate ATE, TT, and TUT under the assumption of ignorability, they are seldom used to study treatment effect heterogeneity by individual characteristics.
A sufficient (but not necessary) condition is that is bounded over [0, 1] × [0, 1]. By the mean value theorem, PRTE(p, αλ(p)) can be written as where p* ∈ [p, p + αλ(p)]. Thus PRTE(p, αλ(p)) is also bounded. By the dominated convergence theorem, the limit can be taken inside the integral.
References
- Angrist Joshua D and Pischke Jörn-Steffen. 2008. Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton university press. [Google Scholar]
- Arabmazar Abbas and Schmidt Peter. 1982. “An Investigation of the Robustness of the Tobit Estimator to Non-normality.” Econometrica 50(4):1055–1063. [Google Scholar]
- Attewell Paul and Lavin David. 2007. Passing the Torch: Does Higher Education for the Disadvantaged Pay Off across the Generations? Russell Sage Foundation. [Google Scholar]
- Bjorklund Anders and Moffitt Robert. 1987. “The Estimation of Wage Gains and Welfare Gains in Self-selection.” The Review of Economics and Statistics 69(1):42–49. [Google Scholar]
- Blundell Richard, Dearden Lorraine and Sianesi Barbara. 2005. “Evaluating the Effect of Education on Earnings: Models, Methods and Results from the National Child Development Survey.” Journal of the Royal Statistical Society: Series A (Statistics in Society) 168(3):473–512. [Google Scholar]
- Borjas George J. 1987. “Self-Selection and the Earnings of Immigrants.” The American Economic Review 77(4):531–553. [Google Scholar]
- Bowen William G and Bok Derek. 1998. The Shape of the River. Long-Term Consequences of Considering Race in College and University Admissions ERIC. [Google Scholar]
- Brand Jennie E and Xie Yu. 2010. “Who Benefits Most from College? Evidence for Negative Selection in Heterogeneous Economic Returns to Higher Education.” American Sociological Review 75(2):273–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breen Richard, Choi Seong-soo and Holm Anders. 2015. “Heterogeneous Causal Effects and Sample Selection Bias.” Sociological Science 2:351–369. [Google Scholar]
- Brinch Christian N, Mogstad Magne and Wiswall Matthew. 2017. “Beyond LATE with a Discrete Instrument.” Journal of Political Economy 125(4):985–1039. [Google Scholar]
- Card David. 2001. “Estimating the Return to Schooling: Progress on Some Persistent Econometric Problems.” Econometrica 69(5):1127–1160. [Google Scholar]
- Carneiro Pedro, Heckman James J. and Vytlacil Edward J.. 2010. “Evaluating Marginal Policy Changes and the Average Effect of Treatment for Individuals at the Margin.” Econometrica 78(1):377–394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carneiro Pedro, Heckman James J and Vytlacil Edward J. 2011. “Estimating Marginal Returns to Education.” American Economic Review 101(773):2754–2781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carneiro Pedro and Lee Sokbae. 2009. “Estimating Distributions of Potential Outcomes using Local Instrumental Variables with an Application to Changes in College Enrollment and Wage Inequality.” Journal of Econometrics 149(2):191–208. [Google Scholar]
- Dale Stacy and Krueger Alan B. 2011. Estimating the Return to College Selectivity over the Career Using Administrative Earnings Data. Technical report National Bureau of Economic Research. [Google Scholar]
- Elwert Felix and Winship Christopher. 2010. “Effect Heterogeneity and Bias in Main-effects-only Regression Models.” Heuristics, Probability and Causality: A Tribute to Judea Pearl pp. 327–336. [Google Scholar]
- Fan Jianqing and Gijbels Irene. 1996. Local Polynomial Modelling and Its Applications. Vol. 66 London: Chapman and Hall. [Google Scholar]
- Gamoran Adam and Mare Robert D. 1989. “Secondary School Tracking and Educational Inequality: Compensation, Reinforcement, or Neutrality?” American Journal of Sociology 94(5):1146–1183. [Google Scholar]
- Hahn Jinyong, Todd Petra and Van der Klaauw Wilbert. 2001. “Identification and Estimation of Treatment Effects with a Regression-Discontinuity Design.” Econometrica 69(1):201–209. [Google Scholar]
- Heckman James J. 1978. “Dummy Endogenous Variables in a Simultaneous Equation System.” Econometrica 46(4):931–959. [Google Scholar]
- Heckman James J. 2010. “Building Bridges between Structural and Program Evaluation Approaches to Evaluating Policy.” Journal of Economic literature 48(2):356–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James J. and Vytlacil Edward J.. 1999. “Local Instrumental Variables and Latent Variable Models for Identifying and Bounding Treatment Effects.” Proceedings of the National Academy of Sciences of the United States of America 96(8):4730–4734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James J. and Vytlacil Edward J.. 2001a. “Local Instrumental Variables.” Nonlinear Statistical Modeling: Proceedings of the Thirteenth International Symposium in Economic Theory and Econometrics: Essays in Honor of Takeshi Amemiya. [Google Scholar]
- Heckman James J. and Vytlacil Edward J.. 2001b. “Policy-Relevant Treatment Effects.” American Economic Review 91(2):107–111. [Google Scholar]
- Heckman James J. and Vytlacil Edward J.. 2005. “Structural Equations, Treatment Effects, and Econometric Policy Evaluation.” Econometrica 73(3):669–738. [Google Scholar]
- Heckman James J. and Vytlacil Edward J.. 2007a. Econometric Evaluation of Social Programs, Part I: Causal Models, Structural Models and Econometric Policy Evaluation. In Handbook of Econometrics, ed. Heckman JJ and Leamer EE. Vol. 6 of Handbook of Econometrics Elsevier; chapter 71. [Google Scholar]
- Heckman James J. and Vytlacil Edward J.. 2007b. Econometric Evaluation of Social Programs, Part II: Using the Marginal Treatment Effect to Organize Alternative Econometric Estimators to Evaluate Social Programs, and to Forecast their Effects in New Environments. In Handbook of Econometrics, ed. Heckman JJ and Leamer EE. Vol. 6 of Handbook of Econometrics Elsevier; chapter 71. [Google Scholar]
- Heckman James J, Humphries John Eric and Veramendi Gregory. 2016. “Returns to Education: The Causal Effects of Education on Earnings, Health and Smoking.” Journal of Political Economy. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James J and Robb Richard. 1986. Alternative Methods for Solving the Problem of Selection Bias in Evaluating the Impact of Treatments on Outcomes. In Drawing Inferences from Self-selected Samples. Springer; pp. 63–107. [Google Scholar]
- Heckman James J., Urzua Sergio and Vytlacil Edward J.. 2006. “Understanding Instrumental Variables in Models with Essential Heterogeneity.” The Review of Economics and Statistics 88(3):389–432. [Google Scholar]
- Heckman James J and Hotz V Joseph. 1989. “Choosing among Alternative Nonexperimental Methods for Estimating the Impact of Social Programs: The Case of Manpower Training.” Journal of the American statistical Association 84(408):862–874. [Google Scholar]
- Heckman James and Navarro-Lozano Salvador. 2004. “Using Matching, Instrumental Variables, and Control Functions to Estimate Economic Choice Models.” The Review of Economics and Statistics 86(1):30–57. [Google Scholar]
- Hill Jennifer L. 2011. “Bayesian Nonparametric Modeling for Causal Inference.” Journal of Computational and Graphical Statistics 20(1):217–240. [Google Scholar]
- Holland Paul W. 1986. “Statistics and Causal Inference.” Journal of the American Statistical Association 81(396):945–960. [Google Scholar]
- Hout Michael. 2012. “Social and Economic Returns to College Education in the United States.” Annual Review of Sociology 38:379–400. [Google Scholar]
- Imbens Guido W. and Angrist Joshua D.. 1994. “Identification and Estimation of Local Average Treatment Effects.” Econometrica 62(2):467–475. [Google Scholar]
- Maestas Nicole, Mullen Kathleen J and Strand Alexander. 2013. “Does Disability Insurance Receipt Discourage Work? Using Examiner Assignment to Estimate Causal Effects of SSDI receipt.” The American Economic Review 103(5):1797–1829. [Google Scholar]
- Maurin Eric and McNally Sandra. 2008. “Vive la Révolution! Long-Term Educational Returns of 1968 to the Angry Students.” Journal of Labor Economics 26(1):1–33. [Google Scholar]
- McCaffrey Daniel F, Ridgeway Greg and Morral Andrew R. 2004. “Propensity Score Estimation with Boosted Regression for Evaluating Causal Effects in Observational Studies.” Psychological methods 9(4):403. [DOI] [PubMed] [Google Scholar]
- Moffitt Robert. 2008. “Estimating Marginal Treatment Effects in Heterogeneous Populations.” Annales d’Economie et de Statistique (91/92):239–261. [Google Scholar]
- Quandt Richard E. 1958. “The Estimation of the Parameters of a Linear Regression System Obeying Two Separate Regimes.” Journal of the american statistical association 53(284):873–880. [Google Scholar]
- Quandt Richard E. 1972. “A New Approach to Estimating Switching Regressions.” Journal of the American Statistical Association 67(338):306–310. [Google Scholar]
- Robins James M, Hernan Miguel Angel and Brumback Babette. 2000. “Marginal Structural Models and Causal Inference in Epidemiology.” Epidemiology 11(5):550–560. [DOI] [PubMed] [Google Scholar]
- Robinson Peter M. 1988. “Root-N-consistent Semiparametric Regression.” Econometrica pp. 931–954. [Google Scholar]
- Rosenbaum Paul R and Rubin Donald B. 1983. “The Central Role of the Propensity Score in Observational Studies for Causal Effects.” Biometrika 70(1):41–55. [Google Scholar]
- Roy Andrew Donald. 1951. “Some Thoughts on the Distribution of Earnings.” Oxford Economic Papers 3(2):135–146. [Google Scholar]
- Sakamoto Arthur and Chen Meichu D. 1991. “Inequality and Attainment in a Dual Labor Market.” American Sociological Review 56(3):295–308. [Google Scholar]
- Smock Pamela J, Manning Wendy D and Gupta Sanjiv. 1999. “The Effect of Marriage and Divorce on Women’s Economic Well-being.” American Sociological Review 64(6):794–812. [Google Scholar]
- Stuart Elizabeth A, Cole Stephen R, Bradshaw Catherine P and Leaf Philip J. 2011. “The Use of Propensity Scores to Assess the Generalizability of Results from Randomized Trials.” Journal of the Royal Statistical Society: Series A (Statistics in Society) 174(2):369–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thistlethwaite Donald L and Campbell Donald T. 1960. “Regression-discontinuity Analysis: An Alternative to the Ex Post Facto Experiment.” Journal of Educational Psychology 51(6):309. [Google Scholar]
- Toomet Ott and Henningsen Arne. 2008. “Sample Selection Models in R: Package sampleSelection.” Journal of statistical software 27(7):1–23. [Google Scholar]
- Vytlacil Edward. 2002. “Independence, Monotonicity, and Latent Index Models: An Equivalence Result.” Econometrica 70(1):331–341. [Google Scholar]
- Willis Robert J. and Rosen Sherwin. 1979. “Education and Self-selection.” Journal of Political Economy 87(5):S7–S36. [Google Scholar]
- Winship Chris and Mare Robert D.. 1992. “Models for Sample Selection Bias.” Annual Review of Sociology 18:327–50. [Google Scholar]
- Winship Chris and Morgan Stephen. 1999. “The Estimation of Causal Effects from Observational Data.” Annual Review of Sociology 25:659–706. [Google Scholar]
- Xie Yu. 2013. “Population Heterogeneity and Causal Inference.” Proceedings of the National Academy of Sciences 110(16):6262–6268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie Yu, Brand Jennie and Jann Ben. 2012. “Estimating Heterogeneous Treatment Effects with Observational Data.” Sociological Methodology 42(1):314–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Xiang. 2018. localIV: Estimation of Marginal Treatment Effects using Local Instrumental Variables. R package version 0.1.0, available at the Comprehensive R Archive Network (CRAN). [Google Scholar]
- Zhou Xiang and Xie Yu. 2016. “Propensity Score-based Methods Versus MTE-based Methods in Causal Inference: Identification, Estimation, and Application.” Sociological Methods & Research 45(1):3–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Xiang and Xie Yu. Forthcoming. “Marginal Treatment Effects from A Propensity Score Perspective.” Journal of Political Economy. [DOI] [PMC free article] [PubMed] [Google Scholar]


