High-Resolution Encoder–Decoder Networks for Low-Contrast Medical Image Segmentation

Abstract

Automatic image segmentation is an essential step for many medical image analysis applications, include computer-aided radiation therapy, disease diagnosis, and treatment effect evaluation. One of the major challenges for this task is the blurry nature of medical images (e.g., CT, MR, and microscopic images), which can often result in low-contrast and vanishing boundaries. With the recent advances in convolutional neural networks, vast improvements have been made for image segmentation, mainly based on the skip-connection-linked encoder–decoder deep architectures. However, in many applications (with adjacent targets in blurry images), these models often fail to accurately locate complex boundaries and properly segment tiny isolated parts. In this paper, we aim to provide a method for blurry medical image segmentation and argue that skip connections are not enough to help accurately locate indistinct boundaries. Accordingly, we propose a novel high-resolution multi-scale encoder–decoder network (HMEDN), in which multi-scale dense connections are introduced for the encoder–decoder structure to finely exploit comprehensive semantic information. Besides skip connections, extra deeply supervised high-resolution pathways (comprised of densely connected dilated convolutions) are integrated to collect high-resolution semantic information for accurate boundary localization. These pathways are paired with a difficulty-guided cross-entropy loss function and a contour regression task to enhance the quality of boundary detection. The extensive experiments on a pelvic CT image dataset, a multi-modal brain tumor dataset, and a cell segmentation dataset show the effectiveness of our method for 2D/3D semantic segmentation and 2D instance segmentation, respectively. Our experimental results also show that besides increasing the network complexity, raising the resolution of semantic feature maps can largely affect the overall model performance. For different tasks, finding a balance between these two factors can further improve the performance of the corresponding network.

I. Introduction

MEDICAL image analysis develops methods for solving problems pertaining to medical images and their use for clinical care. Among these methods and applications, automatic image segmentation plays an important role in therapy planning [1], disease diagnose [2]–[4], and pathology learning [5] strategies. For example, in image-guided disease diagnose for brain cancer, accurately segmented masks of sub-components of a brain tumor enables the physicians to estimate the volume of gliomas (of different grade), and then conduct progression monitoring, radiotherapy planning, outcome assessment, and follow-up studies [5].

The primary challenges for medical image segmentation mainly lie in three aspects. For the ease of understanding, pelvic CT images are selected as an example for illustration, similar conditions also exist in many other segmentation tasks, including brain tumor and cell segmentation. (1) Complex boundary interactions: The main target organs of pelvic CT image segmentation are the three adjacent soft tissues, i.e., prostate, bladder, and rectum. Since these organs are adjacent to each other and their shapes and scales can be changed easily and significantly by different amounts of urine or bowel gas inside the organs, the boundary interaction of these organs can be complicated. (2) Large appearance variation: The appearance of main pelvic organs may change dramatically for the cases with or without bowel gas, contrast agents, fiducial markers, and metal implants. (3) Low tissue contrast: CT images, especially those from the pelvic area, have blurry and vanishing boundaries (see Fig. 1). This last challenge poses the most severe problem for image segmentation algorithms, as compared with the natural or MR images, CT images visibly lack rich and stable texture information (especially on soft tissues). The weak or even vanishing edges caused by low- and noisy-contrast acquisition of the image makes the actual boundaries of organs easily contaminated or even partially concealed by a large number of artifacts. As a consequence, a holistic organ can be accidentally split into isolated parts with various sizes and shapes (i.e., shown by the first sample in Fig. 1), while the independent organs can be visually merged as a whole (i.e., shown by the second sample in Fig.1). The remaining clues for the correct location of boundaries can be trivial and vulnerable (see Fig. 1).

Fig. 1.

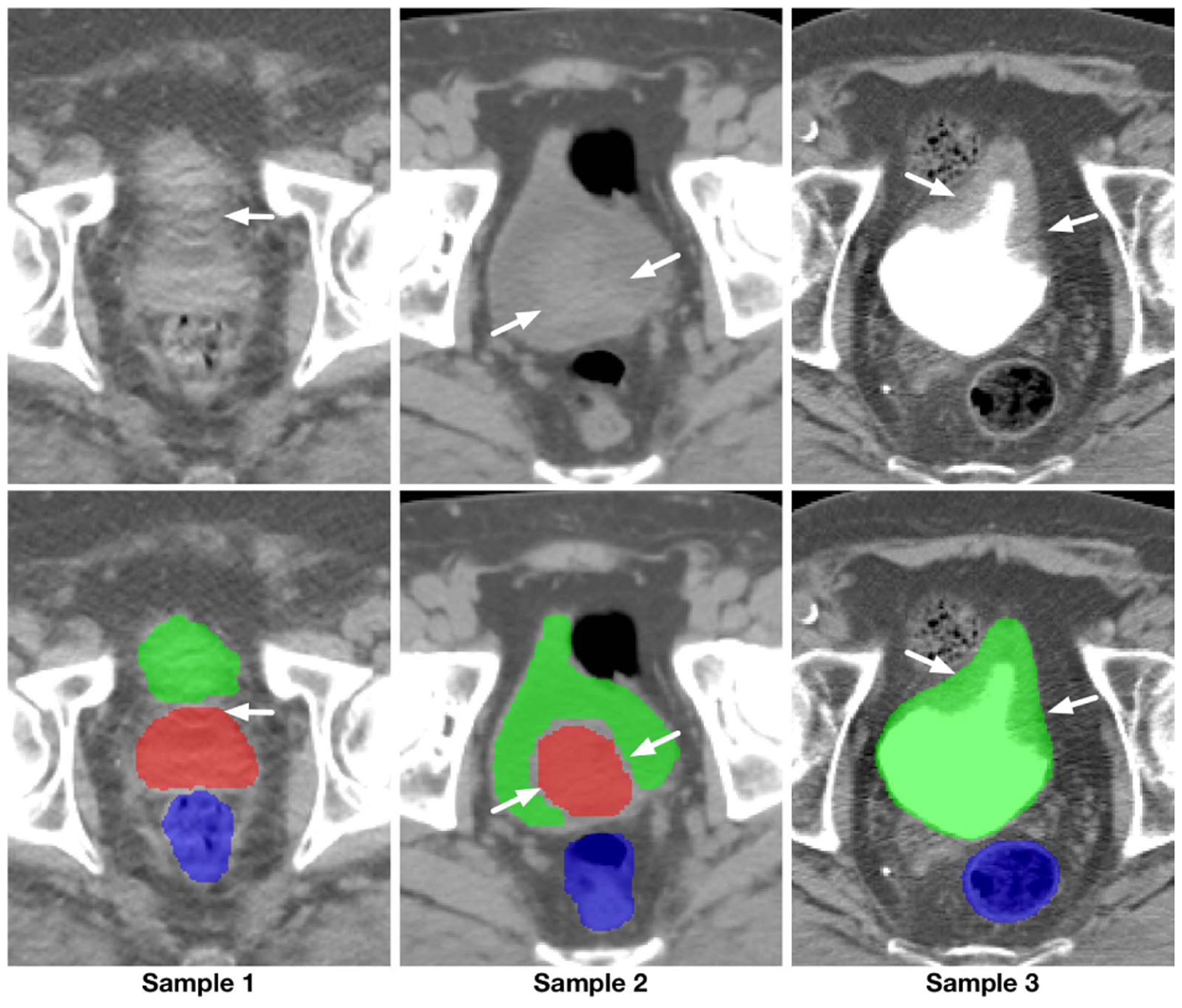
Illustration of the blurry and vanishing boundaries within pelvic CT images. First row: intensity images; Second row: corresponding segmentation ground-truth.

In recent years, considerable improvement has been made to boost the performance of low-contrast medical image segmentation [2], [3], [6] using deep learning-based algorithms. This overwhelming performance gain owes to end-to-end learning mechanisms compared to the traditional shallow learning-based algorithms in many medical image analysis applications [3], [7]–[9]. A common feature in almost all state-of-the-art methods is the encoder-decoder architecture with skip connections. In this structure, downsampling operations together with convolution are utilized to extract robust high-level semantic information, while skip connections are utilized to pass the low-level texture and location information. Although the effectiveness of this structure has been illustrated in many applications, in this paper, we argue that, in the images with blurry or vanishing boundaries, standard encoder-decoder models fail due to two main reasons: (1) Skip connections may fail in preserving the correct location information of blurry boundaries. Different from the high-contrast images, the blurry or missing boundaries resulted by various types of artifacts in medical images make it hard or even impossible for the shallow layers with little context information to delineate the organ boundaries, leaving many nearby fake boundaries (see Sample1 in Fig. 1). (2) In the encoder-decoder pathway, because of the included downsampling operations, important location information is gradually lost to exchange for the invariance property. As a result, the space discriminant capacity of the pathway, which is vital in finding the right boundary among the fake ones, becomes unreliable. To solve this problem, [8], [10], [11] proposed to extract high-resolution semantic information that is accurate in location and rich in contextual information. Although preferable improvement has been achieved, comparing to the encoder-decoder networks, the high memory cost of these models still limits the performance of these algorithms.

In this paper, we propose a novel high-resolution dense encoder-decoder network for low-contrast medical image segmentation. The design of our network is mainly based on the idea of utilizing deeply-supervised high-resolution semantic information to compensate for the deficiency on inaccurate boundary detection of the existing encoder-decoder networks. To this end, we construct our network with three kinds of pathways: 1) skip pathways; 2) high-resolution pathways; and 3) distilling pathways. In these pathways, skip pathway is composed with a simple skip connection, and high-resolution pathway is composed of a series of densely connected dilated convolutional layers, while distilling pathway is composed in an encoder-decoder fashion with dense blocks (see Fig. 2 for more detailed information). In the network, two kinds of semantic information extracted by the high-resolution pathway and the distilling pathway are finely merged to ensure a balance between the location and semantics. By carefully placing the high-resolution pathway in the network, we can achieve better performance with affordable memory consumption. Moreover, to better capture multi-scale structural information and segment possible isolated organ portions with various shapes and sizes, we propose an integrated multi-scale information preservation mechanism. This is done along with a task of contour regression for focusing on accurate localization of the boundaries. Finally, since not all voxels are of equivalent difficulty in segmentation [12], we introduce a difficulty-guided cross-entropy loss to assist the network to pay more attention to the areas with blurry boundaries.

Fig. 2.

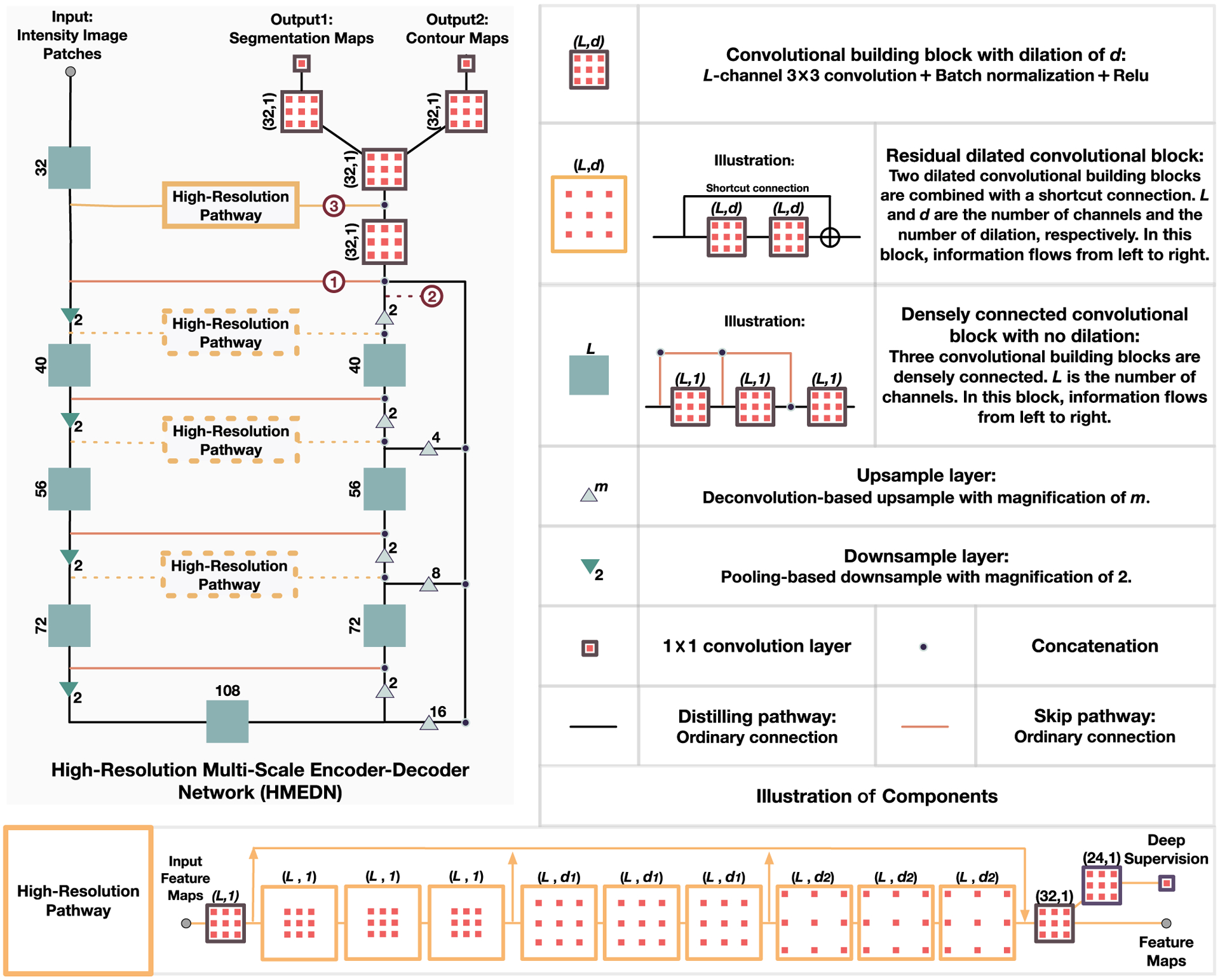
Illustration of the structure of our proposed high-resolution multi-scale encoder-decoder network (HMEDN). The input is a set of intensity image patches and the outputs are segmentation and contour probability maps. Rectangles and triangles represent operations in the network. Three kinds of pathways, i.e., skip connection (pathway ①), distilling pathway (pathway ②) and high-resolution pathway (pathway ②) connect all kinds of operations and form the network.

Contributions.

The main contributions of the paper are three-fold:

1. Through careful analysis and experimental verification, we find an intrinsic problem of the popular encoder-decoder neural networks on low-contrast image segmentation that they lack a mechanism to locate the touching blurry or vanishing boundaries accurately.

2. To solve the problem, a novel high-resolution multi-scale encoder-decoder network (HMEDN) with three different kinds of pathways and a difficulty-aware loss function is introduced. Specifically, in the designed network, the proposed high-resolution pathway is a general plug-in module for encoder-decoder networks to improve performance on low-contrast image segmentation tasks.

3. Extensive experiments on CT, MR and, microscopic image datasets, on both semantic and instance segmentation tasks with 2D and 3D models verify the effectiveness of our proposed network and the high-resolution pathway. Through experiments, we find that the resolution of semantic information is an essential factor to the performance of a segmentation network which has usually been neglected.

II. Related Work

In the literature of deep learning methods for medical image segmentation, two strategies are often incorporated to tackle the problem of low tissue contrast [13]: (1) Introducing shape prior to the segmentation framework as an overall regularization to eliminate unreasonable predictions; (2) Improving the discriminative and reasoning capacity of learned features to allow the network to infer the content at blurry region(s) by checking the surrounding intensity distribution and contour variation tendency.

To implement the first strategy, contour-based methods are combined with deep learning techniques. Specifically, [14] utilized the segmentation results generated by convolutional neural networks (CNN) as initialization, and then fine-tuned the corresponding contours with the level-set and multi-atlas algorithms, respectively. In [15], CNN was used to estimate a reliable vector field that points from a voxel to its closest voxel on the boundary to evolve the Sobolev active contour. In [16], Mo et al. proposed a novel active contour method by modeling the contour delineation problem as finding the limit cycle. In their method, deep learning was utilized to estimate the vector field for a dynamic system. To make full use of the shape information for network training, Tang et al. [17] integrated CNN with a level-set algorithm and trained the whole pipeline iteratively. This setting allowed the output refined by the level-set algorithm to guide the training of CNN, thus allowing the robust shape prior to regularize the training of CNN. To ensure the prediction results to be anatomically meaningful, Oktay et al. [18] modified the convolutional neural network by adding an autoencoder to enforce the prediction of the network to be close to the ground-truth label map in both the original image space and the low dimensional manifold. Recent progress in shape integration using deep learning methods has shown promising results in making the segmentation more robust and reasonable. However, improving these methods also requires enhancing the discriminative capacity of the learned features. This calls for more medical image specific deep learning segmentation methods, which is exactly our goal in this paper.

To improve the representative capacity of the segmentation algorithms, pioneer explorers took advantage of discriminative features learned in an end-to-end manner using patch-based CNNs, outperforming shallower machine learning algorithms with engineered features. For instance, Roth et al. [4] combined and cascaded multiple deep networks to encourage diversity in the extracted semantic information for better segmentation results. Fakhry et al. [19] tailored a deep convolutional network specially for electron microscopy (EM) images by studying the effect of kernel size and also the depth of networks on the segmentation performance. However, segmentation is a dense prediction task, which means each voxel in the image will be given an estimated label. Therefore, the onevoxel-at-a-time predicting manner of patch-based CNN is not only time-consuming but also isolates the highly correlated adjacent voxels, so that the performance of the network is adversely influenced. To overcome the mentioned problems, Long et al. [20] proposed a groundbreaking work, denoted by fully convolutional neural networks (FCN), in which fully connected layers were replaced by multiple upsampling layers to make the size of the network output to be the same as the input. By doing this, both the efficiency and the performance of the networks were largely improved. After FCN, many derivatives have been proposed for medical image analysis. Among these works, Ronneberger et al. [21] designed a skip connection linked symmetric encoder-decoder FCN named U-Net. To further improve the information passing smoothness in U-Net, Drozdzal et al. [22] introduced residual connection [23] into the network. In [24], Chen et al. combined side outputs from multiple levels of FCN to integrate semantic information from different granularity for finer segmentation. Nie et al. [2] integrated three sub-FCNs trained on T1, T2, and fractional anisotropy (FA), respectively, to acquire and fuse complementary information from different modalities for accurate segmentation of infant brain images.

Besides using multiple modalities and adding connections to the network, some researchers also improved segmentation performance by integrating multiple correlated tasks. For example, to improve the segmentation accuracy of the pancreatic cyst, Zhou et al. [25] introduced the segmentation of pancreas, which is simpler but highly correlated with cyst segmentation, as an auxiliary task in a deep supervision fashion to improve the performance on cyst segmentation. In [26], Nogues et al. designed two networks for interior segmentation and contour delineation separately. Then, the results of the two networks are finely combined through structured optimization by boundary neural fields. To further tighten the connection between the two tasks for better results, Chen et al. [3] proposed a network to fuse contour delineation with foreground segmentation in a multi-task learning fashion. To make full use of the learned contour and segmentation results in an end-to-end trained framework for finer fusion of the complementary information, Xu et al. [27] further merged the learned contour and segmentation feature maps with convolution operations. Besides, the combination of convolutional networks with graph models, i.e., conditional random fields (CRF) [28], and Markov random fields (MRF) is also a good way to model the context information [29].

As medical images are often in 3D, many researchers borrowed complementary information from nearby highly correlated slices to estimate the content of the blurry area. However, a better idea is to extend the existing networks into 3D version and enable them to see and learn automatically in the 3D space. Along this direction, 3D U-Net [30] and V-Net [31] are two of the pioneers. After that, many researchers further introduced finer connections, such as residual connections [23], [32], dense connections [33], [34], and deep supervision [35], into the 3D networks to further improve the performance of the networks. On the other hand, some found that 3D CNNs could be too memory costing and computationally intensive, and thus Zhou et al. [25] combined the results of three 2D convolutional networks along three orthogonal directions (axial, sagittal, and coronal directions) as an efficient replacement. In [36], to exploit the intra-slice and inter-slice context, authors introduced the convolutional long short-term memory (CLSTM) [37] into the segmentation pipeline in an end-to-end training manner.

Although the mentioned literature has largely improved the segmentation performance of deep learning algorithms on blurry medical images, the encoder-decoder plus skip connection structure (shared by most of the existing works) limits these networks from accurately locating the boundaries of the target organs. In the following section, we will introduce our solution to this problem in detail, by proposing a novel deep learning framework, denoted as high-resolution multi-scale encoder-decoder network (HMEDN).

III. Method

In this section, we introduce our High-Resolution Multi-Scale Encoder-Decoder Network (HMEDN) for segmentation of low-contrast medical images. Specifically, four strategies are adopted, each discussed in a separate subsection. First, we introduce the distilling network, in which semantic information is carefully distilled and preserved. Then, we elaborate on the high-resolution pathway, which is constructed by densely connected dilated convolution operations for high-resolution semantic information exploitation. Next, we integrate the task of contour regression with the task of organ segmentation for accurate boundary localization. Finally, we force the network to concentrate more on the ambiguous boundary area by designing a difficulty-guided cross-entropy loss function. Fig. 2 illustrates our proposed network.

A. Distilling Network

Our first strategy to segment low-contrast medical image is to provide a more comprehensive multi-scale information collection and fusion mechanism. In general, two structures are usually adopted for multi-scale information preservation in the literature, i.e., U-Net [21] and Holistically-nested Edge Detection (HED) [38]. In the U-Net, multi-scale information is gradually merged by concatenating the upsampled large receptive-field layers with those passed through skip connections with smaller receptive fields (i.e., merging no more than two scales at a time). Comparatively, through fusing the feature maps from multiple scales into the final output at the same time, the HED methods acquire multi-scale information more directly. By doing so, these networks omit the complicated convolution operations in the decoding procedure and bring the multi-scale information together in its original form. To preserve multi-scale information, U-Net gradually integrates and processes the information more delicately, thus making the fusion of the information sufficient, and allows the intermediate results to guide the subsequent fusion. Whereas in the case of HED methods, since all information is processed at the same time, the fusion of multi-scale information can be done more comprehensively.

To take advantage of both types of networks, we inherit the U-Net structure as well as the side outputs of HED networks to construct our network. Moreover, to further encourage smooth information flow between different layers and make the training of the network more manageable, we replace the original plain connections with dense connections initially introduced in [33].

Based on the above intuitions, we propose a densely connected multi-scale encoder-decoder network, to reveal the multi-level structural information comprehensively. This network is denoted by distilling network, due to the use of downsampling layer, which can efficiently enlarge the receptive field and effectively filter the redundant insignificant components. As shown in Fig. 2, the outline of the distilling network (the black pathway, together with the orange skip connections) is a U-Net with four downsampling and four upsampling layers. However, besides the regular skip connections, three extra side channels from intermediate layers with different sizes of receptive fields are also upsampled and merged with the main channel of the network to encourage more comprehensive multi-scale information fusion. Moreover, by linking all the preceding layers to the final layer, we construct dense blocks (i.e., those solid green rectangles in Fig. 2) and use them as the building block to encourage smooth information flow within the network.

B. High-Resolution Pathway

Our second (and main) strategy is to endow the network with a better capacity to extract discriminative high-resolution semantic information. In the task of segmentation, the intuitive tension between what and where has long been realized in [20]. The solution to the problem in the current literature is to combine the coarse layers with fine layers in the encoder-decoder networks by skip connections and allow the networks to make local decisions concerning the global structures. This strategy works well in the high-contrast images with clear and consistent boundaries. However, when it is applied to the images with low contrast, local appearance features extracted by lower layers may fail to refrain from the surrounding hypothetical boundaries and recognize the vanishing boundaries, causing negative effects on the accuracy of these algorithms. Consequently, to achieve accurate boundary localization in blurry images, a mechanism which can provide discriminative high-resolution contextual information is needed. To meet this special demand, the dilated convolution-based pathways are introduced. Given a 2D image X with L channels, the definition of a dilated convolution with kernel w of size 3 is defined as:

$$O_{i,j}:=\sum _{a=0}^2\sum _{b=0}^2\sum _{l=0}^{L-1}{w}_{a,b,l}{\mathcal{X}}_{(i+ad),(j+bd),l},$$ (1)

where d is the dilation factor, O is the output feature map, and (i, j) is the location index in image X. Since this convolution can arbitrarily enlarge the receptive field by tuning the dilation factor d, it can be used to replace the downsample-upsample structure to extract contextual information [8], [10]. This semantic information extraction procedure can deliver two merits to the corresponding network: (1) Because no resolution is lost in the information processing procedure, small and thin objects that can be important for correctly understanding the image are finely preserved. (2) Since no downsampling operation is included, the location information of the generated feature maps can be better conserved.

The building block in these pathways is a residual dilated convolutional block [8]. As shown in Fig. 2 (i.e., the orange squares), it is constructed by two convolution blocks and a shortcut connection. The benefit of this block is two-fold: (1) It improves the training speed and encourages smooth information flow [23]; (2) Combining with the dilated convolutions, skip connections implicitly exploit and fuse information from different scales. Moreover, to further improve the long-term information flow which is weak in the classic dilated residual network [39], we combine dense connection to allow the information from the early stage of the high-resolution pathway to be directly passed to the final layer of the module. This setting also leads to an even finer grain multi-scale information collection of the whole network. After that, to reduce the training difficulties and also to make the pathway discriminative to the true organ (or tissue) boundaries, a deep supervision mechanism is introduced. In our experiments, nine residual dilated convolutional blocks compose the pathway. The first three blocks are with the dilation of 1, the second three with 3, and the last three with 5.

C. Contour Information Integration

In recent studies, neuroscientists have investigated that, in mammal visual system, contour delineation correlates with object segmentation closely [40]. To incorporate these insights to improve the segmentation accuracy, researchers integrate the task of contour detection with the task of segmentation. The advantage of this design is three-fold. (1) It provides extra robust guidance to the task of segmentation. (2) It improves the generalization capacity of the corresponding network. (3) Introducing a task of contour regression can help guide the network to concentrate more on the boundary of organ regions, thus helping overcome the adverse effect of low tissue contrast. In this paper, as shown in Fig. 2, a regression task is added to the end of the network as auxiliary guidance. In the existing studies [3], [27], thanks to the high image contrast, the boundaries are usually clear and stable. As a result, authors in these studies [3], [27] modeled the contour detection as a binary classification problem. However, in our application, due to the blurry nature of images, the voxels near the boundaries are usually highly similar. As a result, it will be more reasonable to model the boundary delineation task as a regression problem, which estimates the probability of each voxel being on the organ boundary.

To extract the contour for training, we first delineate the boundaries of different organs by performing Canny detector [41] on the segmentation ground-truth. Then, on this boundary map, we further exert a Gaussian filter with a bandwidth of δ. In the experiments, we empirically set δ = 2. For other datasets, the setting in landmark heat map generation [42], [43] can be followed (i.e., setting δ from 2 to 3 for good performance). For each voxel v, we generate ${\left\{y_r^v\right\}}_{y_r^v\in Y_r^v}$ as an approximation of the probability map, which describes the certainty of each voxel being on the boundary of an organ. Hence, the regression target is to minimize an Euclidean loss function as defined below:

$${\mathcal{L}}_r\left({\mathcal{O}}_r;\theta \right)=\frac{1}{N}\sum _{o_r\in {\mathcal{O}}_r}{\Vert p\left(o_r\right)-y_r^{o_r}\Vert }^2,$$ (2)

where ${\mathcal{L}}_r$ is the loss of contour regression for the regression feature maps ${\mathcal{O}}_r$, with N voxels and o_r as one of these N voxels, p(o_r) as the probability of o_r being on the boundary. θ represents the network parameters.

D. Difficulty-Guided Cross-Entropy Loss

To balance the frequency of the voxels from different classes, categorical cross-entropy loss is a common choice for multi-class segmentation [2], [3]. Different from the original cross-entropy loss, the categorical version adds a loss weight ν^k for the voxels in the k^th category. This weight is inversely related to the portion of voxels belonging to the k^th category:

$${\mathcal{L}}_c\left({\mathcal{O}}_s;\theta \right)=-\frac{1}{N}\sum _{o_s\in {\mathcal{O}}_s}\sum _{k=1}^K{v}^k{y}_k^{o_s}\text{log}p\left(o_s,y_k^{o_s};\theta \right),$$ (3)

where ${\mathcal{L}}_c$ denotes the categorical cross-entropy loss for the segmentation feature maps ${\mathcal{O}}_s$, with o_s as a voxel in it. K is the number of categories, $y_k^{O_s}\in \left\{0,1\right\}$ denotes whether voxel o_s belongs to the k^th category or not, and p(o_s, $y_k^{O_s}$; θ) denotes the probability of a voxel o_s belonging to the k^th category. This probability is defined by the soft-max over the feature maps of the final convolutional layer.

In a recent work, Li et al. [12] argued that not all voxels are equal and more attention should be paid to the difficult voxels. Inspired by this argument, we propose a difficulty-guided weight map to guide the network and focus more on the ambiguous areas. It is evident that the error of existing networks mainly lies around the borders of both foregrounds and backgrounds. It becomes even larger at the touching boundary of soft tissues. With these observations, we construct the weight map in three steps. (1) We use the Canny operator to calculate the binary boundary image ${\mathcal{B}}_k$ of the category (i.e., organ) k, according to the segmentation ground-truth. (2) We use a Gaussian filter with bandwidth δ₂ to scan each ${\mathcal{B}}_k$ and get the smoothed boundary image $\mathcal{S}{\mathcal{B}}_k$. (3) Finally, all $\mathcal{S}{\mathcal{B}}_k\text{s}$ are summed up and then normalized to construct the final weight map. Hence, the proposed difficulty-guided weight on voxel v will be defined as:

$${\mu }^v={\mu }_0+\sum _{k=1}^K{\mu }_k\cdot \mathcal{S}{\mathcal{B}}_k^v,$$ (4)

where μ₀ is the base weight for all the voxels and μ_k is the importance balancing weight of category k, similar to what is used in Eq. (3). In the experiments, we set μ₀ = 1, and μ₁ = μ₂ = μ₃ = 25 as the ratio of the volume of background to the volume of foreground for prostate, bladder and rectum, respectively. The same strategy is effective for other datasets. For the bandwidth δ₂ of the Gaussian filter, it is set as 8 to achieve a good coverage of the ambiguous boundary regions in all the experiments. In our designed map, we treat the regions of the foreground that are far away from the boundary equally with those from the background. Also, since the area emphasized by different maps could overlap around the touching border, these areas are automatically endowed with the most concentration. Replacing the categorical weight map in Eq. (3) with our proposed difficulty-guided weight map, we propose our loss function ${\mathcal{L}}_s$ for segmentation, which is an improved version compared to ${\mathcal{L}}_c$, as:

$${\mathcal{L}}_s\left({\mathcal{O}}_s;\theta \right)=-\frac{1}{N}\sum _{o_s\in {\mathcal{O}}_s}\sum _{k=1}^K{\mu }^{o_s}{y}_k^{o_s}\text{log}p\left(o_s,y_k^{o_s};\theta \right).$$ (5)

Combining the loss for segmentation and contour regression, our final loss function for network optimization is:

$$\mathcal{L}\left({\mathcal{O}}_s,{\mathcal{O}}_r;\theta \right)={\mathcal{L}}_s\left({\mathcal{O}}_s;\theta \right)+\alpha {\mathcal{L}}_r\left({\mathcal{O}}_r;\theta \right)+\beta \Gamma (\theta ),$$ (6)

where α and β are hyper-parameters used to balance the importance between the terms, and Γ(θ) is the regularization term (the ${\mathcal{l}}_2$ norm of the network parameters). In our experiments, we obtained preferable results by setting α = 1 and regression to be in a comparable magnitude. For β, we followed the suggestion of [44] and set it to a small value as 1×10⁻⁷. Tuning the parameter β improves the performance for 0.5%.

IV. Experiments and Results

In this section, we first showcase the effectiveness of the proposed algorithm on a pelvic CT image dataset, then a multi-modal brain tumor dataset¹ and a microscopic nuclei dataset² are included to demonstrate the generality of our proposed method, especially evaluating the high-resolution pathway. Specially, for the pelvic CT image dataset, considering the large size of pelvic organs, large receptive field on the axial direction is used for accurate segmentation. For computational efficiency, we model the problem as a 2D semantic segmentation problem. For the brain tumor dataset, considering the small tissue size and the diverse structures of the brain tumors, we model the problem as a 3D semantic segmentation problem. Lastly, the nuclei segmentation problem is a typical instance segmentation problem. In the first part of the experiment, we conduct careful ablation studies to verify the effectiveness of each component of the designed network. Then, more experiments are further conducted on the brain tumor and cell segmentation datasets to prove the generalization capacity of the proposed network.

A. Pelvic Organ Segmentation

The evaluation of the proposed method on pelvic CT image dataset starts by comparing the performance of dilated convolutional networks with their encoder-decoder counterparts. Then, we introduce the high-resolution pathway to the encoder-decoder network and test its effectiveness on detecting blurry and vanishing boundaries. Next, we test the effectiveness of the difficulty-guided cross-entropy loss function and the multi-task learning mechanism. After that, we analyze the effectiveness of the main hyper-parameter in our algorithm. Finally, we compare our proposed algorithm with several state-of-the-art medical image segmentation methods.

1). Data Description and Implementation Details:

The dataset used in this experiment is acquired by the North Carolina Cancer Hospital, which includes 339 CT scans from prostate cancer patients. In this task, three important pelvic organs, i.e., prostate, bladder, and rectum are being segmented. For preprocessing, we normalize the images using the common mean and standard deviation. Before experiments, a simple U-Net [21] is first run to extract ROIs for all the compared algorithms, as a rough initial localization. In the experiment, the network patch size is set to 144 × 208 × 5. In each of the extracted patches, five consecutive slices across the axial plane are included as five different channels to introduce space information across slices and to preserve across-slice consistency in the axial direction. In the sampling procedure, we permute the axial slices upside-down to double the number of samples for data augmentation. We randomly divided the data into the training, validation and testing sets with 180, 59 and 100 samples, respectively.

The implementations of all the compared algorithms in this part are based on the Caffe platform [45]. To train the network, we use Xavier method [46] to initialize all the parameters of convolutional layers in the compared networks. To make a fair comparison, we employ the Adam optimization method [47] for all the methods with fixed hyper-parameters. The learning rate (lr) is set to 0.001, and the step size hyper-parameter β₁ is 0.9 and β₂ equal to 0.999 in all cases. The batch size of all compared methods is 10. The models were trained for at least 200,000 iterations until we observed a plateau or over-fitting tendency according to the loss on the validation set. To evaluate the effectiveness of the proposed method extensively, the Dice Similarity Coefficient (DSC) and Symmetric Average Surface Distance (ASD) are reported.

2). Evaluation of Dilated Convolutional Networks:

First, we evaluate the performance of the high-resolution dilated convolutional networks on CT pelvic organ segmentation. To conduct such an evaluation, we design five baseline networks and compare their performances with our method. Among the compared networks, the first three are dilated convolutional networks (see Fig. 3 for an overview of their architecture). Their differences mainly lie in the number of residual dilated convolutional blocks (refer to Fig. 2 for the definition) and the dilation factors (d₁ and d₂). We name these first three networks as DilNet1, DilNet2, and DilNet3 for simplicity. Specifically, DilNet1 and DilNet2 both consist of 9 residual dilated convolutional blocks. Their dilation factors d₁ and d₂ are 3 and 5 for DilNet1, and 2, 4 for DilNet2. DilNet3 has six blocks (without three blocks within the black dotted rectangular in Fig. 3). Its dilation factors d₁ and d₂ are 3 and 5, respectively. The receptive fields of these three networks are 133 × 133, 97 × 97 and 85 × 85, respectively, which are nearly in the receptive filed range of U-Nets [21] with 3 to 4 pooling layers. The fourth and the fifth networks are the distilling networks with four and three pooling layers, respectively. They are designed as representers for encoder-decoder networks, named as Dst-Net1 (Distilling Network 1) and Dst-Net2 (Distilling Network 2), respectively.

Fig. 3.

Illustration of the dilated convolutional network.

All the networks are trained in the same manner as mentioned in Section IV-A.1, with the corresponding DSC and memory consumption listed in Table I. Through experimental results, we can find (1) larger receptive fields and deeper network structures are essential for the performance of both dilated convolutional networks and encoder-decoder networks. (2) The encoder-decoder networks in the experiments tend to provide better performance with smaller memory consumption than the compared dilated networks in CT pelvic organ segmentation. The reasons for its better result may be two-fold. First, the relative plain connection and the smaller number of kernels limit the performance of the dilated convolutional network; Second, without the help of the downsampling operation, dilated convolutional networks are more likely to be adversely affected by the noise in CT images.

TABLE I.

Dice Ratio (%) and Memory Consumption (Mb) Comparison Between Dilated Convolutional Networks and Encoder-Decoder Networks

Network	Prostate	Bladder	Rectum	Memory Consumption
DilNet3	82.2	88.4	81.0	7259
DilNet2	83.4	88.5	81.9	9269
DilNet1	83.5	89.6	83.7	9269
DstNet2	85.4	92.2	85.0	5443
DstNet1	86.2	93.1	84.9	5933

3). Evaluating the Effectiveness of Integrating High-Resolution Pathway:

Although in the last experiment, dilated networks have shown relatively inferior performance than their encoder-decoder competitors, the capacity of providing high-resolution semantic information makes them potentially more suitable than the coarse-grained encoder-decoder networks on accurately localizing the blurry target boundaries, thus improving the segmentation performance. Here, to reveal the limitation of current encoder-decoder networks and show the effectiveness of introducing high-resolution pathways for solving the corresponding problems, we construct and compare two networks. The baseline algorithm is the distilling network (i.e., Dst-Net1) introduced in Section IV-A.2. In the compared network, we add a high-resolution pathway to connect the encoder and decoder at the highest resolution in Dst-Net1, named as high-resolution distilling network (HRDN). The results are listed in Table II. From the results, we can see an approximate 1% improvement in terms of DSC on the two smaller and also more difficult organs with only 0.18M parameters increase. The improvement of ASD on the high-resolution pathway enhanced network is also promising, with 0.143 mm on the prostate and 0.145 mm on the rectum, respectively. The results numerically verify the effectiveness of the high-resolution pathway.

TABLE II.

Result Comparison Between Distilling Network (DstNet1) and High-Resolution Distilling Network (HRDN)

Networks	Prostate	Bladder	Rectum	Param (M)
	DSC(%)
DstNet1	86.2±4.0	93.1±4.5	84.9±5.2	3.2
HRDN	87.5±3.8	93.2±5.5	85.9±5.3	3.38
Networks	Prostate	Bladder	Rectum	Param (M)
	ASD(mm)
DstNet1	1.585±0.437	1.334±0.858	1.543±0.493	3.2
HRDN	1.434±0.425	1.542±2.278	1.395±0.617	3.38

To further exploit the properties of the three kinds of basis pathways, i.e., skip connection, distilling pathway and high-resolution pathway, and then reveal what limitations of the encoder-decoder network have been resolved by the high-resolution pathway intuitively, we visualize and compare some of the salient feature maps generated by the two networks on a representative sample.

First, we illustrate the information conserved by the skip connection and the distilling pathway in Dst-Net1 and that by the high-resolution pathway in HRDN. The exact locations of where the information is collected in the corresponding networks are also marked as ①, ②, and ③ consecutively in Fig. 2. Three representative feature maps with high activation values on the target organs, i.e., prostate, bladder, and rectum, are illustrated and compared in Fig. 4. In this selected sample, as pointed out by the white arrow in the intensity map, due to the effects of artifacts in the CT image, some wavy streaks appear on the three target organs and affect the boundary on the top of the prostate, generating a small visually isolated tissue. Under such circumstance, as can be seen in the activation maps passed by the skip connection (see the first row of Fig. 4), although the skeletons of the organs look more evident since the surrounding small fractions of tissues are filtered, the less obvious but essential texture information is either weakened (e.g., shown in the first and third sub-figures) or strengthened (e.g., shown in the second sub-figure) indistinguishably. As a consequence, with the falsely included tiny texture, the isolated part looks more like a portion of bladder than prostate. Moreover, as little semantic information is contained in this pathway, no organ-specific information is incorporated, leaving the coarse-grained encoder-decoder pathway to select the correct boundary within all these closely located boundary candidates. Considering the feature maps generated by the distilling pathway (the second row of Fig. 4), although the maps are more semantically meaningful, the boundaries of these maps, especially those on the border between bladder and prostate, are inaccurate, since the downsampling operations can undermine the accuracy of location information.

Fig. 4.

Comparison of representative feature maps.

In contrast, since high-resolution semantic information is preserved, the feature maps generated by the high-resolution pathway is more like a combination of the above-mentioned two kinds of feature maps. They contain detailed textural information and yet more semantics. Besides, thanks to the integrated deep supervision mechanism, the hypothetical boundaries are finely weakened or neglected (see the first and second sub-figures of the third row in Fig. 4), making the boundaries in the ambiguous area clear and correct.

Similar with the intermediate activation maps, as can be seen in the final output feature maps and the corresponding prediction maps of the two networks (Fig. 5), due to the falsely located boundary, a large portion at the bottom of the bladder and the top of the prostate is mixed in the distilling network. Comparatively, thanks to the high-resolution pathway, the damaged boundaries are handled more appropriately in HRDN, resulting in a more feasible segmentation.

Fig. 5.

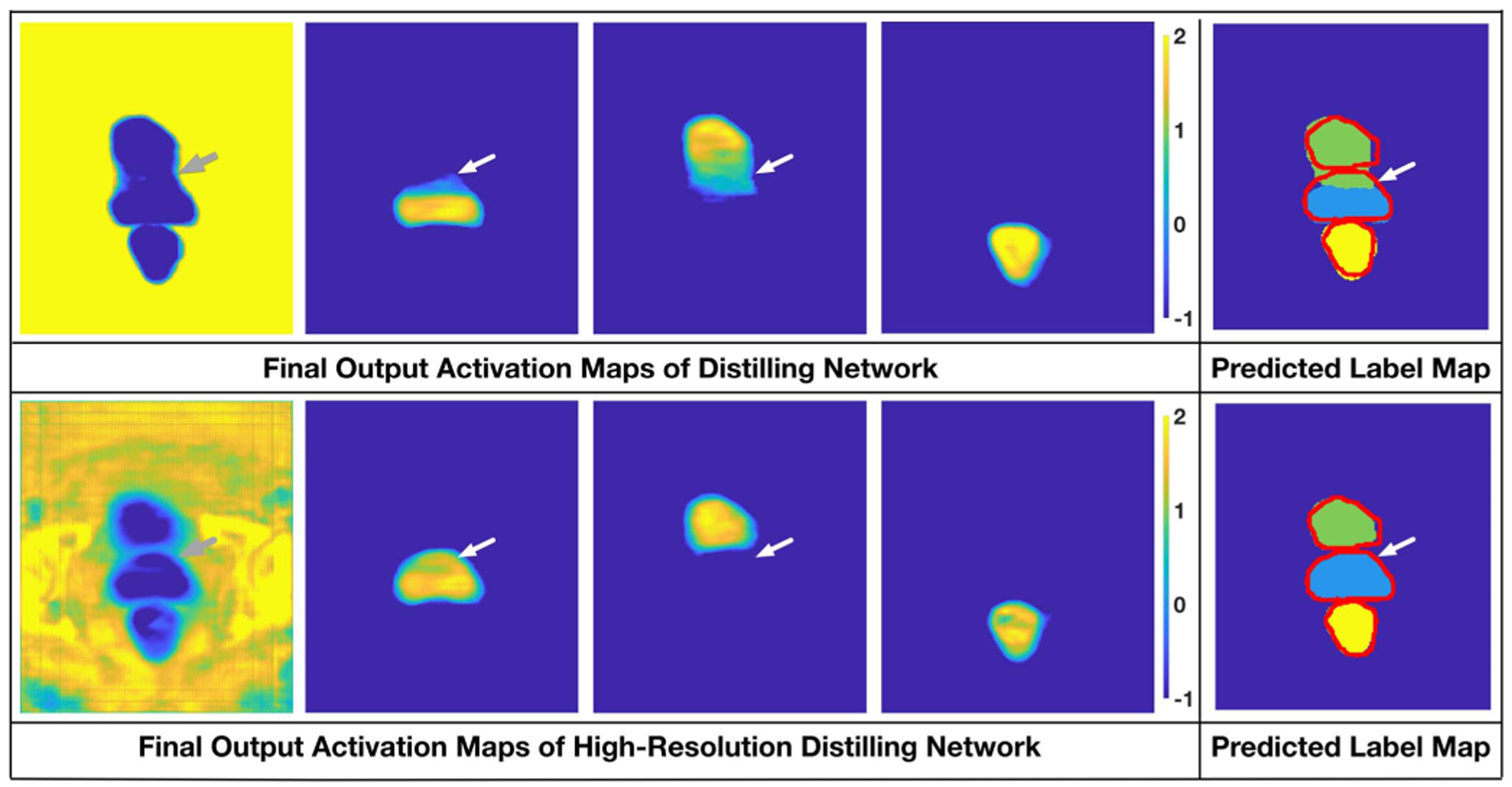
Comparison of the output activation maps of the distilling network and the high-resolution distilling network.

The numerical and qualitative results in this section support our arguments: (1) Simple skip connections can be insufficient to detect the blurry or vanishing boundaries in pelvic CT image segmentation; (2) The downsampling and upsampling operations of the encoder-decoder networks pose potential risks of inaccurate boundary localization and mis-detecting isolated portions of the target; (3) By carefully combining the advantage of the dense connection, residual connection, dilated convolution and deep supervision, the high-resolution pathway can well remedy the limitation of the encoder-decoder network.

4). Balance Between Resolution and Network Complexity:

Although we have shown the effectiveness of introducing high-resolution pathway, considering the large memory cost for convolution operations on high-resolution feature maps, adding the pathway in later stages of the network allows us to use more complex network structure and is also a possible way to improve the network performance. To explore the balance between the network complexity and the resolution of the semantic feature maps, four networks were further designed. In these four networks, the high-resolution pathway is placed on the first stage to the fourth stage of the network, respectively. Here, the first stage indicates the feature extracting stage with no downsampling, the second stage indicates the stage with one downsampling, and so on. The feature number L of the high-resolution pathways is 32, 40, 56, 72, respectively.

In Table III, HRDN-L1 to HRDN-L4 denote the HRDNs with high-resolution pathway on the first stage to the fourth stage, respectively. One can see that tuning the location of the high-resolution pathway does improve the performance of the network, especially on improving the overall segmentation accuracy (reflected by Dice ratio). However, for the pelvic CT image dataset, placing the high-resolution to the third stage provides the best balance between feature resolution and network complexity.

TABLE III.

Testing the Balance Between the Network Complexity and the Resolution of the High-Resolution Pathway. The Boldface Results Indicate no Significant Difference From the Best Result (p-Value < 0.05 of Students t-Test)

Compared Networks	Prostate	Bladder	Rectum
	DSC(%)
HRDN-L1	0.875±0.038	0.932±0.055	0.859±0.053
HRDN-L2	0.875±0.039	0.936±0.047	0.861±0.054
HRDN-L3	0.879±0.039	0.940±0.043	0.868±0.051
HRDN-L4	0.874±0.042	0.936±0.047	0.860±0.060
Compared Networks	Prostate	Bladder	Rectum
	ASD(mm)
HRDN-L1	1.434±0.425	1.542±2.278	1.395±0.617
HRDN-L2	1.438±0.404	1.399±1.600	1.422±0.587
HRDN-L3	1.427±0.483	1.282±1.275	1.397±0.673
HRDN-L4	1.532±0.408	1.362±1.810	1.488±0.745

5). Evaluation of Difficulty-Guided Loss Function and Multi-Task Learning Mechanism:

To evaluate the effectiveness of the difficulty-guided loss function and the multi-task learning mechanism, two networks, including a baseline High-Resolution Distilling Network (HRDN), and a multi-task HRDN with difficulty-guided cross-entropy loss (HMEDN), are designed and tested. The numerical results of these two networks are reported in Table IV. Since the introduced mechanism is mainly proposed to improve the performance on boundary localization, an extra metric, i.e., the Hausdorff Distance [48], which measures the largest distance between two segmentation contours are introduced. As shown in the table, all three metrics, i.e., DSC, ASD, and Hausdorff distance witnessed a stable improvement on all the three organs. Especially on ASD and the Hausdorff distance, which can be easily influenced by the inaccurately located boundaries, the average surface distance of the three organs has been improved by approximately 4%, and 15% on average, respectively.

TABLE IV.

Comparison Between the High-Resolution Distilling Network (HRDN) and the Multi-Task HRDN With Difficulty-Guided Cross Entropy Loss (HMEDN). The Boldface Results Indicate no Significant Difference From the Best Result (p-Value < 0.05 in Student’s t-Test)

Compared Networks	Prostate	Bladder	Rectum
	DSC(%)
HRDN-L3	87.9±3.9	94.0±4.3	86.8±5.1
HMEDN	88.3±4.3	94.4±4.2	87.2±5.5
Compared Networks	Prostate	Bladder	Rectum
	ASD(mm)
HRDN-L3	1.427±0.483	1.282±1.275	1.397±0.673
HMEDN	1.357±0.532	1.175±1.197	1.357±0.796
Compared Networks	Prostate	Bladder	Rectum
	Hausdorff Distance(mm)
HRDN-L3	17.2±21.6	21.6±21.0	20.5±17.0
HMEDN	15.3±20.9	17.5±16.8	17.2±11.1

We also tested the effectiveness of the hyper-parameter α, δ₂, and μ. In this experiment, we tune these parameters in a large range and train the corresponding networks in the same manner. The result is reported in Fig. 6. From the figure, one can see that, although the performance of the proposed algorithm is quite stable in a broad range of the hyper-parameters, tuning these parameters can still boost the performance. The best result is achieved when α = 1, δ₂ = 8, and μ = 25.

Fig. 6.

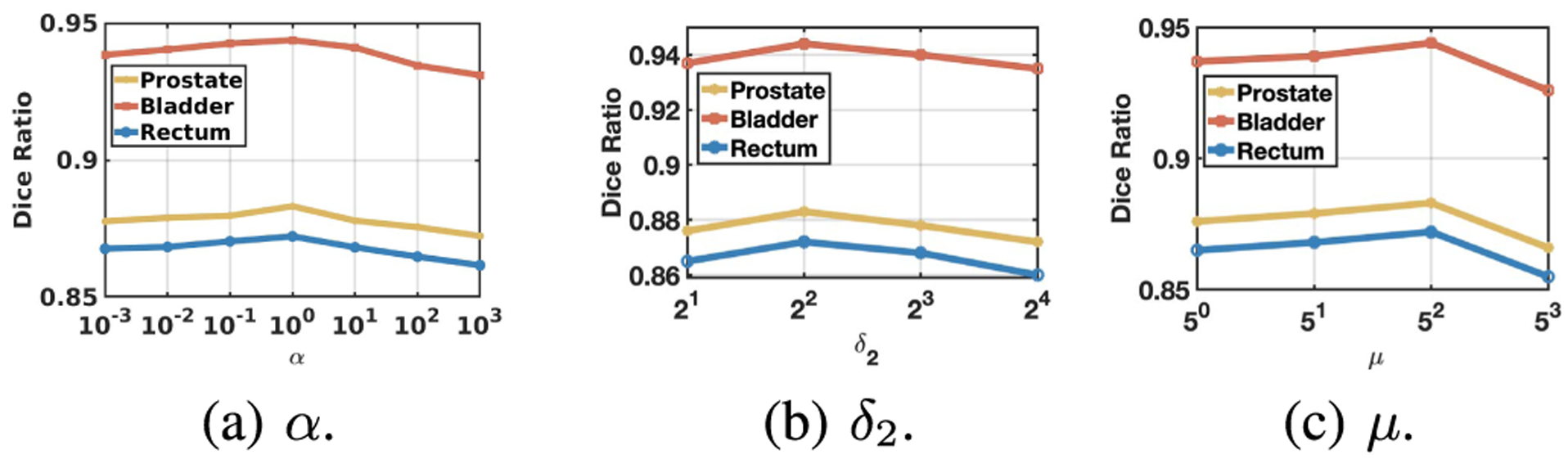
Influence of hyper-parameters. In these figures, the Dice ratio variation against different hyper-parameters are reported. One can see that all the hyper-parameters are effective in improving the performance of the algorithm. Setting α, δ₂, and μ to 1, 8, and 25, respectively, achieves the best performance.

6). Comparing With the State-of-the-Art Methods:

To further evaluate the proposed network, we compared it with several state-of-the-art methods for medical image segmentation. These methods include:

1. U-Net: U-Net [21] is the pioneering work that introduces fully convolutional neural network [20] for medical image analysis. This network achieved the best performance on ISBI 2012 EM challenge dataset [49].

2. FCN: Fully convolutional neural network [20] is the first trial that allows the network directly output a segmentation mask having the same dimension of the input image. The method achieved the state-of-the-art performance on multiple popular benchmark datasets, like PASCAL VOC [50] in 2015.³

3. DCAN: Deep contour-aware neural network [3] has won the 1^st prize in 2015 MICCAI Grand Segmentation Challenge⁴ and 2015 MICCAI Nuclei Segmentation Challenge.⁵

4. 2D DenseSeg: Densely convolutional segmentation neural network [34] introduces dense connections into the HED network to ensure maximum information flow. This method has won the first prize in the 2017 MICCAI grand challenge on 6-month infant brain MRI segmentation.⁶

5. Proposed: Our proposed high-resolution multi-scale encoder-decoder network (HMEDN) is a novel encoder-decoder network enhanced by multi-scale dense connections, high-resolution pathways, difficulty-guided cross-entropy loss function and multi-task learning mechanism.

Table V shows the segmentation results of the compared state-of-the-art methods. To make the final segmentation continuous and smooth, after the segmentation procedure, we conduct an anatomically-constrained merging step for each compared algorithm. This is achieved by absorbing the isolated regions inside the large segmentation targets. In addition, we also discard the tiny isolated regions that reside outside the larger ones. As it is obvious in the results, all algorithms operate similarly well. However, our proposed algorithm still outperforms the second best performance of the state-of-the-art methods by about 1.5 percent in Dice ratio and more than 10 percent in the average surface distance. From Fig. 7, it can be seen that our proposed algorithm tends to not only achieve more accurate segmentation on those easy subjects but also provide more robust results on difficult subjects. More specifically, through the visualization of the segmentation results on two representative samples in Fig. 8, it can be seen that the advantage of our proposed method mainly lies in two perspectives: (1) It can localize the boundary better, especially on those blurry areas; (2) It can better handle the CT artifacts. It is worth noting that hence no deep supervision was involved in DenseSeg [34] and FCN [20] (while DCAN [3] has the deep supervision module, as our algorithm). Therefore, the performance of these two algorithms can be further improved with the deep supervision mechanism.

TABLE V.

DSC and ASD Comparison With the State-of-the-Art Methods on Pelvic CT Image Dataset. The Boldface Results Indicate no Significant Difference From the Best Result (p-Value < 0.05 in Student’s t-Test). The Parameter Number (Param) of Each Network Is Also Reported

Networks	Prostate	Bladder	Rectum	Param (M)
	DSC(%)
U-Net	86.4±5.1	92.4±5.5	85.8±4.9	20.54
FCN	86.5±4.5	93.1±5.3	85.7±5.3	14.72
DCAN	86.7±3.6	92.6±6.8	85.5±5.4	21.06
2D DenseSeg	87.0±4.3	93.0±7.1	85.3±5.5	1.26
Proposed	88.4±4.2	94.5±4.2	87.4±5.4	3.78
Networks	Prostate	Bladder	Rectum	Param (M)
	ASD(mm)
U-Net	1.511±0.465	1.701±1.840	1.451±0.526	20.54
FCN	1.591±0.532	1.588±2.254	1.443±0.578	14.72
DCAN	1.525±0.521	1.357±1.293	1.514±0.747	21.06
2D DenseSeg	1.521±0.536	1.652±2.578	1.721±1.075	1.26
Proposed	1.346±0.531	1.162±1.196	1.332±0.793	3.78

Fig. 7.

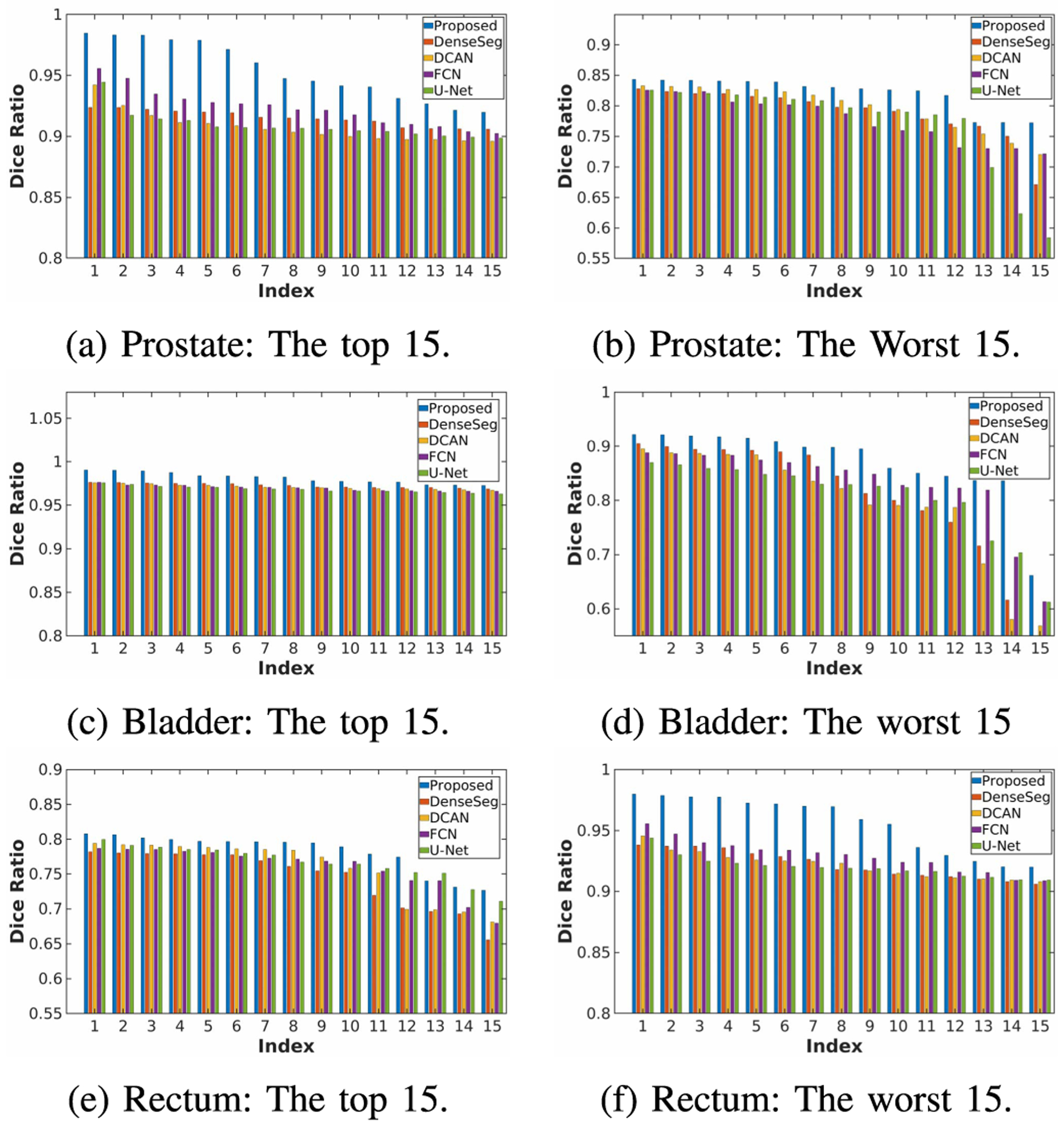
Precision and robustness comparison of the compared algorithms. The sub-figures illustrate the Dice ratio of the 15 best and worst segmented samples of each algorithm.

Fig. 8.

Representative segmentation results of the compared state-of-the-art algorithms on the pelvic CT image dataset. In the first and the fourth rows, the segmentation masks and intensity images in the axial direction are provided. In the second and the fifth rows, the results in the coronal direction are provided. The yellow curves in the segmentation masks indicate the ground-truth contours of the target organs. The third and the sixth rows are the difference map and the segmentation ground-truth in 3D space. The green, red, and blue fragments are the false predictions on prostate, bladder, and rectum, respectively.

B. Experiments on Brain Tumor Segmentation

We also extended our proposed model into a 3D version and evaluated it on a multi-modal brain tumor segmentation dataset [51]. In this dataset, four modalities of MRI scans, including T1, T1-weighted, T2-weighted, and FLAIR volumes were acquired. Experiments on this dataset involve segmenting three regions of interest, i.e., the enhancing tumor (ET), the tumor core (TC), and the whole tumor (WT), See Fig. 9. The highly irregular structure and the tiny isolated tissues of tumors in the brain, together with the low tissue-contrast makes the segmentation task extremely hard. The dataset is comprised of 285 samples. We randomly select 60%, 15% and 25% from the whole dataset for training, validation and testing, respectively.

Fig. 9.

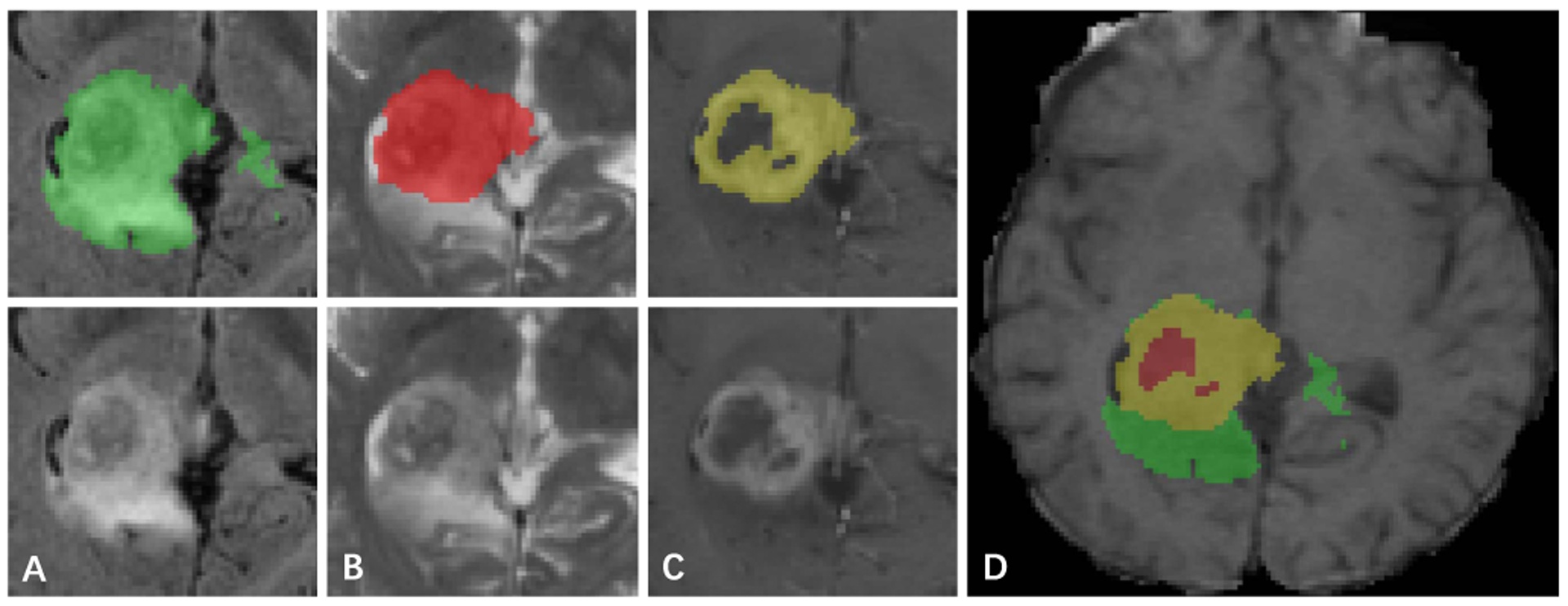
Label and intensity image patches of the brain tumor dataset. The visualized image patches (from left to right) are: (A) the whole tumor in FLAIR, (B) the tumor core in T2, (C) the enhancing tumor structures in T1c, (D) the final labels of the tumor structures (the combination of all segmentations) in T1: edema (green), non-enhancing solid core (red), enhancing core (yellow).

For this 3D version of our method, to make the memory cost affordable, we set the kernel number of each stage in the distilling pathway as 16, 32, 64, 128, 256, respectively. The high-resolution pathway was added to the second and the third stage of the network (with the channel number (L) of 32 and 64, respectively) to find the best balance between semantic resolution and network complexity. Also, to encourage the network to make full use of all four modalities and improve its robustness, dropout was added to the end of each stage of all the compared networks. Moreover, since the structure of the tumors is irregular and highly dispersed, the boundary regression branch was discarded in this task. Four state-of-the-art algorithms, i.e., 3D U-Net [30], Deepmedic [7], 3D DenseSeg [34], and enhanced U-Net (EUNet) [52] are included for comparison. The cropped and resized images that contain only the foreground are utilized for our experiment. Each modality was normalized with z-scores (zero mean and standard deviation of one). The patch size and batch size of Deepmedic were 37 × 37 × 37 and 10 as in [7]. For other compared methods, we adopted the whole brain images with the size of 128 × 128 × 128 as input. One image was utilized for training each time. In this experiment, we followed the training and data augmentation protocol on [53].

Dice ratio and average surface distance of the segmentation are measured for comparison. A visualization of the segmentation is illustrated in Fig. 10. Analyzing at these results, we have several observations: (1) Because of the small and irregular sub-structure of tumors, a finer resolution of semantic information shows to be more preferable. As a consequence, the proposed network with the high-resolution pathway on the second stage outperforms its counterpart, in which the high-resolution is placed in the three stage. (2) The large performance improvement of the other compared algorithms over the baseline 3D U-Net indicates the effectiveness of finer connections, like residual connections [23] and dense connections [33]. (3) Comparing the performance of Deepmedic with the performance of others, we have the observation that algorithms with larger receptive fields tend to have good performance improvement over large targets, like, WT and TC, but this is not necessarily true on small targets, like (ET). (4) The networks with an encoder-decoder network structure, which can carefully integrate semantic information with location information tend to provide better results on smaller targets with smaller size and a complex structure (ET).

Fig. 10.

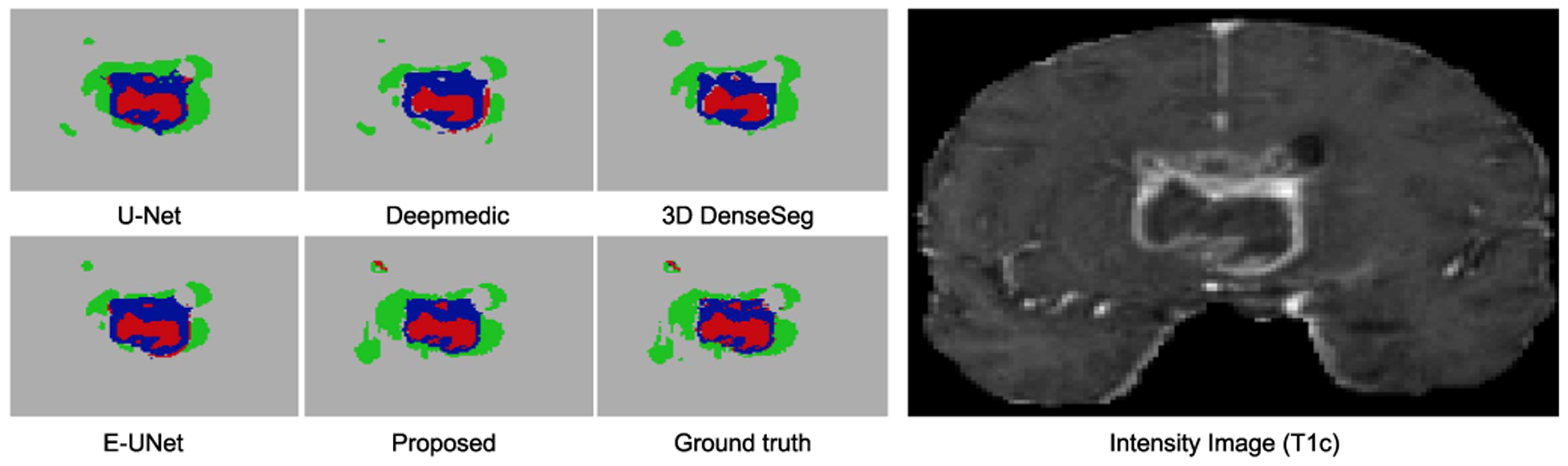
Segmentation results on the brain tumor dataset. In these figures, different colors indicate different tumor categorizations. The T1-weighted image is selected for visualization of the corresponding input images.

C. Experiments on Nuclei Segmentation

Finally, we further integrated the high-resolution pathway with existing popular network structures and tested its performance on a nuclei segmentation dataset to verify the effectiveness of the proposed module. For this task, we segmented different nuclei as independent individuals. Therefore, it is a typical instance segmentation task. However, in this task, the touching nuclei and the highly similar texture of different targets makes the accurate segmentation extremely hard (See sub-figure (g) and (h) in Fig. 11). To solve the problem, we adopted a popular framework [54], which collects the foreground segmentation feature map, boundary feature map and nuclei interior segmentation feature map (generated by a multi-task deep learning network) for a watershed transform algorithm [55] to conduct instance segmentation.

Fig. 11.

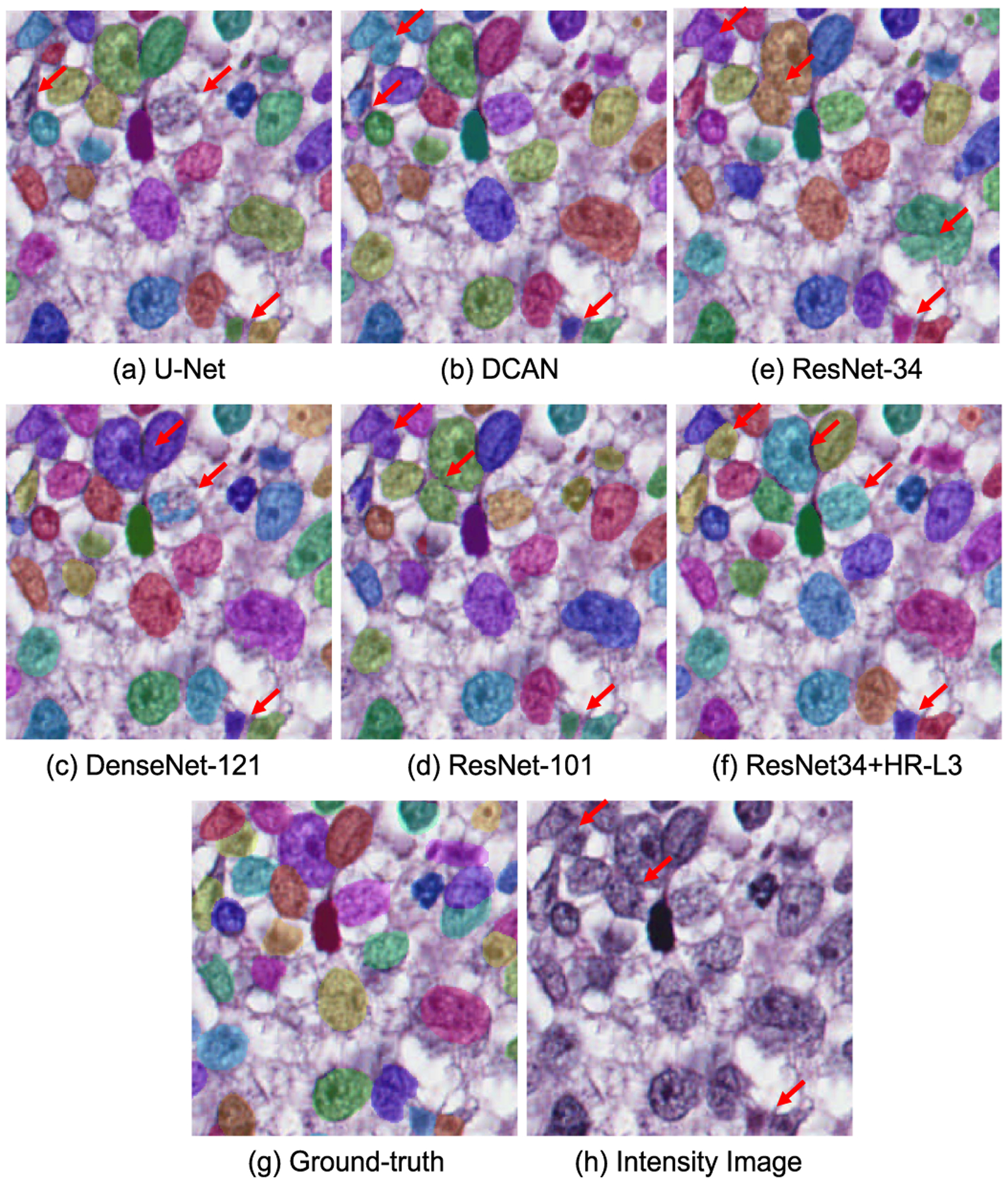
Segmentation results illustration on the nuclei segmentation dataset. In these figures, masks of different colors are corresponding to the segmented nuclei. The red arrows in the figures indicate representative segmentation results and the corresponding intensity map.

In this experiment, we integrated our proposed high-resolution pathway with ResNet-34 as the backbone feature encoder. The high-resolution pathway is placed in the second, third, and fourth stage to find the best balance between the network complexity and the resolution of semantic features. The channel numbers for the high-resolution pathway of the three networks are 128, 256 and 512, respectively. Five state-of-the-art networks, i.e., U-Net [21], DCAN [3], ResNet-34 [23], DenseNet-121 [33], and ResNet-101 [23] are adopted as encoder for comparison. Except for U-Net, all the models are fine-tuned from ImageNet pre-training. The nuclei dataset [54] is comprised of 3627 microscopic images. We randomly divided them into three parts with 2000 samples for training, 627 for validation and 1000 for testing. Heavy data augmentation includes random zooming, cropping, rotation, flipping, channel shifting, elastic transform and adding noise is employed to improve the generalization capacity of the models. We train all models for at least 800 epochs with Adam optimizer [47] until a loss plateau is observed on the validation set.

F1-score, object Dice, and Hausdorff distance of the compared algorithms are reported in Table VII. From the table, we can find that (1) the proposed high-resolution pathway improved the performance of ResNet-34 by 1.8%, 1.3% and 16.6% on F1-score, object dice, and H-distance, respectively in the worst case; (2) The resolution of semantic feature maps did influence the performance of the network. When placed on the fourth stage of the network, the bonus of high-resolution pathway decreased and the corresponding network performed similarly with the ResNet-101 and DenseNet-121; (3) Placing the high-resolution pathway on the third stage of the network achieved the best balance between semantic feature resolution and network complexity. From Fig. 11, we can see that the performance improvement mainly comes from the better detection of fuzzy boundaries of touching nuclei.

TABLE VII.

Result Comparison With the State-of-the-Art Network Structures on the Nuclei Segmentation Dataset. The Boldface Results Indicate no Significant Difference From the Best Result (p-Value < 0.05 in Student’s t-Test). The Parameter Number (Param) of Each Network Is Also Reported

Networks	F1-Score (%)	Object Dice (%)	H-Distance (mm)	Param (M)
U-Net	87.9±13.4	86.8±11.1	6.93±8.73	24.16
DCAN	89.0±12.3	87.3±10.2	6.49±8.83	21.06
ResNet-34	88.5±12.6	87.2±10.5	6.50±7.59	28.03
DenseNet-121	89.9±11.3	88.2±9.7	5.74±7.02	74.90
ResNet-101	90.3±10.3	88.6±8.8	5.53±6.07	96.92
ResNet34+HR-L2	91.2±9.7	89.0±8.6	5.30±7.11	34.96
ResNet34+HR-L3	91.1±10.2	89.1±8.8	5.07±5.88	42.19
ResNet34+HR-L4	90.3±10.9	88.5±9.6	5.42±6.37	67.62

V. Conclusion and Future Work

In this paper, we proposed a high-resolution multi-scale encoder-decoder network (HMEDN) to segment medical images, especially for the challenging cases with blurry and vanishing boundaries caused by low tissue contrast. In this network, three kinds of pathways (i.e., skip connections, distilling pathways, and high-resolution pathways) were integrated to extract meaningful features that capture accurate location and semantic information. Specifically, in the distilling pathway, both U-Net structure and HED structure were utilized to capture comprehensive multi-scale information. In the high-resolution pathway, the densely connected residual dilated blocks were adopted to extract location accurate semantic information for the vague boundary localization. Moreover, to further improve the boundary localization accuracy and the performance of the network on the relatively “hard” regions, we added a contour regression task and a difficulty-guided cross entropy loss to the network. Extensive experiments indicated the superior performance and good generality of our designed network. Through the experiments, we made several observations: (1) Skip connections, which are usually adopted in the encoder-decoder networks, are not enough for detecting the blurry and vanishing boundaries in medical images. (2) Finding a good balance between semantic feature resolution and the network complexity is an important factor for the segmentation performance, especially when small and complicated structures are being segmented in blurry images.

Observing the failed samples of our algorithm, we found that the algorithm fails in cases where the boundaries are totally invisible due to significant amounts of noise incurred by low dose, metal, and motion artifacts, and so forth. To solve these problems, in the future we will combine our algorithm with shape-based segmentation methods and incorporate more robust shape and structural information of target organs.

TABLE VI.

Comparison With the State-of-the-Art Methods on the Brain Tumor Dataset. The Dice Ratio and ASD of the Whole Tumor (WT), Tumor Core (TC) and Enhancing Tumor (ET) Are Reported. The High-Resolution Pathway Was Placed on the Second (Proposed-L2) and the Third Stage (Proposed-L3) to Find a Good Balance Between Semantic Resolution and Network Complexity. The Boldface Results Indicate no Significant Difference From the Best Result (p-Value <0.05 in Student’s t-Test). The Parameter Number (Param) of Each Network Is Also Reported

Networks	WT	TC	ET	Param (M)
	DSC(%)
3D U-Net	84.6±10.4	74.0±20.5	67.7±18.6	6.53
Deepmedic	87.4±6.4	78.8±l5.4	75.4±12.1	2.86
E-UNet	88.5±5.6	80.1±l8.8	77.5±11.3	8.27
3D DenseSeg	88.0±6.7	80.1±l6.6	74.7±15.1	1.26
Proposed-L2	89.7±5.2	83.9±14.4	79.8±10.7	4.39
Proposed-L3	89.0±5.5	82.2±15.0	77.7±13.8	9.64
Networks	WT	TC	ET	Param (M)
	ASD(mm)
3D U-Net	4.261±4.408	7.030±6.775	5.920±6.691	6.53
Deepmedic	1.643±0.624	1.999±l.387	1.069±0.597	2.86
E-UNet	1.467±0.604	1.737±l.621	1.004±0.712	8.27
3D DenseSeg	1.826±1.290	1.799±1.431	1.258±1.168	1.26
Proposed-L2	1.288±0.565	1.481±1.244	0.895±0.582	4.39
Proposed-L3	1.455±0.577	1.676±1.324	0.923±0.563	9.64

Biographies

Sihang Zhou received the bachelor’s degree in information and computing science from the University of Electronic Science and Technology of China (UESTC) in 2012 and the M.S. degree in computer science from the National University of Defense Technology (NUDT), Changsha, China, in 2014, where he is currently pursuing the Ph.D. degree. He was a Visiting Student with The University of North Carolina at Chapel Hill, Chapel Hill, NC, USA. His current research interests include machine learning, pattern recognition, and medical image analysis.

Dong Nie received the B.Eng. degree in computer science from Northeastern University, Shenyang, China, and the M.Sc. degree in computer science from the University of Chinese Academy of Sciences, Beijing, China. He is currently pursuing the Ph.D. degree in computer science with the University of North Carolina at Chapel Hill, Chapel Hill, NC, USA.

His current research interests include image processing, medical image analysis, and natural language processing.

Ehsan Adeli is currently a Researcher and an NIH Fellow with Stanford University, working at the intersection of machine learning, computer vision, computational neuroscience, and medical image analysis with the School of Medicine and the Stanford AI Lab (SAIL). Previously, he was with the University of North Carolina at Chapel Hill and the Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, USA.

Jianping Yin received the Ph.D. degree from the National University of Defense Technology (NUDT), China. He is currently a Distinguished Professor with the Dongguan University of Technology. His research interests include pattern recognition and machine learning. He has published more than 150 peer-reviewed papers, including IEEE T-CSVT, IEEE T-NNLS, PR, AAAI, and IJCAI. He was a recipient of the China National Excellence Doctoral Dissertation’ Supervisor and National Excellence Teacher. He served on the Technical Program Committees of more than 30 international conferences and workshops.

Jun Lian received the B.S. degree in applied physics from Tsinghua University, Beijing, China, and the Ph.D. degree in biomedical engineering from Case Western Reserve University, Cleveland, OH, USA. He is currently a Clinical Associate Professor with the Department of Radiation Oncology, University of North Carolina at Chapel Hill, Chapel Hill, NC, USA. His current research interest includes radiation therapy.

Dinggang Shen (F’18) was a tenure-track Assistant Professor with the University of Pennsylvanian (UPenn) and a Faculty Member with Johns Hopkins University. He is a Jeffrey Houpt Distinguished Investigator and a Professor of radiology with the Biomedical Research Imaging Center (BRIC), Computer Science, and Biomedical Engineering, University of North Carolina at Chapel Hill (UNC-CH). He is currently the Director of the Center for Image Analysis and Informatics, the Image Display, Enhancement, and Analysis (IDEA) Laboratory, the Department of Radiology, and also the Medical Image Analysis Core in the BRIC. He has published more than 1000 papers in international journals and conference proceedings, with H-index 88. His research interests include medical image analysis, computer vision, and pattern recognition. He is a fellow of The American Institute for Medical and Biological Engineering (AIMBE), and The International Association for Pattern Recognition (IAPR). He serves as an editorial board member for eight international journals. He has also served on the Board of Directors, The Medical Image Computing and Computer Assisted Intervention (MICCAI) Society, from 2012 to 2015, and is the General Chair for MICCAI 2019.