Phase precession in the human hippocampus and entorhinal cortex

Summary

Knowing where we are, where we have been, and where we are going is critical to many behaviors, including navigation and memory. One potential neuronal mechanism underlying this ability is phase precession, in which spatially tuned neurons represent sequences of positions by activating at progressively earlier phases of local network theta oscillations. Based on studies in rodents, researchers have hypothesized that phase precession may be a general neural pattern for representing sequential events for learning and memory. By recording human single-neuron activity during spatial navigation, we show that spatially tuned neurons in the human hippocampus and entorhinal cortex exhibit phase precession. Furthermore, beyond the neural representation of locations, we show evidence for phase precession related to specific goal states. Our findings thus extend theta phase precession to humans and suggest that this phenomenon has a broad functional role for the neural representation of both spatial and non-spatial information.

Graphical Abstract

ETOC :

Neurons in the human brain spike in rhythm with local network oscillations to represent spatial position and non-spatial states, highlighting phase procession as a more widespread neuronal mechanism for coordinating spike timing during behavior and cognition.

Introduction

Our brain’s ability to link related experiences is critical to everyday life. One crucial example is spatial navigation, which requires awareness of individual locations and the association between multiple locations, such as those on the same path. Similarly, episodic memory requires the encoding of individual events and associations between sequentially occurring events. Because the hippocampal formation is necessary for spatial cognition and episodic memory (Scoville & Milner, 1957; O’Keefe, 1979; Morris et al., 1982; Burgess et al., 2002), neural activity in this region could underlie our ability to link sequential locations and events. Specifically, one set of theories suggests that the spike timing of hippocampal neurons is critical for learning the associations between events in a sequence (Hebb, 1949; MacKay & McCulloch, 1952; Greenstein et al., 1988; Hopfield, 1995; Markram et al., 1997; Bi & Poo, 2001). Spike timing, in turn, is thought to be coordinated by fluctuations in the large-scale network activity that can be estimated via the local field potential (LFP) (Bragin et al., 1995; Chrobak & Buzsáki, 1998; Manning et al., 2009; Canolty et al., 2010; Zanos et al., 2012; Buzsaki et al., 2012). In this way, a consistent relationship between network oscillations and single-neuron spiking may help to encode sequences and thus play a mechanistic role in complex behaviors or aspects of cognition, such as memory, that rely on relational processing (Siegel et al., 2009; Rutishauser et al., 2010).

Critically, in rodents, neuronal activity in the hippocampal formation exhibits coordination between the LFP and spike timing via phase precession, in which active neurons rhythmically spike in coordination with the local theta frequency (~ 5–10 Hz) oscillation. As such, phase precession may be a potential mechanism for the binding and compressing of sequential events. Phase precession is readily observable in hippocampal place cells (O’Keefe & Recce, 1993) and entorhinal grid cells (Hafting et al., 2005; Reifenstein et al., 2012)—these neurons consistently spike slightly faster than the theta oscillation as the rodent runs through specific locations, resulting in sequences of locations within the field being encoded at different phases of theta oscillations. Consequently, as an animal crosses through consecutive place fields, this phase code ensures that the corresponding sequence of place cells fires in order within a single theta cycle (Skaggs et al., 1996). As such, phase precession may compress spatial trajectories on the scale of behavior into the brief timescale of the theta cycle that is conducive to synaptic plasticity (Lisman & Idiart, 1995; Skaggs et al., 1996; Reifenstein & Kempter, 2020).

In addition to representing space, there is evidence that phase precession’s utility for binding and compressing sequential events may be used by the brain to represent non-spatial features of experience as well. While phase precession is often described in hippocampal place cells or entorhinal grid cells, it has also been observed in a diverse range of brain areas such as ventral striatum (van der Meer & Redish, 2011), subiculum (Kim et al., 2012), basal forebrain (Tingley et al., 2018), and medial prefrontal cortex (Jones & Wilson, 2005). Critically, recent work in rodents has reported phase precession independent of location, encoding elapsed time during REM sleep (Harris et al., 2002), wheel-running (Pastalkova et al., 2008), jumping (Lenck-Santini et al., 2008), fixation (Takahashi et al., 2014), onset of task-relevant stimuli (Aronov et al., 2017; Terada et al., 2017; Robinson et al., 2017) and task context (Tingley et al., 2018). The widespread prevalence of phase precession suggests that this phenomenon has a more general role beyond representing the current spatial location, and that it could be relevant for building neural representations in many regions to support diverse aspects of cognition, learning, and memory.

Many theories suggest a fundamental role for phase precession in neural coding (O’Keefe & Recce, 1993; Burgess et al., 1994; Lisman, 2005; Jaramillo & Kempter, 2017), yet phase precession has almost exclusively been studied in rodents. To examine the prevalence and importance of phase precession in humans, we analyzed simultaneous single-neuron and LFP activity from neurosurgical patients as they performed a virtual spatial memory task and examined the patterns of spike–LFP interaction. Here, we describe spatial phase precession in humans analogous to that observed in navigating rodents. We also describe evidence for phase precession related to the coding of non-spatial variables, in which neurons transiently spike with a rhythm faster than the theta oscillation during trajectories to specific goals. Overall, our findings extend precession to humans and demonstrate its potential use for encoding both spatial and non-spatial features of experience.

Results

Spatial phase precession in hippocampus and entorhinal cortex during navigation.

We analyzed recordings of neuronal spiking from 1,074 neurons in the hippocampus, entorhinal cortex, parahippocampal gyrus, anterior cingulate cortex, orbitofrontal cortex, and amygdala of 13 neurosurgical patients undergoing clinical treatment for drug-resistant epilepsy. During recordings, subjects performed a goal-directed navigation task in a 2D virtual environment on a laptop computer (Jacobs et al., 2010; Miller et al., 2015) (see STAR Methods). The virtual environment contained six goal stores surrounding the perimeter of a square track, with the center of the environment obstructed by buildings. Subjects were able to travel around the track in either clockwise or counterclockwise directions (Fig. 1A).

Figure 1: Virtual environment and hippocampal local-field potential during task.

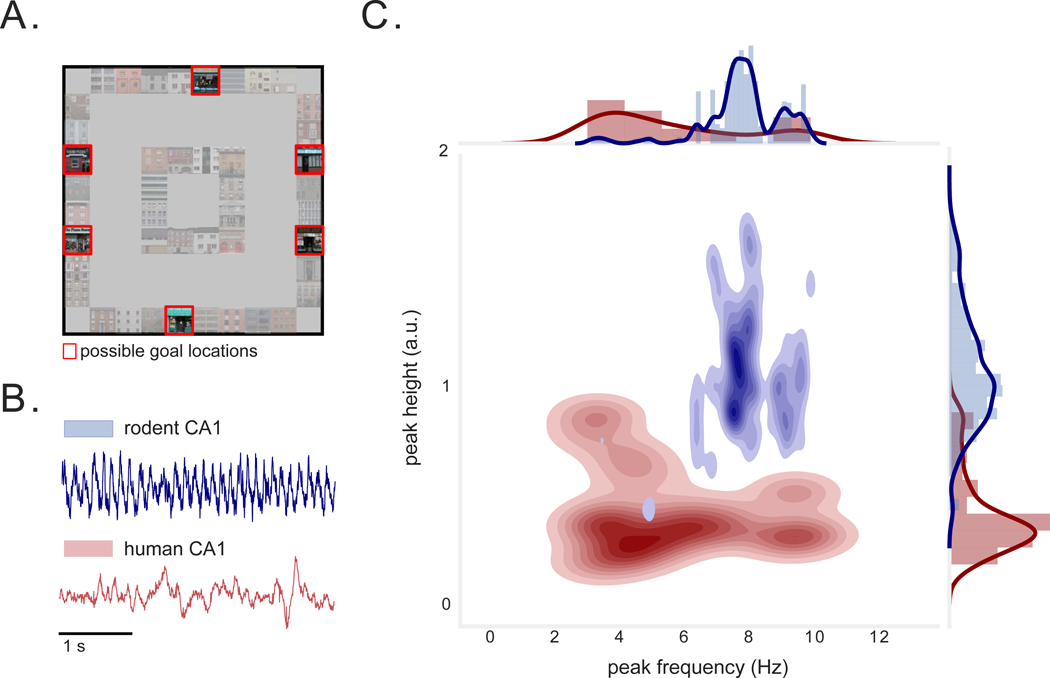
A) Overhead view of task environment. Red squares denote locations of possible goal locations. B) Examples of raw LFP data from rodent (publicly available dataset (Mizuseki et al., 2013)) and human hippocampus. C) Joint distribution depicting the peak frequency and peak height of LFP power spectra (PSD) measured from individual rodent (blue) and human (red) hippocampal electrodes. Different electrodes in the rodent hippocampus exhibit highly stereotyped peaks. Human hippocampal recordings exhibit spectral peaks that are significantly smaller in height, and at significantly lower and broader frequencies (p’s < 4×10⁻⁴). See also Figure S1.

Given our interest in phase coding, we first characterized the prevalence of theta oscillations in the human hippocampus and compared their properties to those seen in rodents, leveraging a publicly-available dataset (Mizuseki et al., 2009a). Compared to rodents, human hippocampal theta spanned a significantly broader range of frequencies (p < 4×10⁻⁴, Levene test), with significantly smaller, lower-frequency peaks in the power spectrum (p’s< 3×10⁻⁸, Wilcoxon rank-sum tests; Figs. 1B–C, S1A). Because human theta appears to span both low and high frequencies (Goyal et al., 2020), and because phase coding may be robust to changes in theta frequencies (Petersen & Buzsáki, 2020), we assessed phase precession with respect to oscillations within a range of LFP theta frequencies (2–10 Hz) (Fig. 1C). Identifying phase precession in this broader range of frequencies would demonstrate that precession might generalize to brain regions and species that exhibit heterogeneous low-frequency signals, in line with recent work identifying phase precession relative to non-rhythmic (2–10 Hz) LFP in bats (Eliav et al., 2018) and shorter theta bouts in humans and non-human primates (Watrous et al., 2013; Jutras et al., 2013; Killian et al., 2012).

To assess phase precession we first identified each neuron whose firing was modulated by the subject’s position in the virtual environment. We labelled the clockwise (CW) and counter-clockwise (CCW) navigation periods and then used a permutation testing procedure to identify 296 spatially modulated neurons that fired significantly more when subjects moved through particular locations in one or both of these directions (Jacobs & Kahana, 2010), after correcting for multiple comparisons (see STAR Methods). Because phase precession in rodents is most predominant near the place-field center (Souza & Tort, 2017) and on short trajectories (Reifenstein et al., 2014), we tested for phase precession during short trajectories through the field center, defined as the peak firing location for each neuron (Fig. 2A–C).

Figure 2: Examples of spatial phase precession in human hippocampus and entorhinal cortex.

A) Schematic illustrating our method for selecting spikes near peak firing bin (see STAR Methods). For each spatially modulated neuron we analyzed phase precession using spikes that occurred early (red), at the midpoint (black), and late (blue) in clockwise (CW) and counter-clockwise (CCW) trajectories through the center of the firing field. Numbers here denote position relative to the center of the field, in virtual units. B) Spike-triggered average (STA) LFP (reconstructed from phase) for early, midpoint, and late trajectory spikes from one neuron. C) Schematic of spike phase as a function of distance from center spike during a trajectory through the field, showing phase precession as a negative progression of phase-by-position. D) Three examples of spatial phase precession. Each row shows an individual neuron. Left: firing rate heat map. Text label indicates average firing rate in peak firing bin, which is noted with an asterisk, as well as spatial information (bits/spike). Brighter colors denote higher firing rates. Dotted lines indicate maximum radius around field in which spiking was assessed. Arrows in the center of the heatmap indicate the navigation direction. Middle: spike phase as a function of location relative to the field center. Spike phases are duplicated vertically to enable visualization of circular-linear regression (red). Rho indicates circular-linear regression coefficient. Right: statistical assessment of circular-linear regression rho using surrogate distribution of circular-linear regression rho values generated by permutation of spike phases. Red line indicates value of real data. Dark gray shading indicates 95^th percentile of surrogate distribution. See also Figure S3.

We observed that some of the spatially tuned neurons showed spiking at progressively earlier phases of the theta oscillation during individual trajectories through their firing field (Figs. 2D, S2A–B). To assess if this was a consistent pattern across trajectories, we leveraged the fact that during phase precession, spikes at later positions in the trajectory should occur at earlier phases, manifesting as a negative correlation between spike-phase and position (O’Keefe & Recce, 1993). In this way, spiking at different phases of the LFP would correspond to different relative positions along the path to a neuron’s firing field center (Fig. 2A–C). We tested for this pattern by measuring the correlation (Kempter et al., 2012) between spike-phase and position using circular statistics (Fisher, 1993) and a shuffle-based permutation procedure (see STAR Methods).

By performing this procedure across all of the identified spatially tuned neurons, we report evidence of phase precession in humans. Figure 2D shows three examples of neurons in the hippocampus and entorhinal cortex whose spiking exhibited significant phase precession during navigation at particular spatial locations (see Fig. S3A–B for additional examples). Each of these neurons increased their firing in a specific region of the environment (Fig. 2D, left). As a person approached the center of that region, the neuron initially spiked at late phases of the 2–10-Hz LFP, but as they continued their trajectory through the center and past it, spikes occurred at progressively earlier phases (Fig. 2D, middle; see also Fig. S3C). This change in spike phases between early positions and late positions is characterized by a significant negative phase–position correlation (Fig. 2D, right).

After testing all spatially tuned neurons in our dataset for phase precession, we found that precession was widespread, with 12% (35/296) of neurons exhibiting this phenomenon (Table S1), which is well above chance (p < 3×10⁻⁶, binomial test; Figs. 3A, S3D). Of these 35 neurons, 22 exhibited uni-directional spatial tuning and precession and 10 exhibited bi-directional spatial tuning and precession. The remaining three neurons exhibited uni-directional precession in one location and bi-directional precession in another. A smaller proportion of neurons (22/296) exhibited a positive correlation between position and phase (Wang et al., 2020) (p = 0.06, binomial test).

Figure 3: Prevalence and characteristics of spatial phase precession in humans.

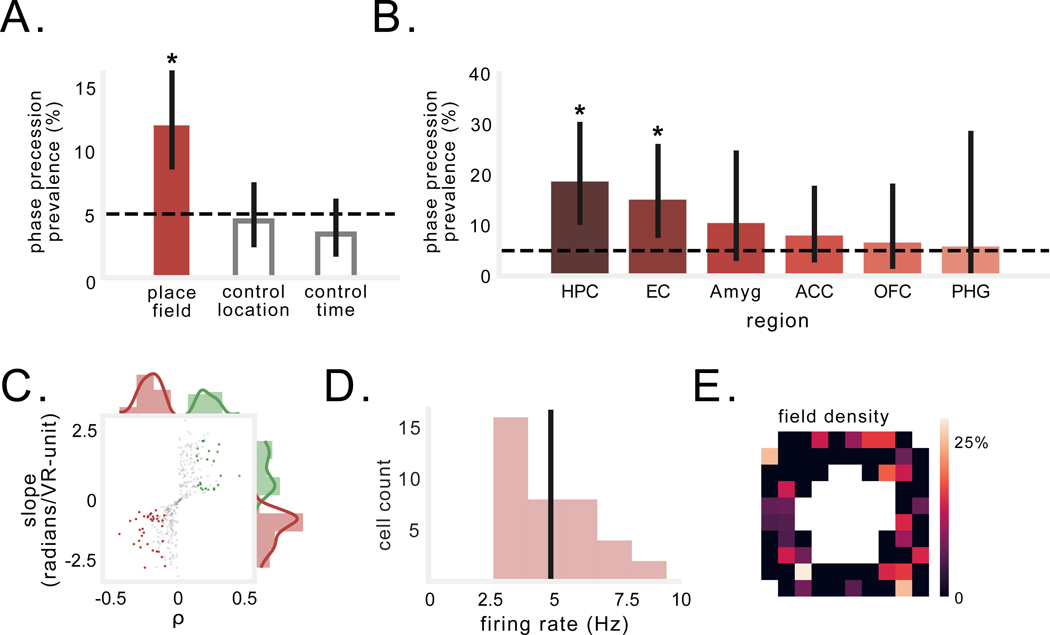
A) Percentage of spatially modulated neurons that exhibit phase precession during trajectories through the firing field (filled bar). Grey bars show control analyses of precession relative to alternative locations, or as a function of time, not position, during spiking episodes (see Fig. S4). Black dotted line denotes chance. Solid black line indicates 95% binomial confidence interval. Asterisk indicates significant proportion of spatially modulated cells exhibiting phase precession during trajectories through the firing field (p < 3×10⁻⁶, binomial test). B) Percentage of spatially modulated cells across regions (HPC=hippocampus, EC=entorhinal cortex, Amyg=amygdala, ACC=anterior cingulate cortex, OFC=orbitofrontal cortex, PHG=parahippocampal gyrus). Asterisk indicates significant proportion of cells exhibit phase precession (ps < 0.002, binomial test). C) Distributions of circular–linear correlation-coefficients between spike-phase and location, and regression slopes for neurons with significant negative (red) and positive (green) correlations. Gray dots denote non-significant correlations. D) Distribution of average firing rate of peak firing bins in which phase precession was observed. Black line denotes the mean of the distribution. E) Prevalence of phase precession across the environment. Colors indicate percentage of firing fields in each bin that exhibited precession.

Notably, we specifically observed significant proportions of spatially modulated cells exhibiting spatial phase precession in the hippocampus and entorhinal cortex (p’s< 0.002, binomial test; Fig. 3B). Phase precessing neurons exhibited an average circular–linear correlation coefficient of ‒0.26±0.09, and an average slope of ‒1.36±0.8 radians/VR-unit (Fig. 3C), suggesting an average phase range of 1.8π radians across the entire field. Phase precessing neurons’ average in-field firing rate was 4.9 ± 1.7 Hz (Fig. 3D), and they had spatial firing fields throughout the environment (Fig. 3E). To test whether spatial phase precession was consistent across an entire behavioral session, we separately computed the phase–position correlation for the first and second halves of the session and found no significant difference in correlation coefficient or slope between halves (p’s > 0.4, paired t-test), with significant negative correlation coefficients in each half when measured individually (p’s < 0.002, one-sample t-tests). We found neurons demonstrating spatial phase precession in all 12 of the subjects with spatially modulated neurons. Overall, these results thus demonstrate the existence of phase precession as a neural code for spatial position in humans during virtual navigation. Specifically, the theta-frequency (2–10 Hz) and regions involved (hippocampus & entorhinal cortex) suggest that this phenomenon in humans is analogous to the phase precession found in rodent place and grid cells.

These analyses specifically tested for phase precession in the location in the virtual environment where the cell was most active. To confirm that precession indicated a spatial phase code relative to these specific locations, we tested two alternative explanations for our results. We assessed whether precession was equally prevalent at randomly selected spatial locations (in which the neuron was sufficiently active), or that precession was actually measuring the advance of spike phase according to elapsed time (see STAR Methods; Fig. S4A, C). Neither alternative model identified significant proportions of phase-precessing cells, and these models resulted in the identification of a smaller number of cells as compared to our primary analyses (χ² = 20.6, p < 4×10⁻⁵, chi-squared test; Fig. 3A; see also Fig. S4B, D). These results indicate that human phase precession occurs more strongly at locations that are associated with elevated firing rates, and that phase precession in spatially tuned neurons during navigation is more closely tied to location than elapsed time. Furthermore, we also found that the position–phase correlation was significantly stronger than the correlations between rate and phase (Huxter et al., 2003; Monaco et al., 2019) (p < 2×10⁻⁸, paired t-test), suggesting that spike phase more strongly encoded position than the instantaneous firing rate (Fig. S3E).

Evidence for phase precession without spatial coding.

While phase precession has been observed most readily relative to specific spatial locations, there is also evidence for precession with respect to non-spatial behaviors and stimuli (Aronov et al., 2017; Harris et al., 2002; Pastalkova et al., 2008; Lenck-Santini et al., 2008; Tingley et al., 2018), and in regions outside the hippocampal formation (Jones & Wilson, 2005; van der Meer & Redish, 2011). These findings suggest that phase precession could be a more general phenomenon that the brain uses to represent diverse types of consecutive, relevant stimuli/states using different frequencies or phases of an oscillation. To examine this possibility, we used a broader analytical method to identify the non-spatially tuned neurons that exhibited phase precession without reference to a specific position. To do this, we measured each neuron’s rhythmic frequency of spiking in comparison to the local theta oscillation (Geisler et al., 2007; Harvey et al., 2009). Identifying a consistent pattern of faster-than-LFP rhythmic spiking would indicate the presence of a precession-like pattern of LFP-coordinated spiking that could bind and compress sequential, non-spatial features of the task—just as spatial phase precession is theorized to do for locations (Bush & Burgess, 2020; Reifenstein & Kempter, 2020).

We identified neurons that showed rhythmic spiking at a frequency faster than the theta oscillation by using a phase-unwrapping method that has identified this pattern both in animals with very stereotyped, 8-Hz theta such as rats (Mizuseki et al., 2009a; Geisler et al., 2010; Kim et al., 2012) and mice (Middleton et al., 2018; Bourboulou et al., 2019), as well as in animals with human-like theta that appears at a range of frequencies, such as bats (Eliav et al., 2018) and non-human primates (Stewart & Fox, 1991; Killian et al., 2012; Jutras et al., 2013). In brief, in this method we first measured the theta phase estimate for each spike from the concurrent 2–10-Hz LFP and “unwrapped” the circular phase time series so that it increased linearly. We then measured the spike-phase spectrum, which we defined as the power spectral density of the time series of unwrapped spike phases (see STAR Methods). In contrast to conventional spectral analysis that measures the frequency of a signal relative to absolute time, the spike–phase spectra reflects the relative frequency of rhythmic spiking compared to the progression of unwrapped phase of the LFP oscillation. If a spike-phase spectra showed a peak at a relative frequency > 1.0 it would indicate that the frequency of a neuron’s rhythmic spiking was faster than that of the concurrent oscillations in the LFP, and thus that the phase of this neuron’s spiking exhibited precession relative to the LFP (Fig. 4A). Importantly, this method ensures that a consistent relationship between the spiking frequency and LFP frequency can be identified even if the LFP shifts in frequency or amplitude, and even though neuronal spike times alone may not show a clear oscillation (Fig. S1B), as is the case in humans and bats (Eliav et al., 2018). We validated this method by applying it to data from rodent CA1 and identifying a consistent > 1.0 relative frequency (Fig. S1C–D), consistent with the spatial phase precession observed in these neurons (Mizuseki et al., 2009a).

Figure 4: Spike-phase spectra reveals precession-like pattern in non-spatially tuned neurons.

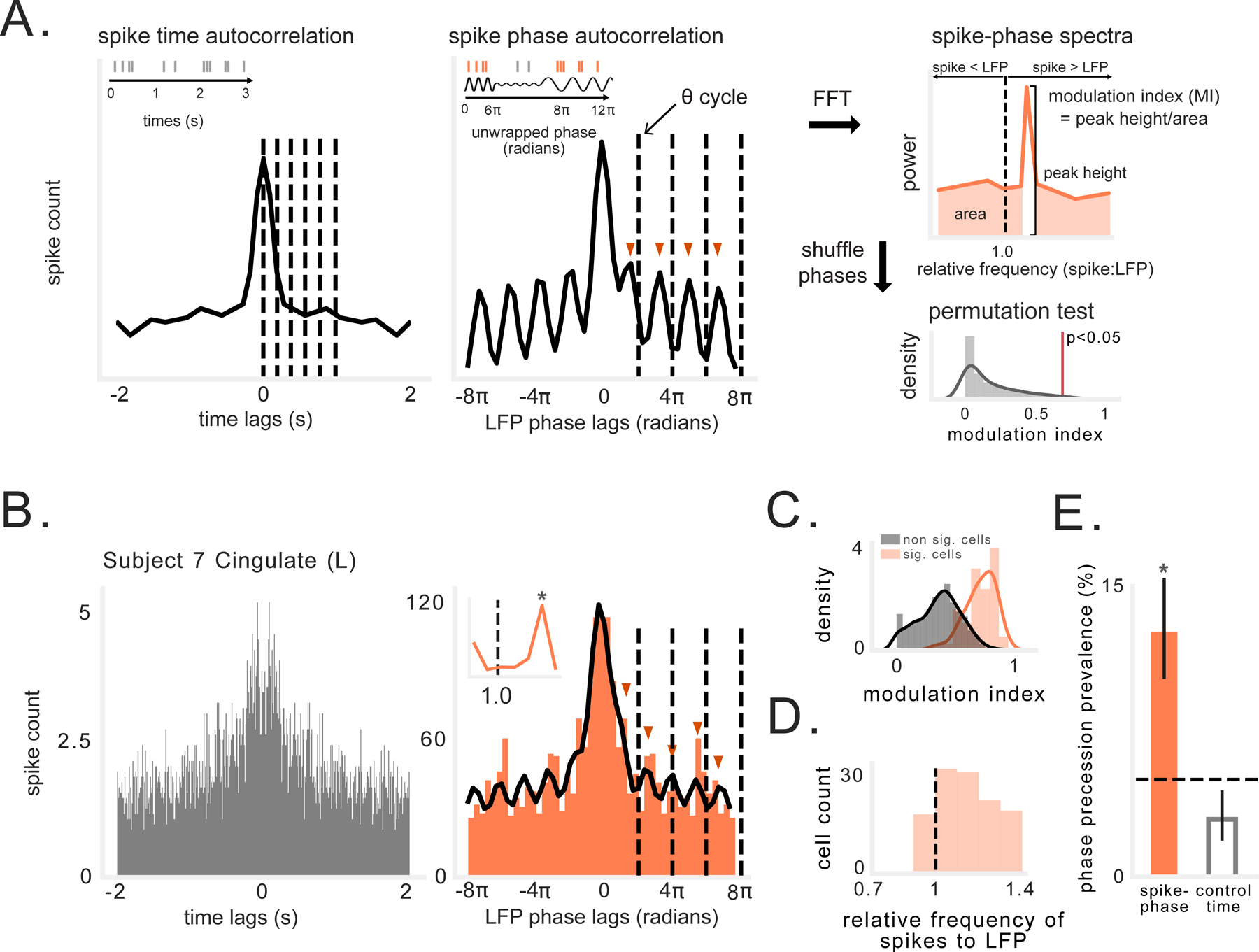
A) Schematic illustrating analysis of rhythmic spiking frequency relative to LFP oscillation (see STAR Methods). Left: Envelope of autocorrelation of spike times (gray), with dotted lines at 200 ms intervals. Middle: Envelope of autocorrelation of unwrapped spike phases, using spikes occurring during the oscillation (orange). Dotted lines indicate one cycle of ongoing LFP in 2–10-Hz band. Red arrows indicate peaks in autocorrelation, which occur progressively earlier than cycles of ongoing LFP. Right: Fourier transform (FFT) of autocorrelation function yields power spectral density(PSD) showing cell spiking frequency relative to ongoing LFP frequency. The spike-phase modulation index (MI) is visualized here as the ratio of the spectral peak height to power at all other relative frequencies. This value is compared to a null distribution of MI values generated by shuffling spike phases in each cycle. B) Left: Spike time autocorrelation showing little evidence of theta modulation, which could not be fit with decaying sine wave function (see STAR Methods). Right: Spike phase autocorrelation (orange) showing cell oscillating slightly faster than ongoing LFP (cycles of 2–10 Hz LFP indicated by dotted line). Black line depicts envelope fit using decaying sine wave function (R² = 0.84). Red arrows indicate peaks in autocorrelation, which occur progressively earlier than cycles of ongoing LFP (and faster than in panel A). Inset shows spike-phase spectra. C) Spike-phase modulation index (MI) of spike-phase spectral peaks for significant vs. non-significant neurons. D) Distribution of relative frequencies for neurons exhibiting significant MI. Values to the right of the black line indicate that the rhythmic spiking frequency slightly exceeded the LFP frequency. E) Percentage of non-spatial cells that exhibit precession-like spiking relative to LFP phase, compared to cell’s exhibiting precession relative to time in a spiking episode. Black dotted line denotes chance level. Solid black line indicates 95% binomial confidence interval. Asterisk indicates significant proportion of cells (p < 7×10⁻¹⁸, binomial test).

To assess whether precession-like rhythmic spiking was evident for non-spatially tuned cells, we used this method to analyze the spiking of the 744 neurons that were active during the task but did not exhibit significant spatial tuning. Figure 4B depicts an example neuron that we identified with this method that showed significant precession. This analysis found that the rhythmicity of this cell’s spiking occurred at a frequency that reliably exceeded the frequency of the LFP (right panel), although no consistent rhythm is apparent from the spike timing alone (left panel). Using this method we found that 20% of non-spatially tuned neurons (146/744) showed a significant relationship between neuronal spiking frequency and LFP frequency (Fig. 4C), with 90 of these neurons showing evidence of precession by having a relative frequency >1.0 (Fig. 4D). Precession-like rhythmic spiking was thus significantly more prevalent than expected by chance (p < 7×10⁻¹⁸, binomial test; Fig. 4E). The set of neurons that showed precession was also larger (χ² = 8.8, p = 0.003) and involved higher mean firing rates (p = 0.04) than the set of cells with a relative spike frequency ≤1.0. None of the 90 neurons exhibiting precession had a mean firing rate exceeding 10 Hz, suggesting that these cells were not theta-modulated interneurons (“theta cells”) (Ranck, 1973).

We performed a control analysis (Fig. S4C) to rule out the possibility that these effects could be explained by the absolute spike timing, though this was unlikely given the relative lack of intrinsic rhythmicity in the spike timing (see Fig. S1B). This analysis confirmed that most of these neurons show phase precession only when spiking is measured relative to the instantaneous ongoing oscillation rather than absolute elapsed time (Petersen & Buzsáki, 2020) (Fig. 4E). These results illustrate how the frequency variability of human hippocampal theta (Goyal et al., 2020) may diminish traditional measures of phase precession, and demonstrate the potential for phase precession in neurons that are not spatially tuned. We next sought to test whether this new non-spatial precession pattern might vary behaviorally in relation to non-spatial, higher-level features of the task, such as prospective goals.

Evidence for phase precession during trajectories to specific goals.

Having shown that non-spatially tuned neurons can exhibit phase precession, we next tested whether this was a tonic pattern (Harvey et al., 2009) or, alternatively, one that emerged selectively to code for specific stimuli or behavioral states. Specifically, recent work has shown that human hippocampal–cortical networks represent goals and their intermediate locations (Brown et al., 2016); furthermore we found previously that this task elicits distinctive patterns of rate- and phase-coding for goals (Watrous et al., 2018). Therefore, we assessed whether phase precession emerged selectively during trajectories to specific goals in service of binding those trajectories for learning and memory.

During each trial of this task, the subject was cued to travel to a randomly selected goal location (Fig. 5A). We found that some neurons specifically showed phase precession only during travel to particular goals. Figure 5B shows an example of a neuron whose spiking shows phase precession during navigation to goal 2, but not the other goals. This effect is evident in the spike–phase autocorrelogram for that goal, which shows that during travel to goal 2 rhythmic spiking occurs at a frequency slightly faster than the ongoing 2–10-Hz LFP. To systematically test for goal-state phase precession, we measured the spike–phase spectrum during trajectories to each goal and compared these spectra between goals, using a permutation procedure and correcting for multiple comparisons across goals (Fig. 5C, see STAR Methods). Figure 5D depicts two example neurons that show this pattern, from the cingulate and amygdala of two different subjects (see Fig. S5 for additional examples). These neurons exhibited rhythmic spiking at faster frequencies than the ongoing LFP while the subjects were en route to specific goals. Critically, this rhythmic spiking was goal-specific and did not appear during trajectories to other goals. These patterns were thus examples of phase precession for a particular goal-state, similar to phase precession in a place field.

Figure 5: Goal-state phase precession.

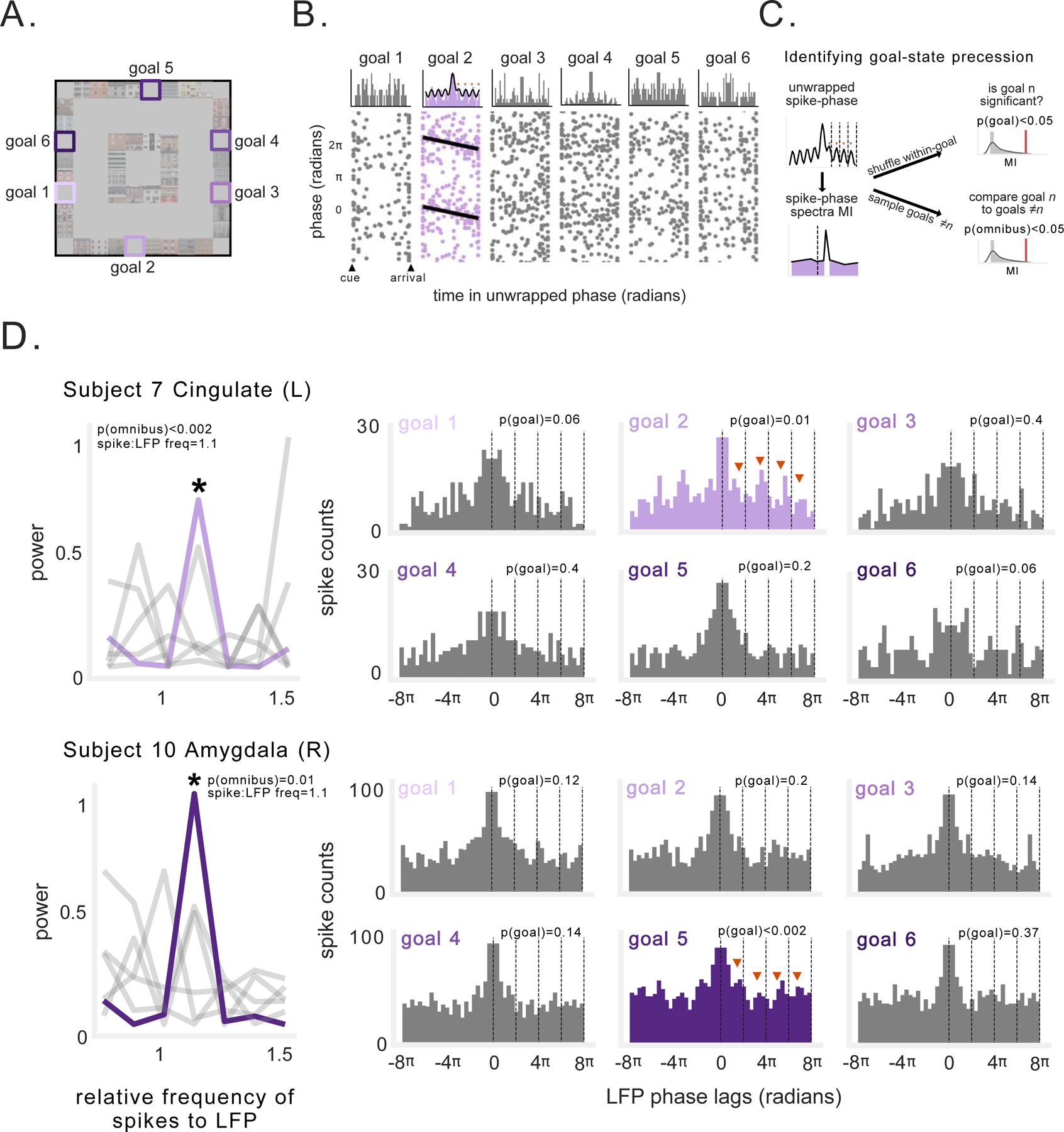
A) Schematic of task environment. Labels indicate goal locations. B) Spike-phases during navigation to different goals for example neuron. Top: unwrapped spike-phase autocorrelograms for each goal. Black line indicates fit of decaying-sine wave function. Spiking frequency transiently exceeded LFP frequency only during navigation to goal 2. Bottom: Spike-phase as a function of duration within each goal epoch. Black line indicates circular-linear regression fit. C) Schematic of method for assessing goal-state phase precession. If a neuron exhibited a significant spike-phase spectral peak at relative frequency exceeding 1 (following multiple comparisons correction), and this effect was significantly stronger than that observed during trajectories to other goals, then this neuron was classified as exhibiting goal-state precession (see STAR Methods). D) Example neurons exhibiting phase precession during navigation to specific goals. Left: Spike-phase spectra depicting frequency of neuronal spiking relative to ongoing LFP. Asterisk denotes spectral peaks that were significant and significantly different from other spike-phase spectra for other goals. Gray lines denote non-significant goals. Right: Spike-phase autocorelograms during navigation to each goal (significant goal epochs depicted in color). Text indicates the p-value for significance tests described in C). See also Figure S5.

We applied this method to the 448 neurons that were sufficiently active during each goal. We excluded spatially tuned neurons, to ensure that spatial phase precession did not confound the analysis. We found a population of neurons exhibiting a significant pattern of faster-than-LFP rhythmic spiking during trajectories to at least one goal (Fig. 6A), across a range of relative frequencies (Fig. 6B). Overall, 11% of the neurons we analyzed (49/448) exhibited significant goal-state precession (Table S2), with at least one neuron exhibiting goal-state phase precession in 10/13 subjects. We examined the specificity of goal-state precession, and found that a majority of these neurons only exhibited significant precession during trajectories to one goal (Fig. 6C); furthermore, other patterns of rhythmic spiking (equal to or slower than theta frequency) were also absent during trajectories to other goals. Next, we found that only 4/49 neurons exhibiting goal-state precession showed consistent spike-phases across the start or end of goal trajectories (as in Fig. 5B), suggesting that the spike–LFP frequency difference may be more important for encoding information than specific phases. Goal-state phase precession was present at significant levels in anterior cingulate, orbitofrontal cortex, amygdala, and hippocampus, but not parahippocampal gyrus or entorhinal cortex (p’s < 0.02, binomial test; Fig. 6D).

Figure 6: Prevalence and characteristics of goal-state phase precession in neurons that are not spatially tuned.

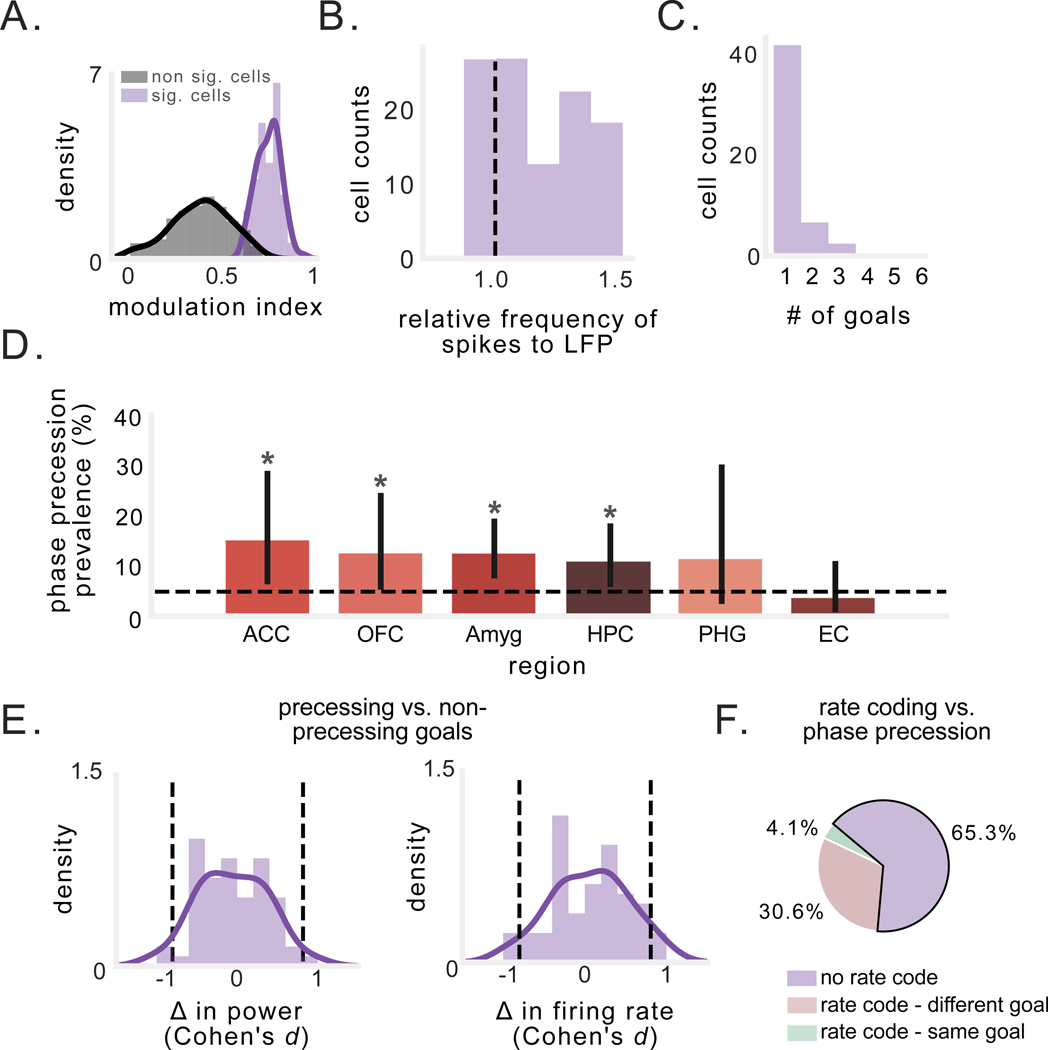
A) Spike-phase modulation index (MI) of spike-phase spectral peaks for significant vs. non-significant goals. B) Peak spike-phase PSD frequency for all goals for which a neuron exhibited a significant MI in the spike-phase spectra. Values to the right of the black line indicate that the neuronal frequency slightly exceeded the LFP frequency, indicating precession. C) Number of goals per neuron for which precession was observed. Most neurons exhibited precession during only one goal. D) Percentage of non-spatial cells in each region that exhibited goal-state phase precession. Asterisks indicate significant proportion of cells (p’s < 0.02, binomial test). E) Distribution of Cohen’s d for the difference in 2–10-Hz power (left) and firing rate (right) between trajectories to goals showing precession vs. those that did not. Black dotted lines indicate effect size of ±0.8. F) Analysis of overlap between goal-state phase precession and rate coding for goals.

To confirm that goal-state precession was stable across an entire behavioral session, we computed the correlation between the goal-specific spike–phase spectra for the first and second halves of the session and found they were significantly positively correlated (ρ = 0.36±0.4; Fig. S6A; p = 0.0001, t-test). We also performed a series of control analyses to test the possibility that our observation of precession for specific goal states was confounded by between-goal differences in LFP power or neuronal firing rate (Fig. 6E). Indeed, neither example neuron in Figure 5 exhibited increased firing rates during goals that showed precession, which suggests that goal-state precession was independent of goal-specific firing rate increases (Watrous et al., 2018). Neurons exhibiting goal-state precession had lower mean firing rates than those that exhibited spatial phase precession (p < 3×10⁻⁴). Furthermore, only 17 of the 49 neurons that showed goal-state precession also showed increased goal-specific firing rate increases (ps < 0.05, one-way ANOVA), and only 2 of 17 of these neurons showed precession and a firing rate increase for the same goal (Robinson et al., 2017) (Fig. 6F). Next, we tested whether subject performance on different goals might be responsible for our results, i.e., whether precession might occur when subjects perform more efficient navigation. However, we measured subject’s performance on each goal (see STAR Methods) and found no significant difference in navigational performance between goals that elicited precession and those that did not (Fig. S6B–C).

We considered the possibility that a neuron might show goal-state precession if that neuron had a place field that only emerged during trajectories to the goal in question. Spatial phase precession through that field might explain any observation of goal-state precession. Therefore we analyzed whether the neurons that showed goal state precession also showed spatial tuning specifically on trajectories to that same goal. We found that this was only the case for 6/49 cells, suggesting that spatial phase precession could not generally explain our finding of goal-related precession. Furthermore, goal-state precession did not differ in strength depending on whether subjects were near or far from goals (p = 0.37, paired t-test), demonstrating that this effect was fairly consistent throughout navigation to the goal. Therefore, it is likely that goal-state precession represents a distinct neural process from spatial phase precession. Overall, because differences in theta power, firing rate, and behavior did not account for our results, our findings indicate that non-spatial phase precession selectively occurs during trajectories to specific goals and may also support the representation of non-spatial, sequential features of behavior.

Discussion

Understanding the nature of the neural code is a fundamental challenge in neuroscience. Our findings show that neurons in the human brain spike in rhythm with local network oscillations to represent spatial position and non-spatial states, in addition to the well-established code based on firing rate. Specifically, we demonstrate the presence of phase precession in humans performing a virtual spatial memory task. We provide evidence for rodent-like spatial phase precession in human hippocampus and entorhinal cortex, in which spatially tuned neurons spike at earlier phases of theta (2–10 Hz) LFP oscillations as subjects moved through the putative place field center. We also provide evidence for the existence of non-spatial, goal-state phase precession, which occurs transiently during trajectories to specific goals. These findings thus extend phase precession beyond rodents, and beyond spatial location, highlighting its potential as a more widespread neuronal mechanism for coordinating spike timing during behavior and cognition.

The spatial phase precession we observed bears important similarities to phase precession in rodents. We found spatial phase precession most predominantly in hippocampus and entorhinal cortex, where place and grid cells, respectively, are canonically found (O’Keefe, 1979; Hafting et al., 2005; Ekstrom et al., 2003; Jacobs et al., 2013). This suggests that the spatial phase precession we observed may be driven primarily by place and grid cells, as it is in rodents, though it is possible that our findings of precession were also associated with neurons with more complex spatial firing fields compared to place or grid cells (Hargreaves et al., 2005; Deshmukh & Knierim, 2011). One key difference between these results and those in rodents is that some spatially tuned neurons in our dataset exhibited activity outside of the firing field, unlike the activity of many rodent place cells where out-of-field spiking is less frequent. This difference in spatial specificity might explain why the tuning of human phase precession is weaker than that observed in many rodent studies, and might be due to difference in ethology or physiology between species. Alternatively, a different possible explanation for certain aspects of our results is that phase precession may simply be less precise or prevalent in virtual reality environments (Aghajan et al., 2014). There are also other distinctive features of our results. Notably we found near-significant proportions of positive phase-position correlations (or “procession”), which had very recently been described in rodents (Wang et al., 2020). Finally, human theta oscillations often appear at a slower and broader range of frequencies compared to those seen in rodents (Jacobs, 2014; Watrous et al., 2013; Goyal et al., 2020), which may explain why phase precession in humans was not previously observed. For this reason, we specifically assessed phase precession relative to the broader range of theta frequency (2–10 Hz) fluctuations of the LFP, in line with the recent discoveries of phase precession in bats (Eliav et al., 2018) and marmosets (Courellis et al., 2019) — two animals with similarly heterogeneous low-frequency field potentials. As a result of these differences in the properties of phase precession between species, it will be important for future studies to determine whether phase precession plays a different functional role in humans than in rodents.

Our discovery of spatial phase precession bears a potentially interesting relationship to the precession observed relative to non-rhythmic fluctuations in bats (Eliav et al., 2018). While many of the electrodes included in this study exhibited (small) spectral peaks, it is possible that non-rhythmic fluctuations in the 2–10-Hz band contributed to the phase estimates in particular epochs, suggesting that human precession shares features with the forms of precession observed in both rodents (relative to oscillatory theta) and bats (relative to non-rhythmic fluctuations). This might hold important mechanistic implications, as only certain models of phase precession are compatible with a non-rhythmic excitatory drive to spatially tuned neurons (Mehta et al., 2002; Eliav et al., 2018). In fact, high-amplitude theta rhythmicity may not be necessary for phase precession at all; recent work in rodents has demonstrated that the theta phase code remains consistent even as theta frequency is altered (Petersen & Buzsáki, 2020). Similarly, rodents continue to show phase precession even when LFP theta power and theta-modulated spiking are reduced (Royer et al., 2010; van der Meer & Redish, 2011; Schlesiger et al., 2015), and recent evidence has emerged in rodents of slower oscillations like those included in this work (<4-Hz), which may exhibit phase precession (Safaryan & Mehta, 2020; Schultheiss et al., 2020). It is thus likely that the spatial phase precession we observed shares features with the precession observed both in rodents and in bats, despite differences in theta range and rhythmicity. Future experiments carefully manipulating theta power and frequency in rodents while measuring phase precession may be able to further link the precession observed here, and in bats, with that observed in rodents.

Phase precession has predominantly been observed during place- or grid- cell spiking (Moser et al., 2008). However, recent work has discovered the presence of phase precession relative to sound (Aronov et al., 2017; Terada et al., 2017), odor (Terada et al., 2017), time in an episode (Harris et al., 2002; Pastalkova et al., 2008; Lenck-Santini et al., 2008), task progression (Tingley et al., 2018), and REM sleep (Harris et al., 2002). Recent work also suggests that time cells in the human MTL may exhibit phase precession during verbal memory encoding (Umbach et al., 2020). These findings highlight the potential generalizability of phase precession to non-spatial domains. In these instances, phase precession may enable the encoding of any successive stimuli or state, with the progression of phases binding a myriad of non-spatial sequences together for learning. By leveraging the idea that any variable may be encoded in spike phase if the frequency of spike rhythmicity exceeds the frequency of the local LFP oscillation (Mizuseki et al., 2009a; Bush & Burgess, 2020), we showed that phase precession also occurs with respect to behavioral states other than inhabiting a specific physical location—in this case, exclusively during trajectories to specific goals. The fact that this result is so specific, only showing up for a subset of goals for each neuron, might suggest an ensemble temporal code responsible for encoding all of the goals in the task (Wikenheiser & Redish, 2015; Meshulam et al., 2017).

The goal-state phase precession we observed was largely independent of rate coding for goals, which has been described previously in human studies (Ekstrom et al., 2003; Watrous et al., 2018; Qasim et al., 2019). The fact that the presence of rate and phase coding for goals is statistically independent is consistent with the observation in rodents that phase precession can appear for specific behavioral states even in the absence of concurrent firing-rate changes (Robinson et al., 2017). These findings support the theory that phase precession is used by the brain to signal behavioral states independent of firing-rate changes (Huxter et al., 2003; O’Keefe & Burgess, 2005). A challenge for future work is to understand the specific features of this phenomenon, such as the precise relationship to spatial precession, and the role of different phases within goal-state precession. For example, goal-state precession could involve multiple cycles of phase precession, in contrast to the shorter ranges typically exhibited during spatial phase precession. If so, one hypothesis is that goal-state phase precession represents a novel kind of frequency-code in the brain, where absolute phases do not encode specific stimuli; instead, shifting LFP frequency can modulate spike-time intervals for synaptic plasticity without affecting the spike-phase, consistent with a variety of computational models of phase precession (Burgess, 2008; Bush & Burgess, 2020), and broader cognitive function (Wutz et al., 2018). Alternatively, spike phases during goal-state precession may help track a person’s “episodic” position within a goal-seeking event. This would align with work in rodents showing phase-precession in “episode” or “time” cells when a rodent runs on a treadmill with a goal (Pastalkova et al., 2008) but not without a goal (Hirase et al., 1999), as well as evidence from human imaging showing that hippocampal and entorhinal cortex population activity correlates with distance to goal (Howard et al., 2014). Furthermore, goal-state phase precession may relate to the phase precession observed in ventral striatum “ramp cells” (van der Meer & Redish, 2011), and medial prefrontal cortex neurons in rodents (Jones & Wilson, 2005). The former exhibited precession as rodents approached reward locations, and the latter exhibited precession that was clearest when rodents approached the decision point in a maze (Jones & Wilson, 2005). Given that we found goal-state phase precession across various brain regions, including frontal cortex, together this body of work supports the hypothesis that precession may represent “episodic” position within high-level behavioral states.

It is important to understand the prevalence of phase precession due to its hypothesized relevance as a neuronal mechanism for binding and compressing sequential events. In brief, phase precession organizes spiking at time intervals below the deactivation time constant of NMDA receptors, facilitating synaptic plasticity between neurons that encode events at behavioral time-scales (Greenstein et al., 1988; Debanne et al., 1998, 1995; Jensen & Lisman, 2000; Bi & Poo, 2001; Reifenstein & Kempter, 2020). Phase precession may thus be a useful mechanism in the brain for encoding associations between stimuli or events into the relative timing of active neurons for learning and memory. Critically, our findings demonstrate the potential generalizability of such a mechanism, extending phase precession to the human brain and showing that precession does not necessarily depend on specific physiological constraints such as a stationary theta oscillation that consistently stays at the same frequency (Royer et al., 2010; van der Meer & Redish, 2011; Schlesiger et al., 2015; Eliav et al., 2018; Bush & Burgess, 2020). Demonstrating this generalization of phase precession supports the broader possibility that the instantaneous phase of brain oscillations such as theta may serve as an internal reference “clock” for neuronal spiking (and behavioral states) (Buzsáki & Tingley, 2018). As the frequency of theta drifts over time, the phase of this signal may become uncorrelated with the progression of clock time in the outside world. Thus, considering oscillation phase as the brain’s internal clock provides new avenues for research into temporal coding mechanisms throughout the brain (Terada et al., 2017; Tingley et al., 2015, 2014). There is evidence of this idea in recent literature, such as the recent finding that hippocampal cell assemblies encoding a rodent’s position were more tightly coupled to the phase of ongoing theta oscillations than to absolute time (Petersen & Buzsáki, 2020). Therefore, our findings suggest the potential utility for phase precession in humans, across diverse brain regions, as a general mechanism for the use of temporal coding to represent experiences.

In summary, we have provided evidence for spatial phase precession in the human hippocampus and entorhinal cortex during virtual navigation and shown that it exhibits features similar to those seen in rodents. Further, we also demonstrated the existence of phase precession that is specific to trajectories to particular goals. These findings suggest that phase precession is a general mechanism for temporal coding in the human brain, despite the heterogeneity in theta rhythmicity in human MTL. Furthermore, the discovery of goal-state phase precession extends the potential for phase coding to be physiologically relevant for an array of experiential features, even when the neurons do not show concurrent firing rate changes for those features. Overall, our results suggest that phase precession is an important neural code across species and brain regions, not only for spatial cognition and memory but also for non-spatial features of experience.

Limitations of the Study

Here, we demonstrate the existence of phase precession in humans. However, because our analysis utilized a wider frequency band and less stringent spatial-tuning criteria than studies of rodent phase precession, a challenge for future work is establish a firm link between rodent and human phase precession. To bridge this gap, future work in rodents may assess whether phase precession occurs in neurons with complex spatial firing fields or out-of-field spiking, and if researchers manipulate the range of theta frequencies to match those in the human brain. Firmly linking rodent and human phase precession would strengthen the idea that precession may hold widespread value as a neural code in the brain across species. Additionally, characterizing precession in animals that have human-like low frequency brain activity, such as bats and non-human primates, would also strengthen the generalizability of phase precession. Furthermore, our study involved epilepsy patients performing spatial navigation tasks on a computer. It is possible, if unlikely, that the epileptic brain alters patterns such as phase precession. It is also possible that virtual navigation elicits different (i.e. weaker) patterns of phase precession than real-world navigation.

STAR Methods

Resource Availability

Lead Contact.

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Joshua Jacobs (joshua.jacobs@columbia.edu).

Materials Availability.

This study did not generate new unique reagents.

Data and Code Availability.

The data that support the findings of this study are available on reasonable request from the Lead Contact. The data are not publicly available because they could compromise research participant privacy and consent. Analysis code is available online (https://github.com/seqasim/human_precession).

Experimental Model and Subject Details

Participants.

The thirteen participants in our study (10 male, mean age = 30.2±11.6 years) were epilepsy patients who had Behnke–Fried microelectrodes (Fried et al., 1999) (Ad-Tech Medical) surgically implanted in the course of clinical seizure mapping at the University of California, Los Angeles. The Medical Institutional Review Board at the University of California-Los Angeles approved this study (IRB 10–000973), and patients provided informed consent to participate in research. For comparison with rodent data we used a publicly available dataset (CRCNS hc-2, hc-3) (Mizuseki et al., 2009a, b, 2013).

Method Details

Data recording.

Microwire signals were recorded at 28–32 kHz, and we used Combinato for spike detection and sorting (Niediek et al., 2016). Manual sorting identified single- versus multi-unit activity versus noise on the basis of previously determined criteria (Hill et al., 2011; Valdez et al., 2013). The local field potential (LFP) for each neuron was recorded from the local microelectrodes and was downsampled to 250 Hz for spectral analysis.

Task.

This behavioral task is described in several previous studies (Jacobs et al., 2007, 2010; Miller et al., 2015; Watrous et al., 2018). Subjects first learned the navigational controls during a 4-delivery training session in a large, wide-open arena. After the practice session, subjects performed the main task, in which they were instructed to drive passengers to one of 6 goal stores in the virtual environment. Upon arrival, on-screen text displayed the name of the next randomly selected destination store. The task was self-paced in order to accommodate patient testing needs. The size of the virtual environment was 10×10 VR units, the width of the road was 2.5 VR units, and the obstructed area in the center of the road was 5×5 VR units. During navigation, subjects had a 60° field of view, a maximum forward speed of 1.25 VR units/s, a maximum backward speed was 0.5 VR units/s, and maximum angular velocity of 40°/s. To encourage subjects to take the shortest route to each destination, subjects received 50 points for each successful delivery and had one point deducted for each second that they spent navigating. Points were constantly displayed on-screen. Patients performed an average of 73±11 deliveries in each session. To assess performance on this task, we measured subjects’ excess path length (EPL) on each trajectory, defined as ratio of the actual path length to the ideal path length. We computed ideal path length on each trial using the A-star search algorithm to identify the most computationally efficient path between goals in the environment (Russell & Norvig, 2010).

Quantification and Statistical Analysis

Statistical methods and software.

All statistical analyses were carried out in Python, primarily using the SciPy (Virtanen et al., 2020) and statsmodels (Seabold & Perktold, 2010) libraries. For comparisons between two groups, we primarily utilized the Wilcoxon rank-sum test unless otherwise specified. For omnibus testing, we used ANOVAs, determining the p-value by comparing the real test-statistic to those from empirically derived null distributions generated by shuffling the true data. All figures were made using the Matplotlib (Hunter, 2007) and Seaborn libraries.

Characterizing place-cell activity.

To assess how neuronal activity related to the subject’s virtual spatial location, first, we binned the environment into a 10×10 spatial grid. We computed the firing rate map for each neuron by dividing the number of spikes by the amount of time spent in each spatial bin. We then used an ANOVA to assess whether the interaction of X and Y spatial bin (and thus 2D position) significantly modulated firing rate. To assess the significance of the ANOVA we circularly shuffled the firing rate and generated 500 surrogate test-statistics, and used this null distribution to determine the shuffle-corrected p-value of the ANOVA using the real data. These p-values were then FDR-corrected for multiple comparisons between the three movement types (CW, CCW, bi-directional). We used an ANOVA to classify spatial-tuning in order to ensure that we captured a wide-range of potentially complex spatial firing fields that might not exhibit high spatial information scores (Hargreaves et al., 2005; Deshmukh & Knierim, 2011), though this method showed significant convergence with spatial information metrics (Fig. S3D). From this ANOVA method, only neurons with critical statistics exceeding 99% of the shuffled data (p < 0.01) were considered to be spatially modulated. We considered spatially-modulated neurons to be analogous to place- and grid- cells because firing rate differed significantly as a function of spatial location. We identified the spatial bin with the highest firing rate (analogous to the center of a place- or grid- field). We only included a spatial bin if the person passed through it at least 3 times, and occupied it for at least 4 seconds. To assess the significance of spatial information metrics (Fig. S3D) we generated 500 surrogate spatial information values by randomly re-assigning spikes to positions from the subject’s shuffled trajectories and re-computing spatial information. If a neuron’s spatial information exceeded the 95th percentile of this surrogate distribution, we considered it to have a significantly higher spatial information than chance.

Spectral analysis of LFP and spike time.

To assess the prevalence and frequency of theta oscillations in the human and rodent LFP, we computed the continuous Morlet wavelet transform (wave number 6) at 20 logarithmically spaced frequencies between 1 and 32 Hz. Then, to identify theta-like oscillations, we utilized an iterative algorithm to subtract the aperiodic background and fit a Gaussian to putative peaks (Donoghue et al., 2020). For this fitting procedure, we restricted the maximum number of peaks to 2, and the maximum peak width to 4 Hz. We only assessed the peak height (parameterized as the height of the Gaussian’s peak relative to the aperiodic background) and the peak frequency (parameterized as the center frequency at which the Gaussian reaches its peak) for the largest peak in the PSD. To assess the prevalence and frequency of theta oscillations in human and rodent spiking, we computed the autocorrelation of spike times, and performed a fast Fourier transform (FFT), yielding the PSD of the spike train.

Phase estimation.

We estimated the instantaneous phase of LFPs in the theta frequency range. Theta oscillations in human hippocampal formation vary from low (2–5 Hz) to high (5–10 Hz) frequencies (Watrous et al., 2013; Jacobs, 2014; Goyal et al., 2020). In order to analyze fluctuations in the LFP, we estimated 2–10-Hz phase by first identifying peaks, troughs, and midpoints in a broader (30 Hz) lowpass-filtered LFP, and then linearly interpolating between these points with respect to the (2–10 Hz) band-pass filtered signal to estimate phase in the desired frequency range. This phase-interpolation method has been used previously to effectively estimate theta phase in bats (Eliav et al., 2018), as well as in rodents (Siapas et al., 2005; Cole & Voytek, 2019), as an alternative to using the Hilbert transform. This is because Hilbert phase estimation utilizes narrow band-pass filters that can lead to phase shifts due to the non-sinusoidal characteristics of the LFP signal, whereas the phase-interpolation method initially relies on a wide-band signal to estimate the true peaks and troughs of the signal (Belluscio et al., 2012; Dvorak & Fenton, 2014; Cole & Voytek, 2019). To ensure that phase estimates were not based on an unreliable low amplitude signal, we computed the instantaneous power of the LFP and discarded those time-points in which the power fell below a 25^th percentile threshold (Eliav et al., 2018). Low (2–5 Hz) and high (5–10 Hz) theta bouts showed weak but significant correlation in these electrodes (mean ϕ = 0.12, p < 0.05). This indicated that phase estimates could be drawn from across a range of low or high frequencies except during bouts of correlation, when only one band would contribute phases.

Spatial phase precession.

To identify phase precession in this dataset, for each spatially modulated cell we first identified every trajectory through the cell’s peak firing location. Following the methods used in some recent studies for measuring phase precession (Huxter et al., 2008; Jeewajee et al., 2014; Eliav et al., 2018), for each such trajectory we first identified the spike closest to the center of the bin as the center spike (our reference point for the center of the bin on each trajectory). We limited our analysis to spikes in close spatial proximity to the center of the peak firing bin. To do so, we only analyzed the 11 closest spikes to the center of the peak firing bin. To ensure that these 11 spikes did not occur too distant from the peak firing bin, we set a diameter threshold of 40% of the environmental width, meaning that we did not analyze spikes that occurred further than 2 VR units from the center of the peak firing bin. This diameter threshold could sometimes result in fewer than 11 spikes on trajectories where the neuron was less active. We re-ran our analyses while varying the inclusion criterion for the number of spikes (9, 11, & 13) and the diameter (40% & 60%) and found that the parameters we selected did not significantly affect the proportion of cells exhibiting spatial phase precession (χ² = 5.25, p = 0.5, chi-squared test). We next tested for phase precession using circular statistics. Specifically, for each cell we measured the relation between spike phase and the subject’s position by computing the circular– linear correlation coefficient (Kempter et al., 2012). We included all data from the navigation period in our analyses because patients were only stationary for short epochs during each trial (15% of time), and because excluding these epochs did not lead to reduced power in the 2–10-Hz band, or altered prevalence of phase precession.

In order to assess the statistical significance of each neuron’s circular–linear correlation, we used a shuffling procedure that compares the observed phase-position correlation for each neuron to shuffled data from the neuron’s own spike train (thus maintaining the mean firing rate for the neuron) (Kempter et al., 2012). To generate the surrogate distribution, we randomly assigned phases to each spike from the distribution of all the spike phases for that neuron (with replacement), and re-computed the circular–linear correlation 500 times. This null distribution effectively scrambled the relationship between spike position and spike phase and controlled for any effect of spurious phase estimates or differences in sample size. Here, a neuron was considered significant only if the circular–linear correlation computed from the true dataset exceeded the 95^th percentile of the distribution of correlation coefficients computed from shuffled (surrogate) datasets.

Control analyses for spatial phase precession.

We performed two control analyses for alternative explanations for the spatial phase precession we observed. The first analysis tested whether the peak firing bin, our analogue to the place-field center, was crucial for observing precession. To do so, we selected control locations for each cell and assessed the strength and prevalence of precession in these control bins. Control bins were chosen as to not overlap with the peak firing bin (at least 30 % of the map width away). Similar to the peak firing bin, these control bins had to be traversed a minimum of 3 times with a minimum firing rate of 0.5 Hz. Furthermore, because we only analyzed the 11 spikes in the immediate vicinity of the peak firing bin, control bins matched the peak firing bin in the sample size of spikes per trajectory, ensuring that effects were not confounded by firing rate differences. Another possible alternative explanation for our findings is that the phase precession we observed here is actually encoding relative time to peak firing, independent of spatial position, with particular spike phases occurring at specific time-intervals within any epoch of elevated firing rate (Ravassard et al., 2013; Aghajan et al., 2014; Umbach et al., 2020). To control for this possibility, we identified epochs of elevated firing rate in the time domain without any information about position, which we refer to as “firing rate motifs” (Ravassard et al., 2013; Aghajan et al., 2014). We identified the spike that occurred closest in time to the peak firing of each motif field, and used the 11 spikes in the immediate temporal vicinity (within 2 seconds before or after) to compute the circular–linear correlation between spike phase and spike time relative to the motif field peak, matching our spatial phase precession analysis. In both cases, we analyzed the paired difference in correlation coefficients (true vs. control precession) for each neuron (Fig. S4).

Non-spatial phase precession.

To measure non-spatial phase precession without reference to place fields, we compared the spiking frequency of each neuron to the frequency of the local LFP, with relatively faster rhythmic spiking classified as phase precession (Geisler et al., 2007; Mizuseki et al., 2009a). However, detecting oscillations in spike times alone is difficult in humans (Fig. S1B) and bats (Eliav et al., 2018), potentially due to the transient, non-stationary nature of theta observed in these species (Watrous et al., 2013; Eliav et al., 2018). Instead, we applied a method introduced by Mizuseki et al. (Mizuseki et al., 2009a) which measures spiking frequency relative to the ongoing LFP. This is a particularly useful method when the ongoing LFP is non-stationary but may still be an important reference “clock” for neuronal spiking. To perform this analysis, we computed the autocorrelation histogram of each neuron based on the timescale determined by the phase of the reference LFP, rather than the conventional method of using absolute time. We computed this autocorrelation using 60° bins with window-length of 4 cycles (Eliav et al., 2018). For visualization, we fit decaying sine wave functions to the autocorrelation histogram (Eliav et al., 2018). We then computed the Fourier transform of the autocorrelation histogram to yield the power spectral density (PSD) of the frequency of spiking relative to the LFP. Here, a peak relative frequency greater than 1.0 indicates that the cell is oscillating at a faster frequency than the reference LFP. We excluded neurons that exhibited both a peak near 1.0 and significant phase-locking (p < 0.05, Rayleigh test) to ensure that we did not mistakenly identify phase-locked neurons (Jacobs et al., 2007) as exhibiting phase precession. To measure the strength of this effect we measured the amplitude of the peak in the PSD, normalized by the total amplitude across all other relative frequencies (Kim et al., 2012), which we refer to as the spike-phase “modulation index” (MI) (Fig. 4A).

In order to ensure that our results did not arise from poor phase estimates due to low LFP amplitude, we discarded spikes that occurred during the lowest 25^th percentile of LFP power in the oscillation of interest (Kim et al., 2012; Eliav et al., 2018). In order to ensure that low spike counts did not confound our estimates we only analyzed cells with more than 100 valid spike-phase estimates for the autocorrelogram. We compared the spike-phase modulation index to the null distribution of spike-phase modulation indices for the peak frequency, which we computed using randomized phases generated by circularly shifting spike phases within each cycle of theta. This shuffling ensured that across-cycle dynamics (such as precession) were disrupted while maintaining slower and more rapid spiking dynamics (Kim et al., 2012; Eliav et al., 2018). The spike-phase modulation index was considered significant if it exceeded the 95^th percentile of this surrogate distribution. Finally, we excluded cells that exhibited significant phase-locking during the entire session (Rayleigh test, p < 0.05) in order to ensure that peaks close to 1.0 did not result from phase-locked spiking.

Goal-state phase precession.

To measure goal-state phase precession, we separately applied our analysis of non-spatial precession to spiking during each of the six goal conditions. We only included neurons for which we observed at least 100 spikes per goal, to ensure a sufficient sample size to analyze non-spatial precession for each goal. We established two tests to characterize significant goal-state phase precession. First, just as with non-spatial precession, the magnitude of detected phase precession (as indicated by a peak in the spike-phase spectra exceeding 1.0) had to be greater than the 95^th percentile of the shuffled distribution. Because we conducted this test for each of the six goals separately, we used the False Discovery Rate procedure (Benjamini & Hochberg, 1995) to correct the resulting p-values for multiple corrections across goals. If a goal exhibited significant non-spatial precession, we then compared the goal-specific modulation index to a surrogate distribution of spike-phase modulation indices generated by selecting 500 random spike-trains from across the entire session. Each null spike-train was generated to match the number of spikes recorded during the significant goal to ensure that firing rate differences did not account for our results. The p value from this procedure compares the magnitude of goal-state precession for the goal in question versus the session as a whole. To test the stability of goal-specific precession, we computed the Pearson’s correlation between the spike–phase spectra of the first and second halves of the session. We then compared this distribution of correlation coefficients to a surrogate distribution that we generated by applying the same procedure to data where the correspondence between the first and second halves of each session was shuffled across cells.

Supplementary Material

Supp.Figures

Supplemental Figure 1: Rodent hippocampal theta oscillations and measurement of precession without position. Related to Figures 1, 4. A) Power spectral density of hippocampal LFPs recorded in navigating rodents (blue) and humans (red). Black line denotes average across channels. Rodent hippocampal LFP shows a clear peak in the 5–10 Hz range in almost all channels, while the human LFP does not. B) Power spectral density from single-unit discharge from rodent (blue) and human (red) hippocampus. Black line denotes average across neurons. Rodent spiking shows clear theta modulation of spike timing while human spiking does not. C) Spike–phase modulation index (MI) of spike–phase spectral peaks for significant vs. non-significant neurons recorded in rodent CA1. D) Distribution of relative frequencies for neurons exhibiting significant MI in the spike–phase spectra. Values to the right of the black line indicate that the neuronal frequency slightly exceeded the LFP frequency.

Supplemental Figure 2: Examples of spatial phase precession during individual passes through a field. Related to Figure 2. A) Spike times and 1–30-Hz filtered LFP data during individual passes through peak firing bins for four neurons that exhibited significant spatial phase precession. Red arrows denote peaks of individual theta cycles. B) Spike times and 1–10-Hz filtered LFP data during individual passes through peak firing bins for two neurons that exhibited significant spatial phase precession. Here, spike times appear to precess with respect to irregular, non-rhythmic low-frequency fluctuations.

Supplemental Figure 3: Additional examples of spatial phase precession. Related to Figure 2. A) The activity of four neurons that show significant spatial phase precession. Left: firing rate heat map. Brighter colors denote higher firing rates. Text label indicates the color scale for the plot with the mean firing rate of the peak firing bin, which is noted with an asterisk. Dotted lines indicate maximum radius around field in which spiking was assessed. Arrows in the center of the heatmap indicate the movement direction for which this plot was computed. Middle: spike phase as a function of location relative to the field center. Spike phases are duplicated vertically to enable visualization of circular–linear regression (red). Text indicates circular-linear regression coefficient (rho). B) Additional examples of significant spatial phase precession. C) Visualization of binned phase-by-position for spikes inside and outside the place field for four example neurons exhibiting significant precession. Colormaps denote circular mean of spike–phase in spatial bin. D) Distribution of spatial information (bits/spike) across all spatially-tuned neurons. Black shading indicates cells with spatial information significantly exceeding chance. The spatially-tuned neurons we identified exhibited higher spatial information content (bits/spike)Skaggs et al. (1993) than non-spatially tuned neurons (χ² =12.1, p < 6×10⁻⁴), or than expected by chance (p < 3×10⁻⁴, binomial test). E) Distribution of position-phase (red) and rate-phase (blue) circular-linear correlation coefficients across all neurons exhibiting significant spatial phase precession. Asterisk denotes significant difference between the distributions (p < 2×10⁻⁸, paired t-test).

Supplemental Figure 4: Location- and time- control analyses for spatial phase precession. Related to Figure 3. A) Example of alternate location selected to test whether peak firing bins exhibited significantly greater phase precession than randomly selected locations. B) Distribution of paired differences in the strength of precession (true location vs. control location), as measured by circular-linear correlation coefficients. C) Schematic of method for identifying elevated firing rate. Firing rate had to exceed a firing rate threshold of 1.5 Hz for at least 250 ms in order to be classified as a firing rate ”motif”. D) Schematic of method for time-based phase precession within motifs of elevated firing rate. E) Example neuron exhibiting significant phase precession relative to elapsed time within a firing rate motif. F) Distribution of paired differences in the strength of precession (location in field vs. time in motif), as measured by circular-linear correlation coefficients.

Supplemental Figure 5: Additional examples of goal-state phase precession. Related to Figure 5. Three example neurons exhibiting phase precession during navigation to specific goals. Left: Power spectral density depicting frequency of neuronal spiking relative to ongoing LFP. Asterisk denotes peaks that were significant and significantly different from other goals. Gray lines denote spike–phase spectra for non-significant goals. Right: Spike–phase autocorrelograms during navigation to each goal (significant goal epochs depicted in color). Text indicates the p-value for both significance tests described in Figure 5C), and relative frequency of spiking to LFP. Black line indicates fit of decaying sine wave function (added to significant examples), depicting oscillation in spike–phase autocorrelogram.

Supplemental Figure 6: Goal-state phase precession is not a function of a differences in navigation performance. Related to Figure 6. A) Top, stability of goal-specific precession across each half of the task session, measured by the Pearson’s correlation (rho) between the spike–phase spectra of the 1st and 2nd halves of the session. Bottom, surrogate distribution of stability generated by shuffling cell labels across the 1st and 2nd half spike–phase spectra used to compute between-half correlations. B) Excess path length as a function of goal. C) Distribution of Cohen’s d comparing excess path length during trajectories to goals that showed precession vs. those that did not. Black dotted line indicates effect size of ±0.8.

• In phase precession neurons code information by spiking faster than local oscillations

• Neurons in the human brain exhibit phase precession during a spatial memory task

• As in rodents, precession occurs relative to space in the hippocampal formation

• In the frontal cortex, non-spatial precession occurs while seeking specific goals