Multimodal Image Analysis of Apparent Brain Age Identifies Physical Fitness as Predictor of Brain Maintenance

Abstract

Maintaining a youthful brain structure and function throughout life may be the single most important determinant of successful cognitive aging. In this study, we addressed heterogeneity in brain aging by making image-based brain age predictions and relating the brain age prediction gap (BAPG) to cognitive change in aging. Structural, functional, and diffusion MRI scans from 351 participants were used to train and evaluate 5 single-modal and 4 multimodal prediction models, based on 7 regression methods. The models were compared on mean absolute error and whether they were related to physical fitness and cognitive ability, measured both currently and longitudinally, as well as study attrition and years of education. Multimodal prediction models performed at a similar level as single-modal models, and the choice of regression method did not significantly affect the results. Correlation with the BAPG was found for current physical fitness, current cognitive ability, and study attrition. Correlations were also found for retrospective physical fitness, measured 10 years prior to imaging, and slope for cognitive ability during a period of 15 years. The results suggest that maintaining a high physical fitness throughout life contributes to brain maintenance and preserved cognitive ability.

Introduction

As we age, our brains are subject to both functional and structural degeneration, such as cortical thinning (Salat et al. 2004), increased white matter atrophy and lesions (Vernooij et al. 2008), decreased functional connectivity (Salami et al. 2014), and increased dedifferentiation among functional regions (Ferreira et al. 2016). There is, however, considerable individual variability, with some individuals appearing to maintain a youth-like brain along with preserved cognition, that is, brain maintenance (Nyberg et al. 2012), while other individuals fall outside the normal range of typical age-related changes, with elevated risk for developing dementia.

Brain age predictions use image-based machine learning methods to identify patterns that differentiate older appearing brains from younger appearing ones (Franke et al. 2010; Cole, Poudel, et al. 2017a). Brain changes can impact distinct pathways, differently affecting a number of regions and functions (Eavani et al. 2019; Smith et al. 2019). In general, older appearing brains can be characterized by global and regional gray matter (GM) and white matter (WM) loss, as well as altered functional connectivity. For example, strong associations have been found between the calculated brain age prediction gap (BAPG) and white matter microstructure in the fornix and anterior thalamic radiation (Smith et al. 2019). By calculating the difference between predicted age and chronological age for a given individual, predictions can be made about their general brain health, which in turn could serve as a brain-based personalized biomarker to detect individuals at risk for future disease. A predicted age higher than the chronological age has, for example, been related to cognitive decline and Alzheimer’s dementia (Franke and Gaser 2012; Gaser et al. 2013; Liem et al. 2017; Pendlebury and Rothwell 2019), and here we expected that a predicted younger age would reflect brain maintenance.

Traditionally, most brain age prediction models are based on structural magnetic resonance images (MRI) (Franke et al. 2010; Cole, Ritchie, et al. 2017b; Gutierrez Becker et al. 2018). However, studies using other modalities, including diffusion tensor imaging (DTI) (Richard et al. 2018), functional magnetic resonance imaging (fMRI) (Dosenbach et al. 2010), or combinations thereof (Liem et al. 2017; Cole 2020; de Lange et al. 2020), have also been presented. In theory, different image modalities should provide unique information to the brain prediction model. Hence, a multimodal approach could not only improve age predictions but also result in a model that captures a wider range of pathologies with stronger associations to various physiological factors. Thus, by identifying several different “brain ages,” reflecting different aspects of the aging process (Cole 2020; de Lange et al. 2020), we could get a deeper understanding of the connection between brain aging and neurological diseases, and thereby improve the selection of which modalities to include depending on specific research questions. However, more studies are needed on the importance of combining data from several modalities into a multimodal model, and how the choice of input data influences the association with other variables and their change over time (see below). The first goal of this study was to compare 5 single-modal and 4 multimodal prediction models, and we hypothesized that by combining several image modalities the associations would be strengthened.

In addition to the choice of input data, the biggest difference between prediction methods is the choice of machine learning method. The level of complexity can vary markedly, from basic regression to more advanced methods including regularizing terms that improve stability (Baldassarre et al. 2017), kernel methods where variable transformations are performed, probabilistic methods where hyperparameters are estimated from the data, or deep learning methods such as convolutional neural networks (Cole, Poudel, et al. 2017a). Some prior studies compared different methods (Franke et al. 2010; Baldassarre et al. 2017; Cole, Poudel, et al. 2017a; Zhai and Li 2019; Jiang et al. 2020), but the number of included methods is generally small and conclusive evidence is lacking. The second goal of this study was, therefore, to investigate whether the choice of prediction method has a significant impact on the resulting prediction. This was accomplished by comparing some of the most frequently used machine learning methods for brain age predictions, using ordinary least square (OLS) regression as the reference.

The third, main goal of this study was to investigate how brain age predictions are related to variables that in past studies have been linked to neurocognitive aging. Since aging can be defined as the gradual accumulation of cell damage or other structural changes (Harman 2001; López-Otín et al. 2013), it should be advantageous to employ a longitudinal perspective in brain age prediction. In the present study, we utilized individual data collected over more than a decade to define the BAPG and assess relations to other variables both cross-sectionally and longitudinally. Given that brain maintenance was introduced to account for relative well-preserved cognition in aging (Nyberg et al. 2012; Nyberg and Pudas 2019), we related the BAPG to cognitive ability over time and predicted that individuals with a predicted age younger than chronological age would have more intact cognition. We further examined the association between predicted brain age and longitudinal study dropout (attrition), since attrition has previously been linked to worse outcomes in aging (Caracciolo et al. 2008; Salthouse 2019). Additionally, we examined whether the BAPG was associated with level of education, which previously has been proposed (Steffener et al. 2016) but not conclusively demonstrated. Based on recent analyses of the role of education in cognitive aging (Lövdén et al. 2020), we predicted relations for cross-sectional but not longitudinal estimates of the BAPG. Finally, we related BAPG to level of physical fitness. Physical fitness has been linked to both structural and functional changes in the brain. For example, higher levels of physical fitness, measured in terms of cardiorespiratory fitness, BMI, and blood pressure, have been associated with greater functional connectivity in age-sensitive networks, primarily the default mode network (Boraxbekk et al. 2016; Voss et al. 2016), as well as higher perfusion and GM volume in associated regions (Boraxbekk et al. 2016). There are also suggestions about a relationship between physical activity and changes in WM structure (Sexton et al. 2016). When linking the number of daily flights of stairs climbed with predicted brain age from imaging data, it was shown that for each additional flight of stairs climbed per day the predicted brain age decreased with 0.58 years (Steffener et al. 2016). We predicted that a high level of physical fitness throughout life would relate to a younger brain age.

Materials and Methods

Participants

All included subjects were part of the Betula prospective cohort study on memory, health, and aging (Nilsson et al. 1997; Nyberg et al. 2020). The Betula study started in 1988, with data collection every 5 years. Subjects with no history of severe neurological illness or events that might cause dementia were recruited at random from the population in Umeå, Sweden. Informed consent, in accordance with guidelines of the Swedish Council for Research in the Humanities and Social Sciences, was signed by all participants. At the first measurement wave (T1), 1000 participants (S1) were recruited, 100 for each of 10 age groups where subjects were 35, 40, 45…80 years at inclusion. At the second measurement wave (T2), an additional longitudinal sample of 963 participants (S3), spanning the same age groups (age 40–85 at this point), was recruited. For more detailed information on subject inclusion in the Betula study, see (Nilsson et al. 1997; Nyberg et al. 2020).

At each time point, health assessment, memory tests, and questionnaires on socioeconomic factors and critical life events were performed (Nilsson et al. 1997). At the fifth and sixth measurement waves (T5 and T6), a subsample of individuals from the original study samples (S1 and S3), as well as an additional sample (S6), underwent structural and functional MRI. Detailed information of this cohort can be found elsewhere (Pudas et al. 2013). In the present study, data from T3-T6 are included, spanning from approximately 10 years prior to baseline brain imaging to approximately 5 years after. See Table 1 for details of the included cognitive and biomedical data. In the current study, subjects (N = 351, 182 women) with structural T1-weighted images, DTI, and resting-state functional magnetic resonance images (rs-fMRI) data, acquired at the T5 wave, were included, and follow-up images (T6) were available for 214 of these subjects (117 women). The age range was from 25 to 83 years (63 ± 13 years) at the time of baseline MR scanning, and 29 to 85 years (65 ± 13 years) at follow-up scanning.

Table 1.

Average values for demographic, biomedical, and cognitive data at each measurement wave

	T3 (1998–2000)	T4 (2003–2005)	T5 (2008–2010)	T6 (2013–2014)
Number of subjects
S1	131	130	131	104
S3	140	139	140	106
S6	–	–	80	62
Total	271	269	351	272
Background information, mean (SD)
Education, years	12.3 (4.2)	12.3 (4.2)	12.7 (4.1)	12.9 (4.2)
Age, yearsa	56 (8)	62 (8)	63 (13)	65 (13)
No. women/men	144/127	143/126	182/169	137/134
Biomedical data, mean (SD)
BMI (kg/m2)	26.1 (3.7)	26.4 (3.6)	26.4 (3.8)	26.5 (3.7)
Waist circumference (cm)	89.5 (10.3)	91.4 (9.9)	92.1 (11.3)	93.2 (10.9)
Diastolic blood pressure (mmHg)	82.5 (9.7)	83.5 (8.7)	80.8 (9.2)	80.6 (8.7)
Systolic blood pressure (mmHg)	138.0 (19.3)	139.6 (18.5)	138.2 (18.8)	138.9 (16.3)
Grip strength right (kg)	–	38.1 (12.8)	35.7 (12.4)	36.2 (13.0)
Grip strength left (kg)	–	42.5 (6.2)	31.5 (10.8)	35.8 (13.7)
Pulse (bpm)	63.5 (8.6)	62.0 (9.2)	61.2 (9.0)	61.3 (8.4)
Cognitive performance, mean (SD)
Free recall	10.1 (2.5)	10.0 (2.36)	9.6 (2.6)	9.3 (3.1)
Fluency A	13.1 (4.2)	13.8 (4.7)	12.3 (4.4)	12.8 (4.8)
Letter Digit	31.7 (6.4)	31.3 (6.3)	30.2 (7.7)	29.1 (8.0)
Block design	31.1 (9.4)	30.2 (8.8)	29.5 (9.7)	28.6 (9.9)

Note: Brain age predictions were calculated from image data at the T5 and T6 wave. S1, S3, and S6 are different study samples, recruited at T1 (1988–1991), T2 (1993–1995), and T5 (2008–2010), respectively.

^aFor T3 and T4, mean and SD are calculated based on the stratified ages, while for T5 and T6, age at time of imaging is used.

Imaging Data

MR images were collected on a 3T scanner (GE Discovery MR 750, Milwaukee, WI, USA) with a 32-channel head coil. T1-weighted structural images were collected with a 3D fast spoiled gradient echo sequence (180 slices; thickness, 1 mm; repetition time (TR), 8.2 ms; echo time (TE), 3.2 ms; flip angle, 12°; field of view, 25 × 25 cm). DTI was collected with a single-shot T2-weighted spin-echo planar sequence (64 slices; spatial resolution, 0.98 × 0.98 × 2 mm; TR, 8000 ms; TE, 84.4 ms; flip angle, 90°; field of view, 25 × 25 cm; b = 1000 s/mm²; 32 directions; 6 B0 images). Rs-fMRI was acquired with a gradient echo planar imaging sequence (37 slices; thickness, 3.4 mm; gap, 0.5 mm; TR, 2000 ms; TE, 30 ms; flip angle, 80°; field of view, 25 × 25 cm; in plane resolution, 2.6 × 2.6 mm). Time series data were acquired over 5 min and 40 s, and participants were instructed to keep their eyes open during the scan and look at a presented fixation cross. All analyses in this study were carried out on a global brain level and no regional comparisons were done, neither within images nor between modalities.

Each image modality was preprocessed separately (i.e., images were not normalized and scaled in the same way). Structural images were preprocessed using Statistical Parametric Mapping software (SPM12) (www.fil.ion.ucl.ac.uk/spm). T1 images were segmented into GM, WM, and cerebrospinal fluid (CSF) using SPM12’s segment, resulting in probability maps for each tissue type, describing the probability that each tissue is found at a specific location in the brain (Ashburner and Friston 2005). These probability maps were then normalized to Montreal Neurological Institute (MNI) space (Evans et al. 2012) using the nonlinear DARTEL method (Ashburner 2007). In DARTEL, the tissue probability maps were used to produce a study-specific template and subject-specific flow fields allowing normalization of images of interest. An affine transformation of the population average template to MNI space was used to bring normalized images into MNI space. For anatomical data, we utilized the option of preserving the amount of signal from each region. To reduce the amount of data, the probability maps were down sampled to isotropic 3 mm resolution and masked using the standard MNI brain mask from SPM to remove nonbrain voxels. The DTI data were processed using the University of Oxford’s Center for Functional Magnetic Resonance Imaging of the Brain (FMRIB) Software Library (FSL) package (http://www.fmrib.ox.ac.uk/fsl). Images were eddy current corrected and skull stripped, and fractional anisotropy (FA) images were calculated with DTIFIT. FA images were nonlinearly registered to the FMRIB58_FA standard space image with an isotropic 1 mm resolution, and values were projected onto the corresponding FA skeleton, through the tract-based spatial statistics (TBSS) pipeline, creating a denser version of the FA image, with improved alignment between subjects. Functional images were also processed in SPM, the data were slice-time corrected and corrected for head movement with realign & unwarp, normalized to MNI space using DARTEL as previously described, smoothed using an 8-mm full-width half-maximum Gaussian filter, and adjusted for B0 inhomogeneity. The data were also high-pass filtered with a cutoff of 130 s, using SPM’s filtering function. For each subject, a connectivity matrix describing temporal correlation between cortical regions was calculated from the rs-fMRI data, using an in-house developed software (DataZ) operating with SPM subroutines. Additional motion correction (the Friston 24 parameter model Friston et al. 1996, which contains 6 motions estimates from the current and preceding volume, plus their squared versions) was used in this process. The seed regions for the connectivity matrix was defined based on the Cortical Area Parcellation from Resting-State Correlations (Gordon et al. 2016) with 333 cortical regions; this atlas was selected since it is specifically developed for functional connectivity analysis.

Each image was reshaped into a one-dimensional feature vector, using each voxel as a feature. Final resolution for the structural images was 3 × 3 × 3 mm, resulting in a total of 114 990 features each for the GM, WM, and CSF tissue probability maps after removing background voxels. The FA images had a final resolution of 1 × 1 × 1 mm and were masked with the sample-specific binary skeleton mask obtained through the TBSS pipeline, resulting in a total of 139 235 features. The connectivity analysis carried out on the rs-fMRI resulted in a symmetric 333 × 333 matrix (FC), describing connectivity between each region; after removing duplicate values, 55 278 features remained. Figure 1 shows examples of these images and how they are used in the brain age prediction process.

Figure 1.

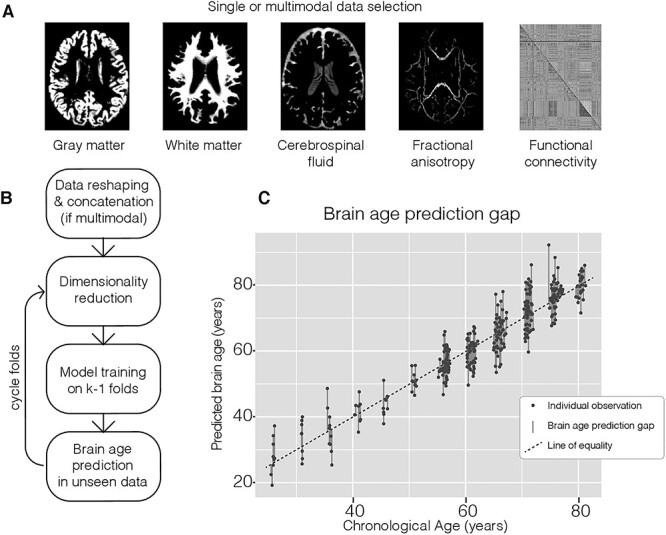
Overview of the brain age prediction process. (A) Example of input modalities that were used in the brain age prediction process. (B) Main processing steps of the prediction method from reshaping image data into 2-dimensional matrixes with one row per subject that could be concatenated to contain all the considered modalities, through the k-fold prediction framework where dimension reduction and model training are performed on k-1 folds and resulting parameters are used in the prediction of age in the unseen fold. (C) Combined output from the prediction method and corresponding calculation of BAPG.

Brain Age Predictions

Figure 1 shows an overview of the brain age prediction pipeline. Single-modal brain age predictions were calculated for each of the 5 images (GM, WM, CSF, FA, and FC). These predictions were compared with 2 different types of multimodal age predictions, using either concatenation or random forest (RF) regression (Liem et al. 2017). In the concatenation model, the feature vectors of all included modalities were joined lengthwise, to a single feature vector for each subject, as the first step in the data processing scheme (Fig. 1).

RF is an ensemble machine learning method based on decision trees. A decision tree can be seen as a flow chart where subjects are sorted into groups giving the lowest training errors. Individual trees have a tendency to overfit to the training data, and to overcome this, a large number of trees, in our case 100, were trained on random subsets of the data, and the predicted values were obtained by averaging the results from all trees. The goal of RF is to improve predictions by combining results from the single-modality models; therefore, the RF model was trained on the age predictions obtained from the single-modality models rather than the full feature vectors (Liem et al. 2017).

For each of the 2 approaches, 2 models were constructed, including either the 3 structural images or all 5 images. For the concatenated data, this resulted in feature vectors of length 344 970 for the structural images and 539 483 for all images combined. For the RF model, which was based on predictions obtained in the previous step rather than raw data, input vectors were of the length of 3 and 5, respectively.

To obtain age predictions for all subjects, 10-fold cross-validation was used. The subjects were divided into 10-folds, the regression methods were trained on data from 9-folds, and the trained method was used to obtain predictions for the subjects in the last fold. This process was repeated for each fold, to obtain predictions for all subjects. The regression methods were trained on T5 data, and predictions were made for both T5 and T6, simultaneously. To reduce the impact of group selection, this process was repeated 50 times, and the average prediction value from all repetitions was used in the analysis. The same methodology was used for both the single-modal models and the models based on concatenated data, but in the latter case, the feature vectors were concatenated to form longer vectors before entering the prediction scheme.

First, each set of data was normalized by calculating the z-score (subtracting the mean and dividing by the standard deviation), and principal component analysis (PCA) was used to reduce the dimensionality of the data by extracting the most important features (Franke et al. 2010; Gutierrez Becker et al. 2018). To avoid contamination between test and training data, both z-score and PCA were calculated based on the training data, and the resulting transforms were applied to the test data. PCA is a linear transformation that calculates orthogonal components from a data set, describing the linear combinations of features that capture the largest amount of the variance in the data. This means that instead of hundreds of thousands of features, many of which contains little unique information, the prediction methods only need to handle a few hundred linear combinations of features, where each PCA component might include data from several modalities. By design, the largest number of components obtained from PCA is equal to the number of observations. The number of principal components in each model was therefore equal to the number of subjects in the training set (315 or 316 depending on fold).

Brain age predictions were carried out using supervised learning regression methods from the scikit-learning package in python. The goal of regression methods is to find the function that best fits the training data, by minimizing training error. Different methods use different definitions of training error and hence might differ in what is considered the best fit. Based on previous studies of brain age predictions, we identified 7 regression methods for comparison. As a reference, we used the most straightforward of the identified methods, OLS (Zhai and Li 2019), where a linear model is fitted to the data by minimizing the residual sum of squares. Some drawbacks of OLS include large variance (Tibshirani 1996), which could increase the risk of unreliable results, especially if the number of predictor variables is much larger than the number of observations, or if there are multicollinearities (Zhai and Li 2019).

Bayesian ridge regression (BRR) (Hoerl and Kennard 1970; Hsiangl 1975; Monté-Rubio et al. 2018) is also a linear model, and the 2 main differences to OLS are that BRR adds a regularization term to the minimizing function, penalizing large coefficients. This term is controlled by a hyperparameter, α, and is proportional to the root of the sum of squares of the coefficients (L2 norm). The other difference is that BRR is a probabilistic method based on Bayesian statistics, meaning that hyperparameters are estimated from the data according to a probability function, rather than set by the user.

Least absolute shrinkage and selection operator (LASSO) (Tibshirani 1996; Baldassarre et al. 2017; Varikuti et al. 2018) does also add a regularization term, controlled by hyperparameter α, proportional to the sum of the absolute values of the coefficients (L1 norm) instead of its square, which shrinks unnecessary coefficients to zero, that is, performing variable selection, which could improve prediction accuracy (Tibshirani 1996).

Elastic net (ENET) (Zou and Hastie 2005; Baldassarre et al. 2017) combines the advantages of both LASSO and ridge regression by adding 2 regulation terms, one with L1 and one with L2 norm, and the proportion between these 2 terms is controlled by a hyperparameter ρ.

In addition to these 4 linear models, we also included 3 kernel methods. These methods differ in that instead of working directly with coordinates in feature space, the features are transformed using a predefined kernel function, working with inner products of feature vectors. The most common kernel method is support vector regression (SVR) (Drucker et al. 1997; Dosenbach et al. 2010; Franke et al. 2010), which focuses on those cases where it is hardest to fit the model. This fit is controlled by 2 hyperparameters, C and ε. Relevance vector regression (RVR) (Tipping 2000; Franke et al. 2010; Su et al. 2013) is analogues to SVR, but uses the Bayesian method where hyperparameters are estimated within the regression model.

The final method in our comparison was Gaussian process regression (GPR) (Rasmussen and Williams 2006; Cole, Poudel, et al. 2017a; Aycheh et al. 2018), another probabilistic model, closely related to ridge regression models, but employing the kernel transformation mentioned above. To find suitable kernels for the 3 kernel methods, standard options were compared. For SVR and RVR (https://github.com/JamesRitchie/scikit-rvm), a linear kernel was used, while GPR used a dot product kernel. For the non-Bayesian methods, hyperparameters can be estimated using cross-validation. We chose to go with the default options, meaning α = 1 for LASSO and elastic net, ρ = 0.5 for elastic net, C = 1 and ε = 0.1 for SVR and a priori values of α1 = α2 = λ1 = λ2 = 10⁻⁶ for BRR, α = β = 10⁻⁶ for RVR and α = 10⁻¹⁰ for GPR.

For each combination of regression method and input data, the corresponding model was fitted to the training data and applied to the test data, and the process was then repeated for the next fold. Just as the other models, the RF models were trained and evaluated using 50 iterations of 10-fold cross-validation. But instead of the full feature vector, the input was the 3 (structural) or 5 (all combined) age predictions for each subject, obtained from the single-modal models. The difference between predicted and chronological age, denoted BAPG, was calculated for each subject and model by subtracting the chronological age from the predicted age. A positive BAPG is therefore equivalent to a predicted age higher than chronological age, and a negative BAPG to a predicted age lower than chronological age. Previous studies have shown noticeable age dependency in BAPG, where the predicted ages are overestimated for young subjects and underestimated for old subjects (Le et al. 2018; Smith et al. 2019; de Lange and Cole 2020). This bias was also observed here and was corrected for using the following linear regression (Beheshti et al. 2019), calculated from the full T5 data:

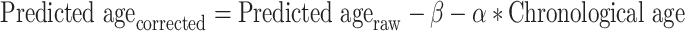where β is the intercept and α the slope of the regression line describing the relationship between chronological age and BAPG. Figure 2 shows results before and after correction. This correction ensured that the BAPG was independent of age, which is necessary to exclude age as a mediating factor between BAPG and other investigated factors.

Figure 2.

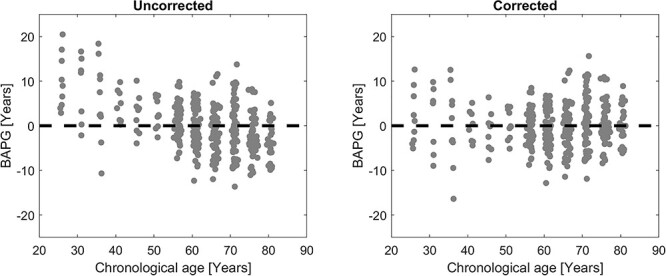
Scatterplot of T5 BAPG versus chronological age for the Conc all model (a) before (MAE = 4.20 years) and (b) after (MAE = 3.64 years) age correction using linear regression. Before correction, young subjects on average get a higher predicted brain age than chronological age, while old subjects get a lower predicted brain age.

BAPG Association with Cognition, Education, Attrition, and Physical Fitness

Associations between BAPG and education and attrition were analyzed cross-sectionally. Education was measured in terms of self-reported number of years of formal education. Attrition was coded as a dummy variable, taking the value of 1 if the subject remained in the study at T6, and −1 if they dropped out. Out of the 351 subjects, 272 returned for further testing at T6.

Associations between BAPG and physical fitness and cognitive ability were investigated both cross-sectionally and longitudinally. For the cross-sectional analysis, data collected at T5, that is, in conjunction with the first imaging session, were used, while data from all 4 time points (T3–T6) were used in the longitudinal analysis of how factors change over time. Physical fitness and cognitive ability were assessed using composite scores as described below.

Cognitive ability, education, attrition, and physical fitness were collectively referred to as investigated factors. Among these, education and physical fitness were identified as potential protective factors that might prevent brain aging, while cognitive ability and attrition are considered outcome factors, related to brain maintenance. The physical fitness score has previously been described in (Boraxbekk et al. 2016). It was based on measurements of resting pulse, resting systolic and diastolic blood pressure, maximum grip strength (left and right hand, not available at T3), BMI in kg/m², and waist circumference in cm. The z-score for each measurement was calculated, and scores from all 7 measurements were averaged. Measurements where a higher value was indicative of poorer health (BMI, waist circumference, pulse, and blood pressure) were multiplied with −1, so that a higher score indicated higher level of fitness. These values were originally calculated from the entire Betula cohort and were therefore renormalized using z-scores, to reflect the distribution of values in the current cohort.

To assess cognitive ability, the g-factor (Spearman 1904; Carroll 1993) was used, where a common factor influencing several cognitive domains is identified and used as a measure of general cognitive ability. To calculate this score, we used 4 cognitive tests spanning different domains: episodic memory (free immediate recall of 16 enacted sentences), semantic memory (1-min generation of words beginning with the letter A), spatial ability (block design), and processing speed (letter–digit substitution test). These tests were selected in accordance with a previous study (Davies et al. 2018); for a more extensive description of these tests, see (Nilsson et al. 1997; Larsson et al. 2004). Test scores were normalized using z-scores, and PCA was used to find the linear combination of these tests that captured the largest amount of variation (the first principal component), based on the T5 data. Normalized loadings were between 0.4 and 0.6 for all 4 tests, and the cognitive ability score for each individual was calculated by multiplying each test score with the corresponding loading and summing them all together.

Longitudinal Analyses

Both physical fitness and cognitive ability were assessed at 4 time points (T3–T6), and the retrospective data were included to investigate if cognitive ability and physical fitness earlier in life were related to brain age later in life. A linear model for each of these measures was fitted for every subject, provided that data were available for at least one retrospective time point (T3 or T4), and at least 2 time points in total. Slope and intercept of these models were then used to investigate longitudinal effects, using correlation analysis as described below. In this context, slope measures the rate of change over time, while intercept can be interpreted as a modified baseline score, indicating an expected value 10 years before baseline brain age prediction, assuming a linear trajectory. Since the data are normalized at each time point, all scores are set in relation to the other subjects in the study, rather than change in absolute values.

Correlation with BAPG

The primary measurement of association between BAPG and the investigated factors in both the cross-sectional and the longitudinal analysis was correlation. We also investigated how much of the variation in each factor could be explained by predicted age in comparison to chronological age. This was done by calculating the coefficient of determination (R²) for a linear regression between each investigated factor and both predicted and chronological age. F-test was then used to determine if there is a significant difference in the amount of explained variance for predicted and chronological age.

For the longitudinal BAPG, correlation between T5 and T6 value was calculated, as well as correlation between baseline value and change in BAPG between the 2 time points. Correlation with investigated factors was also calculated for both T6 BAPG and change in BAPG.

Correlations among the 4 investigated factors were also calculated, as well as the difference in BAPG and years of education between subjects who did or did not return for testing at T6. In total, 20 tests were performed for each model at T5, and an additional 20 at T6. False discovery rate (Benjamini and Hochberg 1995) was used to correct for multiple comparisons. Unless otherwise stated, all analyses were done in MATLAB (Mathworks).

Results

Cross-Sectional Brain Age Prediction

All evaluated regression methods performed at a similar level in terms of average size of the prediction gaps (MAE) at T5 (Fig. 3, Kruskal–Wallis P’s > 0.23), and predicted age was strongly correlated to chronological age for all models (r’s > 0.90). Therefore, the reference method (OLS) was used for all subsequent analyses. The lowest MAE among the single-modal models (3.72 ± 2.90 years) was obtained for the model based on WM (Fig. 3A). GM and FA did also perform well (3.90 ± 3.21 and 4.04 ± 2.88 years, respectively), while CSF and FC had a higher MAE (4.68 ± 3.82 and 4.87 ± 3.50 years, respectively). For the multimodal predictions (Fig. 3B), the models based on concatenated data had a lower MAE than RF, and models combining all 5 modalities had lower MAE than those based on only the structural data (GM, WM, and CSF), (Conc struct: 3.93 ± 3.08, Conc all: 3.64 ± 2.98 years, RF struct: 3.99 ± 3.30, and RF all: 3.72 ± 2.98 years), with the lowest value over all for the full multimodal model (Conc all). Scatterplots of predicted versus chronological age for all models are shown in Figure 4. Table 2 shows the correlation between all the BAPG methods, all models were significantly correlated, and all models except the single-modal FC had r’s > 0.5.

Figure 3.

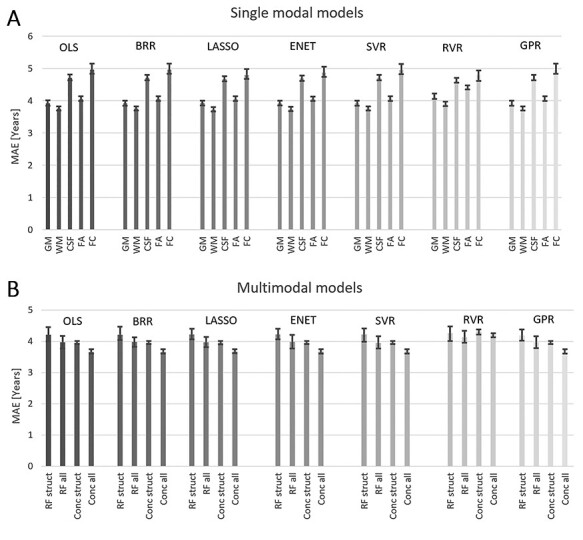
Average mean absolute error (MAE) for each method based on the 50 iterations, error bars show the range of obtained values, (A) single-modal prediction, (B) multimodal predictions.

Figure 4.

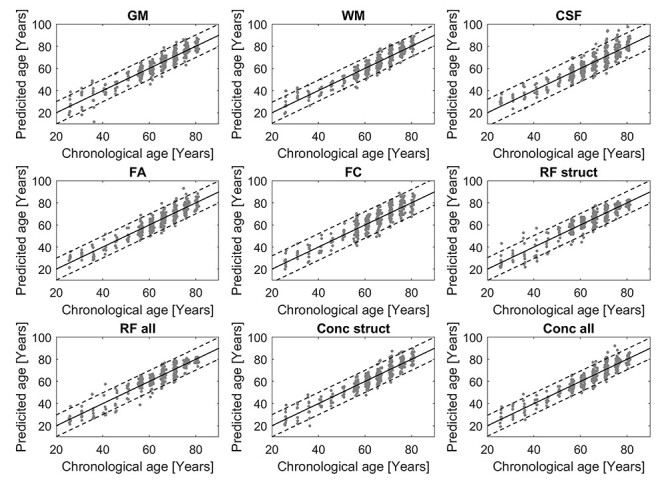
Scatterplots of predicted versus chronological age for all methods, dashed lines indicate M ± 2 SD.

Table 2.

Correlation between BAPG obtained from each investigated cross-sectional model. All correlations were significant at P < 0.0005

	GM	WM	CSF	FA	FC	RF struct	RF all	Conc struct
WM	0.69
CSF	0.61	0.61
FA	0.58	0.59	0.54
FC	0.22	0.21	0.30	0.23
RF struct	0.78	0.73	0.62	0.58	0.21
RF all	0.74	0.69	0.59	0.67	0.33	0.91
Conc struct	0.93	0.75	0.78	0.63	0.28	0.78	0.74
Conc all	0.85	0.70	0.70	0.79	0.44	0.72	0.75	0.91

Longitudinal Brain Age Prediction

The average BAPG, based on the full multimodal model (Conc all), for the participants that were scanned at both time points was −0.33 ± 4.65 years at T5 and −0.46 ± 4.52 years at T6. This means that subjects on average aged 3.87 ± 2.13 years during this period of 4.0 ± 0.2 years. BAPG at T5 and T6 was strongly correlated (r = 0.89). A moderate correlation (r = −0.29) was found between T5 BAPG and change in BAPG, indicating that subjects with a low BAPG at T5 had a higher rate of brain aging than those with a high BAPG at T6. Figure 5 shows individual BAPG trajectories over this period.

Figure 5.

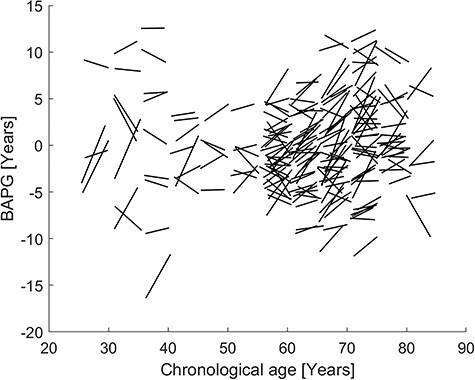
Trajectories of change in BAPG over a 4-year period, each line represents one subject and shows how their BAPG change with their chronological change from T5 to T6.

BAPG Associations with Cognition, Education, Attrition, and Physical Fitness

Table 3 shows the correlations among the 4 investigated factors. Years of education was significantly correlated with physical fitness and cognitive ability, and the latter 2 factors were also correlated with each other. Attrition was only correlated with cognitive ability. All correlations were positive.

Table 3.

Correlations among investigated factors

	Education	PF	CA
Education	–	–	–
PF	0.23	–	–
CA	0.51	0.25	–
Attrition	0.08	0.04	0.26

Note: Bold values are significant at false discovery rate corrected P = 0.05, PF = physical fitness, CA = cognitive ability.

For BAPG, a negative value was considered an indication of good health (a person with a negative BAPG has lower predicted brain age than chronological age, i.e., a brain that more closely resembles the brain of someone younger). Therefore, we expected negative correlations between BAPG and the investigated factors, which was the case for all significant correlations. In the cross-sectional analysis, BAPG measures from 4 of the evaluated models were significantly negatively correlated to physical fitness, cognitive ability, and attrition, while only the predictions based on FC were significantly correlated to education (Table 4). For cognitive ability, all but 2 models showed a significant correlation with BAPG. Figure 6 illustrates the relationship between BAPG and education, physical fitness, and cognitive ability for the models based on WM, FC, and all modalities concatenated.

Table 4.

Correlations between each BAPG measure and the 4 main investigated factors

Correlations	Education		PF T5		CA T5		Attrition
	N = 349		N = 316		N = 350		N = 350
	r	P	r	P	r	P	r	P
GM	−0.06	0.242	−0.17	0.002	−0.14	0.010	−0.15	0.005
WM	−0.07	0.178	−0.17	0.003	−0.21	<0.001	−0.17	0.001
CSF	−0.09	0.086	−0.06	0.320	−0.17	0.002	−0.14	0.009
FA	−0.08	0.150	−0.12	0.031	−0.16	0.003	−0.08	0.146
FC	−0.14	0.007	−0.03	0.613	−0.13	0.017	−0.04	0.467
RF struct	−0.09	0.098	−0.12	0.032	−0.14	0.009	−0.09	0.095
RF all	−0.09	0.081	−0.15	0.010	−0.13	0.013	−0.10	0.065
Conc struct	−0.08	0.130	−0.16	0.004	−0.19	<0.001	−0.16	0.003
Conc all	−0.11	0.040	−0.15	0.007	−0.20	<0.001	−0.12	0.029

Note: Bold values are significant at false discovery rate corrected P = 0.05, PF = physical fitness, CA = cognitive ability.

Figure 6.

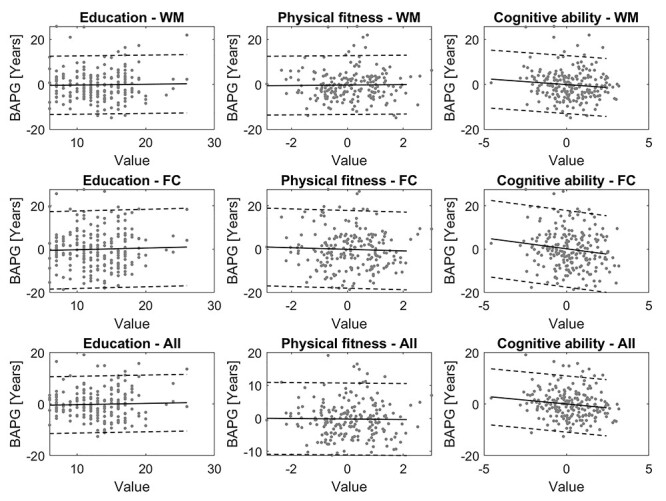
Scatterplots of education, physical fitness, and cognitive ability against BAPG at T5, calculated with WM, FC, and all modalities concatenated. Solid line shows the linear regression fitted to the data, and dashed lines M ± 2 SD.

In the longitudinal analyses of changes in cognition and physical activity over time in relation to BAPG (Table 5), 6 of the 9 models showed correlations between cross-sectional BAPG and slope of cognitive ability, but only one method (FC) showed correlation with slope of physical fitness. However, for physical fitness intercept, correlations were seen with BAPG in several models. This pattern indicates that both cognition and physical fitness relate to BAPG longitudinally, but in different ways. Current and retrospective levels of physical fitness appear to be more related than rate of change, whereas those with low BAPG (younger brains) show less cognitive decline regardless of their level of cognitive ability to begin with.

Table 5.

Correlations of longitudinal variables

Correlations	PF slope		PF intercept		CA slope		CA intercept
	N = 268		N = 268		N = 271		N = 271
	r	P	r	P	r	P	r	P
GM	-0.12	0.059	-0.08	0.193	-0.14	0.025	-0.02	0.751
WM	-0.03	0.650	-0.15	0.013	-0.27	<0.001	-0.003	0.955
CSF	0.11	0.072	-0.18	0.002	-0.18	0.003	-0.02	0.784
FA	0.02	0.758	-0.17	0.005	-0.17	0.005	-0.01	0.863
FC	0.16	0.010	-0.21	0.001	-0.12	0.040	-0.04	0.534
RF struct	0.01	0.822	-0.10	0.107	-0.11	0.063	0.03	0.656
RF all	0.04	0.500	-0.13	0.037	-0.13	0.036	0.07	0.274
Conc struct	-0.03	0.582	-0.14	0.022	-0.18	0.003	-0.03	0.594
Conc all	-0.04	0.566	-0.15	0.012	-0.20	0.001	-0.03	0.577

Note: Bold values are significant at false discovery rate corrected P = 0.05, PF = physical fitness, CA = cognitive ability.

Significant associations between BAPG and physical fitness and cognitive ability remained at T6, meaning that BAPG at T6 was correlated with both current physical fitness and cognitive ability, as well as intercept of physical fitness and slope of cognitive ability (P’s < 0.03). Significant correlation was also found for change in BAPG and education (r = 0.15, P = 0.024), where individuals with longer education aged faster than those with shorter education. No association with any of the other investigated factors was found for the longitudinal difference in BAPG between the 2 imaging sessions (P’s > 0.3), and no clear trend was seen either. Thus, changes in BAPG and changes in cognition or physical fitness were not significantly associated.

Finally, Table 6 shows the results from the analysis of variance that directly compared the relation of chronological versus predicted age with the examined factors. Since no relation between BAPG and intercept of cognitive ability and slope of physical fitness was found, these variables were left out of the analysis. Predicted brain age explained more of the variance than chronological age in both physical fitness and cognitive ability, and for attrition, a similar pattern was seen as for cognitive ability.

Table 6.

Variance explained by age and predicted age

Explained variance	Education			PF T5			CA T5			Attrition			PF intercept			CA slope
	R 2 age	R 2 pred-age	P	R 2 age	R 2 pred-age	P	R 2 age	R 2 pred-age	P	R 2 age	R 2 pred-age	P	R 2 age	R 2 pred-age	P	R 2 age	R 2 pred-age	P
GM	0.169	0.164	0.805	0.192	0.221	0.216	0.301	0.315	0.667	0.018	0.032	<0.001	0.041	0.045	0.406	0.054	0.072	0.024
WM	0.169	0.168	0.995	0.192	0.221	0.224	0.301	0.345	0.207	0.018	0.035	<0.001	0.041	0.055	0.015	0.054	0.010	<0.001
CSF	0.169	0.169	0.992	0.192	0.178	0.496	0.301	0.323	0.509	0.018	0.033	<0.001	0.041	0.067	<0.001	0.054	0.080	0.002
FA	0.169	0.169	0.999	0.192	0.205	0.581	0.301	0.325	0.484	0.018	0.024	0.016	0.041	0.064	<0.001	0.054	0.076	0.005
FC	0.169	0.187	0.330	0.192	0.167	0.206	0.301	0.305	0.916	0.018	0.019	0.608	0.041	0.078	<0.001	0.054	0.063	0.205
RF struct	0.169	0.171	0.873	0.192	0.204	0.593	0.301	0.316	0.657	0.018	0.025	0.003	0.041	0.058	0.005	0.054	0.077	0.005
RF all	0.169	0.174	0.764	0.192	0.213	0.363	0.301	0.314	0.686	0.018	0.026	0.001	0.041	0.069	<0.001	0.054	0.085	<0.001
Conc struct	0.169	0.170	0.954	0.192	0.218	0.269	0.301	0.335	0.322	0.018	0.033	<0.001	0.041	0.056	0.010	0.054	0.081	0.001
Conc all	0.169	0.179	0.593	0.192	0.215	0.316	0.301	0.341	0.248	0.018	0.028	<0.001	0.041	0.059	0.004	0.054	0.084	<0.001

Note: Bold values denotes significant difference at false discovery rate corrected P = 0.05, PF = physical fitness, CA = cognitive ability.

Discussion

In this study, we addressed heterogeneity in brain aging by comparing predicted brain age with chronological age. One of the main advantages of our study is that we have a wide variety of data, including brain images, cognitive tests, and health assessment, covering several decades. A predicted brain age higher than the chronological age is indicative of accelerated aging, while a predicted brain age younger than chronological age could reflect brain maintenance. Overall, we found the chronological and predicted ages to be strongly related, and the additional prediction capacity of BAPG was limited in comparison to that of chronological age. Still, even for the models with the smallest deviation between actual and predicted age, there was a mean absolute difference of 3.5–4 years. Notably, in situations when both measures explained a relatively small portion (<10%) of the variation, the predicted age explained a significantly larger proportion of the variance than chronological age. Thus, our findings are in line with the notion that brain age may go beyond chronological age in capturing some of the vast heterogeneity in neurocognitive aging.

In support of our predictions and attesting to the validity of the brain age concept, our findings indicate that a younger brain age was related to less age-related cognitive change. Specifically, for cognitive ability, BAPG showed an association with rate of decline and current ability. Thus, our findings provided support for the brain maintenance theory of cognitive aging (Nyberg et al. 2012). Here it should be noted that the difference in BAPG between the 2 time points was not correlated with neither level of nor change in cognitive ability. The reasons for the lack of associations for longitudinal BAPG is unclear but may include reduced power and/or the necessity of employing more sophisticated statistical approaches to identify longitudinal effects (see e.g., Tucker-Drob et al. 2019). There have been some studies looking at longitudinal changes in brain age (Franke and Gaser 2012; Høgestøl et al. 2019), and future longitudinal studies of brain age predictions are warranted.

A key finding was that the results supported the hypothesis that physical fitness, both current and retrospective, was related to a younger appearing brain (i.e., brain maintenance). Relatedly, a previous cross-sectional study based on a larger sample also found a connection between BAPG and cognitive ability, as well as walking speed, lung function, and grip strength (Cole, Ritchie, et al. 2017b). The latter measure was also included in our physical fitness score. Our findings indicate that current and retrospective physical fitness is more important for brain maintenance than rate of change. By this view, individuals who have maintained a high physical fitness throughout adult life have a lower predicted brain age than those who may have improved their fitness over the last decade.

We obtained minimal support that level of education was related to apparent brain age. Specifically, with the exception for the FC model, no significant correlation was found between education and BAPG. In fact, if anything, higher education was related to accelerated aging in terms of change in BAPG, and this, however, was not consistent over prediction models and was likely a spurious finding. Taken together, our results do not provide support that longer education will protect against brain aging. Attrition was correlated with cognitive ability and also with BAPG, that is, the subjects who returned had a lower predicted brain age at baseline than those who did not return for follow-up testing. Thus, although the magnitude of the correlation between attrition and BAPG is likely too low for meaningful predictions about future dropout, a high positive BAPG might be considered a risk factor for dropout.

No significant difference was found between regression methods, indicating that brain age predictions are stable in regard to such selection. It should be noted that we settled for the default choices and did not fine-tune the hyperparameters used within these models. Considering that the majority of methods gave almost identical solutions, altering these settings would not likely have improved the predictions significantly.

We used OLS as the reference method, which may have some limitations when working with high-dimensional data (Cole and Franke 2017; Aycheh et al. 2018). This shortcoming was however not manifested in the present study, and, hence, all subsequent analyses were based on the predictions from the OLS method. It is worth noting that since the data were preprocessed with PCA, the OLS approach can also be described as a principal component regression.

All methods included in this study were supervised regression methods. Another popular approach used in brain age prediction is deep learning methods such as convolutional neural networks (Cole, Poudel, et al. 2017a; Jiang et al. 2020). These methods do often produce better predictions but need a much larger set of training data.

The multimodal methods based on concatenation performed better than the ones based on RF, both in terms of MAE and number of significant correlations. Only one of the multimodal models had a lower MAE than the best single modal method but this difference was not significant (paired t-test, P = 0.64), and there was no difference in number of significant correlations. Thus, the multimodal models did not perform noticeably better than the single-modal models. It is possible, however, that a more refined way of combining different modalities could reveal the advantage of multimodal imaging in brain age predictions (Eavani et al. 2019; Smith et al. 2020). Further, making more informed decisions about what features to include, such as cortical thickness, surface area, or subcortical volumes, derived from the structural images (Liem et al. 2017; Gutierrez Becker et al. 2018), rather than using the voxel values from the probability maps (Franke et al. 2010; Cole, Poudel, et al. 2017a), could also result in better predictions. On the other hand, if the number of features is too small, the correlation with age seems to decrease (Cole 2020).

The FC model was based on data derived in a fundamentally different way than the other modalities, since the features were obtained from a functional connectivity analysis rather than directly from the anatomical images. It is therefore reasonable that the predictions obtained from this model differ the most from all other models, as indicated by the lower correlation coefficients in Table 2. It is therefore likely that this model provides complementary information. FC resulted in the highest MAE among all models, although still within acceptable range (Liem et al. 2017; Franke and Gaser 2019).

Previous research suggests that GM is more important than WM in brain age predictions (Cole, Poudel, et al. 2017a; Sajedi and Pardakhti 2019). In this study, the opposite result was found, with both a lower MAE and a stronger correlation with cognitive ability for the age predictions obtained from the WM model. One measure in particular that stands out is the strong correlation between WM-derived BAPG and the slope of cognitive ability (r = −0.27). We suggest that this might be related to WM lesion burden in the ventricular regions, which has been associated with cognitive impairment (Karalija et al. 2019; Kaskikallio et al. 2019). This hypothesis is furthermore supported by the strong correlations with cognitive ability found for the CSF model, since WM lesions are more common in subjects with enlarged ventricles (Breteler et al. 1994), and these lesions might be classified as CSF. Predictions from the FA model, where values represent maximum anisotropy along WM tracts, did also show strong correlations with cognitive ability, although not as strong as the WM model.

One limitation of our study is the relatively small sample size. Several other similar studies are using models trained on cohorts of 2000 subjects or more (Liem et al. 2017; Cole, Ritchie, et al. 2017b). However, by using a single cohort where all images were collected on the same scanner with the same inclusion criteria, unnecessary confounders can be avoided. However, it does come with the shortcoming of smaller sample size and possibly less generalizability. Further, the age distribution in our sample is skewed, with many older and fewer younger subjects.

The age bias observed in both this and many other studies of brain age was corrected using linear regression. This approach was suggested by (Beheshti et al. 2019), although more advanced correction methods have also been suggested (Smith et al. 2019). The most common explanation of this bias is “regression to the mean” (Le et al. 2018; Liang et al. 2019; Rokicki et al. 2020), although there might be other underlying explanations as well, for example, a nonlinear relationship between age and brain measures that would be more effectively captured using a nonlinear modeling approach.

All analyses in this study were carried out on a global level, and no regional comparisons were done, neither within images nor between modalities. By investigating how different regions contribute to the brain age predictions, additional information about the regionalization of brain aging could be obtained. Such approach was, however, outside the scope for this study. For the concatenated models, features from several modalities were combined into the same PCA components, and we have not looked further into how much of the data actually used for regression originated from each modality. The dimensionality reduction was done separately in each cross-validation fold, based on the selected training data, so the composition of the PCA components varied during the prediction process.

It would also be interesting to use commonality analysis to further investigate how the brain age measurements derived from different modalities differ and interact in relations to the investigated factors. We know that the amount of correlation between BAPG and investigated factors varies between models, but it remains unclear whether the explained variance is shared between models, or whether they account for different parts of the variation. Although several of the investigated factors were correlated with each other, this should not affect the results, since each factor was analyzed separately, and such associations would not be weakened by potential collinearity.

Although there are many studies looking at the connection between predicted brain age and various diseases such as schizophrenia (Nenadića et al. 2017), epilepsy (Pardoe et al. 2017), and multiple sclerosis (Høgestøl et al. 2019), studies where these prediction methods are developed and introduced have generally aimed to minimize the difference between predicted and chronological age, by comparing the performance of different methods in terms of MAE (Franke et al. 2010; Liem et al. 2017; Cole, Poudel, et al. 2017a). If the main goal is to construct a biomarker with strong connection to modifiable factors and capacity to predict future pathologies, rather than actual age, this might not be the most effective approach, and it is therefore important to consider other measures of performance besides MAE.

In conclusion, combining several MRI modalities did not significantly improve MAE for brain age predictions but might still contribute with unique information. Choice of input data is more important than choice of regression method. Brain age predictions were associated to attrition, current and retrospective physical fitness, and cognitive ability over time, indicating that maintaining a high physical fitness throughout life contributes to brain maintenance.

Funding

The research is part of the program Paths to Healthy and Active Ageing, funded by Forskningsrådet om Hälsa, Arbetsliv och Välfärd (2013–2056). This publication is based on data collected in the Betula prospective cohort study, Umeå University, Sweden. The Betula Project is supported by a Wallenberg Scholar Grant to L.N. from Knut och Alice Wallenbergs Stiftelse and by grants from Vetenskapsrådet (K2010-61X-21446-01).

Notes

Conflict of Interest: The authors declare no conflict of interest.