Quantitative Analysis of Protein Unfolded State Energetics: Experimental and Computational Studies Demonstrate That Non-Native Side-Chain Interactions Stabilize Local Native Backbone Structure.

Abstract

Proteins fold on relatively smooth free energy landscapes which are biased towards the native state, but even simple topologies which fold rapidly, can experience roughness on their free energy landscape. The details of these interactions are difficult to elucidate experimentally. Closely related to the problem of deciphering the details of the free energy landscape is the problem of defining the interactions in the denatured state ensemble (DSE) which is populated under native conditions, i.e. under conditions where the native state is stable. The DSE of many proteins deviates from random coil models, but quantifying and defining the energetics of the transiently populated interactions in this ensemble is extremely challenging. Characterization of the DSE of proteins which fold to compact structures is also relevant to studies of intrinsically disordered proteins (IDPs) since interactions in the dynamic ensemble populated by IDPs can modulate their behavior. Here we show how experimental thermodynamic and pKa measurements can be combined with computational thermodynamic integration to quantify interactions in the DSE. We show that non-native side chain interactions can stabilize native backbone structure in the DSE and demonstrate that that even rapidly folding proteins can form energetically significant non-native interactions in their DSE. As an example, we characterize a non-native salt bridge that stabilizes local native backbone structure in the DSE of a widely studied fast-folding protein, the villin headpiece helical domain. The combined computational experimental approach is applicable to other protein unfolded states and provides insight that is impossible to obtain with either method alone.

Graphical Abstract

Introduction

Proteins typically folded on smooth free energy landscapes which are biased towards the native state, but even simple topologies which fold rapidly experience roughness on their free energy landscape. An atomic level characterization of interactions that contribute to roughness on the free energy landscape is challenging. A closely related, and also challenging, issue is the characterization of interactions formed in the denatured state ensemble (DSE) populated under native conditions. There is no standard nomenclature for protein unfolded states and in this work we use the term DSE to refer to the unfolded state ensemble populated under conditions where the native state is stable, i.e. under native conditions. The DSE of many proteins clearly deviates from classic random coil models, but quantifying and defining the transiently populated interactions in the ensemble is extremely challenging. It is particularly difficult to precisely define the energetics of these interactions. Interactions in the DSE can influence protein stability and the tendency of proteins to aggregate. These interactions can involve contacts which are found in the folded state (native interactions) as well as interactions which must be broken as the protein transitions to the folded state (non-native interactions). Here we demonstrate a hybrid experimental and computational approach that allows quantification of the energetics of specific interactions in the DSE. The approach is complimentary to MD simulations of unfolded states that provide information about the conformational ensemble, but have difficultly precisely defining the energetics of specific interactions. As an example, we characterize non-native interactions in the DSE of a small three helix protein that folds near the speed limit for folding. We show that non-native side chain interactions can stabilize local native backbone structure in the DSE and demonstrate that that even rapidly folding proteins can form energetically significant non-native interactions in their DSE which must be broken during the folding process.

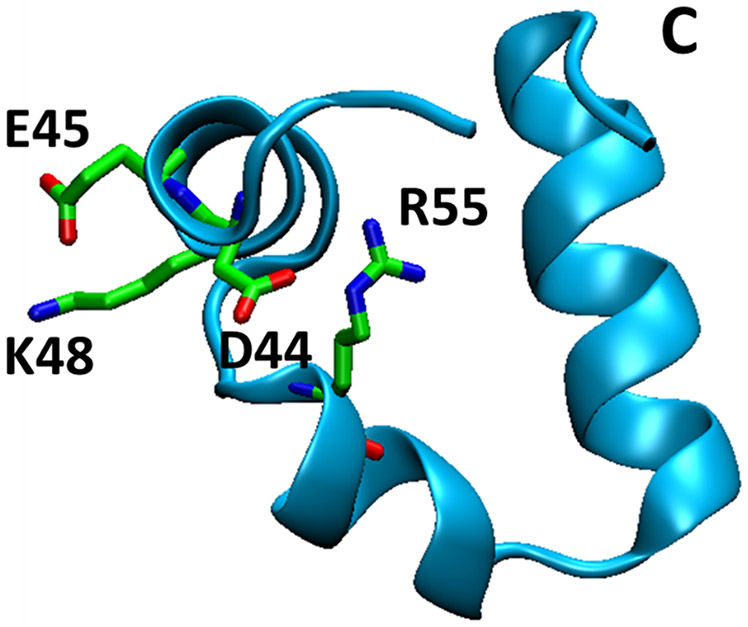
The villin headpiece subdomain (HP36), a 36-residue (or 35-residue depending on the construct used) protein, is one of the smallest naturally occurring proteins that fold cooperatively (Fig 1.)¹. The folding rate of HP36 approaches the theoretical limit for folding. Its small size, simple three-helix topology and rapid folding have made HP36 an extraordinarily popular protein model for both experimental, computational and theoretical studies of protein thermodynamics and folding^2-32. The structure of HP36 is constructed of three α-helices and the folded state contains a well packed hydrophobic core which includes three Phe residues^24-26. The free energy of folding of HP36 is within the expected range for a protein of this size and the midpoint of the thermal unfolding transition is high, owing to the small change in heat capacity (ΔCp) upon unfolding^{5,6, 26}. The small ΔCp is expected and is simply a consequence of the small size of the protein²⁶.

Figure 1.

Cartoon diagram of the structure of HP36 (PDB code 1yrf). D44, E45, K48 and R55 are shown in stick format. The C-terminus is labeled.

Extensive experimental and computational studies have been conducted on the DSE of HP36 and indicate that some native-like local secondary structure exists in the DSE, but the possible role of non-native interactions in the DSE of HP36 are not understood and the energetics of DSE contacts have not been measured^{4, 7-8, 27-31}. Indeed, measurement of the strength of DSE interactions made by specific residues is very challenging and the lack of such information is a significant impediment to a full description of protein unfolded states. A peptide fragment, HP21, composed of helix 1 and helix 2 of HP36, has been used as an experimental model for studying the DSE of HP36. HP21 lacks well defined tertiary structure, but has considerable native helical content^{27-28, 31}. Temperature-jump infrared spectroscopy on intact HP36, in combination with site-specific labeling, indicates that helix 3 is the most stable followed by helix 1 and then helix 2³².

Several computational studies have suggested that residual native and non-native structures may be present in the DSE of HP36^{4, 7-8, 30}, including a non-native salt bridge between D44 and K48^{4, 8}. However, the different MD simulations are not all consistent with each other and the simulations do not provide free energies of DSE interactions. Note the notation used here corresponds to the numbering of this region in the full villin headpiece plus an additional Met. Thus, the first residue in the construct studied here is designated as M41 and the second residue is L42. This notation is adopted to facilitate comparison with earlier work. Recent work has pointed out issues with MD simulations of unfolded states and argues that they may lead to force field dependent and sometimes overly compact structures^33-37. Modifications to protein force fields and water models to overcome these difficulties are ongoing and show considerable promise^38-47, but experimental evidence for specific DSE interactions observed in MD simulations of HP36 is scarce.

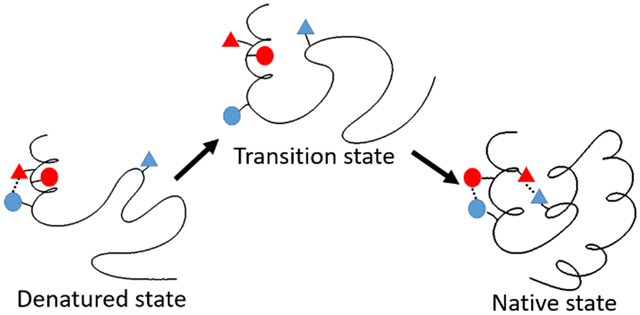
Prior experimental work using mutagenesis and pKa measurements has demonstrated that K48 and E45 form a salt bridge in the native state of HP36⁶. However, a K48M mutation showed enhanced stability relative to wild-type even though it disrupts the native state salt bridge. This effect was proposed to be due to the disruption of favorable interactions involving K48 in the DSE of HP36⁶, but the origin of these effects is not known. Here we use double mutant thermodynamic cycle analysis (Fig 2), combined with pKa analysis of both the DSE and native state and alchemical free energy calculations to show that the D44 and K48 side chains make favorable non-native electrostatic interactions in the DSE of HP36 and we quantify the strength of the interaction. This i to i+3 salt bridge is expected to stabilize the native local helical structure found in the DSE. However, these residues do not form a salt bridge in the native state of HP36, rather D44 forms a tertiary salt bridge with R55 which is located in a different helix, while K48 forms a salt bridge with E45⁶. Thus, the D44 K48 DSE interaction needs to be broken during the transition to the native state and in this sense represents an interaction that contributes to roughness on the free energy landscape.

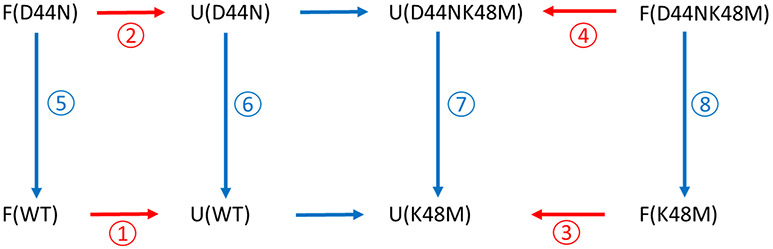
Figure 2.

Thermodynamic cycles for the unfolding of wildtype HP36 and its mutants, HP36D44N, HP36K48M and HP36D44NK48M. The red arrows are the unfolding processes of HP36 and its mutants. Blue arrows are the mutation processes in the context of native/folded state (F) and DSE (U). Circled numbers represent the free energy associated with the processes. The values denoted in red can be experimentally measured; those in blue cannot be, but can be calculated using alchemical free energy methods.

This study reveals that non-native salt bridges with significant strength can exist in the DSE and illustrates how they are compatible with local native-like backbone structure. The combined computational experimental approach illustrated here is applicable to other protein unfolded states and provides insight that is impossible to obtain with either method alone. The assumptions inherent in the analysis are discussed below, but the key for the simplest approach is being able to adequately describe the titration behavior of the native state and DSE as the sum of a set of pKa values.

Methods

Protein expression and purification

HP36 wildtype and mutants were expressed as a fusion protein with NTL9 as described⁵. The factor Xa cleavage was carried out at 23 °C for 16-20 h. The proteins were purified by ion exchange chromatography and reverse-phase HPLC using a gradient of 30-65% buffer B in 70 minutes. The identity was confirmed by matrix-assisted laser desorption and ionization time-of-flight mass spectrometry (MALDI).

Protein stability measurements

Protein stability was measured by CD monitored urea and thermal denaturation experiments. Urea induced unfolding was performed at 25 °C and 222 nm with samples of 15-30 μM protein in 10 mM sodium acetate and 150 mM sodium chloride at pH 6.0 on an AVIV 202SF spectrophotometer. The concentration of urea was increased from 0 to about 10 M in ~0.25 M steps. Urea concentrations were determined by measuring the refractive index. Urea unfolding curves were analyzed by a non-linear least squares fit to standard expression to give the value of ΔG⁰ in the absence of urea. More details can be found in prior work ^5,6,26. Thermal unfolding experiments were performed using an Applied Photophysics Chirascan CD instrument at 222 nm over the range of 2 °C to 94 °C in 2 °C intervals. Thermal unfolding curves provide the midpoint of unfolding, T_m, and the value of ΔH°(T_m). These parameters are combined with the known change in heat capacity upon unfolding, ΔC_p, and used in the Gibbs-Helmholtz equation to obtain ΔG° (25 °C)²⁶. The buffer and protein concentration were the same as used in the urea denaturation experiments. Measurements were made at pH 3.00 and 6.00. The reversibility of unfolding was confirmed by comparing the initial CD signal at the start of the run to the signal measured after the run was completed and the sample was cooled to the starting temperature. The transitions were fully reversible.

Protein pKa measurements

The pKa values of Asp, Glu and the C-terminus in the native state of the HP36D44N and HP36D44NK48M mutants were measured using NMR. The chemical shifts of the Hβ and Hγ protons were collected. The Hα chemical shifts of the C-terminus residue, F76, were used to measure the pKa of the C-terminus. The chemical shift data collected from pH=2 to pH=7 were fit to the standard expression with a Hill coefficient of 1.0 to yield the pKa values⁶. All mutants and wild type HP36 remained fully folded over this pH range and the relevant NMR resonances are well resolved throughout the titration. This enables straight forward determination of the relevant pKa’s.

Free energy calculations for the Asp44-to-Asn44 and K48-to-M48 mutations in the native state of HP36

The PDB file 1YRF was used for the structure of HP36. Hydrogen atoms were added using the MolProbity program⁴⁸. Side chain rotamer states for Asn/Gln were corrected based on suggestions provided by MolProbity. Lys, Arg side chains and the N-terminus were set to be protonated and Asp, Glu side chains and the C-terminus were set to be unprotonated. Waters present in X-ray structures were kept. Sodium and chloride ions were added and the number of sodium and chloride ions was adjusted before the simulations so that the calculation always starts from a neutral system. The concentration of NaCl was ~160mM. The D44-to-N mutation causes a net charge change of 0 to 1 in both wild-type and K48M background. Similarly, the K48-to-M mutation causes a net charge change of 0 to −1 in both wild-type and D44N background. Truncated octahedron boxes were used to solvate the proteins. Free energy calculations were performed using non-softcore thermodynamic integration (TI) implemented in Amber16^49-51. The atom mappings for the transition of D-to-N and K-to-M can be found in supporting Table S1&S2. The Amber force field ff14SB and the TIP3P water model were used for the TI calculations^52-53. The X-ray structure as determined at low temperature, consequently minimization and equilibration under constant pressure⁵⁴ were conducted to heat up and relax the X-ray structures. Energy minimization was conducted using gradient descent algorithm with 100 kcal/mol position restraints on all heavy atoms of proteins. The maximal number of cycles was 10000. A 0.1 ns constant volume MD simulation was then conducted to slowly heat up the structures from 150K to 298K with 100 kcal/mol position restraints on all heavy atoms of proteins. A 0.1 ns constant pressure MD simulation was conducted with 100 kcal/mol position restraints on all heavy atoms of proteins. A 0.25 ns constant pressure MD simulation was conducted with 10 kcal/mol position restraints on all heavy atoms of proteins. To relax the side chains, a 0.1 ns constant pressure MD simulation was conducted with 10 kcal/mol position restraints on all CA, C and N atoms. A 0.1 ns constant pressure MD simulation was conducted with 1 kcal/mol position restraints on all CA,C and N atoms. A 0.1 ns constant pressure MD simulation was conducted with 0.1 kcal/mol position restraints on all CA, C and N atoms. The mutation site (residue 44 or 48) was excluded in the restraints. In the last step 0.25 ns constant pressure MD simulation was conducted with no restraints. A 1 fs step size was used for the equilibration. Production runs were conducted under constant pressure⁵⁴. Pressure scaling was controlled by isotropic position scaling. The pressure relaxation time was set to 0.1 ps. The temperature was set to 298K and no salt ion was included. Langevin dynamics was used to control temperature and the collision frequency was set to be 1.0 ps⁻¹. Particle mesh Ewald methods were used to calculate electrostatic energies⁵⁵. Hydrogen atoms were constrained using the SHAKE algorithm⁵⁶. The cutoff of non-bonded interactions was set to 8 Å. A timestep of 2fs was used. The simulation time length for each λ window was 72 ns. Data from the last 48 ns of each window was analyzed. The trapezoidal rule was used for the integration of all λ windows. Three independent TI calculations were conducted for each mutation with different initial positions of ions. The uncertainty is the standard deviation of the three independent calculations.

Mutation of D-to-N was conducted in one transition step with equally spaced λ from 0 to 1 with an interval of 0.1. Mutation of K-to-M was conducted in two transition steps. In the first step, the charges were changed with equally spaced λ from 0 to 1 with an interval of 0.1. In the second step, the VDW interactions were changed with a series of λ = 0.00922, 0.04794, 0.11505, 0.20634, 0.31608, 0.43738, 0.56262, 0.68392, 0.79366 0.88495, 0.95206 and 0.99078. Amber library files were built for Asp and Met with dummy atoms to match the disappearing atoms in Asn and Lys. The mapping of atoms for D-to-N and K-to-M mutations can be found in Tables S1 and S2 in the supporting information.

Propagation of errors

The accumulation of errors was calculated using the following equation.

$$\Delta =\sqrt{\begin{array}{c}\hfill (uncertaintyof①{)}^2+(uncertaintyof②{)}^2\hfill \\ \hfill +(uncertaintyof③{)}^2+(uncertaintyof④{)}^2\hfill \end{array}}$$ (1)

Results and Discussion

D44 has a suppressed pKa in the denatured state ensemble of HP36.

The pKa of titratable residues reflects the electrostatic interactions they experienced under the circumstances where they are measured^57-62. Titratable residues can experience either favorable or unfavorable electrostatic interactions in the DSE. Again, we use the terminology DSE to refer to the unfolded state in equilibrium with the folded state under native conditions where the folded state is the most stable. The pKa’s of titratable residues in the DSE of various proteins have been studied by using either direct NMR measurements on unfolded states populated under non-native conditions^63-65 or by using the Tanford-Wyman linkage relationship to probe pKa values of the DSE under native condtions^66-70. The latter method is indirect, but provides information about pKa values in the DSE under native conditions. The Tanford-Wyman linkage equation is an exact relationship that relates the change in stability as function of pH to the difference in the number of protons bound to the native state and DSE. If protein stability and proton binding to the native state can be measured as function of pH, the relationship can be used to interrogate the properties of the DSE^67-70.

To apply the Tanford-Wyman linkage relationship, the pKa values of acidic residues in the DSE of HP36 were first estimated following the approach of Shen and coworkers ⁶⁶. In this approach, native state pKa values are combined with pH dependent stability measurements to infer DSE pKa’s Stability measurements for wild type HP36 and its mutants were conducted at pH = 3.0 and pH = 6.0 respectively. Previously measured native state pKa values indicate that the acid residues in HP36 are partially protonated at pH = 3.0 in the native state, (i.e. the protein ensemble contains a mixed population of molecules with protonated and deprotonated individual acidic residues), and are fully deprotonated at pH = 6.0 in the native state⁶. The approach does not require that the sidechains are fully protonated at the low pH; all that is required is that there is a significant change in the population of the protonated and deprotonated forms during the titration. This ensures that the stability difference of HP36 at pH=3.0 and pH=6.0 includes the protonation free energies contributed by the acidic residues. Protein stability was measured using thermal unfolding experiments at pH = 3.0 since lowering the pH further in the presence of urea requires the addition of large amounts of acid due to the protonation of urea and hence involves a change in ionic strength. At pH = 6.0, the stabilities were measured using urea unfolding experiments. The thermodynamic data are listed in Table 1. The unfolding free energy with respect to the pKa values in the folded and unfolded state and of the pH can be expressed as:

$$\Delta \Delta G=\Delta G^{pH1}-\Delta G^{pH2}=RT{\sum }_{i}ln\frac{(1+{10}^{(p{K}_a^F(i)-pH2)})(1+{10}^{(p{K}_a^U(i)-pH1)})}{(1+{10}^{(p{K}_a^U(i)-pH2)})(1+{10}^{(p{K}_a^F(i)-pH1)})}$$ (2)

where ΔG^pH1 and ΔG^pH2 are the unfolding free energy measured at pH₁ and pH₂ respectively. For this study, pH₁ = 6.0 and pH₂ = 3.0 were chosen since the thermodynamic data was measured at these two pH values (Table 1). i represents all titratable residues in wildtype HP36 and mutants.

Table 1.

Thermodynamic parameters for the unfolding of HP36 wildtype and mutants at pH=3.0 and pH=6.0 at 25 °C.

Protein	pH 6.0	pH 3.0
	ΔG° (kcal mol−1)	Tm (°C)	ΔH°(Tm) (kcal mol−1)	ΔG° (kcal mol−1)
HP36 WT	3.39±0.06	52.8±0.2	25.4±0.5	1.70
HP36D44N	2.93±0.12	51.3±0.1	26.5±0.4	1.73
HP36E45Q	2.99±0.11	52.7±0.1	27.8±0.3	1.90
HP36D46N	2.51±0.09	49.7±0.1	25.9±0.4	1.61
HP36E72Q	3.28±0.10	50.4±0.1	25.4±0.3	1.60

The listed uncertainties are the standard errors to the fit. Values at pH 6.0 were determined by fitting urea induced unfolding data. Values at pH 3.0 were determined via fitting of thermal unfolding data to obtain T_m and ΔH°(T_m). These values were combined with the previously determinded value of ΔCp (0.38 Kcal mol⁻¹ deg⁻¹ )to obtain ΔG° at 25 °C ⁵. The thermal unfolding curves and chemical denaturant unfolding curves measured by CD can be found in supporting figures S1&S2.

If we assume the mutation has a negligible effect on pKa of other titratable residues in the DSE.

$$\begin{gathered} \Delta \Delta G^{WT}-\Delta \Delta G^{MU}=\Delta G^{pH1,WT}-\Delta G^{pH2,WT}-(\Delta G^{pH1,MU}-\Delta G^{pH2,MU}) \\ =RTln\frac{\left(1+{10}^{\left(p{K}_a^{F,WT}(j)-pH2\right)}\right)\left(1+{10}^{\left(p{K}_a^{U,WT}(j)-pH1\right)}\right)}{\left(1+{10}^{\left(p{K}_a^{U,WT}(j)-pH2\right)}\right)\left(1+{10}^{\left(p{K}_a^{F,WT}(j)-pH1\right)}\right)}+RT{\sum }_{i\ne j}ln\frac{\left(1+{10}^{\left(p{K}_a^{F,WT}(i)-pH2\right)}\right)}{\left(1+{10}^{\left(p{K}_a^{F,WT}(i)-pH1\right)}\right)}-RT{\sum }_{i\ne j}ln\frac{\left(1+{10}^{\left(p{K}_a^{F,MU}(i)-pH2\right)}\right)}{\left(1+{10}^{\left(p{K}_a^{F,MU}(i)-pH1\right)}\right)} \end{gathered}$$ (3)

where j is the residue of interest. WT and MU stand for wildtype HP36 and HP36 mutant respectively. The mutant has a neutral analog in the place of the residue j. For example, HP36D44N was used as the mutant to determine the pKa of D44 in the DSE of HP36 using this method. The last two terms on the right side of equation 3 will be 0, if we assume that the mutation has negligible effect on the pKa of other residues in the native state. This is the case for HP36⁶_. However, it is important to note that this assumption is not necessary when native state pKa’s can be directly measured, as is the case here.

The basic residues and the N-terminus of HP36 have pKa values higher than 6.0, and thus only acidic residues need to be considered in equation 3. The native state pKa values for wild type HP36 and the K48M mutant have been previously reported⁶. We measured the pKa values for the D44N single mutant and the D44NK48M double mutant. The native state pKa values of the acidic residues and the C-terminus of wildtype HP36 and the mutants are listed in Table 2. The pKa’s in the DSE of HP36 were first estimated using Eq.3 with the assumption that the mutation of residue j has no effect on the pKa’s of other residues in both the native and DSE (Table 3). Control experiments have shown that mutations of HP36 involving single D/N and E/Q substitutions that remove one acidic residue at a time do not perturb the native state pKa values of the other acidic residues. It is harder to test that the titration behavior of the DSE is described as the sum of individually titrating groups. Given the more dynamic nature of the DSE relative to the native state, it is likely that the DSE pKa’s are not significantly impacted by mutation of the other acidic residues, but is not possible to directly test if the mutation of one acidic residue perturbs the DSE pKa of another. We have shown that the acidic residues in peptide fragments of HP36 are not affected by mutation of other acidic residues⁶ and this together with the native state data lends credence to the assumption for the actual DSE.

Table 2.

pKa of acidic residues in the native state of wildtype HP36 and HP36 mutants.

Protein/Residue	D44	E45	D46	E72	C-terminus
HP36WT6	3.04±0.12	3.95±0.02	3.44±0.11	4.37±0.03	2.91±0.08
HP36D44N	N/A	3.86±0.02	3.43±0.05	4.32±0.02	2.85±0.10
HP36K48M6	3.23±0.07	4.68±0.09	3.38±0.05	4.41±0.03	2.90±0.06
HP36D44NK48M	N/A	4.39±0.05	3.49±0.08	4.37±0.03	2.96±0.09

pKa values of HP36WT and HP36K48M were taken from reference⁶. The values for HP36D44N and HP36D44NK48M were measured as part of this work. Curves for the pKa determinations via chemical shift monitored pH titrations can be found in supporting figures S3&S4.

Table 3.

Estimated pKa of acidic residues in the DSE HP36 and measured pKa of acidic residues in the peptide fragments. The fragments chosen were residues 41 to 53 for D44, E45, D46 and residues 70 to 76 for E72. These fragments capture local sequence effects, but are too small for tertiary interactions. The fragments also lack significant secondary structure.

residue	estimated wildtype DSE pKa	pKa in peptide fragment6
D44	3.58	4.00
E45	4.42	4.50
D46	4.12	3.86
E72	4.38	4.15

The pKa of residues in the peptide fragments are taken from reference⁶.

To provide a reference, the DSE pKa values were compared to the pKa values for the same residues in a set of small peptide fragments. The use of reference peptides is not required; they simply provide a convenient benchmark that helps to account for local sequence effects, such as those that might arise from nearby charged residues or residues that could form local hydrophobic clusters ⁶⁹. The reference peptides used here have been shown to be largely unstructured in isolation⁶. The pKa of the acidic residues in the actual DSE of full-length HP36 will be affected by both residual tertiary interactions and any secondary structure in the DSE. The use of peptide fragments as a reference state does not affect the conclusions, but it allows one to distinguish between local sequence effects in the DSE in the absence of significant structure and more interesting effects. E45 has a similar DSE pKa value compared to its counterpart in the appropriate peptide fragment⁶, while D46 and E72 have DSE pKa values 0.23 and 0.26 higher than in their respective peptide fragments. However, the pKa of D44 in the DSE is 0.42 lower than that of the peptide fragment, which indicates that D44 makes favorable electrostatic interactions in the DSE of HP36, beyond those which are captured in the fragment peptides. D44 is part of a tri-acidic sequence comprised of residues 44 through 46 and we tested whether or not altering the local sequence significantly impacts the peptide fragment pKa of D44. A variant peptide with E45 replaced by Q was prepared and the pKa’s measured by NMR. The pKa of D44 and D46 are not shifted in this fragment relative to the wildtype peptide⁶, indicating that the pKa of D44 in the fragment is not significantly altered by its immediate neighbor.

The pKa of E45, D46, E72 and the carboxyl group of C-terminus of HP36 D44N were measured to examine the assumption that the D44-to-N44 mutation has no effect on the pKa of other acidic residues in the native state of HP36. The results are listed in Table 2. For comparison, the pKa of E45, D46, E72 and the carboxyl group of HP36K48M and HP36D44NK48M are also listed. These experiments indicate that the D44N mutation does not significantly alter the native state pKa’s of other acidic residues. The largest shift is only 0.09 pKa units. We also examined the effect of the K48M mutation on the native state pK’s. Notably this mutation only perturbs the pKa of E45 which is consistent with the formation of a K48-E45 salt bridge in the native state. The K48M mutation does not significantly impact the pKa of D44 in the native state.

In order to test the robustness of our DSE pKa calculations, we repeated the calculation of the DSE pKa’s using the native state pKa’s determined for HP36D44N (Table 2) and obtained a DSE pKa of 3.65 for D44, which is very close to the value of 3.58 deduced using the simpler method. In both cases the DSE pKa of D44 is clearly shifted below the peptide fragment value, indicating that D44 experiences favorable electrostatic interactions in the DSE beyond those due to local sequence effects.

Double mutant cycle analysis provides additional evidence that there are favorable interactions between D44 and K48 in the unfolded state

K48 has been suggested to make favorable interactions in the DSE of HP36⁶ and D44 has a suppressed DSE pKa, hence it is likely that they make favorable interactions with each other in the DSE. In order to determine whether they form a favorable interaction in the DSE and to quantitatively estimate the strength of the interaction, a double mutant thermodynamic cycle analysis was designed (Fig. 2) that allows the deconvolution of native and DSE effects. Conventional double mutant cycles usually do not consider the effect of changes in the energetics of the DSE.

In these two thermodynamic cycles, ⑥-⑤=①-② and ⑦-⑧=③-④. These two equations lead to ⑥-⑦-(⑤-⑧) =①-②- (③-④) in which ①, ②, ③ and ④ are the standard unfolding free energies listed in Table 4. If non-electrostatic perturbations are negligible in this thermodynamic cycle, ⑤-⑧ and ⑥-⑦ can be interpreted as the electrostatic interaction strength between D44 and K48 in the native state and in the DSE respectively. Asn and Met are neutral analogs of Asp and Lys respectively which are expected to cause little perturbations to the structure and energetics of HP36 in the native and DSE besides the loss of electrostatic interactions. However, it is formally possible that N44 and M48 introduce unexpected non-electrostatic perturbations into HP36.

Table 4.

Thermodynamic parameters for the unfolding of HP36 WT and the mutants.

Protein	ΔG° (kcal mol−1)	m-value (mol−1 K−1)	Midpoint of the unfolding transition CM (M)
HP36	3.39 ± 0.06	0.52 ± 0.01	6.5
HP36D44N	2.93 ± 0.12	0.63 ± 0.02	4.7
HP36K48M	4.26 ± 0.07	0.52 ± 0.01	8.2
HP36D44NK48M	3.05 ± 0.07	0.49 ± 0.02	6.3

The uncertainties are the standard error to the fits. Experiments were performed at 25 °C with 10 mM sodium acetate and 150 mM sodium chloride, pH 6.0.

Urea unfolding experiments were used to obtain the unfolding free energies of wild-type HP36 (①), HP36D44N (②), HP36K48M (③) and HP36D44NK48M (④) (Table 4). This leads to ⑥-⑦-(⑤-⑧) =①-②- (③-④) = −0.75 ± 0.17 kcal mol⁻¹ and indicates that the interaction of D44 and K48 is −0.75± 0.17 kcal/mol more favorable in the DSE than in the native state. The value is the net difference in interaction strength between the native state and the DSE and needs to be deconvoluted to obtain the absolute interaction strength in the DSE.

In order to estimate the interaction strength between D44 and K48 in the DSE, (⑥-⑦), the interaction strength between D44 and K48 in the native state, (⑤-⑧), must be obtained. It can be estimated by using:

$$⑤\text{-}⑧=2.303RT\Delta pKa$$ (4)

Where ΔpKa is the pKa shift of D44 in the native state caused by the K48 to M48 mutation. Using the known pKa shift ⁶, the electrostatic interaction strength between D44 and K48 in the native state was calculated to be −0.27 kcal/mol. Thus, if the non-electrostatic perturbations caused by the mutations are negligible, D44 and K48 have a favorable electrostatic interaction of −1.02 kcal/mol in the DSE of HP36 (−0.75 kcal/mol – 0.27 kcal/mol). This value is obtained from (⑤-⑧) + (①-②- (③-④)). Note that the value of ①-②- (③-④) obtained from the double mutants cycle also includes any non-electrostatic perturbations caused by the D44-to-N44 and K48-to-M48 mutations. Moreover, an error of 0.1 unit of pKa translates to an error of 0.14 kcal/mol in free energy at 25 °C. Thus, it is desirable to obtain an independent estimate of native state effects. Hence, we used alchemical free energy calculations to independently investigate the effect of the D44-to-N44 and K48-to-M48 mutations in the native state, and to estimate any non-electrostatic contribution that may need to be deconvoluted to more accurately estimate the DSE interactions.

Computational studies confirmed that D44 and K48 make favorable electrostatic interactions in the denatured state ensemble

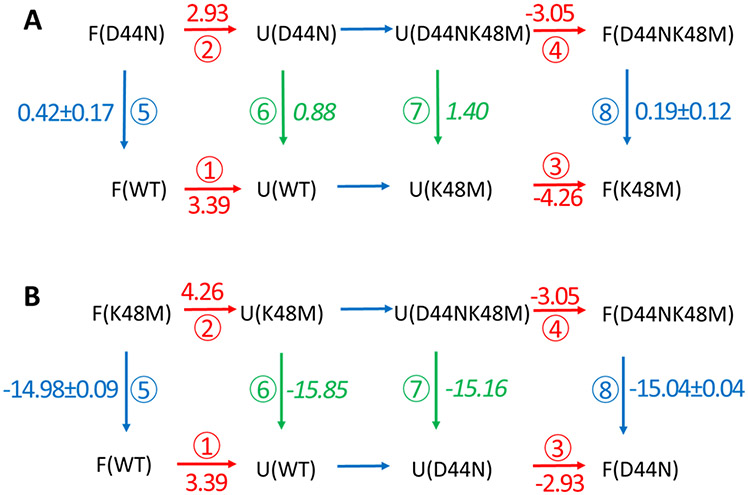
The estimation of the native state effects based upon the pKa shift, ΔpKa, ignores any non-electrostatic perturbation caused by the mutations and only considers the electrostatic interactions between D44 and K48. In contrast, the value of the native state interaction strength between D44 and K48 calculated by free energy calculations, ⑤-⑧, includes all interactions introduced by the mutations. Two thermodynamic integration (TI) calculations of the D44-to-N44 mutation were conducted to provide separate estimates of ⑤-⑧ (Fig. 3), one in the context of wild-type HP36 and the other in the context of HP36K48M. The results show that the overall free energy change introduced by the D44-to-N44 mutations in the native state is ⑤-⑧ = 0.23 ± 0.21 kcal/mol. (Fig 3A) This leads to a refined estimate of the strength of the interaction in the DSE, ⑥-⑦, = −0.52 ± 0.27 kcal/mol. The value of ⑤-⑧ can also be obtained by conducting TI calculations of the K48-to-M48 mutation in the context of wild-type HP36 and HP36D44N (Fig. 3B). These calculations give a value of ⑤-⑧ of 0.06 ± 0.10 kcal/mol, which leads to a value of the DSE interaction, ⑥-⑦, = −0.69 ± 0.20 kcal/mol. This is in excellent agreement with the other estimates.

Figure 3.

Thermodynamic cycles for the transitions among HP36WT, HP36D44N, HP36K48M and HPD44NK48M. (A) Cycle focusing on the D44N mutation. (B) Cycle focusing on the K48M mutation. In both cases F and U denote the folded (native) and the DSE respectively. The red numbers are unfolding free energies measured by experiment. The blue numbers are calculated free energy changes in the folded state. Green numbers in italics are free energy changes in the DSE calculated using two unfolding free energies and one calculated folded state free energy from the same thermodynamic cycle. For example, ⑤ + ① − ② = ⑥. The difference in the green numbers within a given cycle is equal to ⑥-⑦ and is equal to the strength of the D44 K48 interaction in the DSE. The difference in the blue numbers in a given cycle is equal to ⑤-⑧ and is equal to the strength of the D44 K48 interaction in the folded state. All free energies are given in kcal/mol.

Note that the value of ⑥-⑦ includes contributions from any newly formed interactions made by N44 and M48 as well as any contributions from the removal of interactions between D44 and K48 in the DSE of HP36. If N44 and M48 cause little to no perturbation to the DSE beyond their effect on electrostatics, the electrostatic interaction strength between D44 and K48 in the DSE is estimated to range from −0.69 ± 0.20 to −0.52 ± 0.27 kcal/mol. This is in excellent agreement with the independent estimate obtained using native state pKa measurements in combination with stability measurements. The critical point is that the three approaches yield very similar values; this provides another layer of confidence in the analysis.

Conclusions

This study illustrates how experiment and calculations can be combined to provide new insight into the nature and strength of DSE interactions. The approach is complimentary to all atom simulations of the DSE which provide an overall structural description of the conformational properties of the ensemble^71-74. The pKa of D44 was found to be suppressed in the DSE of HP36 and K48 was found to make favorable electrostatic interactions in the DSE of HP36⁶. Together these observations strongly suggest that a non-native salt bridge between D44 and K48 is formed in the DSE. The double mutant cycle analysis presented here revealed that the D44 and K48 DSE electrostatic interaction is 0.75 kcal/mol more favorable than the same interaction in the native state of HP36. Determination of the absolute energetics of the interaction in the DSE requires knowledge of the strength of the interaction in the native state. In this work, two independent approaches were used to deconvolve the native state effects. The native state pKa measurements of D44 in both HP36WT and HP36K48M show that the electrostatic interaction between D44 and K48 is about −0.27 kcal/mol in the native state. Combining these values gives a quantitative estimate of the strength of the D44-K48 electrostatic interaction in the DSE of −0.27 – 0.75 = −1.02 kcal/mol. An alternative estimate can be obtained using TI calculations to deconvolve the effects of native state interactions. Importantly, the TI calculations also consider non-electrostatic contributions caused by the mutations. They show that the strength of the native state interactions between D44 and K48 ranges from +0.06 to +0.23 kcal/mol. Using the high end of this range yields a net DSE effect of 0.23 – 0.75 = −0.52 kcal/mol. Thus, the predicted interaction strength between D44 and K48 in the DSE of HP36 ranges from −0.52 to −1.02 kcal/mol. This interaction involves residues close in sequence and could be able to form early in folding, however it needs to be broken during the transition to the native state as D44 interacts with R55 in a different element of secondary structure and K48 interacts with E45 in the native state. The D44-K48 non-native salt bridge provides an example of an interaction which contributes to roughness on the free energy landscape for folding.

In summary, this work provides an atomic level view of non-native side chain interactions in the DSE and shows how they can stabilize native-like secondary structure. The case examined here shows that non-native interactions can play a role in the free energy landscape, even for fast folding proteins. It is natural to inquire how general such interactions may be. The question is difficult to answer, but there are many examples of electrostatic interactions in the DSE of proteins ^63-70 and there are also many examples of native secondary structure in the DSE including helical structure, thus we suspect other examples of these types of interactions will emerge. The work illustrates how experimental measurements can be combined with alchemical free energy calculations to define the energetics of DSE interactions and shows how the combined approach provides information that cannot be obtained using either experiments or simulations alone. The approach infers information about the energetics of the DSE from information collected on the native state and thus avoids any potential difficulties with sampling issues of long-time MD simulations. The strategy provides reliable estimation of residue-specific energetics in the DSE and is complimentary to methods that focus on a structural overall view of the DSE ensemble and to approaches that examine the effect of mutations on structural parameters such as Rg or specific FRET derived distances. The approach illustrated here is applicable to other proteins that have a high resolution structure, are suitable for NMR studies of native state pKa’s, and for which accurate thermodynamic stability measurements can be made.