Solubility Determination, Hansen Solubility Parameters and Thermodynamic Evaluation of Thymoquinone in (Isopropanol + Water) Compositions

Abstract

This article studies the solubility, Hansen solubility parameters (HSPs), and thermodynamic behavior of a naturally-derived bioactive thymoquinone (TQ) in different binary combinations of isopropanol (IPA) and water (H₂O). The mole fraction solubilities (x₃) of TQ in various (IPA + H₂O) compositions are measured at 298.2–318.2 K and 0.1 MPa. The HSPs of TQ, neat IPA, neat H₂O, and binary (IPA + H₂O) compositions free of TQ are also determined. The x₃ data of TQ are regressed by van’t Hoff, Apelblat, Yalkowsky–Roseman, Buchowski–Ksiazczak λh, Jouyban–Acree, and Jouyban–Acree–van’t Hoff models. The maximum and minimum x₃ values of TQ are recorded in neat IPA (7.63 × 10⁻² at 318.2 K) and neat H₂O (8.25 × 10⁻⁵ at 298.2 K), respectively. The solubility of TQ is recorded as increasing with the rise in temperature and IPA mass fraction in all (IPA + H₂O) mixtures, including pure IPA and pure H₂O. The HSP of TQ is similar to that of pure IPA, suggesting the great potential of IPA in TQ solubilization. The maximum molecular solute-solvent interactions are found in TQ-IPA compared to TQ-H₂O. A thermodynamic study indicates an endothermic and entropy-driven dissolution of TQ in all (IPA + H₂O) mixtures, including pure IPA and pure H₂O.

1. Introduction

Thymoquinone (TQ, Figure 1) is a naturally-derived bioactive compound, which is isolated mainly from the essential oils of Nigella sativa [1,2]. In the literature, a variety of therapeutic/pharmacological effects of TQ have been reported [3,4,5,6,7]. However, a high amount of TQ is required to produce its therapeutic efficacy, due to its poor water solubility [7,8].

Figure 1.

Chemical structure of thymoquinone (TQ).

The solubility data of poorly water-soluble naturally-derived bioactive compounds in cosolvent mixtures have a significant role in various industrial processes, such as purification, recrystallization, drug discovery, and formulation development [9,10,11,12,13]. The potential of isopropanol (IPA) has been proved in enhancing the solubility of various poorly soluble bioactive compounds, such as ferulic acid, hesperidin, iminodibenzyl, and quinocetone in the literature [10,14,15,16]. Various formulation strategies, including nanomedicines and advanced drug delivery systems, have been adopted for the solubility/dissolution and bioavailability improvement of TQ in the literature [17,18,19,20,21,22]. The solubility of TQ in neat water (H₂O) and neat isopropanol (IPA) has been documented well in the literature [7,23,24]. However, the solubility data of TQ in various (IPA + H₂O) mixtures is not studied and reported in the literature.

Therefore, the solubility data of TQ in various (IPA + H₂O) mixtures, including pure IPA and pure H₂O at 298.2–318.2 K and 0.1 MPa, respectively, are studied and reported in this work. The thermodynamic behavior of TQ in various (IPA + H₂O) compositions, including neat IPA and neat H₂O, was also evaluated. The solubility parameters for free TQ, neat IPA, neat H₂O, and various (IPA + H₂O) mixtures free of TQ were also predicted to correlate with experimental solubility data. The activity coefficients of TQ were also determined to evaluate the TQ-IPA or TQ-H₂O interactions at the molecular level. The physicochemical data of TQ in various (IPA + H₂O) combinations reported in this investigation would be applicable in “purification, recrystallization, drug discovery, preformulation studies, formulation development, and preclinical studies” of TQ at laboratory and industrial scale.

2. Results and Discussion

2.1. TQ Solubility Determination

The experimental solubilities of TQ in binary (IPA + H₂O) mixtures, including pure IPA and pure H₂O at 298.2–318.2 and 0.1 MPa, respectively, are included in Table 1. The solubility of TQ in pure IPA and pure H₂O are documented well in the literature [7,23,24]. However, there are no reports on solubility values of TQ in binary (IPA + H₂O) combinations. Some other cosolvents, such as dimethyl sulfoxide, carbitol, and polyethyleen glycol-400, etc., have been studied to solubilize TQ in our previous publication [24]. In this study, only IPA was studied in the solubilization of TQ in H₂O. The equilibrium solubility of TQ in neat H₂O at 298.2 K was reported as 740.63 µg mL⁻¹ (equivalent to 7.75 × 10⁻⁵ in mole fraction) by Salmani et al. [23]. The mole fraction solubility of TQ in neat H₂O at 298.2 K was determined as 8.27 × 10⁻⁵ by Ahmad et al. [24]. The mole fraction solubility of TQ in neat H₂O at 298.2 K was obtained as 8.25 × 10⁻³ in this research (Table 1). The equilibrium solubility of TQ in neat IPA at 298.2 K was reported as 165.54 mg mL⁻¹ (equivalent to 4.55 × 10⁻² in mole fraction) by Kalam et al. [7]. The mole fraction solubility of TQ in neat IPA at 298.2 K was reported as 4.51 × 10⁻² by Ahmad et al. [24]. The mole fraction solubility of TQ in neat IPA at 298.2 K was recorded as 4.47 × 10⁻² in this work. The mole fraction solubilities of TQ in pure IPA and pure H₂O at 298.2–318.2 K have also been reported [24]. The graphical analysis between experimental and literature solubility data of TQ in pure H₂O and pure IPA at 298.2–318.2 are presented in Figure 2A,B, respectively.

Table 1.

Experimental solubilities (x_e) of thymoquinone (TQ) in mole fraction in various isopropyl alcohol (IPA) + water (H₂O) mixtures at 298.2–318.2 K and 0.1 MPa ^a.

m	x e
	T = 298.2 K	T = 303.2 K	T = 308.2 K	T = 313.2 K	T = 318.2 K
0.0	8.25 × 10−5	9.35 × 10−5	1.06 × 10−4	1.28 × 10−4	1.48 × 10−4
0.1	1.59 × 10−4	1.80 × 10−4	2.05 × 10−4	2.45 × 10−4	2.81 × 10−4
0.2	2.96 × 10−4	3.35 × 10−4	3.79 × 10−4	4.51 × 10−4	5.23 × 10−4
0.3	5.50 × 10−4	6.27 × 10−4	7.15 × 10−4	8.47 × 10−4	9.91 × 10−4
0.4	1.06 × 10−3	1.18 × 10−3	1.35 × 10−3	1.60 × 10−3	1.83 × 10−3
0.5	1.95 × 10−3	2.24 × 10−3	2.53 × 10−3	2.93 × 10−3	3.42 × 10−3
0.6	3.68 × 10−3	4.20 × 10−3	4.71 × 10−3	5.46 × 10−3	6.34 × 10−3
0.7	6.84 × 10−3	7.84 × 10−3	8.87 × 10−3	1.06 × 10−2	1.24 × 10−2
0.8	1.30 × 10−2	1.52 × 10−2	1.72 × 10−2	1.93 × 10−2	2.22 × 10−2
0.9	2.41 × 10−2	2.80 × 10−2	3.16 × 10−2	3.58 × 10−2	4.15 × 10−2
1.0	4.47 × 10−2	5.17 × 10−2	5.85 × 10−2	6.56 × 10−2	7.63 × 10−2
x idl	6.16 × 10−1	6.96 × 10−1	7.85 × 10−1	8.83 × 10−1	9.92 × 10−1

^a The average relative uncertainties u_r are u_r (T) = 0.012, u_r (m) = 0.010, u (p) = 0.003 and u_r (x_e) = 0.014.

Figure 2.

Graphical comparison of TQ solubility in (A) neat H₂O and (B) neat IPA with literature values at 298.2–318.2 K; the symbol represents the TQ experimental solubility in (A) neat H₂O and (B) neat IPA, and the symbol represents the TQ literature solubility values in (A) neat H₂O and (B) neat IPA taken from reference [24].

The results depicted in Figure 2A,B showed an excellent correlation of experimental solubility data of TQ with its literature solubilities in neat H₂O and neat IPA at 298.2–318.2 K [24]. The root mean square deviation (RMSD) between experimental and literature solubility values of TQ in H₂O and IPA was found to be 1.82% and 0.86%, respectively. These observations indicated that the experimental solubility values of TQ obtained in this research were in good agreement with its literature solubility values [7,23,24].

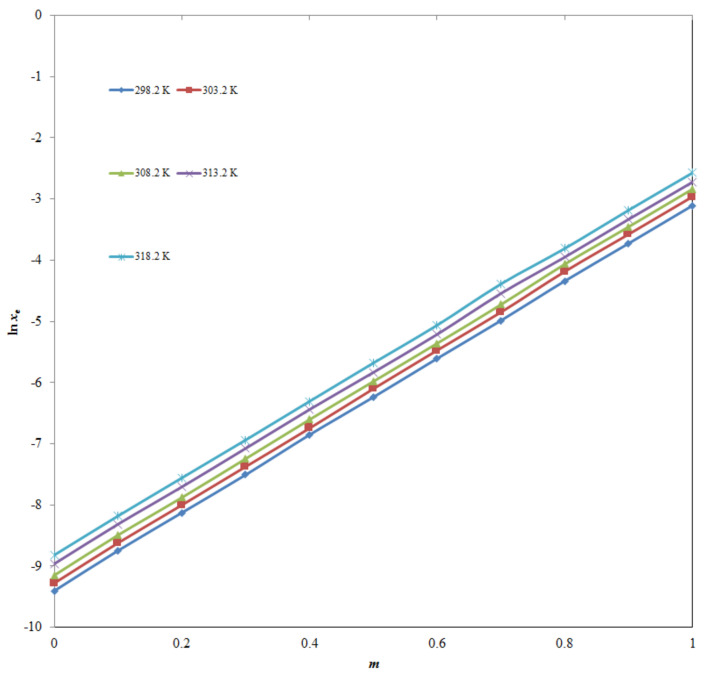
In general, TQ mole fraction solubilities (x₃) were found to be increasing significantly (p < 0.05) with the rise in temperature and IPA mass fraction in (IPA + H₂O) mixtures, and hence, the lowest mole fraction solubility of TQ was recorded in neat H₂O (x₃ = 8.25 × 10⁻⁵) at 298.2 K and the highest one was recorded in neat IPA (x₃ = 7.63 × 10⁻²) at 318.2 K. The effect of IPA mass fraction on TQ logarithmic solubilities at 298.2–318.2 K is summarized in Figure 3. According to results depicted in Figure 3, TQ logarithmic solubility was found to be increased significantly with an increase in IPA mass fraction at 298.2–318.2 K (p < 0.05). The maximum solubilization/solvation of TQ in IPA could be possible due to lower polarity of IPA, maximum solute-solvent interactions between TQ and IPA, and lower activity coefficient of TQ in IPA compared with water [10]. Accordingly, IPA could be utilized as an efficient cosolvent in TQ solubilization.

Figure 3.

Impact of IPA mass fraction (m) on TQ logarithmic solubility at 298.2–318.2 K.

2.2. Computation of Hansen Solubility Parameters (HSPs)

The HSPs are a very important tool for validating experimental solubility values to find out the best solvent for the solubilization of materials. Therefore, various HSPs for TQ, neat IPA, neat H₂O, and binary (IPA + H₂O) compositions free of TQ were determined in this work. The HSPs for binary (IPA + H₂O) compositions free of TQ at 298.2 K are included in Table 2. The total HSP (δ) value of TQ was predicted as 21.00 MPa^1/2, indicating that TQ is the low-polar bioactive compound. The HSP values for neat IPA (δ₁) and neat H₂O (δ₂) were predicted as 22.30 and 47.80 MPa^1/2, respectively. The values of δ_mix for various (IPA + H₂O) combinations free of TQ were predicted as 24.85–45.25 MPa^1/2. The HSP values for neat IPA (δ₁ = 22.30 MPa^1/2) and neat H₂O (δ₂ = 47.80 MPa^1/2) were significantly different (p < 0.05). The HSP of TQ was similar to that of neat IPA; hence, the experimental solubilities of TQ were found to be highest in neat IPA compared to its solubilities in neat H₂O. Overall, the experimental solubility values of TQ in various (IPA + H₂O) mixtures were in accordance with respective HSPs data.

Table 2.

Hansen solubility parameters (δ_mix/MPa^1/2) for binary (IPA + H₂O) compositions free of TQ at 298.2 K.

m	δmix/MPa1/2
0.1	45.25
0.2	42.70
0.3	40.15
0.4	37.60
0.5	35.05
0.6	32.50
0.7	29.95
0.8	27.40
0.9	24.85

2.3. Determination of Ideal Solubility and Activity Coefficients

The results of ideal solubility (x^idl) values of TQ are included in Table 1. The ideal solubilities of TQ were estimated as 6.16 × 10⁻¹–9.92 × 10⁻¹ at 298.2–318.2 K. The ideal solubilities of TQ were significantly higher compared to its experimental solubilities in neat IPA, neat H₂O, and various (IPA + H₂O) mixtures (p < 0.05). The ideal solubilities of TQ were increased significantly with an increase in temperature, which indicated that the dissolution process of TQ was endothermic. The higher ideal solubilities of TQ compared to its experimental solubilities were possible, due to its low melting temperature (352.8 K) [24].

The activity coefficient (γ_i) values for TQ in various (IPA + H₂O) compositions at 298.2–318.2 K are included in Table 3. The γ_i value of TQ was obtained larger in neat H₂O at 298.2–323.2 K. However, the γ_i of TQ was found lowest in neat IPA at 298.2–318.2 K. The larger γ_i values in water were possible, due to the lowest solubility values of TQ in water. However, the smaller γ_i values of TQ were due to the highest solubility values of TQ in IPA [10]. It has been reported very well in the literature that low values of γ_i are associated with maximum solute-solvent interactions at the molecular level [10,24]. The γ_i values of TQ in IPA were lowest compared to the H₂O; therefore, the maximum solute-solvent interactions at the molecular level were considered in TQ-IPA compared to the TQ-H₂O.

Table 3.

Activity coefficients (γ_i) of TQ in binary (IPA + H₂O) compositions (m) at 298.2–318.2 K.

m	γ i
	T = 298.2 K	T = 303.2 K	T = 308.2 K	T = 313.2 K	T = 318.2 K
0.0	7350	7383	7349	6877	6702
0.1	3808	3823	3810	3598	3536
0.2	2049	2057	2064	1955	1898
0.3	1103	1099	1094	1042	1021
0.4	573.9	587.2	577.3	552.5	543.7
0.5	310.2	308.0	309.6	301.3	290.6
0.6	164.9	164.2	166.1	161.7	156.6
0.7	88.66	88.06	88.14	82.92	79.84
0.8	46.47	45.30	45.56	45.79	44.71
0.9	25.14	24.66	24.74	24.68	23.90
1.0	13.54	13.34	13.35	13.44	12.99

2.4. Apparent Thermodynamic Analysis of TQ Solution

The results of various apparent thermodynamic parameters for TQ dissolution in different (IPA + H₂O) mixtures, including pure IPA and pure H₂O, are included in Table 4.

Table 4.

Apparent standard enthalpy (Δ_solH⁰), apparent standard Gibbs energy (Δ_solG⁰), apparent standard entropy (Δ_solS⁰), and R² values for TQ in binary (IPA + H₂O) compositions (m)^a.

m	ΔsolH0/kJ/mol	ΔsolG0/kJ/mol	ΔsolS0/J/mol/K	R 2
0.0	23.47	23.35	0.36	0.9923
0.1	22.74	21.68	3.42	0.9942
0.2	22.65	20.10	8.25	0.9967
0.3	22.70	18.50	13.62	0.9965
0.4	22.10	16.87	16.99	0.9935
0.5	21.85	15.27	21.34	0.9962
0.6	21.31	13.67	24.78	0.9957
0.7	23.69	12.02	37.88	0.9932
0.8	20.51	10.41	32.76	0.9978
0.9	21.03	8.84	39.59	0.9980
1.0	20.66	7.27	43.48	0.9975

^a Average relative uncertainties are u(Δ_solH⁰) = 0.04, u(Δ_solG⁰) = 0.34 and u(Δ_solS⁰) = 0.67.

The apparent standard enthalpy (Δ_solH⁰) values for TQ dissolution in various (IPA + H₂O) mixtures, including pure IPA and pure H₂O, were calculated as 20.51–23.47 kJ/mol, suggesting an endothermic dissolution process of TQ in all (IPA + H₂O) mixtures, including pure IPA and pure H₂O [25,26]. The apparent standard Gibbs energy (Δ_solG⁰) values for TQ in binary (IPA + H₂O) compositions, including pure IPA and pure H₂O, were estimated as 7.27–23.35 kJ/mol (Table 4). The Δ_solG⁰ values for TQ were decreased with an increase in IPA mass fraction in all (IPA + H₂O) compositions. The highest and lowest Δ_solG⁰ values for TQ were found in pure H₂O (23.35 kJ/mol) and pure IPA (7.27 kJ/mol), respectively. The highest and lowest Δ_solG⁰ values for TQ in pure H₂O and pure IPA were possible due to the lowest and highest solubility values of TQ in pure H₂O and pure IPA, respectively. The apparent standard entropy (Δ_solS⁰) values for TQ dissolution in binary (IPA + H₂O) mixtures, including pure IPA and pure H₂O, were calculated as 0.36–43.48 J/mol/K, showing an entropy-driven dissolution process of TQ in all (IPA + H₂O) compositions, including neat IPA and neat H₂O [25]. Based on these observations and results, the overall TQ dissolution was found to be endothermic and entropy-driven in all (IPA + H₂O) combinations, including pure IPA and pure H₂O [25,26].

2.5. Modeling of TQ Solubility

The obtained experimental solubilities of TQ were regressed with six different theoretical models, namely, van’t Hoff model (VHM), modified Apelblat model (MAM), Yalkowsky–Roseman model (YRM), Buchowski–Ksiazczak λh model (BKλhM), Jouyban–Acree model (JAM), and Jouyban–Acree–van’t Hoff (JAVHM) models [26,27,28,29,30,31,32,33,34,35,36]. Results of the VHM model for TQ in binary (IPA + H₂O) mixtures, including pure IPA and pure H₂O, are summarized in Table 5. The RMSDs for TQ in various (IPA + H₂O) mixtures, including pure IPA and pure H₂O, were computed as 0.83–2.09%. An average RMSD for the VHM model was calculated as 1.51%. The determination coefficient (R²) values for VHM were predicted as 0.9921–0.9980.

Table 5.

Resulting data of van’t Hoff model for TQ in binary (IPA + H₂O) compositions (m).

m	a	b	R 2	RMSD (%)	Overall RMSD (%)
0.0	0.02	–2818.90	0.9921	2.09
0.1	0.39	–2731.50	0.9940	1.74
0.2	0.97	–2720.50	0.9926	1.94
0.3	1.62	–2726.90	0.9964	1.34
0.4	2.03	–2655.40	0.9933	1.76
0.5	2.55	–2624.40	0.9961	1.20	1.51
0.6	2.96	–2559.90	0.9956	1.55
0.7	4.54	–2846.30	0.9930	1.74
0.8	3.93	–2464.00	0.9979	0.83
0.9	4.74	–2527.00	0.9980	1.28
1.0	5.21	–2482.30	0.9975	1.22

Results of the MAM model for TQ in various (IPA + H₂O) mixtures, including pure IPA and pure H₂O, are summarized in Table 6. The graphical comparison between the experimental and MAM solubilities of TQ is shown in Figure 4, which showed an excellent correlation between the experimental and MAM solubility data of TQ. The RMSDs for TQ in various (IPA + H₂O) mixtures, including pure IPA and pure H₂O, were predicted as 0.51–1.11%. An average RMSD for the MAM model was predicted as 0.84%. The R² values for the MAM model were estimated as 0.9965–0.9997.

Table 6.

Resulting data of modified Apelblat model for TQ in binary (IPA + H₂O) compositions (m).

m	A	B	C	R 2	RMSD (%)	Overall RMSD (%)
0.0	−423.43	16,530.02	62.93	0.9967	1.10
0.1	−331.45	12,432.20	49.31	0.9970	0.98
0.2	−446.40	17,720.89	66.49	0.9980	0.80
0.3	−273.39	9840.95	40.87	0.9984	0.75
0.4	−325.33	12,303.02	48.65	0.9965	1.11
0.5	−353.02	13,623.04	52.84	0.9997	0.51	0.84
0.6	−361.45	14,091.46	54.16	0.9995	0.58
0.7	−455.99	18,196.27	68.44	0.9982	0.89
0.8	−47.03	−131.00	7.57	0.9977	0.91
0.9	−160.29	5017.23	24.52	0.9987	0.76
1.0	−156.94	4929.95	24.09	0.9966	0.85

Figure 4.

Graphical correlation of TQ solubility with the modified Apelblat model in various (IPA + H₂O) mixtures at 298.2–318.2 K (the modified Apelblat solubility of TQ is indicated by solid lines, and experimental solubility of TQ is shown by the symbols).

Results of the YRM model for TQ in various (IPA + H₂O) compositions are summarized in Table 7. The RMSDs for TQ in various (IPA + H₂O) mixtures were predicted as 1.18–3.33%. An average RMSD for the YRM model was predicted as 2.02%.

Table 7.

Resulting data of Yalkowsky–Roseman model for TQ in binary (IPA + H₂O) compositions (m) at 298.2–318.2 K.

m	Log xYal					RMSD (%)	Overall RMSD (%)
	T = 298.2 K	T = 303.2 K	T = 308.2 K	T = 313.2 K	T = 318.2 K
0.1	−3.81	−3.75	−3.70	−3.62	−3.55	2.40
0.2	−3.53	−3.48	−3.42	−3.35	−3.28	1.29
0.3	−3.26	−3.20	−3.15	−3.07	−3.01	1.18
0.4	−2.98	−2.93	−2.87	−2.80	−2.74	2.62
0.5	−2.71	−2.65	−2.60	−2.53	−2.47	1.71	2.02
0.6	−2.44	−2.38	−2.32	−2.26	−2.20	1.30
0.7	−2.16	−2.10	−2.05	−1.99	−1.93	3.33
0.8	−1.89	−1.83	−1.78	−1.72	−1.65	2.87
0.9	−1.62	−1.56	−1.50	−1.45	−1.38	1.53

Results of the BKλhM model for TQ in binary (IPA + H₂O) compositions are summarized in Table 8. The RMSDs for TQ in various (IPA + H₂O) compositions were predicted as 1.36–3.24%. An average RMSD for the BKλhM model was predicted as 2.43%.

Table 8.

The Buchowski–Ksiazczak λh model parameters (λ and h) and RMSD values for TQ in various (IPA + H₂O) compositions.

Samples	λ	h	RMSD (%)	Overall RMSD (%)
0.1	7.17	380.55	2.59
0.2	6.56	414.57	2.42
0.3	5.93	459.14	2.89
0.4	5.30	500.45	1.98
0.5	4.68	560.08	1.36	2.43
0.6	4.06	629.23	3.12
0.7	3.39	838.70	3.24
0.8	2.80	878.21	1.68
0.9	2.18	2527.00	2.67

Results of the JAM model for TQ in various (IPA + H₂O) mixtures are summarized in Table 9. An average RMSD for the JAM model was predicted as 0.72%.

Table 9.

Resulting data of Jouyban–Acree and Jouyban–Acree–van’t Hoff models for TQ in (IPA + H₂O) mixtures.

System	Jouyban–Acree	Jouyban–Acree-van’t Hoff
		A1 5.21 B1 –2482.30 A2 0.02 B2 –2818.90 Ji 67.38 0.64
(IPA + H2O)	Ji 73.49
RMSD (%)	0.72

Results of the JAVHM model for TQ in binary (IPA + H₂O) compositions are also summarized in Table 9. An average RMSD for the JAVHM model was estimated as 0.64%. According to these observations and results, all investigated theoretical models showed low values of RMSD, which indicated good solubility correlation for TQ with all six theoretical models evaluated.

3. Materials and Methods

3.1. Materials

TQ (mass fraction purity = 0.980) and IPA (mass fraction purity = 0.997) were obtained from “Sigma Aldrich (St. Louis, MO, USA)”. Liquid chromatography grade methanol (mass fraction purity = 0.999) was obtained from “Alfa Aesar (Tewksbury, MA, USA)”. The potassium dihydrogen phosphate buffer (10 mM) was prepared in the laboratory. Water (conductivity < 1.0 µS/cm) was obtained from the “Milli-Q Water Purification Unit (Darmstadt, Germany)”. Biological shaker was obtained from “Grant Scientific (Cambridge, UK)”. High-performance liquid chromatography (HPLC) system was from “Waters Corporation (Milford, MA, USA)”. The information about these materials is summarized in Table 10.

Table 10.

List of materials used.

Material		Molecular Formula	Molar Mass (g/mole)	CAS Registry No.	Purification Method	Mass Fraction Purity	Analysis Method	Source
TQ		C10H12O2	164.20	490–91-5	None	0.980	HPLC	Sigma Aldrich
IPA		C3H8O	60.10	67–63-0	None	0.997	GC	Sigma Aldrich
H2O		H2O	18.07	7732–18-5	None	-	-	Milli-Q

TQ, thymoquinone; IPA, isopropyl alcohol; H₂O, water; HPLC, high-performance liquid chromatography; GC, gas chromatography.

3.2. Preparation of Solvent Mixtures

All (IPA + H₂O) solvent mixtures were prepared on mass, using a “Digital Analytical Balance (Mettler Toledo, Greifensee, Switzerland)” with a sensitivity ± 0.10 mg. The mass fraction of IPA for different (IPA + H₂O) solvent mixtures was varied by 0.10 from 0.10–0.90. Each solvent mixture was obtained in triplicates.

3.3. TQ Solubility Evaluation

An isothermal equilibrium method was applied to determine TQ solubility in various (IPA + H₂O) compositions [m = 0.1–0.9; where m is the IPA mass fraction in (IPA + H₂O) compositions, including neat IPA (m = 1.0) and neat H₂O (m = 0.0)] [37]. The experiment was performed at 298.2–318.2 K and 0.1 MPa in triplicates. Excess amounts of TQ crystals were dispersed into 2.0 g of each (IPA + H₂O) mixture, including neat solvents (IPA and H₂O). Each sample was kept at “OLS 200 Grant Scientific Biological Shaker (Grant Scientific, Cambridge, UK)” after the settings of temperature and rotational speed. The samples were continuously shaken to reach equilibrium. After equilibrium, the samples were taken out from the shaker and centrifuged. The supernatants were carefully withdrawn and diluted with mobile phase and utilized to determine TQ content using the HPLC method at 254 nm, as described in the literature [38]. “Waters HPLC system (Waters Corporation, Milford, MA, USA)” was utilized for TQ analysis. The binary mixture of potassium dihydrogen phosphate buffer (10 mM) and methanol (90:10, v/v) was used as the mobile phase. The flow rate of the mobile phase was kept constant at 1.0 mL/min with an isocratic mode. The injection volume for all samples was 20 µL. The column used for TQ analysis was Waters Symmetry-R RP C-18 (150 × 4.6 mm, 5 µm particle size). The TQ content in the above samples was calculated from the previously constructed calibration curve of TQ. The TQ calibration curve was constructed on a mass/mass basis, which was observed as linear in the range of 1–200 µg/g. The x₃ value of TQ was then calculated using Equations (1) and (2) [10,11]:

$$x_3=\frac{m_1/M_1}{m_1/M_1+m_2/M_2}$$ (1)

$$x_3=\frac{m_1/M_1}{m_1/M_1+m_2/M_2+m_3/M_3}$$ (2)

where, m₁ = TQ mass; m₂ = IPA mass; m₃ = H₂O mass; M₁ = TQ molar mass; M₂ = IPA molar mass, and M₃ = H₂O molar mass.

3.4. Estimation of HSPs

The HSPs of solute, solvent, and cosolvent mixtures are an important tool to predict the best solvent for the solubilization of the solute [39]. Hence, the HSPs for TQ, neat IPA, neat H₂O, and different (IPA + H₂O) compositions free of TQ were predicted to compare the experimental solubility values of TQ. The HSP (δ) for TQ, neat IPA, and neat H₂O was obtained by applying Equation (3) [25,39]:

$${\delta }^2={\delta }_{\mathrm{d}}^2+{\delta }_{\mathrm{p}}^2+{\delta }_{\mathrm{h}}^2$$ (3)

where, “δ = total HSP; δ_d = dispersion HSP; δ_p = polar HSP and δ_h = hydrogen-bonded HSP”. The HSPs for TQ, pure IPA, and pure H₂O were computed by “HSPiP software (version 4.1.07, Louisville, KY, USA)” [39]. However, the HSPs of different (IPA + H₂O) compositions free of TQ (δ_mix) were obtained using Equation (4) [26,40]:

$${\delta }_{\mathrm{mix}}=\propto {\delta }_1+\left(1-\propto \right){\delta }_2$$ (4)

where, α = IPA volume fraction in (IPA + H₂O) combinations; δ₁ = HSP of pure IPA, and δ₂ = HSP of pure H₂O.

3.5. Determination of Ideal Solubility and Activity Coefficients

The x^idl of TQ at 298.2–318.2 K was calculated by applying Equation (5) [31]:

$$\ln x^{\mathrm{idl}}=\frac{-\Delta H_{\mathrm{fus}}\left(T_{\mathrm{fus}}-T\right)}{R{T}_{\mathrm{fus}}T}+\left(\frac{\Delta C_{\mathrm{p}}}{R}\right)[\frac{T_{\mathrm{fus}}-T}{T}+\ln \left(\frac{T}{T_{\mathrm{fus}}}\right)]$$ (5)

In which, T = absolute temperature; T_fus = TQ fusion temperature; R = universal gas constant; ∆H_fus = TQ fusion enthalpy, and ∆C_p = difference in the molar heat capacity of TQ solid state with that of TQ liquid state [9,41]. The quantitative data of T_fus = 318.52 K, ∆H_fus = 19.44 kJ/mol, and ∆C_p = 61.03 J/mol/K were taken from the literature [24]. The x^idl value for TQ was calculated by applying Equation (5).

The γ_i for TQ in binary (IPA + H₂O) compositions, including pure IPA and pure H₂O, were obtained by applying the non-random two-liquid (NRTL) model [42]. Based on the principle of solid-liquid equilibrium, the γ_i can be calculated using the NRTL model with the help of Equation (6) [42,43]:

$$\ln {\gamma }_{\mathrm{i}}=\frac{\Delta H_{\mathrm{fus}}}{R}\left(\frac{1}{T_{\mathrm{fus}}}-\frac{1}{T}\right)-\left(\frac{\Delta C_{\mathrm{p}}}{R}\right)+\ln \left(\ln \frac{T}{T_{\mathrm{fus}}}-\frac{T}{T_{\mathrm{fus}}}+1\right)]-\ln x_3$$ (6)

The value of ∆C_p between the melting and solid states of TQ is very small, and hence, the Equation (6) can be simplified as Equation (7) [43]:

$$\ln {\gamma }_{\mathrm{i}}=\frac{\Delta H_{\mathrm{fus}}}{R}\left(\frac{1}{T_{\mathrm{fus}}}-\frac{1}{T}\right)-\ln x_3$$ (7)

The interactions between TQ and the solvents or solvent mixtures at the molecular level were evaluated based on the recorded TQ γ_i data.

3.6. Apparent Thermodynamic Analysis of TQ Solution

Apparent thermodynamic analysis of TQ in binary (IPA + H₂O) compositions, including pure IPA and pure H₂O, was performed to evaluate TQ dissolution character by applying van’t Hoff and Gibbs Equations. The van’t Hoff Equation was applied to compute the thermodynamic parameters of TQ in various (IPA + H₂O) compositions at mean harmonic temperature (T_hm) = 308 K at 298.2–318.2 K. The Δ_solH⁰ value can be obtained using the Equation (8) [41,44]:

$${\left(\frac{\partial \ln x_3}{\partial \left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$T$}\right.-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$T_{\mathrm{hm}}$}\right.\right)}\right)}_P=-\frac{{\Delta }_{\mathrm{sol}}{H}^0}{R}$$ (8)

By plotting ln x₃ versus $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$T$}\right.-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$T_{\mathrm{hm}}$}\right.$, the Δ_solH⁰ and Δ_solG⁰ data for TQ were determined using Equations (9) and (10), respectively [45]:

$${\Delta }_{\mathrm{sol}}{H}^0=-R{\left(\frac{\partial \ln x_3}{\partial \left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$T$}\right.-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$T_{\mathrm{hm}}$}\right.\right)}\right)}_P$$ (9)

$${\Delta }_{\mathrm{sol}}{G}^0=-R{T}_{\mathrm{hm}}\times \mathrm{intercept}$$ (10)

The Δ_solS⁰ data for TQ in various (IPA + H₂O) combinations, including neat IPA and neat H₂O, were computed by applying Equation (11) [41,44,45]:

$${\Delta }_{\mathrm{sol}}{S}^0=\frac{{\Delta }_{\mathrm{sol}}{H}^0-{\Delta }_{\mathrm{sol}}{G}^0}{T_{\mathrm{hm}}}$$ (11)

3.7. Solubility Correlation With Theoretical/Computational Models

The experimental solubilities of TQ in binary (IPA + H₂O) mixtures, including pure IPA and pure H₂O, were regressed by VHM, MAM, YRM, BKλhM, JAM, and JAVHM models [26,27,28,29,30,31,32,33,34,35,36].

The VHM model is a semi-predictive model, which can correlate the solubility of solutes at different temperatures at the given set of cosolvent mixtures. Therefore, the VHM solubility (x₃^van’t) of TQ in different (IPA + H₂O) mixtures, including pure IPA and pure H₂O, at different temperatures was computed by applying Equation (12) [26]

$$\ln x_3^{{\mathrm{van}}^{\prime }\mathrm{t}}=\mathrm{a}+\frac{b}{T}$$ (12)

where, a and b = model coefficients, and these values were predicted using the least square method.

The regression between experimental and VHM solubility of TQ was performed using RMSD and R² values. The RMSD of TQ was obtained using its standard equation, reported previously [9]. The MAM model is also a semi-predictive model, which correlates the solubility of solutes at different temperatures at the given set of cosolvent mixtures. Therefore, the MAM solubility (x₃^Apl) of TQ in binary (IPA + H₂O) mixtures, including pure IPA and pure H₂O, was predicted by applying Equation (13) [27,28]:

$$\ln x_3^{\mathrm{Apl}}=A+\frac{B}{T}+C\ln \left(T\right)$$ (13)

where, A, B, and C = the model coefficients, and these values were predicted using nonlinear multivariate regression analysis of experimental solubilities TQ included in Table 2 [9]. The regression between experimental and MAM solubility of TQ was performed using RMSD and R². The YRM model is a cosolvency-based model. It is a special case of the JAM model in which adjustable parameters are fixed and equivalent to zero. The logarithmic solubility of the YRM model (log x₃^Yal) for TQ in various (IPA + H₂O) compositions was computed by applying Equation (14) [29]:

$$\mathrm{Log}{x}_3^{\mathrm{Yal}}=m_1\log x_1+m_2\log x_2$$ (14)

where, x₁ = mole fraction solubility of TQ in IPA; x₂ = mole fraction solubility of TQ in H₂O; m₁ = IPA mass fraction, and m₂ = H₂O mass fraction.

The BKλhM model is based on two parameters λ and h. It is also a semi-predictive model, which is widely used for the solubility correlation at different temperatures at the given set of cosolvent compositions. The BKλhM solubility (x₃^λh) of TQ was obtained using Equation (15) [30,31]:

$$\ln [1+\frac{\lambda \left(1-x_3^{\mathsf{\lambda }\mathrm{h}}\right)}{x_3^{\mathsf{\lambda }\mathrm{h}}}]=\lambda h [\frac{1}{T}-\frac{1}{T_{\mathrm{fus}}}]$$ (15)

where, λ and h = the adjustable model parameters of Equation (15).

The regression between experimental and BKλhM solubility of TQ was performed using RMSD. The JAM predicts the solubility of solutes in cosolvent mixtures at the given set of temperatures. The JAM solubility (x₃^JA) of TQ in binary (IPA + H₂O) composition was predicted using Equation (16) [32,33,34,35,36,46]:

$$\ln x_3^{\mathrm{JA}}=m_1\ln x_1+m_2 \ln x_2+\lceil \frac{m_1{m}_2}{T}{\displaystyle \sum }_{i=0}^2{J}_{\mathrm{i}}\left(m_1-m_2\right)\rceil$$ (16)

where, J_i = model coefficient and this value was determined using no-intercept regression analysis, described in the literature [35,47]. The regression between experimental and JAM solubility of TQ was performed using RMSD.

The JAVHM model is based on the combination of VHM and JAM models. It also predicts the solubility of solutes in cosolvent mixtures at the given set of temperatures. The JAVHM solubility (x ₃^JAVHM) of TQ in binary (IPA + H₂O) compositions were predicted using Equation (17) [48]:

$$\ln x_3^{\mathrm{JAVHM}}=m_1\left(A_1+\frac{B_1}{T}\right)+m_2 \left(A_2+\frac{B_2}{T}\right)+\left[\frac{m_1{m}_2}{T} {\displaystyle \sum }_{i=0}^2{J}_{\mathrm{i}}\left(m_1-m_2\right)\right]$$ (17)

where, A₁, B₁, A₂, B₂, and J_i = the model coefficients. The regression between experimental and JAVHM solubility of TQ was performed using RMSD.

3.8. Statistical Evaluation

Statistical evaluation was performed by applying a Kruskal–Wallis test, followed by Denn’s test using “GraphpadInstat software (Version 9.1.1, San Diego, CA, USA)”. The p < 0.05 or equivalent to 0.05 was taken as a significant value.

4. Conclusions

In this research, the solubility of a naturally-derived bioactive compound TQ in binary (IPA + H₂O) mixtures, including pure IPA and pure H₂O, was evaluated at 298.2–318.2 K and 0.1 MPa. The TQ solubility was found to be increasing significantly with the rise in absolute temperature and IPA mass fraction in all (IPA + H₂O) mixtures, including pure IPA and pure H₂O. The experimental solubility values of TQ were regressed well with six different theoretical models, including VHM, MAM, YRM, BKλhM, JAM, and JAVHM models. The results of activity coefficient calculations indicated maximum solute-solvent interactions in the TQ-IPA combination compared to the TQ-H₂O combination. A thermodynamic study suggested an endothermic and entropy-driven dissolution of TQ in all (IPA + H₂O) mixtures, including pure IPA and pure H₂O. The obtained solubility data can be utilized for the drug discovery process, formulation development, and preclinical assessment of TQ.

Author Contributions

Conceptualization, M.G. and F.S.; methodology, M.Y.B. and P.A.; software, F.S. and M.H.A.; validation, M.G.; F.S., H.S.Y. and P.A.; formal analysis, M.H.A.; investigation, F.S.; M.Y.B. and M.G.; resources, M.G.; data curation, H.S.Y.; writing—original draft preparation, F.S.; writing—review and editing, M.G.; P.A.; M.H.A. and H.S.Y.; visualization, P.A.; supervision, F.S.; project administration, F.S.; funding acquisition, M.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Deanship of Scientific Research (DSR) at King Khalid University, Abha, Saudi Arabia through General Research Project under grant number (G.R.P-250-42) and The APC was funded by DSR.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.