Magnetic and Transport Properties of New Dual-Phase High-Entropy Alloy FeRhIrPdPt

Abstract

High-entropy alloys (HEAs) are broadly explored from the perspective of mechanical, corrosion-resistance, catalytic, structural, superconducting, magnetic properties, and so on. In magnetic HEAs, 3d transition metals or rare-earth elements are well-studied compositional elements. We researched a magnetic HEA containing Fe combined with 4d and 5d transition metals, which has not been well investigated, and found a new dual-phase face-centered-cubic (fcc) HEA FeRhIrPdPt. The structural, magnetic, and transport properties were evaluated by assuming that FeRhIrPdPt is a mixture of FeRh₄, FeIr₄, FePd₄, and FePt₄, all with the fcc structure. The dual-phase is composed of a Rh- and Ir-rich main phase and a Pd- and Pt-rich minor one. FeRh₄ and FeIr₄ show spin freezings at low temperatures, while FePd₄ and FePt₄ are ferromagnetic. Two magnetic features can characterize FeRhIrPdPt. One is the canonical spin-glass transition at 90 K, and the other is a ferromagnetic correlation that appears below 300 K. The main and minor phases were responsible for the spin-glass transition and the ferromagnetic correlation below 300 K, respectively.

1. Introduction

High-entropy alloys (HEAs) were initially proposed for simple crystal structures such as face-centered cubic (fcc), body-centered cubic (bcc), and hexagonal close packing (hcp), in which more than five elements, each having an atomic fraction between 5% and 35%, randomly occupy one crystallographic site [1,2]. The HEA concept is now adopted in various crystal structures [3,4]. The high-entropy state contributes to the stability of the solid solution with the desired crystal structure through the relatively large mixing entropy. For example, (Gd_1/6Tb_1/6Dy_1/6Tm_1/6Yb_1/6Lu_1/6)₂Si₂O₇ disilicate shows outstanding thermal stability, which is ascribed to the high-entropy state at the rare-earth site [5]. The significant atomic disorder leads to the severe lattice distortion effect. In particular, bcc HEAs show superior mechanical properties, attracting a great deal of interest. There is also growing interest in the study of HEAs with high ductility, refractory HEAs, those demonstrating superconductivity, as well as HEAs used in anti-corrosion coatings, biomaterials, catalysts, shape memory alloys, magnetic refrigeration materials, and so on [6,7,8,9,10,11,12,13,14,15].

In some HEAs containing 3d transition (Cr, Mn, Fe, Co, and Ni) or rare-earth metals, the magnetic properties are well investigated. Al_xCoCrFeNi exhibits a structural change from fcc to bcc through the mixture of fcc and bcc as x is increased [16]. Al-free CoCrFeNi is ferromagnetic below 120 K, and the Curie temperature T_C tends to be enhanced above room temperature with increasing Al content. In some compositions, spin freezing appears at low temperatures, which is detected as the irreversible magnetization between zero-field-cooled (ZFC) and field-cooled (FC) states. The electrical resistivity of Al_xCoCrFeNi shows metallic temperature dependence, whereas it is rather small due to atomic disorder. NiFeCoCrPd and NiFeCoCrMn Cantor–Wu alloys are famous equimolar HEAs. Both alloys are ferromagnets with T_C = 440 K for NiFeCoCrPd and T_C = 38 K for NiFeCoCrMn, respectively [17,18]. NiFeCoCrMn also shows a spin-glass behavior. The temperature dependences of the electrical resistivity of Cantor–Wu alloys are also weak but metallic. Although the almost-magnetic HEAs display ferromagnetism, Cr₂₀Mn_xFe_yCo₂₀Ni_z (x + y + z = 60) is reported to be an antiferromagnet with the transition temperature ranging from 80 to 190 K, depending on the composition [19]. As for rare-earth-based HEAs, Gd₂₀Dy₂₀Er₂₀Ho₂₀Tb₂₀ forms a single-phase hcp structure and shows relatively good magnetocaloric properties [15].

Research into HEA magnetic materials also shows a growing interest in tailoring magnetic properties by changing the microstructure, especially in dual-phase HEAs as in the present study. In Fe₁₅Co₁₅Ni₂₀Mn₂₀Cu₃₀, a spinodal decomposition occurs after heat treatment [20]. The spinodally decomposed HEA possesses enhanced T_C and magnetization by 48% and 70%, respectively, compared to the homogenized single-phase state. The control of magnetic properties was also achieved in dual-phase CoFeNi_0.5Cr_0.5-Al_x (x = 0, 1.0, and 1.5) or multiphase Al_0.1(Fe_1+xCoCr_1−xMn)_0.9 (x = 0, 0.2, 0.4, 0.6, and 0.8) HEAs [21,22]. The magnetic phases contained in the dual-phase HEAs independently exhibit their magnetic properties.

Up to now, HEAs containing Fe combined with 4d and 5d transition metals, such as Rh, Ir, Pd, and Pt, have not been well investigated. Here we show the results of the new equimolar FeRhIrPdPt. We found that this HEA forms a dual-phase fcc structure, which shows a spin-glass transition at approximately 90 K and a ferromagnetic correlation below 300 K. The phase assignment of these two characteristic magnetic properties was performed by employing FeRh₄, FeIr₄, FePd₄, and FePt₄ under the assumption that FeRhIrPdPt is a mixture of the four binary alloys with fcc structure. This article reports structural investigations of FeRhIrPdPt, FeRh₄, FeIr₄, FePd₄, and FePt₄. The magnetic and transport properties of these alloys were examined by measuring the temperature dependences of magnetization, isothermal magnetization curve, and electrical resistivity.

2. Materials and Methods

Polycrystalline samples, as listed in Table 1, were prepared by a homemade arc furnace using constituent elements Fe (99.9%), Rh (99.9%), Ir (99.99%), Pd (99.9%), and Pt (99.9%) under an Ar atmosphere. The elemental metals were arc-melted to button-shaped samples with a mass of 1.5 g and quenched on a water-chilled Cu hearth. The samples were flipped and remelted several times to ensure homogeneity. In this study, all samples received neither heat treatment nor deformation (e.g., rolling). Room-temperature X-ray diffraction (XRD) patterns of as-cast samples were collected using an X-ray diffractometer (XRD-7000L, Shimadzu, Kyoto, Japan) with Cu-Kα radiation in Bragg–Brentano geometry. We used thin slabs cut from the samples due to their high ductility.

Table 1.

Chemical compositions determined by energy-dispersive X-ray spectroscopy and lattice parameters of the prepared samples.

Sample	Composition	Lattice Parameter (Å)
FeRh4	Fe19.2(8)Rh80.8(8)	3.782(1)
FeIr4	Fe18.5(6)Ir81.5(6)	3.807(1)
FePd4	Fe19.3(9)Pd80.7(9)	3.858(1)
FePt4	Fe19.2(6)Pt80.8(6)	3.871(2)
FeIrRhPtPd	main: Fe15.8(5)Rh24.5(5)Ir32.6(1)Pd10.7(6)Pt16.4(6) minor: Fe23.7(7)Rh14.0(8)Ir5.4(9)Pd32.5(9)Pt24.4(6)	3.834(1)

The metallographic examination of the prepared sample was carried out by a field-emission scanning electron microscope (FE-SEM; JSM-7100F, JEOL, Akishima, Japan). The atomic composition in each sample area was investigated by an energy-dispersive X-ray (EDX) spectrometer equipped to the FE-SEM by averaging several data collection points. The elemental mappings of FeRhIrPdPt were also obtained by the EDX spectrometer.

The temperature dependence of dc magnetic susceptibility χ_dc(T) between 50 K and 400 K and the isothermal magnetization curve were measured by VersaLab (Quantum Design, San Diego, CA, USA). The temperature dependence of ac magnetic susceptibility χ_ac(T) between 70 K and 170 K under the ac field of 15 Oe and the frequency ranging from 20 Hz to 5 kHz was also measured using this apparatus. χ_dc(T) below 100 K and the isothermal magnetization curve at 2 K were measured by MPMS3 (Quantum Design, San Diego, CA, USA). The high-temperature χ_dc(T) between 400 K and 450 K was checked by a vibrating sample magnetometer (BHV-50H, Riken Denshi, Yutenji, Japan). The temperature dependence of electrical resistivity ρ (T) between 3 K and 300 K was measured by a dc four-probe method using a homemade system in a GM refrigerator (UW404, Ulvac cryogenics, Kyoto, Japan). In this equipment, we also measured χ_ac(T) between 3 K and 300 K under the ac field of 5 Oe at 800 Hz.

3. Results and Discussion

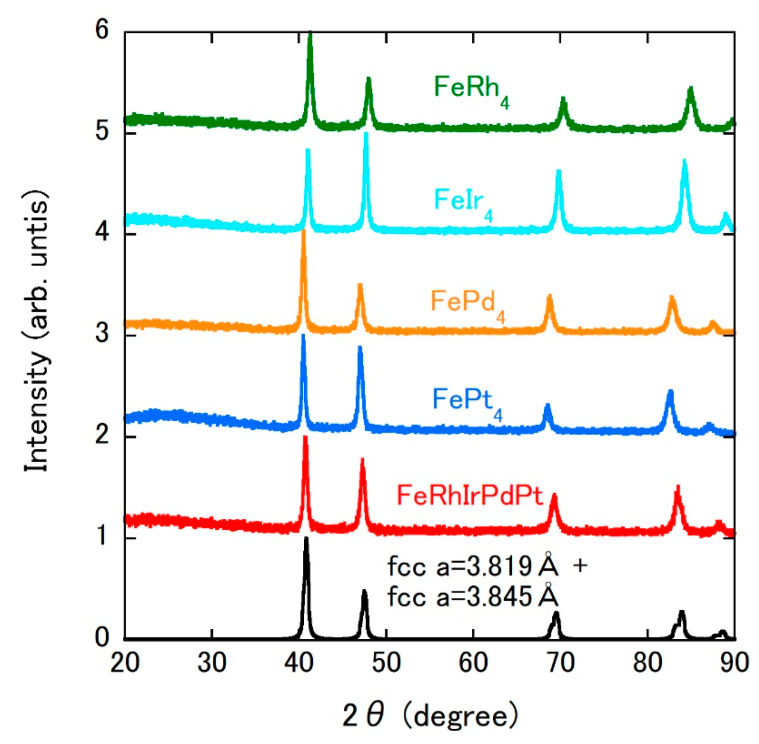
Figure 1 shows the XRD patterns of prepared samples. In each pattern, the diffraction peak positions match those of the fcc structure with the lattice parameters listed in Table 1. The lattice parameters were determined by the unit cell parameter refinement program CellCalc [23]. In the binary alloys, the lattice parameter decreases from FePt₄, FePd₄, and FeIr₄ to FeRh₄. The lattice parameter of FeRhIrPdPt is almost intermediate between those of FePd₄ and FeIr₄. SEM images of the studied samples are displayed in Figure 2a–e. The images of all binary alloys demonstrate their single-phase nature (Figure 2a–d). In each alloy, the chemical composition determined by EDX analysis is consistent with the starting composition listed in Table 1. In contrast, the SEM image of FeRhIrPdPt shows the main phase with the bright image (70 vol.%, 74 wt.%), accompanying the minor phase (30 vol.%, 26 wt.%) precipitated between grain boundaries of the main phase (see the dark image in Figure 2e). Figure 2f shows the elemental mappings of FeRhIrPdPt, especially the Ir and Pd mappings that support the dual-phase nature. For further elucidation of the dual-phase nature in FeRhIrPdPt, transmission electron microscopy images and selected area electron diffraction patterns are desirable. As shown in Table 1, compared to the ideal composition Fe₂₀Rh₂₀Ir₂₀Pd₂₀Pt₂₀, one can say that the main (minor) phase is Rh- and Ir-rich (Pd- and Pt-rich) alloy. We guess that the minor phase also forms an fcc structure with a lattice parameter close to that of the main phase because no extra XRD peak other than the fcc structure in Figure 1 was observed. We tried simulating the XRD pattern of FeRhIrPdPt by the superposition of the main and minor phases. The lattice parameter of each phase was estimated by the composition-weighted average of FeRh₄, FeIr₄, FePd₄, and FePt₄. The obtained parameters are 3.819 Å for the main phase and 3.845 Å for the minor one. The resultant XRD pattern calculated using PowderCell 2.3 software [24] with the weight fractions mentioned above is shown in Figure 1. The simulated pattern agrees with the experimental one.

Figure 1.

X-ray diffraction patterns of FeRh₄, FeIr₄, FePd₄, FePt₄, and FeRhIrPdPt. The simulated pattern for FeRhIrPdPt is also shown. The origin of each pattern is shifted by an integer value for clarity.

Figure 2.

SEM images of (a) FeRh₄, (b) FeIr₄, (c) FePd₄, (d) FePt₄, and (e) FeRhIrPdPt, respectively. (f) Elemental mappings of FeRhIrPdPt.

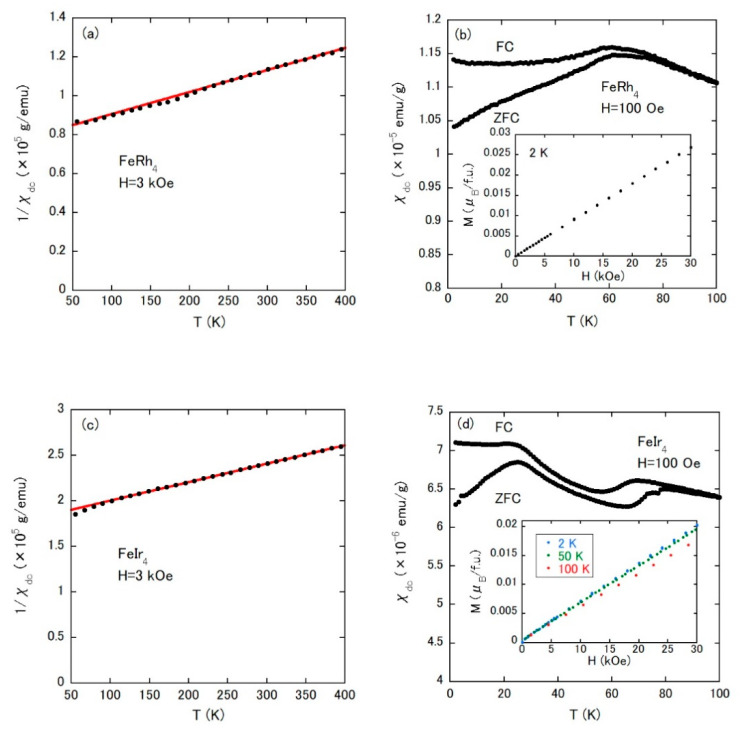
Next, we discuss the static and dynamic magnetic properties within the framework of molecular field. The magnetic properties investigated by χ_dc(T) and M–H (M: magnetization, H: external field) curve measurements are summarized in Figure 3a–d for FeRh₄ and FeIr₄. As shown in Figure 3a,c, the 1/χ_dc(T) of FeRh₄ and FeIr₄ show linear temperature dependences (red lines), which are well-described by the Curie–Weiss law as follows:

χ_dc (T) = C/(T − Θ_CW), (1)

where C is the Curie constant and Θ_CW is the Weiss temperature. The effective magnetic moment μ_eff is derived from C. μ_eff and Θ_CW were obtained as listed in Table 2. In each alloy, the value of μ_eff per Fe atom is close to that of the Fe³⁺ ion (5.92μ_B), which means a well-localized magnetic moment, and the negative Θ_CW indicates a dominance of antiferromagnetic (AFM) interaction between Fe atoms. The low-temperature χ_dc(T) under ZFC and FC conditions with H = 100 Oe for FeRh₄ is given in Figure 3b. Irreversibility between the temperature dependences of ZFC and FC magnetization is common in spin-glass materials. Additionally, the isothermal M–H curve at 2 K demonstrates a featureless magnetization process (see the inset of Figure 3b). FeIr₄ also shows a spin-glass-like behavior (Figure 3d), whereas there are two anomalies, for example, at approximately 23 and 69 K in χ_dc(T) under the FC state. The comparison of M–H curves in the inset of Figure 3d suggests no pronounced feature characteristic for ferromagnetic (FM) or AFM ordering.

Figure 3.

(a) Temperature dependence of 1/χ_dc under an external field of 3 kOe for FeRh₄. (b) Temperature dependence of χ_dc under ZFC and FC conditions with an external field of 100 Oe for FeRh₄. The inset is the isothermal M–H curve at low temperature. (c,d) Experimental results of FeIr₄, corresponding to (a,b), respectively.

Table 2.

Magnetism, magnetic ordering temperature, effective magnetic moment μ_eff, Weiss temperature Θ_CW, and electrical resistivity ρ at room temperature (RT) of prepared samples. SG, FM, and FM corr. refer to spin-glass, ferromagnetism, and ferromagnetic correlation below 300 K, respectively. T_f and T_C are spin-freezing and Curie temperatures, respectively. T_f is the temperature where field-cooled magnetization under the external field of 100 Oe shows the hump.

Sample	Magnetism	Magnetic Ordering Temperature (K)	μeff (μB/Fe)	ΘCW (K)	ρ (RT) (μΩcm)
FeRh4	SG	Tf = 59	5.74	−700	39.0
FeIr4	SG	Tf = 23, 69	5.71	−890	21.2
FePd4	FM	TC = 393	5.44	409	59.5
FePt4	FM	TC = 177, 317	4.11	272	107
FeRhIrPdPt	SG +FM corr.	Tf = 90	3.40	308	70.8

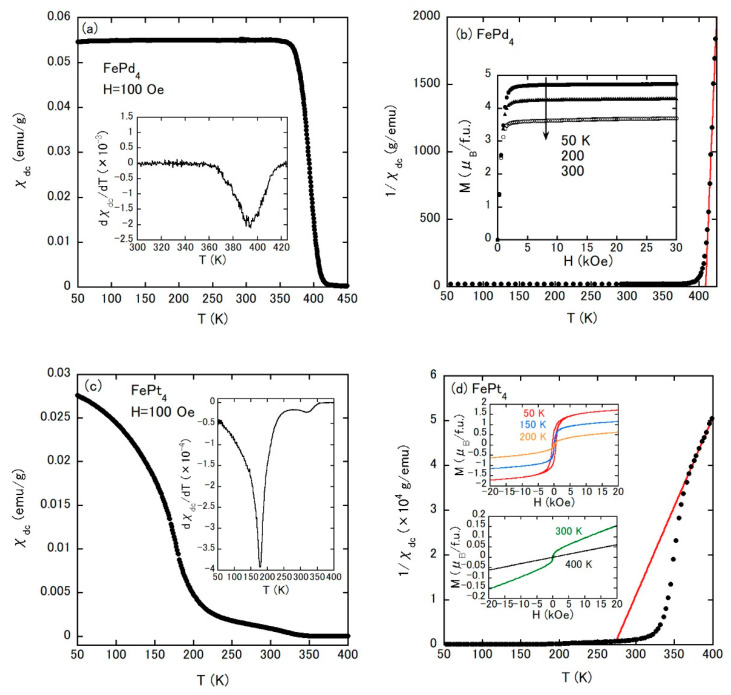
FePd₄ and FePt₄ show FM transitions, which are observed as rapid increases of χ_dc(T) below approximately 400 K and 200 K, respectively (Figure 4a,c). For FePt₄, an additional transition is observed at 317 K, which can be confirmed by the small anomaly in the temperature derivative of χ_dc (see the inset of Figure 4c). The FM nature of these alloys was also checked by the M–H curves, as shown in the insets of Figure 4b,d. Although the M–H curves of FePd₄ measured in increasing and decreasing H show no noticeable difference, a small hysteresis appears in FePt₄. The 300 K isothermal M–H curve of FePt₄ already displays an FM feature. Thus, the additional anomaly at 317 K can be ascribed to the entrance into the FM state. We note here that FeIr₄, the alloy between Fe and 5d element, also possesses two magnetic anomalies. The T_C of each ferromagnet was determined as a minimum on the temperature derivative of χ_dc(T) (see the inset of Figure 4a or Figure 4c). This procedure is frequently employed in ferromagnets [25,26,27]. The χ_dc(T)s of FePd₄ and FePt₄ also show Curie–Weiss behaviors above their T_Cs (red lines in Figure 4b,d). The value of each μ_eff supports the localized magnetic moment for the Fe atom, and the positive Θ_CW is consistent with the FM ground state.

Figure 4.

(a) Temperature dependence of χ_dc under an external field of 100 Oe for FePd₄. The inset is the temperature derivative of χ_dc. (b) Temperature dependence of 1/χ_dc of FePd₄. The inset shows the isothermal magnetization curves of FePd₄ at 50, 200, and 300 K. (c) Temperature dependence of χ_dc under an external field of 100 Oe for FePt₄. The inset is the temperature derivative of χ_dc. (d) Temperature dependence of 1/χ_dc of FePt₄. The insets are the isothermal magnetization curves of FePt₄ at 50, 150, 200, 300, and 400 K.

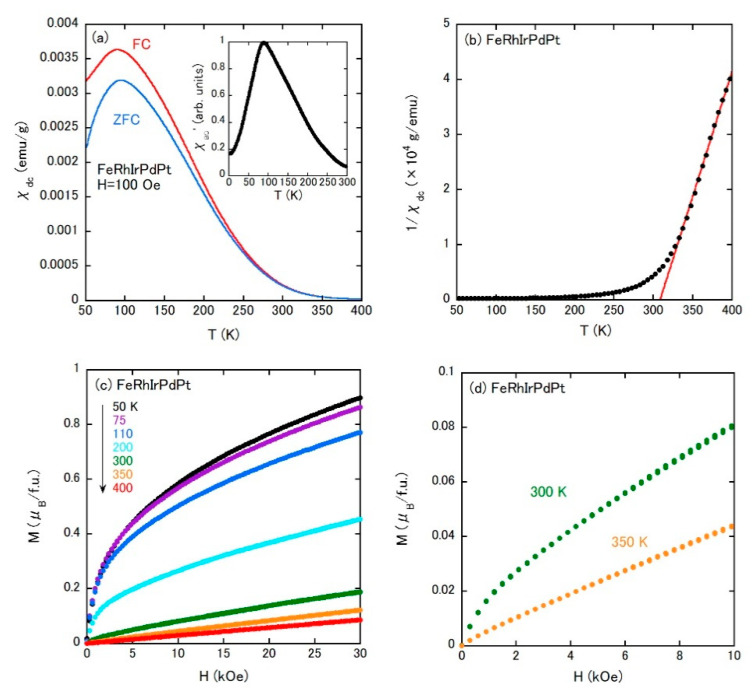
For FeRhIrPdPt, χ_dc was measured as a function of temperature under ZFC and FC protocols with an external magnetic field of 100 Oe (Figure 5a). Both χ_dc(T)s show broad peaks at approximately 90 K, associated with the difference between ZFC and FC data, due to a spin-glass transition as mentioned below. Besides, the irreversible χ_dc(T) between ZFC and FC states already appears below approximately 300 K, which suggests a growth of some magnetic correlation. The inverse χ_dc(T) shows the straight line above 325 K and can be explained by the Curie–Weiss law with μ_eff = 3.40μ_B/Fe and Θ_CW = 308 K (Figure 5b). The effective moment slightly smaller than those of binary alloys is probably due to the influence of the dual phase. The positive Θ_CW indicates the presence of FM correlation. Note that Θ_CW is comparable to 300 K, below which the irreversible χ_dc(T) grows. So, the irreversibility of a magnetic domain could be responsible for the difference of χ_dc(T) between ZFC and FC below 300 K. The FM correlation is further supported by the M–H curves depicted in Figure 5c,d. Although the isothermal magnetization at 350 K shows a paramagnetic behavior, a rather rapid increase of magnetization at the lower field appears below 300 K, close to Θ_CW. With decreasing temperature, the rapid increase at the lower field is pronounced, whereas no saturation is confirmed, which indicates an additional contribution of paramagnetic moments. There seem to be two characteristic temperatures in the magnetism of FeRhIrPdPt: 90 K (spin-glass transition) and 300 K (FM correlation). Especially for the latter temperature, it may be important to investigate a possible long-range ordering. χ_ac(T) is a useful tool for this because the real part of χ_ac(T) can often distinguish respective magnetic ordering as a peak, even in the case that a large χ_dc anomaly due to a strong magnetic interaction masks a small anomaly by a minor magnetic ordering [28,29]. The inset of Figure 5a presents the real part of ac magnetization χ_ac′(T) between 3 K and 300 K, showing no anomaly except for the broad peak due to the spin-glass transition. Therefore, the FM correlation below 300 K would not evolve into a long-range ordering. We note that a similar phenomenon was also observed in another magnetic compound, and is ascribed to an inhomogeneous magnetic state [30,31].

Figure 5.

(a) Temperature dependence of χ_dc measured under ZFC and FC conditions for FeRhIrPdPt. The external field is 100 Oe. The inset is the temperature dependence of the real part of the ac susceptibility χ_ac′(T) of FeRhIrPdPt under an ac field of 5 Oe at 800 Hz. (b) Temperature dependence of 1/χ_dc measured under FC condition for FeRhIrPdPt. Isothermal magnetization curves of FeRhIrPdPt at 50, 75, 110, 200, 300, 350, and 400 K for (c) and at 300 K and 350 K with expanded scale for (d).

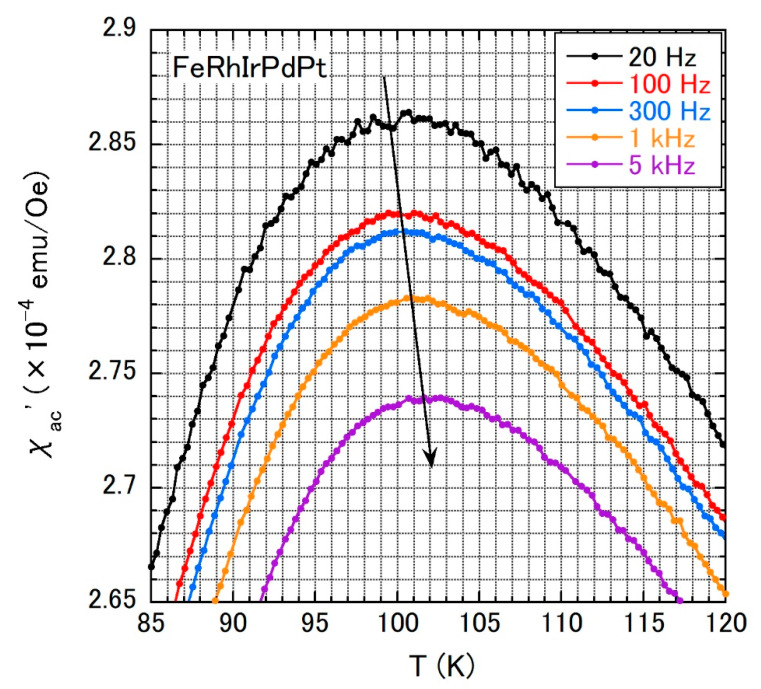
To assess the possible spin-glass transition in FeRhIrPdPt, we measured χ_ac′(T) under several ac frequencies, as shown in Figure 6. χ_ac′(T) shows a broad peak at T_{f_ac}, and as anticipated for a spin-glass transition, T_{f_ac} slightly shifts to higher temperatures as the frequency is increased. We employed two models to explain the shift quantitatively [32]. One is the Vogel–Fulcher law, expressed by

τ = τ₀∙exp [E_a/(k_B(T_{f_ac} − T_SG))]. (2)

Figure 6.

Temperature dependences of χ_ac′ under ac frequencies of 20 Hz, 100 Hz, 300 Hz, 1 kHz, and 5 kHz for FeRhIrPdPt. The arrow is a guide to the eyes.

The other model is the critical scaling approach, as follows:

τ = τ₀∙[T_{f_ac}/T_SG − 1]^−zv. (3)

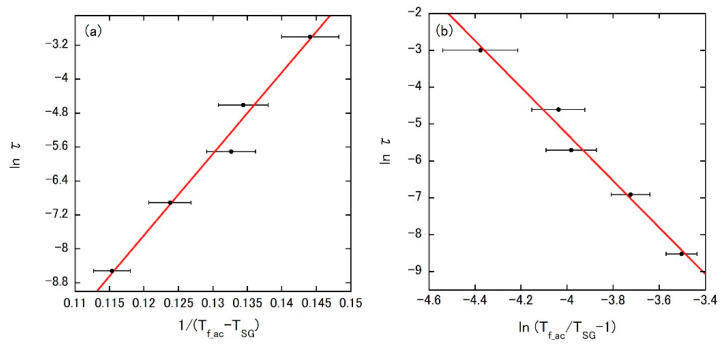
In these equations, τ, τ₀, E_a, T_SG, zv, and k_B are the inverse ac frequency, the spin relaxation time, the activation energy, the spin-glass temperature, the dynamical critical exponent, and the Boltzmann constant, respectively. Figure 7a is the ln τ vs. 1/(T_{f_ac} − T_SG) plot by the Vogel–Fulcher law, which yields the parameters listed in Table 3. The relations E_a ~ 2T_{f_ac} and τ₀ on the order of 10⁻¹⁴ s are consistent with those found in many canonical spin-glass systems [33,34]. The fitting result by the critical scaling approach is given in Figure 7b with a ln τ vs. ln(T_{f_ac}/T_SG − 1) plot. The obtained parameters again fall in the typical range for spin-glass systems [32]. Furthermore, the Mydosh parameter K defined by ΔT_{f_ac}/T_{f_ac}log(Δf) (where f is the ac frequency) is 0.007, comparable to those of canonical spin-glasses such as CuMn and AgMn [35]. Thus, FeRhIrPdPt can be regarded as a canonical spin-glass HEA.

Figure 7.

Fitting results of T_{f_ac} shift in χ_ac′(T) using (a) Vogel–Fulcher law and (b) critical scaling approach for FeRhIrPdPt, respectively.

Table 3.

Fitting parameters obtained by Vogel–Fulcher law and critical scaling approach for FeRhIrPdPt.

Model	τ0 (s)	Ea (K)	TSG (K)	zv
Vogel–Fulcher law	4.8 × 10−14	192	93	-
Critical scaling approach	5.1 × 10−14	-	90	6.3

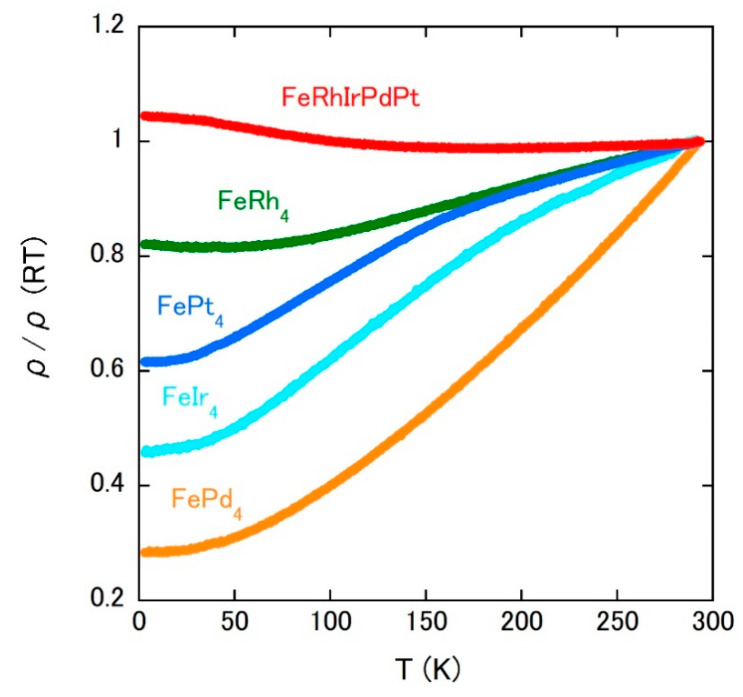
Figure 8 shows the ρ (T) of investigated alloys. Each ρ is normalized by the room-temperature value listed in Table 2. The binary alloys show the metallic behavior; ρ decreases as the temperature is lowered. For the disordered FePd₄, the temperature dependence is rather large in the ferromagnetic state, which is also observed in the other disordered ferromagnets [36]. Contrasted to the metallic behavior of binary alloys, ρ of FeRhIrPdPt slightly increases on cooling, which is a signature of carrier localization and may be due to the atomic disorder higher than those in the binary alloys. It should be noted that the other spin-glass HEAs show metallic temperature dependences [16,18,37].

Figure 8.

Temperature dependences of electrical resistivity of FeRh₄, FeIr₄, FePd₄, FePt₄, and FeRhIrPdPt.

Here we discuss the dual-phase formation in FeRhIrPdPt. Compared to the ideal equimolar Fe₂₀Rh₂₀Ir₂₀Pd₂₀Pt₂₀, the EDX analysis indicates that the main phase is rich in Rh and Ir and poor in Fe, Pd, and Pt, whereas the minor phase shows the reverse tendency (see also Table 1). The enthalpy of formation ΔH_f of each binary compound for constituent elements [38] calculated by Troparevsky et al. can explain the dual-phase formation. Table 4 presents the ΔH_f of stable binary alloy for each component. Although Fe tends to form an alloy with all elements because all pairs Fe–Rh, Fe–Ir, Fe–Pd, and Fe–Pt show negative ΔH_f, Fe–Pd and Fe–Pt pairings would be more robust. Furthermore, alloying between Ir and Rh (Pt and Pd) is also favored. These facts based on the pairwise ΔH_f can explain the dominant elements in each phase of FeRhIrPdPt. A similar discussion has been found in AuPdAgPtCu, also showing a dual-phase microstructure [39]. All binary alloys of noble metals (Rh, Ir, Pd, and Pt) with 1:1 composition form fcc [40,41]. Furthermore, many noble metal HEAs (e.g., PdPtRhIrCuNi and PdPtRhRuCe) are reported to be fcc alloys [39,42]. Therefore, the fcc FeRhIrPdPt would be deeply related to the existing phase diagrams of noble metals.

Table 4.

Enthalpies of each binary compound. The unit is meV/atom. Data from [38].

	Fe	Rh	Ir	Pd	Pt
Fe	0	−57	−63	−116	−244
Rh	−57	0	−21	37	−24
Ir	−63	−21	0	40	11
Pd	−116	37	40	0	−36
Pt	−244	−24	11	−36	0

It is straightforward that the main and minor phases of FeRhIrPdPt independently exhibit their magnetism as in the other dual-phase HEA magnetic materials. The magnetic properties of FeRhIrPdPt can be characterized by the canonical spin-glass plus high-temperature FM correlation. So, in FeRhIrPdPt, the different phases would be responsible for the spin-glass transition and the high-temperature FM correlation. In the binary alloys, FeRh₄ and FeIr₄ are spin-glass materials, while FePd₄ and FePt₄ are ferromagnets. Based on the atomic ratios in the dual-phase of FeRhIrPdPt, we speculate that the main phase rich in Rh and Ir and minor one rich in Pd and Pt exhibit the spin-glass transition and the FM correlation, respectively. As mentioned in the Introduction, dual-phase HEAs would be useful in tailoring magnetic properties via a change of microstructure. In this case, the occurrence of spinodal decomposition is mainly responsible for the change of microstructure. Although the as-cast dual-phase HEA was investigated in this study, it is important to understand the thermal stability of the alloy in order to understand and control the microstructure. This is a future task. The other interesting aspect of dual-phase HEAs is a possible multifunctional magnetic material, in which two magnetic phases offer different magnetic functions.

4. Summary

We synthesized the new dual-phase fcc HEA FeRhIrPdPt and evaluated its structural, magnetic, and transport properties by assuming that the HEA is a mixture of FeRh₄, FeIr₄, FePd₄, and FePt₄, all with fcc structure. The dual-phase alloy is composed of a Rh- and Ir-rich main phase with 70 vol.% (74 wt.%) and a Pd- and Pt-rich minor one with 30 vol.% (26 wt.%). The minor phase could also form an fcc structure with a lattice parameter near that of the main phase. In the binary alloys, FeRh₄ and FeIr₄ are spin-glass materials dominated by antiferromagnetic interactions, whereas FePd₄ and FePt₄ are ferromagnetic. FeRhIrPdPt can be characterized by two magnetic features: one is the canonical spin-glass transition at 90 K, and the other is the ferromagnetic correlation revealed by the irreversible χ_dc(T) under ZFC and FC conditions below 300 K. The latter correlation would not lead to long-range magnetic ordering. Based on each chemical composition of the dual-phase alloy, the main and minor phases would be responsible for the spin-glass transition and the ferromagnetic correlation at high temperatures, respectively. The temperature dependence of the electrical resistivity of FeRhIrPdPt indicates weak carrier localization, which is contrasted with the metallic behaviors of binary alloys. The dual-phase formation of FeRhIrPdPt can be discussed based on the pairwise formation enthalpies of the binary alloys.

Author Contributions

Conceptualization, J.K.; methodology, J.K.; formal analysis, J.K.; investigation, K.B., N.I., T.N., and J.K.; writing—original draft preparation, J.K.; writing—review and editing, T.N. and J.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data sharing is not applicable.

Conflicts of Interest

The authors declare no conflict of interest.