The Influence of X-Ray Computed Tomography Acquisition Parameters on Image Quality and Probability of Detection of Additive Manufacturing Defects

Abstract

X-ray computed tomography (XCT) is a promising nondestructive evaluation technique for additive manufacturing (AM) parts with complex shapes. Industrial XCT scanning is a relatively new development, and XCT has several acquisition parameters that a user can change for a scan whose effects are not fully understood. An artifact incorporating simulated defects of different sizes was produced using laser powder bed fusion (LPBF) AM. The influence of six XCT acquisition parameters was investigated experimentally based on a fractional factorial designed experiment. Twenty experimental runs were performed. The noise level of the XCT images was affected by the acquisition parameters, and the importance of the acquisition parameters was ranked. The measurement results were further analyzed to understand the probability of detection (POD) of the simulated defects. The POD determination process is detailed, including estimation of the POD confidence limit curve using a bootstrap method. The results are interpreted in the context of the AM process and XCT acquisition parameters.

1. Introduction

Metal additive manufacturing (AM) has great potential to transform manufacturing industries. However, many AM processes, including laser powder bed fusion (LPBF) processes, can produce undesired gas pores and lack-of-fusion (LOF) defects, which can be detrimental to mechanical performance of the produced part [1]. Gas pores result from entrapping environmental gas or gas that already exists in metal powders [2,3], and these pores tend to be spherical in shape. LOF defects are attributable to unoptimized processing parameters (e.g., laser power, scan speed, and hatch spacing) [4,5]. These pores tend to be irregular in shape, and multiple pores can be interconnected. If the pore is large enough, it can trap unmelted metal powder [6]. These defects are important considerations for adoption of the technology in applications such as fracture-critical components in the medical and aerospace industries [7]. But a reliable method to detect defects in AM-produced parts with complex internal structures must be developed prior to widespread adoption of metal AM.

X-ray computed tomography (XCT) was identified as the most promising technique to nondestructively inspect AM-produced components with complex geometries [8]. While the technique is promising for inspection, the quality of XCT images is a critical factor for a reliable detection of defects as described in a recent work [6]. Noise in the image can mask defects that we hope to identify, and the noise can be described quantitatively by the standard deviation of image intensity within a homogenous material. The standard deviation, σ, of the pixel gray scale values P_i for N pixels in a homogeneous region is defined in Eq. (1), where μ denotes the mean pixel value and a homogenous region is a region with a uniform material composition. The signal-to-noise ratio (SNR) is the quotient between the mean signal level (μ) and the fluctuation range (noise, σ) and is often used as a measure to describe the image quality (Eq. (2)). Since single-phase materials have a single fixed mean level in XCT images, the noise alone may be used to compare the quality of two images from the same uniform material.

$${\sigma }^2=\frac{1}{N-1}\cdot \sum _{i=1}^N{\left(P_i-\mu \right)}^2$$ (1)

$$\text{SNR}=\frac{\text{Signal}\text{level}}{\text{Noise}\text{level}}=\frac{\mu }{\sigma }$$ (2)

Noise level and thus image quality of XCT images are affected by various acquisition parameters such as source voltage, current, magnification, frame rate (inverse of exposure time per projection), number of images per projection, number of projections, and the CT reconstruction algorithm. In addition to the acquisition parameters, image processing and thresholding/surface detection algorithms strongly affect automatic detection and measurement capability. There are many different thresholding algorithms available, but the influence of different thresholding algorithms is not considered in this study.

Hermanek and Cargmignato [9] recently developed a reference sample containing 72 hemispherical calottes with diameters from 100 μm to 500 μm. A design of experiment (DoE) was used to study the effects of voltage and current on the calotte diameter measurements. Müller et al. [10] studied the effect of various parameters (voltage, current, magnification, frame rate, and number of images per projection) on dimensional measurement as well. They developed a full factorial (3²) DoE, where each factor had three levels, to determine the influence of spatial resolution and pixel noise on dimensional measurements. Our literature review has shown that only a limited amount of research has been focused on the effect of acquisition parameters on dimensional measurements. The large number of acquisition parameters and the wide range of possible variation of those parameters make an experimental investigation difficult. For the first goal of this work, we designed a fractional factorial experiment to rank the influence of six acquisition parameters on image quality while limiting the data acquisition to a reasonable number of experiments.

The detectability of defects of a nondestructive evaluation (NDE) system or procedure can be quantitatively described by the probability of detection (POD). The POD evaluation can be used to compare different NDE systems and also to determine if the NDE system or procedure is suitable for a given inspection task. In an XCT system, the system resolution is often quoted as the limiting capability of the system. For qualification and certification of a fracture-critical component, more rigorous investigation is needed. The concept of POD embraces the statistical nature of detection either by an operator or a system. A defect is said to be detected if a machine signal crosses a pre-specified threhsold. However, the signals are noisy. A different defect of the same size, even the same defect, could produce a different signal at a different time. A good NDE system will detect flaws in structures a high percentage of the time even in the presence of such noise. We analyzed acquired measurements in this paper to estimate POD. As the artifact was not originally designed for a POD study, the study does not strictly follow all the recommended requirements in terms of the number of defects and other aspects mentioned in the MIL-1823A guide [11]. While POD studies have been performed for various NDE systems, only a limited number of studies have been performed for XCT. Therefore, the second objective of this work is to provide an introduction and general procedure for determining POD in XCT measurements using the $\widehat{a}$ versus a model to the AM community. In an $\widehat{a}$ versus a model, a refers to the true size of the defect and $\widehat{a}$ refers to the NDE signal response of the defect. Section 2 describes the artifacts built for the study as well as the fractional factorial design, Sec. 3 describes the experiment and XCT measurement protocols, Sec. 4 describes both the factor ranking analysis and the POD analysis, and Sec. 5 ends with discussion and conclusions.

2. Materials and Methods

2.1. Artifact Development.

A sample incorporating synthetic defects that represent LOF defects with some trapped powder particles was produced with the LPBF process as shown in Fig. 1. The overall dimension of the sample is nominally 5 mm (diameter) × 15 mm (height). Pre-alloyed 17–4 stainless steel powders (GP1) [12] were used to produce the sample with the chemical composition of typical 17–4 stainless steel. The powders were atomized in nitrogen gas, and the powder size, as measured by laser diffraction, was between 5 μm and 80 μm with a peak around 40 μm [13]. Hollow cubes of different nominal edge length (200 μm, 400 μm, 600 μm, 800 μm, 1 mm, and 2 mm) were produced using default processing parameters. Due to the PBF process, these hollow cubes trapped metal powder particles. Individual powder particles are not fully resolved in the image due to their small sizes compared with the targeted voxel size. They appear as a single material with lower contrast in XCT images. The cubes were designed such that one of the body diagonals of the cube is aligned with the vertical axis. This orientation was found to produce an actual geometry closer to the nominal design based on the previous work [14]. Figure 1 shows the picture of the artifact, computer-aided design (CAD), and a vertical cut view through a reconstructed XCT image stack.

Fig. 1.

Artifact incorporating hollow cubes filled with raw metal powders. The XCT image is a section cut (A-A) through the center of the sample, as shown in the CAD.

2.2. Experiment Design.

A fractional factorial experiment [15] in voltage, current, magnification, frame rate, number of images average per projection, and reconstruction algorithm was designed. Three continuous levels were considered for all factors except algorithm, which had only two categorical levels: filtered back projection and iterative reconstruction. The levels of the continuous factors were selected considering the following constraints.

2.2.1. Constraint 1: Geometric Unsharpness.

When selecting voltage and current, it is important to keep the source spot size small enough so that the geometric unsharpness does not exceed the pixel pitch for different magnifications. The relationship of magnification (Mag) and source spot size (s) on geometric unsharpness (λ_g) is shown in Eq. (3). The geometric unsharpness should be less than or equal to the effective pixel pitch (dp) of the X-ray detector, which accounts for any binning or optical magnification. In this case, no binning was applied, and there is no optical magnification in the flat panel detector system. Therefore, dp is just the detector pixel pitch. As the geometric unsharpness exceeds the limit, the actual resolution of the image is degraded, and the highest resolution is not achieved at the given magnification. The spot size of the source is known to be related to the source power. A general rule of thumb is 1 μm per 1 W, and similar information can be found from another Ref. [16]. For a proper comparison between different experiments, we kept the geometric unsharpness of each experiment below the limit.

$$(\text{Mag}-1)\cdot s={\lambda }_g\le dp$$ (3)

2.2.2. Constraint 2: X-Ray Signal Level.

The selected voltage, current, frame rate, and source-to-detector distance combination should also allow enough the X-ray flux incident on the detector by penetration through the sample. The detected signals by X-ray incidence must be higher than the background level for a proper XCT reconstruction. The background signal includes the radiation intensity in the background and any electronic noise in the detector. The X-ray signals also must be lower than the maximum detector dynamic range, which is 16 bits (0–65535) in this case. The detected intensities were kept at about 75–80% of the maximum level. An increase in the voltage and current will increase the X-ray flux and detected signals. A reduction in the frame rate increases the detected signals up to the detector limitation. A decrease in the source-to-detector distance increases the flux level at the detector plane. The X-ray flux proportionally decreases by the square of distance.

2.2.3. Constraint 3: Fixed Source-to-Detector Distance.

The same magnification can be achieved for different combinations of source-to-object distance (SOD) and source-to-detector distance (SDD). To simplify the experiment, a constant source-to-detector distance was chosen while varying the source-to-object distance to achieve different levels of magnification, which simplified the choice of frame rates.

2.2.4. Constraint 4: Physical Filter.

Although it is not a part of the study here, the incident X-ray spectrum typically includes low energy characteristic peaks, which influence the noise level (quality) of the images. A physical filter was applied at the source window to cut off these peaks, thus hardening the beam spectrum. This process also reduced the available flux at the detector. In this case, a 3.05-mm-thick copper filter was used.

The X-ray spectra were simulated using the Tungsten anode spectral model using interpolating cubic splines (TASMICS) software, as shown in Fig. 2 [17]. Even though a 3.05-mm-thick copper filter was used, the predicted spectrum showed some remaining characteristic peaks. These characteristic peaks correspond to a combination of peaks at around 57.4 keV and 66.7 keV–69.5 keV. These characteristic peaks could have contributed to the noise level in the images. Further increase in the filter thickness can reduce the effect of characteristic peaks, but it will also reduce the available X-ray flux at the detector plane resulting in longer acquisition times. The average energies of each spectrum are, from left to right in Fig. 2, 105 keV, 113 keV, and 120 keV, respectively.

Fig. 2.

Simulated spectra for different source voltages with 3.05-mm Cu filter for 1 Gy air Kerma (Kerma is an acronym for kinetic energy released per unit mass, and 1 Gy is 1 Joule per kilogram)

3. Experiment

An industrial XCT system was used for XCT measurements. The system is equipped with a microfocus source, a rotary stage, and a flat panel detector. The microfocus source has a tungsten target. The number of projections was chosen to be more than the theoretically required number of projections. Two different cone beam reconstruction algorithms, Feldkamp–David–Kress (FDK) and simultaneous iterative reconstruction technique (SIRT), as supplied by the open-source software ASTRA, were used [18,19]. For the FDK algorithm, a typical ramp filter (Ram-Lak) was used as the reconstruction filter. The reconstruction filter of the FDK algorithm is known to affect the image quality and noise level for filtered back-projection algorithms [20]. There are different types of iterative reconstruction algorithms, and the results would vary for different algorithms. Based on our study, the number of iterations significantly affects the image quality as shown in the appendix. The 20 measurements that were acquired, based on the fractional factorial design, are listed in Table 1, which also lists the factor level combinations that were used as well as the measurement response, standard deviation of image intensity. The values covered here are at voltages (160 kV–200 kV) chosen at the higher-end of the system (225 kV source), which would be typically used for inspecting a metallic sample. Depending on the material and applications, various magnifications may be employed, which is covered in the study. We covered magnifications from high to coarse in three levels considering the constraints mentioned in the previous section. The voxel sizes were determined by dividing detector pixel pitch (127 μm) by geometric magnification values, and they are listed in the table to help readers identify the data sets. Some of the parameters are chosen based on the limitation discussed in the Sec. 2. While only one image is often acquired per projection, we wanted to study how increasing the number of images may improve the image quality. As more images are averaged per projection, the image SNR theoretically increases by $\sqrt{N}$, where N is the number of images averaged. The trade-off would be the increase of the total acquisition time.

Table 1.

XCT acquisition parameters and standard deviation measurements

Experiment	Voltage (kV)	Current (mA)	Magnification	Voxel size (μm)	Frame rate (frame/s)	Number of images per projection	Reconstruction algorithm	Standard deviation (16-bit gray level)
1	180	90	5.62	22.60	2	4	FDK	697.7
2	180	90	5.62	22.60	2	4	SIRT	809.7
3	160	80	8.39	15.14	3.75	16	SIRT	1144.4
4	200	100	3.18	39.94	3.75	1	SIRT	1267.1
5	180	80	8.39	15.14	1	1	SIRT	1753.4
6	160	80	8.39	15.14	1	16	FDK	643.0
7	180	100	8.39	15.14	3.75	16	SIRT	864.9
8	160	100	3.18	39.94	1	16	SIRT	494.6
9	180	80	8.39	15.14	3.75	1	FDK	2842.9
10	160	80	3.18	39.94	1	1	FDK	915.4
11	180	90	5.62	22.60	2	4	FDK	695.2
12	160	100	8.39	15.14	1	16	FDK	614.5
13	160	80	3.18	39.94	1	16	SIRT	514.2
14	160	100	8.39	15.14	3.75	1	FDK	3042.6
15	160	100	3.18	39.94	3.75	16	FDK	577.8
16	200	100	3.18	39.94	1	1	FDK	686.5
17	200	80	3.18	39.94	3.75	16	FDK	530.2
18	160	100	8.39	15.14	1	1	SIRT	1876.7
19	160	80	3.18	39.94	3.75	1	SIRT	1908.5
20	180	90	5.62	22.60	2	4	SIRT	814.5

The XCT scans acquired at different magnifications were aligned at the same orientation in a three-dimensional (3D) space using an image registration algorithm based on the maximization of normalized mutual information as implemented in the AVIZO software [21]. For a detailed explanation of the general registration method, readers are referred to other papers [22–25]. Once all data were registered to the same location, standard deviations were measured for homogeneous areas (51 × 75 × 550 voxels) within the sample away from the simulated defects.

4. Effect of X-Ray Computed Tomography Acquisition Parameters on Image Quality

4.1. Data Analysis Overview.

The analysis of image quality focuses on three questions: (1) how repeatable are the scans, (2) which of the six factors most impact the image quality, and (3) which experimental factor combination leads to the best image quality. The analysis is performed on the logarithmic scale, a common pre-analysis transformation for inherently positive response variables. The replicated runs (1 paired with 11, and 2 paired with 20) are used to answer question 1, and the least absolute shrinkage and selection operator (LASSO) [26] is used to answer question 2. The GLMNET package [27] for R [28] was used for computations related to the LASSO. The shrinkage parameter for the LASSO was calculated by a 10-fold cross validation and the “one-standard-error” rule described in Ref. [27]. The LASSO has recently been compared with more traditional tools for analyzing fractional factorial experiments and found to be especially useful when, due to missing observations, the orthogonal structure of the designed experiment is disturbed [29]. This is exactly our situation, not because of missing observations, but because of experimental constraints. Question 3 is answered directly from the experimental results. The experimental factor combination with the lowest standard deviation would be considered to have the best image quality out of the 20 experiments.

A second analysis centered on the calculation of POD for XCT was also carried out. The numerical results that we present should not be considered conclusive because as we describe in Sec. 5, it is not possible to directly measure the size of the cuboidal defects in our sample. We feel that there is, however, great value in this description since to our knowledge such a description does not appear in the literature on defect detection for AM. We intend that this description will serve as a roadmap for future work in the area.

4.2. Scan-to-Scan Repeatability.

The replicated points (1 paired with 11, and 2 paired with 20) were used to assess scan-to-scan repeatability, e.g., the level of noise change when a scan is repeated under identical settings of the acquisition parameters. The standard deviations of the logarithm of the measurement results from the replicate runs made with the SIRT algorithm (experiments 2 and 20) and the replicate runs made with the FDK algorithm (experiments 1 and 11) were averaged, which yielded 0.003. Since the analysis is performed on the logarithmic scale, we interpret the number in the following way: if scans are repeated using the same acquisition parameters, the noise level in the image is expected to vary by 0.3%.

4.3. Ranking.

Table 2 lists the factors from the LASSO procedure with non-zero coefficients in order by absolute magnitude. Note that the raw numerical values of the coefficients are not directly interpretable because the input factors are centered and scaled before use. The magnitude and sign of the coefficients directly provide useful information, which is the focus of this section. Clearly, the most important factor is the number of images, with increasing quality (lower standard deviation) as the number of images increases. Magnification and frame rate impact image quality similarly, with a higher magnification and a higher frame rate leading to lower image quality. Voltage is ranked as fourth most important with higher voltage leading to better quality images. The main effect of the reconstruction algorithm and its interaction with the frame rate impact image quality by a similar magnitude, but in opposite directions. The experiments were designed to be able to study the interactions between the six main parameters, and the interaction between the algorithm and the frame rate was the only interaction found to significantly influence the image quality. Surprisingly, the positive coefficient for algorithm factor implies that on average SIRT reconstructions lead to lower image quality. This could be an artifact of the number of iterations used for reconstruction (see appendix). The negative coefficient on the interaction between the number of images and the algorithm implies that for FDK reconstructions the deleterious effect of increasing the frame rate becomes worse, but for SIRT reconstructions, the harmful effect of the increasing frame rate is lessened.

Table 2.

Ranking of the investigated XCT acquisition parameters

Rank	Factor	LASSO coefficient estimate
1	Number of images	−0.32
2	Magnification	0.18
3	Frame rate	0.16
4	Voltage	−0.061
5	Algorithm—frame rate	−0.0016
6	Algorithm	0.0010

4.4. Comparison of the Data With the Lowest and Highest Standard Deviation.

Experiment 8 had the lowest standard deviation (highest image quality), and experiment 14 had the highest standard deviation (lowest image quality), see Table 1. The images are compared in Fig. 3, and the difference in the image quality is quite significant as shown from the grayscale images. Based on a visual inspection, it is possible to detect defects of all sizes. However, an automatic inspection is desired in industrial settings, and an image thresholding process is required. Otsu’s method [30] was used to threshold the grayscale images to binary images as an example. Connected components within the binary images can be used to label each component and quantitatively measure the volume. In the case of experiment 8, the thresholding and labeling processes were successful. Different colors in the labeled image represent different connected components. On the other hand, images in experiment 14 were too noisy to properly segment the components. The main differences with the acquisition parameters are magnification, frame rate, number of images, and reconstruction algorithm as presented in Table 3. Except for the reconstruction algorithm, the trend of high image quality in experiment 8 and low image quality in experiment 14 follows the interpretation of the impact of the factors in Sec. 4.3, e.g., raising the number of images raises image quality.

Fig. 3.

Comparison of the images of the lowest (experiment 8) and highest (experiment 14) standard deviation data sets

Table 3.

Acquisition parameters of experiment 8 and experiment 14

Experiment	8	14
Voltage (kV)	160	160
Current (mA)	100	100
Magnification	3.177	8.394
Frame rate (frame/s)	1	3.75
Number of images	16	1
Reconstruction algorithm	SIRT	FDK
Standard deviation (16-bit gray level)	494.6	3042.6

4.5. Suggestions for Future Experiments.

An X-ray source spectrum is governed by the source voltage, current settings, and filter material and thickness. The source voltage strongly affects the X-ray spectrum and total flux, and it was found to be an important parameter in the current study. In future experiments, it is suggested to fix the source voltage for comparisons of other parameters to reduce measurement uncertainty due to having different X-ray spectra. The simulated energy spectrum also showed that a 3-mm Cu filter was not enough to completely remove the characteristic X-ray peaks, and the filter thickness should be more carefully selected in future experiments. A simulation tool for XCT measurements may help determine the noise level for different conditions not experimentally measured. The voltage would also change the penetration capability, which will affect the number of photons passing through the sample and reaching the detector. While not considered in this project, the effect of material thickness on detection capability would be an important factor to study as well. The POD is expected to significantly decrease with an increase in material thickness and a subsequent reduction of X-ray transmission.

Another consideration for future studies is the type of experiment to run. The fractional factorial experiment used in this work is efficient for screening many factors. Figure 4 plots the residuals from the LASSO procedure against the fitted values. Overall, the residuals are symmetric around zero, as we would expect, but an apparent curvilinear pattern remains, which may signal a need for higher order terms such as quadratic or cubic. The use of efficient response surface designs or even optimal designs that enable fitting higher order terms may be beneficial. However, note that the magnitude of the largest residuals is still quite small, around 5%. Furthermore, the percentage of variability in the data described by our LASSO model is more than 90%. Thus, even in light of the shortcomings, the model fits the data quite well and is adequate for the purpose of ranking the importance of the factors.

Fig. 4.

The residuals plotted against the fitted values from the LASSO procedure

5. Probability of Detection

The acquired data sets were used to determine the POD for the given artifact and XCT acquisition parameters. The NDE flaw size detectability is often denoted as a_90/95, the 95% lower confidence bound for a defect size with 90% POD [11]. In this study, the $\widehat{a}$ versus a approach was used, where a is the actual size of the defect, and $\widehat{a}$ is the NDE measurement response to a defect of that size [31]. Both a and $\widehat{a}$ are volumes in this study, with a being the true volume and $\widehat{a}$ being the volume measured by XCT. The artifact incorporated six simulated defects, which trapped metal powders. The detectability of defects with trapped metal powder can be less than that of a defect with no powder due to additional X-ray attenuation of powders resulting in reduced image contrast when imaged with coarser resolution than the size of powders. For each of 12 acquisition settings, we have six measurements, one for each simulated defect. To perform an $\widehat{a}$ versus a study, the true volume a must be found. Since the simulated defects are fully enclosed, it would require a serial sectioning process to measure volumes, which not only destroys the sample but is also prone to produce errors due to smearing the edges. Instead, we used an XCT measurement system that has spatial resolution that is an order of magnitude higher than the system to be used for routine inspection of AM parts. The ZEISS Versa XM500 system² in NIST Boulder was used to measure the regions of interest of the sample around individual defects as shown in Fig. 5. The system configuration is slightly different from the other XCT system as it incorporates a lens-coupled charge-coupled device (CCD) camera detector. Optical magnification was utilized in addition to geometric magnification. The parameters shown in Table 4 were used. The effective image voxel size of 3.71 μm was achieved, which is a result of magnification (both geometrical and optical) and camera binning. The material and thickness of the filter are proprietary information of the vendor. The reconstruction was performed with FDK algorithm in the vendor’s software. In Fig. 5, examples of XCT images of the largest (nominally 2 mm cube) and smallest (nominally 200 μm cube) defects are shown. The trapped powders are clearly visible. The defect volumes are measured based on sub-voxel determination in the environment of VGSTUDIOMAX 3.1 [32]. The uncertainties are found based on the 1/10th of a voxel uncertainty of surface determination process applied to a cube [33]. Since we measure the true defect size, a, using a higher resolution XCT system than would be used for routine inspections, the reader should treat the POD analysis that follows as expository, not a definitive quantitative statement about POD for LOF defects with XCT systems. A more rigorous POD study would require the true defect size, a, to be measured by a technique that produces metrologically traceable [34] measurements with completely characterized uncertainties. This would require destructive measurements or artifacts for which the defects are not fully enclosed.

Fig. 5.

(a) XCT slice from the lower resolution XCT image and measurements of simulated defect volumes of (b) 2-mm cube (nominal size) and (c) 200-μm cube (nominal size) from higher resolution XCT images

Table 4.

XCT imaging parameters of higher resolution XCT scan

Parameters	Values
Voltage (kV)	160
Current (μA)	62
Filter	HE#6
SDD (mm)	28,999.0
SOD (mm)	15,999.6
Magnification (geometric)	1.81
Magnification (optical)	4.01
Camera binning	2
CCD camera pixel pitch (μm)	13.5
Effective image voxel (μm)	3.71
Frame rate (frame/s)	0.227
Number of images	1
Number of projection	3201
Reconstruction algorithm	FDK

Otsu’s method [30] was again used for thresholding, which enabled volume measurements to be made in the high-resolution XCT images. The measured volumes for each nominal defect sizes are presented for different experiments and reference measurements in Table 5. A binary response curve is shown in Fig. 6, with the horizontal axis depicting the noise level (standard deviation of intensity) of the image. The binary response of 1 means that all defects were clearly thresholded and identified, and the response of 0 means one or more of the defects were not thresholded properly. The experiments with the two lowest standard deviation values in the 0 binary response group properly detected all defects but the smallest. There are more materials around the smallest defect, which reduced X-ray penetration, and the higher local noise level around the smallest defect reduced thresholding capability for the two acquisition settings. Since all defects were not properly detected, the two results are excluded from the following POD analysis. All other experiments in the 0 binary response group had higher standard deviation values than all of the experiments in the 1 binary response group, and the results again indicate the importance of reducing noise level for a proper detection of defects. The acquisition parameters that did not permit automatic defect detection are omitted from Table 5 as well as our POD analyses because we do not expect XCT operators to perform manual inspection in industrial settings.

Table 5.

Volume measurements of defects (the signal response measurements (â) were performed for experiments 1, 2, 3, 6, 7, 8,11, 12,13,15,17, and 20. The true defect sizes (a) are shown in the last row)

Experiment	2-mm cube (mm3)	1-mm cube (mm3)	0.8-mm cube (mm3)	0.6-mm cube (mm3)	0.4-mm cube (mm3)	0.2-mm cube (mm3)
1	9.379	1.274	0.666	0.298	0.100	0.021
2	9.342	1.271	0.662	0.298	0.100	0.020
3	9.393	1.268	0.662	0.304	0.102	0.021
6	9.250	1.256	0.656	0.298	0.098	0.018
7	9.326	1.274	0.667	0.302	0.100	0.020
8	9.528	1.267	0.663	0.293	0.098	0.023
11	9.376	1.273	0.663	0.298	0.100	0.020
12	9.262	1.262	0.660	0.299	0.098	0.019
13	9.569	1.258	0.648	0.299	0.107	0.026
15	9.576	1.271	0.660	0.292	0.098	0.025
17	9.608	1.263	0.649	0.296	0.104	0.026
20	9.334	1.269	0.662	0.299	0.100	0.020
True defect size (a)	9.147 (±0.0266%)	1.204 (±0.0523%)	0.652 (±0.0642%)	0.280 (±0.0851%)	0.0899 (±0.124%)	0.0146 (±0.228%)

Fig. 6.

Binary detection response of 20 experiments

For the $\widehat{a}$ versus a POD study, an arbitrary decision threshold needs to be chosen based on the objective of the POD study [31]. If the threshold changes, the curve does too. In some previous POD studies, the decision threshold was chosen as the NDE instrument detection limit. For an example of ultrasound testing (UT), the lowest signal response that is above the noise level was chosen [35]. In this case, the reliability of the minimum detectable limit is estimated. Here, we want to discuss the choice of decision threshold for screening out the critical defects and whether to accept the part after an inspection for the critical defect size. In instances similar to ours, where the $\widehat{a}$ is a direct estimate of a, the reaction may be to set the threshold to the size of defect that we want to find, which may not be optimal. In contrast, in UT, defect size is measured in a unit of area perpendicular to the sound beam, but the measurement response is maximum echo amplitude (e.g., dB). A threshold in terms of echo height must still be chosen.

One way to choose a threshold is to proceed iteratively. Choose an initial threshold, estimate the POD curve and its lower bound, and examine the POD for defect sizes that are of interest for your application. If they are satisfactory, the chosen threshold can be used to identify defective parts. If not, the threshold should be adjusted up or down depending on if its POD is too high or too low for defect sizes of interest for your application. If the POD for defect sizes of interest for the initial threshold is too low, the threshold should be adjusted down. If the POD is too high, the threshold should be increased. This should be continued until the POD for the defect sizes of interest for your application is acceptable. The reader may note that they can achieve (essentially) POD=1 for their defect size of interest by choosing a low enough threshold. This is true, but it does not come for free. The threshold specifies when a defect is declared to be larger than some critical size. If the threshold is pushed too low, many defects that are smaller than the critical size will still be flagged as larger.

This suggests a second approach for choosing a threshold, balancing the true positive rate (TPR) (the probability of declaring a defect larger than some critical size when it really is) and the false positive rate (FPR) (probability of declaring a defect larger than some critical size when it is not). For example, if the threshold is set to be extremely small so that all defects are classified as larger than the critical size, both the TPR and FPR are one. In contrast, if the threshold is set to be extremely large so that no defects are classified as larger than the critical size, the TPR and FPR are identically zero. The goal is to set a threshold that balances these competing aspects so that the TPR is large and that FPR is small instead of focusing only on the POD. A common plot for simultaneously displaying the TPR and FPR as the threshold changes is the receiver operating characteristic curve, which has found extensive use in a diverse collection of fields such as signal processing [36], diagnostic medicine [37], and more recently machine learning [38]. We do not employ such a strategy here because to calculate the TPR and FPR in the a versus $\widehat{a}$ study, it is necessary to hypothesize a distribution of defect sizes in an AM part to be inspected.

Once a satisfactory decision threshold and a corresponding POD curve are found, the inspector can use the decision threshold to accept or reject an actual part during a future XCT inspection. If there is a defect with a signal response higher than the decision threshold, the part can be rejected with the determined POD and confidence. If one is interested in estimating the detection capability of the XCT setting, an example decision threshold may be chosen as the volume of 8 voxels, which is the minimum measurable size of features based on the Nyquist sampling theorem in 3D [39]. If the geometric unsharpness was not properly addressed as already mentioned in Eq. (2), the number of voxels may have to be increased. Based on this decision threshold, one can determine the reliability of the XCT setting and a_90/95 value for damage tolerance analysis.

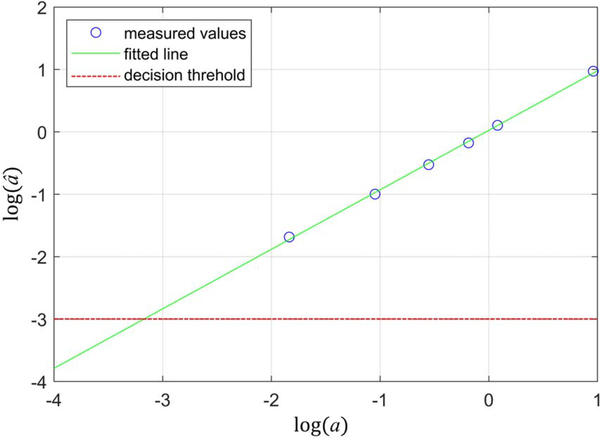
For experiment 1, $\widehat{a}$(lower resolution XCT) is plotted against a (higher resolution XCT) in log-log scale in Fig. 7. A linear relationship was found, and a line was fit to the points. We demonstrate the development of a POD curve using a decision threshold of 0.001 μm³. As an example, we chose a 100-μm cube (0.001 mm³) as the true defect size (a) of interest (e.g., critical defect size). Since our $\widehat{a}$ versus a curve is almost 1:1, we also chose 0.001 μm³ as the decision threshold in the scale of $\widehat{a}$ as an example to describe the process of determining a POD curve. As described in the previous paragraph, the final decision threshold will be iteratively chosen based on the resulting POD curve. The decision threshold is shown in Fig. 7 as the dotted line.

Fig. 7.

Plot of $\widehat{a}$ versus a in log scale of experiment 1

To generate a POD curve, a normal distribution is used with mean values determined by the fitted line and standard deviation determined by the root mean squared error of the linear fit. Figure 8 shows one such normal distribution. The x-axis in Fig. 8(a) is the logarithm of $\widehat{a}$. The POD at each $\widehat{a}$ value is the area under the normal distribution curve above the decision threshold as shown in Fig. 8(b). When the normal distribution curve mean value is centered at log(0.0011) as an example, the POD is 75.8% based on the decision threshold of log(0.001). The POD is estimated from different normal distribution curves with the mean values centered at different $\widehat{a}$ values. The POD values and the corresponding a may be found, leading to the curve shown in Fig. 9 with the x-axis being the actual size of defect (a) and the y-axis being POD. The uncertainty in a is not addressed in our POD analysis because it is much smaller than the error in our fitted lines ($\widehat{a}$ versus a). If the uncertainty in a were closer in magnitude to the error in the linear fits, it would be necessary to use errors in variable regression techniques [40] to fit the lines, and the corresponding Monte Carlo bootstrap procedure used to estimate uncertainty of POD curves should be revised appropriately, too.

Fig. 8.

(a) Determination of POD from normal distribution curve and (b) the normal distribution curve overlaid on the $\widehat{a}$ versus a plot

Fig. 9.

POD curve for experiment 1

An important aspect of POD curves is to be able to account for uncertainty. The 95% lower confidence bound is typically estimated. To estimate the uncertainty of the curve, a parametric bootstrap method was used [41]. The bootstrap method we employ accounts for the mismatch between the fitted line and the values of $\widehat{a}$. On the basis of the fitted line and its root mean squared error, new $\widehat{a}$ values are simulated from a normal distribution with a mean determined by the original fitted line and a standard deviation of root mean squared error from the original linear fit. Based on the new set of $\widehat{a}$ values, a new line is fit, which will have a new slope, a intercept, and a root mean squared error. A new POD curve is generated for the new line. For an example with 1000 repetitions, 1000 data sets and corresponding lines fits are generated as shown in Fig. 10(a), and the corresponding 1000 POD curves are generated as shown in Fig. 10(b). The 95% lower confidence POD curve is found by finding the lower 5th percentile POD values for each a value of interest. The resulting 95% lower confidence bound for the POD curve is shown in Fig. 11. In this study, the POD curve will be interpreted as whether the given inspection setting would be suitable for inspection of the defect of interest (producing a signal response of 0.001 mm³). For experiment 1, the original POD curve provided 100% POD (essentially) at a true defect size of 0.001 mm³, and the 95% confidence curve provided 99.7% POD. If the user does not find the POD values acceptable for the application, a different decision threshold can be chosen to repeat the process until an acceptable POD curve is obtained for the defect size of interest. The 95% lower confidence POD curves for the 12 experiments with clear volume measurements are plotted in Fig. 12. The POD values vary depending on the acquisition parameters, and all experiments provided high 95% confidence POD values for 0.001 mm³ defect. However, it would not be appropriate to rank the acquisition settings based on the POD values. A POD curve is a complex function of the quality of $\widehat{a}$ versus a fit and the choice of decision threshold. Different XCT acquisition settings may be preferred for different decision thresholds.

Fig. 10.

(a) Data generated with bootstrap method and the corresponding line fits for 1000 sets and (b) the corresponding POD curves

Fig. 11.

POD curve of experiment with the 95% lower confidence bound

Fig. 12.

POD curves of 12 experiments detected defects

6. Conclusions

The effect of XCT acquisition parameters on image quality for detection of AM defects was studied, and a method to determine the probability of detection was demonstrated in this paper. Due to the complex external and internal geometry of an AM component, XCT is considered as a promising nondestructive inspection technique. However, XCT is a relatively new NDE technique with many possible acquisition settings, which greatly affects the inspection results. Due to the large number of acquisition parameters and the possible ranges of variation, it is challenging for a novice operator to find a suitable setting. A methodology to determine reliability of XCT inspection is also currently lacking. An artifact incorporating simulated defects was generated using a LPBF AM technique to study the two objectives: effect of acquisition parameters on image quality (in terms of noise level) and probability of detection.

A fractional factorial experiment was conducted by varying six different parameters of XCT acquisition and reconstruction algorithms that affect the noise level in XCT images. The noise level in the image is related to the total X-ray detected fluence, which is affected by the X-ray spectrum, distance from source to detector, frame rate, number of images per projection, sample thickness, and reconstruction algorithm. In this experiment, voltage, current, magnification, frame rate, number of images averaged per projection, and reconstruction algorithm were varied. The standard deviation of image intensity was used as the metric to characterize noise level in the reconstructed images. The LASSO regression procedure was used to identify and rank the most important factors affecting the image quality. The number of images averaged to produce each projection was found to be the most important factor. Other parameters included magnification, frame rate voltage, interaction of reconstruction algorithm with frame rate, and reconstruction algorithm in the order of significance. Repeated measurements were also performed, and the repeatability of image quality was found to be very high. (Standard deviation of the measure (standard deviation of image intensity) was 0.3%.)

A process for determining a POD curve for XCT measurements was also demonstrated based on the measured data. A signal response ($\widehat{a}$ versus a) model was used. For the signal response $(\widehat{a})$ value, the XCT images were thresholded to measure the volume of the defects. For the true defect size (a), defect volumes were measured using a higher resolution (3.71 μm/voxel) XCT system. The data sets with a lower noise level (standard deviation) provided a complete thresholding of all produced defects, and the results indicated the importance of reducing noise level for a reliable detection of defects, in general. A detailed procedure of determining a POD curve was explained, and the uncertainty of the curve (95% lower confidence bound) was also determined by using a parametric bootstrap method. The POD curve provides a reliability statement for the NDE inspection for critical defects. A discussion regarding the choice of decision threshold was also provided where the choice of decision threshold is influenced by the reliability of inspection and economics of inspection. The established methodology will be used as a basis for future POD studies of XCT for different AM defects and part geometries.

Appendix: SIRT Iteration

The simultaneous iterative reconstruction technique (SIRT) [42] as implemented in ASTRA was used for the reconstruction process. A fixed number of iterations were used after qualitatively inspecting the image quality. To understand the effect of number of iterations on image gray level standard deviation, a simple test was performed. It shows that the standard deviation of SIRT-produced images increases as the number of iteration increases. This is due to the inherent noise of the projection data, which the original SIRT algorithm does not account for. Therefore, applying more iteration inevitably increases the noise level. One way to solve the problem is to apply a proper regularization to account for the noise in the system matrix [43,44], which is an active topic of research. At around 1000 iterations, the standard deviation is at a level similar to that produced by the FDK algorithm, as shown in Fig. 13. Therefore, we chose to use 1000 iterations for this project. However, using a lower number of iterations could have reduced the noise level and thereby improved the detection capability.

On the other hand, using a lower number of iterations sacrifices feature sharpness. A line plot across the edge of sample is shown in Fig. 14. The edge transfer function shows a reduced sharpness for a lower number of iterations. Therefore, smaller features could have been missed at lower iteration levels.

Fig. 13.

Standard deviation measurement of FDK and SIRT with different number of iterations

Fig. 14.

Edge transfer function of SIRT with different number of iterations and FDK