Consistency in Monte Carlo Uncertainty Analyses

Abstract

The Monte Carlo method is an established tool that is often used to evaluate the uncertainty of measurements. For computationally challenging problems, Monte Carlo uncertainty analyses are typically distributed across multiple processes on a multi-node cluster or supercomputer. Additionally, results from previous uncertainty analyses are often used in further analyses in a sequential manner. To accurately capture the uncertainty of the output quantity of interest, Monte Carlo sample distributions must be treated consistently, using reproducible replicates, throughout the entire analysis. We highlight the need for and importance of consistent Monte Carlo methods in distributed and sequential uncertainty analyses, recommend an implementation to achieve the needed consistency in these complicated analyses, and discuss methods to evaluate the accuracy of implementations.

1. Introduction

According to the Guide to the Expression of Uncertainty in Measurement - Supplement 1 [1] the Monte Carlo method is an important method for evaluating the uncertainty in measurements. This method uses a priori known probability distributions for input quantities and propagates these uncertainties through transformations to derived quantities. The Monte Carlo method samples the input distributions, transforms this sample to obtain the derived results, and summarizes the resulting distribution. In contrast to sensitivity analysis [2], this method is accurate for both linear and nonlinear transformations; however, it can be computationally intensive as the convergence of sample estimators of the mean and variance to population values is obtained as N^−1/2, where N is the Monte Carlo sample size [3].

Because of the computational cost, Monte Carlo uncertainty analysis is often performed on multiple processes of a distributed memory computer e.g. a multi-node cluster or supercomputer [4]. Additionally, uncertainty analyses are often performed on a particular component that may need to be further propagated through a system. Such analyses occur commonly at National Metrology Institutes, where individual components of a measurement system may be sequentially analyzed in different experiments, in separate laboratories, over long time trames [5]. In order to obtain accurate Monte Carlo uncertainty analyses, which may be distributed over computational processes or processed successively in multiple steps, these analyses must be made consistent. For the purpose of this paper, we define a consistent Monte Carlo analysis as one that uses the same sequence as a Monte Carlo sample of a particular quantity regardless of how many times or where this quantity enters such an analysis.

In this paper, we outline the need for consistency in Monte Carlo uncertainty analyses by showing how inconsistency can lead to incorrect results, recommend an implementation which maintains consistency for these analyses, and discuss the importance of software tools to validate the accuracy and fit for purpose of implementations.

2. Monte Carlo Analysis

The Monte Carlo method is often used in uncertainty analyses to capture the effect of uncertainty of known parameters on derived quantities of interest. The method typically propagates uncertainty in input quantities, for which an a priori probability distribution is known, through a transformation yielding a distribution for an output quantity. Statistics of the resulting distributions can be used to estimate the uncertainty in these quantities.

Although there are many variations of Monte Carlo sampling, some of which can more efficiently estimate statistics of the output distribution (e.g. Latin hypercube [6], importance sampling [3]), these approaches suffer from the curse of dimensionality [7]. Standard Monte Carlo random sampling remains the state of the art for reporting uncertainties in metrology [1].

2.1. Sampled Distributiom

A Monte Carlo uncertainty analysis can be applied to the following transformation

$$\mathit{\text{Y=g(X)}},$$

where g is a transformation of input quantity X, often considered a random variable, into quantity of interest Y, also a random variable. Here the uncertainty in X is specified as X ~ f_X (X) where f_X (X) is a probability distribution of X. The Monte Carlo method proceeds by sampling f_X(X) to obtain an input Monte Carlo sample ${\left\{x_n\right\}}_{n=1}^N$, evaluating the transformation g on these samples to obtain a Monte Carlo sample of y, ${\left\{y_n\right\}}_{n=1}^N$, where

$$y_n=g\left(x_n\right),\text{for}n=1,\dots ,N.$$ (1)

The distribution of the Monte Carlo sample ${\left\{y_n\right\}}_{n=1}^N$ approximates the probability distribution of Y due to variability in X. This sampling distribution can be used in uncertainty analysis to estímate the expected value and variability in the quantity of interest Y.

The input sample distribution, here ${\left\{x_n\right\}}_{n=1}^N$, is typically formed by using a pseudorandom number generator (PRNG), which generates a sequence of pseudorandom numbers with a discrete distribution that agrees with, in some measure, that of the specified distribution.

2.2. Importance of Consistency ure, that

Suppose that we now perform a further uncertainty analysis on quantity of interest Z = h(X,Y), where Y = g(X) and we reuse the Monte Carlo sample calculated inEq. (1). This occurs frequently in practice when one wants to avoid additional costly computation (in reevaluating g(x_n)), doesn’t have the expertise to reevaluate y_n = g(x_n), or wants to maintain traceability to previous analyses for metrology purposes. This analysis then uses both of the Monte Carlo samples ${\left\{x_n\right\}}_{n=1}^N$ and ${\left\{y_n\right\}}_{n=1}^N$ of Eq. (1) to obtain the associated Monte Carlo sample of Z

$$z_n=h\left(x_n,y_n\right),\text{for}n=1,\dots ,N$$ (2)

where yn = g(xn).

In order to maintain the accuracy and validity of the results of this approach, the samples ${\left\{x_n\right\}}_{n=1}^N$ must match in both Monte Carlo uncertainty analyses Eqs. (1) and (2). That is, even if the calculation of ${\left\{y_n\right\}}_{n=1}^N$ has been performed previously, one needs to ensure that the same sequence ${\left\{x_n\right\}}_{n=1}^N$ used in Eq. (1) is also used in Eq. (2). Otherwise, if X ~ f_X(X) is resampled, the resulting sample ${\left\{{\tilde{x}}_n\right\}}_{n=1}^N$ will be independent of ${\left\{x_n\right\}}_{n=1}^N$. Then, calculating

$${\tilde{z}}_n=h\left({\tilde{x}}_n,f\left(x_n\right)\right),\text{for}n=1,\dots ,N,$$ (3)

will produce incorrect results, as the two sequences approximating the distribution of the single quantity X are different. A Monte Carlo method that does not preserve the dependencies of random variables using different sequences to represent the same quantity is inconsistent, whereas an implementation which preserves these dependencies and maintains a single sequence for each unique random variable is consistent.

Obviously the usage of an inconsistent Monte Carlo method is incorrect, although in practice care must be taken to ensure implementing a consistent Monte Carlo method. Mathematically, if variables are dependent upon each other as X and Y are, then this dependence must be preserved. However, in practice tracking these dependencies can become non-trivial in complicated multi-step analyses. Implementations of the Monte Carlo method which perform multi-step analyses must take this into account.

To formalize the above, we introduce the following definition and proposition.

Definition 1.

A consistent Monte Carlo method is one in which the dependencies of random variables are preserved within the Monte Carlo samples. Practically, this requires that each input random variable has a unique Monte Carlo sample associated with it, resulting in the exact same sequence being used no matter how many times or where it appears in the analysis. An inconsistent Monte Carlo method does not preserve these dependencies.

Proposition 1.

Suppose that a random variable Z is a composite function of independent random variables X₁,_;X₂, …, X_m

$$Z=h\left(X_1,X_2,\dots ,X_m,g\left(X_{i_1},X_{i_2},\dots ,X_{i_p}\right)\right)$$ (4)

where g is a function of some subset of the random variables ${\left\{X_{i_k}\right\}}_{k=1}^p\subseteq {\left\{X_i\right\}}_{i=1}^m$ and that there exists a Monte Carlo sample of size N for g

$$y_n=g\left(x_{i_1,n},x_{i_2,n},\dots ,x_{i_p,n}\right)\text{for}n=1,\dots ,N$$ (5)

such that each random variable X_ik, k = 1, …,p, has been independently sampled N times, obtaining ${\left\{x_{i_k,n}\right\}}_{n=1}^N$.

If an inconsistent Monte Carlo sample is drawn such that for any $i_{k_0}=i_0$ the Monte Carlo sample drawn for $X_{i_0}$ and used in Eq. (4) is independent of ${\left\{x_{i_{k_0},n}\right\}}_{n=1}^N$ used in Eq. (5), then the sample variance of the resulting Monte Carlo sample of Z is biased.

Proof.

We prove the proposition for scalar random variables and affine functions g and h. The extension to multivariate and nonlinear functions is straightforward.

For an affine g we can write

$$g\left(X_{i_1},X_{i_2},\dots ,X_{i_p}\right)=a_0+\sum _{k=1}^p{a}_{i_k}{X}_{i_k}.$$

For notational simplicity we can rewrite g to be a function of all of the random variables ${\left\{X_i\right\}}_{i=1}^m$

$$\begin{gathered} g\left(X_{i_1},X_{i_2},\dots ,X_{i_m}\right)=\tilde{g}\left(X_1,X_2,\dots ,X_m\right) \\ =a_0+\sum _{i=1}^m{a}_i{X}_i \end{gathered}$$

where we have replaced each i_k with the corresponding value in ${\left\{i\right\}}_{i=1}^N$ and introduced coefficients a_i = 0 for each $i\notin {\left\{i_k\right\}}_{k=1}^p$. We can now write an affine h as

$$\begin{gathered} h\left(X_1,X_2,\dots ,X_m,\tilde{g}\left(X_1,X_2,\dots ,X_p\right)\right)=b_0+\sum _{i=1}^m{b}_i{X}_i+a_0+\sum _{i=1}^m{a}_i{X}_i \\ =\left(a_0+b_0\right)+\sum _{i=1}^m\left(a_i+b_i\right)X_i \end{gathered}$$

and the second order moment of Z is

$$V(Z)=\sum _{i=1}^m{\left(a_i+b_i\right)}^{2}V\left(X_i\right).$$ (6)

Provided Monte Carlo samples of each $X_{i_k}$, ${\left\{x_{i_k,n}\right\}}_{n=1}^N$, for k = 1, …, p we can write

$$\tilde{g}\left(x_{1,n},x_{2,n},\dots ,x_{m,n}\right)=a_0+\sum _{i=1}^m{a}_i{x}_{i,n}.$$

Denoting separate Monte Carlo samples of X_i; i= 1, …m used in the subsequent evaluation of h as ${\left\{{\tilde{x}}_{i,n}\right\}}_{n=1}^N$ we can write

$$h\left({\tilde{x}}_{1,n},{\tilde{x}}_{2,n},\dots ,{\tilde{x}}_{m,n},\tilde{g}\left(x_{1,n},x_{2,n},\dots ,X_{p,n}\right)\right)=b_0+\sum _{i=1}^m{b}_i{\tilde{x}}_{i,n}+a_0+\sum _{i=1}^m{a}_i{x}_{i,n}$$

For consistent Monte Carlo samples, where ${\tilde{x}}_{i,n}\equiv x_{i,n}$ for all i = 1,...,m and n = 1,..., N, we can write the unbiased sample variance of ${\left\{z_n\right\}}_{n=1}^N$ as

$${\widehat{\sigma }}_z^2=\sum _{i=1}^m{\left(a_i+b_i\right)}^2{\widehat{\sigma }}_{x_i}^2$$

where the ${\widehat{\sigma }}_{x_i}^2$ represents the unbiased sample variance of the ${\left\{x_{i,n}\right\}}_{n=1}^N$.

However an inconsistent Monte Carlo sample, where for any $i_{k_0}=i_0$ the Monte Carlo sample ${\left\{{\tilde{x}}_{i_0,n}\right\}}_{n=1}^N$ is independent of ${\left\{x_{i_{k_0},n}\right\}}_{n=1}^N$, yields a biased sample variance

$${\widehat{\sigma }}_{\tilde{z}}^2=\sum _{\begin{array}{c}i=1\\ i\ne i_0\end{array}}^m{\left(a_i+b_i\right)}^2{\widehat{\sigma }}_{x_i}^2+a_{i_0}^2{\widehat{\sigma }}_{x_{i_0}}^2+b_{i_0}^2{\widehat{\sigma }}_{{\tilde{x}}_{i_0}}^2$$

when both $a_{i_0}$ and $b_{i_0}$ are nonzero. □

As a simple example, suppose that we have a standard normal input distribution, X ~ N(0, 1), and wish to calculated

$$Y\text{=}X\text{+3}$$ (7)

followed by

$$Z\text{=}X\text{+}Y.$$ (8)

First we sample the distribution of X yo obtain ${\left\{x_n\right\}}_{n=1}^N$ and evaluate Eq. (7) yielding ${\left\{y_n\right\}}_{n=1}^N$. Consistently resampling X for Eq. (8) we again produce ${\left\{x_n\right\}}_{n=1}^N$ and so the resulting distribution is

$$\begin{gathered} z_n=x_n+y_n \\ =x_n+x_n+3 \\ =2x_n+3 \end{gathered}$$

and the Monte Carlo sample ${\left\{z_n\right\}}_{n=1}^N$ will approximate that of Z ~ N(3, 4).

On the other hand, if X is not sampled consistently in Eq. (8) and instead a different and independent sample ${\left\{{\tilde{x}}_n\right\}}_{n=1}^N$ is obtained, then

$$\begin{gathered} {\tilde{z}}_n={\tilde{x}}_n+y_n \\ ={\tilde{x}}_n+x_n+3 \end{gathered}$$

the Monte Carlo distribution of $\tilde{z}$ will approximate ${\tilde{z}}_n~N(3,2)$. Here, an estimate of uncertainty, the sample variance, is negatively biased. The independen samples of X leads to incorrect results and can have a large impact on the resulting calculation of uncertainty. In other cases, say when Y = X + 3 and Z = X – Y the inconsistent method will produce a sample that gives positively estimates of uncertainty.

This example demonstrates that similar effects may arise in more complicated, distributed, multi-laboratory analyses where it may not be clear which or how uncertainty mechanisms were accounted for in previous results. In the recommended implementation in Sec. 3.1, each input uncertainty mechanism is given a label which is tracked and used to generate consistent samples avoiding inconsistencies in situations as above.

2.3. Pitfalls of Summary Statistics

Using summary statistics at each stage of the uncertainty analysis may also lead to incorrect results. Here, the sample statistics of Eq. (1) can be calculated and the distribution of Y can be approximated. However, one cannot sample this resulting distribution, obtaining ${\left\{{\tilde{y}}_n\right\}}_{n=1}^N$ as these samples are again independent of the ${\left\{x_n\right\}}_{n=1}^N$.

Thus, when propagating uncertainty through multiple stages of an analysis, either the entire problem must be analyzed at once or the Monte Carlo sample sequences must be consistent across different stages of analysis. The use of summary statistics does not maintain consistency.

2.4. Monte Carlo Samples on Distributed Memory Computers

A similar issue arises when using distributed-memory parallel computation. A common way to perform the Monte Carlo method on a distributed compute is to generate an independent subsequence on each process. In [8] the authors recommend this implementation using the Wichmann-Hill PRNG [9]. However, running one step of the analysis on a certain number of processes but then using a different number of processes for a later step would produce an inconsistent sample.

In order to maintain consistency in a general distributed Monte Carlo implementation, where the number of processes may change from one step to another, each process must obtain a sequence of pseudorandom numbers yielding a consistent sequence no matter how many processes are used. Improper handling of pseudorandom number generation in parallel may lead to inconsistent Monte Carlo samples, lack of reproducibility, or distributions that do not achieve desired statistical properties.

For example, as we will show in Sec. 4.1, applying the Monte Carlo method on the first step of a multiple step uncertainty analysis using P processes but then completing the analysis on a different number of processes requires that the sequences corresponding to the sampled random variables is the same in both cases.

Additionally, as inter-process communication can limit efficiency and scalability of simulations, this communication is to be avoided, so a consistent distributed Monte Carlo implementation should not require any additional inter-process communication (other than possibly an initial setup) in order to maintain efficiency.

2.5. Pseudorandom Number Generators

Before moving on to describe a parallel implementation of a consistent Monte Carlo method, we give a little background on PRNGs. Generally, PRNGs are used in many disparate applications including cryptology, gambling, and simulation. Each of these applications requires specific features from a PRNG. For example, in gambling applications, the ability to prevent an attacker from determining the next number in the pseudorandom sequence is critical. For Monte Carlo uncertainty analysis, the primary concerns are lack of bias, clustering and representative coverage of the distribution. That is, generally, the distribution provided by the PRNG should approximate the specified probability distribution attributed to the PRNG.

Typical PRNGs, like linear congruential generators, operate in the following way. The PRNG is seeded with an initial value, typically a collection of integers, which generates an initial state. Subsequent calls to the PRNG use this state to generate a pseudorandom number and advance the PRNG to the next state. As each state is generated from the previous state, we see that these PRNGs are reproducible^§ in that, for a specified seed, the PRNG will return the same sequence. Thus for typical PRNGs generating the ith pseudorandom number requires i – 1 calls to the generator. However, for Monte Carlo samples that require tens or even hundreds of thousands of samples generated on distributed processes, this can be inefficient.

Moving from a sequential PRNG implementation to a parallel implementation, as required for a distributed Monte Carlo implementation, necessitates additional constraints [11]. Previous work [8, 9] has implemented independent sequences of pseudorandom random numbers on each process of a distributed memory computer. As mentioned in section 2.4, these sequences can be used in Monte Carlo uncertainty analyses which are processed all at once, but become inconsistent when then number of processes changes during the course of a sequential analysis.

For our purposes, in order to maintain consistency over multi-step analyses, an efficient parallel implementation requires the specification of a global pseudorandom sequence and the ability to skip through the sequence to obtain the ith pseudorandom number (and corresponding PRNG state) with much less than i operations. L’Ecuyer [12] shows for multiplicative linear congruential generators (MLCGs), of standard uniform distributions, how to “jump ahead” in the sequence, allowing one to efficiently move to the ith number directly.

2.6. Monte Carlo Sample Size

The Monte Carlo method provides estimates of statistics that converge as the sample size increases, N → ∞. Additionally, obtaining coverage intervals corresponding to high coverage probability (say greater than 95%) may require even larger sample sizes [8]. A suitable Monte Carlo sample size depends upon the typically unknown distribution of the output quantity and so must be uniquely determined for each application, output quantity, and required level of accuracy. Although there are automated techniques to assess the suitability of the size of a sample [1, 13], sample sizes ranging from 10³ to 10⁶ are often used.

In order to produce consistent Monte Carlo samples across a multi-step analysis one must determine a sample size sufficient for all aspects of the analysis and use this size for all Monte Carlo samples. This adds some difficulty in distributed analyses where a specific sample size may be large enough for some components of the analysis but not for latter components (which may only be known at a later time). For this reason, we recommend that a consistent Monte Carlo uncertainty analysis use as large a sample size as is feasible and practical for the first step of the analysis and verify the suitability of that size for every output quantity of interest.

In the following, we assume that the sample size of each Monte Carlo sample is large enough for all aspects of the total uncertainty analysis. In general, care should be taken to ensure an appropriate sample size.

3. Implementation and Evaluation

In the previous section, we showed that preserving the consistency of the Monte Carlo sample in various parts of the analysis is critical to obtain accurate uncertainty results. Here, we outline an implementation which maintains consistency even for multi-step analyses that are distributed over computational resources. We also discuss the evaluation of PRNGs to ensure that the results are suitable for accurate uncertainty analyses.

3.1. Implementation of a Consistent Distributed Monte Carlo Method

An efficient, consistent, distributed Monte Carlo implementation involves (a) creating reproducible pseudorandom number sequences distributed across an arbitrary number of processes, each of which correspond to unique random variables (quantities with uncertainty), that can be recalled throughout the analysis and (b) efficiently indexing through the sequences in parallel on distributed processes.

For task (a) we begin by using a unique text label, say a string, for every input uncertainty mechanism that is to be sampled. This label is used to refer to a specific mechanism of uncertainty and facilitates the tracking of this mechanism through complicated analyses. From this label we then generate a seed to be used for a PRNG. This seed can be generated for example by hashing a string into a sequence of bytes (using, say, Secure Hash Algorithm 256 (SHA256) [14]) and then converting these bytes to form the (typically) integer values required as seeds for PRNGs. These seeds (or, equivalently, the string to be hashed) are then distributed to all processes involved in the calculation in an initialization step.

Task (b) requires a PRNG that efficiently indexes through the pseudorandom number sequence. Although there are other PRNG implementations that can skip to specific indices in the sequence, including Mersenne Twister [15], we use the MLCG from [12] as there is an implementation available in the software package documented in [16]. Our implementation indexes this PRNG to the appropriate point in the pseudorandom sequence for each of our distributed processes. This provides an efficient method to index the sequence in parallel.

Using this PRNG, a consistent Monte Carlo implementation can be completed as follows. Each process p = 1, …,P determines the beginning α_p and ending β_p indices corresponding to its range of Monte Carlo samples to compute. Each process is given the labels for all input uncertainty mechanisms and initializes PRNGs with corresponding seeds and then skips to the α_pth number in each of the sequences. The input Monte Carlo sample is obtained from these PRNGs, the transformation is applied to this sample, and the resulting output sample is saved to disk to be used in further analyses.

When a situation like that of Eqs. (1) and (2) arises, the sequence corresponding to the sample of Y is read from disk, the label for X is again read and used to generate the seed for the PRNG obtaining a Monte Carlo sample for X. This sequence and the sequence used to generate the sample for X used to calculate that of Y are identical and thus the Monte Carlo analysis is consistent. This methodology works for multiple input distributions as well as multivariate data.

Note that additional care may be needed to extend this implementation from uniform distributions to other distributions. Typically, methods like inverse sampling [17] or Box-Muller [18] are used to generate other probability distributions from uniform distributions; these implementations must also preserve a one-to-one (or equivalent) correspondence with the sequence of uniform draws to maintain consistency.

Finally, we note that the NIST Microwave Uncertainty Framework [19] implements a method similar to the above in order to maintain consistent Monte Carlo uncertainty analyses in distributed applications. This software tool is used to evaluate the uncertainty of complicated, multi-laboratory uncertainty analyses of high-frequency electronic applications. This framework facilitates collaboration across laboratories, yielding consistent Monte Carlo analyses for these complicated distributed systems, and providing additional productivity for users of the tool.

3.2. Evaluating Accuracy using Testing Suites

In addition to consistency, the accuracy of the generated PRNG sequence is paramount for Monte Carlo analysis. Note that other applications, e.g. cryptology- or gambling-related applications, may have other quality criteria, such as correlation between replicates, as well [20]. For uncertainty analyses, ensuring that the distribution of the sequence matches that of the specified probability distribution to some level is the primary concern. To verify this one can run tests such as the Kolmogorov-Smirnov test [21]. However, this is just one of many potential tests; In order to obtain better testing coverage and have more certainty of the quality of a PRNG, one should run a suite of many tests. There are several high-quality testing suites available to test the suitability of a PRNG including the Diehard battery [22], the Dieharder test suite [23], the NIST Statistical Test Suite [24] and the TestU01 testing suite [20, 25]. The TestU01 suite contains many tests to evaluate the performance of a PRNG by sampling the PRNG to compute test statistics which are used to test against the null hypothesis that the sampled distribution approximates a standard uniform distribution. These tests are grouped into small (“Small Crush”), medium (“Crush”) and larger (“Big Crush”) collections. As uncertainty analysis practitioners often have expertise outside of pseudorandom number generation, it is important to check the resulting PRNG implementation using a comprehensive test suite like TestU01 to verify that it is fit for purpose for uncertainty analysis. We apply the TestU01 test suite to examples in the next section.

4. Examples and Testing

4.1. Maintaining consistency in Distributed Samples

We return to the example of Section where we

$$\begin{gathered} Y=X+3 \\ Z=X+Y \end{gathered}$$ (9)

but here X is distributed uniformly as U[0, 1].

We illustrate that the recommended implementation maintains consistency even when the number of processes changes between the two steps. This is in contrast to using independent sequences of pseudorandom numbers, one for each process, similar to [8], which can lead to an inconsistent method. Here, we perform the first step of the analysis (evaluating Y = X + 3) using multiple processes and then change the number of processes in the evaluation of the second step (Z = X + Y ).

For the consistent method we proceed by sampling X distributed over 10 processes using the recommended implementation to obtain ${\left\{x_n\right\}}_{n=1}^N$ for a total sample size of N = 10,000 and use this sample to compute ${\left\{y_n=x_n+3\right\}}_{n=1}^N$. For the next step of the analysis, evaluating Z = X + Y, the recommended implementation will recall the same sequence ${\left\{x_n\right\}}_{n=1}^N$ and use this to evaluate ${\left\{z_n\right\}}_{n=1}^N$ resulting in a consistent Monte Carlo sample.

For the inconsistent approach, for each of the 10 processes an independent sequence of numbers is sampled from X in the first step of the analysis, Y = X + 3. For the second step, using a different number of processes generates a different sequence for X, ${\left\{{\tilde{x}}_n\right\}}_{n=1}^N$, which is then an inconsistent Monte Carlo sample.

Histograms of these two Monte Carlo samples, the consistent and inconsistent samples, are shown in Figure 1 where we see that the consistent sample approximates the expected distribution of Z ∼ U[3, 5], whereas the inconsistent distribution is clearly biased.

Figure 1.

Histograms of the consistent and inconsistent distributed Monte Carlo sequences of Eq. 9 for a sample size of 10 × 10⁴. We see that the consistent sample approximates the true distribution U[3, 5] while the inconsistent sample is biased.

4.2. Naїve Usage of Pseudorandom Number Generators

We have highlighted the importance of consistent Monte Carlo implementations. In this section, we show the importance of the correct usage of PRNGs in these implementations. For this we implement a consistent Monte Carlo implementation that naїvely applies PRNGs, we denote this the naїve implementation, and compare this with the recommended implementation in Section 3.1. Although the naїve implementation incorrectly applies PRNGs, it is similar to what could be implemented by one who does not have expertise in PRNGs and uses built-in algorithms provided by standard software packages. The purpose of this comparison is to highlight differences between PRNG implementations that have appropriate statistics and those that don’t, as well as to show the efficacy of methods that evaluate the performance and test the statistics of resulting sequences.

For the naїve implementation, we use the Monte Carlo index i appended to a parameter label to generate a unique string for every Monte Carlo replicate. Then this string is hashed using the Fowler-Noll-Vo 1a-64 hash algorithm (FNV1a-64) [26] to create two 32 bit integers to seed the MLCG from [27] provided in the software package ALGLIB^|| [28] in the routine hqrnd and a single number is taken from each PRNG for each Monte Carlo replicate. We see that this method produces a reproducible sequence even when distributed over an arbitrary number of processes and is therefore consistent.

We compare this method to the implementation recommended in Section 3.1 to demonstrate the effect of implementing a poor distributed PRNG and highlight some tools to evaluate fit-for-purpose of PRNGs. We generate a pseudorandom sequence of a standard uniform distribution with each of these generators using the label “parameter.” Figure 2 shows the histogram of the naїve implementation (a) and the recommended implementation (b) for 5 × 10⁴ replicates. Here we see that, while the numbers are qualitatively well distributed, there seems to be some clustering in the naїve implementation. To investigate the further suitability of these PRNGs we examine the data from each sequence more thoroughly.

Figure 2.

Histograms for the first 5 × 10⁴ numbers from the naїve (a) and recommended (b) sequences.

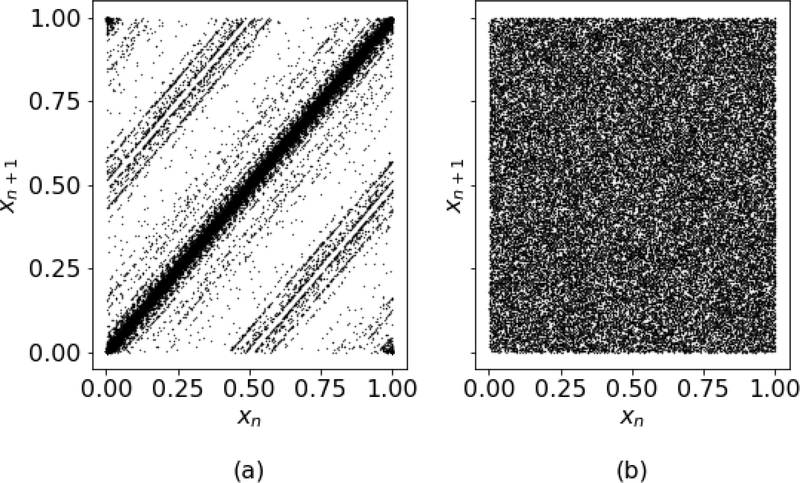
We begin with a lag plot of lag one as shown in Fig. 3. Here, the naїve implementation, Fig. 3(a), shows a considerable amount of correlation between draws, whereas the recommended implementation (b) does not. Note that this behavior is similar to that of the generators discussed in L’Ecuyer [27] (see Fig. 5(a) in that reference). Finally, we investigate this correlation more thoroughly in Fig. 4 which shows the results of an autocorrelation on each of the sequences. There we see that there is substantial correlation in the naїve implementation for many lags.

Figure 3.

Lag plots of lag one for the naїve (a) and recommended (b) sequences. Note the significant structure of the naїve sequence in (a).

Figure 5.

The first 500 values of the naїve (a) and recommended (b) sequences. The naїve sequence show significant clustering as well as lack of coverage in some intervals.

Figure 4.

Autocorrelation of the naїve (a) and recommended (b) sequences. The naїve sequence has significant correlation for many lags. As expected, the recommended sequence shows negligible correlation for all lags larger than zero. Note the different scales in (a) and (b).

Finally, in this case we can intuit the suitability of the PRNGs simply by looking at the values of the pseudorandom numbers. Figure 5 shows a scatter plot of the first 500 pseudorandom numbers versus their index for each of the naїve (a) and recommended (b) implementations. Here we see that there is significant clustering in the naїve implementation as well as intervals where there is undersampling. This undersampling can have serious consequences for uncertainty analyses where some critical regions may not be represented in the resulting Monte Carlo sample.

4.3. Evaluation of PRNGs

The above analysis shows that the naїve method has significant correlation and therefore the generator does not approximate independent sampling. Additionally, Figure 5 shows non-trivial clustering. Here, we press on to see the results of further testing on these implementations. A standard test to determine whether a sampling distribution matches an analytical distribution is the Kolmogorov-Smirnov test. Here the empirical cumulative distribution for the sample and the analytical cumulative distribution function are compared. We present the p-value of this test for each of the distributions in table 1 where we see that the p-value for the naїve implementation, while rather small, would pass many testing criteria.

Table 1.

The results of various tests applied to the naїve and recommended generators. The Kolmogorov-Smirnov test results and the average number of failures for over 100 runs of the Small Crush and Crush test batteries from TestU01 are shown. We see that the although the naїve implementation has strong correlation between draws and fails many TestU01 tests it does pass a few of these tests as well as the Kolmogorov-Smirnov test.

	Kolmogov-Smirnov (p-value)	Small Crush Avg. % failure	Crush Avg. % failure
Naїve	.137	94.2%	87.7%
Recommended	.758	0.333%	0.250%

Finally, we now turn to statistical testing suites to further, in an automated way, evaluate the performance of these generators. For this we use the TestU01 [20, 25] test suite. Of course when performing many statistical tests there is a non-negligible chance that one of the tests will fail so we rerun these tests 100 times using labels “parameter1” through “parameter100” to initialize each generator. We ran the Small Crush, and Crush test batteries^¶, which include 15 and 144 tests respectively, and show these results in table 1. Here we see that the naїve implementation reliably fails nearly every test in these batteries while the recommended implementation reliably passes nearly all of them (as expected from a well-studied PRNG).

Many of the tests included in these batteries assess features outside of the interest of Monte Carlo uncertainty analysis. However, some of the tests in TestU01 test for bias or differences in the spread in the sample, including the svaria SampleMean, svaria SumLogs and svaria WeightDistrib tests, and the naїve method failing these tests shows that this generator is not fit for purpose to be used for uncertainty analysis. Additionally, we follow the guideline in [20] for PRNGs that “the bad ones fail very simple tests whereas the good ones fail only very complicated tests...” and take these results to show that the naїve implementation is not suitable whereas the recommended generator is fit for purpose.

Although the sheer number of tests applied in these batteries can be overwhelming, the thoroughness of the testing gives confidence in the use of a given generator for uncertainty analysis. This is in contrast to simply using one test (say the Kolmogorov-Smirnov test) to evaluate the behavior, as we saw even the naїve implementation, which exhibited extensive clustering, passed some tests. For uncertainty analysis purposes, it is important to run many tests to ensure that the statistics of the PRNG are fit for purpose.

5. Conclusion

Consistency is paramount in Monte Carlo uncertainty analysis; without consistency the analysis is invalid. In complicated uncertainty analyses, which are often distributed across computing platforms, different laboratories, and long time frames, inconsistencies can easily enter the analysis leading to uncertainty estimates that are biased. Additionally, the use of summary statistics in temporally distributed Monte Carlo uncertainty analyses can lead to inconsistent Monte Carlo samples.

We developed a consistent Monte Carlo implementation that is reproducible and efficiently generates pseudorandom sequences in parallel over many processes. For this we used the PRNG in [12] which allows skipping within the pseudorandom number sequence. Combined with using a label for each uncertainty mechanism, this allows us to generate consistent, reproducible pseudorandom number sequences having satisfactory statistics (as evident by passing the TestU01 tests) even for analyses that are distributed across processes or separate analyses. We recommend that Monte Carlo uncertainty analysis practitioners choose an implementation like this based on well studied and documented PRNGs for their analyses. Software tools that evaluate uncertainties, such as the NIST Microwave Uncertainty Framework [19], produce more accurate and robust uncertainty analyses through the such an implementation.

Finally, we highlight the importance of testing the statistics of custom PRNGs using a testing suite similar to TestU01. As many uncertainty analysis practitioners come from backgrounds other than pseudorandom number generation, they may not have the expertise to ascertain that they are implementing an accurate method in their analyses. A test suite like TestU01 can efficiently evaluate the behavior of a PRNG, verifying that it is fit for purpose and providing confidence in its use for Monte Carlo uncertainty analysis.