Dual-comb spectroscopy

Abstract

Dual-comb spectroscopy is an emerging new spectroscopic tool that exploits the frequency resolution, frequency accuracy, broad bandwidth, and brightness of frequency combs for ultrahigh-resolution, high-sensitivity broadband spectroscopy. By using two coherent frequency combs, dual-comb spectroscopy allows a sample’s spectral response to be measured on a comb tooth-by-tooth basis rapidly and without the size constraints or instrument response limitations of conventional spectrometers. This review describes dual-comb spectroscopy and summarizes the current state of the art. As frequency comb technology progresses, dual-comb spectroscopy will continue to mature and could surpass conventional broadband spectroscopy for a wide range of laboratory and field applications.

1. INTRODUCTION

Dual-comb spectroscopy (DCS) combines many of the strengths of conventional broadband spectroscopy and tunable laser spectroscopy into a single platform [1–59]. As with conventional Fourier-transform infrared (FTIR) spectrometers, broad swaths of the optical spectrum can be interrogated, and with the use of only a single photodetector. As with laser spectrometers, the frequency resolution and accuracy is set by the laser rather than the instrument, and the bright single spatial mode output enables long interrogation paths for high sensitivity. Since the first demonstrations [2–4,60], interest in DCS has spawned a large number of proof-of-concept experiments [1–59]. DCS quickly evolved to provide comb-tooth-resolved spectra [6,9], ultimately providing a high signal-to-noise ratio (SNR) over broad optical bandwidths in the near-IR [24,25,50]. From its inception, researchers have explored DCS at longer wavelengths, where spectroscopic signatures are strong [2–7]. Experiments have highlighted its compatibility with enhancement cavities [14,43], multipass cells [25,50,51], gas-filled fibers [56], and turbulent open-air paths [3,21,36,53]. DCS has been applied to ultrabroadband near-IR spectroscopy [50], to near-field microscopy for subwavelength spatial resolution [5,8], to precision metrology of molecular line centers [22,29,50], to a spectral lidar [21,31], and to greenhouse gas monitoring [36,51,53]. Recently, it has been extended to nonlinear spectroscopy for stimulated Raman scattering, comb-based coherent anti-Stokes Raman spectroscopy (CARS) [27,32], and two-photon spectroscopy [40,61]. As DCS continues to mature, this list of applications will continue to expand.

Underlying DCS is the frequency comb laser emitting an array of narrow, phase-coherent spectral lines, or “teeth.” Perfectly spaced in frequency, these teeth can all be simultaneously stabilized to an optical or rf reference [62,63]. Laser frequency combs have had a significant impact on diverse fields and, ever since their invention, have been considered an attractive source for spectroscopy [64,65]. However, the challenge of using frequency combs for broadband spectroscopy was clear from very early on. To exploit the frequency accuracy and spectral resolution provided by the frequency comb structure, one needs to spectrally resolve each individual comb tooth. Comb light could be coupled into conventional spectrometers. However, since the comb tooth spacing is finer than the resolution of nearly all spectrometers, the comb then simply acts as a very bright, collimated light source; its associated frequency resolution and accuracy are lost. To fully capitalize on the underlying comb structure, several high-resolution dispersive spectrometer and Fourier transform spectrometer techniques have been developed for resolving individual comb teeth, including virtually imaged phase array (VIPA) spectrometers [66–68], comb-cavity Vernier spectrometers [69,70], and high-resolution FTIR spectrometers [71–75]. While VIPA and FTIR techniques have seen compelling demonstrations, to date the most widely pursued form of direct comb spectroscopy is DCS, which dispenses with the dispersive spectrometer altogether. This same technique appears in the literature as multiheterodyne spectroscopy, linear optical sampling, coherent Fourier-transform spectroscopy (FTS), and terahertz (THz) asynchronous optical sampling (ASOPS), but the IR/visible community has largely settled on the moniker “dual-comb spectroscopy,” which we use here. This review focuses primarily on DCS in the IR region of the spectrum, although we draw connections to DCS in the THz region. (The THz domain has been discussed in several excellent reviews [7,49].) As mentioned earlier, DCS has a number of advantages over conventional spectrometers in the basic performance metrics of frequency resolution, accuracy, acquisition speed, and SNR, as well as in the potential for a compact system, since its performance is not fundamentally limited by the instrument optical path length as in grating or FTIR spectrometers.

The DCS concept is illustrated in Fig. 1(a). Two combs with slightly different repetition rates are interfered on a photodiode generating an rf comb composed of distinguishable heterodyne beats between pairs of optical comb teeth. This rf comb is easily accessible with rf electronics and contains the relevant spectral information in the optical comb spectra. To perform spectroscopy, a sample is introduced into one or both optical beam paths. The sample’s response is encoded on the comb light; this response is then recovered through heterodyne detection. The exact information recovered will vary depending on the system architecture, as shown in Fig. 1(b). In the first configuration, one comb is transmitted through the sample and then interfered with the second “local oscillator” comb. This asymmetric approach is analogous to the “dispersive” FTIR technique, and the full phase and amplitude response of the sample is measured [76]. In the second, symmetric approach, both combs are transmitted through the sample. This approach is analogous to the typical FTIR configuration and measures only the sample’s absorption, but is more robust to turbulent measurement paths. In either case, the variations in the comb spectrum must be effectively normalized out so that only the sample’s response is measured.

Fig. 1.

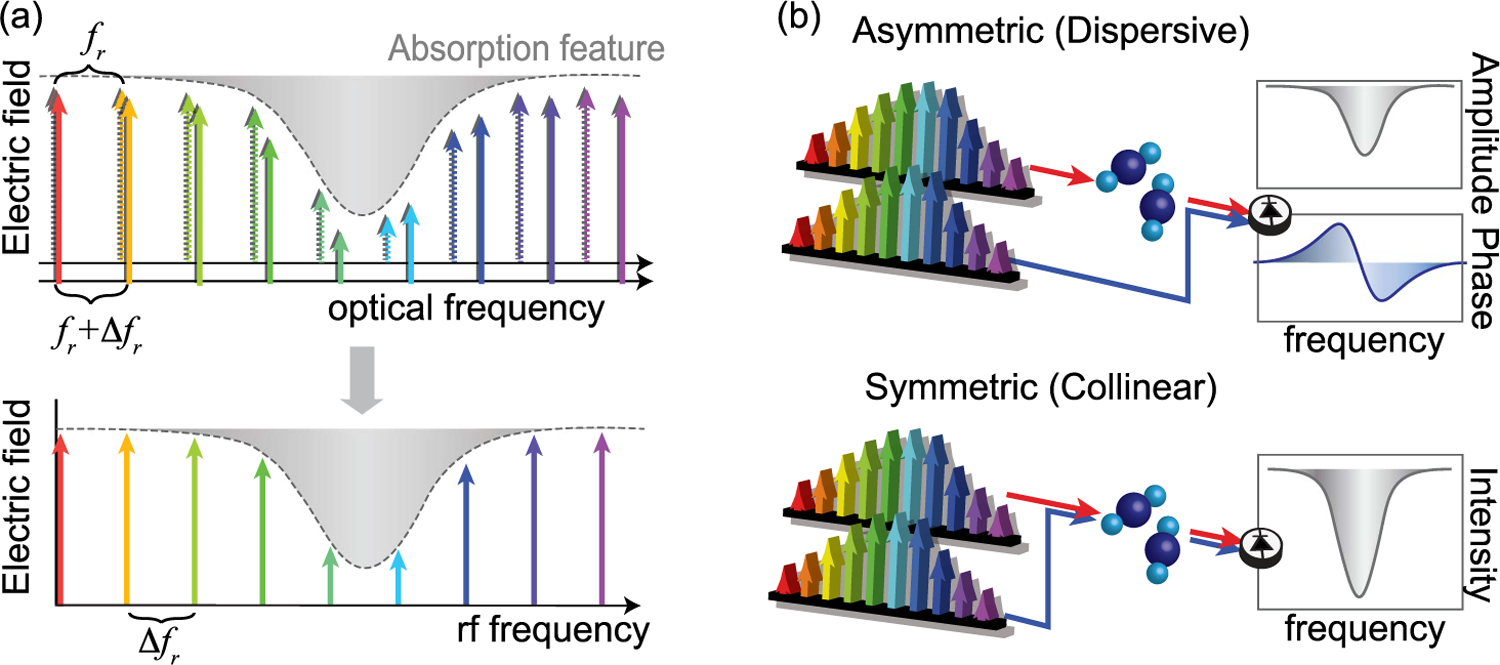
(a) Simple DCS concept. Two combs with repetition rates f_r and f_r + Δf_r are mixed and detected by a single photoreceiver. As a result of the comb structure, each pair of optical teeth yields an rf heterodyne signal at a unique rf frequency. These rf frequencies form an rf comb of spacing Δf_r. The rf teeth can be tightly packed such that >10⁵ comb teeth can be observed simultaneously. For much of the original DCS work, f_r was typically ∼100 MHz and Δf_r was 100 Hz to 1 kHz, but these values can vary considerably across different frequency comb sources. (b) For spectroscopy, either one or both combs are passed through the sample. The resulting absorption (or phase shifts) on the comb teeth is encoded onto the corresponding amplitude (or phase) of the measured rf comb teeth.

To date, DCS has outpaced other comb spectroscopy techniques, as well as swept laser spectroscopy, in terms of spectral coverage, though it is unlikely to ever match the full spectral coverage possible with conventional FTIR. Figure 2 shows an overview of the spectral coverage of DCS demonstrations. These DCS experiments span a wide range in terms of realized resolution, accuracy, SNR, control of systematics, etc. This range reflects the fact that the unique advantages of DCS do come with experimental challenges, and the quality of the DCS spectra largely mirrors the technological sophistication of the frequency combs in the given spectral region. For example, the acquisition of a semiquantitative spectrum with free-running combs is significantly simpler than the acquisition of a high-SNR, high-resolution absorbance spectrum with a fully calibrated frequency axis. DCS in the near-IR can indeed yield the latter and support measurements, for example, of line centers [29,50] or of gas concentrations [36,53]. In the mid/far-IR, DCS is generally still limited to proof-of-concept demonstrations, with the exception of methane concentration and line center measurements [22,51]. However, as mid- and far-IR combs continue to evolve, so too will their DCS spectra.

Fig. 2.

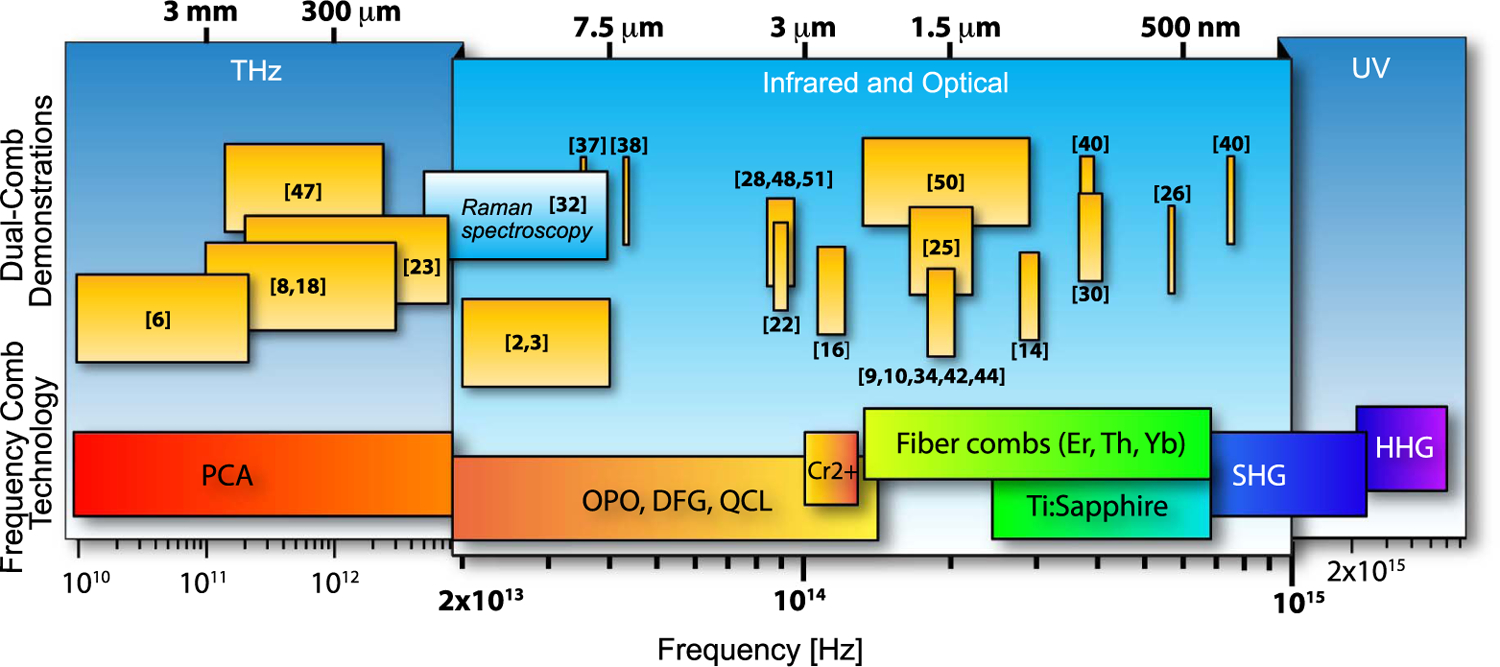
Spectral coverage of dual-comb spectroscopy demonstrations (top band) and underlying frequency comb technologies (bottom band). The span covers over 14 octaves across the THz, IR, and optical. DCS has also been proposed in the extreme UV [77]. Section 4 discusses some of these different demonstrations. PCA, photoconductive antenna; OPO, optical parametric oscillator; DFG, difference frequency generation; QCL, quantum cascade laser; SHG, second-harmonic generation; HHG, high-harmonic generation.

The review is organized as follows. Section 2 provides a brief summary of DCS in the absence of phase noise, with an emphasis on the basic scaling laws. Actual laboratory DCS must contend with the finite linewidths and drift of the combs, and Section 3 categorizes DCS demonstrations by frequency comb coherence. Section 4 summarizes existing DCS demonstrations across different spectral regions. Section 5 is a more complete discussion of SNR limitations and summarizes demonstrations that have pushed these limits. In particular, it discusses coherent averaging, which will serve a critical role in applications of DCS. Section 6 concludes by summarizing current progress and future challenges.

Although we focus here on DCS applied to linear spectroscopy as a broadband coherent system, the same basic technique has been applied to closely related applications. The ability to simultaneously record loss and dispersion has made dual-comb approaches attractive for characterizing telecom components, fiber gratings, and microresonators [78–80]. A modified dual-comb system can monitor active sources such as static and fast-swept cw waveforms [81–84], arbitrary optical waveforms [57,85,86], and even pulsed or incoherent sources [87,88]. All these techniques have the same underlying dual-comb/single-receiver architecture and serve to highlight the versatility of this approach, which is ultimately no more than a simple extension of standard heterodyne laser interferometry to frequency comb sources.

2. DUAL-COMB SPECTROSCOPY: THE IDEAL CASE

A. DCS in the Time and Frequency Domains

In the frequency domain, the DCS output is simply an rf comb [see Figs. 3(a) and 3(b)]. The intensity and phase of the detected rf comb teeth are proportional to the product of the electric fields of the two optical comb teeth. DCS effectively maps the optical spectrum of width, Δν, to an rf spectrum of width, Δν∕m, where $m=f_r/\Delta f_r$. Here, f_r is the comb repetition frequency and Δf_r is the repetition frequency difference between the two combs. Compression factors m of 30,000–1,000,000 are common, and several hundred thousand comb teeth, spanning tens to hundreds of THz, can be mapped into a 100 MHz rf band and digitized. From inspection of Fig. 3, it is clear that the one-to-one mapping from the optical to rf domain is only maintained if the optical spectral bandwidth satisfies

$$\Delta \nu \le \frac{m{f}_r}{2}=\frac{f_r^2}{2\Delta f_r},$$ (1)

which can be doubled for in-phase/quadrature detection. Figures 3(c) and 3(d) provide the complementary time-domain picture of DCS. In this picture the two combs sample each other, with very fine effective time shifts between each consecutive pair of pulses given by

$$\Delta T=\frac{\Delta f_r}{f_r\left(f_r+\Delta f_r\right)}\approx \frac{1}{m{f}_r},$$ (2)

which is in the picosecond to femtosecond range. One can see the analogy to linear optical sampling or a sampling oscilloscope; the sampling gate given by the femtosecond pulses of one comb asynchronously samples the repetitive pulse train from the other comb, allowing observation of a downsampled version of that comb. The resulting time-domain signal is also viewed as an “interferogram” that is highly analogous to FTIRs. The effective sampling time step per point of ΔT imposes a Nyquist condition that is the same as Eq. (1). The time-domain picture also highlights the importance of detector linearity, since an accurate spectrum requires a linear detector response from the strong centerburst to the weaker tails visible in Fig. 3(d). Note that the Fourier transform of a series of interferograms yields the rf spectrum of the frequency-domain picture in Fig. 3(b).

Fig. 3.

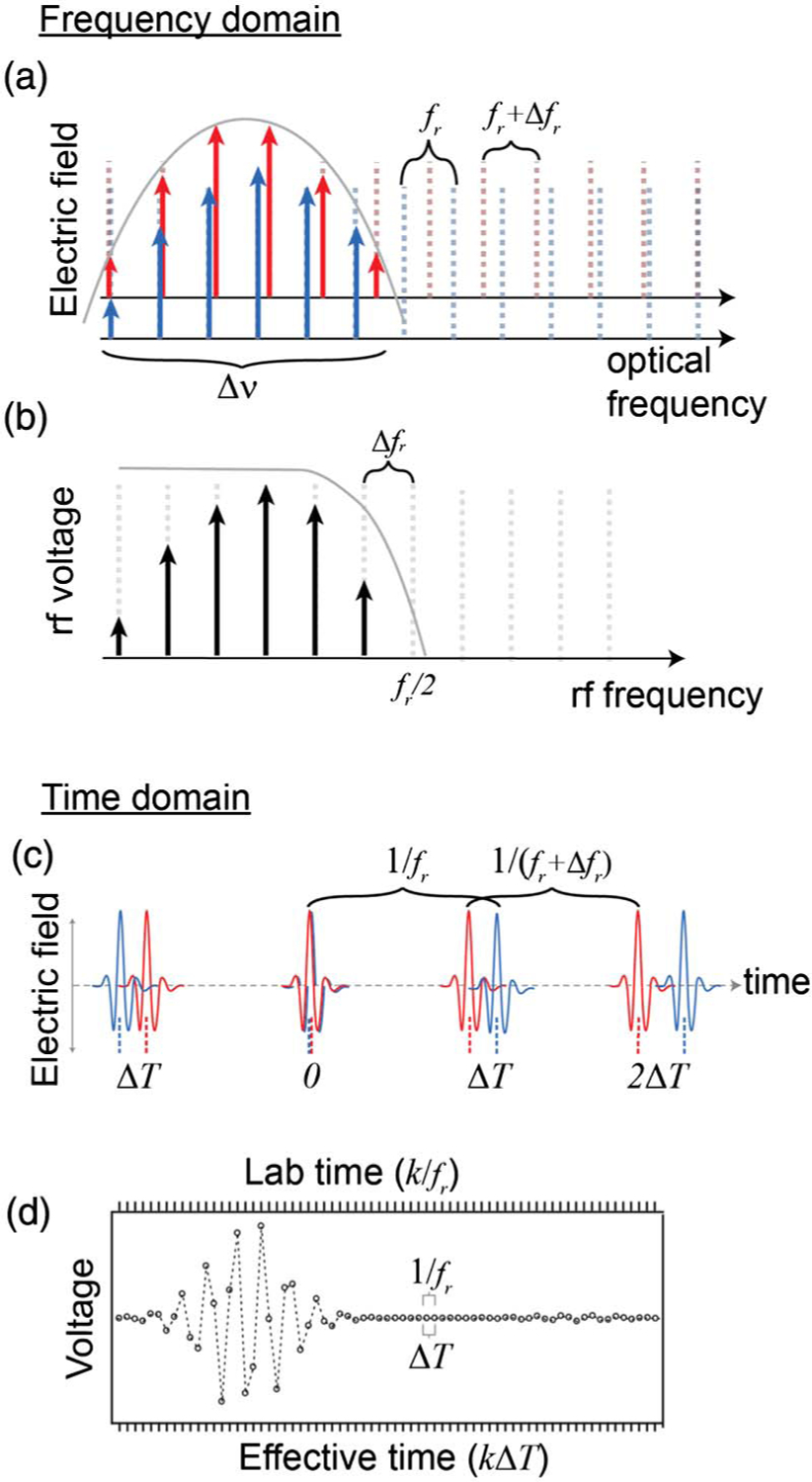
(a) Two frequency combs (red and blue) are mixed to produce (b) the rf comb. Solid gray lines indicate filter functions applied in the rf and optical to avoid aliasing effects. (c) The equivalent time-domain picture showing the pulse-to-pulse walk-off between the two comb pulse trains. (d) The photoreceiver voltage output corresponds to the product of the two comb pulses, integrated over the receiver bandwidth. This output can be viewed in laboratory time, where the samples are at time intervals of 1∕f_r, or in effective time, where the samples are at time intervals of ΔT (as with FTIR interferograms). In both time scales k is the sample number. The large “centerburst” corresponds to the simultaneous arrival of the two pulses. Also visible in the “tail” to the right is a weak ringing containing absorption information of the sample gas.

To obtain the sample response, we must use one of the configurations shown in Fig. 1(b) and normalize by the unperturbed (i.e., sample-free) dual-comb spectrum. The result is the linear response of the sample, which can be viewed equally well in either the time or frequency domain [20].

B. Acquisition Speed

The minimum time to resolve the rf comb teeth, and therefore acquire a single spectrum, is simply 1∕Δf_r. Therefore, with Eq. (1) there is a direct trade-off between optical bandwidth and acquisition speed. Nevertheless, at 100 MHz comb tooth spacing, a single spectrum having over a million spectral elements can be acquired in milliseconds; narrower spectra can be acquired proportionally faster. However, this speed advantage is offset by the low SNR per single spectral acquisition. In practice, multiple spectra must be co-added, and the minimum acquisition time is instead set by the required SNR. Still, the rapid single-shot acquisition is important for measurement in turbulent environments, since the turbulence-induced noise is “frozen” out over a single interferogram [36,89]. Moreover, the development of mid-IR [16,22,28,33,35,41,48,51,58] and far-IR [2,3,5,37,38,52] DCS and long interaction path lengths through optical cavities [14,43], multipass cells [25,43,51], and open paths [36] may relax the need for a high SNR somewhat by providing enhanced absorption signals. Furthermore, note that this speed increases with the square of the comb tooth spacing. Emerging microresonator combs [90], electro-optic modulator (EOM) combs [43,54–57], and quantum cascade laser (QCL) combs [37,38,90] have repetition rates in excess of 10 GHz; with these one can consider recording complete spectra in time scales below 1 μs. The spectral spacing is relatively coarse, but such devices could allow studies of fast dynamic processes such as chemical reactions or rapid measurements of the broad absorption features of liquids or solids [91,92].

Note that the discussion above assumes an entire interferogram is digitized. Instead, only a limited region of the interferogram about the centerburst can be digitized, corresponding to an apodized interferogram in the language of conventional FTS. This apodization nominally shortens the acquisition time of a particular single spectrum, but of course the acquisition rate of consecutive spectra is still Δf_r. Moreover, the frequency comb structure is lost, since the Fourier transform of the apodized interferogram yields a spectrum that is smoothed across comb teeth. This spectral smoothing does lead to an improved SNR per (coarser) spectral point at the cost of lower spectral resolution. The SNR for the detection of a given molecular species remains unchanged, since it will be independent of the spectral smoothing [20].

C. Signal-to-Noise Ratio

One strength of DCS is that only a single detector is needed to record millions of spectral points. However, there is a “multiplexed” penalty associated with the use of a single detector. Essentially, for M spectral elements (i.e., comb teeth), one might expect the SNR per spectral element to scale as $1/\sqrt{M}$ as one spreads a fixed laser power over M spectral elements. However, the use of a single detector leads to an additional multiplexed penalty of $1/\sqrt{M}$, leading to the overall SNR scaling with 1/M [20]. In the ideal shot-noise limit, the $\text{SNR}\approx \sqrt{\tau n_{\text{comb}}}/M$, where τ is the acquisition time and n_comb is the number of detected comb photons per second. However, the actual SNR per spectral element will depend on the dominant noise source, which is discussed in detail in Section 5. Nevertheless, the basic scaling law of $\text{SNR}\approx \sqrt{\tau }/M$ is retained and illustrates the trade-off in SNR versus bandwidth, since $\Delta \nu =M\hspace{0.17em}{f}_r$. It also illustrates the importance of a long coherent averaging time, or equivalently a long effective mutual coherence time between combs, which sets the maximum possible τ. Finally, this scaling drives the choice of a useful figure of merit of $\text{SNR}\approx M/\sqrt{\tau }$, used in Section 5 to compare the SNR across different acquired DCS spectra.

3. DUAL-COMB SPECTROSCOPY WITH IMPERFECT COMBS

The ideal picture of the previous section assumed ideal frequency combs composed of narrow (delta-function-like) comb teeth at well-defined frequencies. Actual frequency combs can approach this ideal performance, but it is experimentally challenging. DCS “doubles” that challenge by requiring two such combs with high mutual coherence. In practice, DCS has been demonstrated over a wide range of frequency comb performance. Coarsely, DCS demonstrations can be broken into three categories: free-running combs, mutually coherent combs, and fully referenced combs, as listed in Fig. 4 and summarized below. Clearly, the experimental challenges increase in moving from free-running combs to fully referenced combs, but so too does the performance in terms of improved spectral resolution, frequency accuracy, and SNR (through increased coherent averaging times).

Fig. 4.

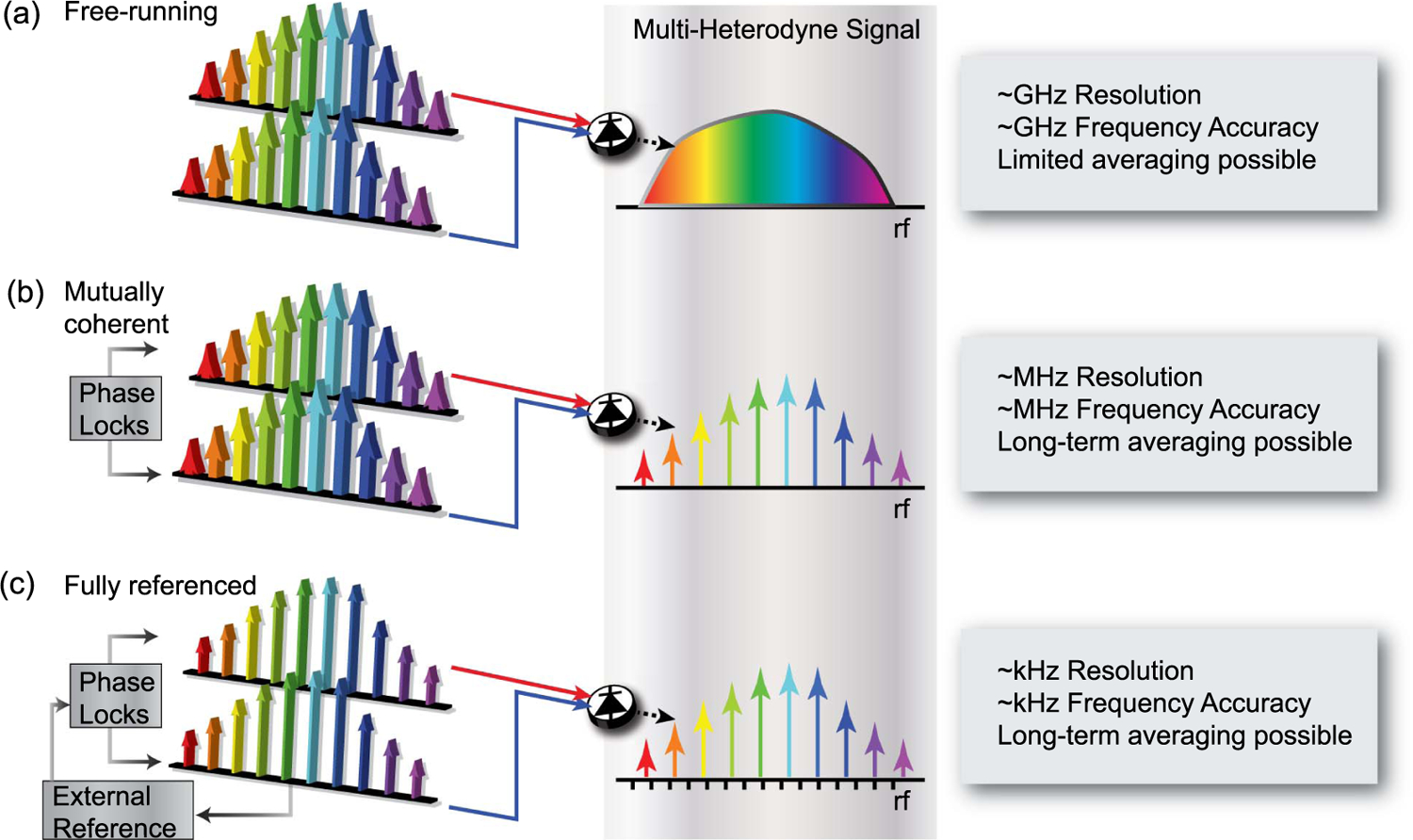
Three different categories of DCS demonstrations. (a) Free-running combs can yield dual-comb spectra, but with low resolution, low frequency accuracy, and low SNR, since only limited signal averaging is possible; (b) mutually coherent combs can yield comb-tooth-resolved spectra that can be averaged for high SNR; and (c) fully referenced combs yield spectra with simultaneous high resolution, absolute frequency accuracy, and high SNR. Text boxes indicate some general rules of thumb for frequency combs based on mode-locked lasers.

Figure 4(a) depicts the case of free-running combs, where the relative optical linewidth between the combs is greater than Δf_r. In that case, there can be varying degrees of overlap or blending with the corresponding rf comb, resulting in a much lower frequency resolution. Nevertheless, demonstrations with free-running combs have been important as basic proof-of-principle experiments, for example, the first demonstration of DCS by Keilmann and coworkers [2,3], cavity-enhanced DCS [14], and many demonstrations with novel comb sources in the mid-IR and far-IR [16,28,33,35,37,38,41,48,51,93].

Figure 4(b) depicts the case of high mutual coherence, where the relative linewidth between the combs is well below Δf_r. The mutual coherence can be enforced through active feedback to the combs and/or signal processing, as discussed later, or through comb designs where the coherence is at least partially inherent [43,54,55,57,94–97]. In this case the individual comb teeth are spectrally resolved, and therefore each comb tooth pair provides a single independent spectral sample. Since the fundamental resolution is set by the comb tooth linewidth, which can be several orders of magnitude smaller that the spectral point spacing, there is minimal cross talk between adjacent spectral elements, i.e., no instrument line shape. This sets DCS apart from conventional broadband spectrometers, where instrument line shapes are always present and will distort the recorded spectra in ways that can shift over time. Moreover, at typical comb repetition frequencies the spectral point spacings are 50–200 MHz, matching the highest resolution FTIRs, traditionally the gold standard of high-resolution broadband spectroscopy. Finally, this point spacing is not the actual resolution limit; if needed, the comb can be scanned for higher point density up to a resolution limit set by the absolute comb tooth linewidths (typically a few kilohertz to megahertz) [22,39,59]. There is an important second consequence to high mutual coherence, namely, it allows for longer acquisition times, τ, and therefore higher SNR, as discussed in Section 2.C and later in Section 5.

Finally, Fig. 4(c) depicts the “ideal” case, where the two mutually coherent combs are referenced back to an absolute frequency standard. This is easiest to achieve for combs based in difference frequency generation (DFG) or with THz combs, where the carrier-envelope offset frequency, f_ceo, is identically zero [5–7,11,18,23,39,45–47,49]. In other cases, f_ceo is not zero; stabilizing f_ceo still allows the comb teeth to reach kilohertz accuracies, so that tooth-resolved DCS spectra exceed the accuracy of conventional broadband spectrometers by many orders of magnitude [9,19,22,25,36,53]. Absolute referencing also removes common-mode frequency drifts of the two combs that would otherwise broaden the instrument line shape over long averaging times, potentially washing out spectral features of interest. Molecular line centers retrieved with fully stabilized DCS have frequency accuracies superior to high-resolution FTIRs, and traceability to the underlying frequency reference. However, spectral distortions can limit line center retrievals to about a part per thousand of the linewidth. [22,29].

4. DUAL-COMB SPECTROSCOPY DEMONSTRATIONS IN DIFFERENT SPECTRAL REGIONS

In this section, we review DCS demonstrations by spectral coverage, following the summary presented in Fig. 2. As emphasized in Fig. 2, the first requirement for DCS is the existence of a frequency comb in the desired spectral range. While near-IR comb technology is becoming more robust [98–101], combs in the mid-IR [16,22,28,33,35,41,48,51,58] and far-IR [2,3,37,38] are still developing. For this reason, most demonstrations using highly coherent [i.e., Fig. 4(b)] or fully stabilized combs [i.e., Fig. 4(c)] have taken place in the near-IR (or THz), and they are discussed first below.

A. Near-IR DCS with Fiber-based Frequency Combs

Figure 5 provides an example of a DCS spectrum acquired in the near-IR using the dispersive configuration and fiber-laser-based frequency combs with 100 MHz repetition rates [15]. The high SNR and flat baseline are due to long-term coherent averaging, time-multiplexed signal and reference measurements, and sequential acquisition over subbands to avoid detector nonlinearity.

Fig. 5.

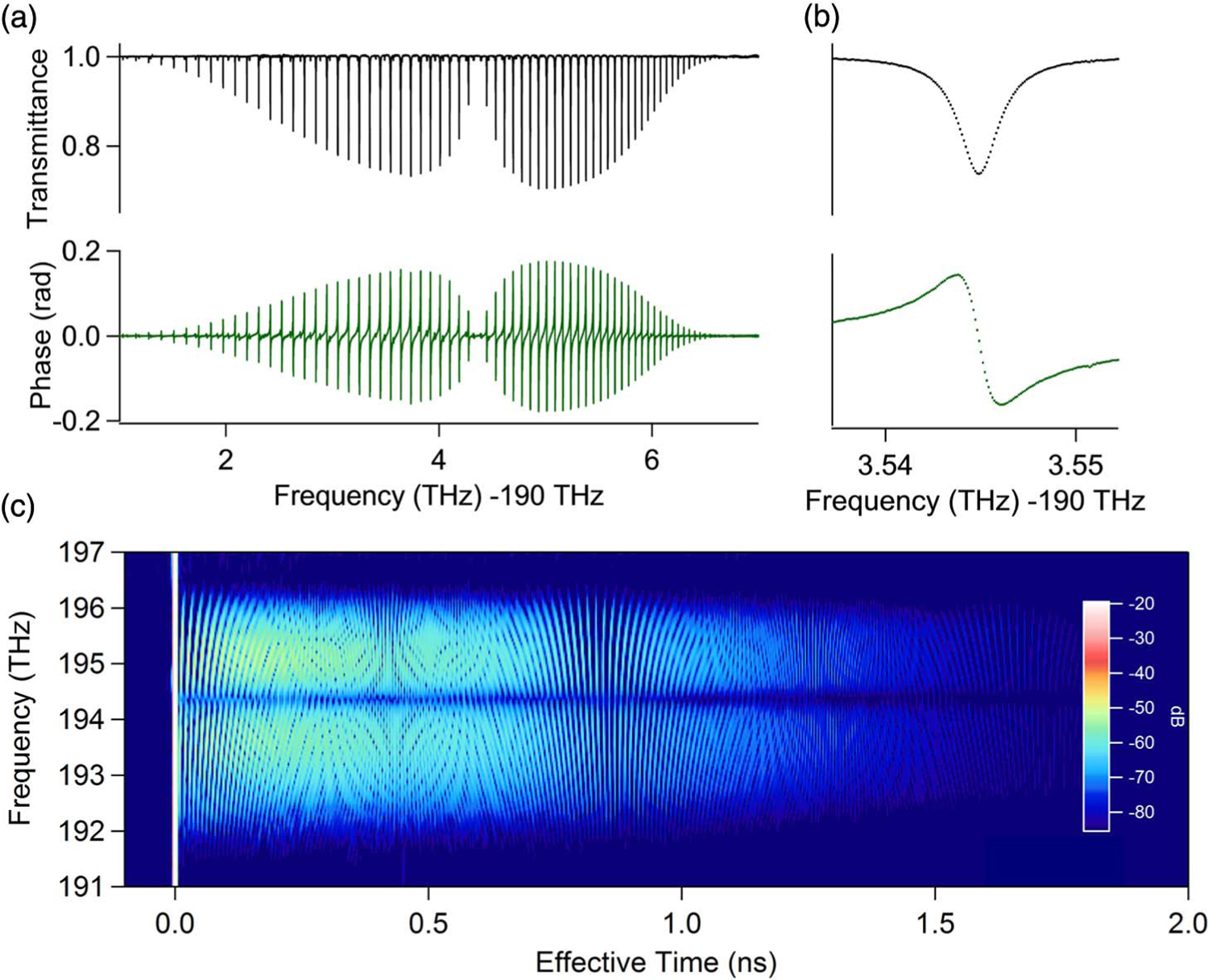
Signature of the full rotational band from the C-H overtone of HCN gas as measured in the dispersive dual-comb spectrometer configuration [19]. (a) The phase and amplitude signature at 100 MHz point spacing has a signal-to-noise ratio per point of ∼4000 with respect to unity transmission; (b) expanded view showing the spectral sampling points; (c) joint time–frequency domain signature from the short-time Fourier transform of the data that clearly shows the free-induction decay signals in the “P” and “R” branches as vertical stripes. The overall decay results from Doppler and collisional dephasing.

The quality of this early data was facilitated in part by the relatively advanced nature of the near-IR optical componentry. Indeed, to date the majority of DCS demonstrations have been performed in the ∼1550 nm telecommunication band, where there are relatively inexpensive and robust erbium fiber frequency combs, fiber-optic components, and high-bandwidth, sensitive photoreceivers [9,10,17,19,24,25,29,34,36,42,44,50,53]. For example, the near-IR saw the first demonstration of tooth-resolved DCS spectra, which was achieved by use of active phase/timing correction of the two combs [9] and also included absolute frequency stabilization. This work was followed closely by the first demonstration of a digital phase/timing correction that essentially imposes mutual phase coherence via signal processing and achieves tooth-resolved spectra [10]. References [42,44] developed an analog adaptive sampling approach that also leads to tooth-resolved spectra and is more accessible to many laboratories.

Section 5.C discusses these important methods of extending the mutual coherence in more detail.

Near-IR DCS demonstrations have also shown that DCS is compatible with nonlinear spectral broadening. Operating in the erbium or ytterbium gain windows provides access to only a small set of molecules. Fortunately, the spectrum of a comb can be broadened in nonlinear fibers. With spectral broadening, Zolot et al. demonstrated tooth-resolved DCS over 43 THz, allowing interrogation of atmospheric trace molecules such as methane, carbon dioxide, and water [25]. Okubo et al. have shown that DCS is possible over an even broader spectrum covering 140 THz or almost the entire 1–2 μm supercontinuum span of Er fiber frequency combs [50].

Near-IR DCS is also one of the few regions, other than the THz, where the technology has ventured beyond instrument demonstrations. It has been used for accurate measurement of molecular line centers [29,50] and, most recently, greenhouse gas monitoring over outdoor air paths [36,53], in both cases providing performance beyond what is possible with conventional broadband spectrometers.

These systems all make use of erbium fiber frequency combs. DCS based on ytterbium fiber frequency combs centered at 1 μm is less common but has been used for a very early demonstration of cavity-enhanced DCS [14]. Further toward the visible spectrum, DCS based on doubled erbium fiber frequency combs at 760–780 has been used for Rb and O₂ spectroscopy [30,40], while DCS based on doubled ytterbium fiber frequency combs at 520 nm has been used for iodine spectroscopy [26].

Finally, the near-IR also saw the first demonstrations of long-term averaging, using techniques discussed in Section 5.D. With these modified schemes, DCS can truly have SNRs comparable to FTIR or grating spectrometers. In Ref. [19], the active phase/timing approach was extended to enable coherent co-adding of interferograms on an FPGA, effectively allowing infinitely long averaging times without incurring dead time. Alternatively, Refs. [17,24] further refined the digital phase/timing correction approach to allowing for similarly limitless continuous real-time coherent averaging on a field programmable gate array (FPGA) and yielding spectral SNRs exceeding all other techniques to date.

B. Near-IR DCS with EOM-based Frequency Combs

Near-IR dual-comb systems can also be based on “electro-optic modulator” frequency combs generated by strong modulation of a cw laser. In fact, as early as 2001 a dual-comb system based on EOM combs was used in a high-speed optical coherent tomography demonstration [60]. EOM-based dual-comb systems have the advantage of a flexible repetition rate that can exceed 10 GHz, high-power comb teeth, and intrinsic mutual coherence between combs, since the two combs are generated from the same cw laser and rf time base [43,54,55,57], but their operation is thus far restricted to relatively narrow spectra comprising ∼50–100 teeth over tens of gigahertz and to the telecom band where efficient modulators are commercially available. As such, they are well matched to rapid, sensitive spectroscopy across single near-IR molecular lines, and EOM-based DCS has been demonstrated in the detection of the complex (phase and amplitude) spectrum of CO₂ [43] and HCN [54,55]. Through external spectral broadening in nonlinear fiber, EOM-based DCS has been demonstrated at up to ∼300 GHz instantaneous bandwidth [56]. With future mid-IR modulators, it should be possible to extend this technique beyond the near-IR. Finally, note that there is no absolute frequency accuracy, unless the cw laser frequency is measured, and any frequency noise on that cw laser will limit the ultimate resolution.

C. Related Near-IR Systems

It is also worth noting that there is a range of emerging techniques that bear a strong resemblance to the dual-comb approach both in concept and in underlying technology. In most cases it is too soon to know where these offshoots will lead, but they offer an interesting trade-off space to explore.

One of the simplest variations of DCS and FTIR is the use of a single frequency comb coupled with an unbalanced interferometer [102–105]. Sometimes referred to as optical scanning by cavity tuning (OSCAT), this technique works by continuously scanning the repetition rate of the comb [106]. This sweeping repetition rate, combined with the significant differential time delay in the unbalanced interferometer (often ∼1 μs), gives two pulse trains with a continuously varying relative timing that can be interfered to create an interferogram similar to DCS, though typically with lower spectral resolution. In a related approach, an acousto-optic tunable filter in one arm of the interferometer can allow for a rapidly changing differential delay even with a static comb, although the maximum path delay and spectral resolution are restricted [107]

A second interesting system is known as dual-etalon cavity ringdown spectroscopy (with the memorable acronym DEFCOM) [108]. Two high-finesse etalons are excited with a single common optical pulse. As both etalons ring down, they emit two trains of pulses that can be interfered to mimic DCS. This technique inherently combines the strengths of cavity ringdown spectroscopy and Fourier transform techniques. However, to date, DEFCOM has been demonstrated only with limited bandwidths.

Finally, there are a number of systems that seek to dispense with the requirement of two mode-locked lasers by generating dual combs with offset repetition frequencies from a single laser system [94–97]. In the near-IR, the recent work of Ref. [97] exhibits very-high-quality dual-comb spectra using this approach.

D. Mid-IR and Far-IR DCS

While DCS does have applications in the near-IR and visible regions, the principle spectral region of interest for molecular spectroscopy is at wavelengths greater than 3 μm, where molecules exhibit much stronger absorption cross sections. This is also the principle area in which DCS lags behind FTIR, the primary workhorse for analytical spectroscopy. Indeed for all its advantages, DCS will never usurp FTIR for many applications until it has much broader spectral coverage into the mid-IR (3–5 μm) and far-IR (6–13 μm). As illustrated in Fig. 2, frequency combs continue to expand into these spectral regions, and there have been a number of interesting DCS demonstrations including the pioneering work of Keilmann and coworkers [2,3].

Mid- and far-IR frequency combs can be generated based on DFG from near-IR sources or directly from mid-IR/far-IR mode-locked lasers, optical parametric oscillators (OPOs), microresonators, or QCLs [109]. An advantage of using DFG-based DCS is that the coherence of the underlying near-IR comb sources can be directly translated into the mid-IR. This high coherence was demonstrated in narrowband mid-IR DCS near 3.4 μm for the accurate line center measurements of methane [22]. In that case, the Er fiber comb was shifted to the mid-IR via DFG with a cw 1 μm laser in periodically poled lithium niobate. Higher-power, broader-bandwidth (and f_ceo-free) combs are generated by DFG with the reamplified 1 μm light generated by supercontinuum generation from the Er fiber comb [51,58]. Reference [51] demonstrated rapid, sensitive methane detection with such a system over 3.17–3.44 μm. Through additional external spectral broadening, future DFG-based systems have the potential to cover the full mid-IR (3–5 μm).

DFG-based combs can also permit DCS further into the IR. As mentioned above, the first DCS demonstrations were based on a Ti:sapphire comb whose output was shifted to the 9–12 μm region through DFG in Ga:Se [2]. This system has been applied to the rapid detection of ammonia over a 44 m outdoor path [3] and to scanning near-field optical microscopy [5]. Furthermore, the Ti:sapphire laser can be replaced with an all-fiber system allowing even greater tunable spectral coverage from 4 to 17 μm with 21 THz of instantaneous bandwidth [110]. Future developments in optically patterned gallium arsenide could make for even more efficient generation, high-power DFG combs in the far-IR [111].

Mid-IR combs can also be generated directly by OPOs at high power and with broad tuning ranges [28,33,35,41,48,68,72, 112,113]. DCS presents the daunting challenge of operating two coherent OPOs. However, there has been a series of single OPOs designs for DCS where two mode-locked lasers at slightly different repetition rates pump a single OPO cavity [28,33,35,41,48]. Nonlinear interaction of the pulses in the OPO cavity can be minimized by counterpropagating the two pump lasers in the OPO cavity [41,48]. With this approach, OPO-based DCS has been demonstrated in spectroscopy of methane and acetylene over 3.1–3.4 μm [35,41,48]. Finally, the use of degenerate OPOs offers the possibility of extremely broadband DCS across the mid-IR [112,114].

Interesting new dual-comb Raman techniques also offer access to the 7–50 μm range [27,32]. This technique combines the advantages of CARS with the resolution/accuracy of combs to probe the far-IR molecular spectrum. As discussed in Ref. [32], this approach has the potential for high-speed broadband CARS and can be applied to spectro-imaging of complex samples.

Finally, mid-IR comb light can also be generated directly from mode-locked lasers. Proof-of-principle DCS experiments have been conducted at 2.4 μm with two Cr²⁺:ZnSe femtosecond lasers, and several groups are actively pursuing mid-IR mode-locked fiber lasers [115,116]. Further into the IR, QCLs provide interesting possibilities, since they can provide a path toward a chip-scale, electrically pumped system for DCS [52]. Preliminary demonstrations of DCS using QCL-frequency combs have been reported at 7–8.5 μm with over 64 comb teeth at 15 GHz separation in the molecular fingerprint far-IR region [37,38,52]. With improvements in spectral coverage, these QCL DCS systems could eventually provide a compact, high-speed far-IR spectrometer.

E. THz DCS

At longer wavelengths one enters the THz region, which is also very attractive for spectroscopy. DCS demonstrations in the THz are as prevalent as in the near-IR and have an earlier inception [4] as well as several excellent reviews [7,49]. In the THz, DCS is effectively equivalent to THz time-domain spectroscopy or ASOPS [4,6–8,11,13,18,39,45–47,49], and commercial systems are available [117]. THz systems often use either Ti:sapphire or fiber-based combs to drive photoconductive antennas that emit broadband THz combs. As with DFG, this process cancels the carrier-envelope offset frequency, and the long wavelengths make the system more tolerant of timing jitter. THz DCS has been demonstrated with absolute frequency accuracy, high SNR through longer integration times, and comb-tooth-resolved spectra [6,11,23,45–47,49].

In the THz region, Doppler broadening is correspondingly smaller than in the near-IR, and for a sufficiently dilute gas the molecular absorption features can be narrower than the comb spacing. Interleaving of comb spectra can fill these gaps [22,39,59], and coherent processing is required to account for time-domain features that can extend across multiple interferograms [39].

5. DUAL-COMB SPECTROSCOPY: SNR

The previous section categorized DCS demonstrations in terms of spectral region. However, as noted, many DCS experiments outside of the near-IR and THz have been limited to proof-of-concept spectra with low SNR. In order for future experiments to exploit the full frequency resolution and accuracy afforded by DCS, a high-SNR spectrum is critical. Otherwise, the strong spectral noise will mask the fine detail present in molecular spectra. This section summarizes the approaches for achieving high-SNR DCS spectra.

Section 5.A summarizes the limitations to the SNR in DCS. Section 5.B defines the figure of merit, $\text{SNR}\approx M/\sqrt{\tau }$, discussed in Section 3.C and summarizes the figure of merit achieved in recent DCS experiments. Of course, this figure of merit is most sensible if the DCS data are acquired for at least 1 s, the normalized acquisition time. Section 5.C discusses the methods for DCS data acquisition over seconds. Finally, Section 5.D discusses two methods that allow for long-term coherent averaging spanning minutes, hours, or even days.

To understand the importance of coherent averaging, consider a DCS spectrometer with a figure of merit of $\text{SNR}\approx M/\sqrt{\tau }={10}^6{\text{HZ}}^{1/2}$. It then requires 10,000 s of averaging to reach an SNR per spectral point of 1000 over 100,000 spectral points. This long-time acquisition over 10,000 s is possible but requires the techniques discussed in Section 5.D.

Note that in this section we focus on spectral SNR, defined as the standard deviation of a normalized transmission spectrum. This spectral SNR is independent of path length and allows use across platforms with widely varying paths and purposes.

A. Practical Limitations to the SNR

Broadband time-domain noise will lead to “broadband” spectral noise, corresponding to uncorrelated point-to-point fluctuations across the measured spectral points (comb teeth). The resulting SNR has been analyzed in detail in Ref. [20]. Note that this SNR of a single spectral point differs from the SNR for the detection of a molecular species. The latter would be integrated over the full absorption spectrum and could be higher or lower depending on the molecule’s summed line strength and, of course, on the total effective path length.

In general, the shot-noise-limited SNR of Section 2 does not apply, as the comb power is either too low, so that the photoreceiver’s noise equivalent power (NEP) dominates, or too high, so that it must be attenuated to avoid photoreceiver saturation. The former case might be encountered in the far-IR, where the comb powers might be lower and NEP higher than in the near-IR. In that case, the SNR is

$${\text{SNR}}_{\text{NEP}}\propto \hspace{0.17em}\frac{1}{M}\frac{\sqrt{P_1{P}_2}}{\text{NEP}}\sqrt{\tau },$$

where P₁ and P₂ are the powers of the two combs at the detector and τ is the averaging time. Clearly, the route to a higher SNR is higher comb power and lower NEP. Since the NEP can be a function of the photoreceiver bandwidth, one can possibly realize lower NEP by compressing the rf comb into bandwidths well below f_r∕2, provided the comb linewidths are sufficiently narrow.

On the other hand, many near-IR or visible comb sources can generate hundreds of milliwatts of optical power, which can easily drive a photoreceiver into nonlinearity or full saturation if not attenuated. In this case, the SNR is effectively limited by the dynamic range of the photoreceiver, D (as in FTIR):

$${\text{SNR}}_{\text{DynRange}}\propto \hspace{0.17em}\frac{D}{M}\sqrt{\tau f_r.}$$

Note that the actual noise floor might be shot-noise limited, but since the dynamic range sets the maximum comb power, we refer to this case as dynamic-range limited. Dynamic ranges vary, but a commercial 100 MHz InGaAs amplified photoreceiver might have a limited D of ∼500 (given by the ratio of the maximum peak power to the NEP integrated over a bandwidth of f_r ). Clearly, the route to higher SNR here is increased dynamic range. One solution is to simply push deeper toward saturation. The first effect at the onset of saturation is the mixing of adjacent rf comb lines, leading to slight distortions (∼1 MHz) of the measured absorption line centers [22,29,50], with distortions in the integrated line strength appearing at yet higher powers. For many applications, such line center shifts are inconsequential, and many DCS demonstrations have operated at least partially into this nonlinear regime. If this dynamic range is set by the rf amplification of the strong centerburst (rather than intrinsic nonlinearity in the photodetection), the peak signal intensity can be reduced by strongly chirping one of the two frequency combs [17]. In the near-IR below ∼1.8 μm, there has been considerable recent progress in the development of high-dynamic-range InGaAs detectors to support microwave photonics [118]. Finally, one could spectrally disperse subbands of the spectrum onto multiple photoreceivers to improve the SNR [20] at the cost of experimental complexity.

This analysis ignores the multiplicative noise from differential phase noise between the combs. This noise will clearly be most prevalent for free-running combs [e.g., Fig. 4(a)]. However, even for mutually coherent combs with linewidths below Δf_r, there is still a residual phase noise pedestal on any given rf tooth. Phase noise at Fourier frequencies below Δf_r will contribute to slow baseline variations [20] and should be removed though interferogram phase correction (see Section 5.D). Phase noise at Fourier frequencies above Δf_r will affect neighboring rf comb teeth, limiting the SNR. The full impact of this higher frequency multiplicative noise has not yet been rigorously examined, but active real-time phase correction as in Ref. [24] will suppress its effects (again, see Section 5.D).

Finally, the goal is to measure the sample’s response, not the comb spectrum. Therefore the comb spectrum must be normalized out. This normalization is common to any spectroscopic system, but here it is exacerbated by the strongly varying comb spectra. While a DCS spectrum can cover 100 THz [50], the broadband comb spectrum will generally have significant structure showing up to 20 dB of intensity variations (which is not captured in Fig. 2), regardless of the wavelength band. Regions of the spectrum may be unusable for spectroscopy due to low power, while other regions may have strong variations over short wavelength spans that are difficult to remove from the final sample spectrum, particularly for broad absorbers. To date, most DCS experiments have interrogated small molecules in the gas phase. Because the resulting absorption linewidths are narrower than the comb variations, a piecewise linear baseline fit can suffice to remove these background variations [36], as in conventional FTIR. Additionally, experiments have explored normalization using a second reference channel, sequential measurements with and without the sample, and even time-interleaved interferograms [15,51]. The best option will depend strongly on the comb spectrum, the optical configuration (e.g., presence of etalons), and the spectral signature of the sample (broad or narrow absorbers). However, as with conventional spectrometers, a “flat” baseline at the parts-per-thousand level is challenging.

B. Figure of Merit for SNR

As shown in the previous section, in the shot-noise limit, dynamic-range limit, or detector-noise limit, the SNR scales as $\frac{\sqrt{\tau }}{M}$. For this reason, we identify a useful figure of merit for DCS as SNR × M at τ = 1 s, which also connects the SNR with the measured optical bandwidth, Δν = Mf_r [20]. It can be challenging to extract values for the SNR and bandwidth from the literature because of variations in whether the peak or average SNR is given and in the definition of optical bandwidth. Nevertheless, Fig. 6 reviews the state of the art for DCS in terms of this figure of merit for a few different demonstrations. All SNRs are scaled to the unapodized value (i.e., resolution equal to the comb tooth spacing f_r) and to 1 s acquisition times. With the exception of Refs. [51,56], which used 250–300 MHz comb tooth spacing, all experiments used approximately 100 MHz comb tooth spacing. (A higher repetition rate shifts the points to wider optical bandwidths for the same nominal figure of merit).

Fig. 6.

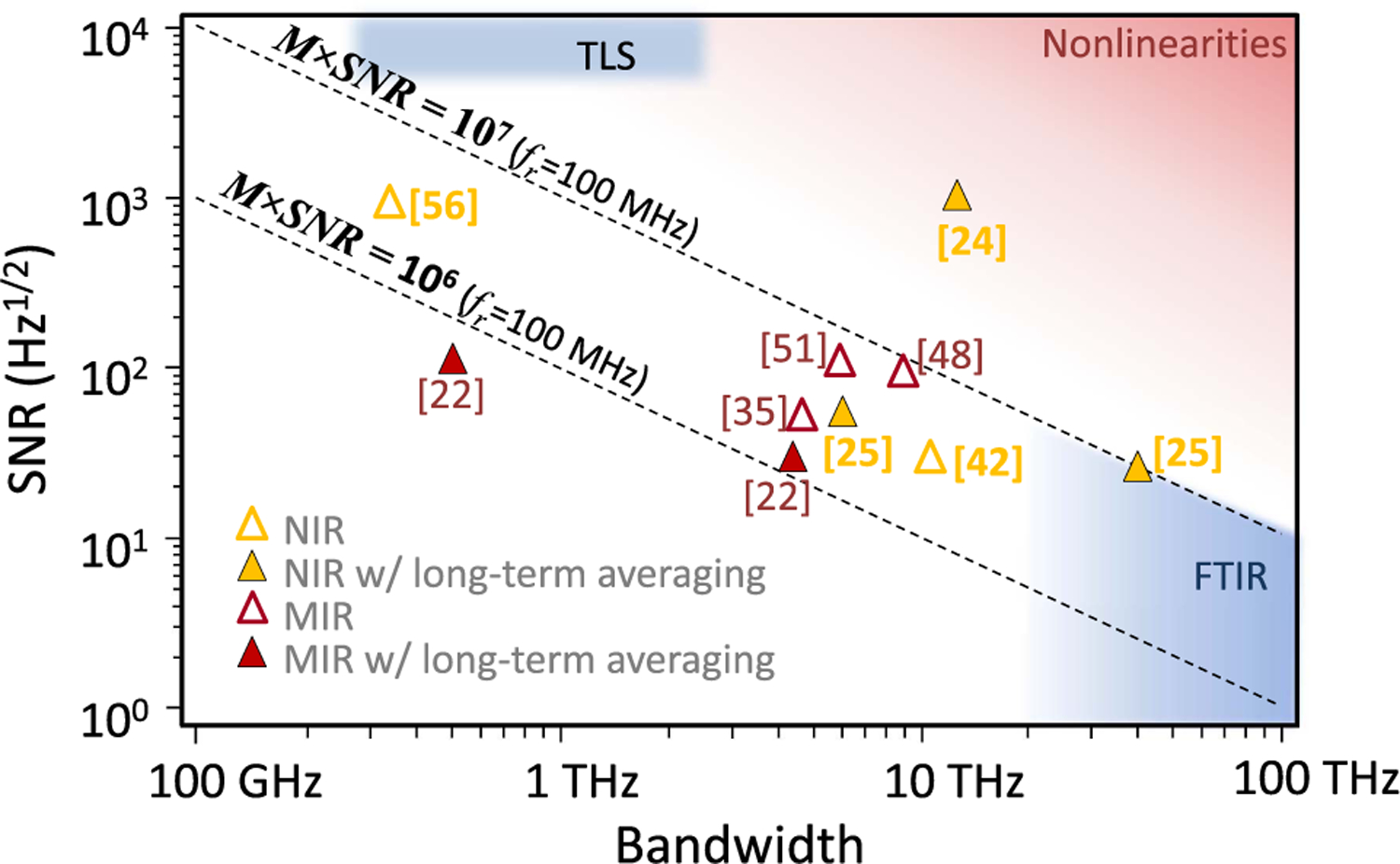
Spectral SNR versus bandwidth for DCS demonstrations in the near-IR (NIR; yellow triangles) and mid-IR (MIR; red triangles). In the near-IR, data points include only experiments that enforced mutual coherence through either active phase/timing feedback [25], digital phase/timing correction [24], or analog adaptive sampling [42]. The solid triangles indicate that coherent averaging was implemented. Approximate regions of operation for FTIR and tunable laser spectroscopy (TLS) are added in blue. The number of spectral elements M is the bandwidth/f_r, where f_r is ∼100 MHz for most demonstrations shown here.

As shown in Fig. 6, most demonstrations so far have a figure of merit in the range of 10⁶–10⁷. Also, Fig. 6 emphasizes the significant advantage of digital phase/timing correction, which, combined with a high dynamic range detector, yields a record figure of merit [24] of ∼2 × 10⁸ Hz^1∕2. Finally, when operating at the highest possible figure of merit, one must be wary of increased nonlinearities that can degrade the instrument line shape (by mixing the response across rf comb teeth) and lead to systematic distortions of the spectrum.

C. DCS with Mutual Coherence Time of Seconds

As discussed above, the SNR improves with the square root of the averaging time, but only up to the mutual coherence time of the two combs, which sets the linewidth of the rf comb teeth. For THz combs or EOM-based frequency combs, this mutual coherence can be established with relatively minimal active control. In the IR, mutual coherence is much harder to enforce because of the higher carrier frequency and broader optical bandwidths.

Three different approaches have been taken in IR DCS to force mutual coherence times on the order of seconds: active phase/timing feedback, digital phase/timing correction, and analog adaptive sampling. In all three cases, the two combs are each compared to a pair of common references, for example, to two cw lasers separated by a few THz [9,17,42]. (Alternatively, Ref. [50] used fully self-referenced combs compared against a single cavity-stabilized cw laser.) The comparison generates two pairs of error signals that reflect the fluctuations in the two combs. In the approach of active phase/timing feedback, these error signals are input to a phase-locked loop that actively stabilizes both frequency combs via high-bandwidth actuators to achieve subhertz residual linewidths and a known, stable repetition frequency [9,19,22,25,36,50,53]. In the approach of digital phase/timing correction, these error signals are digitized along with the interferograms. Signal processing then removes both carrier phase noise and relative timing noise by resampling the interferograms [10,17,24,30,31]. In the approach of analog adaptive sampling, these error signals are input to a set of analog electronics that corrects for any relative carrier phase noise and adjusts the digitizer sampling clock to match the difference in repetition rates [26,42,44].

Both the digital phase/timing correction and the analog adaptive sampling do require low-bandwidth active feedback so that the detected error signals and interferograms remain within useful frequency windows, but they avoid the experimental challenges associated with high-bandwidth active feedback. Analog adaptive sampling can be implemented with readily available rf electronics, but digital phase/timing correction is more powerful, since it can take advantage of modern FPGAs and is readily extended to long-term coherent averaging, discussed next.

D. Coherent Averaging: DCS Acquisition over Hours and Days

When acquiring DCS data over times greater than a few seconds, two problems arise: data overload and interferogram dephasing. The solution is to implement real-time coherent averaging, as described below. Coherent averaging (the analog of co-adding interferograms in FTIR) has been demonstrated both using active phase/timing feedback combined with post processing and using real-time digital phase/timing correction implemented on an FPGA [19,22,24,25,36,39,43,47,50]. The former has allowed for DCS across an open-air path that ran continuously for three days [36]. The latter has enabled real-time, continuous coherent averaging for 24 h with record levels of SNRs on both short timescales (see Fig. 6) and long timescales, reaching an SNR of 316,000 at 100 MHz point spacing [24].

To understand the problem of data overload, the direct 16-bit digitization of both signal and reference interferograms at f_r ∼ 100 MHz generates 3 Gbits/s of data, presenting a significant storage and processing challenge. The solution is to align the two frequency combs such that the interferograms will be identical and comprise an integer number of samples. (This condition is met if the repetition rates of both combs and the difference of their f_ceo frequencies are all integer multiples of Δf_r ). In the case of active phase/timing feedback, this condition is accomplished via careful choice of the rf offsets in the four phase-locked loops that control the combs. In the case of digital phase/timing correction, this condition is easily met by adjusting the interferogram phase and resampling it essentially at will. In either case, sequential interferograms are then co-added point by point on an FPGA over a period up to 1 s, providing a factor of 100–1000 reduction in data load [19,24]. Since the final coherently averaged interferogram is only 1∕Δf_r in length in lab time or 1∕f_r in effective time (see Fig. 3), there may be a misconception that the spectral resolution is limited by this time window. This is not the case, as the coherently averaged interferogram is actually measured over a total acquisition time t_acq, and its Fourier transform is mathematically equivalent to streaming the entire time data to memory, Fourier transforming the time sequence, and then selecting only the power at multiples of Δf_r. The resolution of each spectral point is then the larger of the comb tooth linewidth or the inverse acquisition time.

After a second at most, the interferograms will drift out of phase because of phase/timing drifts between the two combs due to path length variations in the spectrometer that are not detected in the comparison with the common reference lasers. The solution is to apply a phase correction to the interferograms, as is traditionally done in FTIR [76] either in postprocessing software [19] or as part of the real-time digital signal processing [24]. In this approach, the phase at the center of each consecutive, possibly co-added, interferogram [e.g., Fig. 3(d)] is measured, and any difference is applied across the entire interferogram. Timing shifts are also corrected through a linear spectral phase correction in the frequency domain [19] or through resampling in the time domain [24]. These phase-corrected interferograms can then be coherently added up to the desired averaging period. (Conventional FTIR will use even higher order phase corrections than linear, but higher order phase corrections have so far not been necessary for dual-comb spectrometers.)

We emphasize that the digital phase/timing correction approach to full coherent averaging is particularly attractive, as it combines all of the processing discussed above on a single real-time platform and with high effective correction bandwidths [24]. That is, it uses real-time digital signal processing of the combined interferogram signals and common reference signals to force mutual coherence at short times with a high effective bandwidth, implements a real-time interferogram-based phase correction at update times of 1∕Δf_r, and finally implements real-time co-adding for deep averaging.

In the THz, the same need for coherent averaging arises. Here, mutual coherence is easier to establish because of the longer wavelengths, and because it can be sufficient to stabilize the repetition rate [6,7,11,12,39,45–47,49]. For THz signals, a Doppler limited absorption feature can be less than the comb spacing, but the coherent co-added interferogram preserves the resolution of the system to observe this fine structure [46].

6. CONCLUSION

Frequency combs are an ideal source for broadband spectroscopy, as they provide high frequency resolution, broad spectral coverage, and a high-brightness collimated beam. DCS fully exploits these frequency comb properties to measure a sample’s complex response on a comb tooth-by-tooth basis with only a single photodetector. The most extensive demonstrations so far have been conducted in the near-IR, where experiments have demonstrated the full benefits of DCS of bandwidth, resolution, SNR, and accuracy. While proof-of-principle experiments continue, near-IR DCS has also evolved to the point where it can be used as a tool to support practical spectral measurements.

Farther into the IR, DCS is still under development, as mid-IR combs have yet to match their near-IR counterparts in terms of a robust, affordable system that can provide high stability, coherence, and suitably wide spectral bandwidths. Nevertheless, there has been much progress in this region, and DCS remains one of the primary motivations driving mid- and far-IR comb development. With continued development, one can speculate that in the future DCS will become a lithe, agile spectroscopic tool that could replace traditional FTIR in many applications both in the laboratory and in the field, enabling much greater resolution and sensitivity in a much more compact system.