Skip to main content
PMC home page
NIST Author Manuscripts logoLink to NIST Author Manuscripts
. Author manuscript; available in PMC: 2021 Jun 14.
Published in final edited form as: Nat Phys. 2019;15(12):10.1038/s41567-019-0670-x. doi: 10.1038/s41567-019-0670-x

Extreme magnetic field-boosted superconductivity

Sheng Ran 1,2,3,*, I-Lin Liu 1,2,3, Yun Suk Eo 1, Daniel J Campbell 1, Paul M Neves 1, Wesley T Fuhrman 1, Shanta R Saha 1,2, Christopher Eckberg 1, Hyunsoo Kim 1, David Graf 4, Fedor Balakirev 5, John Singleton 5,6, Johnpierre Paglione 1,2, Nicholas P Butch 1,2,*
PMCID: PMC8201648  NIHMSID: NIHMS1670428  PMID: 34131432

Abstract

Applied magnetic fields underlie exotic quantum states, such as the fractional quantum Hall effect1 and Bose–Einstein condensation of spin excitations2. Superconductivity, however, is inherently antagonistic towards magnetic fields. Only in rare cases3–5 can these effects be mitigated over limited fields, leading to re-entrant superconductivity. Here, we report the coexistence of multiple high-field re-entrant superconducting phases in the spin-triplet superconductor UTe2 (ref. 6). We observe superconductivity in the highest magnetic field range identified for any re-entrant superconductor, beyond 65 T. Although the stability of superconductivity in these high magnetic fields challenges current theoretical models, these extreme properties seem to reflect a new kind of exotic superconductivity rooted in magnetic fluctuations7 and boosted by a quantum dimensional crossover8.

It is a basic fact that magnetic fields are destructive to superconductivity. The maximum magnetic field in which superconductivity survives, the upper critical field Hc2, is restricted by both the paramagnetic effect of electron spin polarization due to the Zeeman effect and the orbital pair-breaking effect of electron–cyclotron motion due to the Lorentz force. In a few very rare cases, however, magnetic fields can do the opposite and actually stabilize superconductivity3–5. In these cases, the applied magnetic field is most often compensated by an internal field produced by ordered magnetic moments through exchange interactions, resulting in a reduced total effective field9. A different set of circumstances involving unconventional superconductivity occurs in the ferromagnetic superconductor URhGe (refs. 10,11), in which field-induced superconductivity is attributed to very strong ferromagnetic fluctuations that emanate from a quantum instability of a ferromagnetic phase, strengthening spin-triplet pairing7.

Here, we report the presence of two independent high-field superconducting phases in the recently discovered triplet superconductor UTe2 (ref. 6), for a total of three superconducting phases (Fig. 1). This is an example of two field-induced superconducting phases existing in one system, one of which has the highest lower and upper limiting fields of any field-induced superconducting phase: more than 40 T and 65 T, respectively. It is probable that both of the field-induced superconducting phases are stabilized by ferromagnetic fluctuations that are induced when the magnetic field is applied perpendicular to the preferred direction of the electron spins. The high-field superconducting phase exists exclusively in a magnetic field-polarized state, unique among these superconductors. This discovery provides an excellent platform to study the relationship between ferromagnetic fluctuations, spin-triplet superconducting pairing and dimensionality in the quantum limit.

Fig. 1 |. Magnetic field-induced superconducting and polarized phases of uTe2.

Fig. 1 |

Open in a new tab

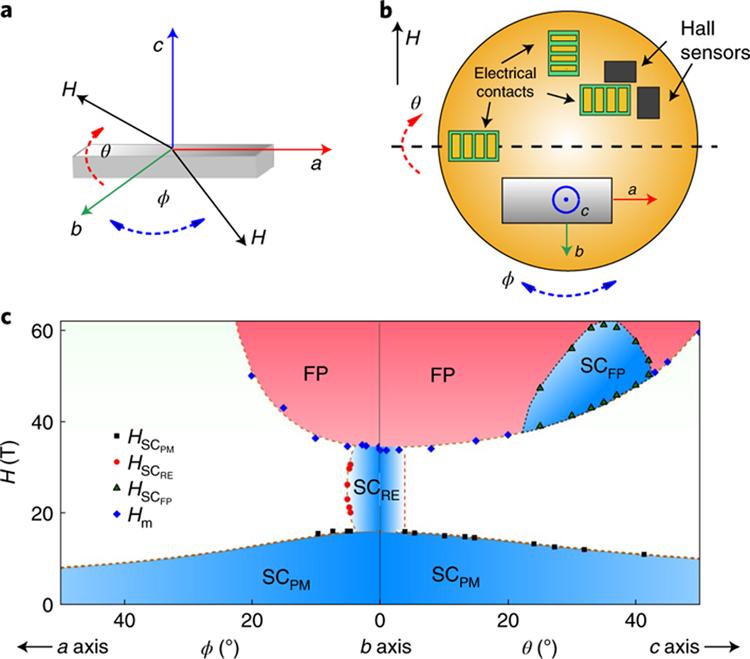
a, Sketch of how the magnetic field is applied with respect to the three crystallographic axes of UTe2. b, Top view of the sample platform with a two-axis rotator used in d.c. field measurements to achieve the best alignment. c, Magnetic field–angle phase diagram showing the three superconducting phases SCPM, SCRE and SCFP. FP is the field-polarized phase. The magnetic field is rotated within the a–b and b–c planes. The critical field values of the SCPM and SCRE phases are based on d.c. field measurements, and those of the SCFP and FP phases are based on pulsed field measurements. The SCRE phase was not observed for angles of θ larger than 3.9° in the b–c plane (Supplementary Fig. 1). The dashed lines are guides to the eye.

UTe2 crystallizes in an anisotropic orthorhombic structure, with the a axis the magnetic easy axis along which spins prefer to align in low magnetic fields. Hc2 is strongly direction-dependent and exceedingly large along the b axis, with an unusual increase in its temperature dependence above 15 T. Hc2 is extraordinarily sensitive to the alignment of the magnetic field along the b axis12, and accurate measurements require the use of a specialized two-axis rotator (Fig. 1b). When the magnetic field is perfectly aligned along the b axis, superconductivity persists up to 34.5 T at 0.35 K (Fig. 2a). A small misalignment of less than 5° from the b axis towards the a axis decreases the Hc2 value by over half, to 15.8 T. However, even this misaligned superconductivity is resilient: when the magnetic field is further increased, superconductivity reappears between 21 T and 30 T. Our measurements show that this re-entrant phase, SCRE, does not persist beyond misalignment greater than 7°. When the field is rotated towards the c axis, SCRE does not persist beyond 3.9° (Supplementary Fig. 1). Future measurements will determine whether this phase boundary exhibits similar curvature.

Fig. 2 |. Re-entrance of superconductivity in uTe2.

Fig. 2 |

Open in a new tab

a, Field dependence of R in UTe2 at T = 0.35 K measured in the d.c. field. The magnetic field is rotated from the b axis towards the a axis. Zero resistance persists up to 34.5 T when the magnetic field is perfectly along the b axis. The same dataset is plotted on a logarithmic scale in the inset. Re-entrance of superconductivity can be clearly seen when the magnetic field is applied slightly off the b axis. b, Magnetoresistance R and f of the PDO circuit (see Methods for technical details) in UTe2 at T = 0.45 K in the pulsed field, with the magnetic field applied along the b axis. c, Magnetization measurements of UTe2 at T = 0.46 K and 1.69 K in the pulsed field, with the magnetic field applied along the b axis. The two-axis rotator is not compatible with measurements in the pulsed field. There is probably a slight angle offset along the perpendicular direction. SCRE is not observed in these measurements. f.u., formula unit.

Although UTe2 is closely related to the ferromagnetic triplet superconductors6, the observation of re-entrant superconductivity in UTe2 resembles neither that of URhGe (refs. 10,11), which is completely separated from the low-field portion, nor the sharp Hc2 cusp in angle dependence13 in UCoGe. The angle dependence of the superconducting phase boundary suggests that SCRE may have a distinct order parameter from the lower-field superconductivity, SCPM. However, unlike the case for both URhGe (refs. 11,14) and UCoGe (refs. 13,15), there is no normal-state change in the underlying magnetic order in UTe2 that would drive a change in the superconducting order parameter symmetry. We discuss the magnetic interactions that stabilize this unusual behaviour after an excursion to an even higher field.

The upper-field limit of SCRE of 35 T coincides with a dramatic magnetic transition into a field-polarized phase (Fig. 2c). The magnetic moment along the b axis jumps from 0.35 to 0.65 μB discontinuously, due to a spin rotation from the easy a axis to the orthogonal b axis. The abrupt change in moment direction is accompanied by a jump in magnetoresistance R and a sudden change of frequency f in the proximity detector oscillator (PDO) circuit (Fig. 2b). The critical field Hm of this magnetic transition has little temperature dependence up to 10 K, but Hm increases as the magnetic field rotates away from the b axis to either the a or c axis (Fig. 1c). Meanwhile, the magnitude of the jump in magnetic moment, 0.3 μB, seems to be direction-independent (Supplementary Fig. 5). This magnetic field scale seems to represent a general energy scale for correlated uranium compounds: weak anomalies are observed in the ferromagnetic superconductor UCoGe (ref. 16), whereas a large magnetization jump occurs in the hidden-order compound URu2Si2 (ref. 17).

As Hm limits the SCRE phase, it gives rise to an even more startling form of superconductivity. Sweeping magnetic fields through the angular range of θ = 20–40° from the b axis towards the c axis reveals a superconducting phase inside the field-polarized state SCFP at high H (Fig. 3). The onset field of the SCFP phase precisely follows the angle dependence of Hm, while the upper critical field goes through a dome, with the maximum value exceeding 65 T, the maximum field possible in our measurements. This new superconducting phase largely exceeds the magnetic field range of all known field-induced superconductors3–5,10. Owing to its shared phase boundary with the magnetic transition, this superconducting phase tolerates a rather large angular range of offsets from the b–c rotation plane. However, it does not appear when the field is rotated from the b axis to the a axis.

Fig. 3 |. angle dependence of the field-induced superconducting and polarized phases of uTe2.

Fig. 3 |

Open in a new tab

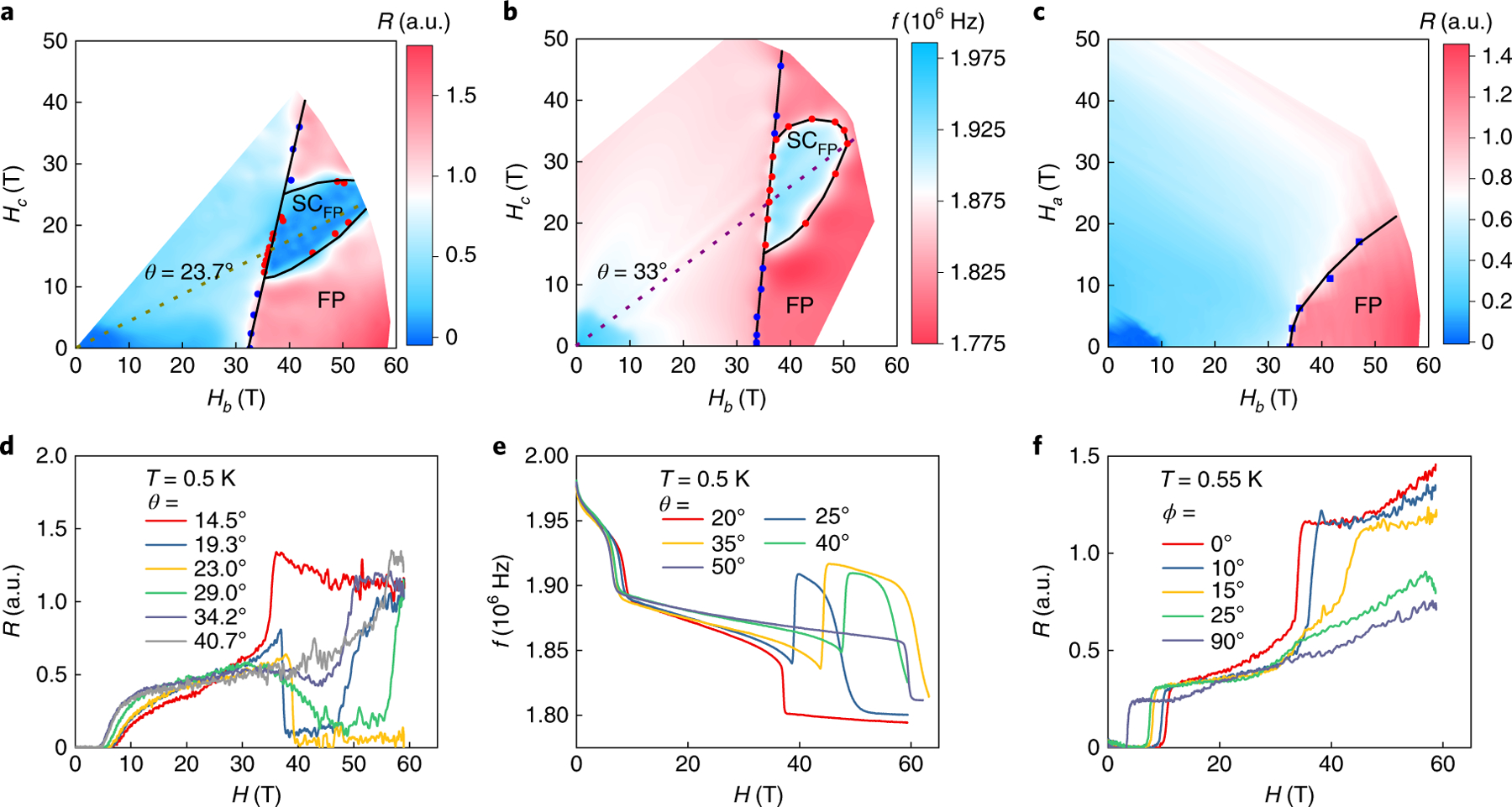
a–c, When the magnetic field is applied at an angle from the b axis towards the c axis (or a axis), it is equivalent to two applied magnetic fields: one along the b axis, Hb = Hcosθ or Hcosϕ, and the other along the c axis, Hc = Hsinθ (or along the a axis, Ha = Hsinϕ). Colour contour plots are shown for magnetoresistance R as a function of Hc and Hb (a), f of the PDO circuit as a function of Hc and Hb (b), and magnetoresistance R as a function of Ha and Hb (c). The blue dots are the critical fields for the field-polarized state and the red dots are the critical fields for SCFP. The dotted lines in a and b indicate the directions along which measurements were also performed at different temperatures, as shown in Fig. 4. d–f, The corresponding data as a function of the applied magnetic fields at selected angles.

Having established the field limits and angle dependence of the SCFP phase, we turn to its temperature stability (Fig. 4). The onset field has almost no temperature dependence, again following Hm, while the upper critical field of the SCFP phase disappears near 1.6 K, similar to the zero-field superconducting critical temperature. This suggests that although it is stabilized at a remarkably high field, the new superconducting phase involves a similar pairing energy scale to the zero-field superconductor.

Fig. 4 |. Temperature dependence of SCFP in uTe2.

Fig. 4 |

Open in a new tab

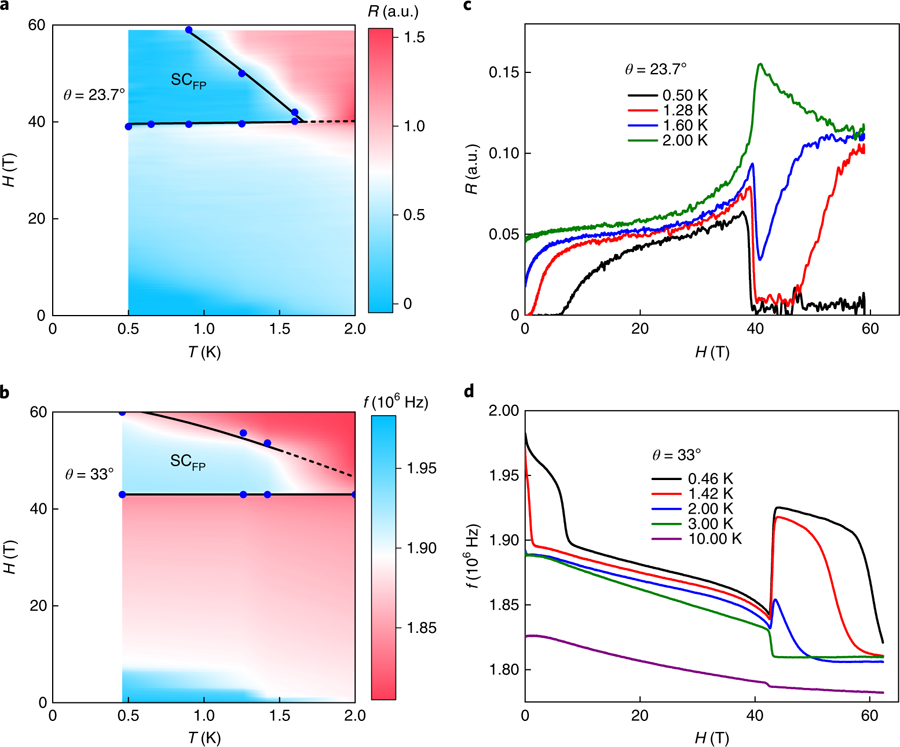
a,b, Colour contour plots of R (a) and f (b) of PDO measurements as a function of T and H at θ = 23.7° (a) and θ = 33° (b). The blue dots are the critical fields for SCFP and the dashed lines are guides to the eye, extrapolated to the region where there are no data. c,d, The corresponding data as a function of the applied magnetic fields at selected temperatures.

The mechanism responsible for the large magnetic field and temperature stability of the SCFP phase is unclear. A natural candidate is the Jaccarino–Peter effect used to describe other re-entrant superconductors9. This antiferromagnetic type of exchange interaction can lead to an internal magnetic field that is opposite the external magnetic field, resulting in a much smaller total magnetic field. This compensation mechanism has successfully explained the field-induced superconductivity in Chevrel-phase compounds and organic superconductors3–5, but it probably does not apply to the SCFP phase of UTe2, which lacks the requisite localized atomic moments. Furthermore, SCFP persists over a wider field–angle range than is typical of the compensation effect18.

The temperature dependence of the SCFP phase and its close relationship with the magnetic transition are reminiscent of the field-induced superconducting phase in URhGe, which has been attributed to ferromagnetic spin fluctuations associated with the competition of spin alignment between two weakly anisotropic axes. In URhGe, a magnetic field transverse to the direction of the ordered magnetic moments leads to the collapse of the Ising ferromagnetism; this instability enhances ferromagnetic fluctuations, which in turn induce superconductivity7.

UTe2, however, is not ferromagnetic. Nevertheless, the similarities between UTe2 and the ferromagnetic superconductors with regard to the relationship between the preferred magnetic axis and the direction of high Hc2 (ref. 6) suggest that strong spin fluctuations transverse to the preferred orientation or easy axis of the magnetic moment play a central role in these superconducting phases7. The Hc2 values and directionality in UTe2 can thus be understood in the following manner. Starting from zero magnetic field, superconductivity is most resilient to a magnetic field applied along the b axis, which is perpendicular to the easy magnetic a axis. A magnetic field applied along the b axis thus induces spin fluctuations that stabilize superconductivity against field-induced pair breaking. At 34.5 T, however, a magnetic phase transition occurs, and magnetic moments rotate from the a axis to the b axis. In the high-field-polarized phase, a magnetic field along the b axis no longer induces transverse spin fluctuations, and superconductivity is suppressed completely. However, it is possible to induce transverse spin fluctuations by applying a magnetic field along the c axis. When viewed as a vector sum of fields along the b and c axes (Fig. 3), it is clear that Hb stabilizes the magnetic phase, while a range of Hc strength values stabilize superconductivity with the highest re-entrant magnetic field values observed.

This ferromagnetic fluctuation scenario is qualitatively consistent with the wider picture of field-induced superconducting phases in UTe2, yet a very important distinction exists between the SCFP phase and the field-induced superconducting phase in URhGe: the SCFP phase exists only in the field-polarized state. This challenges the current theory proposed for URhGe, which allows superconductivity to exist on both sides of the phase boundary7,19,20.

Through the suppression of the orbital limit, reduced dimensionality has been theorized to stabilize high-field superconductivity21. A model proposed by Lebed and Sepper8 invoking spin-triplet pairing predicts re-entrant superconductivity at very high magnetic fields applied transverse to the axis of a quasi-one-dimensional conductor. The field-induced lower dimensionality is field–angle dependent and facilitates the recovery of the zero-field superconducting critical temperature, as we observe in SCFP (Figs. 3 and 4). The possibility that field-stabilizing effects may also exist in quasi-two-dimensional superconductors21 suggests that high-field dimensionality is a useful starting point for understanding the SCFP phase. Furthermore, the suppression of the orbital limit permits superconductivity in a pure material to survive in any magnetic field, making UTe2 an exciting basis for further testing of the limits of high-field-boosted superconductivity.

The existence of the SCFP phase in only the field-polarized state, and in such a high magnetic field, suggests that the superconducting state probably has odd parity with time-reversal symmetry breaking. Odd parity is the cornerstone of topological superconductivity22, and it is certain that the SCFP phase has non-trivial topology. Since time-reversal symmetry is also broken, a special topological superconducting state is highly likely, such as chiral superconductivity23, which hosts Majorana zero modes, the building blocks for topological quantum computing24,25.

Note added in proof: While our manuscript has been under review, we became aware of other independent reports of the field-polarized state26 and the lower-field re-entrant superconductivity27 in UTe2.

Methods

Single crystals of UTe2 were synthesized by the chemical vapour transport method using iodine as the transport agent. Crystal orientation was determined by Laue X-ray diffraction performed with a Photonic Science X-ray measurement system. Magnetoresistance measurements were performed at the National High Magnetic Field Laboratory (NHMFL), Tallahassee, using the 35 T d.c. magnet, and at NHMFL, Los Alamos, using the 65 T short-pulse magnet. PDO and magnetization measurements were performed at NHMFL, Los Alamos, using the 65 T short-pulse magnet.

To perfectly align the magnetic field along the b axis in the d.c. magnet, a single crystal of Ute2 was fixed to a home-made sample mount on top of an Attocube ANR31 piezo-actuated rotation platform (Fig. 1b). Thin copper wires were fixed between the probe and rotation platform, in order to measure the sample and two orthogonal Toshiba THS118 Hall sensors. All three measurements were performed using a conventional four-terminal transport set-up with Lake Shore Cryotronics 372 a.c. resistance bridges. Adjustments to θ were made using a low-friction apparatus28 to find the centre of the range, where the sample resistance was zero at H = 25.5 T. With a lower field of 0.5 T, small changes were then made to the ϕ orientation while monitoring the Hall sensors. With the field aligned near the b axis, the magnetic field was swept to 34.5 T.

The contactless conductivity was measured using the PDO circuit described in refs. 29,30 that has been used to study field-stabilized superconducting phases31. A coil comprising 6–8 turns of 46-gauge high-conductivity copper wire was wound about the single-crystal sample; the number of turns employed depends on the cross-sectional area of the sample, with a larger number of turns needed for smaller samples. The coil formed part of a PDO circuit resonating at 22–29 MHz. A change in the sample skin depth29 or differential susceptibility30 causes a change in the inductance of the coil, which in turn alters the resonant frequency of the circuit. The signal from the PDO circuit was mixed down to about 2 MHz using a double-heterodyne system29,30. Data were recorded at 20 million samples per second, well above the Nyquist limit. Two samples in individual coils coupled to independent PDOs were measured simultaneously using a single-axis, worm-driven, cryogenic goniometer to adjust their orientation in the field.

The pulsed field magnetization experiments used a 1.5-mm-bore, 1.5-mm-long, 1,500-turn compensated-coil susceptometer constructed from 50-gauge high-purity copper wire32. When a sample is within the coil, the signal is proportional to dM/dt, where M is magnetization and t is time. Numerical integration was used to evaluate M. The sample was mounted within an ampoule of 1.3 mm diameter that could be moved in and out of the coil. Accurate values of M were obtained by subtracting empty coil data from that measured under identical conditions with the sample present. These results were calibrated against results from the Quantum Design’s magnetic property measurement system.

Supplementary Material

Supp1

Acknowledgements

We acknowledge helpful discussions with A. Lebed and V. Yakovenko. W.T.F. is grateful for the support of the Schmidt Science Fellows programme in partnership with the Rhodes Trust. Research at the University of Maryland was supported by the US National Science Foundation Division of Materials Research Award No. DMR-1610349 (support for sample preparation), the US Department of Energy (DOE) Award No. DE-SC-0019154 (support for experimental measurements) and the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant No. GBMF4419 (support for materials synthesis). Work performed at NHMFL was supported by NSF Cooperative Agreement No. DMR-1644779, the State of Florida, DOE and through the DOE Basic Energy Sciences Field Work Project Science in 100 T. A portion of this work was supported by the NHMFL User Collaboration Grants Program. Identification of commercial equipment does not imply recommendation or endorsement by NIST.

Footnotes

Online content

Any methods, additional references, Nature Research reporting summaries, source data, statements of code and data availability and associated accession codes are available at https://doi.org/10.1038/s41567-019-0670-x.

Competing interests

The authors declare no competing interests.

Additional information

Supplementary information is available for this paper at https://doi.org/10.1038/s41567-019-0670-x.

Data availability

The data represented in Figs. 1–4 are available as source data in Supplementary Data 1–4. All other data that support the plots within this paper and other findings of this study are available from the corresponding authors on reasonable request.

References

  • 1.Stormer HL Nobel lecture: the fractional quantum Hall effect. Rev. Mod. Phys 71, 875–889 (1999). [Google Scholar]
  • 2.Zapf V, Jaime M & Batista CD Bose–Einstein condensation in quantum magnets. Rev. Mod. Phys 86, 563–614 (2014). [Google Scholar]
  • 3.Meul HW et al. Observation of magnetic-field-induced superconductivity. Phys. Rev. Lett 53, 497–500 (1984). [Google Scholar]
  • 4.Uji S et al. Magnetic-field-induced superconductivity in a two-dimensional organic conductor. Nature 410, 908–910 (2001). [DOI] [PubMed] [Google Scholar]
  • 5.Konoike T et al. Magnetic-field-induced superconductivity in the antiferromagnetic organic superconductor κ-(BETS)2FeBr4. Phys. Rev. B 70, 094514 (2004). [Google Scholar]
  • 6.Ran S et al. Nearly ferromagnetic spin-triplet superconductivity. Science 365, 684–687 (2019). [DOI] [PubMed] [Google Scholar]
  • 7.Mineev VP Reentrant superconductivity in URhGe. Phys. Rev. B 91, 014506 (2015). [Google Scholar]
  • 8.Lebed AG & Sepper O Quantum limit in a magnetic field for triplet superconductivity in a quasi-one-dimensional conductor. Phys. Rev. B 90, 024510 (2014). [Google Scholar]
  • 9.Jaccarino V & Peter M Ultra-high-field superconductivity. Phys. Rev. Lett 9, 290–292 (1962). [Google Scholar]
  • 10.Lévy F, Sheikin I, Grenier B & Huxley AD Magnetic field-induced superconductivity in the ferromagnet URhGe. Science 309, 1343–1346 (2005). [DOI] [PubMed] [Google Scholar]
  • 11.Lévy F, Sheikin I & Huxley A Acute enhancement of the upper critical field for superconductivity approaching a quantum critical point in URhGe. Nat. Phys 3, 460–463 (2007). [Google Scholar]
  • 12.Aoki D et al. Unconventional superconductivity in heavy fermion UTe2. J. Phys. Soc. Jpn 88, 043702 (2019). [Google Scholar]
  • 13.Aoki D et al. Extremely large and anisotropic upper critical field and the ferromagnetic instability in UCoGe. J. Phys. Soc. Jpn 78, 113709 (2009). [Google Scholar]
  • 14.Huxley AD, Yates SJC, Lévy F & Sheikin I Odd-parity superconductivity and the ferromagnetic quantum critical point. J. Phys. Soc. Jpn 76, 051011 (2007). [Google Scholar]
  • 15.Hattori T et al. Relationship between ferromagnetic criticality and the enhancement of superconductivity induced by transverse magnetic fields in UCoGe. J. Phys. Soc. Jpn 83, 073708 (2014). [Google Scholar]
  • 16.Knafo W et al. High-field moment polarization in the ferromagnetic superconductor UCoGe. Phys. Rev. B 86, 184416 (2012). [Google Scholar]
  • 17.De Boer FR et al. High-magnetic-field and high-pressure effects in monocrystalline URu2Si2. Phys. B+C 138, 1–6 (1986). [Google Scholar]
  • 18.Balicas L et al. Superconductivity in an organic insulator at very high magnetic fields. Phys. Rev. Lett 87, 067002 (2001). [DOI] [PubMed] [Google Scholar]
  • 19.Hattori K & Tsunetsugu H p-Wave superconductivity near a transverse saturation field. Phys. Rev. B 87, 064501 (2013). [Google Scholar]
  • 20.Sherkunov Y, Chubukov AV & Betouras JJ Effects of Lifshitz transitions in ferromagnetic superconductors: the case of URhGe. Phys. Rev. Lett 121, 097001 (2018). [DOI] [PubMed] [Google Scholar]
  • 21.Dupuis N & Montambaux G Superconductivity of quasi-one-dimensional conductors in a high magnetic field. Phys. Rev. B 49, 8993–9008 (1994). [DOI] [PubMed] [Google Scholar]
  • 22.Sato M & Ando Y Topological superconductors: a review. Rep. Prog. Phys 80, 076501 (2017). [DOI] [PubMed] [Google Scholar]
  • 23.Kallin C & Berlinsky J Chiral superconductors. Rep. Prog. Phys 79, 054502 (2016). [DOI] [PubMed] [Google Scholar]
  • 24.Sarma SD, Freedman M & Nayak C Majorana zero modes and topological quantum computation. npj Quant. Inf 1, 15001 (2015). [Google Scholar]
  • 25.Karzig T et al. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with Majorana zero modes. Phys. Rev. B 95, 235305 (2017). [Google Scholar]
  • 26.Miyake A et al. Metamagnetic transition in heavy fermion superconductor UTe2. J. Phys. Soc. Jpn 88, 063706 (2019). [Google Scholar]
  • 27.Knebel G et al. Field-reentrant superconductivity close to a metamagnetic transition in the heavy-fermion superconductor UTe2. J. Phys. Soc. Jpn 88, 063707 (2019). [Google Scholar]
  • 28.Palm EC & Murphy TP Very low friction rotator for use at low temperatures and high magnetic fields. Rev. Sci. Instrum 70, 237–239 (1999). [Google Scholar]
  • 29.Altarawneh MM, Mielke CH & Brooks JS Proximity detector circuits: an alternative to tunnel diode oscillators for contactless measurements in pulsed magnetic field environments. Rev. Sci. Instrum 80, 066104 (2009). [DOI] [PubMed] [Google Scholar]
  • 30.Ghannadzadeh S et al. Measurement of magnetic susceptibility in pulsed magnetic fields using a proximity detector oscillator. Rev. Sci. Instrum 82, 113902 (2011). [DOI] [PubMed] [Google Scholar]
  • 31.Singleton J et al. Observation of the Fulde–Ferrell–Larkin–Ovchinnikov state in the quasi-two-dimensional organic superconductor κ–(BEDT–TTF)2Cu(NCS)2. J. Phys. Condens. Matter 12, L641 (2000). [Google Scholar]
  • 32.Goddard PA et al. Experimentally determining the exchange parameters of quasi-two-dimensional Heisenberg magnets. New J. Phys 10, 083025 (2008). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supp1
NIHMS1670428-supplement-Supp1.pdf (1.4MB, pdf)

Data Availability Statement

The data represented in Figs. 1–4 are available as source data in Supplementary Data 1–4. All other data that support the plots within this paper and other findings of this study are available from the corresponding authors on reasonable request.

RESOURCES