CO₂ reduction on pure Cu produces only H₂ after subsurface O is depleted: Theory and experiment

Significance

Electrochemical reduction of CO₂ to fuels and valuable chemicals is a global imperative to address energy and climate challenges. Despite enormous efforts, there is not yet a commercial process. The best catalyst remains Cu metal, but a great deal of controversy revolves around the role of the presence of oxygen in the material. We combine theory and experiments to show that pure Cu without subsurface oxygen leads to no organic products. Thus, maintaining substantial oxygen at Cu surfaces is essential for long-term reduction of CO₂ to organics.

Abstract

We elucidate the role of subsurface oxygen on the production of C₂ products from CO₂ reduction over Cu electrocatalysts using the newly developed grand canonical potential kinetics density functional theory method, which predicts that the rate of C₂ production on pure Cu with no O is ∼500 times slower than H₂ evolution. In contrast, starting with Cu₂O, the rate of C₂ production is >5,000 times faster than pure Cu(111) and comparable to H₂ production. To validate these predictions experimentally, we combined time-dependent product detection with multiple characterization techniques to show that ethylene production decreases substantially with time and that a sufficiently prolonged reaction time (up to 20 h) leads only to H₂ evolution with ethylene production ∼1,000 times slower, in agreement with theory. This result shows that maintaining substantial subsurface oxygen is essential for long-term C₂ production with Cu catalysts.

Anthropogenic carbon emissions, particularly CO₂, are surging primarily because of global fossil fuel consumption, raising serious environmental concerns about global warming (1). Recycling CO₂ via electrochemical (EC) reduction of carbon dioxide (CO₂RR) to fuels and valuable chemicals using renewable energy could play an important role in global efforts to address current energy demand and climate challenges (2). CO₂ can be electrochemically reduced to C₁ products (CO, methane, and formic acid), C₂ products (ethylene, ethane, and ethanol), and C₃ products (n-propanol) (3, 4). The major challenge to make this process economically viable is to increase selectivity to generate higher-hydrocarbon products.

In this context, copper (Cu) remains the only single metal capable of producing significant amounts of higher hydrocarbons, such as C₂ products ethylene or ethanol. Indeed, many experiments report that oxide-derived Cu catalysts lead to higher activity for C₂ products (5–8). However, the role of oxygen in the Cu catalyst and the correlation with the underlying C₂ production mechanism remains a subject of considerable debate (4). We suggested earlier that the optimum catalyst is the partially reduced cuprous oxide (Cu₂O) surface in which surface and/or subsurface oxygen of Cu₂O are adjacent to a reduced Cu⁰ surface, termed MEOM for metal embedded in oxidized matrix (9). Density functional theory (DFT) calculations on model systems showed that MEOM leads to a barrier for CO₂ reduction to CO that is 0.22 eV lower than for pure Cu⁰ and to a barrier for CO dimerization (the first step toward C₂ products) that is 0.39 eV lower than for pure Cu⁰. This result suggests that C₂ production on the MEOM surface could be >5,000 times faster than for pure Cu⁰. Indeed, other groups have recently hypothesized that surface Cu⁺ and/or subsurface oxygen on Cu might play an essential role in promoting CO dimerization and ethylene production (10–14). However, others have argued that such surface or subsurface oxygen species cannot be important because many experiments show that surface oxygen is rapidly depleted under CO₂RR conditions (15, 16), and it is, rather, suggested that surface roughness plays an active role in bolstering ethylene selectivity (16, 17). Hence, fundamental understanding into the relationship between the presence of oxygen and the increased C₂ production activity on Cu catalyst can solve the existing debates.

Here, we combine theory and experiments to disentangle the contributions from both Cu that contains oxygen and fully reduced (or depleted) Cu⁰ to uncover the role of subsurface oxygen in promoting C–C coupling and consequently C₂ production on Cu catalysts. We predict that hydrogen evolution reaction (HER) on pure Cu(111) leads to a turnover frequency (TOF) = 0.32/s, in stark contrast to C₂ production, which we predict to have a TOF = 0.0006/s, which is ∼500 times slower than HER. Our time course experiments confirm these predictions, showing that, when continuing CO₂ reduction for times up to 20 h, the C₂ production rates decrease to a level of 1,600 and 680 times slower than HER on polycrystalline Cu and Cu₂O catalysts, respectively.

In contrast, starting with Cu₂O, we find that the reduction leads to a Cu⁰/Cu₂O structure, with a thin, disordered Cu⁰ surface on top of the Cu₂O substrate. We calculate that this structure leads to TOF = 3.95/s for C₂ production compared to TOF = 10.02/s for HER, which is 2.58 times faster. This result is consistent with our experiments, which find HER production to be 2.1 times higher than C₂ during the first 5 h. In addition, we predict that C₂ production on the Cu⁰/Cu₂O model is a factor of 5,000 times faster than that on pure Cu(111). Indeed, our experiments measured an initial partial current density of ethylene production on Cu₂O of 0.6 to ∼0.8 mA/cm², which becomes negligible after 20 h on fully depleted Cu (∼1/1,000 of the H₂ current).

These calculations of TOF as a function of applied potential (U) use our recently developed grand canonical potential kinetics (GCP-K) methodology that predicts the evolution of the reaction intermediates and transition states (TSs) in solvent to obtain the TOF as a function of U (18). In this approach, the solvated structures and energetics of the intermediates adjust adiabatically as the U is changed, leading to very accurate rates versus U. Here, we apply GCP-K to directly assess the impact of subsurface oxygen on the C₂ production over Cu catalysts. Many theoretical studies have been reported on the product distribution during CO₂RR, but nearly all were carried out for fixed charge, usually zero. None have previously considered optimizing structure and kinetic activation energies as a function of U (19–23). In this study, we consider all thermodynamically stable structures of Cu₂O using GCP-K DFT calculations at U = −1 V_RHE with pH 7, common experimental conditions for examining the activity of Cu-based catalysts in CO₂RR (6, 17). Here, the U is U = −1 V on the reversible hydrogen electrode (RHE) scale. The GCP-K formulation allows the geometries to relax as U is changed so that the microkinetics allows all structures (equilibrium states and saddle points for TSs) to remain optimum for each U. This development enables us to track the free energy continuously with U at a computational cost close to conventional canonical DFT calculations (see SI Appendix for further details of GCP-K method, SI Appendix, Figs. S1 and S2).

First, we performed GCP-K calculations to construct the surface Pourbaix diagram shown in Fig. 1A. Starting from intact Cu₂O(111), we gradually reduced the surface by removing various numbers of oxygen and plotted the free energies of eight states (SI Appendix, Fig. S3 and Table S1), as a function of U. The results show that the disordered Cu⁰/Cu₂O surface is more stable at −1 V_RHE than the MEOM and Cu₂O models. Therefore, we considered the Cu⁰/Cu₂O model as the structure for Cu₂O at −1 V_RHE. We assume for the pure Cu with no O that the catalyst relaxes back to Cu(111) (SI Appendix, Fig. S4), using this as the model for fully depleted Cu₂O or Cu. We consider the MEOM surface for comparison in SI Appendix. We predicted the free energy barriers for HER and for CO dimerization (the dominant step in C₂ formation) for these models.

Fig. 1.

GPC-K DFT calculations for different Cu phases and their relation to C₂ production. Surface free energies as a function of U of various surface phases with different numbers of reduced lattice oxygen potential energy surfaces for the CO dimerization (A), the RDS for C₂ production (B), and the RDS for HER at U = −1 V_RHE and pH 7 on Cu(111), MEOM, and Cu⁰/Cu₂O (C). The RDS are the Heyrovsky step [H_ad+H₂O(l) + e⁻ → H₂(g) +OH⁻(aq)] for Cu(111) and MEOM and the Volmer step [H₂O(l) + e⁻ → H_ad+ OH⁻(aq)] for Cu⁰/Cu₂O. OCCO* geometries on Cu(111) (D), OCCO* geometries on MEOM (E), and OCCO* geometries on Cu⁰/Cu₂O catalysts (F). The Us for each state correspond to −1.25 V_RHE, −1.15 V_RHE, and −1.02 V_RHE, respectively. The C–C bond distances are indicated for all catalysts, and Cu–O bond distance is also indicated for Cu⁰/Cu₂O catalysts.

Our previous full solvent quantum mechanics molecular dynamics studies showed that C–C coupling of two surface CO is the rate determining step (RDS) for producing C₂ products (24). We predict that the ΔG† = 0.72 eV for C–C coupling on the disordered Cu⁰/Cu₂O surface (Fig. 1B) led to TOF = 3.95/s, which is 5,840 times faster than our predicted to 6.77 × 10⁻⁴/s for oxygen depleted Cu(111) surface, which has a barrier of ΔG† = 0.94 eV [close to our previous results (9)]. This enhancement of C–C coupling on Cu⁰/Cu₂O is attributed to its capability of forming a (OCC)O–Cu bond, which greatly stabilizes OCCO*, as shown in Fig. 1F and SI Appendix, Fig. S3.

For HER, we considered the following:

• •Volmer [H₂O(l) + e⁻ → H_ad+OH⁻(aq)] step and
• •Heyrovsky [H_ad+H₂O(l) + e⁻ → H₂(g) +OH⁻(aq)] step.

Fig. 1C examines both steps on Cu(111) as a function of U.

On Cu(111) at U = −1 V_RHE, the RDS for the HER is Heyrovsky, which leads to ΔG† = 0.79 eV (0.16 eV lower than for C–C coupling) and to TOF = 0.32/s.

For Cu⁰/Cu₂O at U = −1 V_RHE, we find the RDS for the HER to be the Volmer reaction with ΔG† = 0.70 eV, only −0.02 eV lower than C–C coupling.

Thus, the C₂ production rate is predicted to be comparable to HER rate on Cu⁰/Cu₂O (0.39 times slower). Whereas on fully depleted Cu(111), the predicted rate for H₂ production is 479 times higher than C₂ production. The predicted ratio of the rate for H₂ production on Cu⁰/Cu₂O versus fully depleted Cu(111) is 3.14 × 10¹. All atomic configurations for catalytic reactions are shown in SI Appendix, Figs. S6–S8.

To validate experimentally the above predictions from theory, we synthesized Cu-based catalysts through EC deposition of Cu₂O on polycrystalline Cu. Compared to the planar surface of polycrystalline Cu, our synthesized Cu₂O samples exhibit polycrystalline grains with a 1-µm thickness (SI Appendix, Fig. S9), which we refer to as thick Cu₂O.

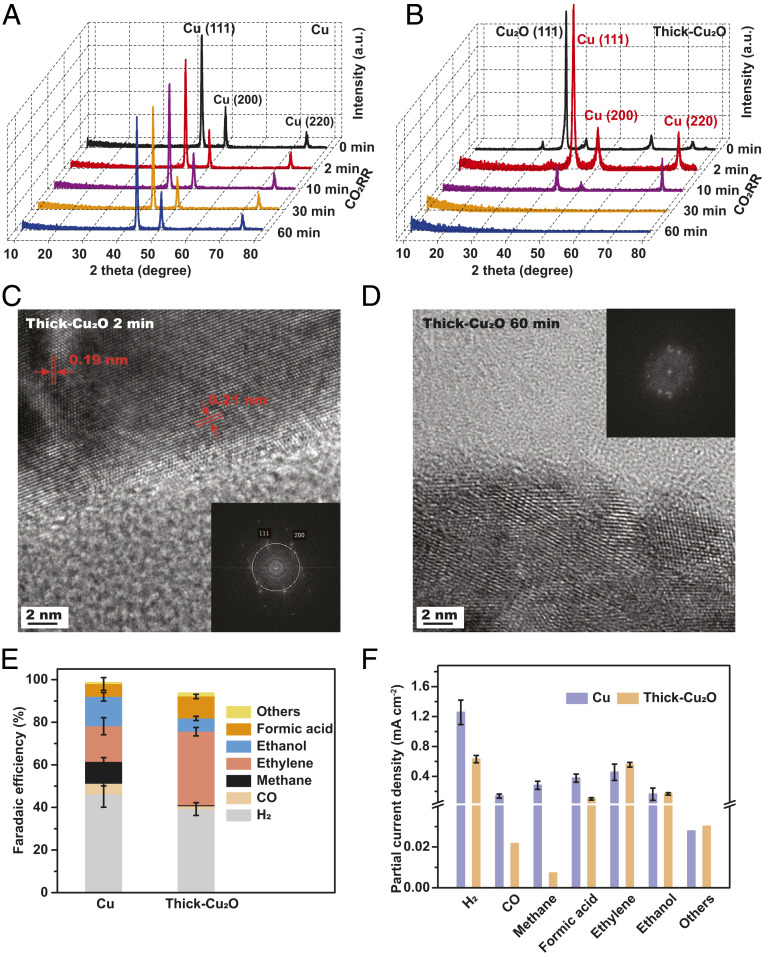
Under bulk electrolysis at −1 V_RHE with CO₂-saturated 0.1 M K₂CO₃ electrolyte for 65 min, the crystalline structures of polycrystalline Cu featuring Cu(111) are retained, as shown in ex situ grazing incidence X-ray diffraction (GIXRD) analysis (Fig. 2A)

Fig. 2.

Stable phases and catalytic activities of polycrystalline Cu and thick Cu₂O under CO₂RR. Ex situ GIXRD analysis of polycrystalline Cu (A) and thick Cu₂O (B) after 0 (as-prepared), 2, 10, 30, and 60 min CO₂RR at −1 V_RHE in 0.1 M CO₂-saturated K₂CO₃ electrolyte (pH 7). High-resolution transmission electron microscopy images of thick Cu₂O under CO₂RR for 2 min (C) with corresponding fast Fourier transform (Inset) and 1 h (D) with corresponding fast Fourier transform (Inset); fragmented Cu-based nanoparticles with lower crystallinity were observed over 1 h CO₂RR. (E) FEs of CO₂RR toward H₂ (gray), CO (gold), methane (black), ethylene (pink), ethanol (blue), formic acid (orange), and others: acetate, ethylene glycol, and 1-propanol (yellow) for Cu and thick Cu₂O at −1 V_RHE. (F) Partial current densities toward H₂, CO, methane, formic acid, ethylene, ethanol, and others: allyl alcohol; n-propanol, normalized by electrochemically active surface area over Cu (purple); and thick Cu₂O (orange) for 1 h CO₂RR at −1 V_RHE in CO₂-saturated 0.1 M K₂CO₃ electrolyte (pH 7). Average values in E and F are based on triplicates, and the errors correspond to the SEM of data points from individual samples in SI Appendix, Table S3.

On the other hand, thick Cu₂O is reduced to Cu⁰ because of removal of lattice oxygen under CO₂RR, leading to disordered Cu⁰ surface over time, as demonstrated by ex situ GIXRD (Fig. 2B). Complementary high-resolution transmission electron microscopy confirms that the surface of thick Cu₂O is readily reduced to crystalline Cu⁰ after 2 min of CO₂RR (Fig. 2C). Then, this crystalline surface evolves into fragmented and disordered Cu-based nanoparticles over 60 min CO₂RR (Fig. 2D), in excellent agreement with GIXRD results. Control experiments further revealed that thick Cu₂O became crystalline Cu⁰ under N₂ saturation at −1 V_RHE and at less negative potentials (−0.6 V_RHE and −0.3 V_RHE) under CO₂RR for 1 h (SI Appendix, Fig. S10). Thus, these experimental observations verify that the theoretically predicted Cu(111) and disordered Cu⁰/Cu₂O model are indeed the thermodynamically stable structure for polycrystalline Cu and thick Cu₂O under CO₂RR at −1 V_RHE.

The initial catalytic activity and selectivity of polycrystalline Cu and thick Cu₂O catalysts toward CO₂RR were examined over 1 h by gas chromatography and high-performance liquid chromatography in a two-compartment flow cell (SI Appendix, Fig. S11). Compared to polycrystalline Cu, we find that using thick Cu₂O catalysts leads to lower selectivity of H₂ evolution, while selectivity toward C₂ (ethylene and ethanol) products over C₁ (CO, methane, and formic acid) products is higher (Fig. 2E), in agreement with previous reports (25, 26). In particular, the C₂/C₁ ratio reaches a value of 5.9 on thick Cu₂O, while that for polycrystalline Cu is only 0.8, based on the faradaic efficiencies (FEs) in Fig. 2E. In addition to FE, to understand the intrinsic activity toward each product, we further plotted partial current density, normalized by electrochemically active surface area, for polycrystalline Cu and thick Cu₂O catalysts in Fig. 2F. These data highlight that the enhanced C₂/C₁ ratio on thick Cu₂O mainly stems from suppression of C₁ products, while similar rates of C₂ (ethylene and ethanol) products were observed on polycrystalline Cu and thick Cu₂O catalysts during the first hour of measurements. Previous studies have shown that the activity and selectivity of C₂ production on Cu are strongly dependent on the surface morphology and chemical composition (14, 17, 27).

To assess the role of surface morphology on Cu and thick Cu₂O catalysts under operating conditions, we employed quasi–in situ EC atomic force microscopy (Fig. 3). Compared to as-prepared polycrystalline Cu (0 min), no dramatic topography change was observed on Cu under CO₂RR with a constant R_a (∼2 nm) (Fig. 3 A–C). On the other hand, EC fragmentation occurred on the thick Cu₂O catalysts along with nanoparticles formation on Cu₂O grains during the first 1 min of EC measurements (Fig. 3 D and E). Afterward, the changes in topography remain small on thick Cu₂O (Fig. 3 E and F), leading to constant R_a (∼21 nm), which is 10 times of that of polycrystalline Cu. The sharp discrepancy in surface topography and roughness of polycrystalline Cu and thick Cu₂O rules out the possibility that surface topography or roughness play a predominant role in the similar C₂ production rate on polycrystalline Cu and thick Cu₂O.

Fig. 3.

Monitoring surface topography or roughness over Cu and thick Cu₂O under CO₂RR. Quasi–in situ EC-AFM images of polycrystalline Cu at 0 min (as-prepared) (A), 1 min (B), and 5 min (C) and thick Cu₂O at 0 min (as-prepared) (D), 1 min (E), and 5 min (F) in 0.1 M CO₂-saturated K₂CO₃ electrolyte (pH 7) at −0.8 V_RHE.

As a result, we argue that a similar initial chemical composition in polycrystalline Cu and thick Cu₂O is key to achieve the similar activity of ethylene production, as supported by the results during the first hour of activity of Cu and thick Cu₂O samples (Fig. 2). Specifically, X-ray photoelectron spectroscopy (XPS) reveals that polycrystalline Cu initially possesses native oxide surface layers (SI Appendix, Fig. S12), as it is well known that Cu is readily oxidized in air (16). The coexistence of native surface oxygen and Cu⁰ substrate makes the polycrystalline Cu surface similar to a very thin MEOM structure. Meanwhile, the disordered Cu⁰ character was naturally formed on thick Cu₂O under CO₂RR, as shown in Fig. 2 B–D. Thus, similar rates for C₂ products obtained on polycrystalline Cu and Cu₂O during 1 h CO₂RR can be interpreted by taking into account that MEOM structure of polycrystalline Cu and the disordered Cu⁰ character of thick Cu₂O share a similar kinetic barrier for C–C coupling, as mentioned earlier. However, as native oxygen on polycrystalline Cu is depleted under CO₂RR at −1 V_RHE, the population of the thin MEOM structure will decrease rapidly over time. In addition, theoretical calculations suggest that disordered Cu⁰ surface in thick Cu₂O would ultimately stabilize to crystalline Cu⁰ after oxygen is fully depleted. In this context, we consider that the long-term CO₂RR selectivity and activity toward ethylene on polycrystalline Cu and Cu₂O catalysts should be time dependent, which is associated with oxygen depletion. As residual oxygen is removed completely and disordered, Cu⁰ transforms to pure crystalline Cu⁰, leading to H₂ as the dominant product, in excellent agreement with the predictions by the DFT calculations.

To validate this hypothesis, we further synthesized a thin Cu₂O with 0.2-µm thickness (SI Appendix, Fig. S13) to compare with the results for thick Cu₂O. We proceeded to carry out long-term measurements (15 to 25 h) of product distributions on polycrystalline Cu, thin Cu₂O, and thick Cu₂O at −1 V_RHE with CO₂-saturated 0.1 M K₂CO₃ electrolyte. We monitored hourly gaseous ethylene and H₂ producing rates over time (Fig. 4), as well as the corresponding full products detection over the measured time (SI Appendix, Figs. S14 and S15). The total FEs are close to 100% for all samples.

Fig. 4.

Long-term CO₂RR measurements on polycrystalline Cu, thin Cu₂O, and thick Cu₂O. (A) FE of polycrystalline Cu; (B) partial current densities of polycrystalline Cu toward H₂, methane, and ethylene, normalized by electrochemically active surface area (ECSA); (C) FE of thin Cu₂O; (D) partial current densities of thin Cu₂O, toward H₂, methane, and ethylene, normalized by ECSA; (E) FE of thick Cu₂O; (F) partial current densities of thick Cu₂O, toward H₂, methane, and ethylene, normalized by ECSA at −1.0 V_RHE in CO₂-saturated 0.1 M K₂CO₃ electrolyte (pH 7) for CO₂RR over time. (G) FE of Cu, thin Cu₂O, and thick Cu₂O at −1.0 V_RHE in CO₂-saturated 0.1 M K₂CO₃ electrolyte (pH 7) after 1 h CO₂RR, 16 h CO₂RR, and Cu, thin Cu₂O and thick Cu₂O experienced 16 h CO₂RR, followed by a regeneration process: allowing the above catalysts to sit in air for about 2 wk.

As expected, selectivity and production rate of ethylene rapidly decayed on polycrystalline Cu catalyst within 1 h because of the depletion of native oxygen, while the HER rates increase with time. Furthermore, we employed a suit of characterizations including cyclic voltammetry, inductively coupled plasma mass spectrometry, and XPS analysis to exclude the role of surface texturing and metal ion contamination in determining the selectivity switch from ethylene to H₂ on polycrystalline Cu (SI Appendix, Figs. S16 and S17 and Table S4).

By contrast, the selectivity and production rate of ethylene on thin Cu₂O and thick Cu₂O slightly increased over the first 4 h, followed by a slow decay over time. Ultimately, C₂ production goes eventually to a level 1,600 times smaller than HER for polycrystalline Cu and 680 times lower for Cu₂O catalysts, in excellent agreement with theory predictions. In particular, for all cases, ethylene production finally became negligible with sufficient time: ∼4 h for polycrystalline Cu, ∼15 h for thin Cu₂O, and ∼20 h for thick Cu₂O.

Moreover, we demonstrated that after 16 h CO₂RR, polycrystalline Cu, thin Cu₂O, and thick Cu₂O catalysts were all able to recover their initial selectivity toward ethylene production: 92, 77, and 78% of their initial activity, respectively (Fig. 4G). This result was obtained by simply allowing the samples to regain a native oxide layer via reoxidization in the air.

Taking these results together, we conclude that the activity and selectivity of polycrystalline Cu and Cu₂O catalysts toward ethylene are influenced dramatically by the oxygen content within the Cu-based catalysts.

This interpretation was further corroborated by angle-resolved XPS (AR-XPS) analysis over as-prepared polycrystalline Cu, Cu after 1 h CO₂RR, and Cu after 16 h CO₂RR (SI Appendix, Figs. S18–S20). To minimize the oxidation of the sample in air, the sample was rinsed, dried with N₂ flow, and transferred to the vacuum chamber of XPS within 2 min after the CO₂RR measurements were completed. The O 1-s spectra show that lattice oxygen decreases with increasing takeoff angle on both as-prepared polycrystalline Cu and Cu after 1 h CO₂RR, indicating that subsurface lattice oxygen is present (28). In contrast, only surface-adsorbed OH/H₂O is observed on polycrystalline Cu after 16 h CO₂RR (SI Appendix, Fig. S18 and Table S5), which is consistent with Cu 2p and Cu Auger transition (Cu L₃M_4,5M_4,5, SI Appendix, Figs. S19 and S20).

It is important to note that in situ Raman measurements at −1 V_RHE indicate that the total reduction of thick Cu₂O was most likely completed in 1 h (SI Appendix, Fig. S21), which is shorter than the critical time for the selectivity switch from ethylene to H₂, observed in Fig. 4. By contrast, we find that the time scale of the relaxation of disordered Cu⁰ into crystalline Cu⁰ is much longer than that one of Cu₂O reduction, which agrees well with the time scale of the switch in selectivity (SI Appendix, Fig. S22). Thus, we propose that the lagging change on C₂ production, compared with Cu₂O reduction, is most likely due to the slow relaxation of disordered Cu⁰ into crystalline Cu⁰. While Raman spectroscopy measurements exclude the presence of an underlayer of (partially reduced) Cu₂O after 1 h, previous studies showed that disordered Cu⁰ can have more labile oxygen in the lattice during CO₂RR (6, 12). Moreover, Cuenya et al. suggested that the K⁺ cation in the electrolyte may be able to retain the removal of subsurface oxygen species under CO₂RR (29).

In addition, our theoretical calculations (SI Appendix, Fig. S4) find that the disordered Cu⁰ relaxes back to Cu(111) after oxygen is fully depleted. While the relationship between slow crystalline relaxation and residue oxygen requires further investigations, the comparison of AR-XPS analysis over as-prepared thick Cu₂O, thick Cu₂O after 1 h, and after 16 h CO₂RR (SI Appendix, Fig. S23 and Table S6) reveals that subsurface oxygen is observed on thick Cu₂O after 1 h CO₂RR but is absent after 16 h CO₂RR. This result implies that residual oxygen is retained in the lattice, even after Cu₂O was reduced.

These findings highlight the essential role of subsurface oxygen in C₂ production on Cu-based catalysts and how this role is related to inducing the formation of disordered Cu⁰. The disordered Cu⁰ structure represents the thermodynamically stable structure of Cu₂O-based catalysts under CO₂RR, which substantially enhances intrinsic C₂ production, compared to pure crystalline Cu⁰. This phase is achieved by dynamic transformation of Cu-based nanocrystals under CO₂RR conditions (6, 30).

While previous studies on subsurface oxygen on Cu demonstrate that subsurface oxygen may not play an essential role in CO₂ adsorption (31), Nilsson and coworkers show that subsurface oxygen on Cu is instrumental in enhancing CO adsorption, which can lead to an improved C₂ selectivity (32, 33).

We calculate C₂ and HER TOFs on various Cu-based models. These results demonstrate that the presence of residual oxygen is essential for retention and long-term stability of the disordered Cu⁰ surface that is active toward C₂ production. This finding can explain why disordered Cu-based catalysts and uncoordinated Cu sites at grain boundaries have higher selectivity for C₂ products (6, 8, 34). Thus, allowing the residual oxygen of Cu catalysts to be replenished from other robust oxides under CO₂RR might be a promising direction to design efficient CO₂RR catalysts with sustained C₂ selectivity. Additionally, the intrinsic ability of Cu to be rapidly oxidized in the air to regain its catalytic ability is beneficial to developing a sustainable/recyclable catalyst. For example, recent findings show that the continuous regeneration of defects and Cu⁺ species favors C–C coupling pathways (14).

In summary, we provide mechanistic insights into C₂ production over Cu-based catalysts by GCP-K DFT calculations, showing that for pure Cu(111) with no subsurface oxygen, the rate of C₂ production is ∼500 times smaller than HER, whereas reduced models starting with Cu₂O led to C₂ production ∼10,000 times faster. Furthermore, we combine time-dependent product detection with a correlative characterization approach to confirm that activity and selectivity of polycrystalline Cu and Cu₂O catalysts toward ethylene is determined by the disordered Cu⁰ character involving oxygen content within Cu-based catalysts. Compared to the MEOM structure, the formation of a disordered Cu⁰ surface induced by the removal of lattice oxygen from Cu₂O is thermodynamically favorable under CO₂RR. After long-term CO₂RR, pure crystalline Cu⁰ without subsurface oxygen leads only to HER at −1 V_RHE in aqueous solutions, in excellent agreement with the DFT calculations. Based on this theoretical and experimental understanding, we conclude that the key for the rational development of highly active electrocatalysts toward C₂ production is to modify the catalyst conditions in such a way as to preserve surface or subsurface oxygen in the Cu catalyst under CO₂RR conditions.

Materials and Methods

Electrodeposition of Cu₂O.

In a typical experiment, a 0.4 M Cu sulfate pentahydrate solution was used as the plating solution, prepared by stirring 4.99 g CuSO₄⋅5 H₂O in 50 mL MilliQ water. A total of 3 M (13.51 g) lactic acid was added to stabilize Cu²⁺ in basic solution, and then, 3 M NaOH was added to the solution until the pH of plating solution reached 12. Thick Cu₂O and thin Cu₂O were deposited on Cu foils (99.999%, Alfa Aesar) for 150 and 15 min, respectively, at a constant current density (−0.1 mA/cm²) in a three-electrode configuration under room temperature. To obtain a uniform coating, the Cu foil was mechanically polished with sandpapers (1,200 g Wetordry sandpaper, 3 M) and electropolished in 85% phosphoric acid at +2.1 V for 5 min, followed by annealing in air at 300 °C for 30 min prior to use. After the deposition, the sample was gently rinsed with MilliQ water and then dried with a nitrogen gun.

Product Detection.

EC experiments were conducted in a two-compartment flow cell fabricated from polyether ether ketone. A Selemion anion-exchange membrane separated the two chambers. A Pt foil was used as the counter electrode. A leak-free Ag/AgCl electrode (LF-1, 1-mm outer diameter, Innovative Instruments, Inc.) was used as the reference electrode.

Computational Details.

Our DFT calculations used the Vienna ab initio simulation package (VASP) (35, 36) with the VASPsol solvation model (37) for geometry optimization, followed by single-point calculations using the charge-asymmetric nonlocally determined local-electric solvation model (CANDLE) (38), as incorporated in the joint density-functional theory (JDFTx) (39).

The electron exchange and correlation were treated within the generalized gradient approximation (40) in the form of the Perdew–Burke–Ernzerhof functional, including the D3 correction for London Dispersion (van der Waals attraction) (41). The interaction between the ionic core and the valence electrons was described by the projector-augmented wave method (42). We used a plane-wave basis up to an energy cutoff of 500 eV. The Brillouin zone was sampled using the 3 × 3 × 1 Monkhorst–Pack grid (43). The convergence criteria for the electronic structure and the atomic geometry were 10⁻⁵ eV and 0.03 eV/Å for initial state (IS) and final state (FS) and 0.01 eV/Å for TS, respectively. We exploited the variational transition state (TS) theory package to search the TS using both climbing-image nudged elastic band method (44) and the dimer method for TS search (45).

The Gibbs free energies were calculated at 298 K and 1 atm as the following:

$$\text{G}=\text{H}-\text{T}\mathrm{\Delta }\text{S}=\hspace{1em}{E}_{DFT}+E_{ZPE}+E_{solv}+\underset{0}{\overset{298}{\int }}{C}_{v}dT-\text{T}\mathrm{\Delta }\text{S},$$

where $E_{DFT}$ is the total energy, $E_{ZPE}$ is zero-point vibrational energy, $E_{solv}$ is the solvation energy, $\underset{0}{\overset{298}{{\displaystyle \int }}}{C}_{v}dT$ is the enthalpy, and $∆\mathrm{S}$ is the change in entropy. The turnover frequency (TOF) of a reaction is given by

$$\mathrm{TOF}=\frac{k_B\mathrm{T}}{h}exp\left(-\frac{∆{\mathrm{G}}^{‡}}{k_B\mathrm{T}}\right)\left[/\mathrm{s}\right],$$

where k_B is the Boltzmann constant, T is the room temperature (298 K), h is the Plank’s constant, and ΔG^‡ is a free energy barrier.

The Cu(111) system was described by four layers of 4 × 4 supercell with two bottom layers fixed. Pristine Cu₂O and oxide-derived Cu were described by four trilayers of 4 × 4 supercell with two bottom trilayers fixed. The model system was described by three layers of 4 × 4 Cu slab with 20 Å of vacuum. The bottom two layers are fixed. All designed models have > 20 Å vacuum.

H₂ and C₂ Production on Cu MEOM Model.

In a previous study, we suggested that the MEOM model’s surface has adjacent-oxidized and metallic regions (9). On MEOM, we predict that C–C coupling has a kinetic barrier of 0.71 eV, which is 0.4 eV lower compared to that on Cu(111). We showed that the enhancement of C–C coupling on this catalyst is due to the attractive electrostatics, involving a carbon on the positively charge Cu⁺ induced by subsurface oxygen next to a C bound to a Cu⁰ site.

In our calculation on this MEOM catalyst using the GCP-K method, we find that C–C coupling has a kinetic barrier of ΔG^† = 0.72 eV, while the RDS for HER (the Heyrovsky reaction) has a barrier of ΔG^† = 1.02 eV. This leads to a C₂/H₂ ratio of 1.23 × 10⁶. Compared to Cu(111), C–C coupling is 7.03 × 10³ times faster, but HER is 1.19 × 10⁻⁴ times slower.

All configurations for IS, TS, and FS of C–C coupling and Volmer and Heyrovsky reactions are depicted in SI Appendix, Figs. S6–S8.

Data Availability

All study data are included in the article and/or SI Appendix.