Significance
For decades, the propulsion of sperms has been traditionally attributed to the beating or rotating of the soft tails. However, this work disclosed an unusual swimming model of Ray sperms whose propulsion is from not only the helical tail but also the unique spiral head (i.e., the head can contribute ∼31% of the force in propulsion). Such a propulsion mechanism provides Ray sperms with high adaptability to large environmental viscosities along with advantages in linearity, straightness, and efficiency. This study expands our knowledge on the microorganisms’ motion and provides inspirations for engineering design.
Keywords: dual-helical propulsion, highly environmental adaptability, bidirectional motion
Abstract
We disclose a peculiar rotational propulsion mechanism of Ray sperms enabled by its unusual heterogeneous dual helixes with a rigid spiral head and a soft tail, named Heterogeneous Dual Helixes (HDH) model for short. Different from the conventional beating propulsion of sperm, the propulsion of Ray sperms is from both the rotational motion of the soft helical tail and the rigid spiral head. Such heterogeneous dual helical propulsion style provides the Ray sperm with high adaptability in viscous solutions along with advantages in linearity, straightness, and bidirectional motion. This HDH model is further corroborated by a miniature swimming robot actuated via a rigid spiral head and a soft tail, which demonstrates similar superiorities over conventional ones in terms of adaptability and efficiency under the same power input. Such findings expand our knowledge on microorganisms’ motion, motivate further studies on natural fertilization, and inspire engineering designs.
Moving in an aquatic environment is an essential requirement for organisms and cells in waters and inside bodies. Over millions of years, organisms have developed unique body shapes to realize efficient propulsions in various environments, such as the flipper of ducks, the tail of fish, the soft body of snakes, and the flagella of bacteria and sperms (1–3). In 1951, a scientist revealed that swimming is highly size affected, and the underlying physical behaviors are significantly different and correspond to the ratio of inertial force and viscous force (4), represented by Reynolds number Re in physics. In recent decades, the soft tail of microorganisms, including bacteria and sperms, attracted great interest because its motion can break the symmetry of deformation in time at low Re, allowing these tiny organisms to swim efficiently. Nowadays, such findings have significantly inspired the design of miniature swimming robots, which has a wide range of applications from environmental to biomedical engineering (5, 6).
In the usual perception, sperms are thought to use the soft tail for swimming by rotating or beating (7–9), and the head is only a container of the genetic material. Some sperms of various species, such as cartilaginous fish (10–12), passerine birds (13–16), some amphibians (17–20), cephalodasys maximus (21), annelida (22), arthropoda (23), monotreme, and epiphanes senta, as reviewed by researchers (24, 25), have a distinctive spiral head. Apart from the morphology studies, some researchers also reported the spinning motion of sperms with spiral head (26–29), including their motility in viscous environments (30–32). Although some studies predicted the coupled relation between the rotational motion and forward motion (33–35), the specific role of the spiral head in the propulsion and the dual helical propulsive mechanism are still unclear. To reveal the role of the spiral head of sperm in propulsion, here, we disclosed an unusual swimming style of sperms, designated as Heterogeneous Dual Helixes (HDH) model, by accounting for the motions of sperms extracted from Javanese Cownose Ray (Rhinoptera javanica) and Black Spotted Ray (Taeniura meyeni) in solutions with various viscosities (36). We illustrate that the Ray sperm contains one soft tail and one rigid spiral head connected by the midpiece, and both the tail and head contribute to propulsion by rotating in the same direction. More interestingly, their contributions are adjustable and correspond to the motion and the liquid environment’s viscosity. Such heterogeneous helical propulsion not only provides Ray sperms high adaptability to a wide range of viscous environments but also leads to superior motion linearity, straightness, bidirectional motion ability, and efficiency. The advantages of this HDH model are also evidenced by designing a miniature swimming robot with a rigid spiral head and a soft helical tail, which demonstrated similar superiorities over conventional ones in terms of adaptability and efficiency under the same power input. These findings provide a perspective to expand our knowledge on the motion of microorganisms, to study natural fertilization, and to inspire engineering designs.
Results and Discussion
Heterogeneous Dual Helical Propulsion of Ray Sperms by a Spiral Head and a Soft Tail.
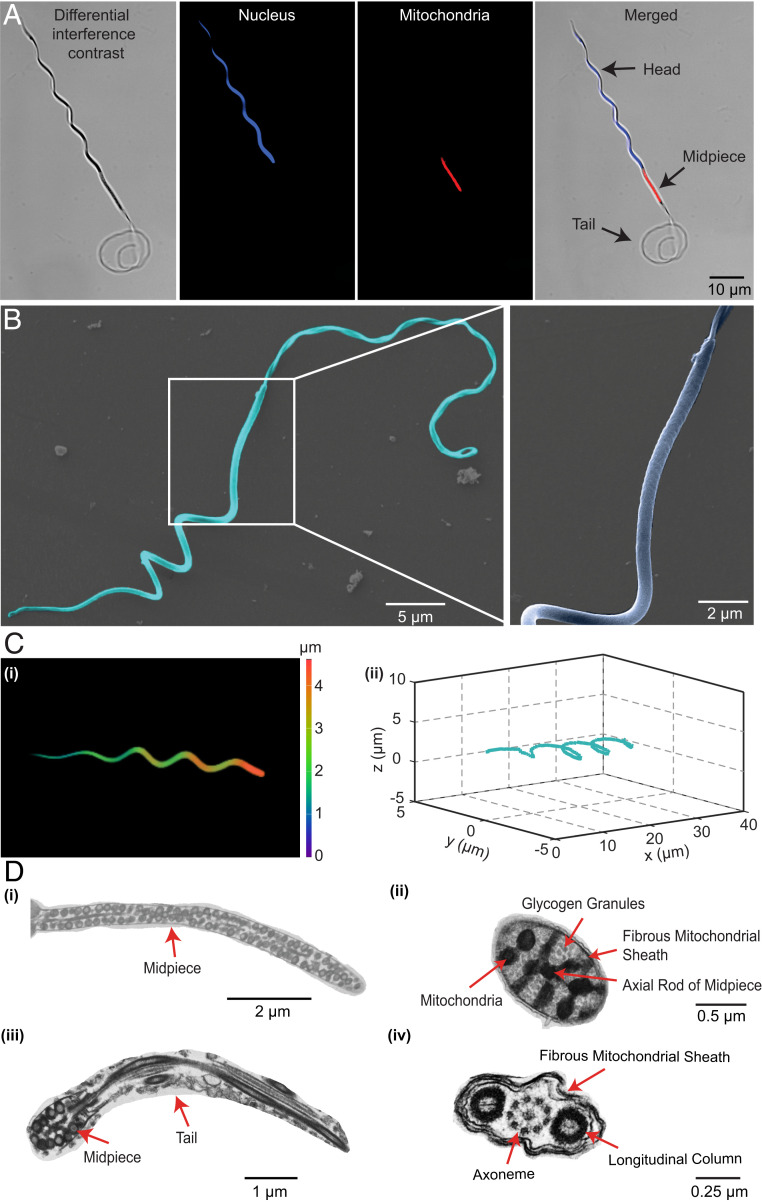
Different from conventional sperms with soft tails only, Ray sperms consist of heterogeneous helical sections, namely, a rigid spiral head and a soft tail, which are connected and actuated by a powered midpiece in the middle. Statistics suggest that the spiral head is 42.9 ± 2.3 μm long with four circles, and the soft tail is 62.6 ± 3.9 μm long with three helical cycles in swimming, while the midpiece is straight and 12.7 ± 1.0 μm long (Fig. 1A and SI Appendix, Fig. S1). The length ratio of the head:midpiece:tail is approximately 3.4:1:4.9, which is quite unique compared with sperms with (nearly) spherical or rod-shaped head (37–40) (SI Appendix, Table S2). To illustrate the structure of Ray sperms in detail, we further characterize them by scanning electron microscopy (SEM) and transmission electron microscopy (TEM). The SEM images (Fig. 1B) show that the head is naturally spiral, similar to that in the semen diluent (normal solution). On the contrary, the tail changes its form from a helical shape when in motion to a random curve in the relaxed state. Moreover, the regular projections of lumps on the midpiece reveal the existence of the mitochondria, which provide energy for sperm motion. The naturally spiral shape of the head of Ray sperms is further confirmed by confocal microscopy (Fig. 1 C, i and ii and SI Appendix, Fig. S2), suggesting that the head is composed of four cycles with the radius and half of the pitch ranges in [0.8, 3.3] μm and [6.5, 8.3] μm, respectively. Additionally, the ultrastructure of the sperm obtained by TEM (Fig. 1D and SI Appendix, Fig. S3) suggests that the head consists of multiple concentric layers with different densities and connects to the midpiece by the axial rod in the center. On the other hand, the tail consists of a “9+2” (doublet + singlet) microtubular axoneme with two longitudinal columns on the two sides. These differences between the head and tail in ultrastructure implies their differences in stiffness.
Fig. 1.
The morphology and ultrastructure of Ray sperms. Images of the Ray sperm observed under the fluorescence microscope (A), SEM (B), confocal microscope (C), and TEM (D). The nuclear DNA stained by Hoechst is blue, and the mitochondria stained by MitoTracker are red. Due to the difference in flexibility, the head exhibited helical shapes while the tail curved under microscopes. The lumps on the midpiece represent the mitochondria, which provide energy for the propulsion of sperms. The three-dimensional (3D) helical structure of the head is observed under the confocal microscope (C, i), and the 3D reconstruction of the head is shown in C, ii. The ultrastructure of the sperm is illustrated in D: longitudinal sections of the midpiece (D, i) and tail (D, iii), cross sections of the midpiece (D, ii), and tail (D, iv).
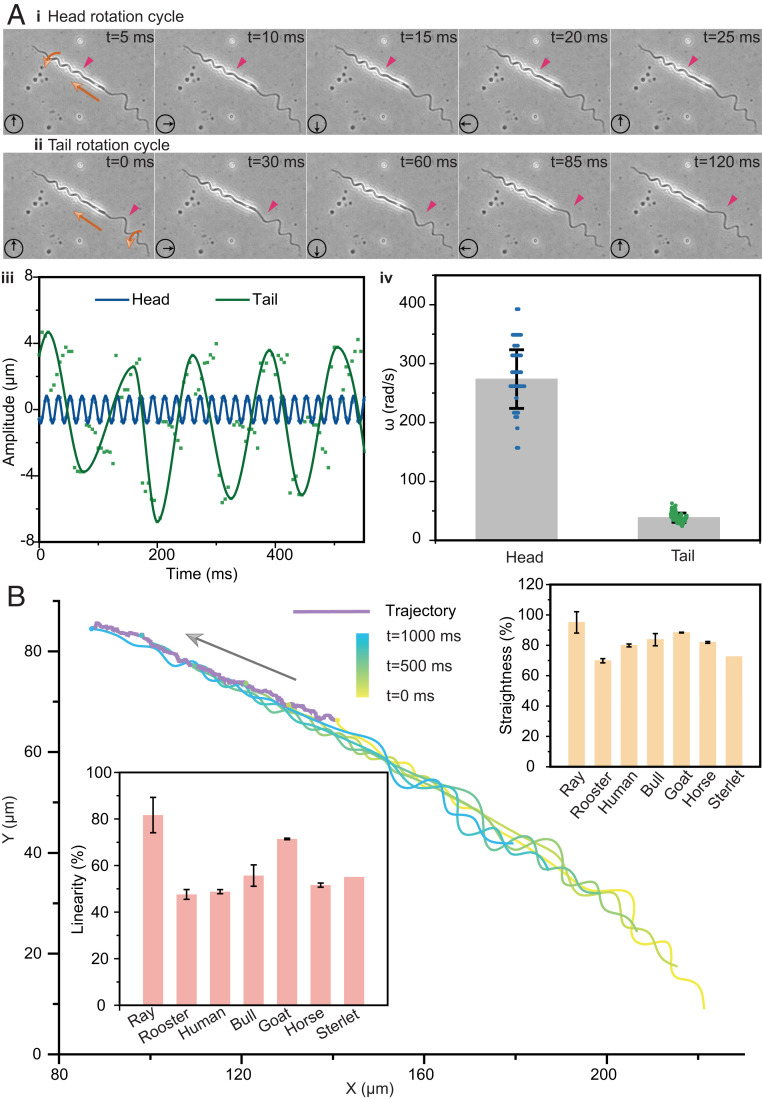
To elucidate the motion of Ray sperms, we track the shape and trajectory of sperms during swimming under the microscope. The results indicate that the rotational radius and half of the pitch of the rigid head change little during swimming (i.e., the coefficients of variation [SD/mean]) of and are less than 12.6% and 10.9% in each half-cycle, respectively. In contrast, the value of and of the tail is less than 43.24% and 21.98%, indicating that the soft tail always deforms in accordance with environmental changes (SI Appendix, Fig. S5). The motion of a representative sperm is shown in Fig. 2 A and B (Movie S2). Given the recorded first of head and tail in Fig. 2A, iii, the head rotates while keeping the spiral shape and the cyclically varied within 1 μm. Conversely, the first of tail irregularly changes with time, and the extreme values change from 3.7 μm to 6.8 μm, which might have been due to its soft specialty. The detailed rotational speeds of six half circles on the tail are shown in SI Appendix, Fig. S6, and the average speeds ranged from 49.1 rad/s to 51.3 rad/s, which are ∼16% of those of the head. A further statistics study based on 33 samples suggests that the mean of the head’s rotational speed is 273 rad/s, which is approximately six times greater than that of the tail, as shown in Fig. 2A, iv.
Fig. 2.
The motion of Ray sperms. The swimming motion of the Ray sperm in semen diluent (normal solution) is observed under the bright-field microscope shown in A and B. According to the images in A, i and ii and the rotational amplitude changes in A, iii, the rotating periods of head and tail were ∼20 ms and 120 ms, respectively. The average rotational speeds of the head and tail were 273.7 rad/s and 38.5 rad/s, respectively, from 33 samples shown in A, iv. Based on the recorded trajectory in B, their linearity and straightness were 81.6% and 95.1% (n = 29), respectively, which were obviously higher than those of the other six species. Bar = mean; error bar = SD.
Moreover, we find that the heterogeneous dual helical propulsion provides Ray sperms better directivity during swimming compared with sperms with helical or beating tails only. We record and draw the shape of sperms and the trajectory of their head tip and provide the data of a representative sperm in Fig. 2B and SI Appendix, Fig. S7. Although some fluctuations exist during the swimming, the real trajectory is nearly a straight line. The average linearity and straightness of Ray sperms’ motions are 81.6% and 95.1%, respectively, which are obviously higher than sperms from many other species (usually around 50% and 80%) (41–47), except for special cases of guppy and zebrafish with linearity over 92% (48, 49).
The Hydrodynamics of the Heterogeneous Dual Helical Propulsion Mechanism.
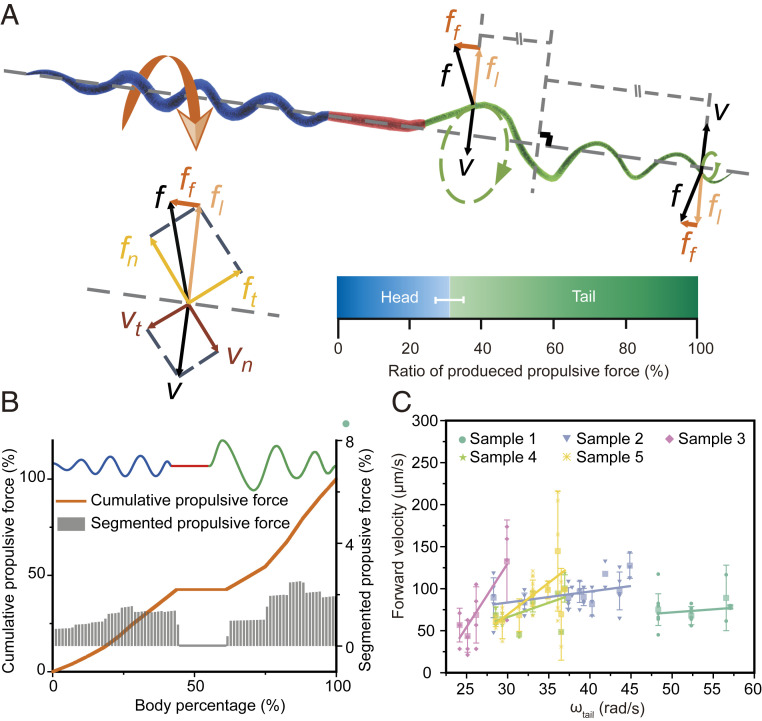
To elucidate the contribution of the head and tail to sperm’s swimming, we construct a model to analyze the sperm’s propulsion based on the resistive force theory (Fig. 3A) (50, 51). Taking into consideration the homogenous rotational speeds and ununiform helixes of the Ray sperm, we introduce the integration in the modeling to improve its generalization. For each rotating segment on the head or tail, its velocity is decomposed into two parts: the normal velocity and the tangential velocity . According to the resistive force theory, this segment sustains two kinds of forces, namely, normal stress and tangential resisting force , which are all linear to the velocity in the same direction with the coefficient of and , respectively. Then, the forward propulsive force is derived from , and is the pitch angle of that segment. The midpiece is modeled as a cylinder, whose structure just produces resisting force in propulsion. As such, the total propulsive force of the sperm can be calculated by the integral of along with the body.
Fig. 3.
Ray sperm propulsion. (A) Schematic diagram of the sperm propulsion. The net drag force , acting on each segment of both head and tail helixes, has a rotational component and the propulsive force , which drives the sperm forward. From 381 samples, the average propulsion contribution from the helical head accounted for 31% of the total body. Bar = mean; error bar = SD. The detailed results of the cumulative (orange) and segmented (gray) propulsive force along with one sperm body are shown in B. The gray bars represent the segmented propulsive force of every 100 segments on the sperm body. (C) Fitting relationship between the rotational speed of tail and the forward speed of the sperm (mean ± SD). The forward speed grew with increasing tail rotational speed and the slopes for the five samples were 0.73, 1.31, 15.17, 3.40, and 7.54, respectively.
Based on the above model and the recorded experimental shape and velocity data (SI Appendix, Figs. S8 and S9), we find that the spiral head contributed ∼31% to the total propulsion, which is a recorded head propulsion in all known sperms (7, 52). This ratio is consistent with the calculation result based on the regularized Stokeslet method (2, 53) (SI Appendix, Fig. S10). Such relatively high contribution comes from the fast rotational speed of the head (seven times of the tail), although the rotational radius is much smaller (20 to 50% of the tail). Furthermore, the relationship among the rotational speeds, forward speed, and the propulsive ratio of the head is statistically analyzed by regression and displayed in SI Appendix, Table S3. It suggests that the head can contribute 13.08% and 45.10% of the propulsive force when the rotational speed and the forward speed in extreme situations, respectively. To further illustrate the role and contribution of every part of the sperm to the propulsion, we calculate the propulsive force of each segment (gray bar) and compared it with the cumulative force (orange line) in Fig. 3B. It shows the cumulative propulsive force increases in both head and tail regions depending on the rotational radius and speeds but remains unchanged along the midpiece.
Similar to the propulsion of other sperms, the forward velocity of Ray sperm is also positively correlated to the rotational speed, although its propulsion comes from both the head and tail. The relationship between the forward velocity and the rotational speed of the tail for five samples is illustrated in Fig. 3C. The scattered points are the experimental measurements of the velocities, and the corresponding lines represent the fitted function between those two velocities based on the first-order linear fitting, and the significance test result is provided in SI Appendix, Tables S4 and S5. Although the slope of each line varies due to the differences among sperms, the swimming speed demonstrates a proportional relation with the tail’s rotational speed, which is in accordance with the proposed HDH model.
The HDH propulsion mechanism offers the Ray sperms high motion efficiency. From a biological perspective, the energy generated from the midpiece would transfer to both the head and tails for propulsion. However, for the normal sperm with a nearly spherical head, the propulsion only comes from the helical or beating motion of the tail, whereas the motion of the head makes no contribution to the propulsion. In comparison, the Ray sperms use both the head and tail for helical propulsion, demonstrating a higher efficiency in the use of biological energy. This could be evidenced by the ratio between the forward speed and rotational/beating frequency of the flagella in SI Appendix, Table S6. The highest propulsion distance per revolution stemming from the Ray sperm can reach 14.8 μm. For comparison, the sperms of Sterlet and Bull can only move 3.85 μm and 5.5 μm within one cycle, which are just 26% and 37% of the propulsion distance of the Ray sperm (54–57), thereby revealing the high energy efficiency of the HDH propulsion mechanism.
Bidirectional and Turning Motion Enabled by the Heterogeneous Dual Helical Propulsion.
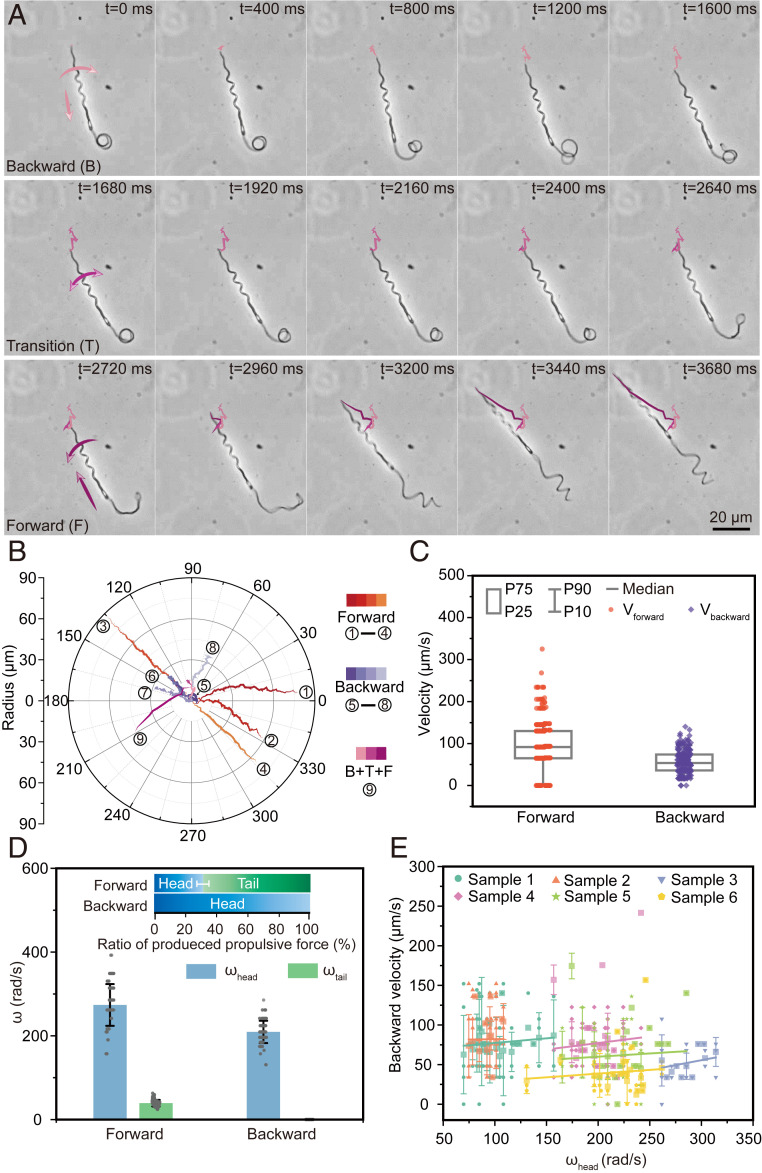
Unlike the motion of other sperms, we find that the unique heterogeneous dual helical structure of Ray sperms offers a unique bidirectional swimming ability. Such an ability could benefit sperms in nature, especially when they encounter obstacles (SI Appendix, Fig. S12 and Movie S3). As discussed above, the propulsive force is determined by the rotational speeds and directions of both head and tail (Fig. 3C). Hence, when the rotational direction changes, such as when the sperm rotates clockwise toward the direction of the head, the sign of the velocity will be negative, which means the produced propulsive force is consequently opposite and the sperm moves backward.
Here, we list three kinds of bidirectional motions of sperms, namely, only forward motion, both backward and forward motions, and only backward motion. The image sequences of a sperm in Fig. 4A (Movie S3) demonstrate a kind of swimming with the above three types of motions (i.e., moving backward, changing direction, and then moving forward). In the backward motion (0 to 1,600 ms), the rigid head holds the spiral shape, but the soft tail intertwines into a circle due to their differences in stiffness, which means the backward force is mainly produced by the head. To change the motion direction, the sperm rotates its body in a different direction. At the beginning of the direction changing process (1,680 to 2,640 ms), the location of the sperm almost has no change, but the sperm starts to shake, and the tail starts to unwrap. Quickly, the sperm moves forward (2,720 to 3,680 ms), and the tail’s shape recovers to a helical structure for propelling along with the head together. Specifically, when the sperm proceeds with the backward movement first (pink curves in Fig. 4B), the speed decreases seriously, and the swing is strongly enhanced due to the anomalous tail. However, when the sperm turns to forward direction, the tail can always recover to the regular helical structure again to maintain the speed and stability of the forward motion.
Fig. 4.
Bidirectional motion of the Ray sperm. (A) Images showing sequences of the Ray sperm swimming backward and forward. The sperm rotated right and moved backward in the first 1,600 ms with the tail twining as a circle. In the next 1,040 ms, the sperm transferred its status from back to forward. Then, the tail unwrapped and returned to the helical structure, which drove the sperm moving forward faster (2,720 to 3,680 ms). (B and C) Trajectories and corresponding moving velocities of forward (orange), backward (purple), and first backward then forward (pink) motions. Box: 25th to 75th percentiles, whisker: 10th to 90th percentiles, and horizontal line: median value. Since the tail twined as a circle in the backward motion and almost made no contribution to the propulsive force, backward motions were much slower than forward ones. (D) Rotational speed and propulsive force in forward and backward motions (n = 495). Bar = mean; error bar = SD. The rotational speeds of the head decreased by over 20% in backward motions compared with those in forward motions. The tail wraps on the head without active rotational motion, resulting in no contribution in propulsive force in backward motions. (E) Fitting relationships between the rotational speeds of head and backward speed. The backward speed (mean ± SD) was correlated with the rotational speed of heads linearly with a fitting slope of 0.117, 0.017, 0.248, 0.165, 0.082, and 0.093, respectively.
Further statistical analyses (Fig. 4 B and C and SI Appendix, Figs. S13–S15) show that the average forward speed (∼90.5 μm/s) is approximately twice of backward speed (∼56.0 μm/s), due to the action and inaction of the soft tail. In the backward motion, the rotational speed of the head drops by ∼23% compared with that in the forward motion (i.e., from 273 rad/s to 209 rad/s), whereas the tail totally wraps on the head with no active helical motion. Hence, the average propulsive contribution of the tail also reduced to 0 in the backward motion correspondingly, indicating that only the head contributes to the backward motion. The relationship between the rotational speed of the head and the backward velocity is provided in Fig. 4E, and the significance test result of the regression is provided in SI Appendix, Tables S7 and S8. Similar to the model’s prediction, the backward swimming velocity also increases with increasing rotational speed of the head even if the slopes differ due to individual variation.
The spiral head also gives Ray sperms a conspicuous active turning ability benefited from the HDH model. Although the turning behavior of sperms has been observed in human sperm under flow (58), the active and smooth turning motion like Ray sperm has not been reported and analyzed. As the images and trajectory illustrated in SI Appendix, Fig. S11, the sperm initially moves toward the right bottom, and the angle between the head and the horizontal line is 37.8°. In this case, the angle between the center axis of the head and tail is 4.7°. Then, the head of the sperm turns right gradually, and the angle difference increases to 11.8° within 300 ms. It can be seen that the whole body of the sperm turns 40.3° following the new direction of the head in a short time of 1.3 s (SI Appendix, Fig. S11C). Such turning motion comes from the difference angle between the two individual helical sections. Considering that both the head and tail contribute to the propulsion, the angle between them will produce a lateral force on the body, resulting in the turning, and revealing the high motion flexibility of the HDH model.
High Environmental Adaptability to a Wide Range of Viscous Environments.
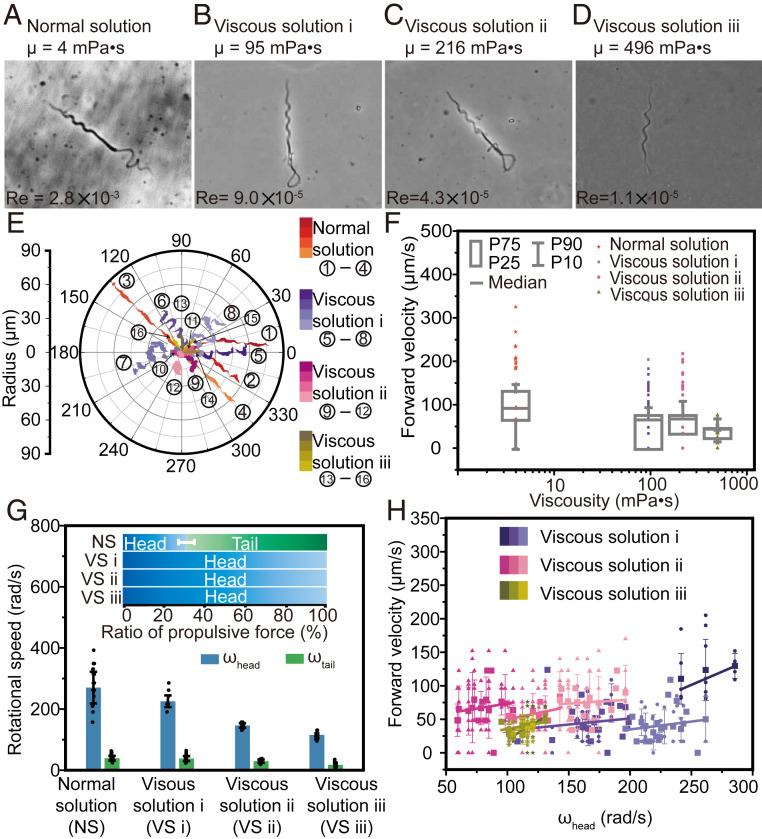
The specific heterogeneous dual helical structure of Ray sperms also demonstrates an advantage in environmental adaptability, which is also a critical competence in nature since the environmental viscosity changes when the sperm moves in the fertilization environment. According to the histochemical results of the elasmobranch’s female reproductive tract reported previously (59–65), sperms were observed inside the oviduct, oviducal gland, isthmus, uterus, and uterine sphincter. Specially, the investigation on the microstructure of the oviducal gland indicates the presence of mucous and/or proteic secretions, such as sulfated acid mucins, neutral mucins, and glycoproteins, thereby showing the viscosity change in the fertilization environment. To evaluate the environmental adaptability of the Ray sperm, we place sperms in solutions with 10 different viscosities, ranging from 4 mPa⋅s to 496 mPa⋅s (SI Appendix, Table S9). Those solutions are prepared by mixing the normal solution with various percentages of alginate, as follows: 0%, 0.1%, 0.2%, 0.3%, 0.4%, 0.5%, 0.6%, 0.8%, 1%, and 1.5%. The motion of sperms in those solutions are illustrated in Fig. 5 A–D (normal solution, viscous solution i [+0.5% alginate], viscous solution ii [+1% alginate], and viscous solution iii [+1.5% alginate]) and SI Appendix, Figs. S16–S19, and the Reynolds numbers of sperms in these solutions are provided in SI Appendix, Table S10. In the normal solution, the sperm can move forward using both the spiral head and helical tail (Fig. 5A). However, in the viscous solutions i to iii (Fig. 5 B–D, SI Appendix, Figs. S16–S18, and Movie S4), only the head can maintain the spiral shape, whereas the tail twins into a circle due to the high viscosity. It is noteworthy that although the shapes of sperms in different solutions vary, all sperms can move forward at a certain speed due to the existence of the spiral head. The raw velocity data are displayed in Fig. 5F, along with the median values in the four solutions, namely, 91.9 μm/s, 66.0 μm/s, 68.0 μm/s, and 45.3 μm/s, respectively. It indicates that the dual helical sections allow the Ray sperms to keep ∼50% of their speed when swimming in an extremely viscous environment even if the tail coils as a ring with no contribution to propulsion.
Fig. 5.
Environmental adaptability of the Ray sperm in viscous solutions. Images (A–D), trajectories (E), and velocities (F) of the Ray sperm swimming in four types of solutions (normal solution, viscous solution i, viscous solution ii, and viscous solution iii) observed through the bright-field microscope. Box: 25th to 75th percentiles, whisker: 10th to 90th percentiles, and horizontal line: median value. Since highly viscous solutions hindered the helical motion of soft material, the tail twined as a circle and almost made no contribution to the propulsive force. The forward velocity in viscous solution i was 28% slower than that in normal solution. (G) Rotational speed and propulsive force in four solutions (n > 34). Bar = mean; error bar = SD. The high viscosity of solutions reduced the rotation of the head and abolished the helical rotation of the tail. (H) Fitting relationships between the rotational speed of the head and forward speed (mean ± SD) in different solutions, showing the rotational speed of the head was correlated with the forward speed positively.
To further analyze the impact of the head and tail on the propulsive force in different solutions, we observe their rotational speed and calculate the corresponding propulsive contributions. As shown in Fig. 5G, the rotational speed of the head decreases from 270.1 rad/s (normal solution) to 225.6 rad/s (viscous solution i),146.4 rad/s (viscous solution ii), and 115.71 rad/s (viscous solution iii) while retaining its spiral shape. Moreover, the tail cannot keep the helical shape due to the high viscosity and rotates as a ring at a lower speed (∼20 rad/s), resulting in no contribution in the propulsive force. Hence, the head’s domination in propulsion in viscous solutions is demonstrated. The relationship between the rotational speed of the head and the forward speed in Fig. 5H and SI Appendix, Figs. S20 and S21 illustrated their positive correlation, consistent with the theoretical representation. The corresponding significant test result of the regression is provided in SI Appendix, Tables S11 and S12.
Compared with other species that usually drop in speed by over 40% in highly viscous solutions (viscosity increasing by 20 orders of magnitude) (66, 67), the velocity of the Ray sperm moving in highly viscous solutions (viscosity increasing by 50 orders of magnitude) only drops by 26% (SI Appendix, Table S14). The specific heterogeneous dual helical morphology, especially the rigid spiral head, allows Ray sperm to move in solutions with a wide range of viscosities, which could indicate prominent competence in nature, and could inspire many engineering designs as well.
Considering that the fertilization in Rays is internal, the sperm should swim through the uterus, oviducal gland, and the oviduct. However, the length of the uterus and oviduct can reach up to 30 to 40 mm (∼200 times the length of the sperm), secretory cells and ciliated cells commonly exist in the female reproduction tract (60–65), and the ciliated microvilli from the ciliated cells hinder the sperm’s motion. These features raise great challenges for sperms moving in the fertilization environment. Benefiting from the HDH model, the swimming linearity, obstacle avoidance ability, and environmental adaptability provide Ray sperms higher competence in motion and efficient propulsion in the female reproductive tract.
Experimental Corroboration of the HDH Model by a Bio-Inspired Robot.
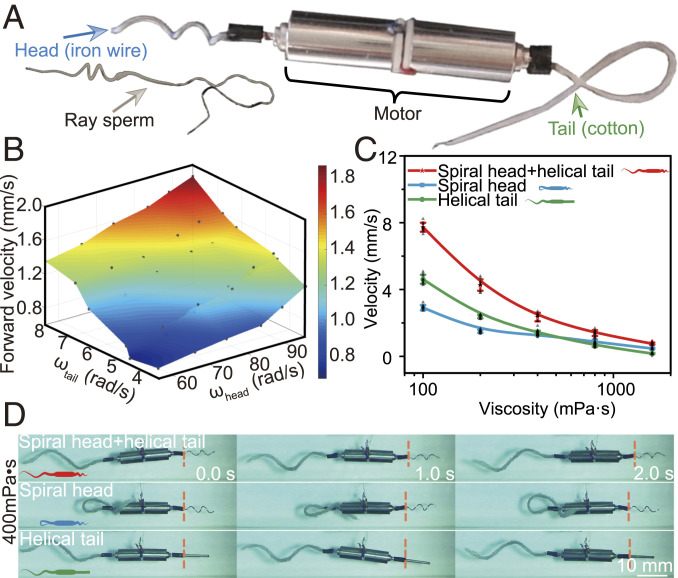
The advantages of the HDH model of Ray sperms in motion directivity, bidirectional motion ability, and the environmental adaptability offer a perspective for the design and fabrication of a small swimming robot. To further determine the potentials of the sperm’s specific structure, we design a bio-inspired robot with a heterogeneous dual helical morphology as shown in Fig. 6A. The robot consists of three parts like the sperm, namely, a spiral head made of rigid iron wire, a helical tail made of soft cotton wire, and two motors as the midpiece for the energy supply. We first place the bio-inspired robot in silicon oil solution with the Reynolds number of , similar order as that of Ray sperms in normal solution. The corresponding rotational speed of the head, tail, and the forward speed of the robot are displayed in Fig. 6B and SI Appendix, Fig. S24. The gray scatters represent the raw velocities. The colored surface is the three-dimensional (3D) fitting function determined through the interpolation method. The forward velocity increases with the growth of the rotational speed of both head and tail, matching the theoretical analysis. Meanwhile, the roles of the head and tail in propulsion have been demonstrated by driving the robot with a single head or tail in different viscous solutions (SI Appendix, Figs. S25 and S26 and Movie S5). The velocity ratio reveals that the tail plays the main role in the dilute solution whereas the head contributes more in the viscous solution.
Fig. 6.
The robot inspired by the dual helical sections of Ray sperms. (A) Structure of the bio-inspired robot. The robot is powered by motors with the rigid helical head and soft tail made of iron wire and cotton wire, respectively. (B) Fitting surface of the rotational speed of head and tail and the forward velocity through the interpolation method. The forward velocity is positively correlated with these two rotational speeds, consistent with the theoretical analysis of sperms’ motions. Forward velocities (mean ± SD) (C) and images (D) of the robot with dual or single helical sections under the same power input (n = 3). The robot with the dual helical sections moves fastest in all solutions, demonstrating its ultra-adaptability in all solutions. The robot with a helical tail relatively adapts to the dilute solution while the robot with a helical head performs better in highly viscous solutions.
To demonstrate the advantages of the heterogeneous dual helical swimming model over the conventional helical ones in various environments, we conduct control experiments by using the robot with heterogeneous dual helical morphology, single helical head, and single helical tail. Those robots are driven at the same power input. The experimental results are presented in Fig. 6 C and D, SI Appendix, Fig. S27, and Movie S5. Compared with the robot only with head or tail, the robot with heterogeneous dual helical morphology is able to adjust its energy distribution on the head (viscous solutions) or tail (dilute solutions) corresponding to the viscosity. Although all the three robots swim slower with increasing solution viscosity, the robot with heterogeneous dual helical morphology always moves fastest, and its velocity is 140 to 420% times those of the other two robots. For instance, the velocities of robots with single propulsion section decreases from 3.2 mm/s to 0.5 mm/s (single head) and 4.5 mm/s to 0.2 mm/s (single tail), respectively, with increasing viscosity from 100 mPa⋅s to 1,600 mPa⋅s. For comparison, the velocity of the robot with heterogeneous dual helical morphology only drops from 7.6 mm/s to 0.8 mm/s. This result is consistent well with the proposed HDH model and demonstrates the great application potentials of the heterogeneous dual helical morphology in engineering.
The inspired robot expertly moves in liquid environment, especially when the viscosity changes, due to the motion linearity, straightness, and especially, the high environmental adaptability of the HDH structure. Such abilities provide great opportunities for the swimming robot design and application inside the human body with complex fluidic environments (e.g., vascular, and enterocelia). Apart from the biomedical applications, the robot with high adaptability to viscosity will also become the solution to some challenging engineering tasks, such as tidal flat exploration.
In summary, as a disclosed swimming style of sperms, the HDH model demonstrates several advantages in environmental adaptability, swimming linearity, straightness, and efficiency. This peculiar motion style breaks the conventional perception of single tail propulsion and illustrates the significant contribution of the helical head. This discovery will expand the knowledge on sperms’ motions and motivates further investigations on natural fertilization and robotics.
Materials and Methods
Semen Collection, Dilution, and Preservation.
Semen was collected from different Ray fishes (Rhinoptera javanica and Taeniura meyeni) raised in the aquarium at the Ocean Park, Hong Kong, through the insertion of a tiny feeding tube attached with a 1-mL syringe through the urogenital papillae to the sperm sac. For each semen collection, we collected semen from two mature Javanese cow nose rays, and we used 20 mature fishes throughout the study. We observed that the average spermatozoa density was about 689 ± 185 × 106 ml−1 for Javanese cow nose rays (n = 20). For the black-spotted stingray, the sperm count was about 300 × 106 ml−1, and there was only one fish from which to collect the semen. Semen was diluted into the semen diluent for cartilaginous fish, also called ocean ringer solution (1:3), within 5 min of the collection at room temperature (22 °C) and transferred to the laboratory in an icebox (4 to 5 °C). In the laboratory, further dilution was performed for getting the concentration of 1 × 106 sperm per ml. A total 1 mL diluted semen (1:10) was kept in an Eppendorf tube (1.5 mL) and then preserved in a refrigerator (4 to 8 °C) for further application. The recipe of ocean ringer solution was as follows: NaCl (240 mM), KCl (7 mM), MgCl2 (4.9 mM), CaCl2 (10 mM), Na2SO4 (0.5 mM), NaHCO3 (2.3 mM), Na2HPO4(0.5 mM), glucose (55 mM), urea (360 mM), and TMANO (60 mM). The pH was kept about 7.8 to 8.0 measured by a pH meter (3510 Jenway).
Sample Preparation.
After the semen collection, semen was diluted into the semen diluent for cartilaginous fish, which is also called ocean ringer solution (1:3) within 5 min after the collection at room temperature (22 °C) and transferred to the laboratory in an icebox (4 to 5 °C). In the laboratory, further dilution was performed to get the concentration of 1 × 106 sperm per ml. A total 1 mL diluted semen (1:10) was kept in an Eppendorf tube (1.5 mL) and then preserved in a refrigerator (4 to 8 °C) for further application. In the motility observations, we first add 1 to 2 μL solution on the slide (LIUSHENG, REF188158, treated with positive charges) to wet it in advance. Then we add 10 μL of the diluted sperm sample solution on the slide and use a glass coverslip on it. Then we add 1 to 2 μL solution on the two sides of the coverslip and then observe the sample under the microscope. The distances between the slide and the coverslip are measured under a microscope (SI Appendix, Fig. S23), which are 86.9 ± 7.1 μm (normal solution), 84.3 ± 11.0 μm (viscous solution i), and 116.6 ± 34.8 μm (viscous solution ii). Compared with the rotating radius of the sperm (within 10 μm), this height is sufficiently large for sperm movement.
Nucleus and Mitochondria Staining.
The nuclear portion of the sperm was identified through staining with Hoechst 33342 (Cell Signaling Technology). In brief, Stock Solution (16.23 mM) of Hoechst 33342 was diluted into a dilution of 1:1,000 in ocean ringer solution to prepare working solution. A total 100 µl sperm sample (1 × 106 cells/mL) was added to 100 µl of Hoechst 33342 working solution and incubated for 30 min in a dark place at room temperature (22 °C). A total 10 µl staining solution was added to the microscopic slides and sealed with a coverslip. The image was taken by using Nikon Ni-E Upright Microscope. An oil immersion lens of 100x with a numerical aperture (NA) of 1.5 was set to capture the image by Zyla 4.2P. USB3 Andor Camera (0.065 µm per pixel).
To identify the mitochondrial area in Ray fish sperms, MitoTracker Red CM−H2X (Life Technologies Corporation) was used. A stock solution (1 mM) of MitoTracker Red was diluted 1:100 in ocean ringer solution to prepare the primary solution (10 µM). A total 2 µl of primary solution was added into a sperm solution of 400 µl and kept in a dark place for 15 min before observing under the microscope. A total 10 µl of this solution was placed on a microscope slide, and a coverslip was used to seal it. Image was captured with a 100x (oil immersion) lens within 30 min to avoid deformation using Nikon Ni-E Upright Microscope.
SEM Image Acquisition.
Sperm samples of 10 × 106 per ml concentration were fixed with 2.5% glutaraldehyde and 4% paraformaldehyde in 0.1 M ocean ringer solution and post fixation done by 2% osmium tetraoxide. After washing with water thrice, the dehydration was performed through an acetone series. Gold coating of the sample for SEM was done under vacuum using a coating unit E5100 (Polaron Equipment Ltd.), and images were taken by SEM (FEI Quanta 250) with a working distance of 8 mm and magnification of 6,000× for the total body and 18,000× for the midpiece.
Video Acquisition.
The videos showing the motion of the sperm were captured with 1) 12.5 fps, 2) 100 fps, 3) 200 fps, and 4) 500 fps using different microscopes. For the 12.5-fps videos, we used an Olympus BX50 phase contrast microscope with a 20× objective. For the 100-fps and 200-fps videos, Nikon Ni-E Upright Microscope was used with 10× and 20× objective lens, respectively. An inverted microscope (Olympus IX73) with the high–time resolution camera (Optronis CP70-1HS-M-1900) was used to capture the high frame rate videos (500 fps) with 40× objective.
Confocal Image Acquisition.
The images of the sperm head captured under the confocal microscope were captured with 30 fps using Nikon A1 HD25 large field-of-view confocal microscope with 40× and 60× objective lens. The sperm samples were prepared following the same protocol used for the nuclear staining method.
TEM Image Acquisition.
Sperm samples of 10 × 107 per ml concentration were fixed in 2.5% glutaraldehyde and 4% paraformaldehyde in 0.1 M ocean ringer solution and kept at 4 °C for 2 h. After three rinses with 0.1 M sodium cacodylate buffer with 10 mM CaCl2 and 0.2M sucrose, cell pellets were embedded in 3% agarose and sliced into small blocks (1 mm3), rinsed with the same buffer three times, and postfixed with 1% osmium tetroxide and 0.8% potassium ferricyanide in 0.1 M sodium cacodylate buffer with 10 mM CaCl2 and 0.2 M sucrose for 1.5 h at room temperature. Cells were rinsed with water and enbloc stained with 4% uranyl acetate in 50% ethanol for 2 h. Cells were dehydrated with increasing concentration of ethanol, transitioned into propylene oxide, infiltrated with Embed-812 resin, and polymerized in a 60 °C oven overnight. Blocks were sectioned with a diamond knife (Diatome) on a Leica Ultracut 7 ultramicrotome (Leica Microsystems), collected onto copper grids, and post stained with 2% aqueous uranyl acetate and lead citrate. Images were acquired on a JEM-1400 Plus transmission electron microscope equipped with a LaB6 source operated at 120 kV using an AMT-BioSprint 16-M charge-coupled device camera.
Viscosity Measurement.
The viscous solution was prepared by mixing 0.1%, 0.2%, 0.3%, 0.4%, 0.5%, 0.6%, 0.8%, 1.0%, and 1.5% sodium alginate along with the ocean ringer solution. Viscosity was measured by NDJ-9SB Digital Rotary Viscometer.
Image Analysis.
The trajectory and morphology shape data of swimming Ray sperms were obtained through the image processing. The rotational speeds of the head and tail were calculated according to the image sequences from the experimental videos with 100 fps, 200 fps, and 500 fps. The shape data, including the rotational radius, half of the pitch, and the helical filament radius of Ray sperms, were measured through the image processing software ImageJ. The morphology of Ray sperms during swimming was extracted from the free available web application WebPlotDigitizer. When acquiring the trajectory of the sperm, we tracked the top point on the sperm head in images based on the custom-written script in Matlab to record the position of the sperm’s head. Furthermore, a custom-written script in Matlab was applied to gain the motion characteristics of Ray sperms. Five parameters described the motility of the sperm, consistent with the current standards, as follows: 1) curvilinear velocity (VCL): the distance between two neighboring tracking points of the sperm/the corresponding time difference; 2) average path velocity (VAP), which is the average path of the sperm/total tracking time; 3) straight line velocity (VSL), which is the distance between the first and the last positions of the sperm/total tracking time; 4) linearity: VSL/VCL; and 5) straightness: VSL/VAP. The average of these parameters and the trajectory were chosen as the characteristic values of each sperm, and the mean of all sperms was the final value for each motility parameter.
Fabrication of the Bio-Inspired Robot.
The swimming robot inspired by Ray sperms was constructed with one soft tail and one rigid helical head, and they were driven by two independent motors in the midpiece (Fig. 6A). The motor has dimensions of 4 mm × 8 mm and a rated power of 0.06 W (Shenzhen Jiechuangsen Technology Co., Ltd). The rigid helix acts as the head and was fabricated by wrapping an iron wire (diameter 250 μm) on a mandrel. The pitch angle, radius, and axial length of the head helix was 45°, 0.8 mm, and 10 mm, respectively. The tail helix was manufactured by coating a polydimethylsiloxane (PDMS, 0.1 equivalent curing agents, Sylgard 184, Dow Corning) layer on a cotton wire (diameter 1 mm). First, the cotton wire was soaked in the PDMS solution for full integration. Then it was wrapped around a mandrel with a radius of 2.7 mm and finally thermal cured in 70 °C for 24 h. The cured PDMS helix acting as the tail could be deformed by force while maintaining a certain spiral shape in a normal state. The tail’s helix had an axial length of 25 mm with a pitch angle of 45°. For the robot with a single helical section used in the comparison experiment, the head of one robot was replaced by a straight iron wire with dimensions of 1 mm × 8 mm while the flexible tail was maintained. The tail of another robot was wrapped around the body manually while the rigid helical head was maintained. Further test results indicated that Young’s modulus of head and tail material was 1.2 × 1011 N/m2 and 2.51 × 107 N/m2, respectively.
The rigid head helix was aligned to the motor axis exactly. The oblique angle between the tail helix axis and the motor axis was 5° to express the large swing of the Ray sperm’s tail. The power for motors was provided by two programmable DC power supplies (eTM-L303SP) with accuracy of 0.0001 A and 0.001 V. The bio-inspired robot was put in a rectangular container (200 mm × 75 mm × 35 mm) filled with dimethyl silicone oil (Density 0.9630, Aladdin Chemistry Co. Ltd.) with the viscosity changing from 100 mPa⋅s to 1,600 mPa⋅s at 25 °C. A foam plate with dimensions of 25 mm × 20 mm × 7 mm was attached to the robot for suspension in the silicone oil solution. The motions of the bio-inspired robot were captured by the KEYENCE VW-Z1 motion analyzing microscope with 500 fps.
Experimental Set-Up of the Bio-Inspired Robot.
To investigate the relationship among the rotational speed of the head and tail and the velocity of the robot, we placed the robot in the 800-mPa⋅s silicone oil, and the dual helixes were driven by two independent motors with powers ranging from 0.025 W to 0.050 W. The rotational speed of the head changed from 8.9 to 15.2 rps and that of tail changed from 0.5 to 1.2 rps. The forward speed of the robot increased along with the rotational speeds in the range of 0.7 to 1.8 mm/s.
The analysis of the propulsive contribution of the helical head and tail in different viscous solutions was then conducted. The bio-inspired robot was driven by a single head or tail with the power of 0.050 W in solutions with viscosity ranging from 100 mPa⋅s to 1,600 mPa⋅s. Considering that the robot did not have a uniform size and the rotational speed of each part also differed, the cubic root of the volume of the whole robot is used as the characteristic length for Reynolds number calculation (68). The detailed parameters for calculation are provided in SI Appendix, Table S10.
To compare the motions of robots driven by dual or single helical sections, we used three kinds of robots: the robot with both helical head and helical tail, the robot with a spiral head and a winded tail, and the robot with a straight head and a helical tail. During the swimming motion, the two motors of each robot were driven in series with the fixed total input power of 0.075 W. The three robots were located in the same rectangular box filled with the silicone oil and had the viscosity levels in the range 100 to 1,600 mPa⋅s. The mechanical behavior of the motor is provided in SI Appendix, Fig. S29.
Roles of the Head and Tail on Propulsion for the Bio-Inspired Robot.
To illustrate the roles of the head and tail in propulsive force, we located the robot in viscous solutions, and the viscosity changed from 100 mPa⋅s to 1,600 mPa⋅s (Movie S5). Then, the same electric power was supplied to the head or tail, and the corresponding rotational speed and forward speed were provided in SI Appendix, Fig. S26 with the image sequences in SI Appendix, Fig. S25. The results indicated that both the rotational speed of the head and tail decreased as the viscosity raised because of the increasing fluid-resisting force. In addition, the rotational speed of the tail dropped from 58.1 rad/s to 3.4 rad/s, because the tail was softer than the head, and it cannot resist the increasing fluid force in viscous solutions. In comparison, the head still rotated with 54.5 rad/s in the highly viscous (1,600 mPa⋅s) solution, supplying propulsive force for the forward motion. Such trend is very similar to that of Ray sperms and consists well with the proposed swimming model.
Moreover, the contribution of the head and tail to the propulsive force also varied with the viscosity (SI Appendix, Fig. S26 and Movie S5). Here, we defined the velocity ratio as the velocity driven by the head () or tail () dividing the sum of those two velocities () to illustrate the performance of the head and tail in different viscous solutions. The velocity ratio of the tail was relatively high in the low-viscosity solution, indicating that the tail played a major role in propulsion in the dilute solution. With increasing viscosity, the velocity ratio of the tail reduced gradually and reached 50% at ∼400 mPa⋅s. As the viscosity increased further, the tail was not able to rotate freely and was not able to produce enough propulsive force. Nevertheless, the rigid head was able to maintain its spiral shape in viscous solutions, and its propulsive efficiency was thus higher than that of the tail, leading to a dominating contribution to the propulsive force with the final value of 61.2%.
Although the midpiece of the bio-inspired robot is a little larger compared with the midpiece of the Ray sperm, it does not influence the contribution of the head and tail on the propulsion. Because the midpiece of the robot is a rigid regular cylinder, the drag force from the midpiece is proportional to the moving velocity according to the textbook, as follows:
| [1] |
where is the drag coefficient, is the density of the solution, is the velocity of the cylinder, D is the diameter, and L is the length. The parameters for calculation are provided in SI Appendix, Table S15. By substituting these values into the above equation, we obtained the drag force from the midpiece is in the order of 10−6 N. We have also estimated the propulsive force from the head and tail based on the resistive force theory, which was in the order of 10−2 N, and was more than four orders of magnitude over the drag force from the midpiece. Thus, the influence of the midpiece was negligible.
Calculation of the Reynolds Number.
The Reynolds number of the sperm and robot was calculated by the following formula:
| [2] |
where is the density of the liquid, is the moving velocity of the sperm or the robot, is the characteristic length, and is the viscosity of the liquid. The specific values of the above parameters are listed in SI Appendix, Table S10. The characteristic length of the sperm was chosen as the total length of the body. The characteristic length of the robot was calculated as the cube root of its volume. Here, the rotational amplitude of the robot head and tail was 0.8 mm and 3.7 mm, respectively, and the diameter of the motor was 4 mm. The axis lengths of the head, motor and tail were 10 mm, 16 mm, and 25 mm, respectively. Hence, the characteristic length of the robot was 10.9 mm.
Shape Analysis.
The head and tail of the sperm are considered to have a helical shape with the radius and pitch changing along with the body length. Here, we use the WebPlotDigitizer tool to acquire the shapes of a sperm in a series of images. Then, the extreme value of each point on the sperm on the X-Y plane and the X-Z plane can be obtained. Based on the above measured data, the position of each point on the y- and z- axis were fitted through the Smoothing Spline method and interpolation method (shape-preserving piecewise cubic hermite interpolating polynomial) in the Matlab. Then, the position of each point on both head and tail were obtained from the above-fitted function. The fitting results are displayed in SI Appendix, Fig. S8. According to the fitting results, we reconstructed the 3D shape of the sperm with the amplitude and pitch continuously changing with the body, as shown in SI Appendix, Fig. S8.
We also conduct the 3D reconstruction based on the confocal images. The acquired confocal image of the sperm is illustrated in SI Appendix, Fig. S2A. Then, the red, green, blue (RGB) values of each pixel in that image are acquired. After that, the image processing, including thresholding, labeling the maximum connected domain, edge detection, and centerline calculation, is conducted for this image to get the edge of the sperm. The processing results of each step is displayed in SI Appendix, Fig. S2 C–F. The centerline of the sperm on the y-axis is chosen as the average of the edge. After the acquisition of the centerline of the sperm, the height information of this centerline can be calculated by matching the RGB value with the color bar of the height. With the combination of the centerline and the height data, the 3D structure of the sperm is reconstructed as shown in SI Appendix, Fig. S2B.
To verify the reliability of the reconstruction based on the two-dimensional (2D) image, the comparison of the reconstruction based on the 2D image and the confocal data are conducted. The positions of the sperm head on the X-Y plane and the X-Z plane based on the above reconstruction results are shown in SI Appendix, Fig. S9. Then, the tendency and values of the two curves are similar, demonstrating the feasibility of the reconstruction method based on the 2D image.
Propulsive Force Calculation.
Resistive force theory.
The calculation of the propulsive force produced by the head and tail is based on the resistive force theory. First, the cell shape, rotational speed, and forward velocity are obtained from the videos. Then, the cell body is segmented to enormous parts with a segment distance of 0.01 μm. For each segment on the helical head or tail, its velocity consists of two elements, namely, the velocity in the normal direction and the velocity in the tangential direction. Meanwhile, the force acting on this segment also can be decomposed into two parts, namely, the normal stress and the tangential resisting force , which are all linear to the velocity in the same direction with the coefficient of and , respectively. Then, the infinitesimal normal stress force and the tangential resistive force acting on each element ds of the head and tail are derived from the following formulas:
| [3] |
| [4] |
and,
| [5] |
| [6] |
where μ is the viscosity of the solution, q is the wavelength of the head or tail, and a is the radius of the helical filament. Then, the infinitesimal propulsive force on each element is as follows:
| [7] |
where φ is the pitch angle of the helix and can be calculated from:
| [8] |
and the ds is the length of the element:
| [9] |
After the calculation of the thrust force in each differential segment along with body, the total propulsive force of the head or tail is the integral of the differential force, as follows:
| [10] |
Here, the head and tail are divided by every 0.01 μm.
The propulsive force from the head and tail is calculated by integrating the segmented force on the head and tail, respectively. The ratio of the head on the propulsive force is estimated by dividing the total propulsive force of the body into the force from the head. Considering the differences on shapes and speeds of individuals, this ratio differs accordingly.
For the backward motion, since the rotational direction of the head is opposite, so the velocity is in the opposite direction, and the propulsive force is hence negative.
The midpiece of the Ray sperm is considered as a cylinder that cannot produce the propulsive force although rotating.
Regularized Stokeslet method.
The regularized Stokeslet method is also used for the calculation of the propulsion force. According to this theory, the relationship between the velocity and the force acting on the filament is as follows:
| [11] |
where is the velocity, is the viscosity of the fluid, is the regularized Green’s function, and is the force acting on the segment.
In this work, we use the cutoff function as follows:
| [12] |
where .
Then, the regularized Stokeslet is as follows:
| [13] |
This regularized Green’s function only depends on the geometry of the sperm filament and the regularized parameter . Thus, for the given velocity, the propulsive force is calculated accordingly. The regularized parameter is chosen as a quarter of the radius of the filament.
Regression of the propulsive ratio.
To compare the propulsive contributions of the head and tail, the regression of the propulsive contribution is conducted. In the regression analysis, the shape of the sperm is fixed, and the variables are set as follows: the rotational speed of head (x1), rotational speed of tail (x2), forward speed (x3), and the ratio of the contribution from the head (y). The estimated values of the parameters in the regression are as follows: b0 = 37.84, b1 = 0.11, b2 = −0.16, and b3 = 0.20. According to the significance test of the regression and the parameters of the regression (SI Appendix, Table S3), the regression is reliable. The extreme values of the rotational speed of the head, rotational speed of the tail, and the forward speed are [157, 24.15, 65] and [392.5, 62.8, 222.09] based on observations. After substituting the extreme values of the speeds, the ratio of the propulsive contribution from the head ranges is [13.08%, 45.10%].
Data Fitting.
The fitting relationship between the moving velocity and the rotational speed of the head or tail of the sperm was obtained using the polynomial method with a degree of 1 in Matlab. The function among the forward velocity and rotational speeds of head and tail of the bio-inspired robot is fitted through the interpolation method in the Curve Fitting application in Matlab.
Ethics Statement.
All procedures were conducted in accordance with the guidelines of the Association of Zoos & Aquariums and approved by the Ethics Committee of the Ocean Park (Hong Kong) for animal experiments under number vet.aqua-2017.01.
Supplementary Material
Acknowledgments
We appreciate the financial support from the National Natural Science Foundation of China (Grants NSFC61922093, NSFC U1813211, 81770099), the Hong Kong Health and Medical Research Fund (Grant 05160296), the Hong Kong Research Grants Council (Grant 21101218), Shenzhen Science and Technology Innovation Fund (Grants JCYJ20170413115637100 and JCYJ20170412152916724), Sanming Project of Medicine in Shenzhen (Grant SZSM201811092), Hong Kong Research Grant Council (RGC) General Research Fund (Grant CityU 11211720), ShenZhen (China) Key Basic Research Project (Grant JCYJ20200109114827177), and the grant from Tung Biomedical Sciences Center to J.S.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2024329118/-/DCSupplemental.
Data Availability
All study data are included in the article and/or supporting information.
References
- 1.Cosson J., et al., Marine fish spermatozoa: Racing ephemeral swimmers. Reproduction 136, 277–294 (2008). [DOI] [PubMed] [Google Scholar]
- 2.Rodenborn B., Chen C.-H., Swinney H. L., Liu B., Zhang H. P., Propulsion of microorganisms by a helical flagellum. Proc. Natl. Acad. Sci. U.S.A. 110, E338–E347 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Birkhead T. R., Hosken D. J., Pitnick S. S., Sperm Biology (Elsevier, 2008). [Google Scholar]
- 4.Taylor G. I., Analysis of the swimming of microscopic organisms. Proc. R. Soc. Lond. A Math. Phys. Sci. 209, 447–461 (1951). [Google Scholar]
- 5.Edd J., Payen S., Rubinsky B., Stoller M. L., Sitti M., “Biomimetic propulsion for a swimming surgical micro-robot” in Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003)(Cat. No. 03CH37453) (IEEE, Las Vegas, NV, 2003), pp. 2583–2588. [Google Scholar]
- 6.Tottori S., et al., Magnetic helical micromachines: Fabrication, controlled swimming, and cargo transport. Adv. Mater. 24, 811–816 (2012). [DOI] [PubMed] [Google Scholar]
- 7.Gaffney E. A., Gadêlha H., Smith D., Blake J., Kirkman-Brown J., Mammalian sperm motility: Observation and theory. Annu. Rev. Fluid Mech. 43, 501–528 (2011). [Google Scholar]
- 8.Nosrati R., Driouchi A., Yip C. M., Sinton D., Two-dimensional slither swimming of sperm within a micrometre of a surface. Nat. Commun. 6, 8703 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gadêlha H., Hernández-Herrera P., Montoya F., Darszon A., Corkidi G., Human sperm uses asymmetric and anisotropic flagellar controls to regulate swimming symmetry and cell steering. Sci. Adv. 6, eaba5168 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 10.Jamieson B. G., Leung L.-P., Fish Evolution and Systematics: Evidence from Spermatozoa: With a Survey of Lophophorate, Echinoderm and Protochordate Sperm and an Account of Gamete Cryopreservation (Cambridge University Press, 1991). [Google Scholar]
- 11.Skinner M. K., Encyclopedia of Reproduction (Academic Press, 2018). [Google Scholar]
- 12.Stanley H. P., The fine structure of spermatozoa of Hydrolagus colliei (Chondrichthyes, Holocephali). J. Ultrastruct. Res. 83, 184–194 (1983). [DOI] [PubMed] [Google Scholar]
- 13.Hermosell I. G., et al., Patterns of sperm damage in Chernobyl passerine birds suggest a trade-off between sperm length and integrity. Biol. Lett. 9, 20130530 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Støstad H. N., “The evolution and function of sperm head morphology in songbirds” (Rep. 13-22, University of Oslo, Oslo, Norway, 2018).
- 15.Schilthuizen M., Langelaan R., Hemmings N., van Oostenbrugge W., Visser S., An unexpected twist: Sperm cells coil to the right in land snails and to the left in song birds. Contrib. Zool. 86, 297–302 (2017). [Google Scholar]
- 16.Jamieson B. G., Hodgson A., Spottiswoode C. N., Ultrastructure of the spermatozoon of Myrmecocichla formicivora (Vieillot, 1881) and Philetairus socius (Latham, 1790)(Aves; Passeriformes), with a new interpretation of the passeridan acrosome. Acta Zool. 87, 297–304 (2006). [Google Scholar]
- 17.Andrietti F., Bernardini G., The movement of spermatozoa with helical head: Theoretical analysis and experimental results. Biophys. J. 67, 1767–1774 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Joshy H., Kuramoto M., Scanning electron microscopic studies on spermatozoa of anurans from India and Sri Lanka. Amphib. Reptil. 22, 303–308 (2001). [Google Scholar]
- 19.Muto K., Kubota H. Y., A novel mechanism of sperm motility in a viscous environment: Corkscrew-shaped spermatozoa cruise by spinning. Cell Motil. Cytoskeleton 66, 281–291 (2009). [DOI] [PubMed] [Google Scholar]
- 20.Mizuhira V., et al., The fine structure of the spermatozoa of two species of Rhacophorus (arboreus, schlegelii). I. Phase-contrast microscope, scanning electron microscope, and cytochemical observations of the head piece. J. Ultrastruct. Mol. Struct. Res. 96, 41–53 (1986). [DOI] [PubMed] [Google Scholar]
- 21.Fischer U., Ultrastructure of spermatogenesis and spermatozoa of cephalodasys maximus (Gastrotricha, Macrodasyida). Zoomorphology 114, 213–225 (1994). [Google Scholar]
- 22.Franzén Å., The spermatozoon of Siboglinum (Pogonophora). Acta Zool. 54, 179–192 (1973). [Google Scholar]
- 23.Smith R. J., Matzke‐Karasz R., Kamiya T., De Deckker P., Sperm lengths of non‐marine cypridoidean ostracods (Crustacea). Acta Zool. 97, 1–17 (2016). [DOI] [PubMed] [Google Scholar]
- 24.Temple-Smith P., Ravichandran A., Horta F., “Sperm: Comparative vertebrate” in Encyclopedia of Reproduction, Skinner M., Ed. (Elsevier, ed. 2, 2018), pp. 210–220. [Google Scholar]
- 25.Pitnick S. S., Hosken D. J., Birkhead T. R., Sperm Biology: An Evolutionary Perspective (Academic Press, 2008). [Google Scholar]
- 26.Comizzoli P., Brown J. L., Holt W. V., Reproductive Sciences in Animal Conservation (Springer, 2019). [Google Scholar]
- 27.Tanaka S., “Comparative morphology of the sperm in chondrichthyan fishes” in Advances in Spermatozoal Phylogeny and Taxonomy, B. G. M. Jamieson, J. Ausio, J.-L. Justine, Eds. (Mémoires du Muséum National d’Histoire Naturel, 1995), pp. 313–320. [Google Scholar]
- 28.Wyffels J. T., et al., Testosterone and semen seasonality for the sand tiger shark Carcharias taurus. Biol. Reprod. 102, 876–887 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Dzyuba V., et al., Sperm motility and lipid composition in internally fertilizing ocellate river stingray Potamotrygon motoro. Theriogenology 130, 26–35 (2019). [DOI] [PubMed] [Google Scholar]
- 30.Dzyuba V., et al., Sperm motility in ocellate river stingrays: Evidence for post‐testicular sperm maturation and capacitation in chondrichthyes. J. Zool. 307, 9–16 (2019). [Google Scholar]
- 31.Minamikawa S., Morisawa M., Acquisition, initiation and maintenance of sperm motility in the shark, Triakis scyllia. Comp. Biochem. Physiol. Part A. Physiol. 113, 387–392 (1996). [Google Scholar]
- 32.Schmoll T., Rudolfsen G., Schielzeth H., Kleven O., Sperm velocity in a promiscuous bird across experimental media of different viscosities. Proc. Biol. Sci. 287, 20201031 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Vernon G. G., Woolley D. M., Three-dimensional motion of avian spermatozoa. Cell Motil. Cytoskeleton 42, 149–161 (1999). [DOI] [PubMed] [Google Scholar]
- 34.Tholl N., et al., Swimming of Xenopus laevis sperm exhibits multiple gears and its duration is extended by egg jelly constituents. Biol. Bull. 220, 174–185 (2011). [DOI] [PubMed] [Google Scholar]
- 35.Støstad H. N., Johnsen A., Lifjeld J. T., Rowe M., Sperm head morphology is associated with sperm swimming speed: A comparative study of songbirds using electron microscopy. Evolution 72, 1918–1932 (2018). [DOI] [PubMed] [Google Scholar]
- 36.Hamlett W. C., Reproductive Biology and Phylogeny of Chondrichthyes: Sharks, Batoids, and Chimaeras (CRC Press, 2011), vol. 3. [Google Scholar]
- 37.Andraszek K., Banaszewska D., Biesiada-Drzazga B., The use of two staining methods for identification of spermatozoon structure in roosters. Poult. Sci. 97, 2575–2581 (2018). [DOI] [PubMed] [Google Scholar]
- 38.Alavi S. M., et al., Effects of osmolality on sperm morphology, motility and flagellar wave parameters in Northern pike (Esox lucius L.). Theriogenology 72, 32–43 (2009). [DOI] [PubMed] [Google Scholar]
- 39.Psenicka M., et al., Morphology and ultrastructure of Siberian sturgeon (Acipenser baerii) spermatozoa using scanning and transmission electron microscopy. Biol. Cell 99, 103–115 (2007). [DOI] [PubMed] [Google Scholar]
- 40.Linhartova Z., Rodina M., Nebesarova J., Cosson J., Psenicka M., Morphology and ultrastructure of beluga (Huso huso) spermatozoa and a comparison with related sturgeons. Anim. Reprod. Sci. 137, 220–229 (2013). [DOI] [PubMed] [Google Scholar]
- 41.Kowalczyk A., Łukaszewicz E., Simple and effective methods of freezing capercaillie (Tetrao urogallus L.) semen. PLoS One 10, e0116797 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Youn J. S., et al., Predictive value of sperm motility characteristics assessed by computer-assisted sperm analysis in intrauterine insemination with superovulation in couples with unexplained infertility. Clin. Exp. Reprod. Med. 38, 47–52 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hoogewijs M. K., et al., Influence of counting chamber type on CASA outcomes of equine semen analysis. Equine Vet. J. 44, 542–549 (2012). [DOI] [PubMed] [Google Scholar]
- 44.Sieczyński P., Glogowski J., Cejko B., Grygoruk C., Characteristics of Siberian sturgeon and sterlet sperm motility parameters compared using CASA. Arch. Pol. Fisheries 20, 137–143 (2012). [Google Scholar]
- 45.Dorado J., Molina I., Muñoz-Serrano A., Hidalgo M., Identification of sperm subpopulations with defined motility characteristics in ejaculates from Florida goats. Theriogenology 74, 795–804 (2010). [DOI] [PubMed] [Google Scholar]
- 46.Contri A., et al., Kinematic study on the effect of pH on bull sperm function. Anim. Reprod. Sci. 136, 252–259 (2013). [DOI] [PubMed] [Google Scholar]
- 47.Abouelezz F. M., et al., Sperm-egg penetration assay assessment of the contraceptive effects of glycerol and egg yolk in rooster sperm diluents. Theriogenology 83, 1541–1547 (2015). [DOI] [PubMed] [Google Scholar]
- 48.Poli F., Immler S., Gasparini C., Effects of ovarian fluid on sperm traits and its implications for cryptic female choice in zebrafish. Behav. Ecol. 30, 1298–1305 (2019). [Google Scholar]
- 49.Breckels R. D., Neff B. D., Rapid evolution of sperm length in response to increased temperature in an ectothermic fish. Evol. Ecol. 28, 521–533 (2014). [Google Scholar]
- 50.Brennen C., Winet H., Fluid mechanics of propulsion by cilia and flagella. Annu. Rev. Fluid Mech. 9, 339–398 (1977). [Google Scholar]
- 51.Lauga E., Powers T. R., The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72, 096601 (2009). [Google Scholar]
- 52.Pitnick S., Hosken D. J., Birkhead T. R., “Sperm morphological diversity” in Sperm Biology, T. R. Birkhead, D. J. Hosken, S. Pitnick, Eds. (Elsevier, 2009), pp. 69–149. [Google Scholar]
- 53.Cortez R., Fauci L., Medovikov A., The method of regularized stokeslets in three dimensions: Analysis, validation, and application to helical swimming. Phys. Fluids 17, 031504 (2005). [Google Scholar]
- 54.Wilson M. C., Harvey J. D., Shannon P., Aerobic and anaerobic swimming speeds of spermatozoa investigated by twin beam laser velocimetry. Biophys. J. 51, 509–512 (1987). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Subramani E., et al., Rotational dynamics of optically trapped human spermatozoa. ScientificWorldJournal 2014, 154367 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Cosson J., Linhart O., Mims S., Shelton W., Rodina M., Analysis of motility parameters from paddlefish and shovelnose sturgeon spermatozoa. J. Fish Biol. 56, 1348–1367 (2000). [Google Scholar]
- 57.Boryshpolets S., et al., Different swimming behaviors of sterlet (Acipenser ruthenus) spermatozoa close to solid and free surfaces. Theriogenology 79, 81–86 (2013). [DOI] [PubMed] [Google Scholar]
- 58.Bukatin A., Kukhtevich I., Stoop N., Dunkel J., Kantsler V., Bimodal rheotactic behavior reflects flagellar beat asymmetry in human sperm cells. Proc. Natl. Acad. Sci. U.S.A. 112, 15904–15909 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Storrie M. T., Walker T. I., Laurenson L. J., Hamlett W. C., Microscopic organization of the sperm storage tubules in the oviducal gland of the female gummy shark (Mustelus antarcticus), with observations on sperm distribution and storage. J. Morphol. 269, 1308–1324 (2008). [DOI] [PubMed] [Google Scholar]
- 60.Moura T., Serra‐Pereira B., Gordo L., Figueiredo I., Sperm storage in males and females of the deepwater shark Portuguese dogfish with notes on oviducal gland microscopic organization. J. Zool. 283, 210–219 (2011). [Google Scholar]
- 61.Serra-Pereira B., et al., The development of the oviducal gland in the Rajid thornback ray, Raja clavata. Helgol. Mar. Res. 65, 399–411 (2011). [Google Scholar]
- 62.Serra-Pereira B., Figueiredo I., Gordo L. S., Maturation of the gonads and reproductive tracts of the thornback ray Raja clavata, with comments on the development of a standardized reproductive terminology for oviparous elasmobranchs. Mar. Coast. Fish. 3, 160–175 (2011). [Google Scholar]
- 63.Henderson A. C., Reeve A. J., Ambu-Ali A., Microanatomy of the male and female reproductive tracts in the long-tailed butterfly ray Gymnura poecilura, an elasmobranch with unusual characteristics. J. Fish Biol. 84, 297–313 (2014). [DOI] [PubMed] [Google Scholar]
- 64.Porcu C., et al., Reproductive aspects of the velvet belly lantern shark Etmopterus spinax (Condrichthyes: Etmopteridae), from the central western Mediterranean sea. Notes on gametogenesis and oviducal gland microstructure. Mediterr. Mar. Sci. 15, 313–326 (2014). [Google Scholar]
- 65.Marongiu M. F., et al., Oviducal gland microstructure of Raja miraletus and Dipturus oxyrinchus (Elasmobranchii, Rajidae). J. Morphol. 276, 1392–1403 (2015). [DOI] [PubMed] [Google Scholar]
- 66.Kantsler V., Dunkel J., Blayney M., Goldstein R. E., Rheotaxis facilitates upstream navigation of mammalian sperm cells. eLife 3, e02403 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Eamer L., Nosrati R., Vollmer M., Zini A., Sinton D., Microfluidic assessment of swimming media for motility-based sperm selection. Biomicrofluidics 9, 044113 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Oliver J., Cervera M., Oller S., Lubliner J., "Isotropic damage models and smeared crack analysis of concrete" in Proc. SCI-C Computer Aided Analysis and Design of Concrete Structures, N. Bicanic, H. Mang, Eds. (Pineridge Press, Swansea, U.K., 1990), pp. 945–957. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or supporting information.