Petrographic carbon in ancient sediments constrains Proterozoic Era atmospheric oxygen levels

Significance

Earth progressed from an oxygen-free planet at birth to the well-oxygenated planet we have today. Life enabled Earth’s oxygenation through the evolution of cyanobacteria, and the subsequent history of oxygen enabled further developments in the evolution of eukaryotic life; mammals, for example, need relatively high oxygen levels to breathe. The relationship between oxygen and life, however, is hampered by uncertainties in the history of oxygen concentrations, particularly during the middle of the Proterozoic Eon when eukaryote ecosystems were first emerging. We explore ancient organic matter cycling through Raman spectrographic analysis of nine geologic formations spanning 1 billion years of Proterozoic time. Our results, when combined with modeling, show that emerging eukaryote ecosystems were not limited by oxygen concentrations.

Abstract

Oxygen concentration defines the chemical structure of Earth's ecosystems while it also fuels the metabolism of aerobic organisms. As different aerobes have different oxygen requirements, the evolution of oxygen levels through time has likely impacted both environmental chemistry and the history of life. Understanding the relationship between atmospheric oxygen levels, the chemical environment, and life, however, is hampered by uncertainties in the history of oxygen levels. We report over 5,700 Raman analyses of organic matter from nine geological formations spanning in time from 742 to 1,729 Ma. We find that organic matter was effectively oxidized during weathering and little was recycled into marine sediments. Indeed, during this time interval, organic matter was as efficiently oxidized during weathering as it is now. From these observations, we constrain minimum atmospheric oxygen levels to between 2 to 24% of present levels from the late Paleoproterozoic Era into the Neoproterozoic Era. Indeed, our results reveal that eukaryote evolution, including early animal evolution, was not likely hindered by oxygen through this time interval. Our results also show that due to efficient organic recycling during weathering, carbon cycle dynamics can be assessed directly from the sediment carbon record.

The history of life has been interwoven with levels of atmospheric oxygen through much of Earth’s history. For example, aerobic life could only prosper after the evolution of cyanobacteria, which introduced oxygen into the environment (1). Furthermore, the oxygen requirements of aerobic eukaryotes, representing most eukaryotes by far, scale positively with their size (2). For example, mammals could not have evolved into a low-oxygen environment that was sufficient for eukaryotic microbes. In this way, the history of atmospheric oxygen has both constrained and permitted evolutionary developments requiring specific oxygen levels (3). However, fully understanding how oxygen has impacted the history of life requires reconstructing the history of atmospheric oxygen.

Direct measurements of atmospheric oxygen concentration over time can be made from air trapped in glacial ice, with a record extending over the past 800,000 y (4), or in evaporitic salt, extending the record to potentially over 1 billion years (5–8). The oxygen record from ice is continuous and precise, but young, while the salt record is infrequent and requires careful screening to ensure samples are appropriate for analysis (9). Otherwise, the history of atmospheric oxygen is estimated from oxygen-sensitive proxies. Oxygen impacts the chemical nature, isotopic composition, and/or concentrations of redox-sensitive substances in the oceans (like molybdenum, e.g., refs. 10 and 11, or cerium, e.g., refs. 12 and 13) and the chemical weathering of redox-sensitive substances on land (like chromium and iron, e.g., refs. 14–16). Oxygen is also directly incorporated into sulfate during redox transformation (17). None of the proxies deriving from these processes represent a direct oxygen barometer, and each requires interpretation through modeling with a variety of assumptions regarding reaction kinetics, isotopic behavior during redox transformations, and the activity level of the ancient biosphere. These approaches are also generally hindered by a limited geologic record.

Furthermore, these approaches do not provide a consensus view as to the history of atmospheric oxygen. For example, some approaches suggest maximum Mesoproterozoic Era (1,600 to 1,000 Ma) oxygen levels of 0.1 to 1% times present levels (PAL) (15, 18), whereas other approaches suggest minimum oxygen levels of 1 to 4% PAL (19–21). Also, different approaches using the same proxy can yield dramatically different results. For example, a kinetic approach to modeling cerium anomalies suggests atmospheric oxygen levels of ≤0.1% PAL from the Mesoproterozoic Era (1,600 to 1,000 Ma) through the latest Neoproterozoic Era (1,000 to 541 Ma) (13), while thermodynamic modeling of the cerium anomaly suggests oxygen levels of 1 to 2% PAL through the same time window (12). Resolving such divergent views is critical, as the Mesoproterozoic Era was a time of emerging eukaryotic ecosystems (22) whose evolution could have been influenced by oxygen availability.

The carbon cycle is also impacted by oxygen in which the weatherability of ancient “geologic” organic matter is a function of oxygen concentration (23). Indeed, existing carbon cycle models suggest that considerable unweathered organic matter should be recycled into marine sediments when oxygen concentrations fall below 10% PAL (24). Thus, the extent of organic matter recycling in the geologic past yields a potential oxygen barometer. Therefore, we have explored with Raman spectroscopy nine geologic formations of relatively low thermal maturity spanning 1 billion years of the Proterozoic Eon (Table 1). We find that recycled organic matter is rare and that organic matter was oxidized during weathering as efficiently then as now, placing rather firm lower limits on levels of atmospheric oxygen through this time.

Table 1.

Number of sampling points and estimates of petrographic carbon concentrations

		Age	# analyses*	#†	TOC	Max	Max	Max	Max
		Ma	graphite/	graphite/	wt%	graphite	kerogen	petro-1‡	petro-2§
Samples	Formation		Kerogen	kerogen		wt%¶	wt%¶
AK-10–53-15	Chuar	742.0	293/43	0/0	20.7	0.0706	0.481	0.552	0.141
SZY-6	Zhengjiaya	1,100	301/45	0/0	9.29	0.0309	0.206	0.237	0.062
WSH-1–2	Wenshuihe	1,200	1101/42	0/0	9.29	0.0084	0.221	0.230	0.017
TZ-21	Taizi	1,330	2510/57	0/0	4.20	0.0017	0.074	0.075	0.003
XML-319–6	Xiamaling Unit 4	1,385	224/49	1/2	0.06	0.0003	0.002	0.003	0.001
XML-365–45	Xiamaling Unit 6	1,395	10/10	0/0	0.06	0.0060	0.006	0.012	0.012
HSZ-538–3	Hongshuzhuang	1,450	277/54	0/0	2.12	0.0077	0.039	0.047	0.015
GYZ-223–6	Gaoyuzhuang	1,570	16/16	0/0	2.45	0.1531	0.153	0.306	0.306
GYZ-299–4	Gaoyuzhuang	1,570	303/75	0/0	0.15	0.0005	0.002	0.002	0.001
MR-9	Reward	1,637	302/54	0/0	4.40	0.0146	0.081	0.096	0.029
MY-2	Wollogorang	1,729	298/80	0/0	1.37	0.0046	0.017	0.022	0.009
MY-7	Wollogorang	1,729	11/11	0/0	1.90	0.1727	0.173	0.345	0.345

^*Number of analyses suitable for the determination of graphite/kerogen. Italics represents samples with too few analyses for meaningful petrographic carbon estimations.

^†Number of identified graphite grains and grains of recycled kerogen.

^‡Max petrographic carbon from summing max graphite and max kerogen.

^§Max petrographic carbon assuming max kerogen is the same as max graphite.

^¶Max graphite or kerogen (wt%) = number of graphite or kerogen grains × TOC (wt%)/number of Raman analyses.

Results and Discussion

Preliminary Raman Analyses.

Raman spectroscopy is a nondestructive analytical technique based on the vibrational energy states of molecules that can be used to determine the degree of structural order in thermally matured organic materials. Progressive thermal cracking (loss of H, O, and other heteroatoms) and the aromatization of biomolecules during diagenesis and low-grade metamorphism lead to the formation of disordered macromolecular kerogen (25) followed by physical molecular alignment and graphitization during metamorphism (26). In preliminary analysis (SI Appendix), we surveyed organic matter from several samples for each formation obtaining Raman spectra that were further evaluated for organic matter maturation temperature T_max using calibrated Raman-based spectral geothermometers. We compared the Lahfid (27) and Kouketsu (28) geothermometers for most of our samples, while utilizing the Beyssac (26) geothermometer for the higher maturity samples (SI Appendix). We compiled the sum of peak widths from the Lahfid geothermometer, with each analysis assigned a field of maturity in a “Sparkes plot” (29) (SI Appendix, Fig. S1).

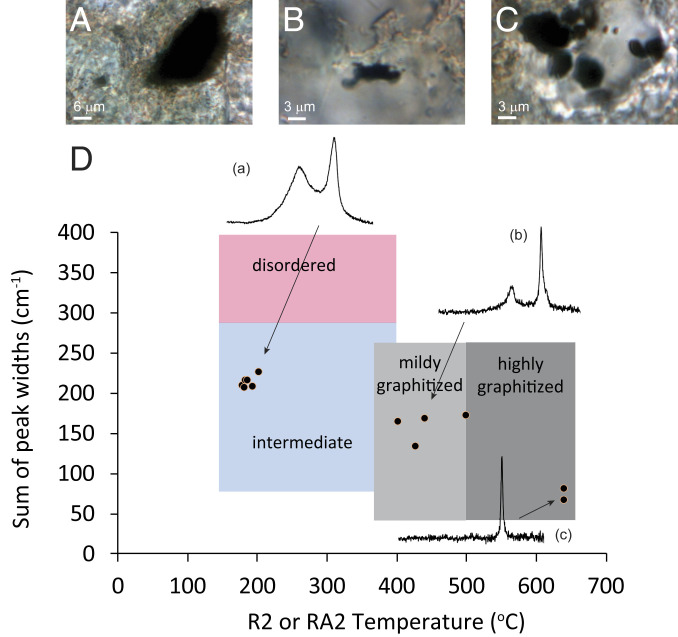
Fig. 1 shows an example from sample XML (Xiamaling Formation) 319.6, a 1,395-Ma-old sedimentary rock from the Xiamaling Formation deposited in a turbidite environment (Table 1). This sample reveals a cluster of kerogens of similar thermal maturity but also several kerogen grains of variable and higher thermal maturity. While most of the analyses from individual formations (SI Appendix, Fig. S1) contained organic matter of similar thermal maturity (SI Appendix, Fig. S1), we identified a total of 11 graphite grains in these preliminary analyses.

Fig. 1.

Raman data for the initial analysis of sample XML 319.6. (A–C) Photomicrographs of selected graphite grains found in the sample. (D) "Sparkes" plot of calculated maturation temperature vs. sum of peak widths, with examples of Raman spectra. Regions of different thermal maturity are also shown after Sparkes et al. (29).

The graphite in our samples clearly reflects organic matter recycled from continental rocks, and graphite itself may be viewed as the highest metamorphic grade of petrographic carbon that also includes rock-derived kerogen (30–32). Recycled petrographic carbon is found in modern river and marine sediments (29, 30, 33–35), and there is also evidence that the recycling becomes more efficient with increasing rates of uplift, denudation, and riverine particle load (e.g., refs. 29, 30, 32, and 36). One might, therefore, expect variability in the amounts of recycled petrographic carbon in marine sediments based on the sediment source.

Petrographic Carbon in Modern Marine Sediments.

Concentrations of graphitic carbon have been determined by others in a few modern marine sediments, with values of 0.031 to 0.09 wt% in Washington shelf sediment (34, 37), 0.016 wt% for sediments of the Mexican margin, 0.012 wt% for sediments of the Equatorial Pacific (37), and 0.01 to 0.11 wt% for sediments of the Gulf of Cádiz (Spain) (38). With this limited data, modern marine sediments seem to contain recycled graphitic carbon with concentrations ranging from around 0.01 to 0.1 wt%.

While recycled kerogen has been identified by Raman spectroscopy in marine and lake sediments derived from rapidly uplifting mountainous terrains in Southern Taiwan (29), the concentrations of recycled kerogen in modern marine sediments are not quantified. However, the flux of riverine petrographic carbon to the oceans, including kerogen, is estimated at 43 × 10⁶ tons ⋅ y⁻¹ (35). This flux would yield a marine sediment petrographic carbon concentration of 0.22 wt% when combined with total sediment discharge of 19,000 × 10⁶ tons ⋅ y⁻¹ (39). If graphite amounts account for 0.01 to 0.1 wt% C of this petrographic carbon, then recycled kerogen may exceed the amounts of recycled graphite. However, riverine-derived petrographic carbon, including kerogen, is also oxidized during river transport (30, 33). We conclude that the concentrations of recycled kerogen in marine sediments are still unresolved and indeed unconstrained by direct measurements.

Raman Analyses of Nine Proterozoic-Aged Geological Formations.

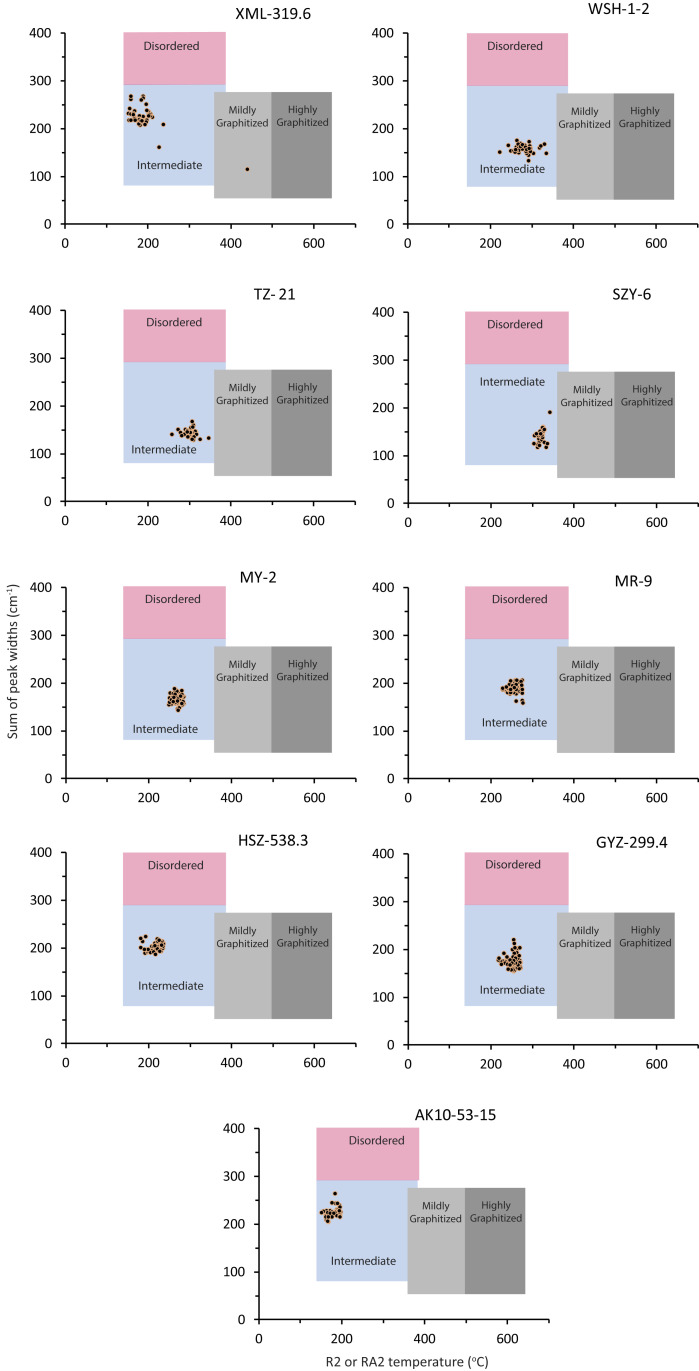
To quantify the amounts of recycled petrographic carbon in our nine geologic formations, we produced Raman spectra for from 224 to 2,510 randomly chosen organic carbon grains (SI Appendix) from thin sections from each formation. All of these randomly produced spectra were of sufficient quality to identify graphite, while between 42 and 80 of them from each formation were of sufficient quality for calculations of T_max. As with our preliminary data, we visualize our results in a “Sparkes” plot (Fig. 2). In a total of 5,646 individual random analyses, we identified only one graphite grain, and this grain was found in sample XML 319.6 (Fig. 2). We found more graphite in our initial Raman analyses of this sample (Fig. 1), but, as noted above, these analyses represented extensive searches during multiple sessions where we were specifically looking to identify graphite. The random Raman analyses are therefore more representative of graphite content than the initial analyses. Overall, our random analyses demonstrate that recycled graphite is rare in the sedimentary rocks that we analyzed.

Fig. 2.

Results from Raman analyses of randomly chosen regions of samples from nine different Proterozoic-aged geological formations with the data plotted on a “Sparkes” plot. Also shown are different regions of thermal maturity (29).

When viewed on the “Sparkes” plot, the kerogens from these different formations form relatively tight clusters (Fig. 2), with the exception of XML 319.6, where two kerogen grains plot well outside of the cluster. Thus, except for this sample, recycled kerogen seems also to be rare in our samples.

We cannot rule out, however, the possibility that in some of our higher maturity samples (e.g., SZY-6, TZ-21), low-maturity kerogen, as found for example in XML-319.6 and AK10-53–15, was recycled but converted to higher maturity kerogen during geological heating of the sedimentary rocks. If this happened, the recycled kerogen would be masked. As source terrains likely contain rocks of variable thermal maturity, we find it highly unlikely that substantial amounts of low-maturity kerogen would be actively recycled in the absence of higher maturity kerogens and graphite, especially as low-maturity kerogens are more easily oxidized than high maturity petrographic carbon during weathering (40). As noted above, in modern terrains experiencing active uplift, petrographic carbon is recycled with a wide range of maturities including graphite (29). Since graphite is rare in our samples, as is obvious recycled kerogen, we suggest that kerogen was also effectively oxidized during the weathering of continental rocks during the time period from 742 to 1,729 Ma, at least as effectively as today.

From our data, we calculate maximum concentrations of graphite ranging from 0.0005 to 0.069 wt% in individual formations based on the concentration of organic matter in the rocks and the assumption that the next random analysis would have yielded a graphite grain (Table 1). For XML 319.6, a single grain was found, so this graphite concentration is not a maximum value. Maximum recycled kerogen concentrations were similarly calculated, noting that for the XML 319.6, two recycled kerogen grains were found, so this calculation is also not a maximum concentration (Table 1). As the numbers of analyses suitable for precise temperature determinations (and used to identify recycled kerogen) were fewer than those suitable to identify graphite, our maximum concentrations for recycled kerogen are higher than those for graphite (Table 1). However, as noted above, kerogen should be more easily oxidized during weathering than graphite. Therefore, a reasonable maximum concentration for recycled kerogen is likely closer to the estimated maximum concentration for recycled graphite in those samples where recycled petrographic kerogen was not found. From these data, we generate two estimates for maximum petrographic carbon concentration for each formation: one summing the separate maximum estimates for graphite and kerogen concentrations (Petro-1) and the other assuming maximum kerogen concentrations were the same as maximum graphite concentrations (Petro-2) (Table 1).

Model Constraints on Atmospheric Oxygen Concentrations.

Our observations on the concentrations of recycled petrographic carbon allow us to place constraints on minimum levels of atmospheric oxygen. To do so, we model the fate of petrographic carbon from weathering in soils through river transport to the final site of deposition in marine sediments. Our weathering model follows that of Bolton et al. (41), incorporating the oxygen dependency of coal oxidation from Chang and Berner (23). As Chang and Berner (23) experimented with bituminous coal, their carbon oxidation rates are appropriate for kerogen but likely overestimate the oxidation rate of more thermally mature graphite (40). We explore some caveats with using these oxidation kinetics in Methods.

The model of Bolton et al. (41) contains a variety of parameters including rate of uplift as it controls the time available for oxidation, the processes controlling oxygen diffusion through rocks and soils as well as the concentrations of organic carbon (and pyrite, also an oxygen sink). In our modeling, we explore uplift rate as a free parameter and use a distribution of organic carbon concentrations consistent with measurements from Mesoproterozoic rocks (SI Appendix) with a pyrite sulfur content (by mass) three times lower (SI Appendix). We also consider that further oxidation of petrographic carbon may occur as particles are transported down river to the oceans and that clastic particles derived from sedimentary and metasedimentary rocks are diluted by particles derived from the weathering of crystalline rocks (SI Appendix).

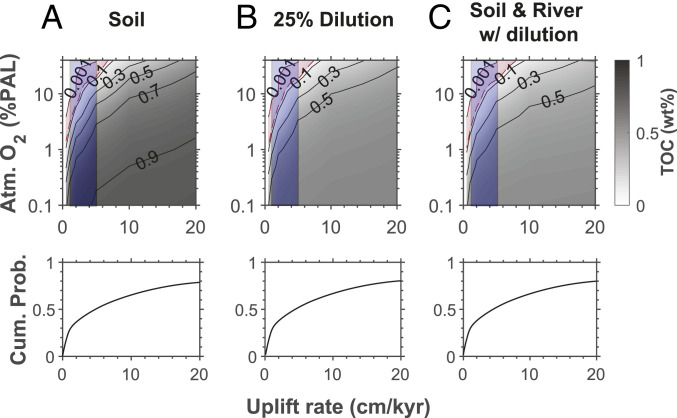
Model results (Fig. 3) show the concentrations of petrographic carbon expected in surface soils (Fig. 3A) and marine sediments without (Fig. 3B) and with (Fig. 3C) river oxidation as a function of atmospheric oxygen (percent PAL) for different rates of uplift. The cumulative probability of uplift rate as estimated from denudation rates in modern river basins (SI Appendix) shows that 20% of all modern rivers, delivering 2.2% of all particles to the ocean, drain landscapes with uplift rates of less than 0.5 cm ⋅ ky⁻¹, while 53% of all rivers delivering 17% of all particles to the oceans drain landscapes with uplift rates less than 5 cm ⋅ ky⁻¹. Thus, with modern rivers as a guide, an uplift rate of 0.5 cm ⋅ ky⁻¹ represents a probable lower limit for the rivers supplying particles to the sedimentary rocks we have sampled, while an uplift rate of 5 cm ⋅ ky⁻¹ represents a conservative upper estimate. This upper estimate is also equivalent to the average rate of continental uplift on the modern Earth (42).

Fig. 3.

Results from our soil carbon oxidation model showing the concentrations of organic carbon for different concentrations of atmospheric oxygen and different rates of uplift. (A) Concentrations of organic carbon in the surface soils. (B) Concentrations of petrographic carbon exported to marine sediments assuming dilution by clastic particles from nonsedimentary rocks. (C) Concentrations of petrographic carbon exported to marine sediments including oxidation during river transport. The blue field shows the likely range of uplift for the terrains supplying particles to the sedimentary rocks of our study. (Bottom) The cumulative probability of uplift rate for modern river basins. See text for details.

As expected (Fig. 3A), organic carbon is more efficiently oxidized at lower uplift rates and higher concentrations of atmospheric oxygen (see also, refs. 24 and 41). In addition, the concentration of petrographic carbon exported to marine sediments is less than in surface soils because of dilution by particles derived from crystalline rocks (Fig. 3B), and river oxidation further reduces the concentration of recycled petrographic carbon (Fig. 3C). The most likely minimum estimates for atmospheric oxygen lie between the predictions based on no river oxidation (Fig. 3B) and those for additional oxidation during river transport (Fig. 3C). We use a length scale for river oxidation of 700 km. This is a conservative upper value, as it is longer than 80% of modern rivers and it also assumes that all particles are introduced in the river headwaters (SI Appendix); particles introduced downstream would experience less oxidation.

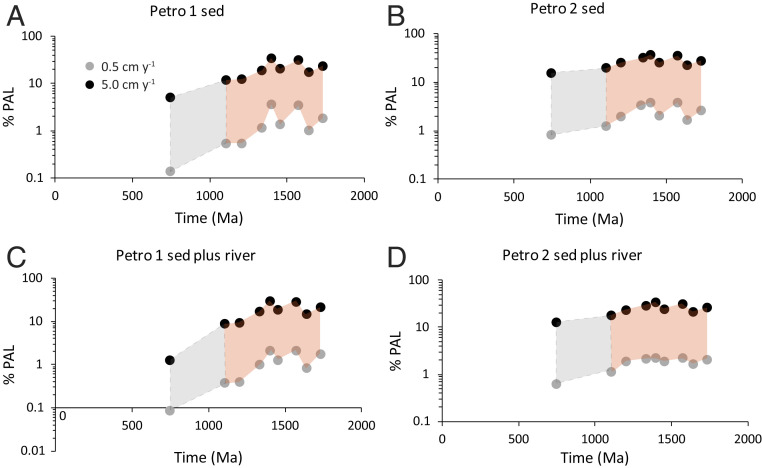
We use these model results to calculate minimum atmospheric oxygen levels from our estimates of maximum petrographic carbon content (Table 1). Our calculations use both the minimum uplift rate of 0.5 cm ⋅ y⁻¹ and our maximum uplift of 5 cm ⋅ y⁻¹ (Fig. 4 and Table 1). In the absence of river oxidation, minimum atmospheric oxygen levels range mostly between 1 to 3.5% PAL and 12 to 35% PAL for Petro-1 (Fig. 4A and SI Appendix, Table S3) and 2 to 4% PAL to 21 to 39% PAL for Petro-2 (Fig. 4B and SI Appendix, Table S3). With 700 km of river oxidation, these minimum oxygen estimates are somewhat reduced to mostly between 0.4 to 2% PAL and 9 to 30% PAL for Petro 1 (Fig. 4C and SI Appendix, Table S3) and 1 to 2 and 18 and 35% PAL for Petro 2 (Fig. 4D and SI Appendix, Table S3).

Fig. 4.

Minimum oxygen estimates as a function of time based on our carbon oxidation model both without (A and B) and with (C and D) oxidation during river transport and for high (Petro 1, A and C) and low (Petro 2, B and D) estimates for maximum concentrations of petrographic carbon. The colored field shows the range of minimum oxygen estimates constrained by uplift rates of 0.5 cm ⋅ y−1 and 5 cm ⋅ y−1. The grey colored field between 742 and 1,100 Ma shows the lower oxygen estimates based on the high petrographic carbon estimates for sample AK10-53–15. We found no recycled petrographic carbon in this sample, and the high resulting petrographic carbon estimates (yielding lower estimates for atmospheric oxygen concentration) are based on the high TOC concentration of the sample. See text for details.

Overall, our lowest rate of denudation (0.5 cm ⋅ ky⁻¹) suggests minimum atmospheric oxygen levels for individual formations ranging from 0.4 to 4% PAL from the period of 1,100 to 1,729 Ma, while for our maximum rate of denudation, 5 cm ⋅ ky⁻¹ (also the Earth-surface average), individual formations have minimum oxygen levels of 9 to 35% PAL (both Petro-1 and Petro-2). These values become slightly elevated (mostly 2 to 4% PAL at 0.5 cm ⋅ y⁻¹ to 20 to 35% PAL at 5 cm ⋅ y⁻¹) if we focus on Petro-2.

The actual minimum estimates for atmospheric oxygen for each formation lie within a band encompassing both the low and high minimum oxygen estimates for that formation (Fig. 4). These rather elevated levels of atmospheric oxygen concentration are compatible with other minimum estimates for Mesoproterozoic Era (1,000 to 1,600 Ma) oxygen concentrations of 1 to 4% PAL (19–21) but extend these minimum estimates from the late Paleoproterozoic Era through nearly all of the Mesoproterozoic Era. While we found no recycled petrographic carbon in the 742 Ma Chuar Formation, its organic carbon concentration was too high to yield meaningful minimum oxygen estimates. Our results, however, do not support that oxygen concentrations at 742 Ma were lower than they were between 1,100 and 1,729 Ma. We have plotted the range of minimum oxygen levels estimated from the Petro 2 sed river model bound by estimates at 0.5 cm ⋅ ky⁻¹ and 0.5 cm ⋅ ky⁻¹ (Fig. 5). We believe these represent a realistic range of minimum oxygen levels as the Petro 1 model likely overestimates petrographic carbon concentrations, yielding unrealistically low oxygen estimates.

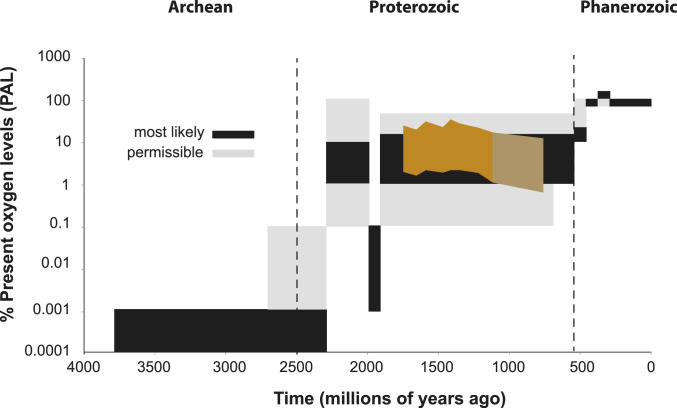
Fig. 5.

Results from the Petro 2 sed plus river analysis of minimum oxygen levels plotted on the long-term trend in atmospheric oxygen evolution that is replotted from ref. 71, including the regions of oxygen levels deemed as "most likely" and "permissible" with available evidence. The separate colored field between 742 and 1,100 Ma designates the lower oxygen estimates based on the high petrographic carbon estimates for sample AK10-53–15.

However, even with the low oxygen estimates of the Petro 1 model, the atmosphere and surface oceans of the middle Proterozoic Eon were not as oxygen starved as has been previously argued (e.g., refs. 13, 15, and 18), although the low end of our minimum estimates overlap with Mesoproterozoic and early Neoproterozoic estimates of 1 to 2% PAL based on the thermodynamic modeling of cerium anomalies (12). We worry, however, that the thermodynamic modeling of cerium anomalies could underestimate minimum oxygen levels as it predicts Paleozoic Era oxygen levels as low as 1% PAL, and such low levels would seem to be incompatible with the likely oxygen requirements of mobile animals at this time (43).

Conclusions

Overall, our estimated minimum oxygen levels in the 2 to 20% PAL range from the late Paleoproterozoic Era into the Neoproterozoic Era were likely sufficient for algae, single-celled eukaryotic protists, and even for early animals (44, 45). Therefore, oxygen was likely not an impediment to the development of early eukaryote ecosystems. Rather, these ecosystems likely evolved in response to other ecological constraints such as nutrient availability, as it controlled the balance between prokaryotes and eukaryotes in the ecosystem (46–48) and evolution, as it controlled developments in feeding, predation, multicellularity, and animal cellular organization (49). Our results provide further critical constraints on interpreting the ancient proxy record of environmental chemistry and generate a foundation for evaluating the relationship between the biological and chemical evolution of the Earth. Finally, our results are the most comprehensive survey of petrographic carbon in sediments of any age, demonstrating active carbon recycling through oxidative weathering through 1 billion years of Proterozoic Eon Earth history. As carbon was actively oxidized during weathering, recycled carbon was not a major component of the sediment carbon pool, meaning that both carbon concentrations and carbon isotopic values reflect, mostly, the activities of the contemporaneous biosphere.

Methods

Raman Spectroscopic Analysis.

Raman spectral analyses were performed on polished thin sections in two different ways: 1) point analyses on selected targets and 2) random point analyses covering a section of the thin section. The first approach was used to obtain bulk grades of maturity. Measurements were made using a 514-nm laser excitation, and the laser was focused below the surface. The second approach was specifically used to determine the relative amounts of recycled petrographic carbonaceous material. Measurements were made using a 532-nm laser excitation, and the laser was rapidly moved along the surface of the thin section. Since the two methods were applied using two different Raman spectroscopes, the analytical details are discussed here separately. We then present our spectral treatment protocols and calculations of T-max using well-known Raman-based geothermometers. In the SI Appendix we provide more background, and provide a short discussion on the excitation wavelength dependency of the Raman spectrum of carbonaceous materials and a discussion on the effects of polishing on the structure of graphitic materials.

Method 1: Individual Point Analyses.

Specific initial point analyses were performed using a Renishaw inVia Raman spectrometer coupled to an Olympus BX61 Confocal microscope within the PARI (Plateau d'analyse haute résolution) analytical platform at the Institut de Physique du Globe de Paris (IPGP). Measurements were made with a 514-nm excitation laser (Ar-ion laser) adjusted to an on-sample intensity of 0.7 mW and a spot size of <2 µm (50× objective). Beam centering and Raman spectral calibration were performed on a pure silicon chip with a specific Raman band at 520.4 cm⁻¹. All spectra were detected using 1,800 l/mm grating and a detector configuration in Streamspot mode, providing a spectral range of >2,000 cm⁻¹ in static mode. Individual spot analyses were obtained in both static mode (2 × 20 s exposure, central position at 1,150 cm⁻¹ with a spectral range of 133 to 2,030 cm⁻¹) and extended mode (1 × 20 s exposure, spectral range 100 to 4,000 cm⁻¹).

Method 2: Random Points Analysis.

To obtain statistically meaningful estimates of the fractions of recycled carbonaceous material, random sets of points were programmed for analysis (SI Appendix, Fig. S2A). These randomized analyses were performed using the LabRAM HR Evolution instrument of the Department for Geosciences, Friedrich Schiller University Jena, Germany. Measurements were made with a 532-nm laser (diode laser) adjusted to an on-sample intensity of 0.25 mW and a spot size of <2 µm (50× objective). All acquired Raman spectra were calibrated for the Raman shift (cm⁻¹) using an internal calibration objective with an imbedded polymer. All spectra were detected using a 600 l/mm grating and a 50 cm⁻¹ cutoff edge filter combined with a 1024 × 128-pixel EM-CCD (electron multiplying charge coupled device) detector. The central position of the spectrometer was set to 1,350 cm⁻¹, recording the spectral region from ca. 530 cm⁻¹ to ca. 2,100 cm⁻¹ (2 × 10 s). The short recording time per point led to spectra of relatively low quality, good enough in all cases to detect the presence of high-grade carbonaceous fractions, but only in some cases of sufficient quality for further spectral treatment. The total number of obtained random spectra per sample, and the number of selected spectra for treatment, are shown in Table 1. For each of the random spectra, a possible graphitic character was determined by visually inspecting spectra and identifying those with a narrow or absent D1 peak and a narrow G peak. These spectra (Fig. 1 and SI Appendix, Fig. S1) were extremely rare but could be effectively detected in the large datasets.

For two samples, TZ-21 and WSH-1–2, it was necessary to revert to the inVia Raman spectrometer at IPGP Paris and to obtain Raman hyperspectral maps with a fixed grid instead of completely random point analyses. Each of these methods, however, provides a random accounting of the different carbon grains within the sample. The data obtained for samples TZ-21 and WSH-1–2 used the same settings as for Method 1 with an on-sample laser intensity of 0.8 mW and an exposure time of 3 s per spectrum. For each sample, three maps were obtained of 800 points each (2,400 points per sample).

Spectral Treatment and T-Max Calculations.

All individual point spectra, as well as selected random point spectra, were treated with the same protocol consisting of the following: 1) truncation, 2) baseline subtraction, and 3) peak fitting. Using the program “Raman Tool Set,” large numbers of individual spectra per sample were uniformly truncated to 800 to 1,900 cm⁻¹, and a background subtraction was performed using a second-order polynomial. Using the curve fitting software Fityk, a peak fitting of spectra was subsequently performed. We employed two established peak-fitting protocols for low-grade (<330 °C) carbonaceous fractions (27, 28) and one for high-grade (>330 °C) carbonaceous fractions (26). The Kouketsu protocol (28) makes use of a selection procedure that is based on the overall band-intensity ratio 1,600/1,350 cm⁻¹. An intensity ratio above 1.5 required a peak fitting as shown in SI Appendix, Fig. S2B. For this procedure, a D1 peak was set with a starting position at ca. 1,350 cm⁻¹. D3 and D4 peaks were set to fixed positions at 1,510 cm⁻¹ and 1,245 cm⁻¹, respectively. The spectral maximum at ca. 1,600 cm⁻¹ was treated as a single peak referred to as the D2 peak. For this procedure, all peaks were set using Voigt functions. The width of D1 (FWHM [full width at half maximum]-D1) was then determined. For an intensity ratio below 1.5, a G peak was set to a fixed position at 1,593 cm⁻¹ with a Lorenz function. All other peaks (D1, D2, D3, and D4) were set using Voigt functions at the positions described above, with the position of the D4 peak fixed to 1,245 cm⁻¹. After peak fitting, the FWHM of the D1 peak was determined with both Raman spectral analytical procedures to apply the geothermometer T = −2.15 (FWHM-D1) + 487 (28).

For the Lahfid protocol (27), spectra were decomposed into the D1, D2, D3, D4, and G peaks (SI Appendix, Fig. S2B) using Lorenz functions with starting positions at 1,360, 1,620, 1,500, 1,180, and 1,580 cm⁻¹ (50). The peak intensity–based ratio RA2 = (D1 + D4)/(D2 + D3 + G) was subsequently calculated, and the geothermometer RA2 = 0.0045T + 0.27 could be determined (27). In the high-grade carbonaceous fractions, the D4 peaks (and in most cases, also the D3 peaks) were absent, and the intensity-based parameter R1 = D1/G and area-based parameter R2 = D1/(D1 + D2 + G) were calculated. From this, the geothermometer T = −445 × R2 + 641 was determined (26).

Modeling.

We used our Raman results from ancient sediments to calibrate ancient levels of atmospheric oxygen through modeling following the approach of Bolton (41) (with some changes) who modeled the oxidation of petrographic carbon in soils. The kinetics of petrographic carbon oxidation are based on the oxygen dependency of carbon in bituminous coal from the study of Chang and Berner (23), and, in particular, we used the results from preoxidized coal with experiments run at a temperature of 24 °C. In the soil oxidation model of Bolton et al. (41), the carbon oxidation kinetics from Chang and Berner (23) were fit to a Michaelis–Menton expression with km (half-saturation constant) of about 0.2 PAL. In contrast, we have chosen to use a power-law dependency of oxygen on a carbon oxidation rate from the same results of Chang and Berner (23). Michaelis–Menten (M–M) kinetics are consistent with biological systems experiencing enzyme saturation, while power-law kinetics are more consistent with surface-reaction control processes (e.g., ref. 51). The power law given by ref. 23 is the following: Rate = 0.28[O₂]^0.4, where Rate is in 10⁻¹² moles O₂ m⁻² ⋅ s⁻¹ and [O₂] is in mM in fresh water at 24 °C, but in making this power law, Chang and Berner (23) did not include their results from the lowest oxygen concentration experiment. If we include these results, the rate law becomes Rate = 0.48[O₂]^0.31 (also see ref. 41). This rate law generates more rapid carbon oxidation at lower oxygen concentrations and therefore yields lower oxygen levels in our modeling results. This rate law also generates more rapid carbon oxidation at low oxygen concentrations compared to the M–M kinetics used by Bolton et al. (41).

Chang and Berner (23) have provided the only available data relevant to the oxygen dependency of petrographic oxidation, but we offer some caveats. As described above, our rate law for petrographic carbon oxidation follows rates of oxygen uptake during the experiments. However, in some cases, CO₂ production was also measured, and these rates are lower than those associated with oxygen uptake. Rates of CO₂ production also seem to follow a M–M-type rate law, with low CO₂ production only at the lowest oxygen levels explored rather than the power-law kinetics that we have used. Chang and Berner (23) argued that the difference between their oxygen uptake and CO₂ liberation rates resulted from the formation of oxygen-rich organic carbon moieties. It is unclear, but possible, that on long time scales, such oxygenated moieties would be more susceptible to terminal oxidation to CO₂, thereby equalizing the rates of oxygen uptake and CO₂ production. In any event, by choosing the more rapid oxygen uptake kinetics, we make a conservative choice on rates of petrographic carbon oxidation, yielding conservatively low estimates for atmospheric oxygen.

There is also evidence that microbes could be involved in petrographic carbon oxidation (e.g., ref. 52), including the oxidation of graphite (53, 54). As Chang and Berner (23) took no special precautions to exclude microbes from their experiments, microbes had a possible, but uncertain, role in the oxidation of carbon in the experiments. Calibrating the work of Chang and Berner (23) to natural weathering conditions, however, will require further work. This may be particularly true for ancient Earth conditions when major groups of modern organisms, like fungi, may have been absent from the ecosystem. Finally, the results of Chang and Berner (23) were obtained from the oxidation of kerogens in coal, and it is uncertain how these rates quantitatively relate to the oxidation of more crystalline graphite. This issue is considered in more detail above in the main text.

To continue with the modeling. we follow Archie’s Law of diffusion as in Bolton et al. (41). In following Bolton et al., and others, we use D_s/D_o = b_t(ϕ_a)^n* (41, 55), where D_s is the diffusion coefficient in the rock/soil, D_o is the diffusion coefficient in air, b_t is a constant, ϕ_a is the air-filled porosity, and n* is an exponential factor related to the tortuous path that solutes or gases take as they diffuse through porous media. An n* value of 2 is typical for diffusion in soils and rocks (e.g., refs. 56–58) and was a value preferred by Bolten et al. (41). We have chosen this value in our modeling. Higher values of n* generate slower diffusion through the rock and yield higher minimum oxygen estimates, while lower values would generate faster diffusion and lower oxygen estimates.

The concentration of organic carbon in rocks significantly affects the distribution of oxygen in weathering profiles and therefore the preservation of organic carbon during weathering. As explored by Bolton et al. (41), higher concentrations of total organic carbon (TOC) lead to more carbon preservation at the surface of the weathering profile at the same rate of uplift. In our modeling, we have used the frequency distribution of TOC measurements from Mesoproterozoic and late Paleoproterozoic sedimentary rocks (SI Appendix, Fig. S3), considering only those rocks with a TOC content of <4 wt%, as we believe that rocks with higher TOC content are likely oversampled. We then separate these analyses into five bins of equal numbers yielding an overall average TOC content of 0.98 wt% and the distribution of TOC concentrations in each bin as indicated in SI Appendix, Table S4. We assume that an average river basin will drain siliciclastic sedimentary rocks with this distribution of TOC values.

Our average TOC values are similar to the modern sediment value of 0.84 wt% for continental margin siliciclastic sediments (59) and nearly identical to the 1% TOC value used by Daines et al. (24) in their modeling. Our average TOC value, however, is much lower than the average of 3 wt% for Mesoproterozoic sedimentary rocks and 2.3 wt% for Paleoproterozoic sedimentary rocks as compiled by ref. 60. As noted above, these high values could reflect a preference for studying high TOC sedimentary rocks leading to an over representation in the literature. The compilation from which our data are derived contains several full sedimentary sequences with both high and low TOC rocks (61). In any event, as noted above, lower values of TOC in the weathering environment generate lower estimates for atmospheric oxygen in our modeling.

After having oxidized TOC in the soil model, we follow the oxidation of weathered petrographic carbon during its transfer in river basins to its final destination in marine sediments. We model river length, noting that 88% of modern rivers have total lengths of 700 km or less (SI Appendix, Fig. S5C) and that petrographic carbon particles will likely not all enter at the river headwaters. Therefore, in using 700 km for river oxidation, we likely overestimate petrographic carbon oxidation during river transport, generating, ultimately, conservatively low estimates of atmospheric oxygen. In modeling river petrographic carbon oxidation, we utilize the carbon oxidation kinetics of Chang and Berner (23), and in modeling petrographic carbon river transport and oxidation, we adapt a standard reaction–transport–diffusion model (62, 63). In our model, we scale diffusion to transport velocity by a Peclet number of 50, while the time step is set by a Courant number of 1.

Effective particle transport velocities are estimated from mean transit times for different large river systems determined by the U-series method (64–66) and a geometrical scaling model for the particle transport/storage in large river systems (67) (SI Appendix, Table S6). The U-series method gives the longest mean transport times for present day large rivers, and thereby the smallest effective transport velocities, resulting in the largest kerogen mass loss (SI Appendix, Fig. S6 and Table S6). The geometrical scaling model of Torres et al. (67) considers lateral channel migration, deposition, and erosion of floodplain sediments, leading to transient sediment storage, and it results in the shortest mean transport times and thereby the least kerogen mass loss (SI Appendix, Fig. S6 and Table S6). Considering the wide range of mean transport times, we take the transport time as a free parameter. In our reaction–transport–diffusion model, we find that the intermediate mean transport time of ∼18,000 y, together with the carbon oxidation kinetics from Chang and Berner (23), reproduce the reported amounts of petrographic carbon oxidation for the Himalayan–Ganges–Brahmaputra river-fan system and the Amazon river system (30, 33) (SI Appendix, Fig. S6). This becomes our preferred transport time in our modeling of riverine petrographic carbon oxidation.

We have also considered the dilution in marine sediments by particles not associated with the weathering sedimentary rocks. We begin with the distribution of different rock types at the Earth’s surface (68) divided into 66% sedimentary rocks, 17% crystalline rocks, and 17% metamorphic rocks. From (69) crystalline rocks are 9% igneous, 8% volcanic, and we assume that metamorphic rock types have the same distribution as sedimentary and crystalline rocks, yielding 80% metasediments and 20% metacrystalline rocks. From ref. 70, sedimentary rocks are composed of 23% carbonate rocks with the remainder siliciclastic rocks. From these values, noncarbonate sediments and metasedimentary rocks comprise 75% of the siliciclastic particles being weathered, while crystalline rocks (igneous and volcanic) contribute 25% and dilute organic matter liberated from the weathering of sediments and metasediments by this amount. These relative proportions of rock types could have been different during Proterozoic times, and they would also likely have varied between different river basins. However, there are no constraints on the original distribution of rock types to weathering through the Proterozoic Eon and even less so on how rock types might have varied in individual ancient river basins. So, we have adopted the modern distribution, recognizing that there will be some uncertainty with our dilution estimate.

Finally, sensitivity analysis of our model with different concentrations of organic carbon in weathering sedimentary rocks is shown in SI Appendix, Fig. S7. These results show, not surprisingly, that terrains with lower initial contents of petrographic carbon export lower concentrations to marine sediments at a given uplift rate and oxygen level. Our model does not include the possible influence of contemporaneous biomass on carbon oxidation and oxygen distribution in soils. We feel this assumption is justified, as the terrestrial biosphere would have likely only consisted of sparsely distributed microbial biomass.

Data Availability

All study data are included in the article and/or supporting information.