Working memory load-dependent changes in cortical network connectivity estimated by machine learning

Abstract

Working memory engages multiple distributed brain networks to support goal-directed behavior and higher order cognition. Dysfunction in working memory has been associated with cognitive impairment in neuropsychiatric disorders. It is important to characterize the interactions among cortical networks that are sensitive to working memory load since such interactions can also hint at the impaired dynamics in patients with poor working memory performance. Functional connectivity is a powerful tool used to investigate coordinated activity among local and distant brain regions. Here, we identified connectivity footprints that differentiate task states representing distinct working memory load levels. We employed linear support vector machines to decode working memory load from task-based functional connectivity matrices in 177 healthy adults. Using neighborhood component analysis, we also identified the most important connectivity pairs in classifying high and low working memory loads. We found that between-network coupling among frontoparietal, ventral attention and default mode networks, and within-network connectivity in ventral attention network are the most important factors in classifying low vs. high working memory load. Task-based within-network connectivity profiles at high working memory load in ventral attention and default mode networks were the most predictive of load-related increases in response times. Our findings reveal the large-scale impact of working memory load on the cerebral cortex and highlight the complex dynamics of intrinsic brain networks during active task states.

1. Introduction

Working memory (WM) is a fundamental cognitive function that allows humans to maintain, manipulate, and control information. It maintains information in an accessible state for a limited time and guides goal-directed behavior (Baddeley, 2012; D’Esposito and Postle, 2015; Eriksson et al., 2015; Miller et al., 2018). WM metrics (e.g., capacity) often predict cognitive measures such as fluid intelligence (Harrison et al., 2015; Wiley et al., 2011). This is not surprising given that WM is an essential component for various domains of human cognition such as executive function, learning, goal-directed behavior, problem solving, and language; and impaired WM is central to many cognitive deficits (Conway et al., 2003; Diamond, 2013; Gathercole and Baddeley, 2014; Titz and Karbach, 2014). While the precise neural mechanisms of WM and how it maintains information in the absence of sensory input are not fully understood, it is thought that interactions between distributed brain networks including prefrontal, parietal, sensory, and motor areas underlie WM maintenance and its executive control (Christophel et al., 2017).

Sustained selective attention is thought to support both encoding and maintenance of information (Eriksson et al., 2015; Petersen and Posner, 2012). This attentional prioritization may explain the limited nature of WM capacity (Conway et al., 2003; Cowan, 2010; D’Esposito and Postle, 2015). However, the impact of WM load on attention and salience networks, as well as other task-related networks remains poorly understood. Functional connectivity is a powerful tool used to characterize brain networks during distinct brain states. Task-based functional connectivity studies have demonstrated that resting state networks largely preserve a core pattern during task states despite subtle reconfigurations (Cole et al., 2014; Gratton et al., 2016, 2018; Krienen et al., 2014; Schultz and Cole, 2016). Supervised machine learning (ML) algorithms have the capacity to assess covariance in connectivity patterns across large number of independent variables and detect such subtle changes (Mahmoudi et al., 2012; Meier et al., 2012). Algorithms such as support vector machines (SVMs) achieve tractability on big data by operating only on the marginal cases (the “support vectors”) that define boundaries between classes (Duda et al., 2001), and have the additional benefit of implicitly guarding against overfitting by minimizing generalization error rather than empirical error (Bishop, 2006; Russell and Norvig, 2010). Furthermore, ML methods have been successful in capturing task-induced variance in functional connectivity (Richiardi et al., 2011). In the current study, we took advantage of the multivariate nature of ML to determine the characteristic connectivity features that produce the most accurate classification of high and low WM load conditions.

In our study, participants underwent fMRI scanning while performing a version of the Sternberg Item Recognition Paradigm (SIRP), which requires short term maintenance of 1, 3, 5, or 7 items in WM. We evaluated functional connectivity among 611 uniformly distributed seed regions covering the entire cerebral cortex, during all four WM load conditions. Each seed was assigned to a cortical network based on the Yeo parcellation (Yeo et al., 2011). We then calculated time series correlations between (611 × 611) seed pairs, and used linear support vector machines and neighborhood component analyses to identify changes in brain connectivity patterns that most robustly indexed WM load. Finally, using a cross-validated analysis, we tested whether task connectivity patterns can be used to predict behavioral performance measured as load-related increases in response time.

2. Methods

2.1. Participants

Study procedures were approved by the Partners Healthcare Human Research Committee and all participants provided informed written consent. The study included 177 healthy young adult participants (age 24.96 ± 3.60, 91 F), who underwent fMRI during resting state and working memory performance. Participants were excluded if they had any history of neurological or psychiatric disease, history of psychotropic medication use, or any MRI contraindications.

2.2. Image acquisition

Participants were scanned at the Martinos Center for Biomedical Imaging at Massachusetts General Hospital using a 3T Skyra magnet (Siemens, Germany) with a 32-channel head coil. The acquisition included a high-resolution T1-weighted image (repetition time/echo time/flip angle = 2530 ms/1.92 ms/7°) with an isotropic voxel size of 0.8 × 0.8 × 0.8 mm³. An interleaved multislice (3 slices) resting-state functional scan was also acquired (repetition time/echo time/flip angle = 1150 ms/30 ms/75°; in-plane resolution = 3 mm × 3 mm; slice thickness = 3 mm, number of volumes = 372), where participants were instructed to keep their eyes open and remain still. Finally, participants performed the Sternberg task while undergoing echo planar imaging (EPI) scans (repetition time/echo time/flip angle = 2000 ms/30 ms/90°; in-plane resolution = 3.6 mm × 3.6 mm; slice thickness = 4 mm, number of volumes = 235).

2.3. Task

A variant of the Sternberg Item Recognition Paradigm was used (Sternberg, 1966). The SIRP is characterized by linear load-dependent increases in response time and brain activation (Kirschen et al., 2005). The task involved encoding a set of consonants and target recognition during probes (Fig. 1). During encoding, a set of 1, 3, 5, or 7 consonants were presented (6 s). After a brief delay screen (1 s), 14 consecutive probes were presented for 1.1 s, separated by a varying intertrial interval (0.6–2.5 s). Participants were asked to indicate, as quickly as possible, whether the probe was a target (presented during encoding) or foil (not presented during encoding) by pressing one of the two keys on a keypad. Each of the four task loads (1, 3, 5, 7) was used twice during the task run (total task duration = ~8 min). Throughout this article we will refer to these four task conditions as 1T, 3T, 5T, and 7T respectively.

Fig. 1.

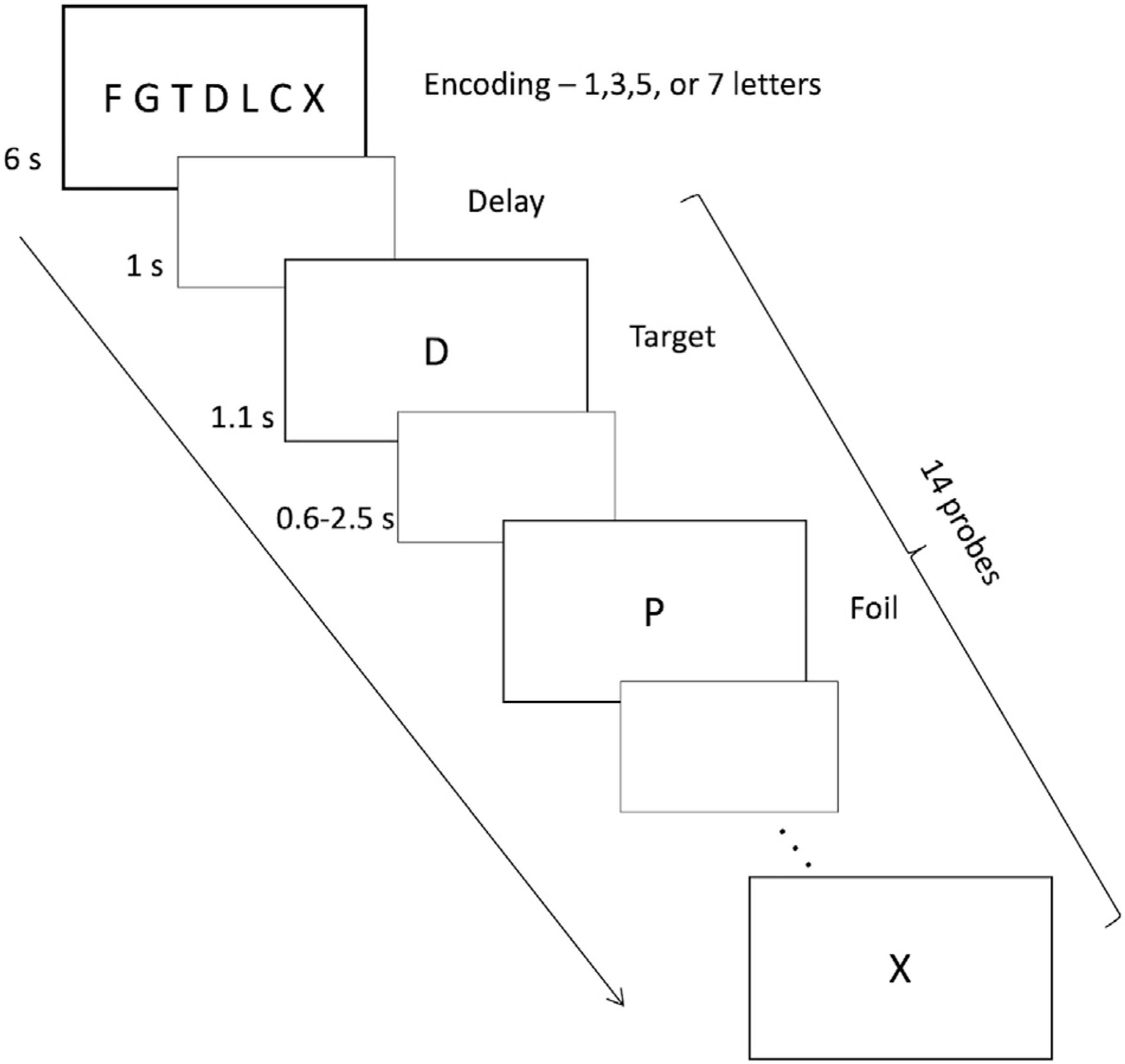
Illustration of the Sternberg task. Each block started with an encoding block where participants were asked to memorize a set of letters (1, 3, 5, or 7 letters). Then, the participants were presented with one letter at a time (probe) to which they were asked to respond by pressing ‘1’ on the keypad if the probe was a foil, and by pressing ‘2’ if the probe was a target. Each WM load was presented twice in an 8-min task run.

2.4. Preprocessing of imaging data and functional connectivity

Functional images first underwent slice timing, realignment, and registration onto an MNI template using affine and nonlinear transforms. They were then resampled to 2-mm isotropic voxels and smoothed using a 6-mm full width half maximum (FWHM) Gaussian kernel. Temporal filtering was applied to eliminate linear trends and retain frequencies below 0.08 Hz. Then, nuisance variables including the signal averaged over the whole brain (global signal), six motion parameters, signal averaged over ventricles and in white matter, and their 12 first temporal derivatives were removed by regression. The residual volumes were used for the functional connectivity analysis. Quality control analysis for head motion was performed using Art Repair (https://www.nitrc.org/projects/art_repair/) and customized scripts (Power, 2017). Framewise Displacement (FD) was computed at each timepoint. The subjects who had average FD > 0.2 mm (over the task run) were excluded from the analysis (n = 5). In addition, volumes with FD > 0.25 mm were scrubbed from the connectivity analysis (see Supplementary Results for additional analysis on FD variation across task conditions). The residual volumes were downsampled to 6×6×6 mm voxels using FLIRT (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FLIRT). In order to reduce dimensionality, we selected 1/8^th of all 6-mm cortical voxels in a uniformly spaced manner using Matlab (Natick, MA, http://www.mathworks.com/), which produced 611 voxels. These voxels were used as seed regions. Each of these 6-mm voxels was assigned a network based on the Yeo parcellation (Yeo et al., 2011). The seed regions were visually inspected and those that were located on Yeo network boundaries (guided by the 2×2×2 mm Yeo MNI template) were moved to the closest location such that they are clearly inside a network. Time courses were then extracted from these 611 seed regions covering the entire cerebral cortex to compute a 611 × 611 correlation matrix for each subject (Fig. 2). Each seed was assigned a cortical network based on a validated cortical parcellation (Yeo et al., 2011). Of the 611 cortical seed regions, 104 were in the visual network (VN), 90 in the somatomotor network (SN), 71 in the dorsal attention network (DAN), 64 in the ventral attention network (VAN), 53 in the limbic network (LN), 91 in the frontoparietal control network (FPCN), and 138 in the default mode network (DMN). In order to compute functional connectivity at different task loads, we extracted time courses at intervals corresponding to the retrieval period (containing 14 probe trials) for a given load (e.g., 1, 3, 5, or 7), during which participants maintained a memorized set, visualized probes, compared them to the memorized set, determined if they were a target (or a foil) and executed a motor response. The time course of each seed was shifted forward by 3 TRs (6 s) in order to account for the hemodynamic lag. This latency was chosen based on the putative peak of the hemodynamic response (Gibbons et al., 2004). For each load, a task correlation matrix (611 × 611) was generated by first appending the time series of all blocks corresponding to that load (total length = 38 time points [76 s]), and then computing the Pearson’s correlation for the time series of all pairs of seeds. Fig. 2 displays the correlation matrices separately for all four loads. The same preprocessing pipeline was used for resting state functional connectivity, which was computed using the full timeseries of the resting state run. Fig. S1 shows the group-averaged resting state correlation matrix.

Fig. 2.

Functional connectivity during four different WM load conditions (N = 177). Correlation matrices were computed using Pearson’s correlations among 611 seed regions on the cerebral cortex covering all 7 Yeo networks. A core pattern characterized by strong within-network connectivity is preserved across different load conditions. Notable changes in connectivity within the ventral attention network, as well as between the ventral attention and default mode networks have been observed. Abbreviations: DAN: dorsal attention network, DMN: default mode network, FPCN: frontoparietal control network, LN: limbic network, SN: somatomotor network, VAN: ventral attention network, VN: visual network.

2.5. Machine learning analysis

Correlation matrices generated for each WM load condition were analyzed using a linear SVM algorithm (fitcsvm) in Matlab. SVMs are a robust supervised ML method that is computationally efficient in large part because they operate on “support vectors” that represent only a small subset of the input data (those data points that sit closest to the hyperplane). SVMs maximize the margin between these support vectors and a separating hyperplane. (Vapnik, 1999). In order to verify the separability of the task conditions needed to meaningfully analyze feature contributions, first we performed binary classification for all possible task condition pairs (1T vs. 3T, 1T vs. 5T, 1T vs. 7T, 3T vs. 5T, 3T vs. 7T, and 5T vs. 7T). Correlation matrices were vectorized to yield 186, 355 unique features representing connectivity between the seed regions. 157,567 of these features encompassed between-network seed pairs (e.g., FPCN-DMN), whereas the remaining 28,788 included within-network pairs (e.g., DMN-DMN). To quantify classifier performance while guarding against overfitting, we calculated the mean out-of-sample accuracy across all folds in a 5-fold cross-validation. For this, we trained an SVM on 80% of the data, tested its performance on the remaining 20%, and repeated with a new SVM for each of five 80/20 splits. This analysis allowed us to assess the separability of each of the task condition pairs.

Next, we further examined the 1T–7T classification to identify the most important features separating low and high WM load conditions. In order to determine which network features contribute most to the classification, we used Neighborhood Component Analysis (NCA) via the fscnca function in Matlab. NCA is a computationally efficient variant of classical “nearest neighbor” methods, which optimizes the classification error by learning a quadratic distance metric. As a nonparametric, unsupervised clustering approach, NCA does not operate on assumptions on distribution of the data and therefore, is more robust to non-Gaussian distributions compared to algorithms using affine transformations (Goldberger et al., 2005). NCA provided us with feature weights for the 1T–7T classification. For the NCA, we used an optimized lambda (regularization parameter) value of 0.02, which minimized classification loss (Yang et al., 2012).

Once the feature weights were computed by the NCA, we ranked all features by their weight and reanalyzed 1T–7T classification using the same 5-fold cross-validation approach. In order to identify the most relevant features, we ran our SVM procedure iteratively using increasing numbers of input features, starting with two and adding one feature at a time until we reached 1000 features (~0.5% of all features). Fig. 3a shows the average classification accuracy resulting from cross-validation at each iteration. In order to select the most relevant features among the top 1000, we assessed the most stable points (where the standard deviation was minimal) in the accuracy plot. For this analysis, we computed the standard deviation of classification accuracy on a sliding window of 100 features (starting from the first 100 features and moving to the right, e.g., 1–100, 2–101, 3–102 … 900–999, 901–1000). Standard deviation for these sliding windows is depicted in Fig. 3b. We then selected 4 local minima (N = 72, N = 252, N = 385, and N = 649), for which the network distributions were generated. We assessed that N = 385 produced a stable solution with peak accuracy and low standard deviation. In order to determine the brain network distribution of these top features that were most relevant to our WM load classification, we first evaluated the number of features in each within- and between-network pair among the top 385 features. Since each network contains different numbers of seeds, the total number of connectivity features across the network pairs differed. For example, while VN-DMN had the most between-network features with 14,352, VAN-LN had the least with 3392. In order to correct for this disparity and account for differences in network size when computing prevalence of each network pair, we multiplied the number of occurrences of a given network pair (among the top 385 features) by a weight representing the ratio of the total number of features of that pair to the total number of all between-network features (or within-network features if the pair in question is a within-network one). The obtained value represented the contribution of that specific network pair (e.g., VN-DMN) to the classification. See Supplementary Methods for details.

Fig. 3.

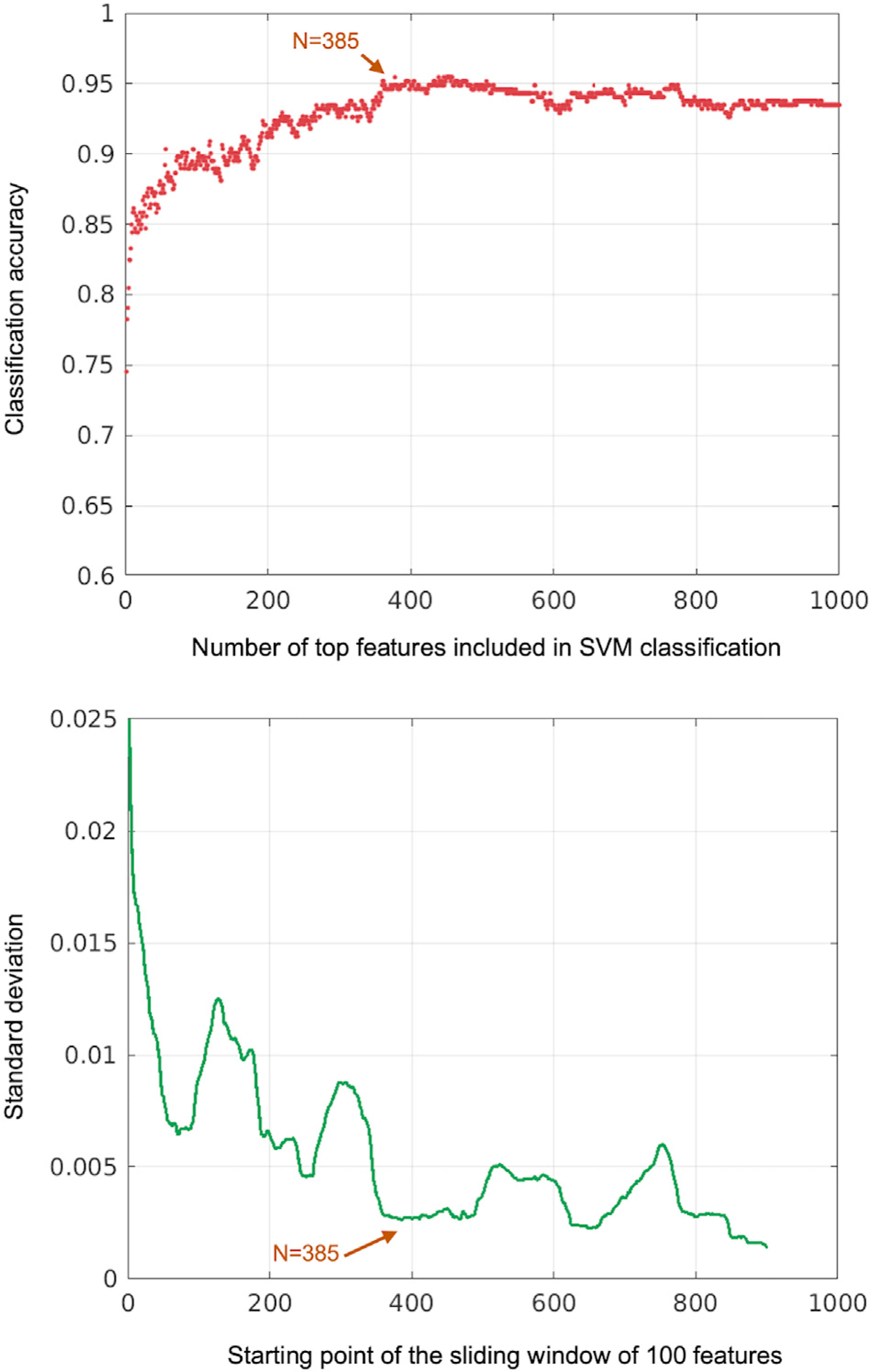
Classification accuracy vs. number of top features included in the SVM analysis. The upper panel shows mean classification accuracy obtained via 5-fold cross validation on SVM classification as a function of top N features included in the analysis. The lower panel shows the standard deviation of mean classification accuracy over a sliding window of 100 features (from top 1–100 to 901–1000). The arrows demonstrate a local minimum (N = 385), where the classification accuracy reaches a stable point.

2.6. Behavioral prediction analysis

In order to examine the behavioral relevance of the functional connectivity features, we tested whether these features could be used to predict behavior. As a behavioral measure, we used the difference in response times for loads 1T and 7T (RT_1T – RT_7T or ΔRT), the characteristic behavioral marker of the SIRP (Sternberg, 1969), which provided us with the degree to which subjects slowed down due to increased WM load. Following previously published methods (Finn et al., 2015), we employed leave-one-out cross-validation (LOOCV) to test whether ΔRT could be predicted by a summary statistic derived from functional connectivity during the most demanding task condition (7T). For this analysis, the highest load was chosen, as we aimed to capture the robust load response in the brain, which most likely underpins the load-dependent increase in response time. In this analysis, one subject’s data (test set) is removed from the rest of the dataset (training set) and the training set is used to first determine the edges that show a significant correlation with behavior (feature selection), and then to build a predictive model. Finally, this model is tested on the subject that was left out (prediction). Each subject is left out once. We conducted 3 separate analyses with 3 different feature selection steps. In the first analysis, we included all edges (within- and between-network) during the feature selection step. This analysis allowed us to test whether a global summary statistic (i.e., network strength) could be used to predict behavior. Secondly, we included all within-network edges (e.g., DAN-DAN, FPCN–FPCN) and built a multilinear regression model with local summary statistic for each network as a separate predictor. Finally, the third analysis restricted feature selection to only (within-network) edges of a single network to directly compare the predictive power among all 7 networks. In order to select the most relevant edges, we computed the correlation between each edge in the feature pool and ΔRT across the subjects in the training set. A feature selection threshold determined the edges with the strongest correlation with ΔRT. We used p = 0.01 for the global and within-network models, whereas p = 0.05 was applied for single-network models to obtain reasonably high edge density. Once the most relevant edges were determined, they were then separated into positive and negative sets depending on the sign of the correlation with ΔRT. Next, we computed a summary statistic (for each subject in the training set), which is defined as the sum of the connectivity values of all edges in the feature sets (i.e., positive and negative) separately. This metric represents the ‘network strength’ (Finn et al., 2015). The relationship between network strength and ΔRT was modeled using linear least squares regression for the global and single-network summary statistics:

$$\Delta {\text{RT}}^{\prime }=a^{*}NS+b$$

where NS stands for network strength, ΔRT′ represents the predicted response time change. Two separate models were built for positive and negative feature sets. For the model that includes all within-network edges, we included a different summary statistic for each network:

$$\Delta {\text{RT}}^{\prime }=a_1^{*}N{S}_1+a_2^{*}N{S}_2+\dots +a_7^{*}N{S}_7+b$$

Finally, network strengths have been calculated in the test subject for positive and negative sets and these models were used to predict the ΔRT for that subject. These analysis steps were iteratively repeated until each subject was used as a test subject. Then, the predictive power of these models was determined by the correlation between observed and predicted ΔRT values (p < 0.05).

3. Results

3.1. Behavioral results

As expected, subjects responded highly accurately to the probes at all WM loads (Table 1). Response time for the Sternberg task is characterized as a linear function of the set size (Fig. S2). Based on the typical characterization of the set size-response time plot (Sternberg, 1969), the intercept represents the total duration of all processes that occur once during the processing of a given probe such as encoding the probe and generating its representation. In contrast, the slope reflects the duration of processes that occur once for each item in the memorized set such as comparison of the probe to an item in the memorized set. Fig. S2 depicts the set size-RT plot, its linear best fit, and the putative processes that take place during the retrieval of a probe stimulus.

Table 1.

Behavioral results. Average working memory accuracy and response time for each load are shown (N = 177).

	WM load
WM task accuracy (% correct)
	1T	98.9 ± 2.4
	3T	97.8 ± 4.1
	5T	91.1 ± 5.9
	7T	90.2 ± 7.8
WM task RT (ms)
	1T	617 ± 77
	3T	692 ± 86
	5T	780 ± 93
	7T	846 ± 111

Abbreviations: WM: Working memory, RT: Reaction time.

^*Mean ± Stdev is shown for quantitative parameters.

3.2. Classification

We tested whether SVMs can reliably decode the WM load from 611 × 611 correlation matrices. SVMs are a robust supervised learning method in which the classifier searches for a relationship between input features (connectivity patterns) and a (binary) output category (WM load). Unlike classical univariate statistical methods, SVMs compare the entirety of the data between conditions. For all our binary classification problems (e.g., 1T–3T, 3T–7T etc.), we used a 5-fold cross-validation (five 80/20 splits of train/test set data) to assess classifier accuracy while guarding against overfitting. Mean accuracy rates for all binary classifications are shown in Table 2. As expected, the greatest classification accuracy was obtained between the lowest and highest WM load conditions (1T vs. 7T). High accuracy rates demonstrated that WM load can be reliably decoded from connectivity matrices even in the case of task conditions with similar difficulty (e.g., 5T vs. 7T).

Table 2. Classification accuracy determined by 5-fold cross-validation using all 186,355 features.

For each classification, the SVM classifier was trained in 80% of the data and tested in the remaining 20% to calculate accuracy. This process was repeated 5 times until each 20% data partition was used as a test set. Mean accuracy reflects the average of all 5 values of classification accuracy, while the range depicts the minimum and maximum accuracy for a given classification.

Classification	Mean accuracy	Range
1T–3T	68%	63%–74%
1T–5T	84%	73%–95%
1T–7T	87%	81%–93%
3T–5T	72%	68%–76%
3T–7T	81%	77%–89%
5T–7T	66%	63%–70%

Abbreviations: 1T, 3T, 5T, 7T: Working memory load representing 1-, 3-, 5-, and 7- letter conditions.

3.3. Discriminative connections

SVM classifiers successfully learned brain connectivity features that could be used to reliably discriminate between task conditions (WM load). Next, we aimed to identify those features to better understand the underlying physiological changes that characterize different states of WM load. To this end, using the most robust classification (1T-7T, which yielded the highest classification accuracy in our SVM analyses) we applied a Neighborhood Component Analysis to the input features. NCA is a supervised learning method which optimizes classification error by learning a quadratic distance metric, and is often used to assess feature importance in linear SVM-solved classification problems (Goldberger et al., 2005). NCA estimated feature weights by minimizing its error term with stochastic gradient descent and the limited memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) algorithm (Bottou, 2010; Liu and Nocedal, 1989). We first identified 1000 connections with the greatest feature weights. In order to determine the optimal number of top features, we ran SVM models iteratively using more features. Starting with top 2 features, we computed 1T–7T classification accuracy adding one feature at a time until we reached the top 1000 features. Fig. 3 shows the accuracy rate at each iteration as well as the standard deviation of accuracy over a sliding window of 100 features. Based on this stability analysis, we identified 4 local minima, for which the network connectivity patterns are demonstrated in Fig. S3. Top 385 features provided an optimal point with high classification accuracy and sufficient number of features for a reliable network characterization. Therefore, we analyzed the distribution of network pairs among these 385 features.

In order to obtain the network distribution, we first identified the number of connections for each network pair within the top 385 features. Within- and between-network pairs were analyzed separately. Importantly, we took into consideration the fact that network pairs consisted of unequal number of connections. For example, our 611 × 611 correlation matrix consists of many more FPCN-DMN seed pairs than DAN-LN pairs. Hence, the probability of a given FPCN-DMN pair to appear in the top 385 features is higher than that of a DAN-LN pair. Therefore, the prevalence of each feature was weighted accordingly to eliminate this disproportionality (see Supplementary Methods for details).

Fig. 4 depicts the distribution of brain networks among the top 385 features. Among between-network features, FPCN-DMN, VAN-DMN, DAN-VAN, and VAN-FPCN connectivity contributed most to 1T–7T classification (23%, 15%, 14%, and 14% respectively). These values correspond to the ratio of weighted prevalence of each network to the total sum of all weighted prevalence values, thus representing the contribution of each network when network size is taken into account. Connectivity within VAN and FPCN were the top contributors among within-network connections (67% and 20% respectively). Table 3 displays, for each within- and between-network pair, the total number of features, calculated weight, number of features among the top 385 features, and a weighted prevalence score. Bar graphs in the lower panel of Fig. S4 demonstrates the actual number of connections among the top 385 features for each network pair, as well as the hypothetical number of connections if every network pair contributed equally to the classification of low vs. high WM load. For details on direction of changes in functional connectivity from low to high WM load, see Supplementary Results.

Fig. 4.

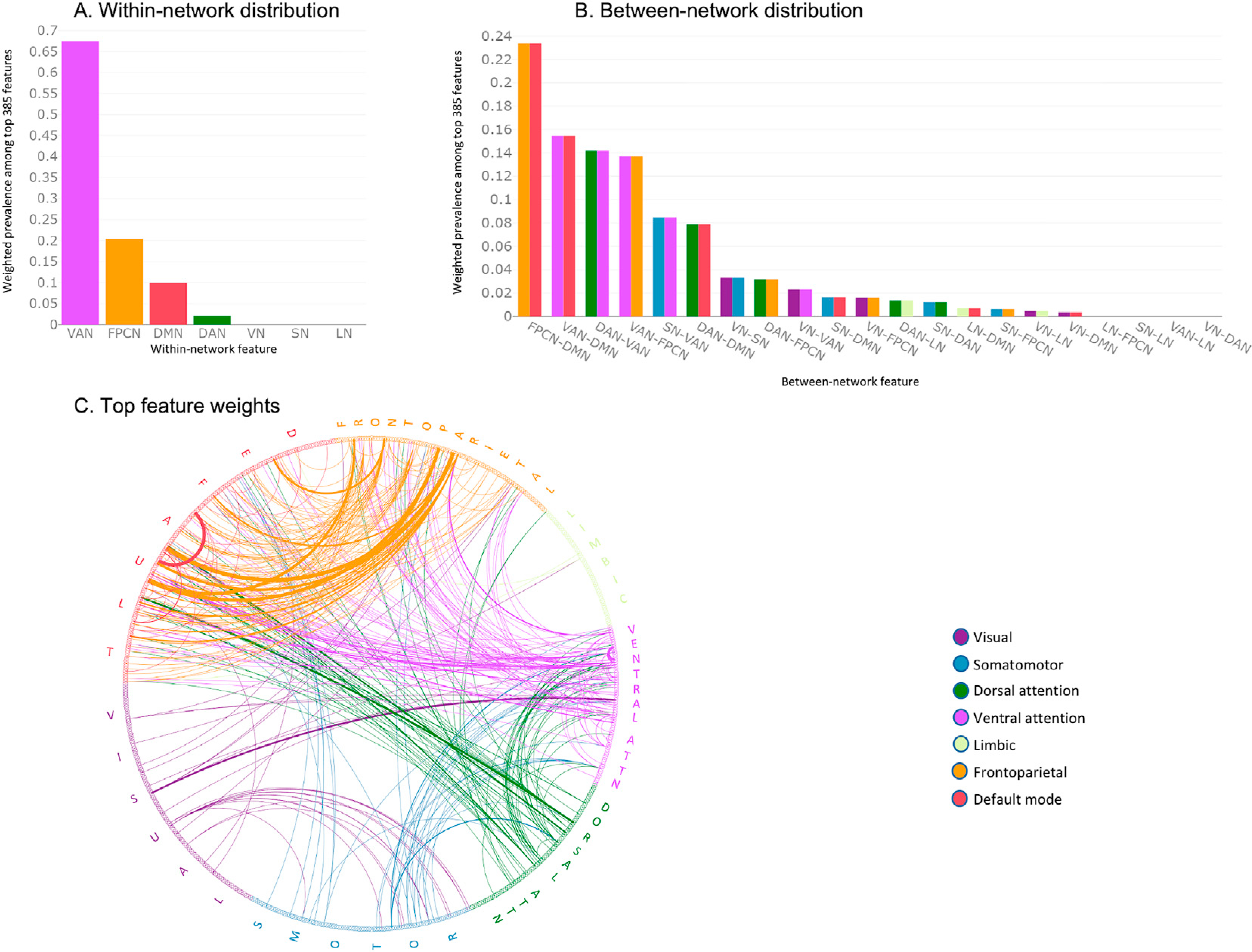
Weighted network prevalence among the primary 385 features separating low vs. high working memory load. Y-axes in the bar graphs shows the ratio of weighted prevalence for each network. A. Weighted prevalence of within-network features for each of the Yeo networks. Coupling within the ventral attention network contributed most to 1T–7T classification. B. Contribution of each between-network set is shown. Functional connectivity among frontoparietal control, ventral attention, and default mode networks contributed most to 1T–7T classification. C. The circular plot depicts feature weights obtained by the Neighborhood Component Analysis for the top 385 features. Line thickness is proportional to the feature weight. Abbreviations: DAN: dorsal attention network, DMN: default mode network, FPCN: frontoparietal control network, LN: limbic network, SN: somatomotor network, VAN: ventral attention network, VN: visual network.

Table 3.

Prevalence of each network pair among top 385 features for 1T–7T classification.

Network pair	Number of features	Weight	Number of features in top 385	Weighted prevalence
Within-network
VAN-VAN	2016	14.28	26	371.28
FPCN–FPCN	4095	7.03	16	112.48
DMN-DMN	9453	3.045	18	54.81
DAN-DAN	2485	7.188	1	7.19
LN-LN	1378	20.891	0	0
SN-SN	4005	11.585	0	0
VN-VN	5356	5.375	0	0
Total	28,788
Between-network
FPCN-DMN	12,558	12.547	114	1430.40
VAN-DMN	8832	17.841	53	945.57
DAN-VAN	4544	34.676	25	866.90
VAN-FPCN	5824	27.055	31	838.71
SN-VAN	5760	27.355	19	519.75
DAN-DMN	9798	16.082	30	482.46
VN-SN	9360	16.834	12	202.01
DAN-FPCN	6461	24.387	8	195.10
VN-VAN	6656	23.673	6	142.04
SN-DMN	12,420	12.687	8	101.50
VN-FPCN	9464	16.649	6	99.89
DAN-LN	3763	41.873	2	83.75
SN-DAN	6390	24.658	3	73.97
LN-DMN	7314	21.543	2	43.09
SN-FPCN	8190	19.239	2	38.48
VN-LN	5512	28.586	1	28.59
VN-DMN	14,352	10.979	2	21.96
LN-FPCN	4823	32.67	0	0
SN-LN	4770	33.032	0	0
VAN-LN	3392	46.453	0	0
VN-DAN	7384	21.339	0	0
Total	157,567

Abbreviations: DAN: dorsal attention network, DMN: default mode network, FPCN: frontoparietal control network, LN: limbic network, SN: somatomotor network, VAN: ventral attention network, VN: visual network.

3.4. Relationship to behavior

In an iterative, cross-validated analysis, we tested whether functional connectivity patterns during the highest WM load condition could be used to predict behavior. As our main behavioral measure, we used load-related increase in response time, ΔRT. We employed leave-one-out cross-validation to test whether ΔRT can be predicted based on the connectivity patterns of a previously unseen subject. As a first pass, we selected features globally. The ΔRTs predicted by the global model significantly correlated with the observed ΔRTs (p = 0.021, r = 0.17 for the positive, p = 0.025, r = 0.17 for the negative set). In a second analysis, features were selected from the within-network pool only. The ΔRTs predicted by the multilinear within-network model strongly correlated (for the positive set only) with the observed ΔRTs (p = 0.00017, r = 0.28). Finally, we selected features from single networks (within-network) to directly compare the predictive power among the 7 Yeo networks. The ΔRTs predicted by the models built using the positive within-VAN and within-DMN features produced the highest correlations (p = 0.011, r = 0.19 for VAN, p = 0.045, r = 0.15 for DMN) with the observed ΔRT values (Fig. 5). Note that these single-network predictions do not reach significance due to multiple comparisons, suggesting that no individual network alone contains sufficient information to characterize ΔRT. In addition, none of the single-network model predictions built with the negative feature sets reached the significance threshold (p = 0.05).

Fig. 5.

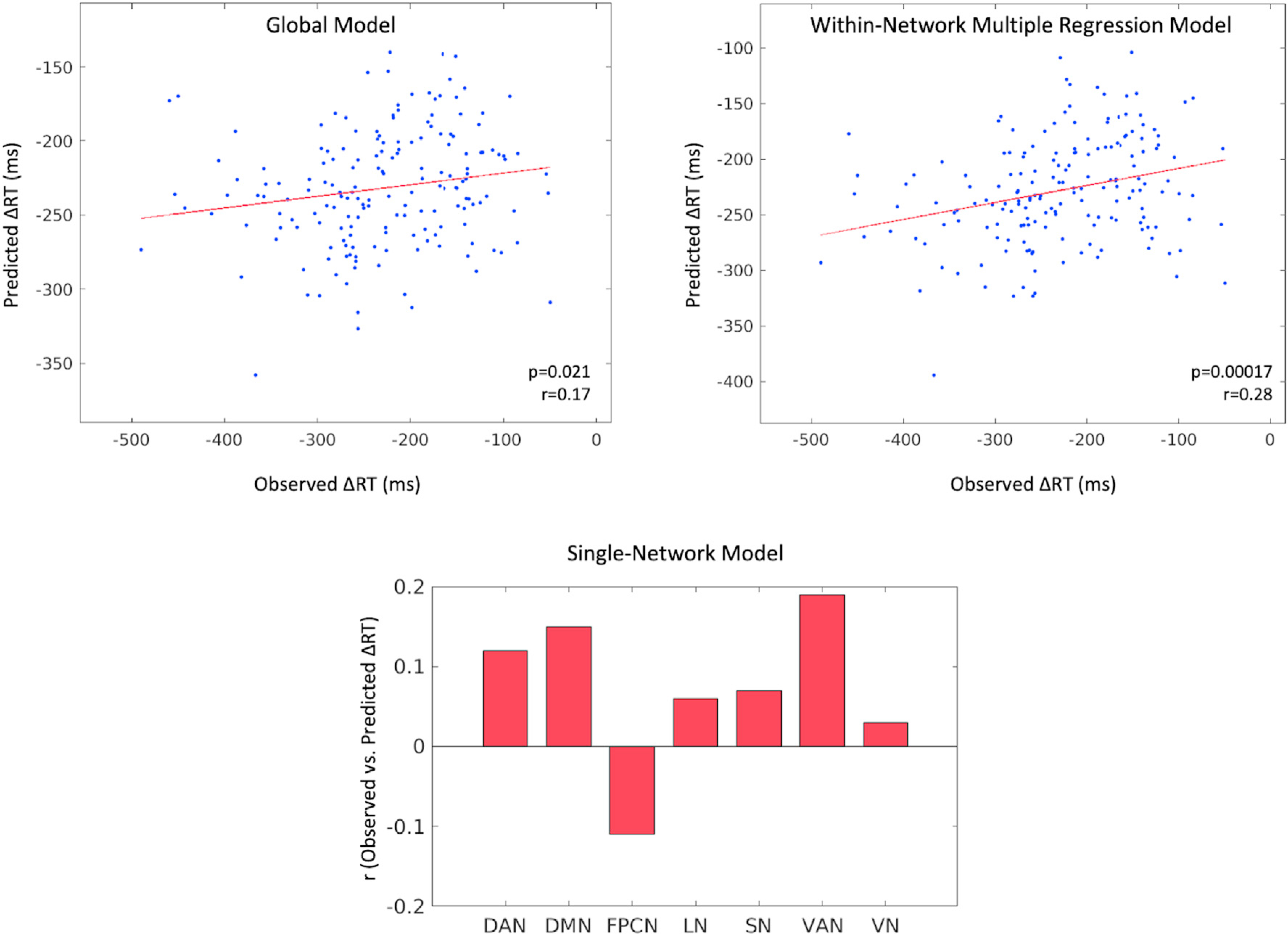
Relationship between connectivity and behavior obtained via an iterative, cross-validated prediction analysis. On the top panel, predicted vs. observed ΔRT values are displayed for the two models that used all possible edges and all within-network edges respectively in the feature selection step. Each dot represents a subject. The bar graph in the bottom panel shows the correlation (r) between observed and predicted ΔRTs for each of the 7 single-network models restricting feature selection to 7 respective within-network feature sets. All plots reflect results from positive feature sets.

4. Discussion

WM is fundamental to human cognition, and its impairment is associated with cognitive deficits in a number of neuropsychiatric diseases (Kasper et al., 2012; Manoach, 2003; Stopford et al., 2012; Williams et al., 2005). WM engages multiple systems including sensory, motor, attention, semantic and episodic memory to support goal-directed behavior (D’Esposito and Postle, 2015). As WM capacity is highly limited, it is important to understand the degree to which these systems are affected by increasing WM load. In this study, using a robust ML method, we first showed that WM load can be decoded from task-based functional connectivity during retrieval periods, even in the case of two task conditions with similar load. Furthermore, we identified that functional coupling within ventral attention and frontoparietal control networks as well as coupling between FPCN-DMN, VAN-DMN, DAN-VAN, and VAN-FPCN play key roles in separating high and low WM conditions. We also found that connectivity patterns within the ventral attention network are the most predictive of load-related changes in response time. Taken together, our findings highlight the primary role of interactions among control, attention and default mode networks in generating adaptive responses to different WM load levels.

Our findings suggest a key role for the VAN (also known as the salience network), which includes the insula and the anterior cingulate cortex (ACC). The NCA revealed that VAN features comprise over 60% of all top within-network features separating high vs. low load. Moreover, functional connectivity of the VAN with DMN, DAN, and FPCN also were among the primary between-network features contributing to the classification. Previous work showed that the salience network is sensitive to WM load, and that its connectivity with DMN and executive control network increases with increasing load (Liang et al., 2016). High prevalence of VAN connectivity with DMN, DAN, and FPCN among the primary discriminative features is also consistent with the putative salience network function of switching between large-scale networks to facilitate access to attentional resources (Goulden et al., 2014; Menon and Uddin, 2010). One possible interpretation is that the salience of the increased WM load may be detected by the VAN and as a result, the internal attention is shifted toward external, task-relevant stimuli.

Human imaging and nonhuman primate studies have consistently documented WM maintenance-related activation in prefrontal and posterior parietal regions (Curtis and D’Esposito, 2003; Ester et al., 2015; Levy and Goldman-Rakic, 2000; Pesaran et al., 2002). While the exact role of delay period activity remains unclear (Lundqvist et al., 2018), it is believed to support maintenance of WM items at an abstract level (Scimeca et al., 2018), reflect top-down signals that allow control of the sensory information (Gazzaley et al., 2005), support storage of WM items (Xu, 2017) or maintain task-relevant goal representations (Sreenivasan et al., 2014). While the difference between these accounts is beyond the scope of this study, the prevalence of within-FPCN connectivity and FPCN-DMN coupling in classifying high vs. low WM load suggests that communication between frontoparietal regions and the default mode network is essential for the appropriate load response, regardless of where stimulus-specific representations are encoded (Scimeca et al., 2018; Xu, 2018). Previous work demonstrated the role of the coupling between FPCN and DMN in supporting goal-directed cognition (Spreng et al., 2010). Therefore, the substantial number of FPCN-DMN connectivity pairs identified as top features in our NCA analysis (Fig. 4) suggests that these two networks work in coordination to support the brain response during high WM loads.

It is important to note that even though the memory set and the probes are first processed visually, the version of the SIRP we used is essentially a verbal task. Thus, it is expected that participants employed subvocal rehearsal strategies to maintain the memory set. Prevalence of connectivity between SN and VAN among the top features separating high vs. low WM load may, therefore, reflect the differences in rehearsal efforts expended to maintain long and short memory sets. The discriminative power of SN-VAN connectivity is also in line with the pivotal role of the VAN in switching between internal and external (e.g., stimulus-driven) attentional states (Uddin, 2015), as high WM load (due to increased external stimuli) is associated with increased motor activity due to phonological loop in the Sternberg task (Baddeley et al., 1998).

Performance in the SIRP is characterized by linear increases in response time with increasing set size (Sternberg, 1969). Indeed, our behavioral results confirmed this linearity as depicted in Fig. S2, which also schematizes the putative cognitive processes that take place during the retrieval period where we computed functional connectivity. Response time can be thought of the combined duration of individual processes. While the intercept of the fit line represents the duration of processes that occur regardless of the set size (e.g., preparation for motor response), the slope reflects the duration of processes that occur once per item in the memory set (e.g., comparison of the probe to an item in the memory set). Therefore, for a given subject, difference between the response times at 7T and at 1T reflects the additional duration of processes occurring once per WM item. We found that this load-dependent change (from 1T to 7T) in response time can be predicted by a global measure representing overall network strength. Moreover, this load-dependent increase in response time can be robustly predicted by a linear model that reflects the combination of network strengths of individual networks. This suggests that the adaptive load response in these networks can be used to gauge the pace at which individuals process and maintain the additional information due to increased load. Finally, our single-network analysis revealed that functional connectivity within the ventral attention and default mode networks at high WM load best predicts the load-dependent response time changes. This finding is consistent with the role of the VAN in detecting behaviorally relevant stimuli, as well as with studies reporting an association between processing speed and areas of the VAN (Genova et al., 2009) and DMN (van Geest et al., 2018).

5. Conclusion

We used robust ML methods in a large fMRI cohort to decode a characteristic task parameter from cortex-wide connectivity matrices and determine key within- and between-network connectivity features associated with changes in WM load. Our findings confirm the distributed nature of WM and reveal the key systems involved in adaptive load responses in WM. Our study also demonstrates that combining ML and functional connectivity can help identify subtle effects that could not be accessed via GLM or univariate connectivity. Future work can take advantage of these robust methods to identify the mechanisms of working memory impairment in neuropsychiatric disease at the system level.