Physical modeling of multivalent interactions in the nuclear pore complex

Abstract

In the nuclear pore complex, intrinsically disordered proteins (FG Nups), along with their interactions with more globular proteins called nuclear transport receptors (NTRs), are vital to the selectivity of transport into and out of the cell nucleus. Although such interactions can be modeled at different levels of coarse graining, in vitro experimental data have been quantitatively described by minimal models that describe FG Nups as cohesive homogeneous polymers and NTRs as uniformly cohesive spheres, in which the heterogeneous effects have been smeared out. By definition, these minimal models do not account for the explicit heterogeneities in FG Nup sequences, essentially a string of cohesive and noncohesive polymer units, and at the NTR surface. Here, we develop computational and analytical models that do take into account such heterogeneity in a minimal fashion and compare them with experimental data on single-molecule interactions between FG Nups and NTRs. Overall, we find that the heterogeneous nature of FG Nups and NTRs does play a role in determining equilibrium binding properties but is of much greater significance when it comes to unbinding and binding kinetics. Using our models, we predict how binding equilibria and kinetics depend on the distribution of cohesive blocks in the FG Nup sequences and of the binding pockets at the NTR surface, with multivalency playing a key role. Finally, we observe that single-molecule binding kinetics has a rather minor influence on the diffusion of NTRs in polymer melts consisting of FG-Nup-like sequences.

Significance

The nuclear pore complex controls the passage of biomolecules between the nucleus and cytoplasm through many sticky flexible proteins (FG Nups) and their interactions with sticky nuclear transport receptors (NTRs). Consequently, the mechanics of these interactions are crucial in keeping the cell alive. Based on comparisons with experiment, here we develop simple models that account for the heterogeneity in FG Nups and NTRs. We find that heterogeneity plays a less important role in overall binding affinity but is important when considering unbinding and binding kinetics. We then further elucidate this by exploring equilibrium diffusion of an NTR in an FG polymer melt. The work here serves as a foundation to understand the physics of FG Nup-NTR interactions.

Introduction

The shuttling of macromolecules between the cytoplasm and nucleoplasm is controlled by nuclear pore complexes (NPCs), selective gatekeepers that permeate the nuclear envelope (1). The NPC is a large (diameter ∼100 nm, mass ∼112 MDa in vertebrates) proteinaceous conduit that allows small (diameter $\lesssim$ 5 nm; mass $\lesssim$ 60 kDa) molecules to passively diffuse through while also hindering the transport of larger molecules (2,3). This size-exclusion barrier arises from the dense (∼100–300 mg/mL) arrangement of intrinsically disordered proteins (FG Nups) that are attached to the inner NPC scaffold (4,5). FG Nups consist of hydrophobic (Phe-Gly) motifs that are separated by more polar/charged regions, and the relative amounts of these—the hydrophobic to charged ratio—defines a cohesiveness spectrum for FG Nups, on which higher amounts of hydrophobicity are associated with higher levels of cohesion (6,7). A large macromolecule can travel through the NPC by binding to one or more nuclear transport receptors (NTRs), forming a cargo complex (8). NTRs are decorated with hydrophobic grooves that have an affinity to the hydrophobic motifs on the FG Nups, thus enabling the cargo complex to overcome the free energy costs of entry (9,10). Remarkably, the NPC can facilitate the rapid transport of thousands of cargoes per second while also maintaining the permeability barrier. The apparent contradiction between fast transport and high selectivity is known as the “transport paradox” (3,11).

Although there is a consensus regarding the importance of FG Nup-NTR interactions in NPC functionality, there is an incomplete mechanistic understanding of the exact roles these interactions play in facilitated transport. The main obstacles to this understanding are 1) an incomplete quantification of FG Nup sequence-specific effects on the selective barrier, 2) a relative scarcity of quantitative data regarding multivalent interactions between FG Nups and NTRs, 3) a difficulty in determining the factors leading to high specificity of NTRs to the FG Nups while maintaining fast unbinding and binding kinetics, and 4) conflicting microscopic and macroscopic binding data on FG Nup and NTR interactions, for which relatively weak per FG-motif binding (with dissociation constant K_D ∼10 mM) is observed in single-molecule studies (12,13) as compared with strong FG Nup-NTR binding (K_D $\lesssim$ 10 μM) as found using other techniques (11,14, 15, 16, 17, 18).

Physical modeling can aid in the interpretation of experiments, incorporating FG Nup and NTR heterogeneity at various levels of detail (5,7,15,19, 20, 21, 22, 23, 24, 25). Modeling approaches accounting for the properties of each amino acid have reproduced elements of FG Nup morphology and FG Nup-NTR interactions (e.g., (5,20)) but require a calibration of many ($\gtrsim$20) interaction parameters, and such a large parameter space makes it difficult to identify/explore the roles of a few key physical elements. In contrast, minimal physical modeling approaches based on a few interaction parameters, determining the salient features of the system, can help to interpret and understand current experimental observations and explore the possible outcomes of future experiments using the smallest set of governing principles (26).

Because both higher-resolution and more coarse-grained modeling approaches aim to describe the same system, they serve complementary purposes. Here, we focus on minimal models: models containing the bare minimum of physical assumptions and parameters to describe experimental observations. The simplest of these models treats FG Nups as homopolymers and NTRs as uniform or isotropic particles. With experimentally determined parameter choices, these have seen surprising success in qualitatively and quantitatively reproducing binding behavior in FG Nup and NTR in vitro assemblies (7,21,22,27). The success of these homopolymer models suggests that many key features of NPC transport can be described by mesoscopic polymer-colloid physics and naturally raises the question of the roles that FG Nup and NTR heterogeneity have in NPC functionality.

Here, we present modeling approaches to explore the roles of FG Nup sequence patterning, surface heterogeneity (or “patchiness”) of NTRs, and multivalency in regulating FG Nup-NTR binding and associated binding kinetics and their effects on the equilibrium diffusion of an NTR in an FG polymer melt. The structure of the study is as follows: first, we present the methodology of our approach; second, we set the parameters and validate the model through comparison with experimental data; third, we provide analytical frameworks for interpreting the results; fourth, we use the model to explore a more physiological FG sequence binding to NTRs; and finally, we make predictions of equilibrium diffusion of an NTR in an FG polymer melt and compare them with experimental data.

Methods

Coarse-grained model

Intrinsically disordered proteins that contain hydrophobic FSFG repeats that are separated by neutral regions containing other amino acids (13) are modeled as freely jointed heteropolymers (see Fig. 1). For simplicity, we only include two types of beads—cohesive and noncohesive—and impose that all polymer beads have the same size, as is commonly done in homopolymer models (7,21,22). To examine the effects of a particular choice of the monomer size d, we test sizes ranging from the approximate diameter of an amino acid (one amino acid per bead (1 apb), d = 0.38 nm) to two amino acids (2 apb, d = 0.76 nm) and finally to that of four amino acids (4 apb, d = 1.02 nm, i.e., in between the size of four closely packed amino acids and a straight line of four amino acids). Two neighboring polymer beads are connected by a stiff harmonic spring defined by the potential U(r)_bond = 1/2k(r − d)², where k is the bond strength and r is the distance between two neighboring monomers.

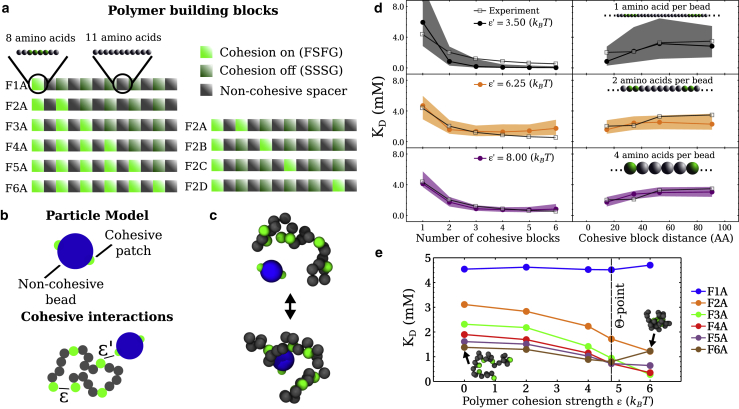
Figure 1.

Setup of the physical model used in this work. (a) Polymer sequences composed of three types of (amino-acid-containing) blocks that mimic synthetic protein sequences for which experimental data are available (13). (b) NTF2 is modeled as a patchy particle and the polymer sequences as chains with cohesive and noncohesive beads. ε and ε′ define the attraction strength between cohesive beads with the chain and between these cohesive beads and the cohesive patches on NTF2, respectively. (c) MD snapshots of unbound and bound NTF2 with an F6A polymer (four amino acids per bead). (d) Parameterization of the particle-polymer cohesion strength ε′, shown for different choices of polymer bead size, using NMR data on the dependence of K_D on the number of cohesive blocks (left) and on the separation of two blocks along the sequence (right) (13). Shaded bands denote ε′ ± 0.25 k_BT. (e) K_D as a function of ε, based on simulations with four amino acids per bead, with a fixed ε′ as determined in (d). The Θ-point, i.e., the point at which the F6A chain has a size that is equal to an idealized (Gaussian) homopolymer chain with the same number of monomers (vertical dashed line); inset snapshots refer to the F6A sequence. To see this figure in color, go online.

We incorporate the size and binder coverage of a nuclear transport receptor in a similarly minimal fashion. In this model, a nuclear transport receptor is treated as a rigid body composed of a sphere of diameter d′₀ that has N spheres (“patches”) of diameter d′ = 0.38 nm (where d′₀ > d′) fixed at specified points on its surface.

We impose excluded volume interactions between all constituent particles via the Weeks-Chandler-Anderson potential

$$U_{vol}\left(r\right)=\{\begin{array}{ll}4{\epsilon }_{vol}\left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right]+{\epsilon }_{vol},\hfill & 0\le r\le r_0,\hfill \\ 0,\hfill & r_0<r,\hfill \end{array}$$ (1)

where ε_vol = 250 k_BT is the interaction strength, σ = 2^−1/6r₀, and r₀ is the distance at which the excluded volume interaction acts. The addition of ε_vol to the potential ensures that U_vol(r = r₀) = 0.0 k_BT. We also imposed a cohesive interaction of strength ε between cohesive polymer beads and an additional cohesive interaction of strength ε′ between cohesive polymer beads and cohesive patches on the particle through the Morse potential

$$\varphi \left(r\right)=\epsilon \left(e^{-2\alpha \left(r-r_0\right)}-2e^{-\alpha \left(r-r_0\right)}\right),$$ (2)

which is truncated and shifted to ensure continuity in both the potential and force for r ≤ 2r₀, where 2r₀ is the cutoff of the cohesive interaction. The resulting cohesive pair potential is then given by

$$\begin{array}{l}{U}_{coh}\left(r\right)={\epsilon }_c{\text{e}}^{(\alpha (-2r-3r_0))}(-2{\text{e}}^{\left(\alpha \left(4r_0+r\right)\right)}+,\\ {\text{e}}^{\left(\alpha \left(5r_0\right)\right)}+{\text{e}}^{\left(\alpha \left(2r+r_0\right)\right)}\left(2r\alpha -1-4\alpha r_0\right),\\ +{\text{e}}^{\left(\alpha \left(2r+2r_0\right)\right)}(2-2r\alpha +4\alpha r_0))0\le r\le 2r_0,\end{array}$$ (3)

where α = 6.0 nm⁻¹ is the decay of the Morse potential and ε_c = Aε or A′ε′ (where A and A′ are constants) recorrects the minimum of the potential that is initially set through either of the two interaction parameters {ε, ε′} because of the truncation and shifting procedure. Combining the pair potentials for excluded volume U_vol and cohesion U_coh then leads to the overall interaction given by

$$U\left(r\right)=\{\begin{array}{ll}{U}_{vol}\left(r\right)+U_{coh}\left(r\right),\hfill & 0\le r\le r_0,\hfill \\ U_{coh}\left(r\right),\hfill & r_0\le r\le 2r_0,\hfill \\ 0,\hfill & r>2r_0,\hfill \end{array}$$ (4)

of which an example plot is shown in Fig. S1. Relevant length scales for the different polymer and particle models are given in Table S1.

Simulation details

Molecular dynamics (MD) simulations were performed using the LAMMPS package (28). We subjected the patterned polymer and patchy-particle system to dynamics at a constant temperature, T, through the implementation of the NVE (constant number of particles N, constant volume V, constant total energy E) time integration algorithm with a Langevin thermostat. This combination results in the total force F acting on a particle as given by

$$\mathbf{F}={\mathbf{F}}_c+{\mathbf{F}}_f+{\mathbf{F}}_r,$$ (5)

where F_c is the conservative force due to the interparticle pair potentials, F_f = −(m/γ)v is the frictional drag force, and F_r ∝$\sqrt{\frac{m{k}_{B}T}{\delta t\gamma }}$ is the force due to solvent particles at a temperature T randomly colliding with the particle. Simulations were performed with dimensionless parameters with T = 1 and γ = 1, where γ is the friction coefficient, and a simulation time step of δt = 0.002τ₀, where τ₀ = 1.707 × 10⁻⁹ s is the unit of time as defined in the supporting material of our previous work (7). The patchy particle was treated as a rigid body so that the resultant force and torque of the body is the sum of the forces and torques of the constituent particles.

To simulate a single polymer (of total volume v) and a single particle (of total volume v′) in the canonical ensemble, we initially placed them in a box, with periodic boundary conditions, of size L³ where typically L³ > C(v + v′), with C > 80 (corresponding to L > 20 nm). Next, we performed a simulation run for 5 × 10⁶ time steps to equilibrate the system, which was checked by inspection of the total energy; a further 30 × 10⁶ time steps were used for data analysis.

To simulate a bulk system consisting of N_p polymers and M_p particles both at packing fractions η in a periodic box of length L = 40 nm, we first placed N_p = ηL³/V_pol-beads polymers and M_p = ηL³/V_par-beads in a cubic box of length L₀ = 120 nm (centered about the origin), where V_pol-beads is the sum of constituent bead volumes of the patterned polymers and V_par-beads is the sum of constituent bead volumes of the patchy particles. Then, to shrink the box to a volume of $L^3$ to obtain a relatively high density (and the desired packing η), we performed an initial run that applied an external force pushing all beads to the center of the box while avoiding particle overlaps. After this, we performed a simulation reducing the box length from L₀ to L and let the system equilibrate (20 × 10⁶ time steps), checked by inspection of the total energy.

Code availability

Example simulation and data analysis scripts are available at https://github.com/patherlkd/PhysicalModellingNPC.

Results and discussion

Minimal models account for NTF2 binding to short FSFG-containing sequences

To develop and test minimal models for how NTRs bind to FG domains, we referred to experiments on the 1:1 binding of NTRs—specifically of NTF2—to short (∼120 amino acids) FSFG-containing sequences (13). These sequences contained various patternings of cohesive (sticker) blocks consisting of cohesive FSFG with two flanking, noncohesive amino acids on either side and noncohesive spacer blocks consisting of 11 noncohesive amino acids. In addition, each FSFG block could be substituted with a noncohesive SSSG alternative. The different sequences are schematically depicted in Fig. 1 a. Briefly, in these sequences, the amount and relative locations of the cohesive blocks were systematically varied; NMR was used to measure the respective single-molecule K_D-values for NTF2 binding to the various sequences (with additional validation by calorimetry) (13).

We model these sequences as beads on a chain with different levels of coarse graining (one, two, and four amino acids per bead), for which the sequence heterogeneity is incorporated in a minimal fashion using appropriate alternations of cohesive (for FSFG-containing blocks) and noncohesive (for the other blocks) beads. The different coarse graining of the polymers, i.e., different choices of the bead size, results in different persistence lengths, with the 2 apb polymer having a persistence length (∼0.38 nm) in line with FG Nups (7,21,22,29). Given that NTF2 has at least two FxFG binding sites (30), we treat NTF2 as a sphere of diameter 3 nm with two cohesive patches. The intra- and intermolecular affinities in this system are defined, respectively, by the strength of interactions between the cohesive beads on the chain, ε, and by the strength of interactions between the cohesive beads on the chain and the cohesive patches on the NTR, ε′ (see Fig. 1 b).

In accordance with previous findings that native and synthetic FG Nup domains behave similarly to Θ-point homopolymers (7,21,22,25,31,32), in which intramolecular repulsion balances intramolecular attraction, we set the polymer-polymer cohesion strength ε = 4.75 k_BT such that the size of the F6A chain is equal to the size of an idealized (Gaussian) homopolymer, with the same chain and Kuhn lengths (which we denote as the “Θ-point”) (see Fig. S2). We chose to set ε based upon the sequence with six cohesive blocks (F6A) because it more closely resembles the symmetry of a homopolymer chain as compared with the other sequences. This leaves us with a single free parameter, the polymer-particle attraction strength ε′, to adjust single-molecule dissociation constants K_D from MD simulations to those derived from experiment (see Fig. 1, c and d). In MD, K_D is essentially computed from the ratio of the number of unbound states (consisting of one free polymer and one free particle) to bound states (consisting of one polymer binding to the particle) that occur in a single long simulation trajectory (7,33,34) (see Supporting materials and methods for details). Encouragingly, such one-parameter fits are sufficient for the simulations to quantitatively reproduce the behavior of K_D as 1) a decreasing function of the number of FSFG motifs in the sequence and 2) as an increasing (but saturating) function of the separation of two FSFG motifs along the chain. The increase in K_D (decrease in overall affinity) with an increase in the separation of two FSFG motifs is due to the decrease in local FSFG concentration and the increased entropic cost of bringing the two motifs together (35). We note that the agreement between the K_D-values as calculated in MD and those inferred from experiments is strictly valid in the single-molecule regime (i.e., very dilute limit) for extrapolation of K_D, as calculated in MD; for much denser bulk scenarios, one must account for local density fluctuations (36). The agreement between simulations and experiment does not significantly depend on the chosen simulation box size (see Fig. S3), and the agreement is robust against the level of coarse graining of the protein sequences (and therefore not strongly dependent on the exact persistence length), with concomitant adjustments of ε and ε′ that were parameterized by the Θ-point for F6A and by the best match with experimental K_D curves, respectively. We note that binding affinities (K_D) exhibited greater sensitivity to changes in ε′ for higher-resolution (less coarse-graining) polymer models (see Fig. 1 d). For computational convenience, we focus on the coarsest model used here, a polymer with four amino acids per bead (4 apb).

For this model, we also investigated how NTF2 binding depends on the intrapolymer cohesion parameter ε. For the sequence with a single cohesive block (F1A), the choice of ε should not—and does not—affect K_D. For sequences containing ≥2 cohesive blocks, K_D decreases (hence, binding affinity increases) upon increasing ε (see Fig. 1 e). This may be attributed to the higher local concentration of polymer cohesive units as the polymer assumes more compact conformations, which increases the probability of the particle rebinding to the polymer (because the particle binding sites are now in closer proximity to the other polymer cohesive units). For the case of F6A, however, K_D increases (hence binding affinity decreases) when ε is increased beyond the Θ-point (ε ≥ 4.75 k_BT). This increase in K_D can be explained by the preference for cohesive beads on the polymer to remain bound to one another, gradually forming a tightly bound globule with the noncohesive polymer regions covering it, thus reducing the accessibility of available binding sites for NTF2 (see Figs 1 e and S2). Accordingly, for such high intrapolymer cohesion, the K_D-values also go up with an increasing number of cohesive blocks for F3A-F6A, inverting the trend observed below the Θ-point (Fig. 1 e). Overall, this decrease in polymer-particle affinity will be defined by the increased polymer cohesion and by the entropic cost of confining noncohesive regions (3,37). We note that for values of ε below the Θ-point (see Fig. 1 e), with other parameters such as the interaction range already set, the resulting qualitative behaviors of K_D as a function of N_coh are similar; thus, in this range of ε, one can still obtain agreement with experimental trends (with an appropriate scaling of ε′). In summary, with the parameterization of ε based on our previous comparisons with other experiments on FG Nups in bulk and polymer film assemblies (7,21,22), our coarse-grained model is able to match experimental K_D trends with a one-parameter fit of ε′.

Having thus established a coarse-grained model that accounts for sequence-dependent variations of how NTF2 binds to FSFG-containing sequences, we next set out to investigate the importance of surface heterogeneity (for NTF2) and sequence heterogeneity (for the FSFG-containing sequences) to quantitatively account for the experimental data. Firstly, we varied the proximity of the two cohesive patches on the NTF2-mimicking particle, through the angle θ. We observed little change in the resulting K_D until the patches were very close, i.e., for θ $\underset{\approx }{<}$ π/5 ($\equiv$ 36°) (see Fig. 2 a). For θ $\underset{\approx }{<}$ π/5, the binding became so strong that NTF2 was barely released from the polymer sequences in our simulations; this strong binding is attributed to the increase in binding energy when a polymer block binds to two NTF2 patches simultaneously. This strong binding was also articulated in the reduction in polymer size (the radius of gyration R_G) for sequences with increasing amounts of cohesive blocks in the sequence. For larger values of θ, with weaker binding, there was an initial mild shrinkage with the number of cohesive blocks, followed by a more pronounced expansion (size increase <10%). Such expansion of polymer size upon binding has also been observed in experiments on NTF2 binding to similar FG domains (38), providing further support for our model.

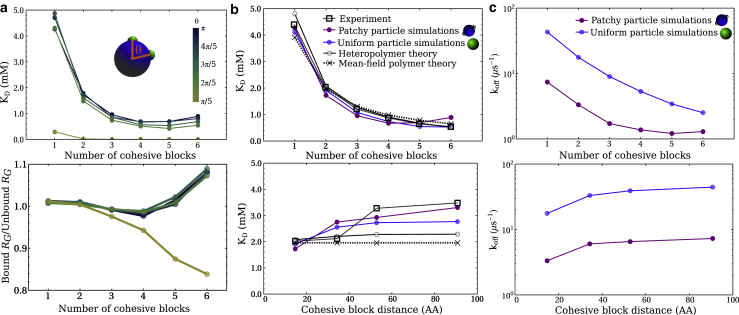
Figure 2.

Effects of surface heterogeneity on a nuclear transport receptor. (a) Effects of varying the patch-patch proximity on binding affinity and polymer size (as measured by the radius of gyration R_G). (b) Effects of surface heterogeneity on the particle and sequence heterogeneity in the polymer using simulations and polymer analytical models. For the patchy-particle simulations, θ = π rads ($\equiv$ 180°) is used. In the uniform-particle cases, the particle interacts with the cohesive polymer beads through its center of mass. As is shown, the cohesion strengths in all cases are set to best-match experiments (13). (c) compares the kinetics between the best-match (of the experimental data) uniform-particle and patchy-particle model used in simulations. The off rate was calculated as k_off = $\langle t_{\text{res}}\rangle$⁻¹, where $\langle t_{\text{res}}\rangle$ is the ensemble-averaged interaction residence time. To see this figure in color, go online.

Noting that we did not observe a major change in K_D with minor variations of the position of the patches on NTF2 (for θ > π/5), we also attempted to model the experimental data ignoring surface heterogeneity altogether and instead modeling NTF2 as a homogeneous or uniform cohesive sphere (of the same size as the noncohesive bead in the patchy particle above). The uniform cohesive sphere is the limiting case of a large number of weakly interacting binding sites spread over the surface of the particle. For the uniform-particle model of NTF2, the cohesive interaction—as imposed through a pair potential—is between the center of the large bead (∼8 times larger than the cohesive NTF2 patch) and the center of the cohesive polymer bead, with an interaction cutoff distance that is ∼3-fold larger than the interaction cutoff distance in the patchy-particle model. As before, we adjusted ε′ to best reproduce the variation of K_D with the number of FSFG blocks and with their separation along the sequence, resulting in a value of ε′ = 5.0 k_BT for the uniform NTF2 model (Fig. 2 b). These results suggest that surface heterogeneity per se is not a relevant factor to determine binding of NTRs to short FG domains, as long as the overall affinity of the NTRs to the FG domains is in the appropriate range. This is largely consistent with experimental observations, which indicate that there are multiple ways to tune NTR surface properties to achieve similar transport properties (39).

Analytical models quantitatively describe effects of multivalency

To explore how the heterogeneity in the polymer sequence dictates the binding affinities as observed in the experimental data, we used an analytical theory that enables quantification of sequence-specific effects on binding (40,41) (see Supporting materials and methods for mathematical details). In line with our results above, we considered the NTF2 as a uniform particle (one bead) binding to a patterned polymer defined by a patterning of cohesive and noncohesive beads. Intra- and intermolecular interactions were incorporated in an approximation of the second virial coefficient B₂ via two terms. The first term is based on a mean-field contribution, in which the heteropolymer is approximated as a smearing of an uncorrelated set of N_coh cohesive monomers that has an effective affinity of strength ∝ ε′N_coh and a range determined by the pair potential (see Table S1) for the NTF2 particle only. The second term is sequence specific and is based on second-order correlations arising between the polymer monomers and also between the polymer monomers and the NTF2 particle. Therefore, the intramolecular polymer correlations implicitly depend on the intrapolymer cohesion strength ε and on an excluded volume parameter ω accounting for the finite size of the polymer beads, and the correlations between the NTF2 particle and cohesive monomers of the polymer depend on ε′. In its simplest form, B₂ is given as (as explicitly shown in the Supporting materials and methods)

$$\begin{array}{l}{B}_2=-\eta \left({\epsilon }^{\prime }\right)N_{\text{coh}}\\ -\int \kappa \left({\epsilon }^{\prime },k\right)\sum _{i,j=1}^{N_m}{s}_i{s}_j\text{exp}\left(-\frac{x_{i,j}{\left(kd\right)}^2|i-j|}{6}\right)\text{d}k,\end{array}$$ (6)

where s_i encodes whether a polymer bead i is cohesive (s_i = 1) or noncohesive (s_i = 0) (with N_coh = ${\sum }_{i=1}^{N_m}{s}_i$), N_m is the total chain length (N_coh + N_noncohesive), d is the bond length, x is a renormalization factor of the bond length that corrects the Gaussian (ideal polymer) correlations for intramolecular excluded volume (dependent on the excluded volume parameter ω) and intramolecular cohesion (dependent on ε) (41), and the integral is over the wave number k defined as the inverse monomer-monomer distance. The functions η and κ are explicitly given in the Supporting materials and methods. To calculate the dissociation constant between one polymer and one particle, we use (details in the Supporting materials and methods)

$$K_D=\frac{P_0}{P_1}\left[c\right]=\frac{V/\left(V-B_2\right)}{1-\left(V/\left(V-B_2\right)\right)}\frac{1}{N_{A}V}=-\frac{1}{N_A{B}_2},$$ (7)

where P₁ is the binding probability, P₀ = 1 − p₁ is the unbinding probability, [c] = 1/N_AV is the concentration (with units mol ⋅ nm⁻³), N_A is Avogadro’s number, and V is the system volume (33,34,40,42). Note that because we are considering the binding of a single polymer to a single particle in a relatively large volume, we use the ratio of the unbinding/binding probabilities K_D ∝ P₀/P₁ (Boltzmann approach), which is practically the same as using K_D ∝ $P_0^2$/P₁ (law of mass action approach) when in the dilute limit (where P₀ ≈ $P_0^2$ ≈ 1) (33,34). The last equality in Eq. 7, which states that K_D ∝ −$B_2^{-1}$, is also valid in the dilute limit (34,40,42). To compare with the experimental K_D data (Fig. 1 d), Eq. 7 is converted to molar units (M) using 1 nm⁻³ $\equiv$ 10⁻²⁴ L.

The intrachain interaction parameters {ε, ω} can be estimated based on a matching of R_G between the heteropolymer theory with those calculated for the simulated sequences (as was similarly done in (41)), and the polymer-particle cohesion strength ε′ is left as a fitting parameter to describe K_D as a function of the number of cohesive blocks. With such parameterization, this analytical heteropolymer model accurately describes the experimental data as a function of the number of cohesive blocks (Fig. 2 b, top). For comparison, we next recalculated K_D without the second term in Eq. 6, with no dependence on {ε, ω}, and thus approximating the heteropolymer as a smearing of a set of uncorrelated monomers. Remarkably, this much simplified model (ignoring any correlations between the polymer units) reproduces the experimental data equally well as the heteropolymer model (Fig. 2 b, top). As per Eqs. 6 and 7, the latter agreement implies that we can describe the increase in polymer-particle affinity with increasing numbers of cohesive blocks in the polymer using a simple approximate relation K_D ∝ 1/N_coh. Indeed, the binding trends as seen in experiments can be well fitted to a function K_D(N_coh) = A/N_coh, with A being a fitting constant (see Fig. S4).

Understandably, the mean-field theory (based on the first term in Eq. 6) could not reproduce the trends in K_D with the distance between (a constant number N_coh = 2 of) cohesive blocks being varied along the sequence. However, the heteropolymer theory—including second-order correlations only—correctly predicts an increase of K_D, though of smaller magnitude than the experimental (and MD) data (Fig. 2 b, bottom). This provides a physical explanation of why binding affinity increases when the FSFG motifs are bought closer together on the sequence; the spatial correlations between the motifs are higher, which results in an increase in local concentration of motifs around the NTR (13).

Effect of NTR surface heterogeneity on unbinding and binding kinetics

Although the most simplified models above accurately describe binding equilibria, it remains unclear to what extent NTR surface heterogeneity needs to be incorporated in a model to account for (un)binding kinetics. To address this question, we calculated the off rate k_off = $\langle {\tau }_{\text{res}}\rangle$⁻¹ from MD simulations, where $\langle {\tau }_{\text{res}}\rangle$ is the ensemble-averaged time over which the binding patches of the NTR remained in the interaction range of at least one cohesive bead on the patterned polymer (Fig. 2 c). This results in predicted residence times of $\langle {\tau }_{\text{res}}\rangle$ < 1 μs. With K_D ∼1 mM as above, such residence times imply on rates k_off/K_D = k_on ∼1 nM⁻¹ s⁻¹ that are consistent with estimates based on stopped-flow experiments (12). We observe that the off rates for the uniform NTF2-equivalent particle (for N_coh ≤ 3) are an order of magnitude faster than for the NTF2 with two separate binding patches and are at least three times greater (for N_coh > 3), despite both particles having (calculated) K_D-values that match the same experimental data (see Fig. 2 b). For the uniform particle to have the same K_D as for the patchy particle, despite having higher k_off (and thus a shorter binding duration t_u < t_p), is for the number of individual binding events to be larger (n_u > n_p) with the condition that t_u/t_p = n_p/n_u. Furthermore, because k_off ∝ k_on, for fixed K_D, the higher k_off for the uniform particle must be compensated with a higher k_on. This implies that the more the NTR-FSFG affinity is smeared out across the NTR surface, the easier it is to unbind the NTR from the FG motifs for a given equilibrium binding constant. In other words, by relying on more spread-out and weaker interactions, FG motifs can achieve the same thermodynamic selectivity for NTRs as would result from having fewer but stronger interactions yet allow for faster off rates. This provides at least part of the explanation for the “transport paradox,” in which on one hand, there is fast (thousands of transport events per second) nucleocytoplasmic transport, whereas on the other hand, the NPC exhibits high selectivity/specificity (3,11), in which many but weak binding spots allow FG motifs in the NPC to have high selectivity for NTRs yet still facilitate fast off rates and hence fast transport.

Accounting for more complex FG sequences and NTRs

Having established our coarse-grained models by comparison with experimental data on short FSFG-containing sequences and NTF2, we next carried out similar MD simulations for a more complex FG sequence and more complex NTRs (Fig. 3 a). Specifically, we devised a longer (∼720 amino acid) sequence with a distribution of 18 FSFG cohesive blocks that is consistent with native Nsp1, an FG Nup that recapitulates salient features of the NPC selective barrier in artificial NPC mimics (27,43,44). For NTRs, we chose NTF2 as well as karyopherin-95 (Kap95, or importin-β), an important and extensively studied cargo-carrying NTR. We model Kap95 as a patchy particle (size ∼5 nm) with N cohesive patches embedded on its surface, with N ranging between 4 and 10 as is expected for Kap95 based on structural data and simulations (Fig. 3 a; (9,10,45)). To further probe the effects of surface heterogeneity and of the proximity of cohesive patches, we used two Kap95 models: one with the N patches equidistant from one another over the whole surface (Kap) and another with the same number of N patches spread equidistantly on one half of its surface (Kap_half).

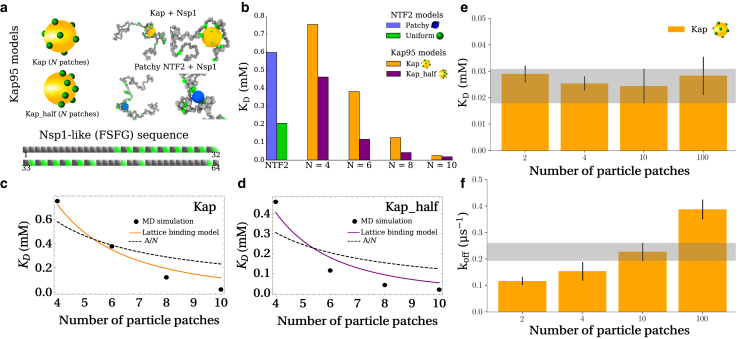
Figure 3.

Single-molecule binding predictions for an Nsp1-like FSFG sequence and NTR particles with varying surface properties, based on coarse-grained MD simulations. (a) Illustration of the particle models for NTRs and the Nsp1-like sequence. Kap95 is modeled as a particle with N binding patches uniformly distributed on its surface (Kap) or a particle with N patches uniformly distributed on one half of its surface (Kap_half). The Nsp1-like sequence is built from the polymer building blocks shown in Fig. 1a (with N_coh = 18 cohesive blocks). (Inset) MD snapshots of Nsp1 binding with selected NTR models. (b) K_D predictions for Nsp1 and the NTR models, with ε = 4.75 k_BT for polymer (FSFG-FSFG) cohesion and ε′ = 8.0 k_BT for polymer-particle cohesion (with ε′ = 5.0 k_BT for the uniform NTF2 particle so as to match the K_D-values of the NTF2 patchy particle with the short sequences (Fig. 2b)). (c and d) Fitting the K_D data from MD simulations (b) with the analytical lattice binding model, in which the N_coh = 18 polymer cohesive blocks and cohesive particle patches interact within a subvolume of a lattice. (e and f) When ε′ is adjusted to yield the same K_D-values (as determined by MD simulations) within standard deviation (SD; gray band is the SD for N = 10) for N = {2, 4, 100} as N = 10 in the Kap model (e), the off rate increases with N (f). In (e) and (f), ε′ = 10.45, 9.55, 8.00, and 2.75 k_BT for N = 2, 4, 10, and 100 patches, respectively. To see this figure in color, go online.

For simplicity, we assume a rather generic nature of the interactions between FSFGs and between FSFG and binding patches on NTRs; hence, we use the same ε = 4.75 k_BT and ε′ = 8.0 k_BT as used for the coarsest model of the short FSFG sequences and patchy NTF2 (see Fig. 1) and ε′ = 5.0 k_BT for the uniform NTF2 particle as before. Firstly, considering the two-patch NTF2 particle (with θ = π rads), we do not observe a substantial drop (∼0.2 mM difference) in K_D going from the F6A (with N_coh = 6) to the Nsp1-like sequence (with N_coh = 18) (see Fig. 3 b), whereas with a scaling K_D ∝ 1/N_coh, we would expect a threefold drop in K_D. This observation could be due to the patchy nature of NTF2 (two patches), with each patch (given finite ranged interactions) having a limit on how many cohesive polymer blocks it can bind to. In other words, when there is an excess of cohesive polymer blocks, the patchy NTF2 can only bind to a small portion of them, reducing the (ensemble-averaged) total number of polymer units bound and thus the total binding affinity. Reassuringly, this observation is supported by experiment in which an equivalent F12A sequence (12 blocks) exhibited a K_D that was similar in value to the F6A sequence (13). It is worthwhile to note that although the Nsp1-like sequence contains more cohesive blocks, it is also six times longer than the F1A-F6A sequences and contains a few larger noncohesive spacer regions that might contribute to some reduction in binding affinity because of entropic effects. In contrast to the patchy particle, a uniformly cohesive NTF2 equivalent does show an ∼3-fold increase in affinity to the Nsp1-like sequence as compared with the F6A sequence, consistent with the scaling K_D ∝ 1/N_coh. This indicates the limitation of the uniform-NTR approximation; it overestimates the binding of NTF2 to long FG domains when there is a large ($\gtrsim$10) excess of FSFG motifs that can access the NTR.

For the Kap95 models, using a constant ε′ = 8.0 k_BT as noted above, we observe a decrease in K_D (increase in overall binding energy) upon increasing in N. Apart from depending on the number of binding sites N on an NTR, K_D also depends on the distribution of these sites over the surface for the Kap95 model particles. Such dependence is rather pronounced when comparing the Kap and Kap_half models. As observed when bringing the binding sites of NTF2 in close proximity (Fig. 2 a), we observed a significantly stronger binding when all N binding sites are located on one side of the NTR (Kap_half) compared with the case in which these binding sites are distributed uniformly over the whole surface (Fig. 3 b; (45)). For the Kap and Kap_half particle with N = 4 patches, the K_D is comparable to that of patchy NTF2, despite having a twofold increase in patch numbers. This observation is the result of the difference in sizes between Kap95 and NTF2 particles, which provides the rationale as to why larger NTRs require more cohesive binding spots (10).

Encouraged by the previous success of our analytical models, we attempted to describe the Kap and Kap_half data using the inverse relationship (K_D ∝ 1/N) that would result from a mean-field treatment of the particle patches (see first term of B₂ in Eq. 6). We found that the simple fitting function K_D(A, N) = A/N (A being a fitting constant), which well described the experimental and simulation trends of K_D on the number of cohesive polymer blocks (Figs. 2 b and S4), resulted in a poor fit to the Kap95 simulation data (see Fig. 3, c and d).

We therefore attempted to develop an analytical model that could describe both the K_D dependence on the number of cohesive polymer blocks N_coh, as seen in the polymer data, and on the number of cohesive patches on the NTR N, as seen in the Kap95 data (see the Supporting materials and methods for a complete derivation). In this model, one considers a system volume V that, for simplicity, is discretized into a large number of M small cubes of volume v_vox = V/M whose centers form a cubic lattice. The N_coh polymer cohesive units and the N cohesive units on the particle occupy a small portion of the M sites. The polymer cohesive units are constrained within a subvolume V′ (consisting of M′ ≪ M sites), and the particle units are also confined to a separate volume that, for simplicity, is also of size V′ (see Fig. S5). In the model, henceforth called the lattice binding model, the polymer cohesive units are assumed uncorrelated and can occupy any of the M′ = (MV′)/V = V′/v_vox sites within V′; the particle units are assumed fixed relative to one another in (analogous to the Kap model in simulations) and are symmetrically distributed among the M′ sites. The polymer and particle units can only interact with one another when their respective subvolumes overlap; when this happens, the free system volume (containing no polymer or particle) goes from V₀ = V − 2V′ to V₀ = V − V′. When an individual polymer unit occupies the same lattice site of a particle unit, it is considered to be bound. Hence, the partition function for this system is given by

$$\begin{array}{l}\mathcal{Z}={\mathcal{Z}}_0+{\mathcal{Z}}_1\\ =\left(\begin{array}{l}M/M^{\text{′}}\hfill \\ 2\hfill \end{array}\right)\left(\begin{array}{l}{M}^{\prime }\hfill \\ N_{\text{coh}}\hfill \end{array}\right)+\frac{M}{M^{\prime }}\stackrel{N}{\sum _{n=0}}\left(\begin{array}{l}{M}^{\prime }-N\hfill \\ N_{\text{coh}}-n\hfill \end{array}\right)\left(\begin{array}{l}N\hfill \\ n\hfill \end{array}\right)e^{-\beta {\epsilon }^{\text{′}}n},\end{array}$$ (8)

where ${\mathcal{Z}}_0$ is the number of noninteracting microstates and ${\mathcal{Z}}_1$ is the number of interacting microstates. The first binomial coefficient $\left(\begin{array}{l}M/M^{\text{′}}\hfill \\ 2\hfill \end{array}\right)=\left(\frac{M}{2M^{\prime }}\right)\frac{M-M^{\prime }}{M^{\prime }}$ is the number of ways of placing the nonoverlapping polymer and particle sublattices (each consisting of M′ voxels) in the system lattice (M), the second binomial coefficient is the number of arrangements of the N_coh units in the polymer sublattice, the M/M′ factor is the number of ways of placing the overlapping (polymer and particle) sublattice in the system lattice, the third binomial coefficient is the number of arrangements of the N_coh − n unbound polymer units among the M′ − N free sites, the fourth binomial coefficient is the number of arrangements of the n bound polymer units among the N particle units, and the last factor is the Boltzmann weight for the system energy E = ε′n (in units of k_BT). The probability that at least one polymer unit is bound is

$$P_1=\frac{\frac{M}{M^{\prime }}{\sum }_{n=1}^N\left(\begin{array}{l}N\hfill \\ n\hfill \end{array}\right)\left(\begin{array}{l}{M}^{\prime }-N\hfill \\ N_{\text{coh}}-n\hfill \end{array}\right)e^{-\beta {\epsilon }^{\text{′}}n}}{\mathcal{Z}},$$ (9)

and the probability for no polymer units being bound is simply P₀ = 1 − P₁. Using the relation K_D = (N_AV)⁻¹P₀/P₁ (as in Eq. 7), one obtains, for arbitrary N_coh and N, an equation for K_D given as (details in the Supporting materials and methods)

$$K_D=\frac{2+\frac{\left(M-M^{\prime }\right)\text{Γ}\left(M^{\prime }\right)\text{Γ}\left(\gamma \right)}{\text{Γ}\left(\gamma +N\right)\text{Γ}\left(\gamma +N_{\text{coh}}\right)}}{2N_{A}V\left({}_{2}F_1\left[-N_{\text{coh}},-N,\gamma ,e^{-\beta {\epsilon }^{\prime }}\right]-1\right)},$$ (10)

where Γ(x) is the Gamma function, ₂F₁[a, b; c; d] is the Gauss hypergeometric function, and γ = 1 + M′ − N − N_coh. As a first test for consistency, we checked whether Eq. 10 reproduced the K_D ∝ 1/N_coh relationship as shown before. Indeed, by setting N = 1 in Eq. 10 and imposing M ≫ M′ > N_coh (dilute limit), we obtain

$$K_D=\frac{e^{\beta {\epsilon }^{\prime }}}{2N_A{N}_{\text{coh}}{v}_{\text{vox}}}.$$ (11)

Next, we performed a one-parameter fit of Eq. 10 to the Kap and Kap_half simulation data by setting N_coh = 18 (for the Nsp1-like sequence) and found that it reasonably describes the trends observed in the coarse-grained MD simulations (Figs. 3, c and d and S6). We note that the lattice binding model only distinguishes between the Kap and Kap_half data through the fitting parameter ε′. We also checked that the results from the lattice binding model were robust against changes to the simplified assumption of how the polymer and particle units bind, i.e., by accounting for a microscopic probability of the units becoming bound (see Supporting materials and methods). Comparing the data in Fig. 3 b with other experiments, we note that the N = 10 result (K_D = 24 μM) is in reasonably good agreement with experimental affinities measured for FG Nups and importins K_D $\underset{\approx }{>}$ 4 M (11,14).

Next, considering the unbinding and binding kinetics using the MD simulations as for the case for NTF2 (Fig. 2 c), we find that for NTRs with more spread-out binding sites, the unbinding off rates k_off are higher when comparing NTR models that yield similar K_D-values (Fig. 3, e and f). That is, if the respective ε′-values are increased for the N = 2 (ε′ = 10.45 k_BT) and N = 4 (ε′ = 9.55 k_BT) Kaps for them to have the same K_D as the N = 10 (ε′ = 8.0 k_BT) particle (Fig. 3 e), we observe that k_off—and therefore also k_on—increases with N (Fig. 3 f). We further verified this observation by simulating a Kap particle with N = 100 patches, i.e., approaching the limit of a uniform sphere for Kap95, which resulted in an ∼2-fold increase in k_off (as compared to the N = 10 case) when ε′ is decreased (to 2.75 k_BT) to match the K_D as calculated for the N = 10 particle. This confirms our result (see also Fig. 2 c) that to facilitate fast kinetics despite having strong binding, it is beneficial for NTRs to have many weak binding sites on their surface rather than a few stronger ones.

Diffusion of NTRs in a polymer melt

After the success of our models in replicating experimental data on single NTRs binding to single FG domains and having used this to study binding equilibria and unbinding and binding kinetics, we next considered how our findings translate to the dynamics on NTRs in a system containing many FG domains. Understanding how “patchy” NTRs and cargoes travel through dense polymeric mediums, such as in the NPC, is an open problem (see (46, 47, 48) for related work). Such considerations are facilitated by available experimental data concerning NTF2 diffusing in a bulk solution of F6A (48). Specifically, we model one NTR diffusing in a bulk solution (polymer melt) of synthetic FG sequences (F1A-F6A) at a physiologically relevant packing fraction (∼0.1) (5,22). To verify that the diffusion measurements can be solely attributed to the movements of the NTR particle relative to the polymer melt and not any codiffusing polymers that could be stuck to it, we tested whether specific polymers showed a significantly higher number of binding events to the particle (as would be the case if particular polymers were stuck to the particle). We observed that the NTR particle uniformly sampled the polymer binding sites, thus ensuring that particular polymers were not stuck to the particle (see Fig. S7).

Having demonstrated that we could measure the diffusion of NTRs with respect to a polymer melt, we next investigated the dynamics of the patchy and uniform NTF2 model particles. Somewhat intriguingly, the instantaneous diffusion coefficients for the patchy NTF2 particle are typically ∼4-fold larger (Fig. 4 a) than for the uniform particle, despite having lower k_off-values for similar K_D-values in the single-molecule simulations (Fig. 2 c). This may be related to the results in Fig. 3 b, which showed that the presence of a larger number of FSFG motifs (18 for the Nsp1-like sequence instead of 1–6 for the synthetic sequences) resulted in significantly tighter binding for the uniform NTF2 model. Indeed, we observed a twofold increase in the number of individual FSFG-particle binding events for the uniform particle as compared with the particle with two patches, which we attribute to the spreading out of NTR affinity through increased numbers of weak binding sites (see Fig. S7). This implies that for the polymer densities and polymer-particle size ratios explored here, there is a dynamical cost in binding to large numbers of FSFG motifs in the melt that is analogous to increased friction/drag on the particle and could provide a physical reason as to why NTRs are not totally covered in binding sites.

Figure 4.

Equilibrium dynamics of a single nuclear transport receptor in a bulk solution of various synthetic FG protein sequences. (a) Instantaneous diffusion coefficients for patchy (left) and uniform (right) NTF2 particles, with equivalent single-molecule dissociation constants for the F1A-F6A sequences, as a function of (lag) time. Bands are SDs from five independent runs. (b) Same as (a) but for the Kap model with N = 10 and 4 with respective cohesion strengths of ε′ = 8.0 k_BT and 9.0 k_BT that give equivalent dissociation constants for the short F1A-F6A sequences. (c) CDFs for patchy and uniform NTF2 for the selected sequence (F6A) alongside two fits: one using a single-mobility model (Gauss) and the other a two-mobility model (bi-Gauss). (d) Same as (c) but for the Kap models. For both (c) and (d), the CDFs are for t ≈ 10⁻²μs (main panels) and t ≈ 10⁰μs (inset panels). To see this figure in color, go online.

As for NTF2, we find for Kap95 that a higher k_off in the single-molecule simulations (Fig. 3, c and d) does not translate into substantially faster diffusion in the polymer melt, as illustrated for the Kap95 models for N = 4 and N = 10 patches with matching single-molecule K_D-values (Fig. 4 b). For both Kap particles, we observe that their dynamics become slower (∼2- to 3-fold difference) upon increasing the number of cohesive polymer blocks from 1 to 6, and they tend to be slower than patchy NTF2 but are comparable with the uniform NTF2 model. Satisfyingly, the diffusion coefficients for the NTR models (∼10 m²/s $\equiv$ 10⁻⁷ cm²/s) are in general agreement with previous experimental data (at similar FG densities as in the NPC) (11,48, 49, 50). It appears that with an appropriately chosen single-molecule K_D, the single-molecule unbinding/binding kinetics does not seem to matter too much for the diffusion in the melt. However, the single-molecule unbinding and binding kinetics might matter more at the peripheries of the NPC, in which faster off rates could determine faster detachment from the mass of FG Nups occluding the pore (we do not explore this here).

Diffusion in crowded biological environments, as well as in crowded polymer melts, can often be characterized as anomalous (non-Fickian), arising from the steric, repulsive, and/or attractive interactions between the molecular components (51, 52, 53). Of relevance, many molecules in the cytoplasm and cell nucleus have been shown to diffuse anomalously (subnormally) (54,55). Because the instantaneous diffusion coefficients decrease with lag time t (Fig. 4), we infer that the NTRs show subnormal diffusion in the polymer melt consisting of FSFG sequences. This can be further analyzed via the cumulative density function CDF(r, t), which is the probability of finding a particle—starting at the origin r = 0 at time t = 0—at a distance r after a time t. We next fitted the CDF(r, t) to one-mobility and two-mobility models, with the latter being defined by two separate ordinary diffusion coefficients (56, 57, 58, 59, 60). The two-mobility model provides more degrees of freedom and may therefore expected to better fit the data; if that is the case, it should be regarded as an indication of deviations from predictions for normal diffusion, not necessarily as an indication for the presence of two discrete modes of diffusion. Indeed, as expected based on the variation of the instantaneous diffusion coefficients with lag time in Fig. 4 a, the computed CDFs are better fitted with a two-mobility, bi-Gauss, anomalous diffusion model (with two parameters) than with a simple one-mobility Gauss model (with one parameter) that applies for normal diffusion (see Fig. 4, c and d and Supporting materials and methods for details).

Interestingly, we find that the patchy NTF2 deviates most from a one-mobility model but can be described well using a two-mobility model with a fast diffusion coefficient (D₁) that is ∼4–5 times greater than the slower one (D₂), with both fast and slow diffusion playing significant roles (35% fast, 65% slow) (see Table S2). Remarkably, the predicted (at t = 1 s) fast (D₁ = {25.7, 21.7} m²/s) and slow (D₂ = {5.5, 5.1} m²/s) diffusion coefficients for patchy and uniform NTF2 particles, respectively, lie close to the experimentally determined diffusion coefficients ({D_free = 23 ± 10, D_bound = 5.6 ± 2.2} m²/s) as found for an NTF2 particle diffusing between a solution of F6A sequences (relating to D_bound) and a reservoir of inert polymers (relating to D_free) (48). Also, the predominance of the slower diffusion (>60%) observed in our simulations is also corroborated by the predominance of bound diffusion in the same experiments. Specifically, we may interpret the faster diffusion coefficient D₁ to represent unbound diffusion, when the NTF2 particle is free of FSFG motifs, and the slower diffusion coefficient D₂ represents bound diffusion, with the caveat mentioned above that this is unlikely to be a sharp distinction.

Expectedly, the two Kap particles (N = {4, 10}) did not show significantly different behavior, as is observed in the instantaneous diffusion coefficients, and showed minor deviations from the one-mobility model. For both Kaps (N = {4, 10}), we found that the slow diffusion coefficient D₂ is similar in value to the one-mobility diffusion coefficient, with a large portion (∼70–80%) of the diffusion arising from D₂, but still a non-negligible portion of faster diffusion (D₁) arose from the two-mobility fits. We note that the size could also be contributing to the slower diffusion (as compared with the NTF2 models). In all cases, we observe that the diffusion coefficients for the mobility models are largely consistent with the independently calculated instantaneous diffusion coefficients. This analysis highlights that the dynamics of NTRs in a heterogenous melt could potentially involve a range of diffusion types, including fast (free or unbound) and slow (bound) diffusion.

Conclusions

In summary, we have presented a physical picture of patterned FG sequences interacting with heterogeneous NTRs. Firstly, our minimal coarse-grained model is in excellent agreement with recent experimental binding data on the level of single molecules by only fitting one interaction parameter (13). We also found that this agreement was maintained even when the surface heterogeneity of the NTR was ignored. This is consistent with our previous observations on NTR uptake in surface-grafted FG domain assemblies as described by mean-field homopolymer models (21,22) and provides a foundation for other computational studies that made similar assumptions (7,19,25,27,61,62). However, we found the uniform-NTR model exhibited much faster binding kinetics (with a high “off” rate ∼10⁶ s⁻¹ and “on” rate ∼10⁹ M⁻¹ s⁻¹) than the two-patch model for the same dissociation constant, owing to a greater spread of the cohesion over the particle. This suggests that care must be taken when inferring kinetic properties from homopolymer type modeling.

Using analytical theories, one based on a sequence-specific polymer theory and the other based on a statistical mechanical lattice binding model, we further confirmed the roles that sequence heterogeneity of the FG sequences have on FG-NTR binding: that the overall number of cohesive blocks largely dictates binding affinity, with variations in the exact distances between those blocks being of lesser importance. These theories provide a physical picture and mathematical framework to understand single-molecule binding of patterned polymers and heterogeneous nanoparticles.

Furthermore, we made predictions on the binding of a more realistic FG sequence based on Nsp1 with NTRs based on Kap95 having more complex surface patterning. We found that an NTR that is larger than NTF2 but with more cohesive patches resulted in a similar overall binding affinity to the FG sequence, highlighting a possible reason for why larger cargoes, e.g., importin-β, have more FG binding grooves and spots to compensate for its size (10). Overall, the number of binding patches on the NTR is critical; we observe a change from ∼1 mM to ∼10 M in the FSFG sequence-NTR binding affinity upon doubling the number of particle cohesive patches.

Our results have potential implications on the large differences between single-molecule K_D-values as inferred from various experiments, including FSFG constructs and native FG Nups, with values including ∼1 mM (12,13), ∼10 M (11,14,15), and $\lesssim$10 M (15, 16, 17, 18). We reconcile these affinity differences through varying degrees of multivalency, in which moderate increases in available binding sites results in large increases in affinity. As such, care must be taken in inferring single-molecule binding affinities from macroscopic systems in which collective effects such as the nonlinear dependence of dissociation on the binding site concentration will carry over into any extrapolated single-molecule binding constant.

Lastly, through exploring the diffusion of an NTR in an FG polymer melt, we found that the observations from single-molecule kinetics do not necessarily carry over to macroscopic systems. Specifically, we did not observe an increase in macroscopic diffusion coefficient upon spreading out the cohesion on an NTR’s surface through more patches, despite this leading to higher k_off-values in the single-molecule simulations. For the NTRs explored here, we find generally fast (∼1–50 m²/s) diffusion in the FSFG polymer melt in accordance with previous experimental data (11,48, 49, 50). Our findings suggest that the macroscopic diffusion of NTRs could be due to a combination of fast and slow modes, with the important caveat that there are many different physical regimes that affect diffusion, and it is not known which one is directly relevant to the NPC. Although we have not explored the precise microscopic mechanism of NTR motion in an FG polymer melt, we expect that our macroscopic picture can be fully reconciled with microscopic pictures of motion such as the “slide-and-exchange” mechanism (46). We speculate that although the overall diffusion in a dense melt is not greatly affected by changes in the surface properties of the NTR, they may be of particular importance at the nucleoplasmic and cytoplasmic entry points of the NPC where high specificity (K_D and k_on) governs uptake and fast unbinding kinetics (k_off) governs release (although cargo transport may not need the NTRs to be released from the NPC).

Overall, we have presented a minimal, yet adaptable, physical framework that sets a solid foundation to further explore specific physical questions regarding selective transport in the NPC while also elucidating future design principles for the components of artificial transport nanomachines.

Author contributions

L.K.D. designed the model, developed the theory, performed and analyzed the simulations and calculations, interpreted the results, and wrote the manuscript. A.Š. advised on MD simulations and analysis and interpreted the results. B.W.H. and A.Z. conceived the study, helped design the model and theory, interpreted the results, supervised the project, and co-wrote the manuscript. All authors provided feedback on the manuscript.

Supporting material

Document S1

. Supporting materials and methods, Figs. S1–S7, and Tables S1 and S2