A Significance Test for Reverberation-Chamber Measurement Uncertainty in Total Radiated Power of Wireless Devices

Abstract

We develop a significance test that determines whether the component of uncertainty due to the finite number of stepped mode-stirring samples or the component due to the lack of spatial uniformity dominates for a particular chamber set-up and stirring sequence, as well as expressions for uncertainty for both cases. The significance test is illustrated with a measurement example comparing unloaded and loaded chambers for the measurement of a large-form-factor machine-to-machine device transmitting the W-CDMA protocol. Based on this example, we illustrate a method that allows users to estimate the minimum number of stepped mode-stirring samples needed to ensure that the component of uncertainty due to spatial uniformity dominates for a given chamber set-up, allowing use of a simplified expression for uncertainty.

I. Introduction

We apply the significance test procedure outlined in the Guide to Uncertainty in Measurement [1] to determine which of two different equations may be used for finding the random, reverberation-chamber-specific component of uncertainty in an estimate of total radiated power (TRP). One equation is applied when the uncertainties related to the finite number of mode-stirring samples and lack of spatial uniformity are comparable, as may be the case for unloaded and lightly loaded chamber configurations. Such configurations are commonly used for electromagnetic susceptibility and emissions measurements, as documented in IEC 61000-4-21 [2]. These tests have been developed with a focus on presenting a known field to the device under test (DUT) (see also [3]), measuring radiated emissions, and/or characterizing antenna parameters such as efficiency or reflection coefficient. These tests are typically performed with continuous-wave signals.

The second equation is applied when the uncertainty due to lack of spatial uniformity dominates, as is common in loaded chambers used for wireless test. Such tests typically involve the reception and demodulation of digitally modulated communication signals, termed “over-the-air” (OTA) tests by the wireless community [5, 6]. In addition to total radiated power (TRP) for modulated signals, other parameters of interest include receiver sensitivity (known as total isotropic sensitivity (TIS) or total received sensitivity (TRS)), bit-error rate, and data throughput [7–12].

These latter metrics require that the channel conditions presented to the DUT are similar to those for which the receiver was designed, allowing verification that the receiver will operate as expected in a realistic channel. This may require broadening the coherence bandwidth (the range over which frequency components of the received signal are significantly correlated) of the channel presented by the reverberation chamber to the wireless device under test [13–15]. The coherence bandwidth for a given chamber set-up is often broadened by loading the chamber with RF absorbing material. Large-form-factor machine-to-machine (M2M) devices made of lossy materials such as plastics or foam may also increase chamber loading [16–18].

Loading has the effect of reducing the amplitude and phase variation of the channel presented to the DUT, which better replicates the channel in which many receivers were designed to operate. However, loading also reduces the mode density in the chamber, hence, reducing the number of uncorrelated measurement samples for a given set-up. Loading also reduces the spatial uniformity of the power density within the chamber.

Both the reduction in the number of uncorrelated samples and the reduction of the spatial uniformity in the chamber may affect the uncertainty in an estimate of total radiated power or other power-based quantities of interest. For a reverberation chamber set-up providing ideal, randomly distributed fields (e.g., those with a large number of modes and mode-stirring mechanisms available for the measurement), the uncertainty ideally decreases by $\frac{1}{\sqrt{N}}$, where N is the number of uncorrelated samples [19]. In this “ergodic-mode” case [20], the uncorrelated stirring samples acquired by various stirring mechanisms including antenna, mechanical paddle, frequency, polarization stirring, contribute equally to the uncertainty and may be interchanged for the calculation of uncertainty.

However, because loading increases correlation between samples, a stirring sequence that provides a sufficient number of samples to meet a given uncertainty threshold in an unloaded chamber may not provide enough samples under loaded conditions. As discussed in [3, 21], for this case, mode-stirring samples based on an antenna’s location within the chamber (e.g., antenna stirring for antennas whose size is negligible relative to the chamber size) and those based on other stirring mechanisms may contribute in different ways to uncertainty. In [3, 21], analytic expressions were developed for finding the uncertainty as a function of the average K factor (the ratio of stirred energy to unstirred energy for a given chamber set-up) and the number of samples given known levels of correlation.

The present work has a different focus: When the unstirred energy in “non-ergodic” modes contributes significantly to the estimate of the quantity of interest, uncertainty in the estimate of that quantity due to lack of spatial uniformity may dominate. In this case, it may be possible to utilize a simplified expression for uncertainty.

For the wireless community, the overall increase in uncertainty due to loading is a necessary trade-off for the measurement of modulated signals. While it is not necessary to load the chamber for TRP measurements, it is often done for expediency to avoid the necessity of two chamber calibration measurements.

Much of the prior work on uncertainty in reverberation-chamber measurements of modulated-signal wireless devices has focused on how specific non-idealities in the set-up affect the spatial uniformity itself. Such work includes the study of a non-zero K factor [3, 15, 21–23], the related issue of number of uncorrelated samples [24–29], and antenna polarization imbalance and the differences between multiple receive antennas [3, 15, 30]. In [31], the variability of the average received power was derived from an analytic model of the modal structure in the chamber for unloaded and loaded conditions under CW excitation. The work here augments these studies by assessing the relative importance of the uncertainty due to the finite number of stepped mode-stirring samples and the lack of spatial uniformity. This is especially important in experiment design for modulated-signal measurements of power-based metrics under conditions where the chamber is loaded with RF absorbing material.

In Section II, we provide an expression for TRP that is consistent with the over-the-air test methodology that is being developed by industry [5, 6]. The expression, derived from flow-graph models in Appendix A, takes into account impedance mismatch between the antennas and the chamber, and the antenna efficiencies. Formulas for de-embedding connecting cables are provided in Appendix B. Our methods are based on “stepped mode-stirring” with samples collected under static, stepped conditions.

In Section III, we derive general expressions for the components of uncertainty due to the limited number of stepped mode-stirring samples and lack of spatial uniformity. A significance test is developed that accounts for the combined effect of these two components. Section IV provides an example where the significance test is applied to measured data for a lossy, large-form-factor M2M wireless device. We compute uncertainty for unloaded and loaded cases, illustrating that, for this set-up, even though there is a significant increase in uncertainty for the loaded case, the total uncertainty does not exceed common thresholds. Finally, we provide an example of the use of the significance test in determining the minimum number of stepped mode-stirring samples required to ensure that utilization of the expression for uncertainty due to lack of spatial uniformity is valid for a given chamber set-up.

While the present work focuses on uncertainty in TRP measurements for cellular wireless devices, the technique for finding the relative significance of various components of uncertainty can be extended to other quantities of interest and other types of wireless devices in a straightforward way.

II. Estimation of Total Radiated Power from Measurement

A. Chamber Configuration

Figure 1 shows a representative configuration for a total radiated power measurement in a reverberation chamber consisting of (a) the DUT measurement and (b) the measurement of the chamber’s reference power transfer function (the “reference measurement”). The reference measurement estimates the loss in the chamber set-up. In Fig. 1, a metallic paddle rotates and stops at various angles where each mode-stirring sample is acquired by the measurement (receive) antenna. The mechanical paddle randomizes the fields by changing the boundary conditions within the chamber. In Fig. 1(a) power samples are measured at each mode-stirring step. Other types of mode stirring could be used [3, 19, 28], including platform stirring, where the DUT is physically moved within the chamber, and polarization stirring, where measurement antennas having different polarizations are utilized.

Fig. 1:

Typical reverberation chamber set-up for measuring radiated power for a wireless cellular device under test. In (a), a base station emulator ensures that the DUT transmits at full power and may also be used to measure the received power. In (b), a VNA connected at the reference planes performs a reference measurement that compensates for the loss in the chamber set-up.

The power samples for the DUT measurement are acquired with a base-station emulator, spectrum analyzer, or other vector receiver. Sampling and averaging the received power from different mode-stirring positions yields an estimate of the total average received power, to within some uncertainty.

For test of a wireless device, the reference measurement is often carried out with a vector network analyzer that acquires S parameter data as a function of frequency over the same stepped mode-stirring sequence as was used for the DUT measurement. These samples are also averaged over the stepped mode-stirring position. Additional averaging is often carried out over the occupied bandwidth of the signal to improve the estimate of the chamber set-up’s transfer function.

To further improve the estimate of the chamber’s reference power transfer function in the presence of non-uniformly distributed fields within the chamber, reference measurements are typically repeated at various locations within the chamber [2, 3] and the mean of these measurements is then used. The standard deviation of these measurements may be used to estimate the component of uncertainty due to lack of spatial uniformity of the fields.

In the following, the same measurement antenna and chamber configuration are utilized for the DUT and reference measurements. RF absorbing objects, including DUTs, must be in place in the chamber during the reference measurement so that this loss will be calibrated out. Procedures for de-embedding of additional cables and adapters not used in the reference measurements and impedance mismatch correction are described in the Appendix.

B. “Within” and “Between” Measurement Samples

We next develop an expression for TRP from stepped mode-stirring samples that occur “within” a given stepped mode-stirring sequence and those that occur “between” antenna locations in the chamber. The within measurements include the various stirring mechanisms such as paddle, antenna position, polarization, or source stirring. They are used to determine the uncertainty due to the finite number of stepped mode-stirring samples.

The between measurements consist of multiple, independent realizations of the mode-stirring sequence carried out at different locations within the chamber. They are used to form an estimate of the reference power transfer function and spatial uniformity for a particular chamber configuration. These locations are typically chosen to cover the working volume of the chamber set-up. Note that the “chamber configuration” includes a given set of antennas and connecting cables, a repeatable stepped stirring sequence, and fixed locations for the absorbing objects within the chamber.

We use notation that allows us to readily identify the relevant components of uncertainty. Specifically, we define:

1. N_W “within” samples of a given stirring sequence, where $W=\left\{w_1,w_2,\dots ,w_{N_{\text{W}}}\right\}$. Each element w_i consists of a single measurement at the i^th stepped mode-stirring position.

2. N_B “between” reference- or DUT-antenna locations $B=\left\{b_1,b_2,\dots ,b_{N_{\text{B}}}\right\}$. Each element b_j corresponds to a different placement of the reference or DUT antenna during a measurement. In the present work, the antenna locations must be spatially uncorrelated.

In the following, we assume that the working volume of the chamber set-up has been chosen to minimize factors such as antenna placement near metallic surfaces [32] and antenna placement near absorbing objects [16–18]. Without loss of generality, we also assume that the chamber configuration (including wall loss, loading and antenna type) will provide a sufficient number of uncorrelated samples to achieve a desired level of uncertainty [24–29] and that uncorrelated samples are used. (Correlated samples can be used if a model is available [3, 21] that accounts for the increased uncertainty.) We consider only uncorrelated samples in the development below. Finally, we assume that the stirring sequence utilizes stepped-mode stirring so that Doppler shift and other effects introduced by continuous mode stirring may be neglected. We then focus on determining the TRP and the uncertainties related to the number of mode-stirring samples and spatial uniformity.

C. Total Radiated Power from the DUT

The objective is to estimate P_TRP, the total power radiated by the DUT in free space, and its associated uncertainty from measurement. We define P_Meas as the average power measured by the receiver at the reference plane indicated in Fig. 1(a) over the occupied bandwidth of the modulated signal. It is typically necessary to average this measurement over many transmitted symbols or frames to obtain a valid estimate. A flow graph model for this measurement is given in Appendix A. Based on this model, the ensemble average over all N_W mode-stirring positions and N_B antenna locations may be given by

$${\langle P_{\text{Meas}}\rangle }_{N_{\text{W}}{N}_{\text{B}}}=\frac{{\eta }_{\text{M}}\left(1-{\left|{\Gamma }_{\text{M}}\right|}^2\right)P_{\text{TRP}}{\langle G_{\text{DUT}}\rangle }_{N_{\text{W}}{N}_{\text{B}}}}{{\left|1-{\Gamma }_{\text{M}}{\Gamma }_{\text{RX}}\right|}^2},$$ (1)

where 〈G_DUT〉 represents the power transfer function of the chamber for the DUT measurement, η_M is the efficiency of the measurement antenna, and Γ_RX is the reflection coefficient of the base-station emulator or spectrum analyzer receiver assembly (including cable, if used). The term Γ_M corresponds to the free-space reflection coefficient of the measurement antenna as defined in Appendix A. We define 〈G_DUT〉 as a gain so that a reduction in power is denoted with a decreasing value of 〈G_DUT〉.

The chamber gain for the DUT measurement 〈G_DUT〉 is often estimated from the chamber reference measurement 〈G_R〉. This reference power transfer function may be estimated from S parameter measurements as

$${\widehat{G}}_{\text{Ref}}\approx {\langle G_{\text{R}}\rangle }_{N_{\text{W}}{N}_{\text{B}}}\equiv \frac{{\langle {\left|S_{21,\text{Ref}}\right|}^2\rangle }_{N_{\text{F}}{N}_{\text{W}}{N}_{\text{B}}}}{{\eta }_{\text{M}}{\eta }_{\text{R}}\left(1-{\left|{\Gamma }_{\text{M}}\right|}^2\right)\left(1-{\left|{\Gamma }_{\text{R}}\right|}^2\right)},$$ (2)

where ensemble averages have been carried out at N_F frequencies with N_W stepped mode-stirring samples conducted at N_B antenna locations for reference measurements. Refer to Appendix A for a detailed derivation of this expression. Note that some derivations refer to the product η_X (1 − |Γ_X|²) as “total efficiency.” Expressions for choices of reference plane other than those shown in Fig. 1(b) are derived in Appendix B.

Typically, the DUT antenna that excites 〈G_DUT〉 will not be identical to the reference antenna that excites 〈G_R〉. This means that the ratio of unstirred energy to stirred energy (the K factor) could be different for the reference and DUT measurements. This, in turn, could result in different correlations and uncertainties. To minimize this effect, current practice is to select a reference antenna that produces a K factor that is similar to that of the DUT. For example, omnidirectional reference antennas are often used to estimate chamber gain 〈G_R〉 for cellular device testing.

Substituting (2) into (1) yields the total radiated power of the DUT from measurement as

$$P_{\text{TRP}}=\frac{{\langle {\text{P}}_{\text{Meas}}\rangle }_{N_{\text{W}}{N}_{\text{B}}}{\left|1-{\Gamma }_{\text{M}}{\Gamma }_{\text{RX}}\right|}^2}{{\eta }_{\text{M}}{\widehat{G}}_{\text{Ref}}\left(1-{\left|{\Gamma }_{\text{M}}\right|}^2\right)}.$$ (3)

Or, in terms of measured quantities P_Meas and S_21,Ref,

$$P_{\text{TRP}}=\frac{{\langle {\text{P}}_{\text{Meas}}\rangle }_{N_{\text{W}}{N}_{\text{B}}}{\left|1-{\Gamma }_{\text{M}}{\Gamma }_{\text{RX}}\right|}^2{\eta }_{\text{R}}\left(1-{\left|{\Gamma }_{\text{R}}\right|}^2\right)}{{\langle {\left|S_{21,\text{Ref}}\right|}^2\rangle }_{N_{\text{F}}{N}_{\text{W}}{N}_{\text{B}}}}.$$ (4)

The DUT measurement ${\langle {\text{P}}_{\text{Meas}}\rangle }_{N_{\text{W}}{N}_{\text{B}}}$ is often made at a single location, that is, N_B = 1 for this term. Equation (4) is similar to (E.1) for radiated power in [2], with ${\langle {\text{P}}_{\text{Meas}}\rangle }_{N_{\text{W}}{N}_{\text{B}}}$ corresponding to P_AveRec, η_R = η_TX, and the term ${\langle {\left|S_{21,\text{Ref}}\right|}^2\rangle }_{N_{\text{F}}{N}_{\text{W}}{N}_{\text{B}}}$ corresponding to the Chamber Validation Factor (CVF) in [2], although the CVF is not averaged over frequency.

The uncertainties associated with the reference measurement are typically used to estimate the DUT measurement uncertainty by assuming that the chamber conditions for the reference measurement are similar to those of the DUT measurement. This requires that the chamber loading remains in place for both the DUT and reference measurements and that the reference antenna be of a similar type to that of the DUT.

III. Uncertainty in Total Radiated Power Measurements

Standard uncertainties of the measured quantities P_Meas, |S_21,Ref|², Γ_M, and Γ_RX can be obtained from repeat measurements in the chamber. The uncertainty in η_R may be obtained from manufacturer’s specifications. Other sources of uncertainty such as VNA calibration errors and drift would also be included in a complete error analysis [3, 18].

We next find the uncertainties associated with the number of stepped mode-stirring samples N_W and the spatial uniformity assessed at N_B reference antenna locations. We then demonstrate how to apply these uncertainties to a single DUT measurement. We assume independence of our uncorrelated samples, as is common practice [24–29].

A. Number of Stepped Mode-Stirring Samples and Lack of Spatial Uniformity

We denote the standard uncertainty due to the stepped mode-stirring samples by s_W, because it originates within a given mode-stirring sequence. We denote the standard uncertainty due to the lack of spatial uniformity in the chamber by s_B, because it originates between reference antenna locations in the chamber. For convenience, we write this uncertainty in terms of the variable G_Ref, with the assumption that uncertainties in the antenna efficiencies do not contribute to this component of uncertainty.

We identify s_W and s_B using a sum of squares (SS) approach based on the decomposition of

$${\sum }_{j=1}^{N_{\text{B}}}{\sum }_{i=1}^{N_{\text{W}}}{\left({\text{G}}_{\text{R}}\left(w_i,b_j\right)-{\widehat{G}}_{\text{ref}}\right)}^2={\sum }_{j=1}^{N_{\text{B}}}{\sum }_{i=1}^{N_{\text{W}}}{\left({\text{G}}_{\text{R}}\left(w_i,b_j\right)-{\langle {\text{G}}_{\text{R}}\left(b_j\right)\rangle }_{N_{\text{W}}}\right)}^2+{\sum }_{j=1}^{N_{\text{B}}}{\sum }_{i=1}^{N_{\text{W}}}{\left({\langle {\text{G}}_{\text{R}}\left(b_j\right)\rangle }_{N_{\text{W}}}-{\widehat{G}}_{\text{ref}}\right)}^2,$$ (5)

which can be written as

$$\text{Total SS}=\text{Within SS}+\text{Between SS}.$$

In particular,

$$s_{\text{W}}{}^2=\frac{(\text{Within SS})}{N_{\text{B}}\left(N_{\text{W}}-1\right)}=\frac{1}{N_{\text{B}}\left(N_{\text{W}}-1\right)}{\sum }_{j=1}^{N_{\text{B}}}{\sum }_{i=1}^{N_{\text{W}}}{\left({\text{G}}_{\text{R}}\left(w_i,b_j\right)-{\langle {\text{G}}_{\text{R}}\left(b_j\right)\rangle }_{N_{\text{W}}}\right)}^2$$ (6)

which has N_B(N_W − 1) degrees of freedom. Likewise

$$s_{\text{B}}{}^2=\frac{(\text{Between SS})}{\left(N_{\text{B}}-1\right)}=\frac{1}{N_{\text{B}}-1}{\sum }_{j=1}^{N_{\text{B}}}{\sum }_{i=1}^{N_{\text{W}}}{\left({\langle {\text{G}}_{\text{R}}\left(b_j\right)\rangle }_{N_{\text{W}}}-{\widehat{G}}_{\text{Ref}}\right)}^2=\frac{N_{\text{W}}}{N_{\text{B}}-1}{\sum }_{j=1}^{N_{\text{B}}}{\left({\langle {\text{G}}_{\text{R}}\left(b_j\right)\rangle }_{N_{\text{W}}}-{\widehat{G}}_{\text{Ref}}\right)}^2,$$ (7)

with N_B − 1 degrees of freedom. Note that the term N_W in the numerator arises from the decomposition of the sum of squares.

To determine whether the variation in the “between” measurements is significant when compared to the variation in the “within” measurements, a significance test may be used. The outcome of the significance test allows us to determine the correct expression for the standard uncertainty to use in our estimate of the total uncertainty in the TRP measurement. As we show below, in many reverberation-chamber measurements, the “between” effect dominates.

B. Calculating Uncertainty from a Significance Test

The statistic for identifying statistically significant differences between the measurement locations is based on an F distribution, which is formed from the ratio of two variances [1]

$$\text{F}\left(s_{\text{B}}{}^2,s_{\text{W}}{}^2\right)=\frac{s_{\text{B}}{}^2}{s_{\text{W}}{}^2},$$ (8)

with N_B − 1 and N_B(N_W − 1) degrees of freedom. The uncertainty associated with reference measurement ${\widehat{G}}_{\text{Ref}}$ will be calculated in one of two ways, depending on the outcome of this test.

1). Case 1: “Between differences” are not significant

If the test is not significant, that is,

$$\text{F}\left(s_{\text{B}}{}^2,s_{\text{W}}{}^2\right)<{\text{F}}_{0.95,N_{\text{B}}-1,N_{\text{B}}\left(N_{\text{W}}-1\right)},$$ (9)

where $F_{\alpha ,n_1,n_2}$ is the α percentile (e.g. 95%) of the F distribution with n₁ and n₂ degrees of freedom, then the uncertainty squared of the reference value is given as the weighted average of s_B² and s_W²

$$u_{\text{Ref}}^2=\frac{1}{N_{\text{B}}{N}_{\text{W}}}\frac{\left(N_{\text{B}}-1\right)s_{\text{B}}{}^2+N_{\text{B}}\left(N_{\text{W}}-1\right)s_{\text{W}}{}^2}{N_{\text{B}}-1+N_{\text{B}}\left(N_{\text{W}}-1\right)},$$ (10a)

$$=\frac{1}{N_{\text{B}}{N}_{\text{W}}\left(N_{\text{B}}{N}_{\text{W}}-1\right)}{\sum }_{i=1}^{N_{\text{W}}}{\sum }_{j=1}^{N_{\text{B}}}{\left(G_{\text{R}}\left(w_i,b_j\right)-{\widehat{G}}_{\text{Ref}}\right)}^2,$$ (10b)

with N_BN_W − 1 degrees of freedom.

2). Case 2: “Between differences” are significant

If the test is significant, that is,

$$\text{F}\left(s_{\text{B}}{}^2,s_{\text{W}}{}^2\right)>{\text{F}}_{0.95,N_{\text{B}}-1,N_{\text{B}}\left(N_{\text{W}}-1\right),}$$ (11)

then the uncertainty squared in the reference value is given as

$$\begin{gathered} u_{\text{Ref}}^2=\frac{s_{\text{B}}{}^2}{N_{\text{B}}{N}_{\text{W}}} \\ =\frac{1}{N_{\text{B}}\left(N_{\text{B}}-1\right)}{\sum }_{j=1}^{N_{\text{B}}}{\left({\langle {\text{G}}_{\text{R}}\left(b_j\right)\rangle }_{N_{\text{W}}}-{\widehat{G}}_{\text{Ref}}\right)}^2, \end{gathered}$$ (12)

with N_B − 1 degrees of freedom. Note that (10) may considerably underestimate $u_{\text{Ref}}^2$ when (11) applies [1].

C. Expanded Uncertainty in the DUT Measurement

By loading the chamber identically for the reference and DUT measurements, we assume that the uncertainty in a single measurement of G_R will be approximately the same as that of a single measurement of P_Meas. The uncertainty squared is given by

$$u_{\text{DUT}}^2=u^2\left({\text{P}}_{\text{Meas}}\left(b_j\right)\right)\cong N_{\text{B}}{u}_{\text{Ref}}^2$$ (13)

with the degrees of freedom corresponding to $u_{\text{Ref}}^2$ from (10b) or (12).

Note that the square root of $\frac{1}{N_{\text{B}}-1}{\sum }_{j=1}^{N_{\text{B}}}{\left({\langle {\text{G}}_{\text{R}}\left(b_j\right)\rangle }_{N_{\text{W}}}-{\widehat{G}}_{\text{Ref}}\right)}^2$ is sometimes used in the literature as a metric to describe the uncertainty due to spatial uniformity [3, 18]. This is equivalent to u_DUT if the between differences are significant.

To find the expanded uncertainty U₉₅ corresponding to a 95 % confidence level, the coverage factor k₉₅ is determined from the degrees of freedom corresponding to $u_{\text{Ref}}^2$ or $u_{\text{DUT}}^2$. The number of degrees of freedom is then used to calculate the coverage factor k₉₅ as recommended in Appendix B3 of [1]. That is, k₉₅ = t₉₅(υ), where t₉₅(υ) is the two-sided 95^th percentile of the Student’s t-distribution having υ degrees of freedom. Note that, depending on the number of measured samples of N_B and N_W, υ can be small. This would make the coverage factor larger than two. Finally, U₉₅ is found as

$$U_{95,\text{Ref}}=k_{95}{u}_{\text{Ref}},$$ (14a)

or

$$U_{95,\text{DUT}}=k_{95}{u}_{\text{DUT}}.$$ (14b)

The above discussion is based on analysis-of-variance techniques for Gaussian random variables. Although each individual measurement of G_R or P_TRP is not Gaussian distributed, the analysis is based on the frequency averaged values and, by the Central Limit Theorem, is expected to meet the model requirement approximately.

IV. Example: Uncertainty for Unloaded and Loaded Chambers

A. Measurement Set-up

The large-form-factor device was a trash compactor with wireless machine-to-machine communications capability, having a metal housing and a solar panel on top [18]. Residing below the solar panel are the communications hardware and an integrated antenna. The device is shown on the left side of Fig. 2. The chamber was loaded with six RF absorber blocks to broaden its coherence bandwidth for measurement of a wideband code-division-multiple-access (W-CDMA) signal with a bandwidth approximately equal to the chip rate of 3.84 MHz. The number of absorber blocks was determined empirically. For this experiment, the trash compactor was configured to transmit in the Personal Communications Service (PCS) frequency band of 1.85 GHz to 2.0 GHz.

Fig. 2:

Interior of a large reverberation chamber configured to measure the total radiated power from a machine-to-machine trash compactor. Six absorber blocks load the chamber to broaden its coherence bandwidth for measurement of a W-CDMA signal. The omnidirectional reference antenna is seen near the absorber. The directional measurement antenna is out of view behind the trash compactor.

Our test set-up included a large reverberation chamber with interior dimensions 4.6 m × 3.1 m × 2.8 m having one mechanical mode stirrer that traces out a cylinder with a radius of approximately 0.50 m and a height of 2.10 m. The loaded condition, shown in Fig. 2, consisted of a stack of RF absorber (360 cm × 60 cm × 15 cm) plus the machine-to-machine trash compactor (1.28 m × 0.70 m × 0.58 m). The Q of the unloaded chamber was ~11,000 and was ~1,290 for the loaded chamber. An omnidirectional discone reference antenna and a directional, dual-ridge guide measurement antenna were used.

The VNA was set to acquire N_F = 145 frequency points spaced by 140 kHz across the 150 MHz PCS band. We measured the S parameters with the calibration reference planes at the input ports to the antennas, as shown in Fig. 1(b). As discussed above, we averaged over frequency to provide a better estimate of the reference power transfer function.

For the unloaded reverberation chamber, the stirring sequence consisted of N_{W_unloaded} = 72 uncorrelated paddle-angle samples for a single reference antenna location, where our correlation threshold was 0.5. The coherence bandwidth for this set-up was calculated to be 0.45 MHz and, for the PCS band, $N_{\text{F}}=\frac{150e6}{0.45e6}\approx 333$ independent frequencies. For the loaded reverberation chamber, the stirring sequence provided N_{W_loaded} = 43 uncorrelated samples, with a coherence bandwidth of 4.46 MHz and $N_{\text{F}}=\frac{150e6}{4.46e6}\approx 34$ independent frequencies. The stirring sequence was repeated N_B = 9 times by moving the reference antenna to three locations in the chamber, each spaced more than 2 λ apart from the others, and making measurements at three orthogonal antenna orientations. These nine measurements were confirmed to be uncorrelated by use of the complex cross correlation function [28].

B. Significance Test Results

To perform the significance test, we measured the S parameters at each of the nine reference antenna locations and calculated the chamber’s reference power transfer function ${\widehat{G}}_{\text{ref}}={\langle {\text{G}}_{\text{R}}\rangle }_{N_{\text{W}}{N}_{\text{B}}}$ for the unloaded and loaded cases. We then determined the degrees of freedom and calculated the within and between uncertainties from (5) – (7) above. We also computed these uncertainties normalized by the mean power, which we refer to as s_{W_norm} and s_{B_norm}. This quantity is sometimes referred to as the coefficient of variation. Finally, we found the test statistic for significance from (8) as the ratio of s_B² to s_W². These values appear in Table I. Recall that these values are unitless because they are based on S-parameter measurements.

Table I.

Standard uncertainty squared for unloaded and loaded reverberation chamber set-ups. The statistic for testing the existence of a between-location effect is given in the last row.

	Unloaded Chamber	Loaded Chamber
sW2	1.84e-07	2.58e-08
sB2	1.66e-06	5.93e-07
$F\left(s_{\text{B}}{}^2,s_{\text{W}}{}^2\right)=\frac{s_{\text{B}}{}^2}{s_{\text{W}}{}^2}$	9.02	22.98

The relative uncertainty in an ideal, unloaded reverberation chamber with perfect mode stirring (no unstirred energy and exponentially distributed power samples), no correlation between measurements, and no measurement noise may be given by [19]

$${\tilde{u}}_{\text{W},\text{unloaded}}=\frac{1}{\sqrt{N_{\text{F}}{N}_{\text{W}}}},$$ (15)

where the tilde represents a non-measurement-based quantity. The value of ${\tilde{u}}_{\text{unloaded}}$ should be the same at all N_B locations in the chamber, so there is no need to evaluate (15) at the N_B antenna locations. This value is calculated from the number of uncorrelated paddle positions and frequency components that were averaged to obtain the value of G_R at each N_B antenna location.

For loaded chambers, we additionally must include the effect of the K factor in the uncertainty, derived, for example, in equation (17) of [21]. The larger the K factor, the worse the expected agreement between the uncertainty in (15) and the measured uncertainty. Because we have based our estimate of G_R on uncorrelated paddle angles and frequency components, we eliminate correlations from (17) of [21] and estimate this component of uncertainty as

$${\tilde{u}}_{\text{W},\text{loaded}}=\frac{\sqrt{K^2+\frac{2K}{N_{\text{W}}{N}_{\text{F}}}+\frac{1}{N_{\text{W}}{N}_{\text{F}}}}}{K+1},$$ (16)

or from the formula of [3], which was largely based on heuristics:

$${\tilde{u}}_{\text{W},\text{K}\_\text{loaded}\_[3]}=\frac{\sqrt{K^2+\frac{1}{N_{\text{W}}{N}_{\text{F}}}}}{\sqrt{K^2+1}}.$$ (17)

In Table II, we compare the uncertainties derived from (15) – (17) to our measured uncertainty normalized by ${\widehat{G}}_{\text{Ref}}$ [21], that is, $u_{\text{W},\text{norm}}=\sqrt{s_{\text{W}}{}^2}/{\widehat{G}}_{\text{Ref}}$. The average K factors for our set-up, derived from measurement, are given in Table IV. The relative difference is given by $\raisebox{1ex}{$\left|{\tilde{u}}_{\text{W},\text{calc}}-u_{\text{W},\text{norm}}\right|$}\!\left/ \!\raisebox{-1ex}{$u_{\text{W},\text{norm}}$}\right.$ where ${\tilde{u}}_{\text{W},\text{calc}}$ corresponds to the values from (15) – (17).

Table II.

Relative uncertainty and relative difference between measurement (u_{W, norm}) and Model (with Tilde)

	Unloaded Chamber		Loaded Chamber
	Relative uncertainty (linear units)	Relative difference (percent)	Relative uncertainty (linear units)	Relative difference (percent)
uW, norm	0.058	--	0.197	--
${\tilde{u}}_{\text{W},\text{unloaded}}$ (15)	0.0065	88.7	0.026	98.6
${\tilde{u}}_{\text{W},\text{loaded}}$ (16)	0.068	17.2	0.253	28.4
${\tilde{u}}_{\text{W},\text{loaded}\_[3]}$ (17)	0.072	24.1	0.320	62.4

Table IV.

Reference power transfer function and standard uncertainties due to lack of spatial uniformity in the reference DUT measurements.

	Unloaded Chamber		Loaded Chamber
	Linear	Decibels	Linear	Decibels
K	0.0724	−11.40	0.337	−4.72
${\widehat{G}}_{\text{ref}}$	7.38e-03	−21.32	8.18e-04	−30.87
uRef	5.05e-05	--	3.91e-05	--
uDUT	1.52e-04	--	1.17e-04	--
uRef,norm	6.84e-03	0.030	0.048	0.20
uDUT,norm	0.020	0.088	0.14	0.58

We see that for both the unloaded and loaded chambers, ${\tilde{u}}_{\text{W},\text{unloaded}}$ is significantly lower than the value of u_{W, norm} derived from measurement. The estimate of uncertainty ${\tilde{u}}_{\text{W},\text{loaded}}$ from (16) is closer to u_{W, norm} because the K factor can be significant, even for an unloaded chamber, when omnidirectional antennas are used. Finally, note that the estimate of uncertainty ${\tilde{u}}_{\text{W},{\text{loaded}}_{-}[3]}$ from (17) tends to be higher than that from (16) for both unloaded and loaded cases.

Percentiles of the F distribution for the 90 %, 95 % and 99 % confidence levels are shown in Table III, where α = (N_B − 1), (7), and β = N_B(N_W − 1), (6).

Table III.

Percentiles of the F-Distribution for the “between” (α) and “within” (β) degrees of freedom for various confidence levels.

	Unloaded Chamber α = 8, β = 639	Loaded Chamber α = 8, β = 378
F0.90,α,β	1.68	1.69
F0.95,α,β	1.95	1.96
F0.99,α,β	2.54	2.56

The test statistic calculated from measurement in Table I was greater than the table values of the F-Distribution for the unloaded and loaded cases and for all confidence levels, indicating that the between effect dominates the uncertainty for both the unloaded and loaded cases. Thus, for this chamber configuration, (12) and (13) should be used to find the uncertainty in the reference and DUT measurements, respectively. The resulting values are shown in Table IV in both linear units and decibels. Table IV shows both the absolute uncertainty and the “coefficient of variation,” given by u_Ref,norm or u_DUT,norm. For the latter, the uncertainty is normalized by ${\widehat{G}}_{\text{Ref}}$. The decibel representation was found as

$$u\left(10{\text{log}}_{10}\left({\widehat{G}}_{\text{Ref}}\right)\right)\approx 10{\text{log}}_{10}\left(\frac{{\widehat{G}}_{\text{Ref}}+u\left({\widehat{G}}_{\text{Ref}}\right)}{{\widehat{G}}_{\text{Ref}}}\right).$$ (18)

Note that, in Table IV, the uncertainties for the unloaded case are significantly smaller than for the loaded case, following the trends discussed in [16]. This indicates that, if desired, a user could reduce the uncertainty in a TRP measurement by reducing or eliminating loading. As mentioned in the Introduction, loading is often needed for measurements that require demodulation of the received signal, resulting in a necessarily higher uncertainty.

The expanded uncertainty for the reference measurement would be found from (14a), with υ = N_B −1 = 8 degrees of freedom, giving k₉₅ = t₉₅(υ) = 2.31. Assuming that the DUT is exposed to a complete stepped mode-stirring sequence at a single antenna location, the expanded DUT uncertainty would be given by (14b).

The TRP from the trash compactor was measured for the loaded chamber configuration. The contributions to the combined uncertainty for this measurement were presented in [18] and found to be 1.36 dB for the PCS band, within the current CTIA limits of 2.2 dB. The TRP performance of the transceiver in the top panel of the trash compactor was previously measured in an anechoic chamber. The difference between the TRP measured in the reverberation chamber and that of the anechoic chamber was approximately 0.2 dB.

C. Use of the Significance Test in Experiment Design

The significance test described in Section III.B can be used to estimate the number of stepped mode-stirring samples or reference-antenna positions for which the between uncertainty dominates for a given chamber set-up. This can be useful in experiment design to find the minimum number of mode-stirring positions needed to obtain a desired level of uncertainty for a stepped mode-stirring sequence, for example. As illustrated below, each chamber set-up will provide different results.

In Figs. 3(a) and (b), we calculate the test statistic from (8) for various numbers of stepped mode-stirring samples (solid curve) and compare this to the 95th percentile of the F Distribution for the unloaded and loaded cases, respectively. The 95^th percentile, ${\text{F}}_{0.95,N_{\text{B}}-1,N_{\text{B}}\left(N_{\text{W}}-1\right)}$, was calculated for the degrees of freedom corresponding to nine antenna locations and various numbers of stepped mode-stirring samples. This is plotted with the dashed curve.

Fig. 3:

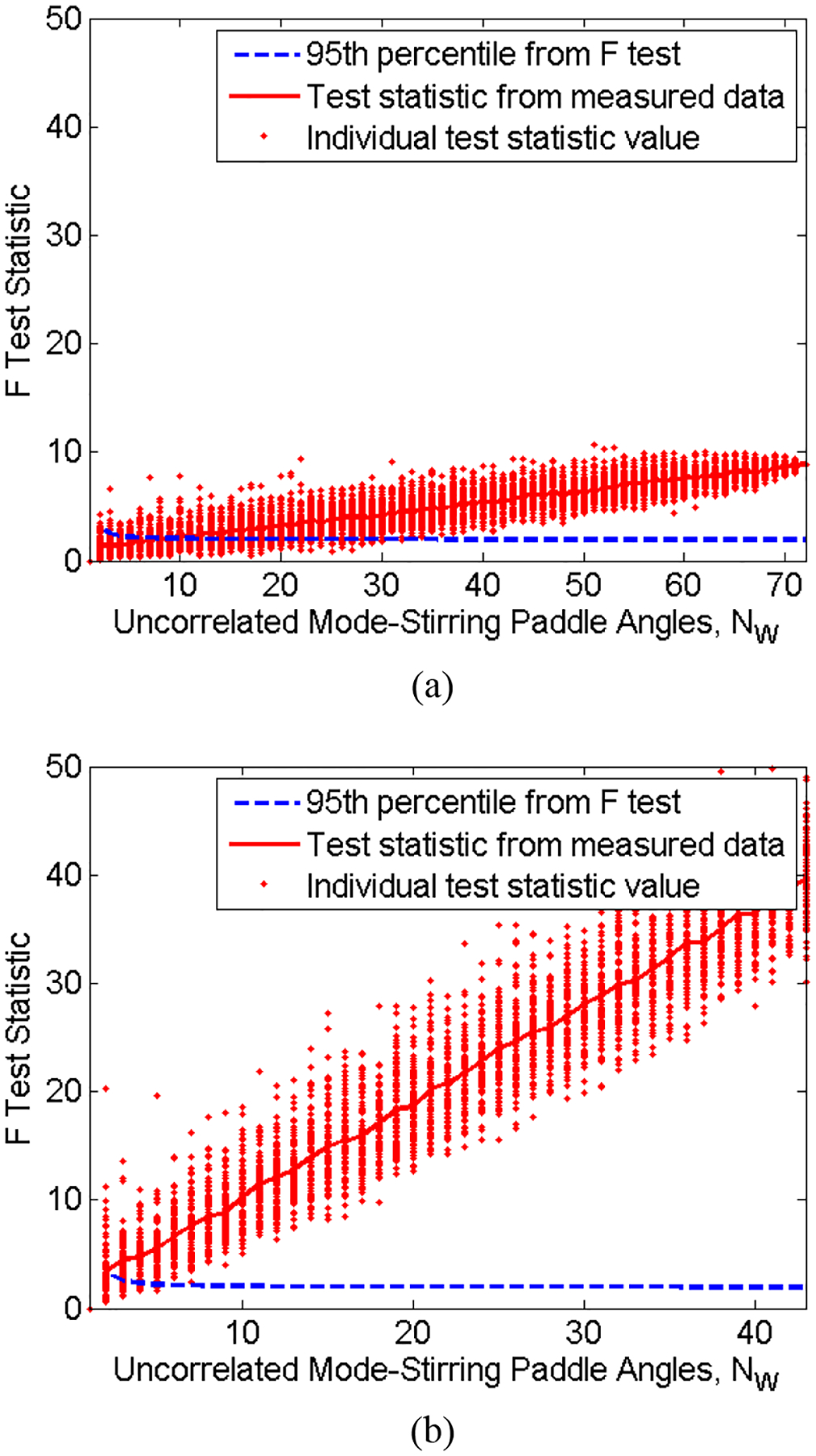
The test statistic from (8) based on an estimate of ${\widehat{G}}_{\text{ref}}$ for increasing values of N_W for the (a) unloaded and (b) loaded reverberation chamber set-ups described in Section IV.A. The red dots represent the test statistic for each of 100 combinations of the measured data and the solid red line corresponds to the average. The 95^th percentile of the F distribution is shown by the dashed line.

To generate the test statistic curve, we averaged multiple realizations of processed data, where for each realization we randomly selected the number of stepped mode-stirring samples from our set of measured data. This approach smooths the test statistic for the reverberation chamber set-up that we used. The dot symbols in Figs. 3(a) and 3(b) represent each individual realization.

As expected, for small numbers of stepped mode-stirring samples, the within effect is more pronounced, shown where the solid curve falls below the F Distribution 95^th percentile values. Because the unloaded chamber provides a high level of spatial uniformity and a wider range of |S_21,Ref| values, the uncertainty due to a limited number of stepped mode-stirring samples is more significant for the unloaded case than for the loaded case. In fact, if fewer than 30 paddle angles were used, it could be concluded that the within effect dominates. Conversely, for the loaded case, the between effect dominates even for very few within samples. This agrees with results from Table I, where we see that the between uncertainty is approximately an order of magnitude higher than the within uncertainty for the loaded case.

We have plotted the same metrics in Figs. 4(a) and (b). However, in Fig. 4, we study the effect of the number of antenna locations N_B on the test statistic. When all of the 100 combinations are considered, the solid line illustrates that the between uncertainty dominates for values of N_B and the use of (7) is indicated for finding the measurement uncertainty in the reference measurement. However, if the metric is formed from fewer than six (unloaded) or four (loaded) antenna locations, the individual measurements show it is possible to conclude that the within effect dominates. These examples illustrate that it is prudent to study multiple combinations of measured data in the design of a reverberation chamber measurement if use of (7) is desired to assess the random component of uncertainty.

Fig. 4:

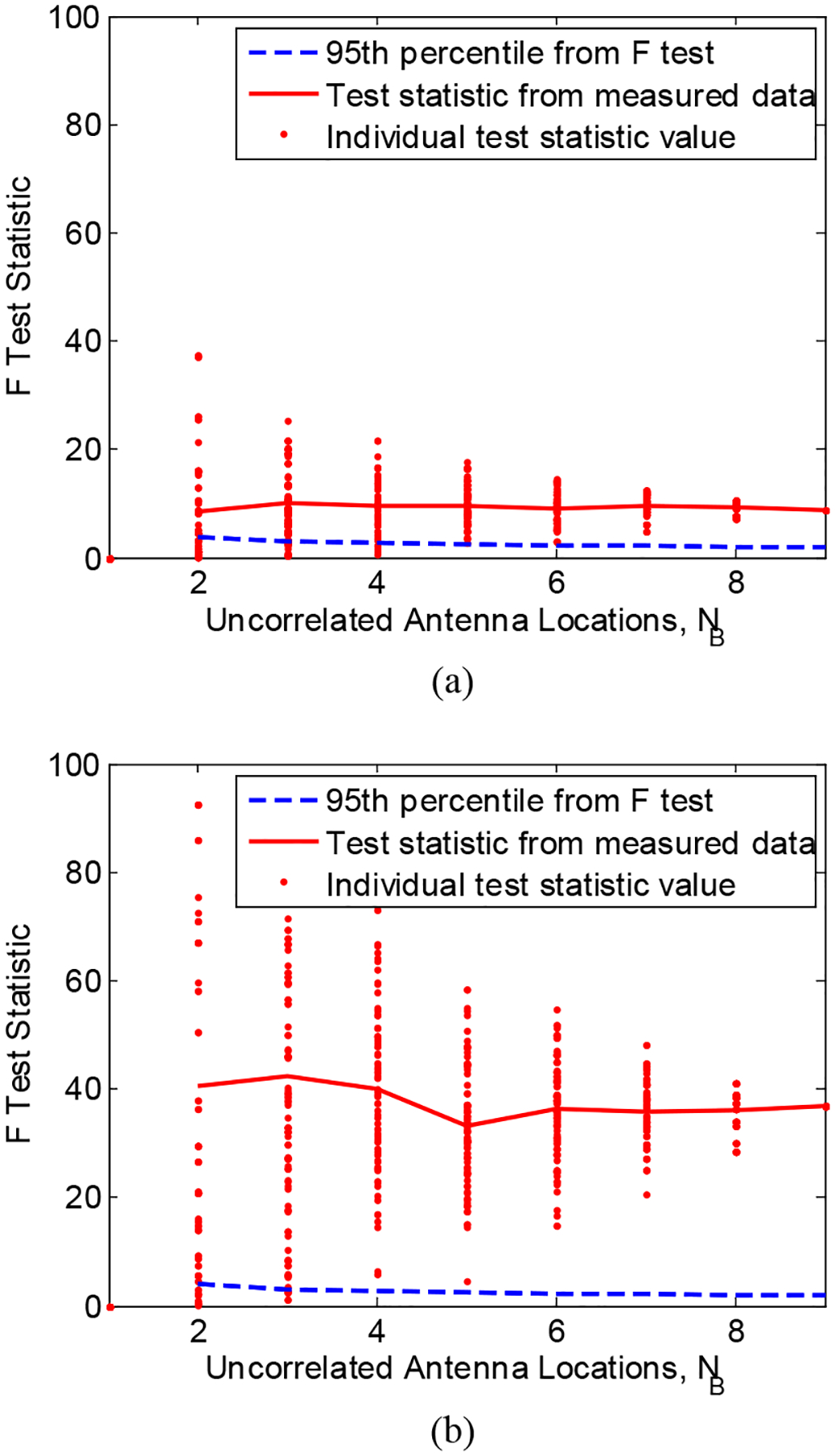
The test statistic from (8) based on an estimate of ${\widehat{G}}_{\text{ref}}$ for increasing values of N_B for the (a) unloaded and (b) loaded reverberation chamber set-ups described in Section IV.A. The red dots represent the test statistic for each of 100 combinations of the measured data and the solid red line corresponds to the average. The 95^th percentile of the F Distribution is shown by the dashed line.

V. Summary and Conclusion

We presented expressions for determining the total radiated power and the related the random component of uncertainty from measurements made in reverberation chambers. Our expressions were derived from fundamental wave parameters by use of flow-graph models. The flow-graph models were extended to allow de-embedding of cable assemblies in the measurement set-up. We then presented a significance test to determine the correct form of uncertainty based on the number of stepped mode-stirring samples and the lack of spatial uniformity in a given chamber set-up.

The significance test was used to determine the correct expression for uncertainty in an estimate of a chamber’s reference power transfer function for an unloaded chamber set-up and a heavily loaded set-up. The loaded set-up was configured to measure the TRP of a large-form-factor M2M device transmitting a W-CDMA signal in the PCS band. Finally, we demonstrated use of the significance test in experiment design to ensure that the simple expression for uncertainty due to lack of spatial uniformity may be used. For this, we determined the number of uncorrelated, stepped, mode-stirring measurements required to form a mode-stirring sequence for a given set-up.

For the chamber set-up we tested, the uncertainty due to lack of spatial uniformity clearly dominated over the uncertainty due to limited number of stepped mode-stirring samples. However, this may not always be the case. For example, when the chamber configuration we studied was not heavily loaded, the uncertainty due to a limited number of stepped mode-stirring samples was on the order of that due to lack of spatial uniformity, as shown in Fig. 3(a) for N_W less than ~30. As well, when the reference power transfer function was found for only a few antenna locations, the user could incorrectly draw the conclusion that the uncertainty due to the limited number of stepped mode-stirring samples was on the order of the uncertainty due to lack of spatial uniformity. Test procedures could be developed that incorporate standardized environments for wireless-device test, as was done in [2] for electromagnetic compatibility testing, but to date, such standards do not exist.

Future work will incorporate expressions for uncertainty involving correlated samples, expand the present work to continuous mode stirring, and study the impact of the different radiation characteristics of the reference and DUT antennas on uncertainty.

Appendix A: Flow-Graph Models for Reverberation-Chamber Measurements

Figure A.1(a) shows a flow-graph representation of a generic reverberation-chamber measurement, where b_g represents the available source power of the VNA for the reference measurement and b₂ represents the measured quantity at the reference plane. For this choice of reference plane, the diagram may be used to derive the relationship between the output and the input quantities as [33–35]

$$b_2=\frac{b_{\text{g}}{S}_{21}}{1-{\Gamma }_{\text{g}}{\text{S}}_{11}-{\Gamma }_{\text{RX}}{\text{S}}_{22}-{\Gamma }_{\text{g}}{\Gamma }_{\text{RX}}\left(S_{21}{S}_{12}-S_{11}{S}_{22}\right)}+ϵ,$$ (A.1)

for a single stepped mode-stirring sample and ϵ represents receiver noise. Because measurements are made well above the noise floor, ϵ is neglected in the following.

Figure A.1:

(a) Flow-graph representation of a general reverberation chamber measurement set-up for a single mode-stirring sample. (b) Flow graph for estimating the chamber gain from a reference measurement. (c) The measured S₂₁ is the cascade of S parameters of the two antennas and the chamber gain.

In (A.1), Γ_g and Γ_RX are the reflection coefficients of the source and calibrated receiver (for example, the base-station emulator in Fig. 1(a)), respectively, and the measured S parameters include the reflection coefficients of the antennas and the effects of the antenna efficiencies η_ant1 and η_ant2. The wave variables in (A.1) have units of the square root of a watt, and are normalized so that the average power P_x,y transmitted across a reference plane is given by $P_{x,y}=\frac{1}{2}\left({\left|a_y\right|}^2-{\left|b_x\right|}^2\right)$ with a reference impedance of 50 Ω.

Because flow-graph models are only applicable to linear, time-invariant circuits, measurements made in the reverberation chamber must be conducted so that both requirements are met. The reverberation chamber provides a linear transmission environment, however when a signal excites the chamber a finite charging time occurs before the mode structure achieves steady state. The charging time was modeled as a double exponential function in [36], and was measured in that work to be less than 25 ns for a large reverberation chamber under various loading conditions. For the reference measurement, the VNA is set to acquire the S parameters only after a delay of at least the charging time, in our case, 10 μs.

A. Model for Antenna Efficiency

As shown in Fig. A.1(b), to find the chamber’s power transfer function, ${\widehat{G}}_{\text{Ch}}$, the antennas are de-embedded from an S parameter measurement of the chamber set-up (See Fig. 1(b) in the main text). We estimate the free-space efficiency η_x of each antenna x = M or R as

$${\eta }_x={\frac{\text{power out},x}{\text{power in},x}|}_{a_{\text{out},x}=0}=\frac{{\left|b_{\text{out},x}\right|}^2}{{\left|a_{\text{in},x}\right|}^2-{\left|b_{\text{in},x}\right|}^2}=\frac{{\left|b_{\text{out},x}\right|}^2}{{\left|a_{\text{in},x}\right|}^2\left(1-{\left|S_{11}^{\text{x}}\right|}^2\right)},$$ (A.2)

where

$${S_{11}^{\text{x}}\equiv \frac{b_{\text{in},x}}{a_{\text{in},x}}|}_{a_{\text{out},x}=0}\text{ and }{S_{21}^{\text{x}}\equiv \frac{b_{\text{out},x}}{a_{\text{in},x}}|}_{a_{\text{out},x}=0}.$$

B. Model for the Reference Measurement

Assuming that reflections from the chamber back into the antennas average to zero and using the notation from Fig. A.1(c) and, we may write the S parameter representation for the reference antenna as

$$\left[\begin{array}{l}{b}_1\hfill \\ b_2\hfill \end{array}\right]=\left[\begin{array}{cc}{S}_{11}^{\text{R}}& S_{12}^{\text{R}}\\ S_{21}^{\text{R}}& 0\end{array}\right]\left[\begin{array}{l}{a}_1\hfill \\ a_2\hfill \end{array}\right],$$ (A.3)

for the chamber as

$$\left[\begin{array}{l}{a}_2\hfill \\ b_3\hfill \end{array}\right]=\left[\begin{array}{cc}0& S_{12}^{\text{Ch}}\\ S_{21}^{\text{Ch}}& 0\end{array}\right]\left[\begin{array}{l}{b}_2\hfill \\ a_3\hfill \end{array}\right],$$ (A.4)

and for the measurement antenna as

$$\left[\begin{array}{l}{a}_3\hfill \\ b_4\hfill \end{array}\right]=\left[\begin{array}{cc}0& S_{12}^{\text{M}}\\ S_{21}^{\text{M}}& S_{22}^{\text{M}}\end{array}\right]\left[\begin{array}{l}{b}_3\hfill \\ a_4\hfill \end{array}\right].$$ (A.5)

From (A.5)

$$a_4=0\Rightarrow a_3=0,$$

and

$$b_4=S_{21}^{\text{M}}{b}_3.$$ (A.6)

From (A.4)

$$a_2=S_{12}^{\text{Ch}}{a}_3=0,$$

and

$$b_3=S_{21}^{\text{Ch}}{b}_2\Rightarrow b_4=S_{21}^{\text{M}}{S}_{21}^{\text{Ch}}{b}_2.$$ (A.7)

From (A.3)

$$b_1=S_{11}^{\text{R}}{a}_1,$$

and

$$b_2=S_{21}^{\text{R}}{a}_1\Rightarrow b_4=S_{21}^{\text{M}}{S}_{21}^{\text{Ch}}{S}_{21}^{\text{R}}{a}_1.$$ (A.8)

With

$$S_{21,\text{meas}}\equiv {\frac{b_4}{a_1}|}_{a_4=0}=S_{21}^{\text{M}}{S}_{21}^{\text{Ch}}{S}_{21}^{\text{R}},$$

then

$${\left|S_{21,\text{meas}}\right|}^2={\left|S_{21}^{\text{M}}{S}_{21}^{\text{Ch}}{S}_{21}^{\text{R}}\right|}^2.$$ (A.9)

Assuming the S parameter measurements of each element in (A.3) – (A.5) are independent and substituting the antenna efficiency from (A.2)

$$\begin{gathered} {\left|S_{21,\text{meas}}\right|}^2={\left|S_{21}^{\text{M}}\right|}^2{\left|S_{21}^{\text{Ch}}\right|}^2{\left|S_{21}^{\text{R}}\right|}^2 \\ ={\eta }_{\text{R}}\left(1-{\left|S_{11}^{\text{R}}\right|}^2\right){\left|S_{21}^{\text{Ch}}\right|}^2{\eta }_{\text{M}}\left(1-{\left|S_{22}^{\text{M}}\right|}^2\right). \end{gathered}$$ (A.10)

We assume that the ensemble average of the measured reflection parameters corresponds to the free-space reflection coefficient of the measurement antenna. $\langle S_{22}^{\text{M}}\rangle \cong \langle S_{22,\text{DUT}}^{\text{M}}\rangle \cong {\Gamma }_{\text{M}}$. Then, for a single mode-stirring sample,

$$G_{\text{Ch}}\equiv {\left|S_{21}^{\text{Ch}}\right|}^2=\frac{{\left|s_{21,\text{meas}}\right|}^2}{{\eta }_{\text{R}}{\eta }_{\text{M}}\left(1-{\left|{\Gamma }_{\text{R}}\right|}^2\right)\left(1-{\left|{\Gamma }_{\text{M}}\right|}^2\right)},$$ (A.11)

which leads to (3) in the main text. Note that Γ_X represents the loss in the antenna and the term (1 − |Γ_X|²) represents the power reflected by the antenna. Other choices of reference plane are discussed in Appendix B.

C. Model for the DUT Measurement

The flow graph of Fig. A.2 was derived from the diagram of Fig. A.1(a) for the DUT measurement. The wave variable a_1,DUT corresponds to the signal emanating from the DUT’s antenna. In this diagram, we assume that the radiated power is not affected by signals that are rereflected from the chamber back into the DUT’s antenna. This may not be a valid assumption depending on the DUT’s impedance matching network. However, for the case studied here, agreement between reverberation-chamber-based and anechoic-chamber-based measurements of TRP was within the measurement uncertainty, indicating that rereflections did not significantly alter the measurement of output power.

Figure A.2:

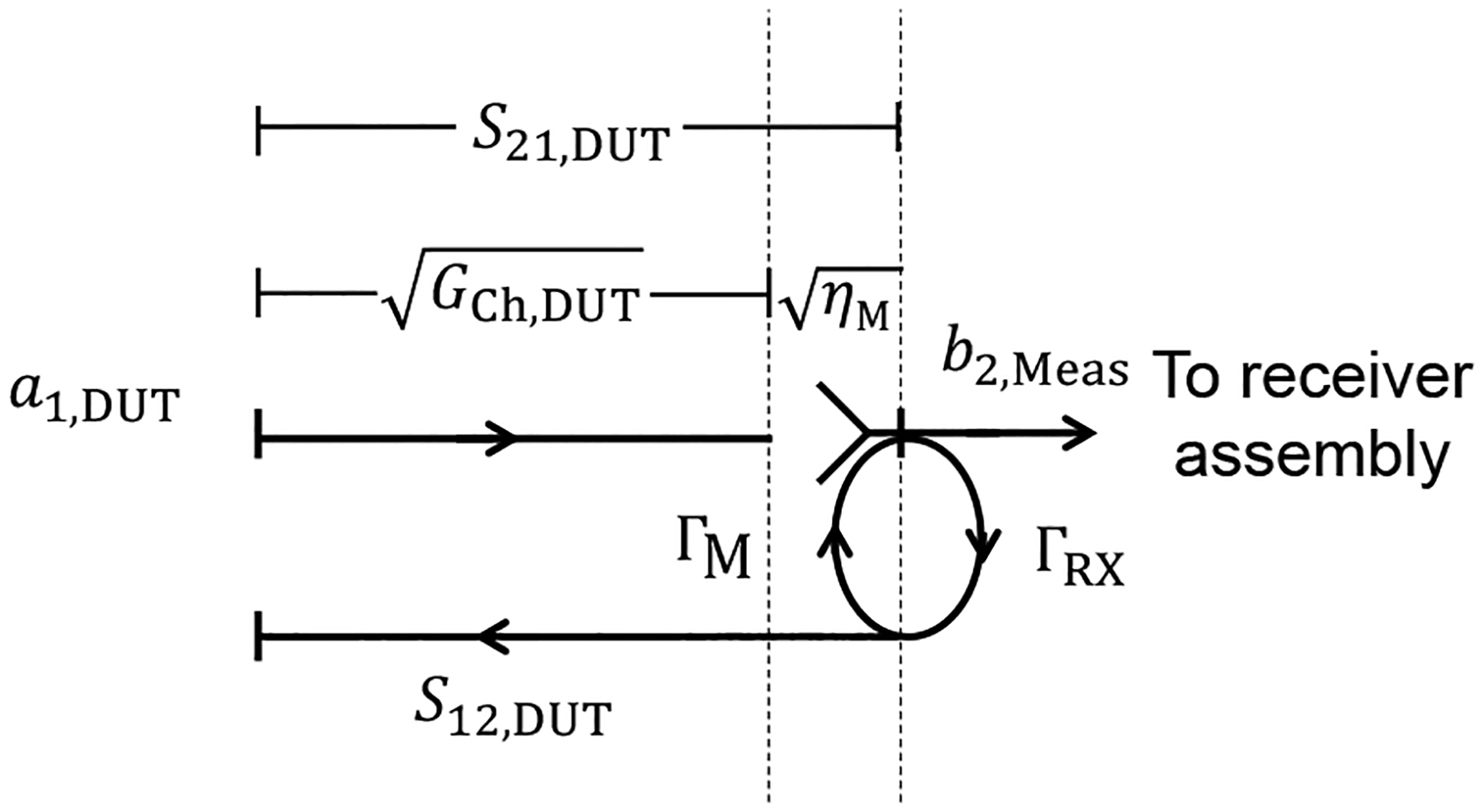
Flow-graph representation of DUT measurement shown in Fig. 1(a), where $P_{\text{TRP}}\approx \frac{1}{2}\langle {\left|a_{1,\text{DUT}}\right|}^2\rangle$ and $P_{\text{Meas}}=\frac{1}{2}\langle {\left|b_{2,\text{Meas}}\right|}^2\rangle$.

From (A.1) and the flow graph in Fig. A.2, we write the measured wave variable b_2,Meas at the input of the receiver assembly for a single stepped mode-stirring sample as

$$b_{2,\text{Meas}}=\frac{a_{1,\text{DUT}}{S}_{21,\text{DUT}}}{\left|1-{\Gamma }_{\text{M}}{\Gamma }_{\text{RX}}\right|},$$ (A.12)

where S_21,DUT is the linear transmission parameter of the reverberation chamber for the DUT measurement, which, for DUTs with integrated antennas, is typically not directly measureable. Γ_RX is the reflection coefficient of the receiver assembly, and Γ_M is the free-space reflection coefficient of the measurement antenna, as defined above.

Figure B.1:

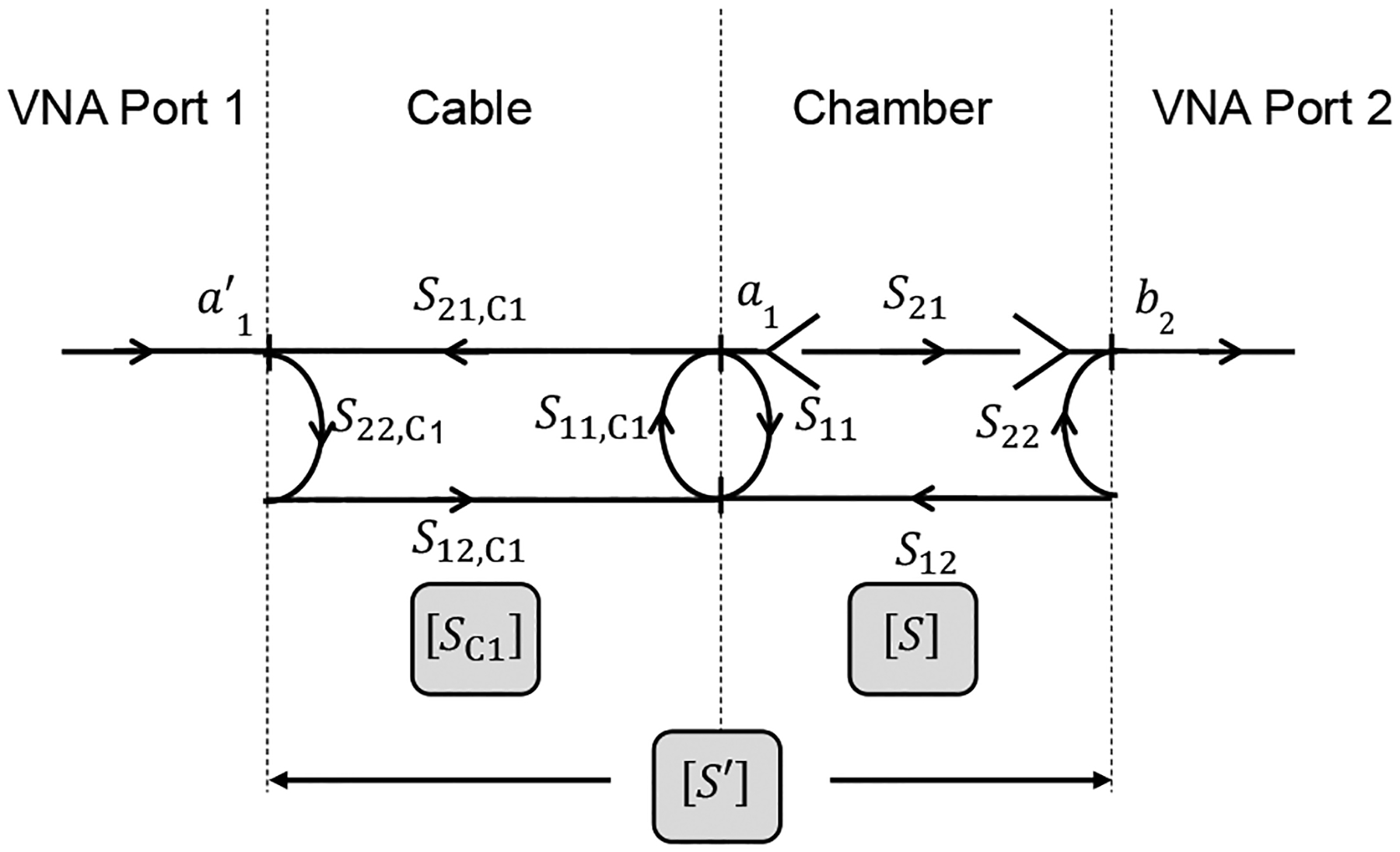
Flow diagram representing the addition of a cable between the excitation and the reference antenna in Fig. A.1(a).

For a single mode-stirring sample, $P_{\text{DUT}}\approx \frac{1}{2}\langle {\left|a_{1,\text{DUT}}\right|}^2\rangle$ and $P_{\text{Meas}}=\frac{1}{2}{\left|b_{2,\text{Meas}}\right|}^2$. We rewrite (A.12) in terms of power-like quantities as

$${\left|S_{21,\text{DUT}}\right|}^2=\frac{P_{\text{Meas}}{\left|1-{\Gamma }_{\text{M}}{\Gamma }_{\text{RX}}\right|}^2}{P_{\text{DUT}}}.$$ (A.13)

With chamber gain G_DUT = S_21,DUT²/η_M(1 − |Γ_M|²), we have¹

$$P_{\text{DUT}}=\frac{P_{\text{Meas}}{\left|1-{\Gamma }_{\text{M}}{\Gamma }_{\text{RX}}\right|}^2}{{\eta }_{\text{M}}{G}_{\text{DUT}}\left(1-{\left|{\Gamma }_{\text{M}}\right|}^2\right)}.$$ (A.14)

Substituting G_Ch = G_R from (A.11) for G_DUT in expression (A.14) and taking the ensemble average leads to the expression for TRP in (4) of the text.

Appendix B: Flow-Graph Models for De-embedding Cables and Other Components

Figures A.1 and A.2 illustrate flow diagrams for measurements where the calibration reference planes are located at the antenna port(s). As mentioned in Appendix A, for the reference measurement, the reference plane may also be located at the output of a cable and/or other components inserted between the measurement antenna and the VNA, as long as they remain in place for both the reference and DUT measurements. If it is necessary to insert additional cables and/or components for the reference or DUT measurements, procedures for de-embedding the loss and mismatch due to these additional components are described below. In the following, the term “cable” could refer to cables or other passive components such as power splitters, couplers, and switches.

Figure B.2:

Flow diagram representing the addition of a cable between the measurement antenna and the receiver in Fig. A.1(a).

A. Cable Connected to the Transmit Antenna

A flow diagram illustrating this configuration is shown in Fig. B.1. For the reference measurement, the VNA measures [S′] and the S parameters of the cable, [S_C1], while [S] is required to find the reference power transfer function. Let $\mathbb{T}$ be the transmission matrix (see, e.g., [38]) of [S], ${\mathbb{T}}_{\text{C}}$ the transmission matrix of [S_C1], and ${\mathbb{T}}^{\prime }$ the transmission matrix of [S′]. Then

$${\mathbb{T}}^{\prime }={\mathbb{T}}_{\text{C}1}\mathbb{T}.$$ (B.1)

To find $\mathbb{T}$, invert its transmission matrix, and compute

$$\mathbb{T}={\mathbb{T}}_{\text{C}1}{}^{-1}{\mathbb{T}}^{\prime }.$$ (B.2)

Once is converted back to S parameters, equations (3) and (4) may be used as written.

B. Cable Connected to the Receive Antenna During DUT Measurement Only

Sometimes the reference measurement is carried out at the measurement antenna reference plane (see Fig. 1(b)), and, subsequently, an additional cable is inserted between this reference plane and the receiver. For this case, the S parameters of the cable [S_C2] may be measured and cascaded with those of the chamber [S] to obtain [S′]. This is represented in Fig. B.2, and may be written in terms of transmission parameters as

$${\mathbb{T}}^{\prime }=\mathbb{T}{\mathbb{T}}_{\text{C}2}.$$ (B.3)

In this way, the chamber/cable assembly [S′] is the same for the reference and DUT measurements, and equations (3) and (4) may be used as written.

C. Cable Connected to the Measurement Antenna During Reference Measurement Only

The flow graph for this situation is the same as that shown in Fig. B.2. However, here, the S parameters of the cable [S_C2] and the cascade of the chamber and cable [S′] have been measured with a VNA and we wish to remove the effects of [S_C2]. This may be accomplished with transmission parameters as follows

$$\mathbb{T}={\mathbb{T}}^{\prime }{\mathbb{T}}_{\text{C}2}{}^{-1}.$$ (B.4)

The S parameter matrix corresponding to the chamber only is then found from $\mathbb{T}$ and used in (3).