Matrix-driven changes in metabolism support cytoskeletal activity to promote cell migration

Abstract

The microenvironment provides both active and passive mechanical cues that regulate cell morphology, adhesion, migration, and metabolism. Although the cellular response to those mechanical cues often requires energy-intensive actin cytoskeletal remodeling and actomyosin contractility, it remains unclear how cells dynamically adapt their metabolic activity to altered mechanical cues to support migration. Here, we investigated the changes in cellular metabolic activity in response to different two-dimensional and three-dimensional microenvironmental conditions and how these changes relate to cytoskeletal activity and migration. Utilizing collagen micropatterning on polyacrylamide gels, intracellular energy levels and oxidative phosphorylation were found to be correlated with cell elongation and spreading and necessary for membrane ruffling. To determine whether this relationship holds in more physiological three-dimensional matrices, collagen matrices were used to show that intracellular energy state was also correlated with protrusive activity and increased with matrix density. Pharmacological inhibition of oxidative phosphorylation revealed that cancer cells rely on oxidative phosphorylation to meet the elevated energy requirements for protrusive activity and migration in denser matrices. Together, these findings suggest that mechanical regulation of cytoskeletal activity during spreading and migration by the physical microenvironment is driven by an altered metabolic profile.

Significance

Mechanical cues from the local microenvironment regulate cell morphology, adhesion, and migration, all of which require energy-intensive cytoskeletal remodeling. Utilizing two-dimensional collagen micropatterns and three-dimensional collagen matrices, we show that oxidative phosphorylation may be necessary to support elevated energy requirements for protrusive activity during cancer cell migration. These findings suggest that the matrix cues can drive changes in metabolism to support cytoskeletal activity during cell migration as a function of the extracellular terrain.

Introduction

Metastasis is a complex series of events in which cells must dynamically adapt their behaviors to the physical properties of their local microenvironment (1), including confinement, rigidity, topology, and adhesivity of the extracellular matrix (ECM) (2). In addition to intrinsic cancer cell mutations, malignant/nonmalignant bidirectional cell-ECM interactions as well as extrinsic ECM cues can influence migration (3,4). During tumor progression, solid tumors progressively remodel and stiffen the ECM, exposing disseminating cancer cells to heterogeneous and aberrant mechanical cues. To navigate through the physical barriers within the microenvironment, cells remodel their cytoskeleton and exert forces to the surrounding matrix fibers (5,6). However, altered mechanical cues within the tumor microenvironment can increase intracellular tension as well as alter cell morphology, cytoskeletal dynamics, and metabolism during invasion (7,8). Cell migration is an energy-demanding process that requires cells to maintain an adequate supply of energy to fuel motility while traversing a heterogeneous microenvironment (9, 10, 11). We have previously shown that the energy utilization of individual migrating cells is affected by the physical properties of the local microenvironment and that intracellular energy state is linked to migratory ability (12). Cancer cells have also been shown to dynamically adapt their metabolic pathways during metastasis (13, 14, 15, 16), and cancer cells display unique metabolic signatures depending on metastatic site (17). These findings suggest that metabolism plays an important role in migration and metastasis. Although matrix confinement and cell mechanics alter cellular energetics during migration (7,12,18), how specific metabolic pathways facilitate cytoskeletal activity and motility in response to microenvironmental cues remains unclear.

Here, we investigated the role of metabolism in supporting migration by examining the relationship between cell elongation and spreading, cytoskeletal activity, migration, and energy production in both two-dimensional (2D) and three-dimensional (3D) microenvironments. We confined MDA-MB-231 highly metastatic breast cancer cells on 2D micropatterns as well as within 3D collagen matrices, and we studied ATP/ADP levels and mitochondrial membrane potential as a metric of oxidative phosphorylation (OXPHOS). Using collagen micropatterns to control cell elongation and spreading, we found that cells increased membrane ruffling in response to increases in elongation and that inhibiting OXPHOS decreased this cytoskeletal activity. When embedded within collagen, cellular protrusive activity and intracellular ATP/ADP ratio increased with increasing collagen density, suggesting that increased cytoskeletal activity is associated with increased energy demands. Inhibition of OXPHOS resulted in lower membrane ruffling, protrusive activity, and migration, suggesting that OXPHOS is necessary for 3D migration. Together, we demonstrate that the physical microenvironment can modulate the metabolic profile of cancer cells and that OXPHOS supports cytoskeletal dynamics during breast cancer cell migration.

Materials and methods

Cell culture and reagents

Highly metastatic MDA-MB-231 breast adenocarcinoma cells (HTB-26; ATCC, Rockville, MD) were maintained at 37°C and 5% CO₂ in Dulbecco’s modified Eagle’s medium (DMEM; Life Technologies, Grand Island, NY) supplemented with 10% fetal bovine serum (Atlanta Biologicals, Flowery Branch, GA), 100 μg/mL streptomycin (Life Technologies), and 100 U/mL penicillin (Life Technologies). MDA-MB-231 cells were transduced with PercevalHR and pHRed as previously described (12). FUGW-PercevalHR (plasmid 49083; Addgene) and GW1-pHRed (plasmid 31473; Addgene) were gifts from Gary Yellen (Harvard Medical School, Boston, MA) and coexpressed in the MDA-MB-231 cell population with the PercevalHR and pHRed lentiviral particles prepared by transient transfection of HEK293T cells (CRL-3216; ATCC, Manassas, VA). To inhibit OXPHOS, cells were treated with 20 μM antimycin A (AMA) in complete media for 6 h. The treatment regime was determined based on a dose curve to give maximal inhibition of OXPHOS based on the mitochondrial membrane potential indicator tetramethylrhodamine methyl ester (TMRM) probe without inducing cell death.

Photolithography-based microfabrication of patterns

Patterns were designed in K-Layout (Matthias Koefferlein, open source developer) and printed using a 101 uPG Heidlberg Mask Writer onto a dark-field soda lime chrome-coated glass mask. S1813 red positive photoresist (S1813) (MicroChem, Newton, MA) was spin-coated onto an O₂-plasma-cleaned and primed silicon wafer (100 mm diameter, 500 μm thickness, Type “P,” <1–10> ohms resolution) (4000 rpm/45 s spin) and soft baked at 115°C. The resist was UV exposed to a dose of 120 mJ/cm² energy in a Karl Suss MA6 mask aligner and developed for 1 min in Microposit MF-319 (MicroChem, MA). Then, the sample was rinsed in deionized water and blow-dried with nitrogen. A Bosch etch process was used to create the micropattern mold with Trion Phantom II, and residual photoresist was removed by rinsing with isophthalic acid, blow-drying with nitrogen, and O₂-plasma treatment. Profilometry was used to verify a feature depth of 10–20 μm for all patterns, and finally, the patterned wafer was silanized by desiccating with trifluorochlorosilane to prevent polydimethylsiloxane (PDMS) from adhering to the patterns during the curing process.

Microcontact printing

The microcontact printing method was adapted from previous methods (19). Sylgard 184 Silicone Elastomer Kit (Dow Corning, Midland, MI) was used to create the PDMS mold by thoroughly mixing the curing agent and the base at a 1:10 ratio (wt/wt). After 20 min of degassing using a house vacuum to remove air bubbles, the mixture was poured onto the wafer in a large petri dish and incubated in the 70°C incubator for at least 1 h. Coverslips (45 × 50 mm, no. 1.5; VWR, West Chester, PA) were activated by 2 min of plasma treatment, a 10-min wash in 1% polyethyleneimine (Sigma-Aldrich, St. Louis, MO) in MilliQ water, 3 × 5 min of MilliQ rinsing, 30 min of 0.1% glutaraldehyde (70% aqueous stock solution; Sigma-Aldrich) in 1× phosphate-buffered saline (Invitrogen, Carlsbad, CA) rinsing, and another 3 × 5 min of MilliQ wash. All procedures were performed step by step at room temperature.

Type I collagen (Corning, Corning, NY) was diluted to a final concentration of 0.01% (wt/vol) in 50 mM HEPES (pH 8.0; Sigma-Aldrich). Diluted collagen was added on top of the PDMS stamps and incubated at room temperature for 30 min, and excess protein was removed using compressed air. The stamp was subsequently pressed against an alcohol-wiped coverslip (22 × 22 mm) for 5 min. An acrylamide solution for 30 kPa polyacrylamide (PA) gels was made with 12% (wt/vol) acrylamide and 0.28% (wt/vol) bisacrylamide in 10 mM HEPES (pH 8.0) (10 kPa PA gels: 7.5% acrylamide and 0.35% bisacrylamide) (Bio-Rad, Hercules, CA). After 20 min of house vacuum degassing, the acrylamide solution, 0.004 mL of N,N,N′,N′-tetramethylethylenediamine (Sigma-Aldrich), and 0.006 mL of 10% ammonium persulfate (Sigma-Aldrich) were added to 20 μmol/mL N-6-((acryloyl)amido)hexanoic acid (N-6) dissolved in ethanol (20) and mixed quickly in a total volume of 1 mL to initiate the polymerization reaction. After pipetting 40 μL of the polymerizing acrylamide solution onto an activated coverslip, the 22 × 22 mm coverslip was gently removed from the stamp and pressed onto the polymerizing acrylamide solution with the stamped side facing down. After polymerization was completed, the sample was immersed in HEPES (pH 8.0) at 4°C for 2–4 h to allow for N-6 linkage completion. The top coverslip was peeled off, and the unreacted N-6 linker was capped with 0.1% ethanolamine (Sigma-Aldrich) in HEPES (pH 8.0). Gels were washed with sterile phosphate-buffered saline, and the coverslips were mounted onto 9.6-cm² round-sized chambers for cell seeding.

2D cell seeding and 3D cell encapsulation

In 2D studies, MDA-MB-231 cells were seeded in a custom chamber with 9.6-cm² surface area at 5000–7500 cells/cm². For 3D studies, MDA-MB-231 cells were embedded at 125,000 cells/mL in 3D collagen matrices prepared from 10 mg/mL acid-solubilized type I rat tail tendon collagen stock solution as previously described (21,22). Collagen solutions were diluted with cooled DMEM medium and neutralized to pH 7.0 with 1 N NaOH to create matrices with a collagen density of 0.5, 0.75, 1, 2, or 5 mg/mL. 500 μL of the neutralized collagen solution was added onto a 24-well glass-bottom plate (MatTek, Ashland, MA) and allowed to polymerize for 1 h in a 37°C incubator. The culture medium was then overlaid onto the polymerized gels. For both 2D and 3D experiments, cells were allowed to adhere and spread overnight in a humidity-controlled incubator at 37°C and 5% CO₂.

Confocal microscopy

PercevalHR and pHRed signal as well as the TMRM mitochondrial membrane potential probe signal were imaged on a Zeiss LSM800 inverted confocal microscope equipped with a 20×/0.8-NA long-working-distance objective and operated by Zen 2.3 software. For intracellular ATP/ADP ratio measurements, PercevalHR was excited using a 488-/405-nm laser corresponding to the ATP-bound and ADP-bound conformation, respectively, with emission light collected through a 450- to 550-nm bandpass filter. pHRed was excited using 561-/488-nm laser, with emission light collected through a 576-nm long-pass filter (23). To examine intracellular ATP/ADP ratio during time-lapse experiments, imaging was performed every 2 min for 2 h for cells on 2D micropatterns or every 20 min for 12 h for 3D migration studies. All time-lapse experiments were conducted in an environmental chamber maintained at 37°C and 5% CO₂. A transmission channel was used to simultaneously image cell morphology.

Confocal reflectance microscopy

Collagen fiber architecture was visualized via confocal reflectance using a Zeiss LSM800 inverted confocal microscope equipped with a 640-nm laser and a 40×/1.1-NA long-working-distance water-immersion objective operated by Zen 2.3 software. Images were taken at least 150 μm above the glass-gel interface.

Quantitative polarization microscopy

The quantification of cell contractility in collagen matrices was performed using a polarization microscope as previously described (24). Briefly, images were acquired using a 20×/1.0-NA polarization objective, and sequences were acquired with 5° intervals of the rotating polarizer over a range of 0–180° with 20-ms acquisition time controlled by Zen software. A pixel-by-pixel retardance map was then obtained by processing the polarized image sequences with a custom MATLAB code (The MathWorks, Natick, MA). The resulting retardance images were subsequently analyzed with ImageJ, and the retardance signal (micromolar) of the whole cell was quantified as the average value of the background-subtracted retardance of the cell area.

Quantification of intracellular ATP/ADP ratio

To investigate the cellular energetics during confinement, MDA-MB-231 intracellular ATP/ADP ratio was acquired using PercevalHR and pHRed probes (12,18,23). PercevalHR and pHRed were imaged simultaneously and analyzed in ImageJ to calculate PercevalHR ratio (F₄₈₈/F₄₀₅) and pHRed ratio (F₅₆₁/F₄₈₈) after background subtraction. For 2D confinement studies, intracellular ATP/ADP ratio was obtained by manually measuring the cell outlines and was calculated from the mean intensity of each background-subtracted channel. For time-lapse studies, ATP levels were collected with PercevalHR and pHRed signals along with cell body centroid measurements and averaged for each cell using a customized macro as previously described (18). Single cells were cropped from the image, with the mean background pixel intensity subtracted for each channel, and channels were converted to a mask using a Li threshold after being merged and subjected to a median filter (25). The mean intensity for each channel was calculated from only pixels containing the corresponding mask-selected fluorescent signal to quantify the PercevalHR/pHRed signal ratio. To estimate energy consumption during migration, the total change in ATP/ADP ratio between time points over the time-lapse was calculated.

A pH calibration was also performed by treating cells with 20 mM NH₄Cl to induce a transient alkalization of the cytosol over a short period. By varying intracellular pH, a calibration curve between the PercevalHR ratio (F₄₈₈/F₄₀₅) and pHRed ratio (F₅₆₁/F₄₈₈) of individual cells was obtained while maintaining a relatively constant intracellular ATP/ADP ratio. A linear correlation equation was then fit from the calibration data, and only cells in the dynamic range of the linear regression model were used in this study. The normalized PercevalHR ratio was measured by dividing the uncorrected PercevalHR signal by the pH-corrected signal.

Quantification of mitochondrial membrane potential

To measure the relative OXPHOS rate of MDA-MB-231 cells, we used the TMRM mitochondrial membrane potential probe, which is a reversible, positively charged fluorescent probe that equilibrates across the mitochondrial membrane (26). MDA-MB-231 cells were incubated in the presence of 150 nM TMRM in serum-free DMEM for 30 min (2D) or 6 h (3D) at 37°C and 5% CO₂ after overnight culture and then imaged using a Zeiss LSM800 confocal microscope equipped with a 20×/0.8-NA objective. TMRM was excited using a 561-nm laser, and the emission was collected over the range of 562–700 nm (26, 27, 28, 29). The cell outline was manually drawn around each cell, and the mean pixel intensity was acquired to determine mitochondrial membrane potential. Background pixel intensity was measured and subtracted from each image. For time-lapse analysis, TMRM signals were collected using a customized macro. The single-cell image was cropped and subtracted with the mean background pixel intensity; it was then converted to a mask using a Li threshold and subjected to a median filter. The mean intensity was then calculated from only pixels containing the corresponding mask-selected fluorescent signal to quantify the TMRM probe signal.

Cell morphology and cytoskeletal activity analysis

Cell size and elongation were analyzed by manually drawing cell outlines to calculate cell area and elongation (aspect ratio/circularity) to quantify the changes in cell morphology in both 2D and 3D environments. Cell elongation factor was quantified as aspect ratio over circularity as previously described (18,30). To measure cytoskeletal activity in 2D confinement, cells were imaged every 2 min for a 2-h period, and cell membrane ruffling was calculated by physically drawing cell outlines and tracking the stepwise cell area difference. For the correlation analysis of intracellular energy levels and cell cytoskeletal activity in 2D, average PercevalHR and pHRed signals were also collected every 2 min for a 2-h period. To better observe these fluctuations in cellular energetics during membrane ruffling for single MDA-MB-231 cells, the stepwise changes in the ATP/ADP ratio and cell size were both normalized to the maximal value and kept as absolute values during the time-lapse.

To measure protrusive activity during 3D migration, cells were imaged after overnight incubation, and images were collected every 20 min for a 12-h period. Stepwise protrusion rate was measured by counting the change in the number of stepwise protrusions and averaging to the number of new protrusions per hour (30); average PercevalHR and pHRed signals were also collected to determine how fluctuations in intracellular ATP/ADP ratio correlated to the number of new protrusions by each cell. Temporal cross correlation of normalized cell membrane ruffling and PercevalHR ratio was calculated in R Studio (version 1.2.1335; RStudio, Boston, MA).

Cell migration analysis

For both 2D and 3D migration studies, cells were imaged after overnight seeding/embedding every 20 min for a 12 h period. Stepwise velocities were calculated by manually tracking the cell body center displacement over 12 h. A cell was considered motile if it has displaced at least one average diameter of a cell (∼10–15 μm) during a 2-h period, and the motile fraction was defined as the ratio of motile cells to total cells. All images were adjusted and modified in ImageJ, including the normalized PercevalHR ratio and temporal RGB time-lapse images of cells, using a customized macro code (12).

Collagen microstructure analysis

To measure collagen fiber orientation, cells were embedded overnight and imaged every 1 h for 12 cycles with confocal reflectance. Fiber directions within 10 μm to cell protrusions were analyzed using the Orientation J plug-in in ImageJ as previously described (31,32). In short, an orientation index was generated after quantifying the orientation distribution and calculating the averaged square cosine of the angle between an individual fiber and the average fiber orientation of the frame. Perfectly random distribution is represented by an orientation index of 0, whereas an orientation index of 1 represents a perfectly aligned distribution.

To measure collagen pore size from confocal reflectance images, a 2D autocorrelation function in MATLAB was used to quantify the characteristic pore size in an image as previously described (21,31). An adaptive Weiner filter (0.625-μm filtering window) and a TopHat filter (0.94-μm strel disk diameter) were used to preprocess the images to remove background noise, and they were finally converted to binary images. The 2D autocorrelation was then computed for each image, from which the characteristic pore size was derived from the decay measured.

Mechanical characterization

The Young’s modulus of patterned PA gel was measured using atomic force microscopy (AFM) in contact mode force (MFP-3D; Asylum Research, Goleta, CA). A total of 60 indentations were performed at a minimum of three regions within each PA gel with force-displacement curves taken at 20 points (4 × 5 grid). Indentations were made at a loading rate of 2 μm/s and trigger force of 5 nN with silicon nitride cantilevers with a nominal spring constant of 0.06 N/m and a 5-μm-diameter spherical polystyrene bead (Novascan, Boone, IA). AFM tips were calibrated before use and had a mean spring constant of 0.06 ± 0.005 N/m. Force-displacement curves were fit to the Hertz model assuming a Poisson’s ratio of 0.45 using the Asylum curve fitting software to determine the elastic modulus.

The stiffness of collagen gels was determined by confined compression as previously described (31,33). In brief, collagen gels were loaded onto a TA Electroforce Model 3100 (TA Instruments, New Castle, DE) that used a 250-g load cell to measure the resulting forces of 5% stepwise displacements. The stress relaxation data were then fit to a linear solid model of viscoelastic behavior via a custom MATLAB script, from which the slope of the stress-strain curve was used to calculate the equilibrium modulus.

Cell viability and metabolic analysis

To create an AMA dose curve, AMA dosage (0.1–40 μM) was dissolved in DMEM media from 10 mM stock solution in DMSO and given to the MDA-MB-231 cells seeded on a glass-bottom 96-well plate (MatTek) at 5000–7500 cells/cm². Cell viability was measured as propidium iodide (PI)-stained cells over the total number of cells by imaging live cells stained with 1 μg/mL Hoechst and 1 μg/mL PI solution after 15 min of incubation at 37°C (34). Staining dye was created by dissolving 10 mg/mL Hoechst 33342 stock solution (Invitrogen) and 1 mg/mL PI (MP Biomedicals, Solon, OH) in DMEM media. PI was excited using a 488-nm laser, with emission collected over a range of 600–700 nm, and Hoechst was excited using a 405-nm laser, with emission collected over a range of 400–600 nm (34). Alamar Blue (10×) stock reagent (Invitrogen) was dissolved in cell media to 1× final concentration with 200 μL of solution added into each well across all conditions for an incubation of 1–24 h. Fluorescence was measured from a plate reader excited at 560 nm and collected at 590 nm (35,36).

Statistical analysis

Data are presented as box-and-whisker plots showing the mean (+), median ± interquartile range (box edges), and 5th–95th percentiles (whiskers) or mean ± SE. Statistical analysis was performed using GraphPad Prism 8.2.1 (GraphPad Software, San Diego, CA), and significance was found using Kruskal-Wallis ANOVA test with Dunn’s post hoc analysis for multiple-group comparison. For two-group comparison, either unpaired t-test or Mann-Whitney rank test was performed (if normality was not assumed with D’Agostino and Pearson test, nonparametric Mann-Whitney rank test was used). All experiments were reproduced at least three independent times. Linear regression models were fitted using the mean ± SE of each group (with single cells, LOWESS smoothing was applied), and the p-value indicated the significance of the slope. To compare the slope of two lines between control (ctrl) and AMA groups, an extra-sum-of-squares F-test was used. R Studio (1.2.1335) was used for temporal cross correlation analysis, with a one-sample t-test used to determine the significance of lag.

Results

Cell elongation and spreading increase ATP/ADP ratio and OXPHOS

Matrix-driven changes in cell morphology have previously been linked with intracellular energy levels (18,37). Therefore, we first examined how cell spreading and elongation influence cellular metabolism. We created microfabricated 2D collagen patterns on PA hydrogels made to mimic the physiological stiffness range of tumors (38,39) and to manipulate cell elongation and spreading area separately (Fig. 1 A). To maintain the elongation but increase cell area, patterns with dimensions of 10 × 10 μm, 20 × 20 μm, and 31.6 × 31.6 μm were used. As such, cell elongation was maintained at 1.2–1.4 (Fig. S1 A), and spreading area was increased. To test the effects of elongation separately from area, patterns with dimensions of 22.4 × 22.4 μm, 50 × 10 μm, and 5 × 100 μm were used to maintain a cell area at 450–550 μm² while increasing elongation (Fig. S1 B).

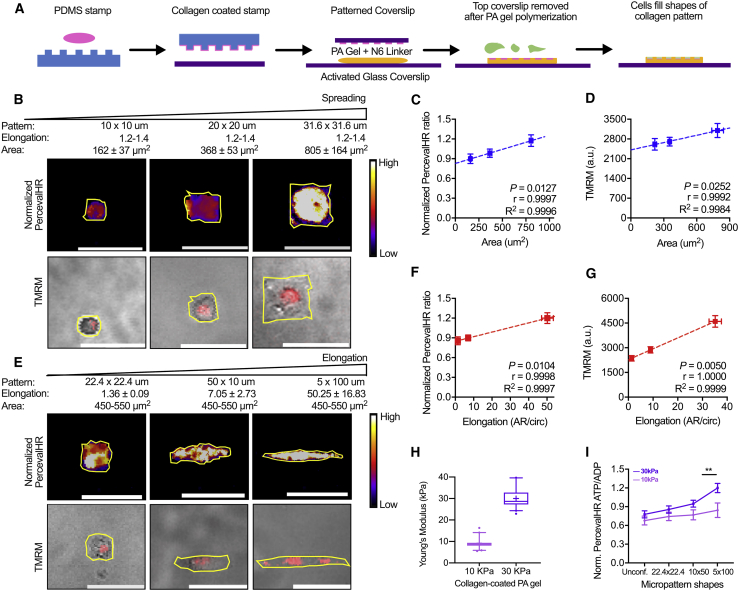
Figure 1.

Intracellular ATP/ADP ratio and OXPHOS increase with cell elongation and spreading on two-dimensional confined patterns. (A) Collagen micropatterning on PA gels with physiological stiffness is shown (blue, PDMS; pink, collagen; purple, cover glass; orange, PA gel; green, cells). (B) Normalized PercevalHR ATP/ADP ratio and TMRM fluorescence intensity for MDA-MB-231 cells with increasing spreading (mean ± SD) while maintaining cell elongation (aspect ratio (AR)/circularity (Circ)) on collagen micropatterns are shown. Quantification of (C) normalized PercevalHR ratio (n = 36–76 cells) and (D) mitochondrial membrane potential via TMRM for cells with increasing spreading is shown (n = 30–155 cells). (E) Normalized PercevalHR ratio and TMRM fluorescence intensity for MDA-MB-231 cells with increasing cell elongation (mean ± SD) while maintaining spreading area on collagen micropatterns is shown. Quantification of (F) normalized PercevalHR (n = 55–64 cells) and (G) TMRM for cells with increasing elongation is shown (n = 40–62 cells). (H) Young’s modulus of collagen-micropatterned PA gels with varying stiffness is shown. (I) Quantification of normalized PercevalHR ratio for MDA-MB-231 cells with increasing elongation on 10- and 30-kPa collagen micropatterns is shown. Data shown as box-and-whisker plots denote mean (+), medians and 25th/75th and 5th/95th percentiles, or mean ± SE; yellow lines show cell outlines; dashed lines show linear regression. ^∗∗p < 0.01 with two-tailed t-test. Scale bars, 50 μm. To see this figure in color, go online.

To study intracellular energy state, highly metastatic MDA-MB-231 cells expressing the genetically encoded intracellular ATP/ADP biosensor PercevalHR (40) were seeded on collagen micropatterns with varying morphology. Previous studies have shown that cells can utilize OXPHOS to meet the high energy demands required during cell metastasis (41, 42, 43). Thus, we also measured changes in OXPHOS using a mitochondrial membrane potential probe, TMRM (26, 27, 28). Cells with larger spreading area exhibited higher ATP/ADP and OXPHOS levels (Fig. 1, B–D). Similarly, with increasing cell elongation, intracellular ATP/ADP ratio and OXPHOS levels increased (Fig. 1, E–G). Because cell adhesion and spreading are mediated in part by substrate rigidity, we also tested the change in intracellular ATP/ADP ratio with increasing elongation on PA hydrogels of varying stiffness (Fig. 1 H; Fig. S1 C). Cells on 30 kPa PA substrates exhibited a more significant increase in ATP/ADP ratio, with increased elongation compared with cells on more compliant 10 kPa substrates (Fig. 1 I). Unconfined cells on collagen-coated PA gels (10 and 30 kPa) demonstrated the lowest energy levels of all conditions regardless of their spreading (Fig. S1, D–F) and elongation (Fig. 1 I; Fig. S1, G–I), suggesting any restriction on cell shape can alter bioenergetics. These data indicate that cellular energy levels and OXPHOS increase with elongation and area regulated by substrate confinement and stiffness.

ATP/ADP ratio and OXPHOS are correlated with membrane ruffling during elongation

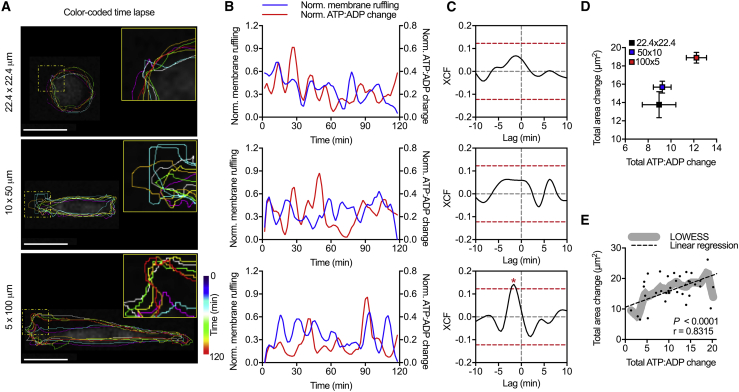
During migration, cells actively remodel their actin cytoskeleton to adapt to the varying architecture and topologies in the ECM (1). Cancer cells, in particular, are characterized by high contractility and cytoskeletal remodeling (44). Because cytoskeleton remodeling is energy intensive (45), we examined the link between energetics and membrane activity with respect to changes in cell elongation. To study 2D cytoskeletal remodeling, MDA-MB-231 cells were seeded on PA gels with collagen micropatterns of varying elongation, and changes in cell area over 2 h were calculated to measure membrane activity (Fig. 2 A). Temporal cross correlation was used to analyze fluctuations in membrane ruffling compared with the intracellular ATP/ADP ratio. A positive correlation with a negative lag exists for the 5 × 100 μm pattern, which is the condition with the most cell elongation, indicating energy was consumed before cytoskeletal remodeling (Fig. 2, B and C). Notably, with increasing micropattern aspect ratio and cell elongation, the significance of this correlation increased (Fig. 2 C). When comparing the total changes in membrane area with the total changes in ATP/ADP ratio over the observation window, more elongated cells on micropatterns with a high aspect ratio had the most change in membrane ruffling and consumed the most energy (Fig. 2 D). Similarly, when we examined individual cells across all conditions and applied LOWESS smoothing to fit the data (46,47), a positive correlation between total ATP/ADP ratio and membrane ruffling was observed (p < 0.0001, r = 0.8315) (Fig. 2 E). Together, these results suggest that energy may be consumed for membrane ruffling and that energy levels are increased with cell elongation to support increased cytoskeletal activity.

Figure 2.

Cytoskeletal activity is correlated with changes in cellular energetics in 2D confinement. (A) The color-coded time-lapse of MDA-MB-231 membrane ruffling is shown. (B) Normalized stepwise cell size change and normalized PercevalHR ratio change of single MDA-MB-231 cell spreading on 22.4 × 22.4 μm, 50 × 10 μm, and 5 × 100 μm collagen micropatterns are shown. (C) Cross correlation (XCF) of single-cell normalized PercevalHR ratio and cell membrane ruffling for cells with increasing elongation (n = 20 cells) is shown. Total membrane ruffling as a function of total normalized PercevalHR ratio (D) averaged for each pattern and for (E) individual control cells is shown (n = 41 cells). Dashed yellow squares show zoomed regions; dashed red lines show one-tailed t-test significance; lines show LOWESS smoothing, and dashed lines show linear regression; ^∗p < 0.05. Scale bars, 25 μm. To see this figure in color, go online.

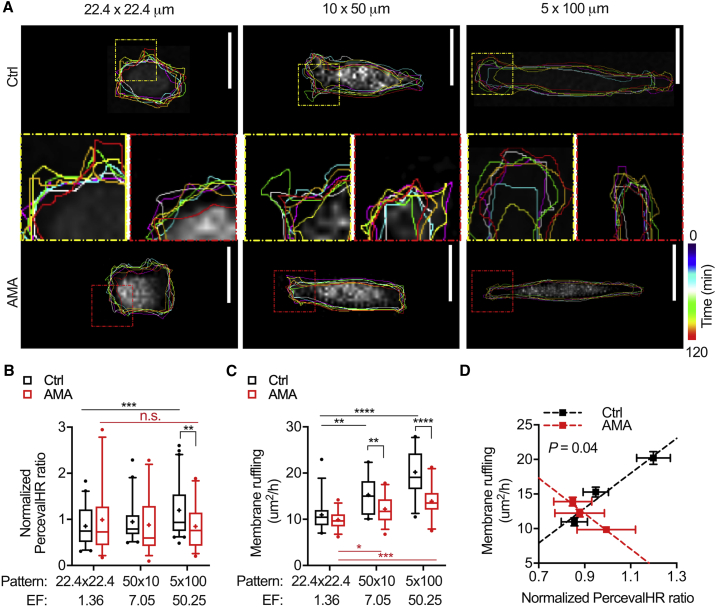
OXPHOS rate and mitochondrial trafficking have been associated with energy-intensive membrane remodeling (48,49). Therefore, we next examined how inhibition of OXPHOS impacts ATP/ADP ratio and membrane activity with changes in cell elongation (Fig. 3 A). To pharmacologically inhibit OXPHOS, cells were treated with 20 μM AMA for 6 h to block electron transfer in the electron transport chain complex III (50, 51, 52, 53). This treatment significantly lowered mitochondrial membrane potential, intracellular energy, and metabolic activity (Fig. S2, A–C) without causing significant cell death (Fig. S2 D). After AMA treatment, cells exhibited a much less significant increase in ATP/ADP ratio and cytoskeletal activity with changes in elongation compared with control cells, and both intracellular ATP/ADP ratio and membrane ruffling increased linearly with pattern elongation (Fig. 3, B and C; Fig. S3, A and B). Inhibiting OXPHOS via AMA treatment resulted in lower membrane activity for all patterns, abolishing the positive correlation between ATP/ADP ratio and membrane ruffling (p = 0.04) (Fig. 3 D). These findings indicate that OXPHOS supports increased energy demands and membrane ruffling when cells adapt to a more elongated morphology.

Figure 3.

Inhibition of MDA-MB-231 OXPHOS lowers cellular energetics and cytoskeletal activity in 2D confinement. (A) The color-coded time-lapse of membrane ruffling of MDA-MB-231 cells after AMA treatment on collagen micropatterns with increasing elongation is shown (dashed squares show zoomed regions; yellow, ctrl; red, AMA). Quantification of (B) normalized PercevalHR ratio (n = 55–64 cells) and (C) membrane ruffling (n = 30–35 cells) after AMA treatment on collagen micropatterns with increasing elongation is shown. (D) Total change in membrane area as a function of normalized PercevalHR ratio averaged for each pattern after AMA treatment is shown (p shows extra-sum-of-squares F-test that compares linear regression). Data shown as box-and-whisker plots denote mean (+), medians and 25th/75th and 5th/95th percentiles, or mean ± SE; dashed lines show linear regression; two-tailed t-test was used when comparing between ctrl and AMA, and multiple comparisons was used with ANOVA when comparing across patterns; n.s., nonsignificant; ^∗p < 0.05, ^∗∗p < 0.01, ^∗∗∗p < 0.001, ^∗∗∗∗p < 0.0001. Scale bars, 25 μm. To see this figure in color, go online.

Collagen density increases cytoskeletal activity and cellular energy

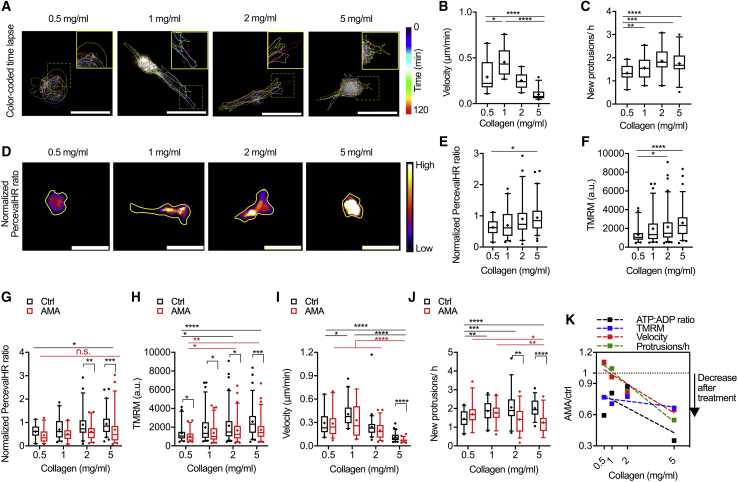
Given that our data and data from others indicate that cellular energy requirements increase with membrane dynamics and that cytoskeletal activity is critical to cell migration (54, 55, 56), we sought to investigate the relationship between energy and OXPHOS in 2D and 3D migration. Our initial experiments indicate that intracellular ATP/ADP ratio and migration speed were not affected by AMA treatment during migration on glass (Fig. S4, A–C), likely due to the fact that migration on a 2D unconfined surface does not challenge cells and large amounts of energy from OXPHOS are not required. Therefore, to challenge the cells, we examined cytoskeletal activity, migration, and energetics of cells in collagen matrices of different densities, where pore size is a function of collagen concentration (Fig. 4 A; Fig. S5, A–C; (12,57)). Collagen densities of 0.5–5 mg/mL were chosen to mimic the tumor tissue microenvironment (57,58). MDA-MB-231 cell size did not significantly change with collagen density; however, elongation exhibited a biphasic response with increasing collagen density, in which elongation is largest at an intermediate collagen concentration (Fig. S5, D and E). Stepwise cell velocity also demonstrated a biphasic response, with cells in the 1 mg/mL collagen matrix having the highest migration speed (Fig. 4 B). These findings are consistent with previous work showing a biphasic response of cell migration to collagen density (57). Protrusive activity increased with collagen density (Fig. 4 C); intracellular ATP/ADP ratio and mitochondrial membrane potential also increased with rising collagen density, suggesting that cells in dense collagen matrices may increase OXPHOS to meet the energy needs necessary for cytoskeletal remodeling and migration (Fig. 4, D–F). Similar to cell elongation and spreading, a positive linear correlation was seen for ATP/ADP ratio and TMRM signal with increased matrix density (Fig. S6, A and B). As ATP/ADP ratio and OXPHOS were correlated with increased protrusive activity and changes in collagen density, these data suggest that protrusive activity in 3D collagen matrices may require a significant amount of energy.

Figure 4.

Inhibition of MDA-MB-231 OXPHOS lowers cellular energetics and cytoskeletal activity in 3D collagen gels. (A) A color-coded time-lapse of MDA-MB-231 protrusive activity in collagen matrices is shown (dashed yellow squares show zoomed regions). Quantification of (B) stepwise cell velocity (n = 33–61 cells) and (C) stepwise cell protrusive activity (n = 30 cells) in matrices of increasing collagen density is shown. (D) Normalized PercevalHR ratio of MDA-MB-231 cells in collagen matrices is shown (yellow lines show cell outlines). Quantification of (E) normalized PercevalHR ratio (n = 33–61 cells) and (F) TMRM fluorescent signal (n = 48–93 cells) in matrices of increasing collagen density is shown. Quantification of (G) normalized PercevalHR ratio (n = 32–61 cells), (H) TMRM fluorescent signal (n = 48–93 cells), (I) stepwise velocity (n = 32–61 cells), and (J) protrusive activity (n = 30 cells) after AMA treatment in matrices of increasing collagen density is shown. (K) Percentage change in cellular energetics, migration speed, and protrusive activity averaged for each collagen density after AMA treatment in comparison to control conditions is shown (AMA/Ctrl; no change = 1; complete inhibition = 0). Data shown as box-and-whisker plots denote mean (+) or medians and 25th/75th and 5th/95th percentiles; dashed lines show linear regression; two-tailed t-test was used when comparing between ctrl and AMA, and multiple comparisons with ANOVA was used when comparing across collagen densities; n.s., nonsignificant; ^∗p < 0.05, ^∗∗p < 0.01, ^∗∗∗p < 0.001, ^∗∗∗∗p < 0.0001. Scale bars, 50 μm. To see this figure in color, go online.

OXPHOS supports cytoskeletal activity and cell migration in 3D collagen matrices

Our results showed that inhibiting OXPHOS lowered increased energy production and membrane activity with cell elongation on 2D collagen micropatterns, suggesting that OXPHOS is important for energy production to support cytoskeletal activity. Previous studies have also suggested that collagen density can alter cytoskeletal remodeling and invasion (48). Therefore, to study the role of OXPHOS in cellular energy and cytoskeletal dynamics during migration in a collagen matrix, we next examined ATP/ADP ratio and protrusive activity over a 12-h time-lapse with AMA treatment to inhibit OXPHOS (Fig. 4, G–J). Both ATP/ADP ratio and mitochondrial membrane potential were reduced in all collagen densities after AMA treatment, and the effect of increased collagen density on ATP and OXPHOS was abrogated (Fig. 4, G and H; Fig. S6, A and B). Cell size was not affected by the AMA treatment, but a significant decrease of elongation was seen, especially with high collagen density (Fig. S6, C and D). Migration velocity and protrusive activity both decreased; however, AMA treatment had a more significant effect on velocity and protrusive activity in high-density collagen gels and no effect in 0.5 and 1 mg/mL collagen (Fig. 4, I and J). Similarly, the total change in energy, cytoskeletal activity, and migration were all greatly decreased in denser collagen gels after OXPHOS inhibition, with the most significant changes occurring in the densest collagen matrices (Fig. 4 K). These results indicate that energy and OXPHOS usage are modulated by matrix cues and associated with cell protrusive activity. As such, OXPHOS plays an important role in providing energy for cytoskeletal dynamics during migration.

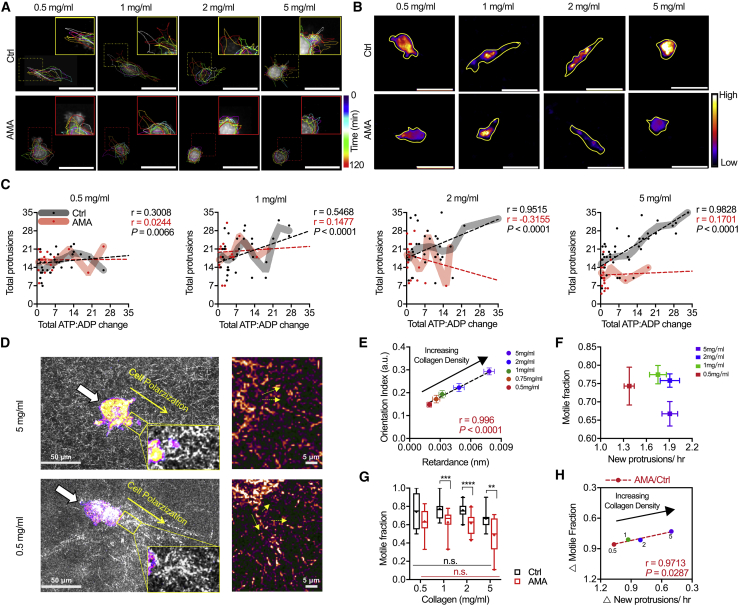
To investigate how OXPHOS may regulate protrusive activity during migration, we further investigated the relationship between energy usage and protrusive activity with respect to cell motility after AMA treatment (Fig. 5, A and B). The number of total protrusions formed and the total ATP/ADP change were positively correlated in control conditions for all collagen densities, with 5 mg/mL density being the most significantly correlated condition (Fig. 5 C; Fig. S6 E). However, AMA treatment attenuated this correlation for all conditions, with cells in 5 mg/mL gels being the most impacted (Ctrl: r = 0.9828; AMA: r = 0.1701; p < 0.0001) (Fig. 5 C). Given the increase in protrusion in high-density matrices, we examined whether the increased number of cell protrusions in high-density matrices may be associated with increased matrix remodeling activities required for migration (Fig. 5 D). Using qPol and confocal reflectance microscopy, we quantified cell contractility and collagen fiber orientation within 10 μm of the protrusions across a wide range of collagen densities (Fig. 5 E; Fig. S7, A and B). Cell matrix remodeling activity by protrusions was measured based on cell contractility and collagen fiber orientation, and we found both factors increased with collagen density (Fig. 5 E). These data suggest that cells may require OXPHOS and protrusions in dense collagen matrices potentially to help with matrix remodeling.

Figure 5.

Protrusive activity is positively correlated with cellular energetics and motility in high-density collagen matrices through OXPHOS. (A) Color-coded time-lapses of MDA-MB-231 protrusive activity and migration after AMA treatment in matrices of increasing collagen density are shown (dashed squares show zoomed regions; yellow, ctrl; red, AMA). (B) Normalized PercevalHR ratio of MDA-MB-231 cells after AMA treatment in matrices of increasing collagen density is shown (yellow lines show cell outlines). (C) Stepwise cell protrusion and total change in ATP/ADP signal of single MDA-MB-231 cell after AMA treatment in collagen matrices are shown (n = 20–40 cells). (D) Normalized PercevalHR ratio of MDA-MB-231 cells in matrices of increasing collagen density with confocal reflectance is shown (small yellow arrows show fiber directions). (E) Quantification of cell contractility and collagen fiber orientation within 10 μm to cell protrusions for MDA-MB-231 cells in matrices of increasing collagen density is shown. (F) Motile fraction as a function of stepwise new protrusions averaged for each collagen density is shown. (G) Quantification of motile fraction (n = 12–20 positions) after AMA treatment in matrices of increasing collagen density. (H) Percentage change in protrusive activity and motile fraction after AMA treatment for MDA-MB-231 cells in matrices of increasing collagen density is shown (AMA/Ctrl; no change = 1; complete inhibition = 0). Data shown as box-and-whisker plots denote mean (+) or medians and 25th/75th and 5th/95th percentiles; lines show LOWESS smoothing, and dashed lines show linear regression with mean ± SE; P represents extra-sum-of-squares F-test when comparing linear regression. n.s., nonsignificant; ∗∗p < 0.01, ∗∗∗p < 0.001, ∗∗∗∗p < 0.0001. Scale bars, 50 μm. To see this figure in color, go online.

Because energy-intensive protrusive activity and ECM remodeling have been largely associated with migration (1,5,59, 60, 61, 62), we examined the relationship between energy-mediated protrusions and cell motility in different collagen densities. By comparing motile fraction with the number of protrusions, cells in the intermediate densities on average had the most motile cells with similar protrusive activity (Fig. 5 F); and AMA treatment had no effect on motility in 0.5 mg/mL collagen gels (Fig. 5 G). Similarly, we observed a greater impact on protrusive activity and motility in response to AMA, which linearly correlates with increasing collagen density (Fig. 5 H). Compared with control conditions, 5 mg/mL is the condition in which protrusive activity and motile fraction were decreased the most after AMA, suggesting that OXPHOS is an important regulator of protrusive activity and migration in high-density matrices. AMA had no significant effect on protrusive activity and migration in 0.5 mg/mL collagen, indicating increased protrusive activity and OXPHOS levels may not be required in matrices with large pores. Together, these findings suggest that intracellular ATP energy and OXPHOS may promote cancer cell protrusive activity, which supports migration in dense microenvironments.

Discussion

We demonstrated that alterations in the geometry of 2D collagen micropatterns and density of 3D collagen matrices drive changes in metabolism to support cytoskeletal dynamics during migration. Specifically, we identified OXPHOS as an important regulator of protrusive activity during migration through dense collagen matrices. Membrane ruffling in 2D and protrusive activity in 3D were correlated with cellular energetics, and OXPHOS was necessary for protrusive activity and migration in 3D matrices. A growing body of work indicates that matrix confinement can impose high energetic costs on cells, which can influence migration path and mode of migration (5,12,18,63). Cell protrusions in 3D tissues have been shown to allow migrating cells to dynamically engage with the ECM fibers, either through ligand binding or matrix remodeling (1,64). This remodeling can result in the formation of tracks of approximately one cell in width for cell migration (65). Dense collagen gels increase cell confinement, limiting cell spreading and migration while also increasing energy utilization during single-cell (12) and collective migration (66). Considering that cells in dense collagen matrix might experience more resistance to send out protrusions, the increased protrusive activity of cells we observed may be associated with matrix remodeling activity required for migration in high-density matrices. Limited by collagen pore size, the new cellular protrusions may be in any direction and are energy driven, as cells may simultaneously search for a migration track in multiple directions (48,67). This is consistent with a previous report that mitochondrial flux toward the leading edge of cells and the associated increase in local ATP concentration contributes to an increased frequency, amplitude, and velocity of actin-rich membrane ruffles (48).

Consistent with our previous work, intracellular ATP/ADP ratio was increased as cells migrated in denser collagen matrices, likely to remodel their cytoskeleton to physically displace the matrix and enable the cells to squeeze and move through smaller pores and/or to proteolytically degrade the denser matrices (12). Active protrusions are important for migration in high-density matrices, which can be inhibited with matrix metalloproteinase inhibition (68). At a single-cell level, a positive relationship between protrusion rate and ATP/ADP ratio was observed for individual cells confined in the same ECM of relatively high density. It indicates that when confined in high-density matrices, high-energy cells are more likely to send out active protrusions for ECM remodeling and migration path generation (1,64,65) as compared with low-energy cells. This increase in ATP/ADP ratio (12,18,69) is likely caused by an increase in OXPHOS activity to meet the associated energy demand during migration (48,67) because inhibition of OXPHOS significantly reduced the ATP/ADP ratio and protrusive activity in a denser matrix. Moreover, we found that cytoskeletal contractility and matrix fiber alignment increase with matrix density, suggesting a more active cytoskeletal function for cells in high-density matrices. Stiffness-mediated stress fiber reorganization was recently shown to regulate cell metabolism via modulating metabolic enzyme activity (8). Similarly, the matrix-density-mediated cytoskeletal activity that we observed may act via a similar mechanism to regulate OXPHOS. Consistent with this idea, our 2D micropattern experiments showed that cellular energetics and OXPHOS increase with substrate stiffness, cell spreading area, and cell elongation, all of which have been previously shown to increase cytoskeletal contractility and fiber organization (70). Increased OXPHOS may further promote cytoskeletal activity, thus forming a positive-feedback loop for cancer cells in high-density matrices.

Although the Warburg effect or aerobic glycolysis remains to be a key feature of metabolism in many cancers, recent work has emerged to refocus on the essential function of mitochondrial OXPHOS in tumor metastasis (41,71, 72, 73). Other research has identified that mitochondrial trafficking is necessary for membrane activity during 2D migration (48) and force generation via actin polymerization at invadopodia during basement membrane invasion, suggesting an important need of OXPHOS to support motility (49). Conversely, other work suggests that the localization of glycolysis proteins is critical for membrane activity (8,74). These conflicting findings may be due to metabolic heterogeneity between cancer types, as cells can adapt their metabolism to the mechanical microenvironment and cells at different metastatic sites have different metabolic profiles (17). Our finding that changes in the collagen matrices can modulate cancer cell metabolism provides context for how the altered ECM promotes metastatic disease.

Interestingly, although cell protrusion rate, intracellular energy, and OXPHOS activity all increased with collagen density, a biphasic response of cell elongation and migration speed to the density of ECM was observed, with optimal migration speed and highest elongation reached in 1 mg/mL collagen. This is consistent with previous reports showing that cells may be sensitive to the ECM mesh size and that an intermediate ECM density may provide cells with optimal fiber alignment and adhesion strength to achieve maximal migration speed (57,75). Notably, ECM geometry can dictate cell migratory mode in both proteolytic and nonproteolytic mechanisms (1,63). The significant cell elongation at an intermediate matrix density with a desirable pore size may further promote cell migration through adhesion dynamics. Cell protrusion dynamics, migration speed, and invasion distance have previously been shown to be modulated by collagen fiber alignment. In high-density collagen (2.5–6 mg/mL), cell migration most effectively depends on invadopodia and matrix metalloproteinase activity (57). Similarly, our results showed that cells in low-density (0.5–2 mg/mL) and high-density collagen (5 mg/mL) exhibited distinct motility regimes. Although cells in lower-density conditions can become efficient “migrators” and adjust to optimized cell elongation and higher migration speed with established protrusions (30), cells in higher-density gels instead send out new protrusions more often throughout the time course. The ability to switch off new protrusion formation and transition to motility is necessary for effective 3D migration in low-density collagen matrices (30). Our data indicate that cells in denser conditions, instead of turning off the new protrusion formation state, may maintain an active matrix probing state in a less-elongated shape to navigate through the ECM. Understanding cell adaptations to different mechanical cues during migration and the role of metabolism plays in fueling these adaptations thus will be an important next step.

Conclusion

The physical properties of the tumor microenvironment, including confinement, stiffness, and topography, are all known to be key regulators of metastasis (2,60,76). Tumor cells adapt their migratory phenotypes in response to an altered mechanical microenvironment, and growing evidence suggests that metabolic changes are important to this response. Utilizing a novel micropatterning method in combination with single-cell measurements of intracellular ATP/ADP ratio and mitochondrial membrane potential, we demonstrated increased membrane ruffling and OXPHOS activity for confined 2D cells with a high elongation. When migrating in 3D, cancer cells require more energy to send out protrusions, potentially for ECM remodeling and migration in denser matrices, and cells actively increase their OXPHOS rate to meet these energy-demanding protrusive activities. Together, these results suggest that the physical properties of local ECM may modulate the cellular metabolic profile to regulate the cytoskeletal activity, thus affecting 3D cancer cell metastatic invasion.

Author contributions

Y.W., M.R.Z., J.Z., and C.A.R.-K. designed the study. Y.W. performed the experiments. Y.W. and M.R.Z. analyzed the data. M.R.Z., J.Z., and C.A.R.-K. supervised the study. All authors contributed to writing the manuscript.

Editor: Paul Janmey.