Energetics and structure of alanine-rich α-helices via adaptive steered molecular dynamics

Abstract

The energetics and hydrogen bonding profiles of the helix-to-coil transition were found to be an additive property and to increase linearly with chain length, respectively, in alanine-rich α-helical peptides. A model system of polyalanine repeats was used to establish this hypothesis for the energetic trends and hydrogen bonding profiles. Numerical measurements of a synthesized polypeptide Ac-Y(AEAAKA)_kF-NH₂ and a natural α-helical peptide a2N (1–17) provide evidence of the hypothesis’s generality. Adaptive steered molecular dynamics was employed to investigate the mechanical unfolding of all of these alanine-rich polypeptides. We found that the helix-to-coil transition is primarily dependent on the breaking of the intramolecular backbone hydrogen bonds and independent of specific side-chain interactions and chain length. The mechanical unfolding of the α-helical peptides results in a turnover mechanism in which a 3₁₀-helical structure forms during the unfolding, remaining at a near constant population and thereby maintaining additivity in the free energy. The intermediate partially unfolded structures exhibited polyproline II helical structure as previously seen by others. In summary, we found that the average force required to pull alanine-rich α-helical peptides in between the endpoints—namely the native structure and free coil—is nearly independent of the length or the specific primary structure.

Significance

We found that the force required to pull an α-helix apart is approximately constant regardless of the degree to which it has already been unfolded or the initial length of the helix. This additive property was determined through adaptive steered molecular dynamics simulations of several alanine-rich peptides with varying sequence and length. The helices were also found to retain partial helical character commensurate with their retained free energy at a given extension. These results provide a sharper view of the stability of the α-helix in proteins. They also have strong implications for the folding and unfolding pathways involving this secondary structure in proteins generally.

Introduction

The α-helix is one of the most fundamental secondary structures found in proteins. Among other things, it helps the formation of tertiary structure and often plays a role in a protein’s function. The allowed combinations of ϕ and ψ angles in an α-helix naturally orient NH and CO groups along the backbone toward each other so as to form hydrogen bonds (1). However, the helix-coil transition is often not a simple two-state reaction. The protein’s landscape can exhibit broad basins with folded and unfolded regimes (2), which confuses the identity of the initial and final structures. A given folding or unfolding protein will thus traverse across several minima and barriers along its pathway. The intermediate (local minimal energy) structures can be quite different from the fully folded or unfolded structures. The compact substructures with frayed ends (3) have been seen to appear along the pathway, for example. The complexity of the landscape plays a role in the Zimm-Bragg (4) and Lifson-Roig (5) theories of the energetics of the transition (6). Meanwhile, the development of sensitive experimental techniques, such as atomic force microscopy and optical tweezers, enables measurements of the conformational change of a single macromolecule (7). These techniques also provide the force required to mechanically unfold a protein, RNA, or DNA (8,9). Steered molecular dynamics (SMD) is carried out in molecular dynamics (MD) simulations to obtain the corresponding unbinding potentials (10,11) and a prediction of the atomic-level-detailed mechanism (12, 13, 14). In this work, adaptive steeted molecular dynamics (ASMD) (15) is used to reveal the energetic trends of the unfolding of a model system such as the helix-coil transition for a series of polyalanines with increasing length, a series of water-soluble alanine-rich proteins with increasing length, and a biologically relevant structure. ASMD is an enhanced sampling method similar to SMD but is performed in several stages to avoid the spread of work that can limit the applicability of SMD. ASMD has been successfully applied to reveal the energetics of decaalanine in vacuum and implicit and explicit solvents (16, 17, 18), neuropeptide Y (15,19), and β-hairpin-containing peptides (20,21). Here, we consider a class of successively larger—that is, longer—helical peptides whose potential of mean force (PMF) profiles can be revealed by ASMD so as to establish the trends in the forces and structure associated with the stretching of a helix as a function of their length.

Polyalanine- and alanine-based peptides have already been used as model systems to address the helix-coil transition both experimentally (22, 23, 24) and theoretically (25). Alanine, with the highest propensity for helical formation (26), has only a methyl group as its side chain. Alanine-rich peptides are a suitable target for addressing the helix-coil transition because of their high tendency for helix formation and in consideration of reducing the computational cost in the simulations. Moreover, the kinetics of the helix-coil transition of alanine-rich peptides has been seen to be sensitive to temperature (24) and peptide length (27,28). Such kinetics are also sensitive to the structure in the initial unfolded proteins; during the process of the helix-coil transition, helices tend to form faster when there is more similarity between the initial coil conformations and the helical structures in the folded state (29). One caveat associated with our choice to focus on polyalanine peptides is that they are insoluble in water. Thus, the determination of the stretching of polyalanine relies on the constraint that it has been submerged in water either by holding both ends therein or because it is part of a larger soluble protein. There has been much debate over which is the stable conformation of polyalanine peptides in solvent, α-helix or random coil. For short alanine-based peptides, both α-helical and 3₁₀-helical conformations have been observed experimentally (30). Advances in the accuracy of model force fields have led to increasingly better model predictions (31, 32, 33, 34, 35, 36). At low temperatures, the Ala₂₁ peptide was seen to exhibit polyproline II (pPII) helical structure in simulations using the AMBER force field (37). The stable structure in Ala₁₂ was found to be a random coil in simulations with the CHARMM force field (38). However, Wales et al. found that increasing the amount of alanine residues from 12 to 16 increases the stability of the α-helical structure in simulations using the AMBER95 force field (39). There is also evidence that suggests that the propensities of the relative orientation of the residues in alanine-rich peptides are highly sensitive to the solvent environment (24,40). To avoid such a confounding factor, in this work we restrict the nature of the solvent environment to be neat water in all cases.

To confirm the role of the trends in helical proteins with their increasing length that we found in polypeptides forced to be in a water solvent, we selected two additional alanine-rich peptides that are known to be soluble. The first peptide of interest is Ac-Y(AEAAKA)_kF-NH₂ (EK peptide) (41, 42, 43, 44, 45). The EK polypeptide exhibits a single α-helical structure for several repeats from k = 4–8 that is, at least, partly a consequence of the helix-stabilizing alanines (39,46), salt-bridge formations, and low temperatures. The series of EK polypeptides are characterized at a temperature of 300 K, at which they are known to be 60% soluble in water (42). The second soluble peptide is the a2N (1–17) (Protein Data Bank, PDB: 2LX4 (47)) peptide with the α-helical structure from Mus musculus V-ATPase. The a2N (1–17) fragment regulates the enzymatic exchange of GDP/GTP of cytohesin-2 (47). It is composed of 17 amino acids including only one alanine residue (sequence: MGSLFRSESMCLAQLFL), and residues 5–17 form an α-helix, whereas residues one to four form a flexible N-terminus (47). Finally, it is notable that ΔH_formation for the helix-coil transition was found to be ∼1 kcal/mol for a large family of helices of lengths ranging from 12 to 19 residues through calorimetry experiments (42,48). Other calorimetry experiments utilizing poly-L-glutamic acid repeats demonstrated that the ΔH_formation was also ∼1 kcal/mol (49). These results indicate that the transition is independent of chain length and type of residues when the peptides are free, in agreement with our findings for the pulling of the proteins when their ends are constrained.

In this work, we determined the energetics and pathway of the force-induced unfolding process for several polypeptides with varying amino acid sequences. The results reveal the generality of the α-helix folding process in leading to corresponding PMFs and hydrogen bonding profiles across different proteins. Our benchmark systems are a series of polyalanine peptides, ranging from 6 to 50 residues in length. We compare the PMF and the hydrogen bonding profiles obtained from the model system to the alanine-rich α-helices and the biologically relevant α-helix structure. The comparison among different alanine-rich peptides demonstrates that the PMF profiles correspond to one another by following the same shape. Furthermore, the hydrogen bonding profiles exhibit the same trends for all types of hydrogen bonds that were observed. Those similarities indicate that the unfolding mechanism for the α-helix is the same for both the model polyalanine peptides and the alanine-rich polypeptides and independent of the side-chain interactions.

Methods

Review of ASMD theory

ASMD has previously been benchmarked on neuropeptide Y in explicit solvent and decaalanine in vacuum and implicit and explicit solvents (15, 16, 17, 18). Our group found that fewer trajectories were required for convergence in comparison with those needed using SMD (10,11). For more details on the criteria required for convergence, please refer to the recent review in (50).

In SMD, a steering force is applied on an auxiliary atom, which is attached to the system of interest with a harmonic potential to guide it along a chosen reaction coordinate or path. A series of nonequilibrium trajectories are then generated and averaged through the Jarzynski equality (JE),

$$G\left({\xi }_t\right)=G\left({\xi }_0\right)-\frac{1}{\beta }\text{ln}\langle e^{-\beta W_{{\xi }_t\leftarrow {\xi }_0}}{\rangle }_0,$$ (1)

which relates the nonequilibrium work values with the equilibrium free energy difference between two states (51, 52, 53). In the JE, G represents the PMF obtained at a particular extension of the reaction coordinate. The constant β is 1/k_BT, where k_B is the Boltzmann constant and T is the temperature. The SMD method has successfully enabled investigations of energetic changes along pathways that are hard to access within the regular timescales of MD simulations, such as protein folding (54) and protein-ligand interactions (55). Even though the combination of SMD and JE has been a powerful tool for computing the PMF of a system, its implementation is often challenging because the requirement of exponential-Boltzmann-weighted calculation requires a large number of simulations to acquire the convergence.

ASMD was developed by Hernandez and co-workers (15, 16, 17) to reduce the sampling size in SMD simulations. The central idea of the method is the segmentation of the whole reaction coordinate into several stages (15). At each stage, a standard SMD simulation is performed, and the PMF is determined using the JE (51, 52, 53). The PMFs are sewn together between stages using a criterion to contract the ensemble at the end of a given stage into one that better approximates the equilibrium ensemble so as to initiate the subsequent stage. In the naïve ASMD method employed throughout this work, we use the simplest such contraction. That is, the trajectory that has the work value closest to the Jarzynski average value at the end of a stage is used as the starting configuration for the next stage. By selecting only one important configuration at the end of each stage, the trajectories that contribute very little to the overall PMF are eliminated, thereby saving computing resources that are otherwise used to propagate trajectories that contribute little to the nonequilibrium ensemble averages. In summary, the PMF for the particle pulled from r_ee(0) to the position r_ee(t) at a given t ∈ (t_{j − 1}, t_j] is obtained iteratively through the corresponding j stages as

$$\overline{W}\left(r_{\text{ee}}\left(t\right)\right)=\overline{W}\left(r_{\text{ee}}\left(t_{j-1}\right)\right)-{\beta }^{-1}\text{ln}\left\{\frac{1}{N}\sum _{i=1}^N{e}^{-\beta W_j\left({\xi }_t^{\left(i\right)}\right)}\right\},$$ (2)

where r_ee(t_{j − 1}) is the position of the auxiliary particle at the end of the stage j − 1 and the nonequilibrium work W_j is obtained for each of the N trajectories ${\xi }_t^{\left(i\right)}$, labeled by i, in the j^th stage. The naïve ASMD method has proven to be efficient and accurate (15,16) for such averages when they are dominated by a single predominant pathway and therefore suffices for the application to polyalanines in this work. Because other versions—e.g., fixed-relaxation ASMD (18) and multibranched ASMD (56)—are not used in this study, we will refer to the naïve method simply as ASMD in the remainder of this work.

Equilibration of target peptides

Polyalanine peptides

Ala homopolymers with lengths 6, 10, 14, 22, 30, 38, and 50 residues were used to represent the family of such single-domain helical peptides. Each structure was built using the VMD plugin molefacture (57). The N-terminus and C-terminus of all the peptides were neutralized using the usual capping procedure—that is, they were acetylated and amidated, respectively. Each helical structure was rotated to the z axis and then placed into a TIP3P water box long enough to accommodate the fully extended peptide, and wide enough to accommodate the initial structure. All simulations were performed with NAMD (58) and the CHARMM36 force field (32). The importance of the torsion-energy terms in leading to a proper description of protein has been reported earlier (35,59, 60, 61). Compared with the CHARMM22 force field, the CHARMM36 force field employed here optimizes the ϕ and ψ dihedral in interaction energies through the CMAP correction terms (32,62). We did not make explicit comparison to other force fields such as those in the AMBER suite because there have been several reports suggesting that they lead to comparable results (63,64). The caveat to this claim is that one must use a force field appropriate to the structures sampled by the particular system (65). Thus, the choice of CHARMM36 is motivated by its benchmarked treatment of the dihedral angles as needed for the appropriate treatment of the α-helical polypeptides of interest in this work.

The whole system was initially equilibrated for 1 ns under NPT conditions at 300 K with the damping coefficient set as 5 ps⁻¹. The pressure was regulated using a Nosé-Hoover Langevin piston with a decay period of 100 fs and a damping time constant of 50 fs. During the NPT equilibration, the C_α ends of each peptide were constrained to allow the water to reach the appropriate density. The system was then equilibrated under NVT conditions at 300 K. A series of 200 ps relaxations were performed with the backbone constrained, using a harmonic potential decreasing from 10.0 to 5.0 to 1.0 kcal/mol Ų. The peptide was then allowed to freely equilibrate under NVT conditions for 1 ns. At the end of that equilibration, the peptide ends are no longer on the z axis. The whole system could then be returned to the z axis through a rotation and translation of the periodic box. We found it easier, however, to rotate and translate only the protein structure to align its ends to the z axis and then resolvate it with TIP3P water. In the end, the system was again equilibrated under NPT conditions for 1 ns at 300 K with the ends constrained. Equilibration was verified through the plateau in the root mean-square deviation analysis obtained via the NAMD plugin.

EK peptides

A soluble polyalanine-rich repeat Ac-Y(AEAAKA)_kF-NH₂ (EK peptide), where k is equal to 4, 5, 6, and 8 corresponding to 26, 32, 38, and 50 residues, respectively, has been observed experimentally to be at least 60$\text{\%}$ soluble in water at 300 K (42). Each experimentally relevant structure was built using VMD plugin molefacture (57). The same end caps and equilibration protocol that were used in the polyalanine study were used in the water-soluble structure study. The resulting structures for all values of k were α-helical.

A2N peptide

A biologically related α-helical structure, a2N (1–17) from M. musculus V-ATPase (PDB: 2LX4 (47)), is also used to determine the PMF and hydrogen bonding profiles. The structure is composed of 17 amino acids including only one alanine residue (sequence: MGSLFRSESMCLAQLFL). Amino acids 5–17 form an α-helix, whereas amino acids 1–4 form a flexible N-terminus (47). The same end caps and equilibration protocol that were used for both polyalanine peptides and EK peptides were used for equilibration in this study.

ASMD simulation parameters for unfolding

The ASMD simulations for the above peptides were carried out in the explicit solvent under NPT conditions at 300 K with NAMD (58) and the CHARMM36 force field (32). For each system, the ASMD simulation was started with the same configuration that was saved from the equilibration phase. Each polypeptide was placed in a rectangular TIP3P water box that was slightly bigger than the corresponding unfolded protein. The first residue C_α-terminus was held fixed, and the other C_α-terminus was attached with the pseudoatom, which would be pulled with an applied force along the z axis direction. Each protein was pulled to a total distance equal to 2 Å times the number of residues, as that is sufficient to break all the intrapeptide bonds (66, 67, 68). The pulling velocity was set to 1 Å/ns because that was slow enough to obtain convergence in the PMF. The parameters are summarized in Table 1. Within each stage, 100 traditional SMD trajectories are carried out, and 100 frames were recorded per trajectory. The conditions for the convergence of the method were recently reported (50), and the convergence of the PMFs in these cases is reported in Fig. S1. Stretching the protein 2 Å per residue results in an unfolded protein, but not necessarily a linear amino acid sequence.

Table 1.

Summary of ASMD simulation parameters for the alanine-rich peptides

Peptide	Length of reaction coordinate (Å)	Number of stages
Ala6	12	5
Ala10	20	10
Ala14	28	10
Ala22	44	20
Ala30	60	25
Ala38	76	25
Ala50	100	50
EK (k = 4)	52	25
EK (k = 5)	64	25
EK (k = 6)	76	25
EK (k = 8)	100	50
a2N (1–17)	34	10

Hydrogen bonding

The hydrogen bonding profiles were calculated for each of the alanine-rich peptides throughout each trajectory. The number of hydrogen bonds was obtained using the MDAnalysis (69,70), and a cutoff of 4 Å between two electronegative atoms and an angle of 140° with the H atom as the vertex were used. The average number of hydrogen bonds along the pulling process,

$$\langle N\left(S_1,S_2\right){\rangle }_t=\frac{{\sum }_{i=1}^N\hat{N}\left(S_1,S_2\right)e^{-\beta W_j\left({\xi }_t^{\left(i\right)}\right)}}{{\sum }_{i=1}^N{e}^{-\beta W_j\left({\xi }_t^{\left(i\right)}\right)}},$$ (3)

was determined by weighting the instantaneous number of hydrogen bonds $\hat{N}$(S₁, S₂) with the corresponding instantaneous work following the notation used earlier in Eq. 2 (8,16,71). The instantaneous number of hydrogen bonds between two selected sets, S₁ and S₂, of functional units—viz. particular residues of the protein or adjacent water molecules—is

$$\hat{N}\left(S_1,S_2\right)=\underset{{\zeta }_k\in S_1,{\zeta }_l\in S_2}{{\sum }^{\text{'}}}\hat{n}\left({\zeta }^{\left(k\right)},{\zeta }^{\left(l\right)}\right),$$ (4)

where $\hat{n}$(ζ^(k), ζ^(l)) is the number of hydrogen bonds (1 for allowed positions and 0 otherwise) between the two functional units, the prime in the sum excludes the case that k = l, and the sum includes all possible units in each set. The form of Eq. 3 can be used to determine other average observables, such as the α-helical character, 3₁₀-helical character, and π-helical character.

Results and discussion

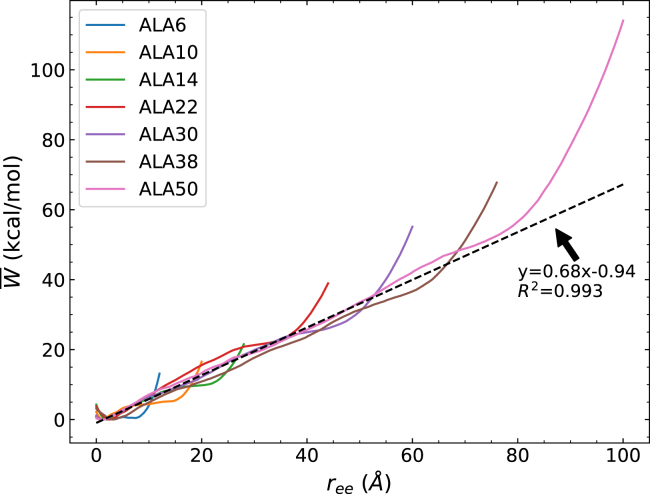
Seven polyalanine peptides were stretched to determine the degree of additivity in the energy and the helix-coil transition as the protein is unfolded. The PMF profiles for a series of polyalanine peptides are shown in Fig. 1. The PMF profiles for a few additional peptides that are known to be soluble in water are also shown in Fig. 2. The PMF profiles for all of these α-helices follow the same trend. The wells seen at the beginning of the stretch for each curve represent the structure with the minimal energy. Starting with the initial compact (helical) structure, the PMF increases approximately linearly with increasing extension along a distance associated with the transition from helix to coil. The pulling force was determined as 0.68 kcal/mol Å (= 47.26 pN), which is comparable to that found in atomic force microscopy measurements of the unfolding poly(γ-benzyl-L-glutamate) in dioxane (72). This agreement may seem surprising because both the solvent environments and sequences of α-helices are different between the two systems. However, both polyalanines and poly(γ-benzyl-L-glutamate) have an α-helical backbone in common, and the unwinding of their α-helical structure appears to present the dominant contribution. That is, because the α-helix is the stabilizing structure in the solvent (46), the extension of the longer α-helix requires the most work. Coronado and co-workers (73) applied the approximate model of Buhot and Halperin (74,75) to determine the force value from the elongation parameters (s) in the Zimm-Bragg model. With the typical values of s at 1.1–1.5 (28), the force values should be around 0.45 kcal/mol Å (73), which is close to those found here (0.68 kcal/mol Å). Furthermore, because the helix-coil transition includes the process of breaking the backbone hydrogen bonds and the formation of peptide-water hydrogen bonds, the PMF is expected to be lower than that for the unfolding of polypeptides in vacuum (data not shown).

Figure 1.

Comparison of the energetics of several polyalanine peptides. The PMFs have been obtained using 100 tps at 1 Å/ns. To see this figure in color, go online.

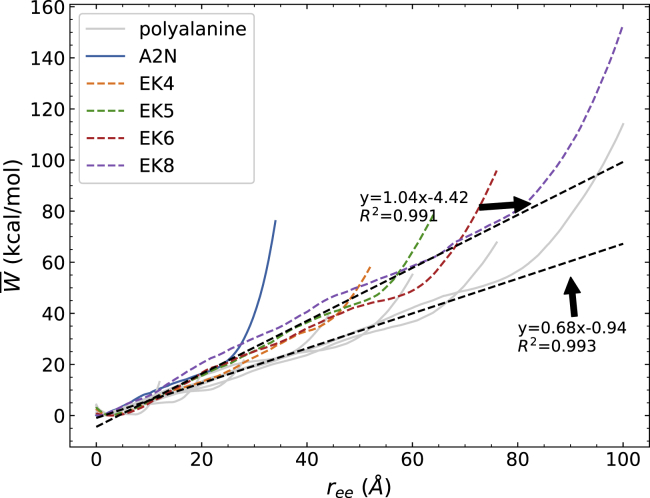
Figure 2.

Comparison of the energetics of several polyalanine peptides, EK peptides, and a2N (1–17) peptide. The PMFs have been obtained using 100 tps at 1 Å/ns. To see this figure in color, go online.

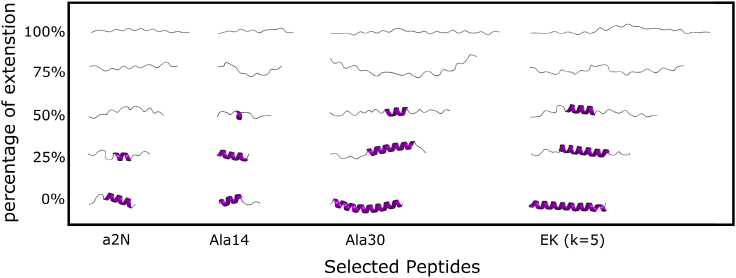
The PMFs for the EK peptides follow the trend seen for the polyalanines in that they share the same slope. The similarity in the required force indicates that the energetics of these α-helices are determined by the same intramolecular interactions, which is hydrogen bonding. The small deviations between the slopes of these two families of proteins may be due to the energy arising from the side-chain interactions between the charged side chains (e.g., Glu and Lys) within EK peptides. Moreover, the large side chain of Lys would also shield water molecules from the backbone, making the EK peptide prefer adopting the α-helix structure (43,76,77). As a consequence, the shielding effect with the salt-bridge formation lets EK peptides have larger final work values than their corresponding polyalanine peptides with similar lengths. As discussed in the next paragraph, this conclusion is also supported by hydrogen bond profiles shown in Figs. 4 and 5. After all the intrapeptide bonds are broken, further stretching of the peptides causes the PMF to increase dramatically, which is due to the covalent bonds stretching. Because we only pull the peptide 2 Å per residue, some peptides may be pulled farther than others. In such a case, the final work will increase to different extents with different degrees of full extension. The a2N (1–17) structure still has a very similar PMF profile as compared to the model system, even though it could have van der Waals interactions in the helix formed between side chains. The a2N (1–17) peptide also has a slope closer to the EK peptide family. Because a2N (1–17) has a completely different sequence with only one alanine residue from the EK peptides, it again illustrates that the precise identity of residues has little influence on helix-coil transition. These conclusions are also apparent in the relative structures of the peptides shown in Fig. 3 along their extension. The helices appear to unfold from their ends and proceed to unfold in a cooperative manner. Both pairs of comparable peptides—viz. (a2N and Ala₁₄) and (EK and Ala₃₀)—have a similar degree of unwinding of the helices along the pulling coordinate in agreement with an apparent nonspecificity in the intrapeptide contacts.

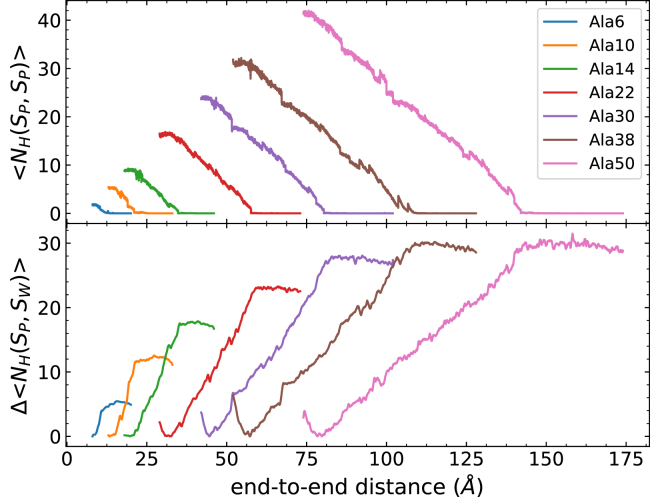
Figure 4.

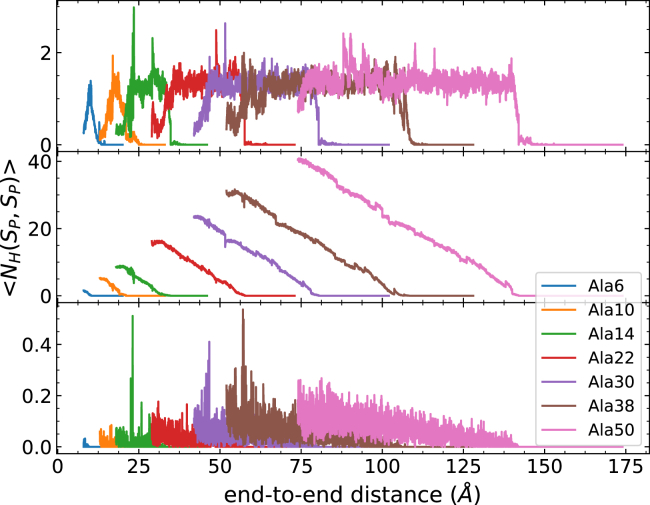
Polyalanine lengths and the corresponding total bonding profile of 100 trajectories at 1 Å/ns. The top panel corresponds to the intrapeptide hydrogen bonds, and the bottom panel corresponds to the peptide-water hydrogen bonds. The rate of losing intrapeptide hydrogen bonds is approximately the same for each polyalanine length. To see this figure in color, go online.

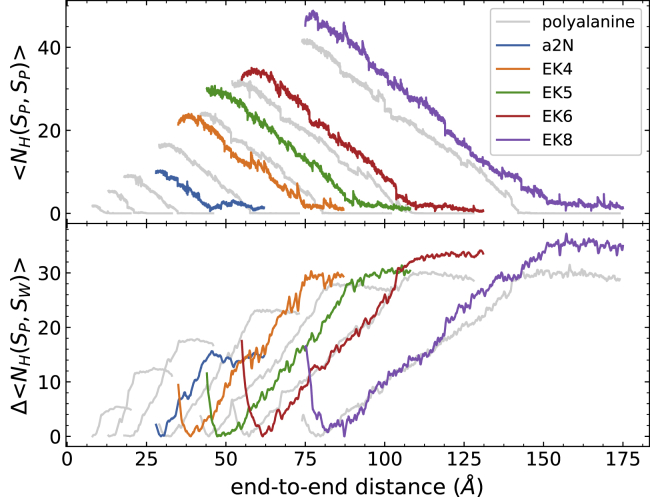
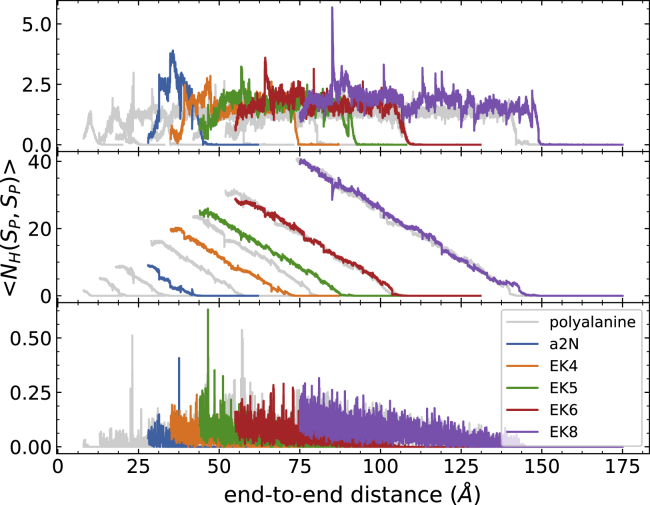
Figure 5.

Various alanine-rich α-helices and the corresponding total bonding profile of 100 trajectories at 1 Å/ns. The top panel corresponds to the intrapeptide hydrogen bonds, and the bottom panel corresponds to the peptide-water hydrogen bonds. The gray color corresponds to the results of polyalanine peptides, which have been shown in Fig. 4. The numbers of peptide-water hydrogen bonds for the EK peptides and a2N (1–17) peptides are higher than the polyalanine peptides because of the hydrophilic side chains. The rate of losing intrapeptide hydrogen bonds is still approximately the same for each type of peptide. To see this figure in color, go online.

Figure 3.

Comparison of structures along the representative ASMD trajectories at several points along the relative extension of the peptides from initial (folded) to final (fully unfolded) structures. The a2N and Ala₁₄ peptides initially have three turns and approximately the same number of residues equal to 17 and 14, respectively. The EK (k = 5) and Ala₃₀ peptides initially have eight turns and approximately the same number of residues equal to 32 and 30, respectively. To see this figure in color, go online.

For the hydrogen bonding profiles (Figs. 4 and 5), all curves are the weighted averages of 100 trajectories per stage (tps) calculated by Eqs. 3 and 4. The hydrogen bond observables are shown along the end-to-end distance in Fig. 4 (in correspondence to the PMFs of Fig. 1) for clarity. The top panel displays the number of intrapeptide hydrogen bonds along the stretching path. Because some peptide-water hydrogen bonds are already formed before the unfolding process starts, the bottom panel is shown as the number of peptide-water hydrogen bonds that are newly formed under the course of unfolding. It is clear that the addition of the helical turn increases the initial number of both intrapeptide and peptide-water hydrogen bonds. As the peptide uncoils, the intrapeptide hydrogen bonds start to be broken, and they are replaced with peptide-water hydrogen bonds. During the unfolding event, each peptide exhibits a similar trend in both the increase of the number of peptide-water hydrogen bonds and the decrease of the number of intrapeptide hydrogen bonds. There are some differences in the number of peptide-water hydrogen bonds between EK peptides with k = 6 (at 100 Å) and 8 (at 120 Å) and the corresponding polyalanine peptides with similar lengths. Some minor discrepancies are caused by the discontinuities that can arise from the connection criteria in ASMD between stages. The selection of only one representative configuration at the end of each stage can lead to instantaneous and abrupt changes in the average number of hydrogen bonds at the transition between stages, but those abrupt changes relax quickly thereafter. The number of hydrogen bonds in the EK peptides also shows additional fluctuations beyond that, but those fluctuations are small compared to the overall magnitudes of the number of hydrogen bonds. The rate of the replacement of peptide-water hydrogen bonds—vis-à-vis the slopes in the curves in the bottom panel of Figs. 4 and 5—decreases with the length of peptides. Consequently, the replacement may relate to the kinetics of peptide unfolding and their association with the surrounding water molecules. A key observation is that the rates—along with their decreasing behavior—between the polyalanine peptides and soluble peptides match as their lengths increase. It is also notable that the soluble peptides reach a higher total number of intrapeptide hydrogen bonds than the corresponding polyalanine peptides with similar lengths. The extra intrapeptide hydrogen bonds are due to those formed between the hydrophilic side chains and the main-chain backbones.

In Figs. 6 and 7, three types of intrapeptide hydrogen bonds formed within the main-chain are classified (3₁₀-helix (top), α-helix (middle), and π-helix (bottom)). Most intrabackbone hydrogen bonds are formed as i → i + 4 bonds (α-helix), and they are lost at the same rate throughout both polyalanine and soluble peptides. The slope is determined as −0.63 H bond/Å. Combined with the slope from the PMF profile, the energy for losing each helical structure is ∼1.08 kcal/mol. According to the free energy surface from the work of Margulis and Berne (78), the transition from the folded to unfolded state for Ala₅ requires ∼1–2 kcal/mol, in agreement with our findings. Moreover, at the pulling speed of 1 Å/ns, the rate of losing the intrapeptide α-helical hydrogen bond was determined to be 0.63 per ns. Therefore, the rate of losing a single helical turn was roughly 6 × 10⁸ s⁻¹, which is in close agreement with previous reports (28,79,80). There is almost no formation of i → i + 5 (π-helix) bonds. The curves for the i → i + 3 bonds (3₁₀-helix) reach a maximal number of one to two contacts during most of the unfolding. Furthermore, at the beginning of unfolding, the number of 3₁₀-helical contacts increases by ∼1 contact. Thereafter, 3₁₀-helical contacts continue to be broken and reformed while maintaining a roughly steady number of only one such contact until other contacts are broken when the protein reaches a random coil structure. That is to say, 3₁₀-helical contacts are involved in the intermediates of the unfolding process, as suggested by other studies (81, 82, 83). As we have described thus far, the peptides begin in α-helical structure, and end in random coils. In between, the peptides also adopt increasing pPII helical structures, which polyalanines are well known to adopt. Notably, the pPII helix structures are not released immediately upon partial unfolding, as indicated in Figs. S2 and S3. Ramachandran plots recording the angles traversed along the unfolding path of each of the peptides reported here are available in Figs. S4 and S5. The most frequently visited angles—corresponding to particular helical structures—are in agreement with the most energetically favorable structures reported in the Ramachandran plots of MacKerell and co-workers (32). Even though all of these simulated peptides have various lengths and sequences, they all share the same corresponding trend during the course of unfolding. In other words, the helix-coil transition for a large number of alanine-rich proteins does not appear to depend on the specific repeat units nor the length of peptides. Based on the behavior exhibited in 3₁₀-helix contacts and α-helix contacts, the proposed mechanism of the helix-coil transition arises from the accumulation of steps in which the contacts from α-helical turns are successively—viz. cooperatively—lost from a single remaining helical subdomain and turn into pPII helix or fully random coils.

Figure 6.

Various alanine-rich α-helices and the corresponding intrapeptide 3₁₀-helical (top), α-helical (middle), and π-helical (bottom) bonding profiles of 100 trajectories at 1 Å/ns. Most of the hydrogen bonds are formed as i → i + 4, and the rate of losing α-hydrogen bonds is about the same, which is determined to be −0.63 H bond/Å. To see this figure in color, go online.

Figure 7.

Various alanine-rich α-helices and the corresponding intrapeptide 3₁₀-helical (top), α-helical (middle), and π-helical (bottom) bonding profiles of 100 trajectories at 1 Å/ns. The gray color corresponds to the results of polyalanine peptides, which have been shown in Fig. 6. Most of the hydrogen bonds are still formed as i → i + 4, and the rate of losing α-hydrogen bonds is also about the same. To see this figure in color, go online.

Conclusion

The main result of this work is the apparent additivity in the unfolding free energy of alanine-rich domains with the number of residues. In particular, we found that the energetics of unfolding polyalanine peptides in an explicit water solvent is additive across a series of such peptides with varying length. In each case, the addition of a helical turn increases the energetic contribution to the PMF, but it does not break the near-linear behavior between free energy and stretching distance. The linear relationship can be summarized by an estimate for the average force per distance required to stretch polyalanines. The additivity in the energetics and the value of this factor was also found in alanine-rich peptides—viz. the EK polypeptide—and even in a peptide, a2N, that contains only one alanine residue. Indeed, the shape of the PMF was similar for all of the polypeptides considered here.

The ASMD method applied in this work improves the overall efficiency of the calculations compared to the standard SMD simulations. For unfolding Ala₁₀ peptide in vacuum, SMD needs 10,000 trajectories with 10 Å/ns pulling speed to obtain converged results (16). However, we had earlier shown that we can achieve similar convergence using ASMD with 100 tps at 10 Å/ns speed for Ala₁₀. Here, we found that a slower pulling speed of 1 Å/ns is required for ASMD to obtain convergence of larger peptides with up to 50 residues. Such a reduction in speed in concert with a large number of tps would make its determination by SMD significantly more expensive and out of reach for most, if not all, present-day computers. Thus, the ASMD method was essential for these calculations and can be a practical tool for studies of larger peptides.

The hydrogen bond profiles along all of these stretching simulations were also observed and led to the finding that the mechanisms of unfolding displayed correspondence between the various alanine-rich α-helices with increasing chain lengths in concert with the additivity in the free energy. That is, the hydrogen bonding profiles exhibited corresponding slopes across the polyalanines, the EK polypeptides, and the a2N peptide. We found that the hydrogen bonding of each polypeptide is mainly composed of α-helical contacts, which are broken at a nearly constant rate in a constant velocity pull. Thus, the corresponding H-bond profiles suggest that the mechanism of the single-molecule pulling is the same for each of the α-helices that were examined in our simulation.

Based on our findings, the helix-to-coil transition of alanine-rich peptides appears to rely primarily on the breaking of the backbone hydrogen bonds rather than from contributions of any side-chain interactions or chain length. During the unfolding, as one α-helical contact is lost with the rest of the α-helical contacts intact, it turns into a 3₁₀-helical contact and then to a pPII helix or a coil through to the end. We have not investigated the energy of hydrogen bonds directly here. It has been reported that the energies of backbone hydrogen bonds within membrane proteins are not sensitive to the local concentration of water changes (84), and other studies also demonstrated that the nature of the solvent could affect the strength of the intramolecular interactions (72,85). Furthermore, the polarity of the residues within the peptide sequence would affect the interactions between the main-chain backbone and water molecules, which, in turn, would influence the tendency of helix formation (82,86). Thus, the direct impacts of the types of solvents and their local concentrations around the peptide backbones on the hydration of peptides with various lengths, as well as on the helix-coil transition, have been seen to be significant, but they remain to be fully resolved.

Author contributions

R.H. and S.Q. designed research, developed methods, analyzed results, and edited the manuscript. Y.Z. and H.R.B. performed research, developed methods, analyzed data, and wrote the manuscript. C.L. and R.B. performed research.

Editor: Jianhan Chen.