Divisive normalization does influence decisions with multiple alternatives

Divisive normalization (DN), an algorithm prominent in sensory processing and viewed as a canonical neural computation¹, has been recently proposed to play a similarly important role in decision making, capturing aspects of both neural value coding and choice behaviour^2–13. In a previous study, DN was proposed to explain context-dependent Independence from Irrelevant Alternatives (IIA) violations, where the relative preference between two given alternatives depends on the value of a third (distracter) alternative¹⁴; however, Gluth et al.¹⁵ conclude in a replication study that there is no effect of distracter value on choice behaviour in their dataset, instead finding an effect on reaction times. Here, we reanalyze the replication dataset, graciously made available by the authors, using econometric techniques specifically designed to test for the presence of divisive normalization in multi-alternative choice datasets; while we observe some differences between their data and the dataset originally reported by Louie et al.¹⁴, overall we find compelling evidence for a DN effect in choice in their dataset. This discrepancy arises primarily from unnecessarily restrictive assumptions used in prior analyses^14,15, emphasizing the importance of deriving the analysis directly from the choice theory itself.

Testing for normalization in choice data

In sensory processing, DN is a prevalent computation observed in multiple brain regions, sensory modalities, cognitive processes, and species from invertebrates to humans¹. Recent studies suggest that DN also plays a crucial role in the neural representation of subjective value, and consequently, choice behaviour. At the neural level, DN captures context-dependent value coding^8,12, characterizes reward-related neural dynamics⁹, and falls within the class of provably optimal methods for encoding value under neural noise¹⁰. At the behavioural level, DN predicts both within-choice and across-choice context effects observed in nematodes⁴, monkeys^13,14, and humans^2,5–7,14. An early example of DN-predicted choice behaviour is a negative distracter effect in trinary choice, in which distracter value diminishes relative choice accuracy¹⁴. However, variable and even opposite distracter effects have also been observed^2,3, emphasizing the importance of replication studies and robust tests for DN in behaviour.

The Gluth et al.¹⁵ replication employed a three-alternative choice experiment that was analyzed with a binary Logit regression on the average valuations of each alternative V₁, V₂, and V₃ in the choice set. This model was estimated both at the subject level (with random effects) and via a hierarchical analysis that allows each subject’s behaviour to arise from a distribution estimated at the level of the pooled sample. While a similar analysis approach was used in Louie et al.¹⁴, we have more recently noted that this method of analysis faces a number of challenges¹¹.

1. A logistic regression is derived from a model of binary choice. The reported experiment offers a choice between three alternatives. While including the third alternative is particularly important when choices of the lowest-valued alternative are frequent, it still improves model estimation even if the third alternative is never chosen. In the analyses reported by Louie et al.¹⁴ and Gluth et al.¹⁵, trials on which subjects chose the lowest valued option were simply dropped from the analysis and the binary Logit model was imposed on the remaining datapoints, a strategy we no longer employ.

2. DN, by design, specifies a non-linear relationship between inputs and outputs. A Logit regression imposes a linear relationship between the log-odds and the regressors (V₁, V₂, and V₃). Given that normalization necessarily predicts a non-linear effect on the log-odds, the Logit regression is thus a severe mis-specification of the theory.

3. In order to test the normalization model using stochastic choice data, an assumption on the distribution of errors must be made. Louie et al.¹⁴ described the predictions of DN under an independent normally-distributed error term. Recently, we have employed a more sophisticated error model that has broadened our understanding of DN and the IIA violations it induces. For example, Webb et al.¹¹ examined the predictions of DN when the errors follow the Gumbel distribution (a standard noise assumption in discrete choice analysis) as well as the more flexible multivariate normal distribution. Ensuring the analysis is robust to assumptions on the error term is critical because any analysis of normalization in choice data is a joint test of normalization and the assumed error distribution¹¹.

A reexamination of the Gluth et al data

To relax Gluth et al.’s assumptions and to take a broader look at normalization effects in choice, we applied a simplified version of the econometric model described in Webb et al.¹¹ to the data from the replication experiment. This choice model uses the same random utility form that underlies standard Logit and Probit regression, but takes as arguments the normalized rather than unnormalized values.

$$U_i=\frac{V_i}{\sigma +\omega {\sum }_n{V}_n}+{\epsilon }_i,$$ (1)

Importantly, this specification allows a fit parameter, $\omega \in [-\infty ,\infty ]$, to govern the degree of normalization in utility. Choice is determined by which of these utilities is largest, with the probability of choosing alternative i given by

$$P_i\left(V\right)=\int \mathbb{1}\left[\frac{V_i-V_j}{\sigma +\omega {\sum }_n{V}_n}>{\epsilon }_j-{\epsilon }_i,\mathrm{ }\forall j\ne i\right]f\left(\epsilon \right)d\epsilon$$ (2)

where f(ε) is the joint probability density of the errors and must be assumed.

If fits of the model indicate that $\omega =0$ and f(ε) is Gumbel, then this indicates that there is no normalization and the model reduces to the standard multinomial Logit in which IIA must hold. Therefore the model allows for a nested hypothesis test (via log-likelihoods) for the presence of normalization, and by extension, whether IIA is violated. We emphasize that - if normalization is not present in a dataset - then ω would be zero and all of the variance in the choice data should be captured by the parameter $\mathcal{o}$. On the other hand, a non-zero ω would support a contextual choice effect captured by normalization: a positive ω replicates the divisive normalization result of Louie et al.¹⁴ whereby larger distracter values (V₃) decrease relative choice performance (P₁/P₂); a negative ω, while rarely employed in sensory normalization models and harder to interpret, predicts – in at least some scenarios - a contrasting facilitatory effect of distracter value that has also been previously reported^2,3.

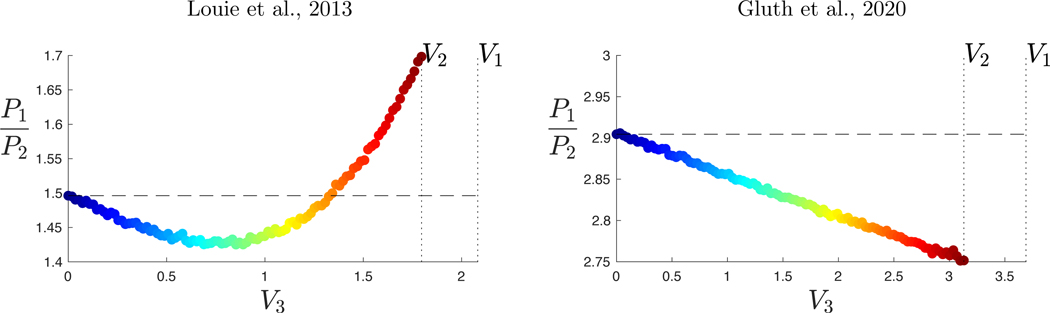
We estimated two versions of this model. The first uses the dataset pooled over all subjects and considers three different distributions of the error term: the Gumbel, the independent standard normal (N), and the multivariate normal (MVN). Across all of them, we find a highly significant effect of normalization (Table 1). The best-performing model uses the Gumbel distribution, where we find a departure from IIA with ω significantly larger than zero $\left(p=.0041, {\chi }^2\left(1\right)\right)$; note that in this analysis, ω was not constrained to be positive. Normalization accounts for 14% of the variance in choice behaviour (calculated at the average of V₁, V₂, and V₃). Figure 1 shows the estimated probability ratio P₁/P₂ as V₃ is varied for the best-fitting model from the two datasets in question: DN with MVN errors for the Louie et al. dataset (i.e. as previously described¹¹), and DN with Gumbel errors for the Gluth et al. dataset (i.e. the estimates reported in Table 1). Two findings are evident: (1) clearly, including normalization allows the model to capture an initial decrease in P₁/P₂ as V₃ increases in both datasets, and (2) the pattern of IIA violations differs between the datasets, with a notable u-shaped non-monotonicity in the Louie et al. dataset. Note that the latter non-monotonicity is consistent with both computational simulations of a normalization model and observed choice patterns in the original dataset¹⁴.

Table 1:

Maximum likelihood estimates for the Gluth et al. replication dataset, pooled over subjects. Standard errors are in parentheses

	No Normalization			Divisive Normalization
f(ε)	Gumbel	N	MVN	Gumbel	N	MVN
σ	1.072	1.064	.994	.927	.794	.783
	(.012)	(.011)	(.016)	(.051)	(.046)	(.044)
ω	0	0	0	.018	.033	.027
				(.006)	(.006)	(.006)
C1			.547			.556
			(.038)			(.039)
C2			.957			.942
			(.019)			(.018)
LL	−16727	−16917	−16898	−16723	−16900	−16886
p-value on X2(1) test for ω > 0				.0041	.0000	.0000
AIC	33456	33836	33802	33450	33804	33780

Figure 1. Best-performing model fits of the P₁/P₂ ratio as V₃ is varied.

Left, the original Louie et al. dataset; right, the Gluth et al. replication. IIA is represented by the dashed line. These fits are generated for the average V₁ and V₂ observed in each sample. In the Louie et al. dataset, Divisive Normalization with the MVN error captures a u-shaped non-monotonic pattern in the P₁/P₂ ratio. In the Gluth et al. dataset, Divisive Normalization with the Gumbel error captures a decreasing pattern. Overall, both datasets show evidence for normalization but differ in the specific pattern of context-dependence, suggesting subtle differences in the choice data.

Our second analysis estimates a hierarchical version of the model that allows both $\mathcal{o}$ and ω to follow a distribution over subjects (i.e. a random effect for both parameters). In this analysis, we assumed Gumbel errors and allowed the ω parameter to follow a Normal distribution over subjects; the $\mathcal{o}$ parameter followed a Gamma distribution. The mean of the distribution for ω = 0.007 was significantly positive ($p<.0001,{\chi }^2\left(2\right)$), and allowing the density for ω to depart from zero captures 36% of the variance in choice behaviour (calculated at the average of V₁, V₂, and V₃ and the mean of the densities for ω and $\mathcal{o}$).

Conclusion

In our re-examination of the Gluth et al. data, all of our analyses display significant evidence of normalization, regardless of assumptions. We believe this discrepancy arises from two factors. First, we employed a more rigorous regression approach that unambiguously indicates that DN is observed in these data. Second, we examined the complete pattern of choice behaviour implied by the model fits and identified a differences between the original and replication datasets. This difference in observed choice behaviour may reflect a general difference between the datasets, consistent with the reported difference in reaction time effects. Furthermore, this difference aligns with the reported variability in the nature of trinary IIA violations³ and may reflect underlying complexity in the generating mechanisms. The shape of IIA violations is a critical and deeply interesting question that we applaud Gluth and colleagues for raising. Like these authors, we are devoting significant energy to understanding the experimental conditions under which IIA violations occur and the proper methodology for analyzing them. However, we believe this new dataset does not materially challenge the evidence for DN: In all of the specifications we estimated, we observed a significant role for normalization in accounting for the variance in choice behaviour. This leads us to the conclusion that in this new dataset, as in others, divisive normalization influences decisions with multiple alternatives.