Point-node gap structure of the spin-triplet superconductor UTe₂

Abstract

Low-temperature electrical and thermal transport, magnetic penetration depth, and heat capacity measurements were performed on single crystals of the actinide superconductor UTe₂ to determine the structure of the superconducting energy gap. Heat transport measurements performed with currents directed along both crystallographic a and b axes reveal a vanishingly small residual fermionic component of the thermal conductivity. The magnetic field dependence of the residual term follows a rapid, quasilinear increase consistent with the presence of nodal quasiparticles, rising toward the a-axis upper critical field where the Wiedemann-Franz law is recovered. Together with a quadratic temperature dependence of the magnetic penetration depth up to T/T_c = 0.3, these measurements provide evidence for an unconventional spin-triplet superconducting order parameter with point nodes. Millikelvin specific heat measurements performed on the same crystals used for thermal transport reveal an upturn below 300 mK that is well described by a divergent quantum-critical contribution to the density of states (DOS). Modeling this contribution with a T^−1/3 power law allows restoration of the full entropy balance in the superconducting state and a resultant cubic power law for the electronic DOS below T_c, consistent with the point-node gap structure determined by thermal conductivity and penetration depth measurements.

The uranium-based superconductors URhGe, UCoGe, and UGe₂ have generated much interest due to the unusual coexistence of a ferromagnetic ground state with superconductivity present in all three systems [1]. Recently, the discovery of superconductivity in UTe₂ [2] has stimulated a flurry of experimental studies on this new actinide superconductor [2–7]. With a ground state close to ferromagnetic order as evidenced by quantum critical scaling of the magnetization [2] and magnetic fluctuations down to millikelvin temperatures [7], the UTe₂ system adds the long-sought paramagnetic end member to the family of uranium-based ferromagnetic superconductors.

The superconducting state of UTe₂ is quite exotic. Strong evidence for spin-triplet pairing is given by a lack of change in the NMR Knight shift upon cooling into the superconducting state, and an upper critical field H_c2 that exceeds the paramagnetic limit for all field directions (i.e., by more than an order of magnitude for H ‖ b) [2]. The NMR 1/T₁ relaxation time and the heat capacity were also observed to exhibit power-law behavior consistent with point nodes in the gap structure [2]. Furthermore, a reentrant superconducting phase was shown to develop in extremely high magnetic fields [4]. Intriguingly, heat capacity measurements in the superconducting state have consistently exhibited an apparent residual fermionic (T-linear) term that appears to equal ∼50% of the normal-state electronic density of states (DOS) [2,3], which has been interpreted as a signature of an unpaired fluid. However, this picture is problematic since a nonunitary pairing state is not formally possible given the orthorhombic crystal symmetry. More important, the entropy balance between normal and superconducting states that is required for a second-order transition (i.e., ${\int }_0^{T_c}\frac{C_{{\text{el}}_s}}{T}dT\ne {\int }_0^{T_c}{\gamma }_{n}dT$, where $C_{{\text{el}}_s}$ is the electronic heat capacity in the superconducting state and γ_n is the normal-state electronic heat capacity) is not obeyed [2,3].

Here, we use thermal conductivity and penetration depth measurements to probe the superconducting gap structure directly by observing the properties of low-energy quasiparticle excitations. Thermal conductivity κ has been established as a powerful directional tool for probing the gap structure of unconventional superconductors [8], and magnetic penetration depth is a well-established tool for finding detailed information about the pairing state [9]. In our thermal transport measurements, we observe a residual quasiparticle contribution which is vanishingly small in the zero-field limit, but is restored by magnetic field much more quickly than would be expected for either clean- or dirty-limit fully gapped superconductivity. Together with a quadratic temperature dependence of the measured magnetic penetration depth, our observations are consistent with a point-node superconducting gap structure in UTe₂. We also present measurements of the specific heat of the same samples used for thermal transport in order to probe the reported residual DOS in the superconducting state. We observe a low-temperature upturn in the T-linear term that is not consistent with a nuclear Schottky contribution, but rather a divergent term consistent with the presence of quantum critical degrees of freedom. Upon subtraction of the divergent term, we recover a complete entropy balance between superconducting and normal states in the electronic specific heat and the previously observed T³ dependence [2,3].

Single crystals of UTe₂ were synthesized using a vapor transport method as described in Ref. [2], using depleted uranium (>99.9% ²³⁸U) and natural abundance elemental ^127.60Te (99.9999% purity). Crystals were shaped into rectangular plates with sample dimensions 1.5 × 0.5 × 0.1 mm³ for the current j ‖ a sample (S1) and 1.8 × 1.0 × 0.3 mm³ for the j ‖ b sample (S2), used for both thermal conductivity and specific heat measurements. Thermal conductivity κ was measured in a dilution refrigerator using a modular one-heater, two-thermometer probe [10], with contacts made by soldering gold wire leads with an In-Sn alloy to evaporated gold pads, resulting in ∼mΩ contact resistances. Electrical resistivity ρ was measured in situ using the same wires and contacts, with samples in the exact position used for thermal transport measurements. Both samples exhibit a residual resistance ratio ρ(300 K)/ρ(0 K) of 22. T_c values of 1.7 K (1.6 K) and H_c2values of 6.2 T (6.5 T) were obtained for S1 (S2) from the in situ resistivity measurements. The resistive T_c values are consistent with T_c measured via heat capacity (Fig. 4). As discussed below, the observation of the Wiedemann-Franz (WF) law in the field-induced normal state confirms the quality of measurements and rules out electron-phonon decoupling issues [11]. Measurements of the low-temperature magnetic penetration depth (λ) were performed using a dielectric resonator technique [12] on two other crystals, labeled S3 and S4, and heat capacity C of samples S1 and S2 was measured using the relaxation time method.

FIG. 4.

Analysis of the low-temperature heat capacity of UTe₂ single-crystal samples S1 and S2 (same crystals used for thermal transport measurements). (a) The total measured heat capacity (open circles) of sample S1 decomposed into a weak power-law divergence (dashed line), phonon term (dashed-dotted line), and electronic heat capacity (solid circles) obtained by subtracting the diverging and phonon terms (see text for details). (b) The obtained electronic heat capacities of samples S1 and S2 plotted vs T². Solid lines are fits to the T² dependence in the superconducting state with T_c determined by balancing entropy.

The superconducting state in UTe₂ has been proposed [2–4] to be a spin triplet based on several experimental observations. Theoretically, because UTe₂ has an orthorhombic lattice that is symmorphic as confirmed at low temperatures by neutron scattering [13], Blount’s theorem must hold [14] so that odd-parity (i.e., spin-triplet) states will either have point nodes or be fully gapped. Conversely, even-parity (spin-singlet) states will have either line nodes or be fully gapped. More formally, assuming strong spin-orbit coupling and invoking the D_2H point group yields the possible gap symmetries shown in Table I. The possible symmetry-imposed nodal structures fall into three types: fully gapped (A_1g, A_1u), axial point nodes (B_1u, B_2u, B_3u with pairs of point nodes along a single high-symmetry axis), or polar line nodes (B_1g, B_2g, B_3g with line nodes perpendicular to a single high-symmetry axis).

TABLE 1.

Candidate superconducting pairing states for the D_2h point group symmetry.

Representation	Representative function	Nodes
A1g	$\text{const}+c_{x}k{x}^2+c_y{k}_y^2+c_z{k}_z^2$	None
B1g	ckzky	Lines
B2g	ckzkx	Lines
B3g	ckxky	Lines
A1u	$c_x{k}_x\widehat{\mathbf{x}}+c_y{k}_y\widehat{\mathbf{y}}+c_z{k}_z\widehat{\mathbf{z}}$	None
B1u	$c_1{k}_y\widehat{\mathbf{z}}+c_2{k}_x\widehat{\mathbf{y}}$	Points
B2u	$c_1{k}_x\widehat{\mathbf{z}}+c_2{k}_z\widehat{\mathbf{x}}$	Points
B3u	$c_1{k}_x\widehat{\mathbf{y}}+c_2{k}_y\widehat{\mathbf{x}}$	Points

Thermal conductivity is a directional probe that can be used to determine the momentum space position of nodes by studying low-energy quasiparticle excitations—as a function of field angle, as shown in the cuprate superconductor YBa₂Cu₃O_7−x (YBCO) [15,16] and heavy fermion compound CeCoIn₅ [17], or as a function of the directional current as shown in UPt₃ [18,19] and CeIrIn₅ [20]. Furthermore, the magnetic field evolution of the electronic thermal conductivity in the T = 0 limit [κ₀(H)] is a reliable probe of both nodal gaps (e.g., UPt₃[18] and KFe₂As₂ [21]) and multiband or anisotropic gap superconductors [22].

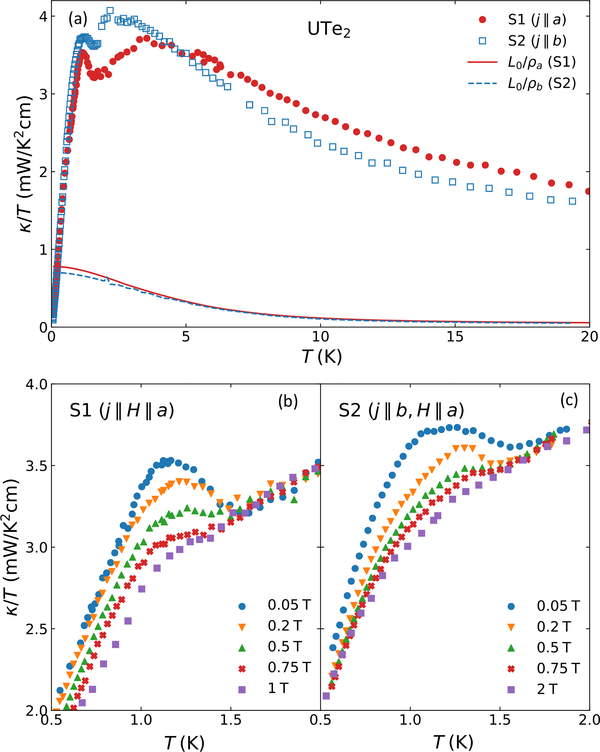
Figure 1(a) presents the total thermal conductivity of UTe₂ samples S1 and S2 measured up to 20 K and compared to the estimated (elastic) charge contribution determined using the in situ measured resistivity ρ for each sample and the WF law [i.e., L₀/ρ, where L₀ = π²/3(k_B/e)²], showing that the majority of the thermal conduction in this range is not electronic. This makes distinguishing the quasiparticle contribution to thermal conductivity quite difficult, even within the superconducting regime. For both samples, there is an abrupt increase in κ/T at T_c as highlighted in Figs. 1(b) and 1(c), similar to that observed in CeCoIn₅ [23,24] and YBCO [25,26], where it is attributed to a suppression of the scattering of heat carriers (electrons and phonons, respectively) by the opening of the superconducting gap. In the case of UTe₂, the enhanced conductivity below T_c is likely due to a combination of electron and phonon carriers being affected by the gap opening, and, more importantly, is an indication of the high crystalline quality of the samples being measured. The rapid suppression of the enhancement in field is likely due to vortex scattering.

FIG. 1.

Thermal conductivity of UTe₂ samples S1 and S2. (a) Measured thermal conductivity in comparison to the estimated (elastic) charge contribution L₀/ρ (solid and dashed lines) determined using the Wiedemann-Franz law and in situ measured electrical resistivities of both samples. L₀/ρ(T) is extrapolated below T_c here assuming the resistivity follows the Fermi-liquid temperature dependence ρ = ρ₀ + AT². (b) and (c) present signatures of the superconducting transition in thermal conductivity measurements for (b) j ‖ a and (c) j ‖ b orientations. The observed increase in κ/T below T_c is thought to arise from a decrease in scattering due to the opening of the superconducting gap, and the suppression with increasing magnetic fields due to vortex scattering.

The nature of the superconducting gap structure can be determined by probing the value of the residual term of κ/T in the T = 0 limit, κ₀/T, and its magnetic field dependence [27]. First, we confirm that the WF law is obeyed in the T = 0 limit in the field-induced normal state at 7 T (a axis). To study the zero-field limit, we apply a small field of 50 mT to ensure soldered contacts are not superconducting and extrapolate to T = 0 by fitting the lowest-temperature data to κ/T = κ₀/T + AT^α with 1 ⩽ α ⩽ 2 and κ₀/T ⩾ 0. As shown in Figs. 2(a) and 2(b), we find that κ/T extrapolates to a vanishingly small residual value for both heat current orientations and rapidly rises with temperature. This is inconsistent with the behavior of a fully gapped superconductor [28], which would not conduct heat until at least ∼20% of T_c, and is more consistent with a gap with nodal excitations [27].

FIG. 2.

Low-temperature thermal conductivity of UTe₂ single-crystal samples (a) S1 and (b) S2, measured with heat current applied along crystallographic a and b axes, respectively, and magnetic fields applied along the a axis. The black × in (a) and (b) represent the converted normal-state charge conductivity L₀/ρ measured in situ at 7 T and calculated using the Wiedemann-Franz law. (c) Magnetic field dependence of T → 0 K extrapolated values [κ₀/T ≡ κ(T → 0)/T] taken from the data in (a) and (b). Error bars correspond to uncertainty in the extrapolation from fitting to a power law over different temperature windows. For comparison we include data for the elemental clean-limit fully gapped superconductor Nb [29] and clean-limit nodal superconductors UPt₃ [18] and KFe₂As₂ [21]. The inset shows a comparison of the detailed low field dependence of Δκ(H)/Δκ_N ≡ [κ(H) − κ(0)]/[κ(7 T) − κ(0)] measured in the field-sweep mode at 100 mK, with the T → 0 extrapolated values from the main panel. (d) Lorenz ratio L/L₀ calculated using the ratio of measured quantities κρ/T at 7 T (a) from and (b) to the Lorenz number L₀. Linear extrapolations to T = 0 show agreement with L₀ to within 8% and 5% for j ‖ a and j ‖ b, respectively. The inset shows the zero-field anisotropy ratio $\overline{\kappa }={\kappa }_b/{\kappa }_a$ normalized to the anisotropy ratio in the normal state ${\overline{\kappa }}_N=\overline{\kappa }(7T)$.

To rule out the possibility of a strongly anisotropic but fully gapped scenario, we study the field dependence of κ₀/T. For a full gap, quasiparticles remain localized to vortex cores and only contribute to the thermal conductivity for fields exponentially close to H_c2, such as shown for the classic experiment on elemental Nb shown in Fig. 2(c) [29]. For a fully gapped superconductor in the dirty limit, κ₀/T increases more quickly in field but still remains exponentially small in the low-field limit [30]. In multiband superconductors with a disparity in gap values, a rapid rise can occur due to a very small field range H* of activated behavior of a small gap Δ₁ (i.e., where ${\Delta }_1/{\Delta }_2~\sqrt{H\ast /H_{c2}}$ [22,31]). For a nodal gap structure, low-energy quasiparticle excitations are not bound and therefore follow a much stronger field dependence that depends on the specific gap structure (e.g., for line nodes, ${\kappa }_0/T\propto \sqrt{H}$ due to the Volovik effect).

Using the same extrapolation method as above, we plot in Fig. 2(c) the field dependence of κ_0a/T and κ_0b/T, which both exhibit a rapid quasilinear rise with magnetic field, further confirmed by detailed 100-mK field-sweep measurements shown in the inset of Fig. 2(c). This behavior rules out a fully gapped scenario, including clean-limit and dirty-limit behaviors, and places a strong constraint on the presence of a very small gap (e.g., ${\Delta }_1\ll {\Delta }_2$). Furthermore, we note that the temperature dependence of κ/T in the presence of such a small gap should show a very rapid increase at low temperatures (or even an apparent residual term), making the extreme multiband scenario unlikely. Rather, the field dependence of κ₀/T in UTe₂ is more reminiscent of that of nodal gap superconductors. Similar behavior was observed in line-node superconductors CeIrIn₅ [8], Sr₂RuO₄ [32], and KFe₂As₂ [21], which are all accompanied by finite residual values in zero field. A line-node (e.g., d-wave) gap is expected to invoke a universal zero-field residual term given by ${\kappa }_0/T=\frac{1}{3}{\gamma }_N{v}_F^2\frac{a\hslash }{2\mu {\Delta }_0}$. Using a conservative upper limit of κ₀/T = 0.1 mW/cm/K² from our experiment together with values 2Δ₀ = 3.5k_BT_c, γ_N = 100 mJ/mol/K², and μ = 2 for a standard d-wave gap slope at the nodes (a is order unity) yields υ_F = 6000 m/s, a very small velocity similar to that of the extremely heavy p-wave superconductor UPt₃ [33]. Interestingly, UPt₃ exhibits both vanishingly small κ₀ in zero field [33] and a linear increase with magnetic field [18], also shown for comparison in Fig. 2(c). Together with this striking similarity, the vanishingly small residual T-linear term and rapid quasilinear rise in magnetic field observed for UTe₂ are most consistent with a point-node gap scenario.

Further information can be garnered from the anisotropy ratio $\overline{\kappa }\equiv {\kappa }_b/{\kappa }_a$, shown in the inset of Fig. 2(d). Normalizing out the normal-state anisotropy by using the ratio $\overline{\kappa }(0.05\text{T})/\overline{\kappa }(7\text{T})$, we find the superconducting state anisotropy approaches ∼0.8 in the low-T limit. This not as large as the value (∼0.5) observed in UPt₃ [19], a more compelling indicator of point-node direction. Rather, the near-unity anisotropy may arise due to nodal excitations directed in both basal plane directions (e.g., accidental), but will require detailed calculations based on candidate gap structures to draw firm conclusions.

Measurements of the low-temperature magnetic penetration depth were performed using a cylindrical rutile dielectric resonator [34], which facilitates a microwave transmission resonance involving the ab-plane electrodynamic response at ≈11 GHz. The temperature dependence of the resonant frequency Δf₀(T ) and the quality factor Q(T) are measured and converted into surface impedance Z_s through a geometrical factor estimated from the geometry of the resonator and the nature of the mode [35]. In the local electrodynamic limit, where the mean free path is smaller than the screening length, Z_s can be converted to the complex conductivity $\tilde{\sigma }={\sigma }_1-i{\sigma }_2$ of the samples through the local relation $Z_s=\sqrt{i{\mu }_0\omega /\tilde{\sigma }}$ [36]. The effective penetration depth is obtained from the imaginary part of the conductivity ${\sigma }_2=1/{\mu }_0\omega {\lambda }_{\text{eff}}^2(T)$, which yields λ_eff(0) = 1126 nm for S3 and 947 nm for S4, both similar to the estimation [λ(0) ≳ 1000 nm] from a recent study [7].

As shown in Fig. 3, the change in screening length, Δλ_eff(T), exhibits a rapid rise with temperature indicative of low-lying excitations [9]. Fitting Δλ_eff(T) to a power-law form aTⁿ + b below 0.3T_c yields a quadratic temperature exponent (n = 2.00 ± 0.01 for S3 and n = 1.92 ± 0.01 for S4), consistent with either a dirty-limit line node [37] or axial point-node scenario [38,39]. Considering the observed vanishingly small κ₀/T values and their magnetic field dependence, we conclude that the quadratic dependence of Δλ_eff(T) is more consistent with axial point nodes aligned in the direction of the vector potential. In our setup, the applied microwave magnetic field generates circulating screening currents in the ab plane [12], so that the direction of the axial point nodes is assumed to lie in the ab plane.

FIG. 3.

Effective penetration depth of UTe₂ samples S3 (red circles) and S4 (blue squares) plotted vs normalized temperature. The solid lines are power-law fits of the form aTⁿ + b, with extracted exponents n = 2.00 for S3 and n = 1.92 for S4. The vertical bars indicate uncertainty for each data set determined by a 5% root-mean-square-error in resonant frequency and quality factor (see text). The inset presents the same data in terms of (T/T_c)² to illustrate the quadratic temperature dependence, with linear dashed lines as guides.

Concerning previous observations of an apparent residual DOS in specific heat [2,3], our observations of a vanishingly small fermionic component of thermal conductivity in the zero-field, zero-temperature limit are inconsistent with a scenario that entails the presence of a sizable residual nonpaired fluid. To confirm this, Fig. 4 presents the measured specific heat of samples S1 and S2, which are the same crystals used for thermal transport. This measurement reproduces the large residual value in C/T observed in previous experiments [2,3], but uncovers a sharp increase in C/T below about 300 mK. Although it appears similar to a nuclear Schottky anomaly, which arises from the splitting of nuclear spin states, such a contribution (C_N) should be negligible since the only isotope with a nuclear spin is ¹²⁵Te, which is only 7% abundant in natural Te and does not have a nuclear quadrupole moment. Moreover, the observed upturn is much broader than the expected form C_N/T ∝ T⁻³. Instead, it is well fit by a weak power-law (C/T ∝ T^−∼1/3) divergence as described below.

Motivated by this, we fit the total heat capacity over the entire temperature range (i.e., 50 mK to 5 K) using

$$\frac{C}{T}=A_{\text{ph}}{T}^2+A_{\text{div}}{T}^{-\alpha }+\{\begin{array}{ll}{A}_{\text{sc}}{T}^2,\hfill & T<T_c,\hfill \\ {\gamma }_n,\hfill & T>T_c.\hfill \end{array}$$ (1)

The result is shown in Fig. 4(a), where the solid line represents the total fit, A_phT² is the phonon heat capacity (dashed-dotted line), A_divT^−α is the power-law divergence (dashed line) where α = 0.35 (0.33) for S1 (S2), and the last term is the electronic heat capacity which varies as T² in the superconducting regime (T < T_c) and is constant (γ_n) above T_c.

The extracted electronic component C_el/T = C/T − A_phT² − A_divT^−α exhibits a nearly perfect entropy balance between normal and superconducting states, which is reflected by the fit result in Fig. 4(a) where the resultant T_c (set by the entropy balance) matches the data very well. Figure 4(b) shows that the specific heat for both S1 and S2 samples follows a cubic power law (i.e., C_el/T ∼ T²) through the superconducting temperature range, consistent with prior fits to raw data above 300 mK [2,3]. While the divergent residual specific heat term requires further investigation, the lack of any sizable contribution to zero-field thermal conduction means that this component arises from either a well-localized DOS, or itinerant fermionic carriers that are heavily scattered in the T → 0 limit.

In conclusion, detailed measurements of thermal conductivity, penetration depth and heat capacity in UTe₂ provide evidence for a superconducting gap structure with point nodes. The vanishingly small residual fermionic term in thermal conductivity, together with rapid increases with both temperature and magnetic field in the zero-field, zero-temperature limits, respectively, confirm the presence of low-energy quasiparticle excitations and the proposed nodal gap structure, and rule out an anistropic or multiband full gap scenario. A quadratic temperature dependence of the low-temperature penetration depth is also consistent with a nodal gap structure, with point nodes within or very near the ab plane. Together with consideration of the D_2H point group symmetry, these results provide evidence for spin-triplet Cooper pairing in UTe₂. The origin of a localized or strongly scattered divergent quantum critical component of the specific heat, which underlies the superconducting state, will require further study to elucidate.