Quantum simulation of hyperbolic space with circuit quantum electrodynamics: From graphs to geometry

Abstract

We show how quantum many-body systems on hyperbolic lattices with nearest-neighbor hopping and local interactions can be mapped onto quantum field theories in continuous negatively curved space. The underlying lattices have recently been realized experimentally with superconducting resonators and therefore allow for a table-top quantum simulation of quantum physics in curved background. Our mapping provides a computational tool to determine observables of the discrete system even for large lattices, where exact diagonalization fails. As an application and proof of principle we quantitatively reproduce the ground state energy, spectral gap, and correlation functions of the noninteracting lattice system by means of analytic formulas on the Poincaré disk, and show how conformal symmetry emerges for large lattices. This sets the stage for studying interactions and disorder on hyperbolic graphs in the future. Importantly, our analysis reveals that even relatively small discrete hyperbolic lattices emulate the continuous geometry of negatively curved space, and thus can be used to experimentally resolve fundamental open problems at the interface of interacting many-body systems, quantum field theory in curved space, and quantum gravity.

I. INTRODUCTION

Non-Euclidean and hyperbolic geometry has inspired thinkers for millennia due to its intriguing properties and perplexing beauty [1]. Besides its aesthetic appeal, the immense usefulness of hyperbolic geometry in physics due to the famous anti–de Sitter and conformal field theory (AdS-CFT) correspondence [2,3] makes field theories and quantum physics in hyperbolic space one of the central themes of current theoretical research. Furthermore, many recent developments in the context of holography and quantum information point towards a deep connection between geometry, entanglement, and renormalization [4–9]. Other exciting applications of hyperbolic geometry emerge, for instance, in the field of fault-tolerant quantum computing [10–12]. To elevate the study of quantum physics in hyperbolic space from pure theory to experimentally verifiable questions, it is crucial to create laboratory setups for exploring the underlying effects in a tunable manner.

Important progress towards the quantum simulation of curved space has been made in nonlinear optical media [13–19], ultracold quantum gases [20–27], and other platforms [28–32], which allowed, for instance, for observation of event horizons [33,34] and Hawking radiation [35,36]. In these experiments, curvature is often emulated in Euclidean geometries through nonlinear field propagation. A complementary path was followed in recent cutting-edge experiments in circuit quantum electrodynamics (QED) [37–41], where hyperbolic geometry was emulated directly through photon dynamics confined to a hyperbolic lattice made from superconducting resonators [42,43]. The setup is highly tunable and can be used to achieve photon interactions, coupling to spin degrees of freedom, or the effects of disorder [44–46]. Hyperbolic lattices have been investigated in the context of classical [47–52] and quantum spin systems [53], and complex networks [54].

In this work, we show that quantum many-body Hamiltonians relevant for circuit QED on hyperbolic lattices can be approximated by a continuum theory on the Poincaré disk. This provides a computational tool to access observables even for otherwise intractable very large lattices, and shows that the discrete setup constitutes a quantum simulation of continuous hyperbolic space. We provide a dictionary between discrete and continuous geometry. To show the strength of our mapping, we quantitatively reproduce the ground state energy, spectral gap, and correlation functions for the noninteracting theory by analytic continuum formulas. We reveal how conformal symmetry emerges on hyperbolic lattices, implying significant computational simplifications in applications.

II. HYPERBOLIC LATTICES

The photon dynamics of the circuit QED experiments of Ref. [42] can be modeled as nearest-neighbor hopping on a hyperbolic graph G; see Fig. 1. We label the graph in Schläfli notation by {p, q}, which corresponds to a tessellation of the plane by regular p-gons with coordination number q. Whereas the three Euclidean lattices (triangular lattice {3, 6}, square lattice {4, 4}, honeycomb lattice {6, 3}) satisfy (p − 2)(q − 2) = 4, one can show that a hyperbolic tessellation is obtained for (p − 2)(q − 2) > 4. In this work, we focus on the heptagonal hyperbolic lattice {p, 3} with p = 7 for concreteness, but point out how to generalize the results to p ⩾ 7. The actual circuit QED experiments realize the line graph of G [43], but their continuum approximation is analogous.

FIG. 1.

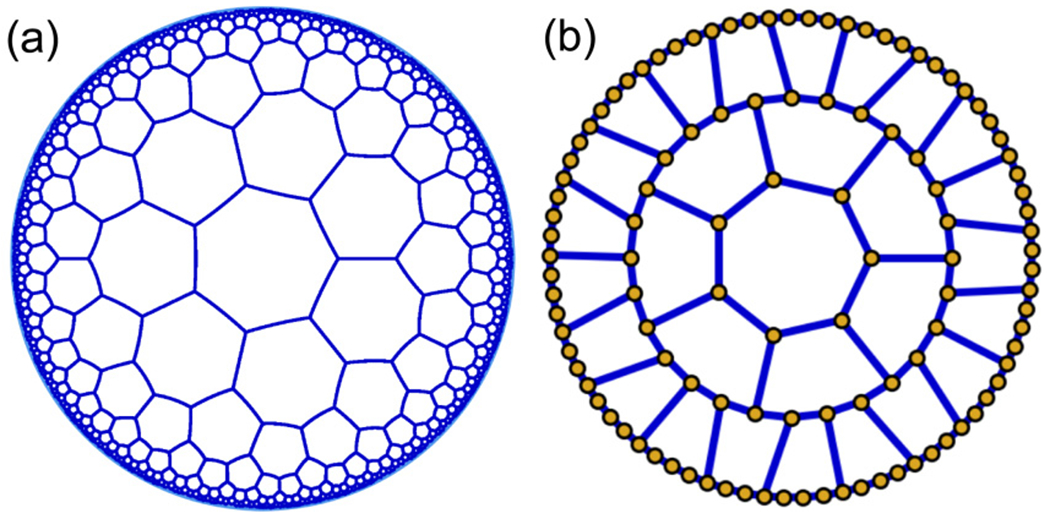
(a) We consider the regular tessellation of the hyperbolic plane with heptagons, embedded into the Poincaré disk with a hyperbolic metric. All neighboring lattice sites have equal hyperbolic distance and the unit disk boundary is infinitely far away from each point in the interior. (b) Finite graphs preserving sevenfold rotation invariance can be constructed by considering subsets that are topologically equivalent to ℓ = 1, 2, 3 … concentric rings, shown here for ℓ = 3.

We consider the nearest-neighbor hopping Hamiltonian

$${\widehat{\mathcal{H}}}_0=-t\sum _{i,j\in G}{\widehat{a}}_i^{†}{A}_i{\widehat{a}}_j,$$ (1)

with ${\widehat{a}}_i^{†}$ the photon creation operator on site i and t > 0. The entry A_ij of the adjacency matrix A is 1 if sites i and j are connected by an edge, and zero otherwise. We construct finite hyperbolic graphs that preserve sevenfold rotation invariance from ℓ = 1, 2, 3, … successive quasi-concentric rings, where ℓ = 1 corresponds to a single heptagon; see Fig. 1. The total number of sites grows exponentially as N ~ 7φ^2ℓ for large ℓ, with $\phi =\left(1+\sqrt{5}\right)/2$ the golden ratio [51,52]; see Table I. Sites in the interior of G have coordination number 3, and sites on the boundary have either 2 or 3. The average coordination number for large ℓ is $3-1/\sqrt{5}=2.553$ and there is always a significant fraction of boundary sites.

TABLE I.

The total number of sites $N=7\left[{\left(\frac{3+\sqrt{5}}{2}\right)}^{\ell }+{\left(\frac{3-\sqrt{5}}{2}\right)}^{\ell }-2\right]$ grows exponentially as a function of the number of rings ℓ. Each finite graph is mapped onto a continuous disk of radius $L=\sqrt{N/\left(N+28\right)}$. The ground state energy E₀ of the hopping Hamiltonian (1), defined as the lowest eigenvalue of the matrix H = −A, can be estimated from the lowest eigenvalue of Δ_g on the finite disk of radius L < 1, which gives $E_0^{\left(\text{cont}\right)}$. Both values agree excellently for sufficiently large ℓ; see also Fig. 3. For ℓ ⩾ 8 we have to resort to less precise sparse matrix methods to estimate E₀.

	Number of rings ℓ
	1	2	3	4	5	6	7	8	9	10
Number of graph sites N	7	35	112	315	847	2240	5887	15435	40432	105875
Effective disk radius L	0.447	0.745	0.894	0.958	0.984	0.994	0.998	0.9990	0.9997	0.9999
Ground state energy (graph) E0	−2	−2.636	−2.787	−2.847	−2.877	−2.894	−2.905	−2.91	−2.92	−2.92
Ground state energy (continuum) $E_0^{(\mathrm{cont})}$	−1.500	−2.570	−2.770	−2.842	−2.876	−2.895	−2.906	−2.914	−2.920	−2.924

For the continuum description, we embed the hyperbolic lattice into the Poincaré disk $\mathbb{D}=\left\{z\in \mathbb{C},\left|z\right|<1\right\}$ with hyperbolic metric

$$d{s}^2\text{=}\frac{d{x}^2+d{y}^2}{{\left(1-{\left|z\right|}^2\right)}^2}.$$ (2)

(We write z = x + iy = re^iϕ.) Let us briefly recall some properties of this space of constant negative curvature [1]: The hyperbolic distance between two points $z,z^{\prime }\in \mathbb{D}$ is

$$d\left(z,z^{\prime }\right)=\frac{1}{2}\text{arcosh}\left(1+\frac{2{\left|z-z^{\prime }\right|}^2}{\left(1-{\left|z\right|}^2\right)\left(1-{\left|z^{\prime }\right|}^2\right)}\right),$$ (3)

which reduces to |z − z′| for |z|, |z′| ≪ 1. The boundary of $\mathbb{D}$ is infinitely far from every point in the interior and the area of a disk of radius L < 1 is πL²/(1 − L²). The isometries (distance preserving maps) of $\mathbb{D}$ are given by conformal automorphisms

$$z\mapsto w\left(z\right)=e^{i\eta }\frac{a-z}{1-z\stackrel{\_}{a}}$$ (4)

with η ∈ [0, 2π) and $a\in \mathbb{D}$. These transformations exchange a with the origin, and so each point in $\mathbb{D}$ is equivalent. The group of mappings (4) is isomorphic to the group $\mathrm{PSL}(2,\mathbb{R})$ of Möbius transformations on the upper half-plane. The embedding assigns a coordinate ${\text{z}}_i\in \mathbb{D}$ to each site i ∈ G so that neighboring sites are separated by a hyperbolic distance d₀ = 0.283 128 [55]; see Appendix A. Importantly, the value of d₀ is determined by the lattice geometry and cannot be varied.

On the Euclidean square lattice, nearest-neighbor hopping Hamiltonians of type (1) are related to the Laplacian through a finite difference approximation, facilitating powerful techniques such as the continuum theory of solids or lattice gauge theory in high-energy physics. The natural generalization of the Laplacian to curved manifolds is the Laplace-Beltrami operator

$${\Delta }_g=\frac{1}{\sqrt{\text{det}g}}{\partial }_i\left(\sqrt{\text{det}g}{\left(g^{-1}\right)}_{ij}{\partial }_j\right),$$ (5)

where the metric tensor g_ij = (1 − r²)⁻²δ_ij is related to the line element in Eq. (2) by ds² = g_ijdx_idx_j. This operator is self-adjoint with respect to the canonical scalar product $\langle f_1,f_2\rangle =\int d{V}_g{f}_1^{*}{f}_2$, with $d{V}_g=d^{2}x\sqrt{\det g}$ the invariant volume element. In our case, we find the hyperbolic Laplacian to be

$${\Delta }_g={\left(1-{\left|z\right|}^2\right)}^2\left({\partial }_x^2+{\partial }_y^2\right).$$ (6)

This operator is invariant under conformal automorphisms [1,56,57].

III. FROM GRAPHS TO GEOMETRY

To understand why Δ_g appears here, note that every function $f:\mathbb{D}\to \mathbb{C}$ induces a function on the graph via i ↦ f(z_i). Consider then a lattice site z_i with coordination number 3 and a sufficiently smooth function f(z); see Fig. 2. We have A_ijf(z_j) = f(z_i+e1) + f(z_i+e2) + f(z_i+e3), where the right-hand side represents the sum over the neighbors of z_i and we implicitly sum over repeated indices. To manipulate this expression, apply an automorphism z ↦ w(z) from Eq. (4) with η = 0 and a = z_i. This exchanges z_i with the origin. Furthermore, the three neighbors of z_i are mapped to form an equilateral triangle with coordinates w₁ = he^iχ_i, w₂ = he^iχ_ie^i2π/3, w₃ = he^iχ_ie^i4π/3, and h = tanh(d₀) = 0.275 798. The phase χ_i depends on the coordinate z_i in a nontrivial manner; see Fig. 5 in the Appendix. Applying the inverse automorphism, we arrive at the identity

$$A_{ij}f\left(z_j\right)=f\left(\frac{z_i-w_1}{1-w_1{\stackrel{\_}{z}}_i}\right)+f\left(\frac{z_i-w_2}{1-w_2{\stackrel{\_}{z}}_i}\right)+f\left(\frac{z_i-w_3}{1-w_3{\stackrel{\_}{z}}_i}\right).$$ (7)

This equation can be expanded in powers of h, with the linear term vanishing due to w₁ + w₂ + w₃ = 0, and the quadratic term being universal and independent of χ_i:

$$A_{\mathit{ij}}f(z_j)=3f(z_j)+\frac{3}{4}{h}^2{\Delta }_{g}f(z_j)+O(h^3).$$ (8)

This relation between the adjacency matrix and the hyperbolic Laplacian remains true for p-gons with p > 7, albeit with a different value of h. We emphasize again that h = tanh(d₀) is fixed by hyperbolic geometry and cannot be tuned. However, the right-hand side of Eq. (7) can be evaluated for every h and so permits a formal finite size scaling limit h → 0. In Appendix B we compute the O(h³) correction to Eq. (8) and discuss the role of boundary sites. In Appendix C, we show that it diminishes as the lattice parameter decreases.

FIG. 2.

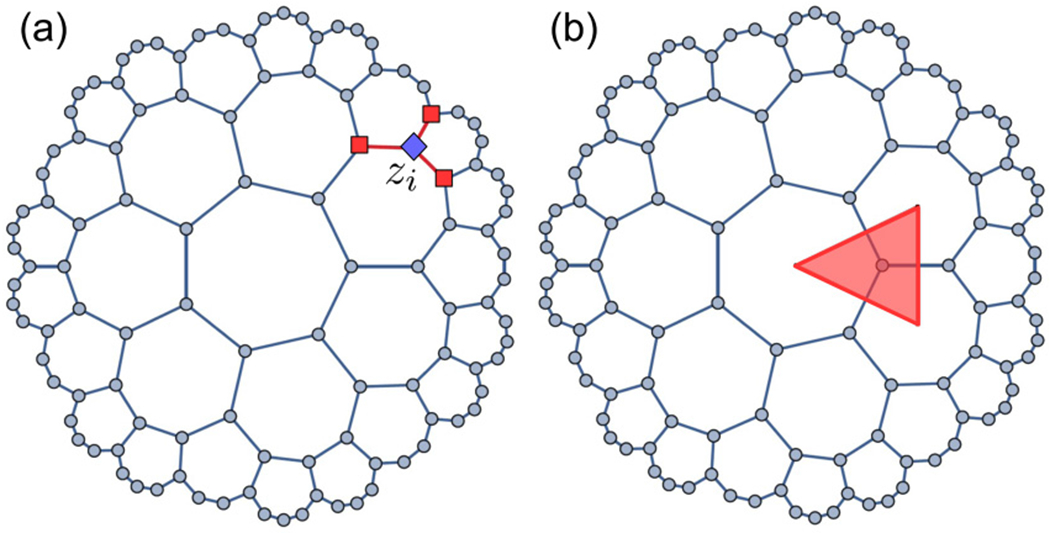
(a) The adjacency matrix can be approximated by the hyperbolic Laplacian in the continuum limit through Eq. (8). To derive this property, we choose an arbitrary site z_i with coordination number 3 (blue diamond). When applying the automorphism $z\mapsto w\left(z\right)=\frac{z_i-z}{1-z{z}_i}$, which maps z_i to the origin, the three neighbors of z_i (red squares) are mapped to an equilateral triangle. This implies Eq. (7), which can be expanded in powers of h to yield the desired relation. (b) Sums over lattice sites are replaced by integrals over hyperbolic space according to Eq. (9). This is achieved by assigning to each site z_i an effective hyperbolic triangle with interior angles 2π/7 and area ${\mathcal{A}}_{\Delta }=\pi /28$.

The next step towards a continuum theory for hyperbolic lattices is a formula to approximate sums over lattice sites by integrals over the Poincaré disk. For suitable functions $f:\mathbb{D}\to \mathbb{C}$, an argument from finite-element triangulations [58–61] implies

$$\sum _{i\in G}f\left(z_j\right)\approx \frac{1}{{\mathcal{A}}_{\Delta }}\underset{\left|z\right|⩽L}{\int }\frac{d^{2}z}{{\left(1-{\left|z\right|}^2\right)}^2}f\left(z\right).$$ (9)

Here, dV_g = d²z/(1 − |z|²)² is the invariant hyperbolic volume element and ${\mathcal{A}}_{\Delta }=\left(\pi -{\gamma }_1-{\gamma }_2-{\gamma }_3\right)/4=\pi /28$ is the area of the hyperbolic triangle of the dual lattice with interior angles γ₁ = γ₂ = γ₃ = 2π/7. Importantly, this implies that a finite graph with ℓ rings and N(ℓ) sites corresponds to a finite continuous disk with effective radius

$$L=\sqrt{\frac{N}{N+28}},$$ (10)

the value of which is determined such that the right-hand side of Eq. (9) yields N when inserting f = 1. We display the first ten effective radii in Table I. In Appendix D, we present an alternative derivation of Eq. (9), which does not utilize the dual lattice. For tessellations with p-gons with p ⩾ 7, we replace $28\to \pi /{\mathcal{A}}_{\Delta }=4p/\left(p-6\right)$.

This dictionary how to approximate A_ij and ∑_i∈G on the hyperbolic lattice by their continuum counterparts comprises the first main result of this work. As an example consider the Bose-Hubbard model Hamiltonian on the hyperbolic lattice,

$$\widehat{\mathcal{H}}=\sum _{i\in G}\left[-t\sum _{j\in G}{\widehat{a}}_i^{†}{A}_{ij}{\widehat{a}}_j-\mu {\widehat{a}}_i^{†}{\widehat{a}}_i+U{\left({\widehat{a}}_i^{†}{\widehat{a}}_i\right)}^2\right],$$ (11)

with chemical potential μ and on-site interaction U. An exciting quantum simulation challenge would be to understand the phase diagram and universality class of the superfluid-to-Mott insulator transition in this model. The associated superfluid in hyperbolic space is then captured by the continuum Hamiltonian

$${\widehat{\mathcal{H}}}^{\prime }=\underset{\left|z\right|⩽L}{\int }\frac{d^{2}z}{{\left(1-{\left|z\right|}^2\right)}^2}\left[{\widehat{\alpha }}_i^{†}\left(-t^{\prime }{\Delta }_g-{\mu }^{\prime }\right){\widehat{\alpha }}_z+U^{\prime }{\left({\widehat{\alpha }}_i^{†}{\widehat{\alpha }}_z\right)}^2\right]$$ (12)

with adjusted parameters $t^{\prime }=\frac{3}{4}{h}^{2}t$, μ′ = μ + 3t, $U^{\prime }=\frac{\pi }{28}U$. The field operators ${\widehat{\alpha }}_z=\widehat{\alpha }\left(z\right)$ satisfy curved-space commutation relations, $\left[\widehat{\alpha }\left(z\right),{\widehat{\alpha }}^{†}\left(z^{\prime }\right)\right]={\left(1-{\left|z\right|}^2\right)}^2{\delta }^{\left(2\right)}\left(z-z^{\prime }\right)$, and we have $\widehat{\alpha }\left(z_i\right)=\sqrt{28/\pi }{\widehat{a}}_i$. More generally, every many-body system with Lagrangian $\mathcal{L}\left(a_i\right)$ where the kinetic term results from nearest-neighbor hopping, especially including multiple species of both bosons and fermions and strong or long-ranged interactions, can be simulated in hyperbolic space by putting it onto a hyperbolic lattice. The resulting continuum theory is described by the action $S=\int d{V}_g\mathcal{L}\left({\alpha }_z\right)$. In this work, we deliberately ignore boundary effects, although holographic models and simulation of bulk-boundary dualities [62–66] are a fascinating application that we leave for future work.

IV. APPLICATIONS

The spectral theory of the hyperbolic Laplacian on the Poincaré disk is well understood [56,57]. We summarize the main aspects here and give some additional details in Appendix E. The eigenvalues of −Δ_g are ε = 1 + k² with eigenfunctions

$${\psi }_K\left(z\right)={\left(\frac{\left(1-{\left|z\right|}^2\right)}{{\left|1-z{e}^{-i\beta }\right|}^2}\right)}^{\frac{1}{2}\left(1+ik\right)},$$ (13)

where K = ke^iβ is a two-dimensional momentum vector. For z → 0 and k → ∞ (corresponding to infinite disk radius and Δ_g → Δ) we have ε → k² and ${\psi }_K\left(z\right)\to e^{\frac{i}{2}\left(K\stackrel{\_}{z}+z\stackrel{\_}{K}\right)}=e^{i\mathbf{k}·\mathbf{x}}$, which is the local Euclidean plane wave limit. In radial coordinates, we write

$${\psi }_K\left(z\right)=\sum _{m=-\infty }^{\infty }{i}^m{g}_{km}\left(r\right)e^{im\left(\varphi -\beta \right)},$$ (14)

generalizing the partial wave decomposition of plane waves. We have

$$g_{km}\left(r\right)\propto P_{\frac{1}{2}\left(-1+ik\right)}^m\left(\frac{1+r^2}{1-r^2}\right),$$ (15)

where $P_{\nu }^m$ is the Legendre function of the first kind. Restricting space to a finite disk of radius L < 1 and imposing Dirichlet boundary conditions, ψ_km(L) = 0, we obtain a discrete energy spectrum ${\epsilon }_n=1+k_n^2$ with k_n > 0, analogous to a particle in a spherical well potential

As a first application of the continuum theory, we estimate ground state energy and spectral gap of the Hamiltonian in Eq. (1). We set t = 1. Since ${\widehat{\mathcal{H}}}_0$ is quadratic this reduces to determining the lowest two eigenvalues of the matrix H = −A, which we label E₀ and E₁ = E₀ + δE with spectral gap δE > 0. Note that the spectrum of H is contained in the real interval (−3, 3). For infinite lattices, the ground state energy is known from mathematical graph theory to lie in the interval [43,67,68] lim_ℓ→∞ E₀ ∈ [−2.966, −2.862]. To estimate the lowest eigenvalues from the continuum limit, we approximate H by the differential operator

$$H^{\left(\text{cont}\right)}=-3-\frac{3}{4}{h}^2{\Delta }_g$$ (16)

with Dirichlet boundary conditions at radius L. Its eigenvalues are the discrete set $E_n^{\left(\text{cont}\right)}=-3+\frac{3}{4}{h}^2\left(1+k_n^2\right)$. As ℓ → ∞, the lowest possible k_n → 0, which yields the ground state energy $E_{\infty }=-3+\frac{3}{4}{h}^2=-\mathrm{2.942\; 95}$, consistent with the graph bound. For finite ℓ ⩾ 1, the first two eigenvalues of H^(cont) are readily computed from ψ_km(L) = 0 for m = 0, 1, respectively. They agree remarkably well with the graph data for ℓ ≳ 4; see Table I and Fig. 3. For ℓ → ∞ we have

$$E_{0,1}^{\left(\text{cont}\right)}~E_{\infty }+\frac{3{\pi }^2{h}^2}{4}\frac{1}{(\ln \phi \ell +c_{0,1}{)}^2},$$ (17)

with $\phi =(1+\sqrt{5})/2$, c₀ = ln 2, and c₁ = ln 2 − 1. Equation (17) is derived in Appendix F.

FIG. 3.

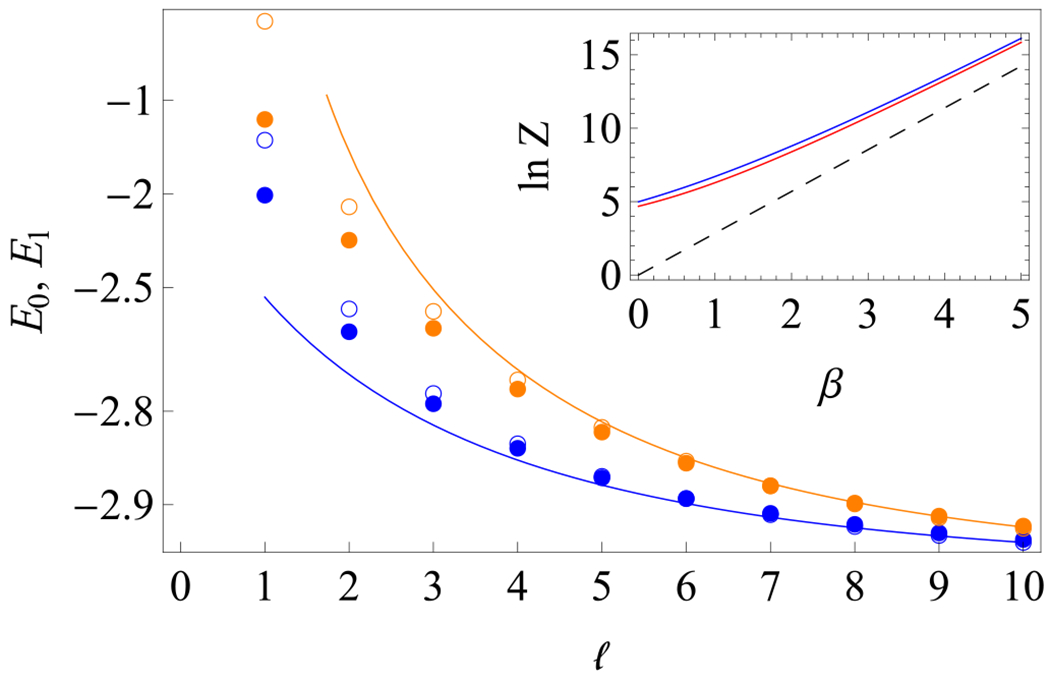
Ground state energy E₀ (blue, lower data) and first excited state energy E₁ (orange, upper data) for the graph (filled circles) and corresponding continuous disk (empty circles). The solid lines are the asymptotic continuum formulas from Eq. (17). Inset: Partition function Z summed over negative energies for the graph with ℓ = 4 (blue) and associated disk (red) as a function of inverse temperature f. The dashed line is the low-temperature asymptote ln Z ~ −βE₀.

As we go to higher energies, the spectra of H and H^(cont) start to deviate. Still, the graph and continuum partition functions $z={\sum }_n\Theta \left(-E_n\right)e^{-\beta E_n}$ and $z^{\prime }={\sum }_n\Theta \left(-E_n^{\left(\text{cont}\right)}\right)e^{-\beta E_n^{\left(\text{cont}\right)}}$ with inverse temperature β agree well; see the inset of Fig. 3. (We limit the sums to negative energies to roughly cut off high energy contributions clearly outside the continuum approximation.) The ability to quantitatively reproduce the low-energy graph spectrum and predict the behavior for large graphs by means of the continuum approximation constitutes the second main result of this work.

Our second application of the continuum theory is the computation of correlation functions on the graph from the continuum Green function. We denote the Green function of H = −A by

$$G_{ij}\left(\omega \right)={\left(\frac{1}{H-\omega }\right)}_{ij}=\sum _{n=1}^N\frac{{\psi }_n\left(i\right){\psi }_n^{*}\left(j\right)}{E_n-\omega }.$$ (18)

Here ψ_n and E_n are the eigenvectors and eigenenergies of H, Hψ_n = E_nψ_n, and $\omega \in \mathbb{C}$ is a complex frequency. G_ij(ω) constitutes the measurable two-point correlation function ${\langle {\widehat{a}}_i\left(\omega \right){\widehat{a}}_j^{†}\left(\omega \right)\rangle }_0$ for the free theory averaged with respect to ${\widehat{\mathcal{H}}}_0$, and can be written as an auxiliary field Gaussian path integral on the graph; see Appendix G. Approximating the latter by the continuum expressions, we obtain

$$G_{ij}\left(\omega \right)\approx \frac{\pi }{21h^2}G\left(z_i,z_j,\frac{4\left(\omega +3\right)}{3h^2},L\right).$$ (19)

Here G(z, z′, λ, L) is the Green function of the hyperbolic Helmholtz operator, i.e., it satisfies

$$\left(\lambda +{\Delta }_g\right)G\left(z,z^{\prime },\lambda ,L\right)=-{\left(1-{\left|z\right|}^2\right)}^2{\delta }^{\left(2\right)}\left(z-z^{\prime }\right)$$ (20)

and Dirichlet boundary conditions G(z, z′, λ, L) = 0 for |z| = L or |z′| = L. Again, the disk radius L is matched to ℓ through Eq. (10). The accuracy of the approximation in Eq. (19) is remarkably good, as shown in Fig. 4.

FIG. 4.

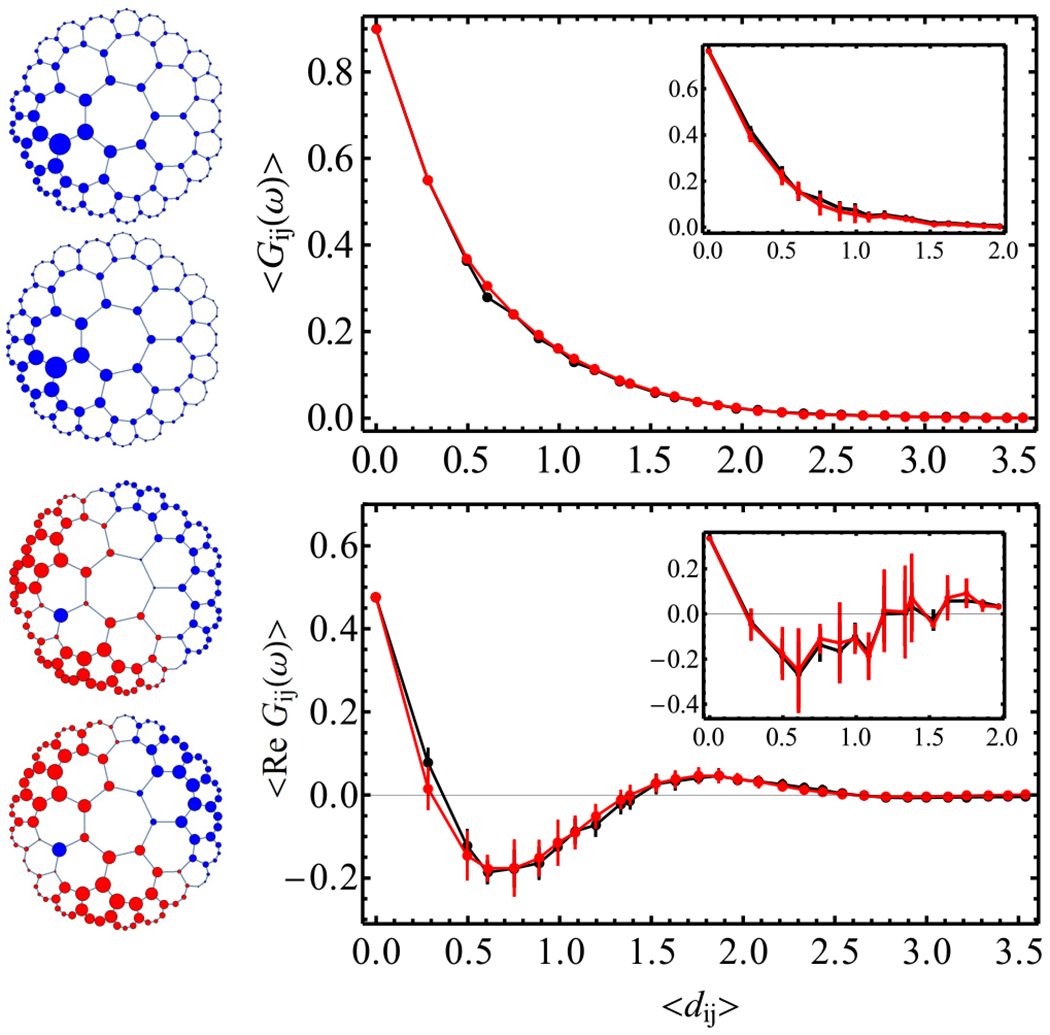
Quantitative match between graph Green function G_ij and continuum Green function G(z_i, z_j). We fix site z_i to be on the second ring, and plot the correlations as a function F_j of site z_j. Upper panel: Results for ω = −2.95 just below E₀. Left: The two plots are F_j = G_ij and F_j = G(z_i, z_j). The size of dots is proportional to |F_j|^1/2, and blue (red) corresponds to positive (negative) sign of F_j. Right: Mean correlation function vs hyperbolic distance d_ij = d(z_i, z_j), where the red (black) data are the graph (continuum) function. To obtain the curves, we make a list of pairs (F_j, d_ij) and compute the average F_j as a function of distance, with the error bar being the standard deviation. The quantitative agreement between graph and continuum is remarkable. Emergent conformal symmetry is reflected by the data points collapsing onto a single curve G_ij = f(d_ij) with some function f for large ℓ. The main plots are for ℓ = 6, the insets for ℓ = 3. Lower panel: The same setting for ω = −2.5 + 0.1i with Re(ω) > E₀. We plot the real part of the correlation function.

The continuum Green function G(z, z′, λ, L) is uniquely specified by the Dirichlet boundary condition [57,69–71]. The full but lengthy analytic expression is derived in Appendix H and summarized in Appendix I. As L → 1, the Green function is solely a function of the hyperbolic distance d(z, z′) due to automorphism invariance. For λ = 0 we have

$$G\left(z,z^{\prime },0,L\right)=-\frac{1}{4\pi }\ln {\left|\frac{L\left(z-z^{\prime }\right)}{L^2-z{\stackrel{\_}{z}}^{\prime }}\right|}^2,$$ (21)

which, indeed, is a function of tanh $d\left(z,z^{\prime }\right)=\left|\frac{z-z^{\prime }}{1-z{\stackrel{\_}{z}}^{\prime }}\right|$ for L = 1. In turn, this implies that also the graph correlation function G_ij(ω) is approximately a universal function of the hyperbolic distance d_ij = d(z_i, z_j) for large ℓ, as shown in Fig. 4. The quantitative matching of graph and continuum Green functions and the finding of emergent conformal symmetry on the hyperbolic lattice constitute our third main result.

V. OUTLOOK

The continuum approximation for hyperbolic lattices that we have put forward shows a path for how quantum many-body systems in continuous hyperbolic space can be reliably simulated using discrete geometries. It also gives a computational framework to efficiently compute observables relevant for experiments simulating curved spaces. In particular, the continuum Green function can be used in diagrammatic techniques to accurately determine interaction effects even for relatively small system sizes. One platform of interest is, of course, circuit QED realizations, where the interplay of curvature and strong interactions between photons and qubit degrees of freedoms can be studied. However, hyperbolic lattices or their topological equivalents can, in principle, also be realized in other experimental platforms that allow for engineered hopping on graphs, including optical lattices for ultracold atoms [72] or electrical circuits [73], and thus can be utilized to simulate other many-body Hamiltonians in hyperbolic space (including fermions or artificial gauge fields). The strong coupling regime in experiment has the potential to uncover novel effects and can be used to benchmark our theoretical description of nonperturbative quantum physics in curved space.

The continuum formalism also naturally connects to statements of AdS-CFT correspondence and the intriguing interplay between boundary field theories and a gravitational bulk. In this context, we want to make the point that simulating bosons in hyperbolic space is related to simulating quantum gravity in two Euclidean dimensions. Although the Einstein-Hilbert action is purely topological in two dimensions, an important alternative theory for metric fluctuations is Liouville quantum gravity [74], which also appears in the context of the Sachdev-Ye-Kitaev (SYK) model [75] and bosonic string theory [76]. Since every two-dimensional metric can be written as g_ij = e^φδ_ij with a scalar field φ, a saddle-point expansion of the Liouville action yields a field theory for φ in a hyperbolic background of constant negative curvature, and fluctuations of φ in that background correspond to fluctuations of the metric g_ij. We conclude that hyperbolic lattices promise a bright future for the genuine simulation of quantum physics in curved space.

APPENDIX A: EMBEDDING COORDINATES

In this Appendix, we explain how the finite graph with ℓ rings is embedded into the Poincaré disk.

We assign a coordinate $z_i\in \mathbb{D}$ to each graph site $\text{i}\in \text{G}$ such that neighboring sites are at hyperbolic distance d₀, with d₀ to be determined. In order to label the coordinates $z_i\in \mathbb{D}$, we have in mind the topologically equivalent graph with ℓ concentric rings; see Fig. 1 in the main text. We enumerate the N graph sites with an index i in a counterclockwise manner by starting on the first ring, then the second ring, and so forth. In this way, the first i = 1, …, 7 sites are on ring ℓ = 1, sites i = 8, …, 35 are on ring ℓ = 2, etc. The number of sites on each ring is summarized in Table II.

The construction of the tessellation starts with the central regular heptagon with |z₁| = ⋯ |z₇| = r₀. For a general hyperbolic lattice {p, q} we have

$$r_0=\sqrt{\frac{\cos \left(\frac{\pi }{q}+\frac{\pi }{p}\right)}{\cos \left(\frac{\pi }{p}-\frac{\pi }{q}\right)}},$$ (A1)

and so for our tessellation {7, 3} we find

$$r_0=\mathrm{0.300\; 743}.$$ (A2)

In particular, the first two coordinates are z₁ = r₀ and z₂ = r₀e^2πi/7 so that

$$d_0=d\left(z_1,z_2\right)=\mathrm{0.283\; 128}$$ (A3)

with d(z, z′) the hyperbolic distance in the Poincaré disk. Starting from the central heptagon, the hyperbolic lattice is generated by iteratively applying the two generators of the symmetry group of the tessellation to the existing sites, which are rotations by 2π/7 through the center of a heptagon and rotations by 2π/3 through a vertex. Alternatively, we can create polygons by iteratively inverting existing polygons on hyperbolic circles along the edges of the polygon.

A list of coordinates {z_i} for the sites of the first ℓ = 6 rings is provided in the Supplemental Material [55]. The list contains 2240 lines, which correspond to the 2240 coordinates for the graph with six rings. The first (second) column of the data constitutes the real (imaginary) part of $i_i \mathbb{D}$. In order to extract the coordinates for a graph with ℓ = 1, 2, 3, 4, 5, 6 rings, restrict to the first 7,35,112,315,847,2240 lines of the data, respectively.

APPENDIX B: DERIVATION OF EQ. (7) AND CORRECTIONS

In this section we present a more detailed derivation of Eq. (7) for approximating the adjacency matrix by the hyperbolic Laplacian. We further discuss the validity of this relation for boundary sites with coordination number 2 and compute the next-to-leading order correction in the expansion in powers of h.

Derivation of Eq. (7).

Choose an arbitrary site z_i of the hyperbolic lattice with coordination number 3. For a test function $f:\mathbb{D}\to \mathbb{C}$ such that f(z_i) = f_i we then have

$$A_{ij}{f}_j=f\left(z_{i+e_1}\right)+f\left(z_{i+e_2}\right)+f\left(z_{i+e_3}\right),$$ (B1)

where z_i+ea with a = 1, 2, 3 stands for the sites adjacent to z_i. The heptagonal lattice is such that all adjacent lattice sites have the same distance with respect to the hyperbolic metric. In particular, this property remains invariant under automorphisms of the Poincaré disk. We apply the transformation $\mathbb{D}\to \mathbb{D}$,

$$z\mapsto w\left(z\right)=\frac{z_i-z}{1-z{\stackrel{\_}{z}}_i},$$ (B2)

$$w\mapsto z\left(w\right)=\frac{z_i-w}{1-w{\stackrel{\_}{z}}_i},$$ (B3)

which exchanges z_i and the origin. We write $f\left(z\right)=\tilde{f}\left(w\left(z\right)\right)$ and have

$$A_{ij}{f}_j=\tilde{f}\left(w\left(z_{i+e_1}\right)\right)+\tilde{f}\left(w\left(z_{i+e_2}\right)\right)+\tilde{f}\left(w\left(z_{i+e_3}\right)\right).$$ (B4)

The adjacent sites in the rotated frame, however, have very simple coordinates: Modulo rotation, they correspond to three sites at hyperbolic distance d₀ from the origin, with mutual relative angle 2π/3. The corresponding Euclidean distance h in the disk is such that

$$d\left(h,0\right)\stackrel{!}{=}{d}_0,$$ (B5)

and so

$$h=\tanh \left(d_0\right)=\mathrm{0.275\; 798}.$$ (B6)

We write

$$w_1=w\left(z_{i+e_1}\right)=h{e}^{i{\chi }_i},$$ (B7)

$$w_2=w\left(z_{i+e_2}\right)=h{e}^{i2\pi /3}{e}^{i{\chi }_i},$$ (B8)

$$w_3=w\left(z_{i+e_3}\right)h{e}^{i4\pi /3}{e}^{i{\chi }_i},$$ (B9)

where the angle χ_i is determined by the coordinate z_i; see below. We have

$$w_1+w_2+w_3=w_1^2+w_2^2+w_3^2=0.$$ (B10)

Applying the inverse automorphism we can parametrize the sites adjacent to z_i as

$$z_{i+e_1}=z\left(w_1\right)=\frac{z_i-w_1}{1-w_1{\stackrel{\_}{z}}_i},$$ (B11)

$$z_{i+e_2}=z\left(w_2\right)=\frac{z_i-w_2}{1-w_2{\stackrel{\_}{z}}_i},$$ (B12)

$$z_{i+e_3}=z\left(w_3\right)=\frac{z_i-w_3}{1-w_3{\stackrel{\_}{z}}_i}$$ (B13)

and so

$$A_{ij}{f}_j=f\left(\frac{z_i-w_1}{1-w_1{\stackrel{\_}{z}}_i}\right)+f\left(=\frac{z_i-w_2}{1-w_2{\stackrel{\_}{z}}_i}\right)+f\left(\frac{z_i-w_3}{1-w_3{\stackrel{\_}{z}}_i}\right).$$ (B14)

The right-hand side is a complex number that depends on the parameter h and can be approximated through Taylor’s formulas by a polynomial in h. We write

$$A_{ij}{f}_j=3f\left(z_i\right)+Q_{1}h+Q_2{h}^2+O\left(h^3\right)$$ (B15)

with

$$Q_1=\frac{d}{dh}[f\left(\frac{z_i-w_1}{1-w_1{\stackrel{\_}{z}}_i}\right)+f\left(\frac{z_i-w_2}{1-w_2{\stackrel{\_}{z}}_i}\right)+f\left(\frac{z_i-w_3}{1-w_3{\stackrel{\_}{z}}_i}\right){]}_{h=0},$$ (B16)

$$Q_2=\frac{1}{2}\frac{d^2}{d{h}^2}[f\left(\frac{z_i-w_1}{1-w_1{\stackrel{\_}{z}}_i}\right)+f\left(\frac{z_i-w_2}{1-w_2{\stackrel{\_}{z}}_i}\right)+f\left(\frac{z_i-w_3}{1-w_3{\stackrel{\_}{z}}_i}\right){]}_{h=0}.$$ (B17)

We use a complex notation where we identify $f\left(z\right)\equiv f\left(z,\stackrel{\_}{z}\right)$ and

$${\partial }_z=\frac{\partial }{\partial z}=\frac{1}{2}\left({\partial }_x-i{\partial }_y\right),$$ (B18)

$${\stackrel{\_}{\partial }}_z=\frac{\partial }{\partial \stackrel{\_}{z}}=\frac{1}{2}\left({\partial }_x+i{\partial }_y\right).$$ (B19)

For a = 1, 2, 3 (with w_a,h := dw_a/dh = w_a/h) we arrive at

$$\begin{gathered} \frac{d}{dh}f{\left(\frac{z_i-w_a}{1-w_a{\stackrel{\_}{z}}_i}\right)}_{h=0} \\ =-\left(1-{\left|z_i\right|}^2\right)\left(w_{1,h}{\partial }_z+{\stackrel{\_}{w}}_{1,h}{\stackrel{\_}{\partial }}_z\right)f\left(z_i\right), \end{gathered}$$ (B20)

$$\begin{gathered} \frac{d^2}{d{h}^2}f{\left(\frac{z_i-w_a}{1-w_a{\stackrel{\_}{z}}_i}\right)}_{h=0} \\ ={\left(1-{\left|z_i\right|}^2\right)}^2\left({\partial }_z^{2}f\left(z_i\right)w_{1,h}^2+{\stackrel{\_}{\partial }}_z^{2}f\left(z_i\right){\stackrel{\_}{w}}_{1,h}^2\right) \\ -2{\stackrel{\_}{z}}_i\left(1-{\left|z_i\right|}^2\right)w_{1,h}^2{\partial }_{z}f\left(z_i\right)-2z_i\left(1-{\left|z_i\right|}^2\right){\stackrel{\_}{w}}_{1,h}^2{\stackrel{\_}{\partial }}_{z}f\left(z_i\right) \\ +2{\left(1-{\left|z_i\right|}^2\right)}^2{\left|w_{1,h}\right|}^2{\partial }_z{\stackrel{\_}{\partial }}_{z}f\left(z_i\right). \end{gathered}$$ (B21)

Summing over the index a and using ${\sum }_{a=1}^3{w}_a={\sum }_{a=1}^2{w}_a^2=0$ and |w_a,h| = 1, this implies

$$Q_1=0$$ (B22)

and

$$Q_2=3{\left(1-{\left|z_i\right|}^2\right)}^2{\partial }_z{\stackrel{\_}{\partial }}_{z}f\left(z_i\right).$$ (B23)

Note that $\Delta =4{\partial }_z{\stackrel{\_}{\partial }}_z$. Thus we have shown that

$$A_{ij}{f}_j=3f\left(z_i\right)+\frac{3}{4}{h}^2{\Delta }_{g}f\left(z_i\right)+O\left(h^3\right)$$ (B24)

for a site with coordination number 3.

Coordination number 2.

Any site z_i with coordination number 2 necessarily lies on the boundary of the graph, which we assume to be built from ℓ rings. Denote the two sites adjacent to z_i in G by z_i+e1 and z_i+e2. The coordinate of the third neighboring site z_i+e3 lies on the (ℓ + 1)th ring outside G, but is otherwise uniquely specified by the heptagonal tessellation of the hyperbolic plane. We then have

$$\begin{gathered} A_{ij}{f}_j=f\left(z_{i+e_1}\right)+f\left(z_{i+e_2}\right) \\ =\underset{0}{\underbrace{[-f\left(z_{i+e_3}\right)+f\left(z_{i+e_3}\right)]}}+f\left(z_{i+e_1}\right)+f\left(z_{i+e_2}\right) \\ =-f\left(z_{i+e_3}\right)+3f\left(z_i\right)+\frac{3}{4}{h}^2{\Delta }_{g}f\left(z_i\right)+O\left(h^3\right). \end{gathered}$$ (B25)

We could now expand the first term to linear order in h, giving f(z_i+e3) = f(z_i) + hδ_nf(z_i), with δ_nf(z_i) a directional derivative along the line from z_i to z_i+e3. On the other hand, for our purposes we need Eq. (B24) only for the case that $f_i={\widehat{a}}_i=\widehat{\alpha }(z_i)$ is an annihilation operator. For any many-body state |Ψ〉 describing the system on graph G we have ${\widehat{\alpha }}_{i+e_3}|\Psi \rangle =0$, since z_i+e3 ∉ G. Consequently

$$A_{ij}{\widehat{a}}_j|\Psi \rangle =\left(3\widehat{\alpha }\left(z_i\right)+\frac{3}{4}{h}^2{\Delta }_g\widehat{\alpha }\left(z_i\right)\right)|\Psi \rangle +O\left(h^3\right),$$ (B26)

and so the linear term should not affect observables. We leave the detailed analysis of these boundary effects to future work, since obviously they do not significantly affect the accuracy of the observables computed in this work.

Third order in h.

It is further possible to determine the coefficient Q₃ in the expansion

$$A_{ij}{f}_j=3f\left(z_i\right)+\frac{3}{4}{h}^2{\Delta }_{g}f\left(z_i\right)+h^3{Q}_3+O\left(h^4\right)$$ (B27)

along the same lines. We have

$$Q_3=-\frac{1}{2}\left[e^{3i{\chi }_i}\mathcal{D}f\left(z_i\right)+e^{-3i{\chi }_i}\mathcal{D}f\left(z_i\right)\right]$$ (B28)

with differential operator

$$\mathcal{D}={\partial }_z^2{\left(1-{\left|z_i\right|}^2\right)}^3{\partial }_z.$$ (B29)

To understand the role of χ_i in this formula, it is instructive to express ∂_z in radial coordinates according to

$${\partial }_z=\frac{e^{-i\varphi }}{2}\left({\partial }_r-\frac{i}{r}{\partial }_{\varphi }\right).$$ (B30)

Consequently only the combination

$${\delta }_i={\chi }_i-{\varphi }_i$$ (B31)

is relevant when applying $\mathcal{D}$ in Eq. (B21). We find that δ_i in most cases (not all) only depends on the radius r_i, and is wildly fluctuating as we go from one lattice site to the other; see Fig. 5. This may explain why the contributions of the operator $\mathcal{D}$, although only suppressed by a power of h, seem to be unimportant for computing the observables we consider in this work.

FIG. 5.

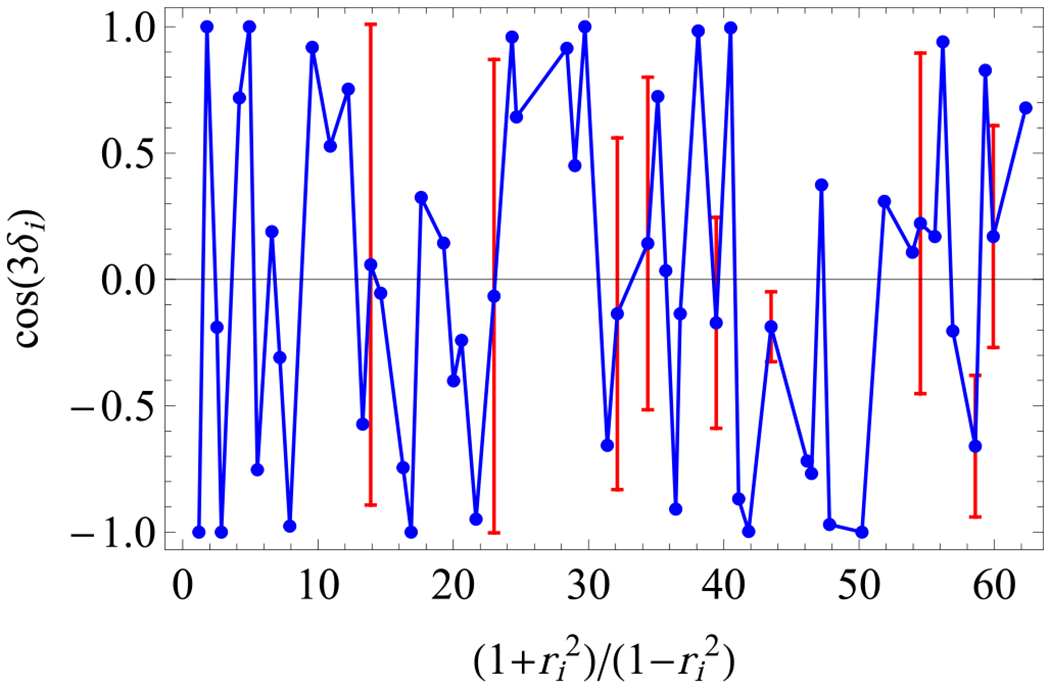
The angle δ_i = χ_i − ϕ_i is heavily oscillating between sites with nearby radius. In most cases, δ_i only depends on the value of the radius |z_i| = r_i. Here we plot the averaged angle δ_i vs site radius r_i for the first five rings (comprising 847 sites). The red “error bars” indicate those cases where the mapping δ_i ↔ r_i is not unique. Still, for any given site i we can unambiguously assign the value of δ_i through Eqs. (B7)–(B9).

TABLE II.

Number of sites on the ℓth ring, N_ring(ℓ), and total number of sites for a graph with ℓ rings, N(ℓ), for the first eight rings.

	ℓ rings
	1	2	3	4	5	6	7	8
Nring(ℓ)	7	28	77	203	532	1393	3647	9548
N(ℓ)	7	35	112	315	847	2240	5887	15435

APPENDIX C: FINITE-SIZE SCALING LIMIT

In this section, we perform a formal finite-size scaling limit h → 0 of Eq. (B14) and show that the higher-order corrections vanish in this formal limit.

The lattice parameter h is fixed by hyperbolic geometry for every {p, 3} lattice through h = tanh(d₀) with d₀ = d(r₀, r₀e^2πi/p) and r₀ from Eq. (A1). Some examples for the lowest (and highest) values of p are

p	7	8	9	10	∞
d0	0.283128	0.36352	0.409595	0.439590	1
h	0.275798	0.348311	0.388129	0.413304	1/2

We observe that the heptagonal lattice has the smallest value of h. As such, the fixed value of h yields a fundamental limit to the accuracy of the approximation in Eq. (B24). However, since h is relatively small, including the O(h³) correction in Eq. (B27) yields virtually exact results.

Remarkably, the right-hand side of Eq. (B14) can be evaluated for every value of h and so allows for a formal finite-size scaling limit h → 0. To see this, let us rewrite the equation as

$$\begin{gathered} {\left({\widehat{A}}_{h}f\right)}_i:=f\left(\frac{z_i-h{e}^{i{\chi }_i}}{1-h{e}^{i{\chi }_i}{\stackrel{\_}{z}}_i}\right)+f\left(\frac{z_i-h{e}^{i2\pi /3}{e}^{i{\chi }_i}}{1-h{e}^{i2\pi /3}{e}^{i{\chi }_i}{\stackrel{\_}{z}}_i}\right) \\ +f\left(\frac{z_i-h{e}^{i4\pi /3}{e}^{i{\chi }_i}}{1-h{e}^{i4\pi /3}{e}^{i{\chi }_i}{\stackrel{\_}{z}}_i}\right), \end{gathered}$$ (C1)

where we defined a formal, h-dependent operator ${\widehat{A}}_h$. Importantly, we can now modify the value of h at will. (But, for h ≠ 0.275 798, the operator loses its interpretation as the adjacency matrix of the heptagonal lattice.)

To simplify the finite-size analysis, let us focus on radially symmetry functions f(r). For most sites i, the expression ${\left({\widehat{A}}_{h}f\right)}_i$ only depends on the radius r_i; see Fig. 5. Consequently, after averaging over the radii, we can plot ${\widehat{A}}_{h}f$ vs the hyperbolic distance from the origin d(r, 0); see Fig. 6. We compare the full expression ${\widehat{A}}_{h}f$ with the quadratic and cubic continuum approximations given by

$${\left({\widehat{A}}_h^{\left(2\right)}f\right)}_i=3f\left(z_i\right)+\frac{3}{4}{h}^2{\Delta }_{g}f\left(z_i\right)$$ (C2)

and

$$\begin{gathered} {\left({\widehat{A}}_h^{\left(3\right)}f\right)}_i=3f\left(z_i\right)+\frac{3}{4}{h}^2{\Delta }_{g}f\left(z_i\right) \\ -\frac{h^3}{3}\left[e^{3i{\chi }_i}\mathcal{D}f\left(z_i\right)+e^{-3i{\chi }_i}\stackrel{\_}{\mathcal{D}}f\left(z_i\right)\right], \end{gathered}$$ (C3)

respectively. We verify that for h → 0 the quadratic approximation is sufficient to approximate the full result ${\widehat{A}}_{h}f$. For general h ⩽ 0.275 798, ${\widehat{A}}_h^{\left(2\right)}f$ always gives a good qualitative and overall approximation. For sizable but small h ~ 0.1, the cubic approximation is sufficient to even capture the quantitative behavior of ${\widehat{A}}_{h}f$, whereas, for the physical value h = 0.275 798, deviations between ${\widehat{A}}_{h}f$ and ${\widehat{A}}_h^{\left(3\right)}f$ are visible, though small.

APPENDIX D: DERIVATION OF EQS. (8) AND (9)

In this section we show how sums of the type

$$\sum _{i\in G}f\left(z_i\right)$$ (D1)

with a suitable function f(z) can be approximated by integrals over the Poincaré disk with a finite radius L < 1. We assume the graph G to consist of $\ell$ rings. We present two methods: Method 1 is geometric in nature and relies on determining the area of the fundamental polygon of the dual lattice, whereas Method 2 is numerical and based on fitting the growth of the number of sites with increasing radial coordinate. The outcomes, Eqs. (8) and (9) in the main text, are the same.

Method 1.

The first method to approximate sums by integrals employs the fact that [58–61]

$$\sum _{i\in G}{\mathcal{A}}_{i}f\left(z_i\right)\simeq \int \frac{d^{2}z}{{\left(1-{\left|z\right|}^2\right)}^2}f\left(z\right)$$ (D2)

With ${\mathcal{A}}_i=\text{area}\left({\mathcal{P}}_i\right)$, where ${\mathcal{P}}_i=\left\{z\in \mathbb{D}:d\left(z,z_i\right)⩽d\left(z,z_j\right)\text{for all}j\ne i\right\}$ is the set of all points in $\mathbb{D}$ that are closer to z_i in comparison to any other lattice point. Equation (D2) is commonly applied for discretization of curved manifold, such as in finite-elements methods for numerical simulations. Due to the high symmetry of the tessellation {p, 3} with regular p-gons, the set ${\mathcal{P}}_i$ is the fundamental triangle of the dual lattice {3, p}; see Fig. 4. Furthermore, the area ${\mathcal{A}}_i={\mathcal{A}}_{\Delta }$ is independent of i in this case, as all sites are equivalent with respect to automorphisms. We then arrive at Eq. (8) from the main text.

In order to compute the area ${\mathcal{A}}_{\Delta }$, we note that the area of a hyperbolic triangle with interior angles α, β, γ is generally given by (π − α − β − γ)/4. In this case, all interior angles are 2π/p. To see this, choose a dual triangle with one vertex at the origin. Clearly, the interior angle at the site at the origin is 2π/p, because the outgoing geodesics are straight lines. However, since the other two vertices of the triangle can be brought to the origin by a suitable Moebius transformation, we conclude that in fact all interior angles are 2π/p. We then arrive at

$${\mathcal{A}}_{\Delta }=\frac{\pi }{4}\left(1-\frac{6}{p}\right),$$ (D3)

as quoted in the main text. For p = 7, we have ${\mathcal{A}}_{\Delta }=\pi /28$.

Method 2.

To simplify the matter let us first assume that f(z) only depends on r = |z|. Define the counting function

$$\mathcal{N}\left(r\right)=\sum _{i\in G}\Theta \left(r-r_i\right).$$ (D4)

Further introduce the hyperbolic invariant ρ via

$$\rho =\frac{1+r^2}{1-r^2},d\rho =4\frac{drr}{{\left(1-r^2\right)}^2}.$$ (D5)

We find that $\mathcal{N}\left(r\right)$ is approximately linear in p and given by

$$\mathcal{N}\left(r\right)\approx 14\rho +b,$$ (D6)

with b a constant; see Fig. 7. Hence $d\mathcal{N}\left(r\right)=14d\rho$. In order to approximate the finite sum by a compactly supported integral, we restrict the integration to a disk of radius L < 1, with L to be determined. We have

$$\begin{gathered} \sum _{i\in G}f\left(r_i\right)\approx \int dN\left(r\right)f\left(r\right)=14\int d\rho f\left(r\right) \\ =14\times \text{4}\underset{0}{\overset{L}{\int }}\frac{drr}{{\left(1-r^2\right)}^2}f\left(r\right) \\ =\frac{\text{14}\times \text{4}}{2\pi }\underset{\left|z\right|⩽L}{\int }\frac{d^{2}z}{{\left(1-{\left|z\right|}^2\right)}^2}f\left(\left|z\right|\right). \end{gathered}$$ (D7)

we fix the effective radius L by matching the total number of sites N to the right-hand side $\frac{14\times 4}{2\pi }\frac{\pi L^2}{1-L^2}$ for f(r) = 1. This yields

$$L=\sqrt{\frac{N}{N+28}}.$$ (D8)

In order to approximate the angular dependence for a more general function f(z) = f(re^iϕ) we can employ standard arguments from Riemann integration. Due to the sevenfold rotation invariance of the lattice we can divide the N lattice sites {i ∈ G} into N/7 “shells,” labeled [i], where each shell contains seven sites with equal radius r_i and angle ϕ_i + 2π j/7 with j = 0, …, 6. Summing over these seven sites for fixed r_i we have

$$\sum _{j=0}^{6}f\left(r_i{e}^{i{\varphi }_i+2\pi ij/7}\right)\approx 7{\int }_0^{2\pi }\frac{d\varphi }{2\pi }f\left(r_i{e}^{i\varphi }\right),$$ (D9)

where we approximated the sum by a Riemann integral. For the total sum over lattice sites we then have

$$\begin{gathered} \sum _{i\in G}f\left(r_i{e}^{i{\varphi }_i}\right)=\sum _{\left[i\right]}\sum _{j=0}^{6}f\left(r_i{e}^{i{\varphi }_i+2\pi ij/7}\right) \\ \approx {\int }_0^{2\pi }\frac{d\varphi }{2\pi }\left(\sum _{\left[i\right]}7f\left(r_i{e}^{i\varphi }\right)\right) \\ ={\int }_0^{2\pi }\frac{d\varphi }{2\pi }\sum _{i\in G}f\left(r_i{e}^{i\varphi }\right) \\ \approx {\int }_0^{2\pi }\frac{d\varphi }{2\pi }14\times 4\underset{0}{\overset{L}{\int }}\frac{drr}{{\left(1-r^2\right)}^2}f\left(r{e}^{i\varphi }\right) \\ =\frac{\text{14}\times \text{4}}{2\pi }\underset{\left|z\right|⩽L}{\int }\frac{d^{2}z}{{\left(1-{\left|z\right|}^2\right)}^2}f\left(z\right). \end{gathered}$$ (D10)

This shows that Eq. (D7) generalizes to functions with nontrivial angular dependence.

FIG. 6.

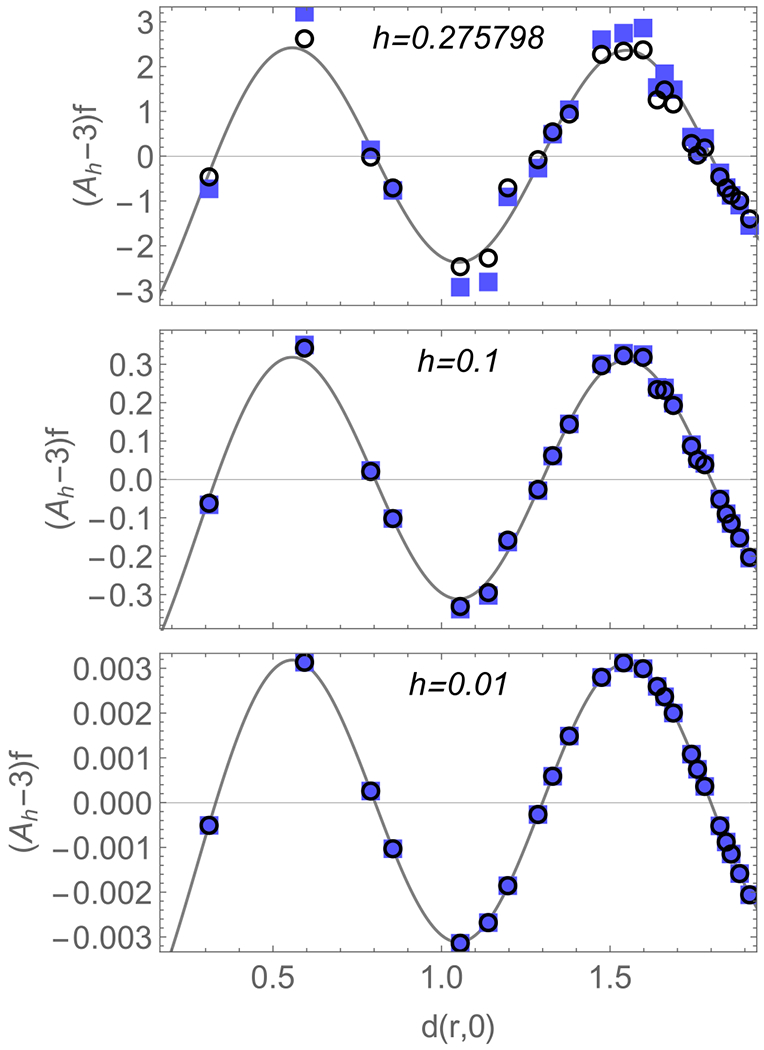
Finite-size scaling. We define the h-dependent operator ${\widehat{A}}_h$ through Eq. (C1), which allows us to connect the physical value of h = 0.275 798 for the heptagonal lattice to a formal h → 0 limit. For the radially symmetric test function f(r) = cos[πd(r, 0)] we show here ${\widehat{A}}_{h}f$ (empty black circles), the cubic approximation ${\widehat{A}}_h^{\left(3\right)}f$ from Eq. (C3) (filled blue squares), and the quadratic approximation ${\widehat{A}}_h^{\left(2\right)}=3f+\frac{3}{4}{h}^2{\Delta }_{g}f$ (gray solid line). We subtract 3f for better visibility of the deviations. The three figures correspond to decreasing values of h, with the individual values given in the plot labels. As h → 0, the quadratic approximation quantitatively reproduces the full expression.

FIG. 7.

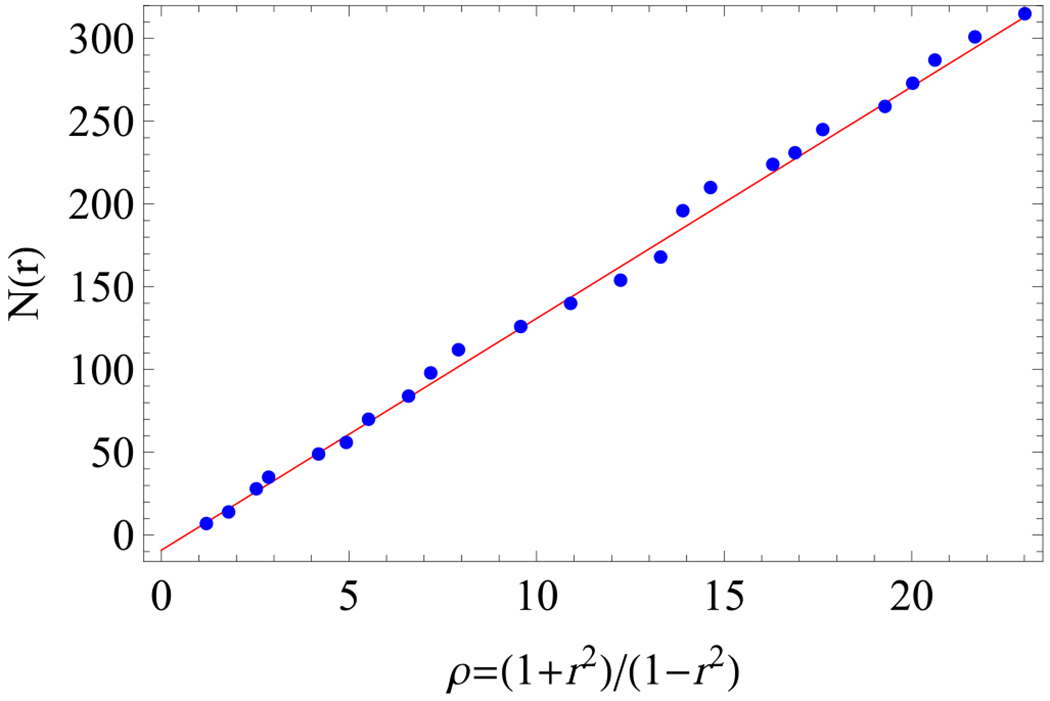
Counting function $\mathcal{N}\left(r\right)$ for radii within the first ℓ = 4 rings versus the linear curve 14ρ + b, with b = −9.096.

APPENDIX E: EIGENFUNCTIONS OF HYPERBOLIC LAPLACIAN

In this section we summarize the spectral properties of the hyperbolic Laplacian, i.e., the eigenvalues and eigenfunctions in different representations.

We label the eigenfunctions of Δ_g on the Poincaré disk by a momentum parameter

$$K=k{e}^{i\beta }$$ (E1)

with k ⩾ 0 the amplitude and β ∈ [0, 2π) a phase. The corresponding eigenfunction is

$${\psi }_K\left(z\right)={\left(\frac{\left(1-{\left|z\right|}^2\right)}{{\left|1-z{e}^{-i\beta }\right|}^2}\right)}^{\frac{1}{2}\left(1+ik\right)},$$ (E2)

and applying ${\Delta }_g=4{\left(1-{\left|z\right|}^2\right)}^2{\partial }_z{\stackrel{\_}{\partial }}_z$ it is easy to see that the corresponding eigenvalue is

$${\epsilon }_K=-\left(k^2+1\right).$$ (E3)

The norm of ψ_K for a disk of radius L < 1 is

$${\Vert {\psi }_K\Vert }^2=\underset{\left|z\right|⩽L}{\int }\frac{d^{2}z}{{\left(1-{\left|z\right|}^2\right)}^2}\left|{\psi }_K\right(z){|}^2=\frac{\pi L^2}{1-L^2},$$ (E4)

which is the hyperbolic volume of the disk. Note how this is analogous to the Euclidean case. Indeed, the Euclidean plane wave solutions

$${\psi }_K\left(z\right)\simeq e^{i\mathbf{k}·\mathbf{x}}=\exp \left[\frac{i}{2}\left(K\stackrel{\_}{z}+\stackrel{\_}{K}z\right)\right]$$ (E5)

are recovered for z ≪ 1 and k ≫ 1, which corresponds to the radius of the Poincaré disk approaching infinity and hence vanishing curvature.

Often it is advantageous to express the eigenfunction in radial coordinates z = re^iϕ. For k ⩾ 0 and $m\in \mathbb{Z}$ we define the radial eigenfunctions g_km(r) corresponding to the eigenvalue −(k² + 1) such that

$${\psi }_K\left(z\right)=\sum _{m=-\infty }^{\infty }{i}^m{g}_{km}\left(r\right)e^{im\left(\varphi -\beta \right)}.$$ (E6)

The ansatz is motivated by the Euclidean formula

$$e^{i\mathbf{k}·\mathbf{x}}=\sum _{m=-\infty }^{\infty }{i}^m{J}_m\left(kr\right)e^{im\left(\varphi -\beta \right)}$$ (E7)

with Bessel functions J_m. We have

$$g_{km}\left(r\right)=i^{-m}\underset{0}{\overset{2\pi }{\int }}\frac{d\varphi }{2\pi }{e}^{-im\varphi }{\left(\frac{1-r^2}{{\left|1-r{e}^{i\varphi }\right|}^2}\right)}^{\frac{1}{2}\left(1+ik\right)},$$ (E8)

which can be solved numerically. However, the functions g_km(r) can be determined in closed form by making the ansatz $g_{km}\left(r\right)=\widehat{g}\left(\frac{1+r^2}{1-r^2}\right)$, which leads to Legendre’s differential equation (H14) for $\widehat{g}$. This yields

$$g_{km}\left(r\right)\propto P_v^m\left(\frac{1+r^2}{1-r^2}\right)$$ (E9)

with $\nu =\frac{1}{2}\left(-1+ik\right)$ and $P_v^m$ the Legendre function of the first kind. The correct prefactor ensuring Eq. (E6) is found to be

$$\begin{array}{l}{g}_{k,m=0}\left(r\right)=P_{\nu }\left(\frac{1+r^2}{1-r^2}\right),\\ g_{k,m>0}\left(r\right)=\frac{1}{{\prod }_{n=0}^{m-1}\left(\nu -n\right)}{P}_{\nu }^m\left(\frac{1+r^2}{1-r^2}\right),\\ g_{k,m<0}\left(r\right)={\left(-1\right)}^m{g}_{k,m>0}\left(r\right).\end{array}$$ (E10)

In the Euclidean limit r ≪ 1 and k ≫ 1, we recover g_km(r) ≃ J_m(kr).

TABLE III.

We compare the ground and first excited state energies for the graph and continuum for ℓ = 1, …, 10. The “asymptotic” continuum formulas for $E_0^{\left(\text{cont}\right)}$ and $E_1^{\left(\text{cont}\right)}$ correspond to Eqs. (F10) and (F16), respectively. For ℓ ⩾ 8 we give an estimate of E₀ and E₁ from sparse matrix methods.

	ℓ
	1	2	3	4	5	6	7	8	9	10
E0	−2	−2.636	−2.787	−2.847	−2.877	−2.894	−2.905	−2.91	−2.92	−2.92
Exact $E_0^{\left(\text{cont}\right)}$	− 1.500	−2.570	−2.770	−2.842	−2.876	−2.895	−2.906	−2.914	−2.920	−2.924
Asymptotic $E_0^{\left(\text{cont}\right)}$	−2.535	−2.738	−2.820	−2.861	−2.884	−2.899	−2.909	−2.916	−2.921	−2.924
E1	−1.274	−2.283	−2.627	−2.762	−2.827	−2.863	−2.884	−2.90	−2.91	−2.91
Exact $E_1^{\left(\text{cont}\right)}$	0.620	−2.085	−2.578	−2.746	−2.821	−2.861	−2.884	−2.899	−2.908	−2.915
Asymptotic $E_1^{\left(\text{cont}\right)}$	15.58	−1.633	−2.507	−2.728	−2.815	−2.858	−2.883	−2.898	−2.908	−2.915

APPENDIX F: COMPUTATION OF LOWEST EIGENVALUES AND DERIVATION OF EQ. (14)

In this section we give details for the determination of the ground state energy and spectral gap of (1) the Hamiltonian H = −A on a graph with ℓ rings and (2) its continuum approximation $H^{\left(\text{cont}\right)}=-3-\frac{3}{4}{h}^3{\Delta }_g$ on a disk of radius $L=\sqrt{N/\left(N+28\right)}$.

Graph Hamiltonian.

Denote the lowest two eigenvalues of H by E₀ and E₁ > E₀. For moderately sized ℓ ≲ 7 we easily find the spectrum of A using matrix diagonalization. For larger ℓ ⩾ 8, due to the exponential increase in the size of the matrix, we use sparse matrix techniques to determine the lowest two eigenvalues. Specifically, we employ the numerical Lanczos algorithm to estimate E₀ and E₁, and estimate the results to be reliable to about three significant digits. Note that the accuracy of the algorithm becomes worse as the spacing between E₀ and E₁ becomes smaller. Since a more precise determination of the values of E₀ and E₁ is not among the goals of the present work, we are not able to test whether the relative error between E_0,1 and $E_{0,1}^{\left(\text{cont}\right)}$ decreases as ℓ → ∞. The results are summarized in Table III.

Continuous Hamiltonian.

The eigenvalues of H^(cont) read

$$E_{nm}=-3+\frac{3}{4}{h}^2\left(k_{nm}^2+1\right),$$ (F1)

where k_nm satisfies the Dirichlet boundary condition

$$P_{{\nu }_{nm}}^m\left(\frac{1+L^2}{1-L^2}\right)=0$$ (F2)

with Legendre function of the first kind $P_v^m$ and $v_{nm}=\frac{1}{2}\left(-1+i{k}_{nm}\right)$. We label the eigenenergies by n = 1, 2, 3, … and $m\in \mathbb{Z}$. The ground and first excited states have azimuthal quantum numbers m = 0 and m = 1, respectively. In order to declutter notation in the following we define

$${\text{k}}_0=k_{1,0},E_0^{\left(\text{cont}\right)}=-3+\frac{3}{4}{h}^2\left(k_0^2+1\right),$$ (F3)

$${\text{k}}_0=k_{1,1},E_1^{\left(\text{cont}\right)}=-3+\frac{3}{4}{h}^2\left(k_1^2+1\right).$$ (F4)

Equation (F2) is readily solved numerically and we present the lowest two eigenvalues $E_0^{\left(\text{cont}\right)}$ and $E_1^{\left(\text{cont}\right)}$ in Table III.

We can employ Eq. (F2) to compute the asymptotic behavior of k₀ as L → 1 (or equivalently ℓ → ∞). For large x → ∞ we have

$$\begin{gathered} P_{\nu }\left(x\to \infty \right)~{\left(\frac{2}{x}\right)}^{\frac{1}{2}\left(1+ik\right)}\frac{\Gamma \left(-ik\right)}{\Gamma {\left(\frac{1}{2}\left(1-ik\right)\right)}^2} \\ +{\left(\frac{2}{x}\right)}^{\frac{1}{2}\left(1-ik\right)}\frac{\Gamma \left(ik\right)}{\Gamma {\left(\frac{1}{2}\left(1+ik\right)\right)}^2} \end{gathered}$$ (F5)

\ with Euler’s Γ function. In order to find the zeros we consider the amplitude

$$\begin{gathered} {\left|P_{\nu }\left(x\to \infty \right)\right|}^2~\left(\frac{2}{x}\right){\left|\frac{\Gamma \left(-ik\right)}{\Gamma {\left(\frac{1}{2}\left(1-ik\right)\right)}^2}\right|}^2\times {\left|1+{\left(\frac{2}{x}\right)}^{-ik}\frac{\Gamma \left(ik\right)\Gamma {\left(\frac{1}{2}\left(1-ik\right)\right)}^2}{\Gamma \left(-ik\right)\Gamma {\left(\frac{1}{2}\left(1+ik\right)\right)}^2}\right|}^2 \\ =\frac{2}{x}\frac{{\cosh }^2\left(\pi k/2\right)}{\pi k\sinh \left(\pi k\right)}\times {\left|1+{\left(\frac{2}{x}\right)}^{-ik}{e}^{i\Phi \left(k\right)}\right|}^2 \end{gathered}$$ (F6)

with

$$i\Phi \left(k\right)=\ln \left(\frac{\Gamma \left(ik\right)\Gamma {\left(\frac{1}{2}\left(1-ik\right)\right)}^2}{\Gamma \left(-ik\right)\Gamma {\left(\frac{1}{2}\left(1+ik\right)\right)}^2}\right).$$ (F7)

The first term in Eq. (F6) is positive. Thus the lowest zero k₀ for L → 1 follows from

$$\begin{gathered} \pi \stackrel{!}{=}-k_0\ln \left(\frac{2}{x}\right)+\Phi \left(k_0\right) \\ =-k_0\ln \left(\frac{2}{x}\right)-\pi +4k_0\ln 2+O\left(k^3\right) \\ =-\pi \text{+}{k}_0\ln \left(8x\right)+O\left(k^3\right) \end{gathered}$$ (F8)

for $x=\frac{1+L^2}{1-L^2}\to \infty$. Consequently,

$$k_0~\frac{2\pi }{\ln \left(8\frac{1+L^2}{1-L^2}\right)}\simeq \frac{\pi }{\ln \left(2{\phi }^{\ell }\right)}.$$ (F9)

We inserted N ~ 7φ^2ℓ with golden ratio $\phi =\left(1+\sqrt{5}\right)/2$ such that $\frac{1+L^2}{1-L^2}~\frac{1}{2}{\phi }^{2\ell }$. The ground state energy for large ℓ follows as

$$E_0^{\left(\text{cont}\right)}~-3+\frac{3}{4}{h}^2+\frac{3{\pi }^2{h}^2}{4}\frac{1}{{\left[\ln \phi \ell +\ln 2\right]}^2}.$$ (F10)

The first excited state energy of H^(cont) can be determined in a fully analogous way from

$$P_{{\nu }_1}^1\left(\frac{1+L^2}{1-L^2}\right)=0,{\nu }_1=\frac{1}{2}\left(-1+i{k}_1\right).$$ (F11)

We have

$$\left|P_{\nu }^1{\left(x\to \infty \right)}^2\right|\propto {\left|1+{\left(\frac{2}{x}\right)}^{-ik}{e}^{i{\Phi }_1\left(k\right)}\right|}^2$$ (F12)

with

$$i{\Phi }_1\left(k\right)=\ln \left(\frac{\Gamma \left(ik\right)\Gamma \left(\frac{1}{2}\left(1-ik\right)\right)\Gamma \left(\frac{1}{2}\left(-1-ik\right)\right)}{\Gamma \left(-ik\right)\Gamma \left(\frac{1}{2}\left(1+ik\right)\right)\Gamma \left(\frac{1}{2}\left(-1+ik\right)\right)}\right).$$ (F13)

Hence k₁ for $x=\frac{1+L^2}{1-L^2}\to \infty$ is found from

$$\begin{gathered} \pi \stackrel{!}{=}-k_1\ln \left(\frac{2}{x}\right)+{\Phi }_1\left(k_1\right) \\ =-k_1\ln \left(\frac{2}{x}\right)-\pi +2\left[2\ln 2-1\right]k_1+O\left(k_1^3\right) \\ =-\pi -k_1\ln \left(\frac{8x}{e^2}\right)+O\left(k_1^3\right). \end{gathered}$$ (F14)

This implies

$$k_1~\frac{2\pi }{\ln \left(\frac{8}{e^2}\frac{1+L^2}{1-L^2}\right)}\simeq \frac{\pi }{\ln \left(\frac{2}{e}{\phi }^{\ell }\right)}$$ (F15)

and

$$E_1^{\left(\text{cont}\right)}~-3+\frac{3}{4}{h}^2+\frac{3{\pi }^2{h}^2}{4}\frac{1}{{\left[\ln \phi \ell +\ln 2-1\right]}^2}.$$ (F16)

APPENDIX G: DERIVATION OF EQ. (16)

In this section we derive the relation between the graph green function G_ij(ω) and the continuum Green function G(z, z′, λ, L) using an auxiliary field path integral representation.

We first recall some path integral identities [70]. If θ_i is a discrete real variable and M_ij a real and symmetric matrix then

$$\langle {\theta }_i{\theta }_j\rangle :=\frac{\int D\theta {\theta }_i{\theta }_j{e}^{-\frac{1}{2}{\theta }_k{M}_{kl}{\theta }_l}}{\int D\theta e^{-\frac{1}{2}{\theta }_k{M}_{kl}{\theta }_l}}={\left(M^{-1}\right)}_{ij}$$ (G1)

with $D\theta ={\prod }_{i}d{\theta }_i$. Furthermore, if θ(x) is a real field and $\widehat{D}$ a differential operator, then $D\theta ={\prod }_{x}d\theta \left(x\right)$ and

$$\langle \theta \left(x\right)\theta \left(y\right)\rangle :=\frac{\int D\theta \theta \left(x\right)\theta \left(y\right)e^{-\frac{1}{2}\int d^{d}r\theta \widehat{D}\theta }}{\int D\theta e^{-\frac{1}{2}\int d^{d}r\theta \widehat{D}\theta }}=-G\left(x,y\right),$$ (G2)

where G(x, y) is the Green function of $\widehat{D}$ according to

$$\widehat{D}G\left(x,y\right)=-{\delta }^{\left(d\right)}\left(x-y\right)$$ (G3)

This can be applied to match the Green function on the graph G_ij to the continuum Green function G(z, z′) evaluated on the graph sites. The graph Green function is given by

$$G_{ij}\left(\omega ,\ell \right)={\left(\frac{1}{H-\omega \mathbb{1}}\right)}_{ij}=\sum _{n=1}^N\frac{{\psi }_n\left(z_i\right){\psi }_n^{*}\left(z_j\right)}{{\epsilon }_n-\omega }$$ (G4)

with H = −A and Hψ_n = ε_nψ_n. Introduce the auxiliary real field θ_i → θ(z_i) and approximate $H\approx -3-\frac{3}{4}{h}^2{\Delta }_g$ and ${\sum }_i\approx \frac{28}{\pi }\underset{\left|z\right|⩽L}{\int }\frac{d^{2}z}{{\left(1-{\left|z\right|}^2\right)}^2}$ to find

$$\begin{gathered} G_{ij}\left(\omega ,\ell \right)=\frac{\int D\theta {\theta }_i{\theta }_j\exp \left[-\frac{1}{2}{\sum }_{i,j}{\theta }_i{\left(H-\omega \mathbb{1}\right)}_{ij}{\theta }_j\right]}{\int D\theta \exp \left[-\frac{1}{2}{\sum }_{i,j}{\theta }_i{\left(H-\omega \mathbb{1}\right)}_{ij}{\theta }_j\right]} \\ =\frac{\int D\theta {\theta }_i{\theta }_j\exp \left[-\frac{1}{2}{\sum }_{i,j}{\theta }_i{\left[\left(3\mathbb{1}-A\right)-\left(\omega +3\right)\mathbb{1}\right]}_{ij}{\theta }_j\right]}{\int D\theta \exp \left[-\frac{1}{2}{\sum }_{i,j}{\theta }_i{\left[\left(3\mathbb{1}-A\right)-\left(\omega +3\right)\mathbb{1}\right]}_{ij}{\theta }_j\right]} \\ \approx \frac{\int D\theta \theta \left(z_i\right)\theta \left(z_j\right)\exp \left[-\frac{1}{2}\frac{28}{\pi }\underset{\left|z\right|⩽L}{\int }\frac{d^{2}z}{{\left(1-{\left|z\right|}^2\right)}^2}\theta \left(z\right)\left[-\frac{3h^2}{4}{\Delta }_g-\left(\omega +3\right)\right]\theta \left(z\right)\right]}{\int D\theta \exp \left[-\frac{1}{2}\frac{28}{\pi }\underset{\left|z\right|⩽L}{\int }\frac{d^{2}z}{{\left(1-{\left|z\right|}^2\right)}^2}\theta \left(z\right)\left[-\frac{3h^2}{4}{\Delta }_g-\left(\omega +3\right)\right]\theta \left(z\right)\right]} \\ =\frac{\int D\theta \theta \left(z_i\right)\theta \left(z_j\right)\exp \left[-\frac{1}{2}{C}^{\prime }\underset{\left|z\right|⩽L}{\int }\frac{d^{2}z}{{\left(1-{\left|z\right|}^2\right)}^2}\theta \left(z\right)\left[-{\Delta }_g-\lambda \right]\theta \left(z\right)\right]}{\int D\theta \exp \left[-\frac{1}{2}{C}^{\prime }\underset{\left|z\right|⩽L}{\int }\frac{d^{2}z}{{\left(1-{\left|z\right|}^2\right)}^2}\theta \left(z\right)\left[-{\Delta }_g-\lambda \right]\theta \left(z\right)\right]} \\ =\frac{1}{C^{\prime }}G\left(z_i,z_j,\lambda ,L\right) \end{gathered}$$ (G5)

with

$$C^{\prime }=\frac{3h^2}{4}\frac{28}{\pi }=\frac{21h^2}{\pi }=0.508,\lambda \text{=}\frac{4\left(\omega +3\right)}{3h^2}.$$ (G6)

Here G(z, z′, λ, L) is the hyperbolic Green function of (Δ_g + λ) on a disk of radius L, i.e.,

$$\frac{1}{{\left(1-{\left|z\right|}^2\right)}^2}\left({\Delta }_g+\lambda \right)G\left(z,z^{\prime },\lambda ,L\right)=-{\delta }^{\left(2\right)}\left(z-z^{\prime }\right).$$ (G7)

We conclude

$$G_{ij}\left(\omega ,\ell \right)=\frac{\pi }{21h^2}G\left(z_i,z_j,\lambda =\frac{4\left(\omega +3\right)}{3h^2},L\right).$$ (G8)

APPENDIX H: CONTINUUM GREEN FUNCTION (COMPUTATION)

In this section, we compute Green’s functions for the hyperbolic Laplacian Δ_g and hyperbolic Helmholtz operator λ + Δ_g (with $\lambda \in \mathbb{C}$) on the disk of radius L ⩽ 1 with Dirichlet boundary conditions. A self-contained summary of the relevant formulas is given in Appendix I.

Definition.

The Green function is defined by

$$\left(\lambda +{\Delta }_g\right)G\left(z,z^{\prime },\lambda ,L\right)=-{\left(1-{\left|z\right|}^2\right)}^2{\delta }^{\left(2\right)}\left(z-z^{\prime }\right)$$ (H1)

with ${\Delta }_g={\left(1-{\left|z\right|}^2\right)}^{2}4{\partial }_z{\stackrel{\_}{\partial }}_z$ acting on z and Dirichlet boundary conditions such that G(z, z′, λ, L) = 0 for |z| = L or |z′| = L. Here (1 − |z|²)²δ⁽²⁾(z − z′) is the δ function with respect to the hyperbolic volume measure. For an arbitrary continuous function $f:\mathbb{D}\to \mathbb{C}$ it is defined by

$$\underset{\mathbb{D}}{\int }\frac{d^{2}z}{{\left(1-{\left|z\right|}^2\right)}^2}{\left(1-{\left|z\right|}^2\right)}^2{\delta }^{\left(2\right)}\left(z-z^{\prime }\right)f\left(z\right)=f\left(z^{\prime }\right).$$ (H2)

In Cartesian coordinates such that z = x + iy we have d²z = dx dy and δ⁽²⁾(z − z′) = δ(x − x′)δ(y − y′).

Spectral representation.

It is always possible to give a closed expression for the Green function in terms of the spectral decomposition of the operator. For this write the eigenfunctions of the hyperbolic Laplacian in radial coordinates by g_km(r)e^imϕ with g_km from Eq. (E10). The normalized eigenfunctions of Δ_g on the disk of radius L < 1 are given by

$${\psi }_{nm}\left(z\right)=\frac{g_{k_{nm}m}\left(r\right)e^{im\varphi }}{\Vert g_{k_{nm}m}\Vert },$$ (H3)

where k_nm solves g_knmm(L) = 0 and the norm is

$${\Vert g_{km}\Vert }^2=2\pi \underset{0}{\overset{L}{\int }}\frac{drr}{{\left(1-r^2\right)}^2}{\left|g_{km}\left(r\right)\right|}^2.$$ (H4)

The Green function can then be written in spectral representation as

$$G\left(z,z^{\prime },\lambda ,L\right)=\sum _{m=-\infty }^{\infty }\sum _n\frac{{\psi }_{nm}\left(z\right){\psi }_{nm}^{*}\left(z^{\prime }\right)}{-\lambda +k_{nm}^2+1}.$$ (H5)

Equation (H1) follows from the completeness of the eigenfunctions and the Dirichlet boundary condition is satisfied due to ψ_nm(z) = 0 for |z| = L. However, the spectral representation is not the most useful form of the Green function since it requires one to determine the discrete momenta k_nm and subsequently to perform the double-sum numerically. Thus we derive a few complementary expressions in the following.

Hyperbolic Laplacian.

First consider the case λ = 0, where Eq. (H1) reduces to

$${\Delta }_{g}G\left(z,z^{\prime },0,L\right)=-{\left(1-{\left|z\right|}^2\right)}^2{\delta }^{\left(2\right)}\left(z-z^{\prime }\right).$$ (H6)

We divide by (1 − |z|²)² and observe that G(z, z′, 0, L) coincides with the Green function of the ordinary Laplacian Δ on a disk of radius L < 1. The latter is given by

$$G\left(z,z^{\prime },0,L\right)=-\frac{1}{4\pi }\ln {\left|z-z^{\prime }\right|}^2+\delta G\left(z,z^{\prime },0,L\right),$$ (H7)

where the first term is the fundamental solution, while the second term is a harmonic function ensuring Dirichlet boundary conditions. We construct δG from a mirror charge outside the disk, whose location is obtained from inversion on the circle, $z^{\prime }\to L^2/{\stackrel{\_}{z}}^{\prime }$. Hence

$$\delta G\left(z,z^{\prime },0,L\right)=\frac{1}{4\pi }\ln {\left|z-\frac{L^2}{{\stackrel{\_}{z}}^{\prime }}\right|}^2+\text{const}$$ (H8)

with a suitably chosen constant. We arrive at

$$G\left(z,z^{\prime },0,L\right)=-\frac{1}{4\pi }\ln {\left|\frac{L\left(z-z^{\prime }\right)}{L^2-z{\stackrel{\_}{z}}^{\prime }}\right|}^2.$$ (H9)

For z′ = 0 we have

$$G\left(r,0,0,L\right)=-\frac{1}{2\pi }\ln \left(\frac{r}{L}\right)=-\frac{1}{2\pi }\ln \left(\frac{\tanh d\left(r,0\right)}{L}\right)$$ (H10)

with d(r, 0) the distance from the origin.

Hyperbolic Helmholtz operator.

Now consider the case of arbitrary $\lambda \in \mathbb{C}$. We construct the Green function by reducing the problem to a one-dimensional Sturm–Liouville problem. We refer to Appendix C of Ref. [71] for a detailed discussion of the procedure. Write

$$G\left(z,z^{\prime },\lambda ,L\right)={\mathcal{G}}_0\left(z,z^{\prime },\lambda \right)-\delta \mathcal{G}\left(z,z^{\prime },\lambda ,L\right),$$ (H11)

where ${\mathcal{G}}_0$ is the fundamental solution and $\delta \mathcal{G}$ is a harmonic function to ensure Dirichlet boundary conditions. To construct these functions, we first solve, for z ≠ 0, the equation

$$\left(\lambda +{\Delta }_g\right)f\left(z\right)=0$$ (H12)

through an ansatz

$$f\left(z\right)=\sum _{m=-\infty }^{\infty }{f}_{\lambda m}\left(\rho \right)e^{im\varphi }$$ (H13)

with $\rho =\frac{1+r^2}{1-r^2}$. Then f_λm satisfies Legendre’s differential equation

$$\left(1-{\rho }^2\right)f_{\lambda m}^{″}-2\rho f_{\lambda m}^{\prime }+\left(\nu \left(\nu +1\right)-\frac{m^2}{1-{\rho }^2}\right)f_{\lambda m}=0$$ (H14)

with $\nu =\frac{1}{2}\left(-1+i\sqrt{\lambda -1}\right)$ or $\frac{\lambda }{4}=-\nu \left(\nu +1\right)$. The two linearly independent solutions are

$$u_m\left(\rho \right)=Q_{\nu }^{\left|m\right|}\left(\rho \right),$$ (H15)

$$v_m\left(\rho \right)=P_{\nu }^{\left|m\right|}\left(\rho \right),$$ (H16)

which are the Legendre functions of the second/first kind, being singular/regular at ρ = 1. Without loss of generality we assume m ⩾ 0 in the following, otherwise replace m → |m|.

Introduce the Sturm-Liouville operator

$$L_m=-4\left(\frac{d}{d\rho }\left[p\left(\rho \right)\frac{d}{d\rho }\right]+q_m\left(\rho \right)\right)$$ (H17)

with

$$p\left(\rho \right)=\left(1-{\rho }^2\right),q_m\left(\rho \right)=\nu \left(\nu +1\right)-\frac{m^2}{1-{\rho }^2}.$$ (H18)

We have

$$\left(\lambda +{\Delta }_g\right)f\left(z\right)=\sum _{m=-\infty }^{\infty }{e}^{im\varphi }{L}_m{f}_{\lambda m}\left(\rho \right).$$ (H19)

The fundamental solution of L_m is defined through

$$L_m{G}_m\left(\rho ,{\rho }^{\prime }\right)=-4\delta \left(\rho -{\rho }^{\prime }\right),$$ (H20)

with the factor of 4 for later convenience. It is given by

$$\begin{gathered} G_m\left(\rho ,{\rho }^{\prime }\right)=C_m{u}_m\left({\rho }_{\max }\right)v_m\left({\rho }_{\min }\right) \\ =C_m[u_m\left(\rho \right)v_m\left({\rho }^{\prime }\right)\Theta \left(\rho -{\rho }^{\prime }\right)+u_m\left({\rho }^{\prime }\right)v_m\left(\rho \right)\Theta \left({\rho }^{\prime }-\rho \right)], \end{gathered}$$ (H21)

where ρ_max(ρ_min) is the maximum (minimum) of ρ and ρ′, and C_m a constant to be determined. To verify Eq. (H20), use L_mu_m = 0 and L_mv_m = 0 and the definition of L_m to find

$$L_m{G}_m\left(\rho ,{\rho }^{\prime }\right)=4C_m{k}_m\left(\rho \right)\delta \left(\rho -{\rho }^{\prime }\right),$$ (H22)

Where

$${\kappa }_m\left(\rho \right)=p\left(\rho \right)\left[{u^{\prime }}_m\left(\rho \right)v_m\left(\rho \right)-u_m\left(\rho \right){v^{\prime }}_m\left(\rho \right)\right]$$ (H23)

$$=-\frac{4^m\Gamma \left(\frac{\nu +m+2}{2}\right)\Gamma \left(\frac{\nu +m+1}{2}\right)}{\Gamma \left(\frac{\nu -m+2}{2}\right)\Gamma \left(\frac{\nu -m+1}{2}\right)}$$ (H24)

is constant and follows from the Wronksian of Legendre’s functions [69]. Thus we have to choose C_m = −1/κ_m and find

$$C_m=\frac{\Gamma \left(\frac{\nu -m+2}{2}\right)\Gamma \left(\frac{\nu -m+1}{2}\right)}{4^m\Gamma \left(\frac{\nu +m+2}{2}\right)\Gamma \left(\frac{\nu +m+1}{2}\right)}$$ (H25)

or

$$C_0=1,$$ (H26)

$$C_{m\ne 0}=\frac{{\left(-1\right)}^{\left|m\right|}}{{\prod }_{n=0}^{\left|m\right|-1}\left[{\left(n+\frac{1}{2}\right)}^2+\frac{1}{4}\left(\lambda -1\right)\right]}.$$ (H27)

We conclude that the fundamental solution of λ + Δ_g is given by

$${\mathcal{G}}_0\left(z,z^{\prime },\lambda \right)=\frac{1}{2\pi }\sum _{m=-\infty }^{\infty }{e}^{im\left(\varphi -{\varphi }^{\prime }\right)}{G}_m\left(\rho ,{\rho }^{\prime }\right).$$ (H28)

Indeed, using ${\sum }_m{e}^{im\left(\varphi -{\varphi }^{\prime }\right)}=2\pi \delta \left(\varphi -{\varphi }^{\prime }\right)$ and

$$\begin{gathered} {\left(1-{\left|z\right|}^2\right)}^2{\delta }^{\left(2\right)}\left(z-z^{\prime }\right)=\frac{{\left(1-r^2\right)}^2}{r}\delta \left(r-r^{\prime }\right)\delta \left(\varphi -{\varphi }^{\prime }\right) \\ =4\delta \left(\rho -{\rho }^{\prime }\right)\delta \left(\varphi -{\varphi }^{\prime }\right) \end{gathered}$$ (H29)

we verify

$$\begin{gathered} \left(\lambda +{\Delta }_g\right){\mathcal{G}}_0\left(z,z^{\prime },\lambda \right)=\frac{1}{2\pi }\sum _{m=-\infty }^{\infty }{e}^{im\left(\varphi -{\varphi }^{\prime }\right)}{L}_m{G}_m\left(\rho ,{\rho }^{\prime }\right) \\ =-\frac{1}{2\pi }\sum _{m=-\infty }^{\infty }{e}^{im\left(\varphi -{\varphi }^{\prime }\right)}\text{4}\delta \left(\rho -{\rho }^{\prime }\right) \\ =-{\left(1-{\left|z\right|}^2\right)}^2{\delta }^{\left(2\right)}\left(z-z^{\prime }\right). \end{gathered}$$ (H30)

Equation (H28) for the fundamental solution ${\mathcal{G}}_0$ allows one to easily construct the correction $\delta \mathcal{G}$ such that the total Green function $G={\mathcal{G}}_0-\delta \mathcal{G}$ satisfies Dirichlet boundary conditions: If either |z| = L or |z′| = L, then ${\rho }_{\max }=\frac{1+L^2}{1-L^2}$. Consequently, we choose

$$\delta \mathcal{G}\left(z,z^{\prime },\lambda ,L\right)=\frac{1}{2\pi }\sum _{m=-\infty }^{\infty }{e}^{im\left(\varphi -{\varphi }^{\prime }\right)}{C}_m{v}_m\left(\rho \right)v_m\left({\rho }^{\prime }\right)\frac{u_m\left(\frac{1+L^2}{1-L^2}\right)}{v_m\left(\frac{1+L^2}{1-L^2}\right)}.$$ (H31)

This is a harmonic function and satisfies ${\mathcal{G}}_0=\delta \mathcal{G}$ whenever |z| = L or |z′| = L. As an illustrative example consider the central correlation function for z′ = 0. We have

$$G\left(z,0,\lambda ,L\right)=\frac{1}{2\pi }\left[Q_{\nu }\left(\frac{1+r^2}{1-r^2}\right)-\frac{Q_{\nu }\left(\frac{1+L^2}{1-L^2}\right)}{P_{\nu }\left(\frac{1+L^2}{1-L^2}\right)}{P}_{\nu }\left(\frac{1+r^2}{1-r^2}\right)\right],$$ (H32)

clearly vanishing for r = L.

The Green function for L = 1 can be given in closed form, because it can only depend on the hyperbolic invariant d(z, z′). Making the ansatz $\mathcal{G}\left(z,z^{\prime },\lambda ,1\right)=F\left(y\right)$ with

$$y=\cosh \left[2d\left(z,z^{\prime }\right)\right]=1+\frac{2{\left|z-z^{\prime }\right|}^2}{\left(1-{\left|z\right|}^2\right)\left(1-{\left|z^{\prime }\right|}^2\right)},$$ (H33)

we find for z ≠ z (or y > 1) that

$$\begin{gathered} 0\stackrel{!}{=}\left(\lambda +{\Delta }_g\right)F\left(y\right) \\ =-2\left[\left(1-y^2\right)F^{″}\left(y\right)-2y{F}^{\prime }\left(y\right)-\frac{\lambda }{4}F\left(y\right)\right], \end{gathered}$$ (H34)

which again is Legendre’s differential equation. The singular contribution gives the fundamental solution, because

$$Q_v\left(y\to 1\right)~-\ln \left(\frac{1}{2}\text{arcosh}\left(y\right)\right)+\text{const},$$ (H35)

and the regular solution is the harmonic correction to ensure the Dirichlet boundary condition. Hence

$$\mathcal{G}\left(z,z^{\prime },\lambda ,1\right)=\frac{1}{2\pi }\left[Q_{\nu }\left(y\right)-\mathcal{C}{P}_{\nu }\left(y\right)\right]$$ (H36)

with

$$\mathcal{C}=\underset{y\to \infty }{\lim }\frac{Q_{\nu }\left(y\right)}{P_{\nu }\left(y\right)}.$$ (H37)

Importantly, since the fundamental solution does not depend on L, it is always given by [57]

$$\mathcal{G}\left(z,z^{\prime },\lambda \right)=\frac{1}{2\pi }{Q}_{\nu }\left(1+\frac{2{\left|z-z^{\prime }\right|}^2}{\left(1-{\left|z\right|}^2\right)\left(1-{\left|z^{\prime }\right|}^2\right)}\right).$$ (H38)

To compute the constant $\mathcal{C}$, the parameter λ needs to be restricted to $\lambda \in \mathbb{C}\backslash \left[1,\infty \right)$, since the spectrum k² + 1 of −Δ_g on the infinite disk is in the interval [1, ∞). For real λ < 1 this implies ν < −1/2. We expand P_ν(y) and Q_ν(y) for large y and arrive at

$$\mathcal{C}=\frac{2^{\nu }{i}^{-\nu }{\pi }^{3/2}\Gamma \left(-\nu \right)}{\Gamma \left(1+\frac{\nu }{2}\right)\Gamma \left(\frac{1+\nu }{2}\right)}[-\cos \left(\frac{\pi \nu }{2}\right)\frac{\Gamma {\left(1+\frac{\nu }{2}\right)}^2}{\Gamma {\left(\frac{1-\nu }{2}\right)}^2}+i\sin \left(\frac{\pi \nu }{2}\right)\frac{\Gamma {\left(1+\frac{\nu }{2}\right)}^2}{\Gamma {\left(-\frac{\nu }{2}\right)}^2}].$$ (H39)

APPENDIX I: CONTINUUM GREEN FUNCTION (SUMMARY)

We summarize the expressions for the Green function G(z, z′, λ, L) derived in Appendix H. We write

$$G\left(z,z^{\prime },\lambda ,L\right)={\mathcal{G}}_0\left(z,z^{\prime },\lambda \right)-\delta \mathcal{G}\left(z,z^{\prime },\lambda ,L\right),$$ (I1)

where the first term is given by

$${\mathcal{G}}_0\left(z,z^{\prime },\lambda \right)=\frac{1}{2\pi }{Q}_v\left(1+\frac{2{\left|z-z^{\prime }\right|}^2}{\left(1-{\left|z\right|}^2\right)\left(1-{\left|z^{\prime }\right|}^2\right)}\right)$$ (I2)

with $Q_{\nu }=Q_{\nu }^{m=0}$ the Legendre function of the second kind and

$$\nu =\frac{1}{2}\left(-1+i\sqrt{\lambda -1}\right).$$ (I3)

The second term reads

$$\begin{gathered} \delta \mathcal{G}\left(z,z^{\prime },\lambda ,L\right)=\frac{1}{2\pi }{P}_{\nu }\left(\rho \right)P_{\nu }\left({\rho }^{\prime }\right)\frac{Q_{\nu }\left(\frac{1+L^2}{1-L^2}\right)}{P_{\nu }\left(\frac{1+L^2}{1-L^2}\right)} \\ +\frac{1}{\pi }\sum _{m=1}^{\infty }{C}_m\cos \left[m\left(\varphi -{\varphi }^{\prime }\right)\right]P_{\nu }^m\left(\rho \right) \\ \times P_{\nu }^m\left({\rho }^{\prime }\right)\frac{Q_{\nu }^m\left(\frac{1+L^2}{1-L^2}\right)}{P_{\nu }^m\left(\frac{1+L^2}{1-L^2}\right)}. \end{gathered}$$ (I4)

with $P_{\nu }^m$ and $Q_{\nu }^m$ the Legendre function of the first and second kind, hyperbolic invariant

$$\rho =\frac{1+r^2}{1-r^2},$$ (I5)

and

$$C_m=\frac{\Gamma \left(\frac{\nu -m+2}{2}\right)\Gamma \left(\frac{\nu -m+1}{2}\right)}{4^m\Gamma \left(\frac{\nu +m+2}{2}\right)\Gamma \left(\frac{\nu +m+1}{2}\right)}.$$ (I6)

In practice, it is sufficient to limit the sum over m to the first few (typically ten or less) terms. For L = 1 we have

$$\delta \mathcal{G}\left(z,z^{\prime },\lambda ,1\right)=\frac{\mathcal{C}}{2\pi }{P}_v\left(1+\frac{2{\left|z-z^{\prime }\right|}^2}{\left(1-{\left|z\right|}^2\right)\left(1-{\left|z^{\prime }\right|}^2\right)}\right)$$ (I7)

with $P_{\nu }=P_{\nu }^{m=0}$ and

$$\mathcal{C}=\frac{2^{\nu }{i}^{-\nu }{\pi }^{3/2}\Gamma \left(-\nu \right)}{\Gamma \left(1+\frac{\nu }{2}\right)\Gamma \left(\frac{1+\nu }{2}\right)}[-\cos \left(\frac{\pi \nu }{2}\right)\frac{\Gamma {\left(1+\frac{\nu }{2}\right)}^2}{\Gamma {\left(\frac{1-\nu }{2}\right)}^2}+i\sin \left(\frac{\pi \nu }{2}\right)\frac{\Gamma {\left(1+\frac{\nu }{2}\right)}^2}{\Gamma {\left(-\frac{\nu }{2}\right)}^2}].$$ (I8)