Abstract
Functional magnetic resonance imaging allows precise localization of brain regions specialized for different perceptual and higher cognitive functions. However, targeting these deep brain structures for electrophysiology still remains a challenging task. Here, we propose a novel framework for MRI-stereotactic registration and chamber placement for precise electrode guidance to recording sites defined in MRI space. The proposed “floating frame” approach can be used without usage of ear bars, greatly reducing pain and discomfort common in standard stereotactic surgeries. Custom pre-surgery planning software was developed to automatically solve the registration problem and report the set of parameters needed to position a stereotactic manipulator to reach a recording site along arbitrary, non-vertical trajectories. Furthermore, the software can automatically identify blood vessels and assist in finding safe trajectories to targets. Our approach was validated by targeting different regions in macaque monkeys and rats. We expect that our method will facilitate recording in new brain areas and provide a valuable tool for electrophysiologists.
Introduction
Neural recordings have been traditionally guided by atlas based stereotactic planning. However, most atlases are based on a single animal1–4, which introduces the problem of inter-subject variability. Furthermore, precise localization and alignment of internal features, such as Bregma and Lambda, on the same plane can be very challenging due to variability in suture appearance. Any deviation from the Bregma-Lambda or Ear Bar Zero (EBZ) plane will introduce significant deviations in deep brain targeting. Another associated problem with atlas based targeting is the risk of hitting a blood vessel. Many region of interests (ROIs) are located directly below major blood vessels, ruling out vertical penetration due to the risk of intracerebral hemorrhage.
With the increased availability of functional localizers it is now possible to pinpoint, with exquisite sub-millimeter precision, brain regions representing visual, auditory, somatosensory information or those participating in higher cognitive functions, such as decision making and language5–9. While fMRI can report activity on a global scale, its temporal and spatial characteristics cannot replace data obtain with electrophysiology, and fMRI activity is only an indirect reflection of underlying activity10,11. Thus, electrophysiological characterization of neural activity in fMRI-identified brain regions is critically needed.
Targeting structures which have been identified in MRI for electrophysiological recording is challenging due to the inherent difference in coordinate systems. While a specific region of interest can be easily and precisely defined in MR space in voxel coordinates, recordings are guided according to stereotactic coordinates. The problem, therefore, is to find a way to register these two systems and to translate a given position and orientation in MR space to a set of parameters that configure the stereotactic arm manipulator to target the intended ROI (Fig. 1).
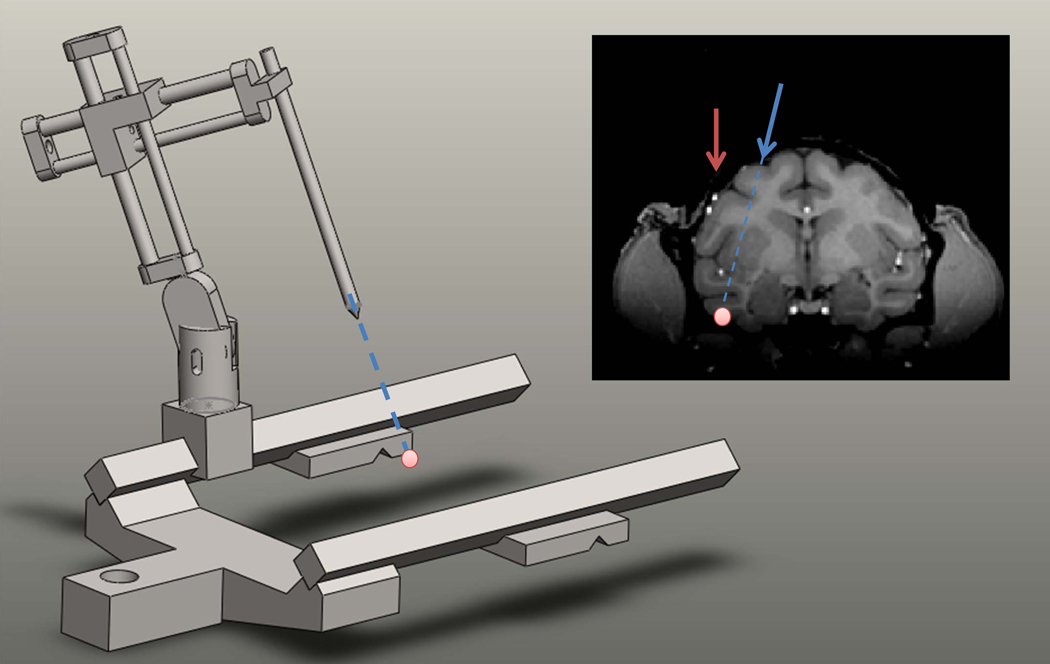
Figure 1. The general targeting problem.
A target in an MR scan (pink dot) is selected according to anatomical or functional considerations. The problem is to position the stereotactic manipulator such that the tip aligns with the desired trajectory. Notice that blood vessels above the target site (small white dots) pose a problem for simple vertical penetration (red line), while a non-vertical trajectory can safely reach the target (blue line).
A traditional solution to the registration problem is to identify in the MR scan a set of features that can be used to determine how the brain would be oriented once the animal is positioned in the stereotactic frame1,3. Physically, stereotactic coordinates are defined by the line passing through the ear canals (AP0) and the horizontal plane passing through the interaural line and the infraorbital ridge. These skeletal features, however, are difficult to localize precisely in anatomical scans: (1) The ear canals are especially vulnerable to magnetic susceptibility artifacts, which can cause spatial mislocalization of the interaural line. (2) The eye orbitals are impossible to see with standard anatomical sequences, leading to use of alignment of the anterior and posterior commissures as an alternate definition of the horizontal plane. Significant mismatch can occur between this definition and the physical definition, leading to a large error during actual stereotactic surgeries.
Here, we propose a novel framework that solves the general registration problem between the MR coordinate frame and the stereotactic frame during the surgical procedure (Fig. 2). The method relies on a machine vision algorithm that finds the optimal transformation between the two coordinate frames by registering a small number of artificial external markers. The framework allows positioning a recording chamber, according to pre-surgery planning, and is not limited to vertical penetrations. Since the registration problem is solved in real time, the stereotactic frame can be physically detached from the animal (ear bars are not inserted to the ear canals). This “floating frame” approach permits implantation of chambers while the animal is simply head fixed in the primate chair, greatly reducing discomfort and complications involved in full stereotactic surgery.
Figure 2. Framework overview.
A brain region is selected for targeting and a virtual chamber is placed. Several external markers are rigidly attached to the skull by drilling into an existing implant or securing a small attachment to the head post (not shown). Marker positions in the MR image is identified. During the surgical procedure the position of the markers is read out using the stereotactic manipulator. This can be done even if the stereotactic frame is not physically attached to the animal, but instead to the primate chair. The software solves the targeting problem given the read out values and outputs the set of parameters that are needed to align the manipulator with the planned virtual chamber position.
We designed general purpose pre-surgery planning software that can be used with various stereotactic frames and manipulators (available for download from http://www.tsaolab.caltech.edu/) and hence is of usage not only for primate research, but also for smaller animals. The software enables visualization of anatomical and functional scans and allows the user to position virtual chambers, cannulae, grids and electrodes that can assist in precise planning of electrodes’ trajectories. The software greatly assists in targeting recording sites by automatically scanning the search space of grid parameters (rotation, tilt angle, hole in grid) and reporting optimal parameters that minimize the distance to a predefined target.
Another novel feature of our software is the ability to automatically identify blood vessels in MR scans and to suggest safe chamber placements and electrode trajectories which avoid passing through them. Such solutions typically require the usage of all degrees of freedom of the stereotactic manipulator. To obtain the values required to position the stereotactic manipulator in such a way we model the stereotactic manipulator as a robotic arm and use an inverse kinematic algorithm to recover the exact parameters needed (Fig. 2). This approach is generic and the system can solve the problem for any stereotactic manipulator, as long as the user can supply a 3D description of its joints.
We envision that this system will be a valuable tool for electrophysiologists and will facilitate recordings in new brain areas, as well as other types of experiments requiring precise stereotactic targeting, e.g., injection of viral vectors or pharmacological compounds to MR-defined targets. Here, we provide experimental validation from monkeys and rats, as well as computer simulations that give the expected chamber placement error in terms of positional and angular uncertainties.
Methods
Animals and Surgery
Three male rhesus macaques, weighing 6–8 kg were used in the experiments. Surgical procedures followed standard anesthetic, aseptic, and postoperative treatment protocols. The head-post was implanted in two surgical procedures separated by several weeks recovery time. First, the monkey was anesthetized (Ketamin / Dexdomitor, 8mg/kg / 0.02mg/kg), then intubated and switched to a maintenance regime of oxygen (1L/min), and isoflurane (0.5–3 %). The monkey’s head was positioned in a stereotaxic frame, and the skull was exposed and cleaned (peroxide 30% and saline). After drilling and thread cutting, ceramic screws were inserted and covered with several layers of acrylic cement, as was all of the exposed skull area. Anesthesia was ended and the monkey was given a period of six weeks or longer to recover. In a brief second surgery, an MR-compatible head-post was attached to the initial implant using acrylic cement. Several small holes were drilled in the existing implant and served as external markers (roughly 1–2mm in diameter).
For chamber implantation in the primate chair, the monkey was head fixed by securing the head post to the primate chair. The stereotactic frame was rigidly attached to the chair using a custom designed adapter, and mounted in reverse (see Supplementary Fig 3). Marker positions were read out using the stereotactic manipulator. A light sedation (Dexdormitor, 2mg/kg) was given and a small region of the existing acrylic implant was drilled away. The chamber was then mounted along the stereotactic manipulator pole and secured with fresh acrylic.
The rat experiments were conducted on a euthanized animal. The animal was mounted in a Kopf 900A stereotactic frame and the skull was exposed. Several holes were drilled and nylon screws were inserted. The skull was then covered with acrylic and a small plastic piece with five markers was attached. Animal was then scanned and a virtual cannula position was selected at random. The planning software was used to find the manipulator coordinates and a MR-compatible cannula (C313GT, Plastics1) was implanted and filled with MR-visible contrast agent.
All procedures conformed to local and US National Institutes of Health guidelines, including the US National Institutes of Health Guide for Care and Use of Laboratory Animals.
MR Scans
Macaques were scanned in a Siemens 3T Tim Trio. Anatomical scans were acquired with an MPRAGE sequence using the following parameters: TR = 2300 ms, TE = 3.37 ms, FOV = 128, slice thickness: 0.5 mm, in-slice resolution: 0.5mm. Functional scans were acquired with an AC88 gradient insert using EPI sequence with the following parameters: TR = 2000 ms, TE = 16 ms, FOV = 100, slice thickness: 1 mm, in-slice resolution: 1 mm.
Rat anatomical scans were obtained in a Siemens 3T Tim Trio with an AC88 gradient insert using following parameters: TR = 2100 ms, TE = 3.47 ms, TI = 1100 ms, FOV = 60, slice thickness: 0.3 mm, in-slice resolution: 0.23 mm.
Results
Framework overview
External markers
The registration framework assumes that one can position MR-visible external markers that are rigidly attached to the animal skull. Such features can be easily prepared in animals that have an acrylic implant, by drilling several small holes in the existing implant and filling them with MR-visible contrast agent such as gadolinium or Vaseline. For animals with only a head post, it is possible to construct a small rigid body attachment with small capsules containing the contrast agent. Markers should be drilled vertically and not perpendicular to the skull surface as it is easier to readout their values in the former case. There is no constraint on marker placement and they can be set at random positions above the skull, as long as they provide a good coverage of the entire implant (i.e., not clustered at one corner). The minimal number of markers that is needed is three, but it is generally advised to have more (7–10) to obtain better registration accuracy.
Planning chamber placement
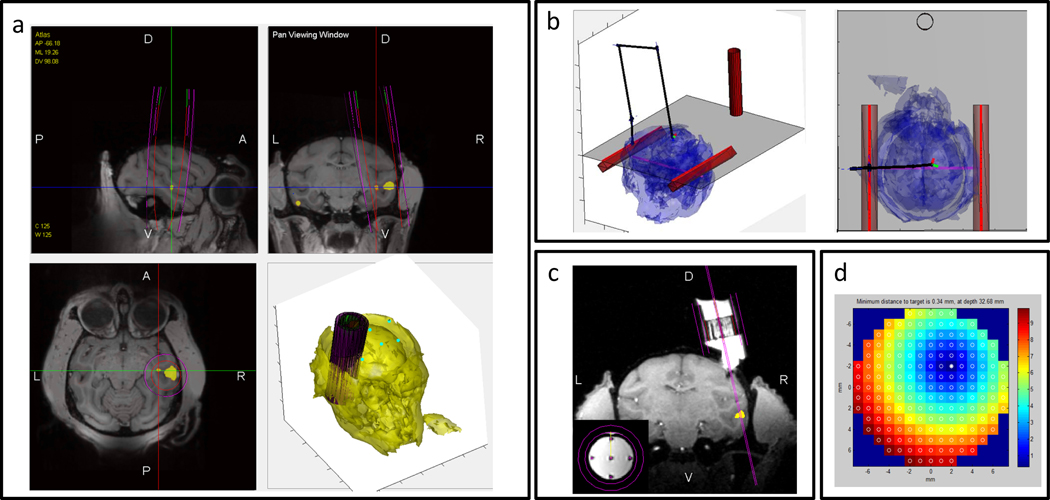
Our pre-surgery planning software allows the user to place a virtual recording chamber in an arbitrary position and orientation (pose) relative to the animal. For a given pose, virtual grids can be inserted to the virtual chamber to guide virtual electrodes into the brain. Various grid designs are available (including tilted grids). For a given grid-hole the user can visualize exactly the expected electrode trajectory and the distance from the desired target site (Fig. 3).
Figure 3. Snapshots from the planning software.
(a) Functional activation map (yellow) is overlaid on top of a structural scan. A virtual chamber is placed (magenta). (b) The stereotactic surgical assistant tool displays the position of the virtual manipulator to reach the desired virtual chamber position. The animal position in the frame is found automatically by registering the markers to their imaged positions. (c) Visualization of the implanted chamber (animal M2) and a virtual electrode to target the desired site. Small inset shows precision of virtual electrodes that align perfectly with five tungsten rods used to fine-calibrate grid rotation (d) Optimal grid analysis automatically finds the best grid tilt angle, orientation and grid hole to use to target the desired site.
Stereotactic manipulator modeling
The stereotactic arm manipulator is modeled using the Denavit-Hartenberg (DH) representation11, which is a standard representation used in the robotics field to describe a manipulator composed of multiple joints. The manipulator is considered to be a chain, composed of rigid links connected at their ends by rotating or prismatic joints. Each link is associated with a scalar value that controls how much the link is extended or rotated.
The main difference between standard stereotactic surgeries and the approach we propose is the following. In our scheme, the user first specifies a target in MR coordinates (coordinate system 1). This is then translated to absolute stereotactic coordinates (X, Y, Z, coordinate system 2) The origin of coordinate system 2 is defined to be on one of the frame rails, just above the mark AP0, and the three axes are defined such that they align with the AP, ML and DV directions. Finally, these coordinates are translated to parameters that directly control the stereotactic manipulator joints (AP, ML, DV, and any additional rotational angles allowed by the manipulator). In standard stereotactic surgeries the frame is used to position a manipulator arm relative to standard landmarks such as AP0 or Bregma. Thus, parameters controlling the stereotactic manipulator need to be explicitly specified.
To convert parameters of the stereotactic manipulator arm to absolute coordinates (X, Y, Z, coordinate system 2) we use the forward kinematic algorithm adopted from the robotics field. The forward kinematic problem is to find the position and orientation of the manipulator tip (or end-effector) in coordinate frame 2, given parameters controlling the arm. The forward kinematic problem can be easily solved by applying a series of rigid body transformations which are defined by the model describing the manipulator link lengths and relative rotations (see appendix 3 for an example of a stereotactic manipulator model described in a DH representation).
Obtaining marker positions in the two coordinate systems
To solve the registration problem between the MR coordinate system and the stereotactic frame coordinate system, two sets of measurements are collected. The first set of measurements is obtained from the MR scan by clicking on the center of each marker (Fig. 2, step 4). The second set is obtained during the surgical procedure by positioning the manipulator tip at each of the markers and reading out the manipulator arm values. To keep things simple, the manipulator is only moved along the three cardinal directions without any rotation, and only ML, DV, and AP are read out. Those values are then translated to absolute stereotactic coordinates by applying the forward kinematic model.
The procedure of obtaining the stereotactic coordinates can either take place while the animal is anesthetized and connected to the stereotactic frame, or in alternative approach which we call the “floating frame”. The floating frame approach is a method for placing a chamber while the animal is in the primate chair. The stereotactic frame is rigidly attached to the chair, but not to the animal (Fig. 2, Step 5, right panel, supplementary fig. 3). This allows moving the manipulator and reading out the coordinates of external markers while the animal is head-fixed in the primate chair, thus reducing complications associated with placing the animal in the stereotactic frame and insertion of ear bars to the ear canals.
Solving the registration problem
We denote by the coordinates of marker i in MR space and by the coordinates of the same marker in the absolute stereotactic coordinate system. The optimal rigid body transformation T, which maps between P and P’, such that is obtained by solving the absolute orientation problem10 (see appendix 1).
Once the mapping between a point in MR space and stereotactic space is found, the planned virtual chamber position and orientation are converted from MR coordinates to absolute stereotactic coordinates. Let us denote by C the 4×4 matrix representing the chamber in MR space. That is, it represents both the position of the tip and its orientation relative to scanned volume origin. The chamber in stereotactic space (C’) can easily be found via the inverse transformation: .
The remaining problem is to find the set of manipulator link parameters that aligns the tip both in position and orientation with C’. For that, the inverse kinematic problem is solved iteratively using psedo-inverse of the manipulator Jacobian15 (see appendix 2). Note that this problem is ill posed. Many solutions exist such that the manipulator tip is aligned with the planned chamber. For example, one can translate the manipulator slightly along the AP direction and apply a counter rotation in the horizontal plane, which would bring the tip exactly to the same place. To circumvent this issue the user can constrain the manipulator by fixing some of its parameters. The software can display the virtual manipulator as well as the animal and the stereotactic frame which greatly assist in visualizing how the arm should be positioned relative to the animal (Fig. 3B).
Experimental validation
To test the proposed framework we have targeted several deep brain structures in three monkeys and one rat. Monkey M1 was implanted with a chamber to target face-selective regions in IT cortex (regions ML and PL 12). Monkey M2 implanted with a chamber to target place-selective regions in the occipital temporal sulcus and parahippocampal cortex. Monkey M3 was implanted with two chambers to target FEF and ML. For the rat experiment, two random locations were selected for cannula placement.
Quantifying misalignment errors
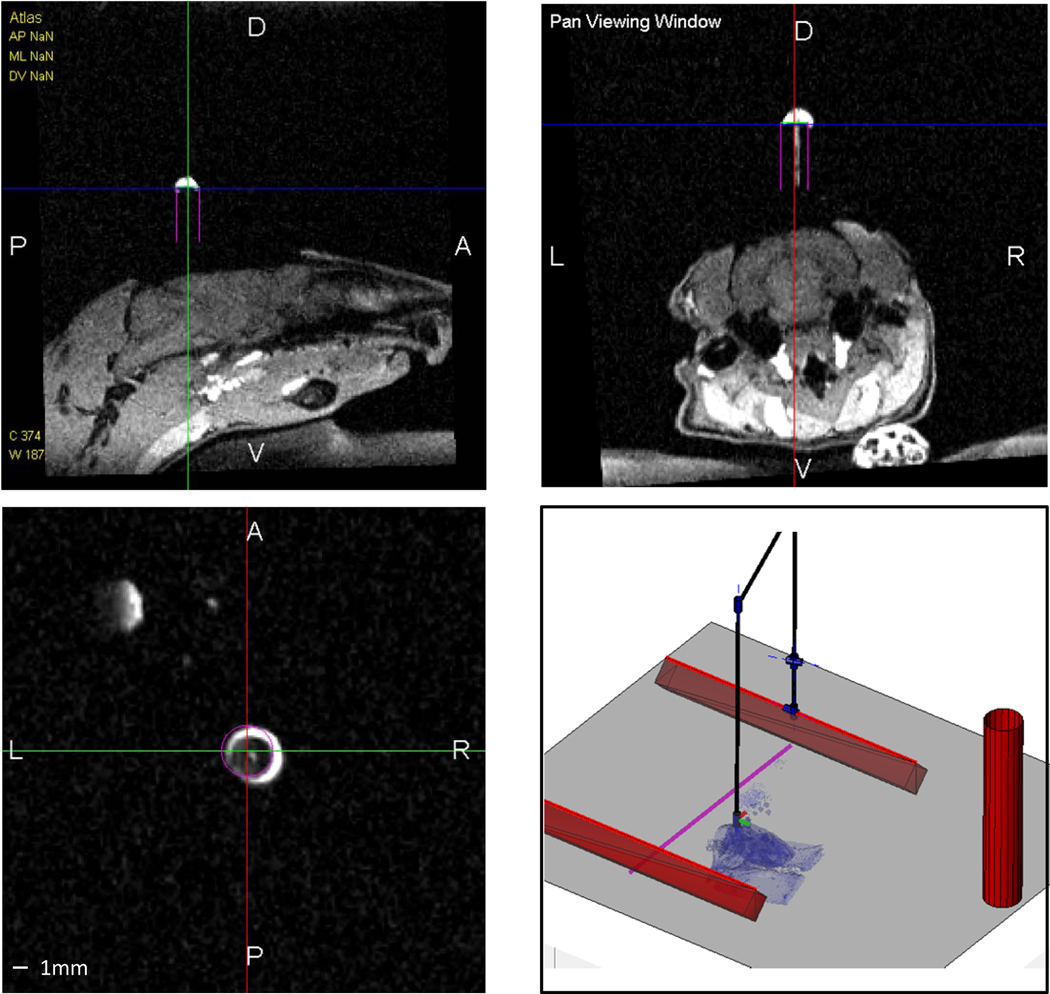
Misalignments between a planned virtual chamber and the implanted chamber were quantified by scanning the animal after the surgery. For monkeys, chambers were filled with gadolinium and a zero degree grid with several thin tungsten rods placed inside plastic guide tubes was inserted. This allowed clear visualization of the chamber axis (Fig. 3C, small inset). For the rat experiment, the cannula was filled with gadolinium which also allowed clear visualization of the direction (Fig. 4), The second scan was registered to the first scan that was used for planning. A second virtual chamber was then placed and aligned with the actual implanted chamber.
Figure 4. MR-Guidded cannula placement in a rat.
Snapshots from the planning software demonstrating the planned cannula position (magenta) and the implanted position (white contrast agent).
The angular error was quantified as the angle between the implanted chamber axis and the planned chamber axis. The positional error was quantified as the minimal distance between the two axes since positional errors along the chamber axis do not affect directly the projected region below.
The positional and angular errors are summarized in Table 1. We found that in the majority of procedures performed, the implanted chamber was within 1 mm and 1 deg from the planned position. The largest error was observed in the rat experiment and is attributed either to a mechanical instability of our stereotactic frame (Kopf 900A) or to the low number of markers used in this experiment. Mechanical instability was observed when values were read out from this manipulator; a large deviation was observed (> 1mm) when the arm was repositioned at the same marker.
Table 1.
Implanted chambers accuracy
| Subject | Number of markers | Chamber positional placement error (mm) | Chamber angular placement error (deg) |
|---|---|---|---|
| Monkey M1 | 7 | 0.07 | 1.61 |
| Monkey M2 | 8 | 0.7 | 0.44 |
| Monkey M3 (Chamber 1) | 9 | 0.83 | 0.89 |
| Monkey M3 (Chamber 2) | 9 | 0.71 | 0.98 |
| Rat R1 (Cannula 1) | 5 | 0.6 | 3.31 |
| Rat R1 (Cannula 2) | 5 | 0.25 | 0.88 |
Error analysis
Many factors determine chamber placement accuracy. The most important ones are the number of artificial markers and the errors in reading out their values, either from the MRI or from the stereotactic manipulator. Other factors that can contribute are errors in 3D modeling of stereotactic manipulator or mechanical instability. Below we describe computer simulations addressing these issues to determine the expected error given uncertainty about the model or read out values.
Marker dependent errors
Errors in determening the exact location of markers in the MR scan or in reading out their values from the stereotactic manipulator will lead to an error in the estimated rigid body transformation (T) between the MR coordinate system and the stereotactic frame coordinate system. Errors in determining marker locations in the MR scan mainly depend on the scanner resolution and on the diameter of drilled markers. These two parameters set a lower bound on how accurately the user can localize the markers in the scan. Our experiments took place with a scanning resolution of 0.5 mm and an average markers’ diameter of 1 mm. Improved resolution and smaller diameter markers may provide better accuracy but come with the cost of collecting more scans to compensate for the reduced SNR.
Errors in pointing markers location using the stereotactic arm depend on the type of manipulator. In our experiments we used a Kopf 1460 manipulator lacking a digital readout, limiting the accuracy of reading out values to about 0.1 mm.
To test the effects of inaccuracies in reading out markers positions’ from the MRI scan we randomly generated markers positions (P) in a volume that approximates a monkey implant (45×45×20 mm) and randomly generated a rigid body transformation (T) to simulate the stereotactic frame placement with respect to those markers. Random Gaussian noise with a standard deviation was added to the marker positions Pn=P+N(0, ) to simulate the uncertainty in reading out markers position. Marker position in the second coordinate frame were then computed by P’=TxP (i.e., assuming no errors in readout using the stereotactic manipulator). The registration algorithm was used to recover T from P’ and Pn.
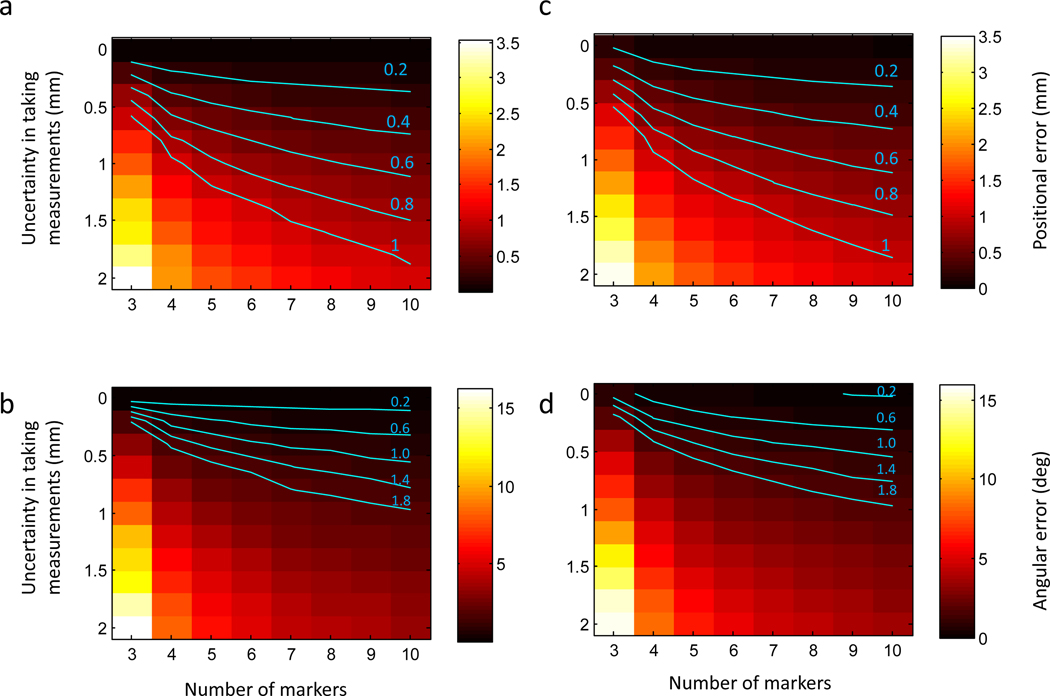
Noise levels were varied between [0, 2] mm to simulate different possible scanning resolutions and the number of markers was varied between [3, 10]. 1000 Simulations were run for a given configuration. The positional and angular errors of the simulation are summarized in Fig. 5 a,b. We found the number of artificial markers to critically determine the accuracy of the registration. For example, given a fixed uncertainty of 0.5 mm, the positional error can be reduced from 1 mm using three markers to about 0.3 mm with 10 markers (Figure 5a).
Figure 5. Predicted positional and angular errors of implanting recording chambers.
(a,b) Predicted positional (a) and angular (b) error as a function of the number of external markers and the uncertainty in annotating markers in the MRI scan. (c,d) Predicted errors when noise is present in both MRI marker positions and read out coordinates from the stereotactic manipulator. Iso-error contours are highlighted in cyan.
To simulate a more realistic scenario, we repeated the simulations but added noise (= 0.1 mm ) to P’ to simulate errors in reading out values with the stereotactic manipulator. Overall, results were very similar (Fig. 5 c,d), indicating accuracies were mainly governed by MRI localization errors.
Marker placement on the implant can also affect accuracy. If markers are packed too closely to each other this can lead to larger errors in estimating the correct rigid body transformation. Simulation with markers that were packed in a smaller region (15×15×10 mm) indicated that the main term that is affected is orientation (Supplementary Fig 1 a, b).
Stereotactic manipulator dependent errors
Another possible source of error is inaccurate Denavit-Hartenberg description of the manipulator. For example, the manipulator arm could have a slight tilt along a certain direction or the user-given constants describing the length of a joint might be inaccurate. We simulated both of these scenarios while varying the number of markers and their placement (Supplementary Fig. 2a,b). Our simulations indicate that angular error in the DH description can lead to both positional and angular errors in chamber placement (Supplementary Fig. 2a), while errors in a joint length can only affect chamber position (Supplementary Fig. 2b). Overall, these analyses stress the importance of having a mechanically stable stereotactic manipulator that is well calibrated.
Correction for surgical placement errors
As described above, small accumulated errors in chamber placement cannot be avoided. The implanted chamber will not align perfectly with the virtual planned chamber due to factors described above. Positional errors less than 1 mm and angular errors less than 1 deg are expected. Errors in chamber placement are also amplified when one is trying to target a deep brain region as a slight angular error will be throw the electrode off the desired trajectory. Generally, a target located d mm below the chamber and an angular error of α can lead to an expected error of d x sin(α) mm to the target. For example, a 1 deg angular error in chamber placement and a target located 50 mm below the chamber would induce an absolute error (closest point between the target and a line passing along the chamber axis) of 0.87 mm.
These errors can be minimized in post-surgery planning by correcting the position/orientation of the virtual chamber to the implanted one. Identification of such errors is possible by filling the chamber with MR contrast agent, placing a zero degree grid and several tungsten rods that serve as markers and can indicate the chamber accurate position and orientation (see Figure 3c. inset). Once properly identified, the optimal trajectory can be recomputed. In practice, this typically results in a shift of one grid hole from the original one.
Blood vessel avoidance
A major concern in targeting deep brain structures for electrophysiology is the presence of blood vessels along the penetration trajectory. Electrodes passing through blood vessels can lead to lesions or seizures induced by internal hemorrhage. Our approach to reduce this risk is to find safe chamber placements in which electrode trajectories do not pass through blood vessels.
The planning software can automatically identify blood vessels in T1-weighted scans using an image-based blood vessel enhancement filter 13. Manual editing is possible and missed blood vessels can be added if image quality is poor. A typical output of the automatic detection is presented in Fig. 6a. Notice that most major blood vessels have been automatically identified. The software can also display the detected blood vessels in any viewing plane. For example, a coronal view is shown in Fig. 6b and detected blood vessels are highlighted in cyan.
Figure 6. Blood Vessel Avoidance.
(a) Output of the automatic blood detection algorithm in a T1-weighted scan. (b) Coronal view (AP +16) showing two ROIs selected for targeting (denoted as red blobs) and detected blood vessels (highlighted in cyan). Notice that the slice is aligned to stereotactic coordinates and that a major blood vessel in the Superior Temporal Sulcus is present directly above the ROI in the left hemisphere. (c,d) Projected blood patterns on the brain surface. 3D maps were generated by casting rays from the ROI (left, right) and highlighting in red rays that cross through blood vessels. (e) Safe chamber placement selected for targeting the left ROI. (f) View aligned to chamber coordinates. Notice that the electrode track (highlighted in magenta) hits the ROI but does not pass through any blood vessels.
Once the user has selected the desired ROIs to be targeted the software can cast rays from the target outward and project the blood vessels pattern on the brain outer surface or skull. Consider for example the scenario presented in Fig. 6b, where two ROIs have been identified using fMRI (denoted as red blobs in the two hemispheres). The projected pattern for the left ROI is shown in Fig. 6c and the projected pattern for the right ROI is shown in Fig. 6d. A red region on the surface indicates that a ray has intersected a blood vessel and is therefore is considered an unsafe position for targeting the ROI. In Fig. 6c,d, yellow regions are considered safe (no blood vessel intersection). Notice that the two patterns differ depending on the position of the ROI.
The scenario in Fig. 6 shows exactly how dangerous a vertical penetration can be for targeting the ROI in the left hemisphere since a major blood vessel in the Superior Temporal Sulcus (Fig. 6b, highlighted in cyan) lies directly above the ROI. By considering the projected blood pattern one can easily find a safe region for chamber placement to target this ROI. An example for such safe placement is shown in Fig. 6e. This placement is further verified by displaying slices aligned with this electrode trajectory (Fig. 6f). Notice that the penetration still passes through the Superior Temporal Sulcus, but not through the blood vessel. Notice that this chamber placement is not vertical along the stereotactic coordinate, yet can easily be placed using the framework proposed in this paper.
Discussion
We have presented a robust framework that allows precise MR-guided placement of chambers, electrodes, catheters, and other devices to target brain regions that have been identified in MRI. We accomplish this by registering a set of external markers that are easily identified in the MR scan to a set of measurements obtained during the surgery. Our method goes beyond the traditional approach of placing chambers vertically or tangentially to the surface of the skull, and can be used to position chambers pointing in arbitrary directions. We verified our technique by implanting chambers in monkeys and rats, and have obtained some theoretical bounds on expected accuracy using computer simulations.
There are many advantages to the proposed framework over existing techniques14–16. It is generic and can be used to target any brain structure with any type of stereotactic manipulator. It uses the existing de-facto platform for performing surgeries and does not require expensive equipment such as real-time camera based tracking or MR-compatible stereotactic frames. It allows more flexibility in the planning stage and greatly assists during the surgery by reporting exactly which parameters to set the manipulator to reach the desired target. The external markers do not require any type of precise calibration and can be drilled into in existing implant or constructed from cheap material and attached to the head post.
Our technique of solving the registration problem makes no assumptions on how the animal is positioned in the stereotactic frame. In fact, if the animal already has a head-post, there is no need for the animal to be physically attached to the stereotactic frame at all. The only requirement is for the stereotactic manipulator arm to be rigidly attached to something relative to the skull. Chamber implantation procedures in our lab took place while the animal was head-fixed in the primate chair, while the frame was rigidly attached to the chair (see Supplementary Fig. 3). This approach greatly reduces complications arising from standard stereotactic surgery.
The proposed planning software automatically identifies blood vessels and assists in finding optimal placement for a chamber to target a desired ROI. The ability to place a chamber along any desired direction can also be used to target multiple different sites from the same chamber. In addition, the software can indicate whether a desired ROI is reachable within the configural space of the stereotactic manipulator.
One drawback of our approach is that it uses the stereotactic device to extract absolute metric information. Stereotactic manipulators are usually designed to infer relative metric information relative to some internal features, such as bregma point. Our method to extract absolute coordinates from the stereotactic frame relies on the ability to have an accurate model describing the manipulator. However, in most cases, such a model is unavailable. The exact lengths of manipulator joints and the exact position of the rotation axes are unknown and need either to be approximated or obtained from the manufacturer. As shown in the error analysis section, inaccuracies in proper description of these parameters can lead to significant errors in the final chamber placement.
Another drawback of the technique is that targeting chambers with arbitrary direction requires precise angular positioning of the manipulator. While most manipulators have a highly precise system for translating the manipulator along the DV, ML and AP dimensions, they typically lack a proper way to have similar precision for rotating the manipulator along those dimensions. In addition, to the best of our knowledge, there are no digital readout for the rotational components of stereotactic manipulators and in most cases, available tick marks are spaced at a resolution of 2 or 5 degrees. We hope future stereotactic manipulators designs will not suffer from this limitation.
Supplementary Material
Appendices
Appendix 1: Solving the absolute orientation problem
A detailed derivation is available in Horn’s original paper 10. Here, we give a brief summary. Let the set of measurements of features in coordinate system A and B be given by . The goal is to find the best rigid body transformation in least square sense, that is: .
The first step is to subtract the center of mass from each point cluster: . Next, we define the following two algebraic operators which are derived from quaternion theory:
We construct the following symmetric matrix : , and compute its eigen-vectors. The largest eigen-vector of M, e4, is used to construct . Finally, the optimal rotation is given by , and the optimal translation is given by .
Appendix 2: Solving the inverse kinematics problem using iterative manipulator Jacobian
The forward kinematic model computes the position and orientation of an end effector by applying a series of rigid body transformation defined according to the arm model. The inverse problem is to find the joint parameters that will position the end effector in a desired position and orientation. The forward model is denoted by function which takes as input the set of joint parameters and converts them to the position T (1×3) and rotation R (3×3) of the end effector. The distance between a given configuration and the goal configuration can be defined according to the following metric:
where denotes the current configuration and the goal configuration and represents the cross product between the x-direction of and the x-direction of . The iterative procedure can be summarized as follows:
Initialization: set to zero (or a random initial solution)
Iteration:
Where J is the manipulator Jacobian
Appendix 3: DH Representation for Kopf 1460 manipulator
We represent the stereotactic frame using Denavit-Hartenberg parameters that allow a minimal representation of the model. Any frame and manipulator can be represented using such representation. Below are the parameters for Kopf 1430 frame with 1460 manipulator mounted on the left rail:
| Joint | Alpha (angle about common normal, from old z axis to new z axis) | A/r (length of the common normal) | Theta (angle about previous z, from old x to new x) | D (offset along previous z to the common normal) | Prismatic / Rotatory | offset |
|---|---|---|---|---|---|---|
| #1 | 0 | 0 | P | 0 | ||
| #2 | 0 | 0 | C1 | R | ||
| #3 | − | 0 | 0 | 0 | R | 0 |
| #4 | 0 | 0 | 0 | 0 | R | |
| #5 | 0 | 0 | 0 | P | C2 | |
| #6 | 0 | 0 | 0 | P | −C3 | |
| #7 | 0 | 0 | 0 | 0 | P | C1+C2 |
| #8 | 0 | 0 | 0 | 0 | R |
Joint #1 specifies the AP position. Joint #2 represents rotation about DV axis. Joint #3 represents rotation about AP axis. Joint #4 represents the 90 degrees discrete rotation of the manipulator. Joint #5 represents the DV position. Joint #6 represents the ML position. Joint #7 represents the length of the last tool tip, Joint #8 represents the rotation of the tip.
The three constants measured from our manipulator were defined as follows:
C1 = 5.395
C2 = 19-C1;
C3 = 12.27;
Footnotes
Our planning software (Planner) is publicly available for research purposes and can be downloaded at http://tsaolab.caltech.edu. The web site contains instruction manuals and video tutorials on how to install and use the software. We have found our planning software to be an extremely valuable tool assisting MR guided electrophysiology.
References
- 1.Paxinos G, Huang XF & Toga AW The rhesus monkey brain in stereotaxic coordinates. (Academic Press, 2000). [Google Scholar]
- 2.Saleem K Atlas of the rhesus monkey brain in stereotaxic coordinates : a combined mri and histology. 1st edn, (Elsevier, 2006). [Google Scholar]
- 3.Saleem KS & Logothetis N A combined MRI and histology atlas of the rhesus monkey brain in stereotaxic coordinates. (Academic, 2007). [Google Scholar]
- 4.Paxinos G & Watson C The rat brain in stereotaxic coordinates. 6th edn, (Academic Press/Elsevier, 2007). [Google Scholar]
- 5.Sereno MI et al. Borders of multiple visual areas in humans revealed by functional magnetic resonance imaging. Science 268, 889–893 (1995). [DOI] [PubMed] [Google Scholar]
- 6.Kayser C, Petkov CI, Augath M & Logothetis NK Functional imaging reveals visual modulation of specific fields in auditory cortex. J Neurosci 27, 1824–1835 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Moeller S, Freiwald WA & Tsao DY Patches with links: a unified system for processing faces in the macaque temporal lobe. Science 320, 1355–1359 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tootell RB et al. Functional analysis of human MT and related visual cortical areas using magnetic resonance imaging. J Neurosci 15, 3215–3230 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tsao DY et al. Stereopsis activates V3A and caudal intraparietal areas in macaques and humans. Neuron 39, 555–568, doi:S0896627303004598 [pii] (2003). [DOI] [PubMed] [Google Scholar]
- 10.Logothetis NK What we can do and what we cannot do with fMRI. Nature 453, 869–878 (2008). [DOI] [PubMed] [Google Scholar]
- 11.Sirotin YB & Das A Anticipatory haemodynamic signals in sensory cortex not predicted by local neuronal activity. Nature 457, 475–479 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tsao DY, Freiwald WA, Tootell RBH & Livingstone MS A cortical region consisting entirely of face-selective cells. Science 670, 670–674 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Frangi A, Niessen W, Vincken K, Viergever M Multiscale vessel enhancement filtering. Medical Image Computing and Computer-Assisted Intervention, 130–137 (1998). [Google Scholar]
- 14.Sperka DJ & Ditterich J Splash: a software tool for stereotactic planning of recording chamber placement and electrode trajectories. Front Neuroinformatics 5, 1, doi: 10.3389/fninf.2011.00001 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Van Essen DC Windows on the brain: the emerging role of atlases and databases in neuroscience. Curr Opin Neurobiol 12, 574–579, doi:S0959438802003616 [pii] (2002). [DOI] [PubMed] [Google Scholar]
- 16.Jing W et al. A new MRI approach for accurately implanting microelectrodes into deep brain structures of the rhesus monkey (Macaca mulatta). J Neurosci Methods 193, 203–209 (2010). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.