Patterns and predictions of drinking water nitrate violations across the conterminous United States

Abstract

Excess nitrate in drinking water is a human health concern, especially for young children. Public drinking water systems in violation of the 10 mg nitrate-N/L maximum contaminant level (MCL) must be reported in EPA’s Safe Drinking Water Information System (SDWIS). We used SDWIS data with random forest modeling to examine the drivers of nitrate violations across the conterminous U.S. and to predict where public water systems are at risk of exceeding the nitrate MCL. As explanatory variables, we used land cover, nitrogen input, soil/hydrogeology, and climate variables. While we looked at the role of nitrate treatment in separate analyses, we did not include treatment as a factor in the final models, due to incomplete information in SDWIS. For groundwater (GW) systems, a classification model correctly classified 79% of catchments in violation and a regression model explained 43% of the variation in nitrate concentrations above the MCL. The most important variables in the GW classification model were % cropland, agricultural drainage, irrigation-to-precipitation ratio, nitrogen surplus, and surplus precipitation. Regions predicted to have risk for nitrate violations in GW were the Central California Valley, parts of Washington, Idaho, the Great Plains, Piedmont of Pennsylvania and Coastal Plains of Delaware, and regions of Wisconsin, Iowa, and Minnesota. For surface water (SW) systems, a classification model correctly classified 90% of catchments and a regression model explained 52% of the variation in nitrate concentration. The variables most important for the SW classification model were largely hydroclimatic variables including surplus precipitation, irrigation-to-precipitation ratio, and % shrubland. Areas at greatest risk for SW nitrate violations were generally in the non-mountainous west and southwest. Identifying the areas with possible risk for future violations and potential drivers of nitrate violations across U.S. can inform decisions on how source water protection and other management options could best protect drinking water.

3. Introduction

For more than two decades, nitrate has been one of the top three contaminants in public drinking water supplies that exceed the National Primary Drinking Water Regulation enforceable maximum contaminant level (MCL).¹ The U.S. federally regulated MCL for nitrate-N is 10 mg/L for Community Watery Systems (CWS) based on risk to infants below six months who could develop blue baby syndrome if they drink water containing nitrate in excess of the MCL.^2–3 Some non-community water systems have an MCL of 20 mg-N/L when approved by the state.⁴ Any public water system (PWS) that has levels above the MCL is considered in violation and is obligated to become compliant.⁵

Nitrate source contributions to waters vary depending on location. The largest contributor to landscape N inputs for the entire conterminous U.S. (CONUS) is through agricultural activities, including synthetic fertilizer application,^6–10 land application of manures from concentrated animal feeding operations (CAFOs), and crop biological N fixation.⁹ Other known drivers of nitrate in surface waters and groundwater include atmospheric deposition,¹¹ wastewater treatment plants,¹² leaking or poorly managed septic systems,¹³ urban runoff,¹⁴ animal waste,⁹ and agricultural runoff after rain events.^15–16 GW nitrate contamination can be especially high in areas with well-drained soils and in places where GW wells are shallow or unconfined.^17–19 Previous studies show that these factors contribute to both elevated GW and SW²⁰ nitrate levels and may also influence nitrate MCL violations.

Almost every state across the CONUS has reported a drinking water nitrate MCL violation sometime between 1978 and 2016.¹ But some states, ecological regions, and certain geological areas or land-use types²¹ have much greater rates of drinking water violations than others. The at risk areas include the Central California Valley, parts of the Great Plains from west central Texas to eastern Nebraska, the Piedmont of Pennsylvania, Coastal Plains of Delaware and adjacent areas of the Piedmont and Coastal Plains extending to southern New Hampshire, and the dairy region of much of central and southern Wisconsin, northeastern Iowa, and parts of central Minnesota.^{1, 21–23} While a national scale model has been developed for predicting nitrate concentrations in private drinking water wells,²² there have been no models developed for predicting public drinking water nitrate concentrations or violations. It is also not known if spatial patterns in nitrate violations are associated with specific anthropogenic or natural drivers. A national-scale model could help to prioritize resources for management and prevention of violations in public drinking water systems.

Many factors may lead to drinking water nitrate violations. Thus, it is advantageous to use a modeling framework that can incorporate many variables and does not require homogeneous or linear datasets when attempting to identify unique geospatial patterns for nitrate violations. Random Forest (RF) models are such an approach and could prove useful for this type of large-scale, multivariate analysis. The RF modeling approach uses many decision trees (a forest) for predicting either discrete classes or continuous variables. Each tree is a subset of the entire dataset and predictions are made by averaging over the trees.²⁴ RF models have a history of use in ecological and water quality studies for spatial predictions.^25–26 However, few studies have applied RF at a national scale.^27–28 RF models have been used to predict nitrate concentrations at less than national scales, such as the Central California Valley²⁹ or the state of Iowa.²⁶ This work builds on these previous studies, but is the first to utilize a model based on data for public drinking water supplies at a national scale.

The objectives of this research were to predict the risk of drinking water nitrate violations across the CONUS and to determine which drivers are most important, using RF modeling. Nitrate violations data from EPA’s Safe Drinking Water Information System (SDWIS).³⁰ are used as response variables and land cover, climate, soil/hydrogeology, and socio-economic data are used as predictor variables in the models. Specifically, we assessed violation risk for areas with 1) PWS that have not yet reported a violation, 2) new or planned PWS, or 3) private groundwater wells, in areas without PWS.

Due to incomplete or insufficient information on PWS engineering factors, such as the presence of advanced nitrate treatment or actions that water operators take in order to meet the MCL (e.g., blending of water or switching water sources), our analysis focuses on environmental drivers, rather than the engineering impacts on nitrate violations. Also, a relatively small percentage of catchments with PWS had reported nitrate treatment technologies (22% of GW and 7.6% of SW catchments with PWS, and the reporting was not consistent for each state, see Figure S1), making the use of treatment at a national scale potentially unreliable. However, we did include nitrate treatment as a predictor variable in separate SW and GW models, to assess the potential role of treatment. It should be noted that without treatment or PWS operation information, the national models will tell only part of the story (the influence of environmental or other factors the effect source waters) because nitrate treatment is known to reduce violation rates when incoming source water is higher than the MCL,³¹ and thus likely plays an important role in regulating nitrate violation rates. Consequently, when interpreting the models, the inability to use treatment or other engineering factors in the final models may mean either: 1) the model may be more likely to produce false positives, predicting high violation risk, due to the presence of environmental drivers like agricultural land with greater nitrogen inputs, in areas where observed violation rates are low due to treatment or the ability of systems to switch and/or dilute the source water, or 2) the models may produce false negatives, predicting low risk in areas even with high nitrogen inputs, due to treatment reducing observed violations. The first possibility would train models to associate high nitrate violation risk with agricultural lands (higher N inputs), while the second possibility would train the models to associate agricultural lands with low nitrate violation risk. The latter is hypothesized to be less likely, assuming the use of nitrate treatment is proportionally less than the prevalence of land use with high N inputs at a national scale.

Based on the literature,^{8, 22, 26} we hypothesized that the following environmental variables would be most important in predicting GW nitrate violations: percent cropland, amount of N inputs, soil permeability, and water table depth. For SW nitrate violations, we expected precipitation and N inputs to be most important, based on evidence that runoff from croplands can increase SW violations.^{1, 16, 32} Given that the models in this analysis do not incorporate information on treatment or managment actions, the goal of this analysis is not to predict which systems are or should be in violation or not, but rather to create models that can be used as risk assessment tools, to predict areas most at risk for having drinking water nitrate violations, based on natural and anthropogenic landscape factors. Because the models are at a national scale, they can be used as a first cut screening tool for identifying areas at risk, before focusing in with more specific and costly tools.

4. Methods

4.1. Preprocessing and Data Validation

The EPA has set a maximum contaminant level (MCL) for nitrate/nitrite-N as 10 mg/L. Approximately 16% of drinking water systems measure nitrate+nitrite and the others measure only nitrate. We included violations for either nitrate or nitrate+nitrate and henceforth, nitrate violations refer to either nitrate or nitrate+nitrite violations. Systems in violation of the nitrate MCL must be reported in the EPA’s Safe Drinking Water Information System (SDWIS). We downloaded data on all PWS which have exceeded the nitrate MCL from EPA’s SDWIS database.³⁰ SDWIS only lists the PWS and their concentrations when they exceed a contaminant MCL. A violation is determined based on whether the average of the original and confirmation sample exceeds the MCL. Note that violations are based on “finished” water ready to be distributed, not raw water. We included violations from all PWS types: community water systems (CWS), transient non-CWS, and non-transient non-CWS. We imported data into the R statistical program³³ for preprocessing, following methods of Pennino, et al. ¹ In brief, we filtered the data to only keep MCL violations data for nitrate and nitrate+nitrite and only states in the CONUS, as most of the predictor variables are limited to those states. We then determined the number of quarters per year a PWS violated the nitrate MCL. We limited our analysis to nitrate violations between 2013 and 2017, because inventory data on the number of active systems was only available for those years, at the time of this analysis.

Each PWS is made up of one or more facilities (i.e., well(s), treatment plant(s), etc.) and we used the location(s) of each facility to associate a PWS with one or more of the 2.6 million National Hydrography Dataset Plus Version 2 (NHDPlusV2, hereafter referred as NHD)³⁴ catchments in the CONUS. It should be noted that catchments are not synonymous with true watersheds within which all surface and/or ground water drains to a particular point. They comprise both true watersheds (i.e., headwater catchments) and portions of watersheds but provide a useful framework of polygons to assess associations among spatial characteristics and water quality.³⁵ Details on how we filtered out facilities and associated catchments with PWS are found in supporting information.

Of the 2.6 million catchments, 57,096 catchments are associated with 117,450 GW PWS and 4,692 catchments are associated with 5,741 SW PWS (Figures 1a–b, S2–S6). Between 2013 and 2017, 748 or 1.3% of the 57,096 GW system catchments had nitrate violations (Figures 1a, S6) and 62 or 1.3% of the 4,692 SW system catchments had nitrate violations (Figures 1b, S6). Note that, 0.8% of all active PWS and 10% of the SW PWS in violation used for the model are designated as GW systems under direct influence of SW (GWUDI).

Figure 1.

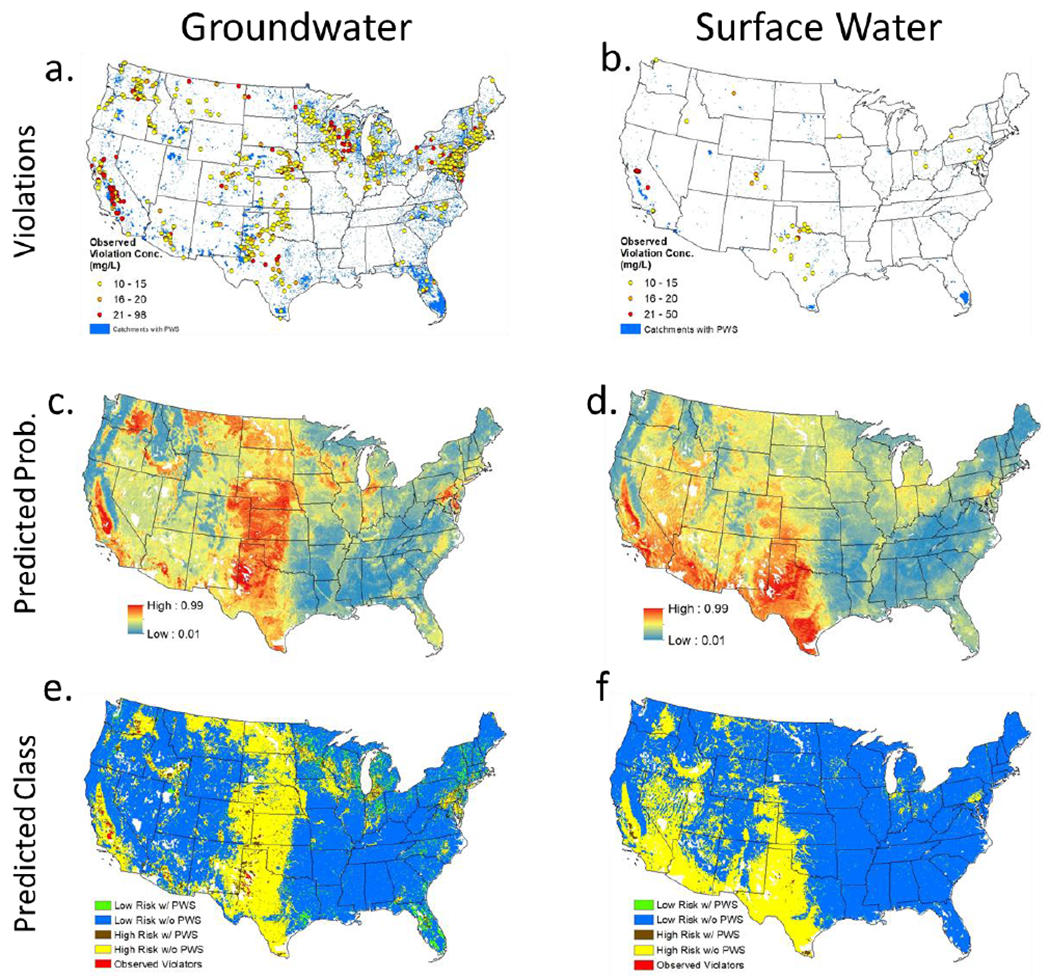
Map of the conterminous U.S. showing a) 88,083 catchments with GW PWS (blue area) and 748 catchments with GW PWS violations (non-blue circles), b) 6,934 catchments with SW PWS (blue area) and 50 catchments with violations (non-blue circles), c) RF classification predicted probability of GW violation, d) RF classification predicted probability of SW violation, e) RF classification prediction for GW, and f) RF classification predictions for SW. Low Risk is < 0.5 probability of violation. High Risk is ≥ 0.5 probability of violation. All observations and predictions are for 2013-2017. The maps in panels c) and d) show the probability of a region being at risk of violation, which is not the same as the percent of systems predicted to be in violation. Also, the maps in panels e) and f) show areas with high or low risk of violation but do not predict which areas are in violation. Note, these maps are risk assessment tools to predict areas most at risk of having drinking water nitrate violations. Also, note that these models only incorporate environmental variables and are not based on nitrate treatment or system management practices.

4.2. Model Development

4.2.1. Model Response Variables

The model response variables were based on nitrate health-based MCL violations data from SDWIS, between 2013 and 2017. For the RF classification approach, a binary response variable was used, i.e., whether the catchment had a violation or not. For the regression approach, a continuous response variable was used, which either was the mean violation concentration above the MCL (mg/L) or the percent of systems in violation per catchment. SDWIS only provides concentration data for PWS that are in violation (≥10 mg N/L).

We calculated the average nitrate concentration above the nitrate MCL, between 2013 and 2017, for each catchment by selecting all violations with a concentration (72.5% of all violations reported the concentration above the MCL) and removing outlying concentrations (two GW systems with concentrations listed above 48,000 mg nitrate-N/L, with the remaining concentrations ≤362 mg nitrate-N/L). Some catchments that had one or more PWS in violation also contained PWS without violations; in such cases, we assigned a value of 5 mg nitrate-N/L (half of the MCL) to each system without violations. This was the case for only 14 of the 748 catchments with GW systems in violation and none of the 62 catchments with SW systems in violation. To calculate the percent of systems in violation per catchment we took the 2013-2017 average of the number of systems in the catchment with a violation per year divided by the average number of active systems in that catchment each year.

4.2.2. Model Predictor Variables

Information on the violations were paired with StreamCat³⁶ landscape variables associated with each catchment. EPA’s StreamCat database contains landscape metric information for all 2.6 million NHD catchments and watersheds (upstream drainage area for a particular catchment) in the CONUS, including data from the national land cover database (NLCD), census population density, nitrogen inputs, soil characteristics, and hydrologic characteristics. StreamCat data have previously been used for making spatial predictions, such as for biotic condition or phosphorus concentrations, across the CONUS.^{24, 28, 37–39} Approximately 210 of the StreamCat variables which were expected to influence N in drinking water sources, based on literature and authors’ judgement, were included in our analysis (Table S1).

We also calculated additional variables not previously included in StreamCat, but are now included (Table S2); these variables include: percent of agricultural land with artificial drainage (i.e., tile drainage), average hillslope, surplus precipitation (precipitation minus potential evapotranspiration), nitrogen surplus^{10, 40} (total nitrogen inputs minus nitrogen outputs from crop removal), net anthropogenic nitrogen inputs (NANI),^41–42 percent of systems with nitrate treatment technologies, and several Census variables (race, income, and education level per catchment). Note that information on treatment for nitrate removal is not complete within SDWIS; also, due to costs, nitrate treatment is not implemented by all PWS. Consequently, treatment was not used in the final models, but used as a supplemental comparison. For our treatment analysis, nitrate treatment was defined as any systems that used reverse osmosis, ion exchange, electrodialysis, or distillation. Also, note that PWS consist of both consecutive (systems that purchase water from other systems) and non-consecutive (systems that obtain their own water) systems and this analysis does not distinguish between these types. That should not impact the analysis much because consecutive systems only make up 3-4% of GW or SW violations.

All additional variables, except Census, treatment, and PWS type, were summarized for each catchment and watershed using the same accumulation and zonal statistics approach as used for the StreamCat variables and have subsequently been added to StreamCat. The supporting information provides further details on the methods for how these variables were calculated. When reporting the results, we placed all variables into one of five different categories: nitrogen inputs (i.e., fertilizer), N Deposition, human land use characteristics (e.g., % cropland), climate/hydrology (e.g., precipitation), natural watershed/geologic factors (e.g., slope, aquifer type) and socio-economic factors (e.g., Census) (Tables 1S & 2S). Note that precipitation during this period was between two and 13 cm above the average for the last 100 years, with 2015 being the wettest year.⁴³

4.2.3. Random Forest (RF) Modeling

RF models⁴⁴ were used to spatially predict the risk of drinking water nitrate levels exceeding the 10 mg N/L MCL and to determine what landscape, geologic, climate, etc. factors best explained the spatial patterns. We modeled GW and SW system violations separately, as the potential causes for the source water violations may differ. RF models use an ensemble or “forest” of many classification trees.⁴⁴ We chose to use a RF model because they are non-parametric and are known to work well for non-linear datasets,^{24, 27–28} can handle large numbers of predictor variables that may be correlated, and are insensitive to overfitting.^28–29

Because of the ability of RF models to handle multiple variables collinear in space,²⁵ we were able to keep all variables in the initial models and for the final models only kept the most important variables that provided the most accuracy (while still potentially keeping collinear variables if model accuracy was improved). The RF model is able to keep collinear variables because each tree is made from only a portion of the predictor variables and thus the variable importance is based on trees made of different variables (see supporting information for more details).²⁵ Also, a previous study showed that RF performs better when multiple correlated variables are kept in the model than when variable selection methods are used.²⁴ The top 10 variables are reported in this paper and all other variables in the final models are reported in supplemental tables. Additionally, a Pearson’s correlation matrix was created for the top 10 variables in each model (Tables S3–S5).

We used the “randomForest” R package⁴⁵ to implement RF classification and regression models on our data. Details on the mechanics of the RF model can be found in the supporting information. In this analysis we use RF classification to classify a binary response variable (violations or no violations) and we use RF regression to model the following continuous response variables: mean violation concentration per catchment and percent of PWS in violation per catchment. Our approach was to first use the RF classification model, using catchments with (748 GW or 62 SW) and without (56,348 GW and 4,630 SW) verified violations, to predict which catchments are in violation. Then, for those catchments predicted to be in violation, we applied the RF regression model to predict the continuous responses (i.e., mean violation concentration or percent PWS in violation). This was done to avoid the difficulty of modeling the continuous predictor variables with a highly zero-inflated dataset, and to model only catchments already predicted to be in violation and not extrapolate to catchments without violations when using the RF regression models. Our approach to deal with zero-inflated data in the classification models is described further in the next section. The same set of candidate predictors was used for both the RF classification and RF regression models, even though final predictors varied.

The RF classification models were used to extrapolate the probability of a violation to all 2.6 million CONUS catchments using the landscape predictors. Note that the catchments to which these predictions are applied may or may not contain PWS (only 93,359 of 2.6 million have a PWS). A catchment is classified as at risk of violating the nitrate standard if the probability of violation exceeds 50%. The maps derived based on the RF classification models can be interpreted as predicting whether a catchment is expected to be at risk for three different conditions: 1) catchments that currently contain at least one PWS, 2) if a PWS were added to a catchment without a PWS, or 3) catchments with private groundwater wells and no PWS, assuming these respond to GW and/or SW conditions similarly to one or more PWS. The maps based on the RF regression models (based only on catchments with violations) represent the predicted concentrations or % of PWS in violation for the catchments previously predicted to be in violation from the RF classification model.

4.2.4. Addressing Imbalanced Data

Due to the highly imbalanced dataset (where catchments with violations are underrepresented statistically, with ~99% of the catchments without violations), we employed two methods to validate the model and ensure it was accurate when applied to both balanced and unbalanced datasets. Method One reports results for the standard 10-fold cross validation technique⁴⁵ and Method Two reports results based on a holdout dataset (a subset of the full dataset that is not used to build the model, but used when testing the model). For both methods, the first step was to pre-balance the dataset using approaches similar to those of Anand, et al. ⁴⁶ and Dal Pozzolo, et al. ⁴⁷ Specifically, prior to training the models, we randomly under sampled the majority class (catchments with zero violations) so that we ran each RF classification model with an equal number (N=748 for GW and 62 for SW) of catchments with and without violations. This randomized pre-balancing was done 10 separate times for each of the 10-fold cross validations.

For Method One, after the pre-balance step, we performed 10-fold cross validations with training and test datasets. Even though the RF algorithm can calculate error rates using out-of-bag data (data automatically held out when training the RF model),^{28, 45} we chose to use cross validation to facilitate comparison with other models in the literature. For the 10-fold cross validation, the RF model was run 10 times, each on a different 90% portion of the dataset, while the remaining 10% of the data was used as a test dataset, ensuring all samples were systematically included as training and test sets separately. The 10 different models created with the training sets were then used to make predictions on their 10 corresponding test sets, and the model results were averaged.

For Method Two, we created a holdout (independent) dataset with 20% of the original samples, representing the original unbalanced dataset, similar to previous studies.^{24, 29} These data were not used in training the model, but used as a means to validate the ability of the trained models to predict on an unbalanced dataset. With the remaining 80% of the original data, we first did the pre-balancing of the dataset and performed 10-fold cross validations with the 90/10 training and test datasets, as described above for Method one. Then the 10 different models were each used to make predictions on the holdout dataset.

4.2.5. Model Validation, Error Estimation, and Bias Correction

To assess the performance of the RF classification model, we calculated the percentage of correctly classified (PCC) catchments as having violations or no violations, the percentage of catchments with violations correctly classified (sensitivity), and the percentage of catchments without violations correctly classified (specificity).²⁵ Another performance metric, called area under the receiver operating characteristic curve(AUC), was also used.⁴⁸ We also calculated the Gmean metric (square root of (sensitivity × specificity)) because it can be a useful performance measure for unbalanced datasets.^46–47 Additionally, when applying each trained model on each 10% test or 20% holdout dataset, we applied a bias correction calculation to correct for this undersampling in the RF classification model, using equation nine from Dal Pozzolo, et al. ⁴⁷:

$$p^{\prime }=\frac{\beta \ast p_s}{\beta \ast p_s-p_s+1}$$

Where $p^{\text{'}}$ = bias corrected probability, $p_s$ = predicted probability, $\beta$ = ratio of number of samples in the positive class to the number of samples in negative class.

The accuracy of the RF regression models was assessed by calculating the R², root mean squared error (RMSE), and model bias.⁴⁹ These accuracy measures were calculated for all 10-fold cross validations estimates and holdout datasets and then averaged. RMSE is calculated as the square root of the squared difference between model predictions and sample observations. The model bias is calculated as the sum of the model predictions minus the sum of the sample observations, divided by the number of samples.

Once the prediction accuracy was optimized for the RF classification and regression models, a final model was run on 10 pre-balanced datasets and then these 10 models were used to make predictions on the original full, unbalanced dataset. Final models were based on ranking the most important variables and then selecting the top predictor variables which provided the highest Gmean for RF classification or R² values for RF regression models.

Maps of the classification errors or residuals were produced for each model. For the classification models, the prediction class error was calculated to show which of the catchments were correctly classified as true positive (catchments with violations that were classified correctly), correctly classified as true negative (catchments without violations classified correctly), classified as false positive (catchments without violations that were classified incorrectly), or classified as false negative (catchments with violations that were classified incorrectly). For the concentration and percent in violation regression models, the residuals were calculated as the predicted values minus the observed values. As a result, these maps will indicate which of the observed violations were correctly or incorrectly classified or how close the regression models came to the actual observed concentrations or % in violation values. Note that these maps are risk assessment tools to predict areas most at risk of having drinking water nitrate violations; they only incorporate environmental variables and are not based on nitrate treatment or system management practices.

4.2.6. Variable Importance and Partial Dependence Plots

The final RF models, applied to the full dataset, were used to determine the relative importance of each predictor variable. For RF classification models, variable importance is calculated as mean decrease in model accuracy for each variable, and for the RF regression models, variable importance is calculated based on the increase in mean squared error (MSE).²⁷ Both measures are calculated and then plotted using the “out-of-bag” data, based on average changes in model accuracy or MSE with and without the variable of interest.^{45, 50} For the top predictor variables, partial dependence plots were used to determine the direction and magnitude of the relationship between response and predictor variables.

4.3. Model Comparison

We compared our SW and GW models predictions to other studies that predicted SW or GW concentrations. In order to show how well our model can make predictions to catchments without PWS, but possibly with private wells, we compared our GW concentration model with the Nolan and Hitt ²² Ground-Water Vulnerability Assessment for Drinking Water (GWAVA-DW) model, which was based on private drinking water wells. To do this, we summarized the GWAVA-DW model predictions for groundwater nitrate concentrations in private drinking water wells to the catchment scale and categorized areas as being in violation if the concentrations exceeded the 10 mg nitrate-N/L MCL. Similarly, we compared our model’s predicted SW violations to the SW concentration data used by Bellmore, et al. ²⁰, based on the U.S. Environmental Protection Agency’s (EPA) National Rivers and Streams Assessment (NRSA) concentration data, collected in 2008–2009. This comparison utilized observed (not modeled) concentration data associated with 1966 NHD stream catchments.

4.4. Separate Model Analyses

While the final RF models did not include nitrate treatment as a predictor variable, we also created RF models using the same above methods, but with nitrate treatment included as an additional predictor variable. This analysis helped assess the potential role of treatment by ranking the importance of treatment with other variables and assessing the partial dependence of treatment with violations. Nitrate treatment was calculated for each catchment as the proportion of systems in each catchment having nitrate treatment. Similarly, we analyzed the impact of PWS type, and PWS population served in separate models. These last two variables were also not included in the final models because not all PWS have this information available, reducing sample size significantly.

5. Results

5.1. Random Forest Classification

Overall, both the GW and SW RF classification models showed a relatively high percent of catchments correctly classified across the CONUS, with similar classification rates for the percent of sites with and without violations correctly classified (indicating balanced models). The RF classification model for GW systems yielded a PCC of 78.7%, a sensitivity of 75.8% (for sites with violations), and specificity of 81.5% (for sites without violations), based on the 10-fold cross-validation test datasets (Table 1). On the unbalanced holdout dataset, the RF GW model obtained a 77.9% PCC, 78.3% sensitivity, and 77.9% specificity (Table 1). The RF classification model for SW systems yielded a PCC of 90.3%, 91.9% sensitivity, and 88.6% specificity for the test datasets. For the unbalanced holdout dataset, the SW model obtained a PCC of 85.7%, a sensitivity of 83.6%, and a specificity of 85.7% (Table 1). An 80% PCC means that the model is able to correctly predict catchments 80% of the time, while incorrectly calculating whether a catchment is likely to have a violation 20% of the time. The similar classification rates between the sensitivity and specificity indicates a balanced model that can predict catchments with or without violations, respectively, equally well. The high and similar classification rate for the unbalanced holdout datasets helps support that the model can do well even when the data is unbalanced (zero inflated), indicating little bias. The SW model performed a little better than the GW model, possibly due to the smaller sample size, with fewer sites to misclassify.

Table 1.

Random Forest Classification Results

Model	PCC	SENS	SPEC	Gmean	AUC	% False Positives	% False Negatives
GW
Test*	78.7	75.8	81.5	78.6	0.85	18.5	24.2
Holdout**	77.9	78.3	77.9	78.1	0.85	22.1	21.7
Final***	78.1	100	77.8	88.2	0.98	22.2	0.0
SW
Test*	90.3	91.9	88.6	90.2	0.92	13.4	8.1
Holdout**	85.7	83.6	85.7	84.7	0.92	14.3	16.4
Final***	85.6	100	85.4	92.4	0.99	14.6	0.0

^*Results for 90/10, 10-fold cross validation on pre-balanced training and test datasets

^**Results for applying 90/10 cross validated model on the unbalanced 20% of holdout of original dataset

^***based on applying model on the unbalanced full dataset

PCC = percent correctly classified; SENS = sensitivity or percent of violators correctly classified; SPEC = specificity or percent of non-violators correctly classified; Gmean = sqrt(SENS × SPEC); AUC = area under the curve; % False Positives = 100-SPEC; % False Negatives = 100-SENS

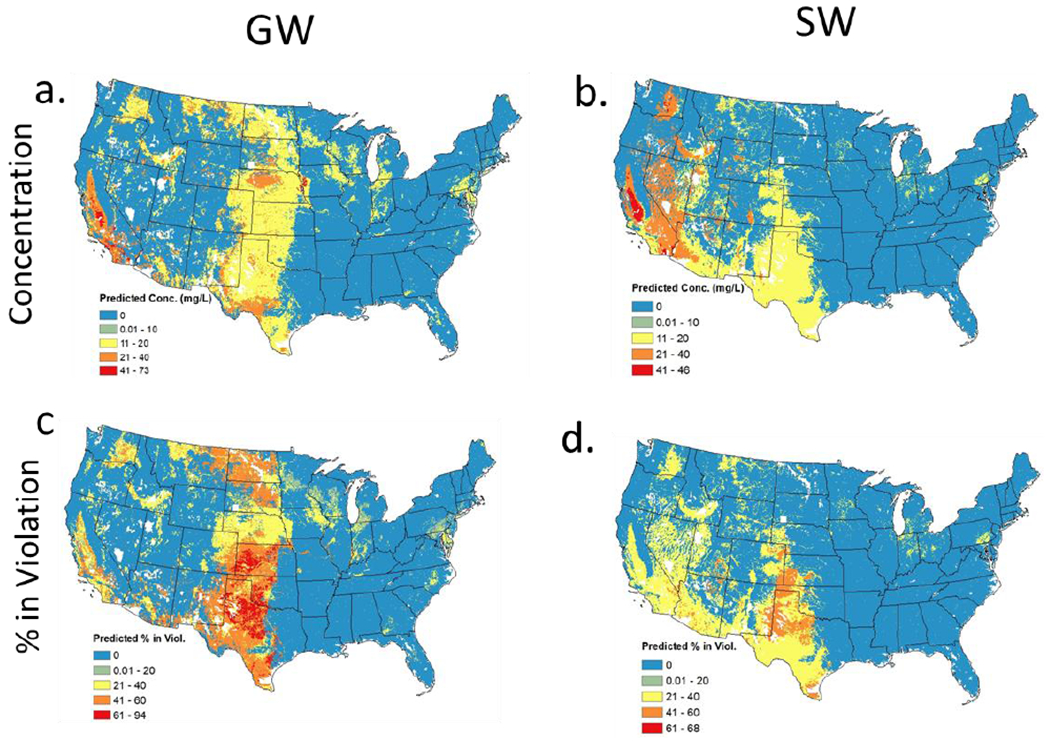
The GW classification model shows a high predicted probability (>0.5) of potential violations in the following regions: 1) The Central California Valley; 2) The Columbia Plateau in Washington; 3) The Snake River Plain in Idaho; 4) The Southern Great Plains from west central Texas to southern Nebraska; 5) Parts of the Northern Great Plains from northern Montana to western North Dakota; 6) Scattered parts of the Upper Midwest centered on the dairy region of much of central and southern Wisconsin, northeastern Iowa, and parts of central Minnesota (1978 and 2012 Census of Agriculture)^{21, 23, 51–52}; and 7) The Piedmont and Coastal Plain of Delaware (Figure 1c). The SW classification model, while also highlighting the Central California Valley as a region at risk of violations, shows the other major regions at risk to be the Southern Great Plains from the U.S./Mexico border to western Kansas and eastern Colorado, and the mostly semi-arid to desert regions of the Madrean Archipelago in Arizona, Sonoran Basin and Range, and Southern California/Northern Baja Coast (Figure 1d).

Of the 2.6 million catchments, 475,890 (19.1 %) are predicted to be at risk of violation for GW systems. We defined risk as a >50% probability of violation. Of the 88,083 catchments with GW PWS, 12,869 or 14.6% have a high risk (>50%) of being in violation. Most catchments (463,021 or 97.3%) predicted to be in violation do not have groundwater PWS currently, though they may have private wells or be potential locations for installing future PWS, due to their current absence of PWS (Figure 1e). Similarly, 390,100 (15.7%) of all catchments are predicted to have a high risk for SW violations and most of these catchments (389,453) do not have surface PWS. On the other hand, 647 (9.3%) of the 6,934 catchments with SW PWS do have high risk of being in violation (Figure 1f).

The proportion of catchments predicted to be in violation for GW (i.e.,14.6%) and SW (i.e., 9.3%) systems is much higher than the observed proportion of systems in violation for GW (0.8%) and SW (0.4%). Regions where the classification models overpredicted (false positives) were mostly in the western states for both models and upper Midwest and Mid-Atlantic for the GW model (Figure 2a,b). These false positive predictions for the final model are due to the model having a specificity (percent of non-violators correctly classified) at 78.8% for GW and 85.4% for SW, indicating that 22.2% and 14.6% of GW and SW catchments, respectively (100 minus specificity) were classified as violators when they were not (Table 1). Depending on the required application of the model, having false positives is a conservative way of seeking which locations are at risk. Also, this model could be considered a screening tool to use for first finding regions with the highest risk and then users of the model could zoom in further with more local scale models to look in depth for distinguishing which locations are at highest risk. It also may be that regions with false positives are due to the presence of nitrate treatment technologies helping to reduce the violation rate in the presence of environmental factors that create high risk. The most important categories of predictor variables for GW violations were land use, followed by climate/hydrology, and then N inputs, while for SW violations they were climate/hydrology, then land use, and N input variables (Figure 3, Table S6). Based on variable importance rankings and partial dependence plots for the top 10 predictor variables in the RF classification model, the likelihood of a catchment having a GW system in violation increases with % cropland, irrigation-to-precipitation ratio, N surplus, and pesticide use, but decreases with agricultural drainage, surplus precipitation, and mean precipitation (Figures 3a, 4). For SW systems, catchments are more likely to have systems in violation with a greater % shrubland, pesticide use (associated with agriculture), intermediate levels of fertilizer use, irrigation-to-precipitation ratio, and canal/ditch/pipeline density, but are less likely with increased surplus precipitation and mean precipitation (Figures 3b, 5).

Figure 2.

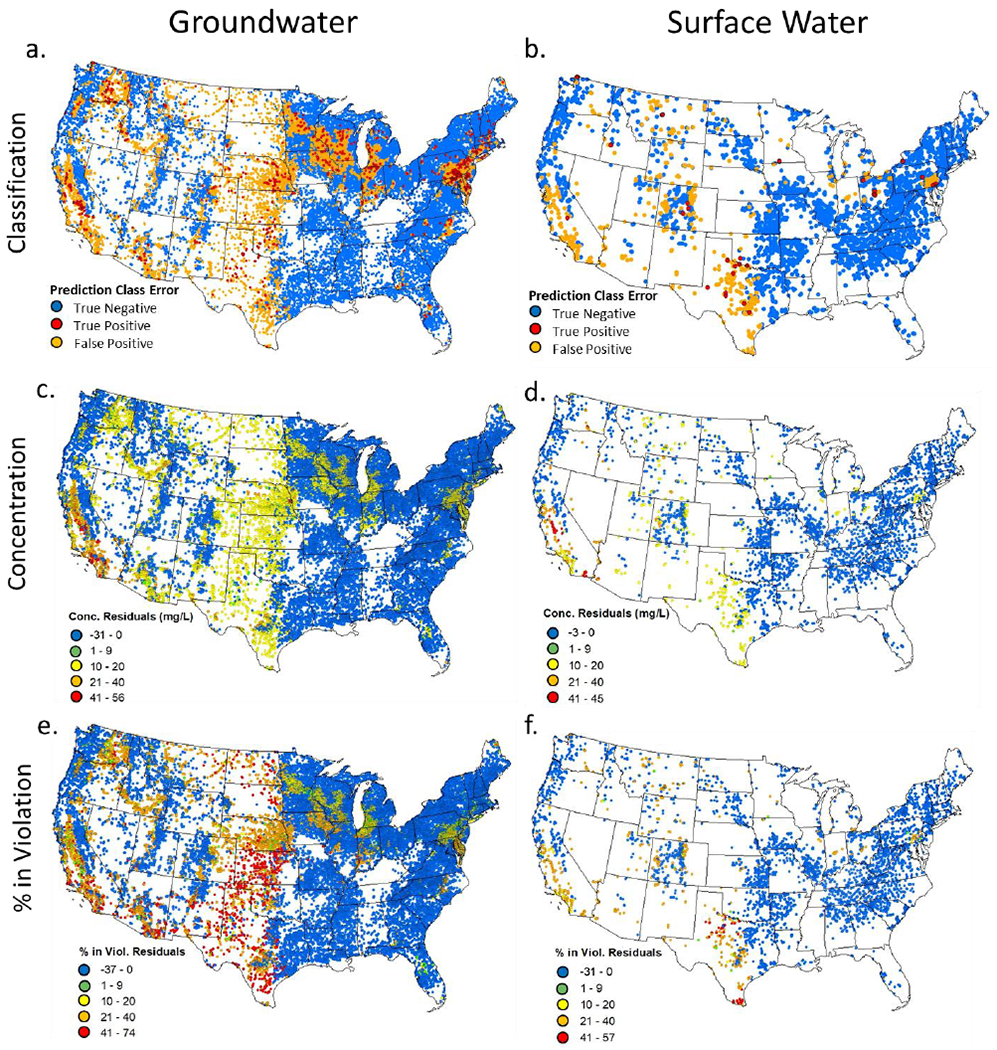
Prediction residuals between observed and predicted a) GW violation class, b) SW violation class, c) mean GW concentration, d) mean SW concentration, e) % of GW systems in violation, and f) % of SW systems in violation per catchment. Prediction Class Error: True Negatives are catchments without observed violations that are predicted to not be in violation, True Positives are catchments with observed violations that are predicted to be in violation, False Positive are catchments without observed violations that are predicted to be in violation. Conc. Residuals and % in Viol. Residuals: the amount of over (positive values) or under (negative values) prediction in mg/L or %, respectively.

Figure 3.

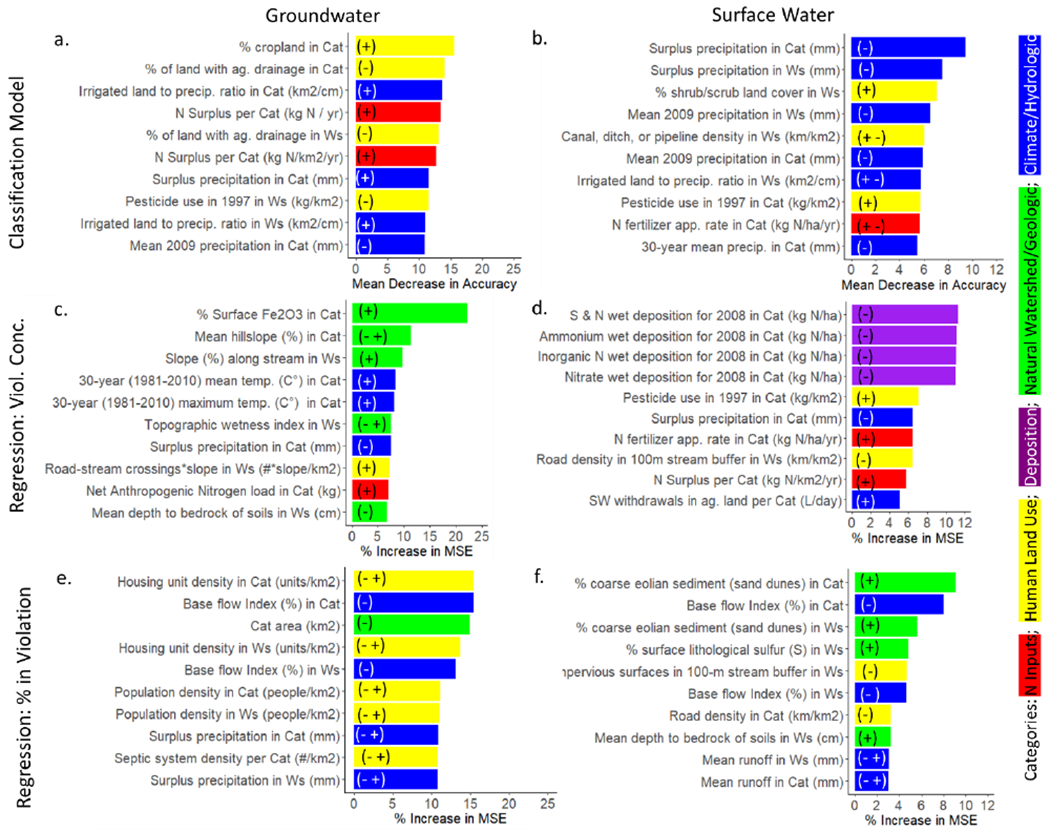
Variable importance rankings for the top 10 variables based on the RF a) GW classification model, b) SW classification model, c) GW concentration model, d) SW concentration model, e) % GW systems in violation model, and f) % SW systems in violation model. The (+) or (−) symbols on the bars mean there was a positive or negative relationship between the predictor and response variables, respectively. And the (− +) symbol indicates there was first a negative then a positive relationship, while a (+ −) symbol indicates there was first a positive then a negative relationship. Cat = catchment; Ws = watershed.

Figure 4.

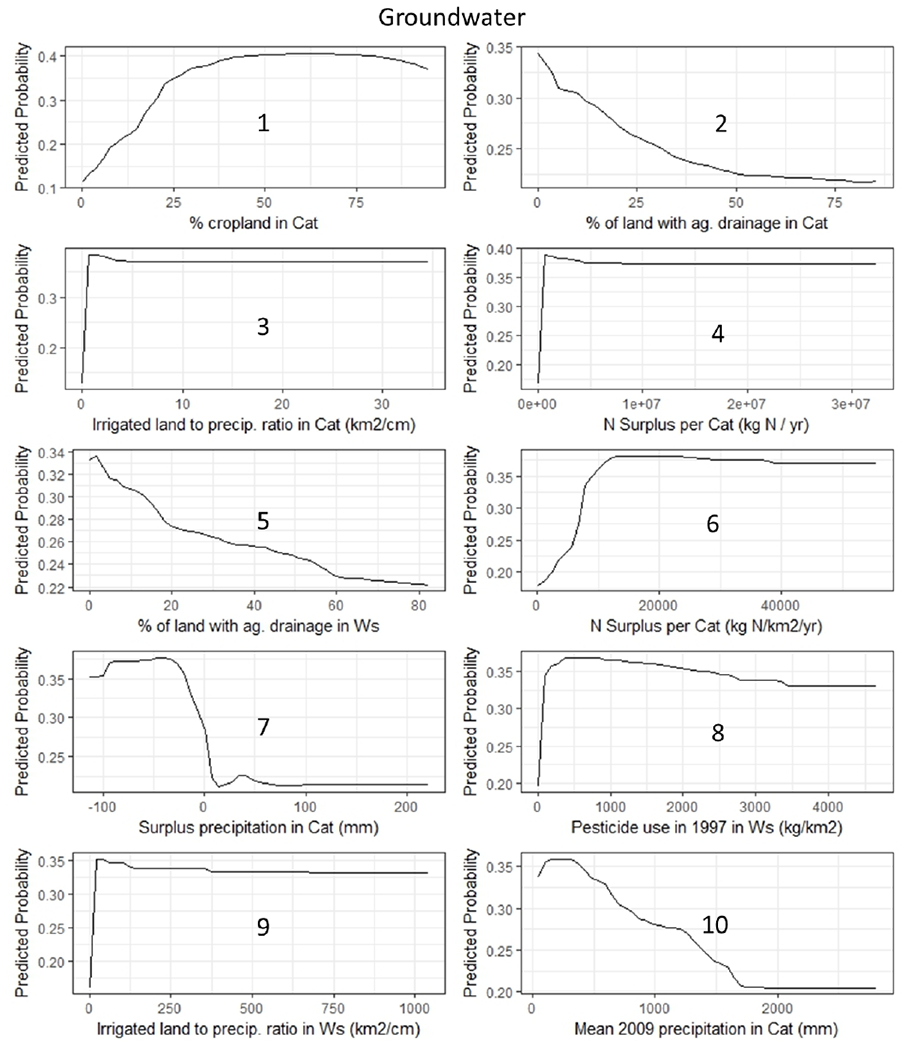
RF classification partial dependence plots for GW, showing the relationship between the top 10 important variables and the violation class. The number on each panel represents the importance ranking.

Figure 5.

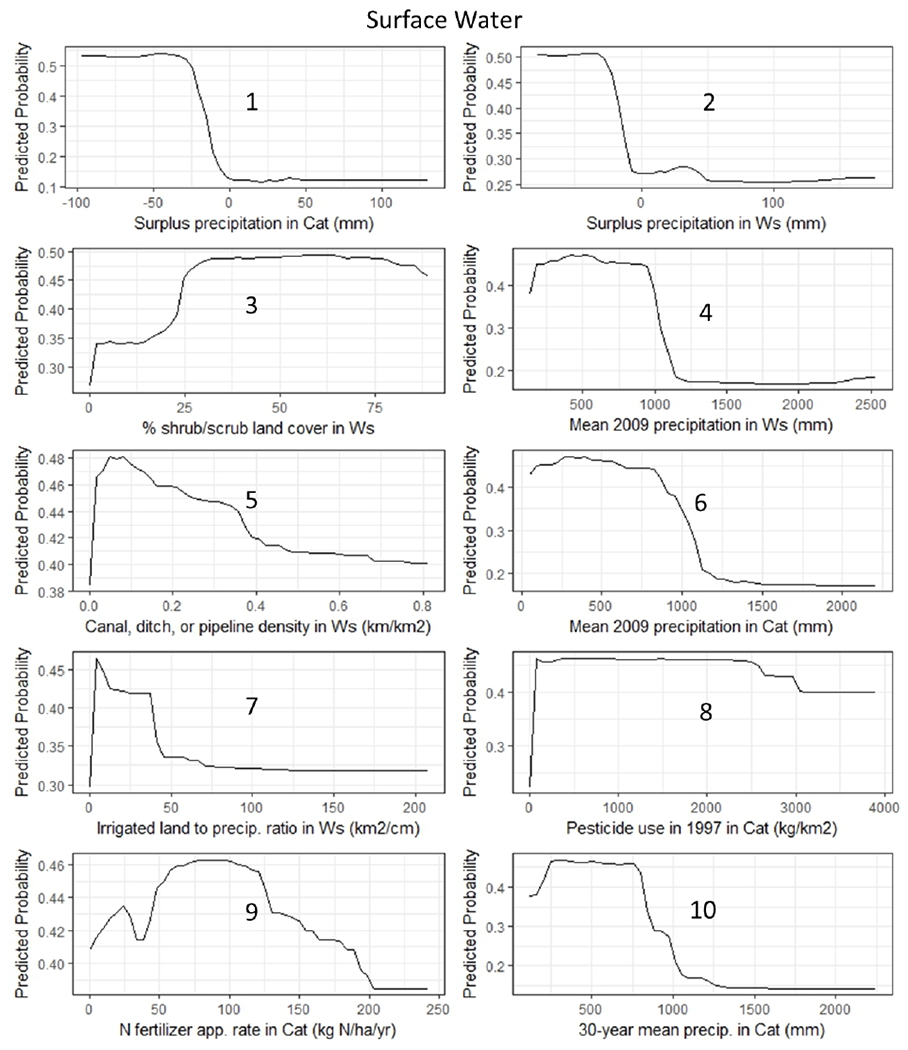
RF classification partial dependence plots for SW, showing the relationship between the top 10 important variables and the violation class. The number on each panel represents the importance ranking.

Many of these important variables show inflection points where a small change in the variable results in a rapid increase in N violations. For example, there is a rapid increase in GW violations when irrigation-to-precipitation ratio goes from 0 to >1, N surplus gets above 7,500 kg N/km²/yr, or >30% cropland, pesticide use is >100 kg/km², or if surplus precipitation <0 mm (Figure 4). There are greater SW violations if surplus precipitation is < −25 mm, irrigation-to-precipitation ratio >1 and <50, pesticide use >10 kg/km², mean precipitation <750 mm, and % shrub/scrubland >25% (Figure 5).

While not included in the final model, three attributes for each PWS in SDWIS (PWS Type, Treatment, and System Size) were used as predictor variables in separate models to determine their effect on nitrate violations. When nitrate treatment was included as a predictor variable in the RF models, treatment was found to not be important for predicting SW violations, but partial dependence plots show that violations decreased with increasing % of PWS, specifying nitrate reduction as a treatment (Figure S7a). For GW systems, treatment was found to be within the top 5 important variables in the RF model, but violations increased with greater % of PWS having treatment technology for nitrate (Figure S7b). For SW systems, violations decreased as the size of the population served by the system increased and had higher violation probability with transient non-CWS (Figure S7c,e). GW systems had similar patterns with population served, and was lowest for community water systems (CWS) and highest for transient non-community water systems, despite the higher 20 mg/L alternative MCL for some non-community water systems⁴ (Figure S7d,f).

5.2. Random Forest Regression Model

The RF regression models can explain 43% and 52% of the variation in mean nitrate concentration per catchment for GW and SW PWS, respectively, based on cross-validation test datasets. When applied to the unbalanced holdout dataset the model explained 35% and 99% of the variation in GW and SW violation concentrations, respectively (Table 2, Figure S8a,b). Potential sources of variability in the data not explained by the model could be due to the concentration data being limited to values above 10 mg-N/L and to the lack of information on nitrate treatment or system operation, as described elsewhere. The RF regression models explained 28% and 21% of the variation in the percent of GW and SW PWS in violations per catchment, respectively, based on cross validation test datasets, and 17% and 40% of the variation in percent GW and SW violations, respectively, for the holdout dataset (Table 2, Figure S8c,d).

Table 2.

Random Forest Regression Results – Comparing Response Variables

Response Variable	R2 Training	RMSE Training	R2 Test	RMSE Test	Bias Test	R2 Holdout	RMSE Holdout	Bias Holdout
Conc. GW	0.88	3.6	0.43	7.8	0.20	0.34	10.6	0.34
Conc. SW	0.98	1.7	0.52	3.5	0.16	0.99	1.6	0.13
Percent GW	0.88	7.9	0.28	19.3	0.70	0.17	19.9	3.65
Percent SW	0.35	15.8	0.21	14.6	−0.49	0.40	13.1	3.84

RMSE = Root Mean Squared Error. Training = average of the 10 cross validated model results that used 90% of the balanced dataset for training the model. Test = average of the 10 cross validated models applied on each of the 10% portions of the balanced dataset that was held back when training the models. Holdout = dataset consisting of 20% of the original zero-inflated and unbalanced dataset that was held back when training the models (based on completely separate model runs from the 90/10 training and testing set model runs).

Based on the RF concentration model for GW systems, the region with the highest predicted nitrate concentrations is the southern California Valley. Other regions with relatively high predicted nitrate concentrations are the remainder of the California Valley, the Southern California/Northern Baja Coast, the Sand Hills of Nebraska, the southern Edwards Plateau of Texas and some adjacent semi-arid areas to the south and west, and a portion of the Western Loess Hills and Plains of western Iowa (Figure 6a). The RF regression SW model for nitrate concentration predicted the highest values in the Central California Valley as well as relatively high concentrations in the Basin and Range ecoregions from western Arizona to northern Nevada, the Snake River Plain in Idaho, and the Columbia Plateau in Washington (Figure 6b). Regions where the models overpredicted (false positives) the nitrate concentrations were mostly in the Great Plains, semi-arid to arid western states, scattered areas in the Upper Midwest, and a region centered on southeastern Pennsylvania and the Delmarva peninsula for the GW model and in the semiarid to arid parts of the western U.S. for the SW model (Figure 2c,d).

Figure 6.

Maps of conterminous U.S. showing a) RF regression predicted concentration for GW, b) RF regression predicted concentration for SW, c) RF regression predicted % of systems in violation for GW, and d) RF regression predicted % of systems in violation for SW. Note that these models only incorporate environmental variables and are not based on nitrate treatment or system management practices.

Unlike the RF regression model for violation concentration, the RF regression model for percent of GW PWS in violation of the nitrate MCL showed higher values in parts of the Great Plains, over the southern two-thirds of the Ogallala aquifer and adjacent areas to the east and south, including much of the Southern Texas Plains, Edwards Plateau, and Chihuahuan Deserts, as well as parts of the northern Great Plains of North and South Dakota and western Montana (Figure 6c). For percent of SW PWS in violation, the highest values were in the Southern Great Plains from northcentral Texas to southwestern Kansas and southeastern Colorado, much of which is over the southern part of the Ogallala aquifer (Figure 6d). Regions where the GW and SW % in violation models overpredicted nitrate violations (false positives) were scattered but mostly concentrated in the southern Great Plains (Figure 2e,f). The RF regression models show that the observed to predicted relationship has smaller variance around the 1:1 line for SW but is larger for GW nitrate concentrations and % in violation. Also, the slope is closer to the 1:1 line for SW than for the GW models (Figure S8).

For the GW model, nitrate concentration increased with surface geology iron oxide content, stream reach slope, mean temperature, maximum temperature, road-stream crossings, and Net Anthropogenic Nitrogen Inputs (NANI), while wetness index, surplus precipitation, and mean depth to bedrock, were negatively related to concentration, and hillslope was negatively related at low slopes, then positively related at higher slopes (Figures 3c, S9, Table S6). For the SW concentration model, pesticide use, N fertilizer application rate, N surplus, and SW withdrawals in agricultural land had a positive relationship, while atmospheric wet deposition from sulfur and nitrogen, ammonium, inorganic N, nitrate, surplus precipitation, and road density had a negative relationship (Figures 3d, S10, Table S6).

For the GW model, % in violation decreased at low levels, then increased at higher levels of housing density in the catchment and watershed, population density in catchment and watershed, surplus precipitation in the catchment, and density of septic systems, but decreased with base flow index within catchment, catchment area, base flow index within watershed, and surplus precipitation in watershed (Figures 3e, S11, Table S6). For the SW model, % in violation increased with coarse eolian sediment in catchment and watershed, soil sulfur content, mean bedrock depth, runoff in watershed and catchment, but decreased with baseflow index, impervious surfaces, and road density in catchment (Figures 3f, S12, Table S6).

Many of these important variables show inflections points where a small change in the variable results in a rapid increase in the response. For GW, higher nitrate concentrations are predicted when % surface iron oxide is >25%, mean temperature >16 °C, NANI load >1×10⁶ kg, and surplus precipitation < −50 mm (Figure S9). For SW nitrate concentrations, steep transitions are predicted when inorganic N deposition is <1 kg N/ha, N surplus >22,000 kg/km²/yr, pesticide use >500 kg/km²/yr, road density <1 km/km², N fertilizer application rate >75 kg N/ha/yr, and irrigation-to-precipitation ratio >0.25 km²/cm (Figure S10). For GW, there is a rapid decrease for % in violation when housing density per catchment is <100 units/km², baseflow index <30, and surplus precipitation in catchment or watershed < −50 mm (Figure S11), while for SW, % in violation steeply rises with baseflow index <20%, road density <20 km/km², and runoff is >600 mm (Figure S12).

6. Discussion

This analysis produced geospatial information to help predict where, at the scale of our analysis, there is potential risk of a nitrate MCL violation for 1) existing PWS, 2) new or planned PWS, or 3) private groundwater wells. This is the first national study to examine the relative importance of a variety of variables that may explain the spatial patterns for both GW and SW sourced nitrate violations in PWS. Information from this analysis can help managers identify the probability for risk based on the characteristics of the GW or SW source and how to focus efforts to reduce violations and, hence, risk to human health.

The models in this analysis predict the locations across the CONUS that have either high or low risk for nitrate MCL violations for GW or SW sources and predict the nitrate concentrations and percent of systems in violation for sites predicted to have high risk of violations. This study also indicates which land use, geology, climate, and other environmental factors most influence nitrate violations. The models, however, were unable to completely assess the impact of nitrate treatment or PWS operation (e.g., switching or blending with other water sources), due to insufficient information in SDWIS. The lack of PWS operation information may be a reason for false positives in the model because sites predicted to be at risk, based on environmental drivers like cropland, may not have violations due to the presence of treatment or ability of the PWS to change sources. Despite this, the models were able show strong prediction accuracy across the entire CONUS, using a variety of predictor variables, for both SW and GW systems. The models in this study are also able to assess risk for areas with both public and private drinking water sources and for both CWS and non-CWS. While this analysis is based on finished water, not raw source water, models can detect if source water poses risks. Overall, the false positives could represent opportunities where the model output could indicate discrepancies between areas where watershed/landscape-based risk differs from actual violations, indicating areas with a tendency towards high violations, where PWS operations have prevented it.

It is also foreseeable that not including treatment in the final models would result in models that incorrectly predict low violation rates (false negatives) in areas that have high N inputs from agriculture, due to widespread use of treatment. We, however, do not believe that not including treatment necessarily resulted in our models being trained to predict low violations in areas that have high N inputs, for several reasons: 1) at the national scale of the model, the environmental and climatic variables were found to be the most dominant predictors, reducing the likelihood that the model was trained to associate high N inputs with low violations, 2) this is also supported by the partial dependence plots that displayed a positive relationship between nitrate violations and N input variables (e.g. Figure 4), 3) a lot of areas where false positives occur (Figure 2e,f) were often areas with known nitrate treatment (Figure S1), particularly for GW, indicating that areas needing treatment were still predicted by the model to likely be at risk for nitrate violations (Figure S7b), and 4) the final GW and SW models had no false negatives, meaning that there were not any observed sites without violations incorrectly predicted to have a high risk for violations. However, the models used on the test and holdout datasets did have 8-24% false negatives, with greater false negatives for GW (Table 1), showing the possibility for the models to predict low risk in unknown areas that have had nitrate violations. This is not necessarily caused by a lack of treatment information in the models, but could also be caused by environmental factors, such as legacy N in GW.⁵³ Further exploration with finer scale models that include treatment information would likely strengthen the prediction and interpretability of the models.

6.1. Classification Models

GW or SW violations do not occur randomly but are concentrated in specific geographic areas. Areas at greatest risk for GW violations (Figure 1), based on the classification model, were correlated with landcover, hydrology/climate, and N inputs (Figure 2), similar to Nolan and Hitt ²². The importance of surplus precipitation and irrigation-to-precipitation ratio, in the GW classification model, indicates that arid landscapes are more vulnerable, particularly where irrigation far exceeds precipitation in croplands. This is because arid landscapes may have a buildup of N inputs that eventually gets infiltrated into GW with irrigation, whereas areas with surplus precipitation may have a dilution of the N inputs, resulting in lower GW concentrations. The importance of N surplus in the GW model indicates that accounting for both N inputs and removals from the system, as advocated by McLellan, et al. ⁵⁴, may be better at predicting nitrate/nitrite drinking water violations than fertilizer inputs alone. Unlike previous studies,^{8, 22, 26, 29, 55} our GW model did not find water table depth (a surrogate for well depth), hydraulic conductivity or aquifer type (e.g., % semiconsolidated sand aquifers) as important. We were not able to specifically use well depth as a variable in the model, as this information is not provided by SDWIS, and well depth is typically greater than water table depth. Soil permeability was a top 20 important variable for the GW classification model, corresponding to increased infiltration to GW aquifers,⁸ However, hydrologic conductivity was not as important, possibly due to its heterogeneity across the landscape and the greater role that N inputs play in source water nitrate levels than geology or soil conditions at the national scale. Only a small number of GW systems were under the direct influence of SW (categorized as GWUDI systems) and so this was not likely a factor. Also, the presence of semiconsolidated sand aquifers likely was not a dominant factor because this and other aquifer types are not evenly distributed throughout the U.S. and so it is not as important at the national scale, compared to local scale models.

Based on the SW classification model, regions at greatest risk for SW nitrate violations (primarily in the southwestern U.S.) were driven largely by geology, climate, agricultural land use. Overall, the regions at risk for SW nitrate violations were specifically associated with a combination of factors, such as agriculture and high N fertilizer use on semi-arid land, where there is less precipitation, but excess irrigation. This indicates that climate, land use, and N inputs all play a key role in governing SW violations. Consequently, optimizing the timing of irrigation and fertilizer inputs in these landscapes could improve source water quality. For example, because SW violations are most strongly influenced by precipitation, one way to manage and reduce SW violations, which may interact with timing of fertilizer, would be to ensure that fertilizer is not added prior to large rain events. Our previous work¹ found that while there are more GW systems in violation, SW systems in violation have the potential to impact more people; therefore, it is important to understand the factors affecting the SW nitrate violations.

6.2. Concentration Models

Regions at risk for the highest nitrate concentrations in GW sourced drinking water (Central California Valley, major parts of the Great Plains in Texas and Nebraska, the Columbia Plateau, the Snake River Plain in Idaho, and the Piedmont and Coastal Plains of Pennsylvania and Delaware) were associated with a combination of anthropogenic N inputs, agricultural lands, and geologic factors (low slope, soil type), as found in other studies.^{22, 26, 29} The regions at most risk were also driven in part by locations of GW PWS (which are not evenly distributed across the U.S.), and which, in turn, are driven by geology, climate, and human population. Factors we identified that were not previously found to drive nitrate in water supplies included climatic factors (high temperatures, excess evapotranspiration) and the presence of high iron oxide. Unlike in the southeast, where high temperatures, rainfall, and soil organic matter result in high denitrification rates and consequently reduced nitrate contamination,⁸ the high temperatures, but low rainfall and low organic matter content in the arid southwest inhibit denitrification, and the low slopes and sandier soils³⁶ likely help foster infiltration of excess nitrate. Also, iron oxide has been shown to increase N mineralization (nitrification) and N mobilization at low pH through increased organic matter decomposition;⁵⁶ based on the USGS’s geochemical soil data of the CONUS,³⁶ iron oxide also happens to be high in the xeric Southwest, the Central California Valley, upper Midwest, southeastern Pennsylvania and Delaware, where violations are highest.

Areas predicted to be at greatest risk of high nitrate concentrations in SW were in parts of southern California, the Central California Valley, and Columbia Plateau in western Washington that correspond with low precipitation, but high N inputs from agricultural land use and where there are high surface water withdrawals for irrigation purposes. Other studies also found that N inputs as well as climate variables like precipitation were important in predicting surface water nitrate concentrations. For example, Bellmore, et al. ²⁰ found that TN input was the best predictor of stream dissolved inorganic nitrogen concentrations, and Nishina, et al. ⁵⁷ found N deposition to be most important followed by slope, temperature, and precipitation. Also, similar to Bellmore, et al. ²⁰, who found atmospheric N deposition to be the most dominant N source in surface water, our model found N deposition variables to be the top four important variables in the SW concentration model. A study by Álvarez-Cabria, et al. ⁵⁸ found the most important variables for predicting river nitrate concentration were % agricultural land, pasture land, and precipitation. Interestingly, predominantly agricultural areas of the Midwest with a few observed SW violations, like in central Ohio, did not result in widespread model predictions for SW violations throughout the Midwest. Even though, agriculture and N loading are major factors in nitrate concentrations in surface source waters,²⁰ the lack of a strong relation to violations might be a result of relatively widespread treatment or other engineering solutions, which reduce violation rates. Additionally, this may indicate that the national scale patterns for SW nitrate violations are more strongly driven by climate and rainfall factors than by land use and N input variables and that spikey violation behavior is difficult for the RF model to detect; this may be particularly true because monitoring is only required quarterly, increasing the likelihood of missing flash rainfall events and subsequent runoff. It may also be that a greater presence of tile drainage in areas like central Ohio may contribute to higher observed SW violations that were not predicted by the model, due to the more local scale of this issue.⁸ Consequently, regional, smaller scale models likely would help better determine local drivers of violations.

6.3. Percent in Violation Models

A greater proportion of GW systems in violation is predicted to be found in more rural areas in semi-arid climates (particularly in much of the western parts of the Great Plains of Texas, Oklahoma, and Kansas, southern Nebraska, and eastern Colorado). This is likely driven by transient non-community water systems (shown to be associated with the greatest amount of GW violations, even though their MCL can be 20 mg-N/L at the discretion of their state⁴) in less populous areas of Western Texas, etc., and by the role of the Ogallala aquifer, which is shallow and more susceptible to groundwater contamination.^{7, 59} Our study also shows that violations increase with smaller PWS population served, thus most violations occur in smaller systems in more rural and less populous areas. This may be due to these systems typically having shallower wells, which are more prone to contamination.⁸ Allaire, et al. ⁶⁰, looking at all reported contaminants in SDWIS, also found that smaller systems and rural areas tended to have more systems in violation. Similarly, population density was also an important driver for the GWAVA drinking water model.²²

The percent of SW systems exceeding the nitrate MCL were predicted to be highest in regions with arid climates, low baseflow, and sandy soils. These regions are primarily in the southwest of the CONUS, areas also predicted to be vulnerable by the other SW and GW models. The higher SW nitrate levels in these arid regions may be due to low rainfall, lower baseflow with less dilution and low organic matter content inhibiting denitrification. Gentle slopes and sandier soils³⁶ also likely help foster infiltration of excess nitrate in surface waters.

6.4. Thresholds

The thresholds at which specific variables are associated with violations, as provided by our models, can be directly useful for watershed managers when assessing risk. For areas with GW systems, knowing that N surplus above 7,500 kg N/km²/yr (75 kg N/ha/yr) or land use >30% cropland increases nitrate violation risk can help managers quantify or set restrictions on N inputs and land use practices. In terms of what regions or climates are most at risk, managers can use the fact that violation risk increases when areas have negative surplus precipitation or when irrigation exceeds precipitation. Managers can also use information from the GW concentration models, which suggest GW systems are at risk for higher nitrate concentrations when surface lithological iron oxide is >50%, due to its stimulation of nitrification,⁵⁶ or where surplus precipitation is < −50 mm, such as in arid climates, mean temperature exceeds 16 °C, or NANI from agriculture is >1,000,000 kg per catchment.

For areas with SW systems, climates most at risk are areas with surplus precipitation < −25 mm (which are areas even more arid than where GW systems are at risk). The risk is also high for SW systems if pesticide use (a surrogate for agricultural practices) is >10 kg/km², or if arid plant cover (shrub/scrubland) is >25%. SW systems also become at risk for high nitrate concentrations when N fertilizer application rate is >75 kg N/ha/yr, N surplus is >22,000 kg/km²/yr (or cropland is approximately >80%), and the location is more rural (road density <1 km/km²). This information can help managers pinpoint which locations are most at risk and where to prioritize money to improve source water protection and/or adjust PWS treatment approaches specific to nitrogen. Many of the predictor variables in the model have a non-linear relationship with nitrate/nitrite violations. There are situations where catchments that are usually below a certain threshold (e.g., low N surplus or low cropland) may be more vulnerable because of a change in land use practices, and situations where catchments above a threshold (e.g., high N surplus or high cropland areas) may not show an increase in violations even when there is an increase in N inputs.⁶¹

6.5. Model Performance

While both classification and regression models performed well compared to previous studies, the classification models overall were better at predictions than the concentration models, likely due to a lack of concentration data below 10 mg N/L, as mentioned earlier.

The prediction accuracy of our national scale RF classification and regression GW and SW models performed similar to other studies done at local scales. The results of the RF classification model for groundwater was not only comparable to other studies, but had more balanced sensitivity and specificities,^{29, 55} likely due to pre-balancing of our zero-inflated datasets. For example, a study which applied a RF classification model to nitrate groundwater concentrations in Iowa found a lower sensitivity (67.1%) compared to specificity (85.8%).²⁶ Additionally, despite the much larger scale of our study and the greater landscape variability of the CONUS, our RF regression GW model for predicting nitrate concentration performed similar to studies using this approach at smaller scales and in less heterogeneous areas. For example, studies in California,²⁹ and Iowa²⁶ both explained ~40% of the variation in groundwater nitrate concentration based on test datasets while ours explained 43% of the variation.

When comparing our RF classification GW model results (Figure 1e, S13a) with the USGS GWAVA-DW model (Figure S13b), 79.9% of the catchments were classified correctly (as either in violation or not in violation), 91.7% of the same catchments with violations were classified correctly for both models, and 79.9% of the same catchments without violations were classified correctly for both models. Additionally, there is a significant positive relationship between predicted SDWIS concentrations above 10 mg nitrate-N/L and the GWAVA predicted concentrations above 10 mg nitrate-N/L, however, there is a low R² (0.16), indicating a large unexplained variance (Figure S13c). This also indicates that it is reasonable to use our RF model to predict violation risk to areas with private drinking water wells, although our model does not account for all sources of variation.

Our RF regression SW models performed similarly to other studies that have applied this approach towards predicting surface water nitrogen concentrations, with an R² of 0.52. A study in Japan⁵⁷ found a test R² of 0.59 and a study in Spain⁵⁸ found a test R² of 0.71 for predicting river nitrate concentrations. This is encouraging since the scale of our model was much larger than the other studies and the SW model had a relatively small sample size. When comparing the SW model results with the surface water concentration data used by Bellmore, et al. ²⁰ we found 79% of the 1966 sites were correctly classified as either exceeding or not exceeding the nitrate MCL, but only 20% of the sites with the MCL exceedance class were correctly matched, possibly due to the small available sample size.

6.6. Limitations of Study

While our national models performed well and comparable to local scale studies (with consistent predictor variables),^{26, 29} there are some limitations to note. Even though the GW and SW models had relatively high prediction accuracies, compared to other similar studies, the models still had a bias towards making false positive predictions (about 15% or 22% of the time for SW and GW systems, respectively), while making no false negative predictions in the final models (Table 1). This may be due to the zero-inflated dataset where only 1% of catchments have drinking water violations, while many catchments without PWS or violations have similar land, geologic, and climate characteristics. For example, most over predictions were in the same regions as catchments with observed violations, particularly in areas of the Great Plains above the Ogallala aquifer and in the Central California Valley, and this is likely because they share similar climate, geology, and land use with the violating catchments. Thus, violations appear to also be driven by additional factors that operate on smaller scales. For example, better knowledge of “engineered” factors within the drinking water treatment plant (e.g., ability of a PWS operator to switch to or mix with other water sources, use improved treatment technologies, or use other management strategies) may improve model performance. Similarly, more local land cover or geology, not characterized at the catchment or watershed scale, would likely help the model. Yet, even though the model overpredicted in certain areas, it is still useful for assessing overall risk and could apply to areas adding new systems. Additionally, because data reporting and quality can differ between states, with 26-38% of health-based violations not reported,^{60, 62} this could mean our model may be “underpredicting” in areas that are underreporting, or that our model’s false positives are in fact accurate predictions for the underreported areas (areas with higher monitoring and reporting violations¹). It also should be noted that it has recently been discovered that nitrification of ammonia within the distribution system can potentially result in increased nitrite or nitrate concentrations at the point of use⁶³ and thus some MCL violations may be missed. Another limitation of the study, due in part to small sample sizes, particularly for the SW models, is that we were unable to regionalize the analyses. An issue associated with trying to determine relationships on a national scale is that the factors that are associated with variation in nitrate in one region often may not be valid in another.⁶⁴ The interrelationships, relative importance, and number of anthropogenic (e.g., road density or Census socio-economic characteristics) and natural drivers (e.g., geology, soils, vegetation, land cover) are more than likely to be very different from one region to another. Thus, some predictor variables that are not important at the national scale may be important at the regional scale for certain regions and vice versa. Consequently, regional models may be necessary for more fine scale predictions and to determine which variables best explain the smaller scale patterns.

Some of the predictor variables had a counterintuitive association with nitrate violations. For example, SW concentrations have a negative relationship with N wet deposition variables and this likely results from the national scale of the model and the fact that there are more observed violations in the southwest, but less N deposition there,¹¹ and more deposition in the northeast, but fewer violations. Similarly, while nitrate treatment technologies have been shown to reduce nitrate violations at the individual system level,^{1, 31} it is surprising that the RF classification GW model predicted nitrate violations to increase with treatment (Figure S7). This may be explained by there being more systems with nitrate treatment in areas already known for having nitrate violations, due to environmental factors, and areas with naturally less nitrate violations will not need the use of nitrate treatment and will thus have less violations. Due to operation costs, not all PWS have advanced nitrate removal treatment technologies, which minimizes the sample sites with treatment to areas where there is a history of violations. Another factor, missed by our model, is that SW treatment plants operate differently under different scenarios, such as during rain events, and that information is not captured in SDWIS. Also, SW violations were highest with intermediate fertilizer use, instead of the expected linear relationship, and this may be due the use of nitrate treatment by PWS in areas with a history of violations. This may also be due to more important variables like surplus precipitation dominating the relationship, with intermediate fertilizer use found at most negative surplus precipitation (Figure 5). Though other studies have shown strong positive relations between agricultural applications and stream nitrate concentrations.⁶⁵

A limitation of the concentration models is that the dataset did not include nitrate concentrations <10 mg nitrate-N/L for non-violating PWS, making it difficult to determine which PWS might be close to being at risk for violating the nitrate standard. Also, the 99% R² for the SW concentration model was due to small sample size (Figure S8b) and the range of sites with low and some with very high concentrations. The RF model results are helpful for finding broader spatial trends for violation risk, but it may not predict intermittent behavior well, such as for certain systems that have violations due to more unusual circumstances, e.g., a concordance of heavy rain and fertilizer application. For those situations, additional information about specific PWS (such as reports of system failures), upstream land use, or local weather, may be needed to predict intermittent behavior.

6.7. Conclusions

Given the potential public health concerns from having excess nitrate in drinking water, the results of this modeling analysis can be used as a screening tool to inform where source waters are most at risk, which can potentially help managers know where to prioritize efforts for source water protection and thereby reduce the likelihood of drinking water nitrate violations. Information from the models on where to prioritize source water protection efforts may particularly be of help to smaller non-CWS, because they more likely lack enough funds for nitrate treatment technology. Thus, the model results can be used to inform smaller systems where, at the NHD catchment scale, they would be less at risk from environmental factors. It may help PWS, with or with nitrate treatment, save money knowing where the least risky regions are, based on the environmental variables that less likely increase nitrate levels in source waters. Also, because nitrate treatment or the ability to change sources are certainly important factors, more local scale models with complete treatment or PWS operation information may better assess the relative role of environmental variables vs. treatment in controlling violation rates.

The results of this model have implications for protection of the environment in the U.S. and beyond. Knowledge of where violation risk is highest due to environmental factors indicates regions where source waters are vulnerable and may need better source water protection measures, to not only reduce violation risk, but also downstream impacts of high nitrate levels, such as coastal eutrophication and harmful algal blooms. Due to our model’s strong prediction capability at the large national scale, similar models could be applied to other regions across the world of varying scales to assess nitrate violation risk for both groundwater and surface water sources.

Because GW violations are most strongly influenced by cropland, irrigation-to-precipitation ratio, agricultural drainage, and N surplus, controlling these variables more efficiently could play a strong role in addressing GW drinking water violations. The fact that N surplus is important indicates that more efficient use of fertilizer into crop harvest could reduce excess N in the landscape⁵⁴ and help prevent GW violations through improved source water quality. Also, as soon as N surplus increases, the probability of a GW violation jumps dramatically, whereas, there is a more gradual increase in the likelihood of violations with an increase in % cropland, indicating N surplus may have a more direct impact.

While there are significantly more nitrate violations from groundwater systems (95% of all violations), surface water system violations typically have the potential to affect more people since surface water systems often serve large urban populations,¹ and are thus important to manage. Though challenging to manage, a number of states have manure timing application tools.^66–68 SW treatment plant operators are also able to adjust their treatment operations during a rain event to reduce violation risk, which is standard practice. Climate plays an important role in determining where PWS are most at risk for violations (e.g., more arid climates), and while that cannot be directly managed, this study highlights areas where it might make sense to prioritize additional funds for managing PWS source water quality by improving irrigation and efficient N application. Additionally, in the future there may be an even greater risk for nitrate violations in the southwest if climate continues to get drier, with more infrequent, but larger storms.⁶⁹

Overall, this study agrees with previous nitrate modeling results in that cropland and N fertilizer application are important drivers of higher nitrate in source waters,^{22, 26, 29} but unlike those studies we found that N surplus is generally more important than fertilizer N alone, and that climate factors (like surplus precipitation) are also important for all models. To help prevent both GW and SW sourced nitrate violations, further consideration on where to prioritize management and source water protection could be for regions predicted to be most at risk. Smaller systems may be most vulnerable to risk of nitrate violations, particularly if they do not have the resources for nitrate treatment technology or the ability to change water sources. Because our models are built using environmental factors, areas where nitrogen inputs, land use, or other environmental variables increase nitrogen in source water can have greater potential for violations. However, as discussed previously, nitrate violations in PWS are not just driven by environmental factors and future analyses and improved data collection need to more fully address the role of treatment and operation of PWS on nitrate violation risk.