Sudden Unexpected Death in Epilepsy

Abstract

Objective

To develop and validate a tool for individualized prediction of sudden unexpected death in epilepsy (SUDEP) risk, we reanalyzed data from 1 cohort and 3 case–control studies undertaken from 1980 through 2005.

Methods

We entered 1,273 epilepsy cases (287 SUDEP, 986 controls) and 22 clinical predictor variables into a Bayesian logistic regression model.

Results

Cross-validated individualized model predictions were superior to baseline models developed from only average population risk or from generalized tonic-clonic seizure frequency (pairwise difference in leave-one-subject-out expected log posterior density = 35.9, SEM ± 12.5, and 22.9, SEM ± 11.0, respectively). The mean cross-validated (95% bootstrap confidence interval) area under the receiver operating curve was 0.71 (0.68–0.74) for our model vs 0.38 (0.33–0.42) and 0.63 (0.59–0.67) for the baseline average and generalized tonic-clonic seizure frequency models, respectively. Model performance was weaker when applied to nonrepresented populations. Prognostic factors included generalized tonic-clonic and focal-onset seizure frequency, alcohol excess, younger age at epilepsy onset, and family history of epilepsy. Antiseizure medication adherence was associated with lower risk.

Conclusions

Even when generalized to unseen data, model predictions are more accurate than population-based estimates of SUDEP. Our tool can enable risk-based stratification for biomarker discovery and interventional trials. With further validation in unrepresented populations, it may be suitable for routine individualized clinical decision-making. Clinicians should consider assessment of multiple risk factors, and not focus only on the frequency of convulsions.

Sudden unexpected death in epilepsy (SUDEP) is the commonest category of epilepsy-related death.¹ Diagnosis requires exclusion of other potential causes of death because there are no pathognomonic autopsy findings.² The reported incidence of 1.2 per 1,000 patients/y in adults³ is an underestimate because insufficient history and ambiguous pathologic findings lead to misclassification.^4,5

Why do some people experience SUDEP after their second seizure while others survive thousands of convulsive seizures? Ongoing convulsions are a major prognostic factor^6,7 but adjusted analyses are less consistent as to whether early age at epilepsy onset, long epilepsy duration, symptomatic etiology, nocturnal convulsions, and a high number or nonadherence of antiseizure medications are independently predictive.^8,9 We cannot, however, accurately predict individualized SUDEP risk.

This is critical for 2 reasons. First, prospective research into EEG, cardiovascular, and imaging biomarkers requires large cohorts followed for long periods unless high-risk subpopulations are targeted.^10,11 A risk assessment tool based on heart rate variability, the SUDEP-7 inventory,¹¹ failed to generalize even at the population level.¹² Predicting individualized risk would help identify SUDEP biomarkers.

Second, most people with epilepsy and families desire information on SUDEP risk even if the probability is low.¹³ Guidelines suggest informing all individuals of average risk but do not specify how to assess personalized risk, leaving individuals poorly informed about their risk. A personalized prediction tool could provide reassurance, motivation to change, or feedback following a clinical intervention.

We used a large SUDEP dataset⁸ to develop and validate a personalized predictive tool optimized for clinical use requiring only routine clinical data.

Methods

Standard Protocol Approvals, Registrations, and Consents

Ethical approval was previously obtained by the original source studies. No additional ethical approval was sought for this re-analysis of data that were de-identified prior to statistical analysis.⁸

Observational Study Description

We reanalyzed 1 US cohort and 3 case–control (England and Wales, Sweden, Scotland) studies⁸ (table 1). SUDEP diagnosis required (1) a history of epilepsy (>1 epileptic seizure within 5 years of study enrolment) and death that was (2) sudden, (3) unexpected, and (4) remained unexplained after investigative efforts, including autopsy. Definite SUDEP required all 4 criteria and probable SUDEP required the first 3 criteria.

Table 1.

Observational Study Descriptions

Predictor Inclusion Strategy

We harmonized the source data to obtain 29 common clinical predictor variables (additional Methods available from Dryad at doi.org/10.5061/dryad.cfxpnvx4c). Of these, 5 had >50% missing data (abnormal imaging, epileptiform features on EEG, psychiatric comorbidity, dementia, brain tumor) and were excluded from further analysis. Levetiracetam was removed from the analysis because it was rarely used in this dataset. Length of epilepsy is the difference between age at epilepsy onset and age at endpoint and was not included to reduce collinearity. We use generalized tonic-clonic seizures (GTCS) to refer to GTCS (previously known as primary GTCS) as well as focal to bilateral tonic-clonic seizures (previously known as secondary GTCS); focal seizures refers to the remaining focal-onset seizures.

All binary variables were represented by single terms where 1 = presence and 0 = absence of the feature. Etiology is an assignment into 1 of 4 categories and was modeled as 4 binary variables. Continuous predictor variables (age at epilepsy onset and age at endpoint) were standardized by removing the mean and dividing by the SD to create a similar scale to the dummy-coded categorical data,¹⁴ facilitating specification of priors. GTCS and focal seizure frequency were standardized by dividing the frequency by an arbitrary number (10), again to put them on a similar scale to other data while keeping a meaningful value for zero.

Model Building Strategy

All analysis was done using RStudio v1.1447 (2016; RStudio, Boston, MA; rstudio.com/) and MATLAB v2018a (The MathWorks, Inc., Natick, MA). We used Bayesian multiple logistic regression to develop a “full” model of SUDEP risk. SUDEP status (a binary variable) was entered as the dependent variable; the remaining clinical variables were entered as predictors. A Bayesian model is specified by the likelihood and the priors.

The logistic regression likelihood is described in equation (1), where y_i = 1 is the SUDEP status for subject i of N and X_i is a J-dimensional vector of predictors for each subject i. The intercept is modeled as 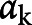; represents the regression coefficient for the jth predictor. We specified a separate intercept for each center (K centers) to account for their differing case:control ratios. As these are a priori known to be different, we did not introduce pooling of these estimates via a further hierarchical term. The prior distribution for regression coefficients (equation 2) and the intercept (equation 3) were chosen to be normally distributed with a mean of 0 and SD of 1. These values were chosen because prior predictive modeling revealed that this resulted in the broad but sensible prior assumption that 95% of standardized adjusted posterior log odds ratios (ORs) would lie between −1.94 and +1.98. A sensitivity analysis was performed (additional Results; data available from Dryad). In order to quantify the improvement in predictive power over current practice, we also developed 2 comparator models. A “baseline” model that had the intercepts (a separate intercept for each center) as predictors but with no other clinical information was used to represent current clinical guidance where only the average population risk is conveyed to individuals with epilepsy. A “baseline GTCS” model that had the population intercepts and also GTCS frequency was also fitted to represent current research practice which relies on GTCS frequency as a surrogate for SUDEP risk. Due to the number of predictors involved and the complexity of the missing data analysis, we avoided modeling interactions within the linear term.

Posterior Estimation

Calculating the Bayesian posterior for such a model can be analytically intractable and therefore posterior parameter estimates were generated using a Markov Chain Monte Carlo (MCMC) procedure. We used RStan software (R package version 2.18.2; mc-stan.org/), which implements Hamiltonian Monte Carlo with No-U-Turn sampling.^14,15 Using the default recommendations, we ran 4 chains from random starting values. After discarding 4,000 warm-up samples (similar but not identical to “burn-in” in other software), posterior estimates were derived from a further 4,000 samples across all chains (no thinning) and were assessed for chain stability and convergence using visualization of trace plots and standard Rhat metrics within the software.¹⁴

Missing Data Analysis

Combining data across heterogeneous studies inevitably results in missing data. Restricting analysis to observations with fully available predictors (a complete-case approach) can cause bias in addition to reducing study power.¹⁶ We used a multiple imputation approach. Assuming that missingness was random conditioned on observed predictors, each variable with missing data was modeled with its own likelihood function and predictors. The benefit of this step is that the resulting regression coefficient estimates are relatively unbiased and that the appropriate uncertainty is propagated to the posterior. The drawbacks are that it is slow—it requires the simultaneous fitting of 12 different likelihood models at each step of the sampling procedure—and requires applied knowledge of the potential causal structure of the data. Continuous missing data were subsequently multiply imputed as part of the posterior sampling procedure, but Stan has the drawback of being unable to sample from discrete distributions.¹⁷ Categorical missing data were, therefore, analytically marginalized over their likelihoods during model fitting instead. Further data are available from Dryad (additional Methods, available at doi.org/10.5061/dryad.cfxpnvx4c).

Model Evaluation and Internal/External Validation

Our strategy was to produce an optimally accurate and well-calibrated model with fully adjusted and unbiased parameter estimates. A variable selection step is often used to reduce the size of clinical prediction models, however, in settings where there are a large number of candidate predictors, this procedure is liable to overfit the data (i.e., some variables are selected or removed by chance).¹⁸ Given these concerns and the desire to reduce the overall number of cross-validated model comparisons, we did not pursue predictor selection beyond the remaining 22 variables.

The overall internal performance of the full, baseline, and baseline GTCS models were assessed with their respective log loss rates,¹⁹ a proper scoring rule based on the residual error that takes into account the entire predictive distribution. Average internal discriminative performance was also assessed with an area under the receiver operating characteristic curve (AUROC); calibration of the baseline GTCS and full models were assessed with a calibration plot (the baseline model will inherently have poor calibration). Beyond internal validity, the question arises as to how well the model will generalize to external unseen data. Especially in scenarios where the model is developed using data from a single center, one risk is that the model predictions will be over-optimistic when applied to individuals from other centers (overfitting). Model generalizability (external validation) is optimally assessed by estimating the model's accuracy on a completely external dataset from a different geographical population or time period, but this was nontrivial in our case because different centers had different case numbers, matching ratios, clinical predictor definitions, and degrees of missing data. Thus, we performed 2 types of external validation: approximate leave-one-subject-out cross-validation and leave-one-center-out cross-validation, each with their strengths and weaknesses. Leave-one-subject-out cross-validation estimates how well the model would perform on new individuals originating from the heterogenous populations already represented (European and North American). In this scenario, external validation can be performed using hold out cross-validation where the data are repeatedly split into training and testing datasets and model performance estimates are summarized on the held-out data over many runs.¹⁷ This procedure is computationally prohibitive in the Bayesian MCMC setting (additional Methods available from Dryad at doi.org/10.5061/dryad.cfxpnvx4c) and information criteria are traditionally used as an alternative way to compare a predictive model's generalizability. Bayesian leave-one-out cross-validation is, however, now computationally tractable due to an approximate technique based on Pareto smoothed importance sampling.¹⁷ This approximation can be assumed to be reliable as long as the Pareto tail parameters (k) fall below 0.7. The resulting external validation metrics are the leave-one-out expected log posterior density (lower is better) and the leave-one-out information criterion (lower is better). The final comparison of how well the full, the baseline, and the baseline GTCS models generalized to new individuals was performed with the paired difference between their respective leave-one-out expected log posterior densities (the worse model has a negative value relative to the preferred model, which has a reference value of 0). We also assessed cross-validated discriminative power with approximate leave-one-subject-out AUROC.

To determine how well the full predictive model generalized to individuals from new source populations, we performed leave-one-center-out cross-validation. Here, each of the smallest 3 datasets (United States, Scotland, Sweden) was held out while the “full” model was trained on the remaining data. The discriminative power of the model was then tested on data from the held-out center with leave-one-out AUROC. The largest center (England and Wales) included too many cases of SUDEP (∼54% of the total) to hold out of the training procedure and so leave-one-center-out cross-validation was only performed on the remaining 3 smaller datasets. We present our results in accordance to the TRIPOD criteria.²⁰

Clinical Utility

The model prediction can be interpreted as an estimate of the latent stochastic SUDEP risk for a given individual characterized by a given constellation of clinical features. In order to demonstrate the utility of this risk prediction in clinical practice, we applied the model to 10 individuals with epilepsy known to one of the authors (B.D.) from her recent clinics and selected by her to demonstrate different clinical scenarios where a risk prediction may have been useful. This required adding a term to the intercept of the logit model (based on the sampling frequencies of cases and controls), which converts expected observed case–control risk to expected population risk²¹ assuming a background incidence of 1.2/1,000 person-years. This assumption is also necessary to translate the unitless model output (a prediction from log ORs) into a prediction with meaningful units (risk of SUDEP per 1,000 person-years). Model evaluations took place initially blinded to the fact that 2 of the individuals had experienced SUDEP.

Data Availability

Requests for data should be directed to the authors of the 4 source studies.^7,22-24 We suggest that this model be restricted to clinical researchers pending external validation in different source populations. We aim to use the model as a basis for a freely available online risk calculation tool for use by clinical researchers only. In the interim, those interested should contact the first author, who will provide analytic support.

Results

Demographics

We included 1,273 cases (287 SUDEP, 986 controls). Baseline demographic data and sampling frequency of all considered 29 predictor variables are available from Dryad (table e1, doi.org/10.5061/dryad.cfxpnvx4c). There were significant missing data (data available from Dryad [table e1], doi.org/10.5061/dryad.cfxpnvx4c), and so only 22 predictors with <50% missing data were taken forward for analysis. The main sources of dataset heterogeneity reflected variation in etiology (an excess of symptomatic cases in Sweden [77.6%) and an excess of cryptogenic cases in Scotland [75.4%], possibly representing overlapping classification criteria across these 2 categories), focal seizure frequency (higher in the United States [4/month] than England and Wales [0.2/month] and Sweden [1.2/month], missing in Scotland), and epilepsy surgery (more frequent in the United States [23.7%] compared with other datasets [1.4% in England and Wales, 0.4% in Sweden], reflecting the variable availability of this treatment across the world).

Predictive Performance

Internal Validation

All MCMC chains converged adequately with Rhat = 1 for all relevant model parameters and there were no reported divergences.¹⁴ Internal validation model performance metrics are provided in table 2 and table e4 (doi.org/10.5061/dryad.cfxpnvx4c) and figure 1. The full model had better predictive performance than either the baseline or baseline GTCS model, having the lowest log loss rate. Overall performance metrics combine evaluation of model calibration and discriminative power, but these aspects were also separately evaluated.

Table 2.

Model Performance

Figure 1. Internal Evaluation of Sudden Unexpected Death In Epilepsy (SUDEP) Model Performance.

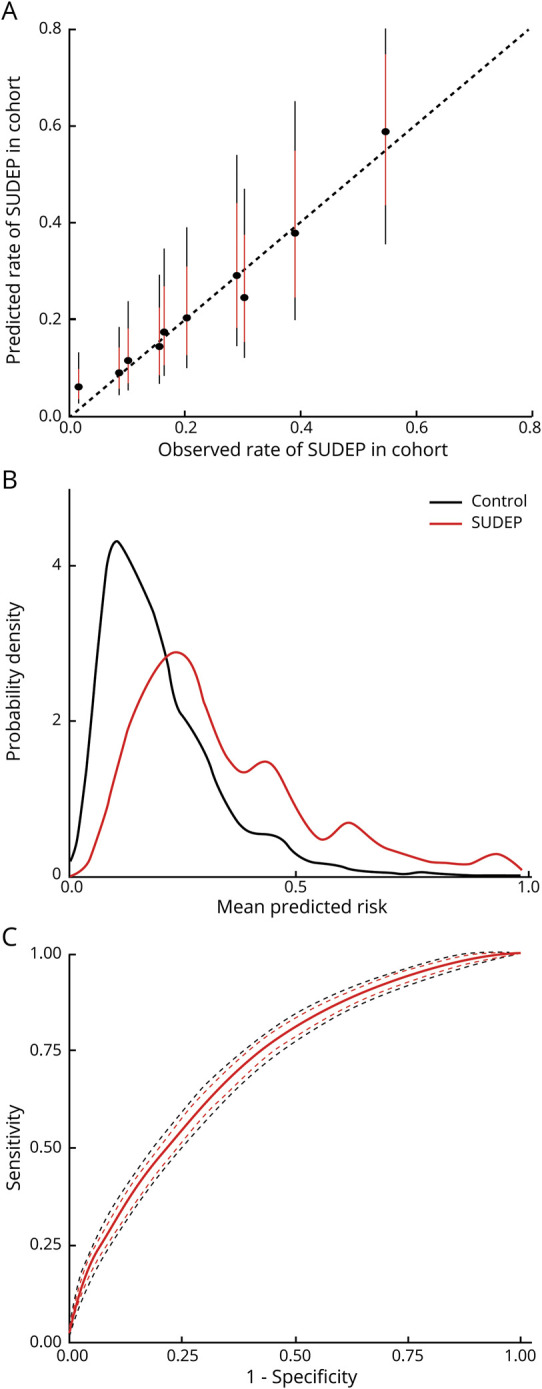
(A) Calibration plot, where the observed cases are sorted into deciles based on the predicted risk from the model. For each subsequent decile, the observed rate of SUDEP in the dataset is plotted against the model prediction (black circle = average, red line 80% credibility interval, black line 95% credibility interval). The model shows excellent calibration—perfect calibration would be aligned along the dotted line where both values are equal. (B) Predicted risk probability distribution functions for SUDEP cases (red) and controls (black). Perfect discrimination would be illustrated by complete separation of the 2 distributions along the x axis; chance discrimination would be illustrated by complete alignment. Discrimination is reasonable but there is still a degree of overlap, suggesting a remaining degree of uncertainty at risk estimates around 0.2–0.4. This is consistent with the receiver operating characteristic curve (C), which shows the specificity and sensitivity of predicting SUDEP in this dataset based on model output (red line = mean, red dash = 80% credibility interval, black dash = 95% credibility interval). The internal area under the receiver operating characteristic curve is 0.72 (95% credibility interval 0.71–0.74), which is reasonable.

Model calibration evaluates the degree to which model predictions fit the observed data across different stratifications. Cases were spilt into deciles ranked by their posterior model risk estimates. The observed SUDEP rate for each decile is plotted against the model prediction in figure 1A and confirms excellent calibration for the full model, compared to poor calibration for the baseline GTCS model (data available from Dryad; figure e1, doi.org/10.5061/dryad.cfxpnvx4c). Calibration for the baseline model is inherently poor as every decile receives the same prediction regardless of the observed rate of SUDEP. Discrimination is the ability of the model to separate observed SUDEP from control cases based on their predicted risk. The risk distributions for both case types are shown in figure 1B; the sensitivity and specificity of the model is shown across all thresholds as a receiver operating characteristic curve in figure 1C. The mean internal (95% credibility interval) AUROC for the full model (0.72 [0.71–0.74]) was better than the baseline GTCS (0.69 [0.68–0.71]) and baseline model (0.57 [0.57–0.57]) (table 2 and table e4, doi.org/10.5061/dryad.cfxpnvx4c).

External Validation

The approximate leave-one-subject-out cross-validation technique was reliable, with only 1 out of 1,273 observations being associated with a Pareto K > 0.7 (0.1%). The full model generalized to new individuals better than either the baseline GTCS or baseline models (paired difference in leave-one-out expected log posterior density full vs baseline GTCS = −22.9, SEM ± 11.0; full vs baseline = 35.9, SEM ± 12.5). Further model comparison measures supported this conclusion (table 2 and table e5, doi.org/10.5061/dryad.cfxpnvx4c). Reweighting model predictions by their Pareto smoothed importance sampling weights also allowed us to approximate the leave-one-subject-out AUROC, as a measure of how well the discriminative power of the model generalizes. The full model generalizes better than the baseline GTCS model or the baseline model to new subjects in terms of AUROC (table 2 and table e5, doi.org/10.5061/dryad.cfxpnvx4c).

We performed leave-one-center-out cross-validation of the full model for the smaller 3 datasets (table e6, doi.org/10.5061/dryad.cfxpnvx4c). When trained on a significantly reduced amount of data and generalized to a sample from an unseen source population, model performance in terms of the AUROC (95% bootstrap confidence interval) was more uncertain but remained on average reasonable for Scotland (0.66 [0.57–0.74]) and Sweden (0.61 [0.52–0.69]). Cross-validated model AUROC (95% bootstrap confidence interval) for the United States was highly uncertain and poor on average (0.55 [0.41–0.69]), but the interpretation of this is difficult as it was also the smallest center (including only 20 cases of SUDEP) with the highest degree of data imbalance (see Discussion).

Inference

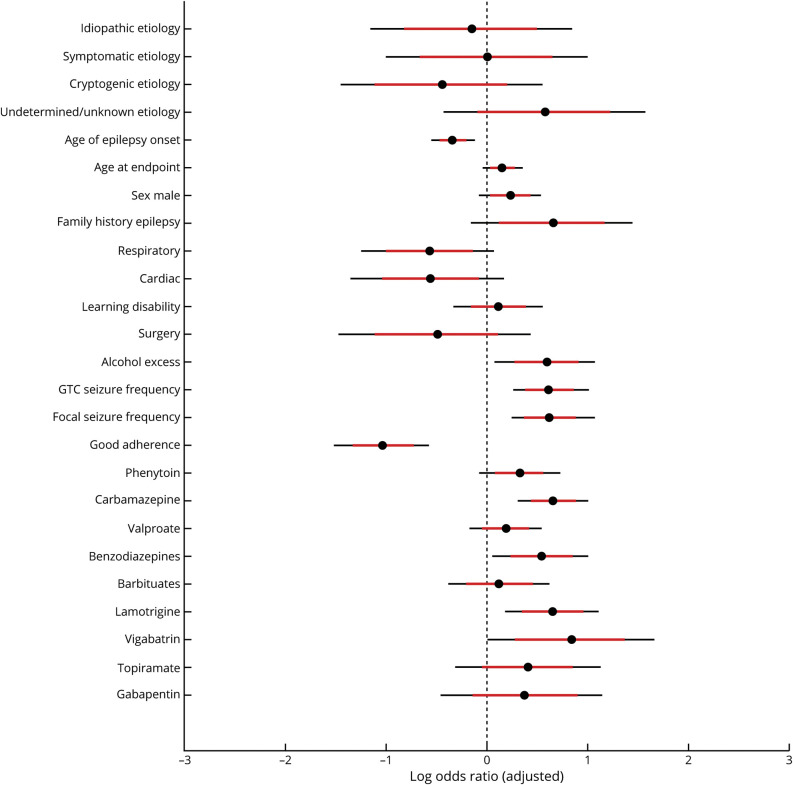
The adjusted posterior log ORs of the fitted logistic regression model are presented in figure 2. Example relations have been transposed onto their natural scales in figure 3, to simplify clinical interpretation. Bayesian models have no arbitrary significance threshold, so we assessed the strength of associations based on the mean effect size (OR) and surrounding uncertainty. Several variables were strongly independently associated with SUDEP; however, the observational nature of observational studies limit causal interpretations (see Discussion).

Figure 2. Adjusted Log Odds Ratios From Bayesian Logistic Regression Model.

Values less than 0 are associated with a reduced risk of sudden unexpected death in epilepsy (SUDEP) and values greater than 0 are associated with an increased risk of SUDEP, relative to the average population sample (black circle = average, red line 80% credibility interval, black line 95% credibility interval). See main text for interpretation, noting that the associations shown are not causal. GTC = generalized tonic-clonic.

Figure 3. Marginal Adjusted Risk.

(A) The marginal (average) predicted noncausal effect of generalized tonic-clonic seizures (GTCS) frequency (top left), focal seizure frequency (top right), age at epilepsy onset (bottom left), and current age (bottom right) on the odds of sudden unexpected death in epilepsy (SUDEP) on their natural scales is shown. These values are relative to a seizure frequency of 0 and to the sample average age at epilepsy onset and current age (red line = mean, red patch 80% credibility interval, gray patch 95% credibility interval). Note that the y axis is a log scale. (B) The combined noncausal association of age at epilepsy onset and current age on SUDEP risk is shown as a grid of values represented by a color scale. Warmer colors represent increased risk and imply that those with a younger age at epilepsy onset have the highest risk and that this risk increases as current age increases.

Individualized Prediction

Over and above the power of the model to discriminate SUDEP cases from controls within an observation period, we can also view the model output as an estimate of latent stochastic SUDEP risk. Variation in this risk across individuals may be clinically useful, even if does not cross a discriminatory threshold. We illustrated the model's potential clinical and research utility by personally forecasting absolute SUDEP risk for 10 individuals with epilepsy (figure 4). The resulting figures show a quantification of risk with uncertainty that may be of benefit in clinical studies aiming to stratify individuals based on risk and potentially in clinical discussions between individuals with epilepsy and their medical team.

Figure 4. Individualized Model Predictions of Sudden Unexpected Death In Epilepsy (SUDEP).

To demonstrate the potential research and clinical utility of this tool, the individualized risk predictions of 10 individuals with epilepsy are shown. These individuals are not known to the model, were drawn from recent practice, and were selected as their SUDEP risk was of clinical interest. The risk is presented on the y axis as a summary measure of a probability distribution (black circle = mean, red line 80% credibility interval, black line 95% credibility interval) for individuals A–J specified on the x axis and ordered by mean predicted risk. Note the y axis is a log scale with risk quantified as a ratio for ease of interpretation. The dotted horizontal line represents the average population risk of 1–2/1,000 patient-years. The predictions are probabilistic, intuitive, and help focus discussions in a time-limited setting such as a clinical consultation. Important prognostic factors vary between the individuals and so multiple factors need to be considered together. For example, in those 5 with the highest risk, focal seizure frequency is particularly important in F, H, and J, generalized tonic-clonic seizures (GTCS) frequency in G, and poor adherence in I. Two of the individuals with highest risk (marked with a red circle next to their names) have died of SUDEP. ASM = antiseizure medications. *The influence of levetiracetam was not modeled.

Discussion

Our model predicted individual risk more accurately than either a model based on GTCS frequency alone or one based on the population-level average even when generalized to unseen subjects. Its ability to discriminate SUDEP from controls was reasonable (leave-one-subject-out AUROC 0.71 [0.68–0.74]). When a version of the model with access to limited training data was generalized to a sample from an unseen source population, the model's discriminative capability was reasonable for Scotland and Sweden, and less certain for the United States, possibly because of its small size, inclusion of children, or distinct data definition and collection procedures (table e6, doi.org/10.5061/dryad.cfxpnvx4c). Use of the model in nonrepresented populations should therefore be done with caution. The AUROC and prediction risk distributions (figure 1, B and C) show that predictions are uncertain. This suggests that risk is a stochastic latent process and categorizing it in binary terms—high-risk vs low-risk—may be misleading; risk should be conveyed as a probability distribution. Our model can stratify individuals based on their risk (figure 4), which may be useful for research studies and has the potential to enhance clinical decision-making and communication. Our model also identified a novel association of focal-onset seizure frequency with SUDEP risk and confirmed previously reported associations with increased GTCS frequency, younger age at epilepsy onset, and male sex. We also found evidence that lamotrigine, benzodiazepines, and carbamazepine are associated with increased SUDEP risk, although the potential causal role of these medications remains undetermined by our current analysis. Combining heterogeneous datasets with different case ascertainment procedures, origin, and risk periods inevitably requires careful harmonization of clinical variables where it is possible and accounting for missing data where it is not (additional Methods available from Dryad at doi.org/10.5061/dryad.cfxpnvx4c). Some clinical predictors were more consistently defined across individual datasets than others.⁸ Antiseizure medications and seizure types were the most consistently defined. Family history was obtained from primary care records in England and Wales as opposed to secondary care records in Scotland. Alcohol use, respiratory and cardiac comorbidities, and learning difficulties had strongly overlapping but distinct definitions in each individual dataset. Adherence was defined according to serum levels of antiseizure medications in the US sample and primary care evaluation of clinical records in the England and Wales sample. These discrepancies may increase the uncertainty of their respective ORs and subsequently impair generalizability between datasets. In spite of this, adherence, family history, and comorbidities all remain individually influential in our model. The combined effect of these inconsistencies between datasets was also tested by the leave-one-center-out analysis. The most uncertain performance was seen when predicting the out-of-sample US outcomes, a finding that may be partly explained by the different definitions used in the US dataset as compared to the others.

Missing data were multiply imputed to reduce bias and appropriately reduce the confidence of subsequent predictions as compared to single imputation or a complete case approach.¹⁶ Potential bias due to heterogeneity in case–control matching ratios and population sampling distributions of each center²¹ was accounted for by explicitly including an intercept for each center. Lastly, any Bayesian approach may be criticized because of the need for prior distributions for the model parameters. We used weakly informative priors consistent with expert knowledge,²⁵ and altering the prior did not alter the model performance substantially.

We developed and evaluated the model to optimize its predictive capabilities but the potential inferential findings require further discussion, particularly as they may be interpreted as challenging previous reports.^8,9 We highlight 2 broad principles. First, due to the impracticability of interventional trials, risk factors are generally derived from observational data and are therefore prognostic rather than causal factors derived from clinical trial data.^1,3,8,26,27 Second, ORs are difficult to compare meaningfully when adjusted by different variable sets—we adjust for an extended set of variables as compared to previous studies. Given such caveats, we confirmed that those with a younger age at epilepsy onset had a higher risk, and that risk increases slowly with age. Men had a slightly higher risk of SUDEP, as previously suggested,⁸ but learning disability did not independently increase risk. This finding is important, as unlike earlier studies,⁷ we adjusted for the effect of multiple factors including etiology, medication adherence, and seizure frequency. Thus, those with learning disabilities have similar risk to other individuals with all other factors being equal and may equally benefit from risk factor modification. A history of epilepsy in first^-degree relatives increased SUDEP risk and was present in ∼4% of our dataset. This may be partially explained by mutations that cause epileptic encephalopathies and treatment-resistant epilepsies such as SCN1A and SCN8A but other more highly prevalent (e.g., DEPDC5) and possibly nonmendelian mechanisms may also contribute.¹

We found that an increased frequency of convulsions (including GTCS and focal to bilateral tonic-clonic seizures) and nongeneralizing focal-onset seizures conferred a higher risk of SUDEP. This is a departure from previous reports that estimate a higher average relative risk from GTCS frequency^8,9 and have found no significant association between focal-onset seizures and SUDEP.^7,9 These differences could be explained by variation in the data themselves or the strategies used for analysis. No significant relation was found between focal-onset seizures and SUDEP from analyses not only in the most recent and homogeneously ascertained data⁹ but also in one of our source studies.⁷ In fact, stratified relative risk from convulsions was higher in a previous analysis of the same combined source data as ours,⁸ suggesting that differences in data can only partially explain the conflicting results. An alternative reason is that, uniquely, our analysis aimed to provide individualized predictions, whereas others aimed to infer average effects over a population.^8,9 Subsequently, we include as many data features as possible in the same single model (22 clinical factors), rather than seeking to interpret the output of multiple smaller models.^8,9 We also removed arbitrary seizure frequency cutoffs (e.g., <3 per year) to improve individualization and interstudy comparability but assumed a monotonic relation between seizure frequency and outcome. We sought to identify prognostic rather than causal risk factors and within these constraints convulsion frequency was not the only predictor of SUDEP risk,¹⁰ and indeed performs poorly if used as the sole predictive factor (table 2). The novel finding that nongeneralizing focal-onset seizure frequency is prognostic conflicts with other major analyses⁹ and requires further investigation as it has potentially wide-ranging implications for clinical practice. Whether nongeneralized focal seizures can directly cause SUDEP or may be proxies for breakthrough tonic-clonic seizure risk in individuals who were previously free of convulsions also remains uncertain. Lastly, some predictors were variably clinically defined and so our interpretations must be made with caution. Even so, medication adherence was associated with reduced risk, while alcohol/drug abuse was associated with increased risk. This highlights 2 modifiable behaviors that, if causal, could reduce risk if addressed.

The independent associations between various treatments and SUDEP risk also require further explanation. Whereas our results support prior studies that have found a protective role for epilepsy surgery,²⁸ almost all antiseizure medications are independently associated with slightly increased SUDEP risk. This needs to be interpreted cautiously since adjusted ORs represent the effect of adding antiseizure medications without any benefit on seizure control—a situation that may either represent increased risk due to the medication or increased risk due to selection of those with treatment resistance. Excluding vigabatrin, which is rarely used and probably falls into the second category, lamotrigine, benzodiazepines, and carbamazepine were associated with increased SUDEP risk compared to other medications, but interventional trials would be needed to determine whether this association is causal or not. Similarly, although cardiac and respiratory comorbidity is associated with reduced risk, this observation may be confounded by a competing risk (these individuals are more likely to die from a non-epilepsy-related cause) or by increased prevalence of coexistent pathologic findings associated with SUDEP misclassification (e.g., 40% left anterior descending coronary artery occlusion).⁵

Regardless of the inferential findings and uncertainties, our model's predictive power remains valid. Its potential ability to either reassure or to motivate individuals by forecasting their current risk (figure 4) will focus discussions on prevention, rather than dwelling on an abstract population estimate of death. Improving antiseizure medication adherence and sleep hygiene, eliminating excess alcohol, employing strategies to reduce seizures in specific settings (e.g., malabsorption of medications due to vomiting or diarrhea), and avoiding seizure-provoking factors in those susceptible (e.g., decongestants, environmental stimuli such as flashing lights) may be emphasized in those at moderate risk. Those with highest risk may consider the use of monitoring (e.g., intermittent observation, seizure detection devices to alarm caretakers), especially with nocturnal convulsions. Lifestyle modifications and monitoring strategies are commonly recommended but remain unproven in reducing SUDEP risk partly due to the logistical challenges of large interventional studies. Our tool could help identify high-risk groups, thereby reducing the number of enrolled individuals needed to establish a treatment effect.

We developed and validated an individualized SUDEP prediction model, which relies on information available during a clinical consultation. This will be developed into an online risk prediction calculator for clinical research use. This prediction remains uncertain, but has potential utility in clinical and research settings. Future prospectively acquired large longitudinal studies are required to improve the model, and to establish its accuracy in nonrepresented populations. Beyond this, a granular understanding of the pathophysiologic factors contributing to SUDEP may contribute towards a mechanistic model that may have even higher accuracy.

Glossary

AUROC

area under the receiver operating characteristic curve

GTCS

generalized tonic-clonic seizures

MCMC

Markov Chain Monte Carlo

OR

odds ratio

SUDEP

sudden unexpected death in epilepsy

Appendix. Authors

Study Funding

The authors report no targeted funding.

Disclosure

This work was carried out at UCLH/UCL Comprehensive Biomedical Research Centre, which receives a proportion of funding from the UK Department of Health's NIHR research centers funding scheme. A. Jha has received support from the Guarantors of Brain, UCLH/UCL Comprehensive Biomedical Research Centre, and honoraria from Sanofi/Genzyme and Novartis. C. Oh and D. Hesdorffer report no disclosures. B. Diehl has received support from the National Institute of Neurologic Disorders and Stroke U01-NS090407 (autonomic and imaging biomarkers of SUDEP). S. Devore reports no disclosures. J.W. Sander receives support from the Dr. Marvin Weil Epilepsy Research Fund, UK Epilepsy Society, and Christelijke Vereniging voor de Verpleging van Lijders aan Epilepsie, The Netherlands. He has received personal fees from Eisai, UCB, Arvelle and Zogenix, grants from Eisai, UCB and GW Pharma, outside the submitted work. O. Devinsky has received funding from Finding A Cure for Epilepsy and Seizures and has equity in Empatica. T. Tomson is an employee of Karolinska Institutet, is associate editor of Epileptic Disorders, has received speaker's honoraria to his institution from Eisai, Sanofi, Sun Pharma, UCB, and Sandoz, and received research support from Stockholm County Council, EU, CURE, GSK, UCB, Eisai, and Bial. T.S. Walczak and M. Brodie report no disclosures. Go to Neurology.org/N for full disclosures.