Leveraging both individual-level genetic data and GWAS summary statistics increases polygenic prediction

Summary

The accuracy of polygenic risk scores (PRSs) to predict complex diseases increases with the training sample size. PRSs are generally derived based on summary statistics from large meta-analyses of multiple genome-wide association studies (GWASs). However, it is now common for researchers to have access to large individual-level data as well, such as the UK Biobank data. To the best of our knowledge, it has not yet been explored how best to combine both types of data (summary statistics and individual-level data) to optimize polygenic prediction. The most widely used approach to combine data is the meta-analysis of GWAS summary statistics (meta-GWAS), but we show that it does not always provide the most accurate PRS. Through simulations and using 12 real case-control and quantitative traits from both iPSYCH and UK Biobank along with external GWAS summary statistics, we compare meta-GWAS with two alternative data-combining approaches, stacked clumping and thresholding (SCT) and meta-PRS. We find that, when large individual-level data are available, the linear combination of PRSs (meta-PRS) is both a simple alternative to meta-GWAS and often more accurate.

Introduction

Polygenic risk scores (PRSs) are a powerful approach to summarize the individual genetic liability to develop a specific disease. They are particularly useful for complex traits and diseases, such as psychiatric disorders,¹ as these are often highly polygenic.² This is because PRSs aggregate the small risk contributions from thousands of variants into a single score, summarizing their overall risk contribution.³ Broadly, the existing polygenic prediction methods differ in the type of data they use for training, i.e., individual-level genotypes/dosages or GWAS summary statistics. Today, GWAS summary statistics are widely available for a broad range of diseases and traits in public databases, e.g., the GWAS catalog contains more than 1,400 summary statistics.⁴ For psychiatric disorders, the Psychiatric Genomics Consortium (PGC) provides GWAS summary statistics based on ever larger sample sizes, as a result of meta-analyzing the individual efforts of many research groups worldwide. Furthermore, many GWAS summary statistics-based PRS methods are broadly used: clumping and thresholding (C+T),5, 6, 7 LDpred,⁸ or more recent methods,9, 10, 11, 12, 13 and have proven successful to identify individuals with significant increased risk of complex diseases such as coronary artery disease.¹⁴

Interestingly, many of these external GWAS summary statistics-based PRS methods approximate the results of the internal individual-level data approaches, making some assumptions in the process (e.g., LDpred-inf⁸ and sBLUP¹⁵ approximate the genomic BLUP,¹⁶ assuming that linkage disequilibrium [LD] patterns in the external data from which the GWAS summary statistics were derived can be captured using an LD reference). Furthermore, phenotype definition, genetic architecture, and/or technical artifacts may affect the prediction accuracy of the derived PRSs.^17,18 Using methods that fit prediction effect sizes jointly on internal individual-level data for training PRSs makes some of these assumptions unnecessary, which can lead to improved prediction accuracy^8,19 (e.g., Privé et al. found that prediction of height using penalized linear regression provides more accurate PRSs compared to C+T [LD clumping an p value thresholding] when trained on individual-level data²⁰). Indeed, a number of powerful alternatives exist for deriving PRSs using individual-level data.20, 21, 22, 23, 24, 25 Until recently, most individual-level datasets have been small, especially in comparison to sample sizes achieved in GWAS meta-analyses, but cheaper genotyping has led to the generation of large genetic datasets (e.g., iPSYCH for psychiatric disorders^26,27 and UK Biobank for a multitude of complex traits²⁸). Therefore, researchers often have access to large individual-level genetic data as well as large published GWAS summary statistics. However, most PRS methods train on either of these data types separately but not directly on both (although many methods do require individual-level data for hyper-parameter optimization). SCT is the only exception that we are aware of, as it does train directly on both types of data.⁷ By combining and leveraging data, we aim to increase the training sample size of PRSs and, ultimately, their prediction accuracy.

In the current paper, we explore and compare different approaches of combining internal individual-level data and external GWAS summary statistics for polygenic prediction. Currently, the most widespread approach is combining the data at the level of GWAS summary statistics by meta-analyzing the marginal effect estimates of different studies, prior to training the PRS (meta-GWAS). We believe this approach is reasonable when the individual-level dataset is small, but may discard its potential for training when larger sample sizes are available. Alternatively, SCT⁷ generates a range of C+T PRSs from the external GWAS summary statistics over a grid of hyper-parameters (e.g., LD clumping parameters and p value thresholds) and then stacks these PRSs by fitting a penalized regression model using individual-level data. This results in a more accurate PRS compared to C+T provided sufficient training data sample size. Based on weighted average PRSs,^29,30 we propose a model with two independently generated PRS (meta-PRS): an internal PRS, derived from the individual-level data; and an external PRS, derived from the GWAS summary statistics; and train the weights using linear regression on a validation dataset. We derive the PRSs with methods that work well for highly polygenic traits—namely we use BOLT-LMM³¹ for deriving the internal PRS and LDpred⁸ for the external PRS. We compare the prediction accuracy of the three approaches presented above (meta-GWAS, SCT, and meta-PRS) through simulations and application to real data of psychiatric disorders and other complex diseases and traits, using individual-level data from two large cohorts (iPSYCH and UK Biobank) as well as large GWAS summary statistics that excluded these cohorts. We show that meta-PRS often outperforms the other compared data-combining approaches in terms of prediction accuracy, while being a simpler approach. We also show that, with larger individual-level datasets, the performance of meta-PRS is expected to increase. Finally, we provide recommendations for selecting a PRS approach when GWAS summary statistics and large individual-level data are available for training.

Material and methods

Approaches for combining internal and external data

We investigated the difference in prediction performance of PRSs that are trained using both external GWAS summary statistics and internal individual-level genetic data, but combined through three different approaches (Table 1). In the first approach (meta-GWAS), the internal individual-level data were used to derive GWAS summary statistics that were subsequently meta-analyzed with the external GWAS summary statistics and finally used for deriving PRSs. For the second approach (SCT), we used the external summary statistics to derive a large number of C+T scores and the individual-level data to fit a penalized regression to linearly combine these C+T scores. In the third approach (meta-PRS), the individual-level data and GWAS summary statistics were used for deriving two independent PRSs. We obtained a weighted average of the two PRSs by fitting a linear regression model.

Table 1.

Overview of the compared data-combining approaches and data utilization

Combining approach	Individual-level data	GWAS summary statistics	Combining strategy	Validation	Test
Meta-GWAS	GWAS	–	$PRS={\sum }_{i=1}^M,Z_i\cdot x_i,$ $Z_i=\frac{\sqrt{n_{int}}\cdot z_{int}+\sqrt{n_{ext}}\cdot z_{ext}}{\sqrt{n_{int}+n_{ext}}}$	select PRS parameters	assess PRS prediction accuracy
SCT	penalized regression of C+T scores	grid C+T scores	$PRS=\sum _{j=1}^k{w}_j\cdot PR{S}_j$	not used
Meta-PRS	derive $PR{S}_{int}$	derive $PR{S}_{ext}$	$PRS=w_{int}\cdot PR{S}_{int}+w_{ext}\cdot PR{S}_{ext}$	select PRS parametersa

Abbreviations: M, number of SNPs; Z, SNP effect size; x, SNP effect allele count; n, effective sample size $n_{eff}=4/\left(1/n_{ca}+1/n_{co}\right)$; int, internal data; ext, external data; k, number of PRSs in grid; w, weights (either regression coefficients or square root of training sample size).

^aWhen the weights for meta-PRS were obtained with linear regression, the validation dataset was also used to train the regression parameters. When the weights were obtained from the training sample size, the validation set was not used.

In the three approaches, the individual-level data were split into training, validation, and test subsets following a 5-fold cross-validation scheme (4-0.5-0.5; 80% training, 10% validation, 10% testing). The selection criterion for all method parameters was the parameter maximizing prediction accuracy in terms of prediction R² in the validation data. Consequently, we obtained five estimates of PRS prediction performance for each method in the test subset and reported the mean. The standard error of the mean prediction accuracy was estimated through 10K bootstrap replicates of this mean.

Computing PRSs

Meta-GWAS

We obtained internal GWAS summary statistics for the individual-level data using linear regression for the simulations and continuous phenotypes and logistic regression for the case-control real phenotypes. For the GWAS, we used the functions big_univLinReg and big_univLogReg from the R package bigstatsr.³² We used sex, age, genotyping batch, and the first 20 principal components (PCs) of each dataset as covariates in the GWAS. We performed an inverse variance-based meta-analysis with the external GWAS summary statistics using the software METAL.³³ We computed PRSs using LDpred v.1.0.10⁸ (note that this version already implements some of the improvements made in LDpred2³⁴), using the infinitesimal model and 7 priors assuming a proportion of causal variants (p = 1, 0.3, 0.1, 0.03, 0.01, 0.003, 0.001). To compute the LD reference panel, we used an LD radius of 500 variants and a random sample of 5k unrelated individuals of European ancestry from each individual-level dataset. We then selected the LDpred PRS with p maximizing the prediction R² in the validation set. We also computed PRSs with LD-clumping and p value thresholding (C+T), selecting the score from a set of C+T PRSs that maximized the prediction R² in the validation set. The C+T PRSs were generated from a grid of parameters: LD pairwise correlation $r^2$ values (0.01, 0.05, 0.1, 0.2, 0.5, 0.8, 0.95), base window sizes (50, 100, 200, 500), and 50 p value thresholds (depending on max and min p value in summary statistics, on a log-log scale).⁷ For LD clumping, the SNP p values were used as a selection variable, i.e., for a pair of correlated SNPs, the SNP with the lowest p value was kept. A total of 1,400 C+T PRSs were derived for each chromosome. We performed logistic regression followed by an inverse variance-based meta-analysis, as this is common practice for GWASs and all the analyzed case-control real traits had GWAS summary statistics from logistic regression. Nevertheless, we observed a slight increase in mean prediction accuracy of the PRSs from linear regression and sample size-based meta-analysis versus logistic regression and inverse variance-based meta-analysis (Figure S1), although with highly overlapping CIs. We also note that some of the variation was expected due to randomness in the cross-validation subsets.

SCT

We computed C+T PRSs using the external GWAS summary statistics and the same grid of parameters as in the section meta-GWAS. The final PRS was computed using the function snp_grid_stacking from the R package bigsnpr,⁷ which performs penalized logistic regression, with the 1400 × 22 C+T scores as predictors and phenotypes as outcomes in the training set.

Meta-PRS

To obtain the meta-PRS, we first computed two independent PRSs: PRS_int and $PR{S}_{ext}$. For $PR{S}_{int}$, we obtained per-SNP prediction betas with BOLT-LMM²⁵ (using the flag –predBetasFile) and computed the PRS as $PR{S}_i=\sum _{=1}^M{\beta }_j\cdot x_{i,j}$, where $M$ are the number of SNPs in the model, ${\beta }_j$. For each sample and trait, we ran BOLT-LMM v.2.3.4 using sex, age, genotyping batch, and the first 20 PCs of the dataset as covariates. Depending on the polygenicity of the trait, BOLT-LMM computes a mixture-of-Gaussians prior on SNP effect sizes or the single-Gaussian BOLT-LMM-inf model, equivalent to best linear unbiased prediction (BLUP). The $PR{S}_{ext}$ was computed with LDpred or C+T, as described in the section meta-GWAS. Finally, we defined the meta-PRS with weights $w_{int}$ and $w_{ext}$ as the linear combination of the two PRSs with these weights, as $MetaPRS=w_0+w_{int}PR{S}_{int}+w_{ext}PR{S}_{ext}$ (lm function in R). To avoid overfitting, we trained the weights in a linear regression model in the validation dataset (lm function in R). For the linear combination, we also used as weights the square root of the respective PRS training data sample size. In these cases, PRSs were standardized prior to being combined. The latter use of weights is highlighted in the text, otherwise the weights in the meta-PRS came from the linear regression model.

Data and quality control

iPSYCH data

We used genotype and phenotype data from the iPSYCH 2012²⁶ and iPSYCH 2015²⁷ case-cohort samples. The iPSYCH2015 is an expansion of the iPSYCH2012 data and includes the samples of the latter. Both datasets were analyzed separately to show the effect of increasing the sample sizes in the method comparison. The iPSYCH2015 case-cohort sample is nested within the entire Danish population born between 1981 and 2008, including 1,657,449 persons. Cases were identified as persons with schizophrenia (SCZ), autism (ASD), attention-deficit/hyperactivity disorder (ADHD), and major depressive disorder (MDD); we identified control subjects as persons from the randomly selected cohort that were not diagnosed with any of the previous disorders. We also included the anorexia nervosa (AN; ANGI-DK) samples from the Anorexia Nervosa Genetics Initiative (ANGI).³⁵ The genetics dataset consists of 134,677 individuals and 8,785,478 SNPs imputed following the RICOLPILI pipeline.³⁶ We computed KING-relatedness robust coefficient³⁷ and excluded at random one of the individuals in the pairs >3rd degree relatedness, resulting in 14,789 individuals excluded. We performed principal component analysis (PCA) following Privé et al.³⁸ and obtained 20 PCs. We also identified 122,197 genetically homogeneous individuals based on these 20 PCs. We define homogeneous individuals as <4.8 log(dist) units from the center of the 20 PCs, calculated using the function dist_ogk from R package bigutilsr.³⁸ This resulted in a subset of 108,623 unrelated individuals of homogeneous ancestry. After removing SNPs with minor allele frequency (MAF) < 0.01 and Hardy-Weinberg p value (${\chi }^2$ (df = 1) test statistic pHWE) < ${10}^{-6}$, we restricted to the HapMap3 variants. The final dataset was composed of 108,623 individuals and 1,184,443 SNPs.

UK Biobank data

We used genotype and phenotype data from the full release of the UK Biobank,²⁸ consisting of 488,377 individuals with genetic information. Specifically, we imported dosage data from BGEN files using the function snp_readBGEN from the R package bigsnpr.³² We identified individuals with either self-reported or ICD-10 diagnosis for breast cancer (BC), coronary artery disease (CAD), type 2 diabetes (T2D), and major depressive disorder (MDD), setting the undiagnosed individuals as control subjects and restricting to women for breast cancer. We also identified individuals with standing height and body mass index (BMI) measurements to use as quantitative traits. We restricted the analysis to unrelated (as described in the section iPSYCH data) and “white British” genetic ancestry individuals. We removed SNPs with MAF < 0.01 and restricted to HapMap3 variants. The final dataset was composed of 337,475 individuals and 1,194,574 SNPs.

Simulations

We simulated case-control phenotypes using 1,194,574 HapMap3 SNPs and the subset of 337,475 unrelated European-ancestry individuals from the UK Biobank. The phenotypes were simulated with two different numbers of causal variants: $M_{causal}=$ 10k and 100k, representing polygenic traits. We also used two different total sample sizes: n = 337,475 (large simulations) and n = 50,000 (small simulations) individuals. Each causal variant was assigned an effect size drawn from $N(0,h^2/M_{causal})$, where the heritability $h^2$ = 0.5. The case-control status was assigned under a genetic liability model, with a simulated prevalence of 0.2. Each simulation scenario was repeated 5 times.

From the sample of individuals, 90% were used as the training set, 5% as the validation set, and 5% as the test set. To represent scenarios with different sample sizes of the individual-level data and GWAS summary statistics, the training set was further split randomly according to the following partitions: 90%–10%, 75%–25%, 50%–50%, 25%–75%, and 10%–90%. One part was used to derive summary statistics and act as the external summary data, while the other part was used as individual-level data. The labels 9:1, 3:1, 1:1, 1:3, 1:9 used in the results reflect the sample size ratio of GWAS summary statistics (left) and individual-level data (right).

Prediction accuracy

The prediction accuracy of the PRSs was assessed in terms of squared correlation (R²) and area under the curve (AUC).³⁹ The PRSs prediction R² were reported as the squared partial correlation⁴⁰ (using sex, age, genotyping batch, and first 20 PCs as covariates) for the quantitative traits and transformed to the liability scale for the case-control data.⁴¹ Additionally, the AUC was reported for the case-control data.

LDSC regression

We obtained estimates of the genetic correlation $r_g$ and intercept from a bivariate LD score regression (LDSC)^42,43 between the internal and external GWAS summary statistics of the traits in Tables 2 and S1. We used the R package GenomicSEM.⁴⁴

Table 2.

Summary of real datasets

Traits	Individual-level sample size	GWAS sample size	Ratio int:ext	rginternal-external (SE)
iPSYCH dataset
Anorexia nervosa (AN)45	7,713	35,274	1:5	0.8147 (0.0945)
Bipolar disorder (BD)46	8,436	48,609	1:6	0.7855 (0.0804)
Schizophrenia (SCZ)47	15,421	48,307	1:3	0.6175 (0.0677)
Autism spectrum disorder (ASD)48	39,068	10,610	4:1	0.6241 (0.0671)
Attention deficit hyperactivity disorder (ADHD)49	43,405	12,214	4:1	1.3137 (0.1216)
Major depressive disorder (MDD)50	49,234	646,483	1:13	0.8115 (0.0477)
UK Biobank dataset
Coronary artery disease (CAD)51	35,457	162,973	1:5	0.8644 (0.0672)
Breast cancer (BC)52	35,707	227,688	1:6	0.9378 (0.085)
Type 2 diabetes (T2D)53	57,086	88,825	1:2	0.9567 (0.0595)
Major depressive disorder (MDD)54	83,900	123,796	1:2	0.8156 (0.0632)
Body mass index (BMI)55	269,106	339,224	1:1	0.9536 (0.0347)
Height56	269,407	253,288	1:1	0.9389 (0.0417)

Effective sample sizes of the six psychiatric disorders in iPSYCH 2015 and ANGI, four diseases and two continuous traits in the UK Biobank, along with the effective sample sizes of the corresponding external GWAS summary statistics. The table reflects sizes of European, unrelated samples (see material and methods).

Results

Performance on simulated data

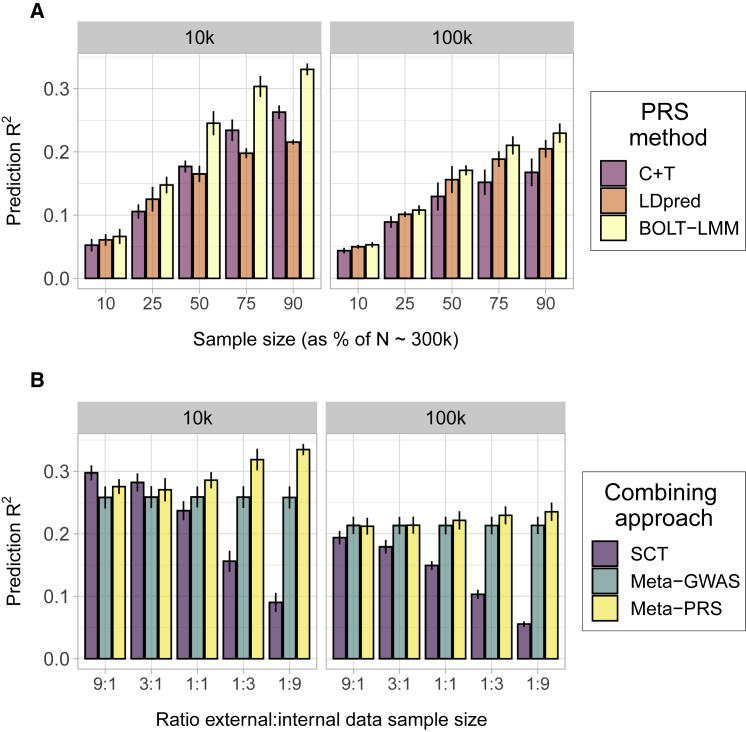
We evaluated the prediction accuracy of the PRSs using simulated data to explore the relationship between the combining approaches and the training sample size. Using the UK Biobank genetic data, we simulated traits with 10,000 (10k) and 100,000 (100k) causal SNPs, aiming at representing the polygenicity range of complex traits, and different sizes of training sample (10%, 25%, 50%, 75%, and 90% of n = 303,728 and 45,000 individuals) of individual-level data (internal) and GWAS summary statistics (external). First, we compared the prediction accuracy of PRSs trained only on internal data (using BOLT-LMM) or external data (using C+T or LDpred) in terms of mean prediction R² (Figure 1A) and AUC (Figure S2A). For all simulated scenarios, the BOLT-LMM outperformed other methods, with a larger relative improvement in the simulations with 10k causal SNPs. The comparison between the GWAS summary statistics-based methods resulted in C+T being generally preferred in the simulations with 10k and LDpred in the ones with 100k causal SNPs. These results highlight the benefits of using the individual-level data for training PRSs over the derived GWAS summary statistics.

Figure 1.

Prediction accuracy of the PRSs in the simulation study

Each panel displays the mean and 95% CI of the PRS prediction ${\mathbf{R}}^2$ (y axis) for each data combining approach. The traits were simulated from a liability threshold model with 10,000 (10k) and 100,000 (100k) causal SNPs and heritability ${\mathbf{h}}^2$ of 0.5, and case-control status was inferred from a disease prevalence of 0.2. Mean and 95% CI of prediction ${\mathbf{R}}^2$ were obtained from 10k non-parametric bootstrap samples of 5 independent replicates.

(A) Effect of training sample size in the PRSs prediction accuracy. The x axis indicates the percentage of individuals from the total training set (n = 303,728) used as individual-level data for BOLT-LMM or GWAS summary statistics for C+T and LDpred.

(B) Effect of the ratio between internal and external data in the combining approaches. The x axis indicates the relative amount of external versus internal data, e.g., 3:1 indicates a scenario where the external data was 75% and the internal data was 25% of the total sample. Figure 1 is a simplified version of Figure S3, selecting a single method per combining approach between C+T and LDpred, where the method maximizing mean prediction ${\mathbf{R}}^2$ was selected.

We also compared the prediction accuracy of PRSs using different data-combining approaches (SCT, meta-GWAS, and meta-PRS) in the simulated traits (Figures 1B, S2B, and S3). The external and internal datasets were matched to create combinations with different ratios of each data type (9:1, 3:1, 1:1, 1:3, 1:9; e.g., 3:1 indicates a scenario where the external data was 75% and the internal data was 25% of the total N ∼300k individuals in the training set). For meta-PRS, we observed a positive relation between the size of the internal data and the mean prediction R². The opposite was observed for SCT, where larger external datasets provided larger mean predictions. The ratio of data showed no effect for meta-GWAS, with constant prediction R² along the simulated ratios (Figure 1B). These results indicated that it was possible to optimize PRS prediction accuracy by selecting a data-combining approach depending on the sample size ratio between the available internal and external data. While the classical meta-GWAS was a valid strategy in ratios of 1:1, scenarios with a more skewed ratio benefit from approaches like meta-PRS (for larger individual-level data) and SCT (for larger GWAS summary statistics), which use the individual-level data for training.

We also performed simulations with smaller effective sample sizes for both individual-level data and GWAS summary statistics (Figure S4). Using a total sample size of 50k individuals, these simulations correspond better to the sample sizes used in the real data analysis. We observed similar mean prediction R² for both meta-PRS and meta-GWAS in these simulations (Figure S4B). The method-specific differences only showed an increase in mean prediction of the BOLT-LMM PRS over the LDpred PRS when the training sample was 90% of the total, i.e., when the effective sample size was 40.5k individuals (Figure S4A).

To better understand the relationship between the sample size and the difference in mean prediction R² between meta-PRS and meta-GWAS, we plotted it as a function of the ratio $nef{f}_{int}\cdot h^2/\sqrt{p}$, where $nef{f}_{int}$ is the effective sample size in the individual-level data, $h^2$ is the heritability, and $p$ is the fraction of causal variants, i.e., 0.1 and 0.01 for the simulations with 100k and 10k causal SNPs, respectively. We note that this ratio is related to the expected prediction accuracy by Daetwyler et al.,⁵⁷ i.e., the larger it is the more accurate predictions we can expect. We found that the observed benefit from applying meta-PRS over meta-GWAS increased as a function of this quantity (Figure S5). Interestingly, we also found that the effective sample size of the external GWAS summary statistics did not influence this relative performance.

Aiming to simplify the construction of the meta-PRS, we attempted to use the square root of the effective sample size ($\sqrt{n_{eff}}$) to weight the internal and external PRSs. This simplified version of meta-PRS is faster and does not need of a validation dataset. In the previously described simulated scenarios, we compared the mean prediction R² of PRSs weighted by $\sqrt{n_{eff}}$ and PRSs weighted by linear regression effect sizes (using a validation dataset). We only observed a small increase in mean prediction R² in the scenarios with large individual-level data (ratios 1:3 and 1:9), with the other remaining the same. We also compared to a meta-PRS between the meta-GWAS and the internally trained PRS with BOLT-LMM, observing no increase in mean prediction R² (Figure S6).

Performance on real data

We investigated the prediction accuracy of the data-combining approaches (meta-PRS, SCT, and meta-GWAS) in real complex traits using internal individual-level data from large genotype cohorts (iPSYCH^26,27,35 and the UK Biobank²⁸) and external GWAS summary statistics. The set of traits selected included the six major psychiatric disorders (ASD, ADHD, MDD, BD, SCZ, and AN), three other complex diseases (BC, T2D, and CAD), and two continuous complex traits (height and BMI) (Table 2). The external GWAS summary statistics were selected to not have sample overlap with the individual-level datasets used. This was confirmed by checking the intercept of a bivariate LDSC regression between the internal and external data (Table S1). Of all traits, only height showed an intercept different from 0 (0.099, SE: 0.0265). Large sample sizes in GWASs (specifically for height) have been reported to cause this effect in the bivariate LDSC regression intercept.⁵⁸ The set of SNPs used for each trait was the intersection between the SNPs in the individual-level data, GWAS summary statistics and the 1,440,616 HapMap3 SNPs.

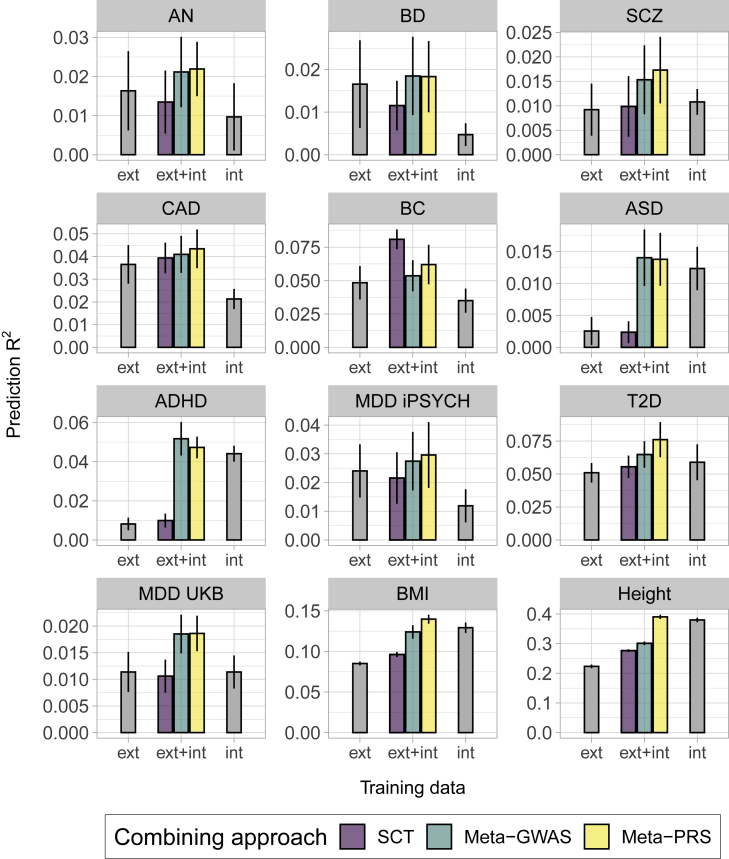
No single combining approach provided the largest mean prediction R² for all traits (Figure 2) or AUC (Figure S7) for all traits. In the cases where the sample size of individual-level data was larger than the summary statistics (int > ext), meta-PRS increased mean prediction R² over SCT and meta-GWAS for height, while both meta-GWAS and meta-PRS had similar results for ASD and ADHD, with large and overlapping CIs. In the cases with equal data training sample sizes (1:1), meta-PRS increased prediction accuracy over meta-GWAS and SCT for BMI and T2D, while the results for meta-GWAS and meta-PRS were similar for MDD UKB. Finally, in the cases where the sample size of the GWAS summary statistics was larger than the individual-level data (ext > int), the results were also diverse. For AN, CAD, SCZ, BD, and MDD iPSYCH, there was no major difference between meta-GWAS and meta-PRS. However, for BC, the data-combining approach with the largest mean prediction R² was SCT.

Figure 2.

Prediction accuracy of the combining approaches in 12 complex traits from iPSYCH 2015 and UK Biobank

Each panel displays the mean and 95% CI of the PRS prediction ${\mathbf{R}}^2$ (y axis) for each data combining approach, of PRS trained on individual-level data (int), GWAS summary statistics (ext), or both (ext+int) (x axis). The prediction ${\mathbf{R}}^2$ was transformed to the liability-scale using a population prevalence of 0.01 (ASD), 0.05 (ADHD), 0.15 (MDD UK Biobank), 0.05 (T2D), 0.01 (AN), 0.03 (CAD), 0.01 (SCZ), 0.07 (BC), 0.01 (BD), and 0.08 (MDD iPSYCH). The methods noted as int and ext were fitted using BOLT-LMM with individual-level data and LDpred or C+T with GWAS summary statistics, respectively. For simplification, only the ext PRS with larger mean prediction ${\mathbf{R}}^2$ is shown, the full results are available in Figure S8. Mean and 95% CI of the prediction ${\mathbf{R}}^2$ were obtained from 10k non-parametric bootstrap samples of the 5 cross-validation subsets.

Generally, the meta-GWAS resulted in a similar mean prediction R² with meta-PRS for the psychiatric disorders, with large and overlapping CIs. This was independent of the sample size ratio of internal versus external data. Results using either iPSYCH 2012 or 2015 were similar, despite the iPSYCH 2015 data having almost twice as many individuals (Figure S9, Table S1). For most outcomes validated in the UK Biobank data, the most accurate approach was meta-PRS, where the largest improvement was for height, BMI, and T2D. For these outcomes, the internal effective sample size was larger than for most of the other outcomes. BC was the only trait where SCT led to the most predictive PRS, even though the ratio internal:external was similar to other traits like CAD.

The difference in mean prediction R² between meta-PRS and meta-GWAS was plotted as a function of the internal effective sample size ($nef{f}_{int}$), SNP-heritability ($h^2$), and proportion of causal variants ($p$) (Figure S10). We observed a similar trend as observed earlier in our simulations (Figure S6). While all of the psychiatric disorders showed small values of $nef{f}_{int}\cdot h^2/\sqrt{p}$, all the other disorders and traits showed an increase in mean prediction R² from using meta-PRS as the data-combining approach over meta-GWAS.

We also compared the meta-PRS constructed with linear regression weights to the one weighed by effective sample sizes ($\sqrt{n_{eff}}$) of training data (Figure S11). As in the simulations, we only observed an increase in mean prediction R² in the traits with large individual-level data (height and BMI). In the rest of the traits, there was no preference for a specific weight type. The use of $\sqrt{n_{eff}}$ as weights is therefore recommended for these traits, as it does not require a validation set. Additionally, we constructed a meta-PRS between the meta-GWAS PRS and the BOLT-LMM PRS. As observed in the simulations, the mean prediction R² of this PRS was similar to the one obtained from the linear regression meta-PRS, which combines the BOLT-LMM PRS to the $PR{S}_{ext}$.

Discussion

With genetic data now available to researchers as both large individual-level datasets and GWAS summary statistics, we want to understand how to best combine these two types of data to optimize polygenic prediction. With this aim, we have evaluated the predictive performance of PRSs generated with different data-combining approaches: meta-GWAS, SCT, and meta-PRS. We find that the simple approach of combining two different PRSs (meta-PRS), trained on individual-level data and GWAS summary statistics separately, may yield more accurate PRSs than a meta-GWAS, particularly in the cases with sufficiently large individual-level datasets. We observe this in simulated data, where meta-PRS consistently increases the mean prediction R² over the widely used meta-GWAS approach, and in the real complex traits with a large individual-level dataset e.g., height, BMI, and T2D. Another advantage of meta-PRS is that it allows to combine multiple pre-calculated PRSs, irrespective of prediction method. When validation data are not available, we show that one can use the square root of the training sample sizes as weights. The same approach could also be used to combine multiple PRSs (e.g., in the PGS Catalog⁵⁹), being standardized and averaged together with their corresponding training sample sizes. As an alternative approach, the scores in a meta-PRS could be weighted using MT-BLUP.⁶⁰ Additionally, we also tried using the meta-GWAS as one of the variables for meta-PRS, which provided similar performance.

In the case of BC, which has several large effects and relatively low polygenicity, the SCT PRS prediction is the most accurate, presumably because it relies more on variant thinning. For psychiatric disorders, we found that the meta-GWAS and meta-PRS generally yielded similar results, despite these disorders being very polygenic and often having relatively large individual-level data sample sizes. We also note that the expected relative improvement of meta-PRS over meta-GWAS is small when polygenicity is large. Our simulations and real data suggest that the relative prediction gain of meta-PRS over meta-GWAS increases as a function of the individual-level data sample size and seems to be independent of the external sample size. This is consistent with the observation that BMI and height display the largest benefit from using meta-PRS over meta-GWAS. As a general rule of thumb, we set the threshold value of $Nef{f}_{int}\cdot h^2/\sqrt{p}$ at 100k. However, we also note that our results suggest that meta-PRS can be applied using smaller sample sizes without loss in prediction accuracy. Meta-PRS may be easier to construct in practice, as it does not require to make a meta-analysis of GWAS summary statistics. In addition, meta-PRS can be updated easily when new external data becomes available, as it only requires one to generate a new PRS on the new external GWAS summary statistics or even take it from a resource like the PGS Catalog.⁵⁹

Our simulations represent an idealized scenario where we assume that the genetic architecture is invariant between cohorts/samples (i.e., genetic correlation is 1). Studies have shown that psychiatric disorders can be quite heterogenous between cohorts.¹⁸ As previously shown by Schork et al.,⁶¹ we have estimated the genetic correlation for psychiatric disorders between external and iPSYCH samples to be between 0.5 and 0.8, while the genetic correlation was larger (>0.8) for the rest of the analyzed complex traits. Similar to disease heterogeneity, differences in genetic ancestry between the training and testing data can also decrease the prediction accuracy of PRSs.¹⁷ In the case of ancestry heterogeneity, the linear combination of PRSs trained independently on different ancestries improves prediction for admixed individuals,⁶² but the extent to which these sample heterogeneities affect each of the prediction accuracies in the compared data-combining approaches should be further studied.

In meta-PRS we combined the BOLT-LMM and LDpred (or C+T) predictions, and therefore the results may not be fully generalizable to other methods, e.g., a more accurate method may lead to more accurate meta-GWAS scores. Nevertheless, given that LDpred generally performs well for polygenic traits in independent comparisons,^63,64 we believe it acts as a good proxy for other similar methods, such as lasso regression,⁹ SBayesR,¹¹ and PRS-CS.¹⁰ In the case of individual-level data and low polygenicity, L1-penalized regression may also provide more accurate PRSs than BOLT-LMM.²⁰

In summary, we found that a simple additive model of two polygenic scores (meta-PRS) often outperformed the accuracy of approaches that first meta-analyzed SNP effects (meta-GWAS) in highly polygenic traits. Fundamentally, the improvement in meta-PRS prediction accuracy stems from the fact that methods that train a polygenic prediction model on individual-level data have access to more training information than methods that only train on a summary of this data and usually make fewer assumptions. However, meta-GWAS has the advantage that each effect estimate is updated separately, possibly making it more robust to small sample sizes and changes in genetic architecture.

Declaration of interests

C.M.B. reports: Shire (grant recipient, Scientific Advisory Board member); Idorsia (consultant); Lundbeckfonden (grant recipient); Pearson (author, royalty recipient). The other authors declare no competing interests.

Published: May 7, 2021

Data and code availability

Access to individual-level Denmark data is governed by Danish authorities. These include the Danish Data Protection Agency, the Danish Health Data Authority, Scientific Ethical Committee, Statistics Denmark, and the European legislation (General Data Protection Regulation). Each scientific project must be approved before initiation, and approval is granted to a specific Danish research institution. International researchers may gain data access through collaboration with a Danish research institution. More information about getting access to the iPSYCH data can be obtained at https://ipsych.au.dk/about-ipsych/. UK Biobank data are available through a procedure described at https://www.ukbiobank.ac.uk/using-the-resource/. All code used is available in the GitHub repository https://github.com/ClaraAlbi/paper_MetaPRS/.

Web resources

• HapMap3, https://www.sanger.ac.uk/resources/downloads/human/hapmap3.html