Atomistic De‐novo Inhibitor Generation‐Guided Drug Repurposing for SARS‐CoV‐2 Spike Protein with Free‐Energy Validation by Well‐Tempered Metadynamics

Abstract

Computational drug design is increasingly becoming important with new and unforeseen diseases like COVID‐19. In this study, we present a new computational de novo drug design and repurposing method and applied it to find plausible drug candidates for the receptor binding domain (RBD) of SARS‐CoV‐2 (COVID‐19). Our study comprises three steps: atom‐by‐atom generation of new molecules around a receptor, structural similarity mapping to existing approved and investigational drugs, and validation of their binding strengths to the viral spike proteins based on rigorous all‐atom, explicit‐water well‐tempered metadynamics free energy calculations. By choosing the receptor binding domain of the viral spike protein, we showed that some of our new molecules and some of the repurposable drugs have stronger binding to RBD than hACE2. To validate our approach, we also calculated the free energy of hACE2 and RBD, and found it to be in an excellent agreement with experiments. These pool of drugs will allow strategic repurposing against COVID‐19 for a particular prevailing conditions.

Schematic diagram of atom‐by‐atom molecule generation, followed by repurposed molecule selection and validation using fre‐energy calculations.

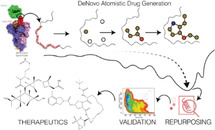
Introduction

SARS‐CoV‐2, the cause of the COVID‐19 pandemic, is a positive strand RNA beta‐coronavirus with large sequence similarities to the SARS‐CoV and BatCoV RATG13 RNA viruses. ^[1] Despite being known from at least early 2019 to as far back as 2006 as found in a report by Tang et al., ^[1] the virus, seemingly incurable and unstoppable, has grown to an enormous scale all across the world.

Therefore, it is essential to find a cure for the virus. Coronavirus is encapsulated by a membrane full of trimeric spike proteins. This spike protein interacts with the peptidase domain (PD) of the human angiotensin‐converting enzyme 2 (hACE2), ^[2] and hence has been alluded to as a potential target to design preventive and curative therapeutics. ^[3] Alternate common targets for viruses are the Main protease (^MPro) and the Non‐Structured Proteins (NSPs). For SARS‐CoV‐2 (Cov2), the high resolution crystal structure of CL3 protease, also known as ^MPro, was resolved recently. ^[4]

However, simulation studies have indicated that the enzymatic active site of ^MPro is highly flexible making it less prone to be inhibited by common viral protease inhibitors. ^[6] Zhou et al. ^[7] mapped protein‐protein interaction in a network for proteins involved in Cov2 and came up with many other targets to be used for drug repurposing.

The detailed structural elucidation of Cov2 and hACE2 (hACE2) interface by Shang et al. ^[8] shows that the spike protein's RBD region remains to be the most important target for drug design for Cov2. The study identifies residues responsible for the interaction and tagged it as receptor binding motif (RBM). RBM is a part of a binding domain called RBD, which again is a part of the S1 region of the spike protein, whose entire structure was solved recently by Wrapp et al. ^[5] This protein is composed of three subunits. Each of these subunits contains a receptor binding domain (RBD). In two of the subunits, the RBD is in the so‐called ‘down’ configuration and in one it is in the ‘up’ configuration. However, the exact structure of the RBD complexed to hACE2 and the interactions involved in the site were redetermined very recently by Yan et al. by X‐ray diffraction. ^[9]

Although the spike protein is trimeric ^[5] and exists in both open and closed forms, ^[10] it is the RBD of the monomer that is responsible for cellular recognition. Its movement is also independent of the rest of the protein. ^[11] Figure 1a shows the structure of the spike protein, where RBD is in the ‘up’ configuration, in contact with hACE2. Figure 1b shows the RBD separately to highlight the interaction hotspot, i. e., RBM ^[8] that serves as the hotspot for a potential inhibitor of interaction between the spike protein and hACE2 peptidase domain.

Figure 1.

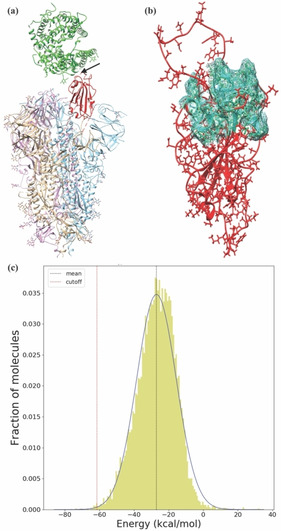
Molecule generation in the RBM. (a) The trimeric structure of the S1 region of the spike protein obtained from the protein data bank with ID 6VSB; ^[5] RBD is shown in red and the hACE2 shown in green. The arrow indicates the target for a new inhibitor design. (b) The magnified version of the modelled RBD (in red) with the RBM (hotspot) shown as a mesh surface in cyan. (c) Distribution of interaction energies with RBD for 13516 DeNovo generated molecules. The mean and standard deviations of the fitted Gaussian distribution is −27.0 kcal/mol and 11.5 kcal/mol, respectively. The cut‐off (redline) is set at three standard deviations lower than the mean, i. e., at −61.5 kcal/mol, the accepted range.

The recent havoc created by the virus resulted in an upsurge of studies towards a remedy. ^[12] Most of the computational studies employed massive‐docking of the existing molecules, sometimes with an implicit solvent‐based MM‐PBSA free energy calculations. ^[13]

Although docking is a quick method to sieve plausible candidates for binding, it often fails to ascertain the correct binding constant due to lack of water, ions, and entropic effects resulting from the fluctuations of proteins, ligands and water molecules. ^[14] Often docking studies provide a wide range of possible lead molecules, making it difficult to choose the best from them. Despite these pitfalls, docking remains a quick method for finding possible repurposable drugs. ^[15] The most reliable and accurate approach to estimate the binding constant, computationally, is to calculate it from an all‐atom, explicit water simulation. ^[16] To the best of our knowledge, no attempt has been made to find out the binding constants of any of the ligands through such rigorous methods for any of the target proteins for COVID‐19. It has been, however, recently attempted for pseudokinase domain of the JAK2 protein. ^[17]

The competitive inhibition by the drug will work if the RBD binds to the drug stronger than it does to hACE2. Therefore, estimating the binding constant accurately is essential. Using surface plasmon resonance experiments, Shang et al. reported a value of 44.2 nM (−10.2 kcal/mol at 300 K) binding affinity for the HIS‐tagged RBD by covalently immobilizing the protein to the sample substrate. ^[8] However, noncovalent association methods, which underestimates the K_d, provide a lower value of 2.9 nM ^[10] and 1.2 nM. ^[10] The K_d measured by Wrapp et al. using biolayer inferometry is 34.6 nM. ^[5] The above values when converted to free energy at 300 K temperature yield a range between −10.3 and −12.3 kcal/mol. We will show later that our computational estimate of the above is very close to the above experimental result.

Therefore, our primary aim for this study is to use a reliable computational method to find a molecule that can bind to the hotspot of RBD with binding free energy lower than −10.3 kcal/mol. For that, we have developed a de novo molecule generation program, called ‘DeNovo’, that creates molecules atom‐by‐atom in the protein's hotspot (a defined structural region of a biomolecule) to optimize the interaction energy between the two. The idea of such a de novo generation stems from the fact that the chemical space is infinite ^[18] and there are molecules in our chemical space that would strongly bind to any given receptor, if only we can find them. Although the program is quite general and can grow molecules for any hotspot, we apply it for the first time here to grow inhibitors for the RBD by targeting the RBM region (Figure 1b). Our approach will be particularly helpful for creating inhibitors where existing drugs have already started facing resistance and a completely new design for a drug is essential. ^[19] The current problem of COVID‐19, however, demands a different solution, where we need to provide molecules worthy of immediate clinical trials.

Hence, from the several de novo molecules we generated, we selected the top 35 and using them we found analogous drugs from the DrugBank ^[20] that could be repurposed for COVID‐19 using a similarity‐based mapping. We have validated our approach by performing the computationally rigorous all‐atom, explicit water well‐tempered metadynamics ^[21] free energy calculations for all these molecules and show that 9 molecules (4 de novo and 5 repurposed drugs) have free energy of binding to the RBD lower than −10.3 (the cut‐off set above), implying their highly promising potential to inhibit the viral attack on human protein. As the benchmark, we calculated the free energy of binding between RBD‐hACE2 which is in good agreement with experiments. Also, performing rigorous well‐tempered metadynamics simulations with multiple coordinates helped us identify the binding mechanism of all these molecules.

Therefore, our study provides a new, viable, and successful approach for finding novel and repurposed drugs for COVID‐19. Our approach is general, and it has the potential to be used for any other receptor‐mediated drug design as well.

Results and Discussion

A. Generation of specific binders for a receptor

Our DeNovo program (see Method) is schematically shown in Figure S1 of the supporting information (SI). Using configurational bias Monte Carlo (CBMC) approach, schematically shown in Figure S2 of SI, we generated 13516 molecules having 10 to 50 heavy atoms to cover a broad spectrum of molecular scaffolds. The distribution of interaction energy between the molecule and the RBD is shown in Figure 1c. We have chosen ∼0.3% of the molecules by selecting those that have interaction energy less than a cut‐off value of −61.5 kcal/mol (Figure 1c), set at three standard deviations lower than the mean energy −27 kcal/mol.

Thus, we gathered 35 molecules (see Figure S3 of SI). The names of the molecules are chosen based on an internal criteria of numbering. At this point, we have a set of good molecules to work with. However, our molecule generation had a few caveats: (1) our hotspot was rigid, (2) there were no water molecules (the screening effect of solvent in the energy calculation of the DeNovo method was accounted for by using dielectric constant of 25.0), (3) and the entropy contributions could not be taken into account.

Therefore, to calculate the exact binding free energy, to the extent that a classical force field can provide, we have subjected the aforementioned molecules to a state‐of‐the art rigorous well‐tempered ^[21] version of metadynamics ^[22] simulation as described later.

B. Route to repurposing

As we will see later, the DeNovo generated molecules are, from a computational point‐of‐view, indeed strong binders and some of which could be candidate drugs. However, synthesis and toxicology study for these molecules may take much longer. Relying on the quality of binding of our de novo molecules ( as shown later via free energy calculations) and building on the concept of similar molecules having similar chemistry, ^[23] we looked for similar molecules in the DrugBank ^[20] using Tanimoto (or Jaccard) ^[24] similarity search which uses bitwise fragment comparison to accurately match structures based on chemical fragments. ^[25] This similarity algorithm generally preserves relative positions of functional groups. We have chosen drugs for each of our 35 molecules with the Tanimoto coefficient ≥ 0.4, following the recommendation of Baldi et al. who showed that a Tanimoto score of 0.4 is significant for a database of over 10,000 molecules. ^[26] This similarity search led to several drug molecules for each of the 35 de novo molecules, listed in Table S1 with their similarity score in brackets. After removing the irrelevant drugs (shown in red) (see the full list and explanation in SI), we ended up with 123 unique drugs. Given the difficulty and time required to perform free energy calculations for all these molecules, we docked all these drugs to the same hotspot (Figure S4 of SI), using docking score purely as a sieving criterion, and selected molecules with a docking score <−8.0 kcal/mol. This narrowed down our list to 20 potentially repurposable drugs. Figure S5 of SI shows the chemical structures of the chosen drug molecules and their docking scores are given in Table S2. As docking score is empirical and varies between different softwares, we carried out the free energy simulations of these drug molecules with well‐tempered ^[21] metadynamics method, as well.

Note that, several other molecules in the DrugBank database could have had docking scores meeting our cut‐offs had we not applied the similarity criteria to narrow down the chemical space of molecules similar to the ones generated by our DeNovo program. Docking, therefore, helps us to narrow down the number of free energy calculations by removing the potentially weak binders.

To capture the relationships between the de novo and drug molecules, we plot the similarity matrix of all the 55 molecules in Figure 2. This matrix is obtained by measuring similarity‐based clustering of each pair of molecules. This matrix provides valuable information on the structural diversity of molecules that have led to favorable properties. We find that there are two separate clusters, one dominated by repurposed drugs and the other dominated by de novo molecules.

Figure 2.

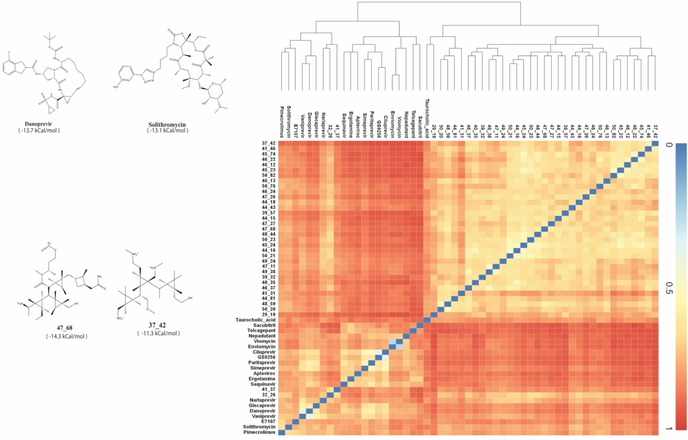
Select drug molecules and similarity heatmap. (left) Two of the best DeNovo generated molecules(bottom) and two repurposed drug molecules(top) with their calculated binding free energies (in brackets underneath each molecule). (right): the heat map of the Tanimoto similarity amongst the chosen list of de novo and repurposed drug molecules. The hierarchical diagram also depicts the similarity between different molecules. Two clusters of de novo molecules and drugs are clearly visible. However, cross similarities are also present.

We note that the molecular similarity reflects on the similarity in binding free energy as well. The best‐binding de novo molecules (as scored based on DeNovo's interaction energy) are in themselves quite similar, as are the best‐binding repurposed drugs among themselves. This is particularly noticeable once the molecules have been mapped to their free energies. Even though it may seem at the first glance that the cross‐similarity is less, there are marked, and sporadically distributed regions of cross‐similarity observed between the de novo molecules and repurposed drugs, which can be attributed to appreciable similarities in their maximal common substructures.

The left panel of Figure 2 shows the structures of some of the best molecules along with their free energy (see discussion below). It is reassuring that we obtained several molecules, both from our de novo generation and repurposing strategy, that are comparable or stronger in binding to RBD than hACE2.

C. Free Energy Surfaces of Protein‐Protein and Protein‐Drug Complexes: An induced fit Mechanism

Free energy calculation with an all‐atom explicit water system is by far the most accurate, albeit expensive, estimate of binding among various computational methods. ^[16] Metadynamics is an extremely popular state‐of‐the‐art method to calculate free energy surface for complex systems ^[27] and it has been shown to reproduce experimental observations closely. ^[28] Recently, attempts to estimate free energy of binding was done for the protease, albeit with an approximate method called MM/PBSA, ^[29] which takes water as a continuum, thus leading to an inaccurate estimation of entropy, and furthermore due to the lack of accurate entropy estimation, it is also not ideally suited for providing mechanistic insights. All‐atom with explicit water free energy calculation not only estimates the free energy more accurately, it also captures the mechanism of the binding. In this study, we have performed the free energy calculations for the huge list of 55 ligand molecules (35 are de novo and 20 are known drug molecules). To the best of our knowledge, this study is the first to perform the free energy calculations for the spike protein's interaction with hACE2 and other ligands.

Before calculating the free energy for all the 55 drugs molecules, we validated our approach by calculating the free energy surface for RBD and hACE2 for comparison. Starting with the available crystal structure of the spike protein and hACE2 (PDB id 6VSB ^[5] ), we first selected only the RBD region, modelled the loop region (see method), solvated the system with water and physiological concentrations of ions and performed multiple, long (∼230 ns) well‐tempered metadynamics simulations against multiple collective variables such as DISTVEC (displacement along a body‐fixed vector) (Figure S6 of SI) and native contact (Figure S7 SI) to study the binding free energy surface of these two proteins. While native contact helps to untangle the interactions between two proteins, DISTVEC is a vectorial displacement coordinate that helps move the proteins apart. These coordinates were used successfully in our previous studies of drug intercalation[ ^28a , ³⁰ ] and protein‐protein interactions. ^[31]

Figure 3 shows the free energy surface of RBD and hACE2, which verifies the crystal structure configuration as the global free energy minimum. A few snapshots of the configuration of both proteins are shown along the unbinding pathway which depicts that the major reason for stability is due to direct protein‐protein interaction. As soon as the proteins detach themselves, the free energy increases. The proteins thus move apart from each other, as reflected in the consequent increase in DISTVEC and a significant decrease in the number of native contacts. From this free energy surface, we estimate the binding free energy to be −13.3 kcal/mol, which is in close agreement with the experimental results. A second metadynamics simulation of the same system yielded free energy estimate of −12.7 kcal/mol making the average −13.0 kcal/mol.

Figure 3.

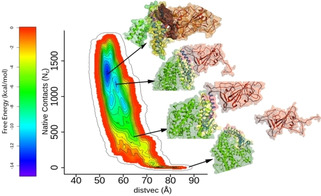
Free Energy of hACE2‐RBD. binding Free energy surface of RBD (brown) binding to hACE2 (green) against two collective variables, native contact (Nc) and DISTVEC (Å). The structures along the path of dissociation are shown along the free energy bar diagram.

Using the same set of collective variables and starting with either the docked configuration for repurposable drug molecules or the DeNovo generated configurations for the novel molecules, we performed metadynamics simulations for all the 55 molecules and calculated their free energy surfaces.

Figure S8 to S11 in SI show the two‐dimensional free energy surfaces (FES) of binding of all the molecules. In Figure 4, we show the FES of three top de novo molecules and 3 top drugs. A representative structure of the most stable configuration obtained from the metadynamics simulation is shown either above or below the FES of the respective molecule. Figure 4 shows that the molecules are nicely packed inside the hotspot region.

Figure 4.

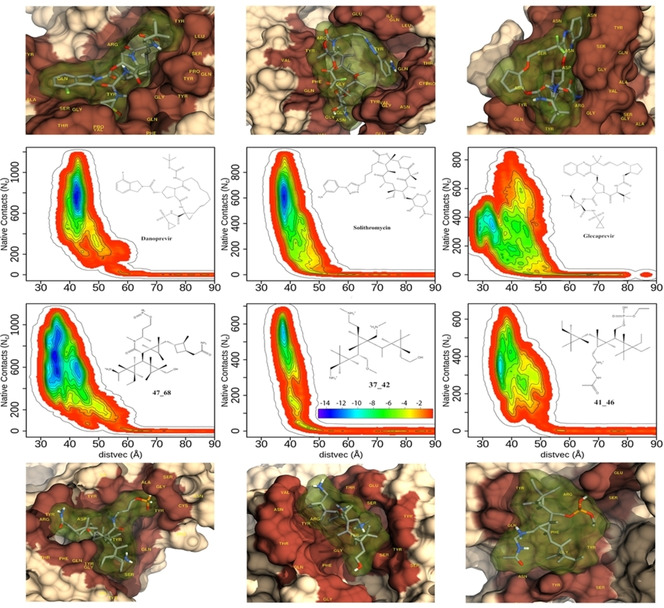
Free energy surfaces (FES) of three best de novo molecules and three best repurposed drug molecules. The chemical structure and name of each molecule are shown in the inset. The free energy bar used to plot FES is shown in the inset of 37_42. The structures of the free energy minimum of each molecule, made using chimera, ^[32] are shown above/below the corresponding FES. The protein is drawn in surface representation while the drug is shown with both stick and surface (with 80% transparency). Note the deep cavity formed by each of these molecules in the protein.

Since each molecule behaves differently, it is not possible to find a unifying trend in their binding mechanism. However, most of the strong binding molecules have a narrow free energy profile along the native contact. Once the contacts (the short distance between the ligand and the protein) are broken, the separation between the ligand and protein quickly increases.

We summarize the results from our metadynamics simulations of all the systems (55 molecules and hACE2) in Figure 5. The details of the system size and the runtime are given in Table S3 of SI. The free energies of the molecules are shown as vertical bar, where the RBD‐hACE2 free energy values (experimental and computational) are shown as horizontal bars. We provided error estimates for the free energy for the hACE2 and some of the strong binding drug molecules by performing multiple free energy calculations. Different experimental techniques provide different estimates for the strength of hACE2 binding to the spike protein, as represented by the grey bar in Figure 5. However, the lower limit of the interaction is −12.3 kcal/mol which is close to our calculated value of −13.0 kcal/mol. The vertical bars show the binding free energy of 35 de novo molecules and 20 repurposed drug molecules. We can see that at least 9 molecules touch or cross the experimental bar indicating that RBD would bind to these molecules comparably or stronger than hACE2. Three molecules (47_68, danoprevir and solithromycin) supersede even the lowest estimate of binding strength of hACE2 with RBD.

Figure 5.

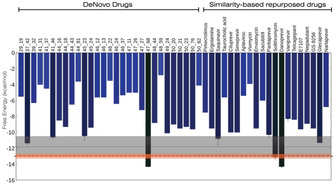
Free energy calculations. Free energy of binding for all the 35 de novo molecules and 20 repurposed drugs to the RBD calculated using all‐atom, explicit water, well‐tempered metadynamics simulations. The horizontal grey bar indicates the experimental range of free energy of binding of RBD and hACE2. The orange bar is the free energy estimate from multiple metadynamics simulations of RBD and hACE2. Error bars, obtained using multiple metadynamics simulations, are shown for some of the strong binding molecules. Note that, with the RBD, many molecules bind comparably or stronger than hACE2.

Figure 4 shows that the strong binding molecules create a cavity within the protein. To understand this better, we investigated the flexible loop (residues 445 to 468) around the hotspot region. We have introduced an angle $\theta$ (see Figure S12 of SI) that categorizes the configuration of the loop near the hotspot into three distinct conformations – closed, open, and semi‐open. We calculated the distribution of $\theta$ from the metadynamics simulations for all the systems including the free protein and hACE2 bound states. We plot the distribution for some of the most stable ligands, free protein, and hACE2‐bound protein in Figure 6. This distribution peaks at high value (155°) in the hACE2‐bound RBD configuration, attributed to the open configuration. The distribution is around 80° in the free state, characterized here as the semi‐open state while the distribution for the most stable ligand bound RBD is around 60°. The loop configurations for the other ligand‐bound states lie between the two extremes of 55° and 155° (between hACE2 and danoprevir bound states). The $\theta$ value for all the other ligand‐bound states are shown in Figure S13 of SI.

Figure 6.

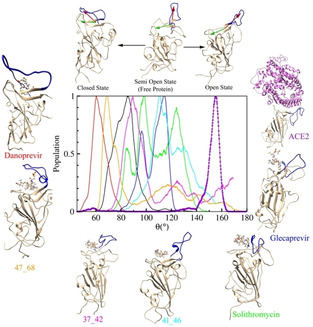
Mechanism of binding hints at competitive inhibition. Distribution of loop configuration in terms of the angle between the red and green vectors (see Figure S11 of SI) from the metadynamics simulation. The top panel shows three categories of loop configurations: open, semi open, and closed states. Representative images of the most stable ligand‐bound states are shown where the structures are arranged from open to closed configurations in clockwise fashion. Note that, while free protein belongs to the semi open configuration, the hACE2‐bound and danoprevir (and 47_68)‐bound RBD lie in the two extremes – open and closed states, respectively.

The above distribution indicates that binding of RBD to hACE2 in contrast to the ligands discussed here generates very different protein configurations. Therefore, we hypothesize that upon binding of these ligands, the RBD configuration will be different, and it will not be able to interact with the hACE2 effectively, potentially achieving the competitive inhibition.

Conclusions and Outlook

The approach to find COVID‐19 therapeutics in this study relies on receptor‐based atom‐by‐atom drug generation and similarity mapping to existing drugs for repurposing. We applied our method to the receptor binding domain of the spike protein and came up with 35 de novo molecules. From the similarity mapping, we obtained another 20 repurposable drug molecules. We validated our approach with state‐of‐the art enhanced sampling method – well‐tempered metadynamics that not only provides with a comparable free energy estimate to that of experiments, it also unearths the mechanism of binding. To show the accuracy of our method, we calculated the free energy of RBD and hACE2 (−13 kcal/mol), which agreed well with experimental value −12.3 kcal/mol. The same protocol was applied to all the 55 molecules (each with more than 100 ns of simulations) to obtain their free energy of binding to RBD. Out of these, we obtained 21 molecules with free energy less than −9 kcal/mol, indicating the success of our approach. Moreover, at least four de novo molecules and five repurposed drug molecules bind to RBD at comparable or higher strength than the hACE2. This implies that these molecules could in principle inhibit the interaction of the RBD with hACE2 and prevent the viral attack on the human cell.

Methods

DeNovo: The atom‐by‐atom synthesis of a strong binder

Here we describe our algorithm of de novo atom‐by‐atom construction of molecules in the hotspot of a receptor. The algorithm is based on the fact that any molecule can be represented as a graph where nodes are atoms and the bonds are edges. The first evidence of graph representation of the molecules dates back to 1867 by Kekule. Recently, a graph‐based algorithm was used to create 166 billion molecules in vacuum from only 17 atoms ^[33] of C, N, O, S, and halogens, which reinforces the fact that the chemical space is infinite and therefore it is possible to get multiple strong binders for each hotspot.

We, however, grow the molecules in the protein hotspot from the similar set of atoms (C, N, O, S, etc.). The classical nonbonding interaction energy (both van der Waals and electrostatic) between the drug and the hotspot is calculated using CHARMM27 ^[34] force field at each stage and the generation proceeds following an algorithm similar to that of the configuration bias Monte Carlo (CBMC) ^[35] (see Figure S1 and S2 and corresponding discussion in SI). Prior to molecular generation, the incomplete residues were completed using xleap of AMBERTools ^[36] and the missing residues of the protein were modelled by Modeller 9.21. ^[37] We targeted a prefixed atom number for the molecule and tried to improve the interaction of the molecule using CBMC criteria. This way, we obtained molecules having between 10 to 50 heavy atoms. Unlike in CBMC, our molecule is made of many different atoms. We used geometric criteria (equilibrium distance and angles) for the formation of rings. Finally, when a molecule reaches the desired number of atoms, we use CBMC criteria to accept it with reference to the previously generated molecule. We repeat this protocol several times until we have the required number of molecules. The program is fully CPU‐parallelized and runs efficiently over several cores (here we used 48 cores for our molecule generation).

Similarity Measurement

We have chosen all de novo generated molecules that interact with the protein with energy lower than our cut‐off −61.5 kcal/mol (see Figure 2). Subsequently, we performed a similarity search using the DrugBank ^[20] search engine employing Tanimoto algorithm. ^[38] All approved and investigational drug molecules with similarity above 0.4, a cutoff based on the studies of Baldi et al., ^[26] were considered. Table S1 of SI lists all the drug molecules for each of the 35 de novo molecules that match the criterion.

Docking of the matched drugs

Based on the similarity measurement, we came up with a list of 123 unique drug molecules from our 35 de novo molecules. We then docked these drug molecules to the hotspot using AutoDock Vina version 1.1.2. ^[39] A box centered around SER443 is created with dimensions 36.7 Å×26.1 Å×40.9 Å and default vina parameters. The docking setup is shown pictorially in Figure S4 of SI. The docking scores for all these molecules are shown in bracket in Table S1. The drug molecules with docking score less than −8.0 kcal/mol were considered for free energy calculations.

Force Field Generation

All drug molecules were optimized using HF (Hartree Fock) theory with 6–31G* basis set using Gaussian 09 software. ^[40] Thereafter, antechamber ^[41] was used for the RESP charge calculation and generation of force field for the molecules. The topology and coordinates were then converted into the GROMACS format by using a python script acpype.py (available at https://github.com/t‐/acpype).

System Setup for Simulation

The starting structure of the SARS‐CoV‐2 spike glycoprotein (PDB ID: 6VSB) was obtained from the Protein Data Bank. Modeller 9.21 ^[37] was used for modeling the missing residues, which predicted five three‐dimensional structural forms using chain A of protein as the template. The best possible structure was predicted considering the DOPE (Discrete Optimized Protein Energy) score. ^[42] All of the simulations were performed using molecular dynamics software GROMACS 2019.6. ^[43] For the study of the protein‐ligand complex, we only considered the RBD region of the protein (residues 302 to 506) and topology was prepared using AMBER99SB force field. ^[44] Each complex system was solvated by ∼23000 TIP3P ^[45] water molecules in a box of dimensions 70×70×180 ų. The physiological concentration (150 mM) of Na⁺ and Cl⁻ ions along with extra Cl⁻ ion were used to neutralize the system.

Equilibration and Simulation

Initially each system was energy minimized using steepest descent method ^[46] for 10000 steps, followed by heating it to 300 K in 200 ps using Berendsen thermostat and barostat ^[47] with coupling constant of 0.6 ps. Restraints of 25 kcal/mol/Ų were applied on heavy atoms during the heating process. Thereafter, equilibration was carried out for 2 ns at constant temperature (300 K) and pressure (1 bar) without any restraints using same thermostat and barostat with coupling constants of 0.2 ps each. The last 100 ps of NPT simulation was used to calculate the average volume the same, which was used in the final 5 ns unrestrained NVT equilibration using the Nosé‐Hoover thermostat ^[48] with coupling constant of 0.2 ps. During the simulation, LINCS algorithm ^[49] was used to constrain all the bonds and Particle Mesh Ewald (PME) method ^[50] was used for electrostatics. The distance cut‐offs for the van der Waals (vdW) and electrostatic long‐range interaction was kept at 10 Å. The time step for each simulation was taken to be 2 fs.

Free energy calculation using Metadynamics

The equilibrated ligand‐bound protein structure was initially simulated for 5 ns. If the ligand was found to be bound after 5 ns simulation, we subjected the system to free energy calculation. To calculate the binding free energy of drugs, well‐tempered metadynamics ^[21] simulations were performed after equilibration using DISTVEC and native contacts as collective variables (see SI for full description). We performed long (∼100 ns) metadynamics simulation with a hill height of 0.2 kJ/mol, a bias factor of 10, and a hills deposition rate of 2 ps. Gaussian widths for DISTVEC and native contacts were taken to be 0.6 Å and 5, respectively. An upper wall restraint was applied at 45° on the angle between two vectors $\widehat{b}$ and $\overrightarrow{d}$ , as shown in Figure S6 of SI. For free‐energy calculations, PLUMED 2.6 ^[51] was used along with GROMACS. The system size and run lengths of all the systems are provided in the Table S3 of SI.

Supporting Information

DeNovo algorithmic flow charts, schematic CBMC profile, image containing all the selected de novo molecules, table showing list of similar drugs, image showing docking region, table of docking scores for selected drugs, table for docking variations, image of all the selected drug molecules, definition and picture of the collective variables used, table showing system size and other information for all the systems, and free energy surfaces of binding to RBD for all the 55 molecules.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

R. Chowdhury, V. Sai Sreyas Adury, A. Vijay, R. K. Singh, A. Mukherjee, Chem. Asian J. 2021, 16, 1634.