Synthesis and characterization of bulk Nd_1–xSr_xNiO₂ and Nd_1–xSr_xNiO₃

Abstract

The recent reports of superconductivity in Nd_1–xSr_xNiO₂/SrTiO₃ heterostructures have reinvigorated interest in potential superconductivity of low-oxidation state nickelates. Synthesis of Ni¹⁺-containing compounds is notoriously difficult. In the current work, a combined sol-gel combustion and high-pressure annealing technique was employed to prepare polycrystalline perovskite Nd_1–xSr_xNiO₃ (x = 0, 0.1, and 0.2). Metal nitrates and metal acetates were used as starting materials, and the latter were found to be superior to the former in terms of safety and reactivity. The Nd_1–xSr_xNiO₃ compounds were subsequently reduced to Nd_1–xSr_xNiO₂ using calcium hydride in a sealed, evacuated quartz tube. To understand the synthesis pathway, the evolution from NdNiO₃ to NdNiO₂ was monitored using in situ synchrotron x-ray diffraction during the reduction process. Electrical transport properties were consistent with an insulator-metal transition occurring between x = 0 and 0.1 for Nd_1–xSr_xNiO₃. Superconductivity was not observed in our bulk samples of Nd_1–xSr_xNiO₂. Neutron diffraction experiments at 3 and 300 K were performed on Nd_0.9Sr_0.1NiO₂, in which no magnetic Bragg reflections were observed, and the results of structural Rietveld refinement are provided.

I. INTRODUCTION

Since the discovery of superconductivity in cuprates, researchers have targeted low-oxidation state nickelates with square planar coordination because they mimic the cuprates in terms of the electronic count and orbital polarization [1–3]. The infinite-layer compounds, RNiO₂ (R = La, Nd), represent perhaps the simplest such structural prototype and were initially investigated as oxygen-deficient phases of RNiO₃ [4–7]. Despite efforts that span nearly three decades of research on these materials, only recently did the first report of superconductivity appear, in which it was observed up to ~15 K in Nd_1–xSr_xNiO₂ thin films grown on SrTiO₃ substrates [8].This intriguing result has rekindled interest in the infinite-layer RNiO₂ compounds, and a number of theoretical studies have been carried out to investigate the electronic structure of these compounds [9–13]. Calculations indicate that although RNiO₂ compounds possess larger charge-transfer energies than cuprates [14,15], they do possess similar long-range to nearest-neighbor hopping ratios and e_g orbital splitting to the cuprates [12]. Unlike cuprates, R 5d states cross the Fermi level [12,15]. Electronic calculations suggest that the parent compounds (i.e. the undoped, Ni¹⁺ end members) should be magnetically ordered [9,14,16]; yet, earlier reports by Hayward et al. for LaNiO₂ [17] and NdNiO₂ [18] evidenced no magnetic order via neutron scattering.

Despite the large number of recent theoretical investigations into RNiO₂ compounds, experimental reports are far more limited. Li et al. recently provided evidence for a super-conducting dome in Nd_1–xSr_xNiO₂ persisting from 0.125 < x < 0.25 and surrounded by weakly insulating states at higher and lower x [19]. Similar results were recently reported by Zeng et al. [20]. Li et al. discussed the nuanced complexities of the epitaxial growth [19]. Hepting et al. measured x-ray-absorption spectroscopy and resonant inelastic x-ray scattering, interpreting that the rare-earth 5d states hybridize with nickel 3d_x²–y² states [15]. There have been no reports of superconductivity in the bulk, but rather, it has been suggested that the superconductivity may be related to an interface effect [21]. Beyond these reports, little has been experimentally evidenced, and the relative dearth of experimental results is most certainly tied to the challenges presented by synthesis.

Concerning the bulk RNiO₂ phase, the only reported approach to synthesize it is to prepare polycrystalline samples of Nd_1–xSr_xNiO₃ and then reduce them to Nd_1–xSr_xNiO₂ via a reducing agent [4,5,17]. However, the formation of Nd_1–xSr_xNiO₃ from NiO involves the oxidation of nickel from Ni²⁺ to Ni^3+x, necessitating the use of high oxygen pressures during synthesis [10]. We note that generally higher pressures are required for smaller R³⁺ species, so that R = Nd growth is more difficult than R = La growth. Although it is unclear what pressures would be required under standard solid-state reaction to produce stoichiometric Nd_1–xSr_xNiO₃ as a function of x, it is certain that the synthesis of Sr²⁺-doped NdNiO₃ would be more challenging because the introduction of Sr²⁺ to NdNiO₃ forces the oxidation state of nickel to exceed 3+. The first report of NdNiO₃ was via solid-state reaction, which required high oxygen pressure of 60 kbar and high temperature of 950 °C [10]. However, an alternative route for producing polycrystalline samples of NdNiO₃ was later developed by Lacorre et al. through sol-gel precursors by using nitrates as starting materials [5,10]. The advantage of the sol-gel route is that precursor powders are ultrafine so that their reactivity is much higher than that of binary oxides and carbonates at reduced temperatures due to the short diffusion path of the ions [11,22]; thus, in principle, synthesis can be carried out at lower temperatures and pressures. Nevertheless, for perovskite nickelates, while this approach does reduce the required pressure, it still involves heat treatment at temperatures greater than 1000 °C and under oxygen pressures as high as 200 bar [23].

Given the recent surge of interest in finding superconductivity in the RNiO₂ phase, we have investigated the synthesis of Nd_1–xSr_xNiO₃ precursors as well as the reduction process of Nd_1–xSr_xNiO₃ to Nd_1–xSr_xNiO₂. Here, we provide details of the procedures that we have used to synthesize the materials, comparing different sol-gel combustion methods for Nd_1–xSr_xNiO₃, performing in situ x-ray diffraction during the reduction process to obtain NdNiO₂, and discussing the challenges in obtaining high-purity, high-quality materials. We characterize the electrical transport properties of the obtained materials, and provide structural Rietveld refinements of neutron diffraction data carried out on Nd_1–xSr_xNiO₂ at 3 and 300 K.

II. EXPERIMENT

A. Synthesis of Nd_1–xSr_xNiO₃

1. Nitrate method

Nd_1–xSr_xNiO₃ (x = 0, 0.1, and 0.2) was synthesized via the citrate-nitrate auto-combustion synthesis as described by Deganello et al. [24]. Metal nitrates Nd(NO₃)₃ · 6H₂O (Strem Chemicals, 99.999%), Ni(NO₃)₂ · 6H₂O (Sigma-Aldrich, 99.999%), and Sr(NO₃)₃ (Alfa Aesar, 99.97%) were used as starting materials. The metal nitrates were dissolved in a minimum amount of distilled water to obtain a clear solution. The exact concentrations of metal nitrates were determined by inductively coupled plasma mass spectrometry to account for variable levels of hydration in the starting materials. Stoichiometric amounts of nitrates were mixed in a beaker to get the desired Nd_1–xSr_xNiO₃ (x = 0 to 0.2) precursor solutions. An aqueous solution of citric acid was then mixed with the precursor solutions at a molar ratio, citric acid to metal ions, of 1.2:1 at room temperature. The pH of the precursor solution was adjusted to ≈7 by adding 30 wt. % aqueous NH₃. The solution was slowly evaporated at 70 °C with continuous mechanical stirring, until a hardened gel was obtained. To carry out the gel decomposition under controlled conditions, the hardened gel was transferred to an alumina crucible, which was then put on a hot plate at 250–300 °C. The gel first turned to black, and then ignited and underwent a vigorous self-sustaining combustion, yielding an ash product. The combusted powders were then fired at 800 °C for 12 h in an oxygen atmosphere at ambient pressure with a flow rate of 0.2 L/min. The resulting black powder was then ground and pressed into pellets with dimensions of 13 mm diameter and about 0.2 mm thickness. The pellets were subsequently fired at 1000 °C under 150–160 bar of oxygen pressure for 12 h in a high-pressure annealing furnace (model AHSO, SciDre GmbH Dresden). For x = 0.10 and 0.20, multiple 12-h firings with intermediate regrinding were carried out.

2. Citrate method

Nd_1–xSr_xNiO₃ (0.0 ⩽ x ⩽ 0.2) was also synthesized using metal acetates, Nd(CH₃CO₂)₃ · H₂O, Ni(CH₃CO₂)₂ · 4H₂O, and Sr(CH₃CO₂)₃, as starting materials. To prevent the formation of carbonate precipitation over time, the pH of the acetate solutions was adjusted to 1 by addition of HNO₃. The rest of the experiment procedure was similar to that described for metal nitrates. Note that the combustion reaction using citrates as starting materials was much less vigorous compared to the nitrates.

B. Reduction of Nd_1–xSr_xNiO₃

The reduction of Nd_1–xSr_xNiO₃ (0.0 ⩽ x ⩽ 0.2) was performed using CaH₂ powder as a reducing agent. From the previously obtained Nd_1–xSr_xNiO₃ (0.0 ⩽ x ⩽ 0.2), 90–100-mg chunks extracted from the thin pellets were wrapped loosely with aluminum foil, which had small holes in it. Then the wrapped samples were loaded together with 0.25 g CaH₂ powder in an Ar-filled glove box and subsequently sealed under rough vacuum (10⁻³ mbar) in an evacuated quartz tube with 11-mm outer diameter, 9-mm inner diameter, and approximately 200-mm length. The tube was then heated to 285 °C at a rate of 1 °C/min and kept at this temperature for 48 h. After reduction, the remaining CaH₂ powder on the sample surfaces was gently removed.

C. Characterization

Powder x-ray-diffraction data were collected at room temperature on all samples using a PANalytical X’Pert Pro powder diffractometer with Cu Kα radiation (λ = 1.5418 Å) in the 2θ range of 20°–70°. Rietveld refinement was performed on the collected data using gsas II software [25].

In situ high-energy synchrotron x-ray diffraction experiments were conducted at beamline 11-ID-C (λ = 0.1173 Å, beam size = 0.5 mm × 0.5 mm), Advanced Photon Source at Argonne National Laboratory. The sample chunk of NdNiO₃ (2 mg), and CaH₂ powder (50 mg) were loaded in a Pyrex glass tube with 1.25-mm inner diameter, and then the loaded tube was sealed under vacuum of 10⁻³ mbar. A specially designed eight-well NMR tube furnace was used to heat the sample. The heating cycle was as follows: ramping at 10 °C/min to 200 °C, and then at 1.6 °C/min to 340 °C, holding at 340 °C for 120 min, then cooling to room temperature at 10 °C/min. Synchrotron powder-diffraction data were collected at 5-min intervals. An amorphous silicon-based area detector (PerkinElmer XRD1621) was used to collect the data, which was then calibrated using CeO₂ images. The data were subsequently reduced from 2-D images to 1-D powder patterns by GSAS-II.

Resistivity measurements of the bulk Nd_1–xSr_xNiO₃ (0.0 ⩽ x ⩽ 0.2) and Nd_1–xSr_xNiO₂ (0.1 ⩽ x ⩽ 0.2) samples were performed in a Quantum Design physical property measurement system in the temperature range of 2–300 K using the Van der Pauw method with contacts made with silver paste.

Powder neutron diffraction experiments were performed on the BT-1 diffractometer at the NIST Center for Neutron Research using the Ge (311) monochromator with λ = 2.079 Å. The mass of the sample was ≈1 g, and the sample was sealed in a vanadium can under helium atmosphere and placed in a closed-cycle refrigerator with a base temperature of 3 K.

III. RESULTS

A. Synthesis of Nd_1–xSr_xNiO₃ (x = 0, 0.1, and 0.2)

The combustion synthesis of citric acid with nitrates produces ultrafine powders, which is confirmed by the size-broadened x-ray diffraction pattern shown in Fig. 1. These as-combusted powders were then annealed in an O₂ flowing atmosphere at ambient pressure at 800 °C for 12 h, after which it was found that the majority phase of the powder was already NdNiO₃ with a small amount of Nd₂NiO₄ and some unreacted NiO and Nd₂O₃ phases (Fig. 1). The black powder was then finely ground and fired again under the same conditions for 84 h. As shown in Fig. 1, some Nd₂NiO₄ and NiO remained, but the quantity of secondary phases was significantly reduced. Because of the poor crystallinity, evidenced by the broadened reflections, and the persistent small amount of secondary phases, the sample was then fired at 1000 °C for 12 h under an oxygen pressure of 150–160 bar. As shown in Fig. 2(a), the crystallinity and purity of the resulting powder was improved markedly over that reached under ambient conditions.

FIG. 1.

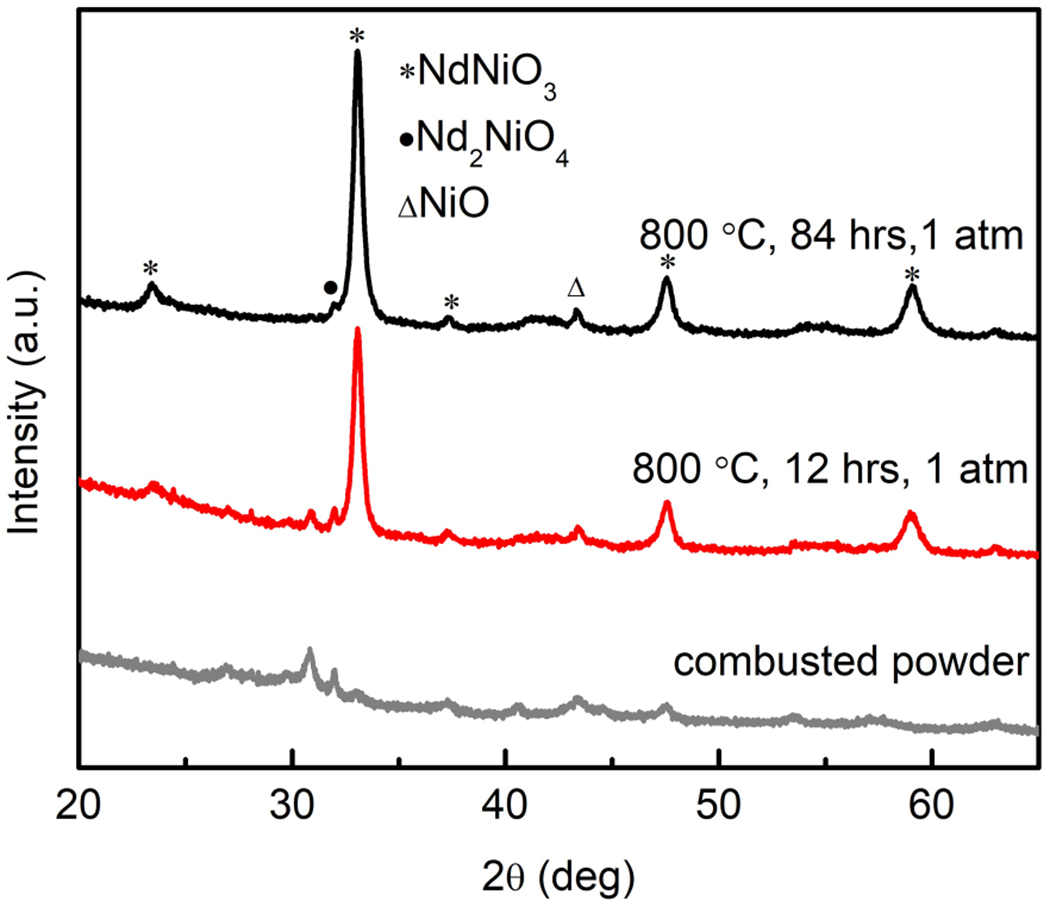
X-ray powder diffraction patterns of combusted Nd_1–x Sr_xNiO₃ (x = 0) powder from nitrate method and after annealing in O₂ at ambient pressure for 12 and 84 h, respectively.

FIG. 2.

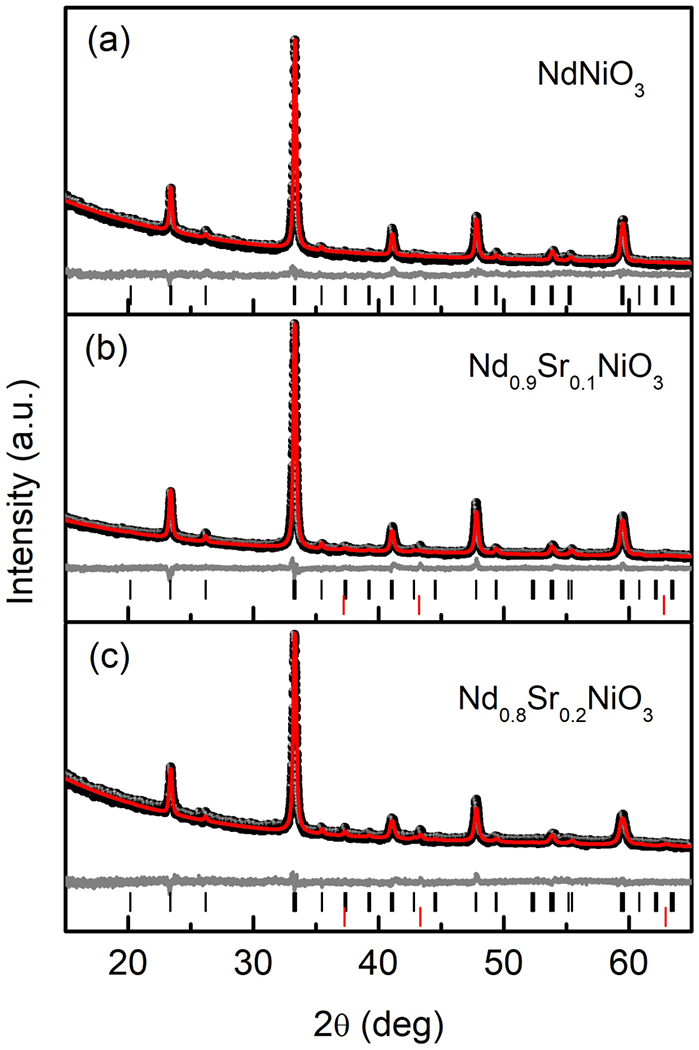
Room temperature X-ray powder diffraction patterns of Nd_1–xSr_xNiO₃ (0.0 ⩽ x ⩽ 0.2) and corresponding Rietveld fitting results using Pbnm space group. The black dots are the observed data, the red line is the calculated fit, and gray line shows the difference between the two. Positions of allowed reflections are indicated by vertical black (Nd_1–xSr_xNiO₃) and red (NiO) lines.

The incorporation of Sr²⁺ into NdNiO₃ increases the formal nickel valence and consequently requires additional high-pressure steps. The main secondary phase involved in the synthesis for both x = 0.1 and 0.2 samples is (Nd, Sr)₂NiO₄ (214), which is more stable at low oxygen pressure. For x = 0.1, a firing at 1000 °C for 12 h under O₂ pressure of 150 bar was needed to remove the 214 impurity, whereas for x = 0.2, multiple firings at 1000 °C under 150 and 160 bar were required to suppress the secondary phase. As shown in Figs. 2(b) and 2(c), both x = 0.1 and 0.2 samples were found to contain small quantities of NiO impurities.

All three compositions were indexed in the orthorhombic, Pbnm space group (Fig. 2), and Rietveld refinement was carried out. The refined parameters and lattice constants are listed in Table I. The variation of the lattice parameters and volume with the Sr content is plotted in Fig. 3. The good agreement factors are consistent with a random substitution of Sr²⁺ for the rare-earth cations. As shown in Fig. 3(a), the lattice parameter c increases with Sr content while b decreases, and a is practically constant over this doping range. The trends in b and c are consistent with those previously reported by Alonso et al. [26], and the values of a are similar, although Alonso et al. reported a monotonic increase in a. To exclude contributions from systematic error, the c/a and c/b ratios were also calculated and listed in Table I. It can be seen that both values increase monotonically with Sr content. This once again suggests that the incorporation of Sr ions into the NdNiO₃ perovskite leads to a lengthening of the c axis.

TABLE I.

Lattice parameters of Nd_1–xSr_xNiO₃ (x = 0.0, 0.1, and 0.2) compounds made from nitrates determined by Rietveld refinement of x-ray data. (Note: GOF stands for “goodness of fit”.)

x	a (Å)	b (Å)	c (Å)	V (Å3)	c/a	c/b	GOF	Rw
0.0	5.3958(8)	5.3758(8)	7.6034(8)	220.55(5)	1.4091	1.4143	1.55	5.70%
0.1	5.394(2)	5.368(2)	7.609 (2)	220.32(2)	1.4106	1.4174	1.41	4.87%
0.2	5.3963(5)	5.3647(5)	7.6133(8)	220.40(3)	1.4108	1.4239	1.21	5.14%

FIG. 3.

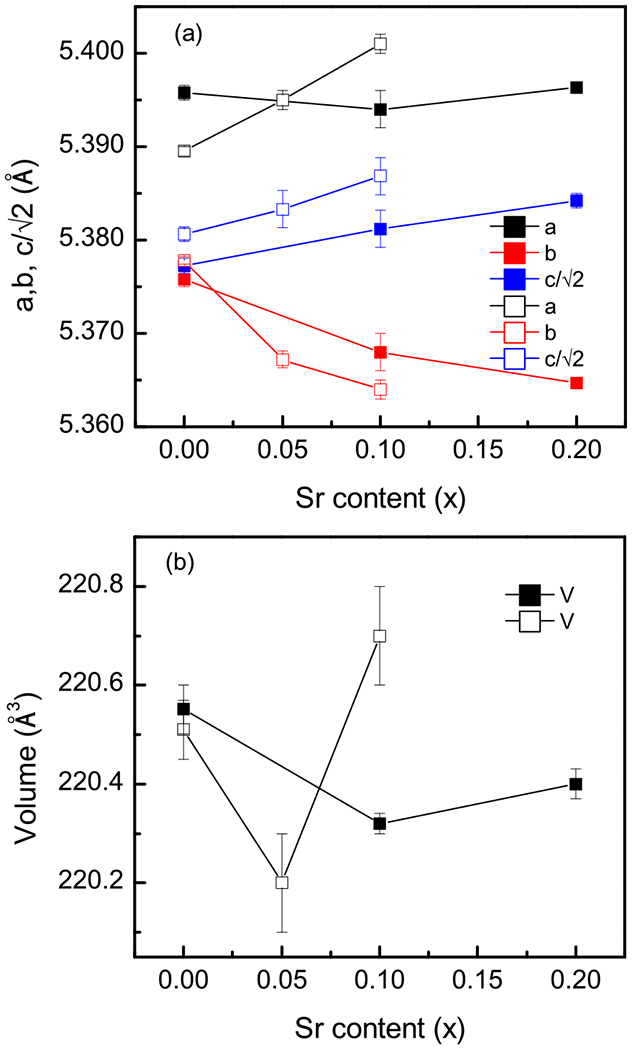
Variation of the (a) unit-cell parameters and (b) cell volume of Nd_1–xSr_xNiO₃ as a function of the Sr content (x). Solid squares: this work; open squares from Ref. [26]. Uncertainties represent one standard deviation.

The observed unit-cell volume [Fig. 3(b)] varies non-monotonically, with a minimum appearing at x = 0.1, though the change in volume is very small (0.1%). Alonso et al. also observed a nonmonotonic behavior, with small changes, though the minimum was observed at x = 0.05 [26]. Given the combination of statistical and systematic uncertainty, it is our contention that the volume is nearly constant with substitution in this doping range and that the nonmonotonic behavior should be considered as a possible, but not definitive, trend. Based on the ionic size of the A-site dopant alone (Nd³⁺ ≈ 1.27 Å, Sr²⁺ ≈ 1.44 Å) [27], one should expect an increase in the unit-cell volume in a Vegard’s law-like fashion. However, additional complications could arise from the increasing propensity for oxygen vacancies to form, which would also be expected to increase the cell volume, and the change in the nickel oxidation state, which would be anticipated to decrease the cell volume. Furthermore, reciprocal trends between lattice constants (e.g., b decreasing, c increasing) can also reflect the perovskite’s propensity to compensate for ionic size effects through rotations of oxygen octahedra. Given the imprecision of x-ray diffraction in determining oxygen positions, we do not further elaborate on this last point.

B. Acetates vs nitrates

Due to the vigor of the reaction using metal nitrates, only approximately 1 g of the hardened gel was burned at a time. In some publications [28,29] describing the preparation of battery materials via sol-gel methods, metal acetates were also employed as oxidants. Therefore, Nd_1–xSr_xNiO₃ (x = 0, 0.1, and 0.2) was also synthesized using metal acetates Nd(CH₃CO₂)₃ · H₂O, Ni(CH₃CO₂)₂ · 4H₂O, and Sr(CH₃CO₂)₃ in a manner similar to that described using nitrates. Combustion of larger quantities (~5 g) could be conducted each time thanks to the less-energetic reaction. Here we take the synthesis of Nd_0.9Sr_0.1NiO₃ using metal acetates as an example. As shown in Fig. 4(a), the combusted powder from metal acetates shows no Bragg reflections at all, while a few peaks from metal oxides were present in the product from the metal nitrates. After annealing at 800 °C for 12 h at ambient conditions, the majority of the sample made from metal acetates was already Nd_0.9Sr_0.1NiO₃. In the case of the sample made from nitrates, there was still about 40% of the (Nd, Sr)₂NiO₄ phase remaining, as estimated from the x-ray diffraction [Fig. 4(b)]. This suggests that the reactivity of the powder obtained from the metal acetates combustion reaction was higher. In the end, Nd_0.9Sr_0.1 NiO₃ was achieved after one single firing at 1000 °C for 12 h in both cases under an oxygen pressure of 150 bar [Fig. 4(c)]. However, it seems the x-ray quality of the final products from metal acetates is slightly better than that of from metal nitrates, e.g., a smaller full width at half maximum for the former [0.261(7)°] than that of the latter [0.291(6)°], indicating better crystallinity of the sample [Fig. 4(d)].

FIG. 4.

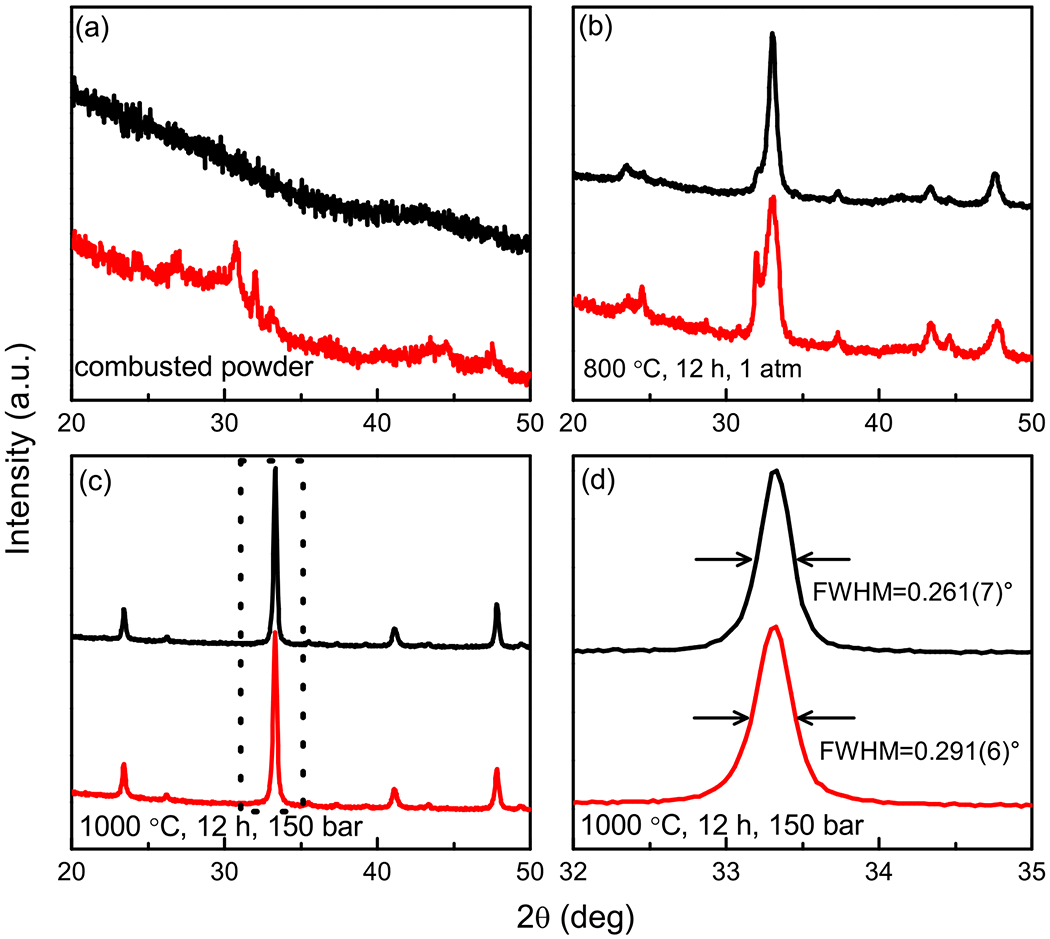
X-ray powder diffraction patterns for samples made from acetates (red) and nitrates (black). (a) Combusted powders, (b) powders annealed at 800 °C for 12 h under ambient pressure, and (c) annealed at 1000 °C for 12 h under oxygen pressure of 150 bar. (d) Enlarged view of the region marked by dashed rectangle in (c).

C. Synthesis of Nd_1–xSr_xNiO₂ by reducing Nd_1–xSr_xNiO₃

As discussed above, the RNiO₂ phase can be obtained by reduction of the RNiO₃ phase. Previous studies have shown that the reduction of NdNiO₃ in flowing, diluted H₂ gas leads to a reported Nd₃Ni₃O₇ phase [5]. The infinite layer Ni¹⁺ containing NdNiO_2+x phase is most easily accessible with the hydride reagents [18]. In the present experiment, the reduction of Nd_1–xSr_xNiO₃ was performed using CaH₂ as a reducing agent. As described in the Experiment section, 90–100-mg chunks extracted from the polycrystalline Nd_1–xSr_xNiO₃ pellets were either directly embedded in CaH₂ powders or loosely wrapped with aluminum foil (with holes) before mixing with CaH₂. It was found that the results from both methods are indistinguishable. In the early work of Hayward et al. [17,18,30–32], in which NaH or CaH₂ was used as reducing agent, the samples were thoroughly ground with the hydride and the reduction has been assumed to be a solid-state reaction. Later, Kobayashi et al. [33] successfully conducted the reduction of SrFeO₃ to SrFeO₂ with physically separated CaH₂, and it was concluded that the reaction proceeded via the release of H₂ by CaH₂. Recently, Page et al. [34] reduced CaMn_0.5Ir_0.5O₃ using NaH and a gas-mediated reaction process was proposed. Here, our results, which are identical for the physically separated and mixed experiments, once again confirm that the reduction using CaH₂ works via H₂ gas instead of solid-state reaction.

Previous work on thin-film LaNiO₃ has shown that reduction induces a series of transformation steps: first to a monoclinic phase LaNiO_2.5, then to c-axis LaNiO₂, followed by a reorientation transition to a-axis LaNiO₂, before subsequent decomposition [5,7,35]. Additionally, a previous study on NdNiO₃ reduction indicated that a fluorite defect phase can be introduced on top of the infinite-layer NdNiO₂ (001) films under certain annealing conditions [36]. These results hinted that it is difficult to stabilize a uniform, single-crystalline infinite-layer NdNiO₂ phase with its formal Ni¹⁺ oxidation state. Indeed, for NdNiO₃, where x = 0.0 in Nd_1–xSr_xNiO₃, our attempts to reduce to NdNiO₂ using CaH₂ were not successful (except for the in situ reduction experiment described below). We tried to optimize the reduction conditions by adjusting reaction time and temperature, but no full transformation to the infinite-layer structure was realized. Given the fact that Hayward et al. succeeded in making NdNiO₂ by grinding the NdNiO₃ with sodium hydride [17], we also tried to grind NdNiO₃ with CaH₂ for the reduction experiment, but this, too, was unsuccessful.

Though the reduction of NdNiO₃ to NdNiO₂ was not successful in our ex situ experiments, we were able to achieve successful reduction via an in situ high-energy synchrotron x-ray diffraction experiment. Figure 5 shows the evolution of phases and the reducing reaction pathway with temperature. As shown in Fig. 5(a), the NdNiO₃ phase diminished rapidly at 200 °C along with the appearance of the Nd₃Ni₃O₇ phase (purple curve). As the temperature was increased, NdNiO₂ began to appear as a secondary phase [Fig. 5(b)], and eventually Nd₃Ni₃O₇ did give rise to NdNiO₂ at 260 °C (black curve), which was stable until the conclusion of the reduction at 340 °C. This suggests that it is possible to prepare NdNiO₂ using CaH₂, but it requires subtleties we do not yet understand. One speculation is that the tube size for the in situ experiment is relatively small, which generates a higher effective H₂ concentration, but further work is needed to confirm this.

FIG. 5.

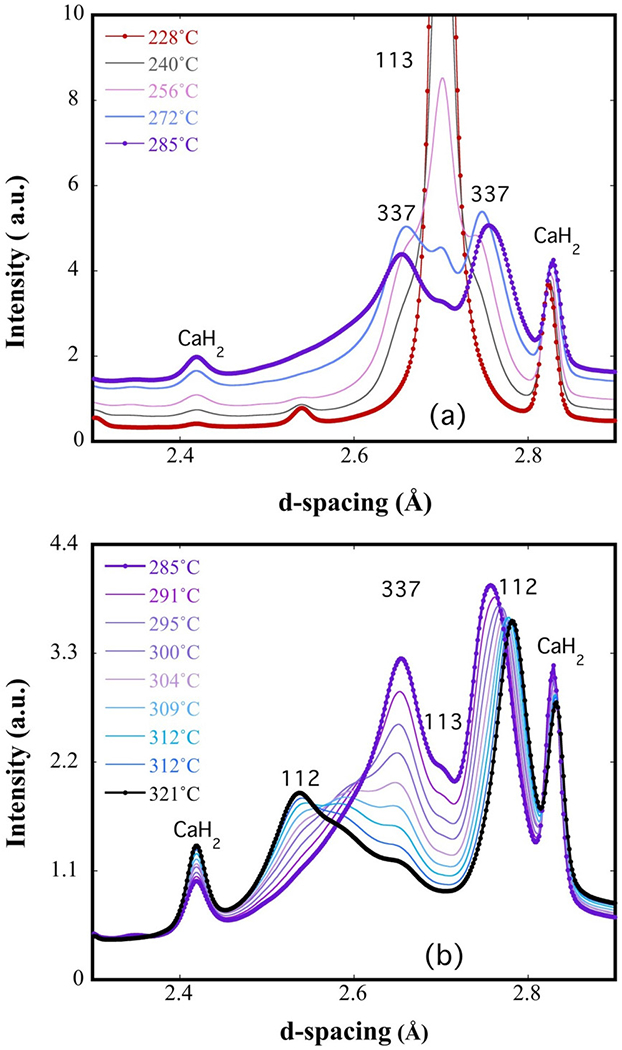
High-energy in situ x-ray data showing the evolution from (a) NdNiO₃ to Nd₃Ni₃O₇ and (b) Nd₃Ni₃O₇ to NdNiO₂. The 113, 112, and 337 denote NdNiO₃, NdNiO₂, and Nd₃Ni₃O₇ phases, respectively.

Although reduction of the parent phase to NdNiO₂ is difficult, we found that hole doping (increasing x) facilitates the reduction process, likely because the formal oxidation state of nickel in the final product is increased. We were able to successfully reduce x = 0.1 and 0.2 samples to Nd_1–xSr_xNiO₂ using the protocol described above, which failed for x = 0. Figures 6(a) and 6(b) display the room-temperature x-ray diffraction measurements and the Pawley refinements of Nd_1–xSr_xNiO₂ (x = 0.1, 0.2) bulk samples. The main phase of both the samples is the infinite-layer phase with a small amount of a nickel impurity. Nickel metal is a common product for the reduction of perovskite nickelates [17,18] and likely arises from the reduction of NiO impurities that were present in the perovskite phase prior to reduction. This realization highlights the fact that achieving high-purity Nd_1–xSr_xNiO₂ requires a high-purity perovskite precursor. In fact, we have a dichotomy: It becomes more difficult to grow the perovskite precursor as x is increased because of the high nickel oxidation state required (3 + x), but once the precursor is produced, it is more difficult to reduce the precursor to the infinite later phase as x is decreased because of the low oxidation state required (1 + x). Considering the challenges involved in both steps, we have found that the easiest infinite-layer composition to synthesize has x ~ 0.1.

FIG. 6.

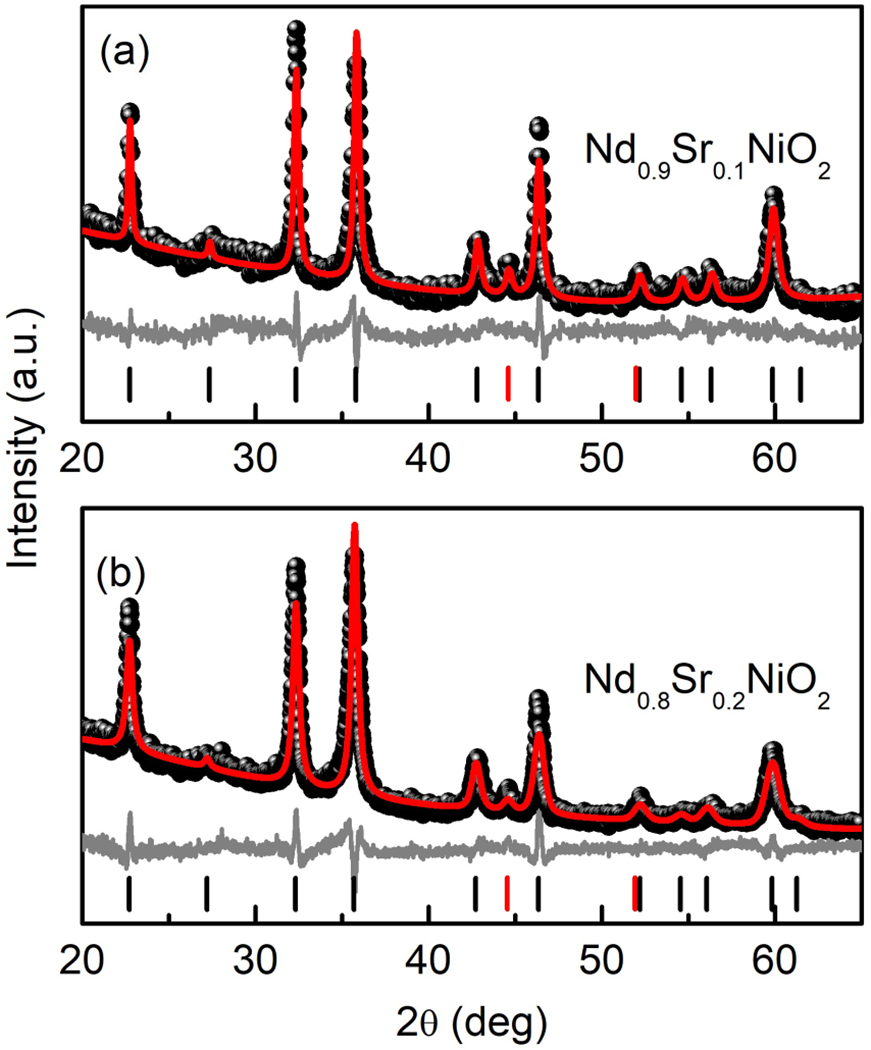
Powder x-ray diffraction of Nd_0.9Sr_0.1NiO₂ (a) and Nd_0.8Sr_0.2NiO₂ (b) and the corresponding Pawley refinement. The black dots are the observed data, the red line is the calculated fit, and gray line shows the difference between the two. Positions of allowed reflections are indicated by vertical black (Nd_1–xSr_xNiO₂) and red (Ni) lines.

In early work on powder synthesis done by Li et al., it was found that the peaks of infinite-layer nickelates are broad, which was attributed to randomly oriented domains with different sizes in the sample [21]. In our case, the infinite-layer phases are also imperfectly crystallized, and the statistics of our x-ray diffraction data are relatively low; therefore, we only applied the Pawley method for the data refinement. A detailed structural analysis on Nd_0.9Sr_0.1NiO₂ by Rietveld refinement is provided by neutron diffraction below. The calculated lattice parameters for Nd_0.9Sr_0.1NiO₂ and Nd_0.8Sr_0.2NiO₂ by Pawley fitting are a = 3.9212(7) Å, c = 3.2681(6) Å and a = 3.9175(5) Å, c = 3.2793(4) Å, respectively. We notice that the in-plane lattice constant c of our Nd_0.8Sr_0.2NiO₂ sample is slightly smaller than that of reported Nd_0.8Sr_0.2NiO₂ thin films (range from 3.34 to 3.38 Å) [8] and bulk sample made by Li et al. (3.34 Å) [21]. Ultimately, however, the results from x-ray diffraction (3.268 Å) and neutron diffraction (3.266 Å) Nd_0.9Sr_0.1NiO₂ are internally consistent.

D. Electrical transport properties

The temperature dependence of the resistivity of Nd_1–xSr_xNiO₃ (x = 0.0, 0.1, and 0.2) and Nd_0.8Sr_0.2NiO₂ is shown in Fig. 7. It can be seen that NdNiO₃ shows the characteristic first-order phase transition from a high-temperature paramagnetic metal to a low-temperature antiferromagnetic insulator and that this transition is suppressed by Sr doping. These results are in good agreement with the results obtained in Ref. [8]. We display the result of Nd_0.8Sr_0.2NiO₂ only as a representative example of the temperature dependence of the measured resistivity. Although it matches well with the report of Li et al. [21], we do not believe that this is truly representative of the intrinsic resistance of Nd_0.8Sr_0.2NiO₂. The issue here is that the temperature dependence is uncharacteristic of an oxide—typically if the actual room-temperature resistivity is on the order of an Ω cm at room temperature [37–39], as we measure here, then the oxide will display semiconducting resistivity with a much higher low-temperature resistance than measured. The reduction process yields fragile pellets with low density, and unfortunately postreduction annealing at higher temperatures causes the infinite-layer phase to decompose. Regardless, we are unable to see any hint of superconductivity in our infinite-layer samples, but we think that the intrinsic resistivity remains an open question.

FIG. 7.

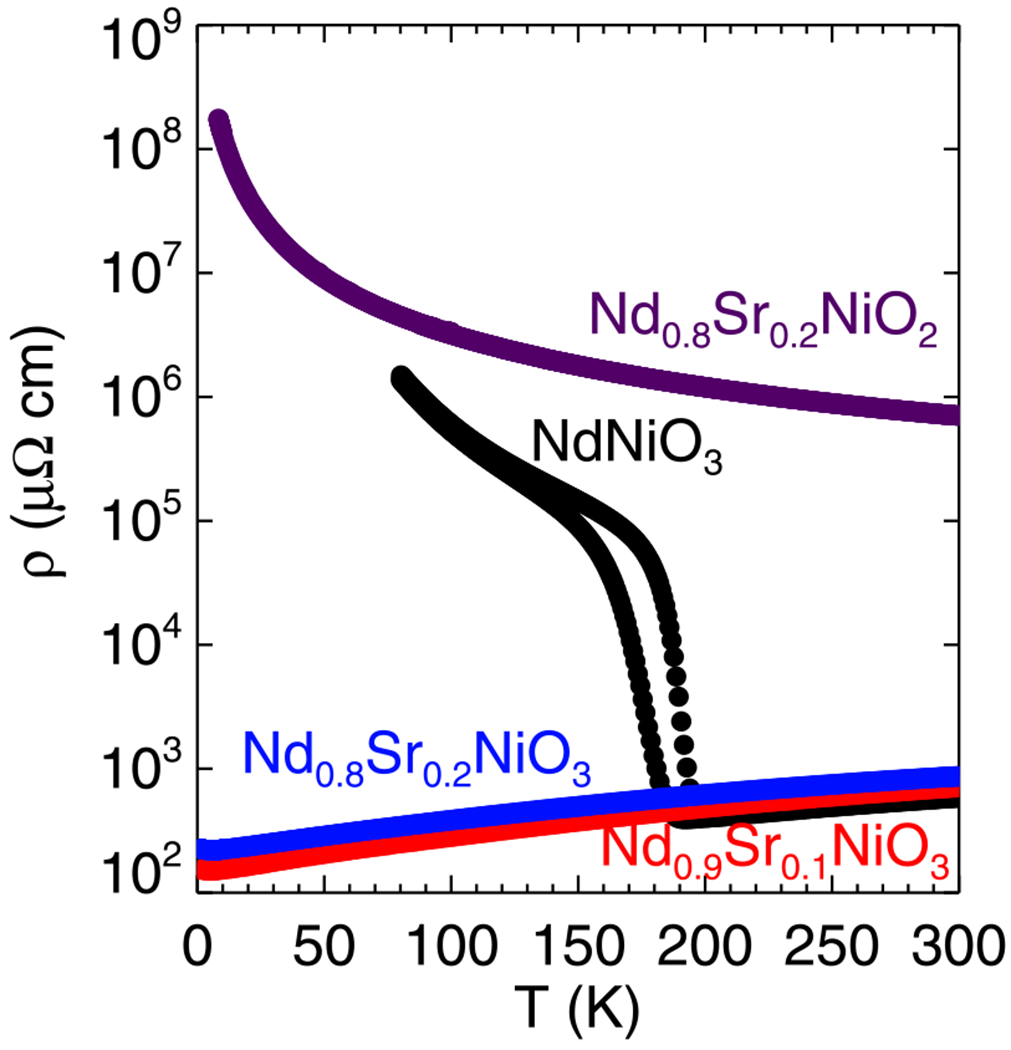
Temperature-dependent resistivity of the Nd_1–xSr_xNiO₃ (x = 0.0, 0.1, and 0.2) and Nd_1–xSr_xNiO₂ (x = 0.2) samples.

E. Neutron diffraction

As described above, powder neutron diffraction measurements were performed on a sample of Nd_0.9Sr_0.1NiO₂ that had been synthesized from acetates. Measurements were taken at both 3 and 300 K and are shown in Figs. 8(a) and 8(b), respectively. Close inspection of the powder patterns revealed neither peak splitting nor the appearance of peaks at 3 K that were not visible at 300 K; thus, we observed neither a structural phase transition nor evidence of long-range magnetic order. In fact, we were able to obtain reasonable fits to the data at both temperatures using a combination of the P4/mmm space group for the 112 phase with an additional fcc nickel second phase. The calculated patterns as well as the difference plots are shown for each of the refinements in Figs. 8(a) and 8(b), and the refined parameters are listed in Table II.

FIG. 8.

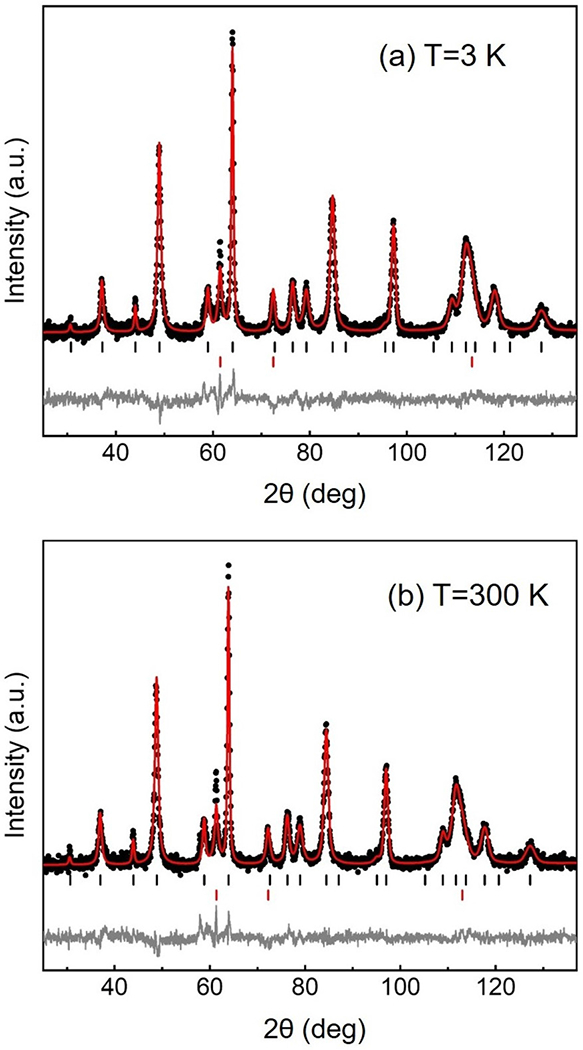
Neutron diffraction and the corresponding Rietveld refinement of Nd_0.9Sr_0.1NiO₂ at 3 K (a) and at 300 K (b). The black dots are the observed data, the red line is the calculated fit, and gray line shows the difference between the two. Positions of allowed reflections are indicated by vertical black (Nd_1–xSr_xNiO₂) and red (Ni) lines.

TABLE II.

Refined crystal structural parameters of Nd_0.9Sr_0.1NiO₂ at 3 and 300 K. a and c are the lattice parameters of the tetragonal crystal, V is volume of unit cell, U_iso is the isotropic atomic displacement parameter. The quality of the agreement between the observed and calculated profiles is measured by various R factors.

		3 K	300 K
a (Å)		3.9132(1)	3.9206(1)
c (Å)		3.2539(3)	3.2664(3)
V (Å3)		49.828(5)	50.208(5)
c/a
Nd	Coordinate	(0.5,0.5,0.5)	(0.5,0.5,0.5)
	100 × Uiso(Å2)	1.25(6)	1.19(7)
Sr	Coordinate	(0.5,0.5,0.5)	(0.5,0.5,0.5)
	100 × Uiso(Å2)	1.25(6)	1.19(7)
Ni	Coordinate	(0,0,0)	(0,0,0)
	100 × Uiso(Å2)	2.06(5)	1.77(6)
O	Coordinate	(0.5,0,0)	(0.5,0,0)
	100 × Uiso(Å2)	1.56(5)	1.45(6)
Nd-O length (Å)		2.5444 (1)×8	2.5513 (2)×8
Ni-O length (Å)		1.9565(6)×4	1.9602 (1)×4
wRp/Rp (%)		4.41/3.46	4.24/3.34

It is useful to compare the results here with those of Hayward and Rosseinsky on NdNiO_2+x [18] with the caveat that their sample contained no Sr. Similar to the present work, they refined their neutron powder data in space group P4/mmm both at high (290 K) and low temperature (1.7 K). In the case of Hayward’s structural refinement, a molar fraction of 18% was refined (5.2% by mass), which is comparable to our neutron refinement, which yielded mass fractions of 94.6% for Nd_0.9Sr_0.1NiO₂ and 5.4% for the nickel impurity. To improve their fit to the data, Hayward et al. introduced a second phase with apical oxygens located in the Nd layer and significant relaxation of the atomic positions vis-à-vis the stoichiometric phase. We found that satisfactory refinement of our Nd_0.9Sr_0.1NiO₂ data did not necessitate addition of this phase. This may very well relate to the composition, as we expect there to be an increased propensity for interstitial apical oxygens to appear as the nickel oxidation state is reduced towards 1+.

In addition, Hayward et al. observed no evidence of antiferromagnetic ordering. Assuming a G-type antiferromagnetic structure, they estimated an upper limit of 0.06_μB/Ni as their sensitivity limit. The sensitivity of our measurement at 3 K to a hypothetical G-type antiferromagnetic structure is significantly poorer, on the order of 0.5_μB. Thus, neither the parent compound nor the 10% Sr-doped compound shows evidence of magnetic order within these estimated sensitivity limits. When considering the lack of observed antiferromagnetic order within the context of the superconductivity observed in thin films, we note that the strained, epitaxial films may exhibit different intrinsic magnetic behavior.

IV. CONCLUSION

In this work, high-quality bulk polycrystalline Nd_1–xSr_xNiO₃ (x = 0, 0.1, and 0.2) samples have been synthesized using a combined sol-gel combustion and high-pressure annealing technique. The evolution from NdNiO₃ to NdNiO₂ was monitored using in situ synchrotron x-ray diffraction during the reduction process. Nd_1–xSr_xNiO₃ (x = 0.1 and 0.2) samples were reduced to Nd_1–xSr_xNiO₂ (x = 0.1 and 0.2) using calcium hydride in a sealed evacuated tube. Our bulk infinite-layer samples showed no sign of superconductivity, although measurements of the intrinsic resistivity are hampered by loose polycrystalline compaction as well as metallic nickel impurities. Neutron diffraction data of the hole-doped infinite-layer phase could be well fit by a combination of the P4/mmm space group with a nickel impurity. Within the limits of our powder diffraction experiment, no evidence of magnetic ordering down to 3 K was observed.