Improved whole-brain SNR with an integrated high-permittivity material in a head array at 7T

Abstract

Purpose:

To demonstrate that strategic use of materials with high electric permittivity along with integrated head-sized coil arrays can improve SNR in the entire brain.

Methods:

Numerical simulations were used to design a high-permittivity material (HPM) helmet for enhancing SNR throughout the brain in receive arrays of 8 and 28 channels. Then, two 30-channel head coils of identical geometry were constructed: one fitted with a prototype helmet-shaped ceramic HPM helmet, and the second with a helmet-shaped low-permittivity shell, each 8-mm thick. An eight-channel dipole array was used for excitation. In vivo maps of excitation flip angle and SNR were acquired.

Results:

Simulation results showed improvement in transmit efficiency by up to 65% and in receive-side SNR by up to 47% on average through the head with use of an HPM helmet. Experimental results showed that experimental transmit efficiency was improved by approximately 56% at the center of brain, and experimental receive-side SNR (SNR normalized to flip angle) was improved by approximately 21% on average through orthogonal planes through the cerebrum, including at the center of the brain, with the HPM.

Conclusion:

Although HPM is used increasingly to improve transmit efficiency locally in situations in which the transmit coil and imaging volume are much larger than the HPM, here we demonstrate that HPM can also be used to improve transmit efficiency and receive-side SNR throughout the brain by improving performance of a head-sized receive array. This includes the center of the brain, where it is difficult to improve SNR by other means.

1 |. INTRODUCTION

Materials having relative electric permittivity (ε_r) much greater than 1 have been used to modify the magnetic field of RF coils. Typically these materials cause an increase in strength of the RF magnetic field near the high-permittivity material (HPM).^1–4 This has become increasingly common in imaging of brain at 7 T, where inhomogeneity of the RF magnetic field for excitation $\left(B_1^{+}\right)$ is notable. In these cases, HPM pads, often containing a mixture of water and ceramic powder,³ are typically placed against the head adjacent the temporal lobes and/or cerebellum,^3,5 where $B_1^{+}$is relatively weak in head-sized volume coils often used at 7 T. Usually the region where $B_1^{+}$ is enhanced by the HPM is small compared with the volume of the transmit coil. In cases in which the transmit volume coil is used for reception as well, an additional improvement in SNR is expected, due to enhancement of the receive sensitivity $\left(B_1^{-}\right)$ of the coil near the HPM.^1,2 The HPM can be made to resonate to greatly enhance local transmit efficiency and SNR of a large volume coil.⁶

Some studies have shown potential advantages of HPM with one or more surface coils.^7–11 These include simulations and experiments for a wide variety of coil, sample, and HPM combinations, and in many cases show improvement in SNR at a desired region (sometimes at the expense of SNR elsewhere) with placement of an HPM, even if that placement causes the coil to be slightly further from the sample.^7,8 Improvement has been shown for cervical spine imaging using a receive array at 3 T, where the region of interest and HPM are small compared with the array and its individual elements,⁹ and for some regions in a cylindrical sample (at the expense of others) within an HPM shell and cylindrical transceiver array.¹⁰ The SNR was improved selectively in the cortex of brain for an HPM cap within a commercial receive array at 3 T, with adverse effects on the transmit field.¹¹

Here we report numerical simulations and experimental measurements of the effects of HPM encompassing the head on SNR throughout the brain for head-sized receive arrays, as well as on transmit efficiency for different excitation coils, at 7 T. Preliminary reports of much of this work have been shown at scientific meetings.^12–16

2 |. THEORY

The ability for an HPM to improve performance of an RF coil is often explained with reference to Maxwell’s fourth equation, Ampere’s Law, with the addition of the displacement current term:

$$\nabla \times B=\mu \left(J+i\omega {\epsilon }_0{\epsilon }_{\text{r}}E\right)$$ (1)

where B is magnetic flux density; J is conduction current density (J = σE); E is electric field strength; μ is magnetic susceptibility; ε_r is relative electric permittivity; ε₀ is electric permittivity of free space; ω is the Larmor frequency; i is the imaginary unit; and bold font indicates vector quantities. At low frequency and ε_r, displacement current (iωɛ₀ ɛ_rE) is also relatively low, and J in the coil is the main contributor to B in the imaging region. At a sufficiently high ω or with sufficiently high ɛ_r, the displacement current can become a significant contributor to B, such that an HPM in a region of high E between the coil and subject can alter the strength and distribution of B for transmit and/ or receive coils. In regions where B is increased without proportional increase in the square root of dissipated power (P_diss) for a given coil, transmit efficiency and/or SNR can be increased.

3 |. METHODS

Numerical simulations were used to explore effects of an HPM on transmit efficiency in a large encircling array and SNR in an eight-element head coil. Experimental coils with and without an integrated HPM helmet were constructed and compared. Further simulations explored effects of moving coils closer to the head in the absence of HPM, and the effects of the HPM on specific absorption rate (SAR) in arrangements similar to experiment.

3.1 |. Numerical simulations

To evaluate transmit efficiency, a helmet was simulated on an anatomical model of an average adult male¹⁷ within a large (15-cm radius), encircling array of 16 stripline antennas.^12,13 Transmit efficiency $\left(\left|B_1^{+}\right|\surd \sqrt{P_{diss}}\right)$ was mapped throughout the head and averaged over the whole brain. Simulated field distributions of receive coils were used to determine sensitivity distributions and noise correlation matrices to calculate SNR for different arrays.¹⁸ Initial SNR evaluations were applied for head arrays with eight elements.¹⁴ These initial evaluations of transmit efficiency and SNR were performed with helmet ε_r values of 1, 50, 75, 100, 107, 125, 150, 175, and 200. Additional simulations were performed to examine the effects of moving receive coils similar to those in the experiment closer to the head by the thickness of the HPM (ε_r = 107, thickness = 8 mm) in the absence of the HPM, and to examine effects of the HPM on SAR for excitation with a dipole array similar to that used in experiment. All simulations were performed with commercially available software (xFDTD; Remcom, State College, PA). A uniform 5-mm isometric grid was used for all simulations except for the 30-channel receive array, which used a 2-mm grid. In all simulations except with the dipole array, the field for each coil was determined by driving it individually with voltage sources across capacitive gaps, producing a voltage distribution as in ideal resonance, and with gaps in all other coils open. In simulations with the dipole array, dipoles were tuned to 297 MHz by adjusting the value of inductors across the off-center gaps, and simulations driving elements individually were used to determine phases necessary for constructive interference at the center of brain in a subsequent simulation, with all elements driven simultaneously. Figure 1 shows the model geometries for evaluating transmit efficiency with the large 16-element stripline array, SNR in the 8-channel and 30-channel receive arrays, and SAR in the dipole array.

FIGURE 1.

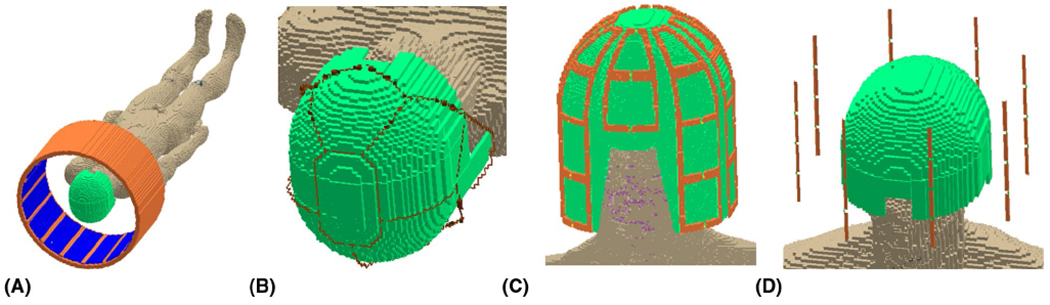
Simulation geometries for 16-element large transmit array used to explore effects of permittivity on transmit efficiency (A), eight-channel receive array used to explore SNR as a function of helmet permittivity (B), 30-channel receive array to explore effects of moving coils closer to head in absence of helmet (C), and eight-channel dipole array for examining effects of specific absorption rate (SAR). (D). Helmet is depicted in light green, and coil elements are depicted in orange

3.2 |. The HPM helmet and coil construction

Two 30-channel receive arrays were built on identical 3D-printed polycarbonate substrates (Fortus 360mc, 21 × 32 × 27 cm³; Stratasys, Rehovot, Israel) designed to closely accommodate helmet-shaped inserts. The HPM helmet array was integrated with a custom ceramic HPM helmet (ε_r = 107 and σ = 0.004 s/m, thickness = 8 mm; HyQRS, State College, PA) that fits tightly into the polycarbonate substrate (Figure 2). The helmet was fabricated from Ba_xSr(_1–x)TiO₃ (0.4 < x < 0.6) powder, in which the Curie temperature was below the ambient operating conditions. The basic formulations were synthesized through a stoichiometric mixture of barium carbonate, strontium carbonate, and rutile. The mixture was calcined at high temperatures (above 1000°C), to decompose the carbonates and react the three components to form a cubic perovskite phase. To create the helmet, phase-pure powder was combined with a binding agent, mixed, pressed at 65 MPa, and heat-treated at a maximum temperature between 1400 and 1500°C for 72 hours per batch. The target ε_r was verified using an established method,¹⁹ and the final structure was machined to geometric tolerances. The second array was fitted with a low-permittivity helmet consisting of a 3D-printed plastic shell with surface geometry identical to the HPM helmet.

FIGURE 2.

Photographs of the three main components of the high-permittivity material (HPM) helmet array. For imaging, the ceramic HPM helmet (left) was placed within the 30-loop receive (Rx) array (middle), which in turn was placed within the 8-dipole transmit (Tx) array. For the array without HPM, a 3D-printed air-filled shell matching the geometry of the HPM helmet was placed within the 30-loop Rx array of identical geometry, but with different capacitor values, which in turn was placed in the same 8-dipole Tx array shown here

The two receive arrays were constructed following a gapped design (Figure 2) previously shown to perform well at 7 T.²⁰ The arrays contain eight rows of two to four coils. Coils were tuned to 297.2 MHz and matched when integrated with the HPM helmet and a tissue-mimicking²¹ head-shaped phantom (ε_r = 65, σ = 0.45S/m) for the HPM helmet array, and when integrated with the air-filled plastic helmet and the same head phantom for the array without HPM. The phantom has dimensions of 14 cm in the left-right direction and 19 cm in the anterior-posterior direction just above the eyebrow, and a distance in the head-foot direction of 20 cm from the chin to the top of the head. The phantom has a neck-like region extending about 9 cm below the chin. Neighboring coils in the head-foot direction were decoupled with geometric overlap, while preamplifier decoupling was used for other coil combinations. One active detuning circuit and one 700-mA fuse were incorporated in each coil to ensure safety. Quality factor (Q) was measured for a representative coil tuned to the same frequency when placed against the side of each helmet, both when unloaded and when loaded with the head phantom.

Excitation was accomplished with an eight-channel dipole array²² surrounding the receive array (Figure 2). Dipoles were tuned and matched in the presence of the head phantom and receive array without HPM. Tuning and decoupling were unaffected by the HPM helmet.

3.3 |. Imaging

Imaging was performed using a whole-body 7T system (MAGNETOM; Siemens Healthineers, Erlangen, Germany) with eight independent transmit amplifiers. Excitation was performed using phase-only $\left(B_1^{+}\right)$ shimming, to achieve constructive interference at a location near the center of brain. All in vivo experiments were performed with approval of our internal review board and informed consent. Maps of $\left(B_1^{+}\right)$ and SNR were acquired using TurboFLASH²³ (TE = 1.9 ms, TR = 10000 ms) and gradient-echo acquisitions (with and without RF excitation, TR = 500 ms, TE = 5 ms, nominal flip angle = 10°). For all images, slice thickness was 5 mm, FOV was 300 mm, matrix was 128 × 128, and bandwidth was 500 Hz/pixel.

4 |. RESULTS

4.1 |. Simulations

When averaged over the whole brain, transmit efficiency for a large encircling array (Figure 3, top) and SNR for the eight-channel head coil (Figure 3, bottom) reached a maximum with a helmet ε_r of 100. Increasing ε_r to 200 resulted in significant reduction of transmit efficiency, especially near the center of brain, and in enhancement of SNR in the cortex but not near the center of brain. With ε_r of 100, use of the helmet resulted in a 65% increase in transmit efficiency and a 47% increase in SNR averaged over the brain. Simulations for the 30-channel head coil showed a 23% increase in SNR at the center of brain and 12.5% average increase in SNR in the brain with use of the HPM helmet, compared with a case with the coils moved closer to the head without HPM (Figure 4, left). For a 1 μT $\left(B_1^{+}\right)$ produced at the center of brain by the dipole array, use of the HPM increased maximum 10-g SAR by 40.0%, decreased head-average SAR by 16.4%, and decreased whole-body SAR by 29.8%. With HPM, the location of maximum 10-g SAR shifted from the frontal lobe to just within the superior surface of brain (Figure 4, right). With the HPM and time-average $\left(B_1^{+}\right)$ of 1 μT at the center of brain, maximum 10-g SAR was 1.88 W/kg and head-average SAR was 0.221 W/kg.

FIGURE 3.

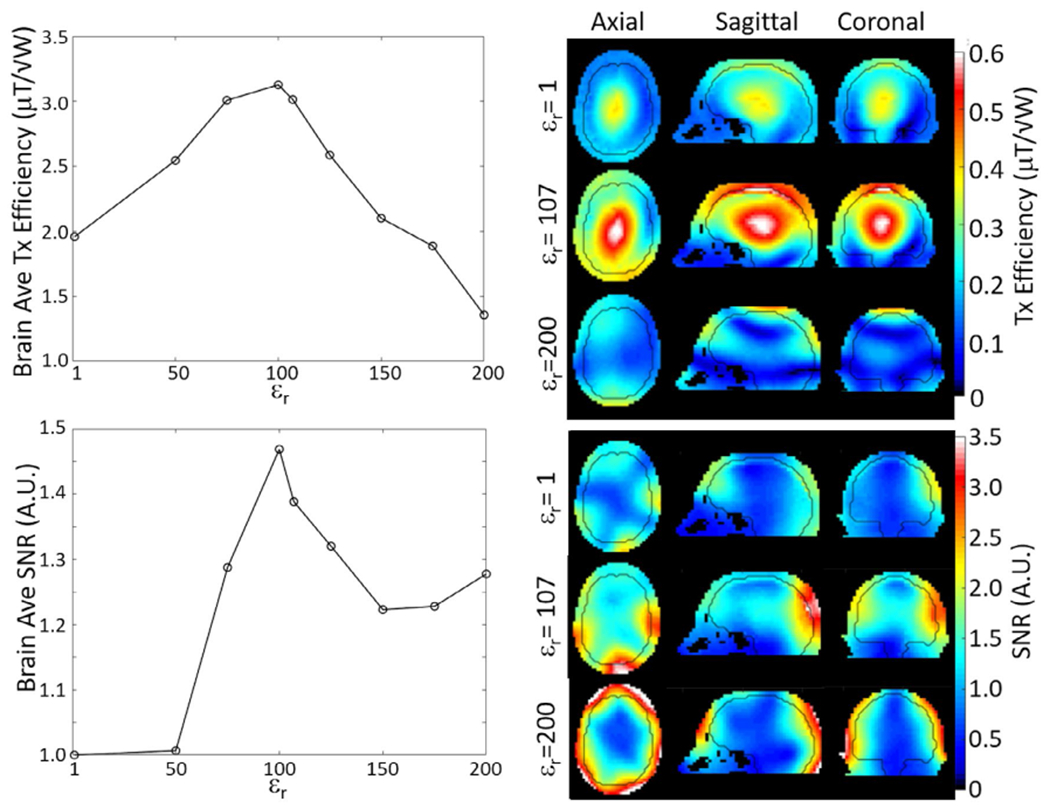
Simulated transmit efficiency (top) and SNR (bottom) averaged over the whole brain (left) and distributed over the three cardinal planes (right) for different helmet permittivities. Nine permittivities are used for line plots of brain average values (left), and three are used in plots of spatial distributions (right). Black contour in the distributions (right) shows the outer surface of the brain

FIGURE 4.

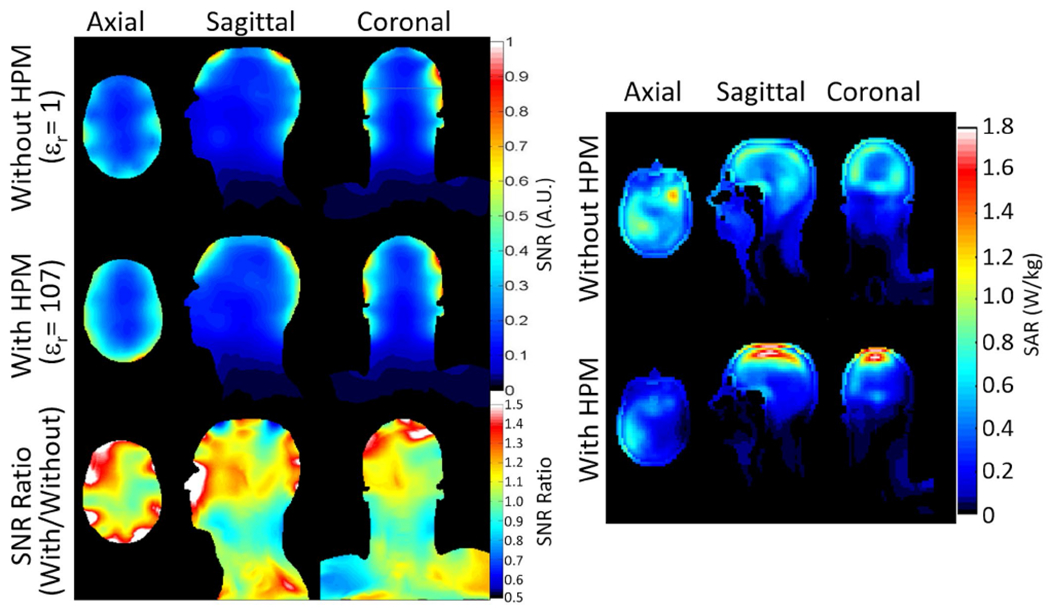
Left: Simulated SNR in a 30-channel array as distributed through the head on three orthogonal planes for 30-channel receive array without HPM and with coils moved closer to the head (top row), with HPM (middle row), and the ratio of SNR with HPM to that without (bottom row). Right: Distribution of 10-g average SAR for 1 μT|$\left(B_1^{+}\right)$| at center of brain for dipole array without (top) and with (bottom) HPM on axial plane through maximum 10-g SAR for case without HPM and on sagittal and coronal planes through maximum 10-g SAR for case with HPM

4.2 |. Bench measurements

For a representative receive coil, the unloaded Q, loaded Q, and capacitance required for tuning were 245, 65 (ratio = 3.8), and 6.8 pF without HPM, and 70, 15 (ratio = 4.7), and 5.6 pF with HPM. All coils were easily tuned and matched both with and without HPM. The average reflection (S₁₁) was approximately −19 dB for elements with and without HPM. The average isolation (S₁₂) between overlapped neighbor elements was −11.1 dB and −11.7 dB for arrays with and without HPM, respectively. Isolation between more distant elements was much better than this on average and was not notably different between arrays with and without HPM. Arrays with and without HPM did not require significantly different coil overlap for geometric decoupling.

4.3 |. Imaging

The HPM helmet improved transmit efficiency ($\left(B_1^{+}\right)$/√P) by approximately 56% at the center of the brain and 55% averaged over the cerebrum in the three planes shown (Figure 5, top). The dipole array with the HPM helmet required a 500-μs, 72.2-V hard pulse to achieve 90° flip angle compared with 121.5-V, 500-μs hard pulse without HPM. The use of the same color scale in cases with and without HPM results in a larger range of colors when the HPM is present, but the relative range of $\left(B_1^{+}\right)$ (more closely related to homogeneity) is similar between the two cases, with the coefficient of variation in |$\left(B_1^{+}\right)$| within brain averaged over the three planes shown being 0.34 with HPM and 0.3 without.

FIGURE 5.

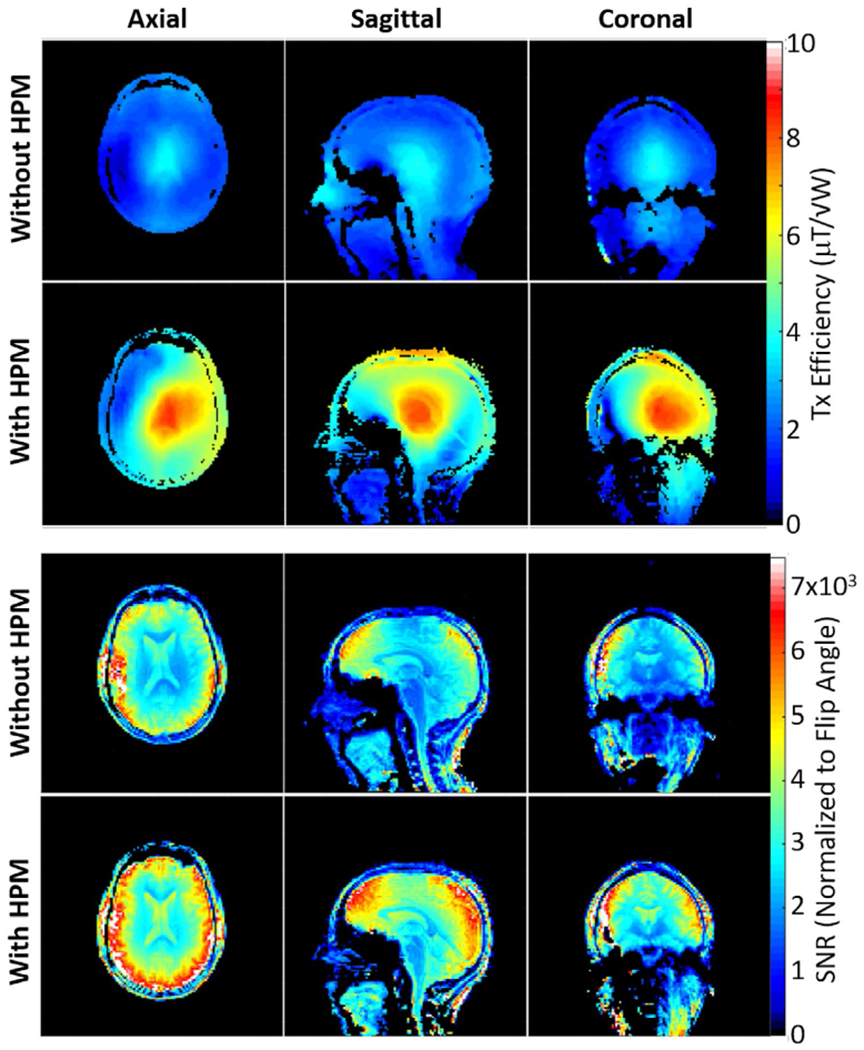
Experimentally acquired maps of Tx efficiency (top) and SNR normalized by the sine of the flip angle (bottom) on three orthogonal planes through the middle of brain, as produced without and with the HPM helmet. The HPM helmet improves the Tx efficiency by 56% and SNR by 20% at the center of the brain

The SNR maps normalized by the sine of the excitation flip angle (approximating SNR specific to the receive array) are presented in Figure 5 (bottom). The HPM helmet improved the receive-array SNR by approximately 20% at the center of brain, and 21% averaged over the cerebrum in the three planes shown.

5 |. DISCUSSION

Both simulations and experiments show that use of an HPM helmet can increase transmit efficiency and receive array SNR throughout brain. Although local HPM pads are typically used to improve signal intensity in targeted regions of otherwise low flip angle, such as the temporal lobes or cerebellum, our encompassing HPM helmet provided both 55% better transmit efficiency and 21% better receive-side SNR, on average, in brain through the three planes shown in Figure 5. Both simulations and the experiment showed significant improvements in the receive-array SNR at the center of the brain, where it is challenging to increase SNR otherwise.²⁴

Although the improvement in transmit efficiency is consistent between experiment and simulations for a similar HPM helmet at 7 T, the SNR improvement achieved experimentally with the 30-channel array did not reach the level in simulations for the eight-channel array or for a 28-channel array.¹⁵ This could be due to a number of differences in configuration between simulation and experiment, such as coil geometry, mutual coupling, and losses. We do not expect that losses in the helmet itself are a significant factor, as simulations with much greater conductivity in the helmet (consistent with a HPM slurry of powder/water mixture rather than the solid ceramic used here) showed minimal effect on the SNR. We expect that coil geometry may be the most significant factor, because simulations with 8-element and 28-element arrays^12,15 showing greater improvement in SNR with use of the HPM having larger individual coils than those in the experimental or simulated 30-channel gapped array used here.

Although homogeneity of the excitation field is slightly worse with HPM than without in these experiments, the significance of this in practice is uncertain, as the RF shimming algorithm used did not attempt to maximize homogeneity, and prior simulations indicated that the presence of the HPM had no adverse effect on achieving homogeneity when that was a goal of the algorithm.¹³

In simulations presented here, the presence of the HPM helmet is associated with an increase in maximum 10-g SAR and a decrease in both head-average SAR and whole-body SAR. In light of both current practices for high-field safety assurance and current safety guidelines, the significance of this on the ability to perform high-SAR sequences with or without the HPM requires further consideration. First, RF shimming algorithms can be designed to constrain maximum local SAR while improving homogeneity,²⁵ and many high-field sites make local SAR their primary measure for ensuring safety, especially when actively performing RF shimming. At the same time, neither the International Electrotechnical Commission nor the Food and Drug Administration recommend limits on local SAR for volume coils, with the International Electrotechnical Commission noting that transmit arrays can be considered volume coils (rather than local coils) when used as such.^26,27 Simulations of temperature with consideration of the relatively high rates of perfusion in brain may help to provide further insight.²⁶

Simulations comparing the effect of the HPM on SNR when coils were moved closer to the head without HPM showed an improvement in SNR with HPM, similar to experiment at the center of brain, but less than in the experiment on average SNR through the brain. Because there is always some electrical insulator between coil conductors and the head, we expect with careful design that it should not be necessary to displace coils by the entire thickness of the HPM in practice.

The mechanism for improvement in transmit efficiency seen here is likely similar to that in other applications, as even the relatively large HPM helmet is much smaller than the 33-cm-diameter transmit array, such that displacement currents in the HPM helmet are significantly closer to the sample. This mechanism cannot as readily explain SNR enhancement by the HPM helmet in the center of the brain. Because the receive array consists of 30 relatively small coils close to the sample, and simulations show that moving these coils closer to the sample in the absence of the helmet does not achieve the SNR enhancement with the helmet in place,¹⁶ a different mechanistic understanding is required. We propose that the displacement current in the helmet associated with each coil be both more distributed than that in the coil and approximate a virtual coil with a larger diameter, such that the effective receive sensitivity for each individual loop extends further into the head, and the combined effect for the coil array is improved sensitivity throughout brain. This understanding of a larger effective coil size is also consistent with the lower unloaded Q and improved Q ratio when the ceramic helmet is present.

A recent experimental study at 3 T showed an HPM cap having ε_r of 1000 or greater within a commercial receive array provided great improvement in receive SNR selectively in the cortex, but with strong adverse distortion of the excitation field,¹¹ similar to results of simulations for a ε_r of 200 shown here (Figure 3). From quasistatic approximations, achieving a similar effect at different frequencies with a given HPM and coil design should require an approximate relationship of ε_r α 1/ ω².^28,29 Extrapolation of results shown here to 128 MHz (3 T) indicate ε_r for optimal whole-brain improvement of transmit efficiency, and receive-array SNR may be closer to 500 or 600, and use of ε_r of 1000 would result in effects like those reported.¹¹

The results presented here show the potential benefit for incorporating HPM into coil design for improving both transmit efficiency and receive array SNR for the entire brain at 7 T. The choices of coil and HPM geometry, and ε_r of the HPM, all depend on the intended use of the array. Although this study includes a first experimental demonstration of advantages of incorporating HPM into a custom head receive array, we expect that further dedicated work in this area will result in further improvements.