A Bayesian dose–response meta-analysis model: A simulations study and application

Abstract

Dose–response models express the effect of different dose or exposure levels on a specific outcome. In meta-analysis, where aggregated-level data is available, dose–response evidence is synthesized using either one-stage or two-stage models in a frequentist setting. We propose a hierarchical dose–response model implemented in a Bayesian framework. We develop our model assuming normal or binomial likelihood and accounting for exposures grouped in clusters. To allow maximum flexibility, the dose–response association is modelled using restricted cubic splines. We implement these models in R using JAGS and we compare our approach to the one-stage dose–response meta-analysis model in a simulation study. We found that the Bayesian dose–response model with binomial likelihood has lower bias than the Bayesian model with normal likelihood and the frequentist one-stage model when studies have small sample size. When the true underlying shape is log–log or half-sigmoid, the performance of all models depends on choosing an appropriate location for the knots. In all other examined situations, all models perform very well and give practically identical results. We also re-analyze the data from 60 randomized controlled trials (15,984 participants) examining the efficacy (response) of various doses of serotonin-specific reuptake inhibitor (SSRI) antidepressant drugs. All models suggest that the dose–response curve increases between zero dose and 30–40 mg of fluoxetine-equivalent dose, and thereafter shows small decline. We draw the same conclusion when we take into account the fact that five different antidepressants have been studied in the included trials. We show that implementation of the hierarchical model in Bayesian framework has similar performance to, but overcomes some of the limitations of the frequentist approach and offers maximum flexibility to accommodate features of the data.

1 Introduction

Dose-response associations examine the effect of different levels of exposure (e.g. levels of smoking or drug doses) on a health outcome.^1,2 In pairwise meta-analysis,^3–5 combining dose–response associations from different studies and settings may lead to more precise and generalizable conclusions.⁶ When aggregate-level data are available from multiple studies, dose–response associations can be synthesized using either a one-stage or two-stage model. The one-stage model is implemented as a linear mixed model, which estimates a dose–response fixed effect and accounts for the heterogeneity by allowing shapes to vary across studies.⁷ In a two-stage model, the dose–response model is fitted first within each study, and then the regression coefficients (or shape characteristics) are synthesized across studies.^8–10

The one-stage model takes into account heterogeneity but provides relevant information via the estimate of a between-studies variance–covariance matrix. The two-stage model employs standard meta-analytical techniques and provides the usual heterogeneity measures, such as I², in case this is of interest. However, to fit non-linear shapes, frequentist implementation of the two-stage model requires multiple dose levels to be reported in each study. For example, if the dose–response curve is assumed to be approximated by a $p$-order polynomial, all studies need to report outcomes for at least $p+1$ dose levels. This situation will result in excluding studies that report $p$ dose levels or fewer levels.

The one-stage and two-stage models are implemented in a frequentist setting, and their performance has been evaluated in simulations and examples.¹¹ Fitting dose–response meta-analysis in a Bayesian framework, in the form of a hierarchical model, is, in our view, highly desirable. Several papers^12,13 have described the advantages of Bayesian evidence synthesis. First, Bayesian models^14,15 can be easily extended to incorporate, for example, study-specific covariates, to combine observational and randomized data, or to deal with multiple outcomes and exposure types. Second, one can employ informative priors for the dose–response shape to reflect expert knowledge or evidence from external data sources. Third, one can easily extend the model to explore the variation in dose–response curves within and across groups of similar exposures or drugs. Finally, probabilistic statements follow naturally as the posterior distributions can be interpreted as the true distributions of quantities of interest as uncertainty about all parameters is incorporated in the results.^16,17

The paper is structured as follow. In Section 2 we present a Bayesian hierarchical dose–response meta-analysis model with normal or binomial likelihood and the cluster-specific dose–response model. The evaluation of the properties of the models follows in Section 3, alongside comparisons with the frequentist model in a simulations study. In Section 4, we re-analyze a dataset of the dose–response association of various doses of antidepressants. Finally, we discuss the strengths and limitations of the model in Section 5.

2 Methods

We introduce a Bayesian hierarchical model for dose–response meta-analysis. We focus on a dichotomous outcome, although the models could easily accommodate continuous outcomes.

2.1 Notation

Table 1 summarizes the notation. Suppose there are $ns$ studies ( $i=1,\mathrm{\hspace{0.17em}}\dots \mathrm{\hspace{0.17em}},\mathrm{ }ns$) and each study has a number of doses $n{d}_i$ ( $j=1,\mathrm{ }\dots ,\mathrm{ }n{d}_i$). Each study reported an empirical estimate of the outcome at each dose level. The doses are denoted by ${\mathrm{ }X}_{ij}$ where the minimum dose $X_{i0}$ is set as the reference level (control group). The observed outcome is expressed as number of events out of total observed or relative treatment effects. The dose-specific number of events is $r_{ij}$ out of a total sample size $n_{ij}$. The estimated change in the outcome from the reference dose $X_{i0}$ to dose $X_{ij}$, summarized for the $n_{ij}$ participants, is indicated by $Y_{ij}$. $Y_{ij}$can be log odds ratio (logOR), log risk ratio (logRR), log hazard ratio (logHR), or any relative treatment effect for continuous outcomes such as mean difference. Relative effects rather than number of events are commonly reported in the context of studying environmental exposures or other exposures examined in observational studies.¹⁸ In this case, the relative effects $Y_{ij}\mathrm{ }$are the estimates from multivariable models adjusted for possible confounding variables. The vector ${\mathit{Y}}_{\mathit{i}}=\left(Y_{i1},\mathrm{ }{Y}_{i2},\mathrm{ }\dots ,\mathrm{ }{Y}_{i(n{d}_i-1)}\right)$ comprises all relative effects, on a natural logarithmic scale, for study $i$.

Table 1.

Notation in aggregated-level data in dose–response meta-analysis.

$i= 1,\dots \mathrm{\hspace{0.17em}},ns$	study id
$j=1,\dots ,n{d}_i$	dose levels in study $i$
$X_{ij}$	dose level $j$ in study $i$
$X_{i0}$	reference dose in study $i$
$r_{ij}$	number of events in dose $j$ within study $i$
$n_{ij}$	sample size in dose $j$ within study $i$
$Y_{ij}$	within study $i$, the relative effect (on a log-scale) of dose $j$ contrasted to the effect in the reference dose ( $X_{i0}$) e.g. log odds ratio
${\mathit{Y}}_{\mathit{i}}=\left(Y_{i1}, Y_{i2},\dots ,Y_{i(n{d}_i-1)}\right)$	vector of all dose-specific (log) relative effects in study $i$
$k=1,\dots p$	number of dose transformations associated with the dose–response shape. For a linear shape $p=1$ and for quadratic and restricted cubic splines $p=2$
$c=1\text{,}2,\dots ,C$	exposure clusters

2.2 Dose–response meta-analysis model

We propose a hierarchical two-level model. In the first level, the dose–response model is fitted within each study assuming either normal (normal dose–response model) or binomial likelihood (binomial dose–response model) for the observed data. In the second level, we synthesize the dose–response regression coefficients across studies. The hierarchical structure allows coefficients to borrow strength across studies, via the exchangeability assumption.

2.2.1 Dose–response model within each study.

Within each study $i$, a multivariate normal distribution is assumed for ${\mathit{Y}}_{\mathit{i}}$

$${\mathit{Y}}_{\mathit{i}}\mathrm{\hspace{0.17em}}\sim \mathrm{\hspace{0.17em}}\mathit{MVN}({\mathit{\Delta }}_{\mathit{i}},\mathrm{ }{\mathit{S}}_{\mathit{i}})$$

where the vector ${\mathit{\Delta }}_{\mathit{i}}=({\delta }_{i1},\dots ,{\delta }_{i(n{d}_i-1)})$ contains the underlying relative effects of dose $X_{ij}$ relative to dose $X_{i0}$. The ( $n{d}_i$−1) $\hspace{0.17em}\times \hspace{0.17em}$( $n{d}_i$−1) variance–covariance matrix ${\mathit{S}}_{\mathit{i}}$ can be estimated assuming a multinomial distribution for the number of events per dose and using the delta-method for large sample sizes.^19,20 For logOR, the elements of ${\mathit{S}}_{\mathit{i}}$ are

$${\widehat{{\mathrm{\sigma }}^2}}_{\mathit{ijm}}=\left\{\begin{array}{c}1/{\mathit{r}}_{\mathit{i}0}+1/{\mathit{t}}_{\mathit{i}0}, \mathrm{if} j\ne m\\ 1/{\mathit{r}}_{\mathit{ij}}\hspace{0.17em}+1/{\mathit{t}}_{\mathit{ij}} + 1/{\mathit{r}}_{\mathit{i}0}+1/{\mathit{t}}_{\mathit{i}0}, \mathrm{if} j=m\end{array}\right.$$

where $t$ refers to the number of non-events and the zero index refers to the quantities in the reference dose. The formula above is suitable when the logORs are estimated from 2 × 2 tables. If the logORs originate from adjusted logistic models from observational studies, then a correction in the correlations between dose strata should be applied to ${\mathit{S}}_{\mathit{i}}$, using the Longnecker and Greenland method^9,10 or the approach suggested by Hamling.²¹

If the data are from a randomized trial and the table of counts is available, it is straightforward to assume a binomial distribution of events

$${\mathit{r}}_{\mathit{ij}}\sim \mathrm{Binomial}\left({\mathit{p}}_{\mathit{ij}},{\mathit{n}}_{\mathit{ij}}\right)$$

where $p_{ij}$ are the underlying probabilities of having an event in dose $j$ within study $i$. Then the underlying relative treatment effects are parametrized as

$$\lambda \left(p_{i0}\right)=u_i$$

$$\mathrm{\lambda }\left({\mathit{p}}_{\mathit{ij}}\right)={\mathit{u}}_{\mathit{i}}+{\mathrm{\delta }}_{\mathit{ij}}$$

with ${\delta }_{ij}$ defined as above. The function $\lambda$is specified based on the effect size we want to estimate; for example, it is the logit function for logOR and the log function for logRR. The parameter $u_i$ is the log-odds of the event in the reference dose level.

Note that continuous outcome data can be accommodated if ${\mathit{Y}}_{\mathit{i}}$ are mean differences or standardized mean differences. Alternatively, if the outcome is available for each dose level, the normal likelihood is used instead of the binomial, and ${\delta }_{ij}$ is parameterized as the mean difference or standardized mean difference.

2.2.2 Dose–response functions.

The underlying relative effect ${\delta }_{ij}$ can be modelled as

$${\delta }_{ij}=f\left(X_{ij};X_{i0};\hspace{0.17em}{\mathit{\beta }}_{\mathit{i}}\right)$$

where $f$ is the dose–response function and ${\mathit{\beta }}_{\mathit{i}}$ are the shape parameters that need to be estimated. Note that the $f$ function could also be any transformation, including linear, quadratic, cubic or fractional polynomials and resulting in ${\mathit{\beta }}_{\mathit{i}}={(\beta }_{ki})$ being a vector of length $p$ and $k=1\text{,}2,\dots ,p$.²² The simplest case is to assume a linear ( $f$ is the identity function) shape $p=1$ where the statistical model needs to estimate only one parameter in study $i$; ${\mathit{\beta }}_{\mathit{i}}={\beta }_i$ and ${\delta }_{ij}=f\left(X_{ij};X_{i0};\hspace{0.17em}{\beta }_i\right)={{\beta }_i(X}_{ij}-X_{i0})$. However, investigating dose–response relations underlying several studies may require non-linear models.²³ A flexible choice is using restricted cubic splines.²⁴ With $m$ knots, there are $p=m-1$ regression coefficients in ${\mathit{\beta }}_{\mathit{i}}$ to be estimated. Setting $m=3$ (say $k_1, k_2, k_3$), will result into $f$ consisting of $p=2$ dose-transformations; $f_1$ is the identity function and $f_2$ is the restricted cubic spline transformation²⁴ with coefficients ${\mathit{\beta }}_{\mathit{i}}=({\beta }_{1i},{\beta }_{2i})$.

$${\mathrm{\delta }}_{\mathit{ij}}={{\mathrm{\beta }}_{1\mathit{i}}\left\{{\mathit{f}}_1\right({\mathit{X}}_{\mathit{ij}})-{{\mathit{f}}_1(\mathrm{X}}_{\mathit{i}0})\}+\mathrm{\beta }}_{2\mathit{i}}\mathrm{\hspace{0.17em}}\left\{{\mathit{f}}_2\right({\mathit{X}}_{\mathit{ij}})-{{\mathit{f}}_2(\mathit{X}}_{\mathit{i}0})\}$$

where

$${\mathit{f}}_1\left({\mathit{X}}_{\mathit{ij}}\right)={\mathit{X}}_{\mathit{ij}},$$

and

$${\mathit{f}}_2\left({\mathit{X}}_{\mathit{ij}}\right)=\frac{{{(\mathit{X}}_{\mathit{ij}}-{\mathit{k}}_1)}_{+}^3-\frac{{\mathit{k}}_3-{\mathit{k}}_1}{{\mathit{k}}_3-{\mathit{k}}_2}{{(\mathit{X}}_{\mathit{ij}}-{\mathit{k}}_2)}_{+}^3+\frac{{\mathit{k}}_2-{\mathit{k}}_1}{{\mathit{k}}_3-{\mathit{k}}_2}{{(\mathit{X}}_{\mathit{ij}}-{\mathit{k}}_3)}_{+}^3}{{\left({\mathit{k}}_3-{\mathit{k}}_1\right)}^2}$$

with ${\left(x\right)}_{+}=x \mathrm{if} x>0$and 0 otherwise.

The total number and location of knots should be identical for all studies, when ${\mathrm{ }\mathit{\beta }}_{\mathit{i}}$ are to be pooled. To set the location of knots, Harrell suggests to use fixed sample quantiles. With three knots, we set them at the 10%, 50% and 90% percentiles of the observed dose range (see Section 2.4 in Harrell²⁴). It has been shown that the location of knots in restricted cubic spline is not very critical in most situations as Stone found in a series of simulations.²⁵ However, we further examine this issue in our simulations study.

2.2.3 Synthesize dose–response functions across studies.

In dose–response meta-analysis, the study-specific regression coefficients ${\mathit{\beta }}_{\mathit{i}}=({\beta }_{1i},{\beta }_{2i},\dots {\beta }_{2p})$ can then be synthesized. Random dose–response coefficients model assumes that the underlying study-specific coefficients ${\mathit{\beta }}_{\mathit{i}}$ are normally distributed with mean $\mathit{B}=(B_1,B_2,\dots B_p)$ and variance–covariance matrix, $\mathit{\Sigma },$ that is

$${\mathrm{ }\mathit{\beta }}_{\mathit{i}}\sim \mathit{MVN}(\mathit{B},\mathit{\Sigma })$$

This model acknowledges the presence of a distribution of true dose–response relationships underlying the studies and is capable of predicting study-specific curves by borrowing strength from their variation across studies. $\mathit{\Sigma }$ is a $p\times p$ variance-covariance matrix with diagonal elements ${\tau }_p^2\mathrm{ }$and in the off-diagonal there are the $p-1$ covariances between the coefficients. To improve estimation, we will assume that ${\tau }_p^2={\tau }^2\mathrm{ }$and we will explore whether the correlations $\rho$ in $\Sigma$ are different from zero. Note that this model assumes that the heterogeneity across the study-specific estimates is fully captured by heterogeneity in the dose–response shapes. For a model with a common dose–response coefficient we set ${\mathit{\beta }}_{\mathit{i}}=\mathit{B}$.

Note that for studies with ${nd}_i<p+1$, ${\mathit{\beta }}_{\mathit{i}}$ is not identifiable. However, because of the exchangeability (or equality) of ${\mathit{\beta }}_{\mathit{i}}$ across studies, we are able to estimate them.

2.3 Dose–response meta-analysis model accounting for clustering in the exposure

Consider an exposure (or drug) variable that can take on different values. For example, daily intake of omega 3 fatty acids in relation to risk of cardiovascular events, possibly accounting for the different assessment of omega 3 (food supplements versus diet with fish and nuts). The differences between these two dose–response curves can be modelled by inserting type-specific regression coefficients ${\mathit{\beta }}_{\mathit{i}}^{\mathit{c}}=({\beta }_{1i}^c,{\beta }_{2i}^c,\dots {\beta }_{pi}^c)$, where

$$c=\left\{1:\mathrm{food}\mathrm{ }\mathrm{supplements},\mathrm{ }2:\mathrm{diet}\mathrm{ }\mathrm{with}\mathrm{ }\mathrm{fish}\mathrm{ }\mathrm{and}\mathrm{ }\mathrm{nuts}\right\}.$$

Overall, for a random of exposure clusters $c=1\text{,}2,\dots ,C$ the relative effects are mapped to the transformed dose as

$${\mathit{\delta }}_{\mathit{ij}}=\mathit{f}\left({\mathit{X}}_{\mathit{ij}};{\mathit{X}}_{\mathit{i}0};{\mathit{\beta }}_{\mathit{i}}^{\mathit{c}}\right)$$

Next, ${\mathit{\beta }}_{\mathit{i}}^{\mathit{c}},$ the vectors of coefficients from study $i$ examining the same cluster of exposures, are synthesized using a multivariate normal distribution with a common mean ${\mathit{B}}^{\mathit{c}}=(B_1^c,B_2^c,\dots B_p^c)\mathrm{ }$and variance–covariance matrix ${\mathit{\Sigma }}^{\mathit{within}}$; that is a $p\times p\mathrm{ }$matrix with diagonal ${\tau }_{\mathrm{within}}^2$ and on the off-diagonal the $p-1$ covariances between the coefficients

$${\mathit{\beta }}_{\mathit{i}}^{\mathit{c}}\sim \mathit{MVN}\left({\mathit{B}}^{\mathit{c}},{\mathit{\Sigma }}^{\mathit{within}}\mathrm{ }\right)$$

At the next step, the cluster-specific dose–response associations ${\mathit{B}}^{\mathit{c}}$are synthesized across the $C$ clusters. Again, a multivariate normal distribution with mean vector $\mathit{B}$ and variance–covariance matrix ${\mathit{\Sigma }}^{\mathit{between}}$is employed. ${\mathit{\Sigma }}^{\mathit{between}}$ has the same dimension as ${\mathit{\Sigma }}^{\mathit{within}}$ and in the diagonal the parameter ${\tau }_{\mathit{between}}^2$ measures the heterogeneity between the clusters

$${\mathit{B}}^{\mathit{c}}\sim \mathit{MVN}\left(\mathit{B},{\mathit{\Sigma }}^{\mathit{between}}\mathrm{ }\right)$$

2.4 Predicting an absolute mean response to a dose

Once the data are synthesized and the dose–response parameters are estimated, we can predict the absolute mean response for any dose within the range of studied dose levels. These predictions are straightforward within a Bayesian model as the total uncertainty in the parameters is propagated in the final predictions. Assume there is a natural reference dose, such as a dose zero or no-exposure (baseline dose). The observations $r_{i0},n_{i0}$ from the zero dose levels can be parametrized to estimate an average summary response to zero-dose $R_0$

$${\mathit{r}}_{\mathit{i}0}\sim \mathrm{Binomial}\left({\mathit{p}}_{\mathit{i}0},{\mathit{n}}_{\mathit{i}0}\right),$$

$$\mathrm{\lambda }\left({\mathit{p}}_{\mathit{i}0}\right)\sim \mathit{N}\left({\mathit{R}}_0,{\mathrm{\sigma }}_0^2\right)$$

Then, the estimated common baseline mean effect $R_0$ (measured on the log or logit probability scale) can be combined with $\mathit{B}$ to obtain the predicted absolute response to any given dose level $X_j$

$${\mathrm{\lambda }}^{-1}\left\{{{\mathit{B}}_1\left\{{\mathit{f}}_1\right({\mathit{X}}_{\mathrm{j}})-{{\mathit{f}}_1(\mathit{X}}_0)\}+\mathit{B}}_2\left\{{\mathit{f}}_2\right({\mathit{X}}_{\mathit{j}})-{{\mathit{f}}_2(\mathit{X}}_0)\}+{\mathit{R}}_0\right\}$$

2.5 Bayesian estimation

We will use Markov chain Monte Carlo (MCMC) techniques to estimate all parameters in a Bayesian setting. An approximate non-informative prior distribution is chosen for the coefficients and the baseline effects $u_{i0}=\mathrm{logit }\left(p_{i0}\right)$ in the binomial model

$${\mathit{B}}_{\mathit{k}}\sim \mathit{N}\left(0,{10}^3\right)$$

$${\mathrm{u}}_{\mathit{i}0}\sim \mathit{N}\left(0,{10}^3\right)$$

Given that both in the simulations and in the example our outcome is dichotomous and measured on the natural log scale, we place a half-normal prior to the heterogeneity parameter

$$\mathrm{\tau }\sim {\mathrm{N}}_0\left(0\text{,\hspace{0.17em}}1\right)$$

This heterogeneity prior is minimally informative in most cases as ORs rarely exceed 5 and hence the underlying values of $B_k$’s should not often exceed |0.2|.

For correlations $\rho$ in the off-diagonal of the variance–covariance matrices, we use a uniform prior

$$\mathrm{\rho }\sim \mathrm{Unif}(-1\text{,\hspace{0.17em}}1)$$

All Bayesian models are implemented in JAGS within R.^26,27 The codes can be found in GitHub at https://github.com/htx-r/DoseResponsePMA. To obtain the spline transformations, we use the rcs function from the rms package.²⁸ To evaluate the convergence of the models, we employed various diagnostic tools for MCMC included in the coda package.²⁹ We explored convergence plots for the MCMC (histograms, trace plots, Geweke plot and Gelman-Rubin plot) and relevant statistics (Raftery and Lewis statistic and Heidelberger and Welch test).³⁰

3 Simulations study

We aim to investigate the agreement between the estimations of the dose–response meta-analysis curve under our two Bayesian models, assuming random-effects for the coefficients, and the frequentist one-stage model.³¹ The codes are available in GitHub.

3.1 Simulation design

We investigated the performance of the three models assuming that the true dose–response function is curvilinear (setting 1), half-sigmoid or log–log (setting 2). Characteristics of the simulated settings are summarized in Table 2.

Table 2.

Description of simulation settings.

Characteristics of the dose–response curve	Function form	Effect size	Number of studies	${\mathrm{\beta }}_1,\mathrm{ }{\mathrm{\beta }}_2$	$\mathrm{\tau }$	Knot positions	Dose distribution	Study sample size	Main finding	Results in Figure/Table
1. True dose–response curve as a restricted cubic spline	$\mathrm{logOR}=\mathrm{ }{{\mathrm{\beta }}_1{\mathrm{f}}_1\left({\mathrm{X}}_{\mathrm{ij}}\right)+\mathrm{\beta }}_2{\mathrm{f}}_2\left({\mathrm{X}}_{\mathrm{ij}}\right)$	OR, RR	40	0, 00.04, 00.1, 0.030.2, −0.2	0.0010.01	25%, 50%, 75%	Unif $\left(1\text{,}10\right)$	Unif $\left(180\text{,}220\right)$	The three models give unbiased estimates	Supplementary Appendix Tables 1 to 3 and 7 to 9Supplementary Appendix Figure 2 and 15
2. Other true dose-response forms	$\mathrm{logOR}=\log \left(\log \left({\mathrm{X}}_{\mathrm{ij}}+1\right)+1\right)$ $\mathrm{logOR}=\frac{{\mathrm{X}}_{\mathrm{ij}}}{\sqrt{1+{\mathrm{X}}_{\mathrm{ij}}^2}}$	OR	20	–	–	10%, 50%, 90%at dose 0, 1, 3	Unif $\mathrm{ }\left(1\text{,}10\right)$ ${\mathrm{\chi }}^2\left(2\right)$	Unif $\left(180\text{,}220\right)$	The three models give biased estimates with high uncertainty for quantile knots and unbiased results for knots at 0,1,3	Figure 1 Supplementary Appendix Figure 6
3. Smaller sample size	$\mathrm{logOR}=\mathrm{ }{{\mathrm{\beta }}_1{\mathrm{f}}_1\left({\mathrm{X}}_{\mathrm{ij}}\right)+\mathrm{\beta }}_2{\mathrm{f}}_2\left({\mathrm{X}}_{\mathrm{ij}}\right)$	OR	20	0, 00.04, 00.1, 0.030.2, –0.2	0.0010.01	25%, 50%, 75%	Unif $\left(1\text{,}10\right)$	Unif $\left(20\text{,}100\right)$	The binomial model gives unbiased estimates	Table 3 Supplementary Appendix Tables 4 to 6 Figure 2
4. Fewer trials	$\mathrm{logOR}=\mathrm{ }{{\mathrm{\beta }}_1{\mathrm{f}}_1\left({\mathrm{X}}_{\mathrm{ij}}\right)+\mathrm{\beta }}_2{\mathrm{f}}_2\left({\mathrm{X}}_{\mathrm{ij}}\right)$	OR	816	0.04, 0.03	0.001	25%, 50%, 75%	Unif $\left(1\text{,}10\right)$	Unif $\left(180\text{,}220\right)$	The three models give unbiased estimates	Supplementary Appendix Figure 3
5. Partially overlapping doses	$\mathrm{logOR}=\mathrm{ }{{\mathrm{\beta }}_1{\mathrm{f}}_1\left({\mathrm{X}}_{\mathrm{ij}}\right)+\mathrm{\beta }}_2{\mathrm{f}}_2\left({\mathrm{X}}_{\mathrm{ij}}\right)$	OR	20	0.04, 0.03	0.001	25%, 50%, 75%	Half the studies from Unif $\left(1\text{,}6\right)$ Half the studies from Unif $\left(4\text{,}10\right)$	Unif $\left(180\text{,}220\right)$	The three models give unbiased estimates	Supplementary Appendix Figure 4
6. Discrete doses	$\mathrm{logOR}=\mathrm{ }{{\mathrm{\beta }}_1{\mathrm{f}}_1\left({\mathrm{X}}_{\mathrm{ij}}\right)+\mathrm{\beta }}_2{\mathrm{f}}_2\left({\mathrm{X}}_{\mathrm{ij}}\right)$	OR	20	0.04, 0.03	0.001	25%, 50%, 75%	sample $\left(1\text{,}10\right)$	Unif $\left(180\text{,}220\right)$	The three models give unbiased estimates	Supplementary Appendix Figure 5

Under the assumption of a curvilinear relationship (setting 1), we used restricted cubic splines with three knots at fixed percentiles (25th, 50th, and 75th) of the dose, with shape defined by the spline coefficients. We modelled the logOR and the logRR. For 40 clinical trials, we simulated study-level aggregated data. For each study, we simulated two non-zero doses from uniform distribution $X_{ij}\sim \mathrm{Unif}($1, 10) and assumed each study reported one zero dose. The study-specific coefficients ${\beta }_{i1}$ and ${\beta }_{i2}$ are generated independently from a univariate normal distribution with means $B_1$ and $B_2$, respectively, and a common heterogeneity $\tau$. Values for $B_1$ and $B_2$ were chosen to represent four dose–response shapes: constant (both equal to zero), linear ( $B_2=0)$, monotonic increasing and umbrella-like shape (see supplementary Appendix Figure 1 and Figure 1). We chose non-zero coefficient values that cover a reasonable range for ORs (0.3–5). We introduced between-study heterogeneity, $\tau =0.001,\mathrm{ }0.01$. The assumed mean and heterogeneity values result in eight scenarios, as shown in supplementary Appendix Tables 1 to 3.

Figure 1.

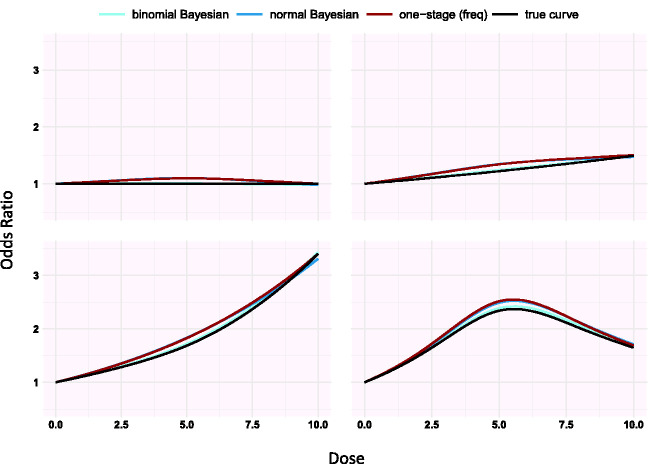
Simulation results from studies with arm sample size generated from Unif(20; 100) (setting 3 in Table 2). True dose–response curves generated from restricted cubic splines (black) along with the three estimated dose–response curves. The panels correspond to scenarios S5–S8 in Table 3.

Using ${\beta }_{1i}$, ${\beta }_{2i}$ and $X_{ij},$we calculated the underlying treatment effect ${\delta }_{ij}=\log O{R}_{ij}={B_1{f}_1\left(X_{ij}\right)+B}_2 f_2\left(X_{ij}\right)$ ( $f_1 \mathit{and} f_2$ are set as explained above in Section 2.2.2). To improve computing time, we assumed that the two shape coefficients ${\beta }_{1i}$ and ${\beta }_{2i}$ are unrelated ( $\rho =0$). Per dose, the observed number of events $r_{ij}$ are generated from binomial distributions with probability $p_{ij}$ and sample size $n_{ij}$. The event rate in the zero-dose group $p_0$is set to 0.1. The underlying event rate at dose $j$ is $p_{ij}=\exp \left({\delta }_{ij}\right)\times p_0$. The sample size per dose is generated from a uniform distribution $n_{ij}\sim \mathrm{Unif}\left(180\text{,}220\right)$. In this way, the number of events and the sample size per dose for each study are generated and used as input for the Bayesian binomial model. Using these counts, we then estimate $\log {\widehat{\mathit{\text{OR}}}}_{ij}$ and their standard errors to use as inputs for the Bayesian normal and frequentist models.³¹

Following the same steps as in logOR above, we simulated the dataset expressing the underlying treatment effect, instead, in terms of risk ratio ${\delta }_{ij}=\log R{R}_{ij}$. The additional concern, particularly for RR, is that we need to confine probabilities within 0 and 1. Therefore, we inserted ${\mathit{maxRR}=\exp \left(\right(B}_k+2\tau )\times \max (f\left(X_{ij}\right)\left)\right)$ and then we set $p_0=0.5/\mathit{maxRR}$. Along with that, we restrict the values of both $p_0$ and $p_1$; $0.05<p_0<0.95$ and $p_1<0.97$, to avoid numerical problems that emerge near the boundaries.

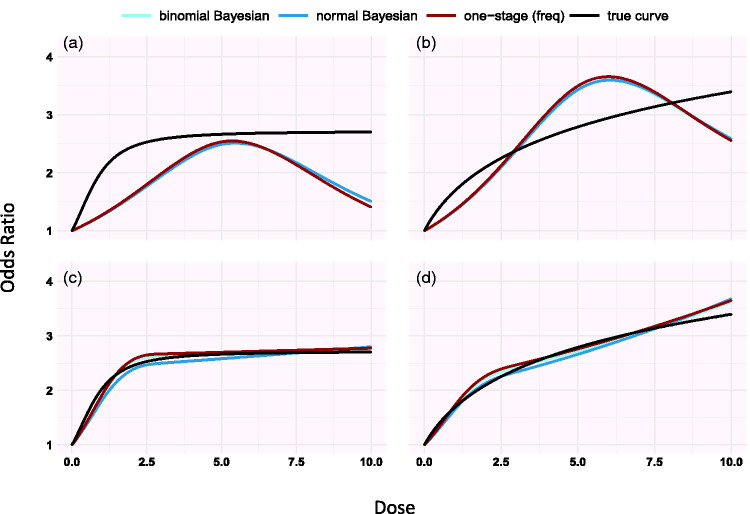
In the second setting (Table 2), we assumed the true shape is log–log ( ${\delta }_{ij}=\log O{R}_{ij}=\log \left(\log \left(X_{ij}+1\right)+1\right)$ and half-sigmoid function ( ${\delta }_{ij}=\log O{R}_{ij}=X_{ij}/\sqrt{1+X_{ij}^2}$). We used two different dose distributions: $X_{ij}\sim \mathrm{Unif}($1, 10) and $X_{ij}\sim {\chi }^2($2). We investigated two different knot positions; at the 10%, 50% and 90% quantiles (1, 5 and 9 for the uniform dose and 0.2, 1.3 and 4.3 for the ${\chi }^2$ distribution) and then at doses 0, 1 and 3 which is where changes in the shape are taking place. This results in eight scenarios for setting 2.

The other four settings in Table 2 result from modifying setting 1. First, we assumed smaller trials by generating the sample size per dose as $n_{ij}\sim \mathrm{Unif}(20, 100)$. Second, we assumed fewer trials; $ns=8 \text{or} 16$. Third, we explored the case of having partially overlapping dose levels across trials, by generating the doses in half of studies from $\mathrm{Unif}(1, 6)$ and the other half from $\mathrm{Unif}(4, 10)$. Finally, we consider the case where doses are discrete by sampling from a list of integer values.

The Bayesian models were estimated using 1× ${10}^5$ iterations with three chains, with a burn-in of 1× ${10}^4$ and a thinning of one. Given that the simulated data was produced assuming $\rho =0$, we did not use bivariate distributions but two independent distributions for ${\beta }_{1i}$ and ${\beta }_{2i}$. Each scenario was studied in 1000 simulations. We used the dosresmeta command to fit the frequentist model.³²

For each method, we estimated the mean bias in the regression coefficients $B_1$and $B_2$ and $\tau$ as the difference between the true coefficient and the corresponding mean estimated value. We computed the mean squared error (MSE) as the sum of the squared bias and the variance of the estimates to quantify the variation in sample estimates. As graphical output is difficult to monitor in a simulation study, the convergence of the MCMC was quantified here only by computing the Gelman statistics $\sqrt{\widehat{R}}$; when $\sqrt{\hspace{0.17em}\widehat{R}\mathrm{\hspace{0.17em}}^\mathrm{\hspace{0.17em}}}\approx 1$ the MCMC converges. Additionally, we report the coverage for each estimate as the proportion of credible intervals that captured the true value. We computed the power to detect $B_k\ne 0$ when the estimated credible interval does not include zero and the mean of the coefficients’ standard error (SE2mean). Finally, we report the Monte Carlo standard error (MCse) to quantify the uncertainty of all the quantities presented above. We present the results from OR for bias and MSE in the main text, whereas the remaining results are presented in the supplementary Appendix.

3.2 Simulation results

3.2.1 Setting 1.

Supplementary Appendix Tables 1 to 3 present the results from the eight scenarios of the first setting for logORs using splines. Supplementary Appendix Figure 2 shows the average estimated curves for scenarios 2 to 4 (results from scenarios 6 to 8 provide similar conclusions to those in supplementary Appendix Figure 2; scenarios 1 and 5 refer to no dose–response association and are not presented in the figure). The three estimated dose–response lines are indistinguishable and all three models perform very well (supplementary Appendix Tables 1 to 3). The binomial Bayesian model has a slightly lower bias in the coefficients than the normal Bayesian and the frequentist approach in all scenarios. The spline coefficients $B_2$ exhibit more bias and are less accurate than those of $B_1$. For both binomial and normal Bayesian models, larger heterogeneity $\tau =0.01$ resulted in less bias than when $\tau =0.001$. The coverage of all estimates exceeds 90%. The power to detect a nonzero linear coefficient $B_1$ ranges between 85% and 93% when $B_1=0.04$ and 100% for $B_1=0.2$. The power to detect a non-linear association ranges between 20% and 28% when $B_2=0.03$ and is 100% when $B_2=$−0.2. The MCMC converged in all simulations as $\sqrt{\widehat{R}}<1.015$. Finally, the largest MCse of bias is $9{\times 10}^{-4}$. The results for logRR agree with the ones based on logOR and are presented in supplementary Appendix Figure 15 and supplementary Appendix Tables 7 to 9.

3.2.2 Setting 2.

Simulating under different shapes, we found that estimations from the three models improves when knots are placed in dose ranges where the risk changes a lot compared to when we set knots at 10%, 50% and 90% percentiles as suggested by Harrell²⁴ (see Figure 1 and supplementary Appendix Figure 6).

3.2.3 Setting 3.

Modifications of setting 1 resulted in similar very good performance of all three models, with one exception. We found that the binomial Bayesian model gives less biased dose–response curve estimates compared with the normal Bayesian and frequentist models (see Table 3, Figure 1, and supplementary Appendix Tables 4 to 6).

Table 3.

Simulations scenarios in setting 3 in Table 2 for a spline dose–response association assuming random effects for ${\mathrm{B}}_1,\mathrm{ }{\mathrm{ }\mathrm{B}}_2$.

(a) Estimated $B_1$
	True values			Binomial Bayesian		Normal Bayesian		One-stage (frequentist)
Scenario	$\tau$	$B_1$	$B_2$	Bias	MSE	Bias	MSE	Bias	MSE
S1	0.001	0	0	2.1	0	23.7	0	22.0	0
S2	0.001	0.04	0	1.7	0	21.4	0	20.1	0
S3	0.001	0.1	0.03	2.1	0	20.3	0	18.9	0
S4	0.001	0.2	−0.2	3.9	0	13.4	0.01	17.2	0.01
S5	0.01	0	0	2.2	0	24.7	0	23.1	0
S6	0.01	0.04	0	4.3	0.01	24.6	0.01	23.3	0.01
S7	0.01	0.1	0.03	4.5	0.01	21.7	0.01	20.2	0.01
S8	0.01	0.2	−0.2	4.2	0	14.5	0.01	17.6	0.01
(b) Estimated $B_2$
	True values			Binomial Bayesian		Normal Bayesian		One-stage (frequentist)
Scenario	$\tau$	$B_1$	$B_2$	Bias	MSE	Bias	MSE	Bias	MSE
S1	0.001	0	0	−7.5	6.0	−35.8	7.0	−30.1	7.5
S2	0.001	0.04	0	−2.5	5.2	−31.0	6.3	−27.0	7.2
S3	0.001	0.1	0.03	2.2	4.4	−28.3	5.8	−22.6	6.2
S4	0.001	0.2	−0.2	−3.2	3.6	−12.2	4.5	−19.6	5.2
S5	0.01	0	0	−5.7	6.0	−35.7	6.9	−30.7	7.8
S6	0.01	0.04	0	−5.9	6.3	−34.5	7.8	−29.8	9.0
S7	0.01	0.1	0.03	−4.7	4.8	−32.6	6.6	−26.9	6.7
S8	0.01	0.2	−0.2	−2.3	4.3	−14.4	5.5	−20.4	6.3
(c) Estimated $\tau$
	True values			Binomial Bayesian		Normal Bayesian
Scenario	$\tau$	$B_1$	$B_2$	Bias	MSE	Bias	MSE
S1	0.001	0	0	32.7	1.2	37.3	1.7
S2	0.001	0.04	0	32.0	1.2	38.0	1.8
S3	0.001	0.1	0.03	28.7	1.0	36.7	1.7
S4	0.001	0.2	−0.2	28.4	0.9	37.0	1.8
S5	0.01	0	0	25.5	0.9	30.5	1.3
S6	0.01	0.04	0	22.7	0.7	30.1	1.3
S7	0.01	0.1	0.03	20.1	0.5	28.8	1.2
S8	0.01	0.2	−0.2	21.2	0.6	29.9	1.4

Note: We assume 20 trials reporting aggregated-level data with three dose-levels each where the sample size is generated from $\mathrm{Unif}(20,\mathrm{ }100)$. The bias and MSE are reported for linear coefficient, spline coefficient and their common heterogeneity (a) ${\mathrm{B}}_1$ (b) ${\mathrm{B}}_2$ (c) $\mathrm{\tau }$, respectively. Bias and MSE are divided by ${10}^3$.

Figure 2.

Simulation results for the half-sigmoid model (panels a, c) and the log-log dose model (panels b, d) estimated using restricted cubic splines (setting 2 in Table 2). Knots are placed in 10%, 50% and 90% quantiles in panels a and b and at doses 0, 1, 3 in panels c and d. The doses are generated from Unif(0, 10).

Overall, the spline coefficients $B_2$ are more biased and less accurate than those of $B_1$. For both binomial and normal Bayesian models, heterogeneity was estimated with considerably more bias than in setting 1 where larger studies have been synthesized (see Table 3 and supplementary Appendix Tables 4 to 6).

Additional results from setting 3 are presented in supplementary Appendix Tables 4 to 6. The coverage of all estimates exceeds 87%; coverage with the binomial Bayesian model is slightly larger than with the normal likelihood models. The power to detect a nonzero linear coefficient $B_1$ ranges from 21% to 40% when $B_1=0.04$ and is 100% for $B_1=0.2$. The power to detect a non-linear association ranges from 4.5% to 7.6% when $B_2=0.03$ and from 85% to 88% when $B_2=-0.2$. The convergence of MCMC is achieved in all simulations as $\sqrt{\widehat{R}}<1.02$. Finally, the largest MCse of bias is $2.6{\times 10}^{-3}$.

3.2.4 Settings 4–6.

In settings 4, 5 and 6, the three estimated dose–response curves are indistinguishable and unbiased, see supplementary Appendix Figures 3 to 5.

4 Dose–response for antidepressants in major depression

We illustrate the methods by synthesizing the dose–response association reported in 60 randomized controlled trials (145 arms, 15,174 participants) examining the efficacy and tolerability of various doses of serotonin-specific reuptake inhibitor (SSRI) antidepressant drugs.³³ Using a previously validated formula, we first transformed the dosages of the different antidepressants into fluoxetine-equivalents.³³ The response to antidepressant is defined as 50% reduction in symptoms. We estimated the dose–response relationship using restricted cubic spline with three knots placed at fixed percentiles of the dose: 10, 20, and 50 mg/day.

The results are displayed in Table 4 and the dose–response curves based on the three approaches are shown in supplementary Appendix Figure 17. The estimated correlation indicates a substantial uncertainty. The two Bayesian models agree to a large extent with the frequentist approach in the estimated linear and spline coefficients and in the precision of the estimations, as shown in results in Table 4. There are immaterial differences between the frequentist and the Bayesian models in the estimation of heterogeneity and correlation $\rho$; the latter is estimated with large uncertainty in Bayesian models.

Table 4.

Dose–response between antidepressants and response to drug.

	Binomial Bayesian		Normal Bayesian		One-stage (frequentist)		Binomial Bayesian with drug clusters
	Mean	SD	Mean	SD	Mean	SE	Mean	SD
$B_1$	0.0214	0.0024	0.0210	0.0037	0.0209	0.0025	0.0213	0.0036
$B_2$	−0.0397	0.0070	−0.0396	0.0085	−0.0376	0.0060	−0.0387	0.0079
$\tau$	0.0087	0.0028	0.0072	0.0031	${\tau }_1=0.0103 {\tau }_2=0.0115$	–	${\tau }_{\mathrm{within}}=$0.0076  ${\tau }_{\mathrm{between}}=0.0050$	0.0028 0.0040
$\rho$	−0.4782	0.4952	−0.2488	0.5652	−1	–	${\rho }_{\mathrm{within}}=-0.3611 {\rho }_{\mathrm{between}}=-0.1064$	0.5153  $0.5508$

Note: Dose is measured as fluoxetine-equivalent in mg/day. The model is fitted with restricted cubic splines and assuming random dose–response coefficients.

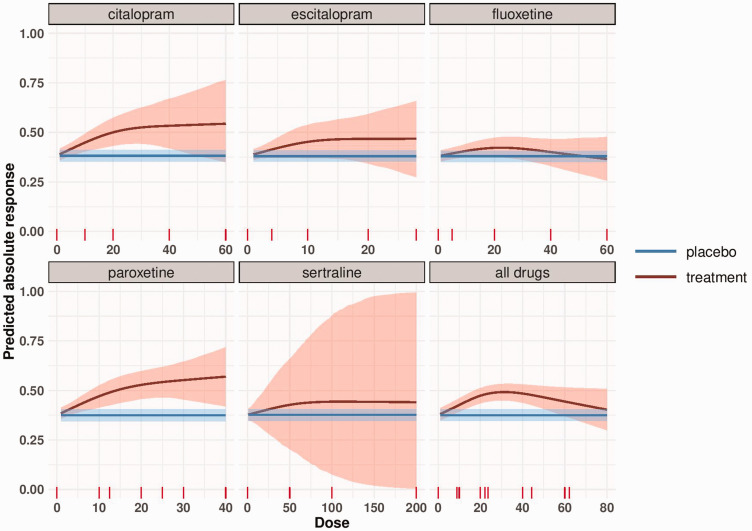
In Figure 3 we present the absolute response using the binomial Bayesian model. The response in the placebo arm was estimated at 37.6% (blue line in Figure 3). We conducted a meta-analysis to synthesize evidence from studies of each drug separately, and we also present the absolute response for all drugs together. The precision in the dose–response curve is high for lower doses and increases for higher doses, as less data are available.

Figure 3.

Dose–response meta-analysis of each SSRI and meta-analysis of all drugs with transformed doses (to fluoxetine-equivalent). The blue line represents the response to placebo as obtained by a meta-analysis of all placebo-arms and its 95% credible region. The red line depicts the absolute response to each antidepressant by dose estimated using the binomial Bayesian model. The shaded area represents the 95% credible region around the absolute dose–response curve.

We also fit the clustered dose–response model where studies have first been synthesized within drugs and then across drugs using the binomial likelihood. The coefficients $B_1, B_2$ were very similar to those estimated from the model that ignores clusters (see Table 4). The within-drug variance ${\tau }_{\mathit{within}}$was estimated 0.0076, a bit smaller than the total heterogeneity from the binomial model ( $\tau =0.0087)$. There were some differences between the eight drugs as indicated from the ${\tau }_{\mathrm{between}}=0.0050$. However, the dose–response shape is practically identical to that of the model that ignores the drug clustering. Finally, the within and between cluster correlations are estimated with large uncertainty like in all models.

We examined the convergence of MCMC for all Bayesian models. Overall, convergence is achieved for all the estimated parameters of the three models, see supplementary Appendix Tables 11 to 16 and supplementary Appendix Figures 18 to 30.

5 Discussion

In this paper, we present a hierarchical dose–response meta-analysis model in a Bayesian framework. At the first level, the dose–response relationship is fitted within each study. Then the curves are combined to get the average dose–response. An additional pooling level can be added, if there are different clusters of exposure or drugs. The exact likelihood of the outcome (binomial or normal) can be employed if arm-level data is available.

We performed extensive simulations under different scenarios, in the majority of which the three tested models (binomial Bayesian, normal Bayesian and one-stage frequentist model) perform equally well and provide unbiased results. When the study sample size is small, we showed that the binomial Bayesian model performs better than the Bayesian or frequentist models that use normal likelihood. This is to be expected because with small sample size the observed logORs are poorly approximated by the normal distribution. One could use a logistic regression to model dose–response within a study; that would provide results equivalent to the binomial Bayesian approach. However, to the best of our knowledge, this approach has not been implemented in any frequentist software. When restricted cubic splines are used to model the association, we showed that prior knowledge about the underlying dose–response shape can direct the choice of the knot location and improve estimation.

Some articles have previously described methods for dose–response meta-analyses.^7,8,11,34,35 Langford et al. proposed four methods to conduct dose–response meta-analysis in a frequentist setting.³⁴ The first two methods focus on the synthesis of arm-level responses which is undesirable in a meta-analysis context, in particular when randomized trials are synthesized. Method 3 is a one-stage approach; the contrasts between the arms are treated as observations to fit the dose–response curve using weighted least squares. Method 4 is a two-stage approach. In the first stage, all possible dose contrasts and their variances are estimated using network meta-analysis (where doses are placed in the network nodes). In the second stage, the obtained dose-specific estimates are used to fit the dose–response curve. Although Methods 3 and 4 are proposed to conduct the analysis based on contrasts, they ignore the correlations between them.

Wu et al. proposed a Bayesian hierarchical dose–response meta-analysis approach.³⁵ The approach aimed to examine the effects of various drugs extracted from living organism (biologics). The analysis was conducted assuming Emax and linear dose–response shapes. Such shapes are common in dose-findings trials. Our approach is, however, more general, in the sense that it can accommodate any dose–response shape. Our approach, additionally, considers both random- and common-effect models, whereas only the latter is considered by Wu et al. Allowing for heterogeneity between studies can be crucial as illustrated by Shi et al. who showed that the associations between breast cancer and alcohol consumption gets substantially weaker when the heterogeneity is incorporated in the model.³⁶

Among the limitations common to all Bayesian approaches, two are particularly challenging for our model.^12,17 First, for some scenarios, the estimation can be sensitive to the prior choice.³⁷ In these cases, sensitivity analysis is recommended with either different prior distributions or by varying the characteristics (hyperparameters) of the specific prior distribution. This is particularly important for the heterogeneity parameter when we have few studies or dose levels.³⁷ Second, time-consuming, intensive computation may be required until MCMC convergence is achieved. In this context, we emphasize the importance of investigating the convergence of MCMC using CODA approaches (e.g. as those presented in our supplementary Appendix). Furthermore, the usual challenges of dose–response meta-analysis apply, including ambiguity in the categorization of the exposure, and the reporting of different categories by different studies or of open-ended categories.³⁸ These issues are discussed in detail elsewhere.¹⁸ Finally, important considerations are to be made, that are specific to the data and context, when the (often continuous) dose has been categorized.³⁹

Simulations under a half-sigmoid and log–log dose–response shape revealed that an agnostic placement of the knots (e.g. in quantiles) might lead to biased and very imprecise estimation. Govindarajulu et al. also showed that restricted cubic splines can’t always capture the true shape.⁴⁰ Restricted cubic splines can perform poorly when most of the change in response is occurring in a narrow exposure interval and knots are located far away from it. In such scenario, subject-matter knowledge can inform the generation of restricted cubic splines by placing the knots where the investigator can anticipate most of the effect to occur, while keeping constant the number of parameters to be estimated. In meta-analysis of dose–response, investigators often know or suspect the underlying dose–response shape or at least the range of doses where the outcome is changing a lot. This should be incorporated in the assumed shape of the modelled dose–response association (e.g. by choosing a piecewise constant) or by locating the knots where changes are expected. In our example of antidepressants, psychiatrists would be interested about the shape in doses lower than 50 mg fluoxetine-equivalent and changes in response are expected to occur between 20 and 40 mg (the minimum therapeutic dose). Therefore, knots have to be placed at these dosages.

A strength of our Bayesian approach is its flexibility. We were able to evaluate whether studies that examine the same drug are more similar than studies examining different drugs by using an extension of our model that adds a layer in the hierarchy according to the specific kind of antidepressant that was studied. We were also able to estimate the absolute response to each dose. Such estimates can also be obtained in a frequentist setting by using best linear unbiased prediction (BULPs) in mixed models.^41,42 However, the process is easier in a Bayesian framework, which also allows the use of external data to estimate the outcome at zero dose. The approach will be particularly valuable in the context of policy- and decision-making where the absolute event rates play a more important role than the relative treatment effects.

The hierarchical structure of the model allows the borrowing of strength across studies.¹⁴ Studies that report only one dose-specific effect can thus be included and a nonlinear dose–response model fitted. This is also possible in a frequentist setting using the one-stage approach; however, our model can be extended to separate between the heterogeneity due to variability in dose–response shape and residual between-study heterogeneity. The latter can be explored by including covariates that may explain this residual variability, which could lead to a dose–response meta-regression. Our model could also be extended to multiple treatments, thus offering an alternative to published network meta-analysis models,⁴³ or it could be used to model simultaneously several outcomes with similar dose–response shapes. Another potential extension, which we have implemented in our paper, is accounting for cluster of the exposure in estimating the dose–response shape. Finally, external knowledge can be incorporated, for example, evidence from observational studies. The use of observational data will be particularly relevant when assessing long-term outcomes, as the majority of RCTs, in psychiatry and elsewhere, are of relatively short duration.¹⁷

In conclusion, we suggest that the Bayesian model with the binomial likelihood could be the default approach as it outperforms the alternative models when the synthesized studies are small. Prior knowledge about the underlying association should be incorporated in the model by defining an appropriate dose–response shape or by locating knots at doses where the outcome is expected to change a lot.