Using Deep Learning to Accelerate Knee MRI at 3 T: Results of an Interchangeability Study

Abstract

OBJECTIVE

Deep learning (DL) image reconstruction has the potential to disrupt the current state of MRI by significantly decreasing the time required for MRI examinations. Our goal was to use DL to accelerate MRI to allow a 5-minute comprehensive examination of the knee without compromising image quality or diagnostic accuracy.

MATERIALS AND METHODS.

A DL model for image reconstruction using a variational network was optimized. The model was trained using dedicated multisequence training, in which a single reconstruction model was trained with data from multiple sequences with different contrast and orientations. After training, data from 108 patients were retrospectively undersampled in a manner that would correspond with a net 3.49-fold acceleration of fully sampled data acquisition and a 1.88-fold acceleration compared with our standard twofold accelerated parallel acquisition. An interchangeability study was performed, in which the ability of six readers to detect internal derangement of the knee was compared for clinical and DL-accelerated images.

RESULTS.

We found a high degree of interchangeability between standard and DL-accelerated images. In particular, results showed that interchanging the sequences would produce discordant clinical opinions no more than 4% of the time for any feature evaluated. Moreover, the accelerated sequence was judged by all six readers to have better quality than the clinical sequence.

CONCLUSION.

An optimized DL model allowed acceleration of knee images that performed interchangeably with standard images for detection of internal derangement of the knee. Importantly, readers preferred the quality of accelerated images to that of standard clinical images.

MRI is the diagnostic imaging modality of choice for multiple diseases and injuries because of its excellent soft-tissue contrast and its ability to gather both morphologic and functional information [1–4]. Most MRI examinations require at least 20–30 minutes, with complex studies taking 60 minutes or longer. The majority of the examination time is used for image acquisition, but some time is used for activities such as bringing patients into and out of the scan room, coil positioning, and room cleaning. Long examination times have multiple disadvantages, including suboptimal image quality from motion artifacts, necessity for anesthesia in pediatric patients, increased costs, and decreased access, particularly in regions with limited numbers of MRI scanners [5].

MRI is slow because data are gathered in a generally sequential and progressive fashion; the greater the spatial resolution and volumetric coverage required, the more data points are needed. When magnetic field gradients are used to encode spatial information, each data point takes time to acquire [6]. Circumventing these basic speed limits means acquiring fewer sequential data points. A number of innovative techniques have been developed in an attempt to accelerate MRI. The most commonly used technique, parallel imaging, allows simultaneous acquisition of some data points using multielement detector arrays [7–9]. However, signal-to-noise ratio (SNR) generally decreases rapidly with increasing acceleration in parallel imaging, and residual artifacts generally increase with increasing acceleration, limiting the achievable speed for images of acceptable quality. For most clinical examinations, the maximum acceptable acceleration factor is 2 [10].

Software approaches to accelerating image acquisition have been explored using compressed sensing and, more recently, deep learning (DL) [11–21] (Knoll F, et al., presented at the International Society of Magnetic Resonance in Medicine [ISMRM] 2017 annual meeting). Recognizing that most images are compressible, compressed sensing approaches gather a reduced set of data points and search for the most compressed image that is consistent with those data (rather than first acquiring a time-consuming full dataset and then compressing it). Compressed sensing tends to preserve SNR better than parallel imaging, but the compression algorithms used tend to oversimplify image content, resulting in residual blurring and a loss of realistic image textures.

DL methods for reconstructing MR images from undersampled data can learn from images of significantly higher complexity than those used for compressed sensing and therefore may allow previously inaccessible levels of acceleration while preserving high image quality [12–21] (Knoll F, et al., ISMRM 2017 annual meeting). In the rapidly advancing field of image generation using DL, photorealistic results have been produced for images of common objects such as faces, dogs, or flowers [22, 23]. However, the use of DL for MR images places constraints on reconstructions beyond photorealism. Reconstructed images must also be diagnostically accurate (i.e., image details must be real and not just plausibly hallucinated). DL methods have yet to make their way into clinical practice because of the challenges in developing approaches that can show, through rigorous clinical interchangeability studies, their ability to achieve the dual and often conflicting goals of high image quality and strict clinical fidelity. Studies have shown progress toward achieving acceptable image quality with a small number of subjects, but a study showing both high quality and high accuracy has not been reported to our knowledge [12, 21] (Knoll F, et al., ISMRM 2017 annual meeting).

We sought to use DL to accelerate MRI to levels compatible with a 5-minute comprehensive examination of the knee, without compromising image quality or diagnostic accuracy. To achieve this goal, we designed a DL model, based on a variational network architecture [12], that explicitly learns MRI detector coil sensitivities, contains several architectural refinements, and is followed by adaptive image dithering to improve the perceived image quality. We chose to show the effectiveness of our approach for the detection of internal derangement of the knee. We collected the largest quantities of dedicated raw MRI data reported, to our knowledge, for such a task and divided the data into training, validation, and testing datasets. We performed a large-scale clinical interchangeability study comparing images obtained using our optimized DL-accelerated protocol with those obtained using our standard clinical MRI protocol. To aid in the further advancement of the field, the code and trained model associated with this study are open source [24].

Materials and Methods

Model Topology

The goal of DL-based image reconstruction is to convert undersampled data to images with full information content. Rather than using blind training for this process, our approach incorporates knowledge about the acquisition process, including the sampling pattern and the knowledge that the measurement was performed with multiple receive coils. Such a physics-guided learning approach reduces the quantity of data required for training and protects against generation of plausible-looking but physically infeasible image structures [12]. Multiple instances of undersampled data from the training set are fed into a model that performs physics-based reconstruction steps (such as gradient descent steps or parallel imaging reconstructions) while learning efficient filters that remove image artifacts introduced because of accelerated acquisition. The results are compared with corresponding ground-truth fully sampled images at each stage of training, and model weights are updated using backpropagation. Once training is complete, new undersampled datasets can be fed into the model and rapidly converted into full images.

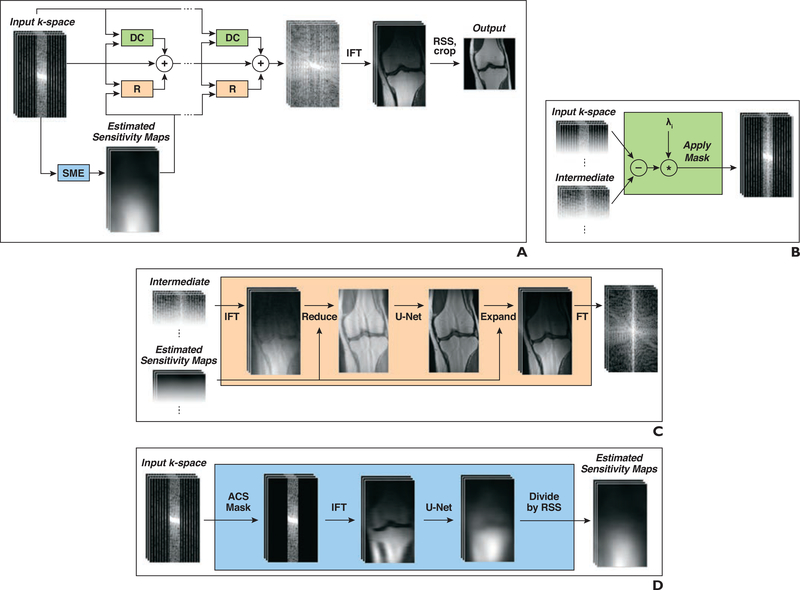
Our particular neural network model is based on the variational network of Hammernik et al. [12], to which we added several architectural innovations that improved the quality of the reconstructions. First, we replaced the pair of convolutional layers from the original network topology with a U-Net architecture [25]. Second, instead of using the ESPIRiT algorithm to estimate sensitivity maps, we included an additional U-Net to estimate these maps from the input k-space data [26]. The U-Net used to estimate sensitivity maps and the U-Nets used to perform reconstruction are trained jointly to optimize the quality of the final reconstruction. We found that such an end-to-end approach is beneficial when the number of central k-space lines is small, which is necessary to obtain higher accelerations. Third, whereas the original variational network performed iterative updates to the complex image representation, our model applied updates directly to the raw k-space data from each coil. Thus, our network gradually refined k-space data instead of refining the combined image from all coils. Figure 1 illustrates the structure of our network, which was selected for this study after comparison of the performance of a variety of alternative network topologies. The sensitivity maps are estimated from fewer low-frequency autocalibration scan lines than are required to construct physically accurate sensitivities, but this reduced set of autocalibration lines is sufficient to produce highly accurate reconstructions via the variational network. The parameters of the model were estimated by minimizing structural similarity index (SSIM) scores on the training set [27]. We used the Adam optimizer with a learning rate of 0.0003 for 100 epochs [28]. A validation set was used to fit the hyperparameters of the model, such as the number of steps in the variational network as well as the number of layers and the number of feature maps in the U-Net. The model contains almost 30 million parameters: 29.5 million in the variational network and 0.5 million in the network that estimates sensitivity maps.

Fig. 1—

Structure of network used for deep learning reconstruction of 3-T knee MR images.

A, Block diagram shows structure of our model, which takes undersampled k-space as input and applies several iterative refinements (R). Each refinement includes residual connection, R module, and data consistency (DC) module. Inverse Fourier transform (IFT) followed by root-sum-of-squares (RSS) transform is applied after final refinement to obtain reconstructed image. SME = sensitivity map estimation.

B, Diagram shows DC module that computes correction map that brings intermediate k-space data closer to input k-space data. Correction is computed only at k-space locations where measurements have been performed.

C, Diagram shows R module that converts multicoil k-space data into single image, applies U-Net, and then converts output back to multicoil k-space data. In first step, IFT is applied to obtain multicoil images, which are then multiplied by conjugate of sensitivity maps and added (Reduce). In final step, image is multiplied by sensitivity maps (Expand) followed by Fourier transform (FT).

D, Diagram shows SME module that estimates sensitivity maps used in R modules. SME selects only autocalibration signal (ACS) lines from input k-space and applies IFT and then U-Net. Finally, output of U-Net is normalized by dividing each individual sensitivity map voxelwise by RSS of all maps.

Multisequence Training

Our clinical knee protocol, which is described in more detail in the Data Collection and Patient Selection section, consists of five separate acquisitions obtained in three distinct image planes, resulting in multiple image contrasts and viewing angles. In a 2018 study that examined multiple sequences, separate specialized reconstruction models were trained for each individual sequence [12]. Although this approach is feasible in a research setting, having a single reconstruction pipeline for all sequences in an imaging protocol reduces the overhead for clinical deployment and improves the potential for generalizability of the trained model. We therefore performed a dedicated multisequence training, in which a single reconstruction model was trained with data from all sequences and was then used to reconstruct data from the complete clinical protocol. Because the images from the disparate sequences in the protocol vary substantially in contrast, SNR, and image content, our model needs a higher computational capacity than is generally required for a specialized sequence-specific model to capture the larger diversity in acquisition parameters. The model was trained for 155.4 hours (or 6.5 days) on eight cloud-based graphics processing units (32-GB Tesla V100, Nvidia).

Acceleration Factor

As mentioned at the beginning of this section, because MRI data acquisition is performed sequentially, the number of acquired data points (or, in technical parlance, the number of acquired phase-encoding steps) is directly proportional to the scan time. In the literature on accelerated MRI, reporting the relative number of steps that are skipped in the undersampling pattern as the “acceleration factor” (R) is common practice (e.g., an acceleration factor of 2 indicates that only every second line in the data space, known as k-space, is acquired). Scanner vendors use the same convention. However, for parallel imaging techniques such as the generalized autocalibrating partially parallel acquisition technique used for our clinical sequences in this study, some number of central k-space lines is always fully sampled for detector sensitivity calibration. Therefore, the true acceleration factor, as compared with a fully sampled case, depends on how many central calibration lines are acquired compared with how many outer lines are undersampled, which in turn depends on the target number of lines in the reconstructed image.

To give an example, for the coronal proton density—weighted acquisitions, a fully sampled acquisition includes 332 phase-encoding lines. The standard clinical protocol with a nominal acceleration factor (or undersampling factor) of 2 therefore acquires 166 phase-encoding lines plus 13 lines at the center of k-space (such that a central region of 26 lines at the center [nRef] are fully sampled), leading to a total of 179 acquired lines and an actual acceleration factor of 1.85 (332/179). In comparison, our accelerated DL reconstruction uses a sampling scheme with a nominal acceleration factor of 4, equidistantly sampled, and a fully sampled nRef region of 16 lines at the center of k-space. This process results in a total of 95 phase-encoding lines and an actual acceleration factor of 3.49 (332/95) compared with fully sampled, nonparallel imaging. Compared with our standard clinical sequences that used twofold accelerated parallel imaging, the DL-reconstructed images were faster by a factor of 1.88 (179/95).

Added Image Noise (Dithering)

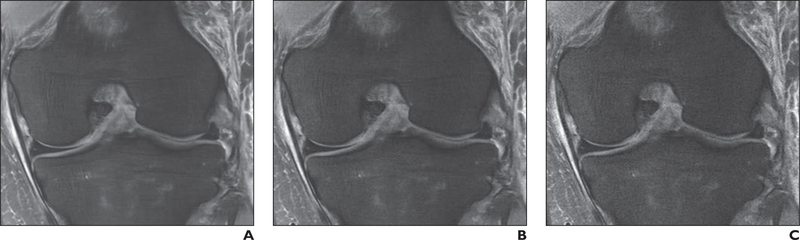
When it comes to subjective image appearance, a common challenge associated with nonlinear reconstruction approaches such as compressed sensing or DL is a residual smoothing of fine image features or background textures. To enhance the subjective perception of sharpness in images, known as acutance in photography, low levels of noise were added back to the reconstructed images (a process known as dithering) [29] (Fig. 2). To avoid obscuring dark areas of the reconstruction by adding too much noise, we adapted the level of noise to the brightness of the image in the vicinity of each voxel. Specifically, we blurred the image we wished to dither with a median filter, taking medians over 11 × 11 patches of voxels, took the square root of the median value at each voxel of the blurred image, and multiplied it by a baseline value (σ) to yield a local SD (σ_local). We then dithered the original unblurred image by adding gaussian noise with 0 mean and SD equal to σ_local at each voxel. Before computing the square root and adding the noise, we normalized every voxel by dividing by the maximum value over all voxels in the cross-sectional slice.

Fig. 2—

34-year-old man with acute knee injury. A–C, Coronal fat-suppressed proton density–weighted images with no added noise (A), baseline noise value (σ) = 0.015 (B), and σ = 0.05 (C) show effect of dithering.

Data Collection and Patient Selection

Institutional review board approval was obtained for this study with a waiver of informed consent. All images and raw data used in this study were anonymized to protect personal health information. Data from 406 consecutive knee examinations acquired on 3-T MRI scanners (Skyra and Biograph mMR, Siemens Healthineers) were collected retrospectively and divided randomly into training (n = 242), validation (n = 56), and test (n = 108) sets. Each MRI examination included our standard knee protocol of five 2D turbo spin-echo pulse sequences acquired in the sagittal, coronal, and axial planes. Each sequence in this protocol used parallel imaging with a nominal acceleration factor of 2; the net acceleration factor accounting for parallel imaging calibration data was closer to 1.85. Table 1 provides the sequence parameters used. We chose to use parallel imaging—accelerated scans for our source data and ground truth, rather than slower fully sampled scans, because parallel imaging with an acceleration factor of 2 is the clinical standard at our institution and many others around the world.

TABLE 1:

MRI Sequence Parameters Used for the 108 Test Patients

Sequence	Time (s)	Turbo Factor	FOV (mm)	Matrix Size		Phase Oversampling (%)	TR Range/TE Range	Slice Thickness (mm)
				Readout	Phase
Axial T2 FS	86–121	9	140 × 140	320	240–256	10–40	4110–7150/59–65	3
Sagittal PD	126–165	4	140 × 140	384	307	50–80	2100–2750/22–23	3
Sagittal T2 FS	80–130	11	140 × 140	320	240–256	50–80	4730–6100/47–50	3
Coronal PD	92–121	4	140 × 140	320	288	5–30	2100–2750/21–27	3
Coronal PD FS	107–143	4	140 × 140	320	288	5–40	2210–3270/27–33	3

Note—T2 = T2-weighted, FS = fat-saturated, PD = proton density–weighted.

The observed performance of trained models in reconstructing data from the independent validation set was used to optimize the model topology used for reconstruction, the extent and pattern of retrospective undersampling performed, and the level of noise added to the reconstructed images.

Interchangeability Study

Once all parameters were optimized, an interchangeability study was performed on the 108 test patients’ examinations [30]. The examinations were performed over 28 days (April 2–29, 2019). Of the 108 patients, 57 (53%) were women and 51 (47%) were men; patient age ranged from 18 to 89 years (median age, 44 years). None of these examinations were used in any way during the design process, training, and validation phases of our neural network. The total scan time required for the test patients ranged from 8 minutes 11 seconds to 11 minutes 20 seconds. The variation in time was mainly due to differences in coverage needed as a result of differences in habitus. The total examination time ranged between 15 minutes and 33 minutes, with a median room time of 21 minutes.

Raw data (in the k-space domain) from each of the five sequences in the examination were retrospectively undersampled with the optimized sampling trajectories and then reconstructed using the optimized model parameters to create accelerated images. The reconstruction was performed on a single graphics processing unit (16-GB V100, Nvidia) that is comparable to the hardware already installed in the host computers of state-of-the-art MRI scanners. Our computation times per slice were approximately 145 milliseconds for the coronal and axial sequences, 180 milliseconds for the sagittal T2-weighted sequence, and 255 milliseconds for the sagittal proton density—weighted sequence. The examinations using the standard clinical sequences and those with the DL-reconstructed accelerated sequences were anonymized and separated into eight equal groups. Each examination was reviewed by six fellowship-trained subspecialized musculoskeletal radiologists with 1–19 years of subspecialty experience. The readers were blinded to all patient information and sequence details. The interpretation scheme consisted of each reader reviewing one group of examinations each week. To limit the potential for recall bias, interpretation of the clinical and accelerated examinations for each subject were separated by a period of 4 weeks, and the readers were blinded to the other readers’ evaluations.

The reader evaluations were recorded on a standardized score sheet using a 4-point Likert scale to assess for internal derangement (meniscal tears, ligament abnormalities, chondral defects, and subchondral bone marrow signal-intensity abnormalities). For the Likert scale, 1 was definitely normal; 2, probably normal; 3, probably abnormal; and 4 definitely abnormal. For scoring of the chondral and subchondral bone marrow abnormalities, the knee was divided into six surfaces (medial and lateral tibial plateaus, medial and lateral femoral condyles, and patellar trochlear surfaces). In addition, each examination was evaluated for sharpness, subjective SNR, presence of artifacts, and overall image quality on a 4-point scale. Each reader also indicated whether they thought the examinations consisted of standard clinical or accelerated sequences.

Statistics

Interchangeability tests the ability of the accelerated technique to replace the clinical sequence by showing that when two readers assess the same patient, the rate of agreement when both readers use the clinical sequence is not substantially higher than that when exactly one of the readers uses the accelerated sequence [30]. For the purposes of this study, a clinically important difference was defined as greater than 5% additional agreement when both readers were interpreting standard images as opposed to when one reader was interpreting standard images and the other was interpreting accelerated images.

For each reader, an exact McNemar test was used to compare the sequences in terms of the percentage of times the reader correctly identified the sequence (clinical or accelerated) that was used to generate an image. An exact paired sample Wilcoxon signed rank test was used to compare the sequences in terms of the image quality scores from each reader. All statistical tests were conducted at the two-sided 5% significance level using SAS software (version 9.4, SAS Institute). For each sequence, an exact test based on the binomial distribution was performed to assess whether the percentage of times a given reader correctly identified the sequence used to derive an image was different from 50%, the rate expected for random guessing.

Results

Optimization Phase

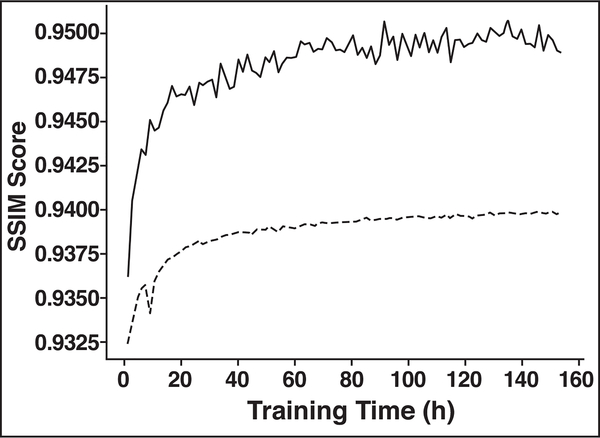
The MR pulse sequences, image plane orientations, and data undersampling patterns used for this study are described in more detail in the Materials and Methods section. Figure 3 shows the SSIM score (or the negative loss) of our model as a function of training time for both the training set and the validation set. Optimized sampling parameters included fourfold nominal acceleration and sampling of 16 calibration lines, which yielded images for each pulse sequence and orientation at a net 3.49-fold acceleration that were difficult to distinguish from the standard clinical images (Figs. 4 and 5). The theoretic scan time of the accelerated sequences ranged between 4 minutes 20 seconds and 6 minutes. With higher acceleration factors, fewer calibration lines, or both, subtle signal abnormalities became less conspicuous (Fig. 6). The optimal baseline SD of noise (σ) added back to the images in the image dithering process described in the Materials and Methods section was determined to be 0.015. With less added noise, the images appeared oversmoothed, with loss of fine detail such as bone trabeculae, whereas greater amounts of added noise led to the images being subjectively too noisy.

Fig. 3—

Graph shows structural similarity index (SSIM) score (or negative loss) as function of training time. SSIM score is computed both on training set (solid line) and on validation set (dashed line).

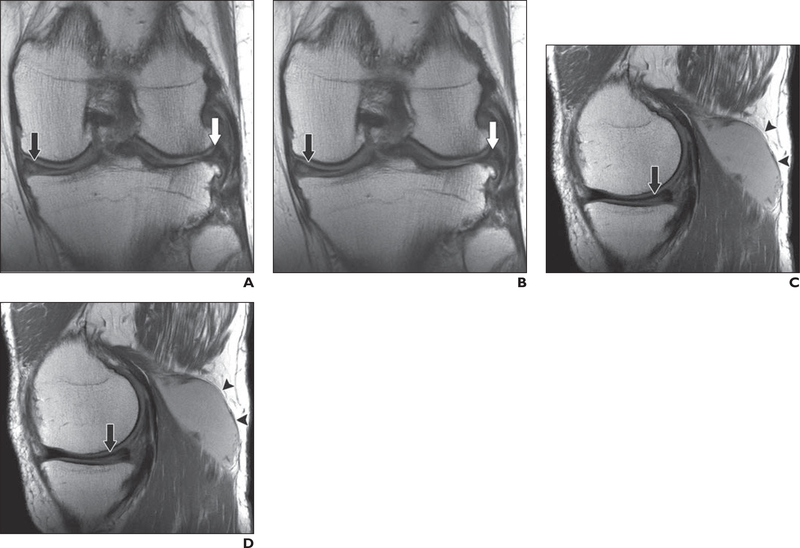
Fig. 4—

64-year-old man with recurrent popliteal cyst.

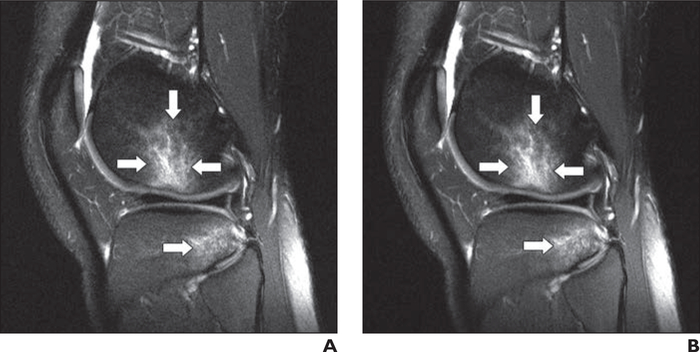
A–D, Coronal clinical (A) and deep learning (DL)-accelerated (B) as well as sagittal clinical (C) and DL-accelerated (D) proton density—weighted images show medial (black arrows) and lateral (white arrows, A and B) meniscal tears and popliteal cyst (arrowheads, C and D). It is difficult to distinguish between clinical and DL-accelerated images.

Fig. 5—

22-year-old man with acute knee injury. A and B, Sagittal clinical (A) and deep learning (DL)-accelerated (B) fat-suppressed proton density—weighted images show bone contusions (arrows) in lateral femoral condyle and lateral tibial plateaus, consistent with anterior cruciate ligament tear. It is difficult to distinguish between clinical and DL-accelerated images. Such indistinguishability is uncommon for traditional acceleration techniques at high acceleration factors, particularly for challenging case of 2D images with strong requirements for spatial resolution and anatomic fidelity.

Fig. 6—

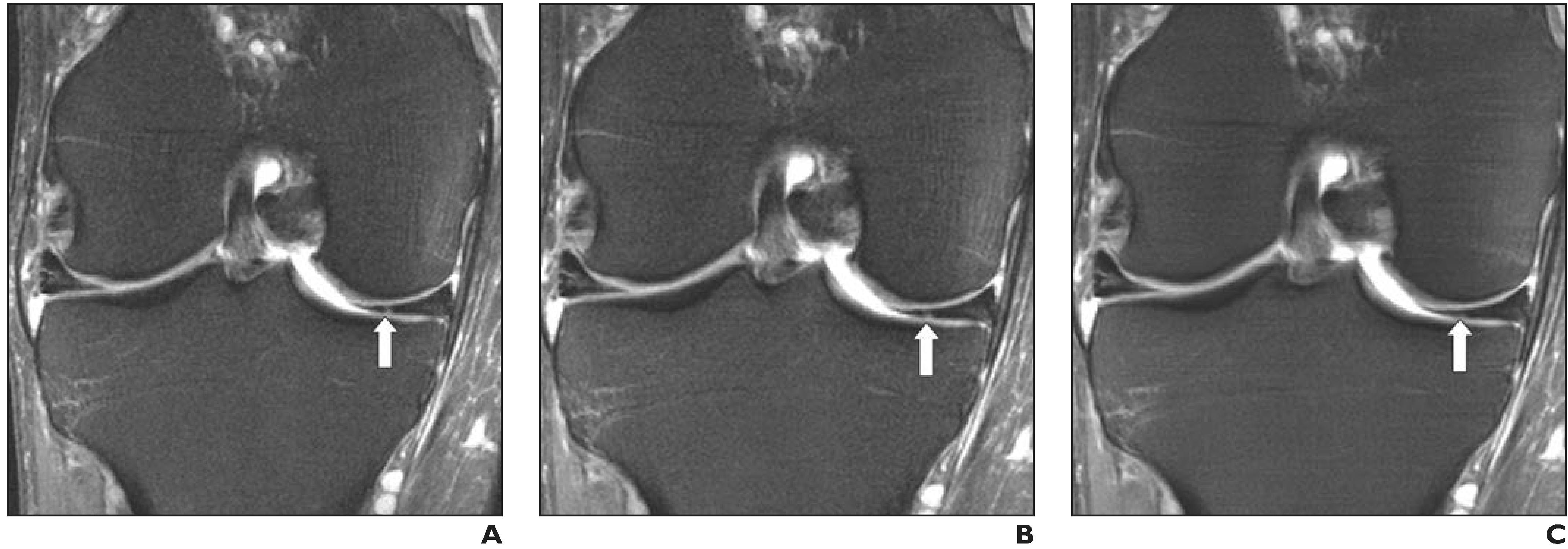
43-year-old man with medial knee pain. A–C, Clinical (A), fourfold (B), and eightfold (C) deep learning—accelerated fat-suppressed proton density—weighted images show subtle signal-intensity change in medial meniscus (arrow) on clinical and fourfold accelerated sequences that is not visible on eightfold accelerated image. Eightfold acceleration was therefore deemed too aggressive for this use of 2D musculoskeletal imaging. However, substantially higher accelerations are likely to be feasible for other clinical applications and for acquisitions that are multidimensional, dynamic, or both.

Interchangeability

Table 2 provides data that support interchangeability of the accelerated and the clinical sequences. They provide 95% confidence that any decrease in the percentage of times two readers would provide concordant opinions that might result from interchanging the sequences will be no more than 4% for any feature that was evaluated. Taking into consideration only abnormalities of the menisci and ligaments, the injuries most commonly treated by operative intervention, the decrease was no more than 1.7%. The number of abnormalities for each structure evaluated is presented in Table 3.

TABLE 2:

Interchangeability of Clinical and Accelerated Images

Anatomic Structure	Decrease (%)	95% CI (%)
Meniscus
Medial	−2.3	−3.5 to −1.1
Lateral	0.7	−0.4 to 1.7
Ligament
Anterior cruciate	0.2	−0.6 to 1.1
Posterior cruciate	0.6	0.2–1.0
Medial collateral	0.8	0.2–1.3
Lateral collateral	0.9	0.2–1.6
Extensor mechanism	−0.7	−1.4 to 0.0
Cartilage
Medial femoral condylar	1.3	0.0–2.6
Lateral femoral condylar	2.7	1.5–4.0
Medial tibial plateau	0.9	−0.2 to 2.1
Lateral tibial plateau	1.4	0.1–2.8
Patellar	1.8	0.6–3.0
Trochlear	0.2	−1.1 to 1.5
Bone marrow
Medial femoral condylar	−0.7	−1.7 to 0.4
Lateral femoral condylar	1.2	0.3–2.2
Medial tibial plateau	−0.4	−1.3 to 0.5
Lateral tibial plateau	0	−0.9 to 0.9
Patellar	0.6	−0.2 to 1.4
Trochlear	0.4	−0.6 to 1.4

Note—Images were evaluated by estimated decrease in the probability of reader agreement that would result when clinical and accelerated sequences were interchanged (based on an ordinal representation of reader assessments).

TABLE 3:

Sum of Readers’ Assessments of Abnormalities for Each Anatomic Structure Seen on Accelerated and Clinical Sequences

Anatomic Structure	Sequence
	Accelerated				Clinical
	1	2	3	4	1	2	3	4
Meniscus
Medial	362	14	26	246	355	29	18	246
Lateral	442	23	23	160	448	14	28	158
Ligament
Anterior cruciate	552	16	11	69	562	18	7	61
Posterior cruciate	638	5	1	4	641	4	0	3
Medial collateral	619	5	2	22	622	5	4	17
Lateral collateral	627	5	7	9	629	4	7	8
Extensor mechanism	628	5	0	15	623	9	4	12
Cartilage
Medial femoral condylar	389	12	24	223	382	8	34	224
Lateral femoral condylar	461	7	26	154	469	9	17	153
Medial tibial plateau	473	15	18	142	466	16	23	143
Lateral tibial plateau	459	17	30	142	446	8	28	166
Patellar	218	12	38	380	227	17	33	371
Trochlear	398	21	22	207	382	24	30	212
Bone marrow
Medial femoral condylar	497	2	3	146	499	0	5	144
Lateral femoral condylar	514	2	3	129	510	0	1	137
Medial tibial plateau	490	0	0	158	486	0	3	159
Lateral tibial plateau	521	2	2	123	522	0	2	124
Patellar	433	2	6	207	429	6	3	210
Trochlear	509	3	3	133	501	1	6	140

Note—Abnormalities were assessed using a 4-point Likert scale, on which 1 was definitely normal; 2, probably normal; 3, probably abnormal; and 4, definitely abnormal.

Image Quality and Sequence Identification

All six readers judged the accelerated sequence to produce better quality than the clinical sequence (Table 4). Irrespective of the sequence actually used to derive an image, only one of the six readers was able to correctly identify the sequence more than 50% of the time. In other words, only one reader was more accurate in identifying accelerated sequences than would be expected by chance alone.

TABLE 4:

Analysis of Image Quality Scores

Feature, Reader	Accelerated	Clinical	Difference	p
Artifacts
1	2.02 ± 0.14	2.04 ± 0.19	0.02 ± 0.19	0.465
2	2.34 ± 0.69	2.35 ± 0.62	0.01 ± 0.69	0.869
3	2.05 ± 0.21	2.05 ± 0.21	0.00 ± 0.19	1.000
4	2.20 ± 0.40	2.21 ± 0.41	0.01 ± 0.44	0.862
5	2.04 ± 0.64	2.10 ± 0.59	0.06 ± 0.78	0.441
6	2.10 ± 0.33	2.10 ± 0.30	0.00 ± 0.41	1.000
Signal-to-noise ratio
1	1.01 ± 0.10	1.49 ± 0.59	0.48 ± 0.59	< 0.001
2	1.98 ± 0.96	2.13 ± 0.81	0.15 ± 0.95	0.139
3	1.06 ± 0.23	1.15 ± 0.36	0.09 ± 0.42	0.052
4	1.12 ± 0.33	1.66 ± 0.58	0.54 ± 0.62	< 0.001
5	1.06 ± 0.23	1.36 ± 0.48	0.31 ± 0.50	< 0.001
6	1.31 ± 0.55	1.81 ± 0.59	0.50 ± 0.66	< 0.001
Sharpness
1	1.21 ± 0.53	1.31 ± 0.62	0.09 ± 0.54	0.110
2	2.06 ± 0.94	2.19 ± 0.83	0.13 ± 0.98	0.219
3	1.12 ± 0.40	1.14 ± 0.40	0.02 ± 0.45	0.737
4	1.75 ± 0.57	1.41 ± 0.58	−0.34 ± 0.69	< 0.001
5	1.20 ± 0.49	1.39 ± 0.54	0.19 ± 0.66	0.012
6	1.46 ± 0.70	1.78 ± 0.70	0.31 ± 0.80	< 0.001
Overall image quality
1	1.16 ± 0.44	1.34 ± 0.61	0.19 ± 0.51	0.001
2	2.06 ± 0.92	2.22 ± 0.81	0.16 ± 0.93	0.095
3	1.10 ± 0.33	1.13 ± 0.36	0.03 ± 0.42	0.560
4	1.75 ± 0.64	1.94 ± 0.69	0.19 ± 0.70	0.019
5	1.25 ± 0.58	1.43 ± 0.63	0.18 ± 0.71	0.025
6	1.50 ± 0.68	1.95 ± 0.68	0.45 ± 0.78	< 0.001

Note—Except for p values, data are mean ± SD. Image quality was rated on a 4-point scale, with 1 being the best quality and 4 being the worst.

Discussion

Our study has shown that an optimized DL network can be used to reconstruct fourfold accelerated images that perform interchangeably with our standard clinical images for the detection of internal derangement of the knee. In particular, the data provide 95% confidence that interchanging the sequences would decrease the likelihood of reader agreement by no more than 4%. Taking into consideration only the menisci and ligaments, the decrease was no more than 1.7%. The fact that accelerated images using DL reconstruction were judged superior to standard clinical images offers promise that such accelerated images can achieve rapid clinical acceptance. In the context of clinical acceptance, an additional benefit of DL reconstruction is that the major computational effort is expended at the stage of training the reconstruction model. Once the training is complete, the computational effort for the time-critical step of reconstructing images while the patient is on the table is relatively low and does not require special computing resources like clusters or cloud computing. As mentioned, our computation times per slice were approximately 145 milliseconds for the coronal and axial sequences, 180 milliseconds for the sagittal T2-weighted sequence, and 255 milliseconds for the sagittal proton density—weighted sequence.

The theoretic scan time that would be required for the knee examination using the fourfold accelerated sequences ranged between 4 minutes 20 seconds and 6 minutes. Although time spent on activities other than imaging has previously accounted for a significant percentage of total MRI examination time, recently described innovative workflow solutions such as dockable tables and dedicated preparation rooms have enabled the time for these activities to be decreased to less than 2 minutes per patient [31]. Combining the DL-accelerated acquisitions with such time-saving workflows could decrease the total examination time for MRI of the knee to less than 10 minutes, which is faster than the time generally allotted for radiography of the knee (15 minutes). If examination time is significantly reduced, the technical reimbursement for knee MRI examinations could also decrease. Currently, radiography is the first step in imaging patients with acute knee trauma because of short examination time and low cost, despite its extremely low sensitivity for such injuries and its use of ionizing radiation [32]. Radiography will continue to play a valuable role in knee imaging particularly for abnormalities that can be difficult to detect on MRI, such as subtle avulsion fractures. However, a low-cost knee MRI examination requiring only a few minutes to acquire has the potential to replace radiography in some clinical situations.

Although various prior studies have investigated the use of DL reconstruction of MR images, they have included small numbers of subjects and have been limited in scope to evaluating image quality rather than diagnostic accuracy. Those studies have predominantly shown inferior quality for DL-accelerated images compared with traditional MR images—a trade-off almost universally encountered in the evaluation of accelerated imaging methods. To our knowledge, ours is the first study to find both high quality and diagnostic interchangeability between a standard clinical MRI protocol and a DL-accelerated protocol.

Our study had several limitations. First, all examinations were performed on MRI scanners produced by a single vendor and only at 3-T field strength. However, all of the accelerated images were reconstructed on a model trained simultaneously on five distinct sequences with markedly different contrast that were obtained in three different planes of orientation, which augurs well for the generalizability of the model. Further studies on multiple vendor platforms and at different field strengths are necessary to fully assess generalizability of our technique. Second, we used retrospective undersampling in this study to simulate the acceleration that could be achieved in clinical practice using prospective undersampling, while still allowing comparison of accelerated images with otherwise identical ground truth images. That said, for knee MRI in particular, in which physiologic motion is limited and dynamic acquisitions are uncommon, our networks would be unlikely to perform differently on prospectively undersampled data. Third, we did not have arthroscopic data with which to judge the diagnostic accuracy of the accelerated sequences. Previous studies, however, have reported excellent accuracy of MRI for the detection of internal derangement of the knee [33]. Therefore, we believe that the interchangeability of accelerated and standard sequences provides evidence that accelerated sequences also had excellent accuracy for the diagnosis of internal derangement. Finally, this study only tested the DL model on knee images. To fully realize its potential positive impact, our DL model needs to be validated on additional anatomic regions and multiple abnormalities. We have since applied the model successfully to images of the brain and liver, and studies are underway to assess diagnostic accuracy [34].

Conclusion

An optimized DL model allowed an additional twofold acceleration of our standard clinical knee images, which are already accelerated by a factor of 2 using parallel imaging. The DL-reconstructed images performed interchangeably with standard images for the detection of internal derangement of the knee. Importantly, the accelerated images were judged better in quality than standard clinical images.