Physical field simulation of the ultrasonic radiation method: An investigation of the vessel, probe position and power

Highlights

• •The most suitable container has been selected.
• •Aluminum foil erosion experiments were performed in Erlenmeyer flasks and beakers.
• •Comparison of the sound field distribution between different instruments.

Abstract

In this paper, the effects of ultrasonic probe position, vessel shape, and ultrasonic input power on the sound pressure distribution in the reactor were investigated by solving the Helmholtz equation using COMSOL Multiphysis^@ software. Three different types of glass containers were used in the study, which are beaker, Erlenmeyer flask, and round bottom flask. The maximum value of sound pressure in the three containers will gradually increase when the distance between the probe and the bottom of the container decreases. When the distance decreases, the area of the high acoustic pressure region in the round bottom flask does not change significantly, while the area of the high acoustic pressure region in the beaker and Erlenmeyer flask increases sharply, which means that the use of the round bottom flask can reduce the influence of the dead zone on the preparation of nanomaterials. In addition, the change in power increases the value of the peak negative acoustic pressure in the vessel, enhancing the response efficiency of ultrasonic cavitation.

1. Introduction

The Ultrasonic irradiation method is widely used in many fields such as organic dye degradation [22], wastewater treatment [6], catalytic conversion of heavy hydrocarbons to light fuels [17], food processing [2], graphene film preparation [8], and production of nanomaterials [14], [21]. Ultrasound is often used in physical and chemical research and is better for driving and enhancing chemical reactions [20]. Ultrasonic cavitation effect occurs when ultrasonic radiation liquid, which refers to when the ultrasonic energy is high enough, the existence of tiny bubbles in the liquid (cavitation nucleus) in the ultrasonic field under the action of vibration, growth, and continuous collection of sound field energy when the energy reaches a certain threshold, the cavitation bubble sharp collapse and closure of the phenomenon. This phenomenon was first proposed by W.T. Richards and A.L. Loomis in the late 1920 s, who found that the acoustic cavitation effect could largely facilitate chemical reaction processes. In 1986, Crum and Fowlkes [5] proposed the idea that ultrasound promotes chemical effects due to the acoustic cavitation bubble effect. These bubbles are generated by pressure oscillations as ultrasound waves propagate through a liquid medium, and they grow, oscillate, and collapse violently, leading to the release of large amounts of energy.

Nanomaterials have attracted a lot of attention due to their small size and unique physical and chemical properties compared to ordinary materials [15], which have a wide range of applications in imaging, sensing, efficient bioenergy, life sciences, etc [9], [10], [19]. Lots of methods have been developed for the synthesis of novel nanomaterials with improved performance like solid-state reaction method, chemical co-precipitation technique, Sol-Gel method, ultrasonic irradiation method, etc [1], [18]. Nanomaterials are generated in two ways: bottom-up aggregation of atoms into clusters of nanomaterials, and top-down fracturing of large particles into nanomaterials by adding different energies [7]. Among the top-down methods, ultrasonic irradiation method is an efficient way to prepare nanomaterials. Ultrasonic irradiation not only accelerates the reactivity of the relevant chemical substances to efficiently obtain the desired product in a short time [16], but also reduces the size of nanoparticles through the cavitation process and acts as a crushing aggregate. Under the effects of ultrasonic radiation method, cavitation bubbles are generated, expanded, oscillated and ruptured with the positive and negative changes of acoustic pressure. The microjets and microwaves generated by cavitation bubble rupture facilitate the synthesis of nanomaterials [23], [24], [25], [26], [27], [28].

Unfortunately, the mechanism by which cavitation affects the particle size and yield of nanomaterials is not known, making it difficult to control particle size and predict the performance of ultrasonic reactors. This is one of the major limitations in optimizing ultrasound for industrial applications [11]. In addition to this, the sound field distribution inside the vessel is closely related to the location of the ultrasonic probe - high acoustic pressure occurs mainly in the solution around the probe, which causes intense local cavitation of the solution, while other parts respond more slowly.

In this study, the effects of ultrasonic probe position, vessel shape, and ultrasonic input power on the acoustic pressure distribution in the reactor were investigated by solving the Helmholtz equation using COMSOL Multiphysis^@software, The influencing factors of acoustic pressure distribution were explained from the geometric level, which provided a new concept for the preparation of nanomaterials by ultrasonic radiation.

2. Experimental details

The numerical simulation in this study aims to explore the effect of ultrasonic probes on the acoustic pressure in the container under different conditions. In addition, ultrasonic radiation of aluminum foils corrosion experiments were also applied in this study. Simulation calculation domain, acoustic pressure simulation, boundary conditions, and apparatus and procedure will be presented in this chapter.

2.1. Simulation calculation domain

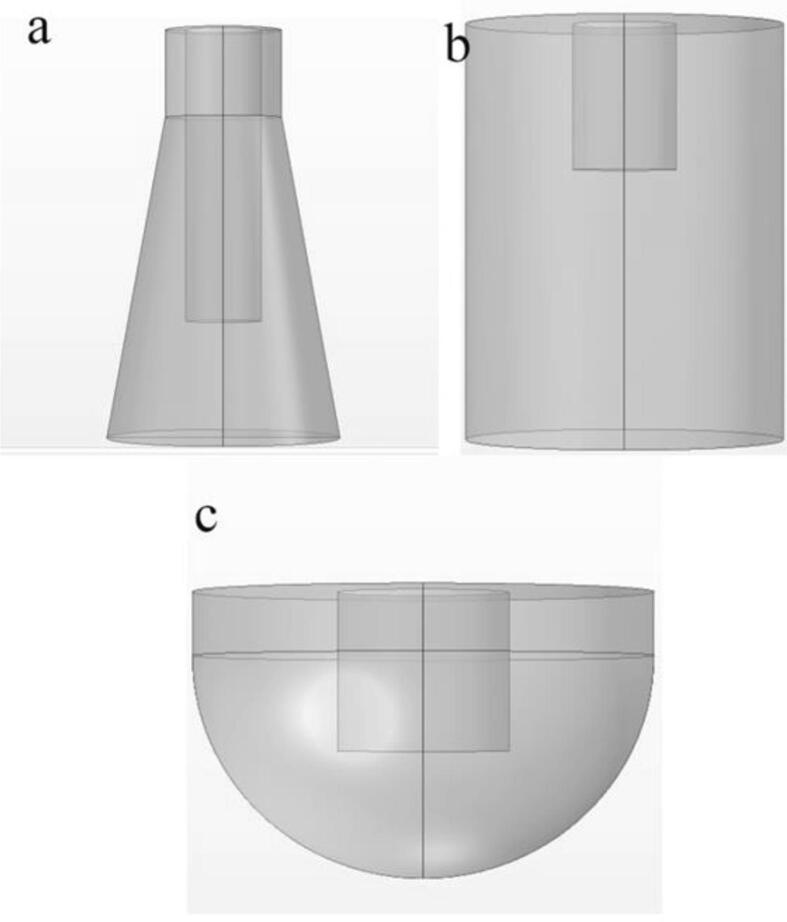
In order to explore the impact of the ultrasonic probe on different containers, this study uses a beaker, an Erlenmeyer flask and a spherical-bottomed flask as the container to perform 3D simulation calculations, as shown in Fig. 1.The upper diameter of the glass Erlenmeyer flask is D_eu = 40 mm, the bottom diameter is D_ed = 80 mm, and the height, H_e = 140 mm with the aspect ratio (H_ed/D_ed) of 1.75. The diameter of the glass beaker is D_b = 80 mm, the height is H_b = 100 mm, and the aspect ratio(H_b/D_b) is 1.25. The diameter of the glass sphere is D_r = 70 mm, the height of the calculation field is H_r = 45 mm, which the aspect ratio(H_r/D_r) is 0.64. The diameter of the iron probe deep into the water is D_p = 26 mm, the frequency f = 20 kHz, and the power P_u = 32 W.

Fig. 1.

Containers used in the simulation. (a) Erlenmeyer flask; (b) beaker; (c) spherical-bottomed flask.

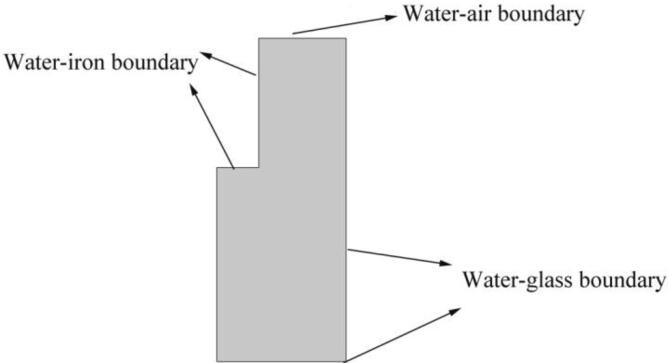
Acoustic impedance boundary is a critical constraint in the simulation. Since the container is axisymmetric, 2D geometry is used in Fig. 2 to show the acoustic impedance boundaries used in this study, which are water–air, water-iron, and water–glass. The density and sound velocity of the material are shown in Table 2

Fig. 2.

Boundary conditions of the model (2D).

Table 2.

Density and sound velocity of the material.

Material	Density(kg/m3)	sound velocity(m/s)
Air	1.2	343
Water	998	1500
Iron	787	5930
Glass	2500	5100

2.2. Acoustic pressure simulation

COMSOL Multiphysics 5.5 ® is a finite element method software, which was used to calculating acoustic pressure in this study. Calculations using the physical field of pressure acoustics studied in the frequency domain, which contains the sound propagation problem controlled by partial differential equations (PDEs). The governing equations are described as the Helmholtz equation:

$$\mathrm{\nabla }·\left(\frac{1}{{\rho }_0}·\mathrm{\nabla }p\right)-\frac{k^{2}p}{{\rho }_0}=0,k=\frac{\omega }{c_0},\omega =2\pi f$$ (1)

where

$$\mathrm{\nabla }=\frac{{\partial }^{2}p}{\partial x^2}+\frac{{\partial }^{2}p}{\partial y^2}+\frac{{\partial }^{2}p}{\partial z^2}$$ (2)

where ρ₀ is the liquid density(m/s), p is scattered pressure field (N/m2),c₀ is sound velocity of liquid, and k refers to the wave number(rad/m), defined by the angular frequency ω(rad/s).

In the process of acoustic pressure vibration, when the acoustic pressure reaches its maximum value, the acceleration of the local area of the medium is expressed as [13]

$$a_n=\omega \sqrt{\frac{2I}{{\rho }_0{c}_0}}$$ (3)

where

$$I=\frac{P_U}{A}=\frac{P_u}{\pi r^2}$$ (4)

Incorporating equation (4) into equation (3), we can obtain the acceleration of the ultrasonic probe vibration as

$$a_n=\omega \sqrt{\frac{8p_u}{\pi {\rho }_0{c}_0{D}_p}}$$ (5)

The required parameters in the formula are shown in Table 1.

Table 1.

Parameters used in the simulation.

f	Ultrasound frequency [kHz]	20
ω	Angular frequency[rad/s]	125,600
Pu	Input power [W]	32
ρ0	Density of liquid [kg/m3]	998
c0	Sound velocity of liquid [m/s]	1500

2.3. Boundary conditions

Acoustic impedance is the complex ratio of the acoustic pressure of the medium in an area of the wave front surface to the volume velocity through this area, which reflects the damping characteristics of a location in the medium to the mass vibration caused by acoustic perturbation. The boundary conditions of this study are shown in Fig. 2, of which the governing equation are as follow:

$$n·(-\frac{1}{{\rho }_0}·\mathrm{\nabla }{p}_u)=p_u\frac{i\omega }{Z_i},Z_i={\rho }_i{c}_i$$ (6)

where Z_i is resistivity [Pa·s/m]. Fig. 3 shows the meshing of the simulation computational domain. The maximum mesh size is 5 mm at ultrasonic probe interface.

Fig. 3.

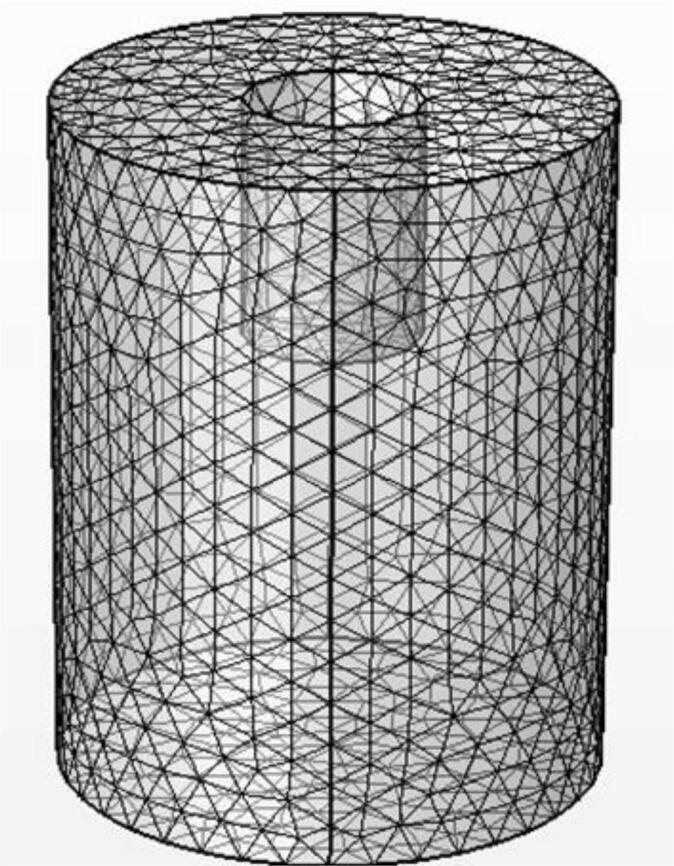
Mesh for acoustic pressure distribution calculationpok.

2.4. Apparatus and procedure

Aluminum foil erosion experiments were performed in JY92-Ⅱ Ultrasonic Cell Crusher shown in Fig. 4. The aluminum foil was placed vertically on the cross-section of the container, and the ultrasonic probe was placed close to the concave surface of the aluminum foil. In order to reduce the influence of water temperature changes on the erosion of aluminum foil, the experiment is implemented in the intermittent sonication method - the sonication time is 20 s, after which the sonication time is stopped for 20 s, each group is cycled 20 times, and the sonication is suspended for 5 min between each group, each aluminum foil is done for a total of 3 groups, that is, 60 times of sonication experiments. To reduce the effect of errors all experiments were repeated three times.

Fig. 4.

Ultrasonic cell crusher used in this experiment.

3. Results and discussion

3.1. Effect of configurations

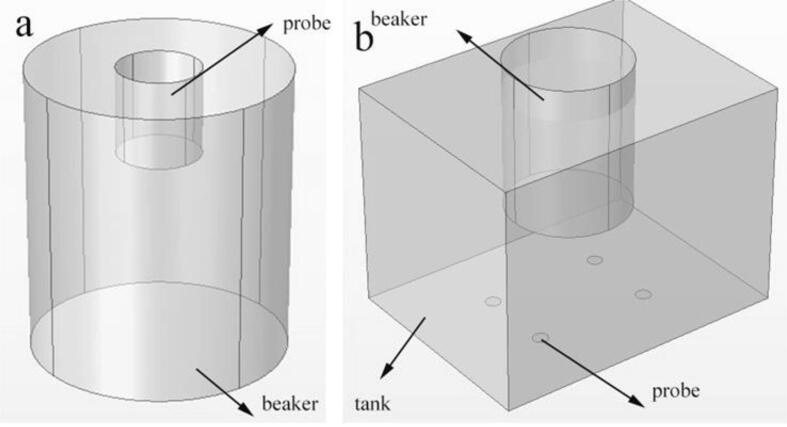
There are two configurations used in this study to introduce ultrasound waves into the reaction vessel, as shown in Fig. 5. These configurations are ultrasonic transducer probe (Fig. 5(a)), and the (Fig. 5(b)). Simulation was operated at an ultrasound frequency of 20 kHz and power of indirect irradiation ultrasonic bath 32 W. Fig. 6 shows the acoustic pressure distribution of two structures.

Fig. 5.

Configurations for ultrasonic irradiation method.

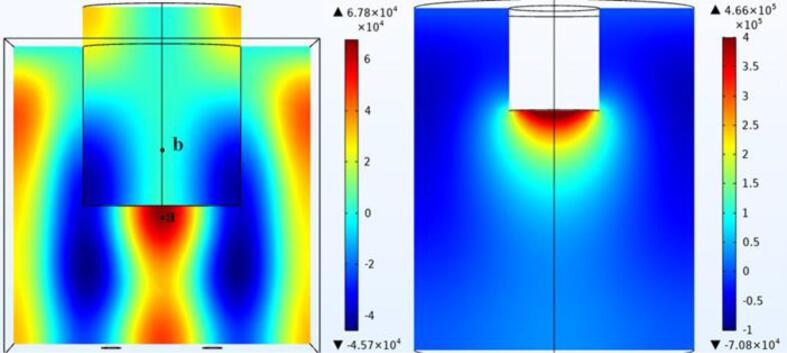
Fig. 6.

Acoustic pressure of two structures.

Under the same circumstances, acoustic pressure introduced by the ultrasonic transducer probe is higher than that of the indirect ultrasonic bath, the highest acoustic pressure of the ultrasound transducer probe is 4.66E5 Pa and the other is 6.78E4 Pa.

The high acoustic pressure of the indirect ultrasonic bath is concentrated above the horn in the water, but the acoustic pressure in the beaker will drop sharply because of the glass container. Acoustic pressure at point a in the tank is 66015 Pa, while the acoustic pressure at point b in the beaker is 1307.4 Pa. It is seen that the maximum acoustic pressure is located in the water below the beaker, which is the effect of the reflection of sound waves on the glass wall and the superposition of sound waves generated by the four probes. On the other hand, as shown in Fig. 6(b), the acoustic pressure region is mainly concentrated in the solution around the ultrasonic probe. Since the probe is inserted directly into the beaker, the value of the acoustic pressure of this kind of device is much larger than that of an indirect ultrasonic bath. Consequently, an ultrasonic transducer probe was used for subsequent ultrasonic radiation simulations.

3.2. Effect of length of ultrasonic horn

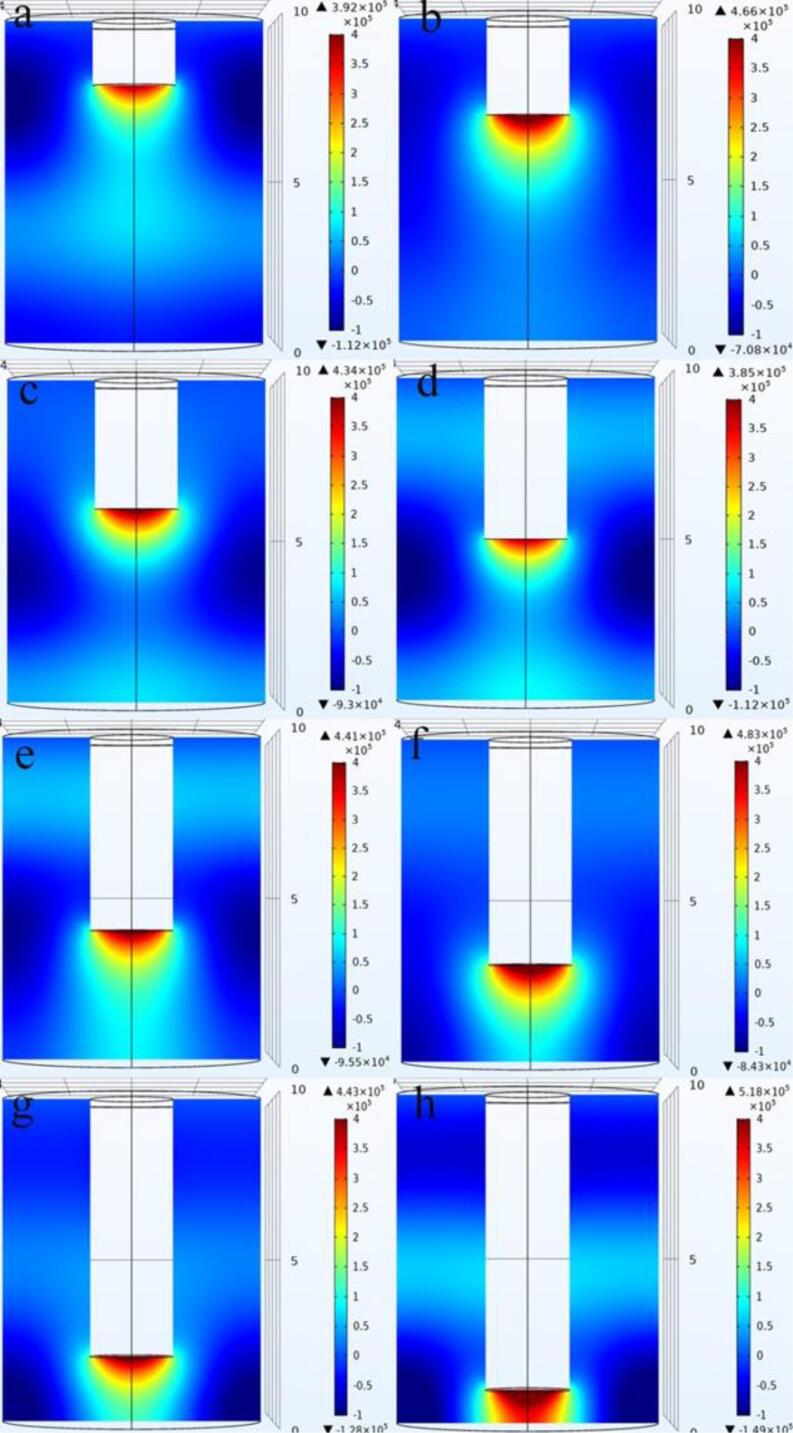
Acoustic pressure simulation of the ultrasonic horn with different horn heights was simulated in the beaker, as shown in Fig. 7. The results show that the position of the ultrasonic probe in the beaker has a significant effect on the acoustic pressure. With references of Fig. 7(a)-(h), it can be seen that the maximum sound pressure occurs at a distance of 10 mm between the probe and wall of the beaker, denoted by H_d = 10 mm in this study, which is caused by the huge impedance difference between the solution and the beaker wall. There is a huge impedance difference between the solution and the beaker wall, and when the ultrasonic transducer is positioned close to the water–glass boundary, the reflectivity of the sound waves will be higher, and thus the maximum sound pressure generated will be slightly higher. In addition to this, it can be seen that the sound pressure gradually increases as H_d decreases. The area of the beaker where the acoustic pressure changes significantly are the largest when H_d = 40, which means that the probe is in this position when the solution affected by the acoustic wave has the largest range and the best effect of ultrasonic radiation [4].

Fig. 7.

Acoustic pressure of beaker (a) 80 mm; (b) 70 mm; (c) 60 mm;(d) 50 mm; (e) 40 mm; (f) 30 mm; (g) 20 mm; (h)10 mm.

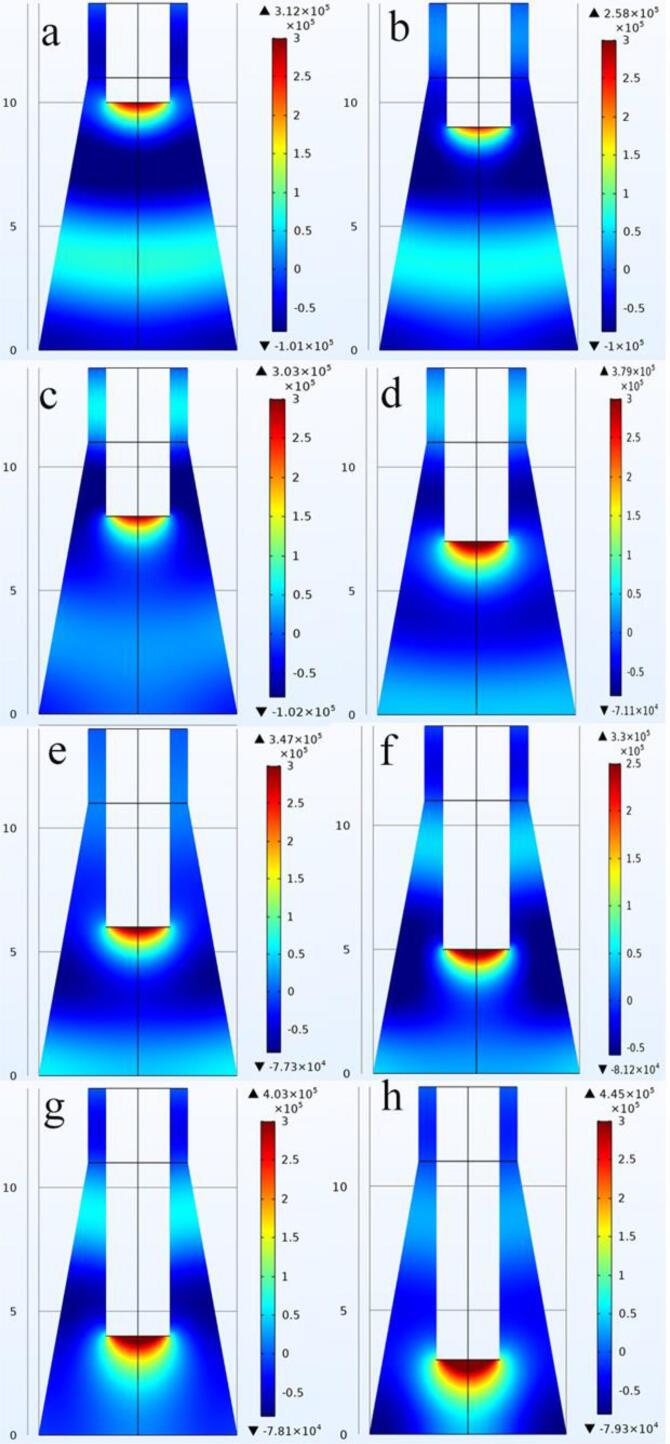
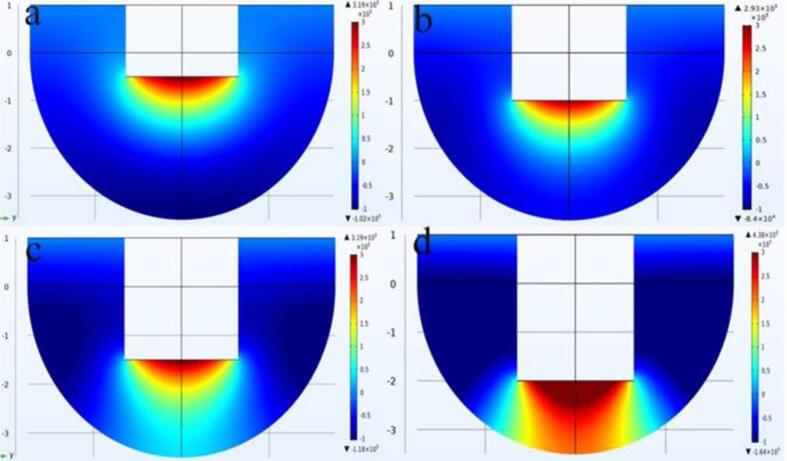
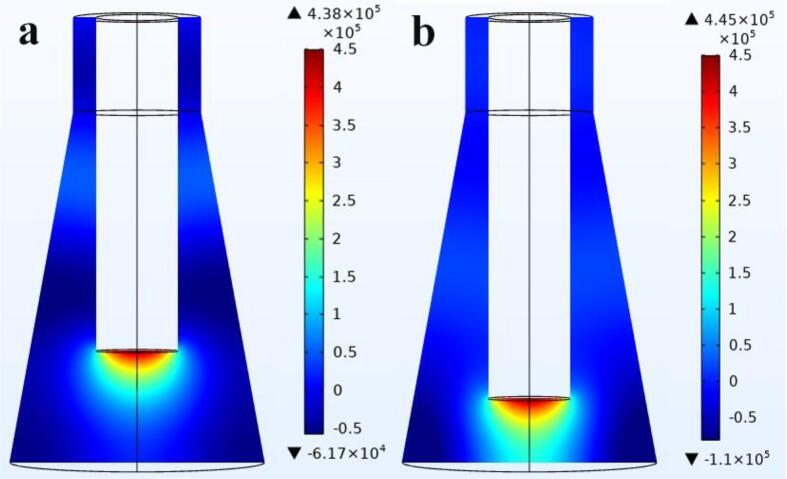
The acoustic pressure distribution of the Erlenmeyer flask is shown in Fig. 8. It can be seen that the maximum value of acoustic pressure increases as H_d decreases, but the value of sound pressure is smaller compared to that of the beaker. When the distance between the ultrasound probe and the bottom surface is H_d = 100 mm and H_d = 90 mm, there is a regular sound field distribution inside the conical bottle, which could be seen from Fig. 8(a) and Fig. 8(b). However, when the distance becomes smaller, the value of acoustic pressure decreases and then increases sharply, which is related to the wavelength (λ). Besides, Fig. 9 demonstrates the acoustic pressure distribution of spherical-bottomed flask with the H_d of 30 mm, 25 mm, 20 mm, and 15 mm. The maximum value of acoustic pressure occurs when H_d = 15 mm, which is 4.38E5 Pa, as shown in Fig. 9(d). High sound pressure region is mainly located near the probe when the distance between the probe and the spherical bottom surface is large, while the area in the vessel where the acoustic pressure changes significantly after the probe moves close to the spherical wall, which indicated the cavitation is this area is intense.

Fig. 8.

Acoustic pressure of Erlenmeyer flask (a) 100 mm; (b) 90 mm; (c) 80 mm; (d) 70 mm; (e) 60 mm; (f) 50 mm; (g) 40 mm; (h)30 mm.

Fig. 9.

Acoustic pressure of spherical -bottomed flask (a) 30 mm; (b) 25 mm; (c) 20 mm; (d) 15 mm;

3.3. Effect of vessel shape

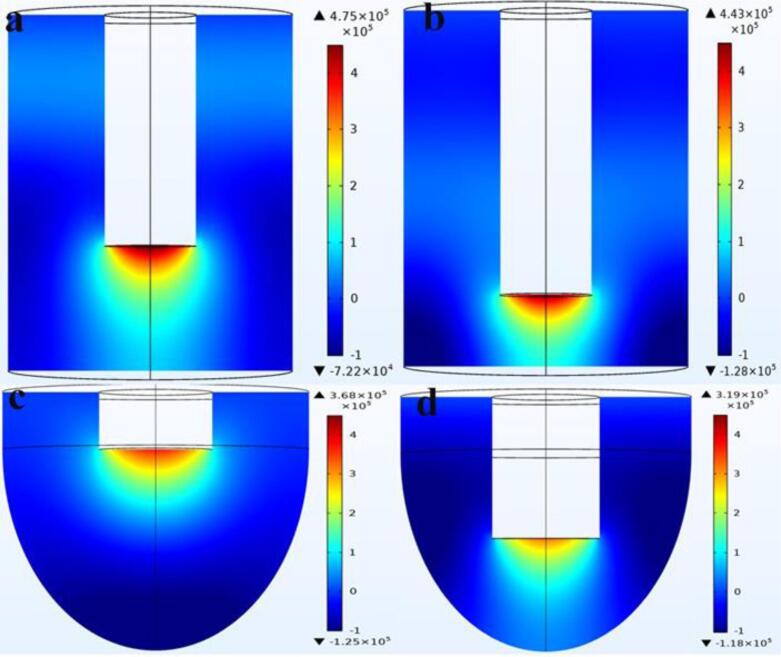
The dead zone where cavitation cannot be achieved is one of the most important parameters to be considered when preparing nanoparticles by ultrasonic radiation method [3], [12]. In order to avoid dead zones, it is most important to keep the distance between the probe tip and the wall container as short as possible [3]. As shown in Fig. 10 there is a clear change in the value and distribution of acoustic pressure when the distance between the probe tip and the bottom of the flat-bottomed beaker is changed. Not only is there a clear color change in the area below the probe, but the difference in peak negative acoustic pressure between H_d = 35 mm and H_d = 20 mm is 5.6E4 Pa. On the other hand, when the depth of the probe varies, the change of the sound pressure distribution in the spherical bottom flask is not significant, and the difference of the peak negative acoustic pressure is 7E3 Pa. Similar to the flat-bottomed beaker, the distribution of sound pressure in the conical flask varies dramatically, as shown in Fig. 11.

Fig. 10.

Acoustic pressure distribution in different vessels (a) flat bottom H_d = 35 mm; (b) flat bottom H_d = 20 mm; (c) spherical bottom H_d = 35 mm; (d) spherical bottom H_d = 20 mm.

Fig. 11.

Acoustic pressure distribution in Erlenmeyer flask (a) 35 mm; (b) 20 mm.

From the above, it can be seen that when the probe position is changed, the spherical-bottom vessel has a more stable acoustic pressure distribution than the flat-bottom vessel, which means that when ultrasonic radiation is performed in the spherical bottom vessel, it is not necessary to shorten the distance between the probe and the bottom of the vessel to avoid the appearance of dead zones.

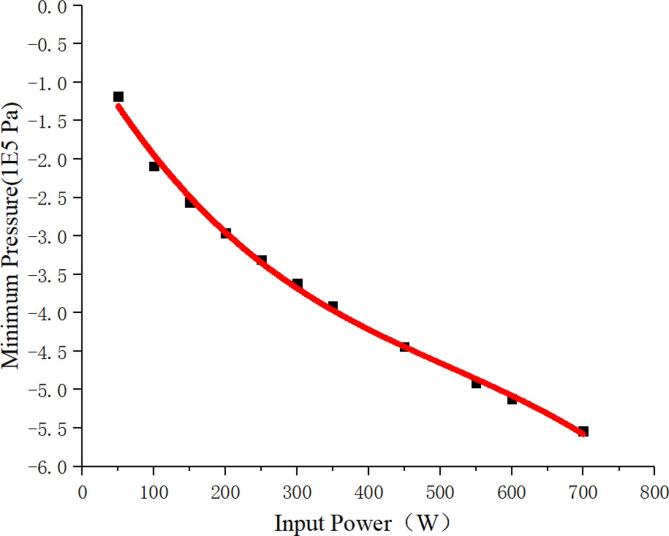
3.4. Effect of input power

The effect of input power on acoustic pressure is presented in Fig. 12 and Fig. 13. As demonstrated in Fig. 13, the increase in sound power leads to a decrease in peak negative acoustic pressure, which affects the cavitation process. Because after the negative acoustic pressure gradually increases and reaches a certain threshold, the bubble will collapse and break due to excessive vibration amplitude, and the bubble is in a transient cavitation state at this time. This process will produce a large amount of light and heat, which will influence the effect of ultrasonic radiation.

Fig. 12.

Effect of input power on acoustic pressure. (a) 50 W; (b) 700 W.

Fig. 13.

Minimum pressure at various input power for spherical bottom vessel.

A cubic equation was fitted to determine the expression for the input power versus the peak negative acoustic pressure as

$$y=-0.55676+B_{1}x+B_2{x}^2+B_3{x}^3$$ (7)

where B₁ = -0.01593, B₂ = 2.29987E-5,and B₃ = -1.49641E-8. The fitted curves are illustrated in Fig. 13, and COD = 0.996.

3.5. Experimental data

Aluminum foil can be used to evaluate the acoustic field distribution inside a vessel. By calculating the area of the aluminum foil eroded by ultrasound, the level of vessel cavitation under the influence of ultrasound can be evaluated. The area of the eroded aluminum foil (cavitation area) is calculated as [7]

$$\mathrm{E}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{a}=\mathrm{I}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{o}\mathrm{f}\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\times \frac{\mathit{Weight}lossofAluminum}{\mathit{Initial}weightofAluminum}$$ (8)

In this study, beakers and Erlenmeyer flasks were selected for the aluminum foil experiment.

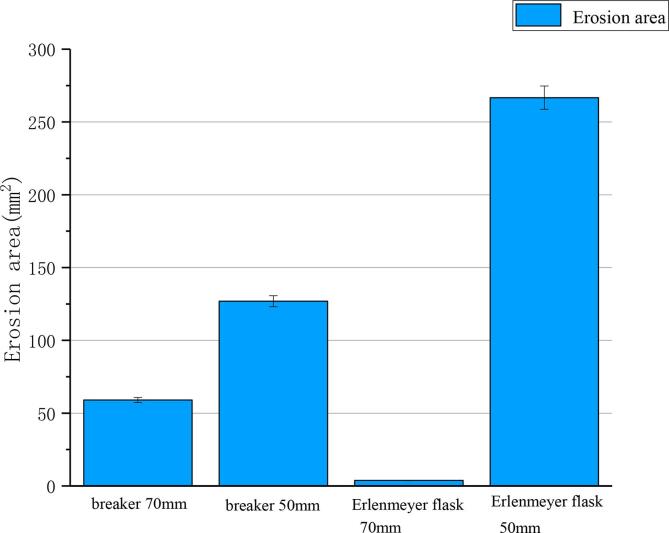
The erosion of the aluminum foil in the beaker and Erlenmeyer flask is shown in Fig. 14. The graph obtained from the calculation (Fig. 15) shows that the erosion area of the aluminum foil increases when the distance between the probe and the bottom of the vessel is close. Meanwhile, as the distance D decreases, the erosion area of aluminum foil in the beaker increases from 59.06 mm² to 126.89 mm², and the erosion area of aluminum foil in the conical flask increases from 3.78 mm² to 266.68 mm². The aluminum foil erosion area in the conical flask changes significantly as D decreases, suggesting that the use of Erlenmeyer flasks results in better cavitation than the use of beakers when considering the problem that too much penetration of the probe into the glass container can cause the container to break.

Fig. 14.

Erosion area of aluminum foil in the beaker (above) and Erlenmeyer flask (bottom).

Fig. 15.

Erosion area (cavitation area) in beaker and Erlenmeyer flask (mm²).

4. Conclusion

This study investigated the effects of ultrasound probe position, vessel shape, and input power on the efficiency of the ultrasound radiation method. The results show that probes that penetrate directly into the vessel produce higher acoustic pressure compared to indirect irradiation ultrasonic bath. Besides, the smaller the distance between the ultrasonic probe and the bottom of the vessel, the higher the maximum sound pressure due to the reflection of the bottom acoustic wave. Although the maximum sound pressure value of the flat-bottomed vessel with H_d = 10 mm is the highest and the ultrasonic radiation effect is the best, the sound pressure value of the flat-bottomed vessel is related to the position of the probe, and the range of the dead zone needs to be reduced by decreasing the value of H_d in specific experiments. On the other hand, the effect of the change of the probe position on the sound pressure distribution in the spherical bottom vessel is not obvious, which indicates that the spherical vessel is more suitable for the realization of ultrasonic irradiation method in specific experiments. Moreover, as the input power increases, the peak negative sound pressure in the vessel tends to decrease and the cavitation effect becomes more intense. In the aluminum foil corrosion experiment, the depth of the ultrasonic probe into the beaker did not have as much effect on the corrosion area as that of the Erlenmeyer flask, which indicates that the shape of the Erlenmeyer flask has a more significant effect on the cavitation results.

The results of this study indicated that a high input power probe and a spherical bottom vessel would be more favorable for the ultrasonic radiation method. Further studies aim to consider the effects of jets generated by cavitation bubble rupture on nanoparticles, nanomaterials and polymers to better understand the mechanism of ultrasonic cavitation in nanomaterial preparation or acoustic pore effects.

CRediT authorship contribution statement

Peilin Cao: Conceptualization, Investigation, Validation, Writing - original draft. Changchun Hao: Writing - review & editing, Project administration, Funding acquisition. Chen Ma: Methodology, Data curation. Haiyan Yang: Formal analysis, Methodology. Runguang Sun: Resources, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.