Abstract
The ionomers distributed on carbon particles in the catalyst layer of polymer electrolyte fuel cells (PEFCs) govern electrical power via proton transport and oxygen permeation to active platinum. Thus, ionomer distribution is a key to PEFC performance. This distribution is characterized by ionomer adsorption and deposition onto carbon during the catalyst-ink coating process; however, the adsorbed and deposited ionomers cannot easily be distinguished in the catalyst layer. Therefore, we identified these two types of ionomers based on the positional correlation between the ionomer and carbon particles. The cross-correlation function for the catalyst layer was obtained by small-angle neutron scattering measurements with varying contrast. From fitting with a model for a fractal aggregate of polydisperse core–shell spheres, we determined the adsorbed-ionomer thickness on the carbon particle to be 51 Å and the deposited-ionomer amount for the total ionomer to be 50%. Our technique for ionomer differentiation can be used to optimally design PEFC catalyst layers.
Introduction
Polymer electrolyte fuel cells (PEFCs) have attracted increasing interest in the context of realizing the UN’s Sustainable Development Goals to achieve a sustainable future. In PEFCs, the thin ionomer coatings in the catalyst layer of the electrode play a pivotal role in the mediation of proton conduction and oxygen permeation.1,2 To reduce the overpotential on the reaction of protons and oxygen with electrons at the catalyst, the coating structure of the ionomer should be optimized on the catalyst support.3,4 Thus, the effect of the ionomer fraction has been investigated to control its structure,5,6 and previous studies have reported improved PEFC performances with an increase in the ionomer distribution homogeneity.7,8
The ionomer distribution on catalyst supports has been studied via state-of-the-art microscopy techniques. A previous study has reported on electron tomography measurements with the use of a high-angle annular dark-field scanning transmission electron microscope (STEM) for a model catalyst layer of a Cs+-stained ionomer and a carbon support with no catalyst.9 A nanometer-scale 3D ionomer distribution was observed on the aggregated carbon particles. Moreover, atomic force microscopy (AFM) was used to observe catalyst-layer cross sections at high humidity and temperature.10 Based on adhesion force mapping, the ionomer thickness was evaluated as the gap between two separated carbon particles. Both these studies focused on the ionomer coating around carbon particles and reported an average coating thickness of 70 Å. On the other hand, scanning electron microscopy (SEM) observations at a low acceleration voltage of 0.5 kV have indicated micrometer-sized ionomer patches in the catalyst layers;11 the size distribution of the ionomer patch reportedly affected the PEFC performance. Here, we note that a hierarchical model of the ionomer distribution from Å to μm is required to optimize proton conduction and oxygen permeation in the catalyst layer.12,13
The ionomer distribution characteristic is determined by the catalyst-layer fabrication process.14 In the wet coating process, the catalyst ink is applied to the substrate with a slot die, a doctor blade, spraying, inkjet printing, and so on. Considering that the ink is a dispersion of the ionomer and catalyst support in an aqueous mixture, researchers have extensively studied the dispersion-medium influence on the catalyst-layer structure.15−19 Via comparing pre- and post-drying dispersion structures, it was shown that a homogeneous catalyst layer is generated by a well-dispersed catalyst ink, whereas a dense aggregated layer is produced by inks with network-structured agglomerates.20 In the structure formation process by drying, the ionomer location in the catalyst ink can influence the final ionomer distribution in the catalyst layer.21,22
In the catalyst ink, the ionomer both adsorbs onto the catalyst-support particles and floats in the dispersion media.23,24 The “adsorbed ionomers” form homogeneous thin ionomer coatings on the particles after drying because the shell of the adsorbed ionomer on the particles forms a monolayer due to electrostatic repulsion against further adsorption of the floating ionomer. Meanwhile, the floating ionomers are concentrated at the throats between particles to form capillary bridges during the drying process due to the surface tension of the inks.25 Thus, the floating ionomers are deposited onto aggregated carbon particles heterogeneously (“deposited ionomers”). Here, we note that adsorbed ionomers with thicknesses of <100 nm typically exhibit properties distinct from the bulk deposited ionomers.26−28 Therefore, when the volume fraction of these two types of ionomers is evaluated, we can calculate specific transport properties of the catalyst layers.29−31 We, thus, propose a minimum structure model expressing the two kinds of ionomers in the PEFC catalyst layer and a quantitative analysis technique to determine the hierarchical structure.
Analysis Methods
The adsorbed and deposited ionomers must be clearly distinguished in addition to discriminating the ionomer from the catalyst support. In this context, small-angle neutron scattering is a versatile tool for nanomaterial evaluation; the scattering length densities (SLDs) of the ionomer and the catalyst support for neutrons are ∼4 × 1010 cm–2 and 6 × 1010 cm–2, respectively, for a typical catalyst layer based on Nafion and platinum/carbon. When the pores in the catalyst layer are filled with a contrast-matched liquid with the catalyst-support particles, we can explicitly obtain the ionomer scattering function. The question here is this: how can the adsorbed ionomer be distinguished from the deposited ionomer? When the ionomer position is observed from a catalyst-support particle, the adsorbed ionomer is always located on the particle surface, whereas the deposited ionomer can randomly distribute in the remaining space. Therefore, an analysis of the correlation function between the ionomer and the catalyst support can be applied for distinguishing the two types of ionomers. Here, we note that the cross-correlation function can be evaluated from the cross-term of the partial scattering function, which was calculated from contrast-variation small-angle neutron scattering (CV-SANS) measurements of the catalyst-ink dispersion.32,33
In this approach, with the partial scattering functions of the scattering vector q, Iij(q), where i, j = C, P, and C and P indicate the catalyst support and the ionomer, respectively, the small-angle scattering from the catalyst layer, d Σ/d Ωn(q), can be expressed as
| 1 |
where 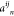 is defined as
(ρi – ρn)(ρj – ρn) with the SLD of the components, ρi and ρj for
the catalyst support
and the ionomer, and ρn for the
pore-filling liquid. It is noteworthy that ρn can be varied by changing the hydrogen/deuterium fractions
without affecting the structure for neutron observations, wherein n indexes the hydrogen/deuterium fraction. Subsequently,
using a transpose vector [ICC(q) ICP(q) IPP(q)]t, we obtain a 3 × n matrix M as
is defined as
(ρi – ρn)(ρj – ρn) with the SLD of the components, ρi and ρj for
the catalyst support
and the ionomer, and ρn for the
pore-filling liquid. It is noteworthy that ρn can be varied by changing the hydrogen/deuterium fractions
without affecting the structure for neutron observations, wherein n indexes the hydrogen/deuterium fraction. Subsequently,
using a transpose vector [ICC(q) ICP(q) IPP(q)]t, we obtain a 3 × n matrix M as
| 2 |
Here, the cross-term of the partial scattering function, ICP(q), and the self-terms, ICC(q) and IPP(q), are calculated from the measurement data of d Σ/d Ωn(q) with n ≥ 3 via the singular value decomposition of M.34
In the study, the three partial scattering functions were first fitted by a model for the fractal aggregation of core–shell spheres, which was introduced for the catalyst inks of the ionomer and the catalyst support.23 The support particles and adsorbed ionomers are expressed as fractal sphere aggregation and a shell of sphere aggregation, respectively. Because catalyst layers are the most condensed form of catalyst inks, we assume that the fundamental structures of the support particles and the adsorbed ionomer are similar. The scattering functions considering the sphere-size distribution are represented as follows
| 3 |
| 4 |
| 5 |
where N denotes the number density, R the core radius, ΔR the shell thickness, ϕshell the shell volume fraction, and ϕ̅ the average volume fraction outside the core–shell. Moreover, S(q) represents the structure factor of fractal aggregation,35 and F(q, R) and W(R) are the scattering amplitude of a sphere and the Schultz distribution of the radius, respectively. We have
| 6 |
| 7 |
| 8 |
where R̅ denotes the average particle radius, Dm the mass-fractal exponent, and Ξ the
cutoff distance related
to the gyration radius for an aggregate. Moreover, Z corresponds to the standard deviation of the Schultz function with 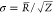 .
.
Experimental Section
The catalyst layer was prepared with an automatic applicator (Toyo Seiki Seisaku-sho, Ltd.) and a baker applicator (YBA, Yoshimitsu Seiki) on a silicon wafer (5 inch diameter × 626 μm thickness, P-type ⟨100⟩, Mitsubishi Materials Corporation). The coating speed was 20 mm/s, and the gap was 70 μm. The wet film was exposed overnight to an ambient atmosphere and dried for 1 h in vacuum at 80 °C. The catalyst-layer thickness was 6 μm. The ionomer-to-carbon weight fraction was set to be 0.75:1. The ionomer and the catalyst support in the catalyst ink were Nafion (D2020, Chemours) and platinum-supported carbon (TEC10V30E, Tanaka Holdings Co., Ltd.), respectively, which were dispersed in aqueous ethanol (water/alcohol ratio = 7/3 in weight) via a planetary mixer/deaerator (KK-50S, Kurabo Industries Ltd.) and an ultrasonic homogenizer (UH-600, SMT Co., Ltd.). The ionomer and catalyst-support volume fractions depend on the void space in the catalyst layer. By measuring the film weight and thickness and employing the component mass density in air, we evaluated the ionomer, catalyst-support, and void volume fractions to be 0.20, 0.27, and 0.53, respectively.
SANS measurements were performed with a TAIKAN time-of-flight instrument at the BL15 beamline of the MLF in J-PARC, Japan.36 The samples included 6 pieces of the catalyst layers on the silicon substrates cut into 15 mm squares from a coated 5 inch wafer. Contrast variation was performed with water/ethanol mixtures (9/1 in volume) to realize 6 different SLDs by changing the hydrogen/deuterium fraction of both water and ethanol. Each sample was immersed in the contrast-variation mixture to fill the pores between the ionomer-coated catalyst support and placed in 1 mm-gap titanium cells with two quartz windows. The scattering data were corrected for the backgrounds and incoherent scattering and normalized to an absolute intensity with a standard glassy carbon.
Results and Discussion
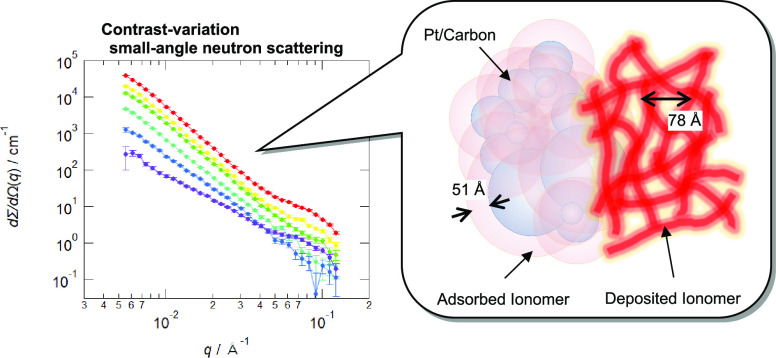
Figure 1 shows the SANS profiles of the catalyst layers with different pore-filling mixtures for contrast variation. The inset shows the SLD values of platinum-supported carbon, Nafion, and the mixture for the contrast-variation measurements. We clearly observe that neutrons are differently scattered by the identically structured catalyst layers depending on the contrast. When the SLD of the mixture of water and ethanol is 6 × 1010 cm–2, those of platinum and carbon are close to this value as shown in the inset of Figure 1. Thus, the SANS profile at the bottom reflects the ionomer structure. From the slope around −2 in the low-q regime, the shape of the ionomer is modeled as a thin film in the catalyst layer. Another SANS profile feature is the shoulder in the high-q regime. As the shoulder disappears when the mixture SLD is comparable with that of Nafion, 4 × 1010 cm–2, we can attribute this shoulder to ionomers with some periodicity. In the case of contrast matching with the ionomer, the SANS profile reflects the structure of the catalyst support. The blue curves are nearly linear in the log–log plot with slopes of −3 to −4, thereby indicating that the catalyst supports have a nature of mass fractal and surface fractal. Here, we can neglect the scattering from the small amount of 2–3 nm-diameter platinum nanoparticles because of the little SLD difference to the carbon. With a further decrease in the mixture SLD, the shoulder and a slope of around −4 are both observed for the top curve, corresponding to the ionomer and the catalyst support.
Figure 1.

Small-angle neutron scattering from a series of catalyst layers with various contrast mixtures in the pores with decreasing scattering length densities (SLDs). The inset presents the SLDs of the mixture (solid line and circles), carbon, Pt, and the ionomer. The color in the inset corresponds to the color of the curves in Figure 1.
To quantitatively determine the structure, we evaluated the partial scattering functions using the singular value decomposition method. Figure 2 shows the three partial scattering functions, Iij(q). The plots of the self-terms for the catalyst support and the ionomer, ICC(q) and IPP(q), are presented in Figure 2a,c, respectively, and that of the cross-term between the catalyst support and the ionomer, ICP(q), is presented in Figure 2b. The reconstructed scattering curves from the partial scattering functions obtained with the use of matrix M show reasonable agreement with the original data (Figure S1). The ICC(q) plots are aligned linearly with a slope of around −4, as expected from the contrast-matching data for the pore-filling mixture with SLD = 4 × 1010 cm–2, and the IPP(q) plots exhibit a shoulder, similar to the curve obtained for the mixture with SLD = 6 × 1010 cm–2 (see Figures S2 and S3). We note here that ICP(q) reflects the cross-correlation between the catalyst support and the ionomer. While the function has a slightly negative value at approximately q = 0.013 Å–1, an upturn to positive values is observed with the q value decreasing below 0.01 Å–1. While the negative regime indicates that the ionomer does not penetrate the catalyst support, the positive correlation proves the existence of a shell layer of the adsorbed ionomer on the catalyst support.37
Figure 2.

Partial scattering functions corresponding to (a) self-term of the catalyst support, (b) cross-term between the catalyst support and the ionomer, and (c) self-term of the ionomer. The solid and dotted lines indicate model fitting with and without the contribution of the deposited ionomer, respectively.
To evaluate the adsorbed-ionomer thickness, we employed a model for the fractal aggregates of the polydisperse core–shell spheres for data fitting, as described by eqs 3–8. The fitting curves for the partial scattering functions are overlaid with dotted lines in Figure 2. The three datasets are globally fitted with each model function, wherein the common parameters are optimized simultaneously with only ϕ̅ being fixed at the measured value of 0.2. Although the calculated curves fit the scattering functions in Figure 2a,b within the error bars, we observe a discrepancy in the high-q regime in Figure 2c. From Figure 2a, we can confirm that the fractal aggregate of polydisperse spheres is an appropriate model for the catalyst support. The slight small deviation from the data could originate from the influence of the surface fractal on the catalyst support. The structure factor S(q), the form factor ∫F2(q, R)W(R)d R, and the distribution function W(R) are presented in Figure 3. Furthermore, the fitting to the cross-term in Figure 2b demonstrates that a core–shell correlation exists between the catalyst support and the ionomer, i.e., the catalyst-support surface is homogeneously coated with a thin ionomer layer. However, the excess scattering corresponding to the self-term of the ionomer, IPP(q), in Figure 2c suggests that the deposited ionomer with a random distribution in the catalyst layer cannot be neglected for the fitting model. Hence, this overlooked nanostructure is considered in addition to the contribution of the adsorbed ionomer shell on the polydisperse spheres. In the study, we assigned the excess scattering to the Nafion cluster structure because the peak at q of ∼0.1 Å–1 is similar to that observed for swollen Nafion membranes (Figure S4, wherein the plots are fitted with the Teubner–Strey (T–S) model represented by eq 9).38 The short-range order in Nafion was expressed by the T–S model, which is applicable for microemulsion systems.39
| 9 |
where Δρ denotes the SLD difference, fd the domain volume fraction, k/2π the inverse of the characteristic for the domain size, and ξ the correlation length. The correlation function is
| 10 |
Next, we combined eqs 9 and 5 and fitted the three partial scattering functions again. The global fitting for the three curves successfully determined the many parameters of the functions. These fitting curves are overlaid with solid curves in Figure 2. The excess scattering in Figure 2c is closely reproduced upon considering the cluster structure of the randomly deposited ionomer, while Figure 2a,b shows little change.
Figure 3.
(a) Form factor for the catalyst-support particles, obtained by fitting with a core–shell sphere model with a radius distribution. The inset shows the Schultz distribution function for the radius. (b) Structure factor for the catalyst-support particles, obtained by fitting with a fractal aggregate model. The slope of the upturn is −3 in the log–log plot.
Table 1 lists the global fitting parameters obtained by the model for the fractal aggregates of the polydisperse core–shell spheres with the deposited ionomer. Here, ΔR = 51.3 Å represents the adsorbed-ionomer thickness on the carbon particles, which is consistent with that for similar systems observed by STEM and AFM, 70 ± 20 Å.9,10 Furthermore, the volume fraction in the shell, ϕshell, is obtained to be 0.74, thereby indicating that the rest of the volume in the ionomer shell contains the water/ethanol mixture. The average catalyst-support radius, R̅, and standard deviation, σ, are evaluated to be 72.3 and 44.0 Å, respectively. The wide distribution with a long tail to a large radius (inset of Figure 3a) demonstrates the polydisperse nature of the carbon particles. The particle aggregation structure was characterized by two parameters, the fractal dimension Dm = 3 and the cutoff length Ξ = 3500 Å, of a mass-fractal object with a clustered network in a limited q range. Thus, an upturn with a slope of −3 from unity could be confirmed in the structure factor (Figure 3b). We note that a fractal dimension, Dm, of ∼3 was estimated for calcium carbonate crystallization,34 corresponding to the measurement and modeling of sedimentary rocks.40−42 The structure factor represents the fractal distribution on the center of the core–shell particles.
Table 1. Fitting Parameters for the Catalyst Layer as Obtained by the Fractal Aggregate Model of Polydisperse Core–Shell Spheres and the Teubner–Strey Modela.
| fitting parameters | ||||
|---|---|---|---|---|
| fractal aggregate model of core–shell spheres | N | (cm–3) | 1.4 × 1016 | |
| ΔR | (Å) | 51.3 | ±0.8 | |
| ϕshell | 0.74 | ±0.01 | ||
| R̅ | (Å) | 72.3 | ±0.5 | |
| σ | (Å) | 44.0 | ±0.3 | |
| Dm | (Å) | 3 | ±0.004 | |
| Ξ | (Å) | 3500 | ±300 | |
| Teubner–Strey model | k | (Å–1) | 0.081 | ±0.001 |
| ξ | (Å) | 32 | ±3 | |
| fd | 0.085 | ±0.007 | ||
For the symbols in the table, see the description of each model in the text. Errors in the table are estimated from standard deviation of the fitting.
The adsorbed-ionomer volume fraction, fa, can be calculated from the specific surface area of the catalyst support SV as
| 11 |
where SV is obtained by fitting to the high-q regime of ICC(q) in Figure 2a with Porod’s law
| 12 |
As SV is evaluated to be (23 ± 1) × 10–4 Å–1 by the fitting at q = 0.04–0.12 Å–1, fa is calculated to be 0.086 ± 0.007. In contrast, the deposited-ionomer volume fraction, fd, is obtained to be 0.085 ± 0.007 from the Teubner–Strey model. The result suggests that the volume fractions of the adsorbed and deposited ionomers are 50 and 50%, respectively. The deposited ionomer exhibits a short-range order with the correlation function given by eq 10 within the patch, which is developed on the catalyst support during the catalyst-ink drying from the dispersion media. The period, 2π/k = 77.6 Å, can be attributed to the repulsive interaction between the rod-like micelles of the ionomer.43 Summing the fa and fd, the total volume fraction of ionomers is 0.171 ± 0.01, which is smaller than the value (= 0.2) evaluated from the macroscopic measurements on the film weight and thickness and the mass densities in air. The SANS measurements, on the other hand, were done for the samples immersed in the mixture of water and ethanol but not in air. In this situation, it is expected that the ionomers and the catalyst layer somehow expanded, leading to the increase in the void fraction. This increase may reduce the volume fraction of total ionomers in the system. This is one of the possible explanations for the discrepancy of the volume fraction between the SANS measurements and the macroscopic measurements.
The SEM micrograph of the catalyst layer is shown in Figure 4a. Primary particles with a diameter of ∼200 Å construct secondary aggregation with a fractal nature, wherein bright spots from Pt nanoparticles are found on the surface. However, it is difficult to distinguish the ionomer and the catalyst support because of their similar composition in terms of the average atomic number. Moreover, the adsorbed and deposited ionomers also cannot be distinguished. Nonetheless, micrographs obtained in the beam-deceleration mode may support the existence of a thin coating for a penetration depth of <20 Å of 0.2 kV incident electrons (as per Monte Carlo simulations). Comparing the two expanded insets, we hardly observe Pt nanoparticles with white spots in Figure 4b, as indicated by arrows. The visibility fluctuation of Pt nanoparticles reflects the thickness distribution of the ionomer coating, which may be affected by the deposited ionomer present on the adsorbed ionomer.
Figure 4.
Scanning electron microscope (SEM) micrographs of the catalyst layer at landing voltages of (a) 0.5 kV and (b) 0.2 kV, obtained by using a Regulus 8230 instrument (Hitachi High-Tech Corporation). The bar in the micrograph represents 1000 Å. A difference in a white spot of a Pt nanoparticle is presented by arrows in the insets. (c) Schematic of the adsorbed and deposited ionomers on the catalyst support, where Pt nanoparticles are omitted for clarity. The two types of the ionomers are distinguished by the positional correlation expressed with the partial scattering functions. A core–shell model and the Teubner–Strey model are used for the fitting.
Figure 4c shows the quantitative nanoscale model of the ionomer on the catalyst layer. We note that some ionomer molecules homogeneously adsorb onto the aggregated carbon particles. In the thin film, the nanostructure in the ionomer is distorted from that in bulk membranes. The adsorbed-ionomer thickness, ΔR = 51 Å, was evaluated from the partial scattering functions via the fractal aggregation model of polydisperse core–shell spheres. Meanwhile, some ionomer micelles in a dispersion may randomly deposit to form patches, where we also observed a short-range-ordered cluster structure with a period of 78 Å. Note that it was hard to model the shape of the deposited ionomer because the q range of the current SANS measurement was limited to 5 × 10–2 Å–1. The two types of ionomers exhibit distinct features in terms of the relative position of the catalyst support and the inner structure of the coating.
The structure parameters for the adsorbed and deposited ionomers are available to validate and improve simulation of the catalyst layer performance. Some models have been proposed to simulate PEFC performance recently, where the proton diffusion and oxygen permeation are directly evaluated from tortuosity in a three-dimensional microstructure model of a catalyst layer.25,44−46 Since the models are based on the porous structure of the carbon particles and the coating structure of the ionomer, focused ion-beam SEM and TEM tomography can provide data for construction of a catalyst-layer structure, respectively.47 However, the limited observation volume, elaborated sample preparation, and inevitable radiation damage require complemental methods. Furthermore, our approach for the ionomer coating structure by considering the positional correlation with the carbon support has an advantage for modeling the catalyst layer more sophisticatedly. The two types of ionomers with different thicknesses and properties should be essential to express the interesting nature of the ionomer in a catalyst layer.
Conclusions
From the three partial scattering functions obtained by CV-SANS, we could distinguish the adsorbed and deposited ionomers based on their correlation with the catalyst support. We applied a fractal aggregate model of polydisperse core–shell spheres to evaluate the adsorbed-layer thickness and volume fraction. The deposited-ionomer amount was found to be sensitive to the peak intensity of the self-term for the ionomer modeled by the Teubner–Strey function. From fitting with a model for a fractal aggregate of polydisperse core–shell spheres, we determined the adsorbed-ionomer thickness to be 51 Å on the carbon particles and the fraction of the deposited ionomer to be 50% of the total ionomer.
Because proton conductivity and oxygen transport in a catalyst layer depend on the ionomer coating structure on the catalyst support, CV-SANS-based structural analysis can critically aid optimal PEFC design.
Acknowledgments
The neutron experiments at the Materials and Life Science Experimental Facility of J-PARC were performed under the aegis of the user program (proposal nos. 2019A0318 and 2019L04). The authors thank Hiroyuki Aoki, Kanae Ito, and Yukinobu Kawakita for their valuable comments. The authors also acknowledge Takahisa Suzuki, Akihiro Shinohara, and Yasutaka Nagai for fruitful discussions.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c01535.
Reconstructed data of scattering, contrast-matching data and partial scattering function for the ionomer and the catalyst support, and scattering data of Nafion (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Holdcroft S. Fuel Cell Catalyst Layers: A Polymer Science Perspective. Chem. Mater. 2014, 26, 381–393. 10.1021/cm401445h. [DOI] [Google Scholar]
- Karan K. PEFC catalyst layer: Recent advances in materials, microstructural characterization, and modeling. Curr. Opin. Electrochem. 2017, 5, 27–35. 10.1016/j.coelec.2017.08.018. [DOI] [Google Scholar]
- Takahashi S.; Mashio T.; Horibe N.; Akizuki K.; Ohma A. Analysis of the Microstructure Formation Process and Its Influence on the Performance of Polymer Electrolyte Fuel-Cell Catalyst Layers. ChemElectroChem 2015, 2, 1560–1567. 10.1002/celc.201500131. [DOI] [Google Scholar]
- Liu Y.; Murphy M. W.; Baker D. R.; Gu W.; Ji C.; Jorne J.; Gasteiger H. A. Proton Conduction and Oxygen Reduction Kinetics in PEM Fuel Cell Cathodes: Effects of Ionomer-to-Carbon Ratio and Relative Humidity. J. Electrochem. Soc. 2009, 156, B970. 10.1149/1.3143965. [DOI] [Google Scholar]
- Sasikumar G.; Ihm J. W.; Ryu H. Dependence of optimum Nafion content in catalyst layer on platinum loading. J. Power Sources 2004, 132, 11–17. 10.1016/j.jpowsour.2003.12.060. [DOI] [Google Scholar]
- Liu Y.; Ji C.; Gu W.; Jorne J.; Gasteiger H. A. Effects of Catalyst Carbon Support on Proton Conduction and Cathode Performance in PEM Fuel Cells. J. Electrochem. Soc. 2011, 158, B614. 10.1149/1.3562945. [DOI] [Google Scholar]
- Ott S.; Orfanidi A.; Schmies H.; Anke B.; Nong H. N.; Hübner J.; Gernert U.; Gliech M.; Lerch M.; Strasser P. Ionomer distribution control in porous carbon-supported catalyst layers for high-power and low Pt-loaded proton exchange membrane fuel cells. Nat. Mater. 2020, 19, 77–85. 10.1038/s41563-019-0487-0. [DOI] [PubMed] [Google Scholar]
- Ahn C.-Y.; Ahn J.; Kang S. Y.; Kim O.-H.; Lee D. W.; Lee J. H.; Shim J. G.; Lee C. H.; Cho Y.-H.; Sung Y.-E. Enhancement of service life of polymer electrolyte fuel cells through application of nanodispersed ionomer. Sci. Adv. 2020, 6, eaaw0870 10.1126/sciadv.aaw0870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez-Haro M.; Guétaz L.; Printemps T.; Morin A.; Escribano S.; Jouneau P. H.; Bayle-Guillemaud P.; Chandezon F.; Gebel G. Three-dimensional analysis of Nafion layers in fuel cell electrodes. Nat. Commun. 2014, 5, 5229. 10.1038/ncomms6229. [DOI] [PubMed] [Google Scholar]
- Morawietz T.; Handl M.; Oldani C.; Friedrich K. A.; Hiesgen R. Quantitative in Situ Analysis of Ionomer Structure in Fuel Cell Catalytic Layers. ACS Appl. Mater. Interfaces 2016, 8, 27044–27054. 10.1021/acsami.6b07188. [DOI] [PubMed] [Google Scholar]
- Orfanidi A.; Rheinländer P. J.; Schulte N.; Gasteiger H. A. Ink Solvent Dependence of the Ionomer Distribution in the Catalyst Layer of a PEMFC. J. Electrochem. Soc. 2018, 165, F1254–F1263. 10.1149/2.1251814jes. [DOI] [Google Scholar]
- Doo G.; Lee J. H.; Yuk S.; Choi S.; Lee D.-H.; Lee D. W.; Kim H. G.; Kwon S. H.; Lee S. G.; Kim H.-T. Tuning the ionomer distribution in the fuel cell catalyst layer with scaling the ionomer aggregate size in dispersion. ACS Appl. Mater. Interfaces 2018, 10, 17835–17841. 10.1021/acsami.8b01751. [DOI] [PubMed] [Google Scholar]
- Sun C.-N.; More K. L.; Veith G. M.; Zawodzinski T. A. Composition Dependence of the Pore Structure and Water Transport of Composite Catalyst Layers for Polymer Electrolyte Fuel Cells. J. Electrochem. Soc. 2013, 160, F1000–F1005. 10.1149/2.055309jes. [DOI] [Google Scholar]
- Hatzell K. B.; Dixit M. B.; Berlinger S. A.; Weber A. Z. Understanding inks for porous-electrode formation. J. Mater. Chem. A 2017, 5, 20527–20533. 10.1039/C7TA07255D. [DOI] [Google Scholar]
- Shin S. J.; Lee J. K.; Ha H. Y.; Hong S. A.; Chun H. S.; Oh I. H. Effect of the catalytic ink preparation method on the performance of polymer electrolyte membrane fuel cells. J. Power Sources 2002, 106, 146–152. 10.1016/S0378-7753(01)01045-X. [DOI] [Google Scholar]
- Chisaka M.; Daiguji H. Effect of Organic Solvents on Catalyst Layer Structure in Polymer Electrolyte Membrane Fuel Cells. J. Electrochem. Soc. 2009, 156, B22. 10.1149/1.3000592. [DOI] [Google Scholar]
- Ngo T. T.; Yu T. L.; Lin H.-L. Influence of the composition of isopropyl alcohol/water mixture solvents in catalyst ink solutions on proton exchange membrane fuel cell performance. J. Power Sources 2013, 225, 293–303. 10.1016/j.jpowsour.2012.10.055. [DOI] [Google Scholar]
- Kim T.-H.; Yi J.-Y.; Jung C.-Y.; Jeong E.; Yi S.-C. Solvent effect on the Nafion agglomerate morphology in the catalyst layer of the proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2017, 42, 478–485. 10.1016/j.ijhydene.2016.12.015. [DOI] [Google Scholar]
- Sharma R.; Andersen S. M. Zoom in Catalyst/Ionomer Interface in Polymer Electrolyte Membrane Fuel Cell Electrodes: Impact of Catalyst/Ionomer Dispersion Media/Solvent. ACS Appl. Mater. Interfaces 2018, 10, 38125–38133. 10.1021/acsami.8b14622. [DOI] [PubMed] [Google Scholar]
- Kumano N.; Kudo K.; Suda A.; Akimoto Y.; Ishii M.; Nakamura H. Controlling cracking formation in fuel cell catalyst layers. J. Power Sources 2019, 419, 219–228. 10.1016/j.jpowsour.2019.02.058. [DOI] [Google Scholar]
- Jung C.-Y.; Kim W.-J.; Yi S.-C. Optimization of catalyst ink composition for the preparation of a membrane electrode assembly in a proton exchange membrane fuel cell using the decal transfer. Int. J. Hydrogen Energy 2012, 37, 18446–18454. 10.1016/j.ijhydene.2012.09.013. [DOI] [Google Scholar]
- Van Cleve T.; Khandavalli S.; Chowdhury A.; Medina S.; Pylypenko S.; Wang M.; More K. L.; Kariuki N.; Myers D. J.; Weber A. Z.; Mauger S. A.; Ulsh M.; Neyerlin K. C. Dictating Pt-Based Electrocatalyst Performance in Polymer Electrolyte Fuel Cells, from Formulation to Application. ACS Appl. Mater. Interfaces 2019, 11, 46953–46964. 10.1021/acsami.9b17614. [DOI] [PubMed] [Google Scholar]
- Shibayama M.; Matsunaga T.; Kusano T.; Amemiya K.; Kobayashi N.; Yoshida T. SANS studies on catalyst ink of fuel cell. J. Appl. Polym. Sci. 2014, 131, 39842. 10.1002/app.39842. [DOI] [Google Scholar]
- Takahashi S.; Shimanuki J.; Mashio T.; Ohma A.; Tohma H.; Ishihara A.; Ito Y.; Nishino Y.; Miyazawa A. Observation of ionomer in catalyst ink of polymer electrolyte fuel cell using cryogenic transmission electron microscopy. Electrochim. Acta 2017, 224, 178–185. 10.1016/j.electacta.2016.12.068. [DOI] [Google Scholar]
- Inoue G.; Ohnishi T.; So M.; Park K.; Ono M.; Tsuge Y. Simulation of carbon black aggregate and evaluation of ionomer structure on carbon in catalyst layer of polymer electrolyte fuel cell. J. Power Sources 2019, 439, 227060. 10.1016/j.jpowsour.2019.227060. [DOI] [Google Scholar]
- Eastman S. A.; Kim S.; Page K. A.; Rowe B. W.; Kang S.; Soles C. L.; Yager K. G. Effect of Confinement on Structure, Water Solubility, and Water Transport in Nafion Thin Films. Macromolecules 2012, 45, 7920–7930. 10.1021/ma301289v. [DOI] [Google Scholar]
- Frieberg B. R.; Page K. A.; Graybill J. R.; Walker M. L.; Stafford C. M.; Stafford G. R.; Soles C. L. Mechanical Response of Thermally Annealed Nafion Thin Films. ACS Appl. Mater. Interfaces 2016, 8, 33240–33249. 10.1021/acsami.6b12423. [DOI] [PubMed] [Google Scholar]
- Ogata Y.; Abe T.; Yonemori S.; Yamada N. L.; Kawaguchi D.; Tanaka K. Impact of the Solid Interface on Proton Conductivity in Nafion Thin Films. Langmuir 2018, 34, 15483–15489. 10.1021/acs.langmuir.8b03396. [DOI] [PubMed] [Google Scholar]
- Das P. K.; Li X.; Liu Z.-S. Effective transport coefficients in PEM fuel cell catalyst and gas diffusion layers: Beyond Bruggeman approximation. Appl. Energy 2010, 87, 2785–2796. 10.1016/j.apenergy.2009.05.006. [DOI] [Google Scholar]
- Zeng R.; Zhang H. Y.; Liang S. Z.; Wang L. G.; Jiang L. J.; Liu X. P. Possible scenario of forming a catalyst layer for proton exchange membrane fuel cells. RSC Adv. 2020, 10, 5502–5506. 10.1039/C9RA09864J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iden H.; Ohma A.; Shinohara K. Analysis of Proton Transport in Pseudo Catalyst Layers. J. Electrochem. Soc. 2009, 156, B1078. 10.1149/1.3169514. [DOI] [Google Scholar]
- Yoshimune W.; Harada M. Effect of Pt Loading on the Adsorption of Perfluoro-sulfonic Acid Ionomer in Catalyst Ink for Polymer Electrolyte Fuel Cells. Chem. Lett. 2019, 48, 487–490. 10.1246/cl.190017. [DOI] [Google Scholar]
- Yoshimune W.; Harada M. Impact of Nonadsorbed Ionomer on Viscosity of Catalyst Inks for Polymer Electrolyte Fuel Cells. Bull. Chem. Soc. Jpn. 2020, 93, 302–307. 10.1246/bcsj.20190321. [DOI] [Google Scholar]
- Endo H.; Schwahn D.; Cölfen H. On the role of block copolymer additives for calcium carbonate crystallization: small angle neutron scattering investigation by applying contrast variation. J. Chem. Phys. 2004, 120, 9410–9423. 10.1063/1.1691736. [DOI] [PubMed] [Google Scholar]
- Teixeira J. Small-angle scattering by fractal systems. J. Appl. Crystallogr. 1988, 21, 781–785. 10.1107/S0021889888000263. [DOI] [Google Scholar]
- Takata S.-i.; Suzuki J.-i.; Shinohara T.; Oku T.; Tominaga T.; Ohishi K.; Iwase H.; Nakatani T.; Inamura Y.; Ito T.; Suzuya K.; Aizawa K.; Arai M.; Otomo T.; Sugiyama M.. The Design and q Resolution of the Small and Wide Angle Neutron Scattering Instrument (TAIKAN) in J-PARC. In Proceedings of the 2nd International Symposium on Science at J-PARC — Unlocking the Mysteries of Life, Matter and the Universe —; JPS Conference Proceedings: 2015. [Google Scholar]
- Kusano T.; Hiroi T.; Amemiya K.; Ando M.; Takahashi T.; Shibayama M. Structural evolution of a catalyst ink for fuel cells during the drying process investigated by CV-SANS. Polym. J. 2015, 47, 546–555. 10.1038/pj.2015.36. [DOI] [Google Scholar]
- Teubner M.; Strey R. Origin of the scattering peak in microemulsions. J. Chem. Phys. 1987, 87, 3195–3200. 10.1063/1.453006. [DOI] [Google Scholar]
- Peng J.; Cantillo N. M.; Nelms K. M.; Roberts L. S.; Goenaga G.; Imel A.; Barth B. A.; Dadmun M.; Heroux L.; Hayes D. G.; Zawodzinski T. Electron Transfer in Microemulsion-Based Electrolytes. ACS Appl. Mater. Interfaces 2020, 12, 40213–40219. 10.1021/acsami.0c07028. [DOI] [PubMed] [Google Scholar]
- Wong P.; Howard J.; Lin J. S. Surface roughening and the fractal nature of rocks. Phys. Rev. Lett. 1986, 57, 637–640. 10.1103/PhysRevLett.57.637. [DOI] [PubMed] [Google Scholar]
- Wong P.; Bray A. J. Porod scattering from fractal surfaces. Phys. Rev. Lett. 1988, 60, 1344. 10.1103/PhysRevLett.60.1344. [DOI] [PubMed] [Google Scholar]
- Giri A.; Tarafdar S.; Gouze P.; Dutta T. Fractal geometry of sedimentary rocks: simulation in 3-D using a Relaxed Bidisperse Ballistic Deposition Model. Geophysical Journal International 2013, 192, 1059–1069. 10.1093/gji/ggs084. [DOI] [Google Scholar]
- Yamaguchi M.; Matsunaga T.; Amemiya K.; Ohira A.; Hasegawa N.; Shinohara K.; Ando M.; Yoshida T. Dispersion of Rod-like Particles of Nafion in Salt-Free Water/1-Propanol and Water/Ethanol Solutions. J. Phys. Chem. B 2014, 118, 14922–14928. 10.1021/jp506814m. [DOI] [PubMed] [Google Scholar]
- Inoue G.; Kawase M. Effect of porous structure of catalyst layer on effective oxygen diffusion coefficient in polymer electrolyte fuel cell. J. Power Sources 2016, 327, 1–10. 10.1016/j.jpowsour.2016.07.037. [DOI] [Google Scholar]
- So M.; Park K.; Tsuge Y.; Inoue G. A Particle Based Ionomer Attachment Model for a Fuel Cell Catalyst Layer. J. Electrochem. Soc. 2020, 167, 013544 10.1149/1945-7111/ab68d4. [DOI] [Google Scholar]
- Matsuda T.; Kobayashi K.; Mabuchi T.; Inoue G.; Tokumasu T. Multiscale simulation of proton transport in the catalyst layer with consideration of ionomer thickness distribution. ECS Trans. 2020, 98, 187. 10.1149/09809.0187ecst. [DOI] [Google Scholar]
- Okumura M.; Noda Z.; Matsuda J.; Tachikawa Y.; Nishihara M.; Lyth S. M.; Hayashi A.; Sasaki K. Correlating Cathode Microstructure with PEFC Performance Using FIB-SEM and TEM. J. Electrochem. Soc. 2017, 164, F928–F934. 10.1149/2.0581709jes. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.