Submillimeter MR fingerprinting using deep learning-based tissue quantification

Abstract

Purpose:

To develop a rapid 2D MR fingerprinting technique with a submillimeter in-plane resolution using a deep learning-based tissue quantification approach.

Methods:

A rapid and high-resolution MR fingerprinting technique was developed for brain T₁ and T₂ quantification. The 2D acquisition was performed using a FISP-based MR fingerprinting sequence and a spiral trajectory with 0.8-mm in-plane resolution. A deep learning-based method was used to replace the standard template matching method for improved tissue characterization. A novel network architecture (i.e., residual channel attention U-Net) was proposed to improve high-resolution details in the estimated tissue maps. Quantitative brain imaging was performed with 5 adults and 2 pediatric subjects, and the performance of the proposed approach was compared with several existing methods in the literature.

Results:

In vivo measurements with both adult and pediatric subjects show that high-quality T₁ and T₂ mapping with 0.8-mm in-plane resolution can be achieved in 7.5 seconds per slice. The proposed deep learning method outperformed existing algorithms in tissue quantification with improved accuracy. Compared with the standard U-Net, high-resolution details in brain tissues were better preserved by the proposed residual channel attention U-Net. Experiments on pediatric subjects further demonstrated the potential of the proposed technique for fast pediatric neuroimaging. Alongside reduced data acquisition time, a 5-fold acceleration in tissue property mapping was also achieved with the proposed method.

Conclusion:

A rapid and high-resolution MR fingerprinting technique was developed, which enables high-quality T₁ and T₂ quantification with 0.8-mm in-plane resolution in 7.5 seconds per slice.

1 |. INTRODUCTION

Quantitative MRI has great potential for the detection and diagnosis of various diseases, including cancer, edema, and sclerosis.^1–3 Although its importance has long been recognized, the adoption of quantitative imaging for clinical practice remains a challenge, which is largely due to the prolonged acquisition times. Magnetic resonance fingerprinting (MRF) is a relatively new MRI framework for quantitative MRI, and can provide rapid and simultaneous quantification of multiple tissue properties.⁴ Compared with conventional quantitative imaging approaches, the MRF technique uses pseudorandom acquisition parameters, such as flip angles and TRs, to obtain unique signal evolutions for each tissue type, and estimates the tissue property values using a template-matching method. Specifically, each observed signal evolution is matched to a precomputed MRF dictionary, which contains a large number of tissue property values and their corresponding signal evolutions simulated by Bloch equations. During the template-matching process, the dictionary entry with the highest correlation to the observed signal is selected and the corresponding tissue property values are retrieved.

Although MRF has demonstrated superior performance as compared with other quantitative techniques for T₁ and T₂ mapping, its spatial resolution is generally lower as compared with the current clinical standard. For example, the original 2D MRF technique was performed with a spatial resolution of 2 × 2 × 5 mm³ for adult brain imaging,⁴ and a recent pediatric study was conducted with 1 × 1 × 3 mm³ for neuroimaging of typically developing children. Further improvement in the spatial resolution of MRF techniques is desired, which will facilitate wide applications especially for pediatric imaging and characterization of small lesions. However, high-resolution MRF, particularly at submillimeter levels, is technically challenging and often requires extended scan times. Since the introduction of the MRF technique in 2013, many different techniques have been proposed to accelerate MRF acquisition as well as postprocessing.^5–14 Most of these advanced methods focus on extracting more information from the MRF data set for improved accuracy and acquisition speed.

Recently, deep learning–based approaches have been proposed for tissue quantification in MRF.^15–22 Compared with the standard template matching algorithm, deep learning can extract more advanced features from the complex MRF signal evolution for improved tissue characterization and accelerated tissue property mapping. Specifically, Cohen et al used a 4-layer neural network and achieved an approximate 300–5000-fold reduction in computation time for tissue property mapping as compared with the standard template matching approach.¹⁵ Fang et al²² proposed a spatially constrained quantification approach that exploits spatial information from neighboring pixels using a convolutional network (i.e., U-Net²³) and achieved accurate quantification using a 4-fold reduction in scan time (i.e., from about 23 to 6 seconds for each 2D MRF data set). Although the spatially constrained quantification method²² enabled accurate quantification with less sampling data, some image blurring was noticed in the estimated tissue maps, which hinders its application for high-resolution tissue quantification. Based on the conventional U-Net method, an improved network architecture, called the residual channel attention U-Net (RCA-U-Net), has been developed in this study. Compared with the standard U-Net structure, which uses stacked convolutional layers for feature extraction, the RCA-U-Net uses residual channel attention blocks (RCABs)²⁵ to enhance high-frequency information in the intermediate feature maps and therefore the final network output. The RCAB also reweights each feature channel based on its contained information for tissue quantification, making the network focus more on the channels with more information and less noise, thus improving the training efficiency and quantification accuracy in high-resolution MRF.

The aim of this study was to develop a rapid, submillimeter 2D MRF method using the RCA-U-Net. The study was established and validated with in vivo brain imaging on 5 healthy adult subjects and 2 pediatric subjects. The performance of the proposed method in terms of quantification accuracy and processing speed was also compared with several existing algorithms for MRF processing.

2 |. METHODS

2.1 |. Magnetic resonance fingerprinting acquisition and image reconstruction

All MRF experiments were performed on a Siemens 3T Prisma scanner (Erlangen, Germany) with a 32-channel head coil. The 2D FISP-based MRF method previously developed for cardiac MRF was adopted^26,27 and applied with a spiral trajectory with 0.8-mm resolution (FOV, 25 cm; matrix size, 304 × 304; slice thickness, 3 mm). Variable acquisition parameters, such as flip angles and inversion pulses, were applied to encode MRF signal in the acquisition. Each MRF image was acquired with a spiral readout, and a golden-angle rotation was further applied between adjacent MRF images to increase spatial inhomogeneities (Supporting Information Figure S1). A uniform spiral trajectory, instead of a variable-density spiral, was used to minimize the readout time and image blurring incurred due to B₀ field inhomogeneities (spiral readout time, 8.0 msec; Supporting Information Figure S2). A total of about 2300 time frames were acquired with variable flip angles ranging from 5° to 12° (Supporting Information Figure S1). Instead of acquiring only 1 spiral arm for each time frame as the conventional MRF approach (in-plane reduction factor of 48), 4 spiral arms were acquired for each time frame (in-plane reduction factor of 12) to reduce the aliasing artifacts and ensure high-quality quantitative maps for the training purpose. The acquisition was designed to acquire the first spiral arm for all time frames and was followed by the sampling of the remaining 3 spiral arms. A constant waiting time of 20 seconds was applied between the sampling of different spiral arms to ensure complete longitudinal relaxation for all brain tissues, including CSF. A constant TR of 10.4 msec was used in the study, and the total scan time for 1 slice was approximately 3 minutes.

After the data acquisition, image reconstruction was performed off-line using MATLAB (R2017a; MathWorks, Natick, MA) on a standalone personal computer. Nonuniform fast Fourier transform was used to reconstruct the highly undersampled MRF images. The MRF dictionary in this study was simulated using Bloch equations for a total of 13 123 combinations of T₁ and T₂ values. Specifically, the T₁ values range from 60 msec to 5000 msec, and T₂ ranges from 10 msec to 500 msec in the dictionary.

2.2 |. Data processing

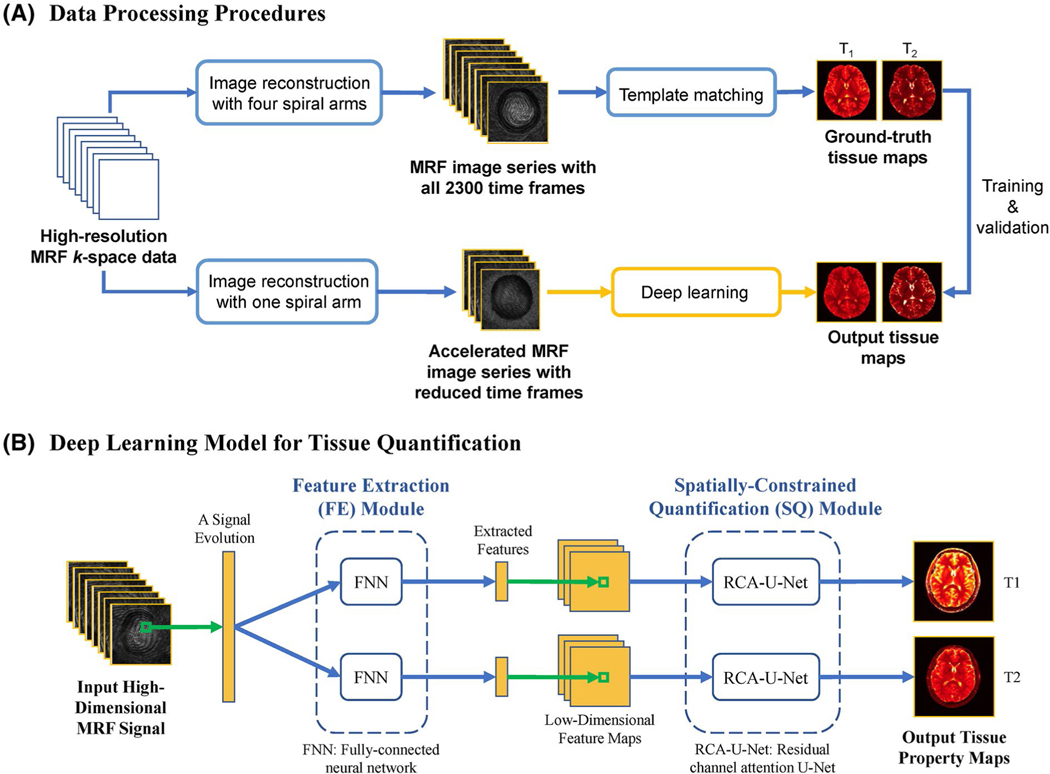
Figure 1A illustrates the framework for data processing in this study. As shown in the upper part of Figure 1A, the MRF images reconstructed with all 4 spiral arms were used to obtain the ground-truth tissue maps. Both T₁ and T₂ maps were obtained using the standard template matching approach with all 2300 time frames. To identify the optimal number of time frames to reduce the MRF acquisition time for rapid high-resolution imaging, MRF images were reconstructed with only 1 spiral arm and reduced the number of time frames, as shown in the lower part of Figure 1A. Specifically, 3 acceleration rates were evaluated in this study (i.e., 2×, 4×, and 8× shortened scan times), corresponding to the cases of using the first 1152 (1/2), 576 (1/4), and 288 (1/8) time points in the original acquisition, respectively. The MRF images generated with less sampled data were used as the input in the deep learning model for tissue quantification, whereas the ground-truth tissue maps obtained from all acquired data and template matching were used for model training and validation. The deep learning model was trained 3 times for 3 different acceleration rates.

FIGURE 1.

A, Diagram of data-processing procedures. The MR fingerprinting (MRF) images were first reconstructed using data from all 4 spiral arms to compute the ground-truth tissue maps with template matching. The images reconstructed with 1 spiral arm and reduced time points were obtained and used as input of the deep learning model for tissue quantification. B, Diagram of the proposed deep learning model for tissue quantification. First, the feature extraction (FE) module extracts a lower-dimensional feature vector from each signal evolution. A spatially constrained quantification (SQ) module is applied to estimate the tissue maps from the extracted feature maps with spatial information. Abbreviations: FNN, fully connected neural network; RCA-U-Net, residual channel attention U-Net

2.3 |. Magnetic resonance fingerprinting tissue quantification using deep learning

Figure 1B shows the structure of the deep learning model used for tissue quantification in this study. Similar to the method proposed in Fang et al,²² the deep learning model consists of 2 different modules. The feature extraction module uses a fully connected neural network to reduce the dimension of signal evolutions and extract useful features. The spatially constrained module uses residual channel attention U-Net, which is an improved version of U-Net, to estimate the tissue maps from the feature maps. The RCA-U-Net extracts spatial information from neighboring pixels to improve the quantification accuracy with reduced data.

As introduced in the literature,²² the input of the fully connected neural network was an MRF signal evolution extracted from 1 pixel. The real and imaginary parts of complex signals were split and concatenated to form a real-value vector. Thus, the input dimension of the fully connected neural network equals 2 times the number of time points. The output of the fully connected neural network is a 64-dimensional feature vector extracted from the input signals. The network consists of 4 fully connected layers, with an output dimension of 64 for each layer.

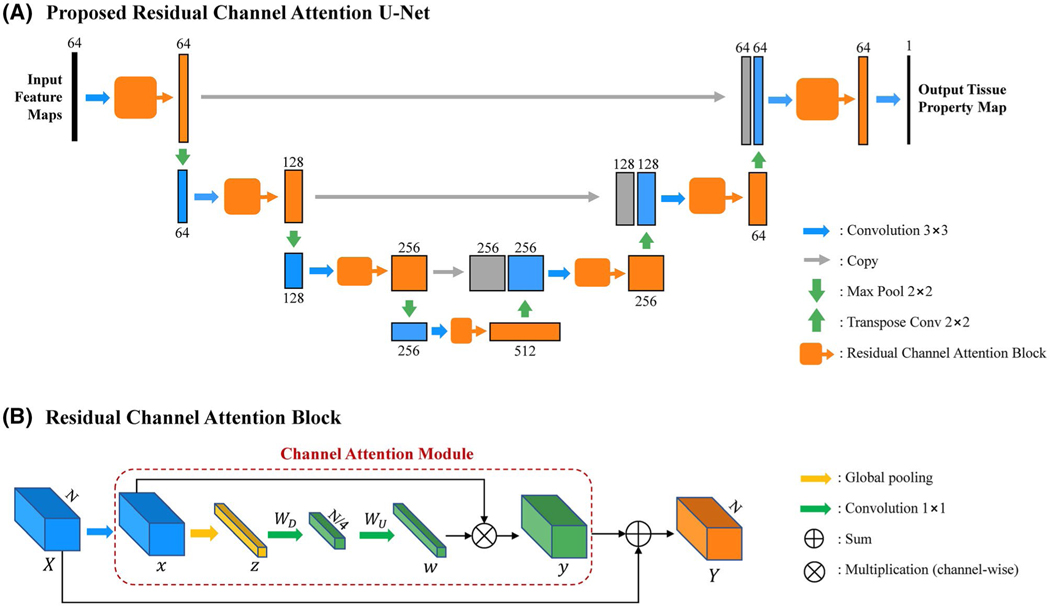
Figure 2 shows the structure of the proposed RCA-U-Net, which has a U-Net-like structure. With 3 down-sampling layers (maximum pooling 2 × 2) and 3 up-sampling layers (transpose convolution 2 × 2), it extracts spatial information from 3 different scales. At each spatial scale, skip connections are used to combine global information with local details. Unlike the conventional U-Net, RCA-U-Net uses RCABs²⁵ to extract more informative features for improved tissue quantification. As shown in Figure 2B, the RCAB integrates a channel attention module into the conventional residual block. The channel attention module first applies global average pooling to each channel of the feature map to generate a channel descriptor. Let x be the input of the channel attention module, with C feature maps at the size of H × W. Each channel descriptor is determined by

$$z_c=\frac{1}{H\times W}\sum _{i=1}^H\sum _{j=1}^W{x}_c(i,j),$$ (1)

where x_c(i, j) is the value at position (i, j) of the cth feature map x_c. Then, two 1 × 1 convolution layers are used to exploit channel-wise dependency for estimation of channel-wise rescaling weights. The rescaling weights w∈ℝ^C are given by

$$w=f\left(W_U\delta \left(W_{D}z\right)\right),$$ (2)

where W_D is the weights of the first 1 × 1 convolution layer, which acts as a channel-downscaling layer with a reduction ratio of 4; W_U is the weights of the second 1 × 1 convolution layer, which acts as a channel-upscaling layer with a ratio of 4; δ(·) denotes sigmoid function; and f(·) represents rectified linear unit activation. Then, the original feature map x is rescaled by the weights through channel-wise multiplication as follows:

$$y_c=w_c\cdot x_c,$$ (3)

where w_c and x_c are the rescaling weight and feature map in the cth channel, respectively, and y_c is the output of channel attention module in the cth channel. In this way, the features containing more information for quantification of the desired tissue property are strengthened, whereas those features containing more noise and less useful information are weakened. The output of the channel attention module is then added to the input of RCAB by residual skip connection to generate the final output of RCAB as

$$Y=X+y,$$ (4)

where X is the input of RCAB and y is the output of channel attention module.

FIGURE 2.

The structure of the proposed RCA-U-Net used in the SQ module. A, Overall architecture of RCA-U-Net. B, Structure of a residual channel attention block

For training purposes, the loss function is defined as the relative L1 difference between network estimation and ground truth, as follows:

$$L={\mathbb{E}}_{{\widehat{\theta }}_x,{\theta }_x}\left|\frac{{\widehat{\theta }}_x-{\theta }_x}{{\theta }_x}\right|,$$ (5)

where ${\widehat{\theta }}_x$ denotes the estimated tissue property (T₁ or T₂) value at pixel x; θ_x denotes the ground-truth value at pixel x; and 𝔼 represents mathematical expectation. In this study, the L1 loss was chosen, instead of L2 loss, as the L2 loss tends to produce smoother tissue property maps, which is not desired for imaging at high spatial resolutions. The Adam optimizer²⁸ was used to train the networks with a batch size of 32. Patches of 64 × 64 pixels were extracted for training. The network weights were initialized from a Gaussian distribution with zero mean and SD of 0.02. The learning rate was initially set as 0.0002, remained the same for 200 epochs, and then linearly decayed to zero in the next 200 epochs. The deep learning algorithm was implemented in Python with the PyTorch library. The whole training process took around 5 to 10 hours (depending on the number of time points used to generate the input data) on a graphics processing unit (GPU; NVIDIA GeForce GTX TITAN XP; Santa Clara, CA). The application of the trained deep learning network for T₁ and T₂ quantification was tested on both the GPU and the CPU (4.2 GHz Intel Core i7 with 4 cores and 16 GB memory).

To evaluate the performance of the proposed method, leave-1-subject-out cross validation was performed using the data set acquired from healthy adult subjects, and the mean quantification error was calculated from all of the subjects. Specifically, in each experiment, the data from 4 adult subjects were used for training, and the data from the remaining subject were used for testing. Three existing methods were also evaluated on the adult data for comparison,^4,7,22 including (1) the standard template matching approach, (2) template matching with singular value decomposition compressed dictionary, and (3) deep learning with conventional U-Net. For template matching with singular value decomposition compression, the rank of compressed dictionary is selected as 17, which retains 99.9% of the total energy of MRF signal evolutions in the dictionary. To identify the optimal acceleration rate for high-resolution MRF acquisition, the mean percentage error values were calculated between the deep learning–derived T₁ and T₂ maps and the ground-truth maps.

2.4 |. Effect of RCA-U-Net on spatial resolution

In this section, we quantitatively evaluated the impact of residual channel attention block on spatial resolution of quantitative maps. Based on the fact that spatial smoothing or degradation of image resolution leads to a decrease of high-frequency energy in the images, the proportion of high-frequency energy in the tissue maps was calculated for quantitative evaluation of the spatial resolution of in vivo brain data. Specifically, the tissue maps were first converted to the frequency domain by 2D Fourier transform. The sum-up of the energy of frequency components within the upper 25% of spectrum was calculated and then divided by the sum-up of the energy of all frequency components to obtain the proportion of high-frequency energy for each tissue property map. To evaluate the effect of RCABs on spatial resolution, we calculated this value for the MRF results obtained using the standard U-Net and the proposed RCA-U-Net. The proportion of high-frequency energy from the ground-truth tissue maps obtained using template matching was also computed as the reference.

2.5 |. In vivo measurements

Five normal adult volunteers (male:female, 3:2; mean age, 29 ± 13 years) were recruited for this study, and informed consent was obtained from all subjects before the MRI measurements. For each subject, a total of 10 axial slices were acquired using the MRF protocol containing 4 spiral arms. The results were used to generate the MRF images and ground-truth T₁ and T₂ maps to train the deep learning model as outlined in Figure 1A.

To evaluate the potential of the developed approach for fast pediatric neuroimaging, 2 healthy pediatric volunteers (2 females; mean age, 9.5 ± 0.7 years) were recruited in the study by obtaining informed parental consent for each subject before the study. The prospectively accelerated MRF scan with the optimal acceleration rate determined from the adult study was applied on both pediatric subjects. The deep learning model trained from adult subjects was used to generate quantitative T₁ and T₂ maps for these scans. To further evaluate the accuracy of the proposed method on pediatric neuroimaging, 1 MRF scan with 4 spiral arms and 2300 time frames was acquired from 1 pediatric subject and prescribed to have the same slice location as 1 of the prospectively accelerated scans. The deep learning model was applied to retrieve T₁ and T₂ maps from retrospectively shortened data and prospectively accelerated data, and the results were compared with the reference maps obtained using 4 spiral arms.

Quantitative T₁ and T₂ values from multiple brain regions, including white matter, gray matter, and subcortical gray matter, were extracted with a region-of-interest analysis. For each subject, multiple regions of interest were drawn manually on T₁ relaxation maps by a neuroradiologist with 16 years of experience in neuroimaging. Because all tissue property maps obtained using MRF were inherently co-registered, the regions of interest were automatically propagated from T₁ maps to T₂ maps to extract both T₁ and T₂ values simultaneously. For adult subjects, the regions of interest were drawn based on the ground-truth maps to extract reference T₁ and T₂ values. The regions of interest were further applied to the maps obtained using deep learning with the retrospectively shortened data set.

2.6|. Statistical analysis

The results are presented as mean ± SD. A paired Student’s t-test was performed to compare the proportion of high-frequency energy in MRF maps obtained using the U-Net and RCA-U-Net methods. A p-value less than 0.05 was considered significantly different in comparison.

3 |. RESULTS

3.1 |. Reference maps using 4 spiral arms versus 1 spiral arm

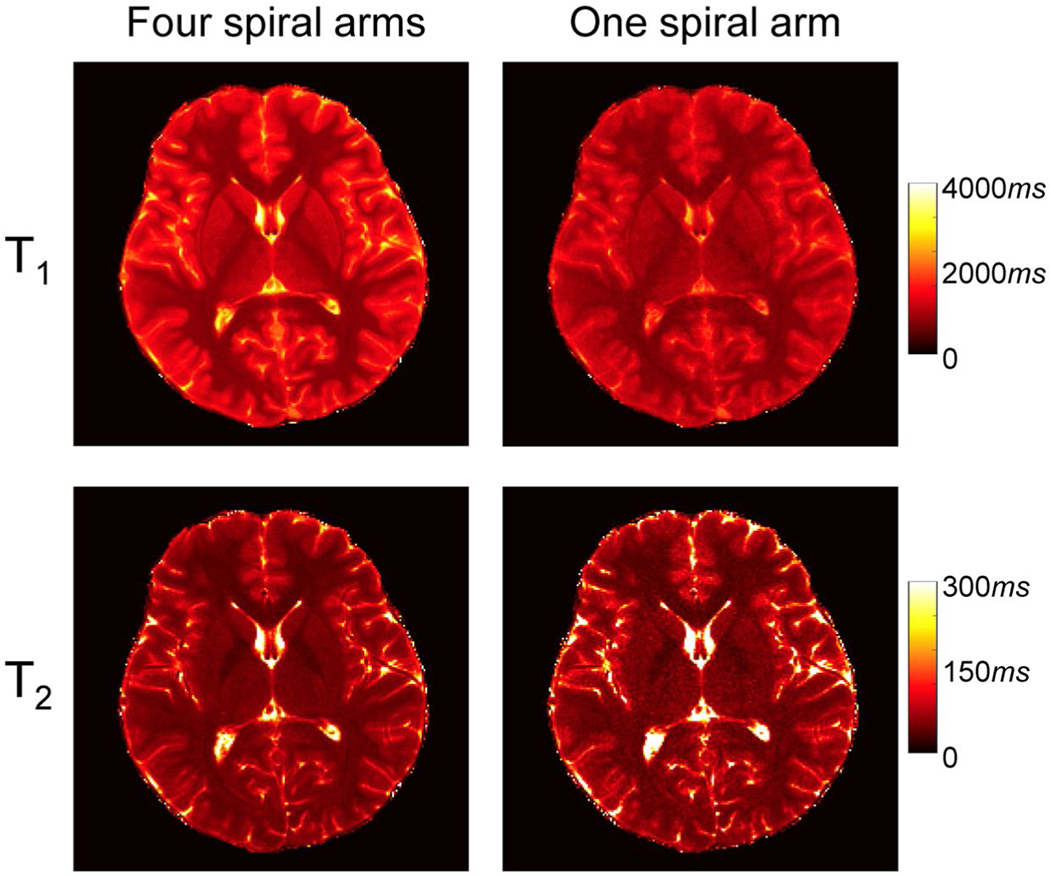
Figure 3 shows representative reference T₁ and T₂ maps obtained from an adult subject using 4 spiral arms. The maps were calculated using template matching and approximately 2300 MRF time frames. The T₁ and T₂ maps obtained from the same MRF scan but using only the first spiral arm are also plotted as a comparison. With the high in-plane resolution of 0.8 mm, the quality of tissue property maps was largely improved. For example, both cortical and subcortical gray matters are better delineated using the 4-arm approach. The noisy appearance in the T₂ map with only 1 spiral arm was also eliminated with the 4-arm approach. Therefore, the tissue maps obtained using 4 spiral arms were chosen as the ground truth, to train the deep learning model in this study.

FIGURE 3.

Representative T₁ and T₂ maps obtained with data from 4 spiral arms versus 1 spiral arm using template matching. All approximately 2300 time points were used for tissue quantification, and the results were obtained from an adult subject

3.2 |. Determination of the optimal acceleration rate

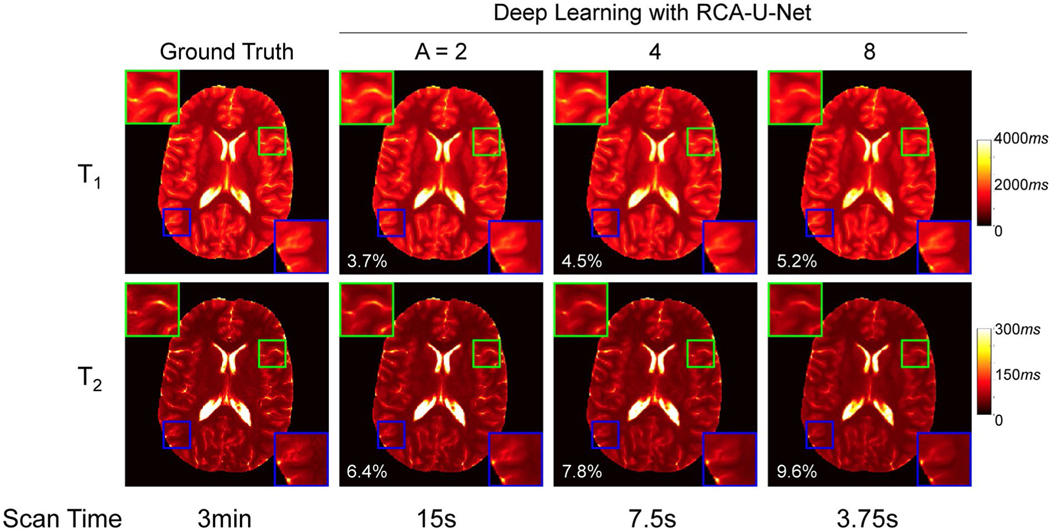
We further evaluated the effect of acceleration rate on the quantification performance of the proposed method. Figure 4 shows the T₁ and T₂ maps obtained using the deep learning method with 1 spiral arm and 3 different acceleration rates. The ground-truth maps obtained using template matching with 4 spiral arms and all time points are also shown for comparison. With an increase in acceleration rate, the mean percentage error values were increased for both T₁ and T₂ maps (Figure 4). Compared with the deep learning results obtained from the acceleration rates of 2 and 4, certain image blurring, especially in T₂ maps as demonstrated in the zoomed-in plots, was observed with the acceleration rate of 8. To balance the image quality and acquisition time, an acceleration rate of 4 was selected for the prospectively accelerated scans performed in the pediatric study. For this scan protocol, about 570 time frames were acquired, and the corresponding acquisition time was about 7.5 seconds per slice.

FIGURE 4.

Representative T₁ and T₂ maps obtained by the proposed deep learning approach using different acceleration rates. Both the ground-truth and the deep learning results obtained with acceleration rates of 2, 4, and 8 (i.e., using 1152, 576, and 288 time frames, respectively) are plotted. The corresponding sampling time is also listed at the bottom of each image. Here, A denotes the acceleration rate

3.3 |. Comparison with existing approaches

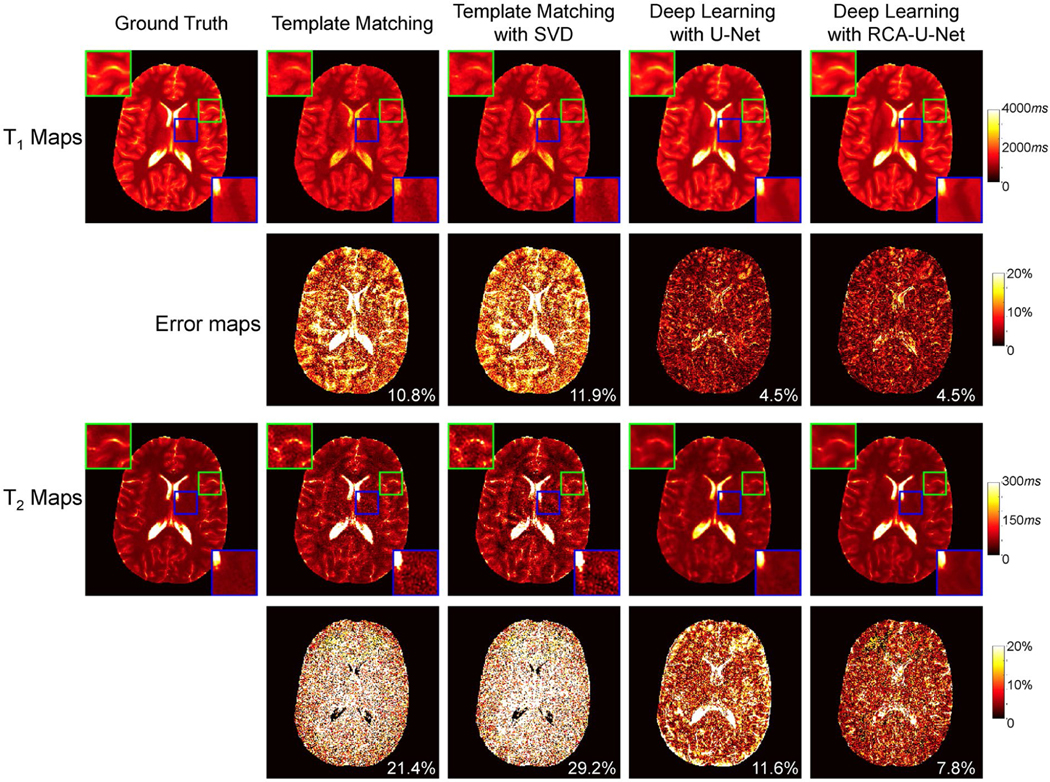
Figure 5 shows representative T₁ and T₂ maps from a healthy adult volunteer with 4-times shortened scan time. In addition to the tissue quantification results from the proposed method (i.e., deep learning with RCA-U-Net), the results from 3 existing methods in the literature are also plotted. For T₁ quantification, the deep learning–based approaches generally perform better than the template-matching-based approaches. Similar mean percentage error values were noticed in the results obtained using the conventional U-Net and the proposed RCA-U-Net methods. For T₂ quantification, the results were largely improved with the deep learning methods as compared with the template matching methods. Furthermore, compared with the conventional U-Net, the proposed RCA-U-Net achieves improved accuracy in T₂ quantification and preserves more high-resolution details in the T₂ maps. Table 1 summarizes the T₁ and T₂ quantification errors yielded by the proposed deep learning method and the existing methods obtained from leave-one-out cross validation. The proposed RCA-U-Net method outperforms the other 3 methods for both T₁ and T₂ quantification, which is consistent with the results shown in Figure 5. In addition, when only about 570 time points were used for tissue quantification, substantial variation across different subjects was noticed in the results obtained with the template matching approach. However, more consistent results were observed with the proposed deep learning method.

FIGURE 5.

Comparison of the proposed method with several existing methods for MRF tissue mapping (4-times shortened scan time). Representative T₁ and T₂ maps and their corresponding error maps from an adult subject are plotted. Abbreviation: SVD, singular value decomposition

TABLE 1.

Mean percentage errors (%) for T₁ and T₂ quantification from 5 adult subjects using 3 existing methods (i.e., template matching, template matching with SVD, and deep learning with U-Net) and the proposed method (i.e., deep learning with RCA-U-Net)

	Subject #	Template matching	Template matching with SVD	Deep learning with U-Net	Deep learning with RCA-U-Net
T1	1	10.7 ± 3.0	11.3 ± 3.2	6.5 ± 1.9	7.1 ± 2.0
	2	26.2 ± 5.0	28.5 ± 5.3	4.6 ± 0.3	4.5 ± 0.5
	3	29.1 ± 5.2	31.5 ± 5.5	5.9 ± 0.8	5.6 ± 0.8
	4	8.0 ± 1.2	8.5 ± 1.2	5.0 ± 0.7	4.8 ± 0.6
	5	7.6 ± 1.8	8.3 ± 2.0	4.9 ± 0.6	4.3 ± 0.7
	Average	16.3 ± 10.5	17.6 ± 11.5	5.4 ± 0.8	5.2 ± 1.1
T2	1	27.9 ± 2.7	36.8 ± 3.6	10.2 ± 1.9	10.1 ± 1.9
	2	25.4 ± 2.7	38.9 ± 5.1	8.0 ± 0.6	8.3 ± 0.7
	3	29.1 ± 4.0	44.2 ± 6.5	9.5 ± 1.0	9.2 ± 0.9
	4	25.6 ± 2.2	34.0 ± 2.9	10.4 ± 1.0	10.3 ± 1.0
	5	20.4 ± 0.9	27.1 ± 1.3	10.9 ± 0.8	7.5 ± 0.6
	Average	25.7 ± 3.3	36.2 ± 6.3	9.8 ± 1.1	9.1 ± 1.2

Note: The results were obtained from MRF data containing 1 spiral arm and approximately 570 time frames (1/4 of the total acquired time frames).

3.4 |. High-resolution MRF with pediatric subjects

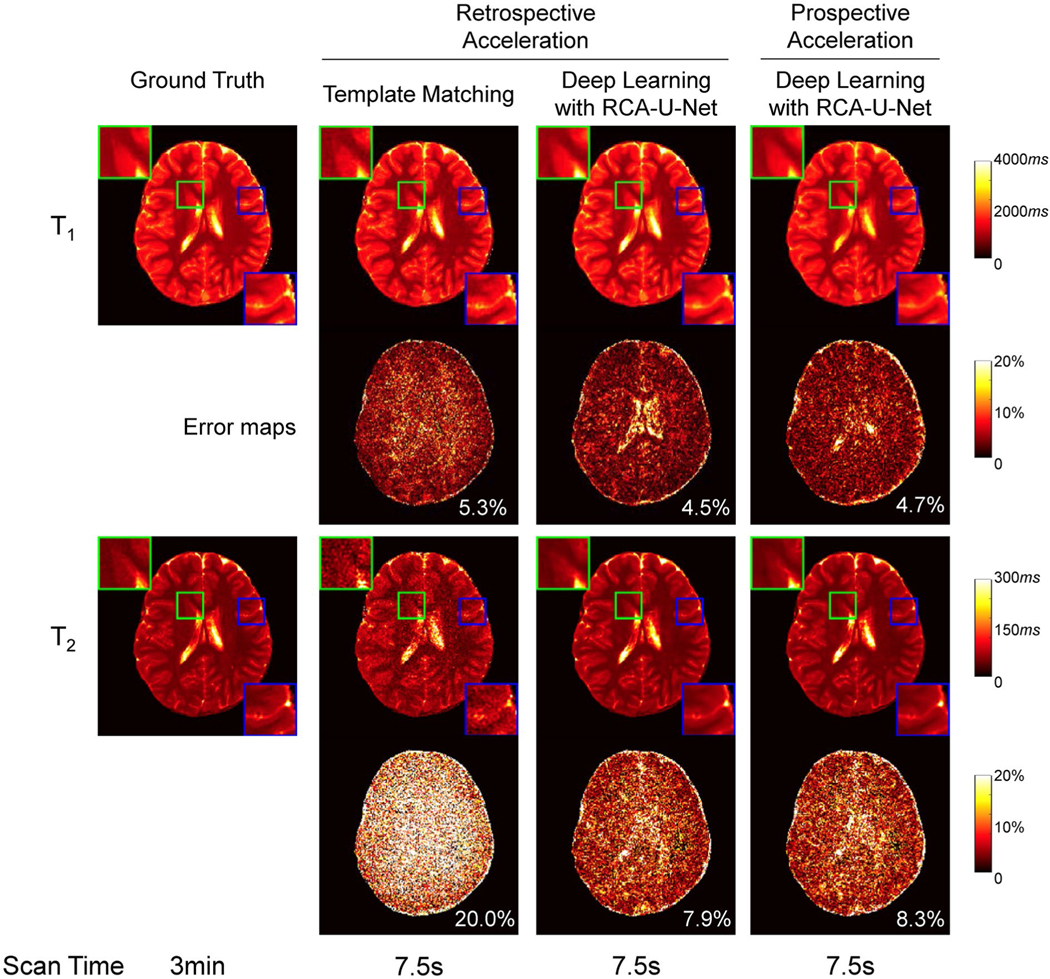
We further evaluated the proposed high-resolution MRF method on pediatric subjects. Before the implementation of the accelerated MRF method, we first evaluated the accuracy of the proposed method with pediatric imaging, and 1 MRF scan with 4 spiral arms was acquired from 1 of the subjects. The T₁ and T₂ maps obtained from retrospectively shortened MRF data (4-times shortened scan time) using template matching and deep learning are shown in the second and third columns of Figure 6. The ground-truth maps are also presented in the first column for comparison. Again, the deep learning approach achieves significant improvement in T₂ quantification accuracy compared with the template matching approach.

FIGURE 6.

(Left 3 columns) Representative T₁ and T₂ maps and their corresponding error maps yielded by the proposed deep learning method and the standard template-matching method using retrospectively accelerated data from a pediatric subject (4-times shortened scan time). The ground-truth maps are also presented for comparison. (Right column) T₁ and T₂ maps obtained at the same slice location using the prospectively accelerated MRF scan

We then applied the prospectively accelerated MRF method on 2 pediatric subjects (4-times shortened scan time; 7.5 seconds per slice). The right column in Figure 6 shows the T₁ and T₂ maps obtained using the deep learning model with prospective acceleration from the same subject at the same slice location as the ground truth. With only 7.5-second scan time, the proposed method using deep learning provides results similar to the ground-truth maps, which took approximately 3 minutes to acquire. It is also worth noting that the errors yielded by the proposed RCA-U-Net for the pediatric subject (Figure 6, with 4.7% for T₁ and 8.3% for T₂) are similar to those obtained from the adult subject (Figure 5, with 4.5% for T₁ and 7.8% for T₂), which suggests similar performance achieved for both adult and pediatric subjects with the proposed method.

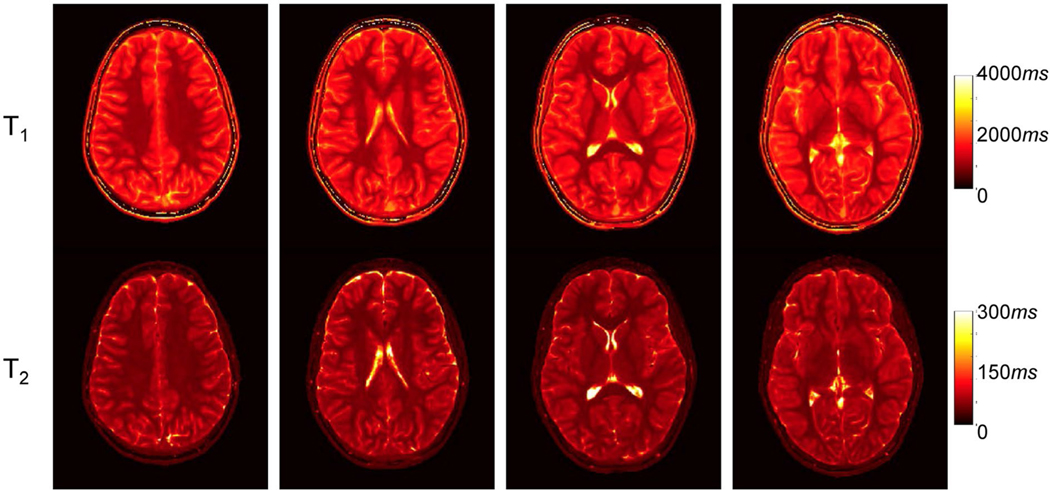
Figure 7 shows axial T₁ and T₂ maps obtained from the other pediatric subject at multiple brain locations with the proposed high-resolution MRF approach. Success was found in conveying minute structural details of the brain, which, in hand with other results, demonstrates the potential of the proposed method for fast and high-resolution pediatric quantitative imaging.

FIGURE 7.

Representative T₁ and T₂ maps yielded by the proposed deep learning method using prospectively accelerated data from the other pediatric subject. Approximately 570 time frames were acquired, and the scan time for each slice was 7.5 seconds

The quantitative T₁ and T₂ values obtained from multiple brain regions for both adult and pediatric subjects are summarized in Table 2. For adult subjects, the mean percentage errors of the deep learning result compared with the ground truth are 2.4% ± 3.4% for T₁ and 3.2% ± 3.2% for T₂, respectively. The values for different brain regions are consistent with those reported in the literature.^29,30

TABLE 2.

Quantitative T₁ and T₂ values obtained from multiple brain regions for both adult and pediatric subjects

	Adult (N = 5)				Pediatric (N = 2)
	Ground truth		RCA-U-Net		RCA-U-Net
	T1	T2	T1	T2	T1	T2
White matter	793 ± 23	39 ± 2	802 ± 12	39 ± 1	821 ± 25	43 ± 2
Cortical gray matter	1472 ± 31	68 ± 3	1465 ± 33	63 ± 2	1513 ± 47	70 ± 2
CSF	4257 ± 79	482 ± 22	3836 ± 126	440 ± 25	4005 ± 89	346 ± 25
Corpus callosum	784 ± 26	45 ± 2	795 ± 13	44 ± 2	777 ± 21	44 ± 1
Caudate	1324 ± 46	56 ± 1	1292 ± 41	56 ± 2	1388 ± 30	61 ± 1
Putamen	1181 ± 41	49 ± 3	1172 ± 39	49 ± 2	1279 ± 25	59 ± 3
Thalamus	1060 ± 48	49 ± 2	1051 ± 41	48 ± 2	1157 ± 44	52 ± 2

Note: The ground-truth results for adult subjects were obtained from the data containing 4 spiral arms and all approximately 2300 time frames using template matching. The deep learning results with RCA-U-Net were obtained from the MRF data containing 1 spiral arm and approximately 570 time frames.

3.5 |. Processing time for tissue quantification

We also compared the processing times of the template matching approach and our deep learning approach for T₁ and T₂ quantification. When both methods were performed with the CPU, a 5-fold acceleration (26.0 versus 5.1 seconds per slice) was achieved by the deep learning approach as compared with the template matching. The processing time can be further improved by 40-fold (0.12 seconds per slice) when using the GPU for the deep learning approach.

3.6 |. Effect of the proposed deep learning network on spatial resolution

We further calculated the proportion of energy in the high-frequency domain of MRF maps, and the results obtained using U-Net and RCA-U-Net are presented in Table 3. Compared with the ground-truth maps, both deep learning methods led to some level of spatial smoothing in the estimated tissue maps. Compared with the conventional U-Net, RCA-U-Net results in a significantly higher proportion of energy in the high-frequency domain for T₂ quantification (P < .001), which demonstrates that the residual channel attention block helps preserve more high-resolution details in the estimated T₂ maps.

TABLE 3.

Proportion of energy in high-frequency domain of the T₁ and T₂ maps estimated by U-Net and RCA-U-Net

	Ground truth	U-Net	RCA-U-Net
T1	1.52 ± 0.37	1.23 ± 0.26	1.23 ± 0.26
T2	3.25 ± 0.99	1.54 ± 0.56	1.71 ± 0.61

Note: The values from the ground-truth tissue maps are also presented as a reference.

4 |. DISCUSSION

In this study, a fast 2D high-resolution MRF technique was developed using deep learning–based tissue quantification. This technique allows fast and high-quality T₁ and T₂ quantification with 0.8-mm in-plane resolution in 7.5-second scan time per slice. The method was developed and validated using the data acquired from normal adult subjects and then applied for fast imaging with pediatric subjects. Our results demonstrate that the proposed deep learning model achieves higher quantification accuracy as well as shorter computation times as compared with the standard template-matching approach.

Compared with the 2D MRF approach developed in the current study, high-resolution MRF has also been explored with 3D acquisitions in the literature.³¹ Although MRF with volumetric imaging can provide better spatial coverage and higher SNR to improve spatial resolution, it typically requires longer scan times and is more sensitive to subject motions, especially with pediatric populations. The proposed fast MRF method can provide high-resolution quantitative imaging while minimizing potential motion artifacts. In the future, our proposed method can be further combined with simultaneous multislice imaging techniques³² to improve spatial coverage and SNR for potentially higher spatial resolutions.

To achieve robust tissue quantification using the deep learning approach, it is critical to obtain accurate ground-truth maps to train the network. In this study, instead of acquiring just 1 spiral arm as the standard MRF method, 4 spiral arms were acquired for each MRF image to reduce the aliasing artifacts. Previous studies have shown that, with a spatial resolution of 1.2 × 1.2 × 5 mm³, accurate T₁ and T₂ measurement was achieved using only 1 spiral arm (in-plane reduction factor of 48).^4,22 However, when targeting at higher spatial resolutions, our results suggest that acquiring more spiral arms could improve the quality of tissue property maps and provide more solid ground truth to train the deep learning model. Although this approach increases the data sampling time, this only applies to the acquisition of the training data set, and not the prospectively accelerated scans. It is worth noting that ground-truth maps obtained with more spiral arms (>4) per MRF time point could potentially provide better map quality. However, this is achieved at a cost of longer scan times, and the results are more prone to subject motions. To balance between map quality and scan time, 4 spiral arms were chosen to acquire the ground-truth maps in this study. Compared with the standard template matching methods, 1 shortcoming of the proposed deep learning method is the need to acquire an additional training data set. When applying the proposed method to a new acquisition protocol (e.g., with a different scan time, k-space sampling pattern, or MRF flip angle pattern), a new network needs to be trained with a new training data set acquired. Cohen et al showed that the training data can be generated using the MRF dictionary.¹⁵ Although the approach has been proven to be effective for fully sampled data acquired using an EPI sequence, its application to highly aliasing MRF data remains to be evaluated. Another potential solution to mitigate this problem is to simulate the training data based on some prior knowledge of tissue property maps and MRF dictionary. With this approach, some key components associated with the actual imaging acquisition, such as noise distribution, aliasing artifacts and multicoil sensitivity maps, need to be considered in the simulation—a feasibility that will be explored in the future.

To apply the deep learning approach for high-resolution MRF, a network that combined U-Net and RCABs, was proposed in this study. Findings in a previous study have shown that using the standard U-Net for spatially constrained tissue quantification in MRF can potentially degrade the spatial resolution of tissue maps due to spatial smoothing.²² To overcome this limitation, we proposed adding RCABs to the conventional U-Net to enhance the high-resolution details in the output tissue maps. Early studies with residual blocks and channel attention have demonstrated that this modification can preserve the high-frequency information in the intermediate feature maps and lead to superior performance in various image processing tasks (e.g., super-resolution imaging).^25,33 Specifically, residual blocks enable the network to focus more on the differences between block input and output, which typically contain rich high-frequency components, and facilitate the gradient backpropagation during training. In addition, the channel attention module adaptively assigns larger weights to more informative feature channels with high-frequency information, enhancing the high-frequency components in the quantification results. As a result, the proposed residual channel attention U-Net preserves more high-resolution details in the tissue maps than the conventional U-Net model.

In the current study, image patches of size 64 × 64, instead of full-scale images, were used for training due to the large size for the MRF data set and limited GPU memory. Previous deep learning studies have been performed to use full-scale images for MR tissue mapping. For example, Liu et al²⁴ proposed a deep learning model called MANTIS to convert undersampled images to quantitative parametric maps for efficient MR parameter mapping. This is an end-to-end mapping technique based on UNet and can achieve high-quality T₂ mapping with high acceleration rates. In the future, the training with full-scale MRF images can be explored with the proposed method when more computational resources are available.

Although template matching has been used widely for tissue property quantification in MRF, 1 potential drawback of this approach is its high computational demand. Both memory and computation time requirements grow exponentially with the number of tissue parameters to be estimated. Consistent with the findings in the literature,^15,16 this study achieves rapid tissue quantification using deep learning–based tissue quantification. For quantification of both T₁ and T₂ for a 2D slice with a matrix size of 304 × 304, the deep learning–based method is about 5 times faster than the template matching using a CPU for computation. Moreover, the deep learning method can be directly implemented on a GPU, which allows further acceleration in computation. The memory and time requirements of the deep learning approach grow only linearly with the number of tissue parameters in this study, which is particularly desirable for quantification of a large number of tissue properties simultaneously using MRF. This method also holds great potential for 3D MRF applications, in which more computational demand is expected with volumetric coverages.

There are some limitations to this study. Some network parameters used in this study, such as the numbers of convolution layers, down-sampling/up-sampling layers and feature channels, were adopted from the previous study for 2D MRF.²² Although reasonable results have been achieved, these network parameters can be further optimized to improve the quantification accuracy of the proposed deep learning model for high-resolution MRF. Besides, the longest T₂ value was set at 500 msec in the MRF dictionary. Further improvement in T₂ measurement, especially for tissues with long T₂ values (such as CSF in the brain), is needed with the MRF method. The sample size for our network training is relatively small. Our experiments show that an insufficient training data set could potentially lead to a decrease in the performance of T₁ and T₂ quantification (Supporting Information Table S1). A future study will be performed to evaluate the proposed model with a larger training data set and with more pediatric subjects across different ages. The current study is focused on quantitative characterization of normal brain tissues. When applied to patients with different pathologies, more training data sets from both normal and abnormal tissues are likely needed to train the proposed network.

5 |. CONCLUSIONS

A rapid and high-resolution MRF technique was developed using deep learning–based tissue quantification, which enables high-quality T₁ and T₂ mapping with 0.8-mm in-plane resolution in 7.5-second acquisition time per slice. The proposed residual channel attention U-Net can better preserve high-resolution details in quantitative tissue property maps. In addition, the computation of tissue property maps with the deep learning model was also 5 times faster than the standard template matching approach.

Supplementary Material

supinfo

FIGURE S1 A, Magnetic resonance fingerprinting sequence diagram. Variable acquisition parameters, such as flip angles and inversion pulses, were applied to encode the MRF signal in the acquisition. Each MRF image was acquired with a spiral readout, and a golden-angle rotation was applied between adjacent MRF images to increase spatial inhomogeneities. B, The flip angle pattern applied in the acquisition. C, Representative MRF signal evolution extracted from the dictionary (T₁, 1000 msec; T₂, 100 msec)

FIGURE S2 Effect of spiral design on high-resolution MRF. The MRF measurements were performed using 2 different spiral trajectories: 1 with 48 spiral interleaves per fully sampled image (readout time, 8.0 msec) and the other with 64 spiral interleaves per image (readout time, 6.3 msec). The MRF maps were obtained at the same slice position using 4 spiral arms per time point (R = 12) as the ground-truth maps. No visual differences were noticed in either T₁ or T₂ maps obtained using the 2 spiral trajectories with different spiral readout durations, which suggests that image blurring due to off-resonance is not significant with the proposed multishot spiral trajectory

TABLE S1 Mean percentage errors (%) for T₁ and T₂ quantifications from RCA-U-Net using different amounts of training data (i.e., 2, 3, or 4 subjects). Note: The results were obtained from MRF data containing 1 spiral arm and approximately 570 time frames (i.e., 1/4 of the total acquired time frames)