Abstract
The rapid growth in virtualization solutions has driven the widespread adoption of cloud computing paradigms among various industries and applications. This has led to a growing need for XaaS solutions and equipment to enable teleworking. To meet this need, cloud operators and datacenters have to overtake several challenges related to continuity, the quality of services provided, data security, and anomaly detection issues. Mainly, anomaly detection methods play a critical role in detecting virtual machines’ abnormal behaviours that can potentially violate service level agreements established with users. Unsupervised machine learning techniques are among the most commonly used technologies for implementing anomaly detection systems. This paper introduces a novel clustering approach for analyzing virtual machine behaviour while running workloads in a system based on resource usage details (such as CPU utilization and downtime events). The proposed algorithm is inspired by the intuitive mechanism of flocking birds in nature to form reasonable clusters. Each starling movement’s direction depends on self-information and information provided by other close starlings during the flight. Analogically, after associating a weight with each data sample to guide the formation of meaningful groups, each data element determines its next position in the feature space based on its current position and surroundings. Based on a realistic dataset and clustering validity indices, the experimental evaluation shows that the new weighted fuzzy c-means algorithm provides interesting results and outperforms the corresponding standard algorithm (weighted fuzzy c-means).
Keywords: Datacenter, Virtual machine, Abnormal behaviour, Workload monitoring, Weighted fuzzy C-means clustering, Starling birds
Introduction
In the current age of virtualization and new technologies, datacenters are undergoing rapid evolution and are facing several challenges in the coming years: the development of predictive analytics, the growth of cloud and serverless, edge computing, the arrival of 5G, and more recently, the COVID-19 epidemic that has snatched the world are among the topics that will be at the heart of their concerns.
The virtual machine (VM), being a core element of the cloud environment, is typically required to perform and maintain the operating system’s operation and storage and ensure the normal functioning of the operating system (OS). As the cloud platform is constantly growing, it is becoming more prominent and more complex. Consequently, a variety of challenges have arisen in terms of the competitive partitioning of the platform’s hardware resources and the resulting VM bugs. Any abnormal behaviour of the VM (the workload executed in the VM, respectively) can disrupt the regular system functioning, leading to a significant loss for the enterprise, which results in a reduced computing capacity or even hinders the successful deployment and operation of cloud computing.
Knowing workloads executed on the system can play a significant role in ensuring efficient resource usage and data security. Identifying workloads that intensively utilize shared resources enables implementing different scheduling models [1]. Several research works have proposed models for either scheduling or live migration of VMs based on workload knowledge. We cite, for example, the work presented in [2]; authors have introduced a machine learning-based model to analyze and predict the resource utilization of co-located applications that share resources; then, a scheduling strategy has been built based on knowledge levied by the prediction model. In the same way, depending on the applications running externally or inside a VM, Ayaz Ali et al. [3] have recently proposed a consolidation technique, consisting of selecting the most efficient migration of an individual VM, a container, or a specific application which runs inside a container. Besides, authors in [4] have used a perturbation tool to discover service and resource dependencies to minimize the system outage and improve data reliability. The authors have confirmed the importance of knowing the most common workloads and their characteristics for distributed system control.
Datacenter operators do not usually recognize which tasks are being executed in the system at a given time. The physical hosts can be shared by numerous users and simultaneously run hundreds or thousands of applications per day [5]. Static workload analysis has been proven to be ineffective in detecting the exact behaviour of the running applications and jobs [6]. Furthermore, the applications executed in a virtualized environment impose a workload expressed as memory utilization, processing time, storage, and network bandwidth. Typically, the actual resource usage is less than the number of resources requested by the customer. Therefore, naive methods for identifying the workload’s behaviour, such as looking at the information given by the users in the form of resource request or a pre-defined service level agreement (SLA), are not useful.
To address the before-mentioned challenges, we focus, in this work, on the employment of a fuzzy clustering approach for workload characterization. For a better understanding of workload characteristics and behaviour, monitoring data is investigated, including extensive information on resource usage such as central processing unit (CPU) usage, network activities, etc., which is collected periodically at runtime from a computing cluster. We propose a new weighted fuzzy c-means (WFCM) algorithm that adopts starling birds’ collective behaviour to build meaningful clusters. A starling naturally diffuses some information to its close neighbours to maintain its position, and subsequently, this information is spread to the whole swarm [7]. According to this analogy, we develop a technique for computing each sample’s weight iteratively based on its current position in the feature space (in relation to its closest neighbours). It is a kind of informational communication between the individual (object) and its nearest neighbours.
The motivation for using an unsupervised approach like fuzzy clustering for the classification of abnormalities is twofold: first, with enough labelled data, supervised learning techniques perform better in terms of accuracy. However, in cases where the available data for certain kinds of anomalies are scarce or the behaviour type is unknown, the use of unsupervised methods such as clustering may be more appropriate. Second, the purpose of using clustering is the elicitation of membership functions of linguistic variables. It is a standard procedure for automatically setting up fuzzy rule-based systems and fuzzy relational systems.
Clustering can refer to different aspects of the grouping concept. This paper is interested in a clustering algorithm that can be considered as a function fitting multiple observations in a finite, unlabeled, multi-variate dataset to partitions. Each observation represents a datum’s features so that the features’ probabilistic or uncertain nature is taken into account. The problem is to divide the dataset into groups (clusters) in a way that the data within a cluster are similar to each other and are as dissimilar as possible from data belonging to other clusters. A defined distance metric determines the similarities. Specifically, the two contributions of this paper are the following:
We introduce the weighted fuzzy c-means clustering algorithm based on starling birds behaviour (sbWFCM): a novel density-based approach involving the exploration of the topological adjacency of neighbours along with the application of a model search improving the performance of the WFCM algorithm. The proposed method yields an interacting algorithm that provides different clustering alternatives depending on the number of iterations of bird movement instructions, and it offers a detailed exploration of different regions of the feature space.
The proposed algorithm is utilized for identifying the abnormal execution of workload within VMs. We use a real-world dataset (monitoring data collected periodically at runtime from a computing cluster [8]). The clustering results are compared to the ground truth (the real classification of the workloads).
The remaining content of the paper is organized as follows. We review, in Sect. 2, the existing clustering algorithms applied to workloads and applications identification in a datacenter. Then, in Sect. 3, we briefly outline the background techniques useful for implementing the proposed work. Section 4 describes the proposed clustering algorithm. Using an experimental dataset, Sect. 5 validates the proposed algorithm. In Sect. 6, we synthesize the present work and highlight some directions for future work.
Related work
Currently, there is a wealth of work that introduces the employment of machine learning-based models for large-scale and distributed systems (datacenter, High-Performance Computing (HPC), etc.) monitoring [9–11], for their proper adaptation to fulfil the requirement of automatic detection of anomalies. Supervised and unsupervised machine learning algorithms are applicable. In supervised learning, abnormal workload behaviour is categorized according to a preliminary understanding of the data that corresponds to regular workload behaviour and abnormalities. We acquire this knowledge through an experimental execution of the algorithm, referred to as the training phase. However, unsupervised learning does not involve prior knowledge and allows for the discovery of unknown irregularities. The following focuses only on this last; more precisely, we address the clustering algorithms used for datacenter workload monitoring.
A large and growing body of literature has investigated clustering techniques for producing a concise representation of the system behaviour while executing different workloads. A study conducted by [12] examined the K-means clustering approach for Customizing the allocation policy for VMs. The clustering model they suggest for allocating cloud resources consists of mapping a group of tasks to VMs. To perform the clustering, they have focused on the CPU, memory, and bandwidth utilization by jobs. They aimed at reducing energy consumption through efficient resource allocation. In [13], authors investigated a co-clustering algorithm to identify workload patterns that are executed on a server during a certain time lapse, which enables the prediction of each VM workload.
Authors in [14] have recently proposed a model that combines kernel fuzzy c-means (KFCM) with an optimal type-2 fuzzy neural network (OT2FNN) classifier to detect potential threats of unauthorized and unlawful access to data in the cloud. The model consists of two learning phases: first, KFCM is used to identify meaningful clusters in the data; second, each resulting cluster is assigned a type-2 fuzzy neural network to label it as a regular or intrusive process. The detection mechanism as a whole is organized following training and test operations.
Likewise, a detection technique has been developed in [15] to identify intrusions at the virtual machine’s monitoring tier. The proposed mechanism starts by using FCM to split large datasets into smaller clusters to allow the support vector machine classifier (SVM) to learn efficiently. Based on the values of the selected cluster, the SVM modules are then trained, and the fuzzy aggregation module is used to combine the eventual results of the hypervisor inspector. It has been shown that the hybrid mechanism (FCM-SVM) can identify anomalies accurately.
Abdelsalam et al. have developed an approach to detect anomalous VM behaviour in scenarios that imply automatic scaling in Infrastructure as a Service (IaaS) clouds using unsupervised learning [16]. A modified version of the K-means sequential clustering algorithm has been used to detect abnormalities based on resource usage variations. These variations can be encountered when insiders or other malware attempts to run malicious tasks on VMs of cloud customers.
In [17], authors have proposed a model that combines K-means clustering along with the Extreme Learning Machine (ELM) to predict VM requirements in a data center. This work involved a combination of clustering of users together with CPU and memory workload in a prediction system. In addition, they conducted a comparative study between k-means clustering and FCM, which were used to analyze VMs and user behaviour so that each VM request was mapped to a single cluster.
Similarly, the performance of the Principal Component Analysis (PCA) and K-means has been investigated in [18]. The authors have evaluated these techniques in a monitored cloud testbed environment where both an attack and a migration occur simultaneously or separately, resulting in measures such as performance measurement. Authors have assumed that the undefined number of unwanted attacks and false alarms produced while migrating VMs from one host to another could make the behaviour of the VM unpredictable. Therefore, they have asserted that the widely-used PCA and K-means clustering methods can be directly involved in the live migration aspect. Mainly, their work has focused on the effect of VM migration on anomaly detection techniques.
The work, proposed by Amruthnath and Gupta [19], was initiated as a testbed to evaluate different unsupervised learning algorithms for early failure detection. They have chosen a simple vibration dataset collected by an extraction fan and adapted different unsupervised learning algorithms such as PCA, hierarchical clustering, K-Means, and FCM. Then, they proposed a methodology to evaluate different algorithms and choose the final model.
In addition, a typical clustering algorithm has been designed for aggregating data, with a similarity metric, into clusters [20]. Given that the VM performance would be monitored continuously round-the-clock by the cloud platform, authors have designed the Incremental VM workload clustering algorithm to gather performance information with similar VM workloads into a single cluster. The experimental results presented in this work have shown that the proposed clustering framework could effectively gather performance information with comparable VM workloads in a single cluster to help prevent negative actions when anomalies are detected.
The work proposed by Zhang et al. [21] consisted of task-level anomaly detection procedure in a software agnostic manner; they applied the unsupervised learning technique DBSCAN to learn the regular behaviour with the accurate task profiling level metrics in the unlabeled historical data. They then used the clustering result to detect the potential performance anomaly. They established the relationship between the task and the network connection.
In [22], a hybrid system for anomaly detection has been introduced. The authors have employed the FCM clustering algorithm with Artificial Neural Networks (FCM-ANN) to detect the abnormal behaviour of VMs. The proposed system detects the attack patterns which are stored previously in a database. This database must be updated frequently. To avoid the manual update, authors have adopted the FCM clustering algorithm to capture the news attacks automatically. Similarly, in our previous work, the Gath-Geva clustering algorithm has been used for identifying similarities between different applications running on an HPC system [23].
Although there have been numerous works using clustering for the detection of the anomalous behaviour of VMs in a datacenter, we argue that all current approaches are far from ideal. Some approaches assume prior knowledge of the workloads running on the VMs. However, our proposed model enables us to act with no previous knowledge required. Moreover, work such as [12, 16, 18] studied the conventional (hard) clustering for detecting workload abnormalities. This requires well-defined boundaries between clusters, which is not the case in many, even most, natural systems. In this work, we propose a fuzzy clustering approach distinguished from hard clustering. It enables an observation to belong to more than one cluster with various degrees of membership. Such factors can express the ambiguity or certainty of an observation’s belonging to a given cluster. More interestingly, clustering algorithms browse a limited region within the partition space. The explored portion is driven mainly by the algorithm and the underlying assumption about the data distribution or the model used. Several steps are involved in exploratory analysis using clustering, including the selection and implementation of the algorithm, the validation based on certain cluster validity indices, and a last, critical step of interpretation. This last is contingent on the domain of applicability and requires domain experts who play a crucial role in identifying relevant clusters, i.e., clusters representing the real structure of the data. Compared to K-means, FCM is shown, in the experimental studies reported in the literature above, to be effective in this domain; however, it does not allow a complete exploration of the data. Our approach provides significant assets over FCM. It enables detailed exploration of different regions of the feature space, and it generates different partitioning alternatives depending on the number of iterations that a domain expert can control.
Background
Weighted fuzzy c-means fundamentals
WFCM is an extended algorithm derived from the FCM clustering algorithm. It consists of attaching, to each data element, a weight value that defines the relative relevance the element while building the clustering solution. For a given set of objects , we associate a set of observations in . represents the characteristic value describing the object . WFCM aims at minimizing the following objective function:
| 1 |
is the corresponding weight of each datum , noting that objects with a high weight have a greater influence on the clustering process than low weighted objects. is being the so-called fuzziness parameter that regulates the influence of the members’ ratings. denotes the membership of observation in the cluster, where and C is the number of clusters. takes values in [0,1], 0 corresponds to non-membership while 1 refers to total membership. Vectors say are arranged as columns of CN-matrix . are computed as follows:
| 2 |
refers to the centroid of the cluster and can be updated by the following equation:
| 3 |
We notice that the cluster prototype (center) is a weighted sum of the feature vectors since each object has a different predetermined impact given by a relative weight . Determining the weight associated with each observation can be carried out following different strategies. We cite, among others, the use of neighbourhood density information of each sample (the number of objects that are near to the sample using a distance threshold) or user-defined constants [24]. The optimization of the objective function 1 through an iterative process builds the fuzzy partitions. The algorithm is outlined in Algorithm 1.
The collective behaviour of starling birds
The collective movement of groups of animals is one of the most spectacular phenomena observed in nature. These collective movements arise from local interactions between individuals and are supported by the formation of large-scale spatial and temporal structures. To understand the characteristics of these collective movements, it is significant to characterize the dynamics of interactions between individuals. To do this, many researchers studied a species of bird, starlings, to develop an algorithm that analyzes the individual trajectories and determines for each bird, and at each moment, how many of its neighbours influence its movement [25, 26]. Similarly, in 1986, a computer scientist, Craig Reynolds, developed rules that simulate the behaviour of clouds of birds, such as schools of fish. He named these virtual birds “boids” (a short-language word for “birds”) [27].
According to Wayne Potts’ study [28], every bird reacts to what surrounds it, and only to that. This means that its behaviour can be modelled so that each bird reacts only to its neighbours. Understanding collective information-processing mechanisms in birds living in groups opens up prospects for the development of bio-inspired algorithms for the distributed control of artificial systems such as automated highway systems [29], co-operative robotic recognition [30], manipulation control [31], group-based flight control [32], distributed sensor network deployment [33], etc.
In this work, we follow the Reynolds simulations that consist of the following. During the flight of starlings, the direction of the movement of each starling depends not only on self-information but also on information provided by other nearby starlings. A starling reacts to its close neighbours in the flock and adapts its flight direction progressively to follow the direction of its fellow starlings, as shown in Fig. 1.
Fig. 1.
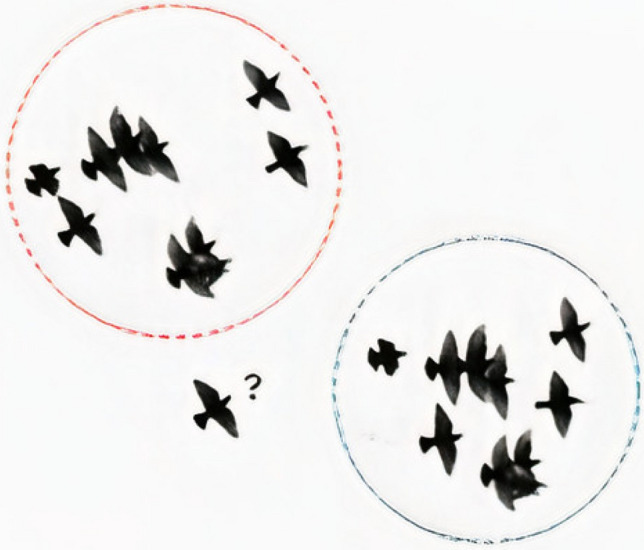
A simplified example of the collective behaviour of starling birds
The proposed sbWFCM clustering algorithm
At its core, the flocking model assumes that there are three basic behavioural steering patterns, which describe how an individual employs the relative position of close peers to decide its next position and direction. Separation means maintaining a minimal distance from surrounding boids; alignment to adapt the direction to that of boids in the vicinity; and cohesion which refers to moving towards the center of the perceived density of birds in the neighbourhood. The three behaviours are modelled as outlined in Table 1. Flocking is a way that an individual i responds to peers in a small area that is defined by a distance and a flight path of the starling boids . As a result, a force is produced, called the social force, consisting of a summation of the three forces , and , to determine the next position of the individual i.
| 4 |
The communication between individuals in the flock involves the dissemination of information to all starlings within the flock after a certain time, with no direct interaction. That way, the consistency of the starling flock can be achieved by grouping the birds with the same direction, while maintaining a distance from the other flocks.
Table 1.
The description and the mathematical formulation of the three elementary behaviours, separation, alignment, and cohesion where is the set of individuals in the interaction area, , , are respectively the separation, alignment, and cohesion weighting factors, is the required avoidance distance between individuals, is the forward direction of each individual, g is the avoidance rate (given as function of the proximity to the neighbour), and is the Gaussian Standard Deviation
| Behaviour | Description | Formula |
|---|---|---|
| Separation 2a | The individual i is guided by a force to flow in the opposing direction from the average of other positions in its proximity | |
| Alignment 2b | The individual i is attracted by a force to be aligned with the mean forward-direction of its neighbour. | |
| Cohesion 2c | The individual i is subjected to a force to move toward the average position of the local flockmates in its neighbourhood |
Fig. 2.
The visual description of the elementary behaviours in the Raynolds simulation model, where a, b, and c correspond respectively to separation, alignment, and cohesion
To develop the proposed algorithm, this metaphor is substantiated as follows. Each object is represented as an individual in the starling flock (cluster), and corresponds to its position in the feature space. Supposedly, the forward direction varies according to the distance to each cluster prototype; it is given by Eq. (5). The social force (given by Eq. 4) is used to update the weight assigned to each object, given the separation, alignment and cohesion expressions defined in Table 1.
Mainly, sbWFCM algorithm performs as described in Algorithm 2. Noting that is a distance given to identify the set of neighbours . Given a set of features X and the initialized parameters, a ponderation coefficient, based on the Reynold’s formulation, can be embodied into the functional cost of sbWFCM. First, we compute the forward direction of X elements. Next, we identify the surrounding of each element by computing the distance (given by ), as well as the forward direction of the surrounding. Each element is driven then by a weight to approach its surrounding. This step is critical to conciliate similar features. Thereafter, we compute the separation force to maintain distance from dissimilar elements that belong to different clusters. Eventually, the three forces are associated to provide the next position of data elements in the feature space.
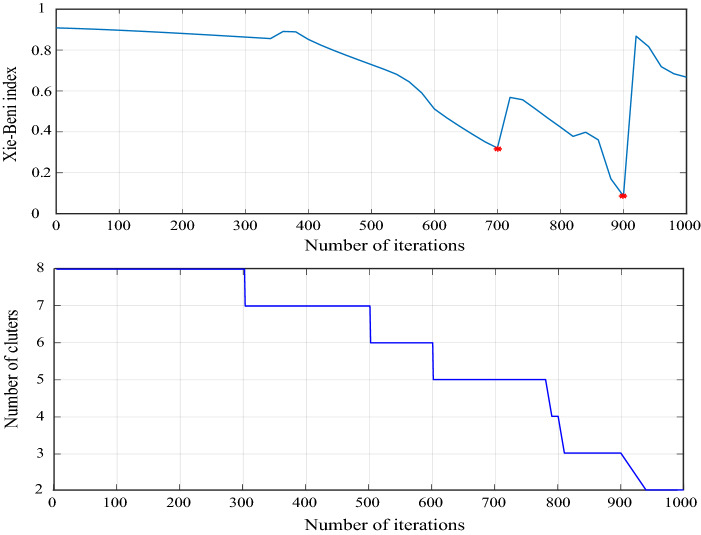
One of the most influential parameters of a partitioning clustering algorithm is the number of clusters C. The clustering process may effectively reveal the actual structure of the data only if C matches the number of existing subgroups. The selection quality of a given C is often assessed by a cluster validity analysis, and one possibility is to run the clustering algorithm repeatedly. Our proposed algorithm is guided by a number of iterations that corresponds to the movement of elements in the feature space. We use an iterative algorithm to find a reasonable number of clusters, which involves successive executions of Algorithm 2 with a variable number of iterations. For each number of iterations, the number of candidate clusters is determined based on the calculation of the internal Xie-Beni Index (XBI) for clustering validation, given in Appendix A. Typically, the number of iterations can be determined dynamically by a domain expert to recognize meaningful clusters that actually constitute the data structure.
Experimental results and discussion
Dataset outlines
To evaluate the proposed algorithm, we use a realistic dataset provided by Jo et al. [8]. More than thirty workloads benchmark suites and applications reflecting real-world loads have been employed. To generate the dataset, the benchmark suites have been performed on a cluster comprising four identical servers with a 4-core Skylake i5-6600 processor, 16 GB memory, a 1 gigabit network card designed for migration traffic, and a SSD-based storage cluster connected via NFS protocol. Many features covering various memory and CPU use pattern characteristics of a VM have been considered. For more details, the interested reader is referred to [8]. In this work, we focus on CPU, I/O, and memory usage patterns generated by running OLTPbenchmark [34], SPECWeb2009 [35], and MPlayer [36] benchmarks.
To adopt the data to our analysis, we consider three performance metrics, downtime, memory consumption, and CPU overload. For each metric, we set a level: low or high. For example, for the downtime metric, if a VM exceeds a certain threshold (given in milliseconds) while performing a workload or while migrating from one physical machine to another, the possibility that the VM causes downtime is high. This way, we define five status that can be assigned to a VM and are described in the Table 2. Moreover, we have verified the distribution of the values of the features, and we have removed outliers using the Thompson Tau method [37].
Table 2.
The defined status of a VM
| Id | Downtime | CPU overload | Memory use |
|---|---|---|---|
| S1 | Low | Low | Low |
| S2 | High | Low | Low |
| S3 | High | Low | High |
| S4 | High | High | Low |
| S5 | High | High | High |
Implementation notes
We assess the results of a typical run of the algorithm where the fuzzifier parameter was set to , data were normalized to zero means, and other parameter settings given in Table 3. The number of iterations is also an important parameter requiring a proper setting. The experiment consists of 50 trials to ensure a statistical evaluation of the algorithm. To validate the different alternatives proposed by the algorithm, internal XBI [38] and external Adjusted Rand Index (ARI) [39] are considered and briefly reviewed in Appendix A. The ARI is one of the most recommendable external validation indices used for measuring the similarity of two partitions. In this work, these partitions are the ground truth, i.e., the actual partition and the hypothetical partition produced by applying the clustering method. For visualization, the classical Sammon data dimensionality reduction approach is used [40]. The Sammon model creates a non-linear projection of a high-dimensional into a lower-dimensional space, aiming to maintain the structure of inter-point distances in both spaces.
Table 3.
Specifications of the hyper-parameters with the default values
| Parameter | Default entry |
|---|---|
| 0.8 | |
| 0.5 | |
| 0.5 | |
| 0.8 | |
| 0.05 | |
| 0.8 |
Clustering results and discussion
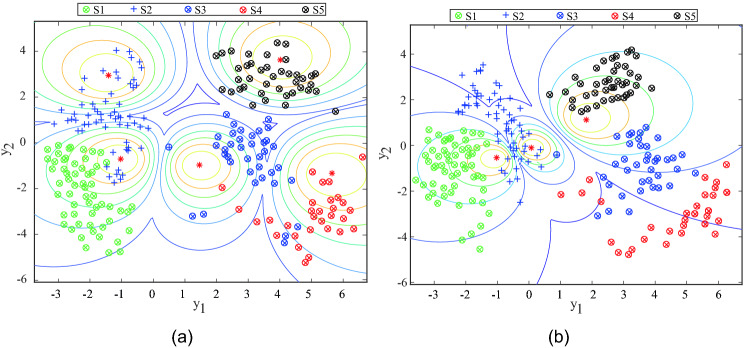
The proposed sbWFCM algorithm is applied to the resulting dataset. Some reasonable partitions were disclosed. Figure 3 shows the quality of the different structural alternatives provided by the algorithm based on the XBI. In this figure, the results correspond to the evolution of the XBI and the corresponding number of clusters as a function of the number of iterations for a typical execution of sbWFCM algorithm. The local minima of the index correspond to a reasonable number of clusters. The analysis of Fig. 3 shows that partitions with a number of clusters equal to 3 and 5 () constitute reasonable structural alternatives. Figure 4 presents illustrations of the two different perspectives using Sammon projection, where the red indicates the center of each cluster; ten solid line curves of different colors ranging from red to dark blue are drawn around it; each curve represents a contour of similar membership rank, i.e., the membership value becomes lower as the curve is further from the center (the darker the blue, the lower the belonging).
Fig. 3.
The evolution of the XBI and the corresponding number of clusters as a function of the number of iterations for a typical execution of sbWFCM algorithm
Fig. 4.
Sammon projection of the resulting feature space into the plane for workloads clustering using sbWFCM algorithm for a 5 clusters reached after 700 iterations and b 3 clusters reached by 900 iterations
Starting from Fig. 4a, we observe that a cluster formed by green symbols (S1), corresponding to workloads that have low CPU and memory usage and low downtime, is formed. Similarly, the cluster constituted by black symbols (S5) is clearly formed. One can say that the cluster formed represents workloads that are likely to cause performance degradation; on the other hand, the cluster containing the green symbols does not influence system performance. Therefore, their separation into two broadly separate clusters is reasonable. Besides, even if the clusters formed by blue and red are roughly in two separate clusters, we notice that some elements of both clusters are misclassified. This can be explained by the fact that both types of workloads have a high downtime impact.
Curiously enough, by increasing the number of iterations, the number of clusters corresponding to reasonable partitioning decreases (from 5 to 3). Passing to Fig. 4b, workloads with low CPU and low memory usage but high downtime (blue ) are always seen by the algorithm as similar to workloads with S1 state. In the same way, the three types of workload that have high downtime (S3, S4, and S5) are merged in one cluster with some misclassified elements. It can be noted that the number of iterations for updating the weight value assigned to each data point is important and can be adjusted by a domain expert.
Since in an actual datacenter it is not possible to recognize all status of VMs while running, we evaluate the robustness of abnormal behaviour detection when executing workloads with unknown configurations. Table 4 presents the ARI values of the different alternatives obtained by running sbWFCM algorithm to detect the abnormal behaviour when downtime, CPU overload, or memory use is not known. We observe that, except for the downtime metric, our algorithm can identify abnormal behaviours with over even when the status of the VMs is not clear. The ARI tends to decrease when the downtime configuration is not available in the ground truth. This decrease can be explained by the fact that a VM’s behaviour with an unknown configuration of a metric may be similar to abnormal behaviour, making the identification and diagnosis more complex. By way of illustration, the downtime metric, where a healthy workload runs with an undefined configuration, may be classified as an abnormal behaviour; however, VMs with normal behaviour can be suspended due to CPU or memory overload or for an eventual migration process.
Table 4.
ARI values obtained by running sbWFCM algorithm with unknown configurations
| ARI | |
|---|---|
| Memory use | 0.83 |
| CPU overload | 0.79 |
| Downtime | 0.57 |
SbWFCM vs. WFCM
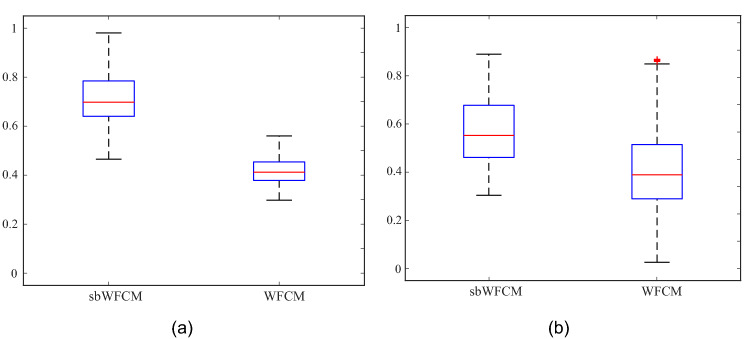
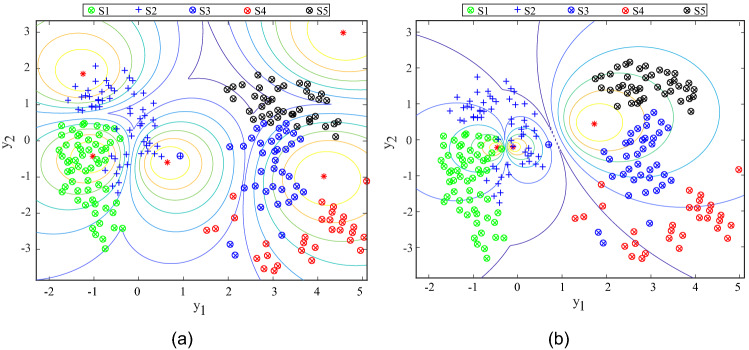
More interestingly, we compare the proposed clustering algorithm sbWFCM to a simple density-based WFCM algorithm. We proceed as if we are interested in the quality of the final results at hand. We statistically evaluate the quality of the obtained partitions, as recorded by the external ARI, for 20 runs of both algorithms for and clusters under the same initial parameter settings. Since the present case does not require any normality or homoscedasticity of the analyzed samples, we use the non-parametric statistical Wilcoxon signed-rank test to analyze the results [41]. In other words, the test serves as a means of addressing the question of how well the quality of partitions can reflect two different populations. The observed distribution of the ARI over 20 independent runs of the algorithms for a varying number of clusters is summarized in Fig. 5 with the corresponding statistical results reached. The significance level considered is given by , referring to a confidence interval of 95%. For example, indicates the existence of a statistically significant difference between the data samples being analyzed. Based on these experiences, we can conclude that the sbWFCM outperforms the standard density-based WFCM for and . Such improvement a purpose of this type of algorithm; it is a convenient spin-off effect of the elementary behavioural technique used to conceive the clustering process. The improvements are noticed for both number of clusters considered. In practical term, this basically implies that, in this case, the simple density-based WFCM is not able to clearly distinguish between data point for the different workload status, as shown in Fig. 6; we notice that the clusters identified by the algorithm are not adequate with the actual classification of the data; for example, in the upper right cluster exhibited in Fig. 6a, the data points symbolized by black are far away from the center of the cluster.
Fig. 5.
Boxplots showing the distributions of ARI over 20 independent runs of sbWFCM and simple density-based WFCM for a 3 clusters and b 5 clusters
Fig. 6.
Sammom projection of the resulting feature space into the plane for workloads clustering using simple density-based WFCM algorithm for a 5 clusters and b 3 clusters
Conclusion
In this paper, we further take advantage of a machine learning technique for workload and VM performance monitoring. We have proposed using our newly developed weighted fuzzy clustering algorithm (sbWFCM) to identify abnormal behaviours of VMs while running given workloads. This algorithm enables to determine the membership of an object to a cluster, based on its position according to its neighbourhood, to build significant clusters, i.e., clusters that correspond to the actual data structure.
The proposed algorithm sbWFCM is inspired by the collective movement of groups of starling birds. According to Reynolds simulations, each starling movement’s direction depends on self-information, along with information provided by other close starlings, during the flight. A starling reacts to its neighbours and adapts its flight direction progressively to follow its fellow starlings. The coherence of the starling flock can thus be ensured by grouping the birds in the same direction while maintaining a distance from the other birds in the flock; the sbWFCM algorithm follows this intuitive mechanism to build clusters. The proposed algorithm involves grouping similar elements of data based on a particular distance metric. This last consists of a weight that drives clusters’ formation, allowing items with the same neighbourhood and direction to belong to the same cluster while maintaining distance from other groups with different position in the feature space.
The experimental results showed that the sbWFCM could provide a number of reasonable partitions for different numbers of iterations pre-defined and validated by a domain expert. Reasonable partitions are determined by an internal validation index, in this case, the XBI. Moreover, an external validity index (ARI) has been used to evaluate the mechanism of anomalous behaviour detection using the proposed algorithm applied to a dataset with missing configurations. Also, we compare sbWFCM with an existing density-based WFCM; results have shown that, for both cases considered in this work, the proposed sbWFCM outperforms this last by producing partitions with better ARI scores.
This paper’s results demonstrate the ability of the proposed clustering algorithm to identify abnormal behaviours of workloads running within given VMs. However, the detection process is of-line, which can be limited when real-time detection is required. As prospects, we will integrate our algorithm into an online unusual behaviour detection framework, which exploits previously observed performance and resource consumption data to build and detect the patterns of previously observed irregularities. Simultaneously, we will explore a new variant of sbWFCM that can automatically scale the number of iterations needed to achieve the optimal partitioning results instead of being adjusted by a domain expert.
Biographies
Saloua El Motaki
received the BSc degree in Mathematics and Computer Science from the University Sidi Mohamed Ben Abdellah, Fez, Morocco (USMBA) and the MSc degree in Imagery and Business Intelligence from the USMBA. She obtained her PhD degree at USMBA. Currently, she is working on the optimization of power consumption in data centers.
Ali Yahyaouy
is a professor at the Faculty of Sciences Dhar El Mahraz, Sidi Mohamed Ben Abdellah University, Morocco. He obtained his PhD degree at University of Technology of Belfort-Montbéliard, France and Sidi Mohamed Ben Abdellah University, Morocco in 2010. He is a member of the LISAC laboratory in Fez. He has been the coordinator of the University Qualification "Software Engineering and Multimedia" since 2014 and of the International Francophone Master "Web Intelligence and Data Science" since 2017. His research activities mainly concern Multi-agent Systems, Intelligent Energy Management, and Smart Grids.
Hamid Gualous
obtained his doctoral thesis at the University of Paris Orsay in 1994. He was appointed Associate Professor at the University of Franche-Comté in Belfort in 1996 and then Professor of Universities in 2009 at the University of Caen Normandy. He has been Director of the LUSAC laboratory in Cherbourg since January 2012. His research activities mainly concern energy Storage for Embedded and Stationary applications, Power Electronics as well as Energy Management and Smart Grids. He is author of more than 70 A-rank publications, two books on Energy Storage and seven chapters in books and more than 60 international conferences.
Jalal Sabor
received the Ph.D. degree in engineering science from the Institut National des Sciences Appliquées (INSA), Rouen, France in 1995. He is currently a professor of industrial computer science at the Ecole Nationale Supérieure d’Arts & Métiers (ENSAM), University Moulay Ismail, Meknes, Morocco. He was a member of the LSMI Laboratory. He was, also, the research team control steering and supervision systems head. Currently, he is the head of the department of Automatic, Electronic, Electro-technical and Electromechanical at ENSAM Engineering School. His main research interests include Intelligent Management of Energy, Smart Grids, Control and Supervision Systems, Architecture based on Multi-agent Systems and Fuzzy Logic.
A. Appendix: Evaluation criteria
The primary purpose of the illustration was to judge the performance of the proposed algorithm. For the standard FCM algorithm and its variants, the number of clusters C is the most significant parameter. If C matches the unspecified number of subsets existing in the data, it is more likely that the clustering process provides an effective insight into the underlying structure of the data. Thus, two cluster validity indices are used to verify the effectiveness of the choice of C.
- The Xie–Beni Index (XBI): is an internal fuzzy clustering index, defined as a ratio between the compactness and the separation of the fuzzy clustering algorithm. The XBI has been mathematically proven by its dependence on Dunn’s index, a robust cluster validity function [38]. The goal is to achieve a clustering structure in which element in the dataset strongly belongs to a certain cluster while maintaining as much separation as possible from the centers of the other clusters. The XBI can be mathematically expressed as follows:
Note that a low value of XBI signifies that the clusters are compact and clearly separated.5 - Adjusted Rand Index (ARI): is an external validation index. It is the bias-adjusted formulation of the Rand Index (RI) [39]. The RI measures the similarity between a partition G, representing the ground truth labels of items in the dataset, and a partition H generated by the clustering process. It is given by the following:
where is the sum of the separated pairs in both G and H partitions; is the total number of pairs that are joined together in both partitions; (, respectively) is the number of pairs that cluster in G (H, respectively) but not in H (G, respectively); is the total number of pairs. As the value of the RI is not stable, ARI is introduced to overcome this drawback by considering the following:6
where is the number of elements belonging to G and H, and are the the number of elements within G and H. We note that ARI takes values in the interval [0, 1]; thus, values around 1 correspond to a high resemblance between the partitions under consideration.7
Author contributions
Conceptualization: SEM and AY; Formal analysis and implementation: SEM and AY; Writing - original draft preparation: SEM; Writing - review and editing: SEM, AY and HG; Supervision: AY, HG and JS.
Funding
The authors of this paper have not received any financial support for research, authorship and/or publication of this article.
Data availability
The data that support the findings of this paper are available from https://csap.snu.ac.kr/software/lmdataset.
Declaration
Conflict of interest
The authors of this paper declare that they have no significant competing financial, professional, or personal interests that might have influenced the performance or presentation of this work.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Chandio AA, et al. Energy efficient VM scheduling strategies for HPC workloads in cloud data centers. Sustain. Comput. 2019;24:100352. doi: 10.1016/j.suscom.2019.100352. [DOI] [Google Scholar]
- 2.Buchaca D, et al. Sequence-to-sequence models for workload interference prediction on batch processing datacenters. Fut. Generation Comput. Syst. 2020;110:155–166. doi: 10.1016/j.future.2020.03.058. [DOI] [Google Scholar]
- 3.Khan AA, et al. An energy, performance efficient resource consolidation scheme for heterogeneous cloud datacenters. J. Netw. Comput. Appl. 2020;150:102497. doi: 10.1016/j.jnca.2019.102497. [DOI] [Google Scholar]
- 4.Bagchi, S., Kar, G., Hellerstein, J.: Dependency Analysis in Distributed Systems using Fault Injection: Application to Problem Determination in an e-commerce Environment. (2001)
- 5.Bari MF, et al. Data center network virtualization: a survey. IEEE Commun. Surv. Tutor. 2013;15(2):909–928. doi: 10.1109/SURV.2012.090512.00043. [DOI] [Google Scholar]
- 6.Egele, M., et al.: Blanket execution: Dynamic similarity testing for program binaries and components. In: 23rd USENIX Security Symposium (USENIX Security 14). pp. 303–317 (2014)
- 7.Hereford, J., Blum, C.: FlockOpt: A new swarm optimization algorithm based on collective behaviour of starling birds. In: 2011 Third World Congress on Nature and Biologically Inspired Computing, pp. 17–22 (2011). 10.1109/NaBIC.2011.6089411.
- 8.Jo, C., Cho, Y., Egger, B.: A machine learning approach to live migration modeling. In: ACM Symposium on Cloud Computing. SoCC’17. Santa Clara, CA, USA (2017)
- 9.Mohamed, S.H., El-Gorashi, T.E.H., Elmirghani, J.M.H.: A Survey of Big Data Machine Learning Applications Optimization in Cloud Data Centers and Networks. (2019). arXiv: 1910.00731 [cs.NI]
- 10.Xiao P, et al. A power and thermal-aware virtual machine management framework based on machine learning. Clust. Comput. 2021;1:1–18. doi: 10.1007/s10586-020-03228-6. [DOI] [Google Scholar]
- 11.Tang X, et al. Energy efficient job scheduling with workload prediction on cloud data center. Clust. Comput. 2018;21(3):1581–1593. doi: 10.1007/s10586-018-2154-7. [DOI] [Google Scholar]
- 12.Rugwiro, U., Chunhua, G.: Customization of Virtual Machine Allocation Policy Using K-Means Clustering Algorithm to Minimize Power Consumption in Data Centers. In: Proceedings of the Second International Conference on Internet of Things, Data and Cloud Computing. New York, NY, USA: Association for Computing Machinery, (2017). 10.1145/3018896.3018947.
- 13.Khan, A., et al.: Workload characterization and prediction in the cloud: A multiple time series approach. In: 2012 IEEE Network Operations and Management Symposium, pp. 1287–1294 (2012)
- 14.Srilatha D, Shyam GK. Cloud-based intrusion detection using kernel fuzzy clustering and optimal type-2 fuzzy neural network. Clust. Comput. 2021;8:1–16. doi: 10.1007/s10586-021-03281-9. [DOI] [Google Scholar]
- 15.Jaber AN, Rehman SU. FCM-SVM based intrusion detection system for cloud computing environment. Clust. Comput. 2020;23(4):3221–3231. doi: 10.1007/s10586-020-03082-6. [DOI] [Google Scholar]
- 16.Abdelsalam, M., Krishnan, R., Sandhu, R.: Clustering-based IaaS cloud monitoring. In: 2017 IEEE 10th International Conference on Cloud Computing (CLOUD), pp. 672–679 (2017). 10.1109/CLOUD.2017.90.
- 17.Ismaeel, S., Miri, A., Al-Khazraji, A.: Energy-consumption clustering in cloud data centre. In: 2016 3rd MEC International Conference on Big Data and Smart City (ICBDSC). pp. 1–6 (2016)
- 18.Shirazi, N., et al.: Assessing the impact of intra-cloud live migration on anomaly detection. In: 2014 IEEE 3rd International Conference on Cloud Networking (CloudNet), pp. 52–57 (2014). 10.1109/CloudNet.2014.6968968.
- 19.Amruthnath, N., Gupta, T.: A research study on unsupervised machine learning algorithms for early fault detection in predictive maintenance. In: 2018 5th International Conference on Industrial Engineering and Applications (ICIEA), pp. 355–361 (2018). 10.1109/IEA.2018.8387124.
- 20.Hui Y. A virtual machine anomaly detection system for cloud computing infrastructure. J. Supercomput. 2018;21:6126–6134. doi: 10.1007/s11227-018-2518-z. [DOI] [Google Scholar]
- 21.Zhang, X., et al.: askInsight: A fine-grained performance anomaly detection and problem locating system. In: 2016 IEEE 9th International Conference on Cloud Computing (CLOUD), pp. 917–920 (2016). 10.1109/CLOUD.2016.0136.
- 22.Pandeeswari N, Kumar G. Anomaly detection system in cloud environment using fuzzy clustering based ANN. Mobile Netw. Appl. 2016;21:494–505. doi: 10.1007/s11036-015-0644-x. [DOI] [Google Scholar]
- 23.El Motaki, S., et al.: Gath-Geva clustering algorithm for high performance computing (HPC) monitoring. In: 2019 Third International Conference on Intelligent Computing in Data Sciences (ICDS). pp. 1–6 (2019)
- 24.Hathaway RJ, Hu Y. Density-weighted fuzzy c-means clustering. IEEE Trans. Fuzzy Syst. 2009;17(1):243–252. doi: 10.1109/TFUZZ.2008.2009458. [DOI] [Google Scholar]
- 25.Bialek W, et al. Statistical mechanics for natural flocks of birds. Proc. Nat. Acad. Sci. USA. 2012;109(13):4786–4791. doi: 10.1073/pnas.1118633109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bialek W, et al. Social interactions dominate speed control in poising natural flocks near criticality. Proc. Nat. Acad. Sci. USA. 2014;111(20):7212–7217. doi: 10.1073/pnas.1324045111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Reynolds, C.W.: Flocks, herds and schools: a distributed behavioral model. In: Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques. SIGGRAPH ’87. New York, NY, USA: Association for Computing Machinery, 25–34 (1987). 10.1145/37401.37406.
- 28.Potts WK. The chorus-line hypothesis of Manoeuvre coordination in avian flocks. Nature. 1984;309(1):344–345. doi: 10.1038/309344a0. [DOI] [Google Scholar]
- 29.Pant A, Seiler P, Hedrick K. Mesh stability of look-ahead interconnected systems. IEEE Trans. Autom. Control. 2002;47(2):403–407. doi: 10.1109/9.983389. [DOI] [Google Scholar]
- 30.Balch T, Arkin RC. Behaviour-based formation control for multirobot teams. IEEE Trans. Robot. Autom. 1998;14(6):926–939. doi: 10.1109/70.736776. [DOI] [Google Scholar]
- 31.Tanner HG, Loizou SG, Kyriakopoulos KJ. Nonholonomic navigation and control of cooperating mobile manipulators. IEEE Trans. Robot. Autom. 2003;19(1):53–64. doi: 10.1109/TRA.2002.807549. [DOI] [Google Scholar]
- 32.Giulietti F, Pollini L, Innocenti M. Autonomous formation flight. IEEE Control Syst. Mag. 2000;20(6):34–44. doi: 10.1109/37.887447. [DOI] [Google Scholar]
- 33.Ogren P, Fiorelli E, Leonard NE. Cooperative control of mobile sensor networks: adaptive gradient climbing in a distributed environment. IEEE Trans. Autom. Control. 2004;49(8):1292–1302. doi: 10.1109/TAC.2004.832203. [DOI] [Google Scholar]
- 34.Difallah DE, et al. OLTP-Bench: an extensible testbed for benchmarking relational databases. Proc. VLDB Endow. 2013;7(4):277–288. doi: 10.14778/2732240.2732246. [DOI] [Google Scholar]
- 35.The Open Systems Group OSG. The SPECweb2009 benchmark. https://www.spec.org/web2009/. Accessed 04 May 2020 (2020)
- 36.MPlayer. The movie player 2017. http://www.mplayerhq.hu/design7/news.html. Accessed 04 May 2020 (2020)
- 37.Dieck, R.H.: Measurement uncertainty: methods and applications. ISA (2007)
- 38.Dunn JC. Well-separated clusters and optimal fuzzy partitions. J. Cybern. 1974;4(1):95–104. doi: 10.1080/01969727408546059. [DOI] [Google Scholar]
- 39.Hubert L, Arabie P. Comparing partitions. J. Classific. 1985;2(1):193–218. doi: 10.1007/BF01908075. [DOI] [Google Scholar]
- 40.Sammon JW. A nonlinear mapping for data structure analysis. IEEE Trans. Comput. 1969;100(5):401–409. doi: 10.1109/T-C.1969.222678. [DOI] [Google Scholar]
- 41.Sheskin DJ. Handbook of Parametric and Nonparametric Statistical Procedures. Boca Raton: CRC Press; 2003. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this paper are available from https://csap.snu.ac.kr/software/lmdataset.