Modeling the Social and Spatial Proximity of Crime: Domestic and Sexual Violence Across Neighborhoods

Abstract

Objectives:

Our goal is to understand the social dynamics affecting domestic and sexual violence in urban areas by investigating the role of connections between area nodes, or communities. We use innovative methods adapted from spatial statistics to investigate the importance of social proximity measured based on connectedness pathways between area nodes. In doing so, we seek to extend the standard treatment in the neighborhoods and crime literature of areas like census blocks as independent analytical units or as interdependent primarily due to geographic proximity.

Methods:

In this paper, we develop techniques to incorporate two types of proximity, geographic proximity and commuting proximity in spatial generalized linear mixed models (SGLMM) in order to estimate domestic and sexual violence in Detroit, Michigan and Arlington County, Virginia. Analyses are based on three types of CAR models (the Besag, York, and Mollié (BYM), Leroux, and the sparse SGLMM models) and two types of SAR models (the spatial lag and spatial error models) to examine how results vary with different model assumptions. We use data from local and federal sources such as the Police Data Initiative and American Community Survey.

Results:

Analyses show that incorporating information on commuting ties, a non-spatially bounded form of social proximity, to spatial models contributes to better deviance information criteria (DIC) scores (a metric which explicitly accounts for model fit and complexity) in Arlington for sexual and domestic crime as well as overall crime. In Detroit, the fit is improved only for overall crime. The distinctions in model fit are less pronounced when using cross-validated mean absolute error (MAE) as a comparison criteria.

Conclusion:

Overall, the results indicate variations across crime type, urban contexts, and modeling approaches. Nonetheless, in important contexts, commuting ties among neighborhoods are observed to greatly improve our understanding of urban crime. If such ties contribute to the transfer of norms, social support, resources, and behaviors between places, they may then transfer also the effects of crime prevention efforts.

1. Introduction

Crime in the United States has been on a downward trajectory nationally since the mid 1990’s but some cities, such as Detroit, Michigan, remain at much higher levels than others. Domestic and sexual violence also remain great problems. Studies show that intimate partner violence accounts for 15 percent of all violent crime (Morgan and Truman, 2014), 1 in 3 female murder victims are killed by intimate partners (Bridges et al., 2008). One in 5 women in the United States experienced completed or attempted rape during her lifetime (Black et al., 2011). About 11 million of these victims reported the first event to have occurred before age 18 (Smith et al., 2018). Over 52 million women (43.6 percent) experienced contact sexual violence victimization in their lifetime (Smith et al., 2018). Victims of domestic and sexual violence experience increased risk of a range of physical and mental health problems, including depression and suicide (WHO, 2013). Children exposed to domestic violence also suffer emotional and behavioral problems (Wolfe et al., 2003).

Urban crime is also known to concentrate in some neighborhoods and places more than others (Sampson, 2012; Weisburd et al., 2016). This differential distribution of crime across neighborhoods within a city has been the focus of research since the early 1900’s (Shaw and McKay, 1942). Moreover, neighborhood contexts have been shown to play important roles in domestic and sexual violence (Benson et al., 2003, 2004; Browning, 2002; Lauritsen, 2001; Lauritsen and White, 2001; Pinchevsky and Wright, 2012; Voith, 2017; Wooldredge and Thistlethwaite, 2003; Wright and Benson, 2010, 2011). Historically, however, the emphasis has been predominantly on internal socio-demographic forces and social processes. In the last few decades, studies of crime have started to highlight more the importance of geographic proximity to crime (or spatial dependencies) (Anselin et al., 2000; Anselin, 2002; Gracia et al., 2015; Graif, 2015; Morenoff et al., 2001; Peterson and Krivo, 2010). Though not focused on domestic or sexual violence in particular, non-spatially bounded social proximity also has been emerging as an intriguing phenomenon with potential great significance for crime (Browning et al., 2017; Graif et al., 2019; Mears and Bhati, 2006; Tita and Radil, 2010; Wang et al., 2016). For instance, research has begun to show evidence that co-offending ties and gangs and gang conflicts connect neighborhoods that are not necessarily geographically proximate (Papachristos et al., 2013; Radil et al., 2010; Schaefer, 2012; Tita and Radil, 2011).

Important insights from research on the crime pattern theory have presented the urban landscape as an environmental backcloth, a collection of nodes connected through pathways that facilitate people’s routine activities (Brantingham and Brantingham, 1993). Indeed, people have been shown to move a great deal between non-nearby areas as a result of commuting for work, changing their home address, traveling for recreation, shopping, or other routine activities (Boivin and D’Elia, 2017; Boivin and Felson, 2018; Felson and Boivin, 2015; Graif et al., 2017; Matthews et al., 2010; Matthews and Yang, 2013; Ong and Houston, 2002; Sampson, 2012; Wikström et al., 2010). These routine activity and mobility patterns are likely related to the configuration of a city’s transportation pathways and the spatial distribution of a city’s land use, industrial, commercial, or residential (Groff et al., 2009; Kinney et al., 2008). Importantly, a lot remains unknown about the consequences for crime of large numbers of people moving routinely across space. However, indications exist that connections between places matter for crime. For example, access to external resources such as mortgage loans from outside people’s neighborhoods has been shown to be associated with to lower crime (Velez et al., 2012).

Beyond material influences, norms, pressures, and social disapproval in people’s extended social circles, including professional and work communities, may affect attitudes and behaviors regarding the acceptability of coercion or violence in dating situations or in resolving domestic conflicts (NAS, 2018; WHO, 2009). Norms and experiences within immediate and extended social contexts such as work places about the roles of men and women in society and in intimate situations may affect people above and beyond the norms and experiences in their kin and friendship networks or home communities. Social isolation from networks of potential support has long been viewed as a key precursor of intimate partner violence (Browning, 2002; Lanier and Maume, 2009; Pinchevsky and Wright, 2012; Wright and Benson, 2010).

Drawing on this emerging line of research, in this study we aim to understand to what extent interconnections between the neighborhoods where people live and the ones where they work contribute to crime in general and to sexual and domestic crime, in particular. Given that domestic and sexual violence are often thought of as “private” crimes, if we observe a connection between commuting ties and such crimes, it would be a more conservative test than observing one for crime overall. Substantively, our focus on the role of social proximity as conceptualized through non-spatially bounded commuting ties, is closely linked to the logic of how spatial proximity typically works. Spatial proximity has often been thought as a specific form of social proximity (Tita and Radil, 2010), likely driven by social interactions, clustering and spillovers that influence people’s attitudes, norms and behaviors from a neighborhood to another. The main difference in our approach is that social proximity, conceptualized through activity ties like commuting, can include spatial proximity but does not depend on it.

We use spatial statistical models to identify the significant community characteristics that may affect domestic and sexual violence by using incident-level crime data as well as local and federal data sources to incorporate socioeconomic characteristics of the neighborhoods. Socioeconomic variables such as unemployment rate and median income are collected from the American Community Survey (ACS), and commuting data, collected from LODES (Longitudinal Employer-Household Dynamics Origin-Destination Employment Statistics) which is run through Census, are used to capture non-spatially bounded social proximity (that can include but is not bounded by spatial proximity) between neighborhoods defined by block groups from Census.

The first location that we choose for our study is Detroit, Michigan, a city that has been shown to be safer than only 2% of US cities (NeighborhoodScout.com, 2018b). The second area of focus is Arlington County, Virginia, in part, because of our engagement with county and the local government agencies including the police department. This partnership allows us to identify issues that are of particular interest to the police department and our findings could be used to inform and impact their decision-making processes. Importantly, in contrast to Detroit, Arlington was rated as safer than 40% of US Cities (NeighborhoodScout.com, 2018a). The diversity of these two sets of urban communities enables us to test the robustness and scalability of our approach.

In this paper, we rely on the conditional autoregressive (CAR) model for analyzing spatially aggregated or “areal” data. CAR models are popular in sociology, political science, epidemiology, and other disciplines. We consider three types of CAR models, all three of which fall under the category of spatial generalized linear mixed models (SGLMMs): the Besag, York, and Mollié (BYM) model, the Leroux model, and the sparse SGLMM (s-SGLMM). Each of the three models can capture social proximity between communities, but does so in different ways. For each model, we consider two versions – one that allows for geographical proximity alone, the standard approach in the literature, and another that combines both geographic and commuting proximity. This study thus seeks to contribute methodologically to quantitative criminology and spatial statistics by comparing these approaches and examining if combining commuting and spatial proximity improves the fit and the performance of the statistical models, for both Arlington and Detroit. We compare the CAR models to more conventional models in criminology, the spatial lag and spatial error models. The study contributes to the literature by investigating the value of a novel measure of social proximity based on population commuting patterns.

An increasing number of studies in the crime literature use microgeographic units of analysis, such As street intersections (Andresen et al., 2017; Curman et al., 2015; Weisburd et al., 2004), and the importance of this work has been established (Weisburd, 2015). For the purposes of our analysis, the smallest geographic areas that data security constraints allow us to use is block groups. Nonetheless, our core focus is on the social relationships between communities. There are few, if any, data sources that can clearly and robustly establish social ties between street intersections. In addition, in our modeling procedure we compare geographic and commuting ties between areal units and control for demographic features of the areal units. We believe that these socioeconomic characteristics of neighborhoods are important to take into account when modeling crime.

The paper is organized as follows. In the next sections, we summarize the literature focused on neighborhood effects related to sexual or intimate partner violence highlighting some of the key the underlying mechanisms. We then discuss this literature in connection to possible social spillovers due to spatial proximity and to commuting proximity. Section 4 describes the aims of the current study from the statistical literature. Section 5 includes details of our proposed methodology, including the models and the model comparison techniques. Specifically, Sections 5.1–5.4 describes the modeling framework and presents the conditional autoregressive (CAR) statistical models used in this study. Section 5.5 outlines the spatial lag and spatial error models- two popular spatial models in the field of criminology. Section5.6 includes our methods for model comparison, including the Deviance Information Criteria and the mean absolute error. Section 6 summarizes the data sources, and in Section 7 we present the results through model comparison and evaluation of spatial autocorrelation. We conclude with a discussion of the results, some caveats and implications in Sections 8 and 9 with brief additional analysis in the appendix in Section 10.

2. Theoretical Framework and Background

Research on social disorganization has found that neighborhood structural features, such as socioeconomic disadvantage, unemployment, and residential heterogeneity, affect overall crime and intimate partner violence, directly or through different mechanisms (Benson et al., 2003, 2004; Browning, 2002; Cunradi et al., 2011; Lauritsen, 2001; Lauritsen and White, 2001; Pinchevsky and Wright, 2012; Wooldredge and Thistlethwaite, 2003; Wright and Benson, 2010, 2011). Several classes of such mechanisms have been highlighted in the literature (Sampson et al., 2002) and tested in empirical studies with respect to all types of crime, including intimate violence. The first category of mechanisms highlights the importance of social ties and interactions. Ties to friends and families in an area increase the social support and social capital of residents, protecting potential victims and deterring potential offenders from committing intimate crime. Social isolation from local networks of support, in turn may contribute to lower levels of social control against, and higher tolerance of, violence (Sampson and Bartusch, 1998), including violence against women (Pinchevsky and Wright, 2012; Wright and Benson, 2010, 2011). Moreover, the quality of social ties matters. Lower intimate partner violence (IPV) prevalence in a women’s social network is shown to be associated with lower IPV victimization (Raghavan et al., 2006). Violence in a male’s network has been found to mediate and moderate the effect of community violence on physical IPV perpetration (Raghavan et al., 2009). Wallis et al. (2010) and Brodsky (1996) indicate that women have to find ways to protect themselves against negative social support in the neighborhood.

The second category of mechanisms involves norms and collective efficacy. Under this umbrella fall expectations that neighbors would come together to solve community problems and high levels of trust and social cohesion in a community. Both are expected to contribute to lower crime in a community, including domestic and sexual crime. With some exceptions, empirical studies have found evidence consistent with this expectation (McQuestion, 2003). Levels of neighborhood collective efficacy were found to be associated with IPV risk (Browning, 2002; DeKeseredy et al., 2003) (also see Emery et al. (2011) who found no association). Lower levels of social cohesion and social control were associated with more IPV (Obasaju et al., 2009). Norms supporting noninterventions were positively associated with IPV risk (Browning, 2002). Higher perceived disorder was positively associated with IPV (Cunradi, 2007) though not significant in DeKeseredy et al. (2003)’s study. Higher levels of legal cynicism (or misstrust in the law) were found to be positively associate with IPV (Emery et al., 2011). Norms regarding the use of aggression against one’s wife at the community level have been shown to make a difference on an individual’s perpetration of physical intimate violence incidents (Koenig et al., 2006).

Two other major categories of mechanisms include routine activities (Cohen and Felson, 1979) and institutional resources. The presence of certain types of organizations, health services, domestic violence shelters, recreational centers, family well-being support centers in the area that can be accessed by the residents may deter crime generally, empower potential domestic violence victims to get support with domestic issues before they turn into violence and send signals to potential offenders that others care, preventing sexual or domestic violence. The balance of residential and commercial land use in a focal neighborhood, the density of transportation nodes may shape local interaction patterns between locals and transient population groups. Daily routine activity routes into the neighborhood by outsiders may contribute to new opportunities for dating, aggression, and sexual violence between residents and outsiders. An increasing number of studies show evidence consistent with these links (Clodfelter et al., 2010). The local presence of drug markets and alcohol outlets may contribute to signals of weakened normative constraints against abuse and aggression (Cunradi, 2010; Cunradi et al., 2011), signs of disorder and aggression (Cunradi, 2007), encourage congregation of at-risk individuals and reinforcing problematic attitudes and behaviors,increase normative tolerance of alcohol abuse and intimate violence (Benson et al., 2004; Boyle et al., 2009; Caetano et al., 2010; Cunradi et al., 2000; Cunradi, 2009; Flake, 2005; Li et al., 2010; McKinney et al., 2009; Stueve and O’Donnell, 2008) (but see Waller et al. (2012) for a non-significant relationship).

3. Neighborhood Mechanisms from a Spatial and Social Proximity Perspective

While traditionally, neighborhoods have been treated as closed systems with little transfer of ideas or behaviors outside their geographic bounds, recent advancements in research on the spatial ecology of neighborhoods have questioned this assumption, focusing on the possibility of boundary permeability between geographically proximate places (Graif et al., 2014; Graif and Matthews, 2017; Taylor, 2015). Spatial analyses of crime have highlighted the importance of accounting for spatial proximity to better understanding violence (Anselin et al., 2000; Graif and Sampson, 2009; Peterson and Krivo, 2010), including intimate partner violence (Cunradi et al., 2011; Gracia et al., 2015) and sexual violence (LeBeau, 1987). Increasingly, criminological studies have been focusing on modeling the diffusion of crime or offenders between neighborhoods or communities that are not necessarily spatially proximate (Tita and Griffiths, 2005; Wang et al., 2016; Wikström et al., 2010). We know however, that the modern ease of travel and communication contributes to local, national, and international transfers of people, attitudes, and customs (Neal, 2012; Sampson, 2012). While studies so far have not yet delved much into the mech anisms underlying spatial or social spillovers, the four major pathways of influence illustrated in the neighborhood effects scholarship could be envisioned to also work through spatial or non-spatial social proximity.

Integrating social disorganization theories with studies that show that social and institutional norms, pressures, resources, and support at work affect people’s attitudes, stress, and behaviors at home, can offer insights into how one may expect work environments to impact home environments. Indeed, research evidence indicates that stress and arguments at work affect stress and arguments at home (Bolger et al., 1989). Access to social support and physical safety at work by victims may not only empower them but also limit the opportunities of offenders to commit intimate violence (Rothman et al., 2007). Work contexts can also re-shape norms and attitudes about gender roles, aggression, and intimate violence among potential victims as well as offenders and bystanders (Banyard et al., 2004, 2007; Banyard, 2011; NAS, 2018; WHO, 2009). For example, a culture at work where employees’ social status and mobility are linked to aggression and sexual bravado may spill over into employees’ behavior and attitudes at home and in increase tolerance of private violence by neighbors.

Drawing on models of routine activities and journey-to-crime, we expect that access to resources and opportunities in the work area to report sexual or domestic violence may contribute to preventing abuse and empowering potential victims. Employee assistance programs are offered by about 58 percent of employers (Galinsky et al., 2008) and they include services such as counseling, referral to local services, leadership training and other educational programs. Access through employers to services like sexual harassment or diversity training and mental health services can empower potential victims and bystanders and even potential offenders suffering from addictions, contributing overall to decreasing incidents of domestic and sexual violence at work and at home (Falk et al., 2001; Maiden, 1996; Pollack et al., 2010).

On the other hand, sexual offenders may also travel via commuting channels. Some people may become victimized outside their home area as a result of routine travel and activities, an idea that gained attention in research on routine activities theory (Cohen and Felson, 1979). Similarly, crime pattern theory suggests that the places where people live, work, and play constitute activity nodes and paths that increases one’s odds to become involved in crime as a victim or offender (Brantingham and Brantingham, 1993, 1995). Indeed, residents’ travel patterns to work, shopping, and recreation, were found to be positively correlated with crime (Felson and Boivin, 2015; Stults and Hasbrouck, 2015). Evidence shows that a majority of violent crimes occur outside of the neighborhood of residence of the involved victim or offender (Groff and McEwen, 2007; Tita and Griffiths, 2005). While intimate violence often occurs “behind closed doors”, it does not necessarily occur in a victim’s home (Wilkinson and Hamerschlag, 2005). National level studies show that 15 percent of domestic violence incidents occurred in public settings (Greenfeld et al., 1998) and 8 percent of female victims and 11 percent of male victims were killed in public spaces (Rennison and Welchans, 2000).

Models of public control (Bursik Jr et al., 1999; Hunter, 1985; Velez, 2001) suggest that community level ties to external resources and influential political or business actors and organizations may lead to investments or disinvestments in the community. Such connections relevant for community outcomes are likely to form through contacts at work (Sampson and Graif, 2009; Sampson, 2012).

In sum, these ideas converge in suggesting the following hypothesis: like spatial proximity, social proximity based on commuting may affect domestic and sexual violence.

4. The Current Study

Building on this important new body of research and thinking, the current study examines the role of both the geographic and non-spatially bounded social proximity between neighborhoods. Geographic proximity has been studied over many years, with a focus on the concentration of crime in specific areas or area clusters (Weisburd et al., 2016). In our modeling framework, we expand the focus to investigate the possibility that, beyond internal area characteristics or street-corner dynamics, the concentration of crime may be associated with connections to spatially distant yet similarly disadvantaged areas or with differential isolation from more resourceful areas across the city, such as employment hubs.

We propose that in addition to geographic links, meaningful social connections might exist between spatially distant neighborhoods, and capturing this will lead to more accurate estimations of crime and inform more effective policing interventions. Social proximity is of growing interest in criminology and social sciences (Graif et al., 2017; Papachristos and Bastomski, 2018; Sampson, 2012). This study addresses this interest by proposing a new technique, to combine social proximity measured through commuting ties and geographic proximity in this modeling framework. With important exceptions, most of the literature on social proximity is focused on social closeness between individuals, not communities. For example, Agrawal et al. (2008) study both spatial and non-spatial social proximity; and measure social proximity based on co-ethnicity in the context of influence and knowledge flows among inventors. There is also important research on social proximity in networks, such as Alba and Kadushin (1976) where individuals’ social closeness is measured through the intersection of social circles.

Recently, a focus on connections between communities has emerged (Graif et al., 2014). For instance, Wang et al. (2016) use taxi data to establish social proximity between neighborhoods for crime rate inference in Chicago. They establish links between areal units where people get in and out of a taxi. We use commuting data, available through the Census, to establish non-spatially bounded social proximity. We believe that commuting data provides a reliable way to estimate social proximity. Commuting data may be thought of as symmetric- if someone goes to work from block group A to B, they will come home from B to A, which reflects a symmetric transfer of information, ideas, and customs. With taxi trips, travelers may be going from work to a restaurant or from bar to bar which may not illustrate as strong or as consistent of a social tie as commuting.

Our study thus considers two kinds of social proximities, which translate to two neighborhood matrices. Neighborhood matrices are often used in network analysis, which has been popular in recent literature in studying gang behavior (Radil et al., 2010; Tita and Radil, 2011) and it is also critical in the spatial models we use in our analysis. Our first model considers only geographic proximities where two communities are considered neighbors if they share a boundary. The second model considers both geographic and commuting proximities; two communities are considered to be neighbors through social proximity if there are a sufficient number of commuters between the communities. Both kinds of proximities are used as proxies for social interactions or shared characteristics between communities, such as voting behavior, demographics, or economic dynamics.

Jensen (2018) also presented a relevant project at the 2018 International Society for Bayesian Analysis (ISBA). Jensen (2018) also incorporates modifications of the neighborhood matrix and the authors mention incorporating social ties between neighborhoods. However, the authors study social barriers between communities, rather than social ties (Jensen, 2018). There is also some recent work in the field of transfer learning. Specifically, Zhao and Tang (2017) suggest a framework to incorporate Point of Interest data, meteorological data, as well as human mobility data. As in Wang et al. (2016), Zhao and Tang (2017) use taxi data as their measure for human mobility, through pick-up and drop-off points. There have also been some applications in the data mining domain that analyze coupled data sources (Do et al., 2017).

CAR models are a type of spatial generalized mixed model (SGLMM) with spatially correlated random effects. There is an extensive literature on the use of conditional autoregressive (CAR) models in public health and disease modeling (cf. Lawson, 2013; Lawson et al., 2016; Lee, 2011). There are also several instances of CAR modeling approaches in criminology and sociology (Britt et al., 2005; Sparks, 2011). However, many recent papers modeling the spatial distribution of crime rely on methods such as geographically weighted regression/spatial regressions (Bernasco and Elffers, 2010; Cahill and Mulligan, 2007; Wang et al., 2016) or fixed effects for the neighborhood (MacDonald et al., 2013; Papachristos et al., 2011). In our study, we compare these, more common, spatial lag and spatial error models to CAR models.

5. Proposed Methods

Our goal is to develop a model that combines geographic and non-spatial social proximity to provide a more comprehensive way to analyze how crime may be related across communities. Typical models rely on geographic proximity but do not incorporate other ways that communities may be connected rather than just sharing a border. We consider three kinds of CAR models as well as the spatial lag and spatial error models. We compare their results when including geographic proximity with their results when simultaneously accounting for both geographic proximity and commuting proximity. The models we consider are the spatial lag/error models as mentioned and the following CAR models: BYM, Leroux, and sparse spatial generalized linear mixed model. The sparse SGLMM, or s-SGLMM, controls for potential spatial confounding present in the BYM and Leroux models. By considering these different models we also demonstrate the robustness of our approach to a variety of assumptions. We also give details on our model comparison metrics and the relevant literature in this section.

5.1. CAR Modeling Framework

In this framework, we assume that our study region $\mathcal{S}$ is partitioned into K non-overlapping areal units. In our study, the areal units correspond to the 969 block groups in Detroit and 181 block groups in Arlington, which are defined by the Census. The aggregated crime counts for each block group are represented by the set of responses Y = (Y₁,…,Y_K). Spatial variation in the response is modeled using a matrix of covariates X_p×K = (x₁,…,x_K) and a spatial structure component ψ = (ψ₁,…, ψ_K) that accounts for any spatial autocorrelation that is not captured by the covariate effects.

We adopt the conditional autoregressive model (CAR) model (Lee, 2013) for analyzing areal unit data. We will use particular specifications of the CAR model, BYM, Leroux, and sparse SGLMM, which are described in detail below. These models are a special case of a Gaussian Markov Random Field (GMRF) (Lee, 2013). We use the implementations of the BYM and Leroux models in the CARBayes package in R and the implementation of the sparse SGLMM model in the ngspatial package in R (Hughes, 2014; Lee, 2013).

We use a Generalized Linear Mixed Model (GLMM) to fit our spatial areal unit data, given in Equation 1 below (Lee, 2013).

$$\begin{gathered} y_k|{\mu }_k~f\left(y_k|{\mu }_k\right)\text{for}\text{k}=1,\dots ,\text{K} \\ g\left({\mu }_k\right)=x_k^T\beta +{\psi }_k \\ \beta ~N\left({\mu }_{\beta },{\Sigma }_{\beta }\right) \end{gathered}$$ (1)

The parameters Y_k, x_k, and ψ_k represent the response, covariates, and spatial structure component, respectively, as defined above. The terminology $x_k^T$ indicates the transpose of the matrix x_k. The expected value of Y_k, E(Y_k) is denoted in the model as μ_k. The vector of regression parameters, denoted by β = (β ₁,… β _p), is assumed to have a multivariate Gaussian prior distribution. The parameters of this covariance matrix, μ_b and Σ_b are specified in the CARBayes package. We specify μ_β as a zero-mean vector and Σ_β as a diagonal matrix, where the diagonal elements are 100,000, which are the default choices. As our response is count data over the areal units, we use a Poisson form of the GLMM. We assume that f (y_k|μ_k) has the form following y_k ~ Poisson(μ_k) and $\mathit{\text{ln}}\left({\mu }_k\right)=x_k^T\beta +{\psi }_k$

In order to model spatial correlation, we define a neighborhood matrix, W, which is a non-negative, symmetric, K×K matrix, where K is the number of areal units. In each of the model specifications below (BYM, Leroux, and sparse SGLMM), the distribution of ψ parameter depends on the form of the neighborhood matrix, W.

We denote the (k, j)^th element of the neighborhood matrix by w_kj, which represents closeness between areal units or communities (${\mathcal{S}}_k$,${\mathcal{S}}_j$). The diagonal elements of this matrix, w_kk, are always 0. In the classical CAR model, positive values of w_kj indicate geographic closeness, and w_kj = 0 indicates non-closeness. The most commonly used structure to indicate closeness is w_kj = 1. In fact, the current framework of many of the statistical models, such as the sparse SGLMM in the R package ngspatial, only allow for binary elements in the neighborhood matrix.

For our purposes, we let w_kj ϵ {0,1}, where w_kj = 1 indicates that two areal units, k and j, are neighbors and w_kj = 0 otherwise. In our future work, we will consider other values of w_kj that will define proximity between areas that are not adjacent. However, in exploratory analysis, we found that the results are not sensitive to our choice of the positive value for w_kj to indicate closeness. In other words, we see that changing the value of w_kj from 0 to 1, to indicate a community is close through a social tie when it was not close geographically, does impact our modeling procedure but changing the entry w_kj from 1 to a higher weighted value, such as the number of commuters between those two communities, does not have a large impact on our results.

In order to combine commuting and geographic proximity, we create a neighborhood matrix, W, for both. To create the geographic proximity matrix, we define neighbors as any two block groups that share a border. To create the commuting proximity matrix, we define as neighbors any two block groups between which commuters travel, from home to work or vice versa. While we recognize that commuting is technically a directed activity, we treat it as undirected and create a symmetric neighborhood matrix, due to the fact that our modeling framework limits us to symmetric neighborhood matrices. However, we believe that ties between the two block groups may be reasonably assumed to have a bidirectional dimension related to the fact that people typically return home after work.

For the purposes of our model, we investigate whether it is necessary to define a specific non-zero cutoff for the number of commuters in establishing meaningful social proximity ties between two block groups. In our case, for both Detroit and Arlington, we defined a tie between two block groups based on whether there was more than 3 people commuting between the two block groups based on our sensitivity analysis included in Section 10.1. If we include too many or too few ties, then our model fit also improves compared to geographic proximity alone, but it is not optimal.

If there was not already a geographic tie between two communities but there is a commuting tie between the two communities, more than our cutoff number of commuters, then we replace the “0” element in the matrix with “1” and consider the two communities/block groups to be social neighbors. In other words, the first model includes only geographic proximity, where neighborhoods share a border. The second model also includes commuting ties between neighborhoods that did not already have a geographic tie through sharing a border. However, as stated earlier, we note that in preliminary analyses, our results were not sensitive to the positive indicator of closeness, whether it be “1”, as stated above, or a weighted matrix. In Table 1 we have included a brief summary of the neighborhood matrices where we consider geographic proximity alone, commuting proximity alone, and when we add geographic and commuting proximity together. In our models, we compare the first and the last forms of the neighborhood matrix.

Table 1:

Descriptive Statistics of Neighborhood Structures

Detroit
Variable	Geographic	Commuting	Geo. & Cmtg.
Number of regions	871	826	871
Number of nonzero links	4,972	7,322	I2,006
Percentage nonzero weights	0.65	I.07	I.58
Average number of weights per unit	5.71	8.86	I3.78
Arlington
Variable	Geographic	Commuting	Geo. &Cmtg.
Number of regions	173	172	173
Number of nonzero links	982	1,758	2,546
Percentage nonzero weights	3.28	5.94	8.51
Average number of weights per unit	5.68	10.22	14.72

In Jensen (2018), the authors are also interested in the modification of the neighborhood matrix of CAR models; specifically, they are interested in removing ties that are actually barriers. In other words, in their modification of the neighborhood matrix, W, they define element w_ij to be 1 if two communities are geographically nearby and 0 if they are not neighbors geographically. Then, Jensen (2018) recognize that some of these geographic borders might have barriers, either geographic or social. Therefore, the authors remove a subset of the geographic neighbors, or entries of 1 in the neighborhood matrix, and replaces them with 0’s, with promising results.

In Figure 1, we see the neighborhood structures depicted on the map of the block groups of Detroit and Arlington County. We are able to visualize how we have defined the geographic proximity neighborhood structure - links are created when block groups share a boundary. In the commuting proximity case, we can see that some folks are commuting across both counties, as there are clearly social hubs in some areas of the city or county where many people commute to/from. For the purposes of Figure 1, we specify a cutoff of 10 commuters for both Detroit and Arlington to define a social tie to avoid too many ties in the figure. In Table 1, we include the same number of ties as in our modeling results below.

Figure 1:

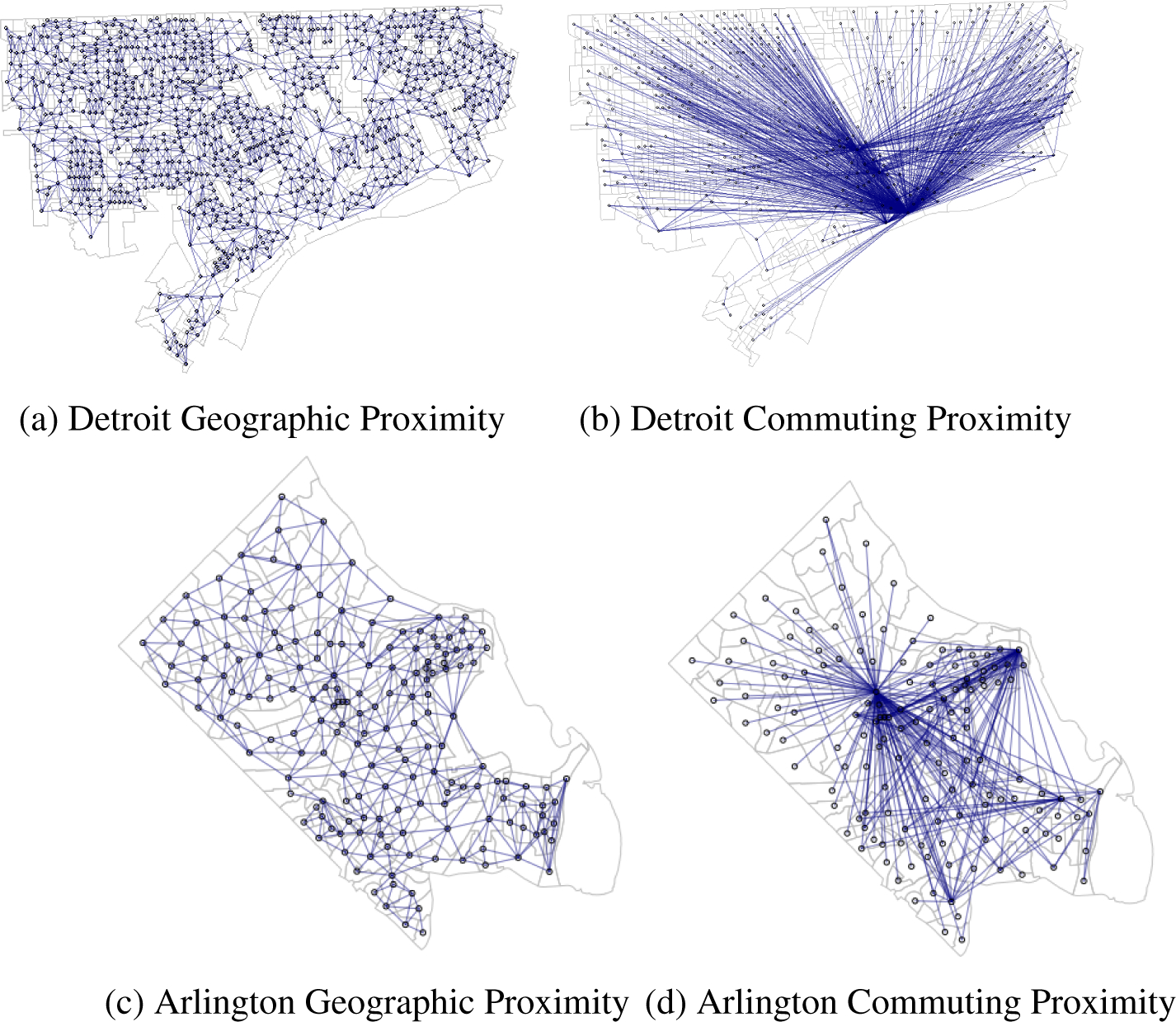
Plot of Neighborhood Structure

5.2. BYM Model

The first model we consider for ψ_k, the spatial random effects that capture the spatial dependence among the observations, is based on the CAR model proposed by Besag, York, and Mollié (BYM) (Besag et al., 1991). It has been widely used, especially in disease mapping. In this model, there are two sets of random effects, spatially autocorrelated and independent. The full model specification in the Bayesian framework is given in Equation 2 below (Lee, 2013).

$$\begin{gathered} {\psi }_k={\varphi }_k+{\theta }_k \\ {\varphi }_k|{\varphi }_{-k},W,{\tau }^2~N\left(\frac{{\sum }_{i=1}^K{w}_{ki}{\varphi }_i}{{\sum }_{i=1}^K{w}_{ki}},\frac{{\tau }^2}{{\sum }_{i=1}^K{w}_{ki}}\right) \\ {\theta }_k~N\left(0,{\sigma }^2\right) \\ {\tau }^2,{\sigma }^2~\text{Inverse-Gamma}(a,b) \end{gathered}$$ (2)

The BYM model requires two random effects to be estimated at each data point, ϕ_k and θ_k whereas only their sum, ψ_k, is identifiable. This is one of the main reasons why the following model, the Leroux Model, was proposed. In Equation 2, W is the neighborhood matrix, where w_ki is the (k,i)th entry of the neighborhood matrix. The parameter τ² allows us to estimate the variability in the random effect ϕ_k. The variability of the random effect θ_k is estimated through the parameter σ². The prior used for both τ² and σ² was Inverse-Gamma(1, 0.01).

5.3. Leroux Model

We adopt the model presented by Brian Leroux et al. as our second model for spatial random effects (ψ_k’s) (Brian et al., 2000). This model provides improved parameter interpretability, particularly of the variance parameters of the spatial random effects. The Bayesian model specification is given in Equation 3 (Lee, 2013).

$$\begin{gathered} {\psi }_k={\varphi }_k \\ {\varphi }_k|{\varphi }_{-k},W,{\tau }^2,\rho ~N\left(\frac{\rho {\sum }_{i=1}^K{w}_k{\varphi }_i}{\rho {\sum }_{i=1}^K{w}_{ki}+1-\rho },\frac{{\tau }^2}{\rho {\sum }_{i=1}^K{w}_{ki}+1-\rho }\right) \\ {\tau }^2~\text{Inverse-Gamma}(a,b) \\ \rho ~\text{Uniform}(0,1) \end{gathered}$$ (3)

The Leroux model uses only a single random effect, ϕ_k, and incorporates another spatial autocorrelation parameter, ρ, and no longer includes θ_k. This version of the CAR model has been widely proposed to be the most appealing CAR model, from both theoretical and practical standpoints (cf. Lee, 2011). Equations 2 and 3 include many of the same parameters, such as ϕ_k as a random effect and τ² as an estimate of variability of the random effect. In the Leroux model, we also include the ρ parameter to estimate both the mean and variance of the random effect. Once again, the prior used for τ² was Inverse-Gamma(1,0.01).

5.4. Sparse SGLMM

Finally, we consider the sparse SGLMM model (Hughes and Haran, 2013). This model addresses potential spatial confounding issues – spatial confounding is the phenomenon by which the spatial random effects act as if they are multicollinear with the covariates (“fixed effects”, in our case the demographic variables). As in standard regression, this multicollinearity can impact our ability to interpret the regression coefficients (β’s). This phenomenon was described by Reich et al. (2006) where, for instance, in the model parameterization given in Equation 1, we observe that $g\left({\mu }_k\right)=x_k^T\beta +{\psi }_k$. Reich et al. (2006) note that if we P is the orthogonal projection onto the regression manifold C(X), and we construct the eigendecomposition of P and I-P to obtain orthonormal bases, such as K_n×p and L_n×(n−p), for C(X) and C(X)^⊥, then Equation 1 can be rewritten as $g\left({\mu }_k\right)=x_k^T\beta +k_i^{\prime }\gamma +l_i^{\prime }\delta$ where γ_p×1 and δ_(n−p)×1 are random coefficients (Reich et al., 2006). This shows how K is the source of the confounding as it is multicollinear with the covariates. Hughes and Haran (2013) resolve this issue by removing K from the model while also reducing the dimensionality of the spatial random effects for computing efficiency. An implementation of this model is available in the R package ngspatial (Hughes, 2014).

5.5. Baseline Models: GLM and Spatial Lag/Error Models

In order to evaluate the CAR models, we compare them to the more frequently used spatial lag models (Anselin, 2013; Ord, 1975). First, we use a Poisson generalized linear model (GLM) and no spatial structure as a true baseline model. Next, we use the spatial simultaneous autoregressive lag model implemented in the spdep R package, with the form described in Equation 4. This is referred to as a mixed regressive spatial autoregressive model, as it includes additional predictor variables (X) to the purely spatially lagged autoregressive model. In this model framework, y is the crime count per block group, W is the neighborhood matrix formulated as above, and r is the spatial autoregression parameter which is estimated by the data (De Smith et al., 2018).

$$y=\rho Wy+\epsilon$$ (4)

We also introduce the spatial error model, which is defined below in Equation 5 (De Smith et al., 2018). We see that the error term is a spatially weighted error vector and a vector of iid errors, or u (De Smith et al., 2018).

$$y=X\beta +\epsilon \text{ where }\epsilon =\lambda W\epsilon +u$$ (5)

The spatial lag model, a type of spatial lag and spatial error models, often called spatial autoregressive model (SAR) differ from conditional autoregressive (CAR) models in several key ways, although they may produce similar results in some applications. In the spatial error models, we model the joint distribution of all of the crime counts per block group, y₁,…,y_n. In the CAR models, we model the conditional distributions of each of the crime counts per a given block group, y_i, given all of the other crime counts per block groups (Smith, 2020).

There are many advantages to both CAR and SAR model types. Both can be implemented in a Bayesian framework, although SAR models are often implemented through maximum likelihood approaches. CAR models assume only that the conditional distribution of each y_i, or crime count per block group, given the crime counts of all the other block groups, is normally distributed (Smith, 2020). Therefore, these distributions are determined by conditional means and variances. These conditional distributions are useful in a Bayesian models. For example, in Gibbs sampling, we can conduct parameter estimation through the specification of the conditional distributions. However, maximum likelihood estimation lends itself well to the spatial lag and spatial error models, where the parameter estimation is fast.

Other recent studies on the relationship between CAR and SAR models illustrate that a “SAR model can be written as a unique CAR model, and white a CAR model can be written as a SAR model, it is not unique” (Hoef et al., 2018). Ver Hoef et al. (2018) note that there are many statistical similarities between the two types of models, such as the fact that they “both rely on a latent Gaussian specification, a weights matrix, and a correlation parameter” (Ver Hoef et al., 2018). Ver Hoef et al. (2018) note that the differences between these models are important due to their effect on inference. Specifically, the authors recommend against the use of spatial lag models as they performed poorly in ecological tests. When comparing spatial error models to CAR models, Ver Hoef et al. (2018) note that two sites that are the same distance apart will have different correlation between the models.

We recognize that both models have their distinct advantages and we present the results for both SAR and CAR models.

5.6. Model Comparison Metrics

Model comparison between the different CAR models (or, for that matter, any areal or lattice models) can be challenging. For our analysis, we rely primarily on the Deviance Information Criteria (DIC). For additional comparisons and discussion, we also calculate the cross-validation based mean absolute error (MAE). DIC is a metric that provides a balance between model fit and complexity and is very widely used in model choice (Arnold et al., 1999; Jin et al., 2005; Ugarte et al., 2016, 2017; Zhu and Carlin, 2000). In contexts where prediction is the primary goal (it is not the primary goal in the lattice data setting in this manuscript), cross-validation based MAE may offer a nice interpretation. However, MAE becomes quite tricky to interpret in the context of CAR models because each time a sample is left out in the cross-validation, the marginal structure of the model changes. This is a problem that is peculiar to CAR models (Besag, 2002) because removing data points in the CAR model alters the marginal distribution of the remaining data.

DIC is a measure that combines the “goodness of fit” of a model and its “complexity” (Spiegelhalter et al., 2002). We measure the fit via the deviance, where D(θ) = −2logL(data|θ). Complexity is measured by the estimate for effective number of parameters, or $p_D=E_{\theta |y}[D]-D\left(E_{\theta |y}[\theta ]\right)=\overline{D}-D(\overline{\theta })$ = posterior mean deviance - deviance evaluated at the posterior mean of the parameters. So, the DIC is defined as in Equation 6 below.

$$\text{DIC}=D(\overline{\theta })+2p_D=D+p_D$$ (6)

A model with a smaller DIC is better supported by the data than a model with a larger DIC, similar to Akaike information criterion (AIC) that is commonly used in model comparison.

In addition to the Deviance Information Criteria (DIC), we also use leave-one-out cross-validation and the mean absolute error (MAE) to compare models. This method has been used in several existing studies for model comparison (Kim et al., 2012; Pardo-Igúzqfiza, 1998) although it is noted to be quite time consuming (Marshall and Spiegelhalter, 2003). In order to perform the leave-one-out cross-validation, we hold out one areal unit at a time, fit the model, and predict the outcome for that areal unit. In our case, we leave out one block group at a time and then predict the crime count for that block group using the coefficients that were estimated from all other block groups. We compute the error in the prediction and then average the absolute error across all block groups that are held out, to calculate the mean absolute error. This method avoids in-sample prediction problems. We repeat this method across all model types to get the mean absolute error for all models in order to conduct model comparison.

This model comparison method is time consuming in our study because the calculation of the leave-one-out cross-validation scales with how many block groups are present in the study. If we have 871 block groups, we need to run the models 871 times in order to get a prediction for each model for each block group when it is left out. To run all of our CAR and SAR models each time takes about 4 hours for Detroit, with 871 block groups. However, Arlington only has 173 block groups. Therefore, we only have to run the models 173 times to calculate the complete mean absolute error under leave-one-out cross-validation. Also, the models take less time to run for Arlington, due to the smaller matrix computations, at about 1 hour for all models. To run the complete cross-validation study for Arlington, it took approximately (1 hour)×(173 block groups) = 173 hours approximately. To run the complete cross-validation for Detroit would have been (4 hours)×(871 block groups) = 3,484 hours approximately. Therefore, we ran the leave-one-out cross-validation for all of the block groups in Arlington and we present results for Detroit with 100 block groups left out one at a time, instead of all 871.

6. Data

In this section, we describe the data sources used in our statistical models. We use crime data from the Police Data Initiative for Detroit, and data provided by Arlington County Police Department. In order to incorporate socioeconomic characteristics of the neighborhoods, as well as the commuting behavior, we use data provided by the US Census Bureau. We describe the data sources in detail below. To use the models described above, with a Poisson distribution, we use crime count data for both Arlington and Detroit. With the ACS demographic information, we incorporate total population per block group into the model formulation as a covariate in our model to ensure that crime frequency is not confounded with the population of the block group.

6.1. Crime

6.1.1. Detroit: Police Data Initiative

The crime data for Detroit, Michigan is available through the Police Data Initiative (PDI) (PoliceDataInitiative, 2017). This data source was created by the Police Foundation to support academic research. They encourage researchers and organizations in the community to use their data in order to create more effective relationships between law enforcement and local citizens. There are several datasets hosted by the PDI, including data on accidents/crashes, community engagement, officer-involved shootings, and complaints. In this study, we focus on the Calls for Service (CFS) which include the individual 911 calls.

For Detroit, the dataset includes 566,553 crime incidents from September, 2016 to November, 2017. There is a location (latitude/longitude) associated with each call, as well as some basic information on crime type and the priority of the call. We use the subset of the data associated with domestic/sexual violence related calls, and obtain 5,669 incidents for this time interval.

For Detroit, we use call description codes such as “rape IP or JH” (rape in progress or just happened) or “assault or sex assault delta”, where delta indicates a high-severity crime on the range alpha to echo. Figure 2 (left) illustrates the number of domestic violence crimes in Detroit by block group. We observe that there is a large peak in crimes in the southeast part of Detroit. Crime is pretty evenly distributed across the city other than this peak.

Figure 2:

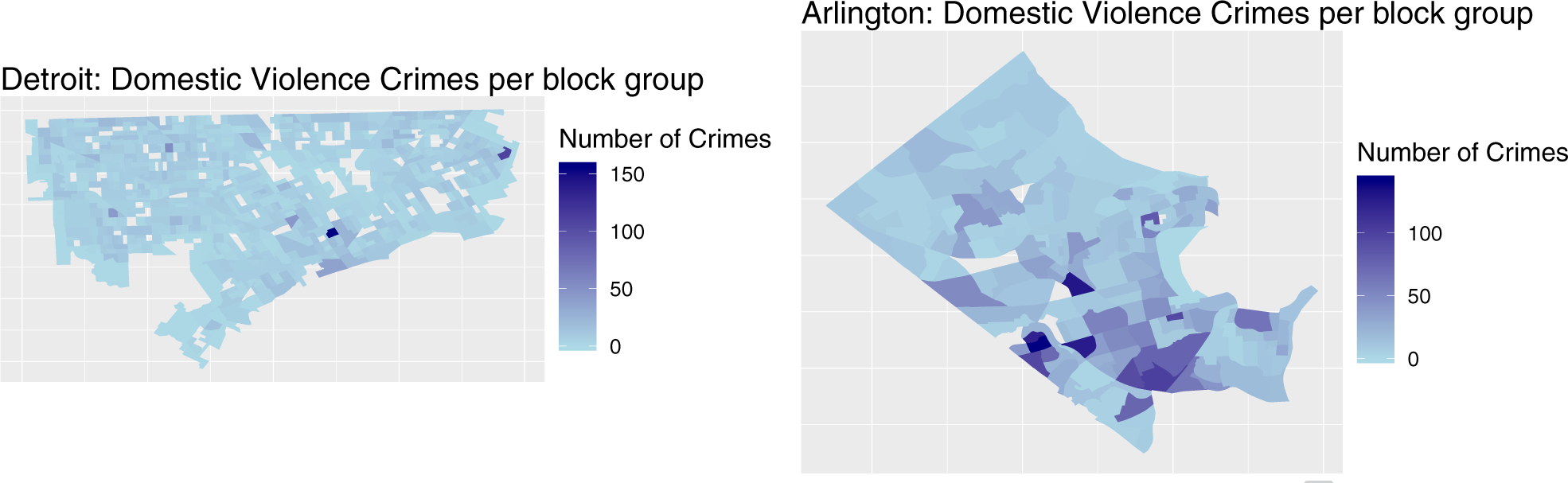
Number of domestic violence incidents by block group in Detroit (left) and Arlington County (right)

6.1.2. Arlington: Arlington County Police Department (ACPD)

For Arlington County, we use Calls for Service (CFS) data provided by ACPD for 2005–2015. This data is not publicly available but instead was provided through a data-sharing agreement and partnership. The dataset includes a total of 1,064,099 CFS, 261,944 incidents, and detailed information such as the time and location (lat/lon) of the call, type of the call and the incident (could be different), responding (dispatched) units, and the individuals involved. We focus again on the domestic/sexual violence incident types, including “assault family, domestic family disturbance” or “rape-gun”. For our analysis, we use the full range of dates available, from 2005 to 2015. The total number of domestic/sexual violence crimes in this time interval is 3,856. There is just 1 block group, out of 181, with no crimes present in this time period. The number of domestic violence incidents in Arlington County by block group is illustrated in the right panel of Figure 2.

6.2. Socioeconomic Characteristics: ACS

We use the American Communities Survey (ACS) to obtain socioeconomic information for all of the block groups in Detroit (Michigan) and Arlington County (Virginia). ACS is a national survey that is released every few years by the US Census Bureau and includes a wide range of variables from household income to migration information. The block groups for Detroit and Arlington County can be seen in Figure 1. In the city of Detroit, there are 969 block groups, of which only 871 have complete publicly available ACS data for our variables of interest, listed below. For Arlington County, 173 of the block groups (out of 181) have publicly available data. The data of the remaining block groups are not released due to concerns of identifiability, a common practice with ACS. The crime rates in these block groups are not high and represent a small portion of the data, so this is not a large concern for our analysis, though this is something we plan to address in future work. We use the 2015 ACS data in order for our data to be representative of the demographics present with the crime data.

The ACS variables that we use are: median income, median age, gender (percentage male), unemployment rate, total population, and race (categorized as white, black/African American, American Indian/Alaska Native, Asian, Native Hawaiian and other Pacific Islander, two or more races, and some other race).

We calculate the Herfindahl Index (HI) (Rhoades, 1993) using the set of variables on race. HI is a measure of concentration that is often used in demography and sociology studies, but has many other applications. For example, it is often used in finance or economics to show the concentration or diversity of a given sector of the economy. This is another effort, in addition to the incorporation of commuting proximity, to attempt to move away from racial profiling in predictive policing by using a measure of diversity rather than variables associated with each individual race. We use HI, shown in equation 7, as a measure of diversity in the block group.

$$HI=1-\left({\left(\frac{\text{\#white}}{\text{total pop}}\right)}^2+{\left(\frac{\text{\#black}}{\text{total pop}}\right)}^2+{\left(\frac{\text{\#Asian}}{\text{total pop}}\right)}^2+\dots \right)$$ (7)

where HI = 0 indicates that the block group is composed of one racial category (i.e., no diversity). The higher the index, the more diverse the block group is.

6.3. Commuting Proximity: LODES

Finally, we incorporate data on commuting to capture social proximity using LODES (Longitudinal Employer-Household Dynamics Origin-Destination Employment Statistics) provided by US Census Bureau. This data is also used as the source for the Census app OnTheMap (Andersson et al., 2008). It shows how many people commute between any two neighborhoods, and how many work in the same area where they reside. Flows between origin and the destination blocks are identified based on Census derived geocodes. As mentioned earlier, we assume commuting to be symmetric, so we define commuting ties if there are any commuters between two block groups, independent of the directionality of the commuting. Using this data source, we create a commuting matrix between all block groups in Detroit and Arlington County, respectively. In this study, we focus on commuting behavior within the boundaries of the county or city and exclude commuters that are leaving the area from the analysis. We plan to incorporate inter-county commuting in future work. We are using this data to establish commuting ties through the modification of the neighborhood matrix, as discussed in Section 5.1. The LODES data was gathered for 2015, the most recent year available for both Michigan and Virginia, for all of the block groups in our study.

7. Results

In this section, we explain our method for assessing spatial autocorrelation and the results of our models. We give details about how the comparisons with and with out commuting proximity in terms of the model fit and we provide evidence regarding spatial confounding in our data.

In the tables in our results, we will refer to the model with only geographic ties as “Geog” or “Geographic”. We will refer to the model that incorporates both spatial and non-spatial commuting ties as “Geog-Cmtg.”

7.1. Spatial Autocorrelation Assessment

Before fitting our models, we want to provide evidence of spatial autocorrelation in the data, which necessitates spatial modeling, based on our two neighborhood matrices. We use Moran’s I, a common method for assessing spatial processes, which is calculated as:

$$\text{I}=\frac{n\sum _i\sum _j{w}_{ij}\left(Y_i-\overline{Y}\right)\left(Y_j-\overline{Y}\right)}{\left(\sum _{ij}{w}_{i\ne j}\right){\left(Y_i-\overline{Y}\right)}^2}$$

For Moran’s I, the null hypothesis states that the spatial processes promoting the observed pattern of values is random chance or it is randomly distributed among the features in your study area (Getis and Ord, 1992). Therefore, for spatial modeling to be appropriate, we would like the p-value to be less than an α of 0.05. In our case, this value of Moran’s I and the associated p-value is a means for making the decision about whether or not spatial modeling is appropriate.

Table 2 summarizes Moran’s I as well as the p-values for this test. For Detroit, we obtain p-values that are less than 0.05, indicating that spatial autocorrelation is present, using the neighborhood matrices for both geographic and combined proximity models. However, the Moran’s I statistic for Arlington is statistically significant only for the model where we combine geographic and non-spatial social proximity. Moran’s I is used to evaluate whether the spatial process is random and therefore depends on the residuals of a non-spatial linear model with crime as the response and including some covariates, such as total population. The Moran’s I test is conducted on the residuals of the non-spatial generalized linear model (GLM) that is also considered in our analysis. Therefore, there is no concern for confounding of crime count and population. Due to the fact that we observe statistical significance in most of these cases, especially in the case when we combine geographic and commuting proximity, we see that spatial modeling is appropriate as the null hypothesis of the spatial process being random chance is rejected.

Table 2:

Moran’s I and p-value

	Detroit		Arlington
Proximity Type	Moran’s I	p-value	Moran’s I	p-value
Geographic	0.44411	0.000999	0.035268	0.I738
Geog-Cmtg.	0.2903	0.000999	0.04407	0.0I399

7.2. Model Comparison: DIC

In this section, we compare eleven models – the BYM, Leroux, and sparse SGLMM CAR models and the spatial lag and spatial error, each for both geographic and combined (geographic and commuting) proximity as well as the GLM with no spatial structure – using the model comparison criteria outlined in Section 5.6.

Tables 3 and 4 illustrate the comparison of the models, using the DIC for both Detroit and Arlington. For Arlington, we observe that when we combine commuting (social) and geographic proximity and compare it to the results of geographic proximity alone, there is an improvement in all of the models in terms of the DIC. All of the models that incorporate both geographic proximity and commuting proximity have lower DICs, indicating a better model fit while also accounting for model complexity (more complex models get penalized). Some differences are small or the values are identical with the spatial lag and spatial error models, but the CAR models all show improvement when adding social ties. However, for Detroit we see mixed results when we consider domestic and sexual violence. We see that for the sparse SGLMM, there is a lower DIC when we include both social and geographic ties than when we include geographic ties alone. For the other CAR models, we see that the DIC is higher when we include commuting ties and for the spatial lag and spatial error models, the DIC is comparable between the two model types.

Table 3:

Sexual and Domestic Violence Deviance Information Criteria (DIC) Model Comparison, Arlington

Arlington
	GLM, no spatial structure
DIC	2,117
	Geog Spatial Lag	Geog-Cmtg Spatial Lag
DIC	1,095	1,093
	Geog Spatial Err	Geog-Cmtg Spatial Err
DIC	1,094	1,094
	Geog BYM	Geog-Cmtg BYM
DIC	1,192	1,182
	Geog Leroux	Geog-Cmtg Leroux
DIC	1,150	1,142
	Geog s-SGLMM	Geog-Cmtg s-SGLMM
DIC	1,722	1,546

Table 4:

Sexual and Domestic Violence Deviance Information Criteria (DIC) Model Comparison, Detroit

Detroit
	GLM, no spatial structure
DIC	7,224
	Geog Spatial Lag	Geog-Cmtg Spatial Lag
DIC	4,406	4,436
	Geog Spatial Err	Geog-Cmtg Spatial Err
DIC	4,427	4,428
	Geog BYM	Geog-Cmtg BYM
DIC	4,370	4,428
	Geog Leroux	Geog-Cmtg Leroux
DIC	4,367	4,447
	Geog s-SGLMM	Geog-Cmtg s-SGLMM
DIC	6,441	6,331

Based on the results in Tables 3 and 4, we see that it is important to consider the model form and the data context when considering adding commuting ties. In the case of Arlington, there is a clear advantage, or no difference, when adding commuting ties to the analysis across all model types. For Detroit, we see there is an improvement in the DIC for some model types but the DIC does not improve across most of the model types. We note that the DIC does improve for the sparse SGLMM which addresses spatial confounding, which we address later in Section 7.5. Therefore, it is valuable to test the fit of both kinds of models- the commonly used spatial model with geographic ties as well as this new model including commuting ties- to see if commuting ties will improve the understanding of the modeled phenomenon.

We also conduct this analysis on the full set of call-for-service data, instead of limiting the scope of our analysis to sexual and domestic violence. We present the results in Tables 5 and 6. We see that for Arlington, there is a universal improvement for all CAR model types when comparing models with geographic proximity alone to models with geographic and commuting proximity combined. There is no difference in the spatial lag and spatial error models between the kinds of proximities. For Detroit, we also see for all of the CAR model types there is an improvement in the DIC when we add commuting proximity to the model. The spatial lag model shows a slight improvement when we add commuting ties as well, with a slight increase in the DIC for the spatial error model. This illustrates once again that the context of the phenomena being modeled should be considered when adding social ties to the model. This is illustrated in detail in the discussion. In Tables 5 and 6, we notice that the DIC is much larger for the CAR models than for the spatial lag and spatial error models. The DIC measure penalizes for model complexity and there are many additional parameters estimated in the CAR models as compared to the spatial error models, as seen in Equations 2, 3, 4, and 5.

Table 5:

All Crimes Deviance Information Criteria (DIC) Model Comparison, Arlington

Arlington
	GLM, no spatial structure
DIC	100,306
	Geog Spatial Lag	Geog-Cmtg Spatial Lag
DIC	1,795	1,795
	Geog Spatial Err	Geog-Cmtg Spatial Err
DIC	1,795	1,795
	Geog BYM	Geog-Cmtg BYM
DIC	46,151	37,525
	Geog Leroux	Geog-Cmtg Leroux
DIC	41,909	34,470
	Geog s-SGLMM	Geog-Cmtg s-SGLMM
DIC	49,853	34,378

Table 6:

All Crimes Deviance Information Criteria (DIC) Model Comparison, Detroit

Detroit
	GLM, no spatial structure
DIC	313,796
	Geog Spatial Lag	Geog-Cmtg Spatial Lag
DIC	8,542	8,540
	Geog Spatial Err	Geog-Cmtg Spatial Err
DIC	8,579	8,582
	Geog BYM	Geog-Cmtg BYM
DIC	158,901	94,725
	Geog Leroux	Geog-Cmtg Leroux
DIC	150,479	128,492
	Geog s-SGLMM	Geog-Cmtg s-SGLMM
DIC	184,770	154,441

7.3. Model Comparison: Cross-Validation and MAE

We also evaluate the models through comparing the mean absolute error (MAE) resulting from leave-one-out cross-validation. We compare the CAR models and the spatial lag and spatial error models to a baseline GLM with no spatial structure. In Table 7, we compare the MAE for Arlington for only sexual and domestic violence crimes and we see that all models represent improvements on the GLM with no spatial structure. For Arlington and these specific crime types, we see that for all models, there is either almost no difference in the mean absolute error when we hold out one block group at a time, with slight improvements for the spatial lag models and spatial error models. In the sparse SGLMM, we see a slight increase in the mean absolute error when we add commuting ties.

Table 7:

Sexual and Domestic Violence Mean Ab solute Error (MAE) for Leave-One-Out Cross Validation Model Comparison, Arlington

Arlington
	GLM, no spatial structure
MAE	20.55
	Geog Spatial Lag	Geog-Cmtg Spatial Lag
MAE	20.23	19.78
	Geog Spatial Err	Geog-Cmtg Spatial Err
MAE	19.70	19.68
	Geog BYM	Geog-Cmtg BYM
MAE	19.70	19.70
	Geog Leroux	Geog-Cmtg Leroux
MAE	19.69	19.69
	Geog s-SGLMM	Geog-Cmtg s-SGLMM
MAE	19.61	19.63

In Table 8, we see once again only slight improvements in the MAE for the BYM and Leroux CAR models as well as the spatial lag model. We see no difference for the sparse SGLMM model and a slight increase in MAE for the spatial error model. Based on the results presented for the MAE in Tables 7 and 8, we see smaller differences in the MAE compared to DIC when we add commuting ties, though we do see slight benefits for some model types, such as the spatial lag model in both cities, when we consider sexual and domestic violence crime.

Table 8:

Sexual and Domestic Violence Mean Absolute Error (MAE) for Leave-One-Out Cross Validation Model Comparison, Detroit

Detroit
	GLM, no spatial structure
MAE	4.85
	Geog Spatial Lag	Geog-Cmtg Spatial Lag
MAE	4.21	4.04
	Geog Spatial Err	Geog-Cmtg Spatial Err
MAE	3.95	4.02
	Geog BYM	Geog-Cmtg BYM
MAE	3.84	3.82
	Geog Leroux	Geog-Cmtg Leroux
MAE	3.86	3.84
	Geog s-SGLMM	Geog-Cmtg s-SGLMM
MAE	3.96	3.96

We also include the leave-one-out cross-validation analysis for all crime types, not subsetting to sexual and domestic violence crimes. In Tables 9 and 10, we see that for both Arlington and Detroit, the MAE indicate very small to no differences between models with geographic proximity alone compared to when we add commuting.

Table 9:

All Crimes Mean Absolute Error (MAE) for Leave-One-Out Cross Validation Model Comparison, Arlington

Arlington
	GLM, no spatial structure
MAE	1,012.12
	Geog Spatial Lag	Geog-Cmtg Spatial Lag
MAE	1,013.68	1,015.66
	Geog Spatial Err	Geog-Cmtg Spatial Err
MAE	1,012.43	1,012.23
	Geog BYM	Geog-Cmtg BYM
MAE	1,012.44	1,012.40
	Geog Leroux	Geog-Cmtg Leroux
MAE	1,012.44	1,012.39
	Geog s-SGLMM	Geog-Cmtg s-SGLMM
MAE	1,012.29	1,012.32

Table 10:

All Crimes Mean Absolute Error (MAE) for Leave-One-Out Cross Validation Model Comparison, Detroit

Detroit
	GLM, no spatial structure
MAE	470.55
	Geog Spatial Lag	Geog-Cmtg Spatial Lag
MAE	470.77	468.24
	Geog Spatial Err	Geog-Cmtg Spatial Err
MAE	467.54	467.14
	Geog BYM	Geog-Cmtg BYM
MAE	466.91	466.87
	Geog Leroux	Geog-Cmtg Leroux
MAE	466.85	466.87
	Geog s-SGLMM	Geog-Cmtg s-SGLMM
MAE	466.64	466.65

7.4. Fitted Values

Next, we compare the CAR models to see the fitted values compared to the actual observed counts per block group. Figure 3 provides the fitted values for all six CAR models for both Detroit and Arlington. For Detroit, we see that the fitted values are quite similar between the geographic alone and the combined models for each of the three types of CAR models. We see that the sparse SGLMM model does not pick up on the peek in crime in a limited number of block groups, but fits a more uniform model.

Figure 3:

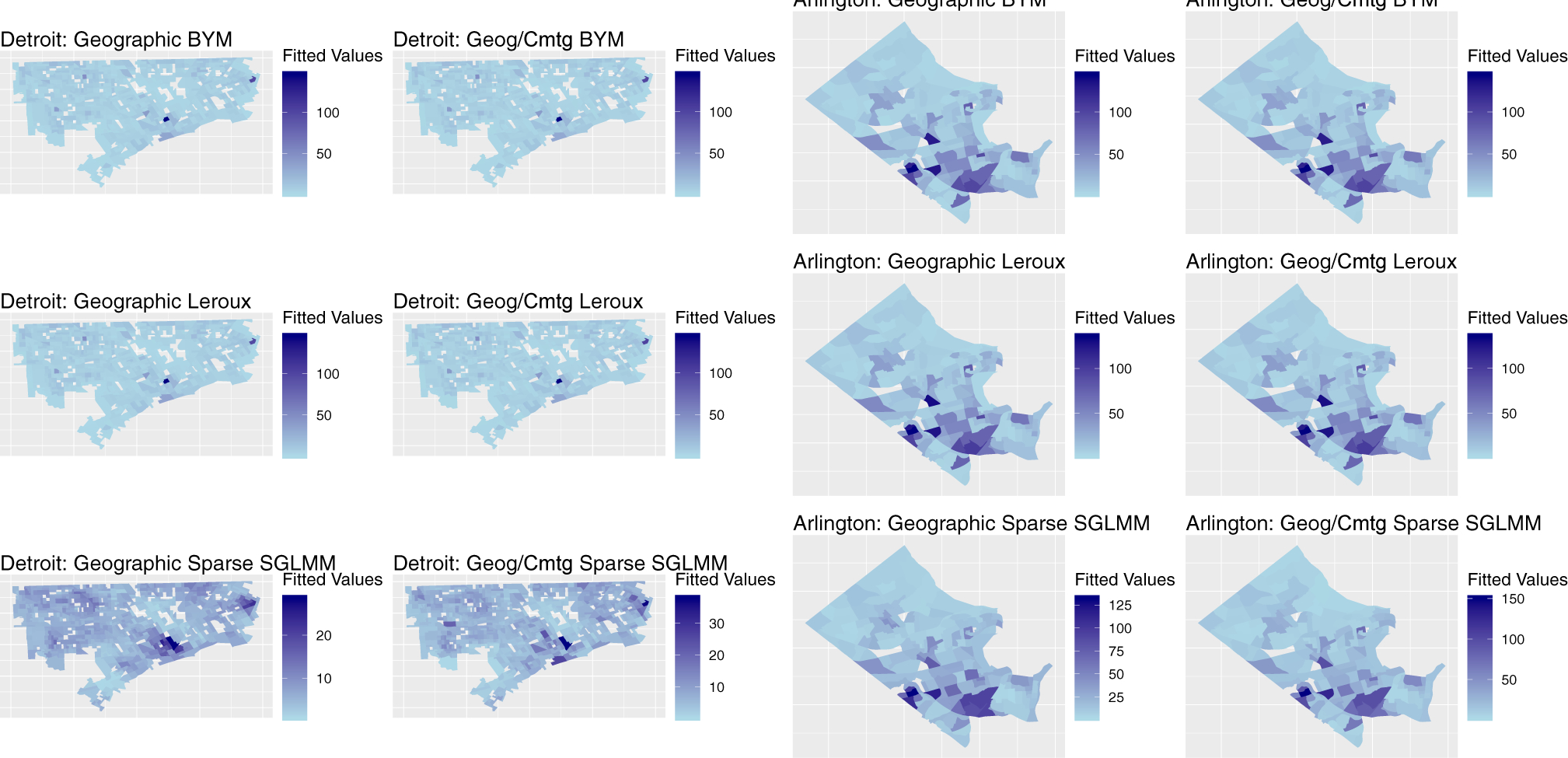
Fitted Values, All CAR Models

For Arlington, the fitted values for the BYM and Leroux models look quite similar to the actual number of crimes in the block groups, shown in Figure 2. The sparse SGLMM model picked up on the peaks as well as the BYM and Leroux models. We do not notice a large difference in the fitted values between geographic alone and the combination of geographic and commuting proximity. However, due to the improvement in DIC, we conclude that adding commuting proximity provides a better model fit.

7.5. Coefficients

In addition to the accuracy of the estimation of crime and the fit of the model, we are also interested in the estimates of the coefficients of the covariates, or the demographic information we have used in our model. Specifically, we are interested to see if there are any problems with spatial confounding in our case. To assess this, we will see if the estimates for the coefficients and their confidence intervals are similar between the BYM/Leroux Model and the sparse SGLMM. We will focus on the comparison between spatial error model, the Leroux model and the sparse SGLMM, the last of which controls for spatial confounding. We chose one of the spatial autoregressive (SAR) models (either spatial error or spatial lag) and one of the CAR models (either BYM or Leroux) based on model performance presented above. The coefficients shown below are for Arlington County and we find similar results for Detroit and omit them here. The estimated values of the posterior median as well as the 95% credible intervals for the model parameters are in Table 11 for the spatial error model, Table 12 for the combined Leroux Model, and in Table 13 for the combined sparse SGLMM model. Our covariates are all of the demographic variables that we collected from Census through the American Communities Survey.

Table 11:

Combined Spatial Error Model, Arlington

	median	credible	interval
Term	0.5	0.025	0.975
Intercept	2.674	2.577	2.767
Median Income	−0.133	−0.291	0.025
Unemployment Rate	−0.007	−0.139	0.125
Total Population	0.332	0.230	0.435
Percentage Male	0.019	−0.085	0.123
Median Age	−0.018	−0.152	0.116
Herfindahl Index	0.406	0.245	0.568

Table 12:

Combined Leroux, Arlington

	median	credible	interval
Term	0.5	0.025	0.975
Intercept	2.656	2.613	2.701
Median Income	−0.151	−0.345	0.023
Unemployment Rate	−0.024	−0.218	0.126
Total Population	0.376	0.258	0.526
Percentage Male	0.018	−0.112	0.198
Median Age	−0.033	−0.187	0.127
Herfindahl Index	0.417	0.216	0.602

Table 13:

Combined Sparse SGLMM, Arlington

	median	credible	interval
Term	0.5	0.025	0.975
Intercept	2.734	2.690	2.777
Median Income	−0.254	−0.332	−0.175
Unemployment Rate	−0.063	−0.128	0.001
Total Population	0.167	0.123	0.213
Percentage Male	−0.047	−0.092	−0.003
Median Age	−0.034	−0.099	0.031
Herfindahl Index	0.234	0.155	0.309

Based on Tables 11, 12, and 13, we see the estimates for the coefficients for all three models. We note that these coefficients are standardized, so that the mean of each of the covariates is 0 and the standard deviation is 1, in order to compare the coefficients and to avoid small coefficients that are uninterpretable for variables such as median income. When we compare Tables 11 and 12 for the spatial lag and Leroux CAR models, we see very similar coefficient estimates. Specifically, we find that the credible interval for median income, unemployment rate, percentage male, and median age all include 0, with similar median estimates. We find similar median estimates across all of the covariates. When we compare these tables to the coefficient estimates for the sparse SGLMM in Table 13, we see some slightly different results. Specifically, we find a negative relationship for median income as well as percentage male. Also, our coefficient estimates differ slightly for the Herfindahl Index, percentage male, total population, median income, as well as the intercept. Spatial confounding is not only the difference that we find here in terms of significant vs insignificant but also the difference in the magnitude of the coefficient. For example, we see that in the spatial error and Leroux models, the credible intervals for the coefficient estimate for the total population does not overlap with the confidence interval for the total population for the sparse SGLMM. All three models agree that there is non-zero positive effect of total population, as is intuitive, but the exact value of the coefficient differs between the Leroux and spatial error models as compared to the sparse SGLMM model, suggesting spatial confounding. Based on this comparison, we find slight concern for spatial confounding and therefore would suggest consideration of the sparse SGLMM model to address this concern, despite the higher DIC values in some cases.

8. Discussion

The results of this study show the following main patterns. We find that, in several important cases, adding social ties improves model fit for the analysis of urban crime. For instance, in Arlington, 7 out of 10 DIC-based model comparisons indicated that including commuting would be preferred and 3 out of 10 indicated a similar fit between models including only geographic ties and the combined commuting models. For Arlington MAE-based comparisons, 5 models slightly prefer adding commuting ties, 3 models slightly prefer the existing model form with no commuting ties, and 2 models find no difference between the models. These results suggest to us that there is added value in considering commuting when studying crime in Arlington – both with respect to overall crime and sexual and domestic crime.

The DIC results for Detroit yielded an approximately even balance of fit between the approaches including and excluding commuting ties. Specifically, 4 models favor the inclusion of commuting ties and 1 favors their absence for overall crime. For sexual and domestic violence, 4 favor the absence, while 1 favors the inclusion of commuting ties. The Detroit results suggest to us that, including commuting may not improve model fit for all crime types in all cities. Together, the results suggest that including or ignoring commuting is best treated as an empirical question rather than an automatic assumption. Combined with reasonable theoretical pathways through which commuting can impact crime, as discussed above, these results provide beginning evidence that, at best, commuting is an important context for crime, and, at least, the role of commuting would need to be tested rather than simply assumed a priori to be irrelevant.

Overall, we find that the models with commuting ties largely improve upon the models without commuting ties in terms of DIC. The MAE results are relatively more equivocal in terms of helping one choose between the two models. However, for the type of data sets we use here, considering model fit and complexity via DIC is preferable for the reasons we mentioned above. Our conclusion is that models including commuting ties provide a theoretically informed, promising new approach that build on and fruitfully extend the models in the existing literature.

The findings of the current study contribute conceptually and methodologically to the literature by highlighting the value of modelling intimate violence using a previously largely ignored feature that measures external social forces based on non-spatially bounded forms of social ties rather than spatial proximity only. We operationalized such social ties though commuting, a form of routine activity, and thus a common form of population mobility and social interaction. The findings that commuting ties matter in understanding neighborhood intimate violence and overall crime advances the scholarship on neighborhoods and crime, which has typically focused on social forces that are predominantly internal or spatially proximate to the neighborhood of interest (Benson et al., 2004; Browning, 2002; Gracia et al., 2015; Lauritsen and White, 2001; Voith, 2017; Wooldredge and Thistlethwaite, 2003; Wright and Benson, 2011). The results are consistent with a rapidly growing body of work that have highlighted the relevance of non-spatially bounded social proximity between neighborhoods, though many focused on more infrequent forms of proximity, such as co-offending, gang conflicts, taxi-trips, or on different outcomes (Browning et al., 2017; Mears and Bhati, 2006; Papachristos et al., 2013; Radil et al., 2010; Sampson, 2012; Schaefer, 2012; Tita and Radil, 2010, 2011; Wang et al., 2016, 2018).

The importance of modeling social proximity through commuting ties indicated in the current study also advances a growing body of research that has shown the importance of day to day mobility of urban residents between places (Boivin and D’Elia, 2017; Boivin and Felson, 2018; Felson and Boivin, 2015; Graif et al., 2017; Matthews et al., 2010; Matthews and Yang, 2013; Ong and Houston, 2002; Sampson, 2012; Wikström et al., 2010). Such mobility may contribute to diffusing norms, social pressures, and resources that may affect local crime risk. Indeed, our findings are consistent with research that shows that connections to resources located outside a neighborhood, such as mortgage loans, decrease local crime (Velez et al., 2012). Furthermore, social and cultural norms have been shown to also matter for domestic and sexual violence (NAS, 2018; WHO, 2009) and may be equally affected by socially proximate environments. For example, cultural and social norms in work places may reinforce or weaken people’s view of the acceptability of using violence, alcohol abuse, or coercion, in dating or domestic conflict situations (Banyard et al., 2004, 2007; Banyard, 2011). To the extent that work communities can function as sources of safety and social support for potential victims (Rothman et al., 2007), social proximity links between places may contribute to lower intimate violence and overall crime. Indeed, research has highlighted the important role of social isolation from support networks for intimate partner violence (Browning, 2002; Lanier and Maume, 2009; Pinchevsky and Wright, 2012; Wright and Benson, 2010). We urge future research to focus in further depth on the mechanisms of transmission between places of norms, social support, and resources that are relevant for crime outcomes.

The second important finding in this study was that commuting ties contributed better to understanding domestic and sexual crime in Arlington than in Detroit. One reason for this may be that in Arlington, a safer and more prosperous city overall than current-day Detroit, employers may be more likely to offer employee assistance programs such as counseling, leadership training, or referral to local mental health services (Galinsky et al., 2008) that can decrease workers’ stress and increase their resources and social support, empowering potential victims of sexual or domestic violence or increasing the chances of bystanders to intervene (Falk et al., 2001; Maiden, 1996; Pollack et al., 2010). Differences across cities in such positive exposures at work may impact the quality of inter-neighborhood ties and the likelihood that safety benefits may transfer between connected neighborhoods. Another possible reason for the difference between the two cities may be that in Arlington, more than in Detroit, high crime neighborhoods may have more connections to low crime neighborhoods, contributing to more channels for diffusing protective influences. To explore this idea, we dug deeper into the connectivity data and, indeed, found that about 97 percent of Arlington neighborhoods in the top thirtile of sexual and domestic violence were connected to neighborhoods in the bottom thirtile. However, only 42 percent of Detroit’s neighborhoods in the top thirtile of such violence were connected to neighborhoods in the bottom thirtile. This is also consistent with recent research that has uncovered violence homophily in commuting connections across neighborhoods in Chicago (Graif et al., 2017), which, like Detroit, is another major Rust Belt city affected by de-industrialization and loss of well-paying jobs.

This difference between the two cities in their segregated connectivity patterns combined with the results for sexual and domestic violence suggests that positive spillovers through commuting, such as access to beneficial resources, social exposures, and support, consistent with routine activity theory (Cohen and Felson, 1979), may be more influential than negative spillovers from crime actors and risk traveling across activity nodes (Felson and Boivin, 2015; Groff and McEwen, 2007; Stults and Hasbrouck, 2015; Tita and Griffiths, 2005; Wilkinson and Hamerschlag, 2005) that crime pattern and journey to crime theories would predict (Brantingham and Brantingham, 1993, 1995). Indeed, studies suggest that the share of domestic violence that occurs in public settings is smaller than the share of other crime (Greenfeld et al., 1998; Rennison and Welchans, 2000), indicating that social mechanisms of external influence at work for this type of crime may be more related to social transfers than to the traveling of crime actors.

A similar difference between the Arlington and Detroit is noticed when examining the data based on thirtiles of all crime types rather than just intimate violence. Yet, the gap is smaller, 80 percent vs 47 percent for Arlington and Detroit respectively, which may explain why for all crime types, commuting ties do improve model estimates even in Detroit. These findings suggest that commuting connections to lower crime neighborhoods may be more influential in protecting against sexual and domestic crime and overall crime, compared to connections to similarly violent neighborhoods. These findings are also consistent with prior work on public control (Bursik Jr et al., 1999; Hunter, 1985; Velez, 2001) suggesting that community level ties to external resources, actors, and organizations, likely to form through contacts at work (Sampson and Graif, 2009; Sampson, 2012), may affect crime through investments or disinvestments in the community. Further research would be valuable in investigating more systematically the relevance for crime of different types of ties, such as ties to less disadvantaged areas, or ties based on different income levels of commuters.

To this end, future research will also benefit from considering measures of social proximity and connectivity that go beyond employment, including social media data. For example, if there are many people tweeting from one community and later from another community, these two communities might be defined to be socially close (Wang et al., 2018) and this closeness may indicate higher potential for exposures to extra-local risk and resources that may affect local crime. Future research would also benefit from considering low income ties between communities. It is possible that low-wage earners may be more vulnerable than higher-wage earners to risk exposures transmitted through commuting channels. Examining variations in the effects of different types of commutes, by wage, age, or industry, will further advance our understanding of different mechanisms of transmission of risks and opportunities through social ties between communities.

This study also makes the following methodological contributions. It builds on recent advances in spatial analyses of crime (Anselin et al., 2000; Graif, 2015; Graif and Matthews, 2017; Taylor, 2015; Wang et al., 2016), of intimate partner violence (Cunradi et al., 2011; Gracia et al., 2015) and sexual violence (LeBeau, 1987), and spatial modeling in statistics (Hughes and Haran, 2013; Jensen, 2018) and extends them through new measures of social proximity and through unique data to advance modeling of the social and spatial ecology crime. The results indicate that adding information on social proximity to adjusted spatial models contributes to a better fit in estimating different types of crime in the the communities of interest in the current study. By using multiple modeling frameworks, we examined variations in results across a variety of different assumptions about the underlying spatial dependence, including to potential confounding between the spatial random effects (representing spatial dependence due to geographic or commuting proximity) and fixed effects (demographic covariates). Still, caveats are necessary, namely, that the data sets we use are observational and there is always the possibility that unmeasured covariates could impact conclusions drawn from such a study.

The methods used here, which combine geographic and commuting links, will be useful to examine other types of crime and, more generally, the spread of risk and influence through social and ecological networks. The results highlight the importance of future research on whether different features of connected neighborhoods affect local crime differently; whether stronger or weaker connections contribute to more or less crime; whether different types of connections affect crime differently; and the extent to which there may be variations in effects as a function of the timing of the flows (Haberman and Ratcliffe, 2015).

Considering the need for further replication of the current study’s approach in other cities and with respect to other types of crime, we refrain from making strong suggestions for policy. What we can say is that, if these results hold in future studies, they will indicate that crime prevention interventions in some neighborhoods may spread farther and wider than in others. Importantly, they would also indicate benefits of policies and programs, such as tax breaks to employers who hire residents from disadvantaged communities or training programs located in disadvantaged or violent areas, which could increase the employment and social connectivity of isolated communities.

9. Conclusions

Overall, the findings show that social proximity based on commuting ties improved DIC model fit scores when estimating both intimate violence and overall crime in Arlington, while in Detroit, social proximity improved DIC model fit for overall crime but not intimate violence. The MAE model comparison metric was generally less helpful in choosing between models, but both DIC and MAE metrics point in the same direction overall. The results contribute conceptually and methodologically to criminology by highlighting important new patterns and informative variations across two very different cities and crime types. The current findings suggest that continuing to account for the citywide patterns of inter-connectivity among neighborhoods in future studies would be valuable for further identifying conditions under which it may affect crime. While, despite important exceptions, social proximity has been largely overlooked in the literature so far, it seems to carry important promise, conceptually and methodologically, as a complementary way to more standard approaches to understanding underlying structural dynamics and mechanisms of risk transmission, above and beyond spatial proximity (Boivin and Felson, 2018; Brantingham and Brantingham, 1993; Browning et al., 2017; Graif et al., 2014, 2019; Mears and Bhati, 2006; Papachristos et al., 2013; Sampson, 2012; Schaefer, 2012; Tita and Radil, 2010, 2011). The study also contributes methodologically to quantitative criminology and to the literature on communities and place, specifically by illustrating the value of importing and adapting innovative approaches from the field of spatial statistics to model commuting ties in order to address an important substantive question in criminology. The results highlight the need for further conceptual development and empirical studies on how external spillover mechanisms such as public control and crime relevant resource and norms flow among city neighborhoods that are socially connected (Sampson, 2012). The approach used in the current study may be expanded in future work to apply social proximity models to a broader range of issues within and outside criminology, such as neighborhood development, education, and public health.

10. Appendix

10.1. Sensitivity Analysis

In this section, we create a sensitivity analysis for our cutoff used to define commuting proximity between two neighborhoods. In order to create a proximity matrix for commuting ties, we created a cutoff of the number of commuters which defined social ties so that if there are more than x number of commuters between two areal units, we define a social tie.

First, for both Detroit and Arlington County, we report the percentage of block groups that have more commuters than our defined cutoff, seen below in Table 14. We see that almost all of the block groups have less than 15 commuters listed for both Detroit and Arlington.

Table 14:

Percent of Areal Units above Cutoffs for Commuters

cutoff	Detroit	Arlington
1	32.9%	52.7%
3	10.9%	23.1%
5	5.9%	12.2%
10	2.0%	3.5%
15	0.8%	1.6%

Next, we analyze the effect of these cutoffs, listed above, on the conclusions that we gain based on model performance. Specifically, we analyze if the commuting proximity combined with geographic proximity is still better than geographic proximity alone, at each level of the cutoff, and we determine if there is an optimal cutoff for the number of commuters to include. We complete this analysis for both Arlington and Detroit. We test all three CAR models included in the full analysis: the BYM and Leroux CAR Models and the sparse Spatial Generalized Linear Mixed Model (s-SGLMM).

We make ten runs of the geographic proximity model in order to assess the variability over repeated measurements (the result is similar when the commuting proximity model is repeated). Therefore, the lines for the Geographic Models in Figure 4 are referring to the mean DIC over 10 runs of the model with geographic proximity alone, as the DIC for this model does not vary with the cutoff other than with random variability as the model does not include commuting ties, and therefore does not include the cutoff. Here, we only include the results for the sparse SGLMM and we find similar results for the BYM and Leroux models.

Figure 4:

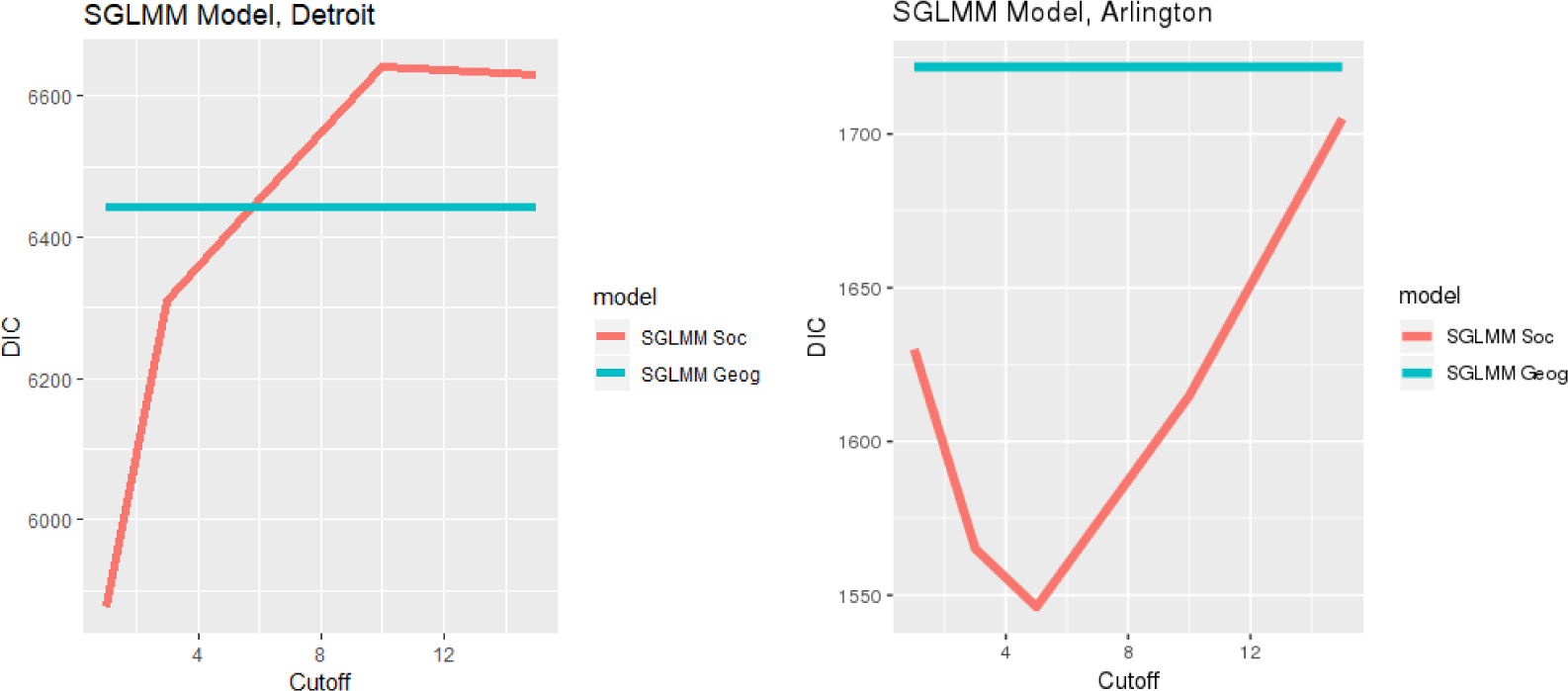
Sensitivity Analysis

In Figure 4, for Arlington we see that for all levels of the cutoff, the model where we combine geographic and commuting proximity still gives us a better model fit (DIC) than the model that includes geographic proximity alone. However, we notice that there does seem to be an optimal level of commuters to include in our analysis. For Detroit, we see that when we include more commuters in the analysis, or when the cutoff for excluding commuters from the analysis is smaller, we obtain a smaller DIC value. When we include more commuters in the analysis, the DIC approaches and even exceeds the DIC of the geographic models.

For both Detroit and Arlington, we see that if we include too few commuters with a large cutoff, where we only define a tie if there are more than 15 commuters between two block groups, our model performance is worse than if we were to include more ties in the model, where the cutoff is smaller for including the social tie in the model.

For our analysis presented in the paper, we defined a social tie between the communities based on whether there are more than 3 commuters between block groups for both Detroit and Arlington, based on this sensitivity analysis. However, more investigation is needed, as LODES uses a confidentially protection algorithm that may affect the interpretation of data at small scales. Therefore, it is important to continue to investigate the implications of the data generating process in future research focused on different geographic scales and different types of ties.