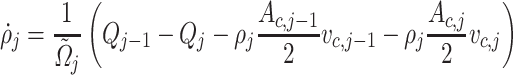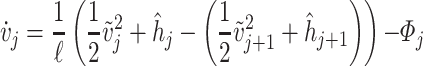Abstract
Lumped elements models of vocal folds are relevant research tools that can enhance the understanding of the pathophysiology of many voice disorders. In this paper, we use the port-Hamiltonian framework to obtain an energy-based model for the fluid–structure interactions between the vocal folds and the airflow in the glottis. The vocal fold behavior is represented by a three-mass model and the airflow is described as a fluid with irrotational flow. The proposed approach allows to go beyond the usual quasi-steady one-dimensional flow assumption in lumped mass models. The simulation results show that the proposed energy-based model successfully reproduces the oscillations of the vocal folds, including the collision phenomena, and it is useful to analyze the energy exchange between the airflow and the vocal folds.
Keywords: port-Hamiltonian systems, fluid–structure interactions, vocal folds, compressible fluids, lumped-parameter models
1. Introduction
The need to better understand the pathophysiology of phonological disorders has motivated the study of vocal fold dynamical behavior through mathematical models (Erath et al., 2013; Samlan et al., 2013; Zañartu et al., 2014). In this sense, infinite-dimensional models have been proposed to obtain a detailed description of intraglottal airflow and vocal folds structure, as shown in Jiang et al. (2017), Shurtz & Thomson (2013) and Zheng et al. (2011). However, these models have strong computational demands in the implementation of the spatial discretization methods used that hamper comprehensive multi-physics descriptions and parametric variations, severely limiting their scope. On the other hand, finite-dimensional models, using mass-spring-damper (MSD) representations of the vocal folds structure (e.g., Ishizaka & Flanagan, 1972; Steinecke & Herzel, 1995; and Story & Titze, 1995; Galindo et al., 2017), are computationally inexpensive and have been successfully used for the exploration of several normal and pathological conditions. One of the most common assumptions in these types of models is to consider the airflow as a quasi-steady behavior one-dimensional flow (Erath et al., 2013). As a consequence of this simplification, the flow is not affected by the dynamics of the vocal folds, limiting the interaction between the vocal folds model and the intraglottal airflow only to the geometry of the flow channel in the glottis to obtain a Bernoulli or jet flow behavior. Flow solutions are pivotal for explaining the energy transfer that sustains (normal and pathological) phonation. According to Mittal et al. (2013) and Thomson et al. (2005), the fluid–structure energy transfer in the glottis is greatly affected by the flow dynamics, however, in traditional lumped-parameter models with a quasi-steady airflow analysis, such as Steinecke & Herzel (1995) and Story & Titze (1995), the pressure over vocal fold contact surface is given by a mapping of subglottal and supragottal pressures only, restricting the analysis of energy transfers between the intraglottal airflow and vocal folds.
In recent years, there has been a growing interest in analyzing the energy flux in the glottis and its influence in vocal folds dynamics and pathogenesis of vocal disorders (Thomson et al., 2005; Titze & Hunter, 2015; Espinoza et al., 2017). In this sense, the port-Hamiltonian framework uses the energy as lingua franca between different physical domains, providing a powerful framework to model the fluid–structure interactions (van der Schaft & Jeltsema, 2014). Additionally, the description of system dynamics in terms of the total energy allows for using system theory (e.g., passivity) to analyze the stability of the model (van der Schaft, 2017). In particular, the dynamics of fluid–structure interaction systems has been described, focusing in the energy flux of the system, for example, using distributed parameters model for a vibro-acoustic system (Trenchant et al., 2015) and a lumped parameters model for the vocal folds (Encina et al., 2015), for the mechanical structure only and for a simple mass description (Hélie & Silva, 2017). Similarly, Mora et al. (2018) propose a port-Hamiltonian-based fluid–structure interaction model for the body-cover formulation of vocal folds; however, the coupling between the fluid and structure domains is given by signal interconnections, limiting the model scalability. In this sense, a scalable power-balanced formulation for the glottal tract is proposed by Wetzel et al. (2019), where the interconnection between adjacent sections of the glottal tract is given by auxiliary junction variables and the coupling with the elastic wall is given by additional connecting springs.
In this paper, we present an energy-based fluid–structure model for the vocal folds. The vocal fold structure is considered as the MSD system proposed by Story & Titze (1995). We assume the intraglottal airflow as a compressible and irrotational fluid. Dividing the glottal tract in 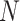 sections for the airflow velocity and density, we obtain a finite-dimensional port-Hamiltonian model of the fluid dynamics from the partial differential equations that describe the conservation laws for the fluid (Bird et al., 2014). This fluid model is coupled in a power-preserving connection to the MSD system. We show in simulations that this finite-dimensional system encompasses all the phenomena involved in fluid–structure interactions, including oscillations and shocks.
sections for the airflow velocity and density, we obtain a finite-dimensional port-Hamiltonian model of the fluid dynamics from the partial differential equations that describe the conservation laws for the fluid (Bird et al., 2014). This fluid model is coupled in a power-preserving connection to the MSD system. We show in simulations that this finite-dimensional system encompasses all the phenomena involved in fluid–structure interactions, including oscillations and shocks.
This paper is organized as follow: in Section 2, a brief introduction to port-Hamiltonian system is presented. In Section 3, models for the vocal fold structure and intraglottal airflow and their coupling are described. Finally, the simulation results and conclusions are presented in Sections 4 and 5, respectively.
2. Port-Hamiltonian systems
The description of mechanical systems, as mass-spring damper systems used in simplified models of vocal folds, is commonly obtained using the classical Euler–Lagrange framework. An alternative to Euler–Lagrange in the modeling of physical systems is the port-Hamiltonian framework. The core of the port-Hamiltonian modeling is the use of the total stored energy of the system to describe the dynamics (van der Schaft & Jeltsema, 2014). Moreover, the port-Hamiltonian formalism is a powerful tool to describe multi-physical systems, providing a framework to model different kinds of systems, for example, chemical reaction networks (van der Schaft et al., 2016), electromechanical systems (Pyrkin et al., 2018) and fluid–structure interactions (Cardoso-Ribeiro et al., 2016, 2017), among others.
In the port-Hamiltonian approach, the system behavior is a function of the gradient of the energy and the input 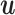 and the output
and the output 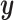 belong to conjugated spaces, such that, the product
belong to conjugated spaces, such that, the product 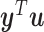 is the instantaneous power supplied to the system (van der Schaft & Jeltsema, 2014; van der Schaft, 2017). In this work, we consider an input-state-output port-Hamiltonian system (PHS) with feed-through term having the from
is the instantaneous power supplied to the system (van der Schaft & Jeltsema, 2014; van der Schaft, 2017). In this work, we consider an input-state-output port-Hamiltonian system (PHS) with feed-through term having the from
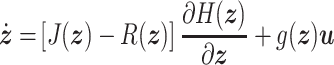 |
(2.1a) |
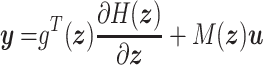 |
(2.1b) |
where 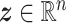 ,
, 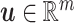 and
and 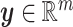 are the state vector, and the input and output ports, respectively. The Hamiltonian
are the state vector, and the input and output ports, respectively. The Hamiltonian 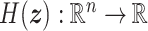 is a positive definite function that represents the total energy of the system.
is a positive definite function that represents the total energy of the system. 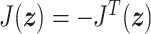 is an
is an 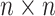 interconnection matrix that describes the energy transfer between energy storing elements;
interconnection matrix that describes the energy transfer between energy storing elements; 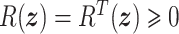 is an
is an 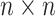 dissipation matrix that describes the energy losses in the system;
dissipation matrix that describes the energy losses in the system; 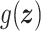 is an
is an 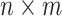 matrix that maps the inputs to the state dynamics; and
matrix that maps the inputs to the state dynamics; and 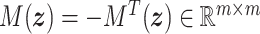 is the feed-through term matrix. For a general formulation of input-state-output port-Hamiltonian systems with feed-through terms, see van der Schaft & Jeltsema (2014, Section 4.2).
is the feed-through term matrix. For a general formulation of input-state-output port-Hamiltonian systems with feed-through terms, see van der Schaft & Jeltsema (2014, Section 4.2).
A special feature of PHS (2.1) is given by the behavior of the Hamiltonian. By the positiveness of 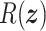 and the skew symmetry of
and the skew symmetry of 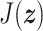 and
and 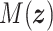 , the time derivative of
, the time derivative of 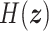 is bounded by the supplied power, i.e.,
is bounded by the supplied power, i.e.,
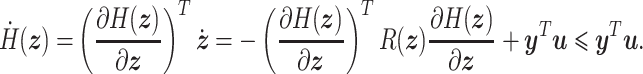 |
(2.2) |
This implies that the change of stored energy in system (2.1) cannot exceed the energy supplied to it, i.e., 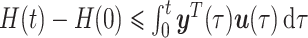 . This, in fact, shows that PHS are passive and, as a consequence, Lyapunov stable (van der Schaft & Jeltsema, 2014). As shown in Haddad et al. (2018) and Nguyen et al. (2019), the passivity is a useful feature in the control and stabilization of linear and non-linear systems.
. This, in fact, shows that PHS are passive and, as a consequence, Lyapunov stable (van der Schaft & Jeltsema, 2014). As shown in Haddad et al. (2018) and Nguyen et al. (2019), the passivity is a useful feature in the control and stabilization of linear and non-linear systems.
To obtain a model of the vocal folds and the intragottal airflow using the port-Hamiltonian theory, in the sequel, we consider that the total energy in the glottis is given by the kinetic and internal energies of the intraglottal airflow and the kinetic and potential energies stored in the mechanical system that represents the vocal folds. Considering that vibratory cycle of vocal folds is stimulated by the subglottal pressure, trachea output pressure, supraglottal pressure and the vocal tract input pressure, it is possible to derive an energy-based model of the vocal folds and the intraglottal airflow as in (2.1), where the output 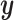 is given by flows and the state variables are defined as
is given by flows and the state variables are defined as 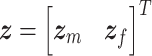 , where
, where 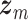 represents the state variables associated with the mechanical model of the vocal folds and
represents the state variables associated with the mechanical model of the vocal folds and 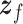 represents the state variables associated with the intraglottal airflow.
represents the state variables associated with the intraglottal airflow.
3. Fluid–structure model
In this section, we present an energy-based fluid–structure model of the glottis. For this purpose, we assume a symmetrical behavior of the vocal folds and, as consequence, only a hemi-larynx is considered, as shown in Fig. 1. In the literature, physical-based models have been used to describe the behavior of the layered tissue-epithelium, lamina propria and muscle of vocal folds (Jiang et al., 2017; Shurtz & Thomson, 2013; Zheng et al., 2011). However, the vibrations of the vocal folds commonly exhibit two dominant eigenfrequencies whose behavior can be described through simplified MSD models (Sváček & Horáček, 2018). Then, for the mechanical structure, we consider the body-cover model (BCM) proposed by Story & Titze (1995), where the bottom surfaces of cover masses, 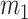 and
and 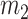 , are in contact with the intraglottal airflow through the surfaces
, are in contact with the intraglottal airflow through the surfaces  and
and 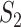 , respectively. Due to the assumed symmetry, the cover masses collide in the midsagittal plane of the glottis. To model the intraglottal flow, we consider the air as an unsteady, compressible and irrotational flow. In the sequel, we use the subindex
, respectively. Due to the assumed symmetry, the cover masses collide in the midsagittal plane of the glottis. To model the intraglottal flow, we consider the air as an unsteady, compressible and irrotational flow. In the sequel, we use the subindex 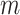 for variables associated with the mechanical structure and the subindex
for variables associated with the mechanical structure and the subindex 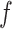 for the variables of the intraglottal airflow.
for the variables of the intraglottal airflow.
Fig. 1.

Hemi-larynx glottis model. Left: lateral view. Right: bottom view.
3.1 Energy-based model of the mechanical structure
From a mechanical point of view, the BCM is a simplified description of the vocal fold behavior, as shown in Fig. 1. Cover masses, 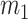 and
and 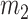 , describe the motion of the epithelial layer and lamina propria layer of the vocal folds and the body mass
, describe the motion of the epithelial layer and lamina propria layer of the vocal folds and the body mass 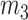 describes the motion of the muscle that is effective in the vibration (see Story & Titze, 1995, for details). Tissue deformations between the epithelial layer and the muscle are described through interconnection of non-linear springs and linear dampers between the cover masses and the body mass. Similarly, one linear damper with coefficient
describes the motion of the muscle that is effective in the vibration (see Story & Titze, 1995, for details). Tissue deformations between the epithelial layer and the muscle are described through interconnection of non-linear springs and linear dampers between the cover masses and the body mass. Similarly, one linear damper with coefficient 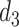 and one non-linear spring with coefficients
and one non-linear spring with coefficients 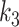 and
and  describe the tissue deformation between the muscle and the glottal wall. The shear strain in the epithelial layer is described through a linear coupling spring, with coefficient
describe the tissue deformation between the muscle and the glottal wall. The shear strain in the epithelial layer is described through a linear coupling spring, with coefficient 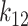 , between the cover masses. This yields the MSD system shown in Fig. 1.
, between the cover masses. This yields the MSD system shown in Fig. 1.
Similarly, when the vocal folds collide another deformation appears. This deformation is given by the tissue compression of the epithelial and lamina propria layers. To describe this phenomenon in lumped-parameter models, it is common to allow the overlap of the cover masses (Ishizaka & Flanagan, 1972; Steinecke & Herzel, 1995; Story & Titze, 1995), i.e., in this case, masses cross the midsagittal plane and have a negative position. Figure 2 shows the collision of the lower half part of vocal folds and its representation by the overlapping of mass 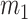 . Then, this tissue compression is characterized by additional non-linear springs interconnected with the cover masses, applying a force normal to the midsagittal plane. These springs are activated only when the collision occurs and are function of the overlapping
. Then, this tissue compression is characterized by additional non-linear springs interconnected with the cover masses, applying a force normal to the midsagittal plane. These springs are activated only when the collision occurs and are function of the overlapping  .
.
Fig. 2.

Description of the collision at lower half side of vocal folds in the glottal tract using the BCM from a coronal view. 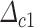 denotes the overlapping of
denotes the overlapping of 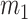 that characterized the corresponding collision spring.
that characterized the corresponding collision spring.
An energy-based model using the port-Hamiltonian framework of a simplified mechanical structure version of the body-cover model is proposed by Encina et al. (2015), where the energy stored by lateral springs given by the displacement of corresponding cover masses, and auxiliary variables are used to describe the elongation of collision springs and no airflow dynamics were considered. Dynamics of these auxiliary variables and the respective spring forces are enable by switches that are activated when the corresponding cover mass is in collision and disable otherwise. However, this formulation can have some drawbacks. For example, some of the state and auxiliary variables need to be appropriately reinitialized to 0 after each collision to avoid numerical errors that increase in time. In this section, we present a more detailed energy-based model of the mechanical structure of the body-cover model, where the stored energy by lateral spring is given by the relative displacement between the cover masses and the body mass and without the use of auxiliary variables to describe the collision behavior. This model is later connected to the airflow (see Section 3.3).
Denoting by 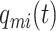 the position with respect to the midsagittal plane of the
the position with respect to the midsagittal plane of the 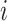 -th mass at the time instant
-th mass at the time instant 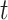 , as shown in Fig. 1, and by
, as shown in Fig. 1, and by 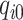 the corresponding equilibrium point at the reference pressure
the corresponding equilibrium point at the reference pressure 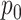 in the glottis. We define
in the glottis. We define 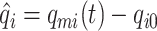 ,
, 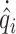 and
and 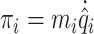 as the transverse displacement, velocity and momentum of mass
as the transverse displacement, velocity and momentum of mass 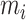 , respectively. To describe the collisions of vocal folds, we define the elongation of collision springs as
, respectively. To describe the collisions of vocal folds, we define the elongation of collision springs as 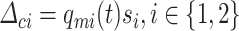 , where
, where 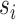 is a switch variable defined as
is a switch variable defined as
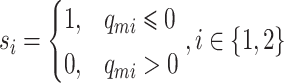 |
(3.1) |
The total energy of the mechanical structure is given by
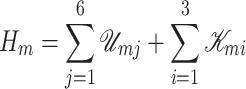 |
(3.2) |
where 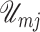 is the stored potential energy in the
is the stored potential energy in the  -th spring and
-th spring and 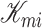 is the kinetic energy of the
is the kinetic energy of the 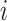 -th mass. The potential and kinetic energies are detailed in Appendix A. The dynamic of mass
-th mass. The potential and kinetic energies are detailed in Appendix A. The dynamic of mass 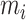 is expressed through the following momentum balance:
is expressed through the following momentum balance:
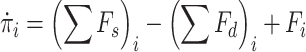 |
(3.3) |
where 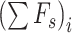 denotes the forces applied by springs,
denotes the forces applied by springs, 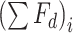 denotes the forces dissipated by dampers and
denotes the forces dissipated by dampers and 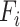 denotes the external force applied over the
denotes the external force applied over the 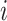 -th mass. Denote by
-th mass. Denote by 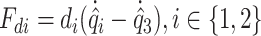 the forces dissipated by the connecting dampers between the cover masses and the body mass, and by
the forces dissipated by the connecting dampers between the cover masses and the body mass, and by 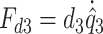 the force dissipated by the damper between the body mass and the gottal wall, see Fig. 1, where
the force dissipated by the damper between the body mass and the gottal wall, see Fig. 1, where 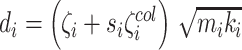 are the damping coefficients, with
are the damping coefficients, with 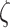 and
and 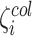 the normal damping factor and the additional damping factor active only when collision occurs, respectively, and
the normal damping factor and the additional damping factor active only when collision occurs, respectively, and 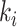 the coefficient of the corresponding lateral spring (Story & Titze, 1995). Then, considering the relationships (A.2) and (A.9) detailed in Appendix A, the PHS that describe the dynamics of the structure of the vocal folds is given by:
the coefficient of the corresponding lateral spring (Story & Titze, 1995). Then, considering the relationships (A.2) and (A.9) detailed in Appendix A, the PHS that describe the dynamics of the structure of the vocal folds is given by:
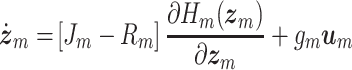 |
(3.4a) |
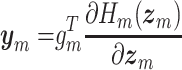 |
(3.4b) |
where 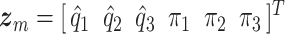 are the state variables,
are the state variables, 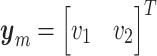 are the cover mass velocities,
are the cover mass velocities, 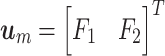 are the forces applied to each mass,
are the forces applied to each mass, 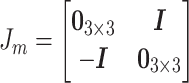 is the interconnection matrix,
is the interconnection matrix, 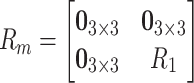 is the dissipation matrix and
is the dissipation matrix and 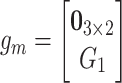 is the input matrix, where
is the input matrix, where
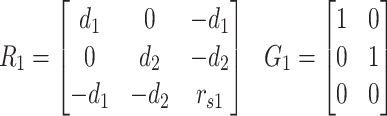 |
and where 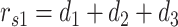 .
.
The model (3.4) describes the dynamics of the masses and includes switches to model the collision when the vocal folds are closed.
3.2 Energy-based model of the fluid
To obtain an energy-based model of the airflow, we use balance equations for mass and momentum that are given by the following partial differential equations:
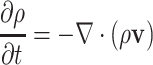 |
(3.5) |
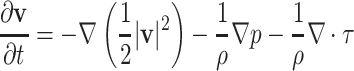 |
(3.6) |
where 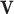 is the velocity field,
is the velocity field, 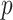 is the pressure,
is the pressure, 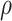 is the fluid density and the Newtonian viscosity tensor is given by
is the fluid density and the Newtonian viscosity tensor is given by 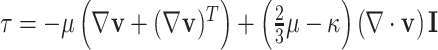 with
with  and
and 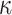 as the viscosity and dilatational viscosity, respectively, and
as the viscosity and dilatational viscosity, respectively, and 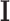 denotes the identity matrix (Bird et al., 2014).
denotes the identity matrix (Bird et al., 2014).
From the ideal gas law, the airflow pressure is given by 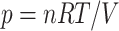 , where
, where 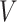 ,
, 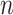 and
and 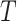 are the volume, number of moles and temperature of the gas, respectively, and
are the volume, number of moles and temperature of the gas, respectively, and 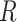 denotes the universal gas constant. Using the molar weight
denotes the universal gas constant. Using the molar weight 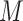 , the airflow pressure can be rewritten as
, the airflow pressure can be rewritten as 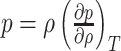 where
where 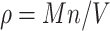 and
and 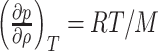 is the isothermal compressibility. Moreover, isothermal compressibility is related to the isentropic compressibility by the thermodynamic formula
is the isothermal compressibility. Moreover, isothermal compressibility is related to the isentropic compressibility by the thermodynamic formula 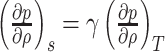 , where
, where 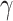 is the specific heat ratio of the gas,
is the specific heat ratio of the gas, 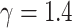 for the air, and
for the air, and 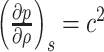 with
with  as the speed of sound (Landau & Lifshitz, 1987, Chapter 8). Then, the pressure of the airflow can be expressed as follows:
as the speed of sound (Landau & Lifshitz, 1987, Chapter 8). Then, the pressure of the airflow can be expressed as follows:
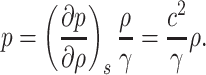 |
(3.7) |
From a port-Hamiltonian point of view, we need to relate the pressure with the energy of the fluid. In this sense, we use the specific form, per unit mass, of the Gibbs equation for a monoatomic fluid, i.e., 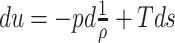 , where
, where 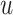 and
and 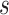 are the specific internal energy and entropy, respectively. Considering the isentropic assumption, this equation is reduced to
are the specific internal energy and entropy, respectively. Considering the isentropic assumption, this equation is reduced to  . Then, the pressure can be expressed as follows:
. Then, the pressure can be expressed as follows:
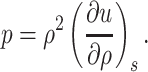 |
(3.8) |
In port-Hamiltonian formulations of fluids, it is common to use the specific enthalpy 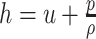 . Considering the pressure description in (3.7) and (3.8), then for an isentropic fluid we obtain the following identity
. Considering the pressure description in (3.7) and (3.8), then for an isentropic fluid we obtain the following identity 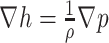 (van der Schaft & Maschke, 2002; Kotyczka, 2013; Matignon & Hélie, 2013) and the internal energy is given by
(van der Schaft & Maschke, 2002; Kotyczka, 2013; Matignon & Hélie, 2013) and the internal energy is given by 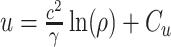 , where
, where 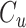 is a constant. Note that depending of the selected value for
is a constant. Note that depending of the selected value for 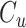 it is possible to obtain negative values for the internal energy. This may be a drawback to analyze the system stability using the total energy as Lyapunov function (van der Schaft & Jeltsema, 2014). On the other hand, in dissipative fluid processes, the temporal evolution of the system depends on the energy available to be converted into mechanical work, and the total energy is replaced by the total available energy (Mackay & Phillips, 2019). In this sense, we use a non-negative availability function for the internal energy.
it is possible to obtain negative values for the internal energy. This may be a drawback to analyze the system stability using the total energy as Lyapunov function (van der Schaft & Jeltsema, 2014). On the other hand, in dissipative fluid processes, the temporal evolution of the system depends on the energy available to be converted into mechanical work, and the total energy is replaced by the total available energy (Mackay & Phillips, 2019). In this sense, we use a non-negative availability function for the internal energy.
In this work, we prefer the use of relative pressure  and relative enthalpy
and relative enthalpy 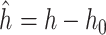 , where
, where 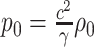 and
and 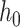 are the pressure and enthalpy at reference density
are the pressure and enthalpy at reference density 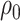 , respectively. Additionally, denoting by
, respectively. Additionally, denoting by 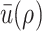 the available internal energy, such that
the available internal energy, such that 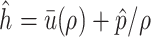 and
and 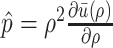 , we obtain the relationship
, we obtain the relationship 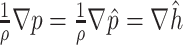 . Moreover, assuming an irrotational flow then
. Moreover, assuming an irrotational flow then 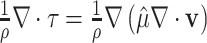 , where
, where 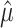 is a function of shear and dilatational viscosities (see Mora et al., 2020, for details). Thus, the momentum equation (3.6) can be rewritten as follows:
is a function of shear and dilatational viscosities (see Mora et al., 2020, for details). Thus, the momentum equation (3.6) can be rewritten as follows:
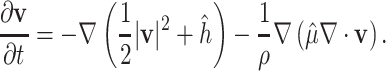 |
(3.9) |
The relative pressure and available internal energy of intraglottal airflow are given by
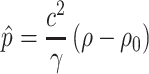 |
(3.10) |
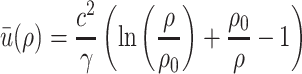 |
(3.11) |
where 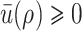 with a minimum at
with a minimum at 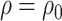 . The relative enthalpy is then given by
. The relative enthalpy is then given by
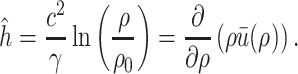 |
(3.12) |
3.2.1 Finite-dimensional fluid model
To simplify the model, we neglect the sagittal component of the airflow, considering a two-dimensional flow. Since we assume an irrotational flow, we can reduce the number of state variables using the following assumption.
Assumption 3.1
Denote by
and
the transverse and longitudinal components of the flow velocity. The gradient of
is uniform in each velocity section and is given by
and
, where
and
denote the longitudinal and transverse axes,
and
are the velocity and position of the glottal wall, respectively, and
.
As a consequence of Assumption 3.1, in each velocity section 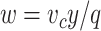 . This implies an algebraic constraint between
. This implies an algebraic constraint between 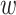 and the glottal wall dynamics. Thus, to complete the flow description, the unknown variable is the longitudinal velocity
and the glottal wall dynamics. Thus, to complete the flow description, the unknown variable is the longitudinal velocity 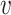 . Additionally, as
. Additionally, as 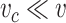 , we can use the following approximation
, we can use the following approximation 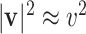 . With these considerations, we reduce the velocity analysis to the longitudinal component, whose momentum equation is described by
. With these considerations, we reduce the velocity analysis to the longitudinal component, whose momentum equation is described by
 |
(3.13) |
To describe the flow velocity and density in the glottis, we divide the fluid domain in 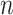 sections of length
sections of length 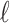 for each variable, as shown in Fig 3(a and b), where
for each variable, as shown in Fig 3(a and b), where 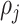 denotes the average density in volume
denotes the average density in volume 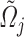 between longitudinal points
between longitudinal points 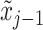 and
and 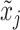 , with
, with 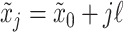 ; and
; and 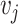 denotes the average velocity in volume
denotes the average velocity in volume  between longitudinal points
between longitudinal points 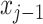 and
and 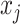 , with
, with 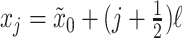 . Then, the fluid dynamics are described using a one-dimensional mesh, as shown in Fig. 3(c), where the boundary conditions are given by the momentum density in the glottis inlet boundary,
. Then, the fluid dynamics are described using a one-dimensional mesh, as shown in Fig. 3(c), where the boundary conditions are given by the momentum density in the glottis inlet boundary, 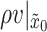 , and the energy plus enthalpy in the outlet boundary,
, and the energy plus enthalpy in the outlet boundary, 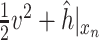 . This mesh is equivalent to the mesh proposed by Trenchant et al. (2018) for one-dimensional discretization of infinite-dimensional port-Hamiltonian systems.
. This mesh is equivalent to the mesh proposed by Trenchant et al. (2018) for one-dimensional discretization of infinite-dimensional port-Hamiltonian systems.
Fig. 3.

Spatial discretization of fluid variables for the finite-dimensional model. (a) Description of the density. (b) Velocity description. (c) Equivalent one-dimensional mesh.
Note that for an arbitrary section with average velocity 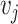 the cross-sectional area
the cross-sectional area 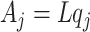 is uniform, with
is uniform, with  and
and 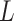 as the height and depth of the
as the height and depth of the 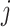 -th velocity section, and the volume is given by
-th velocity section, and the volume is given by 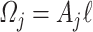 . The contact surface
. The contact surface 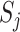 with the mechanical structure have velocity
with the mechanical structure have velocity  and area
and area 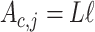 , as shown in Fig. 4(a). For a density section
, as shown in Fig. 4(a). For a density section 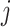 , the volume is given by the combination of the half of adjacent velocity sections,
, the volume is given by the combination of the half of adjacent velocity sections, 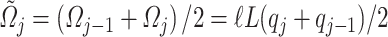 . Similarly, the area of the contact surface is a combination of the areas of adjacent velocity sections, with the corresponding contact velocities, as shown in Fig. 4(b).
. Similarly, the area of the contact surface is a combination of the areas of adjacent velocity sections, with the corresponding contact velocities, as shown in Fig. 4(b).
Fig. 4.

Arbitrary 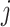 -th sections of the fluid domain. (a) Velocity section. (b) Density section.
-th sections of the fluid domain. (a) Velocity section. (b) Density section. 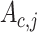 and
and 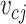 are the area and velocity of the contact surface
are the area and velocity of the contact surface 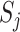 in the velocity section with volume
in the velocity section with volume  and average velocity
and average velocity 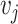 .
. 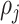 is the average density of the section con volume
is the average density of the section con volume 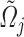 .
.
Proposition 3.1
Consider a fluid domain division as shown in Fig. 3. For the
-th section of density and velocity, the fluid dynamics can be described by the following ordinay differential equations (ODEs):
(3.14)
(3.15) where
and
are the average density and velocity of the corresponding section,
is the mass flow at
,
is the cross-sectional area of
-th velocity section,
and
are the area and velocity, respectively, of the contact surface
on the
-th velocity section,
and
are the kinetic energy by unit mass and relative enthalpy at
and
is the average velocity drop due to energy losses in the
-th velocity section.
Proof.
See Appendix B.
Using (3.14) and (3.15), we can obtain a finite-dimensional port-Hamiltonian model for the fluid dynamics. In this sense, considering the fluid domain division in Fig. 3, we define the fluid total energy as follows:
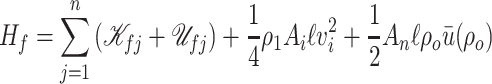 |
(3.16) |
where 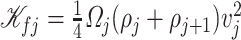 and
and 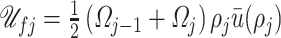 describe the kinetic and potential energies, respectively, in the corresponding fluid section,
describe the kinetic and potential energies, respectively, in the corresponding fluid section, 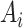 and
and 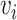 are the cross-sectional area and velocity at
are the cross-sectional area and velocity at 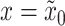 , and
, and 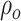 denotes the fluid density at
denotes the fluid density at 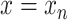 (see Appendix C for details).
(see Appendix C for details).
Considering the fluid effort described in (18), the mass flow at 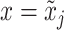 is given by
is given by 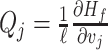 . Similarly, considering
. Similarly, considering 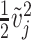 as the weighted mean between the kinetic energy per mass unit of adjacent velocity sections, i.e.,
as the weighted mean between the kinetic energy per mass unit of adjacent velocity sections, i.e., 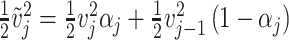 where
where 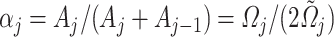 . Then, from (19), the kinetic energy per unit mass plus specific enthalpy at
. Then, from (19), the kinetic energy per unit mass plus specific enthalpy at 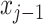 is given by
is given by 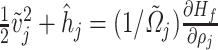 . This implies that the systems (3.14) and (3.15) can be expressed as
. This implies that the systems (3.14) and (3.15) can be expressed as
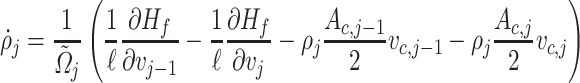 |
(3.17) |
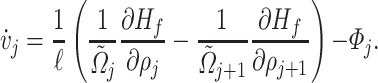 |
(3.18) |
Note that, from the discretization scheme in Fig. 3, the adjacent sections to the inlet and outlet boundaries are given by the first density section and the last velocity section, respectively. Then, to define the inputs and outputs of the system, the ODEs of these systems are written as follows:
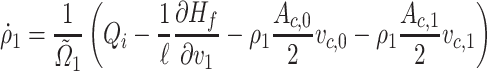 |
(3.19) |
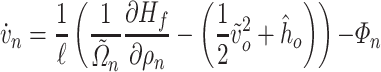 |
(3.20) |
where 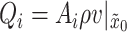 and
and 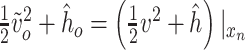 describe the inputs associated with the inlet and outlet boundary conditions, respectively. Similarly,
describe the inputs associated with the inlet and outlet boundary conditions, respectively. Similarly, 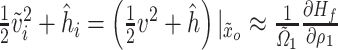 and
and 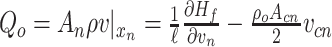 describe the corresponding power conjugated outputs.
describe the corresponding power conjugated outputs.
3.2.2 Energy losses
As shown in Mora et al. (2020), for an isentropic fluid, from an infinite-dimensional port-Hamiltonian point of view, the dissipative elements of the flow are given by the viscosity tensor of the fluid. However, from a macroscopic point of view, other sources of dissipation appear. According to Bird et al. (2014), the dissipated power 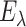 in a volume
in a volume 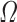 must have the general form:
must have the general form:
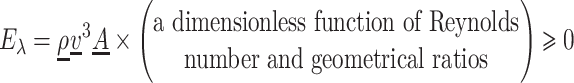 |
(3.21) |
where 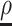 ,
, 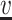 and
and 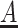 are a characteristic density, velocity and area of the fluid domain in volume
are a characteristic density, velocity and area of the fluid domain in volume 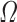 . The dimensionless function in (3.21) can be expressed as
. The dimensionless function in (3.21) can be expressed as 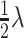 with
with 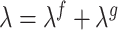 , where
, where 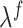 , the friction loss factor, is a function of the Reynolds number, viscous losses, and
, the friction loss factor, is a function of the Reynolds number, viscous losses, and 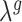 is a loss factor associated with additional resistances determined by the geometry of the fluid way, such as sudden changes in the cross-sectional area, see Bird et al. (2014, Section 7.5) for details. Then, (3.21) can be rewritten as
is a loss factor associated with additional resistances determined by the geometry of the fluid way, such as sudden changes in the cross-sectional area, see Bird et al. (2014, Section 7.5) for details. Then, (3.21) can be rewritten as
 |
(3.22) |
where the term 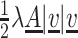 describes the rate of velocity drop in a volume
describes the rate of velocity drop in a volume  due to the energy losses. This term is equivalent to the dissipative terms used in others works. For example, in Kotyczka (2013) the dissipation term, in an infinite-dimensional form, of one-dimensional flow in a rough pipeline is described by
due to the energy losses. This term is equivalent to the dissipative terms used in others works. For example, in Kotyczka (2013) the dissipation term, in an infinite-dimensional form, of one-dimensional flow in a rough pipeline is described by 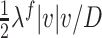 where
where 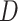 is the pipe diameter and
is the pipe diameter and 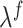 is obtained from the Haaland equation (Bird et al., 2014). Integrating this term in a pipe section of volume
is obtained from the Haaland equation (Bird et al., 2014). Integrating this term in a pipe section of volume 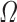 , we obtain
, we obtain 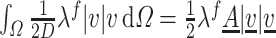 that is equivalent to the rate of velocity drop derived from (3.22).
that is equivalent to the rate of velocity drop derived from (3.22).
In the case of the intraglottal airflow, according to Lucero & Schoentgen (2015), the viscosity effects are relevant at gottal opening and closure, affecting the waveform of the output flow at those instants, decreasing the amplitude at instant of maximum opening (Zhang et al., 2020) and the fluid separation in the glottis (Alipour & Scherer, 2004). On the other hand, the losses associated with geometry of the glottal tract have an impact in the aerodynamics and the energy transfer to the vocal folds, affecting the vibration cycle (Zañartu et al., 2014).
In the 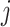 -th velocity section, the characteristic velocity and area are given by
-th velocity section, the characteristic velocity and area are given by 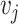 and
and 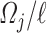 , respectively. Then, the dissipated power described in (3.21) can be expressed as follows:
, respectively. Then, the dissipated power described in (3.21) can be expressed as follows:
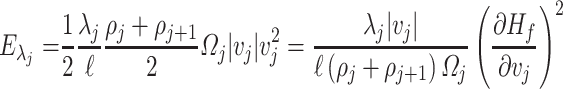 |
(3.23) |
where 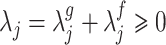 is the loss factor in
is the loss factor in  . Similarly, from a port-Hamiltonian point of view, the dissipation power in the
. Similarly, from a port-Hamiltonian point of view, the dissipation power in the 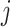 -th velocity section is given by
-th velocity section is given by 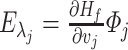 . Comparing with (3.23), we obtain that
. Comparing with (3.23), we obtain that
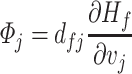 |
(3.24) |
where 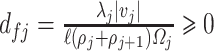 . Given the fluid domain description used in this work, we only consider sudden contractions and expansions. The geometric loss factor
. Given the fluid domain description used in this work, we only consider sudden contractions and expansions. The geometric loss factor 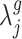 is defined as (Mulley, 2004):
is defined as (Mulley, 2004):
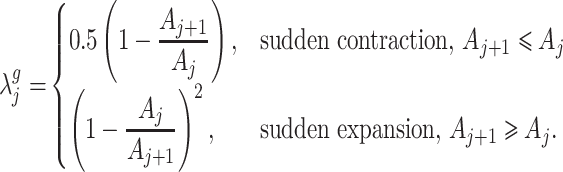 |
(3.25) |
Note that these expressions for sudden contraction and expansion losses are given in textbooks for steady flow and motionless walls. We use these expressions updating the values of areas in each simulation instant.
In the case of the friction factor, we use, for simplicity, a Hagen–Poiseuille formulation, i.e., 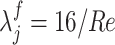 where
where 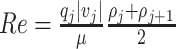 describes the Reynolds number in each velocity section of the glottis (Alipour & Scherer, 2004).
describes the Reynolds number in each velocity section of the glottis (Alipour & Scherer, 2004).
3.2.3 Scalable port-Hamiltonian fluid model
Considering the ODEs in (3.17)–(3.20) and (3.24), the dynamics of 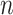 velocity and density sections of the intraglottal airflow can be expressed as
velocity and density sections of the intraglottal airflow can be expressed as
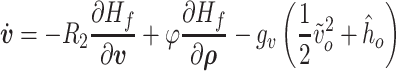 |
(3.26) |
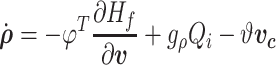 |
(3.27) |
where 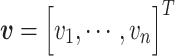 and
and  are the velocity and density sets of fluid sections,
are the velocity and density sets of fluid sections, 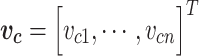 is the set of velocities in the contact surface and
is the set of velocities in the contact surface and 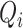 and
and 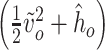 are the inputs in the inlet and outlet boundaries, respectively. The corresponding power conjugated outputs
are the inputs in the inlet and outlet boundaries, respectively. The corresponding power conjugated outputs 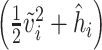 and
and 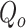 are given by
are given by
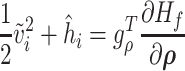 |
(3.28) |
 |
(3.29) |
where
 |
(3.30a) |
 |
(3.30b) |
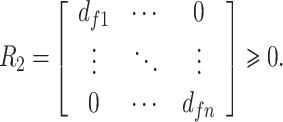 |
(3.30c) |
Defining the set of forces on the contact surfaces 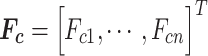 as
as
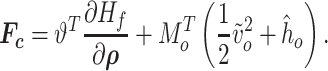 |
(3.31) |
Then, we obtain the following dissipative port-Hamiltonian system with feed-through term (van der Schaft & Jeltsema, 2014) to describe the fluid dynamics:
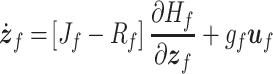 |
(3.32a) |
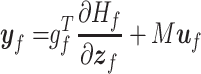 |
(3.32b) |
where 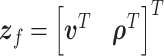 is the state vector,
is the state vector,  are the inputs,
are the inputs, 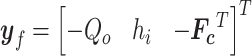 are the outputs and
are the outputs and
 |
(3.33) |
The time derivative of the total energy for the system (3.32a) is described by the power supplied and the total dissipated power, i.e.,
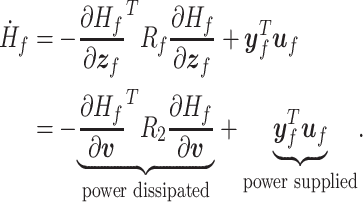 |
(3.34) |
Note that the force 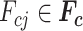 is not the effective force on the contact surface of volume
is not the effective force on the contact surface of volume  with the mechanical structure. This is given by an additional force
with the mechanical structure. This is given by an additional force 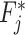 induced by the effects of the structure motion on the variations of fluid section
induced by the effects of the structure motion on the variations of fluid section 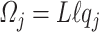 , i.e., the changes in the height
, i.e., the changes in the height 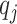 . Forces
. Forces 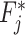 and
and 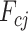 are given by
are given by
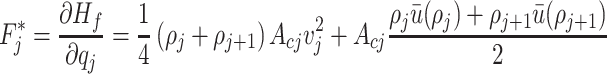 |
(3.35) |
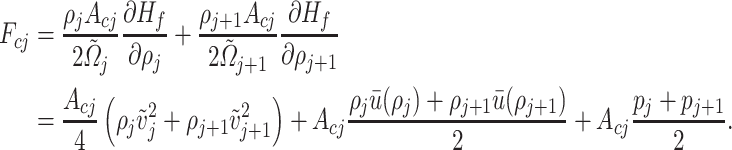 |
(3.36) |
Then, considering that 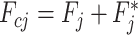 the effective force
the effective force 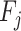 applied on the contact surface of
applied on the contact surface of 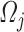 is given by
is given by
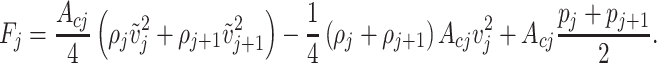 |
(3.37) |
Remark 3.1
Note that the fluid–structure power transfer is given by
, where
is the set of effective forces applied on the structure contact surface. Then, the output
makes it difficult to couple the fluid and the structure systems. This problem with the output forces on the contact surface can be solved using as state variables the heights or volumes of the fluid sections. However, this solution have two disadvantages. First, the state vector increases in
elements. Second, the fluid–structure model obtained would not have a minimum realization, given that the heights and volumes of the fluid sections are proportional to the positions of masses in the structure model. In Section 3.3, we propose a solution based in a fluid–structure power-preserving interconnection and the relationship between the fluid section heights and the positions of the structure elements.
3.3 Overall model
Note that from Assumption 3.1, we obtain two conditions for the transverse airflow velocity in each flow section, 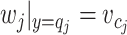 and
and 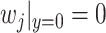 , and as a consequence
, and as a consequence 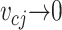 when
when  . This implies a ‘soft’ collision of vocal folds. To obtain the elastic collisions that characterize the motion of vocal folds, we use the approach proposed by Mora et al. (2018). We consider a threshold value
. This implies a ‘soft’ collision of vocal folds. To obtain the elastic collisions that characterize the motion of vocal folds, we use the approach proposed by Mora et al. (2018). We consider a threshold value 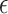 , such that, the fluid dynamics in
, such that, the fluid dynamics in  and its effects on the mechanical structure are disabled when
and its effects on the mechanical structure are disabled when 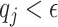 . We define the switch matrix
. We define the switch matrix 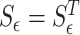 as
as
 |
(3.38) |
where 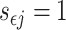 when
when 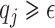 and
and 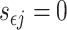 otherwise.
otherwise.
The power transfer between the fluid and the structure systems is given by 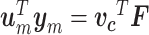 . Then, we define a matrix
. Then, we define a matrix 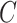 that maps the output and input vectors of the mechanical model of the vocal folds to the corresponding velocities and forces of the fluid model, i.e.,
that maps the output and input vectors of the mechanical model of the vocal folds to the corresponding velocities and forces of the fluid model, i.e., 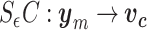 and
and 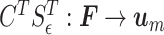 . Thus, we use the following power-preserving interconnection rule
. Thus, we use the following power-preserving interconnection rule
 |
(3.39) |
Using the matrix 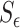 to able and disable the dynamics in each volume
to able and disable the dynamics in each volume  and the interconnection (3.39), we can rewrite the fluid–structure dynamics as follows:
and the interconnection (3.39), we can rewrite the fluid–structure dynamics as follows:
 |
(3.40a) |
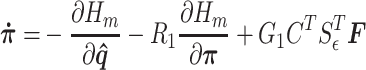 |
(3.40b) |
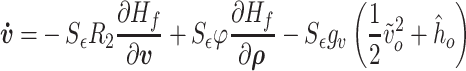 |
(3.40c) |
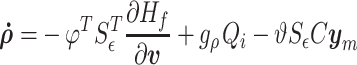 |
(3.40d) |
where 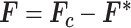 .
.
Note that term 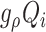 is not switched. This is given by the fact that the inlet mass flows enters through the left half volume
is not switched. This is given by the fact that the inlet mass flows enters through the left half volume 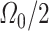 (see Fig. 3), and this part of the fluid domain corresponds to the first lower section of the glottal tract (i.e., the section at the left-hand side of the BCM in Fig. 2). Considering that
(see Fig. 3), and this part of the fluid domain corresponds to the first lower section of the glottal tract (i.e., the section at the left-hand side of the BCM in Fig. 2). Considering that  have motionless walls, it is not necessary the use of switch variables to map
have motionless walls, it is not necessary the use of switch variables to map 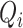 .
.
From (3.35), we have that 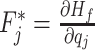 , i.e.,
, i.e., 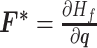 where
where 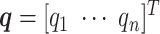 is the set of velocity section heights. Then, considering the definition of
is the set of velocity section heights. Then, considering the definition of 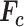 in (3.31), we obtain that
in (3.31), we obtain that
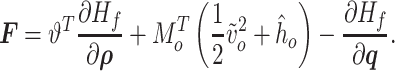 |
(3.41) |
On the other hand, the variation of fluid section heights by the motion of the structure system is given by the following relationship 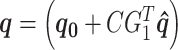 where
where 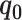 is the set of velocity section heights at the equilibrium point at reference pressure
is the set of velocity section heights at the equilibrium point at reference pressure 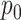 , and the term
, and the term 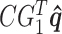 maps the displacement of the structure masses to the variation of fluid section heights. This relationship allows us define the following partial derivative:
maps the displacement of the structure masses to the variation of fluid section heights. This relationship allows us define the following partial derivative:
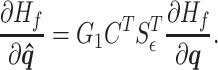 |
(3.42) |
Matrix 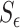 is added to able and disable the corresponding fluid dynamics when the section heights cross the threshold value
is added to able and disable the corresponding fluid dynamics when the section heights cross the threshold value  .
.
Then, using (3.41), (3.42) and the definition of 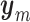 in (3.4a), the fluid–structure model can be rewritten as
in (3.4a), the fluid–structure model can be rewritten as
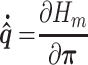 |
(3.43a) |
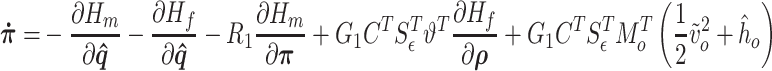 |
(3.43b) |
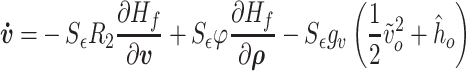 |
(3.43c) |
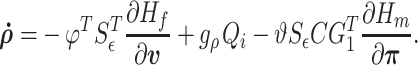 |
(3.43d) |
Remark 3.2
Consider
as the instant where
switches from
to
,
, and
as the instant where
switch from
to
,
. From (3.43a), we obtain that the velocity dynamic in
is disable,
, for the internal
. Additionally, the kinetic energy in the
-th velocity section is negligible, given that
is smaller. Then, to able a soft transition at glottal opening, we set to 0 the corresponding velocity variable. Similarly, for the
-th density section, we set to
the density variable when the corresponding switch variables of adjacent velocity sections are equal to 0.
Finally, considering the total energy of the fluid–structure system as 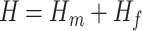 , we obtain the following switched port-Hamiltonian model for the vocal folds:
, we obtain the following switched port-Hamiltonian model for the vocal folds:
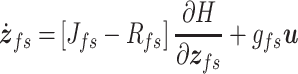 |
(3.44a) |
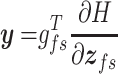 |
(3.44b) |
where the state vector is given by 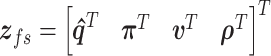 , the input
, the input 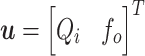 , the output
, the output 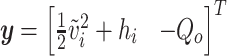 and matrices
and matrices
 |
3.4 Inputs definition
In vocal fold models such as those proposed by Ishizaka & Flanagan (1972), Steinecke & Herzel (1995) and Story & Titze (1995), it is common to use the variation of the subglottal pressure 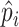 and the supraglottal pressure
and the supraglottal pressure 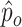 as inputs of the dynamical system. Considering the pressure definition in (3.10), we obtain that the subglottal and supraglottal airflow densities are given by
as inputs of the dynamical system. Considering the pressure definition in (3.10), we obtain that the subglottal and supraglottal airflow densities are given by
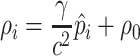 |
(3.45) |
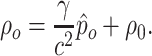 |
(3.46) |
To define the inlet input, we describe the velocity in the inlet boundary 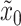 in terms of the pressures in the upper and downer limits,
in terms of the pressures in the upper and downer limits, 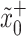 and
and 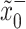 . From (3.15), note that when
. From (3.15), note that when 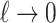 the velocity response tends to be instantaneous. Then, we use the Bernoulli equation to define inlet velocity as
the velocity response tends to be instantaneous. Then, we use the Bernoulli equation to define inlet velocity as 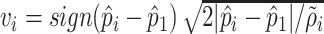 where
where 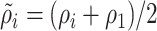 is the density in the inlet boundary and
is the density in the inlet boundary and 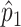 and
and 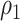 are the pressure and density at
are the pressure and density at 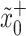 , respectively. Then, the inlet input is given by
, respectively. Then, the inlet input is given by
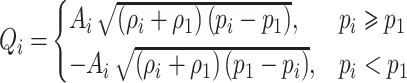 |
(3.47) |
where 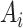 is the cross-sectional area in the inlet boundary.
is the cross-sectional area in the inlet boundary.
To define the outlet input, we neglect the vocal tract influence, i.e., the glottis end is open to the atmosphere (Steinecke & Herzel, 1995). Under this condition, we obtain 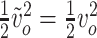 . Thus, considering an average velocity outside the glottis equal to 0, we obtain
. Thus, considering an average velocity outside the glottis equal to 0, we obtain
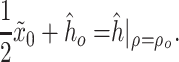 |
(3.48) |
4. Simulation results
In this section, we present simulation results for the proposed fluid–structure port-Hamiltonian model of the vocal folds given in (3.44). For the evaluation of the results, we use as reference the body-cover (BC95) model proposed by Story & Titze (1995) and the port-Hamiltonian fluid–structure model (PH18) proposed by Mora et al. (2018). Simulation parameters for mechanical and fluid systems are summarized in Table 1. Note that the parameters of the mechanical system are in correspondence with the Table II, case C in Story & Titze (1995). Applying the proposed discretization to divide the fluid domain in 38 velocity sections with uniform cross-sectional area and length 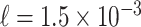 m, the glottal tract can be modeled as shown in Fig. 5, with 14 sections in subglottal part and 12 sections in the supraglottal part of the glottis and 6 sections under each cover mass. The heights of each section are initialized as following:
m, the glottal tract can be modeled as shown in Fig. 5, with 14 sections in subglottal part and 12 sections in the supraglottal part of the glottis and 6 sections under each cover mass. The heights of each section are initialized as following:
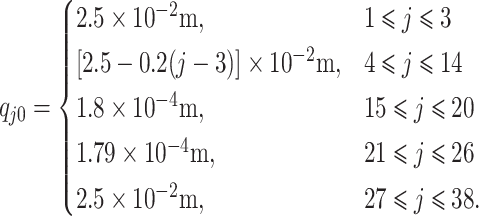 |
(4.1) |
Table 1.
Simulation parameters
| Mechanical parameters | |||
|---|---|---|---|
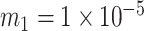 Kg
Kg |
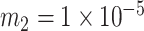 Kg
Kg |
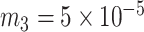 Kg
Kg |
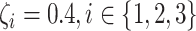
|
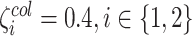
|
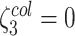
|
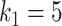 N/m
N/m |
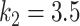 N/m
N/m |
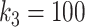 N/m
N/m |
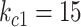 N/m
N/m |
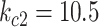 N/m
N/m |
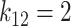 N/m
N/m |
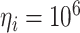 m
m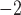 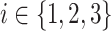
|
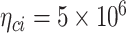 m
m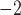 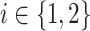
|
||
Fluid parameter at 36 C C |
|||
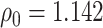 Kg/m
Kg/m |
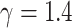
|
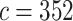 m/s
m/s |
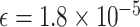 m
m |
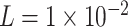 m
m |
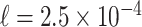 m
m |
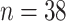
|
|
Fig. 5.

Approximation of the glottal tract using the discretization method proposed, considering fluid sections with uniform cross-sectional areas. Dotted line represents the midsagital plane. Circles denote the number of velocity section in each glottis part.
For the inputs, we have considered the subglottal and supraglottal relative pressures, 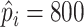 Pa and
Pa and 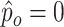 Pa, respectively. Considering a motionless wall in the subglottal and supraglottal sections, we define the interconnection matrix
Pa, respectively. Considering a motionless wall in the subglottal and supraglottal sections, we define the interconnection matrix 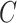 as follows:
as follows:
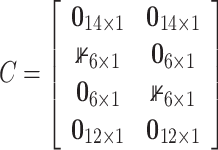 |
(4.2) |
where 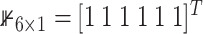 . Note that, given the definition of
. Note that, given the definition of  and
and  , we obtain that
, we obtain that 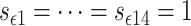 ,
, 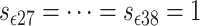 ,
, 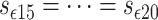 and
and 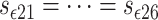 for all simulation time, i.e., from a computational point of view, only two switches are relevant. Simulations were done in Matlab using the solver ODE23tb with an event location function to update the switch variables.
for all simulation time, i.e., from a computational point of view, only two switches are relevant. Simulations were done in Matlab using the solver ODE23tb with an event location function to update the switch variables.
The movement of each mass for BC95, PH18 and the proposed model is shown in Fig. 6. It can be noticed that in the proposed model the masses exhibit oscillations with a fundamental frequency of 129.1 Hz, in contrast with the 127.5 Hz and 139.9 Hz of the BC95 and PH18 models, respectively. The fluid–structure model PH18 presents a displacement almost parallel for the contact masses of vocal folds, lower mass displacement 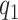 (dash-dot-dotted) and upper mass displacement
(dash-dot-dotted) and upper mass displacement 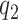 (dashed line), respectively, increasing the oscillation amplitude of
(dashed line), respectively, increasing the oscillation amplitude of 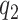 . In contrast, for the proposed model, the movement of the contact masses presents a difference in the amplitude and phase between the oscillations of
. In contrast, for the proposed model, the movement of the contact masses presents a difference in the amplitude and phase between the oscillations of 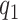 and
and 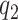 , in correspondence with the wave propagation through the vocal fold structure, obtaining similar oscillations to the BC95 model.
, in correspondence with the wave propagation through the vocal fold structure, obtaining similar oscillations to the BC95 model.
Fig. 6.

Displacement of the masses of the vocal fold mechanical structure. Solid line is the body mass displacement (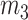 in Fig. 1) and dashed and dash-dot-dotted lines are the displacements of upper and lower cover masses, respectively (
in Fig. 1) and dashed and dash-dot-dotted lines are the displacements of upper and lower cover masses, respectively (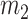 and
and 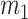 in Fig. 1, respectively).
in Fig. 1, respectively).
In lumped-parameter models of vocal folds, a collision occurs when the contact masses cross the corresponding collision planes. In this work, given the hemi-larynx assumption, the collision plane for the contact masses is the midsagittal plane. Then, the deformation of the vocal folds given by the elastic collision is proportional to the overlapping, 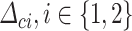 , of cover masses, as shown in Fig. 7. Note that the magnitude of tissue deformation in the PH18 model is around two times the one of the BC95 model. The tissue deformation in the upper section of the vocal folds (solid line) is greater than the deformation in the lower section (dash-dot-dotted line) for the PH18 model, i.e., the impact stress is minor in the lower section of the vocal folds. On the contrary, in the proposed model, the tissue deformation and impact stress are longer in the lower section of vocal folds. This behavior is similar to other lumped-parameter models as the proposed by Ishizaka & Flanagan (1972) and Steinecke & Herzel (1995), and it is consistent with the finite-element study presented by Tao et al. (2006).
, of cover masses, as shown in Fig. 7. Note that the magnitude of tissue deformation in the PH18 model is around two times the one of the BC95 model. The tissue deformation in the upper section of the vocal folds (solid line) is greater than the deformation in the lower section (dash-dot-dotted line) for the PH18 model, i.e., the impact stress is minor in the lower section of the vocal folds. On the contrary, in the proposed model, the tissue deformation and impact stress are longer in the lower section of vocal folds. This behavior is similar to other lumped-parameter models as the proposed by Ishizaka & Flanagan (1972) and Steinecke & Herzel (1995), and it is consistent with the finite-element study presented by Tao et al. (2006).
Fig. 7.

Overlapping of cover masses during the vocal fold collisions. Solid line: deformation for the upper mass (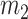 in Fig. 1). Dash-dot-dotted line: deformation for the lower mass (
in Fig. 1). Dash-dot-dotted line: deformation for the lower mass (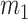 in Fig. 1).
in Fig. 1).
On the other hand, to compare the airflow, we analyze the output flows shown in Fig. 8. In general, the maximum flow occurs in the maximum opening of the glottal tract on the vibrating cycle. In the PH18 model, this happens in the first quarter of the cycle, and in the BC95 and the proposed models the maximum flow occurs in the middle of the cycle. However, the output flow of the proposed model shows a soft increase in the glottis opening with a fast decline when the vocal fold is closing. This shape of the output flow is consistent with the results reported in Shurtz & Thomson (2013, Fig. 7).
Fig. 8.

Output flow in one vibrating cycle.
Figure 9 shows the pressure distribution in the fluid in three instants of the vibration cycle, two instants with a convergent shape of the vocal folds and one instant with a divergent shape. The pressure distributions obtained are consistent with the results of the deep neural network based (DNN) flow model proposed in Zhang et al. (2020, Figs 11–19).
Fig. 9.

Pressure distribution in three instants of the vibrating cycle. Upper row: coronal view of the glottis, where the dots represents the heights of each velocity sections. Bottom row: pressure distribution in the glottis.
Similarly, Fig. 10 shows the behavior of kinetic and potential energies of the mechanical part of the vocal folds, 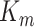 and
and 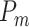 , respectively, and the energies of the fluid,
, respectively, and the energies of the fluid, 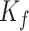 , in one vibrating cycle. Note that for the PH18 model, most of the energy is stored in the mechanical system. The opposite situation is presented by the BC95 model. It is observed that the proposed model presents an intermediate behavior between PH18 and BC95. Note that in the proposed model the maximum potential energy occurs in the maximum opening of mass
, in one vibrating cycle. Note that for the PH18 model, most of the energy is stored in the mechanical system. The opposite situation is presented by the BC95 model. It is observed that the proposed model presents an intermediate behavior between PH18 and BC95. Note that in the proposed model the maximum potential energy occurs in the maximum opening of mass 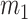 and not in the maximum opening of the glottis as it happens in the PH18 model. It decreases when the glottis is closing and increases slightly again when the glottis is completely closed. The latter is due to the energy stored during the elastic collision of the vocal folds. Regarding the fluid energy note that the potential energy of the proposed model is basically negligible with respect the kinetic energy. Regarding the fluid–structure energy transfer, we evaluated the energy transfer per cycle, i.e.,
and not in the maximum opening of the glottis as it happens in the PH18 model. It decreases when the glottis is closing and increases slightly again when the glottis is completely closed. The latter is due to the energy stored during the elastic collision of the vocal folds. Regarding the fluid energy note that the potential energy of the proposed model is basically negligible with respect the kinetic energy. Regarding the fluid–structure energy transfer, we evaluated the energy transfer per cycle, i.e., 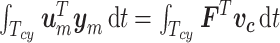 where
where 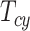 is the vibrating cycle period, obtaining a total of
is the vibrating cycle period, obtaining a total of 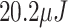 in the model proposed, in contrast with the
in the model proposed, in contrast with the 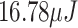 and
and 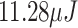 for the BC95 and PH18 models.
for the BC95 and PH18 models.
Fig. 10.

Instantaneous energy in one vibrating cycle. (a) Kinetic energy 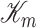 of the mechanical part. (b) Potential energy
of the mechanical part. (b) Potential energy 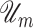 of the mechanical part. (c) Kinetic energy
of the mechanical part. (c) Kinetic energy 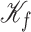 and potential energy
and potential energy 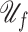 of the fluid part.
of the fluid part.
It is well known that the BC95 model describes appropriately the experimental results on the wave propagation of the real vocal fold motion and the volumetric airflow in the supraglottal section of the glottal tract. However, given the assumptions on the airflow (static and uniform flow), the energy transfers between the fluid and mechanical parts of the model are not completely described and the effects of the closing of the vocal folds on the output airflow are neglected. The proposed model solves this drawback of the BC95 model, keeping the advantages on the mechanical motion of the vocal folds. Additionally, the scalability of the proposed model is a clear advantage over the PH18 model.
5. Conclusion
In this paper, we have presented a novel model of the vocal folds given by a port-Hamiltonian description. The port-Hamiltonian formalism is a framework that has allowed us to obtain an energy-based model of the vocal fold behavior and their interaction with the intraglottal airflow. A scalable port-Hamiltonian model for the airflow has been developed from the balance equations of fluids. This port-Hamiltonian formulation allows the coupling with the mechanical model of the vocal folds using a power-preserving interconnection by ports. The simulation results show that the proposed energy-based model is able to replicate the oscillations and the collisions between the vocal folds. Moreover, the amplitude of masses movements and the airflow velocity are consistent with previous lumped-parameters models and real data. Similarly, the energy transfer estimated with the proposed model is greater than the predicted with BC95 and PH18 models. In future works, we expect to exploit the proposed model for parameter estimation using real clinical data.
Acknowledgements
The authors thank the anonymous reviewers’ comments which greatly improved the final version of this manuscript.
Funding
Research funded by Agencia Nacional de Investigación y Desarrollo (ANID) grants PFCHA Beca Doctorado Nacional 2017-21170472, MEC 80170066, BASAL FB0008, and FONDECYT grants 1181090 and 1191544; Universidad Técnica Federico Santa María grant PIIC 013/2018; National Institutes of Health grant P50DC015446; EIPHI Graduate School contract ANR-17-EURE-0002; also by European Commission Marie Skodowska-Curie Fellowship, ConFlex ITN Network and the INFIDHEM project codes 765579 and ANR-16-CE92-0028. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Appendix A Energy of the mechanical system
This appendix details the kinetic and potential energies associated to the structure and the fluid of the proposed model.
The kinetic energy in the mechanical structure is given by the motion of masses. The kinetic energy associated with the mass 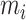 is given by
is given by
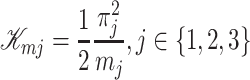 |
(A.1) |
and the total kinetic energy is given by 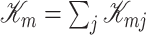 , where
, where
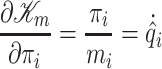 |
(A.2) |
describes the velocity of the 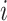 -th mass.
-th mass.
The potential energies in the mechanical structure are stored in six different springs. One coupling spring between the cover masses, two collision springs and three lateral springs. The vocal fold tissue is described as a hyper-elastic or viscoelastic material (Jiang et al., 2017; Shurtz & Thomson, 2013; Zheng et al., 2011). Then, in the BCM (Story & Titze, 1995), lateral and collision springs are described by non-linear forces having the form:
 |
(A.3) |
where 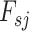 and
and 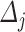 are the force and the elongation of the
are the force and the elongation of the 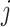 -th spring and
-th spring and 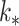 and
and  are the linear and non-linear spring coefficients. Defining
are the linear and non-linear spring coefficients. Defining 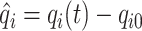 as the displacement of
as the displacement of 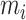 , where
, where 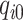 is the equilibrium position of the corresponding mass at reference pressure
is the equilibrium position of the corresponding mass at reference pressure 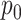 , the stored potential energy in the connecting spring between the cover masses,
, the stored potential energy in the connecting spring between the cover masses, 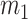 and
and 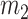 , and the body mass
, and the body mass 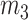 is given by
is given by
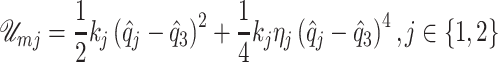 |
(A.4) |
where 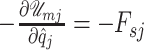 and
and 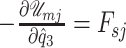 are the corresponding forces over the cover masses and the body mass, respectively. Similarly, the stored energy in the spring that interconnect the body mass with the gottal wall is given by
are the corresponding forces over the cover masses and the body mass, respectively. Similarly, the stored energy in the spring that interconnect the body mass with the gottal wall is given by
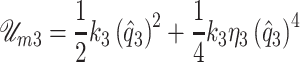 |
(A.5) |
and the force applied over the body mass is given by 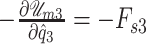 . In the case of collision springs, note that the elongation is given by
. In the case of collision springs, note that the elongation is given by 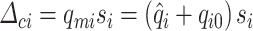 where
where 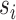 is a switch variable defined in (3.1). Then, the energy stored in the collision springs of cover masses can be expressed as
is a switch variable defined in (3.1). Then, the energy stored in the collision springs of cover masses can be expressed as
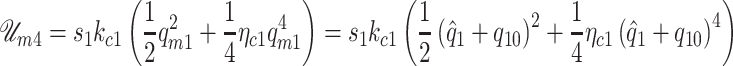 |
(A.6) |
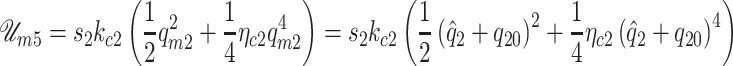 |
(A.7) |
where 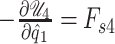 and
and 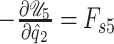 are the forces applied by the collision springs over masses
are the forces applied by the collision springs over masses  and
and 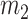 , respectively. Note that these energies and forces imply a switched Hamiltonian. However, as shown in Fig. A1(left), the behavior of the potential energy stored in the collision spring is continuous. This guarantees that the Hamiltonian has no discontinuities. Similarly, the applied force over the cover masses shows a soft transition when the mass
, respectively. Note that these energies and forces imply a switched Hamiltonian. However, as shown in Fig. A1(left), the behavior of the potential energy stored in the collision spring is continuous. This guarantees that the Hamiltonian has no discontinuities. Similarly, the applied force over the cover masses shows a soft transition when the mass 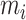 collides,
collides,  , as shown in Fig. A1(right).
, as shown in Fig. A1(right).
Fig. A.1.

Stored potential energy of collision spring (a) and the corresponding applied force over mass 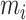 (b). Normalized behavior,
(b). Normalized behavior, 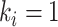 and
and 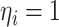 , for
, for 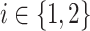 .
.
In BCM, the shear strain of the epithelial layer is modeled through a linear spring whose force takes the form 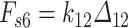 , where
, where 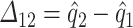 is the spring elongation. Then, the stored potential energy is this spring is given by
is the spring elongation. Then, the stored potential energy is this spring is given by
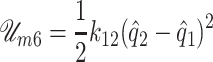 |
(A.8) |
where 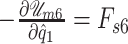 and
and 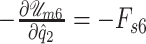 are the corresponding applied forces over masses
are the corresponding applied forces over masses 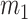 and
and 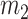 , respectively.
, respectively.
Denote by 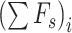 as the sum of forces applied by the springs over mass
as the sum of forces applied by the springs over mass 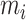 and
and  as the total potential energy of the mechanical system. Then, from the discussion above, we obtain
as the total potential energy of the mechanical system. Then, from the discussion above, we obtain
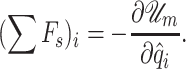 |
(A.9) |
Appendix B Dynamics of the intraglottal airflow
This appendix details the ordinary differential equations that describes the airflow in each section of the glottal tract, as a consequence of Assumption 3.1. In this sense, the fluid dynamics described in Proposition 3.1 is obtained as follows:
Considering a uniform density distribution in the volume 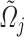 and integrating the continuity equation using the Leibniz integral rule and Gauss divergence theorem (Bird et al., 2014) we obtain
and integrating the continuity equation using the Leibniz integral rule and Gauss divergence theorem (Bird et al., 2014) we obtain
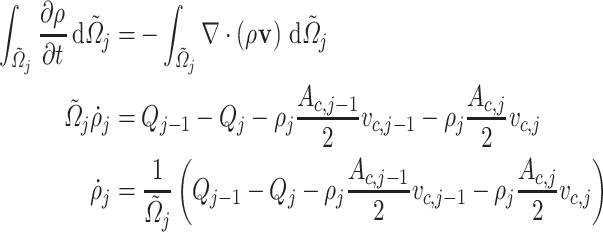 |
(B.1) |
where 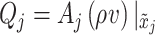 denotes the mass flow at
denotes the mass flow at 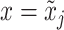 , i.e.,
, i.e., 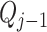 and
and 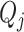 are the mass flow on the inlet and outlet boundaries of
are the mass flow on the inlet and outlet boundaries of 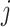 -th density section,
-th density section, 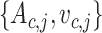 and
and 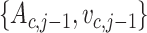 are the area and velocity pairs of the adjacent contact surfaces, as shown in Fig. 4, and
are the area and velocity pairs of the adjacent contact surfaces, as shown in Fig. 4, and 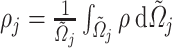 is the average density in volume
is the average density in volume  .
.
Similarly, applying the same procedure in the motion equation (3.13), we obtain
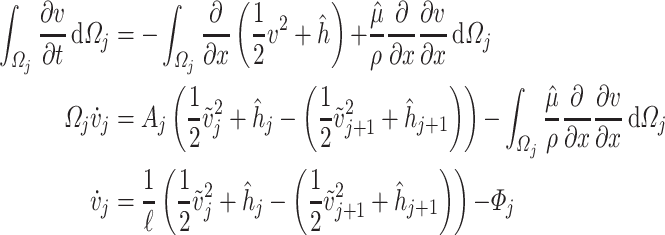 |
(B.2) |
where 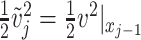 and
and 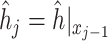 ,
, 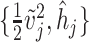 and
and 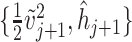 are the pairs of kinetic energy per unit mass and relative enthalpy on the inlet and outlet boundaries of the
are the pairs of kinetic energy per unit mass and relative enthalpy on the inlet and outlet boundaries of the 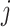 -th velocity section, respectively,
-th velocity section, respectively, 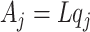 is the corresponding cross-sectional area,
is the corresponding cross-sectional area, 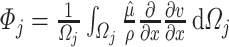 is the average velocity drop due to energy losses in
is the average velocity drop due to energy losses in 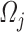 and
and 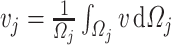 is the average longitudinal velocity in the volume
is the average longitudinal velocity in the volume  .
.
Appendix C Energy of the fluid system
In this appendix, we describe the kinetic and internal energies associated with the velocity and density sections. In case of the  -th velocity section with volume
-th velocity section with volume 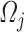 , the corresponding kinetic energy
, the corresponding kinetic energy 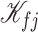 associated with longitudinal velocity is given by
associated with longitudinal velocity is given by
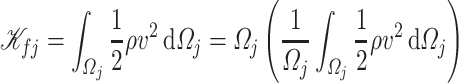 |
(C.1) |
where the term 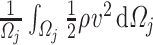 is the average kinetic energy density in volume
is the average kinetic energy density in volume 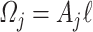 . Denoting by
. Denoting by 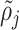 and
and 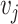 the average density and longitudinal velocity on
the average density and longitudinal velocity on 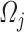 , respectively, then, the average kinetic energy density can be approximated as
, respectively, then, the average kinetic energy density can be approximated as 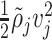 . Note that
. Note that 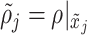 is given by the average of adjacent densities, i.e.,
is given by the average of adjacent densities, i.e., 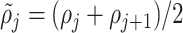 , then,
, then, 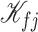 can be expressed as
can be expressed as
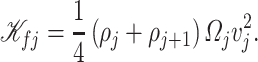 |
(C.2) |
Similarly, the internal energy in a density section with volume 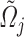 is given by
is given by 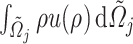 , where
, where 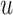 is the internal energy per unit mass of the fluid. However, as previously mentioned, we use a non-negative availability function
is the internal energy per unit mass of the fluid. However, as previously mentioned, we use a non-negative availability function 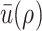 to describe the internal energy. Then, denoting by
to describe the internal energy. Then, denoting by 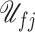 the total internal energy in volume
the total internal energy in volume 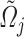 , we obtain
, we obtain
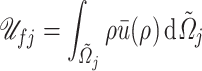 |
(C.3) |
where 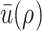 is defined in (3.11). Denoting by
is defined in (3.11). Denoting by 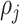 the average density in
the average density in 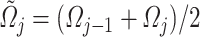 , the average internal energy in the
, the average internal energy in the 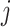 -th density section can be approximated as
-th density section can be approximated as 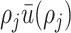 where
where 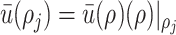 . Then,
. Then, 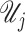 can be expressed as
can be expressed as
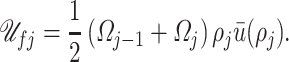 |
(C.4) |
In the case of the first density section, note that 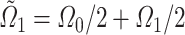 where
where 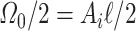 denotes the half volume at the left part of the upstream region (see Fig. 3(b)), with
denotes the half volume at the left part of the upstream region (see Fig. 3(b)), with 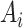 as the cross-sectional area in the inlet boundary. For the
as the cross-sectional area in the inlet boundary. For the 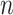 -th velocity section, we have that
-th velocity section, we have that 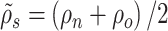 where
where 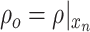 denotes the density in the last half volume
denotes the density in the last half volume 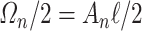 of the right downstream region (see Fig. 3(a)). Then, to complete the characterization in the fluid domain, we define the kinetic energy in
of the right downstream region (see Fig. 3(a)). Then, to complete the characterization in the fluid domain, we define the kinetic energy in 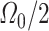 as
as
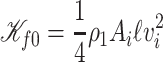 |
(C.5) |
where 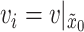 denotes the fluid velocity at
denotes the fluid velocity at 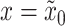 . Similarly, we define the internal energy in
. Similarly, we define the internal energy in  as
as
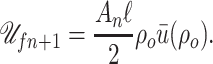 |
(C.6) |
Then, the total energy of the fluid is given by the sum kinetic energy and internal energy of the velocity and density sections, respectively, as shown in (3.16). Defining 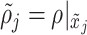 as the average density of the corresponding adjacent sections, i.e.,
as the average density of the corresponding adjacent sections, i.e., 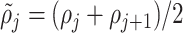 , then, the efforts associated with the velocity and density of each section are given by
, then, the efforts associated with the velocity and density of each section are given by
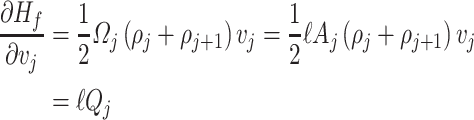 |
(C.7) |
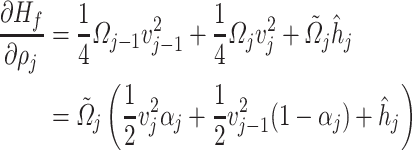 |
(C.8) |
where 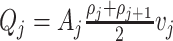 is mass flow at
is mass flow at 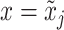 and
and 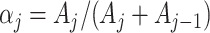 .
.
Contributor Information
Luis A Mora, Department of Electronic Engineering, Universidad Técnica Federico Santa María, 2390123 Valparaiso, Chile; Département AS2M, FEMTO-ST/ENSMM, Université de Bourgogne Franche-Comté, 25000 Besançon, France.
Hector Ramirez, Department of Electronic Engineering, Universidad Técnica Federico Santa María, 2390123 Valparaiso, Chile.
Juan I Yuz, Department of Electronic Engineering, Universidad Técnica Federico Santa María, 2390123 Valparaiso, Chile.
Yann Le Gorec, Département AS2M, FEMTO-ST/ENSMM, Université de Bourgogne Franche-Comté, 25000 Besançon, France.
Matías Zañartu, Department of Electronic Engineering, Universidad Técnica Federico Santa María, 2390123 Valparaiso, Chile.
References
- Alipour, F. & Scherer, R. C. (2004) Flow separation in a computational oscillating vocal fold model. J. Acoust. Soc. Am., 116, 1710–1719. [DOI] [PubMed] [Google Scholar]
- Bird, R. B., Stewart, W. E., Lightfoot, E. N. & Klingenberg, D. J. (2014) Introductory Transport Phenomena. Hoboken, USA: Jhon Wiley & Sons. [Google Scholar]
- Cardoso-Ribeiro, F. L., Matignon, D. & Pommier-Budinger, V. (2016) Modeling by interconnection and control by damping injection of a fluid-structure system with non-collocated actuators and sensors. Proceedings of ISMA 2016—International Conference on Noise and Vibration Engineering and USD2016—International Conference on Uncertainty in Structural Dynamics, Leuven, Belgium, Leuven, Belgium: KU Leuven, pp. 121–135.
- Cardoso-Ribeiro, F. L., Matignon, D. & Pommier-Budinger, V. (2017) A port-Hamiltonian model of liquid sloshing in moving containers and application to a fluid-structure system. J. Fluids Struct., 69, 402–427. [Google Scholar]
- Encina, M., Yuz, J. I., Zañartu, M. & Galindo, G. E. (2015) Vocal fold modeling through the port-Hamiltonian systems approach. IEEE Multiconference on Systems and Control-MSC 2015, Sydney, Australia, Sydney, Australia: IEEE, pp. 1558–1563.
- Erath, B. D., Zañartu, M., Stewart, K. C., Plesniak, M. W., Sommer, D. E. & Peterson, S. D. (2013) A review of lumped-element models of voiced speech. Speech Commun., 55, 667–690. [Google Scholar]
- Espinoza, V. M., Zañartu, M., Van Stan, J. H., Mehta, D. D. & Hillman, R. E. (2017) Glottal aerodynamic measures in women with phonotraumatic and nonphonotraumatic vocal hyperfunction. J. Speech Lang. Hear. Res., 60, 2159–2169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galindo, G. E., Peterson, S. D., Erath, B. D., Castro, C., Hillman, R. E. & Zañartu, M. (2017) Modeling the pathophysiology of phonotraumatic vocal hyperfunction with a triangular glottal model of the vocal folds. J. Speech Lang. Hear. Res., 60, 2452–2471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haddad, N. K., Chemori, A. & Belghith, S. (2018) Robustness enhancement of IDA-PBC controller in stabilising the inertia wheel inverted pendulum: theory and real-time experiments. Internat. J. Control, 91, 2657–2672. [Google Scholar]
- Hélie, T. & Silva, F. (2017) Self-oscillations of a vocal apparatus: a port-Hamiltonian formulation. International Conference on Geometric Science of Information ( F. Nielsen & F. Barbaresco eds). Lecture Notes in Computer Science, vol. 10589. Cham: Springer, pp. 375–383. [Google Scholar]
- Ishizaka, K. & Flanagan, J. L. (1972) Synthesis of voiced sounds from a two mass model of the vocal cords. Bell Syst. Tech. J., 51, 1233–1268. [Google Scholar]
- Jiang, W., Zheng, X. & Xue, Q. (2017) Computational modeling of fluid–structure–acoustics interaction during voice production. Front. Bioeng. Biotechnol., 5. doi: 10.3389/fbioe.2017.00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kotyczka, P. (2013) Discretized models for networks of distributed parameter port-Hamiltonian systems. Proceedings of the 8th International Workshop on Multidimensional Systems (nDS13). Erlangen, Germany: VDE, pp. 63–67. [Google Scholar]
- Landau, L. D. & Lifshitz, E. M. (1987) Fluid Mechanics, 2nd edn. Course of Theorietcal Physics, vol. 6. Oxford, UK: Pergamon Press. [Google Scholar]
- Lucero, J. C. & Schoentgen, J. (2015) Smoothness of an equation for the glottal flow rate versus the glottal area. J. Acoust. Soc. Am., 137, 2970–2973. [DOI] [PubMed] [Google Scholar]
- Mackay, A. T. & Phillips, T. N. (2019) On the derivation of macroscopic models for compressible viscoelastic fluids using the generalized bracket framework. J. Nonnewton. Fluid Mech., 266, 59–71. [Google Scholar]
- Matignon, D. & Hélie, T. (2013) A class of damping models preserving eigenspaces for linear conservative port-Hamiltonian systems. Eur. J. Control, 19, 486–494. [Google Scholar]
- Mittal, R., Erath, B. D. & Plesniak, M. W. (2013) Fluid dynamics of human phonation and speech. Annu. Rev. Fluid Mech., 45, 437–467. [Google Scholar]
- Mora, L. A., Le Gorrec, Y., Matignon, D., Rámirez, H. & Yuz, J. I. (2020) About dissipative and pseudo port-Hamiltonian formulations of irreversible newtonian compressible flows. Proceedings of the 21st IFAC World Congress, Berlin, Germany. Berlin, Germany: IFAC.
- Mora, L. A., Yuz, J. I., Rámirez, H. & Le Gorrec, Y. (2018) A port-Hamiltonian fluid-structure interaction model for the vocal folds. IFAC-PapersOnLine, 51, 62–67. [Google Scholar]
- Mulley, R. (2004) Flow of Industrial Fluids: Theory and Equations. Boca Raton, USA: CRC Press. [Google Scholar]
- Nguyen, T. S., Hoang, N. H., Ha, A. & Hussain, M. (2019) Feedback passivation plus tracking-error-based multivariable control for a class of free-radical polymerisation reactors. Internat. J. Control, 92, 1970–1984. [Google Scholar]
- Pyrkin, A. A., Vedyakov, A. A., Ortega, R. & Bobtsov, A. A. (2018) A robust adaptive flux observer for a class of electromechanical systems. Internat. J. Control, 93, 1–11. [Google Scholar]
- Samlan, R. A., Story, B. H. & Bunton, K. (2013) Relation of perceived breathiness to laryngeal kinematics and acoustic measures based on computational modeling. J. Speech Lang. Hear. Res., 56, 1209–1223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shurtz, T. E. & Thomson, S. L. (2013) Influence of numerical model decisions on the flow-induced vibration of a computational vocal fold model. Comput. Struct., 122, 44–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinecke, I. & Herzel, H. (1995) Bifurcations in an asymmetric vocal-fold model. J. Acoust. Soc. Am., 97, 1874–1884. [DOI] [PubMed] [Google Scholar]
- Story, B. H. & Titze, I. R. (1995) Voice simulation with a body cover model of the vocal folds. J. Acoust. Soc. Am., 97, 1249–1260. [DOI] [PubMed] [Google Scholar]
- Sváček, P. & Horáček, J. (2018) Finite element approximation of flow induced vibrations of human vocal folds model: effects of inflow boundary conditions and the length of subglottal and supraglottal channel on phonation onset. Appl. Math. Comput., 319, 178–194. [Google Scholar]
- Tao, C., Jiang, J. J. & Zhang, Y. (2006) Simulation of vocal fold impact pressures with a self-oscillating finite-element model. J. Acoust. Soc. Am., 119, 3987–3994. [DOI] [PubMed] [Google Scholar]
- Thomson, S. L., Mongeau, L. & Frankel, S. H. (2005) Aerodynamic transfer of energy to the vocal folds. J. Acoust. Soc. Am., 118, 1689–1700. [DOI] [PubMed] [Google Scholar]
- Titze, I. R. & Hunter, E. J. (2015) Comparison of vocal vibration-dose measures for potential-damage risk criteria. J. Speech Lang. Hear. Res., 58, 1425–1439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trenchant, V., Fares, Y., Rámirez, H. & Le Gorrec, Y. (2015) A port-Hamiltonian formulation of a 2D boundary controlled acoustic system. IFAC-PapersOnLine, 48, 235–240. [Google Scholar]
- Trenchant, V., Rámirez, H., Le Gorrec, Y. & Kotyczka, P. (2018) Finite differences on staggered grids preserving the port-Hamiltonian structure with application to an acoustic duct. J. Comput. Phys., 373, 673–697. [Google Scholar]
- van der Schaft, A. J. (2017) L2-Gain and Passivity Techniques in Nonlinear Control, 3rd edn. Communications and Control Engineering. Cham: Springer International Publishing. [Google Scholar]
- van der Schaft, A. J. & Jeltsema, D. (2014) Port-Hamiltonian Systems Theory: An Introductory Overview. Boston, USA: Now Publishers Inc. [Google Scholar]
- van der Schaft, A. J. & Maschke, B. M. (2002) Hamiltonian formulation of distributed-parameter systems with boundary energy flow. J. Geom. Phys., 42, 166–194. [Google Scholar]
- van der Schaft, A. J., Rao, S. & Jayawardhana, B. (2016) A network dynamics approach to chemical reaction networks. Internat. J. Control, 89, 731–745. [Google Scholar]
- Wetzel, V., Hélie, T. & Silva, F. (2019) Power balanced time-varying lumped parameter model of a vocal tract: modelling and simulation. Proceedings of the 26th International Congress on Sound and Vibration, ICSV 2019, Montréal, Canada, Montreal, Canada: International Institute of Acoustics and Vibration, pp. 1–7.
- Zañartu, M., Galindo, G. E., Erath, B. D., Peterson, S. D., Wodicka, G. R. & Hillman, R. E. (2014) Modeling the effects of a posterior glottal opening on vocal fold dynamics with implications for vocal hyperfunction. J. Acoust. Soc. Am., 136, 3262–3271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, Y., Zheng, X. & Xue, Q. (2020) A deep neural network based glottal flow model for predicting fluid-structure interactions during voice production. Appl. Sci., 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng, X., Mittal, R., Xue, Q. & Bielamowicz, S. (2011) Direct-numerical simulation of the glottal jet and vocal-fold dynamics in a three-dimensional laryngeal model. J. Acoust. Soc. Am., 130, 404–415. [DOI] [PMC free article] [PubMed] [Google Scholar]