Estimation of Relative and Absolute Risks in a Competing-Risks Setting Using a Nested Case-Control Study Design: Example From the ProMort Study

Abstract

In this paper, we describe the Prognostic Factors for Mortality in Prostate Cancer (ProMort) study and use it to demonstrate how the weighted likelihood method can be used in nested case-control studies to estimate both relative and absolute risks in the competing-risks setting. ProMort is a case-control study nested within the National Prostate Cancer Register (NPCR) of Sweden, comprising 1,710 men diagnosed with low- or intermediate-risk prostate cancer between 1998 and 2011 who died from prostate cancer (cases) and 1,710 matched controls. Cause-specific hazard ratios and cumulative incidence functions (CIFs) for prostate cancer death were estimated in ProMort using weighted flexible parametric models and compared with the corresponding estimates from the NPCR cohort. We further drew 1,500 random nested case-control subsamples of the NPCR cohort and quantified the bias in the hazard ratio and CIF estimates. Finally, we compared the ProMort estimates with those obtained by augmenting competing-risks cases and by augmenting both competing-risks cases and controls. The hazard ratios for prostate cancer death estimated in ProMort were comparable to those in the NPCR. The hazard ratios for dying from other causes were biased, which introduced bias in the CIFs estimated in the competing-risks setting. When augmenting both competing-risks cases and controls, the bias was reduced.

 

Prostate cancer is one of the most common male cancers, with an estimated 1.2 million newly diagnosed cases in men worldwide each year (1). In the current era of opportunistic prostate-specific antigen (PSA) screening, up to 80% of prostate cancer patients have localized disease (2, 3). The 10-year prostate cancer-specific mortality among men with localized disease varies from 5% to 29%, depending on risk category (4). While radical treatment is generally recommended in cases of high-risk disease, treatment choice for men with low- or intermediate-risk disease poses a clinical dilemma (5). Treatment side effects must be balanced against the risk of dying from competing events and the risk of dying from prostate cancer, and traditional clinicopathological prognostic factors, such as Gleason score, tumor stage, and PSA level at diagnosis, are insufficient to identify those who may benefit from treatment. Hence, there is a strong clinical need to identify additional molecular prognostic factors. However, identifying molecular prognostic markers among men with low- or intermediate-risk prostate cancer is challenging. Because of the low long-term disease-specific mortality in these patients, unfeasibly large tissue repositories with extensive follow-up are needed to identify and validate novel molecular prognostic markers.

The nested case-control study design and other cost-effective cohort subsampling techniques have been developed for the rare-event setting (6, 7). In these studies, relative rather than absolute risks are typically estimated. Estimates of absolute risk are essential, however, if a prediction model is to be clinically useful. Since the late 1990s, different methods for unbiased and efficient estimation of absolute risks in nested case-control settings have been developed (8–14) and extended to the competing-risks setting (10, 15–17). These methods are still underused in clinical epidemiologic practice, and there are very few examples of their practical application.

We have used the National Prostate Cancer Register (NPCR) of Sweden, which comprises a well-defined cohort of virtually all prostate cancer patients diagnosed in Sweden since 1998, to design and conduct a nested case-control study, Prognostic Factors for Mortality in Prostate Cancer (ProMort). The primary aim of ProMort is to identify a tissue-based, molecular signature of lethal prostate cancer for men with low- or intermediate-risk prostate cancer and to develop a clinically useful prognostic model predicting the individual risk of dying from prostate cancer.

In this paper, we describe the ProMort study and provide a practical demonstration of how relative risks of prostate cancer death can be estimated using the weighted likelihood method (11). We further estimate the absolute risks of prostate cancer death in the presence of competing risks by also modeling the relative risks of death from other causes using the same method. Since, in ProMort, cases who died from other causes and their corresponding controls have not been selected using standard incidence density sampling (contrary to what was done for cases who died from prostate cancer), the estimates of the absolute risks of prostate cancer death may be biased to the extent to which the relative risks of death from other causes are biased. Hence, we explore the magnitude of this bias and compare our estimates with those obtained by augmenting competing-risks cases (16)—that is, cases who died from causes other than prostate cancer—and augmenting both competing-risks cases and corresponding controls (17). We also provide a practical description, including Stata programming code (StataCorp LLC, College Station, Texas), of estimation of absolute risks in the presence of competing risks in nested case-control studies.

METHODS

Study population

The NPCR

The NPCR includes incident cases of prostate cancer diagnosed in Sweden since 1998 and covers 98% of all prostate cancers registered in the Swedish National Cancer Register, reporting to which is mandatory by law (18, 19). Detailed descriptions of the NPCR have been published previously (18, 20). In short, the NPCR contains detailed information on mode of detection (PSA screening, lower urinary tract symptoms, other), clinical tumor-node-metastasis (TNM) stage, biopsy tumor differentiation (Gleason score or World Health Organization grade), serum PSA level at diagnosis, and planned primary treatment within 6 months of diagnosis (conservative (active surveillance or watchful waiting), curative (radical prostatectomy or radiotherapy), or noncurative (primary androgen deprivation therapy) treatment). Since 2007, additional information regarding the biopsy procedure (number of cores taken at biopsy, number of positive cores, total length of all biopsy cores, and combined length of cancer in all cores), prostate volume, curative treatment (type of prostatectomy, type of primary radiotherapy, and neoadjuvant hormone therapy), and postoperative Gleason score has been reported to the NPCR. Information on vital status is updated annually by linkage to the Swedish Population Register. For deceased patients, the date and cause of death, coded according to the International Classification of Diseases, Tenth Revision, are obtained through linkage to the Swedish Cause of Death Register. Prostate cancer-specific death is defined as any death for which prostate cancer was coded as the underlying cause of death, and its classification has been shown to be reliable, especially for localized disease (21, 22).

The ProMort study

ProMort is a case-control study nested among all men in the NPCR who were diagnosed with low- or intermediate-risk prostate cancer between January 1, 1998, and December 31, 2011. We defined low- or intermediate-risk prostate cancer as clinical tumor stage T1–T2, Gleason score ≤7 (or World Health Organization grade 1 when information on Gleason score was missing), serum PSA level less than 20 ng/mL, and no signs or nonassessed status of lymph node (N0 or Nx) or distant (M0 or Mx) metastases. At the time of linkage, follow-up was available until December 31, 2012. Among approximately 130,000 men in the NPCR, 57,952 fulfilled these criteria. Emigration occurred among only 0.23% of men in the NPCR and was not accounted for in the present analyses. We selected as cases all men who died from prostate cancer during follow-up (n = 1,735), and we randomly selected 1 control for each case, matched on year and hospital of diagnosis. The control had to be alive at the date of death of the respective case. This sampling scheme is often referred to as incidence-density sampling. Cases without an eligible control within the matching stratum (n = 25) were excluded from the study. The final data set included 1,710 cases and 1,710 matched controls.

We abstracted information on age, clinical stage, Gleason score/World Health Organization grade, and PSA level at diagnosis, as well as vital status and cause of death, from the NPCR. Cause of death was coded as either “prostate cancer-specific” or “other causes of death.” Tumor stage was coded as T1a, T1b, T1c, or T2. We assigned Gleason score ≤6 to the 140 cases and 103 controls with World Health Organization differentiation grade 1 but no information on Gleason score.

Diagnostic slides were retrieved from pathology wards across Sweden and scanned at 40× using the Pannoramic 250 Flash II digital slide scanner (3DHISTECH Ltd., Budapest, Hungary) at Örebro University Hospital (Örebro, Sweden). After scanning, the images were uploaded into specialized software based on the enhanced version of the Open Microscopy Environment Remote Objects (OMERO) platform (created and managed by the Centre for Advanced Studies, Research and Development in Sardinia (Pula, Italy)) for visualizing, managing, and annotating scientific image data (23). Once uploaded into the software, the slides were reviewed by 2 independent genitourinary pathologists and scored according to the 2014 International Society of Urological Pathology modification of the Gleason grading system (24). Prostate cancer patients who are not classified as low or intermediate risk (i.e., Gleason score >7) will be excluded from future main analyses.

Because of the limited amount of tissue available for molecular analysis, we conducted 2 pilot studies to 1) determine the best-performing DNA/RNA extraction kit in terms of the amount of tissue needed for the extraction and the quality of the extracted DNA/RNA (25) and 2) estimate the number and thickness of slices that could be cut from the tissue blocks and the minimum amount of cancer tissue (mm) needed to extract a sufficient amount of DNA/RNA for molecular analyses. Based on the outcome of these pilot studies and on a parallel systematic literature review, the most promising molecular markers for lethal prostate cancer will be prioritized for the main tissue analyses.

Statistical analyses

In nested case-control studies, logistic regression analysis (conditional or unconditional) is typically used to assess the association between the exposure and the outcome. When the interest also lies in absolute risk estimation, the baseline hazard function has to be estimated. Because of the disproportionate representation of controls in nested case-control studies, naive estimates of the baseline hazard result in biased absolute risk estimates (8). However, the sampling probability of the controls can be estimated in the underlying population and used to adjust the contribution of controls. Different methods for calculating this probability have been proposed (10–13), and estimation of absolute risks has been described in the context of the weighted partial likelihood approach, even in the presence of a matched design (8, 9, 11, 12). In such analysis, matching is broken, cases and controls are weighted with an inverse of their marginal probability of being sampled, and unique individuals are pooled for analysis, keeping only 1 control record for controls who were selected more than once and a case record for any control who later became a case (11).

When competing events preclude the occurrence of the primary event of interest, the situation is more complex. Several approaches for dealing with competing risks in the cohort setting (26–35) and the case-control setting (10, 15, 16, 36) have been proposed. Because of the method of control selection for ProMort, in this paper we focus on the cause-specific hazards approach. When a subject is at risk of having K different events, the cause-specific hazard, ${\mathrm{\lambda }}_k\left(t\right)$, denotes the instantaneous rate of event k in subjects who are still alive at time t and can be defined as

$${\mathrm{\lambda }}_k\left(t\right)=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{P(t\le T<t+\mathrm{\Delta }t,K=k|T\ge t)}{\mathrm{\Delta }t}.$$

The cumulative incidence function (CIF) for the event of interest $k$ (i.e., prostate cancer death), $I_k(t)$, is the probability that a subject will die from the event $k$ at the time $t$, accounting for the fact that he can die from other cause(s) (i.e., death from other causes).

$$\begin{array}{c}{I}_k\left(t\right)=P\left(T\le t,K=k\right)\hfill \\ ={\int }_0^t{\mathrm{\lambda }}_k\left(u\right)\exp \left\{-{\int }_0^u\sum _{k=1}^K{\mathrm{\lambda }}_k\left(v\right)dv\right\}du\\ ={\int }_0^t{\mathrm{\lambda }}_k(u)\prod _{k=1}^K{S}_k\left(u\right)du\hfill \end{array}$$

The CIF depends not only on the cause-specific hazard for the event of interest but also on the cause-specific hazard for the competing event(s) (27, 28).

In this paper, we compare the relative risks (i.e., hazard ratios) and absolute risks (i.e., the CIFs) estimated in ProMort using the inverse probability weighting approach with those estimated in the NPCR. Then we use 2 alternative approaches to estimate the hazard ratios and CIFs. In the first approach, denoted method 1, we augment both the competing-risks cases (i.e., cases who died from other causes) and the corresponding controls according to the incidence density sampling principle (17). In the second approach, denoted method 2, we augment only the competing-risks cases (16). The main idea behind the two methods is the reuse of the controls and the cases, selected for one endpoint as controls in the analysis of another endpoint, with or without a new control selection. These two methods are extensions of the inverse probability weighting approach to nested case-control studies with more than one endpoint, including competing risks (16, 17).

The inverse probability weighting methods have been described in the context of the partial likelihood (8, 9, 11, 12). Partial likelihood is used for parameter estimation in the Cox proportional hazards model where the baseline hazard function does not depend on any parameters and is thus not estimated. Since we are interested in both the hazard ratios and the CIFs, in this paper we use the flexible parametric survival model (Royston-Parmar model) (29) instead of the Cox proportional hazards model. The flexible parametric model uses a restricted cubic splines function of log time to model the baseline hazard function, and its parameters are estimated by maximizing the full likelihood (30). In our analysis, we use the weighted full likelihood instead of the weighted partial likelihood. A detailed description of the step-by-step analysis plan for methods 1 and 2 and a formal definition of the weighted full likelihood are presented in Web Appendix 1 (available at https://academic.oup.com/aje).

We calculated the weights as described by Kim (8) and fitted the flexible parametric model as described by Hinchliffe and Lambert (29). We selected the number of knots (1 internal knot, 2 degrees of freedom) and a suitable scale (proportional hazards) by minimizing the values of the Akaike and Bayes criteria (30). The number and location of the knots, however, are often not critical for a good fit of the model (29, 30). We simultaneously estimated cause-specific hazard ratios and corresponding 95% confidence intervals for death from prostate cancer and death from other causes (30, 31), and we obtained the CIFs by combining the cause-specific hazard estimates (16, 17, 32). Time at risk was calculated from the date of diagnosis of prostate cancer to the date of death or the end of follow-up, whichever came first.

Subject-matter knowledge and data availability were used to identify important predictors of prostate cancer death. Age (in 10-year categories: ≤55.0, 55.1–65.0, 65.1–75.0, or >75.0 years), PSA level (<4.0, 4.0–9.9, or ≥10.0 ng/mL), Gleason score (≤6 or 7), and clinical tumor stage (T1a, T1b, T1c, or T2) at diagnosis were included in the prognostic model. Because the matching was broken, we additionally adjusted for the matching variables (8, 13). To avoid unnecessary loss of power due to the large number of matching hospital strata, we joined all the hospitals in the same county and adjusted for county and year of diagnosis. These analyses were performed in both the full NPCR cohort and ProMort.

To further evaluate the method used for relative and absolute risk estimation in ProMort, we drew 1,500 random nested case-control subsamples of the NPCR cohort using the same selection criteria as those used for ProMort (i.e., all cases and a random sample of matched controls). We calculated the absolute bias in hazard ratios (HRs) for death from prostate cancer and death from other causes on the logarithmic scale as log(HR_NCC) − log(HR_NPCR), where log(HR_NCC) indicates the log(HRs) estimated in the 1,500 nested case-control (NCC) subsamples and log(HR_NPCR) indicates the log(HRs) estimated in the NPCR. We also computed the absolute bias in CIFs of dying from prostate cancer at 5, 10, and 15 years of follow-up. The absolute bias was defined as CIF_NCC − CIF_NPCR, where CIF_NCC indicates CIFs estimated in 1,500 subsamples and CIF_NPCR indicates CIFs estimated in the NPCR. In addition, we computed the coverage probability of the CIF 95% confidence intervals estimated in the 1,500 subsamples at 5, 10, and 15 years of follow-up.

All analyses were conducted in Stata, version 12.1 (StataCorp LLC) and R, version 3.3.3 (Institute for Statistics and Mathematics, Vienna, Austria (http://www.Rproject.org)).

RESULTS

Baseline characteristics of all men with low- or intermediate-risk prostate cancer in the NPCR (n = 57,952) and ProMort (1,710 cases, 1,710 controls) are presented in Table 1. Low- and intermediate-risk prostate cancer patients who had died from prostate cancer/cases were on average older at diagnosis and had more aggressive tumors, including higher proportions of Gleason score 7 and stage T2 tumors and higher mean PSA levels at diagnosis, than men who had not died from prostate cancer/controls. Approximately 24% of the men who died from prostate cancer had been treated with curative intent, as compared with over 50% of men who did not die from prostate cancer.

Table 1.

Baseline Characteristics of Low- and Intermediate-Risk Prostate Cancer Patients in the National Prostate Cancer Register and of Cases and Controls in the ProMort Study, Sweden, 1998–2011

Variable	NPCR				ProMort
	Died From PC (n = 1,735)		Did Not Die From PC (n = 56,217)		Cases (n = 1,710)		Controls (n = 1,710)
	No.	%	No.	%	No.	%	No.	%
Year of diagnosis
1998–2000	591	34.06	5,377	9.56	578	33.80	578	33.80
2001–2004	751	43.29	14,339	25.51	741	43.33	741	43.33
2005–2008	336	19.37	19,239	34.22	334	19.53	334	19.53
2009–2011	57	3.28	17,262	30.71	57	3.33	57	3.33
Age at diagnosis, yearsa	73.75 (7.75)		67.21 (7.99)		73.73 (7.75)		67.62 (7.76)
Age group at diagnosis, years
≤55.0	29	1.67	3,168	5.64	29	1.70	80	4.68
55.1–65.0	205	11.82	19,731	35.10	200	11.70	568	33.22
65.1–75.0	699	40.29	23,725	42.20	690	40.35	756	44.21
>75.0	802	46.22	9,593	17.06	791	46.26	306	17.89
Gleason score
≤6	948	54.64	39,114	69.58	927	54.21	1,328	77.66
7	787	45.36	17,103	30.42	783	45.79	382	22.34
Tumor stage
T1	2	0.12	58	0.10	2	0.12	2	0.12
T1a	76	4.38	2,829	5.03	75	4.39	119	6.96
T1b	94	5.42	1,366	2.43	92	5.38	51	2.98
T1c	534	30.78	33,104	58.89	521	30.47	854	49.94
T2	1,029	59.31	18,860	33.55	1,020	59.65	684	40.00
PSA level, ng/mLa	10.36 (4.56)		7.99 (4.08)		10.36 (4.58)		8.77 (4.29)
PSA category, ng/mL
<4.0	116	6.69	7,239	12.88	116	6.78	176	10.29
4.0–9.9	754	43.46	33,659	59.87	740	43.27	933	54.56
≥10.0	865	49.86	15,319	27.25	854	49.94	601	35.15
Follow-up time, yearsb	5.87 (3.58–8.57)		5.55 (3.08–8.35)		5.86 (3.59–8.51)		9.86 (7.56–12.09)
Cause of censoringc,d
Death
Prostate cancer	1,735	100.00			1,710	100.00	80	4.68
Other causes			7,968	14.17			262	15.32
Administrativee			48,249	85.83			1,368	80.00
Initial treatment
Conservative	798	46.80	20,804	37.87	785	46.70	648	38.53
Curative	412	24.16	29,653	53.98	407	24.21	849	50.48
Noncurative	495	29.03	4,476	8.15	489	29.09	185	11.00
Missing data	30		1,284		29		28

Abbreviations: NPCR, National Prostate Cancer Register; PC, prostate cancer; ProMort, Prognostic Factors for Mortality in Prostate Cancer; PSA, prostate-specific antigen.

^a Values are expressed as mean (standard deviation).

^b Values are expressed as median (25th–75th percentile range).

^c No right-censoring was assumed in the study because of the very low percentage (0.23%) of loss to follow-up.

^d For ProMort controls, censoring refers to follow-up after sampling into the ProMort study.

^e Administrative censoring occurred on December 31, 2012.

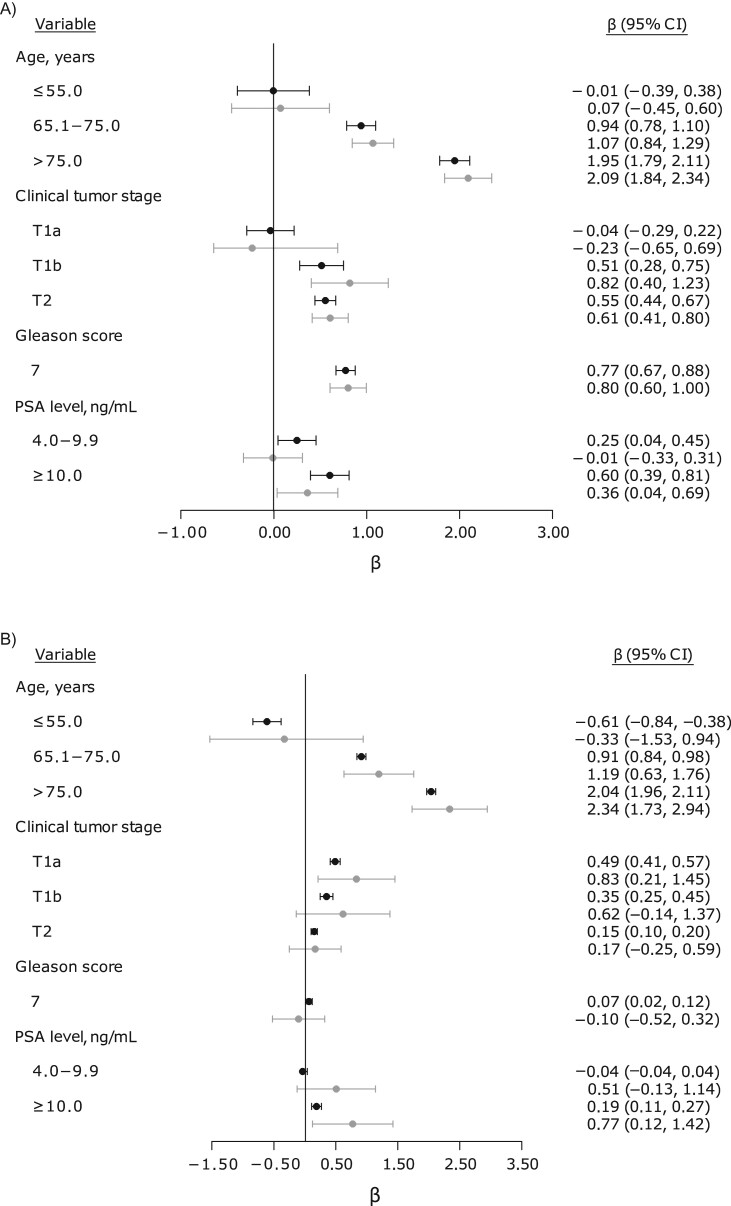
Results from the univariable analyses are presented in Table 2. Age, PSA level at diagnosis, Gleason score, and clinical tumor stage were associated with the hazard of dying from prostate cancer, with comparable point estimates in the NPCR and ProMort. Likewise, in the multivariable analyses, the risk of dying from prostate cancer increased with higher age, PSA level, Gleason score, and clinical tumor stage (Table 2). The point estimates in the NPCR and ProMort were qualitatively similar, though in ProMort they were slightly overestimated for age and clinical tumor stage and underestimated for PSA level (Figure 1A). However, the mean absolute bias in the log(HRs) estimated in the 1,500 subsamples was generally close to zero for all covariates (Web Table 1). The point estimates from the two alternative approaches were also comparable to the NPCR estimates (Web Figure 1). The log(HRs) for death from other causes were generally biased for ProMort, with wide 95% confidence intervals (Figure 1B). The mean absolute bias in the log(HRs) for other causes of death estimated in the 1,500 subsamples was close to zero for clinical tumor stage, Gleason score, and PSA level but not for age (−3.813, −0.118, and 0.118 for ages ≤55.0 years, 65.1–75.0 years, and >75.0 years, respectively) (Web Table 2). Contrary to the other covariates, the distribution of log(HRs) for the age ≤55.0 years category was not normal. Few subjects in the age ≤55.0 years category died from other causes, and when no cases who died from other causes were sampled, the estimated log(HRs) were extreme and unreliable. The log(HRs) for death from other causes in the NPCR were generally comparable with those derived using methods 1 and 2 (Web Figure 1).

Table 2.

Hazard Ratios^a for Death From Prostate Cancer Among Low- and Intermediate-Risk Prostate Cancer Patients in the National Prostate Cancer Register and the ProMort Study, Sweden, 1998–2011

Variable	NPCR				ProMortb
	Univariable		Multivariable		Univariable		Multivariable
	HRc	95% CI	HRd	95% CI	HRc	95% CI	HRd	95% CI
Age group, years
≤55.0	0.92	0.62, 1.36	0.99	0.67, 1.47	1.03	0.64, 1.66	1.07	0.63, 1.82
55.1–65.0	1.00	Referent	1.00	Referent	1.00	Referent	1.00	Referent
65.1–75.0	2.87	2.46, 3.36	2.56	2.19, 2.99	3.12	2.53, 3.86	2.90	2.32, 3.63
>75.0	9.15	7.84, 10.68	7.02	5.97, 8.25	10.34	8.23, 13.00	8.06	6.26, 10.38
PSA level, ng/mL
<4.0	1.00	Referent	1.00	Referent	1.00	Referent	1.00	Referent
4.0–9.9	1.40	1.15, 1.70	1.28	1.05, 1.57	1.22	0.92, 1.63	0.99	0.72, 1.35
≥10.0	2.91	2.39, 3.54	1.83	1.48, 2.25	2.60	1.94, 3.48	1.43	1.03, 1.98
Gleason score
≤6	1.00	Referent	1.00	Referent	1.00	Referent	1.00	Referent
7	2.99	2.71, 3.29	2.17	1.95, 2.40	3.04	2.56, 3.59	2.23	1.84, 2.72
Tumor stagee
T1a	1.21	0.95, 1.55	0.96	0.75, 1.24	1.40	1.00, 1.95	0.79	0.52, 1.20
T1b	2.87	2.29, 3.60	1.67	1.32, 2.12	3.84	2.59, 5.70	2.25	1.49, 3.41
T1c	1.00	Referent	1.00	Referent	1.00	Referent	1.00	Referent
T2	2.61	2.35, 2.91	1.74	1.56, 1.95	3.00	2.54, 3.54	1.83	1.51, 2.23

Abbreviations: CI, confidence interval; HR, hazard ratio; NPCR, National Prostate Cancer Register; ProMort, Prognostic Factors for Mortality in Prostate Cancer; PSA, prostate-specific antigen.

^a Univariable and multivariable flexible parametric proportional hazards models.

^b Duplicate observations (n = 150) were excluded from the analysis.

^c Adjusted for the matching variables (year and county of diagnosis) but not for any other predictor of prostate cancer mortality.

^d Adjusted for the matching variables (year and county of diagnosis).

^e Subjects with a nonsubclassified T1 stage (NPCR: n = 60 (2 cases and 58 controls); ProMort: n = 3 (2 cases and 1 control)) were excluded from the analysis.

Figure 1.

Cause-specific log hazard ratios for the risks of dying from prostate cancer (A) and other causes (B) in the National Prostate Cancer Register (NPCR) and the Prognostic Factors for Mortality in Prostate Cancer (ProMort) study, Sweden, 1998–2011. Reference categories (age 55.1–65.0 years, prostate-specific antigen (PSA) level <4.0 ng/mL, Gleason score ≤6, and clinical tumor stage T1c) and estimates for the matching variables (year and county of diagnosis) are not shown in the figure. Point estimates and 95% confidence intervals (CIs; bars) for the NPCR are presented in black, and those for ProMort are presented in gray.

Web Figure 2 shows CIFs and 95% confidence intervals for prostate cancer mortality for different combinations of risk factors at 5, 10, and 15 years from diagnosis. Overall, the cumulative incidences of prostate cancer death 5, 10, and 15 years from diagnosis were similar in ProMort and the NPCR. However, the bias in the ProMort estimates increased with age and was especially notable at age >75.0 years (Web Figure 2). The mean absolute bias in the CIF estimates across the 1,500 subsamples and across all combinations of covariates was less than 0.008 at all follow-up times (Web Table 3). However, it is worth noting that the mean absolute bias for age >75.0 years was 0.011, 0.025, and 0.025 at 5, 10, and 15 years of follow-up, respectively, while it was less than 0.004 across all other combinations of covariates at all follow-up times. The actual coverage probability averaged over all combinations of covariates was generally conservative at over 97% at all follow-up times (Web Table 3). However, for some combinations of covariates with the age group >75.0 years, the coverage probability was less than the nominal value. CIFs estimated using the two alternative approaches, especially from method 1, were consistently similar to the estimates derived from the NPCR (Web Figure 3).

DISCUSSION

Novel prognostic markers of lethal prostate cancer are needed to aid risk assessment and decision-making for low- and intermediate-risk prostate cancer patients. The aim of ProMort, a large case-control study nested within the well-annotated, population-based NPCR cohort, is to assess new molecular markers of lethal prostate cancer and develop a clinically useful model predicting prostate cancer mortality. ProMort cases and controls were selected using standard incidence-density sampling with the aim of estimating the relative risk of dying from prostate cancer. In this study, we have demonstrated that the relative risks of prostate cancer death estimated in ProMort are comparable to those in the full NPCR cohort. The estimates of relative risks of dying from other causes, on the other hand, are biased, and this introduces some bias in the absolute risks estimated in the competing-risks setting. We have also shown that augmenting competing-risks cases, or both the cases and the controls, reduces the bias in the relative risks of dying from other causes and thus also the bias in the absolute risks of dying from prostate cancer estimated in a competing-risks setting.

With 57,952 study participants and up to 15 years of follow-up, the NPCR comprises, to the best of our knowledge, the largest cohort of men with low- or intermediate-risk prostate cancer with detailed clinicopathological data in the world. Even though death from prostate cancer among low- and intermediate-risk prostate cancer patients is a rare event, our sample size was sufficient to study prostate cancer-specific mortality as the main outcome. One of the limitations of the NPCR is that all data are collected through routine clinical work, and no central histopathological review is conducted (20). Furthermore, information on additional histopathological characteristics potentially useful for predicting lethal prostate cancer, such as primary and secondary Gleason grade pattern, biopsy tumor length (mm), or percentage of biopsy core positivity, is available in the NPCR only for the subset of men diagnosed with prostate cancer from 2007 onwards (20). However, through digitalized diagnostic slide review, we aim not only to obtain information on centrally reassigned Gleason score and minimize bias due to changes in the Gleason scoring system over time and interpathologist variability but also to obtain information on these additional histopathological characteristics for all cases and controls included in ProMort.

Development of prognostic models and prediction of the absolute risk of a disease are traditionally carried out in cohort studies. However, in many chronic diseases, the outcome of interest is rare to the extent that cohort studies become unfeasible, and the nested case-control design may be a viable and cost-effective alternative. Methods for unbiased and efficient estimation of absolute risks in nested case-control studies were developed in the late 1990s (10, 12). However, even though recent studies have confirmed their feasibility (8, 9, 11, 13), these methods are still underused in clinical epidemiologic practice. In this study, we analyzed a real-life nested case-control data set using the inverse probability weighting method proposed by Samuelsen (12), which is easily implemented in standard statistical software (Stata code is provided in Web Appendix 2). The absolute risks estimated using the inverse probability weighting method are shown to be precise in the matched design, even when fine matching is used (11). Furthermore, it has been shown that controls can be reused to make valid inferences on secondary, nonexclusive outcomes (33, 34), and extensions to the competing-risks setting have been developed (15, 16). It is important to note that we did not explore other approaches for estimating absolute risks in the competing-risks setting, such as dealing with a nested case-control study as a missing-data problem (17) or using the approach based on subdistribution hazards (35, 36). We preferred to model the cause-specific hazards because their interpretation is easier when compared with the subdistribution hazards, and proportionality assumed on the hazard scale is mathematically not satisfied on the subdistribution hazard scale (37).

The ProMort study was designed to provide unbiased estimates of the cause-specific hazard ratios for dying from prostate cancer. We showed that the hazard ratios estimated in ProMort were comparable with the estimates derived from the full cohort (NPCR) and that the absolute bias over 1,500 subsamples of the NPCR cohort was close to zero (Web Table 1). On the other hand, the hazard ratios for dying from other causes estimated in ProMort were biased. The absolute bias over 1,500 subsamples was close to zero for PSA, clinical tumor stage, and Gleason score, but it was larger for age, especially age ≤55.0 years (Web Table 2). Because CIF estimates for prostate cancer mortality depend on both cause-specific hazards, the CIFs estimated in ProMort, although generally similar to CIFs estimated in the NPCR, show some bias, especially for age >75.0 years. Similarly, the absolute bias in CIFs over 1,500 subsamples of the NPCR cohort and across all covariate combinations is close to zero 5, 10, and 15 years after diagnosis, and average coverage probability is conservative at all follow-up times. However, for age >75.0 years, the bias in CIF estimates increases and the coverage probability decreases. Alternative approaches with augmented competing-risks cases (16), especially with augmented competing-risks cases and controls (17), resulted in less biased CIF estimates. Therefore, for ProMort, where cases and controls were sampled to gain efficiency, we decided to use a 2-step approach. First, we will use the current data to identify promising molecular markers, and then, if necessary, we will replicate the CIF estimates under the method 1 or method 2 sampling scheme.

To the best of our knowledge, ProMort is the world’s largest series of lethal low- and intermediate-risk prostate cancer patients and constitutes a valid setting for identification of clinically relevant prognostic biomarkers for men with low- and intermediate-risk prostate cancer. By comparing the prognostic models developed in the case-control data with those developed in the underlying cohort, we have demonstrated that accurate estimates of the relative risks of dying from prostate cancer can be made in ProMort. However, in the competing-risks setting, nested case-control studies with augmented competing-risks cases and controls provide more valid absolute risk estimates.

Abbreviations

CIF

cumulative incidence function

HR

hazard ratio

NPCR

National Prostate Cancer Register

ProMort

Prognostic Factors for Mortality in Prostate Cancer

PSA

prostate-specific antigen