Amplifying the Noise: The Dangers of Post Hoc Power Analyses

Abstract

Small sample sizes decrease statistical power, which is a study’s ability to detect a treatment effect when there is one to be detected. A power threshold of 80% is commonly used, indicating that statistical significance would be expected four of five times if the treatment effect is large enough to be clinically meaningful. This threshold may be difficult to achieve in surgical science, where practical limitations such as research budgets or rare conditions may make large sample sizes infeasible. Several researchers have used “post hoc” power calculations with observed effect sizes to demonstrate that studies are often underpowered and use this as evidence to advocate for lower power thresholds in surgical science. In this short commentary, we explain why post hoc power calculations are inappropriate and cannot differentiate between statistical noise and clinically meaningful effects. We use simulation analysis to demonstrate that lower power thresholds increase the risk of a false-positive result and suggest logical alternatives such as the use of larger p-values for hypothesis testing or qualitative research methods.

Bababekov et al. (2019) argue that commonly accepted guidelines for statistical power are inappropriate for surgical studies.¹ As evidence, the authors searched for randomized controlled trials and observational studies with human participants published in three top surgery journals from 2012 to 2016. They then conducted a post hoc power analysis, excluding studies which found significant effects or missing needed information. Not surprisingly, Bababekov et al. found these studies to be grossly underpowered. We believe the authors have mischaracterized the role of power analysis in study design. In this letter, we hope to correct the record and highlight some critical issues when relying on results from post hoc power analyses.

First, it is important to understand why a power analysis is conducted prospectively. Before a study begins, researchers should determine three pieces of information:

1. The minimum effect size that could be considered clinically meaningful. For instance, a surgical intervention which reduces the likelihood of a hospital readmission within 30 dby 0.001% is not clinically meaningful regardless of statistical significance.²

2. The significance level that we will use (e.g., α = 0.10, 0.05, 0.01, and so on). This selection may be based on a variety of factors such as expected sample size, the number of statistical tests conducted, or what is common. The goal here is to minimize type I error: rejection of a true null hypothesis, also known as a “false positive” finding.³

3. The sample size required to reliably find the effect size significant at the selected significance level. Here we would like to minimize the probability of a type II error: failure to reject a false null hypothesis, also known as a ‘false negative’ finding. Naturally, we would like the power to equal 1.0 whenever the null hypothesis is false, but this is infeasible while keeping our significance level small.⁴

The third step often involves a formal power analysis, where the researcher uses simulation analysis to estimate the required sample size. A power threshold of 80% is commonly used, indicating that if the minimum effect size is observed then our statistical test would find that effect significant (a “true positive”) four out of five times. We expect to fail to reject the null hypothesis (a false negative) the remaining one out of five times.

Bababekov et al. are correct when they note that the common power threshold of 80% is arbitrary.¹ This is not unlike the famous (or infamous) P-value threshold of 0.05, which was first proposed by Ronald Fisher in 1925 and has since become standard practice.⁵ However, the authors made three fundamental errors when arguing to abandon the 80% power threshold.

First, encouraging more underpowered studies to proceed would simply increase the number of studies with nonsignificant findings. Alternatively, one could instead select a higher significance level (e.g., α = 0.10) when limited by small sample sizes. If sample sizes are sufficiently small, researchers could instead rely on descriptive statistics and qualitative comparisons without hypothesis testing (e.g., case reports). If the potential implications of the research on clinical practice are substantial and large sample sizes are infeasible, surgical journals could still consider these studies for publication.

Second, the authors’ arguments are tautological; if a study’s results are significant, then its findings are valuable, but if the study’s results are insignificant, then the study was simply underpowered and the findings are still valuable. Although it is true that clinically meaningful but statistically nonsignificant results may occur in underpowered studies,⁶ the authors do not identify clinically meaningful thresholds to make this determination. Moreover, calculating post hoc power with observed effect sizes is simply a transformation of the P-value. The relationship between post hoc power and P-values is necessarily an inverse relationship.⁴ This guarantees that calculating post hoc power with nonsignificant effect sizes will lead one to assert that the studies were “underpowered.”

Third, the authors misunderstand what statistical power refers to. It is a statement about the population being sampled. This is why statistical power is commonly calculated before conducting a study. Conducting a post hoc power calculation with observed effect sizes necessarily assumes that the effect size identified in the study is the true effect size in the population.

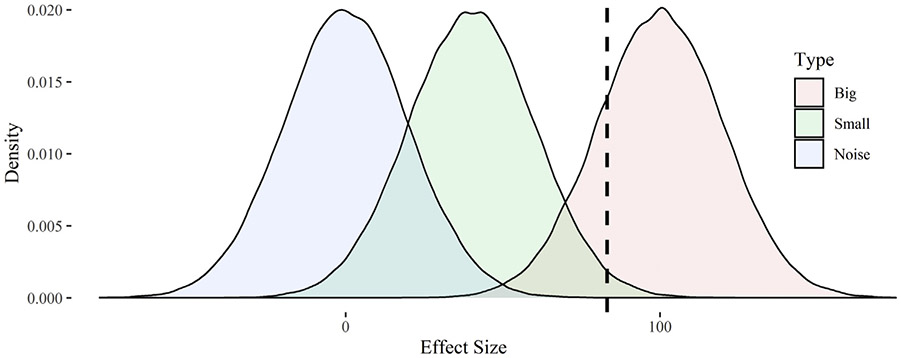
To illustrate the effect of these errors, we propose a stylized simulation. Let us assume the minimum clinically meaningful change in some surgical outcome X is 100 units. For simplicity, let us also assume there are three types of surgical interventions with varying effects on outcomes and these effects are measured with some error: those with clinically meaningful effects (μ = 100, σ = 20), those with less than clinically meaningful effects (μ = 40, σ = 20), and those having no effect (μ = 0, σ = 20). We simulated 100,000 interventions for each type and created density plots for their estimated effects (see Figure). The area to the left of dashed line represents the rejection region at 80% power; 20% of studies with larger effects would fail to reject the null hypothesis, as would approximately 98.5% of studies with smaller effects and 99.994% of studies with no effect. If we calculate post hoc power for these insignificant studies, we will find approximately 38.6% power.

Fig –

Density plots for the effects of simulated surgical interventions. Notes: The chart displays densities for the effects of simulated surgical interventions with big effects (μ = 100, σ = 20), small effects (μ = 100, σ = 20), or an ineffective intervention with noise-only (μ = 0, σ = 20). The dashed line represents the rejection region under 80% statistical power; observed effects to the right of this line are expected to be statistically significant.

When Bababekov et al. calculated post hoc power, their data included all three kinds of studies (excluding those with significant findings) and they found a median power of 16%.¹ This lack of statistical power is not unwanted, it is by design. We want to find clinically meaningful effects to be statistically significant, but not effects that are too small to be clinically meaningful or which are simply the result of noise in our effect estimates. Shifting the rejection region to the left (e.g., by accepting studies with higher P-values than 0.05) may result in more true positives and reduce type II error, but we would also expect to find more false positives and increase our type I error.

In conclusion, although we understand the challenges of small sample sizes in surgical science, we believe there are other more logical alternatives than abandonment of standard thresholds for prospective power analyses. These include selection of a higher significance level or omitting formal hypothesis testing. Analytical approaches under the latter option could rely instead on descriptive statistics or case studies. Researchers who calculate post hoc power analyses should be aware of the dangers in doing so; by “empowering the underpowered study”, they may simply be amplifying the noise.