Improved generalized raking estimators to address dependent covariate and failure-time outcome error

Abstract

Biomedical studies that use electronic health records (EHR) data for inference are often subject to bias due to measurement error. The measurement error present in EHR data is typically complex, consisting of errors of unknown functional form in covariates and the outcome, which can be dependent. To address the bias resulting from such errors, generalized raking has recently been proposed as a robust method that yields consistent estimates without the need to model the error structure. We provide rationale for why these previously proposed raking estimators can be expected to be inefficient in failure-time outcome settings involving misclassification of the event indicator. We propose raking estimators that utilize multiple imputation, to impute either the target variables or auxiliary variables, to improve the efficiency. We also consider outcome-dependent sampling designs and investigate their impact on the efficiency of the raking estimators, either with or without multiple imputation. We present an extensive numerical study to examine the performance of the proposed estimators across various measurement error settings. We then apply the proposed methods to our motivating setting, in which we seek to analyze HIV outcomes in an observational cohort with EHR data from the Vanderbilt Comprehensive Care Clinic.

1 |. INTRODUCTION

Modern biomedical studies are increasingly using nontraditional data sources such as electronic health records (EHR), which are not primarily collected for research purposes. These data sources have enormous potential to advance research of population-level health outcomes due to their large sample sizes and low cost compared to prospectively collected data (Beresniak et al., 2016; Hillestad et al., 2005; Jensen et al., 2012; van Staa et al., 2014). EHR data, however, have also been shown to be vulnerable to measurement error (Botsis et al., 2010; Duda et al., 2012; Floyd et al., 2012; Kiragga et al., 2011; Weiskopf & Weng, 2013). If such errors are not accounted for in the data analysis, estimated effects of interest can be biased, which in turn can mislead researchers and potentially harm patients.

The measurement error found in EHR data can be complex, consisting of errors in both an outcome and covariates of interest, which in turn can be dependent. This complexity stems from the fact that variables of interest are often not directly observed in EHR data; instead, they need to be derived from other existing variables in the data. For example, HIV/AIDS studies might be interested in evaluating the association between a lab value at the date of antiretroviral therapy (ART) initiation and the time from ART initiation to some event of interest. Both the exposure and outcome in the above example depend on the ART initiation date; thus, if the initiation date is incorrect, the outcome and covariate in the analysis will both contain measurement error that is dependent (in addition to potential misclassification of the event).

Covariate measurement error, particularly classical measurement error or extensions of it, has been well studied in the literature, and methods to correct the bias resulting from such error have been well developed (Carroll et al., 2006). Although less attention has been given to errors in an outcome of interest, there has been some recent work looking at errors in binary outcomes (Magder & Hughes, 1997; Edwards et al., 2013; Wang et al., 2016), discrete time-to-event outcomes (Hunsberger et al., 2010; Magaret, 2008; Meier et al., 2003), and to a lesser extent, continuous time-to-event outcomes (Gravel et al., 2018; Oh et al., 2018). There has been even less work to understand the impact of errors in both covariates and a time-to-event outcome, but it has recently been shown that ignoring such errors can cause severe bias in estimates of effects of interest (Boe et al., 2020; Giganti et al., 2020; Oh et al., 2019).

In some cases, errors can be handled by retrospectively reviewing records and correcting all data points; however in most scenarios, this will be too time consuming and expensive to feasibly carry out. Instead, one can use a two-phase design, which involves reviewing and correcting only a subset of the records, to obtain consistent estimates of effects of interest. There have been some methods proposed recently that employ this framework to incorporate the large error-prone data with the smaller validated data to improve statistical inference, including regression calibration (Boe et al., 2020; Oh et al., 2019), multiple imputation (Giganti et al., 2020), and generalized raking (Oh et al., 2019). Generalized raking in particular has been shown to be robust to the structure of the measurement error, which can be quite complex for EHR data (Han et al., 2019; Oh et al., 2019). Specifically, generalized raking estimators use the error-prone data as auxiliary variables to improve the efficiency of the analysis of the validated data without having to model the error structure, making them appealing for EHR settings where the true structure is likely unknown. Thus, we focus on the generalized raking methods in this article.

In the measurement error setting, an error-prone version of the target variable is generally available on all subjects at phase one, which can be used to construct auxiliary variables for raking. While generalized raking estimators are robust, their statistical efficiency is dependent on the quality of the raking variables. Specifically, the efficiency of raking estimators depends on the (linear) correlation between the auxiliary variables and the target variable (Deville & Särndal, 1992). We show that for a time-to-event outcome, where the event indicator is subject to misclassification, this linear correlation is generally low and results in inefficient estimates. In this article, we propose generalized raking estimators that utilize multiple imputation to construct improved auxiliary variables using imputed values of either the error-prone data or direct imputation of the auxiliary variables themselves to improve the linear correlation and, ultimately, the efficiency of the raking estimator.

Our contributions in this article are twofold. First, we develop generalized raking estimators that utilize multiple imputation to construct improved auxiliary variables in the presence of event indicator misclassification. Second, we evaluate the performance of various sampling designs with respect to their impact on the efficiency of the standard or proposed raking estimators. The rest of the paper proceeds as follows. We present our time-to-event outcome model and measurement error framework, and we introduce generalized raking estimators in Section 2. Section 3 discusses how the auxiliary variables relate to the efficiency of raking estimators and the need for their improvement in time-to-event settings with event indicator misclassification. Section 4 develops the proposed generalized raking estimators using multiple imputation. Section 5 compares the relative performance of the proposed estimators with simulation studies for various parameter settings and study designs. In Section 6, we apply our methods to evaluate HIV outcomes in an HIV cohort with error-prone EHR data. We conclude with a discussion in Section 7.

2 |. MODEL SETUP AND DESIGN FRAMEWORK

This section introduces the design and estimation framework, including the time-to-event outcome model, measurement error framework, and generalized raking methods used to estimate parameters of interest.

2.1 |. Time-to-event outcome model

Let T_i and C_i be the failure time and right censoring time, respectively, for subjects i = 1, …, N on a finite follow-up time interval, [0, τ]. Define U_i = min(T_i, C_i ) and the corresponding failure indicator ${\text{Δ}}_i=I\left(T_i\le C_i\right)$. Let $Y_i(t)=I\left(U_i\ge t\right)$ and $N_i(t)=I\left(U_i\le t,{\text{Δ}}_i=1\right)$ denote the at-risk indicator and counting process for observed events, respectively. Let X_i be a p-dimensional vector of discrete and/or continuous covariates that are measured with error and Z_i a q-dimensional vector of precisely measured discrete and/or continuous covariates that may be correlated with X_i. We assume C_i is independent of T_i given (X_i, Z_i ) and that (T_i, C_i, X_i, Z_i ) are independently and identically distributed.

In this paper, we consider estimating the parameters of a Cox proportional hazards model. Let the hazard rate for subject i at time t be given by ${\lambda }_i(t)={\lambda }_0(t)\exp \left({\beta }_X^{\prime }{X}_i+{\beta }_Z^{\prime }{Z}_i\right)$, where ${\lambda }_0(t)$ is an unspecified baseline hazard function. Then to estimate $\beta =\left({\beta }_X,{\beta }_Z\right)$, we solve the partial likelihood score equation

$$\sum _{i=1}^N{\int }_0^{\tau }\left\{{\left\{X_i,Z_i\right\}}^{\prime }-\frac{\sum _{j=1}^N{Y}_j\left(t\right){\left\{X_j,Z_j\right\}}^{\prime }\exp \left({\beta }_X^{\prime }{X}_j+{\beta }_Z^{\prime }{Z}_j\right)}{\sum _{j=1}^N{Y}_j\left(t\right)\exp \left({\beta }_X^{\prime }{X}_j+{\beta }_Z^{\prime }{Z}_j\right)}\right\}d{N}_i\left(t\right)=0.$$ (1)

2.1.1 |. Error framework

Instead of observing (X, Z, U, Δ), we observe (X^⋆, Z, U^⋆, Δ^⋆), where X^⋆, U^⋆, and Δ^⋆ are the error-prone versions of X, U, and Δ, respectively. We do not impose any assumptions on the structure of the measurement error except that the error must have finite variance. In addition, we allow any of the errors to be correlated.

2.2 |. Two-phase design

We consider a retrospective two-phase design where at phase one, a set of possibly error-prone covariates and outcome information is collected on a large group of subjects. At phase two, the large cohort is augmented by selecting a subset of the subjects (n < N) to be validated, that is, to have error-free covariates and outcome information measured. As a result, the phase two data are often referred to as the validation subset. Since the validation subset is selected retrospectively, the sampling probabilities are known. This type of sampling strategy accommodates both fixed subsample sizes (e.g., simple random sampling) as well as more complex designs with random subsample sizes (e.g., case-cohort). Specifically, let R_i be the indicator for whether subject i = 1, …, N is selected to be in the validation subset with known sampling probability $0<{\pi }_i\le 1$. Then the observed data are given by $\left(X_i^{\star },Z_i,U_i^{\star },{\text{Δ}}_i^{\star }\right)$ for $R_i=0$ and $\left(X_i^{\star },X_i,Z_i,U_i^{\star },U_i,{\text{Δ}}_i^{\star },{\text{Δ}}_i\right)$ for $R_i=1$.

2.3 |. Generalized raking

To estimate parameters in the two-phase design framework, we use generalized raking, a design-based estimator that combines the error-prone phase one data with the error-free phase two data to obtain more efficient estimates that take advantage of all the measured data. Let β₀ denote the parameter defined by the population-estimating equations ${\sum }_{i=1}^N{\psi }_i\left({\beta }_0\right)=0$. One classical estimator for two-phase designs is the Horvitz-Thompson (HT) estimator, ${\widehat{\beta }}_{\text{HT}}$, which is defined as the solution to ${\sum }_{i=1}^N\frac{R_i}{{\pi }_i}{\psi }_i(\beta )=0$. Under suitable regularity conditions, ${\widehat{\beta }}_{\text{HT}}$ is a consistent estimator of ${\beta }_0$; however, it has been shown to be inefficient due to not using all of the available data at phase one (Robins et al., 1994). Let A_i denote a vector of auxiliary variables that are available for all N phase one subjects and correlated with the phase two data. Then generalized raking estimators modify the HT estimator design weights to new weights that incorporate the auxiliary variables such that ${\sum }_{i=1}^N{A}_i$, the known population total of auxiliary variables, is exactly estimated by the phase 2 subset. However, the new weights are constructed so that they are as close as possible to the HT weights while still satisfying the constraint. Specifically, for some distance measure d(.,.), the objective can be written as

$$\text{ minimize }\sum _{i=1}^N{R}_{i}d\left(\frac{g_i}{{\pi }_i},\frac{1}{{\pi }_i}\right)\text{ subject to }\sum _{i=1}^N{A}_i=\sum _{i=1}^N{R}_i\frac{g_i}{{\pi }_i}{A}_i,$$

where $\frac{g_i}{{\pi }_i}$ are the raking weights that can be solved for using Lagrange multipliers (Deville & Särndal, 1992). Note that the constraints above are known as the calibration equations. Therefore, the generalized raking estimator is defined by the solution to

$$\sum _{i=1}^N{R}_i\frac{g_i}{{\pi }_i}{\psi }_i(\beta )=0.$$ (2)

Under suitable regularity conditions and an asymptotic framework where n tends to infinity with N (Isaki & Fuller, 1982), the solution to (2) has been shown to be a $\sqrt{N}$ consistent and asymptotically normal estimator of ${\beta }_0$ (Saegusa & Wellner, 2013). When β₀ are the regression parameters from a correctly specified Cox proportional hazards model, ${\psi }_i(\beta )=\psi \left(X_i,Z_i,U_i,{\text{Δ}}_i;\beta \right)$ is the Cox partial score equation (1) and the distance measure $d(a,b)=a\log (a/b)-a+b$ is used. Let λ denote a vector of Lagrange multipliers. Then solving the constrained minimization problem yields $g_i=\exp \left({\widehat{\lambda }}^{\prime }{A}_i\right)$, where $\widehat{\lambda }={\widehat{B}}^{-1}\left({\sum }_{i=1}^N\frac{R_i}{{\pi }_i}{A}_i-{\sum }_{i=1}^N{A}_i\right)+O_p\left(n^{-1}\right)$ and $\widehat{B}={\sum }_{i=1}^N\frac{R_i}{{\pi }_i}{A}_i^{\prime }{A}_i$ (Deville & Särndal, 1992).

3 |. CONSTRUCTION OF BETTER AUXILIARY VARIABLES

To quantify the gain in efficiency of raking estimators compared to the HT estimator, it is useful to consider the calibration equations, which constrain the raking weights to exactly estimate the known population total of the auxiliary variables. Deville and Särndal (1992) argued that “weights that perform well for the auxiliary variable also should perform well for the study variable” to provide support for such a construction. Note that study variable in this context represents the variable that is only observed in the phase two sample. Furthermore, there is an implicit assumption underlying this argument; namely that there exists a linear relationship between the variable of interest and the auxiliary variables of the form $S_i={\gamma }_0+{\gamma }_1{A}_i+{ϵ}_i$, where S_i and A_i are the variable of interest and auxiliary variables, respectively, and ${ϵ}_i$ is a random error. Thus, the efficiency gain of raking estimators depends directly on the (linear) correlation between the variable of interest and auxiliary variables. (For more details, see Lumley et al., 2011). The true relationship between S_i and A_i determines how to best use the auxiliary variables, which we hope to capture with the working model. If the true relationship between the study variable and auxiliary variables is nonlinear, standard generalized raking could be quite inefficient.

Assessing whether a linear working model is appropriate requires precise definitions for the variable of interest and auxiliary variables. In the setting of estimating regression parameters, many common estimators can be written as a population mean of influence function (or efficient influence function for semiparametric models) terms, ${\tilde{\mathcal{l}}}_0\left(X_i,Z_i,U_i,{\text{Δ}}_i\right)$, using their asymptotically linear expansion. Thus, ${\tilde{\mathcal{l}}}_0\left(X_i,Z_i,U_i,{\text{Δ}}_i\right)$ is considered to be the variable of interest, and the auxiliary variables should be constructed to be highly correlated with the influence function contributions. The optimal auxiliary variable was shown by Breslow et al. (2009) to be $\text{E}\left({\tilde{\mathcal{l}}}_0\left(X_i,Z_i,U_i,{\text{Δ}}_i\right)\mid V\right)$, where $V=\left(X^{\star },Z,U^{\star },{\text{Δ}}^{\star }\right)$, which is unavailable in practice. Oh et al. (2019), however, proposed an approximation, ${\tilde{\mathcal{l}}}_0\left(X_i^{\star },Z_i,U_i^{\star },{\text{Δ}}_i^{\star }\right)$, as the auxiliary variable, motivated by settings involving correlated measurement error in covariates and a censored event-time only.

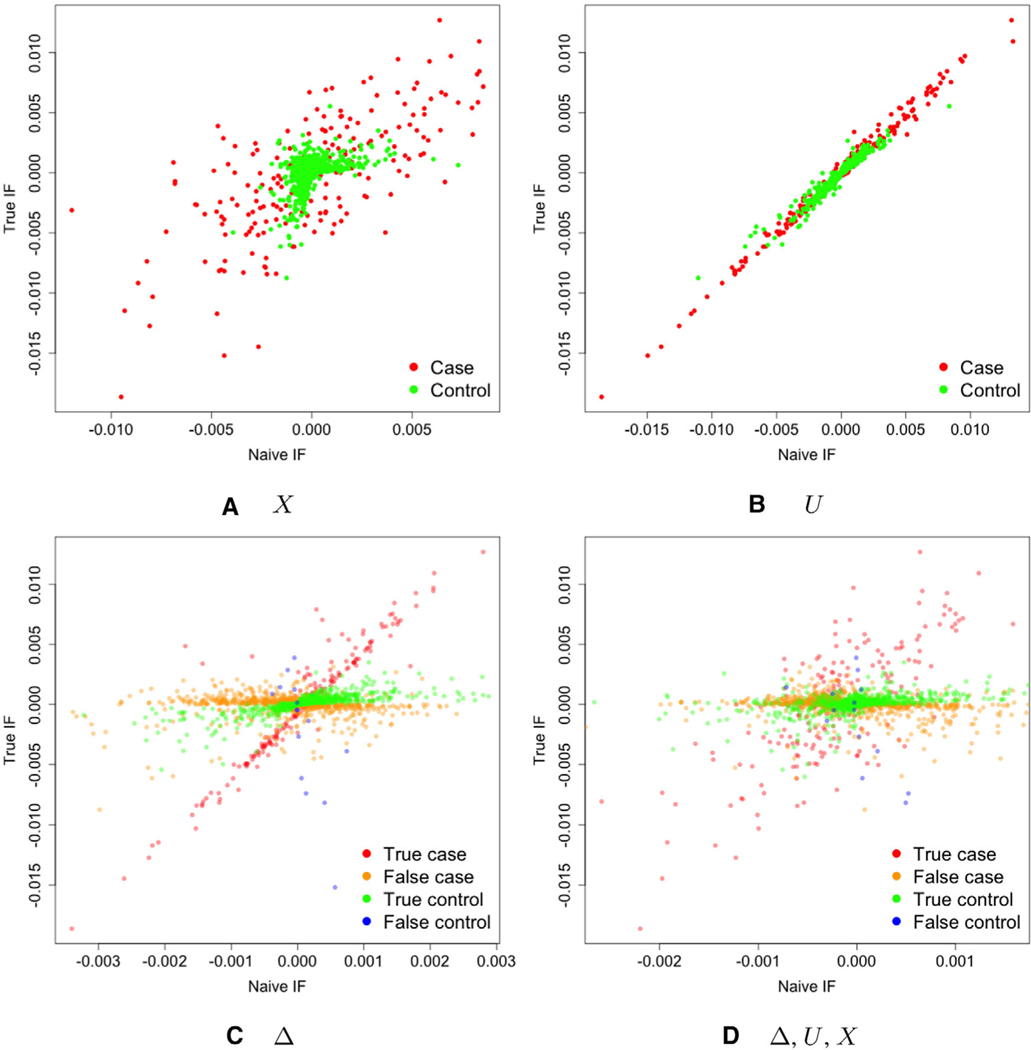
Thus, the linear working model underlying the estimator from Oh et al. (2019) is given by ${\tilde{\mathcal{l}}}_0\left(X_i,Z_i,U_i,{\text{Δ}}_i\right)={\gamma }_0+{\gamma }_1{\tilde{\mathcal{l}}}_0\left(X_i^{\star },Z_i,U_i^{\star },{\text{Δ}}_i^{\star }\right)+{ϵ}_i$. To assess whether the linear fit is appropriate, we plot ${\tilde{\mathcal{l}}}_0\left(X_i,Z_i,U_i,{\text{Δ}}_i\right)$ against ${\tilde{\mathcal{l}}}_0\left(X_i^{\star },Z_i,U_i^{\star },{\text{Δ}}_i^{\star }\right)$ from simulated data for various measurement error scenarios. Specifically, we plot empirical approximations of ${\tilde{\mathcal{l}}}_0$ using delta-beta residuals (see Oh et al., 2019, for more detail on their calculation) for settings with covariate error, time-to-event error, and misclassification only, as well as combinations of all three in Figure 1. The plots of ${\tilde{\mathcal{l}}}_0\left(X_i,Z_i,U_i,{\text{Δ}}_i\right)$ against ${\tilde{\mathcal{l}}}_0\left(X_i^{\star },Z_i,U_i^{\star },{\text{Δ}}_i^{\star }\right)$ for additive errors in the time-to-event or covariate show that the assumption of a linear relationship is mostly justified, albeit with some heteroscedasticity. However, when there is misclassification of the event indicator, a linear working model appears to be a very poor fit and including additional errors in variables as in Figure 1D worsens the fit.

FIGURE 1.

Plots of the true influence function ${\tilde{\mathcal{l}}}_0\left(X_i,Z_i,U_i,{\text{Δ}}_i\right)$ against the error-prone version ${\tilde{\mathcal{l}}}_0^{\star }$ with the variables subject to measurement error noted in the graph subtitle. For example, (A) displays ${\tilde{\mathcal{l}}}_0\left(X_i,Z_i,U_i,{\text{Δ}}_i\right)$ against ${\tilde{\mathcal{l}}}_0\left(X_i^{\star },Z_i,U_i,{\text{Δ}}_i\right)$. Univariate and normally distributed X and Z were generated. Survival times were generated from an exponential distribution with rate ${\lambda }_0\exp \left({\beta }_{X}X+{\beta }_{Z}Z\right)$, where ${\lambda }_0=0.1,{\beta }_X=\log (1.5)$, and ${\beta }_Z=\log (0.5)$, with 90% independent censoring. The error was generated as $X^{\star }=0.2+X-0.1Z-0.4\text{Δ}+0.25U+ϵ,U^{\star }=U+{\sigma }_v\cdot 3-0.2X-1.05Z+v$, and ${\text{Δ}}^{\star }=\text{Bernoulli}(\text{expit}(-1.1+3\text{Δ}-0.3X-0.2U+0.1Z))$, where $(ϵ,v)$ were normally distributed with $\left({\mu }_{ϵ},{\mu }_v\right)=(0,0)$, variances $\left({\sigma }_{ϵ}^2,{\sigma }_{\nu }^2\right)=(0.5,0.5)$, and ${\rho }_{ϵ,v}=0.5$

3.1 |. Model calibration

Wu and Sitter (2001) proposed an alternative calibration method to handle settings where the true relationship between the variable of interest and the auxiliary variables may be nonlinear. Specifically, they assume the relationship between S_i and A_i can be characterized by the first and second moments, with the first moment equals to $\text{E}\left(S_i\mid A_i\right)=\mu \left(A_i;\theta \right)$, where μ is a known function of A_i and θ. Then using the validation subset, one obtains fitted values of $\mu \left(A_i;\theta \right),\mu \left(A_i;\widehat{\theta }\right)$ and performs the raking procedure using them as auxiliary variables. Specifically, the generalized raking objective can be written as

$$\text{ minimize }\sum _{i=1}^N{R}_{i}d\left(\frac{g_i}{{\pi }_i},\frac{1}{{\pi }_i}\right)\text{ subject to }\sum _{i=1}^N\mu \left(A_i;\widehat{\theta }\right)=\sum _{i=1}^N{R}_i\frac{g_i}{{\pi }_i}\mu \left(A_i;\widehat{\theta }\right)0.$$ (3)

Wu and Sitter (2001) showed that this method yields more efficient estimates than the traditional raking estimator but still retains all of its statistical properties for a true nonlinear relationship between the variable of interest and auxiliary variables. Inspired by the model-calibration approach, we propose a data imputation approach that imputes the true Δ to obtain an auxiliary variable that has higher linear correlation with ${\tilde{\mathcal{l}}}_0\left(X_i,Z_i,U_i,{\text{Δ}}_i\right)$ than ${\tilde{\mathcal{l}}}_0\left(X_i^{\star },Z_i,U_i^{\star },{\text{Δ}}_i^{\star }\right)$ does. Additionally, we propose a novel application of the Wu and Sitter (2001) approach that directly imputes ${\tilde{\mathcal{l}}}_0\left(X_i,Z_i,U_i,{\text{Δ}}_i\right)$ based on a (potentially nonlinear) working model.

4 |. PROPOSED MULTIPLE IMPUTATION METHODS FOR GENERALIZED RAKING

In this section, we propose methods to improve the efficiency of the generalized raking estimators under measurement error settings involving event indicator misclassification. Our methods use multiple imputation to impute the event indicator and then construct new auxiliary variables using the imputed values to solve the raking estimating equation. For settings involving errors beyond just misclassification (e.g., additional time-to-event and/or covariate error), we propose a method using the fully conditional specification multiple imputation procedure that additionally imputes the other error-prone variables iteratively. These methods are related to those of Han (2016), who proposed combining an empirical likelihood approach with multiple imputation to construct multiply robust estimators that are consistent if one of the sampling models or data-generating models are correctly specified. Our approach differs in that we assume known phase two sampling probabilities possibly specified using a complex sampling design and study specific efficiency issues for time-to-event data. We additionally consider directly imputing the true population influence functions via a working model to use as auxiliary variables as a novel application of Wu and Sitter (2001). Lastly, we consider various study designs, including outcome-dependent sampling designs, for the selection of the validation subset in the two-phase design framework and discuss their varying impact on the efficiency of the proposed methods.

As alluded to in Section 2.3, our estimators are $\sqrt{N}$ consistent and asymptotically normal estimators of β₀. We provide a brief explanation of the conditions required in Appendix A in the Supporting Information. The proposed methods all focus on adjusting the working model of the population influence functions to construct auxiliary variables closer to the optimal auxiliary variable. If the working model is misspecified, or does not capture the true relationship well, the proposed estimators still yield consistent and asympotically normal estimates (Breslow et al., 2009). If, however, the working model is correct, the estimators will yield the most efficient design-consistent estimator (Han, 2016). We note that imputing the auxiliary variables as we propose to do will not add any bias to the parameter estimates under regular working models. We provide justification for this in Appendix A in the Supporting Information.

4.1 |. Multiple imputation for the event indicator

Traditional multiple imputation in missing data settings (Rubin, 2004) involves developing statistical models for the distributions of the variables subject to missingness conditional on the fully observed variables. The missing variables are sampled M times from their distribution to generate M imputations of the missing data. The original data are augmented with the imputations, yielding M complete imputed datasets. Each of the M imputed datasets are then used to separately estimate the parameters of interest and the average of the M estimates is the multiple imputation estimator. The variance of the estimates can be calculated using Rubin’s rules (Barnard & Rubin, 1999) or the estimators proposed by Robins and Wang (2000).

Multiple imputation for generalized raking follows similarly, with the exception that the M imputed datasets are first used to construct auxiliary variables for the influence functions for the target parameters.

First, we posit an imputation model for $\text{Δ},f\left(\text{Δ}\mid {\text{Δ}}^{\star },X^{\star },U^{\star },Z;\eta \right)$, with parameter vector $\eta$, and specify a noninformative prior distribution, $f(\eta )$. We then fit the imputation model using the validation subset, generate the posterior distribution for $\eta$, and then sample M times from this posterior distribution to obtain ${\eta }_{\star }^{(1)},\dots ,{\eta }_{\star }^{(M)}$. The parameter draws are used to sample ${\widehat{\text{Δ}}}_i^{(m)}\sim f\left(\text{Δ}\mid {\text{Δ}}_i^{\star },X_i^{\star },U_i^{\star },Z_i;{\eta }_{\star }^{(m)}\right)$ for all N phase one subjects and $m=1,\dots ,M.{\widehat{\text{Δ}}}^{(1)},\dots ,{\widehat{\text{Δ}}}^{(M)}$ are then augmented with the phase one data to yield M complete imputed datasets. Then for m = 1, ... , M, the estimating equation ${\sum }_{i=1}^N\psi \left(X_i^{\star },Z_i,U_i^{\star },{\widehat{\text{Δ}}}_i^{(m)};\beta \right)=0$ is solved to obtain ${\widehat{\beta }}^{(m)}$. For each subject i = 1, ... , N, the auxiliary variable ${\widehat{A}}_i$, is defined as

$${\widehat{A}}_i=\frac{1}{M}\sum _{m=1}^M{\tilde{\mathcal{l}}}_0\left(X_i^{\star },Z_i,U_i^{\star },{\widehat{\text{Δ}}}_i^{(m)};{\widehat{\beta }}^{(m)}\right),$$

where ${\tilde{\mathcal{l}}}_0\left(X_i^{\star },Z_i,U_i^{\star },{\widehat{\text{Δ}}}_i^{(m)}\right)$ is the influence function for the estimating equation from the mth imputation and can be empirically approximated as

$$\begin{array}{c}{\tilde{\mathcal{l}}}_0\left(X_i^{\star },Z_i,U_i^{\star },{\widehat{\text{Δ}}}_i^{(m)}\right)\approx {\widehat{\text{Δ}}}_i^{(m)}\left\{{\left\{X_i^{\star },Z_i\right\}}^{\prime }-\frac{S^{(1)\star }(\beta ,t)}{S^{(0)\star }(\beta ,t))}\right\}\\ -\sum _{i=1}^n{\int }_0^{\tau }\frac{\exp \left({\beta }_X^{\prime }{X}_i^{\star }+{\beta }_Z^{\prime }{Z}_i\right)}{S^{(0)\star }(\beta ,t)}\left\{{\left\{X_i^{\star },Z_i\right\}}^{\prime }-\frac{S^{(1)\star }(\beta ,t)}{S^{(0)\star (\beta ,t))}}\right\}d{\widehat{N}}_i(t),\end{array}$$

where $S^{(r)\star }(\beta ,t)=n^{-1}{\sum }_{j=1}^n{Y}_j^{\star }(t){\left\{X_j^{\star },Z_j\right\}}^{\prime \otimes r}\exp \left({\beta }_X^{\prime }{X}_j^{\star }+{\beta }_Z^{\prime }{Z}_j\right)$ ($a^{\otimes 1}$ is the vector a and $a^{\otimes 0}$ is the scalar 1), $Y_j^{\star }(t)=I\left(U_j^{\star }\ge t\right)$ t), and ${\widehat{N}}_i(t)=I\left(U_i^{\star }\le t,{\widehat{\text{Δ}}}_i^{(m)}=1\right)$.

Finally, to obtain estimates of the parameter of interest, we solve the raking estimating equation with adjusted weights calculated using ${\widehat{A}}_i$ as auxiliary variables in (2).

4.2 |. Fully conditional specification multiple imputation

If there exists measurement error in variables beyond just the event indicator (e.g., additional time-to-event and/or covariate error), it is possible to gain efficiency by additionally imputing all error-prone variables iteratively using the fully conditional specification multiple imputation (FCSMI) method (Van Buuren, 2007). FCSMI involves specifying univariate models for the conditional distribution of each of the variables observed only at phase two given all phase one variables. Each missing variable is repeatedly imputed using the specified models and conditioning on the most recent imputations of the other variables. We explicate the FCSMI method for generalized raking in the presence of misclassification, covariate error, and time-to-event error. The method assumes a working model for the censored time-to-event that takes the form $U^{\star }=U+W(\text{Δ},X,Z)$, where W(Δ,X,Z) is an arbitrary function of Δ,X, and Z. Note that if the working error model is misspecified, the raking estimator will still be consistent, albeit with some loss of efficiency.

First, we posit imputation models for Δ,X, and W, as well as noninformative prior distributions for their parameter vectors $\eta ,\theta ,\text{ and }\omega$, respectively, to generate posterior distributions. We then draw parameters from their posteriors as follows: ${\eta }_{\star }^{(0)}\sim f\left(\text{Δ}\mid {\text{Δ}}^{\star },X^{\star },U^{\star },Z;{\eta }_V\right)f\left({\eta }_V\right)$,

${\theta }_{\star }^{(0)}\sim f\left(X\mid {\text{Δ}}^{\star },X^{\star },U^{\star },Z;{\theta }_V\right)f\left({\theta }_V\right)$ and ${\omega }_{\star }^{(0)}\sim f\left(W\mid {\text{Δ}}^{\star },X^{\star },Z;{\omega }_V\right)f\left({\omega }_V\right)$. Then Δ,X, and U are imputed for all N phase one subjects by sampling from the imputation models using the initial parameter draws: ${\widehat{\text{Δ}}}^{(0)}\sim f\left(\text{Δ}\mid {\text{Δ}}^{\star },X^{\star },U^{\star },Z;{\eta }_{\star }^{(0)}\right),{\widehat{X}}^{(0)}\sim f\left(X\mid {\text{Δ}}^{\star },X^{\star },U^{\star },Z;{\theta }_{\star }^{(0)}\right)$, and ${\widehat{U}}^{(0)}=U^{\star }-{\widehat{W}}^{(0)}$, where ${\widehat{W}}^{(0)}\sim f\left(W\mid {\text{Δ}}^{\star },X^{\star },Z;{\omega }_{\star }^{(0)}\right)$. Then for iteration $l=1,\dots ,L$, the algorithm proceeds as follows:

$${\eta }_{\star }^{(l)}\sim f\left(\text{Δ}\mid {\text{Δ}}^{\star },{\widehat{X}}^{(l-1)},{\tilde{U}}^{(l-1)},Z;\eta \right)f(\eta )$$

$${\widehat{\text{Δ}}}^{(l)}\sim f\left(\text{Δ}\mid {\text{Δ}}^{\star },{\widehat{X}}^{(l-1)},{\widehat{U}}^{(l-1)},Z;{\eta }_{\star }^{(l)}\right)$$

$${\theta }_{\star }^{(l)}\sim f\left(X\mid {\widehat{\text{Δ}}}^{(l)},X^{\star },U^{(l-1)},Z;\theta \right)f(\theta )$$

$${\widehat{X}}^{(l)}\sim f\left(X\mid {\widehat{\text{Δ}}}^{(l)},X^{\star },{\widehat{U}}^{(l-1)},Z;{\theta }_{\star }^{(l)}\right)$$

$${\omega }_{\star }^{(l)}\sim f\left(W\mid {\widehat{\text{Δ}}}^{(l)},{\widehat{X}}^{(l)},Z;\omega \right)f(\omega )$$

$${\widehat{U}}^{(l)}=U^{\star }-{\widehat{W}}^{(l)},\text{ where }{\widehat{W}}^{(l)}\sim f\left(W\mid {\widehat{\text{Δ}}}^{(l)},{\widehat{X}}^{(l)},Z;{\omega }_{\star }^{(l)}\right).$$

The algorithm continues sampling and imputing $\widehat{\text{Δ}},\widehat{X},$ and $\widehat{U}$ for L iterations, after which it is assumed a stationary distribution has been reached. The above steps are repeated for M iterations, where ${\widehat{\text{Δ}}}^{(L)},{\widehat{X}}^{(L)},\text{ and }{\widehat{U}}^{(L)}$ are taken to be the imputed values of Δ,X, and U, respectively, for each $m=1,\dots ,M.{\widehat{\text{Δ}}}^{(m)},{\widehat{X}}^{(m)},\text{ and }{\widehat{U}}^{(m)}$ are then augmented with the phase one data to yield M complete imputed datasets. Then for m = 1, ...,M, the estimating equation ${\sum }_{i=1}^N\psi \left({\widehat{X}}_i^{(m)},Z_i,{\widehat{U}}_i^{(m)},{\widehat{\text{Δ}}}_i^{(m)};\beta \right)=0$ is solved to obtain ${\widehat{\beta }}^{(m)}$. Then the auxiliary variable for each subject, ${\widehat{A}}_i$ is defined as

$${\widehat{A}}_i=\frac{1}{M}\sum _{m=1}^M{\tilde{\mathcal{l}}}_0\left({\widehat{X}}_i^{(m)},Z_i,{\widehat{U}}_i^{(m)},{\widehat{\text{Δ}}}_i^{(m)};{\widehat{\beta }}^{(m)}\right)$$

and ${\tilde{\mathcal{l}}}_0\left({\widehat{X}}_i^{(m)},Z_i,{\widehat{U}}_i^{(m)},{\widehat{\text{Δ}}}_i^{(m)}\right)$ can be empirically approximated as

$$\begin{array}{l}{\tilde{\mathcal{l}}}_0\left({\widehat{X}}_i^{(m)},Z_i,{\widehat{U}}_i^{(m)},{\widehat{\text{Δ}}}_i^{(m)}\right)\approx {\widehat{\text{Δ}}}_i^{(m)}\left\{{\left\{{\widehat{X}}_i^{(m)},Z_i\right\}}^{\prime }-\frac{{\widehat{S}}^{(1)}(\beta ,t)}{{\widehat{S}}^{(0)}(\beta ,t))}\right\}\\ -\sum _{i=1}^n{\int }_0^{\tau }\frac{\exp \left({\beta }_X^{\prime }{\widehat{X}}_i^{(m)}+{\beta }_Z^{\prime }{Z}_i\right)}{{\widehat{S}}^{(0)}(\beta ,t)}\left\{{\left\{{\widehat{X}}_i^{(m)},Z_i\right\}}^{\prime }-\frac{{\widehat{S}}^{(1)}(\beta ,t)}{{\widehat{S}}^{(0)}(\beta ,t))}\right\}d{\widehat{N}}_i(t),\end{array}$$

where ${\widehat{S}}^{(r)}(\beta ,t)=n^{-1}{\sum }_{j=1}^n{\widehat{Y}}_j(t){\left\{{\widehat{X}}_j^{(m)},Z_j\right\}}^{\prime \otimes r}\exp \left({\beta }_X^{\prime }{\widehat{X}}_j^{(m)}+{\beta }_Z^{\prime }{Z}_j\right)$ ($a^{\otimes 1}$ is the vector a and $a^{\otimes 0}$ is the scalar 1), ${\widehat{Y}}_j(t)=I\left({\widehat{U}}_j^{(m)}\ge t\right)$, and ${\widehat{N}}_i(t)=I\left({\widehat{U}}_i^{(m)}\le t,{\widehat{\text{Δ}}}_i^{(m)}=1\right)$.

Lastly, to obtain estimates of the parameter of interest, we solve the raking estimating equation with adjusted weights calculated using ${\widehat{A}}_i$, as auxiliary variables in (2).

4.3 |. Model-calibration multiple imputation

We propose a multiple imputation application of the Wu and Sitter (2001) model-calibration approach by specifying a working model for the population influence function and using the fitted values as auxiliary variables for raking in repeated iterations. First, we impute the error-prone variable(s) using MI or FCSMI as described in Sections 4.1 and 4.2. For the purposes of exposition, assume that FCSMI is used to impute Δ,X, and U to obtain ${\widehat{\text{Δ}}}^{(m)},{\widehat{X}}^{(m)}$, and ${\widehat{U}}^{(m)}$. We posit a working model

$$\text{E}\left({\tilde{\mathcal{l}}}_0\left(X_i,Z_i,U_i,{\text{Δ}}_i\right)\mid {\tilde{\mathcal{l}}}_0\left({\widehat{X}}_i^{(m)},Z_i,{\widehat{U}}_i^{(m)},{\widehat{\text{Δ}}}_i^{(m)}\right)\right)=\mu \left({\tilde{\mathcal{l}}}_0\left({\widehat{X}}_i^{(m)},Z_i,{\widehat{U}}_i^{(m)},{\widehat{\text{Δ}}}_i^{(m)}\right);{\gamma }^{(m)}\right),$$

where ${\tilde{\mathcal{l}}}_0\left({\widehat{X}}_i^{(m)},Z_i,{\widehat{U}}_i^{(m)},{\widehat{\text{Δ}}}_i^{(m)}\right)$ is constructed using the empirical approximation given in Section 4.2. Here, μ can capture nonlinear relationships, and the model is fit on the validation subset to obtain ${\widehat{\gamma }}^{(m)}$. The above steps are repeated m = 1,..., M iterations to obtain ${\widehat{\gamma }}^{(1)},\dots ,{\widehat{\gamma }}^{(M)}$. The auxiliary variable for each subject, ${\widehat{A}}_i$ is then defined as

$${\widehat{A}}_i=\frac{1}{M}\sum _{m=1}^M\mu \left({\tilde{\mathcal{l}}}_0\left({\widehat{X}}_i^{(m)},Z_i,{\widehat{U}}_i^{(m)},{\widehat{\text{Δ}}}_i^{(m)}\right);{\widehat{\gamma }}^{(m)}\right).$$

Finally, estimates of the parameter of interest are obtained by solving the raking estimating equation with adjusted weights calculated using ${\widehat{A}}_i$, as auxiliary variables in (2).

4.4 |. Sampling design considerations

In validation study settings, such as those considered in this article, researchers can define the phase two sampling probabilities as functions of the phase one data to select more informative subjects for increased efficiency. For example, researchers may want to oversample cases in rare-event settings or oversample subjects at underrepresented levels of informative covariates. Although generalized raking can easily accommodate such designs, the interplay between sampling designs and raking has not been well studied. We consider the effects of three different sampling designs on the efficiency of raking estimates: simple random sampling (SRS), case-control (CC), and covariate stratified case-control (SCC).

5 |. SIMULATION STUDY

In this section, we study the finite sample performance of the proposed raking estimators utilizing multiple imputation in the presence of event indicator misclassification. We compare these estimators to the raking estimator that constructs auxiliary variables using the naive error-prone data (GRN), the HT estimator, and the true estimator, that is, the Cox proportional hazards model fit with the error-free data for all subjects. We considered three different measurement error scenarios where different variables are observed with error: (1) (X, Z, U, Δ*), (2)(X, Z, U*,Δ*), and (3) (X*, Z, U*, Δ*). For each error scenario, we considered the proposed raking estimator utilizing MI to impute the event indicator only, referred to as generalized raking multiple imputation (GRMI) hereafter. For error scenarios 2 and 3, which include errors in other variables besides the event indicator, we additionally considered the proposed raking estimator utilizing FCSMI to impute all error-prone variables iteratively, referred to as generalized raking fully conditional specification multiple imputation (GRFCSMI) hereafter. We refer to these estimators as encompassing the data imputation approach. For all three error scenarios, we also considered the corresponding model-calibration multiple imputation methods described in Section 4.3, which we similarly refer to as encompassing the influence function (IF) imputation approach. We present % biases, average model standard errors (ASE), empirical standard errors (ESE), relative efficiency (RE) calculated with respect to the HT ESE, mean squared errors (MSE), and 95% coverage probabilities (CP) for varying values of the log hazard ratio β_X, % censoring, cohort and validation subset sizes, and validation subset sampling designs. We additionally present type 1 error results for β_X = 0 and α = 0.05. All standard errors were calculated using sandwich variance estimators. Source code to reproduce the results is available as Supporting Information on the journal’s web page (http://onlinelibrary.wiley.com/doi/10.1002/bimj.202000187/suppinfo).

5.1 |. Simulation setup

All simulations were run 2000 times using R version 3.6.2 (R Core Team, 2019). Cohort and validation subset sizes of {N,n} = {2000,400} and {N, n} = {10000,2000} were considered. Univariate X and Z were considered and were generated as a bivariate normal distribution with means $\left({\mu }_X,{\mu }_Z\right)=(0,2)$, variances $\left({\sigma }_X^2,{\sigma }_Z^2\right)=(1,1)$, and ${\rho }_{X,Z}=0.5$. The true log hazard ratios were set to be ${\beta }_X\in \{\log (1.5),\log (3)\}\text{ and }{\beta }_Z=\log (0.5)$. The true survival time T was generated from an exponential distribution with rate equal to ${\lambda }_0\exp \left({\beta }_{X}X+{\beta }_{Z}Z\right)$ where ${\lambda }_0=0.1$. Censoring times were simulated for each β_X and β_Z to yield 50%>,75%>, and 90%> censoring rates. Specifically, they were generated from Uniform distributions of varying lengths to mimic studies of different lengths.

The error-prone data were generated as follows:

• 1. Scenario 1: (X, Z, U, Δ *), where

$${\text{Δ}}^{\star }=\text{ Bernoulli}(\text{expit}(-1.1+3\text{Δ}-0.3X-0.2U+0.1Z))$$

• 2. Scenario 2: (X, Z, U*, Δ *), where

$${\text{Δ}}^{\star }=\text{ Bernoulli}(\text{expit}(-1.1+3\text{Δ}-0.3X-0.2U+0.1Z))$$

$$U^{\star }=U+W=U+{\sigma }_v\cdot 3-0.2X-1.05Z+v$$

• 3. Scenario 3: (X*,Z, U*, Δ*), where

$${\text{Δ}}^{\star }=\text{ Bernoulli}(\text{expit}(-1.1+3\text{Δ}-0.3X-0.2U+0.1Z))$$

$$U^{\star }=U+W=U+{\sigma }_v\cdot 3-0.2X-1.05Z+v$$

$$X^{\star }=0.2+X-0.1Z-0.4\text{Δ}+0.25U+ϵ.$$

Note that the choice of the intercept term in the event time error model is such that the error-prone time is a valid event time (i.e., greater than zero) with high probability. The few censored event times that were less than 0 were reflected across 0 to generate valid outcomes. For scenario 3, the error terms $(ϵ,\nu )$ were generated from a bivariate normal distribution with means $\left({\mu }_{\in },{\mu }_{\nu }\right)=(0,0)$, variances $\left({\sigma }_{\mathrm{\in }}^2,{\sigma }_v^2\right)=(0.5,0.5)$, and ${\rho }_{ϵ,v}=\mathrm{0.5.}\nu$ was generated from a univariate normal distribution for scenario 2 with the same mean and variance as in scenario 3. Supplementary Materials Table 1 presents the sensitivity, specificity, positive predictive value, and negative predictive value for the misclassified event indicator across all error scenarios.

For the working imputation models, we fit logistic regression models for Δ and linear regression models for X and W. Under the error-generating process considered in this section, analytical expressions for the true imputation models do not exist. Therefore, we considered two types of working imputation models: those including only main effects and those additionally adding all possible interaction effects to potentially specify an imputation model closer to the truth. Specifically, the imputation models including only main effects (referred to as generalized raking multiple imputation simple (GRMIS) and generalized raking fully conditional specification multiple imputation simple (GRFCSMIS) hereafter) were specified as follows:

• 1. Scenario 1: (X,Z,U,Δ*)

$$\text{logit}\left(P(\text{Δ}=1)\mid {\text{Δ}}^{\star },X,U,Z\right)={\eta }_0+{\eta }_1{\text{Δ}}^{\star }+{\eta }_{2}X+{\eta }_{3}U+{\eta }_{4}Z$$

• 2. Scenario 2: (X, Z, U*,Δ *)

$$\text{logit}\left(P(\text{Δ}=1)\mid {\text{Δ}}^{\star },X,U^{\star },Z\right)={\eta }_0+{\eta }_1{\text{Δ}}^{\star }+{\eta }_{2}X+{\eta }_3{U}^{\star }+{\eta }_{4}Z$$

$$\text{E}\left(W\mid {\text{Δ}}^{\star },X,Z\right)={\omega }_0+{\omega }_1{\text{Δ}}^{\star }+{\omega }_{2}X+{\omega }_{3}Z$$

• 3. Scenario 3: (X*,Z, U*,Δ*)

$$\text{logit}\left(P(\text{Δ}=1)\mid {\text{Δ}}^{\star },X^{\star },U^{\star },Z\right)={\eta }_0+{\eta }_1{\text{Δ}}^{\star }+{\eta }_2{X}^{\star }+{\eta }_3{U}^{\star }+{\eta }_{4}Z$$

$$\text{E}\left(W\mid {\text{Δ}}^{\star },X^{\star },Z\right)={\omega }_0+{\omega }_1{\text{Δ}}^{\star }+{\omega }_2{X}^{\star }+{\omega }_{3}Z$$

$$\text{E}\left(X\mid {\text{Δ}}^{\star },X^{\star },U^{\star },Z\right)={\theta }_0+{\theta }_1{\text{Δ}}^{\star }+{\theta }_2{X}^{\star }+{\theta }_3{U}^{\star }+{\theta }_{4}Z.$$

The imputation models containing interaction terms (referred to as generalized raking multiple imputation complex (GRMIC) and generalized raking fully conditional specification multiple imputation complex (GRFCSMIC) hereafter) include the same predictors as above as well as all possible interaction terms. For each error scenario and all parameter settings, the number of imputation iterations was set to 50 and the FCSMI estimators performed 500 iterative updates to the imputed variables per imputation iteration. Appendix C provides further detail on the implementation of the multiple imputation procedures. For the IF imputation approach, linear regression models were fit for the working models of the true influence function for each covariate. For example, the following model was fit for error scenario 1:

$$\begin{array}{c}\text{E}\left({\tilde{\mathcal{l}}}_0\mid {\widehat{\tilde{\mathcal{l}}}}_0\right)={\gamma }_0+{\gamma }_1{\widehat{\tilde{\mathcal{l}}}}_0+{\gamma }_2\widehat{\text{Δ}}+{\gamma }_{3}U+{\gamma }_{4}X+{\gamma }_{5}Z\\ +{\gamma }_6\left({\widehat{\tilde{\mathcal{l}}}}_0\times \widehat{\text{Δ}}\right)+{\gamma }_7\left({\widehat{\tilde{\mathcal{l}}}}_0\times U\right)+{\gamma }_8\left({\widehat{\tilde{\mathcal{l}}}}_0\times X\right)+{\gamma }_9\left({\widehat{\tilde{\mathcal{l}}}}_0\times Z\right).\end{array}$$

For error scenarios 2 and 3, the same models were fit except U and X were replaced by $\widehat{U}$ and $\widehat{X}$.

We considered validation subsets selected via simple random sampling for all three error scenarios. For the rare-event setting of 90% censoring in error scenarios 2 and 3, we additionally compared the performance of the estimators using validation subsets selected via case-control sampling and stratified case-control sampling. For these sampling design comparisons, we considered {N, n} = {4000,800} and generated the error-prone event indicator according to the model described in Supplementary Materials Table 2. The covariate and time-to-event error were generated using the same previous models. To perform case-control sampling, all error-prone cases were selected and a simple random sample of error-prone controls was selected to yield a nearly one-to-one ratio of error-prone cases to controls. To perform stratified case-control sampling, we stratified the continuous covariate X (or X* for settings involving covariate error) into four discrete categories by setting cutpoints at the 20th, 50th, and 80th percentiles. We then selected an equal number of subjects from each of the eight strata defined by the combinations of the error-prone case status and the covariate strata (i.e., the balanced sampling design proposed by Breslow & Chatterjee, 1999). Note that for CC and SCC sampling, the data imputation models and influence function working models for the IF imputation approach were inverse-probability weighted to account for the sampling design of the validation subsets. For the proposed raking estimators utilizing MI or FCSMI for data imputation only, the imputation models were not weighted as we included all stratification variables in the models (Cochran, 2007), and we noticed no empirical differences between including weights or not.

5.2 |. Simulation results

In the scenarios considered, all of the considered estimators were nearly unbiased for all settings, as expected, with the exception of a few specific rare-event settings with {N, n} = {2000,400} and simple random sampling, due to relatively few true events (40 on average) in the validation subset. Since the proposed estimators construct improved auxiliary variables to increase efficiency compared to GRN, we focus on the ESE, RE (with respect to the HT estimator), MSE, and CP and how these performance measures differed across settings.

Table 1 presents the relative performance under error scenario 1 for estimating ${\beta }_X\in \{\log (1.5),\log (3)\}$ using the data imputation approach for {N, n} = {2000,400}, {50%, 75%, 90%} censoring, and simple random sampling of the validation subset. GRN had increased efficiency compared to HT with the RE ranging from 1.24 for 50% censoring to 1.06 for 90% censoring. However, GRMIS and GRMIC both had higher RE than GRN for nearly all parameter settings, ranging from 1.41 for 50% censoring to 1.16 for 90% censoring. GRMIS and GRMIC had comparable REs, lower MSE than HT and GRN, and CPs near 95% for all parameter settings.

TABLE 1.

Simulation results for estimating β_x using the data imputation approach for error scenario 1 (error only in event indicator) with N = 2000, n = 400, and simple random sampling. The % bias, empirical standard error (ESE), relative efficiency (RE), average standard error (ASE), mean squared error, and coverage probabilities (CP) are presented for 2000 simulated datasets

βz	% Cens	βx	Method	% Bias	ESE	RE	ASE	MSE	CP
log(0.5)	50	log(1.5)	True	−0.03595	0.039644	2.289193	0.039422	0.001572	0.956
			HT	1.228958	0.090753	1	0.087874	0.008261	0.949
			GRN	1.40684	0.07401	1.226214	0.072528	0.00551	0.95
			GRMIS	−0.08937	0.065693	1.381469	0.06386	0.004316	0.948
			GRMIC	−0.42527	0.064598	1.404892	0.063389	0.004176	0.946
		log(3)	True	0.041168	0.041582	2.453957	0.04415	0.001729	0.948
			HT	0.631089	0.10204	1	0.097775	0.01046	0.939
			GRN	0.282312	0.082568	1.235824	0.080447	0.006827	0.942
			GRMIS	0.108883	0.072166	1.413959	0.069818	0.005209	0.948
			GRMIC	0.007399	0.072275	1.411835	0.069152	0.005224	0.948
	75	log(1.5)	True	0.119394	0.051672	2.266392	0.053276	0.00267	0.954
			HT	0.781363	0.117109	1	0.118644	0.013725	0.952
			GRN	0.916624	0.097339	1.203106	0.096548	0.009489	0.945
			GRMIS	0.188371	0.093537	1.252017	0.091773	0.00875	0.944
			GRMIC	0.096736	0.096302	1.216058	0.090939	0.009274	0.94
		log(3)	True	−0.01311	0.06088	2.241353	0.059211	0.003706	0.949
			HT	1.034735	0.136454	1	0.131041	0.018749	0.938
			GRN	0.386125	0.119288	1.143905	0.113786	0.014248	0.934
			GRMIS	0.197862	0.102954	1.325384	0.102518	0.010604	0.943
			GRMIC	0.040924	0.101157	1.348933	0.101394	0.010233	0.944
	90	log(1.5)	True	0.0138	0.084364	2.222885	0.083155	0.007117	0.947
			HT	1.805251	0.187531	1	0.184444	0.035222	0.943
			GRN	0.30929	0.167181	1.121725	0.165789	0.027951	0.94
			GRMIS	0.192308	0.161702	1.159732	0.160033	0.026148	0.944
			GRMIC	−0.55691	0.159657	1.174587	0.158312	0.025495	0.936
		log(3)	True	−0.04654	0.088525	2.315872	0.089229	0.007837	0.95
			HT	1.160558	0.205013	1	0.197598	0.042193	0.938
			GRN	0.945284	0.194363	1.054793	0.187058	0.037885	0.941
			GRMIS	0.26163	0.175215	1.17007	0.16969	0.030708	0.94
			GRMIC	−0.31527	0.17402	1.178102	0.169034	0.030295	0.939

Supplementary Materials Table 3 presents the relative performance under error scenario 2 for estimating ${\beta }_X\in \{\log (1.5),\log (3)\}$ using the data imputation approach for {N, n} = {2000,400}, {50%>, 75%>, 90%>} censoring, and simple random sampling of the validation subset. GRN again had increased efficiency compared to HT with the RE ranging from 1.21 to 1.07. GRMIS, GRMIC, GRFCSMIS, and GRFCSMIC, however, all had higher RE than GRN for all parameter settings, ranging from 1.43 to 1.14 for GRMI and 1.45 to 1.14 for GRFCSMI. Comparing GRMIS to GRMIC and GRFCSMIS to GRFCSMIC, we observed nearly no difference in efficiency. Comparing GRMI to GRFCSMI, GRFCSMI had higher or equal RE for nearly all settings, although the difference was sometimes small. In addition, GRMI and GRFCSMI had lower MSE than HT and GRN and CPs by 5–6% for all settings.

Table 2 presents the relative performance under error scenario 3 for estimating ${\beta }_X\in \{\log (1.5),\log (3)\}$ using the data imputation approach for {N, n} = {2000,400}, {50%, 75%, 90%>} censoring, and simple random sampling of the validation subset. In this more complex error scenario, GRN had a small improvement in efficiency over HT, with its RE peaking around 1.05 across all settings. GRMIS and GRMIC similarly showed minor efficiency improvements compared to HT with its RE ranging from 1 to 1.06. However, GRFCSMIS and GRFCSMIC had appreciable gains in efficiency, with RE ranging from 1.12 to 1.25 for all settings except for 90% censoring, where the RE was less than 1.1. These efficiency gains suggest that, in the presence of covariate measurement error that depends on the outcome, multiply imputing all error-prone variables was advantageous over only imputing the misclassified event indicator. Overall, GRFCSMI had lower MSE than all other estimators (albeit with some bias for 90% censoring) and CPs that ranged from 94 to 95% for all settings.

TABLE 2.

Simulation results for estimating β_x using the data imputation approach for error scenario 3 (errors in event indicator, failure time, and X) with N = 2000, n = 400, and simple random sampling. The % bias, empirical standard error (ESE), relative efficiency (RE), average standard error (ASE), mean squared error, and coverage probabilities (CP) are presented for 2000 simulated datasets

βz	% Cens	βx	Method	% Bias	ESE	RE	ASE	MSE	CP
log(0.5)	50	log(1.5)	True	0.07661	0.039569	2.328964	0.039418	0.001566	0.95
			HT	1.342474	0.092155	1	0.088213	0.008522	0.937
			GRN	2.100967	0.093898	0.98143	0.087678	0.008889	0.928
			GRMIS	1.308134	0.092762	0.993454	0.088003	0.008633	0.935
			GRMIC	1.276032	0.092487	0.996408	0.088048	0.008581	0.935
			GRFCSMIS	0.798683	0.075276	1.224217	0.074605	0.005677	0.948
			GRFCSMIC	0.407051	0.073879	1.247364	0.074138	0.005461	0.942
		log(3)	True	−0.00837	0.041674	2.491381	0.04412	0.001737	0.951
			HT	0.777852	0.103825	1	0.097835	0.010853	0.944
			GRN	1.177403	0.101197	1.02597	0.097568	0.010408	0.943
			GRMIS	0.846726	0.103247	1.005597	0.097632	0.010747	0.944
			GRMIC	0.816276	0.103057	1.007453	0.097623	0.010701	0.945
			GRFCSMIS	0.60425	0.088082	1.178736	0.087678	0.007802	0.939
			GRFCSMIC	0.333361	0.088859	1.168426	0.087836	0.007909	0.938
	75	log(1.5)	True	−0.11172	0.050646	2.445003	0.053272	0.002565	0.946
			HT	2.494616	0.12383	1	0.119095	0.015436	0.945
			GRN	3.469044	0.121951	1.015403	0.116576	0.01507	0.944
			GRMIS	3.493033	0.123515	1.002552	0.117963	0.015456	0.94
			GRMIC	3.755253	0.123088	1.006027	0.117855	0.015383	0.938
			GRFCSMIS	1.830123	0.107038	1.156879	0.103193	0.011512	0.946
			GRFCSMIC	1.848374	0.106441	1.163367	0.102455	0.011386	0.947
		log(3)	True	−0.01819	0.05804	2.37266	0.05929	0.003369	0.948
			HT	0.939605	0.13771	1	0.13192	0.019071	0.95
			GRN	1.291495	0.133879	1.028617	0.129447	0.018125	0.947
			GRMIS	1.13204	0.134928	1.020621	0.130678	0.01836	0.948
			GRMIC	1.21211	0.137343	1.002675	0.130285	0.01904	0.947
			GRFCSMIS	0.749482	0.123367	1.116261	0.119853	0.015287	0.946
			GRFCSMIC	0.725826	0.120588	1.14199	0.119671	0.014605	0.944
	90	log(1.5)	True	0.0138	0.084364	2.227607	0.083155	0.007117	0.947
			HT	2.839981	0.18793	1	0.184457	0.03545	0.944
			GRN	4.005694	0.180168	1.043079	0.178185	0.032724	0.94
			GRMIS	4.361114	0.177508	1.05871	0.17808	0.031822	0.937
			GRMIC	4.460343	0.178246	1.054326	0.176558	0.032099	0.936
			GRFCSMIS	1.373064	0.176884	1.062444	0.170686	0.031319	0.943
			GRFCSMIC	2.936905	0.173456	1.08344	0.169147	0.030229	0.938
		log(3)	True	−0.04654	0.088525	2.300257	0.089229	0.007837	0.95
			HT	0.99248	0.203631	1	0.198896	0.041584	0.945
			GRN	1.644558	0.192597	1.05729	0.193718	0.03742	0.942
			GRMIS	1.503862	0.196311	1.037287	0.192159	0.038811	0.945
			GRMIC	1.581827	0.19941	1.021165	0.19132	0.040067	0.943
			GRFCSMIS	1.162629	0.195142	1.043502	0.189566	0.038243	0.947
			GRFCSMIC	1.150689	0.196691	1.035282	0.188478	0.038847	0.946

Results for {N, n} = {10000,2000}, keeping all other parameters the same as Table 1, Supplementary Materials Table 3, and Table 2, are presented in Supplementary Materials Tables 4, 5, and 6, respectively. The conclusions for these large cohort settings were similar to those with {N, n} = {2000,400}. For error scenario 1, GRMI provided appreciable efficiency gain over GRN. For error scenario 2, both GRMI and GRFCSMI provided comparable and significant efficiency gain over GRN. For error scenario 3, only GRFCSMI yielded appreciable efficiency gain over GRN and both GRMI and GRFCSMI were nearly unbiased even with 90%> censoring.

We present the type 1 error results under error scenario 3 for estimating β_X = 0 using the data imputation approach for {N, n} = {10000,2000}, {50%, 75%, 90%} censoring, and simple random sampling of the validation subset in Supplementary Materials Table 7. For the 50% and 75% censoring levels, the type 1 error of the proposed GRMI and GRFCSMI estimators ranged from 0.052 to 0.064. For the 90%> censoring setting, the number of cases in the phase two data was very small at 40, and the type 1 error ranged from 0.068 to 0.072 for the proposed methods. However, we note that the type 1 error could likely be improved by using the bootstrap to calculate standard errors instead of the sandwich variance estimators (see Oh et al., 2019, for more detail).

Results for the IF imputation approach under error scenario 3 for {N, n} = {2000,400}, keeping all other parameters the same as Table 2, are presented in Table 3. We note that the RE of the proposed estimators cannot be directly compared to those from the data imputation tables due to the HT ESE varying slightly. Overall, the conclusions for this approach were very similar to those of the data imputation approach. Comparing the IF imputation estimators to the data imputation estimators, the ESE was very similar across all settings; this suggests that in the relatively simple error settings considered, the data imputation improved most of the auxiliary variable nonlinearity issues. Similar tables for error scenarios 1 and 2 are presented in Supplementary Materials Tables 8 and 9, and similar conclusions were reached. Results for the IF imputation approach for {N, n} = {10000,2000}, keeping all other parameters the same as Supplementary Tables 4, 5, and 6, are presented in Supplementary Materials Tables 10,11, and 12, respectively. The efficiency conclusions were similar to those observed under {N, n} = {2000,400}, with the larger sample sizes again removing any observed bias.

TABLE 3.

Simulation results for estimating β_x using the IF imputation approach for error scenario 3 (errors in event indicator, failure time, and X) with N = 2000, n = 400, and simple random sampling. The % bias, empirical standard error (ESE), relative efficiency (RE), average standard error (ASE), mean squared error, and coverage probabilities (CP) are presented for 2000 simulated datasets

βz	% Cens	βx	Method	% Bias	ESE	RE	ASE	MSE	CP
log(0.5)	50	log(1.5)	True	−0.03595	0.039644	2.357942	0.039422	0.001572	0.956
			HT	0.968647	0.093478	1	0.087968	0.008754	0.944
			GRN	2.48905	0.092254	1.013273	0.087589	0.008613	0.942
			GRMIS	1.27812	0.095618	0.977622	0.082415	0.00917	0.904
			GRMIC	0.702605	0.094581	0.988339	0.082057	0.008954	0.912
			GRFCSMIS	1.176668	0.076746	1.218027	0.072894	0.005913	0.932
			GRFCSMIC	0.766525	0.076361	1.224153	0.072638	0.005841	0.938
		log(3)	True	0.041168	0.041582	2.490834	0.04415	0.001729	0.948
			HT	0.313211	0.103573	1	0.097851	0.010739	0.942
			GRN	0.725322	0.104082	0.995114	0.097532	0.010897	0.945
			GRMIS	1.421894	0.102001	1.015417	0.091883	0.010648	0.924
			GRMIC	1.487215	0.102937	1.006184	0.091601	0.010863	0.926
			GRFCSMIS	0.262352	0.096256	1.076016	0.08654	0.009274	0.934
			GRFCSMIC	0.102202	0.095132	1.088739	0.08656	0.009051	0.934
	75	log(1.5)	True	0.119394	0.051672	2.316876	0.053276	0.00267	0.954
			HT	1.004049	0.119718	1	0.118566	0.014349	0.948
			GRN	1.661829	0.119968	0.997919	0.116507	0.014438	0.945
			GRMIS	4.68564	0.122646	0.976125	0.107653	0.015403	0.92
			GRMIC	5.039218	0.121839	0.98259	0.107163	0.015262	0.916
			GRFCSMIS	1.012435	0.104425	1.146449	0.100447	0.010921	0.948
			GRFCSMIC	1.16514	0.108355	1.104869	0.099865	0.011763	0.946
		log(3)	True	−0.01311	0.06088	2.250031	0.059211	0.003706	0.949
			HT	0.836351	0.136982	1	0.131293	0.018849	0.952
			GRN	1.114833	0.133936	1.022745	0.12923	0.018089	0.952
			GRMIS	1.098573	0.134396	1.019243	0.119741	0.018208	0.931
			GRMIC	1.354594	0.135155	1.013522	0.119708	0.018488	0.93
			GRFCSMIS	−0.52327	0.128106	1.069285	0.115569	0.016444	0.928
			GRFCSMIC	−0.46431	0.127535	1.074077	0.115312	0.016291	0.934
	90	log(1.5)	True	0.0138	0.084364	2.251745	0.083155	0.007117	0.947
			HT	1.897751	0.189966	1	0.183082	0.036146	0.94
			GRN	1.897914	0.183304	1.036344	0.176042	0.03366	0.942
			GRMIS	8.193088	0.198884	0.955159	0.163381	0.040658	0.902
			GRMIC	8.29543	0.195141	0.97348	0.162322	0.039211	0.894
			GRFCSMIS	4.745953	0.177903	1.067808	0.159259	0.03202	0.918
			GRFCSMIC	3.798847	0.181029	1.049366	0.157469	0.033009	0.908
		log(3)	True	−0.04654	0.088525	2.348938	0.089229	0.007837	0.95
			HT	0.928622	0.207941	1	0.196985	0.043343	0.939
			GRN	1.061707	0.203441	1.022115	0.192655	0.041524	0.943
			GRMIS	4.095097	0.206598	1.006498	0.181218	0.044707	0.913
			GRMIC	3.94024	0.205562	1.011573	0.180065	0.044129	0.91
			GRFCSMIS	1.614577	0.194645	1.068304	0.175683	0.038201	0.906
			GRFCSMIC	1.290465	0.198216	1.049058	0.174164	0.039491	0.904

Table 4 presents the relative performance under error scenario 3 for estimating β_X using the data imputation approach comparing simple random sampling to case-control and stratified case-control sampling, where {N, n} = {4000,800} and censoring was 90%. GRFCSMI had increased efficiency compared to HT and GRN for nearly all designs, whereas GRMI did not; however, the absolute gain in efficiency varied by sampling design. The RE for GRFCSMI was higher for SRS than for CC and SCC, ranging from 1.10 to 1.15 for SRS compared to 0.99 to 1.11 for CC and SCC. Although the RE for the proposed estimators was lower for the CC and SCC designs than for SRS, the actual standard errors (ESE and ASE) themselves were lower under these outcome-dependent designs. HT was quite inefficient under SRS, leading to a greater gain in efficiency for GRFCSMI; in contrast, HT under SCC was often nearly as efficient as GRFCSMI under SRS. For instance, the ESE of HT for β_x = log(3) and SCC is 0.126, compared to the ESE of 0.128 for GRFCSMIC for SRS. Similar conclusions were observed for error scenario 2 in Supplementary Materials Table 13, with all other parameters the same as Table 4, except both GRMI and GRFCSMI had slightly increased efficiency compared to HT and GRN for all designs. Thus, we observed less overall efficiency gain in the outcome-dependent sampling designs for the proposed methods but still constructed more efficient estimators generally. Results for the IF imputation approach, keeping all other parameters the same as Supplementary Materials Table 13 and Table 4, are presented in Supplementary Materials Tables 14 and 15, respectively. The conclusions follow very similarly to those of the data imputation approach.

TABLE 4.

Simulation results for estimating β_x using the data imputation approach for error scenario 3 (errors in event indicator, failure time, and X) with N = 4000, n = 800 comparing simple random sampling (SRS), case-control sampling (CC), and stratified case-control sampling (SCC). The % bias, empirical standard error (ESE), relative efficiency (RE), average standard error (ASE), mean squared error, and coverage probabilities (CP) are presented for 2000 simulated datasets

βz	% Cens	βx	Design	Method	% Bias	ESE	RE	ASE	MSE	CP
log(0.5)	90	log(1.5)	SRS	True	−0.19575	0.056825	2.306052	0.058701	0.00323	0.953
				HT	1.348122	0.131041	1	0.130666	0.017202	0.943
				GRN	0.599619	0.123075	1.064728	0.120298	0.015153	0.942
				GRMIS	1.352229	0.120274	1.089521	0.121238	0.014496	0.942
				GRMIC	1.064436	0.12481	1.049923	0.120657	0.015596	0.938
				GRFCSMIS	0.372602	0.116359	1.126176	0.115015	0.013542	0.938
				GRFCSMIC	0.262224	0.118828	1.102777	0.114345	0.014121	0.936
			CC	True	−0.19575	0.056825	2.307166	0.058701	0.00323	0.953
				HT	1.278795	0.131104	1	0.121309	0.017215	0.938
				GRN	1.295066	0.128054	1.023824	0.120734	0.016425	0.943
				GRMIS	1.925384	0.129153	1.015113	0.122768	0.016741	0.942
				GRMIC	1.665403	0.12981	1.009974	0.123029	0.016896	0.94
				GRFCSMIS	1.221831	0.119855	1.093861	0.11281	0.01439	0.938
				GRFCSMIC	0.804186	0.117846	1.112503	0.112475	0.013898	0.938
			SCC	True	−0.19575	0.056825	1.941845	0.058701	0.00323	0.953
				HT	−0.6459	0.110345	1	0.110845	0.012183	0.957
				GRN	−0.09306	0.109473	1.00797	0.110642	0.011984	0.952
				GRMIS	0.081196	0.110714	0.996668	0.111346	0.012258	0.954
				GRMIC	−0.02695	0.108453	1.017446	0.111431	0.011762	0.954
				GRFCSMIS	−0.16322	0.101909	1.082777	0.105767	0.010386	0.954
				GRFCSMIC	−0.10748	0.100555	1.097364	0.105699	0.010111	0.952
		log(3)	SRS	True	0.1293	0.064842	2.25486	0.06303	0.004206	0.954
				HT	0.974558	0.146209	1	0.140603	0.021492	0.948
				GRN	0.744679	0.129418	1.129747	0.130516	0.016816	0.94
				GRMIS	0.713557	0.131614	1.110893	0.131276	0.017384	0.942
				GRMIC	0.650456	0.131029	1.115852	0.131065	0.01722	0.94
				GRFCSMIS	0.627308	0.127227	1.149195	0.127457	0.016234	0.942
				GRFCSMIC	0.60765	0.128461	1.138158	0.126735	0.016547	0.944
			CC	True	0.1293	0.064842	2.208732	0.06303	0.004206	0.954
				HT	1.422661	0.143218	1	0.130477	0.020756	0.928
				GRN	1.646294	0.141186	1.014393	0.129232	0.020261	0.927
				GRMIS	1.614425	0.1409	1.016452	0.130462	0.020167	0.931
				GRMIC	1.506875	0.139858	1.024024	0.130487	0.019834	0.926
				GRFCSMIS	1.395031	0.13998	1.023132	0.124715	0.019829	0.925
				GRFCSMIC	1.32011	0.137537	1.041307	0.124594	0.019127	0.922
			SCC	True	0.1293	0.064842	1.938671	0.06303	0.004206	0.954
				HT	0.82001	0.125707	1	0.123465	0.015883	0.938
				GRN	0.693561	0.126412	0.99442	0.122793	0.016038	0.94
				GRMIS	0.733702	0.126538	0.99343	0.123577	0.016077	0.94
				GRMIC	0.70857	0.127711	0.984303	0.123601	0.016371	0.936
				GRFCSMIS	0.771774	0.127503	0.985911	0.119766	0.016329	0.944
				GRFCSMIC	0.614896	0.124678	1.008254	0.119554	0.01559	0.946

We considered the relative performance of our proposed methods under error scenario 3 where the misclassification generation process additionally included interaction terms (shown in Supplementary Materials Table 16). Results for estimating β_X using the data imputation and IF imputation approaches are shown in Supplementary Materials Tables 17 and 18, respectively, with {N, n} = {2000,400} and simple random sampling of the validation subset. While the conclusions regarding the comparisons of GRMI and GRFCSMI to GRN were very similar to previous tables under error scenario 3, the efficiency gains of GRFCSMI were much larger than under the more simple misclassification scenarios. Overall, the RE ranged from 1.03 to 1.34 and the reduction in MSE compared to that of GRN was appreciable across all settings. These results suggest that our methods yield larger efficiency gains with increased nonlinearity. In addition, we observed greater efficiency gains for GRFCSMIC compared to GRFCSMIS, especially for 75%o and 90%> censoring where the positive predictive value (PPV) was very low. This high censoring and low PPV setting is common for EHR studies and thus suggests that more complex multiple imputation models to model potential nonlinearity would be helpful. The same set of results for error scenarios 1 and 2, namely with added interaction terms into the error models, was also generated (not presented), and we observed even greater efficiency gains for both GRMI and GRFCSMI with the more complex imputation approaches.

To evaluate the robustness of our estimators, we considered the performance of our proposed methods under error scenario 3 where the imputation models for the event indicator and the covariate X were badly misspecified as the true error-generating processes involved significant nonlinearities. Results for estimating β_X using the data imputation approach are shown in Supplementary Materials Table 19 with {N, n} = {2000,400} and simple random sampling of the validation subset. Overall, there are little to no efficiency gains for any of the raking estimators; however, GRFCSMIC has RE at least that of HT in all but one setting, demonstrating that even in badly misspecified settings, raking performs no worse than HT.

6 |. VCCC DATA EXAMPLE

In this section, we applied the proposed raking methods to EHR data on 4797 patients from the Vanderbilt Comprehensive Care Clinic (VCCC), a large HIV clinic. Health care providers at the clinic routinely collect and electronically record data on patients, including demographics, laboratory measurements, pharmacy dispensations, clinical events, and vital status. A recent project at the VCCC performed a full chart review for all records to validate important clinical variables, including antiretroviral dispensations and AIDS-defining events (ADEs). Due to the comprehensive chart reviews, two full datasets were available; the first, which we refer to as the unvalidated data, contains the values for all patients prior to chart review, and the second, which we refer to as the validated data, contains the true values after chart review. Additional details on the study design and data validation are in Giganti et al. (2020).

In this example, we were interested in estimating the association between the covariates CD4 cell count and age at the time of ART and the outcome of time from the start of ART to the first ADE. As is common for studies based on EHR data, the outcome and covariates used in the analysis were derived variables. Specifically, CD4 cell count and age at the time of ART were extracted from tables of laboratory measurements and demographics, respectively, by matching the test date or visit date to the ART start date. In addition, the time from ART start to first ADE is extracted by finding the date of first ADE and the ART start date and calculating the time elapsed. A comparison of the unvalidated data to the validated data revealed errors in the ART start date in about 41%₀ of subjects, which led to downstream errors in the covariates and outcome of the statistical analysis. In addition, the ADE event was very rare with 93.8%> censoring and was subject to appreciable misclassification at 11%, suggesting that raking estimators that ignore the misclassification will be inefficient. The misclassification yielded sensitivity, specificity, positive predictive value, and negative predictive value of 0.879,0.892, 0.351, and 0.991, respectively. The exact eligibility criteria used for the analysis and degree of measurement error in the covariates and outcome are given in Appendix K.

For this analysis, we considered the validated data to be the “truth” and defined the hazard ratio (HR) estimates calculated using the entire validated dataset to be the true, gold-standard estimates. The naive estimator that calculates the HRs using the entire unvalidated dataset was also considered, along with the HT estimator, the GRN estimator proposed by Oh et al. (2019), and the proposed raking estimators using multiple imputation (GRMI and GRFCSMI) for both the data imputation and IF imputation approaches. Although we had a fully validated dataset, we retrospectively sampled 100 different validation subsets as if we did not have validated data for all records in order to examine the estimators’ performance. Due to the rare-event setting, we considered two different validation subset sampling designs: CC and SCC. Two variants of SCC were considered: (1) stratified case-control balanced (SCCB), which is described in Section 5.1, and (2) stratified case-control Neyman allocation (SCCN), where the number of subjects sampled in each strata is proportional to the product of the phase one stratum size and the within-stratum (error-prone) influence function standard deviation. In addition, we considered two different validation subset sizes, 340 and 680, representing roughly 21% and 43% of the cohort, respectively. For CC, all 248 error-prone cases were selected along with a random sample of 92 (or 432) error-prone controls. For SCCB and SCCN, CD4 count was stratified at cutpoints of 100, 200, and 400 to create four discrete covariate groups for sampling. These cutpoints were selected to strategically oversample more informative subjects. Specifically, given that CD4 count is an important indicator of HIV severity, someone with CD4 count below 200 cells/mm³ is considered to be at high risk of getting an ADE. Thus, we selected cutpoints at 100 and 200 cells/mm³ to oversample subjects clinically defined as high risk for an ADE to try to select more true cases and increase efficiency. For each sampling design, the same imputation models (both with and without interaction terms) and influence function working models were fit as described in the Simulation section for error scenario 3 with CD4 cell count and age at ART start corresponding to X* and Z, respectively.

The median of the 100 HRs and the median of their corresponding 95% confidence interval (CI) widths for the proposed methods using the data imputation approach are presented in Table 5. For each subset size and sampling design, the naive estimator had significant bias (calculated with respect to the true estimator) for both covariates (31.3% for CD4 and 31.1% for age). In contrast, HT and all of the raking estimators yielded nearly unbiased estimates of the true estimates for both covariates. In addition, GRN had narrower 95% CI widths than that of HT for all sampling designs. For a subset size of 340, GRMI and GRFCSMI both had narrower CI widths than those of GRN for all sampling designs. However, the degree of efficiency gain differed by sampling design; namely, we observed a larger increase in efficiency (around a 5% decrease in CI width) from GRMI and GRFCSMI under CC sampling compared to SCCB or SCCN (at most a 3% decrease in CI width). GRMI and GRFCSMI under CC sampling had the narrowest median CI widths among all estimators for the 340 subset size. When the validation size was 680, the efficiency gain from GRMI and GRFCSMI over GRN was comparable across sampling designs and the median widths of the CIs were similar. The more modest efficiency gains from GRMI and GRFCSMI over GRN compared to those observed in the simulations can likely be attributed to relatively poor imputation models. The small number of cases at phase one and low PPV of the error-prone event indicator made imputation models difficult to build due to the validation subset containing an extremely small number of true cases. Across the 100 sampled validation subsets, the average area under the receiver operating characteristic curve (ROC AUC) for the imputed event indicator ranged from 0.652 to 0.670 across all sampling designs, suggesting that the imputations of the event indicator were poor. Interestingly, GRMI had comparable, if not narrower, CI widths than GRFCSMI across sampling designs and subset sizes. This is likely due to the fact that the amount of covariate error present was very small, which corresponds to error scenario 2 in the simulations where GRMI and GRFCSMI had comparable efficiency. Supplementary Materials Table 20 presents the median HRs and 95% CI widths across the 100 validation subsets for the IF imputation approach. The conclusions about the comparisons of the naive, HT, and GRN estimators are very similar to those of the data imputation approach. For both subset sizes, GRMI and GRFCSMI under CC and SCCB were less efficient than GRN, except for GRMIC under SCCB for the 340 subset size. GRMI and GRFCSMI under SCCN had slightly better performance, with narrower CI widths for the 340 subset size but not the 680 subset size. The lack of efficiency gains observed for the IF imputation approach can be attributed to the very poor influence function imputation working models. Across the 100 sampled validation subsets, the average R-squared for the CD4 influence function working models ranged from 0.099 to 0.194, indicating a lack of predictive accuracy. In small samples, such low correlation between the target and auxiliary variables can limit the improvement over the HT estimator, indicating the need to carefully examine the performance of the imputation working models, especially under complex error scenarios. In the rare event setting, validation sampling strategies that target missed true cases, such as by stratifying on risk factors that may be less prone to error, will also help efficiency.

TABLE 5.

The median hazard ratios (HR) and their corresponding 95% confidence interval (CI) widths calculated using the data imputation method from 100 different sampled validation subsets for a 100 cell/mm³ increase in CD4 count at ART initiation and 10-year increase in age at CD4 count measurement

Subset size	Sampling	Method	CD4 HR	CD4 CI width	Age HR	Age CI width
340	CC	True	0.693	0.19	0.829	0.361
		Naive	0.91	0.125	1.087	0.275
		HT	0.669	0.313	0.829	0.579
		GRN	0.674	0.274	0.819	0.465
		GRMIS	0.679	0.26	0.824	0.44
		GRMIC	0.678	0.264	0.83	0.438
		GRFCSMIS	0.675	0.265	0.824	0.444
		GRFCSMIC	0.677	0.261	0.824	0.44
	SCCB	True	0.693	0.19	0.829	0.361
		Naive	0.91	0.125	1.087	0.275
		HT	0.686	0.283	0.823	0.573
		GRN	0.687	0.28	0.82	0.494
		GRMIS	0.689	0.272	0.835	0.496
		GRMIC	0.689	0.278	0.826	0.491
		GRFCSMIS	0.687	0.275	0.839	0.498
		GRFCSMIC	0.689	0.276	0.814	0.495
	SCCN	True	0.693	0.19	0.829	0.361
		Naive	0.91	0.125	1.087	0.275
		HT	0.69	0.308	0.779	0.665
		GRN	0.688	0.308	0.807	0.599
		GRMIS	0.684	0.303	0.813	0.608
		GRMIC	0.684	0.299	0.807	0.596
		GRFCSMIS	0.687	0.302	0.818	0.614
		GRFCSMIC	0.69	0.297	0.803	0.598
680	CC	True	0.693	0.19	0.829	0.361
		Naive	0.91	0.125	1.087	0.275
		HT	0.692	0.237	0.826	0.412
		GRN	0.693	0.23	0.825	0.385
		GRMIS	0.693	0.228	0.826	0.38
		GRMIC	0.697	0.228	0.826	0.382
		GRFCSMIS	0.693	0.228	0.826	0.383
		GRFCSMIC	0.696	0.229	0.821	0.382
	SCCB	True	0.693	0.190	0.829	0.361
		Naive	0.910	0.125	1.087	0.275
		HT	0.695	0.234	0.837	0.416
		GRN	0.695	0.233	0.830	0.395
		GRMIS	0.693	0.232	0.829	0.393
		GRMIC	0.697	0.233	0.831	0.393
		GRFCSMIS	0.693	0.231	0.826	0.393
		GRFCSMIC	0.694	0.232	0.832	0.394
	SCCN	True	0.693	0.19	0.829	0.361
		Naive	0.91	0.125	1.087	0.275
		HT	0.69	0.229	0.826	0.43
		GRN	0.689	0.228	0.821	0.406
		GRMIS	0.689	0.226	0.823	0.404
		GRMIC	0.689	0.228	0.825	0.401
		GRFCSMIS	0.689	0.226	0.822	0.403
		GRFCSMIC	0.689	0.228	0.821	0.406

7 |. DISCUSSION

The increasing availability of EHR data collected on large patient populations has allowed researchers to study possible associations between a wide array of risk factors and health outcomes rapidly and cost-effectively. However, estimating such associations without bias requires precisely measured data on the variables of interest, an assumption that is often not met with EHR data due to errors in derived variables, error-prone record entry, or other error mechanisms. To address such bias, Oh et al. (2019) proposed validating a subset of records and applying generalized raking estimators, including GRN studied in this article. However, we demonstrated in this article that GRN, which builds the raking variables from the error-prone data, is inefficient in the presence of event indicator misclassification. In addition, we proposed two classes of generalized raking estimators utilizing multiple imputation to estimate the optimal auxiliary variable, one that yields the optimal efficiency. Both MI approaches yield estimates of the expected value of the influence function for the target parameter based on the error-free data. The data imputation estimators impute either the event-indicator or all error-prone variables (if applicable) to construct auxiliary variables with increased degree of linearity with the true population influence functions. The IF imputation estimators take the data imputations and then fit a (potentially flexible, nonlinear) working model of the true population influence functions to construct auxiliary variables. These raking estimators are very appealing for the analysis of EHR data because their validity is not sensitive to the true measurement error structure nor do they require correct specification of the imputation or influence function working models, all of which are generally unknown for such large observational data. These features do, however, affect their efficiency and thus constructing estimators with increased efficiency has been the main focus of this article.

Overall, the proposed raking estimators using multiple imputation performed well, yielding nearly unbiased estimators, the highest RE, and the lowest MSE across all simulation settings. For settings involving misclassification only or misclassification and event-time error, both GRMI and GRFCSMI had large efficiency gains compared to GRN for all parameter settings. For the most complex error setting involving errors in the covariates, event-time, and event indicator, GRFCSMI had appreciable efficiency gains compared to GRN and GRMI for all parameter settings, which increased when nonlinear error functions were simulated. For all error scenarios, we observed more appreciable efficiency gains under 50% and 75% censoring compared to 90%> censoring. It is of note that these simulations involved error settings with very low sensitivity or PPV to mimic real EHR analysis scenarios. In simulations with higher sensitivity or PPV (not presented), larger efficiency gains were realized for GRMI and GRFCSMI, with RE greater than 1.5. The data analysis, which involved an event with over 90% censoring and very low PPV, resulted in similar conclusions. Nevertheless, we observed that GRMI and GRFCSMI yielded around a 5% reduction in CI widths for both covariates, an appreciable gain in a data poor setting. In addition, we considered outcome-dependent sampling designs to select the validation subset to increase efficiency in rare event settings where the number of cases is small. Specifically, we evaluated case-control and stratified case-control sampling designs and found that while the gain in efficiency for GRMI or GRFCSMI over GRN is smaller compared to the efficiency gain under SRS, the overall standard errors are lower, yielding more efficient estimates across all designs. While good imputation models are difficult to construct in rare events settings, one can still obtain more precise estimates overall by selecting more informative subjects to be validated at phase two.

Another possible estimation approach for the considered settings is the direct multiple imputation estimator, which uses MI to impute the error-prone variables and plug into the Cox model to obtain estimates without the use of raking. Giganti et al. (2020) considered this approach using discrete failure time models but noted challenges with correctly specifying the imputation model. While the MI estimator will be more efficient than raking estimators if the regression and imputation models are correctly specified, Han et al. (2019) showed that in the nearly true model framework of Lumley (2017), even slight misspecification of the models result in bias and worse MSE than raking. This robustness makes raking a very appealing approach in practical settings where the true models are generally unknown. An alternative approach to handle the nonlinear influence functions is to separate them into parts that may not be so nonlinear and calibrate separately. While this approach is appealing, there is an important trade-off to consider. Namely, there could be efficiency gained from the improved raking of each part as the linearity assumption is more reasonable and no imputation is required; however, there could be efficiency loss from the increased number of parameters to estimate with multiple calibration equations. This trade-off would be of particular importance when the validation subset is relatively small, where it is more plausible that the efficiency loss from the increased number of parameters outweighs any gain from improved raking. It is likely that in the small validation subset setting, there would need to be a careful evaluation of the trade-off between the number of separate parts to calibrate and the number of parameters to estimate, which would be very problem dependent. Moreover, this trade-off would be very difficult to evaluate in practice as the increase in standard errors from estimating more parameters is a second-order property. We believe more research is needed to properly understand how to evaluate this trade-off.

The two-phase design framework considered in this article is a specific missing data setting where the data are missing by design. This missing data lens allows us to consider the augmented inverse probability weighted (AIPW) estimators proposed by Robins et al. (1994), who showed that the class of AIPW estimators contains all regular asymptotically linear estimators consistent for the design-based parameter of interest. There is a close relationship between AIPW and raking estimators, in that the class of AIPW estimators contains the raking estimators, but the raking estimators include all of the best AIPW estimators (Lumley et al., 2011). Thus, raking estimators are asymptotically efficient among design-based estimators and provide simple, easy to compute AIPW estimators. In particular, the raking estimators utilizing multiple imputation proposed in this article yield practical methods to approximate the optimal AIPW estimator in settings involving complex measurement error that is often seen in EHR data. In addition, these estimators are consistent without requiring correct specification of the imputation or working models; however, they yield the most efficient design-based estimator if the models are correctly specified. The proposed raking estimators, however, do not improve efficiency if the auxiliary variables have no correlation with the variables of interest. We believe that this will generally not be an issue for settings similar to those considered in our paper, namely settings where the phase one data are error-prone versions of the phase two data. That is, in practice, useless error-prone variables would not be considered for use in analysis.

In this work we proposed a novel estimation method to improve raking estimators and showed additional efficiency could be gained by pairing these estimators with a more efficient two-phase sampling design. While this article considered outcome-dependent sampling designs to improve efficiency in rare-event settings, we believe that more theoretical and empirical work studying sampling designs and their effects on efficiency for failure time outcomes is needed. In particular, constructing multiphase sampling designs would be a fruitful avenue for future work. (See McIsaac & Cook, 2015, Chen & Lumley, 2020, and Han et al., 2020, for some initial work.) These authors considered designs where a pilot sample could initially be selected from the cohort to obtain information on the validated data that can be used to guide follow-up sampling waves. We believe more work is needed to understand how best to take advantage of such strategies for the continuous failure time setting.