Abstract
Purpose:
Diffusion weighted imaging (DWI) is sensitive to head movements, which may cause signal losses due to motion-induced gradient imbalances. Prospective motion correction using fast optical tracking can attenuate these artifacts. Approaches include quasi-continuous updates of gradients and RF pulses or dynamically applying a rebalancing gradient to restore the gradient balance, but these prior methods used bipolar diffusion gradients. The goal of this project was to develop and evaluate a motion-insensitive implementation for the more common monopolar diffusion sequence.
Methods:
A mono-polar diffusion sequence was developed with motion updates prior to each RF pulse and each diffusion weighting gradient. The sequence was tested in a phantom and human brain, at b=1000s/mm2 and rotational velocities up to 20°/s. Motion sensitivity, signal losses, and in vivo image profiles were compared between scans with and without intra-sequence motion updates.
Results:
With typical motion parameters, intra-sequence motion updates with optimal parameters reduced the motion-sensitivity of DWI (motion-induced gradient moment imbalance) 7-fold. Optimal results were achieved by matching the echo time of the pulse sequence to an even multiple of the tracking system frame-to-frame period. Average signal losses and the frequency of signal dropouts in phantom and in vivo measurements were reduced when intra-sequence updates were enabled, and quality measures of DTI analyses were improved.
Conclusion:
A correction scheme for the monopolar DWI sequence can reduce the motion-sensitivity of brain DWI up to 7-fold compared to an implementation without intra-sequence updates.
Keywords: Diffusion, MRI, motion, prospective correction, brain
INTRODUCTION
Diffusion weighted imaging (DWI) can provide diagnostic information in clinical practice, for instance, in the diagnosis of acute stroke (1). Both the apparent diffusion coefficient (ADC) and fractional anisotropy (FA) are used in clinical diagnostics (2). DWI uses strong gradients to assess the microscopic motion of water molecules (3,4). However, these strong diffusion gradients also increase the sensitivity of DWI to head movements (5,6). Uncorrected translational head movements induce localization errors and global phase shifts that can cause artifacts in multi-shot acquisitions. Rotational movements can cause imbalanced gradient moments in the direction perpendicular to the diffusion gradient vector and the rotation axis. These gradient imbalances can result in complete signal loss for a given DWI acquisition (7), or signal attenuation that may be indistinguishable from that due to the microscopic tissues diffusivity. This can lead to difficulties interpreting clinical DWI scans, or incorrect values for quantitative measures in research studies (8,9).
Here, we focus on single shot DWI, which can produce high-quality images of the brain without compromising on sensitivity (10). Previous approaches to reducing motion artifacts include prospective navigator echoes (5), retrospective motion correction (11), and real-time correction of gradients using navigator echoes (12). However, these methods may not be able to recover acquisitions with complete signal losses or correct for through-plane artifacts (6,13,14).
As reported (15), we track head movements with a set of optical cameras fastened to the magnet bore and update the scanning parameters (e.g. slice positions, field-of-view offsets, and rotation matrices) in real-time to ensure that slices are properly aligned. Additionally, movement-induced signal losses due to gradient imbalances can be reduced by quasi-continuous updates of gradients and RF pulses during diffusion-encoding (9) or by applying a single dynamic update to restore the gradient balance prior to data acquisition (8). Since both prior approaches used the double-spin echo sequence (16), we aimed to develop a correction scheme for the monopolar DWI sequence (3). As before (8), the monopolar implementation involves a slice update for each RF pulse (excitation and refocusing) to ensure slices are aligned properly, both across repetitions and within acquisitions. Furthermore, the rotation matrices were updated immediately prior to each diffusion sensitizing gradient, which essentially eliminates first-order gradient moments effects (due to constant rotational velocities).
THEORY
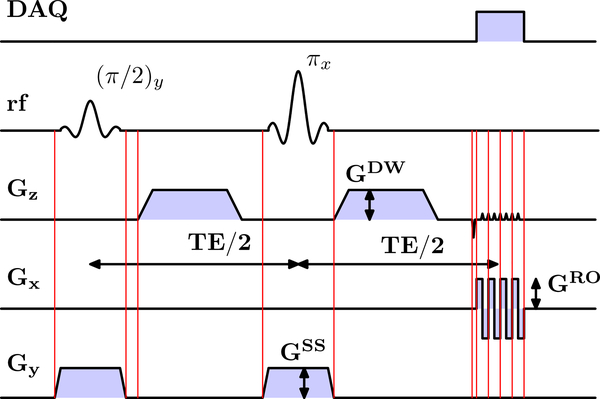
The DTI sequence is based on a monopolar Stejskal-Tanner (3) sequence from the manufacturer, modified to enable real-time gradient and slice updates prior to the excitation and refocusing pulses and diffusion gradients (Fig.1).
Figure 1:
Timing diagram of monopolar DWI sequence. Red vertical lines indicate motion updates. Abbreviations: DAQ: Data acquisition. rf: radio frequency. Gx/y/z: x/y/z gradient. GDW: diffusion weighting gradient (could be applied on any axis). GRO: readout gradient. GSS: slice selection gradient. Note: the interval between some of the motion updates is relatively short and no new tracking information might be available.
We briefly summarize the effects of head motion, assuming the head is a rigid body. Using the notation from Gumus et al. (8), we describe the rotational component of the movement between excitation (t=0) and readout by a time-dependent rotation matrix . With the gradient vector time course, the rotational movement during the interval [0, T] (excitation to readout) induces a gradient moment and moment imbalance (difference between moments with and without motion) :
| [Eq.1a] |
| [Eq.1b] |
Notably, in a spin-echo sequence, the refocusing pulse reverses the gradient moment (8). Furthermore, the effect of intra-sequence motion updates is to reset the rotation angle to zero.
We now consider a head rotation about the y-axis with a time-dependent diffusion gradient and rotation angle θ(t) [with θ(0) = 0]. The motion-induced gradient moment imbalance is then
| [Eq.2] |
For realistic human movements, the head cannot rotate more than a few degrees between excitation and readout (T~100ms). Therefore, we can perform a second-order Taylor expansion of Eq.2:
| [Eq.3a] |
| [Eq.3b] |
| [Eq.3c] |
Thus, to first-order (θ ≪ 1), the gradient moment imbalance along an axis perpendicular to the rotation axis is driven by the diffusion gradient along the third axis (i.e. for a y-rotation, the x-axis imbalance is determined by , and vice versa). The gradient moment imbalance is zero along the rotation axis.
Further approximating the time dependence of the rotation angle to second order, with rotational velocity ωr and rotational acceleration , i.e. θ(t) , yields:
| [Eq.4a] |
| [Eq.4b] |
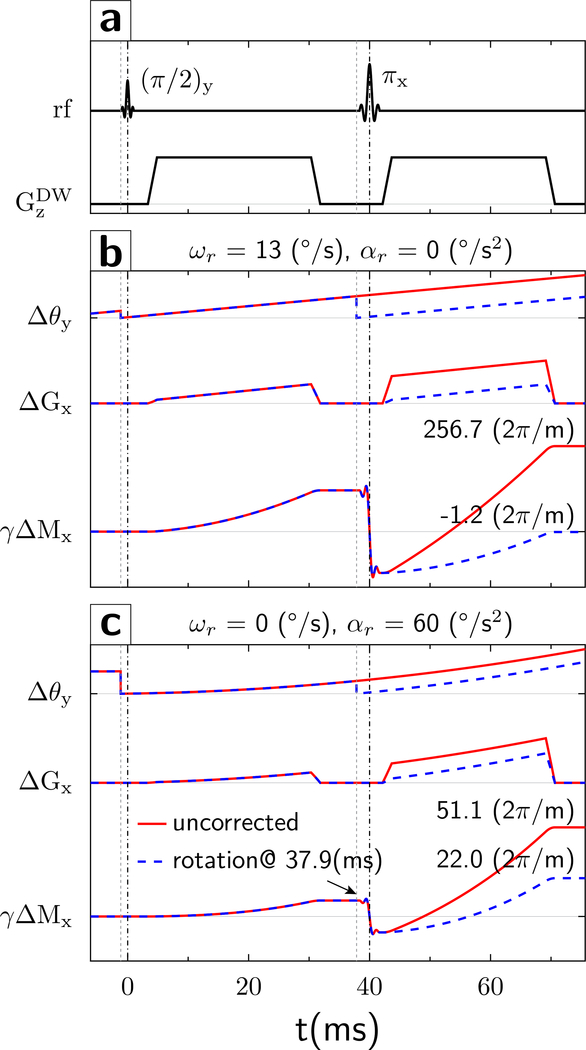
Using Eqs.4, we simulated the evolution of the gradient moment using the parameters of the monopolar diffusion sequence (readout gradient ; dwell time Δt = 3.6μs) at TE=80ms (diffusion gradients , rise-plateau-fall lengths 1.52, 25.47, 1.52 ms; Fig.2) and TE=68 ms (); the effect in phase-encoding direction is the same due to the similarity of Eqs.4a and 4b. The TE values were selected in part based on properties of the optical tracking system (see Results). For an initial first-order simulation, we assumed a constant angular velocity ωr = 13°/s (based on the motion observed in vivo). A gradient moment γΔMx accumulates quadratically during the first TE/2 period (Fig.2b; γΔMx; solid red curve), which is reversed by the refocusing pulse. Without a motion update, the misalignment Δθ between the brain axis and diffusion gradient continues to increase. Consequently, γΔMx accumulates at an accelerating rate and more than doubles at the end of the second diffusion gradient (Fig.2b γΔMx, red curve), totaling (TE=80ms) and (TE=68ms).
Figure 2:
Evolution of gradient waveforms (a) and gradient moments. (b) For a y-rotational motion with constant angular velocity of ωr = 13°/s (no acceleration) relative to the stationary diffusion gradient in z-direction (Δθ), the spins experience an effective x-gradient (ΔGx) that continues to increase throughout the experiment. Thus, a non-zero gradient moment starts to build up quadratically in the first TE/2 period (γΔMx, solid red line). The refocusing pulse reverses the gradient moment at TE/2. Without an additional motion update, the gradient moment continues to accumulate rapidly (γΔMx solid red line) and reaches a non-zero value at TE. However, if the rotation matrix is updated prior to the refocusing pulse, then the axis of the object is re-aligned with the gradient axis (Δθ, dashed blue line). This results in a final residual gradient moment γΔMx that is markedly smaller (γΔMx, dashed blue line) compared to that obtained without the additional motion update (γΔMx, solid red line). (c) Rotational motion with constant rotational acceleration of (0 constant velocity). The overall evolution of the gradient moment is similar to that described in (b) but follows a third-order term in time. Again, without an intra-sequence motion update, the gradient moment continues to accumulate rapidly in the second TE/2 period (γΔMx, solid red line) and reaches a non-zero value at TE. If the rotation matrix is updated prior to the refocusing pulse, the final residual gradient moment is smaller (γΔMx, dashed blue line) compared to that obtained without the additional motion update (γΔMx, solid red line) but still deviates from zero due to the third-order evolution of the gradient moment.
Next, we simulated the gradient moment evolution with an additional motion update immediately prior to the second diffusion gradient. The additional update realigns the diffusion gradient orientation with the rotating head axis, and the gradient moment increase in the second TE/2 period is similar to that in the first TE/2 period (Fig.2b γΔMx, dashed blue), such that the accumulated gradient moment at the end of the second diffusion gradient is almost zero.
Since k-space is defined by gradient moments, any residual gradient moment induced by rotations alters the position of the echo center in k-space. In fact, the motion-induced gradient moment imbalance can be sufficiently large to push the echo outside of the k-space sampling window, leading to complete signal loss (7). For our sequence parameters ( per k-space point, the echo is shifted to the k-space edge at , which corresponds to ωr = 5.6°/s (TE=80ms) and 6.2°/s (TE=68ms) without intra-sequence updates. With intra-sequence updates, these rotational velocities shift the echo <1 k-space point; therefore, the sequence is expected to tolerate markedly higher rotational velocities before the echo is shifted outside of k-space.
Second-order motions were simulated using the peak acceleration of αr = 60°/s2 from in vivo measurements (Fig.2c). Of note, gradient moments induced by first and second order motions are additive (Eqs.4). Acceleration-induced moments are without and 22 with motion updates at TE=80ms, and 40 and 17 at TE=68ms. Therefore, without motion updates, residual gradient moments are dominated by first order motions. Importantly, intra-sequence motion updates can attenuate, but not eliminate, acceleration-induced moments.
Rotation-induced signal losses can also occur in the slice direction, due to dephasing (8). At Δy = 5mm slice thickness, the gradient moment imbalance required to lose half the signal satisfies [(8), Eq.8], or and ωr = 6.1° / s for our parameters. Furthermore, without motion correction, through-plane rotations can cause misalignment ∂θ between the excitation and refocusing pulses (9). This causes a linear signal attenuation over a distance d from the rotation axis, and total signal loss beyond d. Using [(9), Eq.7] and ∂θ~0.5° for our studies, the cutoff distance is d = 286mm. We therefore do not expect substantial signal dropouts due to slice misalignments.
METHODS
Experiments were performed on a Siemens 3T Prisma scanner. An MR-compatible stereovision tracking system (KinetiCor Inc, Honolulu, HI) was used to track the movements of a marker attached to the phantom or the subject’s nose bridge. Tracking data were sent to the internal scanner network at 60 frames/s via User Datagram Protocol (UDP) packets containing the current marker translation and rotation and timing information. The real-time motion correction software dynamically updated gradient axes and RF objects based on the pose of the most recent tracking packet received relative to a reference pose, without accounting for the timing of packets received. The product monopolar diffusion sequence was modified to enable real-time motion updates immediately prior to the excitation and refocusing RF pulse, and immediately prior to each diffusion gradient (Figure 1, vertical lines).
Phantom studies were performed using the body coil (to maximize motion range). A tracking marker was attached to a 200mm gel phantom. Single-slice coronal diffusion scans were prescribed with a diffusion gradient of b=1000s/mm2 along x, z, or 45° in x-z (echo-planar readout along x-axis, TE=68ms or 80ms, TR=500ms, raw acquisition matrix 128×64, FOV=300mm, 5mm slice, bandwidth 2170Hz/Px, 216 repetitions plus one repetition with b=0s/mm2). The phantom was mounted on a wooden stick and rotated manually in place about the y-axis in an approximately sinusoidal movement.
In vivo study:
A healthy subject gave oral and written consent under a protocol approved by the IRB of the University of Maryland in Baltimore. A tracking marker was placed on the subject’s nose bridge, and the subject was placed in the 20-channel head coil. Following a brief localizer, a monopolar DWI sequence was run, using the multi-slice axial Multi-Directional Diffusion Weighting (MDDW) protocol with echo-planar readout in x-direction (TE/TR=68/3000ms, acquisition matrix 128×64, FOV=300mm, 5mm slices, bandwidth 2170Hz/Px, 30 isotropically-distributed diffusion directions with 1 repetition at b=1000s/mm2, one repetition with b=0s/mm2, slices=25). Five scans were acquired: one without motion, and two each (intra-sequence motion correction On and Off) with quasi-periodical head rotation in the up-down (x-rotation) or left-right (z-rotation) direction.
Data analysis
For human and phantom studies, the goals were to determine the sensitivity of the monopolar DWI sequence to rotational movements and compare the motion sensitivity between scans with and without intra-sequence updates. We estimated the motion-induced gradient moment imbalance for each acquisition by calculating the offset of the echo peak from the k-space center, using an in-house algorithm (Matlab).
Motion parameters were analyzed using a log file on the scanner; each entry includes the current translation, rotation θ(ti), and a time stamp ti. The rotational velocity was computed as , and rotational accelerations as . For acquisitions within a given condition, we then determined the slope of the offset versus the rotational velocity ωr as a proxy for its “motion sensitivity” that is independent of rotational velocity. Accordingly, a smaller slope of a trend line ( versus ωr) means smaller k-space offsets induced per rotational velocity, and ultimately a greater range of velocities that can be tolerated before the echo is shifted outside of the k-space window.
For the in vivo scan, we further calculated the signal loss for 480 individual images acquired per condition (16 slices * 30 diffusion directions), by comparing the mean signal intensity (magnitude) in each image relative to that acquired without motion. Additionally, we analyzed each in vivo data set using the MRI Cloud (17), and determined the “normalized error” for each DTI volume (18), which reflects the mean absolute deviation between raw and fitted tensor data after normalizing to the background noise level.
Results
Phantom
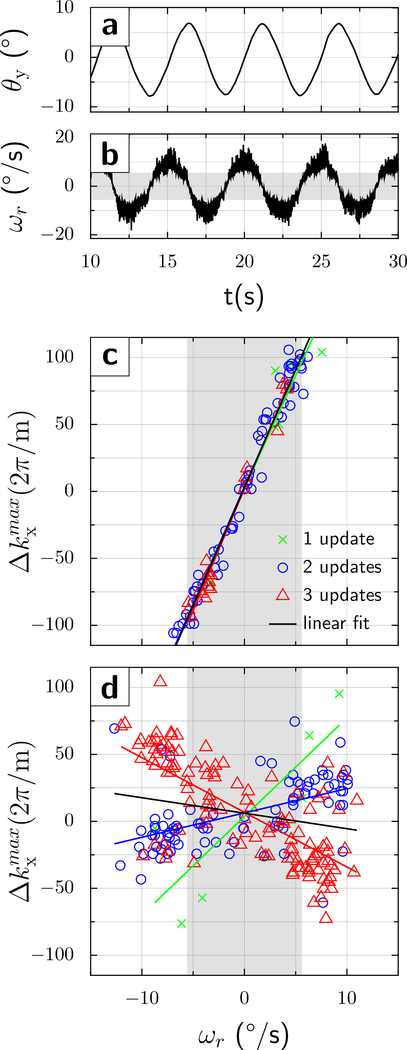
Fig.3.a shows that the phantom’s y-rotation angle θ is essentially periodic (amplitude ~8°; peak velocity ; Fig.3.b). Since the phantom motion was not synchronized with the MRI scanner, the various DWI acquisitions experienced a random sample of rotational velocities. Figs.3c and d show the echo center shift () against the rotational velocity for each of the 216 time points.
Figure 3:
Phantom results at TE=80ms. A gel phantom was manually and quasi-sinusoidally rotated about the y-axis. (a) The phantom was moved back and forth between two turning points by ±8°, with (b) an angular velocity of about 10°/s. The trajectories shown were acquired with motion correction On, but those with motion correction Off are similar. The dependence of the echo center shift (y-axis) on the rotational velocity (x-axis) is presented in (c) and (d). Without motion correction (c), the echo center was within the sampled k-space window only for velocities . (d) In contrast, when motion correction was On, the shift of the echo signal maximum from the center of the k-space fell within the sampling window for almost all (214/216) acquisitions. However, the graph (d) shows 2 major sub-populations, one when 2 tracking packets were received between the excitation and refocusing pulse (blue circles, positive slope) and one when 3 tracking packets were received (red triangles, negative slope). A few acquisitions saw a single motion update only (green crosses). Also, a few acquisitions were probably misclassified (2 versus 3, and 1 versus 2), causing the regression lines to deviate from the main clusters to some degree. The gray vertical band indicates the range of velocities that the original DWI sequence without intra-sequence updates can tolerate before the echo is shifted outside of k-space.
Initial experiments were performed at TE = 80ms. Without intra-sequence updates (Fig.3c), each 1°/s velocity change causes an echo-center shift of 17.7 [14.5 at TE=68ms; Fig.4c). An experiment with variable diffusion direction (x, z and 45° x-z) altered the slope only marginally [16.55 and 16.94 per °/s; not shown]. When intra-sequence updates were enabled (Fig.3.d), the range of the residual gradient moment was reduced to approximately ±60.
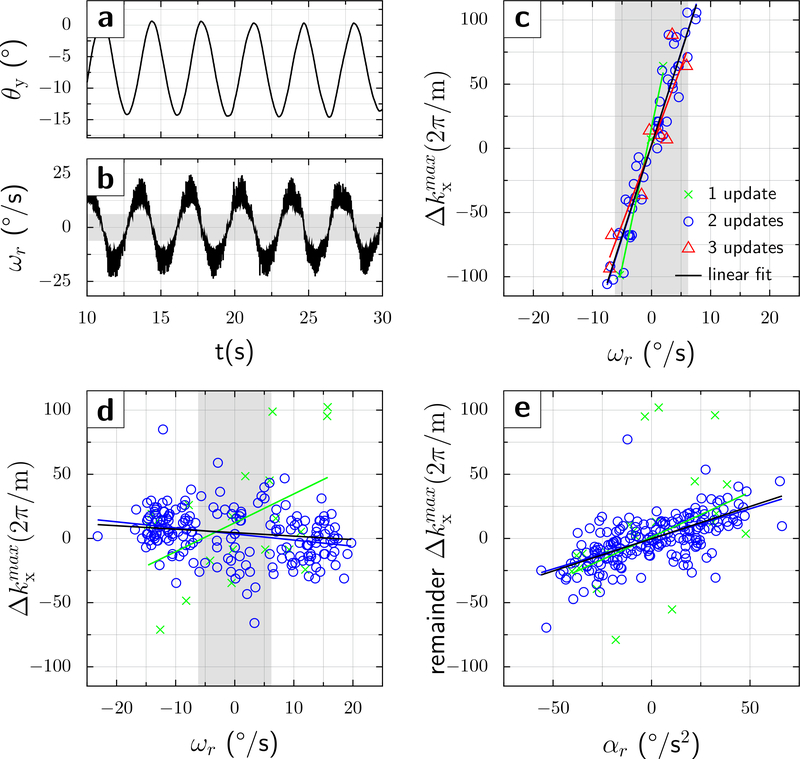
Figure 4:
Phantom results at TE=68ms. a) and b) the same as in Fig.3 but the maximum angular velocity is about 20°/s. Without motion correction (c), the echo was within the sampled k-space window for velocities . (d) In contrast, when intra-scan motion correction was On, the shift of the echo signal maximum from the center of the k-space fell within the sampling window for almost all (212/216) acquisitions. Also, almost all acquisitions received 2 tracking packets (blue circles), and no split into sub-populations was observed when intra-scan motion updates were applied. The slopes of a linear fit are c) a=14.35, b=2.86, r2=0.91; and d) a=−0.47, b=3.47, r2=0.07 (subpopulation with two tracking packets received, blue circles). (e) The residual k-space echo shift (after removal of first-order motion term, i.e. velocity) shows a clear linear dependence upon rotational acceleration ∝r. Parameters from a bivariant linear fit are: a1=−0.47, a2=0.47, b=3.15, with r2=0.45. The gray vertical band indicates the range of velocities that the original DWI sequence without intra-sequence updates can tolerate before the echo is shifted outside of k-space.
Curiously, the graph at TE=80ms shows two subpopulations; one having a positive and one having a negative slope of k-space shift against velocity. Thus, k-space shifts have a residual dependence upon rotational velocities, which may cause signal losses at higher velocities. We hypothesized that this bifurcation might be caused by whether two or three UDP packets arrived between the first and second diffusion gradient. Therefore, the experiment was repeated at TE/2=34ms, which matches the interval of 2 UDP packets (i.e. 2*17ms). Almost all acquisitions now experienced two UDP packets (blue circles in Fig.4d, bottom right). Importantly, the slope of the k-space shift versus rotational velocity was close to 0, and no subpopulations were noticeable. Intra-sequence updates further reduced the range of residual k-space shifts to ±40, which is 7-fold lower compared to the acquisition without intra-sequence updates (±280) over the velocity range studied (±20°/s).
At the two TE-values studied, without intra-sequence updates, the echo center was shifted outside of the sampling window for rotational velocities , close to the predicted values. Over half of acquisitions (123/216 at TE=80ms and 158/216 at TE=68ms) showed complete signal loss. Conversely, fewer than 5 acquisitions showed complete signal loss with intra-sequence motion updates.
Finally, there was a clear effect of measured rotational accelerations on k-space shifts at TE=68ms (Fig.4e). The r2 value of 0.45 suggests that compensating for 2nd order terms would further reduce the residual variance in k-space shifts from 40 to ~25.
In vivo study
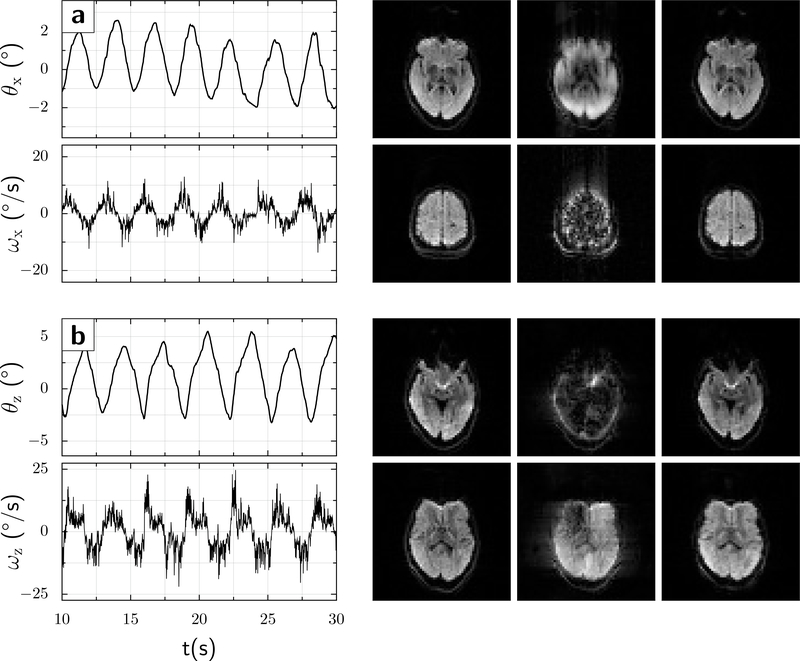
For the up-down motion (x-rotation), the range was approximately θx ≈ ±3° with velocities up to 7.2°/s (Fig.5a). The left-right motion (z-rotation) was larger, with amplitudes θz ≈ ±5.5° and velocities up to 13°/s (Fig.5b).
Figure 5:
A volunteer moved his head quasi-periodically in two separate experiments. (a) nodding in the up-down direction (x-rotation), turning points θx ≈ ±3° (solid red line), and peak rotational velocity ≈ 7.2°/s (solid blue line). (b) Left-right head rotation (z-direction), turning points θz ≈ ±5.5° (solid red line), and peak rotational velocity ≈ 13°/s (solid blue line). The images show 2 representative slices for each motion condition, as follows: Left column: No movement; Center column: Movement but motion correction Off; and Right column: Movement with motion correction On. In both instances, the scans with motion but no intra-sequence updates show markedly more motion artifacts or signal losses.
For the up-down rotation, the median signal drop across slices and diffusion directions was 8.6% without motion correction, but only 3.4% with intra-sequence updates (p<10−10; Wilcoxon rank sum test). For the left-right-rotation, the difference was even more pronounced, with median signal drops of 9.9% without versus 4.8% with motion correction (p<10−7); see Supplemental Figure 1 for histograms of signal changes. These differences are also apparent in the number of images showing a substantial signal loss. For instance, for the z-rotation, 16/480 images without intra-sequence updates showed signal losses over 50%, compared with only 1/480 images when intra-sequence updates were enabled.
Using the quality measures from MRI Cloud, intra-sequence updates decreased the “normalized error” for in vivo scans with motion (up-down: 0.86±0.12 versus 1.07±0.23 without; left-right: 1.01±0.13 versus 1.73±0.24; p ≤ 5*10−5 paired t-test for both). However, all motion scans had larger normalized errors than the acquisition without motion (0.42±0.07).
Discussion
DWI is sensitive to head movements, which can cause partial or complete signal loss of acquisitions even in single-shot mode. Since post-processing methods cannot recover complete signal dropouts, we developed a real-time PMC scheme for a monopolar product sequence. The motion update before the excitation pulse ensures that slices are aligned across TR periods, and the update before the refocusing pulse ensures alignment of slices within a given acquisition. Together with additional motion updates for each diffusion gradient, this markedly reduced the motion sensitivity of the sequence.
The result of simulations was in general agreement with measurements in a moving phantom. First, without intra-sequence motion updates, the measured rotational velocity at which the sampled signal (echo center) is pushed outside of the k-space window is close to the value determined by simulations. Second, intra-sequence motion updates reduced motion-induced gradient imbalances, predominantly by eliminating first-order effects (constant velocity). Our particular implementation decreased the motion sensitivity up to 7-fold, but this value depends upon the details of the motion trajectory and the timing of sequence and motion updates. While our work has focused on signal losses due to k-space shifts, the reduction in gradient imbalances benefits signal dephasing in slice direction as well. Of the residual variance in echo shifts, 45% was explained by accelerations (which the current implementation cannot correct). Further variance is likely caused by latencies between the tracking system and the MRI scanner, shot-to-shot noise in the tracking data, and tracking errors (e.g. due to the skin attachment).
Our data show that the choice of TE relative to the tracking rate can induce sub-populations in the dependence of echo shifts upon rotational velocity. This occurs since the motion correction algorithm on our scanner (and other scanners as well, to our knowledge) uses the most recent data packet from the tracking system to calculate motion updates relative to a reference packet, without accounting for the sequence timing. Therefore, updates to rotation matrices reflect discrete increments in the time base of the tracking system (~17ms in our setup) rather than the relevant “time base” of the spin system (TE), causing discretization errors and sub-optimal correction of gradient moments. Our results also suggest that increasing the effective temporal resolution of the pulse sequence (9) may have only limited benefits if there is a timing mismatch between pulse sequence and tracking system.
Notably, applying intra-sequence updates reduces the motion-sensitivity even when the TE is suboptimal for the tracking rate. However, it is important to resolve discretization errors, since each sub-population shows a residual dependence on rotational velocity; hence, higher angular velocities than those used in our study may still result in echoes being shifted outside of sampled k-space or causing dephasing in slice direction. For instance, with reference to Fig.3d and by interpolating the red regression line to the k-space cutoff of 110 , rotational velocities >25°/s would cause total signal loss when 3 packets are received.
One solution to the discretization problem is to match TE/2 to a multiple of the tracking data interval. In this case, the change in rotation determined from the UDP packets received is close to that experienced by the spin system, yielding a slope of almost 0 between k-space shifts and rotational velocities. The resulting reduction in variance in k-space shifts made it possible to observe the effect of rotational accelerations (Fig.4e). However, due to the asynchronous nature of the process, it is still possible for the incorrect number of packets to arrive within a TE/2 period, causing residual errors in gradient moment updates.
The Gumus approach (8) might avoid many of the drawbacks discussed. It relies on buffering multiple (5–10) motion tracking packets, estimating the residual gradient moment as per Eq.1, and applying a single dynamic update (“blip”) to restore the gradient balance prior to data acquisition. Since the numerical integration for the residual gradient moment utilizes the correct tracking rate, the method should not be affected by the discretization error. Another general solution would be to update rotation matrices based on predicted rotational changes using the frame rate of the tracking system and sequence timing. However, this would require a complete reimplementation of the software to update rotation matrices in real-time, which is beyond the scope of this paper.
Our in vivo results further demonstrate that applying intra-sequence updates can substantially decrease the sensitivity of the DWI sequence to head motion (signal dropouts). However, intra-sequence motion updates did not completely remove motion artifacts on quantitative measures of image quality. A larger study would be required to determine which of the various PMC approaches would afford the most robust reduction in motion artifacts, and how to further reduce residual errors.
A general issue with skin attached markers is that the skin and skull may not fully represent brain motion. However, high resolution MRI studies (15) suggest that these tracking errors are on the order of 0.1°, and therefore not likely a major impediment for correcting motion during DWI, although they may contribute to residual echo shifts. Another issue is that of pulsatile motion in some posterior parts of the brain (19,20), which can be corrected using 2D navigator echoes (21) or cardiac gating (22) but not camera-based PMC.
Conclusion:
The proposed correction scheme for the monopolar DWI sequence can reduce the motion-sensitivity of DWI compared to a sequence without intra-sequence motion updates, but residual artifacts remain. A larger study would be required to demonstrate utility in the clinical setting.
Supplementary Material
Acknowledgements:
This work was supported by NIH grant 1R01 DA021146 (BRP). We would like to acknowledge support by Drs. Pan Su and Tobias Kober from Siemens Healthineers for providing technical assistance and expertise, and Drs. Kenichi Oishi, Susumu Mori, and Yue Li from Johns Hopkins University School of Medicine for helpful discussions.
References
- 1.Heiss WD, Zaro-Weber O. Extension of therapeutic window in ischemic stroke by selective mismatch imaging. Int J Stroke 2019;14(4):351–358. [DOI] [PubMed] [Google Scholar]
- 2.Mascalchi M, Filippi M, Floris R, Fonda C, Gasparotti R, Villari N. Diffusion-weighted MR of the brain: methodology and clinical application. Radiol Med 2005;109(3):155–197. [PubMed] [Google Scholar]
- 3.Stejskal E, Tanner J. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys 1965;42:288. [Google Scholar]
- 4.Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology 1986;161(2):401–407. [DOI] [PubMed] [Google Scholar]
- 5.Ordidge RJ, Helpern JA, Qing ZX, Knight RA, Nagesh V. Correction of motional artifacts in diffusion-weighted MR images using navigator echoes. Magnetic resonance imaging 1994;12(3):455–460. [DOI] [PubMed] [Google Scholar]
- 6.Trouard TP, Sabharwal Y, Altbach MI, Gmitro AF. Analysis and comparison of motion-correction techniques in diffusion-weighted imaging. Journal of magnetic resonance imaging : JMRI 1996;6(6):925–935. [DOI] [PubMed] [Google Scholar]
- 7.Wedeen VJ, Weisskoff RM, Poncelet BP. MRI signal void due to in-plane motion is all-or-none. Magn Reson Med 1994;32(1):116–120. [DOI] [PubMed] [Google Scholar]
- 8.Gumus K, Keating B, Poser BA, Armstrong B, Chang L, Maclaren J, Prieto T, Speck O, Zaitsev M, Ernst T. Prevention of motion-induced signal loss in diffusion-weighted echo-planar imaging by dynamic restoration of gradient moments. Magn Reson Med 2014;71(6):2006–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Herbst M, Maclaren J, Weigel M, Korvink J, Hennig J, Zaitsev M. Prospective motion correction with continuous gradient updates in diffusion weighted imaging. Magn Reson Med 2012;67(2):326–338. [DOI] [PubMed] [Google Scholar]
- 10.Norris DG. Implications of bulk motion for diffusion-weighted imaging experiments: effects, mechanisms, and solutions. Journal of magnetic resonance imaging : JMRI 2001;13(4):486–495. [DOI] [PubMed] [Google Scholar]
- 11.Leemans A, Jones DK. The B-matrix must be rotated when correcting for subject motion in DTI data. Magn Reson Med 2009;61(6):1336–1349. [DOI] [PubMed] [Google Scholar]
- 12.Weih KS, Driesel W, von Mengershausen M, Norris DG. Online motion correction for diffusion-weighted segmented-EPI and FLASH imaging. MAGMA 2004;16(6):277–283. [DOI] [PubMed] [Google Scholar]
- 13.Aksoy M, Forman C, Straka M, Skare S, Holdsworth S, Hornegger J, Bammer R. Real-time optical motion correction for diffusion tensor imaging. Magn Reson Med 2011;66(2):366–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Anderson AW, Gore JC. Analysis and correction of motion artifacts in diffusion weighted imaging. Magn Reson Med 1994;32(3):379–387. [DOI] [PubMed] [Google Scholar]
- 15.Maclaren J, Armstrong BS, Barrows RT, Danishad KA, Ernst T, Foster CL, Gumus K, Herbst M, Kadashevich IY, Kusik TP, Li Q, Lovell-Smith C, Prieto T, Schulze P, Speck O, Stucht D, Zaitsev M. Measurement and correction of microscopic head motion during magnetic resonance imaging of the brain. PLoS One 2012;7(11):e48088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Alexander AL, Tsuruda JS, Parker DL. Elimination of eddy current artifacts in diffusion-weighted echo-planar images: the use of bipolar gradients. Magn Reson Med 1997;38(6):1016–1021. [DOI] [PubMed] [Google Scholar]
- 17.Mori S, Wu D, Ceritoglu C, Li Y, Kolasny A, Vaillant M, Faria A, Oishi K, Miller M. MRICloud: Delivering High-Throughput MRI Neuroinformatics as Cloud-Based Software as a Service. Comput Sci Eng 2016;18(5):21–35. [Google Scholar]
- 18.Li Y, Shea SM, Lorenz CH, Jiang H, Chou MC, Mori S. Image corruption detection in diffusion tensor imaging for post-processing and real-time monitoring. PLoS One 2013;8(10):e49764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Poncelet BP, Wedeen VJ, Weisskoff RM, Cohen MS. Brain parenchyma motion: measurement with cine echo-planar MR imaging. Radiology 1992;185(3):645–651. [DOI] [PubMed] [Google Scholar]
- 20.O’Halloran RL, Holdsworth S, Aksoy M, Bammer R. Model for the correction of motion-induced phase errors in multishot diffusion-weighted-MRI of the head: are cardiac-motion-induced phase errors reproducible from beat-to-beat? Magn Reson Med 2012;68(2):430–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Atkinson D, Counsell S, Hajnal JV, Batchelor PG, Hill DL, Larkman DJ. Nonlinear phase correction of navigated multi-coil diffusion images. Magn Reson Med 2006;56(5):1135–1139. [DOI] [PubMed] [Google Scholar]
- 22.Nunes RG, Jezzard P, Clare S. Investigations on the efficiency of cardiac-gated methods for the acquisition of diffusion-weighted images. J Magn Reson 2005;177(1):102–110. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.